Prediction of In-Plane Shear Properties of a Composite with Debonded Interface

Abstract

An analytical approach is established to analyze the mechanical behavior of a unidirectional (UD) composite subjected to an in-plane shear. The effects of the interface debonding on the in-plane shear strength and plasticity of the composite are evaluated respectively. The volume-averaged internal stresses of the fiber and matrix are calculated through Bridging Model. Owing to the stress fluctuation in the matrix caused by other phases (such as the imbedded fiber and interface crack), the homogenized matrix stresses must be converted into true values based on a stress concentration factor (SCF). A new in-plane shear SCF of a composite with debonded interface is derived and applied to the predictions of strain and strength in this paper. Moreover, the contribution of the relative slippage between fiber and matrix to the non-linear shear deformation of the composite is analyzed. Finally, the efficiency and accuracy of our theory are verified with a series of examples. The approach is very efficient because the calculation can be achieved with explicit expressions mainly based on the constituent material properties. The comparisons between predicted strength and deformation with the experimental results show that our analytical approach can give out reliable underlying data for multi-scale analysis. Moreover, this theoretical method can tell if and how much the interface of a composite needs to be modified for a given load environment.

1 Introduction

In-plane shear stress components widely exist in the application scenarios of modern advanced composite materials. Engineering constructional elements subjected to torsion or lateral loads, such as wing skins, bolted joints, spar caps and bonded joints, are typical such examples. Moreover, some key mechanical problems such as kinking failure are closely related to in-plane shear property of a composite. Test methods [1,2,3,4] for obtaining the in-plane shear behavior of a composite have various shortcomings [3, 5,6,7,8], e.g., dispersed measured data and high costs. As described by Purslow [9], there are many doubts about the mechanism and regularity of the shear-induced deformation and failure. Therefore, researchers attempt to develop analytical models to predict the composite properties under in-plane shear. Until recently, there are still meaningful continuous efforts made to study the mechanical response under in-plane shear [10,11,12,13,14,15].

In engineering applications, most formulae used for predicting the in-plane shear strength based on properties of constituent materials are empirical or semi-empirical [16,17,18]. Researchers admitted that it is still quite hard to accurately predict the mechanical behavior of a composite subjected to in-plane shear loading [19,20,21]. In summary, studying the regular and principal failure and deformation of a composite under in-plane shear and then building a corresponding mechanical prediction model is challenging but has great theoretical and practical significance. The main objective of this paper is to put forward a micro-mechanical method for predicting the debonding moment, ultimate strength and strain response of a composite subjected to an arbitrary loading dominated by in-plane shear, mainly using the original properties of the constituent materials. The other important objective is to understand interface behavior simply and accurately, by telling a discount in a composite strength and rigidity due to the interfacial debonding.

In this work, the objectives above will be achieved by analyzing the stresses and strains in the constituents with a micro-mechanical method. It must be noted that the volume-averaged stresses given by any micro-mechanical theory cannot be directly used for determining the mechanical behavior of a composite. This obstacle has been overcome by applying a stress concentration factor (SCF) theory [22,23,24]. It is well known that a plate with a hole suffers stress concentration under in-plane tension. When the hole is filled by a fiber, or other filler with different properties, a stress concentration occurs as well [25,26,27,28]. Multiplied by the corresponding stress concentration factors (SCFs), the homogenized stresses of the matrix can be converted into the true values, which can be directly used in a failure detection or plasticity evaluation.

The definition and application of the SCFs are mostly based on a perfect interface bonding assumption, which is often not consistent with the practical situation. Interfacial cracks caused by in-plane shear widely exist among composites in engineering applications [9, 29,30,31,32,33,34,35], playing an important role in the mechanical behavior of the composite [25, 35, 36]. In fact, perhaps the most widely used test methods to characterize an interface behavior, such as single fiber pull out or push in test [37], were designed based on an assumption that a shear load will cause the interface debonding to occur. For a composite with an initial perfect and later debonded interface, as the common case being, the stress distribution and fluctuation will change after the interface debonding. Therefore, two SCFs of a composite, with and without interfacial crack, are both needed in a mechanical analysis.

To definite a SCF, two necessary conditions are required. The first is the stress field of the matrix in a representative volume element (RVE) of the composite material, which can be obtained using an elasticity approach. A traditional SCF is defined as a ratio of the maximum point-wise stress and the averaged stress on a surface. Similarly, our SCF is a ratio of averaged stress on a line and that of the whole volume of the representative volume element. The volume-averaged stress is given by Bridging Model and the line-averaged stress is calculated through line integral of the stress filed function. Therefore, the second condition is determination of the integration path, which is perpendicular to the fracture surface of the composite [22,23,24]. For the composite under an in-plane shear, the feature of the shear cracks and fracture surface of the composite can be shown better on a longitudinal section [19, 20, 29, 38], while the stress fields are generally represented in a transversal cross-section [39,40,41]. Therefore, stereoscopic physical models of a composite with and without an interfacial crack are built in this work to gain comprehensive information.

The SCF thus derived is to be used for calculation of the matrix true stresses to quantify the effect of an interface debonding. An analytical approach will be carried out to predict the interface debonding, deformation and ultimate strength of a composite subjected to an in- plane shear, mainly using the original properties of the constituent materials. The homogenized stresses of the constituents are calculated through Bridging Model [42], and the true stresses are obtained accordingly by virtue of the SCFs. As the values of SCFs before and after an interface debonding are different, an incremental solution strategy is generally employed. Moreover, when estimating a deformation, not only the elastic–plastic response of a constituent but also a strain fluctuation and a relative sliding displacement between the fiber and matrix after their interface debonding should be taken into consideration. With the improved SCF theory and the interface slippage model, a more accurate prediction of the in-plane shear strength and the deformation can be achieved. To illustrate our theory, a variety of UD composites are chosen as examples. Only the constituent properties and the transverse tensile strengths are needed for input. The influence of the stress fluctuations due to the embedded fiber and the interface debonding on the matrix SCFs is discussed. The loading level corresponding to an interfacial crack initiation is estimated, and the nonlinear stress–strain response of the composite under in-plane shear up to the ultimate failure is predicted. The accuracy and predictability of our theory has been verified by comparing the predictions with the available experimental data.

2 Internal Stresses in Constituents

To achieve the goal of calculating the properties of a composite using only the fiber and matrix data, the internal stresses of its constituents are obtained with a micromechanical method. A homogenization treatment leads to

$$\sigma_i = \frac1{V'}\int_{V'}\widetilde{\sigma_i}dV=V_f\sigma_i^f+V_m\sigma_i^m,\;i=1,\;2,\;\dots,\;6$$

(1)

In Eq. (1), $\sigma_i$ and $\tilde\sigma_i$ are the volume-averaged and point-wise stresses of the composite, respectively. The subscript i represents the direction of the stress component. In this paper, i equals to 1, 2 or 3 indicates a normal stress along the fiber axial, transverse, or thickness direction of a laminate, whereas to 4, 5, or 6 represents the corresponding shear stress component. V stands for volume content and V’ is an infinitesimal volume. f or m located at superscript or subscript indicates that the volume or stress is related to the fiber or matrix. For example, $\sigma_1^f$ represents the matrix stress in the fiber axial direction and $\sigma_2^m$ indicates the matrix stress in transversal direction.

Correlating the internal stresses in the fiber and matrix with a bridging equation [38],

$\left\{\sigma_i^m\right\}=\left[A_{ij}\right]\left\{\sigma_i^f\right\}$, and combining it with Eq. (1), the internal stresses can be expressed as

$$\left\{\sigma_i^f\right\}=\left(V_f\left[I\right]+V_m\left[A_{ij}\right]^{-1}\right)\left\{\sigma_j\right\}$$

(2)

$$\left\{\sigma_i^m\right\}=\left[A_{ij}\right]\left(V_f\left[I\right]+V_m\left[A_{ij}\right]\right)^{-1}\left\{\sigma_j\right\}$$

(3)

With the bridging tensor, $\left[A_{ij}\right]$, defined by Bridging Model [42], the non-zero internal stresses in a UD composite under in-plane shear, σ₁₂, are given as follows.

$$\begin{aligned}&\sigma_{12}^f=\frac{\sigma_{12}}{V_f+V_ma_{66}},\\&\;\sigma_{12}^m=\frac{a_{66}\sigma_{12}}{V_f+V_ma_{66}},\\&\;a_{66}=\alpha+\left(1-\alpha\right)\frac{G^m}{G_{12}^f}=0.3+0.7\frac{G^m}{G_{12}^f}\end{aligned}$$

(4)

In the above formula, $\sigma_{12}^f$ and $\sigma_{12}^m$ are in plane shear stress of fiber and matrix. $G_{12}^f$ and G^m are the longitudinal shear moduli of the fiber and matrix, respectively. a₆₆ is an element in bridging tensor, $\left[A_{ij}\right]$, related to the in-plane shear stress component. The parameter α in Eq. (4) has a value of 0.3. The expressions of elements in bridging tensor and volume-averaged stresses of the constituents under an arbitrary load are summarized in Appendix A.

3 Derivation of In-Plane Shear SCF after Interface Debonding

3.1 Definition of SCF and True Stress

Different from a classical approach, a SCF of the matrix in a composite is defined as the ratio of a line-averaged stress of the matrix over the corresponding volume-averaged quantity of it. The integration line for the line averaging is along the outward normal to the failure surface of the composite within the RVE, starting from the inner surface and ending at the outside one of the matrix cylinders [22,23,24]. The stress distribution of the matrix is obtained based on a concentric cylinder assemblage (CCA) model. The SCF expressions already available [22,23,24] are given in Appendix B.

Due to the stress fluctuation in the matrix caused by the embedded fiber, the homogenized internal stresses of the constituent materials cannot be directly used for a failure prediction. Instead, the homogenized stresses of the matrix must be converted into the true values to represent the effect of the stress fluctuation [22,23,24]. In our model, x₁ and x₃ axes are along fiber axial and plate thickness directions, respectively. Accordingly, the direction of stress can be read from the subscript of a symbol. For example, $\sigma_{11}^f$ represents the axial stress in the fiber and $\sigma_{12}^m$ represents the in-plane shear stress in the matrix. Let the homogenized stresses of the matrix be $\left\{\sigma_{11}^m,\sigma_{22}^m,\sigma_{12}^m\right\}$,which can be calculated using Eq. (3). The corresponding true stresses $\left\{\overline\sigma_{11}^m,\overline\sigma_{22}^m,\overline\sigma_{12}^m\right\}$ are obtained from

$$\left\{\overline\sigma_{11}^m,\overline\sigma_{22}^m,\overline\sigma_{12}^m\right\}=\left\{\sigma_{11}^m,K_{22}^m,\sigma_{22}^m,K_{12}^m,\sigma_{12}^m\right\}$$

(5)

$$K_{22}=\left\{\begin{array}{l}K_{22}^t,\mathrm{if}\quad\sigma_{22}^m>0\quad \mathrm{and\;with\;perfect\;interface}\\\hat K_{22}^t,\mathrm{if}\quad\sigma_{22}^m>0\quad \mathrm{and\;with\;debonded\;interface}\\K_{22}^c,\mathrm{if}\quad\sigma_{22}^m>0\end{array}\right.$$

(6)

$K_{22}^t$ and $\hat K_{22}^t$ are, respectively, the transverse tensile SCFs of the matrix before and after the interface debonding. $K^{c}_{12}$ and K₁₂ are the transverse compressive and longitudinal shear SCFs of the matrix with a perfect interface. It is noted that under a longitudinal tension or compression, the stresses in the matrix are uniform [43], thus non SCF is applied in front of $\sigma_{11}^m$ in Eq. (5).

3.2 Stress Field of a Composite with Debonded Interface Under Longitudinal Shear

The in-plane shear SCF given in Appendix B is derived based on an assumption that the interface keeps perfect bonding until the ultimate failure [44, 45]. In this case, the stress transfer of a RVE under in-plane shear loading is indicated by Fig. 1. a is the radius of the fiber and b is the radius of RVE volume. b and a are correlated as $b=\frac a{\sqrt{V_f}}$. The schematic and actual drawing of inclined cracks in the matrix caused by shear-resulting maximum principal stress are shown in Fig. 1(a) and Fig. 1(c). From the transversal cross section, the matrix in the region singed by the vertical line is responsible for transferring the applied stress to the fiber. Therefore, the fracture of the composite generally occurs when the stress of this part of matrix reaches ultimate failure strength. Based on the defining method of a SCF, the integral line see Fig. 1(a) and (b) must be perpendicular to the matrix crack, locating in the region with the vertical lines in Fig. 1(b).

Fig. 1

Schematic of stress transfer and matrix cracks under in-plane shear in the (a) longitudinal and (b) transversal sections of a RVE of a composite with complete interface (c) matrix cracks in actual composites[25]

In reality, interface debonding often occurs during the loading process and affects the mechanical properties of the composite. This influence is often attributed to the hindering effect of an interfacial crack on the stress transfer between fiber and matrix. As shown in Fig. 2(b), the stress cannot be transferred smoothly because of the free surface on the interface crack. In fact, an increase of the stress fluctuation after interface debonding also plays a role in the change of mechanical properties, which will be quantified by virtue of a new in-plane shear SCF in this paper. Moreover, the slippage between fiber and matrix will produce an extra in-plane shear deformation, $\gamma_{12}^{int}$, which constitutes the final composite’s deformation ($\gamma_{12}^{comp}$), with the deformation of matrix and fiber ($\gamma_{12}^{mf}$), as shown in Fig. 2.

Fig. 2

Schematic of interface cracks and the resulting extra deformation under in-plane shear in the longitudinal and transversal sections of a RVE of a composite

As mentioned earlier, the corresponding stress field is the foundation of deriving a SCF. As shown in Fig. 1, there is a curved crack on the fiber/matrix interface. Ideally, the debonding can be supposed to occur symmetrically with respect to, e.g., x₃ coordinate, producing two interfacial cracks. However, the interface debonding rarely occurs on both sides simultaneously in reality for following reasons. Considering the minute differences between the interfaces of two sides, the interface debonding crack is very likely to initiate on the weaker side. Once the interface crack initiates on one side, the matrix around the crack loses its bearing capacity and the stress on the opposite side also decreases (as shown by stress nephogram in Fig. 3), reducing the possibility of appearance of symmetrical cracks.

Fig. 3

Stress nephogram around a single fiber of a composite under unit in-plane shear (a) before and (b) after interface debonding

Let us employ the central angle of an interfacial crack to evaluate the size of the debonding part and use a parameter, 2ψ, to stand for it. In a CCA model, Zhang and Hasebe obtained the stress fields of the fiber and matrix in Fig. 1 under an applied in-plane shear, $\sigma_{12}^0$ [46]. After simplification, the expression of stress distribution in the matrix, $\widetilde\sigma_{12}^m$, is given as:

$$\widetilde\sigma_{12}^m=\sigma_{12}^0\;\mathrm{Re}\left\{\frac{G^m}{G^m+G_{12}^f}\left(1-\frac{\alpha^2}{z^2}\right)+\frac{G_{12}^f}{G^m+G_{12}^f}\times\left(z-ae^{i\psi}\right)^{-0.5}\left(z-a\cos\left(\psi\right)-\frac{a^3}{z^2}+\frac{\cos\left(\psi\right)a^2}{z^2}\right)\right\}$$

(7)

In Eq. (7), a is the fiber radius and z = x₂ + ix₃ is the coordinate of the matrix point under consideration. The corresponding stress concentration gradients around a fiber of the RVE under an in-plane shear before and after the interface debonding are represented by stress nephogram in Fig. 3, from which the stress inhomogeneity of the transversal section under a unit shear stress can be seen clearly.

3.3 Determination of Integration Path

Except for obtaining the stress field, the other key requirement for derivation of a SCF is to determine the integration path. According to the universal definition for a SCF, this path should be perpendicular to the failure surface of the composite within the RVE. Existing observational experiments have reported that the micro-cracks in the matrix of a composite under in-plane shear are along a direction approximately in 45° with the fiber axis [9, 20, 26, 30]. Accordingly, one can use Fig. 4 to describe the development of the matrix cracks in a composite under the in-plane shear, where the interface between the fiber and matrix of a composite is supposed to be perfectly bonded during the whole loading process. However, there are some other phenomena widely observed in composites after an in-plane shear failure [9, 29,30,31,32,33,34,35]: the fiber with little matrix covering on it, fiber-like imprints on the matrix, bare fiber pulled out, etc. as shown in Fig. 5. These phenomena are signs of fiber/matrix interface debonding. Thus, a new model containing interfacial crack is needed.

Fig. 4

Stereo model of a composite with perfectly bonded interface under a longitudinal shear (a) initiation of matrix cracks (b) the matrix cracks close to final failure

Fig. 5

Fracture surface of a composite under a longitudinal shear [47] (load direction is shown for ease of understanding)

Let us assume that x₁ is in the fiber axial direction and the shear stress is applied in x₁-x₂ plane. Based on the observations in Fig. 5, a stereoscopic model can be built as indicated in Fig. 6 and Fig. 7. In the x₁-x₂ plane, both of the initial matrix cracks in Fig. 4 and Fig. 6 are approximately in 45° with the fiber axis, perpendicular to the direction of the principal tensile stress. Different from the micro-crack distribution in a composite with the perfect interface (Fig. 4(a)), the matrix cracks caused by the interface debonding are initiated from the boundary of the debonding area in Fig. 6 (a) (or to say, from the tip of an interfacial crack on the x₂-x₃ plane). After a full development (Fig. 6(b)), the matrix cracks induced by the interface debonding will propagate along the x₃ direction, leading to the final fracture (Fig. 7). The schematic morphology shown in Fig. 7 is consistent with that in Fig. 5.

Fig. 6

(a) (b) Stereo model of a composite with interface crack under in-plane shear and (c) corresponding enlarged drawing [48] (the arrows denote the crack propagation)

Fig. 7

(a) Stereo model of a failed composite under a longitudinal shear and (b)(c)(d) actual plane images of it from various perspectives[27]

In all diagrams, it is clear that the cracks are only distributed in a part of matrix due to a stress concentration. The stress level in this part governs the in-plane shear strength of the composite. Accordingly, the definition of an in-plane SCF of the matrix with a perfect interface is based on a physical model similar to that represented by Fig. 4 [44, 45]. In a similar way, the in-plane SCF of the matrix after the interface debonding should be defined based on the model represented by Fig. 6 and Fig. 7.

It is widely believed that the interfacial crack will initiate from a point on the intersecting line of fiber surface and a symmetry plane parallel to the loading direction [25, 40, 41, 49], for example, at the point (x₂ = a, x₃ = 0) in Fig. 8 (b). For a relatively small half-cracked angle, ψ, the interfacial crack hinders the stress transfer thus reduces the load-bearing capacity of the matrix above the debonding region. The matrix area marked with vertical lines in Fig. 8(b) will carry more stresses than the same area of a model under the same loading condition but with the perfect interface (Fig. 8(a)), thus will be more likely to produce cracks. In particular, when the center angle is zero, the composite will turn back to the case of the perfect interface. In another situation, with an expansion of the center angle ψ, the main load bearing area of the matrix will move from the middle to the sides, as shown in Fig. 8(c). Obviously, the actually observed distribution of the matrix cracks on the fracture surface (Fig. 5) is in accordance with the model in Fig. 8(c) instead of Fig. 8(a) or Fig. 8(b).

Fig. 8

Interfacial crack expansion and corresponding distribution of potential matrix crack in a RVE under in-plane shear

The half-cracked angle ψ is a key parameter that effects the distribution of the matrix cracks and the integration line for defining the SCF. On one hand, according to the result obtained with an analytical method [40, 41, 49], this half-cracked angle ψ can reach a value of 90⁰, indicating that a debonding crack can propagate to occupy half of the interface. On the other hand, if the debonding curve expands more than half of the interface, the crack propagating path to form the final fracture surface is depicted in Fig. 9(a), which is longer and more energy-consuming than that in Fig. 9(b). Therefore, it is reasonable to assume that the center angle, 2ψ, is 180°.

Fig. 9

Transversal sections of a composite with a half-cracked angle of (a) over 180°and (b) 180°

To prove this viewpoint, the picture of transversal plane of a composite after an in-plane shear failure is taken from Ref. [50]. After measuring the center angles in Fig. 10(a), an averaged value of 175°is obtained. It is clear in the picture that the sizes of the debonding parts around fibers differ widely from each other due to a non-uniform fiber distribution, but their averaged value is close to our expectation. More evidences can be found on the fracture surface plane [51,52,53], e.g., Fig. 10(b), where the width of a fiber imprint is close to that of the uncovered fiber (marked with both end arrows in Fig. 10(b)).

Fig. 10

(a)Transversal section of a carbon fiber reinforced composite after in-plane shear failure under confocal laser microscope [50](b) Fracture surfaces of a carbon fiber/PEEK epoxy composite after in-plane shear failure [51]

In conclusion, the crack propagation process is as follows: an interfacial crack will initiate from a single point and propagate to about half of the interface, and further connect with the cracks in the matrix rich region to form the final fracture surface. Based on this process, the value of ψ and the schematic in Fig. 2 and Fig. 8(c), a transverse cross-section of the fractured composite with debonded interface under an in-plane shear is finally depicted in Fig. 11, with the crack distribution in the matrix marked with vertical lines parallel to the x₂ axis.

Fig. 11

Schematic of a RVE used in defining SCF of a composite after interface debonding subjected to an in-plane shear

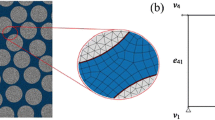
The integration line for defining a SCF is mainly based on the inclined direction of the matrix induced fracture surface. According to the crack distribution in Fig. 11, let us consider a certain longitudinal cross-section containing matrix cracks located at $x_3=x_3^0,\;\alpha\leq x_3^0\leq b$. According to the general definition for a SCF (Appendix B), the stress integration line should be perpendicular to the fracture surface of a microscopic matrix crack. For example, for the longitudinal plane of $x_3^0=\alpha$, the integration line starts from the fiber surface (point (0, 0, a) in Fig. 12(a)) and ends at the matrix outside surface of the RVE, i.e., the point ($\sqrt{b^2-a^2},-\sqrt{b^2-a^2},\;a$) in Fig. 12(a). For a certain longitudinal plane of, the integration line is determined as shown in Fig. 12(b), from the starting point (0,0,$x^{0}_{3}$) to the ending one ($\sqrt{b^2-\left(x_3^0\right)^2},-\sqrt{b^2-\left(x_3^0\right)^2},\;x_3^0$), so that the line connecting the two points is perpendicular to the surface of microscopic matrix shear crack.

Fig. 12

Schematic for defining SCF of matrix under in-plane shear at (a) transversal and longitudinal sections at x₃ = a, (b) transversal and longitudinal sections at $x_3=x_3^0,\alpha\leq x_3^0\leq b$ 

After determination of the integral line, the in-plane shear SCF after interface debonding, can be obtained as

$$\begin{aligned}&{\hat K}_{12}=\{\frac{G^m}{G^m+G_{12}^f}\left(1+V_f\right)+\frac{G_{12}^f}{\left(G^m+G_{12}^f\right)\left(b-a\right)}\lbrack\frac{\alpha\pi}2\left(1-\sqrt{V_f}\right)+\mathrm{Im}(\left(b^2-\alpha^2-2ai\sqrt{b^2-a^2}\right)^{0.5}\\&+\alpha\ln\frac{\left(b^2-\alpha^2-2\alpha i\sqrt{b^2-\alpha^2}\right)^{0.5}}b-i\sqrt{a^2-b^2}-a\ln\frac{\sqrt{a^2-b^2}-a}b\\&+a\ln\left(\left(b^2-a^2-2\alpha i\sqrt{b^2-\alpha^2}\right)^{0.5}-\sqrt{b^2-\alpha^2}+ai\right)-\alpha\left(1+\frac{\alpha^2}{b^2-2a^2-2ai\sqrt{b^2-\alpha^2}}\right)\\&-a\ln(\sqrt{\alpha^2-b^2+bi}))\rbrack\}\frac{V_fG_{12}^f+V_m\left(0.3G_{12}^f+0.7G^m\right)}{0.3G_{12}^f+0.7G^m}\\&=\{\frac{G^m}{G^m+G_{12}^f}\left(1+V_f\right)+\frac{G_{12}^f}{G^m+G_{12}^f}\lbrack\frac{\pi\sqrt{V_f}}2+\frac{\sqrt{V_f}}{1-\sqrt{V_f}}Im({(\frac1{V_f}-1-2i\sqrt{\frac1{V_f}-1})}^{0.5}\\&+\ln({(1-V_f-2i\sqrt{\frac1{V_f}-1})}^{0.5}-\sqrt{V_f})-i\sqrt{1-\frac1{V_f}}-\ln(\sqrt{V_f-1}-\sqrt{V_f})\\&+\ln({(\frac1{V_f}-1-2i\sqrt{\frac1{V_f}-1})}^{0.5}-\sqrt{\frac1{V_f}-1}+i-{(1+\frac{V_f}{1-2V_f-2i\sqrt{V_f-\left(Vf\right)^2}})}^{0.5}\;\\&-\ln(\sqrt{1-\frac1{V_f}}+\frac i{\sqrt{V_f}}))\rbrack\}\frac{V_fG_{12}^f+V_m\left(0.3G_{12}^f+0.7G^m\right)}{0.3G_{12}^f+0.7G^m}\end{aligned}$$

(8)

The detailed derivations can be found in Appendix C. In Eq. (8), a is the radius of the fiber, $b=a/\sqrt{V_f}$ 

4 Role of $\hat K_{12}$ 

The SCF formula, Eq. (8), is valid once an interface debonding occurs. The moment when the debonding will occur must be determined. In general, the fiber/matrix interface is bonded perfectly at the beginning of loading, and the interface debonding would happen when the applied load reaches a critical level. A transverse tension is believed to cause an interface debonding more potentially to occur than any other uniaxial load condition. Thus, a transverse tensile strength should be provided to determine the moment of the interface debonding. A criterion for detecting an interface debonding has been established in our previous work [44], which states that.

$$\bar\sigma_e^m\geq\hat\sigma_e^m\;\mathrm{and}\;\bar\sigma_m^1\geq0$$

(9)

$\bar \sigma^{m}_{12}$ is the Mises stress of the matrix corresponding to matrix true stress components ($\bar \sigma^{m}_{11}, \bar \sigma^{m}_{22}, \bar \sigma^{m}_{12}$) or matrix average stress components ($\hat \sigma^{m}_{11}, \hat \sigma^{m}_{22}, \hat \sigma^{m}_{12}$). $\hat \sigma^{m}_{e}$ is the critical Mises true stress of the matrix. $\bar \sigma^{1}_{m}$ is the first true principal stress of matrix. For a composite under transversal loading, if the stress applied at the moment of interface debonding, $\hat \sigma^{0}_{22}$, is known. $\hat \sigma^{m}_{e}$ in Eq. (9) can be given by [44, 54].

$$\hat\sigma_e^m=\sqrt{\left(\hat\sigma_{11}^m\right)^2+\left(K_{22}^t\hat\sigma_{22}^m\right)^2-K_{22}^t\hat\sigma_{11}^m\hat\sigma_{22}^m}$$

(10)

$$\hat\sigma_{11}^m=\frac{V_f\alpha_{12}}{\left(V_f+V_m\alpha_{11}\right)\left(V_f+V_m\alpha_{22}\right)}\hat\sigma_{22}^0$$

(11)

$$\hat\sigma_{22}^m=\frac{0.3E_{22}^f+0.7E^m}{\left(V_f+0.3V_m\right)E_{22}^f+0.7V_mE^m}\hat\sigma_{22}^0$$

(12)

$$\hat\sigma_{22}^0=\frac{\hat K_{22}^tY}{\hat K_{22}^t-K_{22}^t}\frac{\left(V_f+0.3V_m\right)E_{22}^f+0.7V_mE^m}{\left(0.3E_{22}^f+0.7E^m\right)\left(\hat K_{22}^t-K_{22}^t\right)}\sigma_{u,\;t}^0$$

(13)

a₁₁, a₂₂ and a₁₂ are elements of bridging tensor, for which the expressions can be found in Appendix A. In Eq. (13), Y is the transverse tensile strength of the UD composite. $\hat\sigma_{u,t}^m$ is the matrix tensile strength. $\hat\sigma_{22}^0$ is the applied loading at the moment of interface debonding of the composite under transversal tension. $E^{f}_{22}$ is the transverse modulus of fiber. $K^{t}_{22}$ and are, respectively, the transverse tensile SCFs of the matrix before and after the interface debonding. In Eq. (9), $\bar\sigma_{e}^m$ and $\bar\sigma_{m}^1$ are the Mises and the first principal stresses of the matrix, respectively, calculated from its true stress components, given by Eq. (6). Namely [54],

$$\bar \sigma_e^m=\sqrt{\left(\bar\sigma_{11}^m\right)^2+\left(\bar\sigma_{11}^m\right)^2-\bar\sigma_{11}^m\bar\sigma_{22}^m+3\left(\bar\sigma_{12}^m\right)^2}$$

(14)

$$\bar\sigma_m^1=0.5\left(\bar\sigma_{11}^m+\bar\sigma_{22}^m\right)+0.5\sqrt{\left(\bar\sigma_{11}^m-\bar\sigma_{22}^m\right)^2+4\left(\bar\sigma_{12}^m\right)^2}$$

(15)

When the composite is subjected to an in-plane shear, the interface debonding will occur once the applied load reaches $\bar\sigma^{0}_{12}$, at which the Mises true stress of the matrix attains $\bar\sigma^{m}_{e}$ . Thus, the loading process up to a composite ultimate failure is separated by into two stages. In the first stage, the composite has a perfect interface bonding and the in-plane shear SCF, K₁₂, of the matrix should be applied to determine its true stress. In the latter stage with the debonded interface, the SCF, $\hat K_{12}$, derived in the last section is applicable. Let $\sigma^{m,S}_{12}$and $\sigma^{m}_{12}$ be the matrix homogenized stresses corresponding to the failure and the debonding loads, respectively, under the in-plane shear. The failure condition of the composite under in-plane shear is given by

$$K_{12}\widehat\sigma_{12}^m+{\widehat K}_{12}\left(\sigma_{12}^{m,S}-\widehat\sigma_{12}^m\right)=\sigma_{u,s}^m$$

(16)

$$\sigma_{12}^u=\frac{\alpha_{66}\sigma_{12}^{m,S}}{V_f+V_m\alpha_{66}},\widehat\sigma_{12}^m=\widehat\sigma_e^m/\sqrt3$$

(17)

$\sigma^{m}_{u,s}$ is the matrix shear strength, and $\sigma^{u}_{12}$ is the in-plane shear strength of the composite. From Eqs. (16) and (17), one can estimate the debonding load and the strength of the composite under in-plane shear if its transverse tensile strength, Y, is available.

In a certain longitudinal cross-section (located at $x_{3} = x^{3}_{0}$) of the composite under the in-plane shear, there is a relative sliding displacement along the x₁ direction between the debonded interfaces of the fiber and matrix. An overall strain of the composite is consisted of not only the strain contributed from the fiber and matrix deformations but also that caused by the interfacial slippage displacement. The relative slippage strain, $\gamma_{12}^{int}$, is found to be [55]

$$\gamma_{12}^{int}=\frac{V_f\left(G_{12}^f-G_m\right)\left(\psi_1+\sin\left(\psi_1\right)\cos\left(\psi_1\right)\right)\left(f_1\left(\psi_1\right)+f_1\left(\psi_1\right)\right)}{\pi G_m\left(G_{12}^f+G_m\right)}\sigma_{12}^0$$

(18)

$\sigma_{12}^0$ is the in-plane shear load applied to the composite. The expressions for the $f_1\left(\psi_1\right)$ and$f_2\left(\psi_1\right)$ in Eq. (18) are summarized in Ref. [55]. It is noted that the G_m in Eq. (18) is an instantaneous shear modulus of the matrix, which should be defined upon the current Mises true stress of Eq. (14). More details can refer to Ref. [55]. The angle ψ₁ is defined as.

$$2\psi_1=\frac{\left(\sigma_{12}^0-\hat\sigma_{12}^0\right)}{\left(\sigma_{12}^u-\hat\sigma_{12}^0\right)}\pi,\;\hat\sigma_{12}^0=\frac{V_f+V_m\alpha_{66}}{K_{12}\alpha_{66}}\hat\sigma_{12}^m$$

(19)

To deal with debonded interface, an incremental solution strategy should be applied to evaluate step by step displacements from Eqs. (19). $\hat\sigma^{0}_{12}$ and $\hat\sigma^{m}_{12}$ are applied loading and matrix stress corresponding to interface crack initiation. $\sigma^{u}_{12}$ is the composite’s in-plane shear strength. The a₆₆ is calculated with Eq. (4).

An additional comment regarding the interface debonding angle is made herein. At the beginning of an interface debonding, the debonding angle is zero. This angle expands to the half plane with 2ψ = π when the composite attains an ultimate failure subjected to an in-plane shear load. The Eq. (19) is obtained by assuming that the ultimate failure load corresponds to the half plane debonding [55]. However, in deriving the matrix in-plane shear SCF, , after the interface debonding, the largest debonding plane angle, i.e., 2ψ = π, has been used. This usage does not mean that the SCF, , would play a role only at an interface debonding angle of 2ψ = π. Instead, when ψ ≤ 0 or when the in-plane shear load is smaller than the critical one, $\sigma^{0}_{12}$ ≤ $\hat\sigma^{0}_{12}$, the perfect interface bonding based SCF, K₁₂, is active. However, when ψ > 0 or $\sigma^{0}_{12}$ > $\hat\sigma^{0}_{12}$, $\hat K ^{0}_{12}$ the must be used.

5 Illustration

5.1 Materials and Calculation Method

Only original fiber and matrix properties plus a transverse tensile strength of a UD composite are necessary for predictions of, e.g., the interface debonding load, the ultimate strength of the composite, and the deformation up to failure. The original properties of the constituent materials of a total number of 10 UD composites taken from Refs. [56,57,58,59]. are summarized in Table 1. The SCFs of the matrices in the composites necessary for the predictions are calculated as per the formulae in Sect. 3 and Appendix B. They are listed in Table2.

Table 1 Constituent property of 10 UD composites

Table 2 SCFs of matrices in the 10 UD composites

Using the data of Tables 1 and Tables 2, the in-plane shear strengths of the 10 composites are calculated with and without incorporation of the SCFs as well as the interface debonding. Results are shown in Table 3. Measured counterparts taken from the respective sources and their corresponding measuring methods are also given in the Table 3 to verify the accuracy of our predicted in-plane shear strength.

Table 3 Predicted strengths and relative errors in correlation with measured data of the 10 UD composites

For deformation prediction, the stress–strain curves of a carbon fiber and a glass fiber reinforced composite under in-plane shear until failure are applied as illustrations. Four different kinds of prediction schemes have been made. The first is done based on the homogenized stresses of the matrix (i.e., all the SCFs are set to 1) and no interface slippage is considered. In the second prediction, the SCF of a perfect interface bonding, K₁₂, is used throughout without any interface slippage considered. The third (labeled as “prediction with interface slippage 1”) is made by taking both the SCF K₁₂ and the interface slippage into consideration. In other words, although the contribution from the interface slippage displacement has been considered in the third prediction, the in-plane shear SCF of the matrix, K₁₂, is used throughout. The last prediction (labeled as “prediction with interface slippage 2”) is obtained with the method developed in this paper, incorporated with the two in-plane shear SCFs of the matrix, K₁₂ and, at different loading stages and the interface slippage displacement altogether. The predictions are plotted in Fig. 13 for the AS4/8552 and in Fig. 14 for the E-Glass/ M750 material systems, respectively.

Fig. 13

Predictions and measurements [60] for stress–strain curves of AS4/8552 UD composite under in-plane shear load

Fig. 14

Predictions and measurements [57] for stress–strain curves of E-glass/M750 UD composite under in-plane shear loading

5.2 Result and Discussion

The main contribution of this paper is to derive and apply a new stress concentration factor, $\hat K_{12}$. It is seen from Table 2 that the transverse tensile SCFs are generally higher than the in-plane shear SCFs. In general, the transverse tensile strength is the lowest of the uniaxial strengths of a UD composite, sometimes even lower than half of the original tensile strength of the matrix. On the other hand, the in-plane shear strength of the composite is usually higher than the corresponding matrix shear strength. This difference confirms that the stress concentration caused by the embedded fiber and the interfacial crack is more serious to a transverse tension than to an in-plane shear. Moreover, comparing the data in the third and fourth columns of Table 2, the corresponding transverse tensile SCFs after the interface debonding are more than double of those before the interface debonding. On the other hand, the differences between the in-plane shear SCFs before and after the interface debonding are not very much significant.

Let us analyze the predicted strengths in Table 3. According to the predicted strengths with and without SCFs, the use of an in-plane shear SCF is very effective, and the consideration of the interface debonding could further improve the accuracy of the predicted strength. The accuracy of predictions given by the method proposed in this paper (last row of Table 3) is generally satisfactory. However, it must be noted that the corresponding strength measuring methods of material systems are different, as shown in Table 1. These test methods have their respective characteristics and defects. For example, the tension test of ± 45° laminates [1] is simple to use but easily affected by fiber rotation during loading, or to say, “scissors factors” [5, 6]. The short beam shear test will be affected by a mixed stress state [4]. Contrarily, the Iosipescu shear test [2] could provide a state of pure shear stress but will be influenced by stress concentration near the notch [3].

Due to these characteristics and defects, significant discrepancies sometimes exist among shear strengths measured by different methods [7]. For instance, the value of in-plane shear strength of AS4/3501–6 was reported to be 96 MPa [60], obtained from an Iosipescu measuring method, while the reference value given by a thin-walled tube torsion test was chosen to be 79 MPa [61] by the organizers of WWFE. In fact, other published values are in the range of 71–110 MPa [21, 62,63,64]. Therefore, the difference between the predicted strength and the experimental value can be partly attributed to the measurement error. For example, the relatively error of prediction of AS /epoxy given by our proposed method in the Table 3 is relatively high (11.2%). This is probably because the measurement has been overvalued as the only one given by an Iosipescu test.

Except for the measurement deviation, the relative error can also come from calculation process. For example, the relative error of shear strength of the T300/PR319 reaches 38.8%, which is obviously too high. In fact, the shear strength of RP319 matrix provided by WWEF organizer is 41 MPa, being much lower than strengths of other matrices. The organizers of the WWFEs admit that the data of RP319 resin ‘‘are considered to be low.’’ Therefore, this high relative error can be attributed to the unreasonable raw data of component materials. Similarly, for another material system with a relative error higher than 10%, AS4/3501–6, the mechanical properties of component materials might be doubtful. The tensile, compressive, and shear strengths of the matrices of other material have an approximately quadratic relationship: $\sigma_{u,s}^m \approx 0.5 \sqrt{\left(\sigma_{u,t}^m-\sigma_{u,c}^m\right)}$. However, the given shear strength of the 3501–6 epoxy, 50 MPa, is far away from the value of. It is possible that the measurement or record of the data of this epoxy is not accurate. Another possibility is that the shape of the failure envelope of 3501–6 epoxy is special. Thus, our universal matrix failure criterion is less applicable to it.

With above discussion, the causes of all relative errors higher than 10% have been analyzed. Considering these causes, it is reasonable to believe that our method for calculating in-plane shear strength of a composite is reliable. Next, let us carry out deformation prediction for two composites, AS4/8552 and E-Glass/ M750, under in-plane shear up to failure. In Fig. 13 and Fig. 14, the first (calculation without any SCF) and the second kinds (calculation with K₁₂ and an assumption of a perfect interface) of predictions deviated with the experiments significantly, implying that only the constituent deformations cannot make up the large deformation of a composite under an in-plane shear. It is the relative slippages between debonded fiber and matrix interfaces that dominate the nonlinear in-plane shear stress–strain curve of the composite during a later loading stage. Although significant difference between the predicted stress–strain curve from the second scheme and those from the third and last schemes exists, the predicted ultimate strengths from all of them are comparable with each other. The last prediction scheme, that is, the approach proposed in this paper correlates overall the best with the experiments.

Similar to the strength prediction, the error source and data credibility also need to be discussed for deformation prediction. The methods generally used for measuring in-plane shear deformation include Iosipescu test, ± 45° tension test and 10° off-axis tension test. Among these methods, the discreteness of experimental results given by Iosipescu test is often very high [21, 65, 66]. On the contrary, the corresponding measurement obtained with 10° off-axis test is less discrete but generally too small [66]. For example, the failure shear strain of a Kevlar/epoxy composite is 2.02% for Iosipescu test and 1.73% for ± 45° tension test, but is 1.03% for 10° off-axis tension test. Therefore, we have chosen two illustrations measured with the torsion [57] and ± 45° tension tests [67], to decrease measurement error.

Although the given shear strains of torsion and ± 45° tension are often close in value, the latter is considered to be better because of its easy operation and low standard deviation [66, 68]. According to references [66], for the same material, the coefficient of variation of failure shear strains given by repetitive torsion tests can be several times large as of that corresponding to ± 45° tension test. It means the measurements of AS4/8552 material system is more reliable (Fig. 13), of which our prediction is in very good agreement with the experimental data for the whole loading range. Considering the possible measurement error for the illustration of E-glass/epoxy composite (Fig. 14), simulation results calculated with FE codes have been studied as references [69,70,71]. The results of these simulations are coincided with the measured curve well, indicating that the data of E-glass/epoxy composite’s shear response is also credible. In summary, the results of illustrations in Fig. 13 and Fig. 14 can confirm the accuracy of our strain prediction model.

According to the illustrations, there are two potential application value of the method proposed in this paper. Compared with the macro-mechanical method, the micro-mechanical model only needs the original mechanical property data of component materials to predict the properties of composites, which can greatly reduce the testing cost. Besides, designing of a composite’s properties can be done according to the specific engineering requirements. As long as the component material performance database is established in advance, the mechanical properties of any composite produced with these component materials can be calculated directly through the explicit formula, with high efficiency. Another practical application of our theory is interface evaluation. The general interface strength test can only give a numerical value, which cannot characterize the performance of composite interface under a certain loading condition. On the contrary, with the new SCF and the interface slippage model, our theory can tell the discount of the material’s effective strength and rigidity due to interfacial debonding, giving guidance for interface modification according to the specific bearing condition of composite.

6 Conclusion

In this paper, a three-dimensional geometric model is developed to represent a composite containing both interfacial cracks and matrix shear cracks, and the in-plane shear SCF of the matrix in a composite with a debonded interface is derived. The research has the following main conclusions:

• 1. The discount of the in-plane shear strength due to the interface debonding is attributed to an increase of the stress concentration in the matrix. Thus, it is necessary to introduce SCFs when calculate the ultimate strengths of a composite.

• 2. The decrease of the effective in-plane shear stiffness after the debonding mainly comes from a relative slippage between the debonded matrix and fiber interfaces.

• 3. The interface debonding must be taken into consideration for predicting the strain of a composite under an arbitrary loading containing an in-plane shear stress component.

• 4. The main advantages of the method proposed in this paper includes that it needs less in-put data and minimum calculation, but can give a realistic physical model and reliable predictions. The accuracy of our predicting method can be further improved if the yield point of matrix can be located more precisely.

7 Data Availability Statements

All data generated or analyzed during this study are included in this published article (and its supplementary information files).

Appendices

Appendix A. Homogenized Internal Stresses by Bridging Model

For a UD composite with both fiber and matrix in an elastic deformation stage, the relationships between internal stresses of the fiber and matrix and the stresses applied on the composite are expressed as [42]

$$\left\{\sigma_i^f\right\}=\left(V_f\left[I\right]+V_m\left[A_{ij}\right]^{-1}\left\{\sigma_j\right\}\right)$$

(20)

$$\left\{\sigma_i^m\right\}=\left[A_{ij}\right]\left(V_f\left[I\right]+V_m\left[A_{ij}\right]\right)^{-1}\left\{\sigma_j\right\}$$

(21)

The first coordinate, x₁, is along the fiber axial direction. x₃ is along plate thickness directions. The arbitrary stress vector applied on the composite has six components as {σ_j} = {σ_11, σ_22, σ₃₃, σ₂₃, σ₁₃, σ₁₂}^T, and the vectors $\left\{\sigma_i^f\right\}$ and $\left\{\sigma_i^m\right\}$ have the same form. V_f and V_m (= 1-V_f) are the fiber and matrix volume fractions and [I] is a unit tensor. Explicit expressions for the bridging tensor [A_ij] in Eqs. (20) and (21) are given as [42]

$$\left[A_{ij}\right]=\begin{bmatrix}\alpha_{11}&\alpha_{12}&\alpha_{13}&0&0&0\\0&\alpha_{22}&0&0&0&0\\0&0&\alpha_{33}&0&0&0\\0&0&0&\alpha_{44}&0&0\\0&0&0&0&\alpha_{55}&0\\0&0&0&0&0&\alpha_{66}\end{bmatrix}$$

(22)

$$\alpha_{11}=\frac{E^m}{E_{11}^f}$$

(23)

$$\alpha_{22}=\alpha_{33}=\alpha_{44}=\beta+\left(1-\beta\right)\frac{E^m}{E_{22}^f}\;\left(0.3<\beta<0.6\right)$$

(24)

$$\alpha_{55}=\alpha_{66}=\alpha=\alpha+\left(1-\alpha\right)\frac{G^m}{G_{22}^f}\;\left(0.3<\alpha<0.6\right)$$

(25)

$$\alpha_{12}=\alpha_{13}=\frac{v_mE_{11}^f-E^mv_{12}^f}{E^m-E_{11}^f}\;\left(\alpha_{11}-\alpha_{22}\right)$$

(26)

In the equations above, $E_{11}^f$, $E_{22}^f$, $G_{12}^f$ and $v_{12}^f$ are, respectively, longitudinal, transverse and in-plane shear moduli, and longitudinal Poisson’s ratio of the fiber. E^m, G^m and ν^m are Young’s and shear moduli and Poisson’s ratio of the matrix. α and β are bridging parameters, which can be calibrated from comparison between the predicted in-plane shear and transverse Yong’s moduli of the composite, respectively. It is noted that

$$E_{22}=\frac{\left(V_f+V_m\alpha_{11}\right)\left(V_f+V_m\alpha_{22}\right)}{\left(V_f+V_m\alpha_{11}\right)\left(V_fS_{22}^f+\alpha_{22}V_mS_{22}^m\right)+V_fV_m\left(S_{21}^m-S_{21}^f\right)\alpha_{12}}$$

(27)

$$G_{12}=\frac{G_{12}^fG^m\left(V_f+V_m\alpha_{66}\right)}{V_fG^m+V_mG_{12}^f\alpha_{66}}$$

(28)

If no adjustment from an experiment is applicable, both α and β can be assumed to be 0.3 in most cases [42].

Appendix B. Expressions of Matrix SCFs

Definition of a SCF of the matrix in a composite is generally given by [23]

$$\begin{aligned}K_{ij}=\frac1{\left|\overrightarrow R^b-\overrightarrow R^\alpha\right|}\int_{\left|\overrightarrow R^\alpha\right|}^{\left|\overrightarrow R^b\right|}\frac{\widetilde\sigma_{ij}^m}{{\left(\widetilde\sigma_{ij}^m\right)}_{BM}}d\left|\overrightarrow R\right|\end{aligned}$$

(29)

$K_{ij}$ is the SCF related to $\sigma_{ij}^m$ or $d\sigma_{ij}^m\cdot{\left(\sigma_{ij}^m\right)}_{BM}$ is the matrix stress calculated from Bridging Model $\widetilde\sigma_{ij}^m$ and is a point-wise matrix stress generally obtained through an elasticity on a CCA (coaxial cylinder assemblage) model. $\overrightarrow R$ is a vector along a line perpendicular to the fracture surface of the composite under the given load. $\overrightarrow R^{a}$ and $\overrightarrow R^{b}$ are the vectors of ending at the surfaces of the fiber and matrix cylinders, respectively. a is the radius of the fiber. b and a are correlated as $b=\frac\alpha{\sqrt{V_f}}$. Explicit formulae for the SCFs of matrix in a composite are listed as follows [22,23,24].

The transverse tension SCF of the matrix having a perfect interface bonding with the fiber, $K_{22}^{t}$ is given by

$$K_{22}^t=\left[1+\frac{\sqrt{V_f}}2A+\frac{\sqrt{V_f}}2\left(3-V_f-\sqrt{V_f}\right)B\right]\frac{\left(V_f+0.3V_m\right)E_{22}^f+0.7V_mE^m}{0.3E_{22}^f+0.7E^m}$$

(30)

The expression of transverse compressive SCF of the matrix, $K_{22}^{c}$, is

$$\begin{aligned}K_{22}^c&=\Bigg\{\Bigg[1-A\sqrt{V_f}\frac{\sigma_{u,c}^m-\sigma_{u,t}^m}{4\sigma_{u,c}^m}+\frac B{2\left(1-\sqrt{V_f}\right)}\Bigg[-V_f^2\Bigg[1-2\left(\frac{\sigma_{u,c}^m-\sigma_{u,t}^m}{2\sigma_{u,c}^m}\right)^2\Bigg]{+} \\& \frac{\left(\sigma_{u,c}^m-\sigma_{u,t}^m\right)}{\sigma_{u,c}^m}\left(1+\frac{\sigma_{u,c}^m-\sigma_{u,t}^m}{\sigma_{u,c}^m}\right)-\sqrt{V_f}\Bigg[\frac{\sigma_{u,c}^m-\sigma_{u,t}^m}{\sigma_{u,c}^m}+1-2\left(\frac{\sigma_{u,c}^m-\sigma_{u,t}^m}{2\sigma_{u,c}^m}\right)^2\Bigg]\Bigg]\Bigg]\Bigg\} \\ &\frac{\left(V_f+0.3V_m\right)E_{22}^f+0.7V_mE^m}{0.3E_{22}^f+0.7E^m}\end{aligned}$$

(31)

$$A=\frac{2E_{22}^fE^m\left(V_{12}^f\right)^2+E_{11}^f\left\{E^m\left(V_{23}^f-1\right)-E_{12}^f\left[2\left(v^m\right)^2+v^m-1\right]\right\}}{E_{11}^f\left[E_{22}^f+E^m\left(1-v_{23}^f\right)+E_{22}^fv^m\right]-2E_{22}^fE^m\left(v_{12}^f\right)^2}$$

(32)

$$B=\frac{E^m\left(1+v_{23}^f\right)-E_{22}^f\left(1+v^m\right)}{E_{22}^f\left[v^m+4\left(v^m\right)^2-3\right]-E^m\left(1+v_{23}^f\right)}$$

(33)

$E_{11}^f$, $E_{22}^f$, and $G_{12}^f$ are, respectively, longitudinal, transverse, and in-plane shear moduli of the fiber, $v_{23}^f$is its transversal Poisson’s ratio, $v_{12}^f$ and is its longitudinal Poisson’s ratio. E^m and G^m are Young’s and shear moduli of the matrix, respectively, and ν^m is its Poisson’s ratio.

The formula of in-plane shear SCF of the matrix, is shown as

$$K_{12}=\left\{1-V_f\frac{G_{12}^f-G^m}{G_{12}^f+G^m}\left(W\left(V_f\right)-\frac13\right)\right\}\frac{V_f+A_{66}V_m}{A_{66}}$$

(34)

$$W\left(V_f\right)=\int\limits_0^a\frac1\alpha\sqrt{1-\frac{x_3^2}{\alpha^2}}\sqrt{\frac1{V_f}-\frac{x_3^2}{\alpha^2}}dx_3\approx\pi\sqrt{V_f}\left[\frac1{4V_f}-\frac4{128}-\frac2{512}V_f-\frac5{4096}V_f^2\right]$$

(35)

$G_{12}^f$ and G^m are the longitudinal shear moduli of the fiber and matrix, respectively.

Besides, the transverse tension SCF of the matrix after the interface debonding, is given by

$$\begin{aligned}\hat K_t^{22}=\hat K_t^{22}\left(\psi\right)=Re\Big\{e^{-2i\psi}M\left(be^{i\psi}\right)\left(\alpha^2/b-b\right)-e^{-2i\psi}\left(N_2-N_1\left(\frac{\alpha^2}be^{-i\psi}\right)\right)\\+e^{-i\psi}\left(2+e^{-2i\psi}\right)\left[N\left(be^{i\psi}\right)-N_3\right]\Big\}\frac{\left(V_f+0.3V_m\right)E_{22}^f+0.7V_mE^m}{2\left(b-a\right)\left(0.3E_{22}^f+0.7E^m\right)}\end{aligned}$$

(36)

The functions in Eq. (35), N, N₁, N₂ and N₃, are given by

$$N\left(z\right)=Fz+\frac{a^2k}z-\left(z-\alpha e^{i\psi}\right)^{0.5+i\lambda}\left(z-\alpha e^{i\psi}\right)^{0.5-i\lambda}\left[\left(F-0.5\right)-\frac D{\alpha^2z}\right]$$

(37)

$$N_1\left(z\right)=Fz+\frac{a^2k}z+\frac1\xi\left(z-\alpha e^{i\psi}\right)^{0.5+i\lambda}\left(z-\alpha e^{i\psi}\right)^{0.5-i\lambda}\left[\left(F-0.5\right)-\frac D{\alpha^2z}\right]$$

(38)

$$N_2=\alpha Fe^{-i\psi}+\alpha ke^{i\psi},\;N_3=Fae^{i\psi}+e^{-i\psi}\alpha k$$

(39)

$$M\left(z\right)=F\frac{\alpha^2k}{z^2}-\left[\left(F-0.5\right)z+H+\frac Cz+\frac D{z^2}\right]\chi\left(z\right)$$

(40)

$$F=\frac{1-\left[\cos\left(\psi\right)+2\lambda\sin\left(\psi\right)\right]\mathrm{exp}\left[2\lambda\left(\pi-\psi\right)\right]+\left(1-k\right)\left(1+4\lambda^2\right)\sin\left(\psi\right)}{{\displaystyle\frac4k}-2-2\left[\cos\left(\psi\right)+2\lambda\sin\left(\psi\right)\right]\mathrm{exp}\left[2\lambda\left(\pi-\psi\right)\right]}$$

(41)

$$H=\alpha\left(0.5-F\right)\left(\cos\left(\psi\right)+2\lambda\sin\left(\psi\right)\right)$$

(42)

$$C=\alpha^2\left(k-1\right)\left[\cos\left(\psi\right)-2\lambda\sin\left(\psi\right)\right]exp\left[2\lambda\left(\psi-\pi\right)\right]$$

(43)

$$D=\left(1-k\right)\alpha^3\mathrm{exp}\left[2\lambda\left(\psi-\pi\right)\right]$$

(44)

$$\chi\left(z\right)=\left(z-\alpha e^\psi\right)^{-0.5+i\lambda}\left(z-\alpha e^\psi\right)^{-0.5-i\lambda}$$

(45)

$$k=\frac{\mu_1\left(1+\kappa_2\right)}{\left(1+\xi\right)\left(\mu_1+\kappa_1\mu_2\right)}$$

(46)

$$\lambda=-\left(\ln\xi\right)/\left(2\pi\right),\;\xi=\left(\mu_2+\kappa_2\mu_1\right)/\left(\mu_1+\kappa_1\mu_2\right)$$

(47)

$$\kappa_1=3-4v^m,\;\kappa_2=\frac{3-v_{23}^f-4v_{12}^fv_{21}^f}{1+v_{23}^f}$$

(48)

$$\mu_1=\frac{E^m}{2\left(1+v^m\right)},\;\mu_2=\frac{E_{22}^f}{2\left(1+v_{23}^f\right)}$$

(49)

$$b=\alpha/\sqrt{V_f}$$

(50)

The debonding half angle, $\psi$ is the solution to the following equation [44]:

$$\mathrm{Re}{\left\{\left(G_0-\frac1k-\frac{2\left(1-k\right)}{k\;\mathrm{exp}\left(i\varphi\right)}\mathrm{exp}\left[2\lambda\left(\psi-\pi\right)\right]\right)R\left(e^{i\varphi}\right)\right\}}_{\varphi=\psi-\gamma}=0$$

(51)

$$R\left(exp\left(i\varphi\right)\right)=\left[exp\left(i\left(\varphi\right)\right)-e^{i\psi}\right]^{0.5+i\lambda}\left[exp\left(i\left(\varphi\right)\right)-e^{i\psi}\right]^{0.5-i\lambda}exp\left(-i\left(\varphi\right)\right)$$

(52)

$$G_0=\frac{1-\left[\cos\left(\psi\right)+2\lambda\sin\left(\psi\right)\right]\mathrm{exp}\left[2\lambda\left(\pi-\psi\right)\right]+\left(1-k\right)\left(1+4\lambda^2\right)\sin\left(\psi\right)}{2-k-k\left[\cos\left(\psi\right)+2\lambda\sin\left(\psi\right)\right]\mathrm{exp}\left[2\lambda\left(\pi-\psi\right)\right]}$$

(53)

$$\gamma=\left\{\begin{array}{l}\frac{2\lambda\left(J_1^2+J_2^2\right)}{J_1^2+J_2^2-2J_2J_3},\;if\;\xi<1\\-\frac{2\lambda\left(J_1^2+J_2^2\right)}{J_1^2+J_2^2-2J_2J_3},\;if\;\xi>1\end{array}\right.$$

(54)

$$J_1=kG_0-1-2\left(1-k\right)\xi\;\mathrm{exp}\left(2\lambda\psi\right)\cos\left(\psi\right)$$

(55)

$$J_2=2\left(1-k\right)\xi\;exp\left(2\lambda\psi\right)\;\sin\left(\psi\right)$$

(56)

$$J_3=2\left(1-k\right)\xi\;exp\left(2\lambda\psi\right)\left[J_1\;\cos\left(\psi\right)-J_2\;\sin\left(\psi\right)\right]/J_2$$

(57)

If = 1, no solution for $\psi$ is available, and the corresponding interface crack is singular. But, one can always adjust a fiber or matrix property so that 1, as deviation exists in measurement of it $v_{23}^f$. is the transverse Poisson’s ratio of the fiber. $\sigma_{u,\;t}^m,\;\sigma_{u,\;c}^m$, and $\sigma_{u,\;s}^m$ are, respectively, the matrix tensile, compressive and shear strengths.

Appendix C. Integration After Interface Debonding

For a certain longitudinal section located at $x_3=x_3^0,\alpha\leq x_3^0\leq b$, the length of the integration line between the starting and the ending points is $\sqrt{2\left[b^2-\left(x_3^0\right)^2\right]}$. Thus, the matrix shear SCF along this line is given by

$${\hat{K}}_{12\vert\psi=0.5\pi,a\leq x_3^0\leq b}=\frac{1}{\sqrt{2(b^2-{(x_3^0)}^2)}}\int\limits_0^{\sqrt{2(b^2-{(x_3^0)}^2)}}\frac{\sigma_{12}^m}{{(\sigma_{12}^m)}_{BM}}dS$$

(58)

Note that $b=a/ \sqrt{V_f}$, where V_f is the fiber volume fraction and S is along the integration line. In Eq. (57), ${\left(\sigma_{12}^m\right)}_{BM}$ is the matrix in-plane shear stress calculated through Bridging Model. is a point-wise stress in the matrix given by Eq. (7). Since dS equals (-$\sqrt2$  dx₂) on the integration line (the value of x₃ is a constant), the line integration of Eq.(57) is changed to (noticing that  $x_3^0=x_3$).

$${\hat K}_{12\vert\psi=0.5\pi,\;\alpha\leq x_3^0\leq b}=\frac1{\sqrt{b^2-\chi_3^2}}\int_{-\sqrt{b^2-\chi_3^2}}^0\frac{\sigma_{12}^m}{{\left(\sigma_{12}^m\right)}_{BM}}dx_2$$

(59)

Substituting ψ = 0.5π into Eq. (7), one has

$$\sigma_{12}^m=\sigma_{12}^0\;Re\left\{\frac{G^m}{G^m+G_{12}^f}\left(1-\frac{a^2}{z^2}\right)+\frac{G_{12}^f}{G^m+G_{12}^f}\left(z-ai\right)^{-0.5}\left(z+ai\right)^{-0.5}\left(z-\frac{a^3}{z^2}\right)\right\}$$

(60)

Replacing z in Eq. (59) with x₂ + ix₃ and taking the integration along the x₂ axis gives

$$\begin{aligned}&\int_{-\sqrt{b^2-x_3^2}}^0\;\sigma_{12}^mdx_2\\&=\sigma_{12}^0\;\int_{-\sqrt{b^2-x_3^2}}^0\;Re\left\{\frac{G^m}{G^m+G_{12}^f}\left[1-\frac{\alpha^2}{\left(x_2+x_3i\right)^2}\right]+\frac{G_{12}^f}{G^m+G_{12}^f}N\left(x_2+x_3i\right)\right\}dx_2\end{aligned}$$

(61)

$$N\left(x_2+x_3i\right)=\chi\left(x_2+x_3i\right)\left(x_2+x_3i-\frac{\alpha^3}{\left(x_2+x_3i\right)^2}\right)$$

(62)

$$\chi\left(x_2+x_3i\right)=\chi\left(x_2+x_3i+\alpha i\right)^{-0.5}\left(x_2+x_3i-\alpha i\right)^{-0.5}$$

(63)

Now let us derive the integration on the function N with respect to $x_{2}$ 

Setting $R_0\left(x_2\right)=\left(x_2+x_3i-\alpha i\right)^{0.5}\left(x_2+x_3i-\alpha i\right)^{0.5}$, its derivative with respect to $x_{2}$ is

$$\begin{aligned}&\frac{dR_0}{dx_2}=\frac{d\left[\left(x_2+x_3i-\alpha i\right)^{0.5}\left(x_2+x_3i+\alpha i\right)^{0.5}\right]}{dx_2}=0.5\times\frac{\left(x_2+x_3i+\alpha i\right)^{0.5}}{\left(x_2+x_3i-\alpha i\right)^{0.5}}+0.5\frac{\left(x_2+x_3i-\alpha i\right)^{0.5}}{\left(x_2+x_3i+\alpha i\right)^{0.5}}\\&=\frac{x_2+x_3i}{\left(x_2+x_3i-\alpha i\right)^{0.5}\left(x_2+x_3i+\alpha i\right)^{0.5}}=\left(x_2+x_3i\right)\chi\left(x_2+x_3i\right)\end{aligned}$$

(64)

Similarly, setting $R_1\left(x_2\right)=\frac{\alpha\left(x_2+x_3i-\alpha i\right)^{0.5}\left(x_2+x_3i+\alpha i\right)}{x_2+x_3i}$ and taking a derivative with respect to $x_{2}$ results in

$$\begin{aligned}&\frac{dR_1}{dx_2}=d\left[\frac{\left(x_2+x_3i-\alpha i\right)^{0.5}\left(x_2+x_3i+\alpha i\right)^{0.5}}{x_2+x_3i}\right]/dx_2\\&=\frac{\alpha\left(x_2+x_3i-\alpha i\right)^{0.5}\left(x_2+x_3i+\alpha i\right)^{0.5}}{\left(x_2+x_3i\right)^2}+\frac\alpha{x_2+x_3i}\frac{d\left[\left(x_2+x_3i-\alpha i\right)^{0.5}\left(x_2+x_3i+\alpha i\right)^{0.5}\right]}{dx_2}\\&=\frac{\alpha\left(x_2+x_3i-\alpha i\right)^{0.5}\left(x_2+x_3i+\alpha i\right)^{0.5}}{\left(x_2+x_3i\right)^2}+\frac\alpha{\left(x_2+x_3i-\alpha i\right)^{0.5}\left(x_2+x_3i+\alpha i\right)^{0.5}}\\&=\frac\alpha{\left(x_2+x_3i\right)^2}\chi\left(x_2+x_3i\right)\end{aligned}$$

(65)

Based on Eqs. (63) and (64), one can obtain that

$$\int_{-\sqrt{b^2-x_3^2}}^0\;N\left(x_2+x_3i\right)dx_2=\mathrm{Re}\left[R_0\left(x_2\right)+R_1\left(x_2\right)\right]\;\left|\begin{array}{c}0\\-\sqrt{b^2-x_3^2}\end{array}\right.$$

(66)

Therefore, the integration on Eq. (60) is found to be

$$\begin{array}{l}\int_{-\sqrt{b^2-x_3^2}}^0\sigma_{12}^mdx_2=\sigma_{12}^0\left\{\frac{G^m}{G^m+G_{12}^f}\left(x_2+\frac{x_2\alpha^2}{x_2^2+x_3^2}\right)+\frac{G_{12}^f}{G^m+G_{12}^f}\mathrm{Re}\left[R_0\left(x_2\right)+R_1\left(x_2\right)\right]\right\}\vert_{-\sqrt{b^2-x_3^2}}^0\\=\sigma_{12}^0\left\{\frac{G^m\left(1+V_f\right)}{G^mG_{12}^f}\sqrt{b^2-x_3^2}+\frac{G_{12}^f}{G^mG_{12}^f}\mathrm{Re}\lbrack\frac{\alpha+x_3i}{x_3i}\left(x_3i-\alpha i\right)^{0.5}\left(x_3i-\alpha i\right)\right. \\ \left.-(1+\frac\alpha{-\sqrt{b^2-x_3^2+x_3i}})\left(-\sqrt{b^2-x_3^2}+x_3i-\alpha i\right)^{0.5}\rbrack\right\}\end{array}$$

(67)

Substituting Eq. (66) into Eq. (58), one obtains

$$\begin{array}{l}{\hat K}_{12\vert\psi=0.5\pi,\;\alpha\leq x_3^0\leq b}=\frac{\sigma_{12}^0}{{\left(\sigma_{12}^m\right)}_{BM}\sqrt{b^2-x_3^2}}\{\frac{G^m\left(1+V_f\right)}{G^m+G_{12}^f}\sqrt{b^2-x_3^2}\\+\frac{G_{12}^f}{G^m+G_{12}^f}Re\lbrack\left(1+\frac\alpha{x_3i}\right)\left(x_3i-\alpha i\right)^{0.5}\left(x_3i+\alpha i\right)^{0.5}\\-(1+\frac\alpha{-\sqrt{b^2-x_3^2+x_3i}})\left(-\sqrt{b^2-x_3^2}+x_3i-\alpha i\right)^{0.5}\rbrack\}\end{array}$$

(68)

It should be noted that Eq. (67) is obtained only for a particular longitudinal cross-section. As done in Ref. [44], the matrix in-plane shear SCF must be determined based on an average along the thickness direction from to. This gives rise to

$${\hat K}_{12}=\frac{\int_\alpha^b{\hat K}_{12\vert\psi=0.5\pi,\;\alpha\leq x_3^0\leq b}dx_3^0}{b-\alpha}=\frac{\int_\alpha^b\lbrack\int_{-\sqrt{b^2-x_3^2}}^0\sigma_{12}^m\left(x_2,x_3\right)dx_2/\sqrt{b^2-x_3^2}\rbrack dx_3}{\left(b-\alpha\right){\left(\sigma_{12}^m\right)}_{BM}}$$

(69)

Letting $m=-\sqrt{b^2-x_3^2}+x_3i$ and $R_2=-\left(\sqrt{b^2-x_3^2}+x_3i-\alpha i\right)^{0.5}\left(-\sqrt{b^2-x_3^2}+x_3i-\alpha i\right)^{0.5}=\left(m-\alpha i\right)^{0.5}\left(m+\alpha i\right)^{0.5}$

Eq. (68) is changed to

$$\begin{array}{l}{\hat K}_{12}=\frac{\delta_{12}^0}{\left(b-\alpha\right){\left(\sigma_{12}^m\right)}_{BM}}\int\limits_a^b\{\frac{G^m}{G^m+G_{12}^f}\left(1+V_f\right)+\frac{G_{12}^f}{G^m+G_{12}^f}\mathrm{Re}\lbrack\frac{\alpha+x_3^2}{x_3i\sqrt{b^2-x_3^2}}\left(x_3i-\alpha i\right)^{0.5}\left(x_3i+\alpha i\right)^{0.5}\\-(\frac{R_2}{\sqrt{b^2-x_3^2}}+\frac{\alpha R_2}{\sqrt{b^2-x_3^2}(-\sqrt{b^2-x_3^2}+x_3i)})\rbrack\}dx_3\end{array}$$

(70)

The expression in Eq. (70) containing R₂ is hard to integrate, and must be converted into a function of m. However, $(m-\alpha{i})^{0.5}(m+\alpha{i})^{0.5}$ might equal to $(m^{2}+\alpha^{2})^{0.5}$ or $-(m^{2}+\alpha^{2})^{0.5}$. We need to choose the correct form within the integration range. Because x₃ ∈ [a, b], the phase angles of $(m-\alpha{i})$ and $(m+\alpha{i})$ are within [0.5π, π]. Thus, the phase angles of both and are in between [0.25π, 0.5π]. Hence, the phase angle of is in the second quadrant, indicating that its imaginary part is positive.

As $(m^2+\alpha^2)^{0.5}=({(b^2-2x_3^2+\alpha^2)-2x_3i\sqrt{b^2-x_3^2})}^{0.5}$ and $\mathrm{Im}(-2x_3i\sqrt{b^2-x_3^2})<0$, the phase angle of $(b^2-x_3^2+\alpha^2)-2x_3i\sqrt{b^2-x_3^2}$ is in between -π and 0. The corresponding square root is within [-0.5π,0], and the imaginary part of $(m^2+\alpha^2)^{0.5}$ is negative. Overall, for x₃ ∈ [a, b] and $m=-\sqrt{b^2-x_3^2}+x_3i$, one has $(m-\alpha{i})^{0.5}(m+\alpha{i})^{0.5}=-(m^2-\alpha{2})^{0.5}$ 

Next, from $\frac{dm}{dx_3}=\frac{x_3}{\sqrt{b^2-x_3^2}}+i=\frac{x_3+i\sqrt{b^2-x_3^2}}{\sqrt{b^2-x_3^2}}=\frac{x_3-i\sqrt{b^2-x_3^2}}{\sqrt{b^2-x_3^2}}=\frac m{i\sqrt{b^2-x_3^2}}$, one derives

$$\begin{array}{l}\int_\alpha^b\mathrm{Re}\left\{\frac{R_2\left(x_3\right)}{\sqrt{b^2-x_3^2}}\right\}dx_3=\mathrm{Re}\left\{\int_\alpha^b\frac{-\left(m^2+\alpha^2\right)^{0.5}}{\sqrt{b^2-x_3^2}}dx_3\right\}=\mathrm{Re}\left\{\int_{-\sqrt{b^2-\alpha^2+\alpha i}}^{bi}\frac{-i\left(m^2+\alpha^2\right)^{0.5}}mdm\right\}\\=-\mathrm{Re}\left\{i\left(m^2+\alpha^2\right)^{0.5}+\alpha\;\ln\frac{\left(m^2+\alpha^2\right)^{0.5}-\alpha}{\left|m\right|}\left|\begin{array}{c}bi\\-\sqrt{b^2-\alpha^2}+\alpha i\end{array}\right.\right\}=-Re\left\{i\lbrack\left(b^2-\alpha^2-2\alpha i\sqrt{b^2-\alpha^2}\right)^{0.5} \right.\\ \left. +\alpha\;\ln\frac{\left(b^2-\alpha^2-2\alpha i\sqrt{b^2-\alpha^2}\right)^{0.5}-\alpha}b-i\left(\alpha^2-b^2\right)^{0.5}-\alpha\;\ln\frac{\left(\alpha^2-b^2\right)^{0.5}-\alpha}b\rbrack\right\}\end{array}$$

(71)

Similarly, 

$$\begin{aligned}&\int_\alpha^b\frac{\alpha R_2\left(x_3\right)}{\left(-\sqrt{b^2-x_3^2+x_3i}\right)\sqrt{b^2-x_3^2}}dx_3=\mathrm{Re}\;\int_{-\sqrt{b^2-\alpha^2+\alpha i}}^{bi}\;\frac{-\alpha\left(m^2+\alpha^2\right)^{0.5}}{m^2}dm\\&=\mathrm{Re}\left\{-\alpha i\lbrack-\left(1+\frac{\alpha^2}{m^2}\right)^{0.5}+\ln({(m^2+\alpha^2)}^{0.5}+m)\rbrack\; \Bigg|\begin{array}{c}bi\\-\sqrt{b^2-\alpha^2+\alpha i}\end{array}\right\}\\&=\mathrm{Re}\left\{\alpha i\lbrack\ln\left(\left(b^2-\alpha^2-2\alpha i\sqrt{b^2-\alpha^2}\right)^{0.5}-\sqrt{b^2-\alpha^2}+\alpha i\right)\right. \\ &\left. -(1+\frac\alpha{-\sqrt{b^2-x_3^2+x_3i}})\left(-\sqrt{b^2-x_3^2}+x_3i-\alpha i\right)^{0.5}\rbrack\right\}\end{aligned}$$

(72)

Now, let us derive the integration for the other part of Eq. (68), which contains

$$Re\left\{\left(\frac{\alpha+x_3i}{x_3i\sqrt{b^2-x_3^2}}\right)^{0.5}\left(x_3i-\alpha i\right)^{0.5}\left(x_3i+\alpha i\right)^{0.5}\right\}$$

(73)

As $\left(x_3i-\alpha i\right)^{0.5}\left(x_3i+\alpha i\right)^{0.5}=i\sqrt{x_3^2-\alpha^2}$, Eq. (73) equals to $\frac{\alpha\sqrt{x_3^2-}\alpha^2}{x_3\sqrt{b^2}-x_3^2}$ 

The integration on Eq. (73) becomes

$$\int\limits_a^b\frac{a\sqrt{x_3^2-a^2}}{x_3\sqrt{b^2-x_3^2}}dx_3=-\int\limits_{\sqrt{b^2-a^2}}^{0}\frac{a\sqrt{x_3^2-a^2}}{x_3^2}d(\sqrt{b^2-x_3^2})=\int\limits_0^{\sqrt{b^2-a^2}}\frac{a\sqrt{b^2-a^2-x^2}}{b^2-x^2}dx$$

(74)

In order to get the explicit integral expression, the parameter $x(0\leq x\leq\sqrt{b^2-\alpha^2})$ in Eq. (74) is replaced with $(\sqrt{b^2-\alpha^2}\sin\left(\theta\right),\;0\leq\theta\leq0.5\pi)$. It becomes

$$\begin{aligned}&\int\limits_0^{\sqrt{(b^2-a^2)}}\frac{a\sqrt{(b^2-a^2)(1-\sin^2(\theta))}}{b^2-(b^2-a^2)\sin^2(\theta)} d{\sqrt{(b^2-a^2)}\sin(\theta)}=a\int\limits_0^{\frac{\pi}{2}}\frac{(b^2-a^2)\cos^2(\theta)}{a^2+(b^2-a^2)\cos^2(\theta)} \\ &=\int\limits_0^{\frac{\pi}{2}}a\lbrack1-\frac{2a^2}{2a^2+(b^2-a^2)(1+\cos(2\theta))}\rbrack d\theta\\ &=\frac{a\pi}2-\int\limits_0^{\frac{\pi}{2}}\lbrack\frac{a^2}{(b^2-a^2)\cos(\theta)+(b^2+a^2)}\rbrack d\theta\end{aligned}$$

(75)

Making use of the integral formula

$\int\frac1{\alpha+b\;\cos\left(x\right)}d\left(x\right)=\frac2{\alpha+b}\sqrt{\frac{\alpha+b}{\alpha-b}}\;{\mathrm{arc}\tan}\left(\sqrt{\frac{\alpha-b}{\alpha+b}}\tan\frac x2\right)$,

Eq. (75) is simplified to $\frac{\alpha\pi}2-\alpha\left[\sqrt{V_f}\;arc\tan\left(\sqrt{V_f}\;\tan\frac\theta2\right)\right]\left|\begin{array}{c}\pi\\0\end{array}=\right.\frac{\alpha\pi}2\left(1-\sqrt{V_f}\right).$ 

Combining Eqs. (67), (70), (71), (72) and (75), one finally obtains the expression of the in-plane shear SCF with debonded interface as Eq. (8).