1 Introduction

Owing to their excellent mechanical properties at elevated temperatures, SiC/SiC composites offer promise for aeronautical and astronautic high-temperature applications [1, 2]. Strength is one of the key properties of SiC/SiC composites since the strength affects the judgment on the failure of a structure. Considering the varying working temperature in the aeronautical and astronautic applications, e.g., turbine blades of aero-engines, it is essential to obtain the influence of the temperature on the strength of SiC/SiC composites i.e., the temperature sensitivity.

Many researchers have studied the influence of temperature. Guo et al. [3] carried out tensile tests on plain-woven SiC/SiC composites between 298 and 1400 K and found that the strength remained nearly constant up to 800 K and dropped significantly at 1200 K. Jing et al. [4] performed tensile tests on 3D four-directional SiC/SiC composites at room and elevated temperatures. The result showed a big decline of strength from a room temperature value of 350 MPa to 220 and 200 MPa at 1100 ℃ and 1300 ℃. Zhang et al. [5] also found that the tensile strength of 3D SiC/SiC composites showed a significant decline from room temperature to elevated temperatures.

In the above works, the tests were all carried out in the air, and the decline of strength at elevated temperatures was mainly induced by oxidation [4]. To investigate the influence of the temperature itself, the high-temperature strength in an oxygen-free environment should also be obtained since the strengths in oxidation and oxygen-free environments vary greatly [6]. However, little research has been done into the sensitivity of strength via temperature for SiC/SiC composites in an oxygen-free environment due to the experimental difficulties.

Besides the experimental study, the theoretical analysis of the temperature sensitivity is also important. Guo et al. [3, 7, 8], Jing et al. [4] and Deng et al. [9] developed respective temperature-dependent strength models to analyze the temperature sensitivity. In their models, the strength of SiC/SiC composites is predicted based on that of SiC fibers. As the reinforcement, the strength of SiC fiber has a great influence on that of the SiC/SiC composites. Therefore, in the above models, the variation of the fiber strength at different temperatures is considered. Due to the random flaws in fibers, the strength of a single fiber is stochastic which means that the statistical strength distribution of fibers should be obtained.

The strength distribution of SiC fibers at room temperature has been studied sufficiently. Kotani et al. [10], Wu et al. [11] and Chen et al. [12] have performed tests at room temperature and found that the fiber strength follows a Weibull distribution. For the high-temperature problems, most of the studies focus on the effects of heat treatment on the strength of SiC fibers [13,14,15]. However, the heat-treated fibers are all tested at room temperature in these works. The strength distribution of the heat-treated fibers at room temperature is not equal to that of the as-received fibers at elevated temperatures and the obtained strength properties cannot be used to predicted the high-temperature strength of SiC/SiC composites.

In fact, the strength property of fibers at elevated temperatures is difficult to obtain. In the above literature [3, 4, 7,8,9], the strength of a single SiC fiber is determined from its high-temperature fracture surface and then the strength distribution is obtained. According to this method, the strength of a single fiber S can be determined by the radius of the smooth mirror region rm on its fracture surface.

$$S = \frac{{{A_{\text{m}}}}}{{\sqrt {r_m} }}$$
(1)

where Am is an empirical constant. However, the boundary of the smooth mirror region is not always distinct [16] and the empirical constant Am cannot be determined exactly which makes the strength distribution obtained not precise enough. Pysher et al. [17] performed single fiber tensile tests at elevated temperatures. However, only the average fiber strength was obtained by them. This is because that a large number of samples are needed to determine the distribution character [16] which are difficult to obtain considering the time-consuming single fiber tests at elevated temperatures.

In summary, the sensitivity of strength via temperature for SiC/SiC composites and SiC fibers in an oxygen-free environment is not explicit. In the present work, the temperature sensitivity is studied through experimental and theoretic methods. A new precise and efficient method is developed to obtain the strength distribution of SiC fibers at elevated temperatures. Tensile tests are performed on the SiC/SiC minicomposites and SiC fiber bundles at different temperatures in an oxygen-free environment. The sensitivity of strength via temperature for SiC/SiC minicomposites and Weibull parameters of SiC fibers are then obtained. The fracture model of minicomposites is developed based on which the temperature sensitivity is analyzed theoretically.

2 Material and Experimental Procedure

2.1 Material

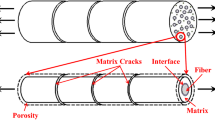
The SiC/SiC minicomposites are used in the present study to investigate the temperature sensitivity. A SiC/SiC minicomposite is defined as the combination of a SiC fiber bundle, the SiC matrix that surrounds the fibers and the interphase between the fiber and the matrix [18,19,20]. Due to their relatively simple architecture (see Fig. 1a) and micromechanical model, minicomposites are an appropriate choice for the study of the temperature sensitivity for SiC/SiC composites. The SiC/SiC minicomposites in the present study are manufactured using the chemical vapor infiltration (CVI) process where the pyrocarbon interphase and SiC matrix are deposited onto the SiC fiber bundle. The data for the material properties of the SiC/SiC minicomposites are listed in Table 1. Here, subscripts f and m denote the fiber and matrix, respectively. Additionally, E is the elasticity modulus, v is the volume fraction, α is the thermal expansion coefficient, r is the diameter, τ is the interfacial shear stress and ΔT is the difference between room temperature and the operation temperature.

Fig. 1
figure 1

Specimen of SiC/SiC minicomposite (a) and SiC fiber bundle (b)

Full size image
Table 1 Material properties of SiC/SiC minicomposites
Full size table

The SiC fibers are provided by Fujian Leadasia New Material Co., Ltd. with a trade name of Cansas-3203. These fibers are manufactured using the preceramic polymer pyrolysis process and are a type of low-oxygen and high-carbon fibers. The general properties are listed in Table 2. Note that the fiber bundles are not resin-impregnated to make the single fibers independent of each other. As shown in Fig. 1b, both ends of the fiber bundle specimen are glued into an aluminum tube using epoxy adhesive (Model DP760, 3 M Company, St. Paul, MN, USA). The gage length of the specimen is 100 mm.

Table 2 Properties of the Cansas-3203 fibers
Full size table

2.2 Tensile Test of Minicomposites and Fiber Bundles

Due to the similar shapes of specimens, monotonic tensile tests of minicomposites and fiber bundles are performed using the same test system. As shown in Fig. 2, the whole test system is composed of an electronic testing machine, a high-temperature furnace and a vacuum chamber. The electronic testing machine is used to apply the tensile load on the specimen and measure the load and the deformation. The high-temperature furnace can heat the specimen and the vacuum chamber can ensure a vacuum degree of 10–3 Pa and therefore avoid the oxidation of the specimen at elevated temperatures. The tensile test is under a constant displacement rate of 0.1 mm/min. The strain of the specimen is calculated based on the cross-head displacement. The stress–strain responses of SiC/SiC minicomposites and SiC fiber bundles at room temperature, 500 and 1000 ℃ are obtained.

Fig. 2
figure 2

High-temperature and oxygen-free tensile test system

Full size image

3 Determination of Fiber Strength Distribution

The commonly used Weibull model [21,22,23,24,25] which is based on the hypothesis of the weakest link is used in the present study to describe the strength distribution of SiC fibers. For a two-parameter Weibull model, the probability that a fiber fractures is

$$P = 1 - \exp \left[ { - \frac{{{L_{\text{f}}}}}{{L_0}}{{\left( {\frac{\sigma }{{\sigma_0}}} \right)}^m}} \right]$$
(2)

where Lf is the length of the fiber, L0 is the reference length taken to be 1 m and σ is the fiber stress. σ0 and m are the statistical parameters and they reflect the characteristic of the fiber strength distribution.

For a SiC fiber bundle, if the strain is εb, the stress in a single fiber is

$$\sigma = {\varepsilon_{\text{b}}}{E_{\text{f}}}$$
(3)

where Ef is the elastic modulus of the SiC fiber. Then the stress of the fiber bundle is

$${\sigma_{\text{b}}} = \sigma \left( {1 - P} \right) = {\varepsilon_{\text{b}}}{E_{\text{f}}}\exp \left[ { - \frac{{{L_{\text{f}}}}}{{L_0}}{{\left( {\frac{{{\varepsilon_{\text{b}}}{E_{\text{f}}}}}{{\sigma_0}}} \right)}^m}} \right]$$
(4)

Equation (4) is the equation of the stress–strain curve of the fiber bundle and it reveals that the Weibull parameters can be derived from some feature points of the stress–strain curve. The ultimate strength of the fiber bundle can be determined by taking the derivative of Eq. (4).

$${\sigma ^{\prime}_{\text{b}}}\left( {{\varepsilon_{\text{b}}}} \right) = {E_{\text{f}}}\exp \left[ { - \frac{{{L_{\text{f}}}}}{{L_0}}{{\left( {\frac{{{\varepsilon_{\text{b}}}{E_{\text{f}}}}}{{\sigma_0}}} \right)}^m}} \right]\left[ {1 - \frac{{{L_{\text{f}}}}}{{L_0}}m{{\left( {\frac{{{\varepsilon_{\text{b}}}{E_{\text{f}}}}}{{\sigma_0}}} \right)}^m}} \right]$$
(5)

Setting \({\sigma ^{\prime}_{\text{b}}}\left( {{\varepsilon_{\text{b}}}} \right) = 0\) and then the extreme point \(\left( {\varepsilon_{\text{b}}^*,\sigma_{\text{b}}^*} \right)\) of the stress–strain curve is derived.

$$\left\{ \begin{gathered} \varepsilon_{\text{b}}^* = \frac{{\sigma_0}}{{{E_{\text{f}}}}}{\left( {\frac{{L_0}}{{m{L_{\text{f}}}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m}}} \hfill \\ \sigma_{\text{b}}^* = {\sigma_0}{\left( {\frac{{L_0}}{{m{L_{\text{f}}}}}} \right)^{{1 \mathord{\left/ {\vphantom {1 m}} \right. \kern-\nulldelimiterspace} m}}}\exp \left( { - \frac{1}{m}} \right) \hfill \\ \end{gathered} \right.$$
(6)

Therefore, the Weibull parameters σ0 and m can be determined from the coordinate of the extreme point (see Fig. 3) and the initial slope of the stress–strain curve of the fiber bundle according to Eq. (6). The flow of determination of the fiber strength distribution is shown in Fig. 4.

Fig. 3
figure 3

Extreme point of the stress–strain curve

Full size image
Fig. 4
figure 4

Flow of determination of the fiber strength distribution

Full size image

4 Prediction of the Strength for Minicomposites

The strength distribution of SiC fibers obtained above can be used to predict the mechanical behavior of SiC/SiC minicomposites. According to the shear-lag theory [26], the stress distributions of an intact and broken fiber in minicomposites are presented in Fig. 5 and Eqs. (7) and (8).

$$\left\{ \begin{gathered} \frac{d\sigma \left( x \right)}{{dx}} = \frac{2\tau }{{{r_{\text{f}}}}},L/2 - d \leqslant \left| x \right| \leqslant L/2 \hfill \\ \sigma \left( x \right) = {\sigma_{{\text{f}}0}}, \, \left| x \right| \leqslant L/2 - d \hfill \\ \end{gathered} \right.$$
(7)
$$\left\{ \begin{gathered} \frac{d\sigma \left( x \right)}{{dx}} = \frac{2\tau }{{{r_{\text{f}}}}} \hfill \\ \sigma \left( x \right) = 0,x = L/2 - {L_{{{\text{b}}_i}}} \, \hfill \\ \end{gathered} \right.$$
(8)
Fig. 5
figure 5

Stress distributions in an intact fiber (a) and a broken fiber (b)

Full size image

where σf0 is the fiber normal stress if the composite is undamaged, L is matrix crack spacing, d is the length of the debonded region and \({L_{{{\text{b}}_i}}}\) is the distance from the matrix crack plane to the nearest fiber break plane as shown in Fig. 5b.

With the stress distributions of intact and broken fibers, the average stress of the minicomposite on any matrix crack plane can be derived.

$${\overline \sigma_{\text{c}}} = \frac{{{v_{\text{f}}}}}{N}\sum\limits_{i = 1}^N {\sigma_{\text{f}}^i}$$
(9)
$$\sigma_{\text{f}}^i = \left\{ \begin{gathered} \frac{\sigma }{{{v_{\text{f}}}}},{\text{intact fiber}} \hfill \\ \min \left( {\frac{\sigma }{{{v_{\text{f}}}}},\frac{2\tau }{{{r_{\text{f}}}}}{L_{{{\text{b}}_i}}}} \right),{\text{broken fiber}} \hfill \\ \end{gathered} \right.$$
(10)

where N is the total amount of fibers in the minicomposite, \(\sigma_{\text{f}}^i\) is the normal stress of the ith fiber in a matrix crack plane. \(L_{b_i}\) is obtained by the stress distribution in Fig. 5a and the strength distribution of the fiber. As shown in Fig. 5, each single fiber is divided into many segments and each segment is a fiber element. To determine the location of the fiber break, i.e., whether a fiber element will break, a random number is first generated computationally. If the random number is less than the probability P, the fiber element breaks.

The average strain of the minicomposite is equivalent to that of the intact fiber.

$$\begin{aligned}{{\bar \varepsilon }_{\text{c}}} & = {{\bar \varepsilon }_{\text{f}}} \\& = \frac{2}{{{E_{\text{f}}}L}}\int_0^{L/2} {{\sigma_{\text{f}}}\left( x \right)dx} + \left( {{\alpha_{\text{f}}} - {\alpha_{\text{c}}}} \right)\Delta T \\& = \frac{2}{{{E_{\text{f}}}L}}\left[ {\int_0^{L/2 - d} {{\sigma_{{\text{f0}}}}dx} + \int_{L/2 - d}^{L/2} {\left( {\frac{\sigma }{{{v_{\text{f}}}}} + \frac{2\tau }{{{r_{\text{f}}}}}\left( {x - \frac{L}{2}} \right)} \right)dx} } \right] + \left( {{\alpha_{\text{f}}} - {\alpha_{\text{c}}}} \right)\Delta T \\& = \frac{2}{{{E_{\text{f}}}L}}\left[ {\frac{\sigma }{{{v_{\text{f}}}}}d - \frac{\tau }{{{r_{\text{f}}}}}{d^2} + {\sigma_{{\text{f0}}}}\left( {\frac{L}{2} - d} \right)} \right] + \left( {{\alpha_{\text{f}}} - {\alpha_{\text{c}}}} \right)\Delta T \\ \end{aligned}$$
(11)

where the matrix crack spacing L is determined from the matrix cracking model in the literature [16].

$$\frac{1}{L} = \frac{1}{{{L_{{\text{sat}}}}}}\left\{ {1 - \exp \left[ { - {{\left( {\frac{\sigma }{{{\sigma_{{\text{m}}0}}}}} \right)}^{{m_{\text{m}}}}}} \right]} \right\}$$
(12)

where Lsat is the saturated matrix crack spacing, and σm0 and mm are the statistical parameters. In the present study, Lsat = 3.3 mm, σm0 = 600 MPa and mm = 5. The flow of determination of the minicomposites strength is shown in Fig. 6.

Fig. 6
figure 6

Flow of determination of the minicomposites strength

Full size image

5 Results and Discussion

5.1 Test Results of Minicomposites and Fiber Bundles

Figure 7 shows the stress–strain responses of SiC/SiC minicomposites and SiC fiber bundles at different temperatures obtained through the tensile tests in Sect. 2.2. The stress–strain curve of SiC/SiC minicomposites can be divided into three parts, i.e., the initial linear part, the nonlinear part and the second linear part. At a low-stress level, the fibers and matrix in minicomposites are nearly undamaged which matches the initial linear part. The nonlinearity is caused by the matrix cracking and the fiber/matrix interfacial debonding. In the second linear part, the stress–strain curve recovers its linearity due to the saturation of matrix cracks and the completely debonded interface.

Fig. 7
figure 7

Stress–strain response of SiC/SiC minicomposites (a) and SiC fiber bundles (b)

Full size image

The stress–strain curve of SiC fiber bundles can also be divided into three parts: the initial linear part, the nonlinear part and the decline part. The nonlinear response and the decrease of stress are both caused by the gradual fracture of single fibers. At the beginning of the tensile test, all the single fibers are intact owing to the low-stress level and therefore the fiber bundle exhibits linearity. When the stress increased, single fibers begin to fracture gradually due to their stochastic strengths. This stage matches the nonlinear part of the stress–strain curve. With the further increase of the number of fractured single fibers, the loading capacity of the fiber bundle declines significantly and the stress of the fiber bundle begins to decrease. This stage matches the decline part of the stress–strain curve.

The strength retentions at different temperatures are listed in Table 3. As shown in Table 3, the temperature sensitivity of minicomposites and fibers varies greatly. The strength of SiC/SiC minicomposites and SiC fiber bundles both decrease as the increase in temperature, but their strength retentions are different and are 94% and 67% at 1000 ℃, respectively. Then, a question is brought up: why the temperature has a significant effect on the strength of the fiber but nearly does not affect the minicomposites? The mechanism will be explained in Sect. 5.3.

Table 3 Strength retentions at different temperatures
Full size table

5.2 Effects of Temperature On the Strength Distribution of SiC Fibers

Figure 8 shows the Weibull parameters of SiC fibers at different temperatures determined by the stress–strain response of fiber bundles and the method in Sect. 3. The temperature has a significant influence on the strength distribution of SiC fibers. As shown in Fig. 8, the Weibull parameters σ0 and m both decrease as the temperature increases. Note that m is the shape parameter and that a higher m means better uniformity. Therefore, the scatter of the strength of SiC fibers is aggravated at higher temperatures. The large scatter results from the new flaws in SiC fibers induced by the high temperature. Note that there are impurities, e.g., oxygen in SiC fibers. At elevated temperatures, the escape and decomposition reactions of the impurities can induce surface flaws in fibers. On the other hand, the crystallization of the amorphous phase and grain growth of fine grains [11, 12, 27] at elevated temperatures can also decrease the average strength and aggravate the scatter of the strength of SiC fibers.

Fig. 8
figure 8

Weibull parameters at different temperatures

Full size image

To verify the accuracy of the determined strength distribution, the stress–strain responses of SiC fiber bundles are simulated according to Eq. (4) and the derived Weibull parameters. As shown in Fig. 9, the simulated stress–strain curves at different temperatures are in good agreement with the experimental results which verifies the accuracy of the method. Moreover, compared with the single fiber tensile test [17], the present method is more efficient and more appropriate to obtain the strength distribution at elevated temperatures.

Fig. 9
figure 9

Simulated stress–strain responses of SiC fiber bundle

Full size image

A comparison between the predicted stress–strain responses and strengths of SiC/SiC minicomposites and the experimental results at different temperatures are presented in Fig. 10 and Table 4. The prediction is based on the obtained strength distribution of SiC fibers and the strength model of minicomposites in Sect. 4. The predicted and experimental results are in good agreement which verifies further the accuracy of the obtained strength distribution of SiC fibers.

Fig. 10
figure 10

Stress–strain responses of SiC/SiC minicomposites

Full size image
Table 4 Comparison between the predicted and experimental results
Full size table

5.3 Reasons for the Low Temperature Sensitivity of SiC/SiC Composites

The test results of fiber bundles and minicomposites (see Fig. 7) reveal that the temperature has a significant influence on the strength of fiber bundles but nearly does not affect that of the minicomposites. To investigate the reason, the stress–strain responses of fiber bundles and minicomposites with different Weibull parameters are predicted using the models in Sects. 3 and 4.

For SiC fiber bundles, as shown in Figs. 11 and 12, the influence of m is limited. However, the strength is very sensitive to σ0. The strength of the fiber bundle decreases with the decrease of σ0. Since σ0 decreases as the temperature increases, the strength of the SiC fiber bundle declines dramatically at a high temperature.

Fig. 11
figure 11

Stress–strain responses of SiC fiber bundles with different m

Full size image
Fig. 12
figure 12

Stress–strain responses of SiC fiber bundles with different σ0

Full size image

For SiC/SiC minicomposites, the influences of m and σ0 are both significant. As shown in Fig. 13, the strength of minicomposites decreases with the increase of m. Figure 14 shows that the strength of minicomposites increases with the increase of σ0. Therefore, the effects of m and σ0 are opposite. Since m and σ0 both decrease with the increase of the temperature (see Fig. 8), their influences are offset. Therefore, the change of the strength of minicomposites at different temperatures is not obvious. This accounts for the low temperature sensitivity of SiC/SiC composites.

Fig. 13
figure 13

Stress–strain responses of SiC/SiC minicomposites with different m

Full size image
Fig. 14
figure 14

Stress–strain responses of SiC/SiC minicomposites with different σ0

Full size image

Note that the fiber/matrix interfacial shear stress also affects the strength of SiC/SiC composites. The microstructure of the pyrocarbon interphase will be changed from an amorphous structure into a highly-ordered layer graphite structure at elevated temperatures [28]. However, this change of microstructure needs a temperature much higher than 1000 ℃ [27]. Therefore, the microstructure of the pyrocarbon interphase and the interfacial shear stress are constant in the present work.

6 Conclusions

The sensitivity of strength via temperature for SiC/SiC composites and SiC fibers is a key issue since they are always used at elevated temperatures. The influence of the temperature on the strength of SiC/SiC composites and SiC fibers is investigated through experimental study and theoretical analysis.

Tensile tests are performed on SiC fiber bundles at room temperature, 500 and 1000 ℃ in an oxygen-free environment. The fiber strength distribution (or Weibull parameters) is then determined from the stress–strain curves of fiber bundles. Results show that the strength distribution of SiC fibers is sensitive to the temperature in an oxygen-free environment. Not only the strength declines at elevated temperatures but also the scatter of the strength is aggravated.

Tensile tests are also performed on SiC/SiC minicomposites at different temperatures. Test results show that, unlike SiC fibers, the strength of SiC/SiC minicomposites is not sensitive to the temperature in an oxygen-free environment. The strength of SiC/SiC minicomposites at 1000 ℃ is 94% of that at room temperature. To explain this phenomenon, the strength model of minicomposites is developed. The theoretical analysis reveals that the low sensitivity of strength via temperature for minicomposites results from that the influences of the changes of the Weibull parameters m and σ0 of SiC fibers at elevated temperatures are offset.