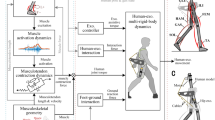
ABSTRACT
We implemented direct collocation on a full-body neuromusculoskeletal model to calculate muscle forces, ground reaction forces and knee contact loading simultaneously for one cycle of human gait. A data-tracking collocation problem was solved for walking at the normal speed to establish the practicality of incorporating a 3D model of articular contact and a model of foot–ground interaction explicitly in a dynamic optimization simulation. The data-tracking solution then was used as an initial guess to solve predictive collocation problems, where novel patterns of movement were generated for walking at slow and fast speeds, independent of experimental data. The data-tracking solutions accurately reproduced joint motion, ground forces and knee contact loads measured for two total knee arthroplasty patients walking at their preferred speeds. RMS errors in joint kinematics were < 2.0° for rotations and < 0.3 cm for translations while errors in the model-computed ground-reaction and knee-contact forces were < 0.07 BW and < 0.4 BW, respectively. The predictive solutions were also consistent with joint kinematics, ground forces, knee contact loads and muscle activation patterns measured for slow and fast walking. The results demonstrate the feasibility of performing computationally-efficient, predictive, dynamic optimization simulations of movement using full-body, muscle-actuated models with realistic representations of joint function.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
INTRODUCTION
The ability to perform predictive simulations is arguably the last grand challenge for bio-scientists and engineers interested in computational modelling of human movement. Model simulations that predict biomechanical function may aid in the design of more effective (targeted) exercise-based therapies for patients with movement abnormalities resulting from stroke,13 cerebral palsy5 and osteoarthritis.9,39 Predictive biomechanical simulations of movement may also assist in pre-operative planning of orthopaedic surgical procedures such as knee-ligament reconstructions and joint replacement, while the ability to predict novel movements would be valuable to sport scientists and coaches aiming to improve the techniques used by Olympic-calibre athletes to achieve exceptional performance.
Dynamic optimization or optimal control theory is well suited to exploring the interactions between the neuromuscular and musculoskeletal systems because it enables all quantities of interest (i.e., joint motion, external (ground reaction) forces and muscle coordination patterns) to be predicted, independent of experiment. Hatze12 pioneered the application of this approach to the study of human motion biomechanics by predicting the neuromuscular patterns needed to produce a minimum-time kicking motion. Since then, dynamic optimization has been used to simulate various other tasks, including jumping,3,28,30,31,45 cycling,14,32 walking1,4,6,25 and running26 (see also Pandy29 for a review). Many other studies have applied an alternate formulation of the optimal control problem called ‘data-tracking’ (known more commonly as ‘state estimation’ in the literature on control systems theory), where model-computed joint kinematics, ground reaction forces, and sometimes muscle activations as well, are constrained to reproduce corresponding experimental data obtained in vivo.36,42 Data-tracking enables efficient calculation of the internal states of the system, for example, the time histories of individual muscle forces and muscle-fibre lengths; however, it is fundamentally descriptive and not amenable to generating novel movements.
We recently implemented an implicit computational method called ‘direct collocation’ on a complex neuromusculoskeletal model with foot–ground contact to generate 3D data-tracking simulations of human locomotion.23 Here we deploy direct collocation on a model of even greater complexity to perform predictive simulations of walking at different speeds. Our specific aims were firstly, to solve a data-tracking collocation problem for normal gait (i.e., walking at the preferred speed) using a full-body neuromusculoskeletal model in which the knee is represented as a 6-DOF joint with articular contact; and secondly, to perform predictive simulations of walking at slow and fast speeds using the data-tracking solution for normal gait as an initial guess.
MATERIALS AND METHODS
Gait Experiments
Experimental data were obtained from the Third and Fourth “Grand Challenge Competitions to Predict In Vivo Knee Loads.”10,16 Data were collected from two participants (participant 1: female; age, 69 years; mass, 78 kg; height, 1.70 m; and participant 2: male, age, 80 years; mass, 68 kg; height, 1.70 m) implanted with instrumented knee replacements which measured the net tibiofemoral contact force.8,17 Data for participant 1 were obtained from the 3rd competition and that for participant 2 from the 4th competition. Both participants walked over ground at their preferred speeds (1.1 and 1.3 m/s for participants 1 and 2, respectively) and participant 2 also walked at the much slower speed of 0.8 m/s on a treadmill. Skin-marker motion, ground reaction forces, knee contact forces, and muscle electromyographic (EMG) signals were recorded simultaneously for each trial. The measured ground reaction forces and knee contact forces were used to directly validate the corresponding model-predicted quantities, while the EMG data were used to qualitatively verify the sequence and timing of the calculated muscle excitations. Data were extracted and processed so that one complete stride cycle began and ended at ipsilateral heel strike. The leg with the knee implant was selected as the ipsilateral limb (participant 1, left leg; participant 2, right leg).
Neuromusculoskeletal Model of the Body
A full-body musculoskeletal model of each participant was created in OpenSim.7 The body was represented as a 25-degree-of-freedom (DOF) skeleton actuated by 80 muscle–tendon units. The pelvis was connected to the ground by a 6-DOF free joint and articulated with the torso via a 3-DOF ball-and-socket back joint. Each hip was represented as a 3-DOF ball-and-socket joint, each ankle as a 2-DOF universal joint, and the contralateral knee as a 1-DOF translating hinge joint. The ipsilateral knee was represented as a 6-DOF joint with articular contact between the femur and tibia simulated using a model of surrogate joint contact.21,22,46 The surrogate contact model was developed to perform computationally efficient contact analyses within multi-body dynamic simulations by eliminating repeated geometry evaluations required by deformable-body-contact models. Details of the creation of the surrogate contact model are given by Walter and Pandy.46 The model skeleton was actuated by 80 muscle–tendon units with each unit represented as a Hill-type muscle in series with an elastic tendon. Muscle excitation–contraction (activation) dynamics was represented as a first-order model with activation and deactivation time constants of 10 and 40 ms, respectively.47 To reduce computational time during a simulation, tendon was assumed to be inextensible whenever tendon slack length was less than the optimum fibre length of the corresponding muscle.33 Twenty-two of the 80 muscle–tendon units were comprised of a rigid tendon based on this assumption (see Supplementary Material). Foot–ground interaction was simulated with six Hunt-Crossley contact spheres placed under each foot: four under the hind foot and two under the toes. Normal forces at each contact sphere were generated by a nonlinear spring-damper system while shear forces were simulated by applying a model of Coulomb friction. The foot–ground contact model was based on that described by Lin and Pandy.23 Details of the neuromusculoskeletal model used in this study can be found at https://simtk.org/home/DCwithJtContact/.
Data-Tracking Collocation Problem
Direct collocation was used to calculate a set of states and controls needed to reproduce measurements of the time histories of body-segmental motions and ground reaction forces obtained from both participants walking at their preferred speeds. The states were comprised of 25 generalized coordinates, 25 generalized speeds, 80 muscle activations, and 58 muscle-fiber lengths, while the controls consisted of 80 muscle excitations. Only 58 muscle-fiber lengths were included as states because the remaining 22 muscle–tendon units possessed rigid tendons, and the associated muscle-fiber lengths were therefore determined by the measured generalized coordinates. The time histories of the states and controls were each discretized on a grid of 80 evenly-spaced nodes over one gait cycle.
Each collocation problem was solved by minimizing three sources of errors that arise during a simulation of movement: defect errors, data-tracking errors, and the violation of periodic boundary conditions. Defect errors consisted of (25 + 25 + 80 + 58) × 79 = 14,852 equations, which represented the errors resulting from trapezoidal approximations of the dynamic equations of motion (see Eq. (2) in Lin and Pandy19); defect errors were calculated 79 times (number of nodes − 1) for each state variable because the trapezoidal approximation was applied to each pair of two adjacent nodes. Data-tracking errors consisted of two sets of 6 × 80 = 480 equations: the first set of these equations accounted for differences between the six measured and calculated ground reaction forces at each instant during the gait cycle (three components of the ground force acting under each foot, hence 6 ground forces in total); the second set of equations represented the errors between the measured and calculated pelvic generalized coordinates (6 coordinates in total) over the entire gait cycle. Periodic boundary conditions consisted of 268 − 6 = 262 equations, which required all control and state variables (268 in total) to be identical at the start and end of the gait cycle, except for the six tracked pelvic generalized coordinates.
Each data-tracking problem was formulated as a nonlinear least-squares problem as there were more unknowns than equations. Specifically, each data-tracking problem consisted of 21,440 control and state variables (80 × 80 = 6400 control variables plus 188 × 80 = 15,040 state variables) and 16,074 equations (14,852 defect error equations + 2 × 480 data-tracking error equations + 262 equations for violation of the periodic boundary conditions). A nonlinear system solver called ‘fsolve’ was used in conjunction with a Levenberg–Marquardt algorithm available in MATLAB (Mathworks,Natick, MA, USA) to solve the least-squares problem by minimizing sum of the squares of the residuals of the 16,074 equations.
Static optimization was used to generate an initial guess for each data-tracking collocation solution. First, an inverse kinematics analysis was performed to calculate the generalized coordinates corresponding to the measured marker motion. This step involved solving a weighted least-squares optimization problem which minimized the sum of the squares of the differences between the positions of virtual markers defined in the model and reflective markers mounted on the subject.24 All three tibiofemoral translations as well as the knee abduction–adduction angle were set to zero during this analysis due to the effect of soft-tissue artefact resulting from skin-mounted markers.2,40 Knee internal–external rotation was determined by the inverse kinematics analysis because X-ray fluoroscopy studies have shown that this motion is less affected by soft-tissue artefact than the abduction–adduction angle during gait.2,40 The resulting generalized coordinates and generalized speeds were used together with the force-plate data to calculate the net moments exerted about each joint. The muscle force-joint moment redundancy problem was then solved by applying static optimization and minimizing the sum of the squares of all muscle activations subject to each muscle’s force–length-velocity property. The entire procedure was performed in OpenSim without including either the foot–ground contact model or the surrogate joint contact model. Thus, the values of the generalized coordinates, generalized speeds, muscle fiber-lengths and muscle activations derived from static optimization were used as an initial guess for the states, while the values of the muscle activations were equated to the muscle excitations and used as an initial guess for the controls.
Predictive Collocation Problem
Direct collocation was also used to perform predictive simulations of slow and fast walking for participant 2. The data-tracking solution derived for walking at the preferred speed was used as an initial guess in these simulations. The optimization problem was to find a set of states and controls needed to reproduce the prescribed walking speed (0.8 m/s and 2.0 m/s for slow and fast walking, respectively) while minimizing the cost of transport, J (Joules/kg m), over one stride cycle, thus:
where the metabolic rate, \(\dot{E}\) (Joules), represents the sum of the activation heat rate, maintenance rate, shortening heat rate, and mechanical work rate of each muscle; Δx represents the horizontal displacement of the center of mass of the pelvis over one stride cycle; and m is the mass of the whole body. The final time, T, was left free and included as an additional design variable in the optimization problem. \(\dot{E}\) was calculated using the model of muscle energy expenditure described by Umberger44 via an OpenSim API (version 3.3) function called ‘Umberger2010MuscleMetabolicsProbe’.
The predictive collocation problem was solved subject to a set of equality path constraints, boundary constraints, and path bounds. The equality path constraints were identical with the trapezoidal approximations of the system dynamic equations derived for the data-tracking collocation problem described above. A set of boundary constraints were formulated to impose periodic boundary conditions on all of the states and controls, except the anterior–posterior translation of the pelvis. An additional boundary constraint was included to ensure the target walking speed (V) was achieved:
Upper- and lower-bound constraints were also imposed on the control and state variables at each time instant as follows:
where \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{u}\) is a 80 × 1 vector of muscle excitations; \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{a}\) is an 80 × 1 vector of muscle activations; \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{l}^{\text{m}}\) and \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{l}_{\text{o}}^{\text{m}}\) are 58 × 1 vectors of muscle-fiber lengths and optimum muscle-fiber lengths, respectively; \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q}\) and \(\dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} }\) are 25 × 1 vectors of generalized coordinates and generalized speeds, respectively; \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q}_{\text{DT}}\) and \(\dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} }_{\text{DT}}\) are 25 × 1 vectors of generalized coordinates and generalized speeds obtained from the data-tracking collocation solution; and \(\Delta \underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q}_{\text{DT}}\) and \(\Delta \dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} }_{\text{DT}}\) are 25 × 1 time-independent vectors defining the range of each DOF specified in \(\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q}_{\text{DT}}\) and \(\dot{\underset{\raise0.3em\hbox{$\smash{\scriptscriptstyle-}$}}{q} }_{\text{DT}}\), respectively. The predictive collocation solution was computed using a nonlinear programming algorithm called ‘fmincon’ available in MATLAB.
For both the data-tracking and predictive collocation problems, the derivatives of the performance criterion and constraints were calculated using central differences as described by Porsa et al.31 Articular contact forces for the ipsilateral knee were calculated using the surrogate contact model while the joint reaction force acting at the contralateral knee was found using the Joint Reaction Analysis available in OpenSim.41 All calculations were performed on a 3.4 GHz desktop computer (Intel® Core™ i7-4770 Processor) and parallelized across four cores using the Matlab Parallel Computing Toolbox.
RESULTS
The data-tracking collocation solutions accurately reproduced the body-segmental displacements, ground reaction forces and knee contact loads measured for both participants walking at their preferred speeds (Table 1 and Figs. 1, 2). The measured pelvic motion was tracked with RMS errors < 0.3° for rotations and < 0.3 cm for translations whilst RMS errors for all remaining generalized coordinates were < 2.2° (Table 1 and Fig. 1). The measured ground forces were tracked with RMS errors < 0.03 body weight (BW), 0.08 BW and 0.03 BW in the fore-aft, vertical, and mediolateral directions, respectively (Table 1 and Fig. 2). Although not explicitly tracked, the model-computed knee-contact loads were also in good agreement with corresponding measurements obtained from the instrumented implants, with RMS errors of < 0.4 BW (Table 1 and Fig. 2).
The patterns of muscle excitations predicted by the data-tracking solutions were temporally consistent with EMG activity measured for walking at the preferred speed (Fig. 3; see also Supplementary Material). In both the model and the subjects, the vasti and ankle plantarflexors were activated during early and late stance, respectively, while the gluteal muscles (maximus and medius) remained active for the duration of the stance phase. Some differences in timing between model and experiment were also evident, particularly in relation to the muscle excitations predicted for vasti and gluteus maximus during terminal swing.
Comparison between model-predicted muscle excitations (blue solid lines) and measured EMG data (red dashed lines) obtained for two participants walking at their preferred speeds. EMG data for GMAX and GMED were obtained from Lin et al.20 as data were not available for the two TKA participants. Muscle symbols are as follows: LVAS, vastus lateralis; LGAS, lateral gastrocnemius; SOL, soleus; GMAX, gluteus maximus; GMED, gluteus medius.
The predictive collocation solutions obtained for slow and fast walking were also consistent with experiment (Figs. 4, 5, and 6). Stride cycle times predicted for slow and fast walking were 1.30 and 0.92 s, respectively, which agreed well with the average times of 1.45 and 0.93 s measured for the subjects. There was also good agreement between the measured and predicted generalized coordinates for both walking speeds, although some differences were evident in hip rotation and ankle dorsiflexion at the slower speed (Fig. 4). The predicted ground reaction forces and knee contact loads were similar in shape and magnitude to the results obtained from the gait experiments (Fig. 5). However, the first peak in the vertical ground force predicted for fast walking was 0.4 BW greater than the second peak, in contrast to experiment where two peaks of similar magnitude were registered by the force plate.
Model-predicted kinematics (blue solid lines) obtained for Participant 2 walking at a slow speed (0.8 m/s, top panel) and a fast speed (2.0 m/s, bottom panel). The shaded regions in the top panel represent ± 1 standard deviation of the mean kinematics data recorded for Participant 2 walking at the slow speed of 0.8 m/s, while those in the bottom panel represent ± 1 standard deviation of the mean kinematics data measured from 10 young subjects walking at 2.1 m/s (Lai et al.18).
Model-predicted ground reaction forces (blue and red solid lines) and knee contact loads (blue solid lines, right-most panel) obtained for Participant 2 walking at a slow speed (0.8 m/s, top panel) and a fast speed (2.0 m/s, bottom panel). The shaded regions in the top panel represent ± 1 standard deviation of the mean experimental data recorded for Participant 2 walking at the slow speed of 0.8 m/s, while those in the bottom panel represent ± 1 standard deviation of the mean experimental data obtained from 10 young subjects walking at 2.1 m/s (Lai et al.18).
Model-predicted muscle excitations (blue solid lines) obtained for Participant 2 walking at a slow speed (0.8 m/s, top panel) and a fast speed (2.0 m/s, bottom panel). The shaded regions in the top panel represent ± 1 standard deviation of the mean EMG data recorded for Participant 2 walking at the slow speed of 0.8 m/s, while those in the bottom panel represent ± 1 standard deviation of the mean EMG data measured from 10 young subjects walking at 2.1 m/s (Lai et al.18). EMG data for GMAX and GMED were not available for slow walking.
The time histories of muscle excitations predicted for slow and fast walking were consistent with EMG measurements and showed that peak muscle excitations increased with walking speed (Fig. 6). For example, peak soleus and gastrocnemius excitations predicted for fast walking were approximately 2.5 times greater than those calculated for slow walking.
Muscle and knee contact forces computed for the ipsilateral and contralateral legs were similar for walking at the slow and preferred speeds, while larger differences were evident at the fast speed (Figs. 7 and 8). For the knee-spanning muscles, the peak force developed by the contralateral gastrocnemius was higher than that developed by the ipsilateral gastrocnemius for both participants across all speeds, while the peak force developed by the contralateral vasti was higher than that developed by the ipsilateral vasti for participant 2 walking at the fast speed. For the non-knee-spanning muscles, the peak force developed by the contralateral gluteus medius was higher than that developed by the ipsilateral gluteus medius for both participants at all speeds. Differences in knee contact force between the ipsilateral and contralateral legs were most pronounced at the fast walking speed (Fig. 8).
Comparison of muscle forces calculated from a 6-DOF knee (ipsilateral knee) and a 1-DOF knee (contralateral knee) for both participants walking across all speeds. Symbols appearing in the diagram are: HAMS, biceps femoris long head, biceps femoris short head, semimembranosus and semitendinosus combined; VAS, vastus medialis, vastus intermedius and vastus lateralis combined; RF, rectus femoris; GAS, medial and lateral portions of gastrocnemius combined; SOL, soleus; GMAX, superior, middle and inferior gluteus maximus combined; GMED, anterior, middle and posterior compartments of gluteus medius.
CPU time required to converge to a predictive collocation solution was considerably greater than that needed to generate a data-tracking solution. Collocation took 3 and 5 h of CPU time, respectively, to solve the data-tracking problems for participants 1 and 2 walking at their preferred speeds. By comparison, 17 and 13 h of CPU time were needed to compute the predictive dynamic optimization solutions for slow and fast walking, respectively.
DISCUSSION
We implemented direct collocation on a full-body 3D neuromusculoskeletal model to calculate muscle forces, ground reaction forces and knee contact forces simultaneously for one cycle of human gait. A data-tracking collocation problem was solved for normal gait (walking at the preferred speed) to establish the feasibility of incorporating a 6-DOF model of articular contact and a model of foot–ground interaction explicitly in a dynamic optimization simulation of movement. The data-tracking solution then served as an initial guess for solving predictive collocation problems, where novel patterns of movement were generated for walking at slow and fast speeds, independent of experimental data.
A novel contribution of the present study is demonstrating the feasibility of performing computationally-efficient, predictive, dynamic optimization simulations of movement using a 3D neuromusculoskeletal model consisting of a 6-DOF knee model with articular contact and a model of foot–ground interaction. A free-final-time optimal control solution was computed for a target walking speed without tracking any experimental data. Guess et al.11 performed forward-dynamic simulations of walking using a whole-body musculoskeletal model that included a 12-DOF knee model (6 DOFs for each of the tibiofemoral and patellofemoral joints) and a foot–ground contact model. They used a proportional-integral-derivative (PID) feedback control scheme to track joint angles and muscle–tendon lengths derived from inverse kinematics. Meyer et al.25 used direct collocation to predict novel movement patterns for walking at 1.1 m/s without reference to experimental data. While these authors included a subject-specific ground contact model to simulate foot–ground interaction, the knee was represented as a 1-DOF hinge joint and the final simulation time was fixed.
In contrast to our previous work,23 the process of solving a data-tracking collocation problem was simplified in the present study. Lin and Pandy23 recommended that the defect errors associated with the initial states and controls be minimized before these variables are amalgamated into an initial guess for a data-tracking optimization problem. Specifically, we proposed that the Matlab function ‘fsolve’ be implemented to minimize the defect errors before another function called ‘fmincon’ is used to track the measured ground forces. Whereas ‘fsolve’ required less than half an hour of CPU time to converge to a least-squares solution, at least 2 h of CPU time was required by ‘fmincon’ to solve a nonlinear constrained optimization problem.23 In the present study, the defect errors associated with the initial guess and the tracking errors corresponding to the ground forces were minimized simultaneously using ‘fsolve’ alone. This simplification obviated the need for ‘fmincon’ and enabled a more efficient solution of the data-tracking optimization problem.
The accuracy of our data-tracking simulations is comparable to that derived by previous investigators using forward-dynamics methods and the same Grand Challenge dataset. Guess et al.11 reported RMS errors of 0.07 BW, 0.15 BW and 0.02 BW for the ground forces computed in the fore-aft, vertical and mediolateral directions when participant 2 walked at 1.4 m/s, slightly faster than this subject’s preferred speed of 1.3 m/s. Thelen et al.43 simulated five overground gait trials using a modified version of the computed muscle control (CMC) algorithm and reported an average RMS error of 0.51 BW in the calculated knee contact force when participant 2 walked at the preferred speed. More recently, Walter and Pandy46 used force-feedback-control to determine knee contact forces for participants 1 and 2 walking at their preferred speeds. They reported an average RMS error of 0.36 BW in the knee contact force, calculated over five gait trials for each participant. RMS errors obtained in the present study were of similar magnitudes, with peak errors in the ground reaction force and knee contact load being < 0.1 BW and < 0.4 BW, respectively (Table 1). We note here that while the knee contact force may also be calculated accurately using more computationally-efficient methods such as inverse dynamics optimization,27,35 this approach is not suitable for predicting novel movements because experimental force and motion data are used explicitly in the optimization calculations.
The data-tracking collocation solutions accurately reproduced the knee contact loads measured for both participants walking at their preferred speeds. In contrast to the ground forces, measurements of the knee contact loads were not explicitly tracked in these simulations. Ground reaction forces have been used as force-feedback control terms in forward-dynamic simulations to constrain the knee contact force within physiological limits.39 Unfortunately, erroneous values of ground forces and knee contact loads result when the generalized coordinates and generalized speeds obtained from an inverse kinematics analysis are applied directly to a full-body model with foot–ground contact. These errors arise mainly from inconsistencies between the foot–ground forces calculated in the model and the joint motions obtained from experiment.23 For example, RMS errors in the model-computed ground forces for participant 2 walking at the preferred speed were 0.21 BW, 0.3 BW and 0.19 BW in the fore-aft, vertical, and mediolateral directions, respectively, while the corresponding RMS error in the knee contact load was 1.46 BW. These errors decreased substantially once the nonlinear system solver ‘fsolve’ was applied to the inverse kinematics solution: RMS errors in the vertical ground force decreased from 0.3 BW to 0.04 BW, and in the knee contact force, from 1.46 BW to 0.32 BW. We conclude, therefore, that accurate estimates of ground reaction forces are necessary to ensure reasonable estimates of articular contact forces at the knee. This result can be especially useful when in vivo measurements of articular contact loading are not available for direct validation of model-computed joint contact forces.
Model-computed muscle forces and knee contact loads were similar for the ipsilateral and contralateral legs in the simulations of walking at the slow and preferred speeds, but substantial differences were observed at the fast speed (Figs. 7 and 8). Many studies have calculated muscle forces and knee contact loading sequentially, where muscle forces are first found using a full-body musculoskeletal model with the knee represented as a planar 1-DOF translating hinge.15,37,38 The calculated values of muscle forces are then applied to a separate 3D knee model, and a quasi-static analysis performed to determine the articular contact forces transmitted at the joint. A few studies also have calculated muscle forces and knee contact loading simultaneously using a single musculoskeletal model with articular contact simulated at the knee.11,21,27,30,46 No study to our knowledge has compared model-computed muscle forces and knee contact loading using two different knee models (i.e., a 1-DOF hinge knee without articular contact and a 6-DOF knee with articular contact) implemented in the same simulation. The results of Figs. 7 and 8 suggest that a planar 1-DOF hinge-knee model may be sufficient for accurate determination of muscle and knee contact forces when humans walk at or below their preferred speeds.
In contrast, larger differences were observed in the muscle and knee contact forces calculated for the ipsilateral and contralateral legs at the much faster walking speed of 2 m/s (Figs. 7 and 8). Peak forces developed by the contralateral vasti and gastrocnemius muscles were, respectively, 2.0 BW and 0.5 BW higher than the forces developed by the corresponding ipsilateral leg muscles. These increases in muscle forces were understandably reflected in a higher knee contact force estimated for the contralateral leg, because vasti and gastrocnemius are major contributors to the first and second peaks, respectively, of the resultant force transmitted at the knee.34,37,38 Thus, muscle forces and knee contact loading computed for walking at faster speeds (e.g., near the transition speed of 2.0 m/s), and presumably for running as well, should be interpreted with caution due to the dependence of these calculations on knee model complexity.
The predictive collocation problems were formulated by prescribing a target walking speed and leaving both stride length and stride duration (inverse of stride frequency) free to be determined by the performance criterion and physiological constraints (e.g., the force–length-velocity properties of the leg muscles). The collocation algorithm altered stride length more than stride duration in computing the optimal solutions for slow and fast walking. For slow walking, stride length decreased by 24% relative to its value at the initial guess whereas stride duration increased by 21%. For fast walking, stride length increased by 33% while stride duration decreased by just 14% relative to their values at the initial guess. Lim et al.19 performed a series of gait experiments using prescribed combinations of step length and step frequency to quantify the effects of these two variables on leg-muscle function across a range of walking speeds. They found that walking biomechanics and leg-muscle function were more heavily influenced by changes in step length compared to step frequency. These results may explain why varying stride length rather than stride duration was favoured in the predictive dynamic optimization solutions derived here.
The principal limitation of the present study was that experimental gait data from only two subjects were used to evaluate the model simulation results. Similar previous studies exploiting the same Grand Challenge dataset used measurements recorded from multiple gait trials performed by a single subject.11,25,43 Deriving data-tracking and predictive simulations for a larger cohort of subjects and for a broader range of activities, for example, walking up and down ramps and stairs, would help to increase confidence in the proposed simulation methods. A second potential limitation involves the motion of the metatarsal joint, which was prescribed using the values obtained from the inverse kinematics analysis performed for walking at the preferred speed. Constraining the motion of the metatarsal joint is likely to have affected the muscle and ground reaction forces computed near toe-off in the predictive simulations of gait.
Change history
14 May 2018
In the “Materials and Methods” section, the link provided at the bottom of the second paragraph should be https://simtk.org/home/dcwithjtcontact/.
REFERENCES
Ackermann, M., and A. J. van den Bogert. Optimality principles for model-based prediction of human gait. J. Biomech. 43:1055–1060, 2010.
Akbarshahi, M., A. G. Schache, J. W. Fernandez, R. Baker, S. Banks, and M. G. Pandy. Non-invasive assessment of soft-tissue artifact and its effect on knee joint kinematics during functional activity. J. Biomech. 43:1292–1301, 2010.
Anderson, F. C., and M. G. Pandy. A dynamic optimization solution for vertical jumping in three dimensions. Comput. Methods Biomech. Biomed. Eng. 2:201–231, 1999.
Anderson, F. C., and M. G. Pandy. Dynamic optimization of human walking. J. Biomech. Eng. Trans. ASME 123:381–390, 2001.
Correa, T. A., R. Baker, H. K. Graham, and M. G. Pandy. Accuracy of generic musculoskeletal models in predicting the functional roles of muscles in human gait. J. Biomech. 44:2096–2105, 2011.
De Groote, F., A. L. Kinney, A. V. Rao, and B. J. Fregly. Evaluation of direct collocation optimal control problem formulations for solving the muscle redundancy problem. Ann. Biomed. Eng. 44(10):2922–2936, 2016.
Delp, S. L., F. C. Anderson, A. S. Arnold, P. Loan, A. Habib, C. T. John, E. Guendelman, and D. G. Thelen. OpenSim: open-source software to create and analyze dynamic simulations of movement. Trans. Biomed. Eng. 54:1940–1950, 2007.
D’Lima, D. D., S. Patil, N. Steklov, S. Chien, and C. W. Colwell, Jr. In vivo knee moments and shear after total knee arthroplasty. J. Biomech. 40(Suppl 1):S11–S17, 2007.
Fok, L. A., A. G. Schache, K. M. Crossley, Y. C. Lin, and M. G. Pandy. Patellofemoral joint loading during stair ambulation in people with patellofemoral osteoarthritis. Arthritis Rheum. 65:2059–2069, 2013.
Fregly, B. J., T. F. Besier, D. G. Lloyd, S. L. Delp, S. A. Banks, M. G. Pandy, and D. D. D’Lima. Grand challenge competition to predict in vivo knee loads. J. Orthop. Res. 30:503–513, 2012.
Guess, T. M., A. P. Stylianou, and M. Kia. Concurrent prediction of muscle and tibiofemoral contact forces during treadmill gait. J. Biomech. Eng. Trans. ASME 136(2):021032, 2014.
Hatze, H. The complete optimization of a human motion. Math. Biosci. 28:99–135, 1976.
Higginson, J. S., F. E. Zajac, R. R. Neptune, S. A. Kautz, and S. L. Delp. Muscle contributions to support during gait in an individual with post-stroke hemiparesis. J. Biomech. 39:1769–1777, 2006.
Kaplan, M. L., and J. H. Heegaard. Predictive algorithms for neuromuscular control of human locomotion. J. Biomech. 34:1077–1083, 2001.
Kim, H. J., J. W. Fernandez, M. Akbarshahi, J. P. Walter, B. J. Fregly, and M. G. Pandy. Evaluation of predicted knee-joint muscle forces during gait using an instrumented knee implant. J. Orthop. Res. 27:1326–1331, 2009.
Kinney, A. L., T. F. Besier, D. D. D’Lima, and B. J. Fregly. Update on grand challenge competition to predict in vivo knee loads. J. Biomech. Eng. 135:021012, 2013.
Kirking, B., J. Krevolin, C. Townsend, C. W. Colwell, and D. D. D’Lima. A multiaxial force-sensing implantable tibial prosthesis. J. Biomech. 39:1744–1751, 2006.
Lai, A., A. G. Schache, Y. C. Lin, and M. G. Pandy. Tendon elastic strain energy in the human ankle plantar-flexors and its role with increased running speed. J. Exp. Biol. 217:3159–3168, 2014.
Lim, Y. P., Y. C. Lin, and M. G. Pandy. Effects of step length and step frequency on lower-limb muscle function in human gait. J. Biomech. 57:1–7, 2017.
Lin, Y. C., L. A. Fok, A. G. Schache, and M. G. Pandy. Muscle coordination of support, progression and balance during stair ambulation. J. Biomech. 48:340–347, 2015.
Lin, Y. C., R. T. Haftka, N. V. Queipo, and B. J. Fregly. Two-dimensional surrogate contact modeling for computationally efficient dynamic simulation of total knee replacements. J. Biomech. Eng. Trans. ASME 131(4):041010, 2009.
Lin, Y. C., R. T. Haftka, N. V. Queipo, and B. J. Fregly. Surrogate articular contact models for computationally efficient multibody dynamic simulations. Med. Eng. Phys. 32:584–594, 2010.
Lin, Y. C., and M. G. Pandy. Three-dimensional data-tracking dynamic optimization simulations of human locomotion generated by direct collocation. J. Biomech. 59:1–8, 2017.
Lu, T. W., and J. J. O’Connor. Bone position estimation from skin marker co-ordinates using global optimisation with joint constraints. J. Biomech. 32:129–134, 1999.
Meyer, A. J., I. Eskinazi, J. N. Jackson, A. V. Rao, C. Patten, and B. J. Fregly. Muscle synergies facilitate computational prediction of subject-specific walking motions. Front. Bioeng. Biotechnol. 4:77, 2016.
Miller, R. H., and J. Hamill. Optimal footfall patterns for cost minimization in running. J. Biomech. 48:2858–2864, 2015.
Moissenet, F., L. Cheze, and R. Dumas. A 3D lower limb musculoskeletal model for simultaneous estimation of musculo-tendon, joint contact, ligament and bone forces during gait. J. Biomech. 47:50–58, 2014.
Ong, C. F., J. L. Hicks, and S. L. Delp. Simulation-based design for wearable robotic systems: an optimization framework for enhancing a standing long jump. IEEE Trans. Biomed. Eng. 63:894–903, 2016.
Pandy, M. G. Computer modeling and simulation of human movement. Annu. Rev. Biomed. Eng. 3:245–273, 2001.
Pandy, M. G., F. E. Zajac, E. Sim, and W. S. Levine. An optimal control model for maximum-height human jumping. J. Biomech. 23:1185–1198, 1990.
Porsa, S., Y. C. Lin, and M. G. Pandy. Direct methods for predicting movement biomechanics based upon optimal control theory with implementation in OpenSim. Ann. Biomed. Eng. 44:2542–2557, 2016.
Raasch, C. C., F. E. Zajac, B. M. Ma, and W. S. Levine. Muscle coordination of maximum-speed pedaling. J. Biomech. 30:595–602, 1997.
Rajagopal, A., C. L. Dembia, M. S. DeMers, D. D. Delp, J. L. Hicks, and S. L. Delp. Full-body musculoskeletal model for muscle-driven simulation of human gait. IEEE Trans. Biomed. Eng. 63:2068–2079, 2016.
Sasaki, K., and R. R. Neptune. Individual muscle contributions to the axial knee joint contact force during normal walking. J. Biomech. 34:2780–2784, 2010.
Serrancoli, G., A. L. Kinney, B. J. Fregly, and J. M. Font-Llagunes. Neuromusculoskeletal model calibration significantly affects predicted knee contact forces for walking. J. Biomech. Eng. 2016. https://doi.org/10.1115/1.4033673.
Seth, A., and M. G. Pandy. A neuromusculoskeletal tracking method for estimating individual muscle forces in human movement. J. Biomech. 40:356–366, 2007.
Shelburne, K. B., M. R. Torry, and M. G. Pandy. Contributions of muscles, ligaments, and the ground-reaction force to tibiofemoral joint loading during normal gait. J. Orthop. Res. 24:1983–1990, 2006.
Sritharan, P., Y. C. Lin, and M. G. Pandy. Muscles that do not cross the knee contribute to the knee adduction moment and tibiofemoral compartment loading during gait. J. Orthop. Res. 30:1586–1595, 2012.
Sritharan, P., Y. C. Lin, S. E. Richardson, K. M. Crossley, T. B. Birmingham, and M. G. Pandy. Musculoskeletal loading in the symptomatic and asymptomatic knees of middle-aged osteoarthritis patients. J. Orthop. Res. 35:321–330, 2017.
Stagni, R., S. Fantozzi, A. Cappello, and A. Leardini. Quantification of soft tissue artefact in motion analysis by combining 3D fluoroscopy and stereophotogrammetry: a study on two subjects. Clin. Biomech. 20:320–329, 2005.
Steele, K. M., M. S. Demers, M. H. Schwartz, and S. L. Delp. Compressive tibiofemoral force during crouch gait. Gait Posture 35:556–560, 2012.
Thelen, D. G., F. C. Anderson, and S. L. Delp. Generating dynamic simulations of movement using computed muscle control. J. Biomech. 36:321–328, 2003.
Thelen, D. G., K. W. Choi, and A. M. Schmitz. Co-simulation of neuromuscular dynamics and knee mechanics during human walking. J. Biomech. Eng. 136:021033, 2014.
Umberger, B. R. Stance and swing phase costs in human walking. J. R. Soc. Interface 7:1329–1340, 2010.
Vansoest, A. J., A. L. Schwab, M. F. Bobbert, and G. J. V. Schenau. The influence of the biarticularity of the gastrocnemius-muscle on vertical-jumping achievement. J. Biomech. 26:1–8, 1993.
Walter, J. P., and M. G. Pandy. Dynamic simulation of knee-joint loading during gait using force-feedback control and surrogate contact modelling. Med. Eng. Phys. 48:196–205, 2017.
Winters, J. M., and L. Stark. Estimated mechanical-properties of synergistic muscles involved in movements of a variety of human joints. J. Biomech. 21:1027–1041, 1988.
Acknowledgments
This work was supported by a Discovery Projects Grant from the Australian Research Council (DP160104366).
Author information
Authors and Affiliations
Corresponding author
Additional information
Associate Editor Estefanía Peña oversaw the review of this article.
Electronic supplementary material
Below is the link to the electronic supplementary material.
Rights and permissions
About this article
Cite this article
Lin, YC., Walter, J.P. & Pandy, M.G. Predictive Simulations of Neuromuscular Coordination and Joint-Contact Loading in Human Gait. Ann Biomed Eng 46, 1216–1227 (2018). https://doi.org/10.1007/s10439-018-2026-6
Received:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10439-018-2026-6