1 Introduction

Microelectromechanical system (MEMS) is one of the active research areas in engineering. The growing demand for better microelectronic devices requires the creation of new technologies. Reviews of some of these devices can be found in Refs. [1,2,3]. An important component in modeling of MEMS devices is the physical properties of the material. There are many materials which are good candidates for MEMS applications, but they have nonlinear mechanical properties. The most commonly used materials for MEMS applications are polysilicon, aluminum, titanium alloys, etc. [1, 4]. The materials at various temperatures exhibit power-law stress-strain relationship, which can be characterized by the Hollomons constitutive equation

$$\begin{aligned} \sigma =K|\varepsilon |^{n-1} \varepsilon , \end{aligned}$$
(1)

where \(\sigma , \varepsilon , K\), and \(n\in (0,1)\) denote the stress, the strain, the strength coefficient, and the strain-hardening (or work-hardening) exponent, respectively [5]. For polysilicon, the true stress and true strain curve can be modeled by the power-law equation in the temperature greater than 25 \(^{\circ }\)C, see Refs. [6,7,8]. Materials modelled by Eq. (1) are called work-hardening materials, sometimes referred to as Ludwick materials [9, 10]. The power-law constitutive equation is a well-known empirical relation that represents the experimental non-linear stress-strain relation of annealed metals, such as annealed copper and No. 8 nickel plated (N.P.8) aluminum alloy [11, 12]. The values of K and n for some common annealed metals can be found in engineering literature [6, 13]. The parameters for several types of power-law materials are specified in Table 1.

We propose to study a natural generalization of the Kelvin-Voigt damping for the power-law materials in the following form:

$$\begin{aligned} \sigma =K|\varepsilon |^{n-1}\varepsilon +c_{d}|{\dot{\varepsilon }}|^{m-1}{\dot{\varepsilon }}, \end{aligned}$$
(2)

where \(c_{d}\) denotes the strain-rate damping coefficient, m is the strain-rate sensitivity exponent [6]. Typical ranges of m for metals are up to 0.05 for cold-working, 0.05–0.4 for hot-working, and 0.3–0.85 for superplastic materials, respectively. The values of strain-rate effects for several materials are shown in Table 2.

Table 1 Physical properties of some well-known power-law materials [6, 13]
Full size table
Table 2 Strain rate effects of different materials for MEMS [6, 13, 14]
Full size table

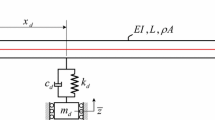
The structural elements of typical microelectromechanical resonators include a low-mass movable electrode and a fixed electrode, which are separated by a micro-gap. A non-deformable platform attached to a spring is used as a movable electrode in some cases. The plane of the platform is parallel to the flat surface of the fixed electrode, as shown in Fig. 1. The fixed electrode is coated with a dielectric layer, of which thickness is h and dielectric constant is \(\varepsilon _r\). The function of the spring is performed by an elastic micro-cantilever beam of length \(\ell \). Let d denote the distance from the point of attached of the spring to the surface of the dielectric, and V be the electrostatic potential difference between the electrodes. As a result of the interaction of the elastic force of the spring, the inertia force, and the electrostatic attraction force due to the potential difference between the electrodes, high-frequency oscillations of the platform occur. The resistance forces due to the air layer between the electrodes are assumed to be negligible.

Fig. 1
figure 1

Design scheme of the microelectromechanical resonator

Full size image

For linear materials, \(n=1\) and \(c_d=0\). The design of micro-resonator with elastic elements in form of strained film, clamped-clamped beam, and cantilever beam were investigated [15,16,17]. When external damping exists, Ref. [18] gave the design of micro-resonator with elastic elements in form of clamped-clamped beam. In the case of \(n=1\) and \(c_{d}\ne 0\), similar problems with different conditions and forces were considered [19, 20]. In Ref. [21], the damping ratio included the strain-rate and the air damping components for the linear materials was presented. And results showed that the strain-rate damping coefficient is proportional to structural stiffness. In this work, the corresponding proportionality is shown for nonlinear materials. The stiffness coefficients for the power-law Euler-Bernoulli beams without damping subjected to different types of boundary conditions were derived in Ref. [22]. The derivation of the approximation formula for the effective internal and external damping coefficients in the cases of the cantilever and hinged-hinged beams were published in the separate paper [23]. Lumped-parameter models for the cantilever beams were useful for modeling energy harvesting devices [24,25,26]. The first lumped-parameter model for an electrostatically actuated device was introduced by Nathanson et al. [27]. For lumped-parameter models, Zhang et al. [28] specified that the dynamic pull-in described the collapse of the moving structure caused by the combination of kinetic and potential energies. In general, a dynamic pull-in required a lower voltage to be triggered compared to the static pull-in threshold [29, 30].

The first goal of this paper is to provide the mathematical model for a microelectromechanical resonator beam based on Eq. (2) of power-law materials with internal damping. This is an extension of the procedure developed in Ref. [31] to a more general class of resonators with damping. The second goal is to provide a lumped-parameter model for the beam partial differential equation (PDE) model and perform analysis of dynamic pull-in of the beam by using the lumped-parameter model. Our lumped-parameter model gives MEMS designers a good account of the pull-in effects, amplitudes, and frequencies of the beam before a more sophisticated simulation using the PDE model is performed.

The paper has six sections. Section 1 is introduction. In Sect. 2, the PDE model for the microelectromechanical resonator is presented. In Sect. 3, the lumped-parameter model is introduced to study the dynamical properties of the resonator. The approximations of the generalized stiffness and damping parameters for power-law cantilever beam under the load at its tip are presented. In Sect. 4, the dynamic pull-in conditions are provided by the lumped parameters. In Sect. 5, the hysteresis loops for solutions of oscillatory types are demonstrated for energy dissipation analysis. In Sect. 6, the electrostatic force is approximated by a cubic polynomial for numerical simulations of the amplitudes and frequencies of the resonator. The paper ends with the conclusions.

2 Mathematical model for a microelectromechanical resonator

Fadeev et al. [17] provided the physical model of the microelectromechanical resonator, as shown in Fig. 1, is used to demonstrate the motion of the non-deformable platform with point mass \(M_c\) under the influence of electrostatic Coulomb force \(F_e\) applied at the platform.

With \(0<x<\ell \) and \(t>0\), let the function u(t, x) be the vertical deflection of the cantilever beam. The deflection at the tip \(u(t,\ell )\) is equal to the deflection of the non-deformable platform denoted by \(u_c (t)\). The distance between the surface of the platform and the surface of the dielectric equals to \(d-u_c (t)\). And the electrostatic force \(F_e\), acting on the platform, is given by

$$\begin{aligned} F_{e}=\frac{\varepsilon _{0}V^{2}S}{2\left[ d+\frac{h}{\varepsilon _{r}}-u_{c}(t)\right] ^{2}}, \end{aligned}$$
(3)

where S is the area of the platform and the electric constant of air \(\varepsilon _{0}=8.85\times 10^{-12}\). The mathematical model for the deflection of the cantilever beam under the influence of the movement of the platform with mass \(M_c\) applied at its tip (\(x=\ell \)) is described by the following nonlinear PDE model

$$\begin{aligned}&{\rho }{A}{u_{tt}}(x,t)+\frac{\partial ^{2}}{\partial \,x^{2}}\left[ c_{d}I_{m}\left| \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right| ^{m-1}\frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right] +\nonumber \\&\quad \frac{\partial ^{2}}{\partial \,x^{2}}\left[ KI_{n}\left| \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right| ^{n-1}\frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right] =0. \end{aligned}$$
(4)

The initial conditions are

$$\begin{aligned} u(x,0)=0,\quad \frac{\partial u(x,0)}{\partial t}=0, \quad 0<x<\ell , \end{aligned}$$

and boundary conditions are

$$\begin{aligned}&u(x,t)=0, \quad \frac{\partial u(x,t)}{\partial x}=0, \quad x=0, \,\, t>0, \nonumber \\&KI_{n}\left| \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right| ^{n-1}\frac{\partial ^{2}u(x,t)}{\partial \,x^{2}} \nonumber \\&\quad + c_{d}I_{m}\left| \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right| ^{m-1} \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}=0, \quad x=\ell , \,\, t>0, \nonumber \\&\frac{\partial }{\partial \,x}\left[ KI_{n}\left| \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right| ^{n-1}\frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right. \nonumber \\&\quad + \left. c_{d}I_{m}\left| \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right| ^{m-1} \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right] = M_{c}u_{tt}(x,t),\nonumber \\&x=\ell , \,\, t>0, \end{aligned}$$
(5)

for \(x\in (0,\ell ), \,\, t>0, \,\, n,m\in (0,1)\). The derivation of Eq. (4) is similar to that in Refs. [17, 32]. In the above equations, \(\rho \) denotes the density of material, A is the cross-sectional area, and \(I_n\), \(I_m\) are the moments of inertia of the cross-sectional area of the beam relative to the neutral axis. Here, note that the tip mass as well as the damping moment are represented in the boundary conditions.

In Eq. (5), the acceleration at the tip \(u_{tt} (\ell ,t)\) equals the acceleration of the platform \(\frac{\text {d}^2 u_c (t)}{\text {d} t^2}\) with mass \(M_c\). The electrostatic Coulomb force \(F_e\), the spring elastic restoring force \((-F_c)\) and the spring damping force \((-F_d)\) acting on the platform together with the platform inertia force obey the force balance equation,

$$\begin{aligned} {\left\{ \begin{array}{ll} \left( M_{c}+m_\mathrm{eff}\right) \frac{\text {d}^{2} u_{c}(t)}{\text {d} t^{2}}+F_{d}+F_{c}=F_{e}, \\ u_{c}(0)=0, \quad \frac{\text {d} u_{c}(0)}{\text {d} t}=0, \quad t>0, \end{array}\right. } \end{aligned}$$
(6)

where \(m_\mathrm{eff}\) is the generalized effective mass coefficient for power-law Euler-Bernoulli cantilever beam [27].

The solution \(u(\ell ,t)=u_c (t), \quad t>0\), to the initial problem (6), describes the motion of the platform, which is assumed to be a point of mass \(M_c\). Consequently, the coupled system of equations for the mathematical model of the micro-resonator reads as follows

$$\begin{aligned}&{\rho }{A}{u_{tt}}(x,t)+\frac{\partial ^{2}}{\partial \,x^{2}}\left[ c_{d}I_{m}\left| \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right| ^{m-1}\frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right] \nonumber \\&\quad + \frac{\partial ^{2}}{\partial \,x^{2}}\left[ KI_{n}\left| \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right| ^{n-1}\frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right] =0, \end{aligned}$$
(7)
$$\begin{aligned}&u(x,t)=0, \quad \frac{\partial u(x,t)}{\partial x}=0, \quad x=0, \quad t>0, \nonumber \\&KI_{n}\left| \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right| ^{n-1}\frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\nonumber \\&+c_{d}I_{m}\left| \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right| ^{m-1} \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}=0, \quad x=\ell , \,\, t>0, \nonumber \\&u(x,0)=0,\quad \frac{\partial u(x,0)}{\partial t}=0, \quad 0<x<\ell , \nonumber \\&u(\ell ,t)=u_c (t), \nonumber \\&\left( M_{c}+m_\mathrm{eff}\right) \frac{\text {d}^{2} u_{c}(t)}{\text {d} t^{2}}-\frac{\partial }{\partial \,x}\left[ KI_{n}\left| \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right| ^{n-1}\frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right. \nonumber \\&+ \left. c_{d}I_{m}\left| \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right| ^{m-1} \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right] \nonumber \\&=\frac{\varepsilon _{0}V^{2}S}{2\left[ d+\frac{h}{\varepsilon _{r}}-u_{c}(t)\right] ^{2}}, \quad x=\ell , \,\, t>0,\nonumber \\&\qquad u_c (0)=0, \quad \frac{\text {d} u_c (0)}{\text {d} t}=0. \end{aligned}$$
(8)

In this paper, we investigate the solutions behavior of the micro-resonators (7), (8) at the tip \(x=\ell \). In order to analyze the micro-resonator behavior at the tip \(x=\ell \), it is needed to study the solution of the Cauchy problem (6). Note that the Cauchy problem (6) is equivalent to the initial value problem (8). However, the second and third terms are unknown in the left side of Eq. (8) regarding to u(x, t). Therefore, to describe the platform behavior, these terms have to approximate through the lumped-parameter model. In the next section, the derivation of the lumped-parameter model will be shown. And for linear elastic materials, lumped-parameter models for Euler-Bernoulli beams in MEMS devices are well-known in Ref. [1].

3 Lumped-parameter model

In this section, we consider the lumped-parameter model for investigation of the micro-resonator vibration at the tip \(x=\ell \). Lumped-parameter models for the Euler-Bernoulli beams with linear materials were collected in Ref. [1]. The generalized stiffness and mass effective coefficients for power-law Euler-Bernoulli beams were presented in Ref. [22]. The connection of the generalized stiffness coefficients with the strain-rate damping coefficients are shown below. Let U(x) be a solution of the initial boundary value problem (4), which satisfies the following system

$$\begin{aligned} {\left\{ \begin{array}{ll} (KI_{n}|U_{xx}|^{n-1}U_{xx})_{xx}=0,\\ U(0)=0,\quad U_{x}(0)=0, \\ KI_{n}|U_{xx}(\ell )|^{n-1}U_{xx}(\ell )=0,\\ \left. (KI_{n}|U_{xx}|^{n-1}U_{xx})_{x}\right| _{x=\ell }=-F_{c}, \end{array}\right. } \end{aligned}$$

where for \(x\in (0,\ell ),\) \(0<n<1\). The function U(x) describes the stationary equilibrium of an elastic nonlinear beam under the influence of a concentrated force \(F_{c}\) at the tip. From Ref. [10], we can obtain that

$$\begin{aligned} U(x)=F_c^{\frac{1}{n}}G(x,\ell ), \end{aligned}$$
(9)

where

$$\begin{aligned}&G(x,\ell )=\frac{1}{(KI_{n})^{\frac{1}{n}}}\left[ \frac{(\ell -x)^{\frac{1}{n}+2}}{(\frac{1}{n}+1)(\frac{1}{n}+2)}+\frac{{\ell }^{\frac{1}{n}+1}}{\frac{1}{n}+1}x-\right. \\&\quad \left. \frac{{\ell }^{\frac{1}{n}+2}}{(\frac{1}{n}+1)(\frac{1}{n}+2)}\right] . \end{aligned}$$

And due to \(U(\ell )\) coincides with \(u_c (t)\),

$$\begin{aligned} F_{c}=\frac{|u_{c}(t)|^{n-1}u_{c}(t)}{|G(\ell ,\ell )|^{n-1}G(\ell ,\ell )}. \end{aligned}$$

The restoring force for the power-law materials implies \(F_{c}=k_{n}|u_{c}(t)|^{n-1}u_{c}(t)\). According to Ref. [22],

$$\begin{aligned} k_{n}=\frac{KI_{n}}{l^{1+2n}}\left( \frac{1+2n}{n}\right) ^{n}. \end{aligned}$$
(10)

Since \(u(\ell ,t)=u_c (t)\), it follows that

$$\begin{aligned} u(x,t)\approx \frac{G(x,\ell )}{G(\ell ,\ell )}u_{c}(t), \quad x \approx \ell . \end{aligned}$$
(11)

Thus, we have remark 1. The next approximation holds

$$\begin{aligned}&\left. \frac{\partial }{\partial \,x}\left[ KI_{n}\left| \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right| ^{n-1} \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right] \right| _{x=\ell }\approx \nonumber \\&\quad -k_{n}|u_{c}(t)|^{n-1}u_{c}(t). \end{aligned}$$
(12)

Considering Eq. (11), we can rewrite Eq. (12) in the form

$$\begin{aligned}&\left. \frac{\partial }{\partial \,x}\left[ KI_{n}\left| \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right| ^{n-1} \frac{\partial ^{2}u(x,t)}{\partial \,x^{2}}\right] \right| _{x=\ell }\nonumber \\&\left. \approx \frac{\partial }{\partial \,x}\left\{ KI_{n}\left| \frac{\partial ^{2}\left[ \frac{G(x,\ell )}{G(\ell ,\ell )}u_{c}(t)\right] }{\partial \,x^{2}}\right| ^{n-1} \frac{\partial ^{2}\left[ \frac{G(x,\ell )}{G(\ell ,\ell )}u_{c}(t)\right] }{\partial \,x^{2}}\right\} \right| _{x=\ell }\nonumber \\&=\left. \frac{\partial }{\partial \,x}\left\{ KI_{n}\left| \frac{\partial ^{2}\left[ \frac{G(x,\ell )}{G(\ell ,\ell )}\right] }{\partial \,x^{2}}\right| ^{n-1} \frac{\partial ^{2}\left[ \frac{G(x,\ell )}{G(\ell ,\ell )}\right] }{\partial \,x^{2}}\right\} \right| _{x=\ell }\cdot |u_{c}(t)|^{n-1}u_{c}(t). \end{aligned}$$
(13)

In analogy to remark 1, we can obtain the approximate expression of remark 2,

$$\begin{aligned}&\left. \frac{\partial }{\partial \,x}\left[ c_{d}I_{m}\left| \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right| ^{m-1} \frac{\partial ^{3}u(x,t)}{\partial \,x^{2}\partial \,t}\right] \right| _{x=\ell }\approx \nonumber \\&\quad -\frac{c_{d}}{K}k_{m}\left| \frac{\text {d}{u}_{c}(t)}{\text {d}t}\right| ^{m-1}\frac{\text {d}{u}_{c}(t)}{\text {d}t}, \end{aligned}$$
(14)

where \(k_m\) is the stiffness coefficient and it is given by Eq. (10) in analogy to the linear case in Ref. [21]. Taking into account Eqs. (12) and (14), the initial value problem (8) for the motion of the platform reads as follows

$$\begin{aligned}&(M_{c}+m_\mathrm{eff})\frac{\text {d}^{2}u_{c}(t)}{\text {d}t^{2}}+\frac{c_{d}}{K}k_{m}\left| \frac{\text {d}{u}_{c}(t)}{\text {d}t}\right| ^{m-1}\frac{\text {d}{u}_{c}(t)}{\text {d}t}+\nonumber \\&\quad +k_{n}|u_{c}(t)|^{n-1}u_{c}(t)= \frac{\varepsilon _{0}V^{2}S}{2\left[ d+\frac{h}{\varepsilon _{r}}-u_{c}(t)\right] ^{2}}, \end{aligned}$$
(15)

and has zero initial conditions

$$\begin{aligned} u_{c}(0)=0, \quad \frac{\text {d}u_{c}(0)}{\text {d}t}=0. \end{aligned}$$
(16)

The solution \(u_c (t)\) of the Cauchy problem (15) determines the motion of the mass \(M_c\) under the influence of electrostatic attraction \(F_e\), the elastic force springs \(F_c\) with stiffness coefficient \(k_n\), and damping force \(F_d\) with damping coefficient \(\frac{c_{d}}{K}k_{m}\). As a result, the nonlinear PDE model for the boundary value problem turns to the lumped-parameter model having single degree-of-freedom with a damping.

4 Dimensionless lumped mass model equation

Following the ideas from Ref. [18], the dimensionless time \(\tau ,\) deflection y, quality factor of a mechanical system Q, and voltage parameter B are defined as follows

$$\begin{aligned}&\tau =\left[ \frac{k_{n}\left( d+\frac{h}{\varepsilon _{r}}\right) ^{n-1}}{M_{c}+m_\mathrm{eff}}\right] ^{1/2}t,\,\,\,y(\tau )=\left( d+\frac{h}{\varepsilon _{r}}\right) ^{-1}u_{c}(t), \end{aligned}$$
(17)
$$\begin{aligned}&Q={\frac{K}{{c_d}{k_m}}}{{k_n}^{\frac{2-m}{2}}}{\left( d+\frac{h}{\varepsilon _r}\right) ^n}{\left[ \frac{\left( d+\frac{h}{\varepsilon _r}\right) ^{n+1}}{M_{c}+m_\mathrm{eff}}\right] ^{-\frac{m}{2}}}, \nonumber \\&B=\frac{\varepsilon _{0}V^{2}S}{2\left( d+\frac{h}{\varepsilon _{r}}\right) ^{n+2}k_{n}}. \end{aligned}$$
(18)

In the sequel, we denote the first and second derivatives of y with respect to the dimensionless time \(\tau \) by \({\dot{y}},\) \(\ddot{y}\) respectively. Then, we obtain from Eq. (15) the following dimensionless single-degree model equation

$$\begin{aligned} \ddot{y}+\frac{1}{Q}|{\dot{y}}|^{m-1}{\dot{y}}+|y|^{n-1}y=\frac{B}{(1-y)^{2}}, \end{aligned}$$
(19)

which is subject to

$$\begin{aligned} y(0)=0,\,\,\,{\dot{y}}(0)=0, \end{aligned}$$
(20)

where \(0<n,m\le 1,\) \(Q> 0\), and \(B\ge 0.\) The case of \(n=m=1,\) \(Q=\infty \), and \(B=0\) corresponds to the classical harmonic oscillator. The static pull-in voltage analysis for the linear case has been investigated in Ref. [1]. It is corresponding to

$$\begin{aligned} B_{stat}(1)=\frac{4}{27}. \end{aligned}$$

The dynamic pull-in voltage

$$\begin{aligned} B^{*}_{1}=\frac{1}{8}<B_{stat}(1), \end{aligned}$$

can be seen in Refs. [17, 30]. In the case of \(n=1,\) \(Q\ne 0\), and \(B \ne 0\), dynamic pull-in voltage analysis has been investigated in Ref. [18]. The case of \(n\ne 1, \, m>0\), and \(Q=\infty \), and \(B>0\), dynamic pull-in voltage analysis has been presented in Ref. [31]. The dynamic pull-in voltage

$$\begin{aligned} B^{*}_{n}=\frac{1}{(n+1)^2}\left( \frac{n}{n+1}\right) ^{n}. \end{aligned}$$

It has found that if

$$\begin{aligned} 0<B<B^{*}_{n}, \end{aligned}$$
(21)

autovibrations of the platform arise when the micro-resonator is started, else there are no autovibrations at \(B>B^{*}_{n} \).

The platform performs autovibrations can be described by the Cauchy problem (19), (20) with the condition (21) and \(\tau <T_{imp}\), where \(T_{imp}\) is a duration of start. The action of the electrostatic attraction stops at the moment of time \(\tau =T_{imp}\), and the movement of the platform continues by inertia in the form of damped vibrations. Suppose that \({\hat{y}}(T_{imp})=y(T_{imp})\) is the solution and \(\frac{\text {d} {\hat{y}}}{\text {d} \tau }\left( T_{imp}\right) ={\dot{y}}(T_{imp})\) is its derivative of the initial value problem (19), (20), then it can be rewrited as

$$\begin{aligned} \ddot{y}+\frac{1}{Q}|{\dot{y}}|^{m-1}{\dot{y}}+|y|^{n-1}y=0, \quad T_{imp}<\tau , \end{aligned}$$
(22)

which is subject to

$$\begin{aligned} y(T_{imp})={\hat{y}}(T_{imp}),\qquad {\dot{y}}(T_{imp})=\frac{\text {d} {\hat{y}}}{\text {d} \tau }\left( T_{imp}\right) . \end{aligned}$$
(23)
Fig. 2
figure 2

Solution profiles for \(B = 0.2\): (a) strain-rate exponent \(m=0.07\); (b) strain-rate exponent \(m=0.17\)

Full size image

When n is equal to 0.54, for different values of m, several solutions with respect to non-damped and damped vibrations for the beams are compared in Fig. 2. In the case of no damping, \(B=0.2\) is less than \(B^{*}_{n}\), the dynamic critical pull-in voltage \(B^{*}_{n} = 0.239\). Figure 2a and 2b show that the model has periodic solutions. Different values of Q are chosen to numerically solve the initial problem (19), (20) with damping by the standard Maple ordinary differential equation (ODE) solver. And the embedded Runge-Kutta method can be used to justify the predicted behavior of the solution \(y(\tau )\). In several solutions, the amplitudes, which are the corresponding amplitudes of the non-damped systems, do not exceed 0.15. In our study, the amplitudes do not exceed 0.33 when voltage is \(B^{*}_{n}\), and the amplitudes do not exceed 0.5 for the linear case \((n=m=1)\) [18].

For \(B = 0.245\), the pull-in solutions corresponding to the non-damped vibrations are shown in Fig. 3a, and the behaviors of the solutions are preserved for the different values of \(Q > 0\). If the value of B is close to \(B^{*}_{n}\), for example, when B is equal to 0.242, some values of Q will show different behaviors of the pull-in solutions to the solutions of the systems with damping, see Fig. 3b.

Fig. 3
figure 3

Solution profiles for different values of Q and \(m=0.17\): (a) \(B=0.245\); (b) \(B=0.242\)

Full size image

Figures 2 and 3 demonstrate the dependency of vibration of the microelectromechanical resonator on the strain-rate damping of the materials. Let \(n = 0.54,\,\, m=0.17,\,\, Q=200,\,\, B=0.15, \,\, B^{*}_{n} = 0.239\), and \(T_{imp}=2\), then \({\hat{y}}(2)=0.074\), \(\frac{\text {d} {\hat{y}}}{\text {d} \tau }(2)=0.00012\). The behavior of the solution is presented in Fig. 4a. Let \(n = 0.54,\,\, m=0.17,\,\, Q=130,\,\, B=0.245,\,\, B^{*}_{n} = 0.239\), and \(T_{imp}=3\), then \({\hat{y}}(3)=0.286\), \(\frac{\text {d} {\hat{y}}}{\text {d} \tau }(3)=0.066\). The behavior of the solution is presented in Fig. 4b.

Fig. 4
figure 4

Solution profiles for different values of Q and B: (a) duration of start \(T_{imp}=2\); (b) duration of start \(T_{imp}=3\)

Full size image

Figure 4 shows that the vibrations of the micro-resonator can be controlled. For example, in Fig. 4a the solution is pull-in at \(\tau =6\). When a damped solution exist, we can fix \(T_{imp}=3\), as shown in Fig. 4b. And the analogy analysis for vibrations of microelectromechanical resonators with the linear materials without damping were done in Ref. [17].

5 Hysteresis loop

In this section, the non-dimensional strain-stress relation form of hysteresis loops for power-law materials corresponding to Eq. (2) are constructed by some numerical examples

$$\begin{aligned} \sigma =|\varepsilon |^{n-1}\varepsilon +\eta \,|{\dot{\varepsilon }}|^{m-1}{\dot{\varepsilon }}, \end{aligned}$$

where \(\eta =\frac{c_d}{K}\). The corresponding model with one degree-of-freedom has the form:

$$\begin{aligned} N(y,{\dot{y}})=|y|^{n-1}y+\frac{1}{Q}|{\dot{y}}|^{m-1}{\dot{y}}, \end{aligned}$$
(24)

where \(N:=N(y,{\dot{y}})\) is the generalized force, y is the generalized coordinate, and Q is a reduced damping coefficient.

Fig. 5
figure 5

Hysteresis loops for different values of \(n,\,m,\,Q\), and B: (a) strain-hardening exponent \(n=0.54\), the strain-rate exponent \(m=0.17\); (b) strain-hardening exponent \(n=0.2\), the strain-rate exponent \(m=0.23\)

Full size image

During cyclic deformation, model (24) can be used to show the difference between the loading and unloading curves in the \(N-y\) axes. This phenomenon is called hysteresis. Areas bounded by loading and unloading curves (hysteresis loop), express the energy that is dissipated in each one cycle of the deformation. The energy consumed in each cycle of vibration equals to the work performed by an external force for the cycle. In Fig. 5a and 5b, the hysteresis loops of the initial value problem (19), (20) for different values of \(n,\,\, m,\,\, Q\), and B, are shown. In the linear case \((n=m=1)\), the hysteresis loops for vibration of one degree-of-freedom system with external harmonic force were investigated in Ref. [33]. Our hysteresis loops analysis for vibration of one degree-of-freedom system with electrical force are calculated analogy to the method used in Ref. [33].

The energy dissipation for various exponent values of stiffness and damping terms can be calculated by

$$\begin{aligned} W= & {} \int _{0}^{T} N(y, {\dot{y}}) \text {d}y\nonumber \\= & {} \int _{0}^{T} \left( |y|^{n-1}y+\frac{1}{Q}|{\dot{y}}|^{m-1}{\dot{y}}\right) {\dot{y}} \,\text {d}t, \end{aligned}$$
(25)

where T is the period of one cycle of the oscillation. Using numerical results from Runge-Kutta method based on polynomial interpolation, energy for each cycle is computed by integral (22). The energy lost for first three cycles of oscillation are provided in Fig. 6.

Fig. 6
figure 6

Energy dissipation for three cycle for various value n and m: (a) for \(n = 0.54,\, m={0.11, \,0.14, \,0.17}\); (b) for \(n = 0.45,\,m={0.11,\, 0.14,\, 0.17}\)

Full size image

These results can be useful for design of microelectromechanical resonators of power-law materials with energy considerations due to material internal damping.

6 Approximation of the electrostatic force

Nonlinearity in MEMS system comes from a large variety of sources [34]. One of them is the nonlinearity of the applied force. In this section, we consider an approximation of the electrostatic force \(F_e\) by the following Taylor expansion

$$\begin{aligned} F_{e}=\frac{B}{(1-y)^2}\approx B(1+2y+3y^2+4y^3+\dots ). \end{aligned}$$
(26)

Using the cubic term in Eq. (26), the approximate solutions of the initial value problem (19), (20) are developed, which is able to show the relationship between the amplitudes and frequencies in the case with different values of Q and B. This gives the following equation

$$\begin{aligned} \ddot{y}+\frac{1}{Q}|{\dot{y}}|^{m-1}{\dot{y}}+|y|^{n-1}y\approx B(1+2y+3y^2+4y^3),\nonumber \\ \end{aligned}$$
(27)

which is subject to the initial conditions in Eq. (20).

Fig. 7
figure 7

Behavior of solutions for \(n = 0.54,\,m=0.17\), B is in the neighborhood of \(B^{*}_{n}\): (a) \(B=0.24\); (b) \(B=0.245\)

Full size image

In Figs. 7 and 8, we plot the solutions of the initial problems (19), (20) and (24), (20), which are obtained by using the standard Maple ODE solver with the embedded Runge-Kutta method. Figure 7 shows that when B is in the neighborhood of \(B^{*}_{n}\) and the value of Q is small, the two solutions will agree well. And in Fig. 8, when B is less than \(B^{*}_{n}\) and the values of Q are various, the two solutions also agree well.

Fig. 8
figure 8

Behavior of solutions for \(n = 0.54,\,m=0.17\), \(B<B^{*}_{n}\)

Full size image

There are examples of one degree-of-freedom models with other types of nonlinear damping, which are approximated with cubic term of electrostatic force, as shown in Ref. [34] and its references.

7 Conclusions

A Kelvin-Voigt type model of a microelectromechanical resonator made of power-law materials taking into account the internal strain-rate damping is presented. In the interval (0, 1), the power-law exponents of the materials, which considering the stiffness and the strain-rate damping in the model, can be used in the analysis of the resonator. The pull-in solutions of this model are analyzed under the critical load of the cantilever beam subjected to tip loads. The control of the pull-in solutions is shown based on the duration start of the electrical force. Hysteresis loops are constructed numerically to demonstrate the energy dissipations due to material internal damping. When the voltage is less than the static pull-in critical voltage, for the resonator with internal damping, the amplitudes and frequencies are constructed numerically by using a cubic approximation of the electric force.