Constitutive modeling of viscoelastic–viscoplastic behavior of short fiber reinforced polymers coupled with anisotropic damage and moisture effects

Abstract

In this paper, a combined viscoelasticity–viscoplasticity model, coupled with anisotropic damage and moisture effects, is developed for short fiber reinforced polymers (SFRPs) with different fiber contents and subjected to a variety of strain rates. In our model, a rate-dependent yield surface for the matrix phase is employed to identify initial yielding of the material. When an SFRP is loaded at small deformation before yielding, its viscoelastic behavior can be described using the generalized Maxwell model, while when plasticity occurs, a scalar internal state variable (ISV) is used to capture the hardening behavior caused by the polymeric constituent of the composite. The material degradation due to the moisture absorption of the composite is modeled by employing another type of ISV with different evolution equations. The complicated damage state of the SFRPs is captured by a second rank tensor, which is further decomposed to model the subscale damage mechanisms of micro-voids/cracks nucleation, growth and coalescence. It is concluded that the proposed constitutive model can be used to accurately describe complicated behaviors of SFRPs because the results predicted from the model are in good agreement with the experimental data.

1 Introduction

Short fiber reinforced polymers (SFRPs) are increasingly applied in a wide range of industrial applications due to their attractive properties such as specific strength/stiffness to density ratio, high corrosion resistance, and ease of processing. Especially for the parts used in automotive industry such as dashboards, bumper beams, sunroof frames, and the like, SFRPs has been widely used to replace traditional metallic materials. However, such materials are sensitive to environment conditions and their mechanical behavior is very complicated. Due to the existence of fibers with large aspect ratios in the matrix, SFRPs display a strong directional dependence (anisotropy) in their mechanical, thermal, and damage behaviors. In addition, numerous interdependent phenomena exhibited by SFRPs have been experimentally observed, including rate/time dependence, moisture effects, permanent strain, and material deterioration due to subscale cracks/voids. It is therefore of great interest to formulate an accurate constitutive relationship for such materials to properly capture their plasticity and damage behaviors.

In the past decades, a large number of works have modeled the aforementioned phenomenological behaviors of SFRPs, though only a few of them could cover all or most of those behaviors. The viscoelastic phenomenon of SFRPs has been modeled, in a proper way, by Nguyen et al. [1], and Andriyana et al. [2] with the concept that the entire composite material system is interpreted as a spring-dashpot mechanical device. On the other hand, Klinkel et al. [3] and Notta-Cuvier et al. [4] proposed elastoplasticity models aimed at describing the post-yielding behaviors of SFRPs. Deterioration of the composite material due to damage was theoretically studied by Voyiadjis and Deliktas [5], where anisotropic tensorial damage variables were introduced to represent the material surface discontinuity in the form of microcracks. In addition to the above phenomenological behaviors exhibited by the SFRPs, it is also well known that most polymers absorb moisture in humid conditions, which leads to the degradation of polymer-based composites [6]. This moisture degradation effect on composite materials was recently modeled by Pan and Zhong [7] with the introduction of internal state variables (ISVs). However, none of the current models are capable of capturing the very comprehensive and complicated behaviors of composites as featured with viscoelasticity, viscoplasticity, thermoelasticity, thermoplasticity, and damage, still fewer can reveal the dominant micromechanisms of those materials at different loading and environmental conditions. A general modeling method concerning the complicated mechanical responses of composite materials and their governing mechanisms still remains unclear. Therefore, we propose in this paper a comprehensive theoretical modeling framework based on combined viscoelasticity–viscoplasticity and damage mechanisms to capture the general behavior of composite materials during different strain rate processes in a universal sense by properly addressing the coupling effects of anisotropic damage and moisture effects. The modeling strategy follows the ISV theory presented by Horstemeyer and Bammann [8] and involves the following features.

• (1) The modeling framework in the present study is taken from the works of Nguyen et al. [1], Klinkel et al. [3], and Notta-Cuvier et al. [4], in which SFRPs are considered as an isotropic continuum medium embedded with several bunches of fibers with different orientations. The fibers are assumed to exhibit different behaviors from the matrix phase, so these two constituents are modeled in different manners.

• (2) The elastic behavior of SFRPs is assumed to be time dependent (viscoelasticity). The viscoelastic constitutive equations are taken from the generalized Maxwell model (spring-dashpot mechanical system) that additively decomposes the total stress of the composites into a pure elastic part (spring-like part) and a time-dependent part (dashpot-like part). The viscoelastic model is then modified, with the help of ISVs proposed by Pan and Zhong [7], to account for material degradation due to the moisture absorbed by the SFRPs. The coupling between the elastic and moisture effects is modeled in a similar manner to that used in continuum damage mechanics when dealing with damage effects.

• (3) The viscoplasticity is modeled using the polymer ISV equations proposed by Bouvard et al. [9]. A scalar ISV is introduced to physically represent the internal strain caused by polymeric entanglement points, which is assumed, based on molecular dynamic simulations, to be the micromechanisms that govern the macroscopic hardening exhibited by the material. The rate-dependent yield surface of the composites is a modification of the metallic crystal plasticity model [10] for polymeric materials.

• (4) The coupling between damage and viscoelasticity–viscoplasticity is achieved by employing the effective variable concept [11] and the anisotropic tensorial damage variable is taken from Murakami [12]. Based on experimental observations obtained by Rolland et al. [13,14], the total damage tensor is further additively decomposed into damage nucleation, growth, and coalescence tensors. Each of them is determined with physically based evolution equations [15]. Those equations are different from the damage evolution equations of composites used by Voyiadjis and Deliktas [5], which were motivated by the unified damage evolution equations of Lemaitre and Chaboche [16].

Standard notation is used throughout this paper. For example, tensors are denoted with bold face characters with capital letters to represent the second and fourth order tensors and lower case letters of the vectors. Scalar variables are represented with standard text font. The symbol colon “:” represents the scalar product of two second order tensors $\varvec{A}$ and $\varvec{B}$, in which the index notation is $\varvec{A}:\varvec{B} \Rightarrow A_{ij} :B_{ij}$. Other tensor operations used in this paper include: $\varvec{AB} = \varvec{A} \cdot \varvec{B} \Rightarrow A_{ij} B_{jk}$, $\varvec{a} \otimes \varvec{b} \Rightarrow \left( {\varvec{a} \otimes \varvec{b}} \right)_{ij} = a_{i} b_{j}$, and $\left\| \varvec{A} \right\| = \sqrt {A_{ij} A_{ij} }$.

2 Constitutive formulation

This section is dedicated to the constitutive description of the coupled thermal viscoelastic–viscoplastic damage model for SFRPs. It is assumed that these composites are made of a polymeric matrix uniformly embedded with several short fiber families. (Fibers that share a similar orientation in the matrix phase are grouped into one family.)

Due to the large aspect ratio of the short fibers, they are assumed to be one-dimensional media that deform only along their own direction. This method of approximating the fiber phase as a one-dimensional medium has been adopted by many other researchers [1,3,4], and is extended in this study by considering a more general case that takes both elastic and inelastic behaviors of the composites into account. It is worth mentioning that the polymeric materials, when reinforced by short brittle fibers, usually exhibit small strains before their failure [17]. It is therefore reasonable to decompose the total strain of the matrix and fiber families in the framework of infinitesimal deformation into the following components

$$ \varvec{\varepsilon}=\varvec{\varepsilon}_{\text{ve}}^{m} +\varvec{\varepsilon}_{\theta }^{m} +\varvec{\varepsilon}_{\text{vp}}^{m}, \quad \varepsilon^{fi} = \varepsilon_{\text{e}}^{fi} + \varepsilon_{\theta }^{fi} \, \left( {i = 1,2, \ldots, n} \right), $$

(1)

where the superscripts “m” and “f” denote the matrix and the fiber phases, respectively. Because there may be more than one fiber family in the material system, the superscript “i” indicates different fiber families. The total local strain of the matrix phase is assumed to be the same as that of the composites ($\varvec{\varepsilon}$) and is decomposed into the components of viscoelasticity ($\varvec{\varepsilon}_{\text{ve}}^{m}$), thermal expansion ($\varvec{\varepsilon}_{\theta }^{m}$), and the viscoplasticity ($\varvec{\varepsilon}_{\text{vp}}^{m}$). The one-dimensional fiber family is assumed to exhibit only pure elasticity ($\varepsilon_{\text{e}}^{fi}$) and thermal expansion ($\varepsilon_{\theta }^{fi}$) due to the brittle nature of many fiber materials such as glass and carbon fibers. It should be noticed that the damage deformation in the current kinematic formulation is not taken as an independent component, but is considered to implicitly occur in both the elastic state and the inelastic state [5]. The local strain $\varepsilon^{fi}$ measuring the extension/compression of the fiber families can be obtained by using a set of structure tensors [1,3,4] as follows

$$ \varepsilon^{fi} = \varvec{A}^{fi} :\varvec{\varepsilon},\quad \varvec{A}^{fi} = \varvec{a}^{i} \otimes \varvec{a}^{i} \,\left( {i = 1,2, \ldots, n} \right), $$

(2)

where the vector $\varvec{a}^{i}$ represents the orientation of the i-th fiber family. The structure tensor $\varvec{A}^{fi}$ can be considered as a projection tensor that maps the total strain ($\varvec{\varepsilon}$) of the composites into a local one-dimensional strain along the fiber direction. The thermal expansion of both matrix and fiber families are assumed to be linearly dependent on the temperature change, so the corresponding strain components are defined as

$$\begin{gathered} \varvec{\varepsilon }_{\theta }^{m} = \varvec{\beta }_{\theta }^{m} \times \left( {\theta - \theta _{{{\text{ref}}}} } \right), \hfill \\ \varepsilon _{\theta }^{{fi}} = \beta _{\theta }^{{fi}} \times \left( {\theta - \theta _{{{\text{ref}}}} } \right)\quad \left( {i = 1,2, \ldots, n} \right), \hfill \\ \end{gathered}$$

(3)

where $\theta$ and $\theta_{\text{ref}}$ are the current temperature and the reference temperature, respectively. The term $\beta_{\theta }^{fi}$ represents scalar coefficients of thermal expansion (CTE) for the fiber families, while a tensorial CTE ($\varvec{\beta}_{\theta }^{m}$) is used for the matrix phase. When the material made of the matrix phase deforms equally along different directions under a thermal condition, $\varvec{\beta}_{\theta }^{m}$ becomes an isotropic tensor and can be fully described with a scalar such as $\varvec{\beta}_{\theta }^{m} = \beta_{\theta }^{m} \varvec{I},$ where $\varvec{I}$ is the identity tensor. The viscoplastic strain component ($\varvec{\varepsilon}_{\text{vp}}^{m}$) of the matrix will be determined by a flow rule given in Sect. 2.2.

2.1 Viscoelasticity coupled with moisture effects

Based on the thermodynamic framework proposed by Notta-Cuvier et al. [4], the total stress ($\varvec{\sigma}$) of the composites can be written in terms of the local stress of the fiber families ($\varvec{\sigma}^{fi}$) and the matrix phase ($\varvec{\sigma}^{m}$) as the following

$$ \varvec{\sigma}= \mathop \sum \limits_{i = 1}^{n} \varphi^{fi} \varvec{A}^{i}\varvec{\sigma}^{fi} \varvec{A}^{i} + \varphi^{m}\varvec{\sigma}^{m} , $$

(4)

where $\varphi^{fi}$ and $\varphi^{m}$ are the volume fractions of the i-th fiber family and the matrix phase, respectively. The local stress $\varvec{\sigma}^{fi}$ is defined with respect to the material coordinate system and the structure tensor $\varvec{A}^{i}$ in Eq. (4) acts as a transformation tensor that maps $\varvec{\sigma}^{fi}$ along the global (loading) system. The polymeric matrix phase is assumed to have a viscoelastic behavior before yielding, so its corresponding local stress ($\varvec{\sigma}^{m}$) can be described by the generalized Maxwell model as

$$ \varvec{\sigma}^{m} =\varvec{\sigma}_{\text{eq}}^{m} + \mathop \sum \limits_{j = 1}^{k}\varvec{\sigma}_{\text{neq}}^{mj} , $$

(5)

where $\varvec{\sigma}_{\text{eq}}^{m}$ is the equilibrium stress that describes the pure elasticity of the matrix material while a set of non-equilibrium stresses $\varvec{\sigma}_{\text{neq}}^{mj}$ denote the time-dependent (viscosity) nature of the polymeric matrix. Based on the stress decomposition in Eq. (5), constitutive relationships can be obtained for $\varvec{\sigma}_{\text{eq}}^{m}$ (linear elasticity) and $\varvec{\sigma}_{\text{neq}}^{mj}$ (linear viscoelasticity) as

$$ \begin{aligned}\varvec{\sigma}_{\text{eq}}^{m} &= 2\mu^{m} \left( \theta \right)\varvec{\varepsilon}_{\text{ve}}^{m} + \lambda^{m} \left( \theta \right){\text{tr}}\left( {\varvec{\varepsilon}_{\text{ve}}^{m} } \right)\varvec{I}, \\\varvec{\sigma}_{\text{neq}}^{mi} & = \mathop \int \limits_{0}^{t} \varrho_{j} { \exp }\left[ { - \frac{{\left( {t - x} \right)}}{{\tau_{j} }}} \right]\frac{{\partial\varvec{\varepsilon}_{\text{ve}}^{m} \left( x \right)}}{\partial x}{\text{d}}x\quad \left( {j = 1,2, \ldots, N} \right), \\ \end{aligned} $$

(6)

where t represents the current time instant and $\varrho_{j}$ is a non-dimensional free energy factor that is defined as the ratio of the instantaneous elastic stored energy to the total free energy in the material [18]. The relaxation time $\tau_{j}$ is defined as the ratio of viscosity to stiffness of the material, which can physically represent the time that the material needed to reach an equilibrium state in a stress relaxation process. The temperature-dependent shear modulus $\mu^{m} \left( \theta \right)$ and Lamé constant $\lambda^{m} \left( \theta \right)$ can be expressed in terms of the Young’s modulus $E^{m} \left( \theta \right)$ and Poisson’s ratio $v^{m}$ of the polymeric matrix material as follows

$$ \begin{aligned} \lambda^{m} \left( \theta \right) & = \frac{{E^{m} \left( \theta \right)v^{m} }}{{\left( {1 + v^{m} } \right)\left( {1 - 2v^{m} } \right)}},\quad \mu^{m} \left( \theta \right) = \frac{{E^{m} \left( \theta \right)}}{{2\left( {1 + v^{m} } \right)}}, \\ E^{m} \left( \theta \right) & = C_{1}^{m} + C_{2}^{m} \left( {\theta - \theta_{\text{ref}} } \right), \\ \end{aligned} $$

(7)

where $C_{1}^{m}$ and $C_{2}^{m}$ are two material constants. For the fiber families, simple one-dimensional linear elasticity equations are used, given as the following

$$ \begin{aligned} & \sigma^{fi} = E^{fi} \left( \theta \right)\varepsilon_{\text{e}}^{fi}, \\ & E^{fi} \left( \theta \right) = C_{1}^{fi} + C_{2}^{fi} \left( {\theta - \theta_{\text{ref}} } \right)\quad \left( {i = 1,2, \ldots, n} \right), \end{aligned} $$

(8)

where $C_{1}^{fi}$ and $C_{2}^{fi}$ are two material constants for the i-th fiber family. It is well known that polymeric materials and their corresponding composites are sensitive to humidity changes in the environment due to the fact that polymer-based materials absorb moisture in humid conditions. Moisture absorption, observed by experiments [6], leads to a strong degradation of mechanical properties of the composites. Therefore, we modify the constitutive relationships of the matrix and fiber families (Eqs. (6) and (8)) by employing the moisture effect equations proposed by Pan and Zhong [7]. The modified equations incorporate the moisture degradation effect and are given as

$$\begin {aligned} &\varvec{\sigma}_{\text{eq}}^{m} = \left[ {2\mu^{m} \left( \theta \right)\varvec{\varepsilon}_{\text{ve}}^{m} + \lambda^{m} \left( \theta \right){\text{tr}}\left( {\varvec{\varepsilon}_{\text{ve}}^{m} } \right)\varvec{I}} \right] \\ &\quad\times \left[ {1 - \varphi^{f} \beta_{1} \left( {\varphi^{f} } \right)\alpha } \right],\\ &{\text{with}} \; \beta_{1} \left( {\varphi^{f} } \right) = \bar{\beta }_{1} \times \left( {\varphi^{f} } \right)^{2}, \\ &\sigma^{fi} = E^{fi} \left( \theta \right)\varepsilon_{\text{e}}^{fi} \times \left( {1 - \beta_{2} \alpha^{i} } \right), \\ &\varphi^{f}= \mathop \sum \limits_{i = 1}^{n} \varphi^{fi} ,\quad \alpha = \frac{1}{n}\mathop \sum \limits_{i = 1}^{n} \alpha^{i} , \\ \end{aligned}$$

(9)

where $\bar{\beta }_{1}$ and $\beta_{2}$ are two material parameters that physically represent the degrees to which the moisture affects the stiffness of the matrix and fiber phase, respectively. $\alpha^{i}$ is an ISV that represents the swelling process of the i-th fiber family, which varies from 0 (dry state) to 1 (saturated state). To simplify the model, the average value (α) of these ISVs is used for the matrix phase instead of introducing a new ISV for that phase. In order to solve Eq. (9), evolution equations for $\alpha^{i}$ are needed. Here, the following equations proposed by Pan and Zhong [7] are used

$$ \frac{{\dot{\alpha }^{i} }}{{1 - \alpha^{i} }} = \frac{{\varphi^{fi} q^{i} \mu^{fi} }}{D}\quad \left( {i = 1,2, \ldots, n} \right), $$

(10)

where $q^{i}$ is a material constant and D is defined as a fiber content independent parameter that governs the rate of energy dissipation as well as the moisture absorption. $\mu^{fi}$ is the shear modulus for the ith fiber family.

2.2 Viscoplasticity

Because of our assumption that the viscoplastic behavior of a polymer-based composite is contributed solely by its polymeric constituent, the ISV proposed by Bouvard et al. [9] for polymers is used in this model to capture the viscoplasticity of the composites. Considering that fiber reinforced composites usually fail at small strain levels, only the scalar strain-like ISV ($\xi^{m}$) is used, which physically represents internal strain due to the presence of defects/obstacles such as entanglement points in the polymers. It is well known that the intensity of the topological restriction of molecular motion by other chains (entanglement density) has a significant effect on the material behavior of polymers. In this paper, we consider this entanglement to be a microscopic defect (similar to the dislocation defect for metallic materials) that constrains the motion of polymer molecular chain, thus, we introduce an internal strain ($\xi^{m}$) to indicate such a defect-induced internal strain. In the view of thermodynamics, there should be a thermodynamic force (also the thermodynamic conjugate to the internal strain) that governs the change of this internal strain; this thermodynamic stress is given below Eq. (12) and is considered in our work as the isotropic hardening variable used in classical plasticity. The evolution equation for $\xi^{m}$ is given as

$$ \dot{\xi }^{m} = H^{m} \left( {1 - \frac{{\xi^{m} }}{{\xi^{*m} }}} \right)\dot{\gamma }_{\text{vp}}^{m} ,\quad \dot{\xi }^{*m} = \left[ {\xi_{\text{sat}}^{*m} \left( \theta \right) - g_{0}^{m} \left( \theta \right)\xi^{*m} } \right]\dot{\gamma }_{\text{vp}}^{m} , $$

(11)

where $H^{m}$ is a temperature independent hardening modulus; $\xi^{*m}$ is the internal strain threshold for polymer chain slippage, with a temperature-dependent saturated value of $\xi_{\text{sat}}^{*m} \left( \theta \right)$; $\dot{\gamma }_{\text{vp}}^{m}$ is the viscoplastic strain rate of the polymeric matrix and will be determined by the corresponding flow rule; $\xi_{\text{sat}}^{*m} \left( \theta \right)$, $g_{0}^{m} \left( \theta \right)$, and the initial value ($\xi_{0}^{*m}$) of $\xi^{*m}$ at time $t = 0$ are assumed to have a linear dependence on the temperature as

$$ \begin{aligned} \xi_{\text{sat}}^{*m} \left( \theta \right) & = C_{3}^{m} + C_{4}^{m} \left( {\theta - \theta_{\text{ref}} } \right),\quad g_{0}^{m} \left( \theta \right) = C_{5}^{m} + C_{6}^{m} \left( {\theta - \theta_{\text{ref}} } \right), \\ \xi_{0}^{*m} \left( \theta \right) & = C_{7}^{m} + C_{8}^{m} \left( {\theta - \theta_{\text{ref}} } \right). \\ \end{aligned} $$

(12)

The thermodynamic stress-like conjugate ($\kappa^{m}$) with respect to $\xi^{m}$ is taken from the work of Bouvard et al. [9] as $\kappa^{m} = 2C_{\kappa }^{m} \mu^{m} \left( \theta \right)\xi^{m}$, where $C_{\kappa }^{m}$ is a material parameter. In viscoplasticity, $\kappa^{m}$ acts as an isotropic hardening variable and will be introduced into the flow rule to describe the expansion of the yield surface. Based on this, the viscoplastic flow rule for the composites is given following Bammann’s approach [10] as

$$ \dot{\varvec{\varepsilon }}_{\text{vp}}^{m} = \frac{{\dot{\gamma }_{{{\text{vp}}0}}^{m} }}{\sqrt 2 }{ \sinh }\left[ {\frac{{\tau_{\text{eq}}^{m} - Y^{m} \left( \theta \right)}}{{N^{m} \left( \theta \right)}}} \right]\varvec{N}_{\text{vp}}^{m} , $$

(13)

where $\dot{\gamma }_{{{\text{vp}}0}}^{m}$ is a parameter representing the reference viscoplastic strain rate; $\tau_{\text{eq}}^{m}$ is defined as the effective shear stress acting on the polymeric matrix to cause its viscoplastic flow, and can be calculated based on the local stress $\varvec{\sigma}^{m}$ and hardening variable $\kappa^{m}$ as $\tau_{\text{eq}}^{m} = \frac{{\varvec{\sigma}^{{m^{\prime } }} }}{\sqrt 2 } - \kappa^{m}$, where “′” is a deviatoric operator; $\varvec{N}_{\text{vp}}^{m}$ determines the flow direction of the matrix phase and is calculated as $\varvec{N}_{\text{vp}}^{m} = \frac{{\varvec{\sigma}^{{m^{\prime } }} }}{{\left| {\left| {\varvec{\sigma}^{{m^{\prime } }} } \right|} \right|}}$; $Y^{m} \left( \theta \right)$ and $N^{m} \left( \theta \right)$ are two parameters that represent the rate-independent and rate-dependent components of the initial yield surface [10] and are assumed to be temperature dependent as $Y^{m} \left( \theta \right) = C_{9}^{m} + C_{10}^{m} \left( {\theta - \theta_{\text{ref}} } \right)$ and $N^{m} \left( \theta \right) = C_{11}^{m} + C_{12}^{m} \left( {\theta - \theta_{\text{ref}} } \right)$.

2.3 Anisotropic damage

The modeling of progressive damage phenomena in SFRPs [13,14] is addressed in this work using the physics-based continuum damage mechanics method [15], which considers the deterioration of the composites as a process of microvoids/cracks nucleation, growth and coalescence. In general, the damage process of the fiber reinforced composites under deformation is a complicated procedure including fiber breakage, interfacial debonding, matrix cracking [13,14]. However, for models aimed at capturing damage degradation phenomena of composites at macroscale, those damage mechanisms have to be properly represented in the models. In the present model, a single damage variable is used to represent all the damage mechanisms occurring at the microscale. This approach of treating the damage mechanisms was also used by Voyiadjis and Deliktas [5]. For a more complicated damage model that uses different equations for different damage mechanisms, the reader is referred to the work of He [19]. In order to capture the anisotropic damage nature of fiber reinforced composite materials, a second damage tensor, $\varvec{\phi}$, is introduced and further additively decomposed as follows

$$ \dot{\varvec{\phi }} = \dot{\varvec{\phi }}_{\eta } + \dot{\varvec{\phi }}_{\nu } + \dot{\varvec{\phi }}_{c} , $$

(14)

where the principal components of the total damage tensor ($\varvec{\phi}$) physically represent the area reduction densities measured at three principal planes of the material system [12]. $\varvec{\phi}_{\eta }$, $\varvec{\phi}_{\nu }$, and $\varvec{\phi}_{c}$ are the second order damage tensors for nucleation ($\eta$), growth ($\nu$), and coalescence ($c$), respectively. In our work, the damage nucleation represents the point at which the microscopic voids/cracks start to appear in the material during deformation; the volume or area change of these nucleated microvoids/cracks is termed as damage growth; when the voids/cracks grow up to the point that adjacent microvoids/cracks link together, such process is termed as damage coalescence. The total damage tensor $\varvec{\phi}$ could not be calculated until all of its components are uniquely determined by corresponding evolution equations.

The evolution equation for the damage nucleation tensor is obtained by slightly modifying the anisotropic damage law proposed by Hammi and Horstemeyer [15] and Lemaitre et al. [20], which is given as

$$ \dot{\varvec{\phi }}_{\eta } = \left( {\frac{{Y_{\text{e}} }}{H}} \right)^{h} \frac{\chi }{{K_{\text{IC}} }}\varvec{P}:\left| {\dot{\varvec{\varepsilon }}} \right|, $$

(15)

where $Y_{\text{e}}$ is the strain energy release rate density of the composites, which can be expressed in terms of energies from the matrix and fiber families as $Y_{\text{e}} = \frac{1}{2}\varvec{\sigma}^{m} :\varvec{\varepsilon}_{\text{ve}}^{m} + \frac{1}{2}\mathop \sum \nolimits_{i = 1}^{n} \sigma^{fi} \varepsilon_{\text{e}}^{fi}$. It is well understood that the material damage process is also an energy-release process. The high speed of damage evolution in materials usually results in a high energy dissipation rate. Therefore, according to Lemaitre et al. [20], the damage evolution rate is assumed to be proportional to the strain energy release rate as given in Eq. (15), $H$ and $h$ are two material constants, $K_{\text{IC}}$ is the fracture toughness of the bulk composite material, the parameter $\chi$ has two definitions depending on whether the fiber fracture ($\chi = d^{1/2} /\varphi^{f1/3}$) or the crazing of polymer matrix ($\chi = M_{\text{w}}$) is the dominant mechanism of the void/crack nucleation in composites, where $d$ is the average length of the fibers and $M_{\text{w}}$ is the molecular weight of the polymeric matrix [21]. When $\left| \cdot \right|$ is applied to a second order tensor, it would return the absolute value of its principal components. The fourth order tensor $\varvec{P}$ is introduced to acount for the effects of loading/stress states and the density and orientation of microvoids/cracks during damage nucleation [15]. Its index notation in the Cartesian coordinate system is represented as

$$ P_{{\left( {ijkl} \right)}} = \frac{1}{{C_{\text{load}} }}\left[ {1 + \frac{{\rho_{{\left( {ij} \right)}} \left(\varvec{\phi}\right)}}{\varvec{\phi}}N_{{c\left( {ij} \right)}} } \right]\delta_{{\left( {ik} \right)}} \delta_{{\left( {jl} \right)}} \quad \left( {{\text{no}}\;{\text{sum}}\;{\text{on}}\;i\;{\text{and}}\;j} \right), $$

(16)

where $\delta_{{\left( {ik} \right)}}$ and $\delta_{{\left( {jl} \right)}}$ are the Kronecker delta; $C_{\text{load}}$ is a parameter that has different values for different stress/loading states such as tension, compression and torsion. The choice of $C_{\text{load}}$ is dependent on the sign of the components of the deformation direction tensor $N_{{c\left( {ij} \right)}}$ of the composites, as illustrated in the following equation

$$C_{{{\text{load}}}} = {\text{ }}\left\{ {\begin{array}{*{20}l} {C_{{{\text{tension}}}} } \hfill &\quad {{\text{if}}\quad N_{{c\left( {ij} \right)}} \geqslant 0,\quad i = j}, \hfill \\ {C_{{{\text{compression}}}} } \hfill &\quad {{\text{if}}\quad N_{{c\left( {ij} \right)}} < 0,\quad i = j} \hfill \\ {C_{{{\text{torsion}}}} } \hfill &\quad {\forall N_{{c\left( {ij} \right)}} ,\quad i \ne j}, \hfill \\ \end{array} } \right., $$

(17)

where the direction tensor is calculated with $\varvec{N}_{c} = \frac{\varvec{\sigma}}{{\left\|\varvec{\sigma}\right\|}}$; $\rho_{{\left( {ij} \right)}} \left(\varvec{\phi}\right)$ in Eq. (16) is a symmetric damage density tensor representing the amount and orientation of microvoids/cracks in the material system and can be expressed as [22]

$$ \varvec{\rho}\left(\varvec{\phi}\right) = \frac{15}{8\uppi }\left[ {\iint {\rho \left( \varvec{n} \right)\varvec{n} \otimes \varvec{n}{\text{d}}S - \frac{{\rho_{0} }}{5}\varvec{I}}} \right], $$

(18)

where $\rho \left( \varvec{n} \right)$ is a microvoids/cracks area density distribution function and is direction dependent ($\varvec{n}$ is a direction vector), $\rho_{0}$ represents the density of all damages that occur within a representative volume element (RVE).

Apart from damage nucleation, growth of microvoids and cracks is another mechanism that might affect the degradation of the composites. Although in most cases, the microvoids/cracks nucleated within the composites have irregular geometric features and would change both their shapes and volumes during the deformation process, we assume that all the nucleated voids/cracks can be treated as having spherical shapes and only undergo volumetric change during the entire deformation process. Thus, it would be sufficient to use a scalar variable to describe the damage growth state; its evolution equation is given as [23]

$$ \dot{\phi }_{v} = \frac{{\sqrt 3 \aleph \dot{\varvec{\varepsilon }}}}{{2\left( {1 - g} \right)}}\sinh \left[ {\sqrt 3 \left( {1 - g} \right)\frac{{\sqrt 2 I_{1} }}{{3\sqrt {J_{2} } }}} \right], $$

(19)

where $\aleph$ is a material constant and $g$ represents the strain hardening effect contributed by the polymeric matrix phase. It is well known that the damage growth is strongly dependent on the stress triaxiality state ($I_{1} /\sqrt {J_{2} }$) of the material, where $I_{1}$ and $J_{2}$ are two stress invariants defined as $I_{1} = {\text{tr}}\left(\varvec{\sigma}\right)$ and $J_{2} = \frac{1}{2}\varvec{\sigma}^{\prime } :\varvec{\sigma}^{\prime }$, respectively. The damage growth tensor, $\varvec{\phi}_{\nu }$, is then expressed as a isotropic tensor as $\varvec{\phi}_{\nu } = \varvec{\phi}_{v} \varvec{I}$.

Similar to the microvoids/cracks nucleation model given in Eq. (15), the tensor $\dot{\varvec{\phi }}_{c}$ that captures the change of damage rate due to voids/cracks coalescence is also assumed to be governed by the total strain rate of the composites. According Ref. [15], that tensor can be expressed as

$$ \dot{\varvec{\phi }}_{c} = C_{c} \left[ {\frac{{Y_{\text{e}} }}{{S_{c} }}} \right]^{{s_{c} }}\varvec{\varPi}\left(\varvec{\phi}\right):\left| {\dot{\varvec{\varepsilon }}} \right|,\quad \varPi_{{\left( {ijkl} \right)}} = \left( {\phi_{{\left( {ij} \right)}} - \phi_{c} } \right)\delta_{{\left( {ik} \right)}} \delta_{{\left( {jl} \right)}} , $$

(20)

where $C_{c}$, S_c, and s_c are three material constants that need to be identified through appropriate damage quantification tests. $\phi_{c}$ is a critical value of $\phi_{{\left( {ij} \right)}}$ that governs the initiation of damage coalescence. After choosing the damage variables and their corresponding evolution equations, the damage degradation effects on the mechanical properties of the composite materials can be addressed within the framework of continuum damage mechanics using the concept of effective stress [11] as the following

$$ \tilde{\varvec{\sigma }} = \varvec{T}\left(\varvec{\phi}\right):\varvec{\sigma}\text{,} $$

(21)

where the Cauchy stress $\varvec{\sigma}$ is transformed, through a fourth order tensor $\varvec{T}\left(\varvec{\phi}\right)$, into an effective stress tensor $\tilde{\varvec{\sigma }}$. It is defined with respect to an equivalent net area without damage. The strain equivalence principle [16] is then adopted. This principle assumes that the constitutive equation for a damaged material can be obtained by simply replacing the stress of the corresponding undamaged material with an effective stress, while keeping the strain unchanged. The damage effect tensor, $\varvec{T}\left(\varvec{\phi}\right)$ is given in a diagonal matrix form [15] as

$$ \varvec{T}\left(\varvec{\phi}\right) = \left[ {\begin{array}{*{20}c} {\frac{1}{{\sqrt {1 - \phi_{{\left( {11} \right)}} } }}} & 0 & 0 & 0 & 0 & 0 \\ 0 & {\frac{1}{{\sqrt {1 - \phi_{{\left( {22} \right)}} } }}} & 0 & 0 & 0 & 0 \\ 0 & 0 & {\frac{1}{{\sqrt {1 - \phi_{{\left( {33} \right)}} } }}} & 0 & 0 & 0 \\ 0 & 0 & 0 & {\frac{1}{{\sqrt {1 - \phi_{{\left( {12} \right)}} } }}} & 0 & 0 \\ 0 & 0 & 0 & 0 & {\frac{1}{{\sqrt {1 - \phi_{{\left( {13} \right)}} } }}} & 0 \\ 0 & 0 & 0 & 0 & 0 & {\frac{1}{{\sqrt {1 - \phi_{{\left( {23} \right)}} } }}} \\ \end{array} } \right]. $$

(22)

2.4 Adiabatic heating

The viscoplasticity of composites is a dissipative process that is usually associated with significant amounts of energy released in the form of heat. When the material is loaded at a low strain rate level, the heat introduced by viscoplasticity has sufficient time to conduct through the material. However, in a high or even moderate strain rate condition [24], the temperature increase in the material becomes adiabatic because the time afforded for such heat conduction is very short. Based on that, the localized temperature change in the composites is assumed to be solely contributed by the viscoplasticity of the polymeric matrix phase and has the following expression

$$ \dot{\theta } = \frac{{\omega \varphi^{m}\varvec{\sigma}^{m} :\dot{\varvec{\varepsilon }}_{\text{vp}}^{m} }}{{\rho_{c} C_{c} }}, $$

(23)

where $\rho_{c}$ is the average mass density of the composite material and $C_{c}$ is the average specific heat capacity. Parameter $\omega$ is a conversion factor that denotes the fraction of the viscoplastic dissipation ($\varvec{\sigma}^{m} :\dot{\varvec{\varepsilon }}_{\text{vp}}^{m}$) which has been converted to heat.

3 Examples of numerical application

Before numerical implementation of the developed model, a flowchart that illustrates the organization of the paper is given in Fig. 1, which follows a sequence of model development, calibration, and validation. Model development was presented in the previous section and in this section, model calibration and validation will be given. The deformation and damage behaviors of two different short fiber reinforced composites are simulated using the developed constitutive model. The first composite is a unidirectional sisal fiber reinforced benzylated wood [7,25]. This example is used to calibrate the material constants related to the moisture degradation effects on the mechanical properties of the short fiber reinforced composites and to validate the accuracy of the present model. It is worth mentioning that due to the lack of experimental data of moisture degradation effects and the evolution of absorbed water content in polymer-based composites, we only use wood-based composites here to investigate the capacity of the present model in capturing the moisture effects. An experimental study on polymer-based composites will be conducted in the future. The second material is a short glass fiber reinforced polyamide 6,6 [2,13,14,17], which is used for testing the capacity of our model in predicting other material behaviors such as viscoelasticity, viscoplasticity, and damage. The constitutive equations given in Sect. 2 are rendered into Matlab code to predict all the aforementioned mechanical behaviors.

Fig. 1

Proposed theoretical approach of model development, calibration, and validation

In the first example, three samples of unidirectional sisal fiber reinforced benzylated woods with different volume fractions (10.2%, 19.7%, and 30.4%) were immersed in water for moisture absorption for a given period of time, and then their elastic moduli along the fiber direction were measured through mechanical tests [25]. In the current model, the predicted elastic modulus ($E_{{\left( {11} \right)}}$) of the composites is obtained by taking the derivative of the total stress $\sigma_{{\left( {11} \right)}}$ in Eq. (4) with respect to the total viscoelastic strain ($\varepsilon_{{{\text{ve}}\left( {11} \right)}} = \varepsilon_{{{\text{ve}}\left( {11} \right)}}^{m}$) as follows:

$$ \begin{aligned} E_{{\left( {11} \right)}} & = \left. {\frac{{{\text{d}}\sigma_{{\left( {11} \right)}} }}{{{\text{d}}\varepsilon_{{{\text{ve}}\left( {11} \right)}}^{m} }}} \right|_{{\varepsilon_{{{\text{ve}}\left( {11} \right)}}^{m} = 0}} \\ & = \left. {\frac{{\varphi^{f} {\text{d}}\sigma^{f} + \varphi^{m} {\text{d}}\sigma_{{{\text{eq}}\left( {11} \right)}}^{m} + \varphi^{m} \mathop \sum \nolimits_{j = 1}^{k} {\text{d}}\sigma_{{{\text{neq}}\left( {11} \right)}}^{mj} }}{{{\text{d}}\varepsilon_{{{\text{ve}}\left( {11} \right)}}^{m} }}} \right|_{{\varepsilon_{{{\text{ve}}\left( {11} \right)}}^{m} = 0}} \\ & = \varphi^{f} \left[ {E^{f} \times \left( {1 - \beta_{2} \alpha } \right)} \right] + \varphi^{m} \\ &\quad \left\{ {\left( {2\mu^{m} + \lambda^{m} } \right) \times \left[ {1 - \bar{\beta }_{1} \times \left( {\varphi^{f} } \right)^{3} \alpha } \right]} \right\} + 2\varphi^{m} \mathop \sum \limits_{j = 1}^{k} \varrho_{j} . \\ \end{aligned} $$

(24)

In the above equation, we ignore the temperature dependence of elastic constants of the material and consider only a single viscous contribution by letting $k = 1$ , such that $\varrho = \varrho_{1}$. Because the matrix phase is reinforced by unidirectional fibers, the number of fiber families is reduced to 1 (i = 1) and the elastic modulus of the fiber phase along the loading direction (same as the fiber direction) is denoted as $E^{f} = E^{f1}$. Similarly, the ISV representing the absorbed water content of the fiber family becomes $\alpha = \alpha^{1}$. Combining Eq. (24) and the evolution equation for α (Eq. 10), there are five parameters ($\lambda^{m}$, $\varrho$, $\bar{\beta }_{1}$, $\beta_{2}$, and $\bar{D} = \frac{q}{D}$) that need to be calibrated before the model can be used for numerical analysis. Other elastic constants can be found in published literature [7,26] as $E^{f} = 37,\!000\,{\text{MPa}}$, $\mu^{f} = 9818.2\,{\text{MPa}}$, and $\mu^{m} = 140\,{\text{MPa}}$. In order to calibrate the first four parameters ($\lambda^{m}$, $\varrho$, $\bar{\beta }_{1}$, $\beta_{2}$), theoretical predictions of elastic moduli ($E_{{\left( {11} \right)}}$) of the composites at dry ($\alpha = 0$) and moisture saturation ($\alpha = 1$) states with respect to different fiber volume fractions are first obtained by introducing these two conditions ($\alpha = 0$ and $\alpha = 1$) into Eq. (24). The predicted results are then fitted to the experimental data [7,25] to determine values for the four parameters. The curve fitting processes are plotted in Figs. 2 and 3 with the material constants determined as $\lambda^{m} = 220\,{\text{MPa}}$, $\varrho = 8\,{\text{MPa}}$, $\bar{\beta }_{1} = 146$, and $\beta_{2} = 0.662$.

Fig. 2

Calibration of material constants $\lambda^{m}$ and $\varrho$

Fig. 3

Calibration of material constants $\bar{\beta }_{1}$ and $\beta_{2}$

To calibrate the parameter $\bar{D} = \frac{q}{D}$, the moisture evolution equation (Eq. 10) is solved for α and the result is fitted to the experimental data for the composite sample with fiber volume fraction of $0.197$. The calibration process is drawn in Fig. 4 and the calibrated parameter $\bar{D} = 3.9 \times 10^{ - 9}$. After calibrating the five parameters, the present model is used to predict the moisture effect on the elastic modulus of the material, and the numerical results are compared with the experimental data [7,25] to validate this model. The comparison results are displayed in Fig. 5. From that figure it can be seen that the calculated elastic moduli of the composites with fiber volume fraction of 0.197 and 0.304 are in good agreement with the experimental data. However, for the composite with a fiber volume fraction of 0.102, the present model overestimates the evolution of its elastic modulus. By carefully checking the model and the experimental data, we found that the difference between the numerical predictions and the experimental results in Fig. 5 may arise from the inaccurate prediction of the initial modulus ($E_{{\left( {11} \right)}}$) of the composite in its dry state ($\alpha = 0$). This inaccuracy might be caused by the inconsistency of the experimental data taken from Pan and Zhong [7] and Lu et al. [25]. As shown in Fig. 2, the experimental data show a linear dependence of the modulus on the fiber volume fraction. However, in Fig. 3, this dependence becomes nonlinear. Since our model is calibrated using the linear dependence of modulus on the fiber volume fraction as given in Fig. 2, the numerical prediction of the modulus at the very beginning in Fig. 5 does not agree well with the experimental data. One way to improve the agreement is to test more samples and obtain more consistent average experimental data for the modulus evolution, as well as its dependence on the fiber volume fraction.

Fig. 4

Calibration of material constant $\bar{D}$. The fiber volume fraction of the composites is 0.197

Fig. 5

Comparison of the numerical prediction and experimental data of the elastic modulus evolution

In the second example, the present model is calibrated for a short E-glass fiber reinforced polyamide 6,6 (PA66GF), and the calibrated model is then used for numerical analysis to predict the damage-coupled viscoelasticity, viscoplasticity of that material. The numerical results are compared with the experimental data obtained by Andriyana et al. [2], Rolland et al. [13,14], and Mouhmid et al. [17] for validation of the developed model. Material properties of PA66GF have been published in Refs. [17,27], and are listed in Table 1.

Table 1 Material properties of the polyamide/glass (PA66GF) composite

In this example, the fibers in the matrix are assumed to align along the uniaxial tensile loading direction, so the damage state ($\varvec{\phi}$) of the composites can be expressed in terms of a diagonal matrix form [5] under the loading coordinate system as

$$ \varvec{\phi}= \left[ {\begin{array}{*{20}c} {\phi_{11} } & 0 & 0 \\ 0 & {\phi_{22} } & 0 \\ 0 & 0 & {\phi_{33} } \\ \end{array} } \right], $$

(25)

where each damage tensor physically represents the microcracks/voids area density defined with respect to principal plane of the damage state. $\phi_{11}$ is defined on the plane that is perpendicular to the loading direction while $\phi_{22}$ and $\phi_{33}$ are defined on corresponding transverse planes. Due to the symmetries of the loading state, damage state and the microstructure of the composites, it is reasonable to assume that $\phi_{22} = \phi_{33}$. Since there is a lack of experimental data about the temperature dependence on the viscoelasticity, viscoplasticity, and damage behaviors of the SFRPs, we neglect the temperature effect by setting relevant parameters to 0. However, the temperature increment in the material due to viscoplasticity is taken into account with Eq. (23).

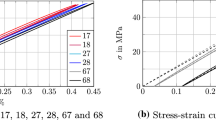
In this case, the viscoelastic part of the model is first calibrated and validated using the stress relaxation data of PA66GF obtained by Andriyana et al. [2], the comparisons results are displayed in Fig. 6. The stress relaxation data obtained from the test started at a strain level of 0.02 mm/mm is used to identify the corresponding viscoelastic parameters ($\tau = 400\,{\text{s}}$ and $\varrho = 8\,{\text{MPa}}$), and another set of data for the strain level of 0.01 mm/mm is used for validation. From Fig. 6, it can be found that although the initiation point at which the stress starts to relax is slightly underestimated by the model at the strain level of 0.01 mm/mm, the trend of the relaxation curve is well predicted with our model. The inaccurate numerical prediction of the initial normalized stress associated with the strain level of 0.02 mm/mm may arise from the viscoelastic contribution of the fiber phase in stress relaxation tests. In the present model, we assume that the viscoelasticity of the composites is solely contributed by its matrix phase, however, the existence of the fibers in the matrix may also contribute or at least affect the total viscoelastic behavior of the composites. In the future study, an interaction term will be added in the viscoelastic model so as to improve the model accuracy in predicting viscoelasticity. As for the viscoplastic part of the model, it can be calibrated and validated through the tensile experiment data obtained from pure matrix materials (polyamide 6,6) by Mouhmid et al. [17] based on the assumption that the viscoplasticity of a composite material is solely contributed by its matrix phase. The comparison results are displayed in Fig. 7. It can be deduced from that figure that the present model could properly predict the flow stress of PA66GF at a strain rate of 0.0011 s⁻¹ but slightly overestimates the flow stress at the rate of 0.056 s⁻¹. The experimental data in Fig. 7 show a work hardening strain rate sensitivity of the polyamide 6,6 when the material starts to yield. When the strain rate increases, the hardening rate of the material decreases and the polyamide 6,6 exhibits a phenomenon of recovery, which can be clearly seen in Fig. 7 when the strain rate is 0.056 s⁻¹. However, the present model lacks a recovery term to capture this phenomenon and thus results in a difference between the numerical results and the experimental data, especially at the strain rate of 0.056 s⁻¹ as shown in Fig. 7. The model will be modified in the future to capture the rate-dependent material recovery. The calibrated parametric values related to viscoplasticity of the SFRPs are listed in Table 2.

Fig. 6

Comparison of the stress relaxation test data and the model prediction for PA66GF. These tests started from the strain levels of 0.01 mm/mm and 0.02 mm/mm

Fig. 7

Comparison of the tension test result and the model prediction for polyamide 6,6. The model was calibrated to the test data measured at strain rate of 0.0056 s⁻¹ and then was validated with respect to the experimental data collected at 0.056 s⁻¹ and 0.0011 s⁻¹

Table 2 Calibrated values of the viscoplastic parameters for polyamide 6,6

Figure 8 compares the average stress–strain response of PA66GF measured under uniaxial tension at the strain rate of 0.0056 s⁻¹ [17] with the numerical results yielded from this model. For the PA66GF with 15 wt% and 30 wt% fiber contents, the numerical results agree very well with the experimental data at the small strain level, while they are slightly less than the experimental data as the strain level increases. For the material with the 50 wt% fiber content, the overall trend of the stress–strain curve is well captured by the model despite small deviations between the experimental data and the numerical results. The deviations shown in Fig. 8 may be caused by the fact that the short fiber reinforced composite samples used in those tests were not ideal unidirectional fiber reinforced composites and the short fibers did not orient perfectly along the same direction in the matrix. To account for the non-perfect fiber orientation effect, the approach proposed by Mouhmid et al. [17] was followed to introduce a fiber orientation parameter in the numerical model. However, the value of the fiber orientation parameter was somehow underestimated (this is equivalent to overestimating the fiber disorientation effect), which results in a composites model with less stiffness compared with the experimental data at the fiber content of 50 wt%. Damage parameters are calibrated by fitting the numerical results to the macroscopic stress–strain data measured from the material with the 30 wt% fiber content (Fig. 8) and taking into account the physical consistency with the work of Rolland et al. [13,14]. In Rolland’s work, the observed total damage volume fraction in the tensile specimen of PA66GF with the fiber content of 30 wt% did not exceed 1%. Table 3 lists the calibrated values for the damage parameters and the corresponding total damage evolution curves (longitudinal and transverse to the fiber direction) for PA66GF with the 30 wt% fiber content are plotted in Fig. 9. The predicted evolution of the damage area can be obtained by solving the damage evolution equations given in Sect. 2.3 with the calibrated damage parameters. In experiments, those damage areas can be obtained by cutting the composite samples along different principal directions and measuring the crack/void areas or area density on each principal plane using scanning electron microscope (SEM). For a detailed description, the readers are referred to the work of Voyiadjis and Venson [28].

Fig. 8

Comparison of the tensile test data and the model prediction for PA66GF with different fiber contents (15 wt%, 30 wt%, and 50 wt% glass) at an applied strain rate of 0.0056 s⁻¹

Table 3 Calibrated damage parameters for PA66GF

Fig. 9

Damage (area fraction) of the constitutive model showing the damage progression of different damage components for the 30 wt% PA66GF. The loading condition is a tension load applied at a strain rate of 0.0056 s⁻¹

4 Conclusion

This study develops a constitutive relationship for SFRPs with different fiber contents to properly identify their damage and moisture effects coupled viscoelastic, viscoplastic behaviors subjected to a range of strain rate levels. The numerical model is developed based on the additive decomposition of the total strain, evolving ISVs are introduced to the formalism to account for the expansion mechanism of the yield surface exhibited by the polymeric constituent of the SFRPs. The damage part of the model is formulated based on the mechanisms of micro-voids/cracks nucleation, growth, and coalescence as observed by Rolland et al. [13,14] and can properly predict the anisotropic damage progression of such materials. The theoretical predictions of the proposed model are overall in a good agreement with the experimental data within a broad range of moisture absorption content, strain rate, and fiber content.