1 Introduction

In order to avoid numerical oscillations in solving compressible inviscid flows and to obtain uniform high-order accuracy both in time and space, Harten and Osher [1] proposed an essentially non-oscillation (ENO) scheme with easing restrictions of non-growing total variation and allowing small increase in total variation. Most of key functions of ENO scheme are applied only on the smooth stencil among all the stencils to evaluate variables at the cell interface for maintaining high-order accuracy in the smooth region and suppressing oscillations in the non-smooth region [2]. To overcome the drawback of ENO scheme, i.e. other stencils are abandoned except the smoothest stencil, Liu et al. [3] proposed a weighted ENO (WENO) scheme using a convex combination of all candidate stencils instead of only using the optional smooth stencil. Furthermore, WENO scheme was improved by Jiang and Shu [4] and Shu [5], in which a general form of smoothness indicators and nonlinear weights was specified in detail. WENO scheme has been significantly improved in terms of accuracy and resolution, compared with ENO scheme. After that, finite difference WENO (FD-WENO) scheme [4, 6] and finite volume WENO (FV-WENO) scheme [7, 8] have been greatly developed, and Shu [5] strongly suggested using FD-WENO scheme in practice owing that it has higher accuracy, higher resolution and a small amount of calculations. In recent decades, WENO scheme has been used well to solve the problems with strong shocks, contact discontinuities and rarefaction waves [9,10,11,12].

An important component of WENO scheme is the calculation of numerical fluxes. In most of various fluxes in the literature, the numerical fluxes that are based on the smooth function approximation [13, 14] and exact or approximate Riemann solvers are widely used , such as the Lax-Friedrichs (LF) numerical flux, Harten-Lax-van Leer (HLL) flux [15], HLLC flux [16] (a modification of the HLL flux), a flux limiter centered (FLIC) flux [17] and multi-stage predictor-corrector (MUSTA) flux [18]. The flux solver based on smooth function approximation cannot resolve discontinuity problems such as compressible flows with shock wave, and the flux solver based on Riemann solver or approximate Riemann solver usually pursues approximate solution of 1D Euler equations along the normal direction to the cell interface. An alternative approach is gas kinetic flux solver which is based on Boltzmann equation [19]. This solver can be well applied for simulation of both compressible flow and incompressible flow [20,21,22,23]. Most of existing gas kinetic schemes are developed on the basis of the Maxwellian distribution function [19, 24, 25]. Owing to complexity of the Maxwellian distribution function, its are usually more complex and rather inefficient than conventional flux solves.

Recently, lattice Boltzmann method (LBM) has received much attention for studying different complex fluid flows [26,27,28,29,30,31], due to its natural parallel characteristic, simplicity and clear physical background. However, the conventional LBM is limited to viscous flows, uniform mesh and tie up of time interval and space step. To develop a more efficient solver for compressible flows, a lattice Boltzmann flux solver (LBFS) was proposed by Ji et al. [32], which is based on the local solution of lattice Boltzmann equation (LBE). Different from conventional flux solvers, which are based on the smooth function approximation [13, 14] or Riemann solver approximation [33,34,35], LBFS applies local reconstruction of solution of lattice Boltzmann equation (LBE) [36, 37] to evaluate the inviscid flux at the cell interface. It was further improved and extended to simulate incompressible flows by Yang et al. [38] and Shu et al. [39, 40]. The LBFS can provide good positivity property for simulation of flows with shock waves [38] and can be well applied to simulate both compressible and incompressible flows [20, 40,41,42,43,44]. However, in the existing LBFS, the inviscid flux at the cell interface is directly computed by using the distribution functions that streamed from neighboring points. Since non-free parameter D1Q4 model is only used along the normal direction to the cell interface, the existing LBFS can be only applied to simulate inviscid flows [38]. Furthermore, the distribution function at cell interface makes up for the equilibrium part and non-equilibrium part. From the Chapman-Enskog expansion analysis [45, 46], the equilibrium distribution function acts on the inviscid flux, while the non-equilibrium distribution function acts on the viscous flux. The non-equilibrium part of the distribution function is regarded as numerical viscosity, and the dimensionless collision time is viewed as the weight of the numerical viscosity. Basing on the above reviews, Yang et al. [44] presented two kinds of LBFS. One is inviscid LBFS (LBFS I) which only considers the equilibrium part, while the other is viscous LBFS (LBFS II) which takes the equilibrium part and non-equilibrium part into consideration and the coefficient in front of the non-equilibrium part is equal to 1. The existing LBFS is viscous LBFS II [32, 39]. Inviscid LBFS I is used to obtain the primitive variables in a straightforward way, while viscous LBFS II is used to directly compute the inviscid flux. On the other hand, in simulating the compressible inviscid flow, the numerical viscosity has benefit of capturing complex wave structures and strong shock waves, but it will affect the solution of smooth problems. Hence, taking control of the numerical viscosity is the key to simulate the inviscid flows. As a consequence, inviscid LBFS I can accurately calculate the solution of smooth regions, but it may diverge or oscillate for simulation of hypersonic flows, while viscous LBFS II has good performances on capturing strong shock waves, but it has an influence on smooth solution. To overcome the drawbacks and combine the advantages of inviscid LBFS I and viscous LBFS II, a hybrid lattice Boltzmann flux solver (denoted as hybrid LBFS III hereafter), which involves a governing function to realize the switch between inviscid LBFS I and viscous LBFS II, was proposed by Yang et al. [44, 47]. The hybrid LBFS III cannot only accurately calculate a smooth solution, but also effectively capture strong shock waves.

In the previous work [48], we systematically studied and compared the performance of WENO scheme combining viscous LBFS II, LF, HLLC, MUSTA and FLIC fluxes. It indicated that the viscous WENO-LBFS II scheme has better performance when all factors including the cost of CPU time, numerical errors and resolution in the solution near discontinuities and shock waves are considered. In this paper, the hybrid WENO-LBFS III scheme combines the advantages of WENO scheme, inviscid LBFS I and viscous LBFS II. In the meantime, we present a hybrid WENO-LBFS IV scheme. Different from the hybrid WENO-LBFS III scheme in which the governing function is the maximum value of the governing function of the left and right control volumes, the governing function in the hybrid WENO-LBFS IV scheme is determined by all the neighboring control volumes of the cell. Comparing with the inviscid WENO-LBFS I scheme and the viscous WENO-LBFS II scheme, we demonstrate the accuracy and efficiency of the present hybrid WENO-LBFS III scheme and hybrid WENO-LBFS IV scheme.

The rest of the paper is organized as follows: In Sect. 2, four WENO scheme-based LBFS for simulation of compressible inviscid flows are outlined in detail, including the inviscid WENO-LBFS I scheme, viscous WENO-LBFS II scheme, hybrid WENO-LBFS III scheme and hybrid WENO-LBFS IV scheme. In Sect. 3, the present hybrid WENO-LBFS III scheme and hybrid WENO-LBFS IV scheme are used to solve continuous flows and compressible flow problems with contact discontinuities, strong shock waves and complex wave structures. Comparisons among the inviscid WENO-LBFS I scheme, viscous WENO-LBFS II scheme, hybrid WENO-LBFS III scheme and hybrid WENO-LBFS IV scheme are also given in Sect. 3. Numerical results indicate that the present hybrid WENO-LBFS III scheme and hybrid WENO-LBFS IV scheme can not only accurately calculate smooth solutions, but also can effectively capture contact discontinuities and strong shock waves. Finally, the conclusions are given in Sect. 4.

2 Methodology

2.1 Euler equations discretized by finite difference method

In this work, the governing equations of compressible inviscid flows, which are conventional Euler equations, are given as

$$\begin{aligned} \frac{\partial \varvec{U}}{\partial t} + \frac{\partial { \varvec{F}({\varvec{U}})} }{\partial x} + \frac{\partial { \varvec{G}({\varvec{U}})} }{\partial y} = 0, \end{aligned}$$
(1)

with

$$\begin{aligned}&\varvec{U}= \begin{pmatrix} \rho \\ \rho u \\ \rho v \\ \rho E \end{pmatrix}, \quad \varvec{F}({\varvec{U}})= \begin{pmatrix} \rho u\\ \rho u^{2}+p\\ \rho uv\\ (\rho E+p)u \end{pmatrix},\nonumber \\&\varvec{G}({\varvec{U}})= \begin{pmatrix} \rho v\\ \rho uv\\ \rho v^{2}+p\\ (\rho E+p)v \end{pmatrix}, \end{aligned}$$
(2)

where \(\rho \) and p are density field and pressure field, respectively. (u, v) is velocity field. The total energy of the mean flow E is defined as

$$\begin{aligned} E=e+\frac{1}{2}(u^{2}+v^{2}), \end{aligned}$$
(3)

here \( e=p/[(\gamma -1)\rho ] \) is the potential energy of the mean flow, and the specific heat ratio is \( \gamma =1.4 \) for diatomic gas.

For finite difference method, the spatial derivative is discreted by a conservative approximation, and then spatial semi-discretization of Eq. (1) could be given as

$$\begin{aligned} \frac{\mathrm{d} {\varvec{U}}_{ij}(t)}{\mathrm{d} t}= & {} -\frac{1}{\Delta x} \left( \hat{{\varvec{F}}}_{i+\frac{1}{2},j} - \hat{{\varvec{F}}}_{i-\frac{1}{2},j}\right) \nonumber \\&-\frac{1}{\Delta y} \left( \hat{{\varvec{G}}}_{i,j+\frac{1}{2}} - \hat{{\varvec{G}}}_{i,j-\frac{1}{2}}\right) . \end{aligned}$$
(4)

For convenience, the first order ordinary differential equation (ODE) system of Eq. (4) could be rewritten as compact form

$$\begin{aligned} \frac{\mathrm{d} {\varvec{U}}(t)}{\mathrm{d} t} = \mathcal {L} \left( {\varvec{U}}\right) . \end{aligned}$$
(5)

Usually, a three-step Runge-Kutta method is applied to solve the first order ODE system of Eq. (5), which is described as Ref. [2]

$$\begin{aligned} \begin{aligned} {\varvec{U}}^{(1)}&= {\varvec{U}}^{n}+\Delta t \mathcal {L}( {\varvec{U}}^{n}), \\ {\varvec{U}}^{(2)}&= \frac{3}{4} {\varvec{U}}^{n} +\frac{1}{4} {\varvec{U}}^{(1)} +\frac{1}{4} \Delta t \mathcal {L}( {\varvec{U}}^{(1)}), \\ {\varvec{U}}^{n+1}&= \frac{1}{3} {\varvec{U}}^{n} +\frac{2}{3} {\varvec{U}}^{(2)} +\frac{2}{3} \Delta t \mathcal {L}( {\varvec{U}}^{(2)}), \end{aligned} \end{aligned}$$
(6)

where \(\mathcal {L}\) is spatial discretization operator and \(\Delta t\) is updated time step. Obviously, the key of solving Eq. (4) is to evaluate the inviscid fluxes \( \hat{\varvec{F}} \) and \( \hat{\varvec{G}} \). Next, a lattice Boltzmann model to evaluate the inviscid fluxes used in this paper will be introduced.

2.2 Non-free parameter D1Q4 model to evaluate the inviscid fluxes \(\hat{{\varvec{F}}} \) and \(\hat{{\varvec{G}}}\)

A lattice Boltzmann flux solver (LBFS) [32, 38,39,40], which uses a local reconstruction of solution of 1D lattice Boltzmann equation (LBE) to evaluate the inviscid flux, can effectively simulate compressible inviscid flows. Next, the non-free parameter D1Q4 model used in this paper will be discussed in detail.

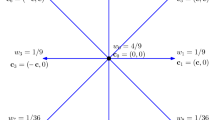
In this paper, the non-free parameter D1Q4 model proposed by Yang et al. [38, 49] is adopted. The equilibrium distribution functions \(f_{\alpha }(\rho , u, p)\) and lattice velocities \(e_{\alpha }\) are given as following

$$\begin{aligned}&\begin{aligned} f_1(\rho , u, p)&= \frac{\rho \left( -d_1d_2^2 - d_2^2 u + d_1u^2 + d_1c^2 + u^3 + 3uc^2\right) }{2d_1\left( d_1^2-d_2^2\right) }, \\ f_2(\rho , u, p)&= \frac{\rho \left( -d_1d_2^2 + d_2^2 u + d_1u^2 + d_1c^2 - u^3 - 3uc^2\right) }{2d_1\left( d_1^2-d_2^2\right) }, \\ f_3(\rho , u, p)&= \frac{\rho \left( d_1^2d_2 + d_1^2 u - d_2u^2 - d_2c^2 - u^3 - 3uc^2\right) }{2d_2\left( d_1^2-d_2^2\right) }, \\ f_4(\rho , u, p)&= \frac{\rho \left( d_1^2d_2 - d_1^2 u - d_2u^2 - d_2c^2 + u^3 + 3uc^2\right) }{2d_2\left( d_1^2-d_2^2\right) }, \end{aligned} \end{aligned}$$
(7)
$$\begin{aligned}&\begin{matrix} e_{1}(\rho , u, p) = d_{1}, &{} e_{2}(\rho , u, p) = -d_{1}, \\ e_{3}(\rho , u, p) = d_{2}, &{} e_{4}(\rho , u, p) = -d_{2}, \end{matrix} \end{aligned}$$
(8)

with

$$\begin{aligned} \begin{aligned} d_1&= \sqrt{u^2 + 3c^2 - \sqrt{4u^2c^2+6c^4}}, \\ d_2&= \sqrt{u^2 + 3c^2 + \sqrt{4u^2c^2+6c^4}}, \end{aligned} \end{aligned}$$
(9)

and \(c = \sqrt{p/\rho }\) is the peculiar velocity of particles.

Furthermore, this model can be used to simulate hypersonic flows with strong shock waves (see Refs. [38, 39, 49] for more details). Consider the following 1D Riemann problem

$$\begin{aligned} (\rho , u, p) = {\left\{ \begin{array}{ll} (\rho ^{-}, u^{-}, p^{-}), &{} x < 0, \\ (\rho ^{+}, u^{+}, p^{+}), &{} x \geqslant 0. \\ \end{array}\right. } \end{aligned}$$

Thus, the equilibrium distribution function \(f_\alpha (0,t)\) at the cell interface could be decided by the location of the point \(x=0\). Specifically, \( f_\alpha (0,t) \) can be given as

$$\begin{aligned} f_\alpha (0,t) = {\left\{ \begin{array}{ll} f_\alpha ^L, &{} \quad \text{ if } ~~ \alpha = 1, 3, \\ f_\alpha ^R, &{} \quad \text{ if } ~~ \alpha = 2, 4, \end{array}\right. } \end{aligned}$$
(10)

where \( f_\alpha ^L \) and \( f_\alpha ^R \) are the equilibrium distribution function at the two sides of cell interface, respectively. \(f_\alpha ^L \) and \( f_\alpha ^R \) can be rewritten as

$$\begin{aligned} \begin{aligned} f_{1}^{L} = f_1(\rho ^{-}, u^{-}, p^{-}),&\quad f_{2}^{R} = f_2(\rho ^{+}, u^{+}, p^{+}), \\ f_{3}^{L} = f_3(\rho ^{-}, u^{-}, p^{-}),&\quad f_{4}^{R} = f_4(\rho ^{+}, u^{+}, p^{+}), \end{aligned} \end{aligned}$$
(11)

with the corresponding lattice velocities given as

$$\begin{aligned} \begin{aligned} e_{1}^{L} = e_1(\rho ^{-}, u^{-}, p^{-}),&\quad e_{2}^{R} = e_2(\rho ^{+}, u^{+}, p^{+}), \\ e_{3}^{L} = e_3(\rho ^{-}, u^{-}, p^{-}),&\quad e_{4}^{R} = e_4(\rho ^{+}, u^{+}, p^{+}). \end{aligned} \end{aligned}$$
(12)

According to the physical conservation laws, the density \( \rho \), velocity u and pressure p at the point \( x=0 \) can be given as

$$\begin{aligned} \begin{aligned}&\rho = \sum \limits _{\alpha =1}^4 f_\alpha ^k, \\&\rho u = \sum \limits _{\alpha =1}^4 f_\alpha ^k e_\alpha ^k, \\&\left( \frac{1}{\gamma -1} p + \frac{1}{2} \rho uu \right) = \sum \limits _{\alpha =1}^4 f_\alpha ^k \left( \frac{1}{2} e_\alpha ^k e_\alpha ^k + \lambda ^k \right) , \\&\left( \frac{\gamma }{\gamma -1} p + \frac{1}{2} \rho uu \right) u = \sum \limits _{\alpha =1}^4 f_\alpha ^k \left( \frac{1}{2} e_\alpha ^k e_\alpha ^k + \lambda ^k \right) e_\alpha ^k, \end{aligned} \end{aligned}$$
(13)

where k is the index of the left and right sides, and \( \lambda =[1-(\gamma -1)/2]e \) is the potential energy of particles.

Now, the non-free parameter D1Q4 model is used to evaluate the inviscid flux. In general, the distribution function \(f_\alpha (0,t)\) is formed from the equilibrium part \( f_\alpha ^\mathrm{eq}(0,t) \) and non-equilibrium part \(f_\alpha ^\mathrm{neq}(0,t)\), i.e.,

$$\begin{aligned} f_\alpha (0,t) = f_\alpha ^\mathrm{eq}(0,t)+f_\alpha ^\mathrm{neq}(0,t). \end{aligned}$$
(14)

From the discrete velocity Boltzmann equation, \(f_\alpha ^\mathrm{neq}\) can be written as

$$\begin{aligned}&f_\alpha ^\mathrm{neq}(0,t) = -\tau _0\left( \frac{\partial f_\alpha }{\partial t}+e_\alpha \cdot \nabla f_\alpha \right) . \end{aligned}$$
(15)

Using Taylor series expansion in space and time for the above equation, the distribution function \(f_\alpha (0,t)\) at the cell interface can be given as

$$\begin{aligned}&f_\alpha (0,t) = f_\alpha ^\mathrm{eq}(0,t)-\tau ,\nonumber \\&\left[ f_\alpha ^\mathrm{eq}(0,t) -f_\alpha ^\mathrm{eq}(-e_\alpha \delta t,t-\delta t) \right] +O(\delta t^2), \end{aligned}$$
(16)

here \( \tau =\frac{\tau _0}{\delta t} \) is the dimensionless collision time and \(\delta t\) is streaming time step. \(f_\alpha ^\mathrm{eq}(-e_\alpha \delta t,t-\delta t)\) is the equilibrium distribution function at the surrounding point of the cell interface. From the Chapman-Enskog expansion analysis [45, 46], the equilibrium distribution function acts on the inviscid fluxes. Hence, for simulating compressible inviscid flows, the non-equilibrium part of the distribution function is regarded as numerical viscosity, and the dimensionless collision time is viewed as the weight of the numerical viscosity. Basing on the value of \(\tau \), Yang et al. proposed three kinds of LBFS [44]. Next, the descriptions of evaluating the inviscid flux \(\varvec{\hat{F}}\) in the x-direction at the cell interface are given (see Refs. [44] for more details).

2.2.1 Inviscid lattice Boltzmann flux solver [44]

When \(\tau \) is set to 0, this kind of LBFS is noted as inviscid LBFS (inviscid LBFS I). According to Eq. (13), the density, momentum and energy in normal direction at the cell interface can be calculated by

$$\begin{aligned} \varvec{W}_{x,\alpha +\frac{1}{2}} = \left[ \rho , \rho u, \frac{1}{2}\rho uu+\rho e \right] ^\mathrm{T} = \sum \limits _{\alpha =1}^4\varvec{\phi }_\beta f_\alpha ^\mathrm{eq}(0,t), \end{aligned}$$
(17)

where \( \varvec{\phi }_\beta \) can be defined by

$$\begin{aligned} \varvec{\phi }_\beta = \left( 1, e_\alpha , \frac{1}{2}e_\alpha ^2+\lambda \right) ^\mathrm{T}. \end{aligned}$$
(18)

The consistency condition [50] gives

$$\begin{aligned}&\sum \limits _{\alpha =1}^4 \varvec{\phi }_\beta f_\alpha ^\mathrm{neq}(0,t)\nonumber \\&=-\sum \limits _{\alpha =1}^4 \varvec{\phi }_\beta \tau [f_\alpha ^\mathrm{eq}(0,t)-f_\alpha ^\mathrm{eq}(-e_\alpha \delta t,t-\delta t)] =0. \end{aligned}$$
(19)

The above two equations give

$$\begin{aligned} \varvec{W}_{x,\alpha +\frac{1}{2}} = \sum \limits _{\alpha =1}^4 \varvec{\phi }_\beta f_i^\mathrm{eq}(-e_\alpha \delta t,t-\delta t), \end{aligned}$$
(20)

where \(f_i^\mathrm{eq}(-e_\alpha \delta t,t-\delta t)\) can be computed by Eq. (10). Basing on non-free parameter D1Q4 model, the density \(\rho \), normal velocity u and pressure p at the cell interface can be evaluated by Eq. (13). However, another velocity component v at the cell interface should be evaluated, which is given as

$$\begin{aligned} \rho v = \sum \limits _{\alpha =1,3} f_\alpha ^k \cdot v^- + \sum \limits _{\alpha =2,4} f_\alpha ^k \cdot v^+. \end{aligned}$$
(21)

By Eqs. (13) and (21), the density, normal velocity, tangential velocity and pressure can be obtained. Substituting these primitive variables into Eq. (2), the inviscid flux in the x-direction at the cell interface can be evaluated. An alternative indirect way is to substitute these primitive variables into Eqs. (7)–(9) to evaluate \(f_i^\mathrm{eq}(0,t)\). Then, the inviscid flux \(\varvec{\hat{F}}\) in the x-direction at the cell interface can be calculated by

$$\begin{aligned} \varvec{\hat{F}}^\mathrm{(I)} = \begin{pmatrix} \rho u \\ \rho uu+p \\ \rho uv \\ \left( \rho E+p \right) u \end{pmatrix}. \end{aligned}$$
(22)

The inviscid flux \(\varvec{\hat{G}}\) in the y-direction is similar to \(\varvec{\hat{F}}\). It only needs that u is replaced by v.

2.2.2 Viscous lattice Boltzmann flux solver [38, 39, 44]

When \(\tau \) is equal to 1, this kind of LBFS is noted as viscous LBFS (viscous LBFS II). After obtaining the density, normal velocity and pressure at the cell interface computed by Eq. (13), the inviscid flux \(\hat{{\varvec{F}}}\) in the x-direction can be evaluated as following

$$\begin{aligned} \hat{{\varvec{F}}}^\mathrm{(II)} = \begin{pmatrix} {\hat{F}}_{1} \\ {\hat{F}}_{2} \\ {\hat{F}}_{3} \\ {\hat{F}}_{4} \\ \end{pmatrix} =\begin{pmatrix} \sum \limits _{\alpha =1}^{4} f_\alpha ^{k} e_\alpha ^{k} \\ \sum \limits _{\alpha =1}^{4} f_\alpha ^{k} e_\alpha ^{k} e_\alpha ^{k} \\ {\hat{F}}_1 v \\ \sum \limits _{\alpha =1}^{4} f_\alpha ^{k} e_\alpha ^{k} \left( \frac{1}{2}e_\alpha ^{k} e_\alpha ^{k} + \lambda ^k \right) + \frac{1}{2} {\hat{F}}_1 v^2 \end{pmatrix}, \end{aligned}$$
(23)

where \(f_{\alpha }^{k}\) and \(e_{\alpha }^{k}\) are computed by Eqs. (11) and (12). The tangential velocity at the cell interface v is given as

$$\begin{aligned}&\rho uv = \sum \limits _{\alpha =1,3}e_\alpha ^L f_\alpha ^L v^- +\sum \limits _{\alpha =2,4}e_\alpha ^R f_\alpha ^R v^+, \end{aligned}$$
(24)
$$\begin{aligned}&\rho uv^2 = \sum \limits _{\alpha =1,3}e_\alpha ^L f_\alpha ^L (v^-)^2 + \sum \limits _{\alpha =2,4}e_\alpha ^R f_\alpha ^R (v^+)^2. \end{aligned}$$
(25)

Similar to \(\hat{{\varvec{F}}}\), the inviscid flux \(\hat{{\varvec{G}}}\) in the y-direction can be evaluated as

$$\begin{aligned} \hat{{\varvec{G}}}^\mathrm{(II)} = \begin{pmatrix} {\hat{G}}_{1} \\ {\hat{G}}_{2} \\ {\hat{G}}_{3} \\ {\hat{G}}_{4} \end{pmatrix} =\begin{pmatrix} \sum \limits _{\alpha =1}^{4} f_\alpha ^{k} e_\alpha ^{k} \\ {\hat{G}}_1 u \\ \sum \limits _{\alpha =1}^{4} f_\alpha ^{k} e_\alpha ^{k} e_\alpha ^{k} \\ \sum \limits _{\alpha =1}^{4} f_\alpha ^{k} e_\alpha ^{k} \left( \frac{1}{2}e_\alpha ^{k} e_\alpha ^{k} + \lambda \right) + \frac{1}{2} {\hat{G}}_1 u^2 \end{pmatrix}, \end{aligned}$$
(26)

with

$$\begin{aligned} \begin{aligned} e_{1}^{L} = e_1(\rho ^{-}, v^{-}, p^{-}),&\quad e_{2}^{R} = e_2(\rho ^{+}, v^{+}, p^{+}), \\ e_{3}^{L} = e_3(\rho ^{-}, v^{-}, p^{-}),&\quad e_{4}^{R} = e_4(\rho ^{+}, v^{+}, p^{+}), \end{aligned} \end{aligned}$$
(27)

The tangential velocity at the cell interface v is replaced by u given as

$$\begin{aligned}&\rho uv = \sum \limits _{\alpha =1,3}e_\alpha ^L f_\alpha ^L u^- +\sum \limits _{\alpha =2,4}e_\alpha ^R f_\alpha ^R u^+, \end{aligned}$$
(28)
$$\begin{aligned}&\rho u^2v = \sum \limits _{\alpha =1,3}e_\alpha ^L f_\alpha ^L (u^-)^2 + \sum \limits _{\alpha =2,4}e_\alpha ^R f_\alpha ^R (u^+)^2. \end{aligned}$$
(29)

2.2.3 Hybrid lattice Boltzmann flux solver [44]

Introduce a governing function to combine inviscid LBFS I with viscous LBFS II. Particularly, a governing function \(\mu \) which ranges from 0 to 1 is defined as

$$\begin{aligned} \mu = \tanh \left( C \frac{|p^- - p^+|}{P^- + P^+} \right) , \end{aligned}$$
(30)

here \(\hbox {tanh}(x)\) is the hyperbolic tangent function, and \(C=10\) applied in this paper is a coefficient. Hence, the inviscid fluxes across the cell interface can be evaluated by

$$\begin{aligned} \begin{aligned} \varvec{F}^\mathrm{(III)}&= (1-\mu )\varvec{F}^\mathrm{(I)} + \mu \varvec{F}^\mathrm{(II)}, \\ \varvec{G}^\mathrm{(III)}&= (1-\mu )\varvec{G}^\mathrm{(I)} + \mu \varvec{G}^\mathrm{(II)}. \end{aligned} \end{aligned}$$
(31)

This kind of LBFS is noted as hybrid LBFS III. On one hand, hybrid LBFS III can achieve transformation between inviscid LBFS I and viscous LBFS II because \(\mu \) is a variable, which enables the governing function to switch into inviscid LBFS I for continuous problems and change into viscous LBFS II for strong shock waves. On the other hand, to remove oscillations in simulating hypersonic flows, a new governing function referred to as hybrid LBFS \(\mathrm III^*\) [44] is given as

$$\begin{aligned} \mu ^*= & {} \max (\mu ^L, \mu ^R), \end{aligned}$$
(32)
$$\begin{aligned} \mu ^L= & {} \max \limits _{l=1,\cdots ,N_l}(\mu _l), ~~ \mu ^R = \max \limits _{r=1,\cdots ,N_r}(\mu _r), \end{aligned}$$
(33)

where \(N_l\) and \(N_r\) are the number of the faces of the left and right control volumes, respectively. Correspondingly, Eq. (31) can be rewritten as

$$\begin{aligned} \begin{aligned} \varvec{F}^\mathrm{(III^*)}&= (1-\mu ^*)\varvec{F}^\mathrm{(I)} + \mu ^* \varvec{F}^\mathrm{(II)}, \\ \varvec{G}^\mathrm{(III^*)}&= (1-\mu ^*)\varvec{G}^\mathrm{(I)} + \mu ^* \varvec{G}^\mathrm{(II)}. \end{aligned} \end{aligned}$$
(34)

Basing on the hybrid LBFS III, we propose a hybrid LBFS IV in which the governing function \(\mu ^{*}\) is the maximum value of the governing function of all the neighboring control volume at the cell. Hence,

$$\begin{aligned} \begin{aligned} \varvec{F}^\mathrm{(IV)}&= (1-\mu ^{*})\varvec{F}^\mathrm{(I)} + \mu ^* \varvec{F}^\mathrm{(II)}, \\ \varvec{G}^\mathrm{(IV)}&= (1-\mu ^{*})\varvec{G}^\mathrm{(I)} + \mu ^* \varvec{G}^\mathrm{(II)}. \end{aligned} \end{aligned}$$
(35)

2.3 WENO scheme to reconstruct the values \(\rho ^{\pm }\), \(u^{\pm }\), \(v^{\pm }\) and \(p^{\pm }\)

Consider the reconstruction of the flow variables \(\rho ^{\pm }\), \(u^{\pm }\), \(v^{\pm }\) and \(p^{\pm }\) in the x-direction at point \((x_{i+\frac{1}{2}}, y_{j})\). Usually, the conservation variables \({\varvec{U}}^{\pm }\) are reconstructed in physical space directly, and then the flow variables can be computed. Unfortunately, the reconstruction process cannot deal with the problem of shock waves very well, as discontinuous solution with low resolution and numerical oscillations. Owing to that, we adopt another way proposed by Shu [5], where the reconstruction process is done in characteristic space. The details of the whole reconstruction process are given, here.

As the conservation variables \({\varvec{U}}\) are known on all grid nodes \((x_{i}, y_{j})\), we have the local left eigenvectors \({\varvec{L}}^{F}\) and right eigenvectors \({\varvec{R}}^{F}\) of the Jacobian matrix \( \left. \frac{\partial {\varvec{F}}}{\partial {\varvec{U}}}\right| _{x_{i+\frac{1}{2}}, y_{j}} \) as following

$$\begin{aligned} {\varvec{R}}^{F}= & {} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 \\ u-c &{} u &{} u &{} u+c \\ v &{} 0 &{} 1 &{} v \\ \gamma e+\frac{u^{2}+v^{2}}{2}-uc\ \ &{} \frac{u^{2}-v^{2}}{2}\ \ &{} v+\frac{u^{2}-v^{2}}{2}\ \ &{} \gamma e +\frac{u^{2}+v^{2}}{2}+uc \\ \end{pmatrix}, \nonumber \\ \end{aligned}$$
(36)
$$\begin{aligned} {\varvec{L}}^{F}= & {} \begin{pmatrix} \frac{u^{2}+v^{2}}{4\gamma e}+\frac{u}{2c} &{} -\frac{1}{2c}-\frac{u}{2\gamma e} &{} -\frac{v}{2\gamma e } &{} \frac{1}{2\gamma e } \\ 1-\frac{u^{2}+v^{2}}{2\gamma e }+\frac{v(u^{2}+v^{2})}{2\gamma e} &{} \frac{u-uv}{\gamma e} &{} \frac{v-v^{2}}{\gamma e}-1 &{} \frac{v-1}{\gamma e} \\ -\frac{v(u^{2}+v^{2})}{2\gamma e} &{} \frac{uv}{\gamma e} &{} 1+\frac{v^{2}}{\gamma e} &{} -\frac{v}{\gamma e} \\ \frac{u^{2}+v^{2}}{4\gamma e}-\frac{u}{2c} &{} \frac{1}{2c}-\frac{u}{2\gamma e} &{} -\frac{v}{2\gamma e} &{} \frac{1}{2\gamma e } \end{pmatrix}, \end{aligned}$$
(37)

here the average state \({\varvec{U}}_{i+\frac{1}{2},j}\) is computed by the simple mean as following

$$\begin{aligned} {\varvec{U}}_{i+\frac{1}{2},j} = \frac{1}{2} \left( {\varvec{U}}_{i,j} + {\varvec{U}}_{i+1,j} \right) . \end{aligned}$$
(38)

Then, we transform the conservation variables \({\varvec{U}}_{k,j}\) to the local characteristic variables \({\varvec{V}}_{k,j}\) by using the left eigenvectors \({\varvec{L}}^{F}\) as

$$\begin{aligned} {\varvec{V}}_{k,j} = {\varvec{L}}^{F} {\varvec{U}}_{k,j}, ~~ i-2 \leqslant k \leqslant i+3. \end{aligned}$$
(39)

Furthermore, the local characteristic variables \({\varvec{V}}_{i+\frac{1}{2},j}^{\pm }\) could be reconstructed. In general, the 5th order WENO reconstruction formulas of \({\varvec{V}}_{i+\frac{1}{2},j}^{-}\) are given. And for this, the local characteristic variables \({\varvec{V}}_{i-1,j}, {\varvec{V}}_{i,j}\), \({\varvec{V}}_{i+1,j}\), \({\varvec{V}}_{i+2,j}\) and \({\varvec{V}}_{i+3,j}\) are chosen, then we have

$$\begin{aligned} {\varvec{V}}_{i+\frac{1}{2},j}^{-} = \omega _{1} {\varvec{V}}_{i+\frac{1}{2},j}^{(1)} + \omega _{2} {\varvec{V}}_{i+\frac{1}{2},j}^{(2)} + \omega _{3} {\varvec{V}}_{i+\frac{1}{2},j}^{(3)}, \end{aligned}$$
(40)

where

$$\begin{aligned}&{\varvec{V}}_{i+\frac{1}{2},j}^{(1)} = -\frac{1}{6}{\varvec{V}}_{i-1, j} +\frac{5}{6}{\varvec{V}}_{i , j} +\frac{1}{3}{\varvec{V}}_{i+1, j}, \nonumber \\&{\varvec{V}}_{i+\frac{1}{2},j}^{(2)} = \frac{1}{3}{\varvec{V}}_{i , j} +\frac{5}{6}{\varvec{V}}_{i+1, j} -\frac{1}{6}{\varvec{V}}_{i+2, j}, \nonumber \\&{\varvec{V}}_{i+\frac{1}{2},j}^{(3)} = \frac{11}{6}{\varvec{V}}_{i+1, j} -\frac{7}{6}{\varvec{V}}_{i+2, j} +\frac{1}{3}{\varvec{V}}_{i+3, j}, \end{aligned}$$
(41)
$$\begin{aligned}&\omega _{r} = \frac{\sigma _{r}}{\sum \limits _{r=1}^{3} \sigma _{r}}, \quad \sigma _{r} = \frac{\theta _{r}}{(\epsilon + \beta _{r})^{2}}, \end{aligned}$$
(42)
$$\begin{aligned}&\beta _{1} = \frac{13}{12}({\varvec{V}}_{i-1,j}-2{\varvec{V}}_{i,j}+{\varvec{V}}_{i+1,j})^{2}\nonumber \\&\quad \qquad +\frac{1}{4}({\varvec{V}}_{i-1,j}-4{\varvec{V}}_{i,j}+3{\varvec{V}}_{i+1,j})^{2}, \nonumber \\&\beta _{2} = \frac{13}{12}({\varvec{V}}_{i, j}-2{\varvec{V}}_{i+1,j}+{\varvec{V}}_{i+2,j})^{2}\nonumber \\&\quad \qquad +\frac{1}{4}({\varvec{V}}_{i+2,j}-{\varvec{V}}_{i,j})^{2}, \nonumber \\&\beta _{3} = \frac{13}{12}({\varvec{V}}_{i+1,j}-2{\varvec{V}}_{i+2,j}+{\varvec{V}}_{i+3,j})^{2}\nonumber \\&\quad \qquad +\frac{1}{4}(3{\varvec{V}}_{i+1,j}-4{\varvec{V}}_{i+2,j}+{\varvec{V}}_{i+3,j})^{2}, \end{aligned}$$
(43)
$$\begin{aligned}&\theta _{1} = \frac{3}{10}, \quad \theta _{2} = \frac{3}{5}, \quad \theta _{3} = \frac{1}{10}. \end{aligned}$$
(44)

Similar to the reconstruction process of \({\varvec{V}}_{i+\frac{1}{2},j}^{-}\), \({\varvec{V}}_{i+\frac{1}{2},j}^{+}\) can be reconstructed by the local characteristic variables \({\varvec{V}}_{i-2,j}, {\varvec{V}}_{i-1,j}\), \({\varvec{V}}_{i,j}\), \({\varvec{V}}_{i+1,j}\) and \({\varvec{V}}_{i+2,j}\).

Finally, we transform the local characteristic variables \({\varvec{V}}_{i+\frac{1}{2},j}^{\pm }\) to the conservation variables \({\varvec{U}}_{i+\frac{1}{2},j}^{\pm }\) by using the right eigenvectors \({\varvec{R}}^{F}\) as

$$\begin{aligned} {\varvec{U}}_{i+\frac{1}{2},j}^{\pm }= {\varvec{R}}^{F} {\varvec{V}}_{i+\frac{1}{2},j}^{\pm }. \end{aligned}$$
(45)

Thus we can get the flow variables \(\rho _{i+\frac{1}{2}, j}^{\pm }\), \(u_{i+\frac{1}{2}, j}^{\pm }\), \(v_{i+\frac{1}{2}, j}^{\pm }\) and \(p_{i+\frac{1}{2}, j}^{\pm }\).

The reconstruction processes of the flow variables \(\rho ^{\pm }\), \(u^{\pm }\), \(v^{\pm }\) and \(p^{\pm }\) in the y-direction at point \((x_{i}, y_{j+\frac{1}{2}})\) are the same as in the x-direction. Here, the local left eigenvectors and right eigenvectors of the Jacobian matrix \(\left. \frac{\partial {\varvec{G}}}{\partial {\varvec{U}}}\right| _{x_{i}, y_{j+\frac{1}{2}}}\) are given as

$$\begin{aligned} {\varvec{R}}^{G}= & {} \begin{pmatrix} 1 &{} 1 &{} 1 &{} 1 \\ u &{} 0 &{} 1 &{} u \\ v-c &{} v &{} v &{} v+c \\ \gamma e+\frac{u^{2}+v^{2}}{2}-vc\ \ &{} \frac{v^{2}-u^{2}}{2}\ \ &{} u+\frac{v^{2}-u^{2}}{2}\ \ &{} \gamma e+\frac{u^{2}+v^{2}}{2}+vc \end{pmatrix}, \nonumber \\ \end{aligned}$$
(46)
$$\begin{aligned} {\varvec{L}}^{G}= & {} \begin{pmatrix} \frac{u^{2}+v^{2}}{4\gamma e}+\frac{v}{2c} &{} -\frac{u}{2\gamma e } &{} -\frac{1}{2c}-\frac{v}{2\gamma e} &{} \frac{1}{2\gamma e } \\ 1-\frac{u^{2}+v^{2}}{2\gamma e }+\frac{u(u^{2}+v^{2})}{2\gamma e} &{} \frac{u-u^{2}}{\gamma e}-1 &{} \frac{v-uv}{\gamma e} &{} \frac{u-1}{\gamma e} \\ -\frac{u(u^{2}+v^{2})}{2\gamma e} &{} 1+\frac{u^{2}}{\gamma e} &{} \frac{uv}{\gamma e} &{} -\frac{u}{\gamma e} \\ \frac{u^{2}+v^{2}}{4\gamma e}-\frac{v}{2c} &{} -\frac{u}{2\gamma e } &{} \frac{1}{2c}-\frac{v}{2\gamma e} &{} \frac{1}{2\gamma e } \end{pmatrix}.\nonumber \\ \end{aligned}$$
(47)
Table 1 \( L_{1} \) and \( L_{\infty } \) errors of the density \( \rho \)
Full size table

Finally, the whole procedure of the WENO-LBFS scheme is given as following

  1. Step 1

    Reconstruct the values \(\rho ^{\pm }\), \(u^{\pm }\), \(v^{\pm }\) and \(p^{\pm }\) by WENO scheme

    1. Step 1.1

      Transform the conservation variables \({\varvec{U}}\) to the characteristic variables \({\varvec{V}}\) based on the local left characteristic vectors \({\varvec{L}}^{F}\) and \({\varvec{L}}^{G}\) by using Eqs. (37), (47) and (39);

    2. Step 1.2

      Reconstruct the characteristic variables \({\varvec{V}}^{\pm }\) by using Eqs. (40)–(44);

    3. Step 1.3

      Transform the characteristic variables \({\varvec{V}}^{\pm }\) to the conservation variables \({\varvec{U}}^{\pm }\) based on the local right characteristic vectors \({\varvec{R}}^{F}\) and \({\varvec{R}}^{G}\) by using Eqs. (36), (46) and (45);

    4. Step 1.4

      Transform the conservation variables \({\varvec{U}}^{\pm }\) to flow variables \(\rho ^{\pm }\), \(u^{\pm }\), \(v^{\pm }\) and \(p^{\pm }\).

  2. Step 2

    Evaluate numerical fluxes \(\hat{{\varvec{F}}}\) and \(\hat{{\varvec{G}}}\) based on the non-free parameter D1Q4 model.

    1. Step 2.1

      Compute the equilibrium distribution function \(f_{\alpha }^{k}\) and lattice velocities \(e_{\alpha }^{k}\) by using Eqs. (7)–(27);

    2. Step 2.2

      Evaluate the numerical fluxes \(\hat{{\varvec{F}}}\) and \(\hat{{\varvec{G}}}\) by using Eqs. (22) or (23), (26) or (31) or (35).

  3. Step 3

    Solve the spatial semi-discretization Eq. (4) by using the three-step Runge-Kutta method of Eq. (6) to update the conservation variables \({\varvec{U}}\).

3 Numerical results

In this section, many numerical tests are performed to compare the results of WENO scheme based on the four different lattice Boltzmann flux solvers outlined in the previous section. The detailed numerical study is mainly performed for the 1D and 2D system cases. Without special statement, the CFL numbers are taken as 0.45 and 0.475 for 1D and 2D states, respectively.

3.1 Accuracy test

First, we should have an accuracy test for compressible flow problems with smooth solution to validate that WENO scheme combining with inviscid LBFS I, viscous LBFS II, hybrid LBFS III and hybrid LBFS IV (the inviscid WENO-LBFS I scheme, viscous WENO-LBFS II scheme, hybrid WENO-LBFS III scheme and hybrid WENO-LBFS IV) can keep high-order accuracy and high efficiency.

Example 1

Consider the two dimensional Euler equations (1). The initial conditions are set to be \(\rho (x,y,0)=1+0.2\sin (\uppi (x+y)), u(x,y,0)=0.7, v(x,y,0)=0.3, p(x,y,0)=1 \) with a 2-periodic boundary condition. The final computational time is up to \(t=2\). The exact solution is \(\rho (x,y,t)=1+0.2\sin (\uppi (x+y-(u+v)t)), u(x,y,t)=0.7, v(x,y,t)=0.3, p(x,y,t)=1 \).

The numerical errors and the orders of accuracy for the density are shown in Table 1. From this table, it can be seen that all of WENO scheme based on the above four kinds of LBFS can achieve desired orders of accuracy. All these schemes are of fifth order of convergence of \(L_{1}\) and \(L_{\infty }\) errors. The error of the WENO-LBFS II scheme is the largest among all scheme, and there is no difference between the WENO-LBFS I, hybrid WENO-LBFS III and hybrid WENO-LBFS IV schemes. In other words, for this smooth problem, the hybrid scheme switches into the inviscid WENO-LBFS I scheme that can better solve continuous problem than the viscous WENO-LBFS II scheme.

3.2 Test 1D cases with shock waves

The problems of compressible flows usually arise shock waves, which demand that the numerical algorithms are robust. This robustness often performs avoiding numerical oscillations and high resolution to shock-capturing. Here, several classical shock problems are presented to test the performance of the inviscid WENO-LBFS I scheme, viscous WENO-LBFS II scheme, hybrid WENO-LBFS III scheme and hybrid WENO-LBFS IV scheme.

Example 2

Shu–Osher problem. The initial condition is

$$\begin{aligned} (\rho , u , p )= {\left\{ \begin{array}{ll} (3.857143,2.629369,10.333333) &{} \quad \text{ for } ~~ x \leqslant -4, \\ (1+\varepsilon \sin (5x),0,1) &{} \quad \text{ for } ~~ x > -4, \end{array}\right. }\nonumber \\ \end{aligned}$$
(48)

where \( \varepsilon \) is set to be 0.2. The computational domain is \([-\,5, 5]\) covered with \(N=300\) grid points. The compact boundary condition is used for the left boundary, and the inflow boundary condition is applied on the right boundary.

The classical elementary waves in solution of Shu–Osher problem include high-frequency waves and shock waves. Figure 1 depicts the density \(\rho \) at time \(t=1.8\) against the reference solution computed by the WENO-LF scheme using 2000 grids. This figure is zoomed at the region \( x\in [0.5,2.5], \rho \in [2.5,5.0] \) which contains high-frequency waves to facilitate comparative analysis. The comparisons of WENO scheme combining with four kinds of LBFS are described clearly in Fig. 1. From this figure, it can be found that the results of the WENO-LBFS1 scheme, the WENO-LBFS III scheme and the WENO-LBFS IV scheme have almost no difference. And the results of these three schemes are slightly better than that of the WENO-LBFS II scheme. Based on the above, WENO scheme based on the hybrid LBFS shows good performance to capture high-frequency waves. For the weak shock waves, WENO scheme based on the hybrid LBFS scheme tends to that of the WENO-LBFS I scheme.

Fig. 1
figure 1

Shu–Osher problem at \(t=1.8\). Solid line: the “exact” reference solution from the WENO-LF scheme with 2000 grid points. Symbols: the results from the WENO-LBFS I, WENO-LBFS II, WENO-LBFS III and WENO-LBFS IV schemes with 300 grid points

Full size image

Example 3

The extension of Shu–Osher problem [18]. The initial condition is

$$\begin{aligned} (\rho , u , p )= {\left\{ \begin{array}{ll} (1.515695,0.523346,1.80500) &{} \quad \text{ for } ~~ x \leqslant -4.5, \\ (1+\varepsilon \sin (20\uppi x),0,1) &{} \quad \text{ for } ~~ x > -4.5. \end{array}\right. }\nonumber \\ \end{aligned}$$
(49)

where \( \varepsilon \) is set to be 0.1. The computational domain is \([-\,5, 5]\) covered with \(N=2000\) grid points. The compact boundary condition is used for the left boundary, and the inflow boundary condition is applied on the right boundary. The simulation time is up to 5.0. The CFL number is set to be 0.6 in this case.

The extension of Shu–Osher problem is yielded by a right facing shock wave of Mach number 1.1 impacting on a high-frequency density perturbation. Figure 2 shows the density \(\rho \) at time \(t=5.0\) against the reference solution computed by the WENO-HLLC scheme with 8000 grid points. Particularly, the result obtained from the WENO-LF scheme with 2000 grid points is also given for comparisons. The solution of this figure is zoomed at region \( x\in [-\,2.2,3.6], \rho \in [0.9,1.7] \) which contains the smooth structures and the moving shock wave to facilitate comparative analysis. From Fig. 2, it can be clearly observed that there is no difference among the WENO-LBFS I, WENO-LBFS III and WENO-LBFS IV schemes, which are more accurate than the WENO-LBFS II scheme, and the WENO-LF scheme is the worst among all schemes. For this problem, the hybrid WENO-LBFS III and WENO-LBFS IV schemes switch into the inviscid WENO-LBFS I scheme.

Fig. 2
figure 2

Extension of Shu–Osher problem at \(t=5.0\). Solid line: the “exact”reference solution from the WENO-HLLC scheme with 8000 grid points. Symbols: the results from the WENO-LBFS I, WENO-LBFS II, WENO-LBFS III, WENO-LBFS IV and WENO-LF schemes with 2000 grid points

Full size image

Example 4

Woodward–Colella blast wave problem [18]. The initial condition is

$$\begin{aligned} (\rho , u , p )= {\left\{ \begin{array}{ll} (1,0,1000) &{} \quad \text{ for } ~~ 0 \leqslant x< 0.1, \\ (1,0,0.01) &{} \quad \text{ for } ~~ 0.1 \leqslant x < 0.9, \\ (1,0,100) &{} \quad \text{ for } ~~ x \geqslant 0.9. \end{array}\right. } \end{aligned}$$
(50)

The computational domain is \( x \in [0,1] \) covered with \(N=300\) grid points. The reflective boundary condition is used for the left and right boundaries. The final simulation time is up to 0.038.

The solution of Woodward problem involves complex wave structures yielded by the interaction of two shock waves. In Fig. 3, the density \(\rho \) at \(t=0.038\) is plotted against the reference solution computed by the WENO-LF scheme using 2000 grids. This figure is zoomed at the region \( x\in [0.53,0.88],\rho \in [0,7] \) which contains complex wave structures to facilitate comparative analysis. The comparisons of WENO scheme combining with four kinds of LBFS are described clearly in Fig. 3. From this figure, it can be seen that the resolution of the inviscid WENO-LBFS I scheme is the highest among all schemes. The results computed by the hybrid WENO-LBFS IV scheme are almost same as that of the hybrid WENO-LBFS III scheme. The performance of the hybrid WENO-LBFS IV scheme is better than that of the WENO-LBFS II scheme and slightly inferior to that of the WENO-LBFS I scheme.

Fig. 3
figure 3

Woodward problem at \(t=0.038\). Solid line: the “exact” reference solution from WENO-LF scheme with 2000 grids. Symbols: the results from the inviscid WENO-LBFS I, viscous WENO-LBFS II, hybrid WENO-LBFS III and hybrid WENO-LBFS IV schemes with 300 grids

Full size image

Example 5

Riemann problem with the initial condition:

$$\begin{aligned} (\rho , u , p )= {\left\{ \begin{array}{ll} (5.99924,19.5975,460.894) &{} \quad \text{ for } ~~ x \leqslant 0.5, \\ (5.999242,-\,6.19633,46.095) &{} \quad \text{ for } ~~ x > 0.5. \end{array}\right. }\nonumber \\ \end{aligned}$$
(51)

The computational domain is \( x \in [0,1] \) covered with \(N = 200\) grid points. The outflow boundary condition is imposed for the left and right boundaries. The simulation time is up to 0.035.

The classical elementary waves in a solution of the Riemann problem include shock waves. In Fig. 4, the density \(\rho \) at \(t=0.035\) is plotted where the comparisons of WENO scheme based on four kinds of LBFS are described clearly. This figure is zoomed at the region \( x\in [0.4,1], \rho \in [5,35]\) which contains shock waves to facilitate comparative analysis. Especially, the solution obtained by the WENO-LF scheme with grid size \(N=1600\) as the reference solution is given.

From Fig. 4, it is clearly seen that the resolution of the hybrid WENO-LBFS scheme is the highest and the resolution of the inviscid WENO-LBFS I scheme is the lowest among all schemes. The performance of the hybrid WENO-LBFS IV scheme is slightly superior to that of the viscous WENO-LBFS II scheme. There is no difference between the hybrid WENO-LBFS III scheme and the hybrid WENO-LBFS IV scheme. It should be noted that the results of the inviscid WENO-LBFS I scheme show oscillations near discontinuity \( x=0.5\), and the errors between the results computed by the WENO-LBFS I scheme and the reference solution are very large at the region \( x\in [0.5,0.8]\). For this shock waves problem, the hybrid WENO-LBFS III scheme and hybrid WENO-LBFS IV switch into the viscous WENO-LBFS II scheme for better capturing shock waves.

Fig. 4
figure 4

Riemann problem at \(t=0.035\). Solid line: the “exact” reference solution from the WENO-LF scheme with 1600 grids. Symbols: the results from the inviscid WENO-LBFS I, viscous WENO-LBFS II, hybrid WENO-LBFS III and hybrid WENO-LBFS IV schemes with 200 grids

Full size image

3.3 Test 2D cases with shock waves

In the previous section, 1D cases with shock waves and contact discontinuities are tested. Based on the numerical results, it is known that the hybrid WENO-LBFS III scheme and hybrid WENO-LBFS IV scheme have good performances to capture some complex wave structures (including shock waves, contact discontinuities, etc.). Next, 2D cases with the complex wave structures are used to test the ability of WENO scheme based on hybrid LBFS.

Example 6

Double Mach reflection [51]. The computational domain is \( [0,4] \times [0,1] \). Initially a right-moving Mach 10 shock is positioned at \(x=\frac{1}{6}\), \( y=0 \) and makes a \(60^{\circ }\) angle with x-axis. For the top boundary, the flow values are set to describe the exact motion of a Mach 10 shock. For the bottom boundary, the exact post-shock condition is imposed for the range \(0 \leqslant x \leqslant \frac{1}{6}\), and the reflecting wall is at rest. For the left and right boundaries, inflow boundary and outflow boundary are adopted respectively. The computational time is up to t = 0.2.

Fig. 5
figure 5

Double Mach reflection problem at \(t=0.2\). The results with \( h=\frac{1}{480} \) computed by WENO scheme based on five kinds of LBFS and the results with \( h=\frac{1}{960} \) computed by the WENO-LF scheme

Full size image

This problem is often provided as a case to test high-resolution schemes. Figure 5 shows the density contours with grid size \( h=\frac{1}{480} \) for WENO scheme based on different LBFS. Especially, the solutions obtained by the WENO-LF scheme with grid size \( h=\frac{1}{960} \) and the hybrid WENO-LBFS \(\mathrm III^*\) scheme with mesh \( h=\frac{1}{480} \) as the reference solutions are given. The figure is zoomed at the region \([2,2.875]\times [0,1],\) which contains complex wave structures to facilitate comparative analysis, and the density is plotted by 30 equally spaced contour lines from \( \rho =1.5 \) to \( \rho = 22.8 \). From this figure, it can be observed that the number of capturing complex wave structures of the inviscid WENO-LBFS I scheme is most among all schemes, but it exhibits oscillations and instability. The reason may be the viscidity of the WENO-LBFS I scheme is too small. The hybrid WENO-LBFS III scheme can capture more vortices than viscous WENO-LBFS II scheme. It should be noted that it has almost no difference between the hybrid WENO-LBFS III scheme and the hybrid WENO-LBFS \(\mathrm III^* \) scheme, but the vortices of the hybrid WENO-LBFS \(\mathrm III^*\) scheme may be smeared out. The more important feature is that the performance of the hybrid WENO-LBFS IV scheme to shock-capturing is better among all hybrid scheme for this problem.

Example 7

Implosion problem [49]. The initial condition is

$$\begin{aligned} (\rho , u , v, p )= {\left\{ \begin{array}{ll} (1,0,0,1), &{} \quad |x|-0.15 \leqslant y \leqslant -|x|+0.15, \\ (0.125,0,0,0.14), &{} \quad \text {otherwise.} \\ \end{array}\right. }\nonumber \\ \end{aligned}$$
(52)

The computational domain is \( [-0.3,0.3] \times [-0.3,0.3] \). The reflective boundary condition is imposed for the left, right and button boundaries. For the top boundary, the outflow boundary is applied. The final simulation time is up to 0.8.

Fig. 6
figure 6

Implosion problem at \(t=0.8\). Left: the pressure computed by the WENO-LBFS II scheme and the WENO-LBFS IV scheme with grid size of \(400\times 400\). Right: the pressure computed by the WENO-LBFS III scheme with grid size of \(400\times 400\) and computed by the WENO-LF scheme with grid size of \(800\times 800\)

Full size image
Fig. 7
figure 7

Implosion problem at \(t=0.8\). Left: the Mach number computed by the WENO-LBFS II scheme and the WENO-LBFS IV scheme with grid size of \(400\times 400\). Right: the Mach number computed by the WENO-LBFS III scheme with grid size of \(400\times 400\) and computed by the WENO-LF scheme with grid size of \(800\times 800\)

Full size image

Implosion problem is used to illustrate the ability of WENO scheme based on four kinds of LBFS for 2D problems.

Figures 6 and 7 respectively show the pressure and Mach number contours with uniform grid size of \(400\times 400\) for WENO scheme based on different LBFS. Especially, the solution obtained by the WENO-LF scheme with uniform grid size of \(800\times 800\) as the reference solution is given. The pressure is plotted by 35 equally spaced contour lines from \( p=0.54 \) to \( p=1.19 \), and the Mach number is depicted by same contour lines from Mach = 0.01 to Mach = 0.2 to facilitate comparative analysis. Particularly, it should be noted that the WENO-LBFS I scheme can not be applied to simulate the implosion problem when the mesh size is \(400\times 400\). It may be that the WENO-LBFS I scheme is an inviscid scheme, so it can not capture strong shock waves. From Figs. 6 and 7, it can be observed that the WENO-LBFS II scheme can capture more complex wave structures than the WENO-LBFS III scheme and the WENO-LBFS IV scheme. Owing to that the results of the WENO-LBFS \(\mathrm III^*\) scheme and the WENO-LBFS III scheme have no significant difference, the result computed by the WENO-LBFS \(\mathrm III^*\) scheme is not shown in Figs. 6 and 7. Obviously, the wave structures of the WENO-LBFS III scheme at the center are not symmetrical. The result is not our expectation according to the reference solution. Based on the above, the present WENO scheme based on the hybrid LBFS has good performance to capture the complex wave structures.

Example 8

2D Riemann problem with four planar shocks [23]. The initial condition is given as follows

$$\begin{aligned}&(\rho , u , v, p )\nonumber \\&= {\left\{ \begin{array}{ll} (1.5,0,0,1.5) &{} \quad \text{ for } ~~ x> 0.8, y> 0.8, \\ (0.5323,1.206,0,0.3) &{} \quad \text{ for } ~~ x \leqslant 0.8, y > 0.8, \\ (0.138,1.206,1.206,0.029) &{} \quad \text{ for } ~~ x < 0.8, y \leqslant 0.8, \\ (0.5323,0,1.206,0.3) &{} \quad \text{ for } ~~ x \geqslant 0.8, y \leqslant 0.8. \\ \end{array}\right. }\nonumber \\ \end{aligned}$$
(53)

The computational domain is \( [0,1] \times [0,1] \) with a mesh size of \(400 \times 400\). The compact boundary condition is applied at all boundaries. The simulation time is up to 0.65.

This problem, whose solution produces multi-scale wave structures resulting from shock wave interactions, is used to validate the capability of WENO scheme-based four kinds of LBFS capturing small-scale wave structures. Figure 8 displays the density distribution, where the density is plotted by 16 equally spaced contour lines from \( \rho =0.2\) to \(\rho =1.7\). From Fig. 8, it can be seen that the inviscid WENO-LBFS I scheme can capture more complex wave structures in all schemes, while it seems that the viscidity of the inviscid WENO-LBFs I scheme is too small to be unstable. The ability of the hybrid WENO-LBFS III and WENO-LBFS IV schemes is slightly better than that of the viscous WENO-LBFS II scheme. For this shock wave problem, the hybrid WENO-LBFS scheme changes into the viscous WENO-LBFS II scheme to better capture complex wave structures.

Fig. 8
figure 8

Density distribution for Riemann problem with four planar shocks at \(t=0.65\)

Full size image
Fig. 9
figure 9

Density distribution for Riemann problem with four planar contact discontinuities with same sign vortex sheets at \(t=0.3\). The initial pressure is uniform \((p=1.0)\)

Full size image
Fig. 10
figure 10

Density distribution for Riemann problem with four planar contact discontinuities with different sign vortex sheets at \( t=0.25 \). The initial pressure is uniform \((p=1.0)\)

Full size image

Example 9

2D Riemann problem with four planar contact discontinuities with same sign vortex sheets [23]. The initial data is given as follows

$$\begin{aligned} (\rho , u , v, p )= {\left\{ \begin{array}{ll} (1,0.75,-\,0.5,0.3) &{} \quad \text {for} ~~ x> 0.5, y> 0.5; \\ (2,0.75,0.5,0.3) &{} \quad \text {for} ~~ x \leqslant 0.5, y > 0.5; \\ (1,-\,0.75,0.5,0.3) &{} \quad \text {for} ~~ x < 0.5, y \leqslant 0.5; \\ (3,-\,0.75,-\,0.5,0.3) &{} \quad \text {for} ~~ x \geqslant 0.5, y \leqslant 0.5. \\ \end{array}\right. } \end{aligned}$$
(54)

The computational domain is \( [0,1] \times [0,1] \) with a grid size of \(400 \times 400\). All boundaries are treated with the compact boundary condition. The final simulation time is to be 0.3.

The problem consists of four planar contour discontinuities, whose instantaneous interaction results in a complex wave pattern. Figure 9 presents the density distribution, which is plotted by 20 equally spaced contour lines from \(\rho =0.2\) to \(\rho =3.5\). Due to the initial pressure distribution is uniform which is equal to 1, the Mach number is relatively large. Therefore, the solution of this problem can display more small scale structures. It can be observed in Fig. 9 that the capability of the WENO-LBFS I, hybrid WENO-LBFS III and hybrid WENO-LBFS IV schemes is better than that of the WENO-LBFS II scheme. For this problem involving four planar contact discontinuities with same sign vortex sheets, the hybrid WENO-LBFS scheme switches into the inviscid WENO-LBFS I scheme.

Example 10

2D Riemann problem with four planar contact discontinuities with different sign vortex sheets [23]. The initial condition is given as follows

$$\begin{aligned} (\rho , u , v, p )= {\left\{ \begin{array}{ll} (1,-\,0.75,-\,0.5,1) &{} \quad \text {for} ~~ x> 0.5, y> 0.5, \\ (2,-\,0.75,0.5,1) &{} \quad \text {for} ~~ x \leqslant 0.5, y > 0.5, \\ (1,0.75,0.5,1) &{} \quad \text {for} ~~ x < 0.5, y \leqslant 0.5, \\ (3,0.75,-\,0.5,1) &{} \quad \text {for} ~~ x \geqslant 0.5, y \leqslant 0.5. \\ \end{array}\right. } \end{aligned}$$
(55)

The computational domain is \( [0,1] \times [0,1] \) with a uniform mesh of \(400 \times 400\). All boundaries are implemented by the compact boundary condition.

In this case, four planar contact discontinuities support vortex sheets with different signs, which generate totally different flow patterns. The solution of this problem contains so-called delta-shocks. The density distributions at \(t=0.25\) are shown in Fig. 10 where the density is plotted by 20 equally spaced contour lines from \( \rho =1.2 \) to \( \rho =4.0 \). From this figure, it can be clearly seen that there is almost no difference among the WENO-LBFS I, hybrid WENO-LBFS III and hybrid WENO-LBFS IV schemes. In these three schemes, more small scale vortices are observed, compared with the WENO-LBFS II scheme. For this problem involving four planar contact discontinuities with different sign vortex sheets, the hybrid WENO-LBFS scheme tends to the inviscid WENO-LBFS I scheme.

Example 11

A Mach 3 wind tunnel with a step. The computational domain is the red region in Fig. 11. The reflective boundary condition is imposed on the top and bottom boundaries. For the left boundary, the inflow boundary condition is applied. For the right boundary, the outflow boundary condition is used. The final simulation time is up to 4.0.

A Mach 3 wind tunnel with a step is used to illustrate the ability of the hybrid WENO-LBFS III scheme for multi-block domains to obtain a stable solution. Figure 12 shows the density and pressure contours with uniform grid size of \( 120 \times 40 \) and \( 240 \times 80 \) for the hybrid WENO-LBFS III scheme. The density is plotted by 30 equally spaced contour lines from \( \rho =1 \) to \( \rho =6 \), and pressure is depicted by same contour lines from \( p=0.5 \) to \( =11.5 \) to facilitate comparative analysis. Particularly, it should be noted that the inviscid WENO-LBFS I scheme can not be applied to simulate this problem. It may be because the numerical viscosity of the iviscid WENO-LBFS I scheme is too small to capture strong shock waves. From Fig. 12, it can be observed that the hybrid WENO-LBFS III scheme can capture shock waves in no special entropy correction for cell at the corner. This implies that the hybrid WENO-LBFS III scheme can obtain a stable solution for a stationary Mach 3 flow hitting a rectangular step owing that the hybrid WENO-LBFS III scheme combines the advantages of the inviscid WENO-LBFS I scheme and the viscous WENO-LBFS II scheme. It should be referred that the results of the hybrid WENO-LBFS IV scheme and the hybrid WENO-LBFS III scheme have no difference for this problem.

Fig. 11
figure 11

Regine of a Mach 3 wind tunnel with a step \( [0,3] \times [0,1] \). The step is from \(x=0.6\) to \(x=3.0\) and is 0.2 length units high

Full size image
Fig. 12
figure 12

Mach 3 wind tunnel with a step at \(t=4.0\). Left: the density computed by the hybrid WENO-LBFS III scheme with grid size of \(120\times 40\) and \(240\times 80\). Right: the pressure computed by the hybrid WENO-LBFS III scheme with grid size of \(120\times 40\) and \(240\times 80\)

Full size image

4 Conclusions

In this paper, compared with the inviscid WENO-LBFS I scheme and viscous WENO-LBFS II scheme, the good properties of the hybrid WENO-LBFS scheme are investigated for simulation of compressible flows. Through simulations with smooth solution, contact discontinuities, strong shock waves and complex wave structures, numerical results show that WENO scheme based on inviscid LBFS I, viscous LBFS II, hybrid LBFS III and hybrid LBFS IV all can achieve high-order accuracy. For smooth problems, the inviscid WENO-LBFS I scheme can more accurately calculate the solution than the viscous WENO-LBFS II scheme, and the hybrid WENO-LBFS scheme switches into the inviscid WENO-LBFS I scheme. For shock waves problems, the viscous WENO-LBFS II scheme can capture more complex wave structures and has higher resolution than the inviscid WENO-LBFS I scheme, and the hybrid WENO-LBFS scheme changes into the viscous WENO-LBFS II scheme. Thus, the present hybrid WENO-LBFS scheme has high-accuracy, high-resolution and high-efficiency. What’s more, it can not only accurately calculate the solution of smooth regions, but can effectively capture shock waves without oscillations.