1 Introduction

Interfaces exist in numerous materials and structures, either natural or man-made. The fundamental objective of interface fracture mechanics is to develop a criterion for predicting the extension of interface cracks, by extending Irwin’s pioneering work [1]. In 1957, Irwin identified three independent modes of the singular stress field near a crack tip in a homogeneous isotropic body, and characterized each mode by a corresponding normalized parameter, called the stress intensity factor (SIF). Then, Irwin [1] defined a new material property, fracture toughness, as the critical SIF that a material can sustain. This idea leads to the now well-established, SIF-based fracture mechanics criterion.

In 1959, Williams [2] found that, under in-plane loading, the singular exponent of a crack resting on the interface of two bonded isotropic materials is a complex number, \(1/2+\mathrm{i}\varepsilon \), where \(\varepsilon \) is a constant related to the elastic properties of two isotropic materials and known as the oscillatory index. Thus, if \(\varepsilon \ne 0\) (as it is for most cracks in dissimilar media), the singular stress field near the interface crack tip is oscillatory [2]. Later, to complicate the case further, England [3] demonstrated the existence of crack/contact interference near the tip of an interface crack. Such pathological singularity at an interface crack tip caused the delay of an appropriate fracture criterion governing interface crack extensions.

In 1988, Rice [4] extended Irwin’s concept to interface cracks. Given that the two in-plane modes of an interface crack are coupled, he ignored the pathological phenomena in the vicinity of the interface crack tip and defined the complex stress intensity factor \(K=K_1 +\mathrm{i}K_2 \) as a new crack tip characterizing parameter [5]. \(K_1 \) and \(K_2\) are the SIFs of the Mode I and Mode II components of an interface crack tip field, respectively. However, the dimension of K is dependent upon \(\mathrm{i}\varepsilon \), hence, it is difficult to employ K to establish suitable fracture criterion for interface cracks. One year later, to address this critical issue, Suo [6] introduced the combination \(Kl^{\mathrm{i}\varepsilon }\) (l being an arbitrary length) so that combination \(Kl^{\mathrm{i}\varepsilon }\) has the same dimension as the classical SIF. While the real and imaginary parts of the combination \(Kl^{\mathrm{i}\varepsilon }\) depend on the value of l, it does not affect the amplitude of the combination. He then introduced \(\psi =\tan ^{-1}\left[ {\hbox {Im}({Kl^{\mathrm{i}\varepsilon })}/{\hbox {Re}(Kl^{\mathrm{i}\varepsilon })}} \right] \) as the phase angle of an interface crack to develop an interface fracture criterion based on the strain energy release rate G, namely, \(G\left( \psi \right) =G_\mathrm{C} (\psi )\) [6]. For a given bimaterial, the critical strain energy release rate \(G_\mathrm{C} \left( \psi \right) \), known as toughness of the interface, depends on the phase angle \(\psi \) [6, 7]. Thereafter, Yuuki and Xu [8] presented a criterion based on the maximum tangential stress theory while Yuuki et al. [9] proposed the empirical elliptical fracture criterion \((K_\mathrm{1}/K_\mathrm{1C})^\mathrm{2}+(K_{2}/K_\mathrm{2C})^{2}= 1\), which can well describe the experimental results. Recently, assuming that the interface possesses deformation capacities for volume and distortional deformation energy, Cai and Xu [10] developed a fracture criterion for an interface crack and an interfacial debonding criterion for a perfectly bonded interface. Banks-Sills [11] summarized comprehensively the progress in interface fracture mechanics. Conceptually, despite the significant efforts made by many scholars, it appears that the G–based fracture criterion is so far the best criterion.

The aim of the current study is to establish a SIF-based fracture criterion for interface cracks, which is not only conceptually sound but also overcomes the limitations associated with the G-based fracture criterion. To this end, firstly, the dimension of the complex SIF K is re-investigated. For an interface crack, its complex SIF is split into two parts, i.e., \(K=\hat{K}s^{-\mathrm{i}\varepsilon }\), where s is a characteristic length of the dissimilar media containing the crack, and \(\hat{K}\) has the same dimension as the classical SIF and characterizes the interface crack tip field. Secondly, the quasi Mode I and Mode II crack tip fields are then defined and distinguished from the crack tip fields of general coupled modes. Finally, based on fracture criteria involving quasi Mode I and Mode II SIFs, the fracture criterion involving SIFs for the mixed mode is proposed. Validation of the new criterion is carried out using existing experimental results.

2 Stress intensity factor (SIF)

2.1 Dimensional dilemma

Rice solved the eigenvalue problem of a semi-infinite traction-free crack lying along the interface between two isotropic half planes with Muskhelishvili’s method, and expressed the singular stress field near the crack tip [5] as

$$\begin{aligned} \sigma _{ij} =\frac{1}{\sqrt{2\uppi \!r}}\left[ \hbox {Re}(Kr^{\mathrm{i}\varepsilon })\hat{{\sigma }}_{ij}^\mathrm{I} (\theta ,\varepsilon )+\hbox {Im}(Kr^{\mathrm{i}\varepsilon })\hat{{\sigma }}_{ij}^\mathrm{II} (\theta ,\varepsilon )\right] ,\nonumber \\ \end{aligned}$$
(1)

where the imaginary part of the singularity exponent \(\varepsilon \) is termed as the oscillatory index, K is the complex SIF, and \(\hat{{\sigma }}_{ij}^\mathrm{I} (\theta ,\varepsilon )\) and \(\hat{{\sigma }}_{ij}^\mathrm{II} (\theta ,\varepsilon )\) are the dimensionless angular distribution functions for Mode I and Mode II tip fields, respectively.

Typically, the unit of K is \(\mathrm{MPa}\sqrt{\mathrm{m}}\mathrm{m}^{-\mathrm{i}\varepsilon }\), which depends on the elastic properties of the two bonded materials via the oscillatory index \(\varepsilon \). As a result, the material dependent unit of K causes difficulties when the system of units is changed [5], hence, the dilemma of using K for constructing a fracture criterion.

The dimension of K is:

$$\begin{aligned} K=\left[ \mathrm{stress} \right] \left[ \mathrm{length} \right] ^{1/2-\mathrm{i}\varepsilon }. \end{aligned}$$
(2)

Dimensional analysis dictates that K should be composed of two parts:

$$\begin{aligned} K=\hat{K}s^{-\mathrm{i}\varepsilon }, \end{aligned}$$
(3)

where s is a characterizing length (see next section) and the normalized SIF \(\hat{K}\) has the same dimension as the classical SIF defined by Erwin [1], as

$$\begin{aligned} \hat{K}=\left[ \mathrm{stress} \right] \left[ \mathrm{length} \right] ^{1/2}. \end{aligned}$$
(4)

Substitution of Eq. (3) into Eq. (1) leads to:

$$\begin{aligned} \sigma _{ij}= & {} \frac{1}{\sqrt{2\uppi \!r}}\left\{ \hbox {Re}\left[ \hat{K}\left( \frac{r}{s}\right) ^{\mathrm{i}\varepsilon }\right] \hat{{\sigma }}_{ij}^\mathrm{I} (\theta ,\varepsilon )\right. \nonumber \\&\left. +\,\hbox {Im}\left[ \hat{K}\left( \frac{r}{s}\right) ^{\mathrm{i}\varepsilon }\right] \hat{{\sigma }}_{ij}^\mathrm{II} \left( \theta ,\varepsilon \right) \right\} . \end{aligned}$$
(5)

Since \(\hat{K}\) characterizes the interface crack tip field as showed in Eq. (5), a criterion for interface cracks may be formulated directly with \(\hat{K}\), as Irwin did in classical fracture mechanics.

2.2 Expression of SIF

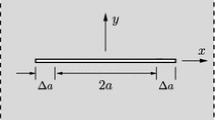
Practically, the complex SIF K can only be determined by solving a specific boundary value problem. Throughout this study, the problem of an infinite bimaterial plane containing an interface crack of length 2a subjected to in-plane stressing \((\sigma _{yy}^\infty ,\sigma _{xy}^\infty )\) at infinity is taken as a typical example. According to the solution of Rice [5], K can be expressed as

$$\begin{aligned} K=(1+2\mathrm{i}\varepsilon )\left( \sigma _{yy}^\infty +\mathrm{i}\sigma _{xy}^\infty \right) (2a)^{-\mathrm{i}\varepsilon }\sqrt{\uppi \! a}, \end{aligned}$$
(6)

where 2a is the length of the interface crack, and the real and imaginary parts of K are:

$$\begin{aligned} K_1= & {} \sqrt{\uppi \! a}\left\{ \cos [\varepsilon \ln (2a)]\left( \sigma _{yy}^\infty -2\varepsilon \sigma _{xy}^\infty \right) \right. \nonumber \\&\left. +\,\sin [\varepsilon \ln (2a)]\left( \sigma _{xy}^\infty +2\varepsilon \sigma _{yy}^\infty \right) \right\} ,\end{aligned}$$
(7)
$$\begin{aligned} K_2= & {} \sqrt{\uppi \!a}\left\{ \cos [\varepsilon \ln (2a)]\left( \sigma _{xy}^\infty +2\varepsilon \sigma _{yy}^\infty \right) \right. \nonumber \\&\left. -\,\sin [\varepsilon \ln (2a)]\left( \sigma _{yy}^\infty -2\varepsilon \sigma _{xy}^\infty \right) \right\} . \end{aligned}$$
(8)

It is seen from Eq. (6) that \((2a)^{-\mathrm{i}\varepsilon }\) in the expression of K is the origin of its dimensional dilemma. To critically address this issue, let K be re-expressed as

$$\begin{aligned} K=\hat{K}(2a)^{-\mathrm{i}\varepsilon }, \end{aligned}$$
(9)

where

$$\begin{aligned} \hat{K}=(1+2\mathrm{i}\varepsilon )(\sigma _{yy}^\infty +\mathrm{i}\sigma _{xy}^\infty )\sqrt{\uppi \!a}. \end{aligned}$$
(10)

The real and imaginary parts of \(\hat{K}\) are:

$$\begin{aligned} \hat{K}_1= & {} \sqrt{\uppi \!a}(\sigma _{yy}^\infty -2\varepsilon \sigma _{xy}^\infty ),\end{aligned}$$
(11)
$$\begin{aligned} \hat{K}_2= & {} \sqrt{\uppi \!a}(\sigma _{xy}^\infty +2\varepsilon \sigma _{yy}^\infty ). \end{aligned}$$
(12)

In contrast to the conventional definition of complex SIF K as showed in Eq. (6), the newly introduced complex SIF \(\hat{K}\) has the same dimension as the classical SIF.

In Eqs. (11) and (12), although the two in-plane modes are coupled even if the interface crack is subjected to simple tension or pure shear at remote, the quasi Mode I or quasi Mode II crack tip fields can be defined as shown below.

2.3 Quasi Mode I and Mode II crack tip fields

For the case of \(\sigma _{xy}^\infty =0, \hat{K}_1 \) and \(\hat{K}_2 \) of Eqs. (11) and (12) are reduced to:

$$\begin{aligned} \hat{K}_1= & {} \sqrt{\uppi \!a}\sigma _{yy}^\infty ,\end{aligned}$$
(13)
$$\begin{aligned} \hat{K}_2= & {} 2\varepsilon \sqrt{\uppi \!a}\sigma _{yy}^\infty . \end{aligned}$$
(14)

It is seen that \(\hat{K}_1\) and \(\hat{K}_2\) are not mutually independent, both depending on \(\sigma _{yy}^\infty \). The singular crack tip field is not a pure Mode I but one with substantial Mode I component, and hence it may be called the quasi Mode I. Let \(\hat{K}_\mathrm{QI} \) act as the characterizing parameter of the quasi Mode I crack tip field. Then, Eqs. (13) and (14) become:

$$\begin{aligned} \hat{K}_1= & {} \hat{K}_\mathrm{QI},\end{aligned}$$
(15)
$$\begin{aligned} \hat{K}_2= & {} 2\varepsilon \hat{K}_\mathrm{QI}. \end{aligned}$$
(16)

For the case of \(\sigma _{yy}^\infty =0, \hat{K}_1 \) and \(\hat{K}_2 \) read as

$$\begin{aligned} \hat{K}_1= & {} -2\varepsilon \sqrt{\uppi \!a}\sigma _{xy}^\infty ,\end{aligned}$$
(17)
$$\begin{aligned} \hat{K}_2= & {} \sqrt{\uppi \!a}\sigma _{xy}^\infty . \end{aligned}$$
(18)

For the same reason, this is not a pure Mode II singularity but one with substantial Mode II component, so it may be called the quasi Mode II. Let \(\hat{K}_\mathrm{QII} \) represent the characterizing parameter of the quasi Mode II crack tip field, then:

$$\begin{aligned} \hat{K}_1= & {} -2\varepsilon \hat{K}_\mathrm{QII},\end{aligned}$$
(19)
$$\begin{aligned} \hat{K}_2= & {} \hat{K}_\mathrm{QII}. \end{aligned}$$
(20)

For an interface crack of \(\varepsilon =0\), the quasi Mode I and quasi Mode II degenerate exactly to Mode I and Mode II, respectively.

2.4 Phase angle of mixed mode crack tip fields

For the case of combined loading \(\sigma _{yy}^\infty \) and \(\sigma _{xy}^\infty , \hat{K}_1 \) and \(\hat{K}_2 \) are:

$$\begin{aligned} \hat{K}_1= & {} \hat{K}_\mathrm{QI} -2\varepsilon \hat{K}_\mathrm{QII},\end{aligned}$$
(21)
$$\begin{aligned} \hat{K}_2= & {} \hat{K}_\mathrm{QII} +2\varepsilon \hat{K}_\mathrm{QI}. \end{aligned}$$
(22)

This is a mixed mode of \(\hat{K}_\mathrm{QI} \) and \(\hat{K}_\mathrm{QII} \), and the corresponding phase angle is defined as

$$\begin{aligned} \hat{\psi }=\tan ^{-1}\left( \frac{\hat{K}_\mathrm{QII} }{\hat{K}_\mathrm{QI} }\right) . \end{aligned}$$
(23)

Quasi Mode I and Mode II are the particular cases corresponding to \(\hat{\psi }=0\) and \(\hat{\psi }=\uppi /2\), respectively.

3 Stress intensity factor based fracture criterion for interface cracks

Based on the new SIF expression for interface cracks detailed in the previous section, the SIF-based fracture criterion is presented below.

3.1 Criterion for quasi Mode I and Mode II

Equations (15) and (16) suggest that once \(\hat{K}_\mathrm{QI}\) is determined, \(\hat{K}_1 \) and \(\hat{K}_2 \) are determined. In other words, one may use \(\hat{K}_\mathrm{QI}\) to establish a fracture criterion for quasi Mode I cracks. Accordingly, the quasi Mode I criterion governing the extension of an interface crack takes the form:

$$\begin{aligned} \hat{K}_\mathrm{QI} =\hat{K}_\mathrm{QIC}, \end{aligned}$$
(24)

where \(\hat{K}_\mathrm{QIC} \) is the critical SIF for quasi Mode I to be determined by experiments.

Similarly, one may use \(\hat{K}_\mathrm{QII}\) to establish a fracture criterion for quasi Mode II cracks, it takes the form:

$$\begin{aligned} \hat{K}_\mathrm{QII} =\hat{K}_\mathrm{QIIC}, \end{aligned}$$
(25)

where \(\hat{K}_\mathrm{QIIC} \) is the critical SIF for quasi Mode II to be determined by experiments.

3.2 Criterion for mixed mode

It is proposed that the SIF-based fracture criterion for a mixed mode interface crack can be expressed in the following form:

$$\begin{aligned} F(\hat{K}_\mathrm{QI},\hat{K}_\mathrm{QII})=F_\mathrm{C}, \end{aligned}$$
(26)

where \(K_\mathrm{QI} \) and \(K_\mathrm{QII} \) are separately the quasi Mode I and Mode II SIF components of a mixed mode crack tip field.

At present, the exact expression of function F in terms of \(K_\mathrm{QI} \) and \(K_\mathrm{QII} \) is not known. In the present study, as a first approximation, it is assumed that:

$$\begin{aligned} \left( {\frac{\hat{K}_\mathrm{QI} }{\hat{K}_\mathrm{QIC} }} \right) ^{2}+\left( {\frac{\hat{K}_\mathrm{QII}}{\hat{K}_\mathrm{QIIC}}} \right) ^{2}=1, \end{aligned}$$
(27)

where \(\hat{K}_\mathrm{QIC} \) and \(\hat{K}_\mathrm{QIIC} \) are the critical stress intensity factors defined in Sect. 3.1 for quasi Mode I and Mode II, respectively. The validity of Eq. (27) will be checked against experimental results in Sect. 5.

4 Energy release rate-based fracture criterion for interface cracks

The fracture criterion of interface cracks can be formulated either in terms of SIF or energy release rate, G. For interface cracks between dissimilar media, the relation between SIF and G is [12]:

$$\begin{aligned} G=\frac{\left| K \right| ^{2}}{E^{*}\cosh ^{2}\left( {\uppi \!\varepsilon } \right) }, \end{aligned}$$
(28)

where

$$\begin{aligned} \frac{1}{E^{*}}=\frac{1}{2}\left( \frac{1}{\overline{E}_1 }+\frac{1}{\overline{E}_2 }\right) , \end{aligned}$$
(29)

and

$$\begin{aligned} \overline{E}=\frac{E}{1-\nu ^{2}}. \end{aligned}$$
(30)

On account of \(\left| K \right| ^{2}=\left| {\hat{K}} \right| ^{2}\), substitution of Eqs. (21) and (22) into Eq. (28) leads to:

$$\begin{aligned} G=\frac{\left( {1+4\varepsilon ^{2}} \right) \left( {\hat{K}_\mathrm{QI} ^{2}+\hat{K}_\mathrm{QII}^{2}} \right) }{{E}^{*}\cosh ^{2}\left( {\uppi \!\varepsilon } \right) }. \end{aligned}$$
(31)

As a result, the general G-based criterion may be formulated in an alternative form, as

$$\begin{aligned} G\left( {\hat{\psi }} \right) =G_\mathrm{C} \left( \hat{\psi }\right) . \end{aligned}$$
(32)

The new expression of G-based criterion (Eq. (32)) is advisable because \(\hat{\psi }\) and the mixed mode have a one-to-one relationship. The new expression of G-based criterion (Eq. (32)) and the original expression of G-based criterion \(G\left( \psi \right) =G_\mathrm{C} (\psi )\) are substantially identical, for the phase angle \(\hat{\psi }\) and phase angle \(\psi \) can be mutually conversed with a given oscillatory index \(\varepsilon \) and arbitrary length l.

In addition, let \(G_\mathrm{I}\) and \(G_\mathrm{II}\) denote separately the energy release rate contributed by \(\hat{K}_\mathrm{QI}\) and \(\hat{K}_\mathrm{QII}\), the SIF-based fracture criterion (Eq. (27)) can be equivalently transformed into a criterion based on the energy release rate, as

$$\begin{aligned} \left( {\frac{G_\mathrm{I}}{G_\mathrm{IC} }} \right) +\left( {\frac{G_\mathrm{II} }{G_\mathrm{IIC} }} \right) =1, \end{aligned}$$
(33)

where \(G_\mathrm{IC}\) and \(G_\mathrm{IIC}\) represent the critical energy release rate for quasi Mode I and Mode II, respectively. In view of Eq. (33), the toughness curve \(G_\mathrm{C}\left( {\hat{\psi }} \right) \) may be characterized using two material property constants \(G_\mathrm{IC}\) and \(G_\mathrm{IIC}\), as

$$\begin{aligned} G_\mathrm{C} \left( {\hat{\psi }} \right) =\frac{G_\mathrm{IC} \left( {1+\tan ^{2}\hat{\psi }} \right) }{1+\left( G_{\mathrm{IC}} /G_{\mathrm{IIC}} \right) \tan ^{2}\hat{\psi }}. \end{aligned}$$
(34)

The derivation of Eq. (34) is given in Appendix 1.

The new expression of G-based criterion (Eq. (32)) coupled with Eq. (34) has a distinctive advantage: \(G_\mathrm{C} \left( {\hat{\psi }} \right) \) is a function of phase angle \(\hat{\psi }\) and depends on two material constants \(G_\mathrm{IC}\) and \(G_\mathrm{IIC}\) only, so a tedious experimental task is not needed to determine \(G_\mathrm{C} \left( {\hat{\psi }} \right) \). \(G_\mathrm{IC}\) and \(G_\mathrm{IIC}\) are determined either by experiments or by Eq. (31) once \(\hat{K}_\mathrm{QIC} \) and \(\hat{K}_\mathrm{QIIC} \) are known.

5 Validation against experimental results

It is noted that Liechti and Chai [13] measured the critical interface toughness with a plane strain specimen as showed in the insert of Fig. 1. The problem associated with the interface crack in this specimen has been solved analytically by Rice [14]. The test specimen had a thickness h of 12.7 mm and a length longer than the thickness. The bimaterial system used was epoxy/glass with the properties: \(E_1 =2.07\) GPa, \(\nu _1 =0.37\), and \(E_2 =68.9\) GPa, \(\nu _2 =0.20\). The oscillatory index \(\varepsilon \) was 0.06. The loading was restricted between \(\hat{\psi }=-76^{{\circ }}\) and \(\hat{\psi }=65^{{\circ }}\).

The existing experimental data on the critical interface toughness depicted in the \(G_\mathrm{C}\sim \psi \) plane (see Fig. 13 in Ref. [7]) are re-plotted in the \(G_\mathrm{C}\sim \hat{\psi }\) plane with hollow symbols, as shown in Fig. 1, (The relation between \(\psi \) and \(\hat{\psi }\) is given in Appendix 2). The experimental critical energy release rate for the quasi Mode I is \(G_\mathrm{IC} =4.17~\mathrm{{J/m^{2}}}\). As the critical energy release rate for the quasi Mode II \(G_\mathrm{IIC} \) is not included in the experimental results, we may estimate the value of \(G_\mathrm{IIC} \) indirectly by Eq. (34) with another appropriate data point, such as \(\hat{\psi }=-74^{\circ }, G_\mathrm{C} =32~\mathrm{{J/m^{2}}}\). Accordingly, the critical energy release rate for the quasi Mode II is assumed approximately as \(G_\mathrm{IIC} =70.6~\mathrm{{J/m^{2}}}\). Knowing \(G_\mathrm{IC} =4.17~\mathrm{{J/m^{2}}}\) and \(G_\mathrm{IIC} =70.6~\mathrm{{J/m^{2}}}\), the interface toughness curve predicted by Eq. (34) is also depicted in Fig. 1 with a solid curve. It is seen that the predictions of the G-based fracture criterion agree well with the experimental results.

It should be pointed out that, as the experimental data of Liechti and Chai [13] lacks values of \(G_\mathrm{IIC}\) as well as \(G_\mathrm{C}\) when \(\hat{\psi }\) is close to \({\pm \uppi \!}/2\), further experimental verification is needed.

Fig. 1
figure 1

Predicted toughness curve \(G_\mathrm{{C}}\left( {\hat{\psi }} \right) \) compared with experimental results [13]

Full size image

6 Concluding remarks

The widely accepted fracture criterion for predicting the extension of an interface crack has been based on an energy release rate \(G\left( \psi \right) \), whereas in classical fracture mechanics such a criterion for monolithic cracks is formulated in terms of the SIF. In the current study, by modifying the definition of SIF for interface cracks so that it has the same dimension as the classical SIF, a SIF-based fracture criterion is formulated. Thereupon, three types of fracture criterion for interface cracks are developed: the \(\hat{K}_\mathrm{QI} \sim \hat{K}_\mathrm{QII} \) criterion, the \(G_\mathrm{I} \sim G_\mathrm{II} \) criterion, and the \(G\left( {\hat{\psi }} \right) \) criterion with empirical toughness curve \(G_\mathrm{C} \left( {\hat{\psi }} \right) \). The validity of the proposed fracture criteria is checked against existing experimental data, with good agreement achieved.

Up to now, oscillatory singularity and crack/contact interference are obstacles facing the further investigation of interface fracture mechanics. However, the existing study demonstrates that a fracture criterion for interface cracks can be developed adequately. Then an obvious question is raised: why the fracture criterion for interface cracks can bypass the oscillatory singularity and crack/contact interference near the tip of an interface crack? Future investigation of this critical issue is needed to provide further insight into the nature of stress singularities associated with interface cracks.