Study on Mach stems induced by interaction of planar shock waves on two intersecting wedges

Abstract

The properties of Mach stems in hypersonic corner flow induced by Mach interaction over 3D intersecting wedges were studied theoretically and numerically. A new method called “spatial dimension reduction” was used to analyze theoretically the location and Mach number behind Mach stems. By using this approach, the problem of 3D steady shock/shock interaction over 3D intersecting wedges was transformed into a 2D moving one on cross sections, which can be solved by shock-polar theory and shock dynamics theory. The properties of Mach interaction over 3D intersecting wedges can be analyzed with the new method, including pressure, temperature, density in the vicinity of triple points, location, and Mach number behind Mach stems. Theoretical results were compared with numerical results, and good agreement was obtained. Also, the influence of Mach number and wedge angle on the properties of a 3D Mach stem was studied.

Graphic abstract

1 Introduction

In supersonic and hypersonic flight in the atmosphere, shock/shock interaction and shock/boundary layer interaction often occur in the vicinity of aircraft or inside the inner duct of the propulsion system. On the surface of hypersonic vehicles, those shock interactions between body and aerofoil always result in a sharp increase of heat flux. In a hypersonic inlet, 3D shock/shock interactions take place due to the compression from inlet walls and cause serious total pressure losses. In most practice, the regional zones of high heat flux or low total pressure often occur behind Mach stems induced by 3D shock/shock interaction. The properties of 3D Mach stems are significant to the design of hypersonic aircraft.

The earliest study on Mach stems can be traced back to the work of Mach in 1878, who observed and recorded Mach reflection (MR) phenomena in his experiments [1]. If Mach reflection of shock waves happens, the hypersonic flow field is characterized by incident waves, reflected waves, Mach stem and slip lines in experiments. Von Neumann built analytical approaches to describe 2D MR wave configuration, called three-shock theory (3ST) [2, 3]. Three-shock theory makes use of inviscid conservation equations across oblique waves together with appropriate boundary conditions and gives the analytical solution to 2D MR. Kawamura [4] proposed that the use of $(p,\theta )$-polars could be an effective tool to understand Mach reflection, where p is the flow static pressure and $\theta$ is the flow deflection angles. $(p,\theta )$-polar theory has been a powerful tool to analyze 2D shock reflection and 2D shock/shock interaction. However, current $(p,\theta )$-polar theory is confined to two-dimensional situations. For three-dimensional shock reflection or 3D shock/shock interaction, there is not a direct theory analogous to $(p,\theta )$-polars.

The properties of 2D Mach stems involves their height and the shape. About five decades ago Courant and Friedrichs (1959) and Liepmann and Roshko, and later Emanuel and Ben-Dor and Takayama, pointed out that the height of the Mach stem of a 2D Mach reflection wave configuration was not uniquely determined by von Neumann three-shock theory [5–8], and the three-shock theory is incapable of predicting the actual size of the Mach stem height since it is inherently independent of any physical length scale.

Hornung and Robinson [9] did a series of experiments to study the effect of wedge angle on the height of 2D Mach stems. They pointed out that Mach stems can be expressed in the general form as a function of specific heat capacity ratio, incoming flow Mach number, reflecting wedge angle, and exit cross-sectional area given trailing edge and wedge length. A physical model for predicting the height of 2D Mach stems was suggested by Azevedo and Liu (1993) [10]. However, Li and Ben-Dor [11] raised some doubts about Azevedo’s model. They presented a modified model, which provided a better agreement with the experimental results. In Li and Ben-Dor’s model, the single wedge model was replaced with a symmetrical model in order to avoid viscous boundary wall effects, and curved Mach stems, reflected waves, and slip lines were adopted so that it was in accordance with practical situations. Furthermore, the centered expansion fan that emanates from the trailing edge of the shock-generating wedges and its interactions with the reflected wave and slipstream were also considered.

Later, the height of 2D Mach stems was studied by researchers of shock waves. At the beginning, a Mach stem was considered a shock wave of small curvature or a normal wave because there was not good understanding of its shape [10]. A study by Dewey and McMillin [12] conducted a series of experiments on the shape of Mach stems. They found that the Mach stem wasn’t always perpendicular to the reflective surface, and it has an inclination angle of $1^{\circ }$. The shape of Mach stems can be fitted by using the circular arc or polynomial approximation techniques. Then Dewey and McMillin [13] built an empirical model, which assumes that Mach stems can be fitted by an arc and be perpendicular to the reflective surface. The curve fits for 2D Mach stems agrees well with the experimental results. Li and Ben-Dor [11] suggested that the exact analytical expression can’t be obtained theoretically because the shock shape is also determined by the downstream subsonic condition. Tan et al. [14, 15] suggested that the subsonic flow just behind Mach stems can be described by the isentropic small-disturbance equation if the angle between the slip line and reflecting plane is sufficiently small. By using this analytical model, they obtained a very simple algebraic expression for the shape of the 2D Mach stem, and it was consistent with Dewey’s hypothesis. Gao and Wu [16] considered the interaction between the various expansion or compression waves. They obtained a Mach stem height, the shape and position of the slip line, and reflected shock wave.

Up to now, most studies on MR phenomena focus on two-dimensional situations, and the inflow Mach number is below 2. For real applications, most shock/shock interactions (SSI) are three-dimensional. Three-dimensional SSI is of great importance, and its analytical theory is necessary. Recently, we built a new approach called “spatial dimension reduction” to analyze 3D steady SSI. The basic idea is that one spatial dimension of 3D steady SSI is handled as a temporal dimension, by which the problem of 3D steady SSI over 3D intersecting wedges can be transformed into the 2D moving SSI on cross sections perpendicular to the intersecting line of incident shock waves. With such a new approach, the flow field induced by 3D steady SSI could be solved theoretically. Then the configuration of Mach interaction can be determined and the location, length, and strength of the 3D Mach stem can be calculated.

In this paper, the detailed procedure of analytic approach is presented in Sect. 2, including the location and strength of the 3D Mach stem. In Sect. 3, numerical simulations are performed to verify theoretical results. The effects of inflow Mach number and wedge angle on 3D Mach stems are also studied theoretically and numerically. Conclusions are summarized in Sect. 4.

2 Theoretical analysis approach and its procedure

Charwat and Watson [17, 18] conducted the earliest research work on 3D SSI over two intersecting wedges. They noted that the wave configurations on cross sections were self-similar so that the schematic illustration on a cross section can be used to show the whole 3D wave configuration. Recently, we found that the shock configurations in 3D steady SSI have similar shock configurations in 2D moving SSI. We propose a “spatial dimension reduction” approach to the theory of 3D SSI. With the approach of “spatial dimension reduction”, the problem of 3D steady SSI can be transformed into that of 3D steady SSI. There are various wave configurations in 3D steady SSI, such as regular interaction, Mach interaction and weak shock interaction. According to different shock interaction configurations, different analytical theory should be used. Mach interaction is a typical wave configuration in 3D steady SSI. There is a Mach stem bridge between the incident shock waves, behind which the gas flow is compressed seriously and causes an increase of heat flux and total pressure loss.

In this paper, the properties of Mach interaction of 3D steady SSI is mainly concerned theoretically and numerically. The theoretical approach is based on the following assumptions:

• (1) The gas is perfect, and its heat capacity ratio is constant $(\gamma =1.4)$.

• (2) The viscosity and thermal conductivity are neglected, so the boundary layer is not considered.

• (3) All Mach stems are infinitely thin and planar.

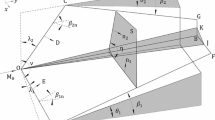
Figure 1 presents the 3D Mach interaction (MI) induced by two intersecting wedges, where $\lambda _1$ and $\lambda _2$ are the sweep angles, $\theta _1$ and $\theta _2$ are the wedge angles, v is defined as the angle between the two bottom planes of wedges. The coordinate system used is also shown, the y coordinate is the inflow direction and is aligned along the intersecting line of two bottom wedges. The x coordinate is chosen in the plane of the horizontal wedge and is normal to y. The third coordinate z is taken as normal to both x and y and is in the plane of the vertical wedge only if the dihedral angle is $90^{\circ }$.

Fig. 1

Schematic illustration of 3D Mach Interaction of steady shock waves

The two incident shock waves induced by the two wedges interact with each other in the corner and a Mach stem bridge forms. The inflow Mach number is $M_0$, $\beta _1$, and $\beta _2$ are the shock angles on cross sections of wedges that parallel to y-axis, while $\beta _{1n}$ and $\beta _{2n}$ are the shock angles induced by wedges perpendicular to $\overrightarrow{OA}$ and $\overrightarrow{OC}$, respectively. A characteristic direction parallel to the two incident waves is defined first. It is not difficult to reveal that the intersecting line OB is the unique characteristic direction. The velocity parallel to $\overrightarrow{OB}$ in the whole field is identical. Thus, the direction $\overrightarrow{OB}$ is the characteristic direction, and the cross sections perpendicular to $\overrightarrow{OB}$ are the characteristic planes. Thus, the spatial dimension in the characteristic direction can be treated as the temporal dimension and the problem of 3D steady SSI can be transformed into an 2D moving SSI in the characteristic planes with time evolution.

Fig. 2

Schematic illustration of 2D Mach interaction of moving shock waves

The 3D wave configuration can be determined by shock-polar analysis on the characteristic planes. For Mach interaction of 3D steady SSI, the problem of 3D steady flow can be regarded as a pesudo-steady flow of two moving incident shock waves along a virtual wall in a two-dimensional plane (see Fig. 2), the definition of a virtual wall is that it is always perpendicular to the Mach stem. The length of the Mach stem grows with the propagation of two moving waves and their interactions. In Fig. 2, $\gamma _1$ and $\gamma _2$ are the angles between the loci of triple-points and the virtual wall. $\eta$ is the angle between $M_{\mathrm{s}1}$ and $M_{\mathrm{s}2}$, and $\theta _\mathrm{v}$ is the angle between the horizontal direction and the virtual wall.

$M_{\mathrm{s}1}$ and $M_{\mathrm{s}2}$ are the decomposed vectors of inflow Mach number, and they can be calculated as following:

$$\begin{aligned} M_{S1}=M_0\mathrm{sin}{\beta _{1n}} \mathrm{cos}{\lambda _1}, M_{S2}=M_0\mathrm{sin}{\beta _{2n}} \mathrm{cos}{\lambda _2}. \end{aligned}$$

(1)

The vector $\varvec{OB}$ and the angle $\eta$ can be obtained by the following equations:

$$\begin{aligned}&{{\varvec{OB}}}={{\varvec{n}}_2}\times {{\varvec{n}}_1}, \end{aligned}$$

(2)

$$\begin{aligned}&\mathrm{cos} \eta =\mathrm{cos}({{\varvec{n}}_2},{{\varvec{n}}_1}). \end{aligned}$$

(3)

The vector ${{\varvec{n}}_1}$ and ${{\varvec{n}}_2}$ on cross sections can be expressed as:

$$\begin{aligned} {{\varvec{n}}_1}= & {} {\varvec{OA}}\times {{\varvec{E}}}=(\mathrm{cos}\lambda _1\mathrm{tan}\beta _{1n}, -\mathrm{cos}\lambda _1\mathrm{cot}\lambda _1\mathrm{tan}\beta _{1n}, \mathrm{cot}\lambda _1) \end{aligned}$$

(4)

$$\begin{aligned} {{\varvec{n}}_2}= & {} {{\varvec{D}}}\times {\varvec{OC}}\nonumber \\= & {} (\mathrm{cot}{\lambda _2}\mathrm{sin}{\nu }+\mathrm{cos}\lambda _2 \mathrm{cos}\nu \mathrm{tan}\beta _{2n},-\mathrm{csc}\lambda _2 \mathrm{cos}^2\lambda _2\nonumber \\&\,\times \mathrm{tan}\beta _{2n}, \mathrm{cos}\lambda _2 \mathrm{tan}\beta _{2n} \mathrm{sin}\nu -\mathrm{cot}\lambda _2 \mathrm{cos}\nu ), \end{aligned}$$

(5)

where ${{\varvec{E}}}$ is the vector in shock plane $S_1$ normal to the leading edge of bottom wedge, and ${{\varvec{D}}}$ is the vector in shock plane $S_2$ normal to the leading edge of lateral wedge. With the definition of virtual wall suggested by Xie et al. [19], the angle of Mach stem can be acquired by solving the problem of Mach reflection of moving shock waves on both sides of the virtual wall.

$\theta _\upnu$ and Mach number $M_\mathrm{m}$ behind the Mach stem can be calculated with the following equations [20, 21]:

$$\begin{aligned}&\mathrm{\tan }\theta _\upnu =\left( \frac{M_\mathrm{m}}{M_{\mathrm{s}2}}\right) \frac{\left[ 1-\left( \frac{M_{\mathrm{s}2}}{M_\mathrm{m}}\right) ^2\right] ^\frac{1}{2} \left\{ 1-\left[ \frac{f(M_\mathrm{m})}{f(M_{\mathrm{s}2})}\right] ^\frac{1}{2}\right\} }{1+\frac{f(M_\mathrm{m})M_\mathrm{m}}{f(M_{\mathrm{s}2})M_{\mathrm{s}2}}}, \end{aligned}$$

(6)

$$\begin{aligned}&\tan \left( \uppi -\eta -\theta _\upnu \right) =\left( \frac{M_\mathrm{m}}{M_{\mathrm{s}1}}\right) \frac{\left[ 1-\left( \frac{M_{\mathrm{s}1}}{M_\mathrm{m}}\right) ^2\right] ^\frac{1}{2} \left\{ 1-\left[ \frac{f(M_\mathrm{m})}{f(M_{\mathrm{s}1})}\right] ^\frac{1}{2}\right\} }{1+\frac{f(M_\mathrm{m})M_{\mathrm{m}}}{f(M_{\mathrm{s}1})M_{\mathrm{s}1}}}.\nonumber \\ \end{aligned}$$

(7)

They are related to upstream properties through the oblique shock wave relations, where f(M) is a function in terms of Mach number M, and its expression is

$$\begin{aligned} f(M)=\mathrm{exp}\left[ -\int \frac{2M\mathrm{d}M}{(M^2-1)K(M)}\right] , \end{aligned}$$

(8)

K(M) is a slowly varying function and its expression is

$$\begin{aligned} K(M)=2(2\mu +1+M^{-2})^{-1}\left( 1+\frac{2}{\gamma +1}\frac{1-\mu ^2}{\mu }\right) ^{-1}, \end{aligned}$$

(9)

where $\mu =\left[ \frac{(\gamma -1)M^2+2}{2\gamma M^2-(\gamma -1)}\right] ,$ which represents the Mach number for the propagation of a moving shock relative to the flow field behind it. The expressions of $\gamma _1$ and $\gamma _2$ are

$$\begin{aligned} \gamma _1= & {} \mathrm{arc}\mathrm{tan}\left[ \frac{M_\mathrm{m}+\mathrm{sec}(\eta +\theta _\upnu )M_{\mathrm{s}2}}{-\mathrm{tan}(\eta +\theta _\upnu )M_\mathrm{m}}\right] , \end{aligned}$$

(10)

$$\begin{aligned} \gamma _2= & {} \mathrm{arc}\mathrm{tan}\left( \frac{M_\mathrm{m}-\mathrm{sec}\theta _\upnu M_{\mathrm{s}2}}{{\mathrm{tan}\theta _\upnu }M_\mathrm{m}}\right) , \end{aligned}$$

(11)

they are related to the interaction of decomposed inflow Mach numbers $M_{\mathrm{s}1}$ and $M_{\mathrm{s}2}$ and their interaction. With the above theoretic approach, wave configurations of 3D steady shock/shock interaction can be determined. For 3D Mach interaction, the strength and location can be obtained by solving Eqs. (6–11).

3 Results and discussion

Figure 3 presents the comparison between analytical results and numerical results, as well as the experimental results of West in 1972 [18]. Numerical results are obtained by solving 3D Euler invisid equations with 2nd order TVD scheme on a grid system of $200\times 200\times 110$ and the experimental results. The coordinates x and z are scaled with y so that they become conical, self-similar variables. $z_0$ and $x_0$ represent the distances of the bottom wedge and the top wedge (see Fig. 1). The error bars are the experimental results of West in 1972. It can be seen from the figure that the theoretical results of the location of incident waves and Mach stem agree well with the experimental and numerical results. For the strength of Mach stem, the theoretical solution is $M_\mathrm{m}=1.84$, and the numerical solution is about $M_\mathrm{m}=1.82$.

Fig. 3

Analytical results versus experimental and numerical results of sectional flow field ($M_0=3,\nu =90^{\circ },\lambda _1=\lambda _2=0^{\circ },\theta _1=\theta _2=9.5^{\circ }$)

Fig. 4

Shock-polar analysis of Mach interaction for $M_0=1.8-5,\nu =90^{\circ },\lambda _1=\lambda _2=0^{\circ },\theta _1=\theta _2=12.2^{\circ }$

In the following sections, the effects of Mach number and wedge angle on the properties of 3D Mach stem will be discussed.

3.1 The effect of inflow Mach number

Figure 4 shows the shock-polar with different inflow Mach numbers; the horizontal axis $\theta$ is the flow deflection angle and the vertical axis $\xi$ is the static-pressure ratio. For the cases of $M_0=2.0-5.0$, $\nu =90^{\circ }$, $\lambda _1=\lambda _2=0^{\circ }$, $\theta _1=\theta _2=12.2^{\circ }$, the reflected polar $R_1$ and $R_2$ do not intersect with each other, it indicates that the wave configurations is Mach interaction (see Fig. 4). As the Mach number increases, the incident polar and reflected polar grow bigger. The reflected polar $R_1$ and $R_2$ do not intersect with each other even if the Mach number is 5, and this means that Mach interactions take place in the range of $M_0=2.0-5.0$. For lower Mach numbers in the range of $M_0=1.6-2.0$, the reflected shock-polars are totally inside the incident shock-polars. This means that the interactions are weak shock interactions (WSI). If $1.1{\leqslant }M_0\leqslant 1.6$, the incident shock waves become detached, but this will not be studied in this paper.

Figure 5 presents theoretical and numerical results of the Mach stem’s location and length. The symbol labelled with a circle at the top-right corner is the Mach stem for the Mach interaction. The M axis is non-uniform for inflow Mach number, which is gradually denser with increase of inflow Mach number. The theoretical results labelled with solid lines are the trajectories of three shock points on both sides of Mach stem. We can see that for Mach interaction, the Mach stem is almost straight. The hypothesis of thin and planar Mach stem can be applied for 3D Mach interactions. However, for WSI, the Mach stem is obviously a curved line, and the hypothesis for the Mach stem in Sect. 2 is inapplicable. The theoretical results agree well with the numerical results for the case of Mach interaction. Also, for WSI, the analytical results of Mach stem length is longer than the numerical results. With the increase of inflow Mach number, the Mach stem gets shorter and closer to the wall.

Figure 6 shows the analytical and numerical solution to the Mach stem strength. The variation of Mach stem strength $M_m$ is almost linear with the increasing of inflow Mach number. The theoretical results agrees well with the numerical results, both for MI and WSI.

Fig. 5

The theoretical and numerical solutions to the location of Mach stem for $M_0{=}1.8-6,\nu =90^{\circ },\lambda _1=\lambda _2=0^{\circ },\theta _1=\theta _2=12.2^{\circ }$

Fig. 6

The theoretical and numerical solutions to Mach number behind Mach stem $M_m$ for $M_0=1.8-6,\nu =90^{\circ },\lambda _1=\lambda _2=0^{\circ },\theta _1=\theta _2=12.2^{\circ }$

3.2 The effect of wedge angle

The effect of wedge angle on the properties of 3D Mach stem are obtained by varying the wedge angle from $5^{\circ }$ to $29.6^{\circ }$, and the inflow Mach number is fixed at 3.17. Figure 7 displays the analytical results by shock-polar analysis for $M_0=3.17$ ,$\nu =90^{\circ }$, $\lambda _1=\lambda _2=0^{\circ }$, $\theta _1=\theta _2=4.1^{\circ }, 5^{\circ }, 10^{\circ }, 15^{\circ }$. As shown in Fig. 7, $\theta =4.1^{\circ }$ is the detached-criterion point according to von Neumann’s detachment criterion [2, 3]. If the wedge angle is below $4.1^{\circ }$, the two reflected polars interact with each other, and this means that regular interaction (RI) takes place. For RI configurations, there is no Mach stem between the two incident waves, and this will not be considered in this paper. If the wedge angle is above 4.1, $R_1$ and $R_2$ do not interact with each other, and this indicates that MI should appear. As the wedge angle increases, $R_1$ and $R_2$ become narrow and thin. Therefore, the wave structures are Mach interactions in the range of $5^{\circ }{\leqslant }\theta {\leqslant }29.6^{\circ }$.

Fig. 7

Shock-polar analysis of Mach interaction for $M_0=3.17, \nu =90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=\theta _2=4.15^{\circ }, 5^{\circ }, 10^{\circ }, 15^{\circ }$

Figure 8 shows the trajectory of three-shock points on both sides of the Mach stem with increasing wedge angle. The $\theta$ axis is non-uniform for the wedge angle, which is gradually denser with decreasing wedge angle. The numerical simulations for various situations demonstrate that the Mach stem is always straight for 3D Mach interaction. As we can see, the theoretical analysis could predict the location and the length of Mach stem well. For lower wedge angles, the influence of wedge angles on the location and length of Mach stem is small, while for larger wedge angles, the effect is larger. For example, the length of Mach stem at $\theta =29^{\circ }$ is about two times that at $\theta =25^{\circ }$. For the transition criteria from RI to 3D MI, we can see that the transition point can be determined by the condition of the length of Mach stem being equal to zero, which corresponds to the mechanical-equilibrium criterion of 2D pseudo-steady shock reflection. The numerical results shows that the larger the wedge angle is, the more complex the corner flow becomes. With increasing wedge angle, the wave structure transforms from a single Mach interaction to a double Mach interaction. For larger wedge angle, the wave configuration may be multi-shock Mach interaction. The influence of wedge angle on Mach stem and wave configuration is great.

Fig. 8

Theoretical and numerical solutions to the location of Mach stem for $M_0=3.17, \nu =90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=\theta _2=5^{\circ }-29.6^{\circ }$

Fig. 9

Theoretical and numerical solutions to Mach number behind Mach stem for $M_0=3.17, \nu =90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=\theta _2=5^{\circ }-29.6^{\circ }$

The effect of wedge angle on the strength of Mach stem is shown in Fig. 9. The variation of $M_\mathrm{m}$ for various wedge angle is almost a straight line. It should be noted that at $\theta =29.6^{\circ }$, the strength of the Mach stem is about 3, which is near the inflow Mach number. Thus, the temperature and total pressure loss are very high behind the Mach stem for larger wedge angle.

4 Conclusion

In this paper, a new analytical solution to solve 3D shock/shock interaction over two symmetrically intersecting wedges is introduced. By using the approach of “spatial dimension reduction”, the properties of 3D Mach stem for corner flow are studied theoretically. The results agree well with the experimental and numerical results. Also, the influence of inflow Mach number and wedge angle on 3D Mach stem are also studied. The results of this paper could be summarized as follows:

• (1) The 3D wave configuration can be determined by using the “spatial dimension reduction” approach and shock-polar analysis. For Mach interaction, the location and the strength of 3D Mach stem can be obtained analytically, and they agree well with experimental and numerical results.

• (2) For Mach interaction with higher inflow Mach number, the Mach stem is always straight. For weak shock interaction with lower inflow Mach number, the Mach stem is curved.

• (3) With increasing inflow Mach number, the Mach stem becomes closer to the wall, and its length gets longer. With increasing wedge angle, the Mach stem gets farther away from the wall, and its length gets longer and its strength increases linearly.

• (4) The transition from regular interaction to Mach interaction of 3D steady shock/shock interaction can be determined by the length of Mach stem $l=0$.