1 Introduction

The reflection and interaction of shock waves are fundamental problems in the field related to high-pressure explosions, detonations, and shock waves. The reflection of a shock wave usually means that a moving or steady shock wave impinges on the surface of walls or other obstacles blocking its path. Complex shock reflection phenomena exist, which greatly depend on how an impinging shock wave encounters the walls or obstacles. On the other hand, the problem of shock interaction mostly deals with the situations in which two or more shock waves interact with each other. Based on the special features of shock wave reflection and interaction, the research in this field has been developed to a separate direction in compressible gas dynamics.

There has been plenty of research work, including theoretical, experimental, and numerical investigations, on two-dimensional (2D) reflection and interaction of shock waves in the past hundred years due to its importance in interpreting the basic behavior. The most frequently encountered configurations of shock reflection were clarified in seminal publications like [1]. The book of Shock Wave Reflection Phenomena [1] gives a good summary of the possible shock wave configurations when a 2D shock wave reflects off a wall surface, for either a steady shock wave or a pseudo-steady shock wave.

This paper mainly concerns the three-dimensional (3D) interaction of two planar shock waves induced by two intersecting wedges. The concepts of shock reflection and shock interaction are defined separately here, although they can be analytically transformed to each other in many situations. Shock reflection is defined as a shock impinging onto a wall surface, and shock interaction is defined as two shock waves in a 2D situation (or two planar shock waves in a 3D situation) interacting with each other. The 3D interaction of shock waves is widely observed in engineering tasks related to aerodynamics because a real aircraft is always three dimensional. The research on 3D shock waves and their interaction with boundary layer is an important topic of hypersonic aerodynamics, for example the 3D interaction of shock waves and boundary layers in a hypersonic inlet and the interaction region of hypersonic wing/rudder and body. In the hypersonic 3D inlet, multiple oblique shock waves interact with each other and make the flow rather complex and non-uniform, and they lead to a serious total pressure loss of the inlet flow. In the interaction region of hypersonic wing/rudder and body, 3D shocked flow causes a complex heat flux distribution on the surface of the aircraft. Until now, there is no commonly accepted correlation method for the prediction of local heat flux of hypersonic complex flow. It is clear that the interaction of shock waves and boundary layers increases the local gasdynamic heating in both 2D and 3D situations. For example, the flow patterns of hypersonic shocked flow in which a 2D shock wave is impinging on a cylinder is classified into six types [2], which have different effects on the local heat flux to the surface of the cylinder. It has been concluded that the type IV interaction of a 2D shock/boundary layer causes a sharp increase in local heat flux. For the 3D interaction of shock waves and boundary layers, the physical mechanisms have not been fully revealed and the theoretical analysis of this configuration is scarce.

It can be seen that the 3D interaction of shock waves is a basic problem for studying the physical mechanisms of 3D interaction of shock waves and boundary layers, that is, the shock/shock interaction (SSI) of two planar shock waves in three-dimensional situations. The earliest approach for studying such shock/shock interaction (SSI) in three-dimensional situations was experimental investigations. Charwat and Redekeopp [3] conducted several experiments to analyze the wave configurations and pressure distribution of the surface along the corner of intersecting wedges with both symmetrical and asymmetrical models. Stainback and Weinstein [4] performed experimental studies on aerodynamic heating in the vicinity of corners at Mach 8. Watson and Weinstein [5] studied corner flow interaction at Mach 20 in helium and found that the basic features of the flow field previously observed at low Mach numbers also occur at high Mach numbers. West and Korkegi [6] conducted experimental investigations on supersonic interaction at high Reynolds numbers and found that the flow structures were conically invariant for turbulent boundary layers. Skews and Naidoo et al. [7,8,9] carried out further research on corner flows and discovered that the flow is no longer self-similar if the sharp corner is replaced by a camber. Most of the above studies focused on the Mach reflection and used symmetrical models, while other complex wave configurations of symmetrical and asymmetrical models were scarcely investigated due to the limitations imposed by the experimental setups. Recently, Yang et al. [10,11,12,13,14] used a spatial dimension reduction approach to analyze the problem of steady 3D SSI. The basic idea is that one spatial dimension of the steady 3D SSI is handled as a temporal dimension, and the problem of the steady 3D SSI over 3D intersecting wedges can be transformed into that of 2D SSI of two moving shock waves on the cross sections normal to the intersecting line of the incident shock waves. With such a new approach, the wave configurations of asymmetrical steady 3D SSI could be determined theoretically just by considering the 2D SSI of two moving shock waves in a 2D plane.

The purpose of this study is to explore the 3D asymmetrical wave configurations induced by two intersecting wedges in supersonic or hypersonic flow. The method used includes theoretical analysis and numerical simulation. The theoretical work is very helpful for understanding the complex mechanisms of 3D steady SSI and those complex phenomena observed in recent and future experiments.

2 Analytical approach and numerical methods

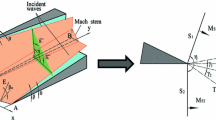
The most commonly observed 3D regular interaction (RI) and Mach interaction (MI) induced by two intersecting wedges are depicted in Fig. 1, where \(\lambda _1\) and \(\lambda _2\) are the sweep angles, \(\theta _1\) and \(\theta _2\) are the wedge angles, and v denotes the angle between the two bottom planes of wedges. The difference between the two configurations is that, in the case of MI, a surface of Mach stem \({ OJK}\) is necessary to satisfy the pressure and deflection angle conditions. The coordinate system used includes the y-coordinate, which indicates the inflow direction and is aligned along the intersecting line of the two bottom wedges. The x-coordinate is chosen in the plane of the horizontal wedge and is normal to y, while the third coordinate z is taken as normal to both x and y.

Fig. 1
figure 1

Schematic illustration of a 3D regular interaction (RI) and Mach interaction (MI)

Full size image
Fig. 2
figure 2

a Schematic illustration of a 2D moving regular interaction in a characteristic plane and b schematic illustration of a 2D moving Mach interaction in a characteristic plane

Full size image

The detailed procedure of the “spatial dimension reduction” method has been published [12,13,14]. First, the relations between the 3D steady problem and 2D unsteady problem should be obtained. If the inflow condition and the geometric parameters of two wedges are given, the two incident oblique shock waves induced by the two wedges will inevitably interact with each other in the corner. Here, we define the inflow Mach number as \(M_0, \beta _1\) and \(\beta _2\) as the shock angles on the cross sections of wedges paralleled to the y-axis, and \(\beta _{1n}\) and \(\beta _{2n}\) as the shock angles induced by the wedges perpendicular to \(\overrightarrow{\mathrm{OA}}\) and \(\overrightarrow{\mathrm{OC}}\), respectively. The direction of the interacting lines of two shock planes \(\overrightarrow{\mathrm{OB}}\) is defined as the characteristic direction, and the planes perpendicular to \(\overrightarrow{\mathrm{OB}}\) are defined as the characteristic planes. The velocities in the flow field can be decomposed into two separate components in the characteristic direction and in the characteristic planes. Thus, the 3D SSI is projected onto the 2D characteristic planes, and the spatial dimension in the characteristic direction can be treated as the temporal dimension. Accordingly, the problem of steady 3D SSI can be dealt with as that of 2D SSI of two moving shock waves in the characteristic planes with time evolution (see Figs. 1, 2).

For the RI configuration, the trajectory of the reflection point can be defined as a virtual wall, and the moving reference frame can be set on the reflection point (Fig. 2a). Such a problem of 2D SSI can be analyzed theoretically by the theory of 2D steady shock wave interaction. For the MI configuration, the virtual wall is defined as a line perpendicular to the Mach stem, and then, the frames of reference can be attached to \(T_1\) and \(T_2\), respectively (as shown in Fig. 2b) [8,9,10]. The Mach number of the Mach stem \(M_\mathrm{m}\) and the angle \(\theta _\nu \) between the virtual wall and the horizontal line can be obtained by solving the problem of Mach reflection at both sides of the virtual wall [15].

Then, the wave configurations can be determined by using the following equation:

$$\begin{aligned} \tan \theta =\frac{\xi -1}{{\gamma }M^2-(\xi -1)} \sqrt{\frac{\frac{2\gamma }{\gamma +1}(M^2-1)-(\xi -1)}{\xi +\frac{\gamma -1}{\gamma +1}}} \end{aligned}$$
(1)

where M is the decomposed Mach number in the direction of the reflection point, \(\gamma \) is 1.4 for an ideal diatomic gas, and \(\xi \) is the ratio of the pressures across the shock.

Finally, the wave configurations can be determined by shock polar analysis in the characteristic plane. Wave configurations and their determinations will be introduced in detail in the following sections.

The governing equations of numerical simulation are the 3D Euler equations, and their discretization is done using the second-order non-oscillatory, non-free parameters, dissipative (NND) scheme [16]. The computational mesh uses the orthogonalized uniform structured mesh. Message passing interface (MPI) parallel computation technology is adopted in the numerical simulation to speed up the calculations. Mesh independence tests are performed to ensure that all the numerical results produced are independent of the type of mesh chosen. The inlet boundary of the computational zone is given the fixed supersonic inflow condition, the far-field boundaries are given non-reflecting boundary conditions, and the wall boundaries are given solid-slipping conditions. The computations are conducted on an 8-core Dell computer.

3 Results and discussion

Charwat et al. [3, 5, 6] noted that the wave configurations of 3D SSI on cross sections are self-similar, so the schematic illustration on a cross section can be used to show the whole 3D wave configuration. The coordinates x and z are scaled with y so that they become conical, self-similar variables. For the ideal gas, the initial conditions of pressure, density, and temperature are non-dimensionalized to unit one.

In the following sections, various 3D asymmetrical wave configurations will be discussed and analyzed. Also, theoretical results are compared with the results of numerical simulations.

3.1 Regular interaction

For 2D supersonic and hypersonic flows, the wave configuration of RR often occurs for small sweep angles and low wedge angles, and it consists of two shock waves, the incident wave and the reflected wave, which meet at the reflection point. For the 3D corner flows induced by two intersecting wedges, numerical simulations and theoretical analysis show that the wave configuration of 3D RI often occurs in the case of small sweep angles and low wedge angles (or sufficiently small dihedral angles with large wedge angles) [17, 18]. The 3D RI includes two incident and two reflected wave planes, which meet at the reflection line OB (Fig. 1a).

The shock polars for different dihedral angles are shown in Fig. 3; the horizontal axis \(\theta \) is the flow deflection angle, and the vertical axis \(\xi \) is the static pressure ratio. In the case of \(M_0=3, \nu =60^{\circ }\)–\(90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=5^{\circ }, \theta _2=3^{\circ }\), shock polar analysis shows that the wave configuration is RI (Fig. 3). With the increase in dihedral angle, the incident polar I and the reflected polar R grow smaller and move to a lower starting point. The reflected polar of bottom wedge \(R_i\) and the reflected polar of upper wedge \(R_{i'}\) intersect at two points, which match the same pressure and angle behind the two reflected waves. If the principle of minimal entropy generation is assumed, the lower point O with lower pressure is physically possible. Also, the variation of dihedral angle has little influence on the flow field near the reflection point. By using the approach of spatial dimension reduction, all the parameters near the reflection line in the 3D flow field can be theoretically obtained. The theoretical solutions to the moving Mach number of incident shock and reflected shock are \(M_1=1.1786, M_{1'}=1.0959, M_2=1.1042, M_{2'}=1.1695\), and they agree well with numerical results.

Fig. 3
figure 3

Shock polar analysis in a characteristic plane for \(M_0=3, \nu =60^{\circ }{-}90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=5^{\circ }, \theta _2=3^{\circ }\). Note \(I_i, I_{i'}\)—incident polar, \(R_i, R_{i'}\)—reflected polar. [\(i=1\) \((\nu =60^{\circ }\), dashed line), 2 (\(\nu =70^{\circ }\), dotted line), 3 (\(\nu =80^{\circ }\), long-dashed line), 4 (\(\nu =90^{\circ }\), solid line)]

Full size image
Fig. 4
figure 4

Numerical results of regular interaction in a characteristic plane for \(M_0=3, \lambda _1=\lambda _2=0^{\circ }, \theta _1=5^{\circ }, \theta _2=3^{\circ }\). a \(\nu =60^{\circ }\); b \(\nu =70^{\circ }\); c \(\nu =80^{\circ }\); d \(\nu =90^{\circ }\). Note \(0, 0'\)—wall, \(1, 1'\)—incident shock, \(2, 2'\)—reflected shock, 3—internal bridge-shaped shock, \(4, 4'\)—near-wall Mach shock, \(5, 5'\)—contact discontinuity

Full size image

The numerical results of the wave configurations in the characteristic planes are shown in Fig. 4, where the incident shock and reflected shock can be clearly observed. However, a special wave configuration, namely transitioned regular interaction (TRI), occurs when the dihedral angle is sufficiently small [16]. It is different from RI, even though the analytical result is in the domain of regular reflection. The TRI often takes place in an unsteady 2D flow and cannot be observed in steady and pseudo-steady 2D flow. According to the analytical flow pattern of a TRI, an internal bridge-shaped shock 3 forms behind the reflection point, and the reflected shock near the wall curves into a near-wall Mach shock 4 and \(4'\) (Fig. 4a–c). As the dihedral angle \(\nu \) increases, the internal bridge-shaped shock moves closer to the reflection point and becomes shorter until it vanishes. The near-wall Mach shock \(4'\) on the larger wedge (\(\theta _1=5^{\circ }\)) is obviously longer than the Mach shock 4 on the smaller wedge (\(\theta _2=3^{\circ }\)). It is an asymmetrical SSI configuration and very different from the symmetrical configuration. For the TRI, the wall boundary plays an important role in the formation of the internal bridge-shaped shock. As the wall boundary is inviscid and slips, the reflected shock in the vicinity of the wall is normal to the wall boundary in order to match the boundary condition. At \(\nu =80^{\circ }\)–\(90^{\circ }\), the angle between the reflected shock and the wall boundary is close to \(90^{\circ }\), at which the reflected shock impinges the wall, and no clear internal bridge-shaped shock and near-wall Mach shock is formed. As the dihedral angle decreases, the reflected shock near the wall curves into a near-wall Mach shock to match the boundary condition, and a clear internal bridge-shaped shock occurs (Fig. 4a, b).

3.2 Mach interaction

Mach reflection was first observed and recorded in studies performed by Mach [19]. In the Mach reflection of a 2D shock wave, a clear incident shock, reflected shock, Mach stem, and slip line can be seen. Ben-Dor [1] systematically summarized Mach reflection in a pseudo-steady flow in his book. According to Ben-Dor, the Mach reflection can be further divided into three types: single Mach reflection (SMR), transitional Mach reflection (TMR), discovered by Smith [18], and double Mach reflection (DMR). For the SSI induced by 3D symmetrical wedges, single Mach interaction (SMI), transitional Mach interaction (TMI), and double Mach interaction (DMI) have been observed in numerical simulations and experiments. Until now, the research on asymmetrical wave configurations for 3D asymmetrical SSI is very limited due to its complexity.

The theoretical analysis and numerical results of the SMI for \(M_0=4, \nu =90^{\circ }, \lambda _1=3^{\circ }, \lambda _2=10^{\circ }, \theta _1=\theta _2=10^{\circ }\) and \(M_0=5, \nu =90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=10^{\circ }, \theta _2=5^{\circ }\) are shown in Fig. 5a–d. There are two different SMIs here. For the first SMI (Fig. 5a, b), the reflected polar of lower wedge \(R_1\) and the reflected polar of upper wedge \(R_2\) intersect with \(I_1\) and \(I_2\), respectively, and the intersecting points are on the positive side and negative side of the \(\theta \)-axis, respectively. This indicates that the foot of the virtual wall originating from the corner rib and the Mach stem is on the Mach stem. For the second SMI (Fig. 5c, d), \(R_1\) and \(R_2\) intersect with \(I_1\) and \(I_2\), respectively, and the intersecting points are both on the positive side of the \(\theta \)-axis. This means that the foot of the virtual wall and the Mach stem is on the extension line of the Mach stem, which is called an inverse single Mach interaction (ISMI).

Fig. 5
figure 5

Shock polar analysis and numerical results in a characteristic plane. a, b Single Mach interaction for \(M_0=4, \nu =90^{\circ }, \lambda _1=3^{\circ }, \lambda _2=10^{\circ }, \theta _1=\theta _2=10^{\circ }\); c, d inverse single Mach interaction for \(M_0=5, \nu =90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=10^{\circ }, \theta _2=5^{\circ }\); e, f transitional double Mach interaction for \(M_0=6, \nu =90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=20^{\circ }, \theta _2=15^{\circ }\). Note \(0, 0'\)—wall, \(1, 1'\)—incident shock, \(2, 2'\)—reflected shock, 3—Mach stem, \(4, 4'\)—contact discontinuity, 5—spiral vortices, 6—secondary reflected shock, 7—near-wall Mach shock

Full size image

For the 3D ISMI, the virtual wall perpendicular to the Mach stem does not intersect with the Mach stem surface. If the wedge angle is in the domain of the SMI, the ISMI often occurs when the disparity of the wedge angle on both sides is sufficiently large. For the case of \(M_0=6, \nu =90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=20^{\circ }, \theta _2=15^{\circ }\), the wave configuration is a transitional double Mach interaction (TDMI) (Fig. 5e, f). In this situation, the wedge angles on both sides are sufficiently large, so that the contact discontinuity originating from the triple points rolls up into the spiral vortices 5, and the reflected waves 2 and \(0'\) near the wedge become more concave in shape. The bending of the reflected shock wave is due to the action of compression waves from the walls 0 and \(0'\). A near-wall shock wave 7 and a secondary reflected shock wave 6 are established to match the wall boundary condition. The wave configuration on the side of the larger angle \(\theta _1=20^{\circ }\) has no clear near-wall shock wave and secondary reflected shock wave, whereas the side of the angle \(\theta _2=15^{\circ }\) has a clear structure of double Mach reflection. The above wave configurations are different from those in 3D symmetrical situations. The larger the wedge angle, the more complex the wave configuration is in 3D asymmetric situations.

3.3 Weak shock interaction

According to Ben-Dor [1], the weak shock reflection could be divided into three types, depending on whether the solution of non-standard three-shock theory is physical or non-physical. If it is physical, the resulting reflection is either a von Neumann reflection (vNR) or a Guderley reflection (GR) [1, 20, 21]. If it is non-physical, the resulting reflection could be a Vasilev reflection (VR) [22]. The major difference between the GR and VR lies in whether the flow after the Mach stem is supersonic or not. Tesdall and Hunter [23] indicated that an expansion fan originates at each triple point according to their numerical results. Skews and Ashworth [20] carried out experiments to demonstrate the presence of expansion waves behind the reflected wave and make the GR physical.

Earlier studies of the weak shock reflection focused on 2D cases, and the inflow Mach number was rather low. In this section, the 3D weak shock interaction induced by two intersecting wedges will be presented numerically and theoretically. In the case of \(M_0=1.5, \nu =90^{\circ }, \lambda _1=0^{\circ }, \lambda _2=1^{\circ }, \theta _1=5^{\circ }, \theta _2=10^{\circ }\), specifically, two reflected polars, \(R_1\) and \(R_2\), are totally inside the incident polar, \(I_1\) and \(I_2\), and it means that the weak shock interaction (WSI) occurs (Fig. 6a). The numerical simulations in Fig. 6b also show that the type of 3D shock interaction is WSI, which is similar to the 2D pseudo-steady shock reflection with a weak incident shock wave and thin wedges. When the WSI occurs, one clear Mach stem, two reflected waves and one Prandtl–Meyer expansion fan can be observed. However, there are some differences between the 3D weak shock wave interaction and the 2D weak shock wave reflection. For example, in 2D pseudo-steady flow the shock is sufficiently weak, whereas in the 3D steady flows with high Mach number and large sweep angle the weak interaction of the shock wave may result in a 3D effect (Fig. 6c, d). Additionally, numerical simulations show that the 3D effect depends largely on the change in the sweep angle. With a larger sweep angle, the 3D effect is more obvious and the weak shock wave interaction is more likely to occur. Theoretical analysis reveals that the decomposed Mach number in the cross-sectional planes is sufficiently small to lead to the occurrence of the weak interaction of shock waves in 3D steady flows.

In the case of \(M_0=2, \nu =90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=10^{\circ }, \theta _2=2^{\circ }\) and \(M_0=4, \nu =90^{\circ }, \lambda _1=30^{\circ }, \lambda _2=0^{\circ }, \theta _1=5^{\circ }, \theta _2=20^{\circ }\), shock polar analysis in the characteristic planes indicates that one reflected polar, namely \(R_1\), intersects with the incident polar \(I_1\), while the other reflected polar \(R_2\) is totally inside the incident polar \(I_2\) (Fig. 6e, f). This means that the weak single Mach interaction (WSMI) occurs, where the disparity of the wedge angle on both sides is sufficiently large. However, the reflected polar \(R_2\) in Fig. 6g is different from the one in Fig. 6e. Specifically, the Mach number of the weak reflected wave (2) is 1.6, whereas it is below 1 in Fig. 6g, where the reflected polar collapses into a point. For the WMSI, the wave structure on the side of the large wedge angle is a weak shock interaction, where the reflected shock reduces into an expansion fan [see \((2')\) in Fig. 6f, h]. For small wedge angles, the SSI is a single Mach interaction, where the reflected shock can be clearly seen [see \((2')\) in Fig. 6f, h].

Fig. 6
figure 6

Shock polar analysis and numerical results in a characteristic plane. a, b Weak shock interaction for \(M_0=1.5, \nu =90^{\circ }, \lambda _1=0^{\circ }, \lambda _2=1^{\circ }, \theta _1=5^{\circ }, \theta _2=10^{\circ }\); c, d weak shock interaction for \(M_0=3, \nu =90^{\circ }, \lambda _1=30^{\circ }, \lambda _2=25^{\circ }, \theta _1=\theta _2=5^{\circ }\); e, f weak single Mach interaction for \(M_0=2, \nu =90^{\circ }, \lambda _1=\lambda _2=0^{\circ }, \theta _1=10^{\circ }, \theta _2=2^{\circ }\); g, h weak single Mach interaction for \(M_0=4, \nu =90^{\circ }, \lambda _1=30^{\circ }, \lambda _2=0^{\circ }, \theta _1=5^{\circ }, \theta _2=20^{\circ }\). Note \(0, 0'\)—wall, \(1, 1'\)—incident shock, 2—reflected wave, \(2'\)—expansion waves, 3—Mach stem

Full size image

For all the above weak shock configurations, the incident shock is almost parallel to the Mach stem; in other words, the Mach number of the incident shock and the Mach shock are very similar. The flows passing through the Mach stem and the incident wave experience similar changes across the shocks, which results in the reflected shock reducing to an expansion fan. For example, for \(M_0=4, \nu =90^{\circ }, \lambda _1=30^{\circ }, \lambda _2=0^{\circ }, \theta _1=5^{\circ }, \theta _2=20^{\circ }\), the theoretical solutions to the Mach stem and incident wave are 2.35 and 2.147, respectively, which exhibits little discrepancy.

4 Concluding remarks

In this paper, an analytical solution termed “spatial dimension reduction” is used to determine the 3D wave configurations over two asymmetrically intersecting wedges. Numerical simulations with the NND scheme are conducted to validate the theoretical analysis, and good agreement is obtained. Several 3D wave configurations in asymmetrical situations are studied theoretically and numerically. The results of this study can be summarized as follows:

  1. 1.

    The 3D asymmetrical wave configuration can be determined by using the approach of “spatial dimension reduction” and shock polar analysis, such as RI, TRI, SMI, ISMI, TDMI, WSI, and WSMI.

  2. 2.

    For the 3D regular interaction with a small sweep angle, TRI occurs due to the interaction of the wall boundary and the reflected wave.

  3. 3.

    For the 3D Mach interaction, an inverse Mach interaction can occur in which there is a big difference between the wedges on both sides. As the wedge angle increases, the wave configuration becomes more complex.

  4. 4.

    If the inflow Mach number is low or the sweep angle is large enough, a weak shock interaction often occurs. For 3D WSI, there is little difference between the Mach number of the Mach stem and that of the incident shock, their properties are almost the same, and the reflected shock will be reduced to an expansion fan.