1 Introduction

A nanofluid is a material made out of nanometer-sized particles or nanoparticles. These nanoparticles are generally developed from metals, oxides, carbides, or nanotubes, air, ethylene glycol, and oil are common basic liquids. Investigations have been sought to improve the thermal conductivity of fluids. The advancement of nanofluids is because of the notable idea of acquainting HTF strong particles with improved thermal conductivity. Choi and Eastman (1995) pioneered the improved heat transfer rate in technology on base liquids, through the utilization of nanoparticles. Buongiorno (2006) proposed significant progression in heterogeneous diffusion of nano-particles for the improvement of heat transfer. Buongiorno also established possible slipping strategies for thermophoresis and Brownian motion in nanofluids. Alblawi et al. (2019) pursued the Buongiorno method to examine the fluid flow over a stretching sheet, stretched out in all networks. Eid et al. (2020) discussed the performance of the boundary layer stream of Carreau nanofluid over a non-linear surfaces with generation/absorption in a permeable medium. Shah et al. (2020) introduced an article that manages the conveyance of blood and the exchange of thermal by methods for a gold micropolar nanofluid in a penetrable pipeline. He et al. (2020) elaborated the stream and heat transfer of CuO-water nanofluid was tried utilizing single-stage and two-stage (mixed) adaptations of various solids (1–4 percent) tube sizes. Gonçalves et al. (2020) opined that there is a quick need to create arrangements that can assist with overcoming current energy utilization and utilization imperatives. Bazdar et al. (2020) demonstrated that the progression of turbulence and heat transfer within a three-dimensional waved miniature channel. Saqib et al. (2019) pronounced the progression of disulfide dependent on generalized nanofluid ethylene glycol over the vertical isothermal plaque. Nasiri et al. (2019) investigated the compressible smooth molecule hydrodynamics (WCSPH) in the nano-liquid stream and heat transfer along the horizontal ring with Reynolds numbers up to 250 is investigated. Jilte et al. (2019) opined that non-renewable energy source fuelled engine vehicles must occur in a cleaner climate. Mir et al. (2020) observed that 0–6 percent volume fraction of nanoparticles with Re = 150–700 in curved geometry to be dictated by a small volume technique utilizing two-stage water/ag nanofluid stream and heat transfer. Khan et al. (2019) studied various slips from the radiation and chemical response over the stretching layer of the magnetohydrodynamic axisymmetric liquid surge. Punith Gowda et al. (2021a) studied magnetic dipole of nanofluid flow over a stretching sheet along with chemical reaction. Abbasi et al. (2021) elaborated water-based nanofluid with temperature-dependent viscosity. Ramesh et al. (2021) studied slip effects of time-dependent micropolar-based Casson nanofluid. Punith Gowda et al. (2021b) elaborated activation energy and chemical reaction impact of Marangoni driven boundary layer flow of a non-Newtonian nanofluid. Similar work on nanofluid using nano-particles was done by (Ahmad et al. 2021; Yahya et al. 2021; Ahmad et al. 2021)

As per general consideration, the implementation of the activation energy in some engineering advances, for example, compact heat exchangers, metallurgy, casting, liquid metal filtration, nuclear reactor cooling, and fusion control, thermal magnetic flux, and heat transfer mechanism. Alamri et al. (2019) appraised the consequences of heat and mass transfer on the second-grade fluid flow, which is subjected to the relaxation of the time. Ellahi et al. (2019a) presented an unconventional mathematical formulation for the electroosmotic of Poiseuille and Couette nanofluids flow. Ahmed et al. (2019) observed the unsteady flow for heat transfer in carbon nanotubes (CNT’s) with viscosity over a shrinking surface. Owing to heated, bi-phase, pressure-driven flow in two slippery walls was discussed by Ellahi et al. (2019b).

Microorganisms are the only cellular sorts that live everywhere, like in animals, humans, and plants. Bio-convection is shaped by the zigzag motion of microorganisms in the fluids. These gyrotactic organisms are much denser than water waving in an upward motion. Applications for mixed convection include biofuels, chemicals, ethanol, amino acid microsensors, biotechnology, and various ecosystems. Specific bio convection mechanisms occur, especially due to the movement of different forms of micro-organisms. Bio-convection exists when moving micro-organisms float upwards, which are even thicker than liquids. When the upper surface of the thin suspension becomes too dense due to mobility, the gradient of density reaches a critical point, gravity is destabilized, and eventually, microorganisms fall for bio-convection. Bhatti and Michaelides (2020) observed the features of thermo-bioconvection nanofluid flow with activation energy over a Riga Plate in the presence of microorganisms. Srinivasacharya and Sreenath (2020) discussed the bioconvection aspects in squeezing a flow of a couple of stress fluids across a non-vertical channel. Shi et al. (2021) discussed the microorganisms with activation energy effects magneto-cross nanofluid. Hamid et al. (2021) discussed the bio-convection flow of magneto-Cross nanofluid with gyrotactic microorganisms. Yusuf et al. (2021) studied the magneto-bioconvection flow of Williamson nanofluid with gyrotactic microorganisms using entropy generation.

The effects of radiation on the thermal transfer properties of liquids through extended surfaces are currently being studied by a number of researchers. Many important uses in chemical and industrial radiation technologies are material manufacturing, space exploration, glass production, and open-fire room lighting. The use of radiation from lung treatment in radiation therapy persists today.Almheiri et al. (2020) pointed out in this case we show that the long distance between Hawking and the unit operation specifications is resolved by adding news addles to the gravitational path as defined by von Neumann entropy. Bassett et al. (2020) showed the radiation hydrodynamic equations for the smoothing of the hydrodynamics of the particles are derived from the radiation division and hydrodynamics terms of the operator, including the required material motion conditions and the separation of each sequence of equations in time and space. Gorny et al. (1988) analyzed Earth’s satellite thermal (STI) images in the 10.5-11.3 mcm spectral range showed that the outgoing radiation flux was stable in both time and space compared to the adjacent blocks in a number of linear settings from the seismically active Middle Asian region (Kopet-Dagh, Talasso-Ferghana, and other failures). Adshead et al. 2020 showed the dark radiation is the curvature in Neff during Big Bang nucleon synthesis contributes to spatial variability with helical and deuterium primordial abundances.

The term “Magneto-hydrodynamic” was introduced by Haanas Alfren in 1942 which is defined as the study of fluids that accommodate electrical properties and magnetic behavior. In the current duration, the interpretation of Magneto nano-fluid has precise apprehension in the range/field of chemistry, medical sciences, physics, engineering, geography, and industries. In numerous aspects of life, abundant researches are done on MHD. The effects of magnetohydrodynamics a non-Newtonian fluid flow using a stretching sheet was discussed by Sarada et al. (2021). Abdal et al. (2020) studied time-dependent MHD mixed convection of micropolar nanofluid over a shrinking/stretching sheet. Abdal et al. (2021a) studies uniqueness of MHD Casson nanofluid flow across an extending cylinder. The porous medium and Stefan blowing effects on MHD flow with active and passive control of nanoparticles over the rotating disk is investigated by Rauf et al. (Rauf et al. 2019a; Mabood et al. 2021; Rauf et al. 2019b). Ali et al. (2021) discussed the phenomena of magnetohydrodynamic mass and heat transport over a stretching sheet. Abdal et al. (2021b) discussed the development of heat transportation over an extendable sheet. Abdal et al. (2015), Ali et al. (2020a), Ali et al. (2020b), Habib et al. (2021) deliberated the distinct flow features of magneto-hydrodynamic.

Our inspiration from the above submissions was developed to explore time depending magnetohydrodynamics of nanofluids over enlarging sheet with bioconvection and radiative implications. Two different sets of thermal heating process are studied, that is prescribed surface temperature (PST) and prescribed heat flux (PHF). Influence of several physical parameters namely unsteady parameter A, mixed convection parameter \(\omega\), bioconvection Rayleigh parameter Nc, buoyancy ratio parameter Nr, Reynolds number Re, Magnetic parameter M, activation energy parameter E, Brownian motion parameter Nb, thermophoresis parameter Nt, Prandtl number Pr, Peclet number Pe, Eckert number Ec, Lewis number Le, bioconvection Lewis number Lb, microorganisms difference parameter \(\delta\), radiation parameter Rd, R suction and injection if \((R > 0, R < 0)\) respectively, chemical reaction \(\gamma\) are analyzed graphically and tabular form in detail.

2 Physical model and mathematical formulation

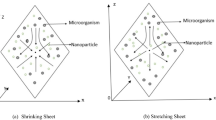
The current description is based on unsteady bioconvection of magneto-hydrodynamics, two-dimensional, incompressible, electrically conducting, nanofluid flow over a stretching sheet with chemical reaction and thermal radiation. The applied electric and magnetic fields have respective strengths \(E_1\) and B. The velocity components are u, v. Ohm law is followed by electric and magnetic law \(J = \sigma (E + V*B)\), here J is joule current, V denotes fluid velocity, \(\sigma\) stands for electrical conductivity (see (Habib et al. 2022)). In the presence of a small magnetic Reynolds number, it overcomes the impact of Hall current and induced magnetic field. \(u_w(x,t)\) is presenting velocity of the linearly stretching sheet while \(v_w(x,t)\) denoting velocity of mass transfer, stretching surfaces gives x-axis and y-axis components of the velocity and t is time. \(T_w\), \(\phi _w\) and \(N_w\) are the temperature, concentration, and motile microorganism of the nanofluid, \(T_\infty\), \(\phi _\infty\) and \(N_\infty\) represents ambient temperature, concentration, and microorganisms respectively, at the surface of the stretching sheet (see Fig. 1). Boundary-layer constitutive equations are simulated using the Buongiorno model (Buongiorno 2006). The governing equations for the given problem are as follows (Abdal et al. 2021c, d; Ali et al. 2019):

Continuity Equation

$$\begin{aligned} \partial _x u +\partial _y v = 0, \end{aligned}$$
(1)

Velocity Equation

$$\begin{aligned}&\partial _t u + u \partial _x u + v \partial _y u = \nu (\partial _{xx} u + \partial _{yy} u) - \left(\frac{1}{\rho _f}\right) \partial _x p + \left(\frac{\sigma ^*}{\rho _f}\right) (E_l B - B^2 u)+ \left(\frac{1}{\rho _f}\right)\\&\bigg ( (1-\phi _f)\rho _f \beta ^{**} g^* (T-T_\infty ) - (\rho _p - \rho _f) g^* (\phi -\phi _\infty ) - (N-N_\infty ) g^* \gamma (\rho _m - \rho _f) \bigg ), \end{aligned}$$
(2)

Temperature Equation

$$\begin{aligned}&\partial _t T + u \partial _x T + v \partial _y T = \bigg (\frac{k}{(\rho c)_f}\bigg ) (\partial _{xx} T + \partial _{yy} T) + \bigg (\frac{\sigma }{(\rho c)_f}\bigg )\,\,(uB - E_l)^2 - \bigg (\frac{1}{(\rho c)_f}\bigg )(\partial _y q_r)\\& + \bigg (\frac{\mu }{(\rho c)_f}\bigg ) (\partial _x u + \partial _y v)^2 + \tau \bigg (D_B \bigg ((\partial _x \phi )(\partial _x T)+(\partial _y \phi )(\partial _y T)\bigg )\,\,+ \left( \frac{D_T}{T_\infty }\right) {(\partial _x T)^2 + (\partial _y T)^2}\bigg ),\end{aligned}$$
(3)

Concentration Equation

$$\begin{aligned}&\partial _t \phi + u \partial _x \phi + v \partial _y \phi = D_B (\partial _{xx} \phi + \partial _{yy} \phi ) + \left( \frac{D_T}{T_\infty }\right) & (\partial _{xx} T + \partial _{yy} T) -(Kr)^2 (\phi -\phi _\infty )\left(\frac{T}{T_\infty }\right)^2 \exp \left(\frac{-E_a}{k_1 T}\right), \end{aligned}$$
(4)

Motile density Equation

$$\begin{aligned}&\partial _t N + u \partial _x N + v \partial _y N +[(\partial _y N)(\partial _{yy} C)]\bigg (\frac{b W_c}{(C_w - C_\infty )}\bigg )& = D_m (\partial _{yy} N). \end{aligned}$$
(5)

The suitable form of boundary conditions is express below (Abdal et al. 2021b):

$$\begin{aligned} \left. \begin{aligned}&u =u_w (x,t) + r_1 \partial _y u, v=v_w (x,t), T= T_w (x,t)=T_c - \frac{cx}{1-\alpha t} (PST),\\&\quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\,\,-K\frac{\partial T}{\partial y}= q_w (x,t)=T_c - \frac{Dx}{1-\alpha t} (PHF),\\&\quad\quad\quad\quad\quad\quad\phi = \phi _w (x,t) + r_2 \partial _y \phi ,N=N_w (x,t) + r_3 \partial _y N \, {\text{as}} \, y=0,\\&\quad\quad\quad\quad\quad\quad\quad\quad\quad u\rightarrow 0, N\rightarrow 0, T\rightarrow T_c, \phi \rightarrow \phi _\infty, \, {\text{as}}\, y \rightarrow \infty . \end{aligned}\right\} \end{aligned}$$
(6)
Fig. 1
figure 1

The schematic flow diagram

Full size image

Here, \(r_1 = r_{11} \sqrt{1-at}\), \(r_2 = r_{22 }\sqrt{1-at}\), \(r_3 = r_{33} \sqrt{1-at}\), signifies the velocity slip factor, concentration slip parameter, motile slip parameter,\(D_B\), \(D_T\) and \(D_m\) are the thermophoresis, Brownian motion and microorganisms coefficients, \(\tau = \frac{(\rho c)_p}{(\rho c)_f}\) is heat capacitance ratio, \(k_1 = \frac{k_0}{(1-at)}\) is the heat capacity of the fluid, and kr is rate of chemical reaction (Fig. 2). Here \(u_w (x,t)=\frac{bx}{(1-at)}\) is velocity of the linear stretching sheet \(v_w (x,t)= \frac{-v_0}{\sqrt{1-at}}\), is the wall mass transfer, where \(v_w <0\) denotes injection and \(v_w >0\) indicates suction. \(\sigma ^*\) stand for electric conductivity, \((\rho c)_f\) indicated the specific heat, component of deformation is \(\pi\), \(T_w\), \(\phi _w\) and \(N_w\) depicts the temperature of fluid, concentration of nanoparticles and microorganisms concentration at wall, thermal conductivity is \(k_1\), \(\phi _\infty\) express the ambient concentration, \(E_a\) is the activation energy. The modified Arrhenius function define as \((\frac{T}{T_\infty })^2 exp(\frac{-E_a}{k_1 T})\), \(W_c\) show the maximum cell speed of microorganisms and \(N_\infty\) stand for ambient concentration of microorganisms.

The expression for \(q_r\) (Habib et al. 2021),

$$\begin{aligned} q_r = -\left( \frac{4\sigma ^{**}}{3 k^*}\right) \partial _y T^4 \end{aligned}$$
(7)

where \(k^*\) denotes the mean absorption coefficient and \(\sigma ^{**}\) is Stefan–Boltzmann constant. Taylor’s series expansion is use for \(T^4\) about \(T_\infty\). We have (Daniel et al. 2017):

$$\begin{aligned} T^4 = 4 T_\infty ^3 - 3 T_\infty ^4 \end{aligned}$$
(8)

Then Eq. (7) becomes;

$$\begin{aligned} \partial _y q_r =-\left(\frac{16 T_\infty ^3 \sigma ^{**}}{3 k^*}\right)\partial _{yy} T \end{aligned}$$
(9)

and Eq. (4) is;

$$\begin{aligned}&\partial _t T + u \partial _x T + v \partial _y T = \bigg (\frac{k}{(\rho c)_f}\bigg ) (\partial _{xx} T + \partial _{yy} T) + \bigg (\frac{\sigma ^*}{(\rho c)_f}\bigg )(uB - E_l)^2 - \bigg (\frac{1}{(\rho c)_f}\bigg )(\partial _y q_r)\\&+ \bigg (\frac{\mu }{(\rho c)_f}\bigg ) (\partial _x u + \partial _y v)^2 + \tau \bigg (D_B \bigg ((\partial _x \phi )(\partial _x T)+(\partial _y \phi )(\partial _y T)\bigg )+ \left( \frac{D_T}{T_\infty }\right) {(\partial _x T)^2 + (\partial _y T)^2}\bigg ) \end{aligned}$$
(10)

Using boundary-layer approximation (Ibrahim and Shankar 2013),

\(u>>v\)

\(\partial _y u>> \partial _x u, \partial _t v, \partial _x v, \partial _y v\)

\(\partial _y p = 0\),

the reduced form of Eq. (1) to Eq. (5) are as follows;

$$\begin{aligned} \partial _x u +\partial _y u = 0 \end{aligned}$$
(11)
$$\begin{aligned}&\partial _t u + u \partial _x u + v \partial _y u = \nu (\partial _{xx} u + \partial _{yy} u) - \left( \frac{1}{\rho _f}\right) \partial _x p + \left( \frac{\sigma ^*}{\rho _f}\right) (E_l B - B^2 u)+ \left( \frac{1}{\rho _f}\right)\\&\bigg ( (1-\phi _f)\rho _f \beta ^{**} g^* (T-T_\infty ) - (\rho _p - \rho _f) g^* (\phi -\phi _\infty ) - (N-N_\infty ) g^* \gamma (\rho _m - \rho _f) \bigg ) \end{aligned}$$
(12)
$$\begin{aligned}&\partial _t T + u \partial _x T + v \partial _y T = \bigg (\frac{k}{(\rho c)_f}\bigg ) (\partial _{yy} T) + \bigg (\frac{\sigma }{(\rho c)_f}\bigg )(uB - E_l)^2 + \bigg (\frac{1}{(\rho c)_f}\bigg )((\frac{16 T_\infty ^3 \sigma ^{**}}{3 k^*})\partial _{yy} T)\\&+ \bigg (\frac{\mu }{(\rho c)_f}\bigg ) (\partial _x u + \partial _y v)^2 + \tau \bigg (D_B \bigg ((\partial _x \phi )(\partial _x T)+(\partial _y \phi )(\partial _y T)\bigg )+ \left( \frac{D_T}{T_\infty }\right) {(\partial _x T)^2 + (\partial _y T)^2}\bigg ) \end{aligned}$$
(13)
$$\begin{aligned}&\partial _t \phi + u \partial _x \phi + v \partial _y \phi \,=\, D_B (\partial _{yy} \phi ) + \left(\frac{D_T}{T_\infty }\right)(\partial _{xx} T + \partial _{yy} T) -(Kr)^2 (\phi -\phi _\infty )\left(\frac{T}{T_\infty }\right)^2 \exp\left(\frac{-E_a}{k_1 T}\right) \end{aligned}$$
(14)
$$\begin{aligned}&\partial _t N + u \partial _x N + v \partial _y N +[(\partial _y N)(\partial _{yy} C)]\bigg (\frac{b W_c}{(C_w - C_\infty)}\bigg) = D_m (\partial _{yy} N) \end{aligned}$$
(15)

The critically investigative assumption of high Reynolds number (Noghrehabadi et al. 2014), The under discussed dimensionless quantities are use to generate the equations (18-21), which are reduced dimensionless form.

$$\begin{aligned}&\eta = \sqrt{\frac{b}{\nu (1-at)}y}, \quad \psi = \sqrt{\frac{b\nu }{(1-at)}x}f(\eta ), \quad \theta (\eta ) = \frac{T-T_\infty }{T_w - T_\infty }, \phi (\eta ) = \frac{C-C_\infty }{C_w - C_\infty }, \xi (\eta ) = \frac{N-N_\infty }{N_w - N_\infty }, \\&\quad T_w (x,t)= T_\infty + T_0 (\frac{bx}{2\nu (1-at)^2}), \quad \phi _w (x,t)= C_\infty + C_0 (\frac{bx}{2\nu (1-at)^2}),\quad N_w (x,t)= N_\infty + N_0 (\frac{bx}{2\nu (1-at)^2})\end{aligned}$$
(16)

The stream function can be define as

$$\begin{aligned} u = \partial _y \psi , \quad u = -\partial _x \psi \end{aligned}$$
(17)

Utilizing expression (10) then (1-9) becomes

$$\begin{aligned}&f'''-f'^2-A(\frac{\eta }{2}f''+f')+ff''+M(E_1-f') +\omega (\theta - Nr\phi - Nc\xi )=0 \end{aligned}$$
(18)
$$\begin{aligned}&(1+(\frac{4}{3})Rd)\theta ''+Pr\bigg (f\theta '-2f'\theta +Nb\theta ' \phi '\nonumber \\&\quad +Nt\theta '^2-A(\frac{\eta }{2}\theta '+2\theta ) +Ecf''^2+MEc(f'-E_1)^2 \bigg ) =0 \end{aligned}$$
(19)
$$\begin{aligned}&\phi ''+LePr(f\phi '-2f'\phi -A(\frac{\eta }{2}\phi '+2\phi )-\gamma \nonumber \\&\quad \phi -\sigma (1+\delta _1 \theta )^n exp (\frac{-E_a}{1+\delta _1 \theta }))+(\frac{Nt}{Nb})\theta '' =0 \end{aligned}$$
(20)
$$\begin{aligned}&\xi ''+Lbf\xi '-2Lbf'\xi -A(\frac{\eta }{2}\xi '+2\xi )\nonumber \\&\quad -Pe[\phi ''(\xi +\delta )+\xi ' \phi ']=0 \end{aligned}$$
(21)

The transform form of boundary conditions (6) are

$$\begin{aligned} \left. \begin{aligned}&f(0)=R, f'(0)=1+R_1 f'', \theta (0)=1 (PST),,\\&\theta (0)=-1 (PHF), \phi (0)=1+R_2 \phi ', \xi (0)=1+R_3 \xi ' at \ \eta = 0,\\&f'=0, \ \theta = 0,\ \phi = 0, \ \xi = 0 \ at \ \eta \rightarrow \infty . \end{aligned}\right\} \end{aligned}$$
(22)

Here \(A(= \frac{a}{b})\) represents the unsteady parameter, \(R_1(=r_1\sqrt{\frac{b}{\nu }})\) signify the velocity slip parameter, \(R_2(=r_2\sqrt{\frac{b}{\nu }})\) shows the solutal slip factor for concentration and as well as, \(R_3(=r_3\sqrt{\frac{b}{\nu }})\) is use for solutal slip parameter for motile microorganisms, \(\omega (=\frac{\beta ^{**} g^*(1-\phi _\infty )(T_w - T_\infty )}{u_w b})\) stand for mixed convection parameter, \(Nc (=\frac{\gamma (\rho _m-\rho _f)(N_w - N_\infty )}{\beta ^* \rho _f (1-\phi _\infty )(T_w - T_\infty )})\) witnessed the Rayleigh number, \(Nr (=\frac{(\rho _p-\rho _f)(\phi _w - \phi _\infty )}{\beta ^* \rho _f (1-\phi _\infty )(T_w - T_\infty )})\) is buoyancy ratio parameter, \(M(=\frac{\sigma ^* B_0^2}{b\rho _f})\) is use for magnetic parameter, \(E_1(=\frac{E_a}{K T_\infty })\) is activation energy parameter, \(Nb(=\frac{(\rho c)_p D_B (\phi _w - \phi _\infty )}{\nu (\rho c)_f T_\infty })\) summarized the Brownian motion parameter, \(Nt(=\frac{(\rho c)_p D_T (T_w - T_\infty )}{\nu (\rho c)_f T_\infty })\) express the thermophoresis parameter, \(Pr(=\frac{\nu }{\alpha })\) represents the Prandtl number, \(Pe(=\frac{bW_c}{D_m})\) denote the Peclet number, \(Ec(=\frac{u_w^2}{c_p(T_w - T_\infty )})\) signifies the Eckert number, \(E_a(=\frac{E_1}{u_w B})\) is implies the electric field parameter, \(Le(=\frac{\alpha }{D_B})\) is custom for Lewis number, \(Lb(=\frac{v_f}{D_m})\) is stand for bioconvection Lewis number, \(\delta (=\frac{N_\infty }{(N_w - N_\infty )})\) is stance for microorganisms difference parameter, \(Rd(=\frac{4\sigma ^{**}T_\infty ^3}{kk^*})\) is the radiation parameter, \(h(=\frac{v_0}{\sqrt{\nu b}})\) is use for suction and injection if \((h>0, h<0)\) respectively, \(\gamma (=\frac{k_0}{b})\) is stance for chemical reaction.

3 Physical quantities

The corporal manufacturing quantities of practical interest for engineers are (Abdal et al. 2021b):

3.1 Surface drag force

The skin friction coefficient is defined as

$$\begin{aligned} C_f = \frac{\tau _w}{\rho u_w^{2}(x,t)}, \end{aligned}$$

where, \(\tau _w\) signify shear stress and is defined as

$$\begin{aligned} \tau _w = \mu (\partial _y u) \ \ \ at \ y = 0, \end{aligned}$$

Thus

$$\begin{aligned} C_f Re^{0.5} = 2 \left[ f''(0)- \left( \frac{\alpha _1}{3} \right) f''^3(0) \right] . \end{aligned}$$

3.2 Heat transfer rate

The local Nusselt Number is defined as:

$$\begin{aligned} N_u = \frac{xq_w}{k(T_w-T_{\infty })}, \end{aligned}$$

where, \(q_w\) symbolize surface heat flux and defined as:

$$\begin{aligned} q_w = \frac{k+16 \sigma ^* T_\infty ^3}{3k^*}\partial _y T \ \ \ at \ y = 0, \end{aligned}$$

Thus

$$\begin{aligned} N_u Re^{0.5} = - \left( \frac{1}{1-n_1} \right) \left( 1+\frac{4}{3}Rd \right) \theta '(0). \end{aligned}$$

3.3 Sherwood number

The local Sherwood Number is interpreted as:

$$\begin{aligned} Sh_x = \frac{x q_m}{D_B(\phi _w - \phi _\infty )}, \end{aligned}$$

where, \(q_m\) represents surface mass flux and defined as:

$$\begin{aligned} q_m = -D_B(\partial _y \phi ) \ \ \ at \ y = 0, \end{aligned}$$

Thus

$$\begin{aligned} S_h Re^{0.5} = -\left( \frac{1}{1-n_2} \right) \phi '(0). \end{aligned}$$

3.4 Density number of micro-organisms distribution

The local density number of micro-organisms is defined as:

$$\begin{aligned} N_n = \frac{x q_i}{D_m(N_w - N_\infty )}, \end{aligned}$$

where, \(q_i\) characterize motile micro-organisms flux and defined as:

$$\begin{aligned} q_i = - D_m(N_y \phi ) \ \ \ at \ y = 0, \end{aligned}$$

Thus

$$\begin{aligned} N_n Re^{0.5} = - \left( \frac{1}{1-n_3} \right) \xi '(0). \end{aligned}$$

4 Implementation of method

In this segment, the numerical result of resulting dimensionless nonlinearity coupled ordinary differential equations Eq. (19) to Eq. (22) with boundary conditions Eq. (23) are integrated by MATLAB built-in raft (bvp4c). This computational software MATLAB is utilized for the substantiation of results of the shooting technique. To execute this numerical method, the differential equation Eq. (19-22) is transformed into a first-order ordinary differential equation by introducing some new notations and its implementation of some new variables expressed as below:

Let

\(f=y_1, f'=y_2, f''=y_3, f'''=y_3', \theta =y_4, \theta '=y_5, \theta ''=y_5'\)

\(\phi =y_6, \phi '=y_7, \phi ''=y_7', \xi =y_8, \xi '=y_9, \xi ''=y_9'\)

\(y_3'=y_2^2-y_1 y_3+A((\frac{\eta }{2})y_3+y_2)-M(E_1+y_2)-\omega (y_4-Nr y_6 - Nc y_8)\)

\(y_5' = \frac{-Pr[Nb y_5 y_7 + Nt y_5^2 + Ec M (y_2+E_1)^2 -2 y_2 y_4 + y_1 y_5 +Ec(y_3)^2- A((\frac{\eta }{2})y_5+2y_4)]}{(1+(\frac{4}{3})Rd)}\)

\(y_7' = -\frac{Nt}{Nb}y_6' - Le Pr[-y_1y_7 -y_2y_6 - \sigma [1+\delta y_4]^n exp[\frac{-E_a}{1+\delta y_4}]-\gamma y_6-A((\frac{\eta }{2})y_7+2y_6)]\)

\(y_9' = -Lb y_1y_9 + 2Lb y_2y_8 +A((\frac{\eta }{2})y_9+2y_8)- Pe[y_9y_7 + (\delta + y_8)_7']\)

\(y_1=R, y_2=1+R_1 y_3, y_4=1, y'_4=-1, y_6=1+R_2 y_7, y_8=1+R_3 y_9,\, {\text{at}}\,\eta = 0\)

\(y_2=0, y_4=0, y_6=0, y_8=0\, {\text{as}}\,\eta \rightarrow \infty\)

Fig. 2
figure 2

Flow chart

Full size image

5 Results and discussion

The analysis clearly shows the relationship of numerical results. It is clear from Table 1 and Table 2 that there are close agreements among the results for the parameters under discussion \(\delta\) and Pr individually. The purpose of the present section is to describe the effect of physical and numerical results. The above code is run for acceptable ranges of the controlling parameters. Findings are obtained for velocity \(f'(\eta )\), temperature \(\theta (\eta )\), nano-particle volume fraction \(\phi (\eta )\) and micro-organism distribution \(\xi (\eta )\). The numerical scheme is validated.

Table 1 Comparison of skin friction coefficient for various values of \(\delta\)
Full size table
Table 2 Comparison of Nusselt number for various values of Pr
Full size table

The impacts of various physical parameters like magnetic parameter M, activation energy parameter \(E_1\), mixed convection parameter \(\omega\), buoyancy ratio parameter Nr, Rayleigh number Rb, unsteady parameter A, Eckert number Ec, Brownian motion parameter Nb, thermophoresis parameter Nt, Prandtl number Pr, radiation parameter Rd, electric field parameter \(E_a\), chemical reaction \(\gamma\), Lewis number Le, bioconvection Lewis number Lb, Peclet number Pe, microorganisms difference parameter \(\delta\) on physical quantities are noticed for both PST and PHF cases. The values of \(M=0.1\), \(h=0.5\), \(S_1=S_2=S_3=A=\omega =Nr=Nc=\delta _1=Lb=Pe=0.1\), \(E_1=0.01\), \(Rd=Ec=0.2\), \(Pr=0.733\), \(Nb=Nt=\sigma =n=0.5\), \(E_a=0.3\), \(\gamma =1\), \(Le=5\) are fixed in computational procedure.

The influence of the magnetic field parameter on velocity \(f'(\eta )\) is demonstrated in Fig. 3a. A retarding trend is shown for velocity profile with the uplifting of magnetic parameter M. The basic reason for retardation is resistance to flow due to Lorentz force. Figure 3b discloses the effective outcomes when activation energy parameter \(E_1\) is applied on velocity distribution. The arising curve depicts that the velocity curve rises when the activation energy parameter is intensified. The effect of parameter \(\omega\) on velocity distribution is depicted in Fig. 4a. It is observed that \(\omega\) is responsible for increasing boundary layer distribution in the presence of PST and PHF cases. The experimental behavior of buoyancy ratio parameter Nr over velocity field distribution is plotted through Fig. 4b. The decreasing trend is observed when parameter Nr is uplifted. The upthrust effect becomes stronger with stronger buoyancy force. Figure 5a is presenting the effect of Rayleigh number Nc for velocity distribution. The stronger points of combined convection of natural and forced convection give downward grades executing over stretching sheet for MHD Flow of unsteady flow. Figure 5b demonstrate the impact of unsteady parameter A on the velocity profile. It is seen from the figure that the velocity profile gets decreasing for both PST and PHF cases with the increasing values of A. Due to decreasing behavior of velocity profile, the thickness of momentum boundary also reduces. The magnetic effect over thermal distribution is sketched in Fig. 6a. The increasing values of magnetic parameter intensify the heat distribution along the stretching sheet for both PST and PHF cases. The influence of activation energy for temperature distribution is exhibited in Fig. 6b. It can be visualized that activation energy causes a decreasing effect of temperature coefficient on enlarging \(E_1\). Another significant parameter that is used to characterize heat transfer dissipation is discussed along temperature coefficient is pictured through Fig. 7a. The outcomes revealed that temperature \(\theta (\eta )\) is intensified when the Ec parameter is increased. The temperature of the fluid is also when the mixed convection parameter \(\omega\) is intensified as shown in Fig. 7b. It is observed that when mixed convection parameter is uplifted, it reduces the temperature of nanofluid. On the other hand, Fig. 8 and b illustrate the firmness between Brownian motion Nb and thermophoresis parameter Nt on both cases for PST and PHF. These two parameters show similar behavior on the increasing values of temperature. The impact of buoyancy ratio parameter Nr on thermal boundary layer distribution is described in Fig. 9a. Plots describe that when buoyancy ratio has uplifted the nanofluid comprising MHD flow have a larger amount of temperature \(\theta (\eta )\). Figure 9b illustrates the effect of Prandtl number Pr over-temperature distribution. The findings show that increasing Pr decreases the temperature of nanofluid. The effect of radiation parameter Rd over temperature is discussed in Fig. 10a. The input effects came to conclude that large values of the Rd parameter take to a higher amount of temperature coefficient. Figure 10b shows the behavior of unsteady parameter A on temperature distribution for PST and PSH. It is observed that with the rising values of unsteady parameter A, the temperature decreases monotonically. The impact of unsteady parameter A is seen more projecting for temperature than the velocity profile. Figure 11a presents the influence of parameter \(\sigma\) on concentration profile. Increasing the amount of \(\sigma\) causes to decrease in concentration profile. The opposite behavior for activation energy parameter \(E_a\) is shown in Fig. 11b. A significant parameter affecting the concentration profile while the execution of MHD flow of unsteady nanofluid is the chemical reaction parameter \(\gamma\) . The physical results depict that the concentration profile is reduced when \(\gamma\) is intensified. The result report can be visualized in Fig. 12a. Figure 12b shows that the nanoparticle concentration decreases as the fitted rate constant n increases. The physical behavior for concentration profile for a significant parameter i.e. Brownian motion is sketched by Fig. 13a. Observing the trends shows that the concentration profile decreases down while uplifting the Nb parameter. To disclose the physical behavior of thermophoresis parameter over concentration distribution for MHD flow of nanofluid Fig. 13b is drawn. It is brought to conclude that the rising Nt parameter leads to an increment in concentration distribution. As Nt is the phenomenon of the combined effect of moving particles of the fluid in which different forces of temperature gradient are the reason of increment in concentration field. Observing the effect of Lewis number Le with respect to the concentration profile, it is seen that \(\phi (\eta )\) is reduced. The evidence report of the above conclusion is reported in Fig. 14a. The physical impact of unsteady parameter A over the concentration field is displayed in Fig. 14 (b). Unsteady parameter produces a decreasing curve for the concentration distribution. Figure 15a is the illustration of bioconvection Lewis number Lb and its effect upon motile microorganism distribution. The traces reveal that motility of the nanofluid decreases when the Lb parameter is raised. The physical effect of Peclet number Pe and motile microorganism distribution is deployed in Fig. 15b. Motility profile is observed rising in curves as Peclet number is given larger amount. Microorganisms difference parameter is a significant parameter affecting the motility of nanofluid having MHD flow. An increase is observed when \(\delta\) is intensified as depicted in Fig. 16a. The impact of an unsteady parameter over motile microorganism distribution is discussed in Fig. 16b. It is visualized that when a large amount of unsteady parameter is given as an input, it gives a rising curve of motile microorganism profile.

Fig. 3
figure 3

Fluctuation of \(f'(\eta )\) with M and \(E_1\)

Full size image
Fig. 4
figure 4

Fluctuation of \(f'(\eta )\) with \(\omega\) and Nr

Full size image
Fig. 5
figure 5

Fluctuation of \(f'(\eta )\) with Nc and A

Full size image
Fig. 6
figure 6

Fluctuation of \(\theta (\eta )\) with M and \(E_1\)

Full size image
Fig. 7
figure 7

Fluctuation of \(\theta (\eta )\) with Ec and \(\omega\)

Full size image
Fig. 8
figure 8

Fluctuation of \(\theta (\eta )\) with Nb and Nt

Full size image
Fig. 9
figure 9

Fluctuation of \(\theta (\eta )\) with Nr and Pr

Full size image
Fig. 10
figure 10

Fluctuation of \(\theta (\eta )\) with Rd and A

Full size image
Fig. 11
figure 11

Fluctuation of \(\phi (\eta )\) with \(\sigma\) and \(E_a\)

Full size image
Fig. 12
figure 12

Fluctuation of \(\phi (\eta )\) with \(\gamma\) and n

Full size image
Fig. 13
figure 13

Fluctuation of \(\phi (\eta )\) with Nb and Nt

Full size image
Fig. 14
figure 14

Fluctuation of \(\phi (\eta )\) with Le and A

Full size image
Fig. 15
figure 15

Fluctuation of \(\xi (\eta )\) with Lb and Pe

Full size image
Fig. 16
figure 16

Fluctuation of \(\xi (\eta )\) with \(\delta\) and A

Full size image

6 Conclusions

An investigation for bioconvection and radiative effects for MHD time-dependent flow of nanofluids due to an extending domain is made theoretically and numerically. Velocity, temperature, concentration, and motile microorganisms’ profiles are evaluated for two types of thermal conditions namely, PST and PHF with varying inputs of pertinent parameters. The requirement of efficient heat transfer is managed by nanoparticle diffusion with enhancement of thermal conductivity of crude base fluid. The bioconvection of self motile microorganisms can be useful to avoid undesired sedimentation. The findings of this communication can find applications in heat exchangers, microelectronics and cooling of nuclear reactors.

  • Velocity trends are enhanced for higher mixed while it shows a decrement for magnetic and buoyancy ration parameter in the presence of the electric field.

  • Concentration is uplifted for a larger amount of Biot number while reduction is observed for Brownian motion.

  • The motility of the nanofluids shows declination for greater values of Peclet number and bioconvection Lewis number.

  • Thermalboundary layer distribution is decreased when Prandtl number under the cases of slip (PST) and (PHF).

  • The concentration of nanoparticles increased for a larger solutal Biot number.

  • The microorganism concentration reduces for various variations of Peclet number and bio convection Lewis number.

  • The current model refers to an enhanced approach to the thermal conductivity of the base fluid and used in nanotechnology.