1 Introduction

Microfluidic droplet operations with high volume precision is of paramount importance for many scientific applications such as chemical synthesis, compound separation, drug discovery, and quantitative analysis of biomedical assays (Dittrich and Manz 2006; Rose 1999). The volume precision of a series of micro droplets can be evaluated by droplet volume inconsistency, which is also referred to as droplet volume reproducibility in some literature (Berthier et al. 2006; Ren et al. 2004; Rose 1999) and defined as the ratio of the standard deviation of a series of droplet volumes to their mean value. It was reported that the inconsistency is preferably between ±5 % and needs to be controlled to within ±2 % or even less for some particular biomedical requirements (Rose 1999).

Over the last decade, a great deal of effort has been devoted to the studies of microfluidic droplet operations in which several effective techniques including electrostatic force (Washizu 1998), thermocapillary effect (Sammarco and Burns 1999), electrochemical gradient (Böhm et al. 2000), dielectrophoresis (Jones et al. 2001), and magnetic fields (Nguyen et al. 2006) have been utilized as the driving mechanism for droplet motions. Due to recent rapid development of microelectromechanical systems (MEMS) and lab-on-a-chip (LOC) devices, considerable effort has also been put into electrowetting-based digital microfluidic manipulations, which facilitates the investigations of discrete droplet operations within parallel-plate electrowetting-on-dielectric (EWOD) devices (Cho et al. 2003; Fair 2007; Guan and Tong 2015a, b; Pollack et al. 2002; Walker et al. 2009; Wheeler et al. 2004). As one of the fundamental microfluidic droplet operations, the investigation of droplet dispensing, which refers to the process of aliquoting a larger volume of liquid into smaller unit droplets for further actions, has been carried out for years due to the increasing demand for excellent droplet volume consistency in various digital microfluidic research works (Berthier et al. 2006; Cho et al. 2003; Fair 2007; Fouillet et al. 2008; Gong and Kim 2008; Jang et al. 2007; Pollack et al. 2002; Ren et al. 2004; Wang et al. 2011; Yaddessalage 2013).

Pollack et al. (2002) were among the early researchers who conducted experiments on micro droplet dispensing in parallel-plate electrowetting-based LOC systems. It was shown that droplets of similar sizes were generated from a large sample drop in the reservoir. Similar dispensing experiment was later performed by Cho et al. (2003) with deionized (DI) water as the working liquid. Droplets were successfully dispensed from a liquid reservoir in a parallel-plate EWOD device which consists of two small electrodes alongside the main dispensing path. It was found that without these two side electrodes, the pinch-off location would not be fixed and the droplet sizes would consequently not be consistent. An experimental method combining electrowetting actuation and built-in capacitance feedback was developed by Ren et al. (2004) for droplet dispensing from a self-contained LOC device using KCl solution as the working liquid. Smaller volume inconsistency was obtained compared with devices without capacitance feedback. The inconsistency was found to increase with droplet viscosity and production rate. Berthier et al. (2006) numerically modeled droplet dispensing process based on the surface energy minimization approach. It was demonstrated that decent volume inconsistency could be achieved when the cutting and generating electrodes were of the same size. Fair (2007) summarized recent development of electrowetting-based digital microfluidics and LOC applications. The dispensing mechanism was also examined by investigating the pressure differences across the liquid boundary at critical dispensing stages. It was reported that fewer cutting electrodes were needed for successful dispensing when the device had a smaller channel height and a larger generating electrode. A real-time feedback control EWOD system was developed by Gong and Kim (2008) for on-chip droplet dispensing experiments, in which droplet consistency was notably improved compared with devices with external pump or open-loop control system. Wang et al. (2011) studied water droplet dispensing from an EWOD-based microfluidic device. It was illustrated that the length of the neck in the cutting stage played a significant role in the volume of generated droplet. Better volume consistency could be acquired when the cutting electrode was of a smaller size. Yaddessalage (2013) carried out experimental studies on micro droplet dispensing from parallel-plate EWOD devices with three different reservoir designs. It was reported that better volume consistency could be achieved by shortening the length of the neck in the cutting stage. Samiei and Hoorfar (2015) recently conducted an experimental study of micro droplet dispensing from a parallel-plate EWOD device in which the generating electrodes were divided into several sub-electrodes with various shapes. The effect of channel height, applied voltage, and generating electrode shape on droplet volume was investigated. It was discovered that the applied voltage needed to be set close to the minimum voltage required for dispensing in order to achieve optimum volume accuracy.

Even though micro droplet dispensing based on the electrowetting effect has been studied for years, the key elements affecting volume inconsistency are still not completely understood. Due to the complex two-phase flow patterns associated with the dispensing process which occurs at the microscale, it is often challenging to perform experimental study to capture clear droplet motion images at crucial time instants. Other issues including arduous work of EWOD system fabrication and droplet volume measurement are also impediments to exploring the dispensing mechanism. Numerical methods, on the other hand, can provide vital information such as the pressure and velocity profiles within the liquid, which may serve as an excellent alternative for systematically analyzing the dispensing process. Besides, clear droplet image and reliable volume data can be directly extracted from numerical results, which are not readily available in experiments.

The objective of the present study is to numerically investigate the physics involved in micro droplet dispensing process within parallel-plate EWOD devices with different reservoir designs as well as the key factors affecting volume inconsistency of generated droplets. A brief review of the parallel-plate EWOD model is given next followed by a description of the numerical formulation and results and discussion in which the details of the reservoir designs are discussed.

2 EWOD in a parallel-plate device

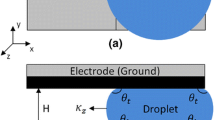
The schematics of the top and cross-sectional views of a parallel-plate EWOD device are shown in Fig. 1. Note that the figure is not to scale with a much narrower channel height in the actual device. It consists of two parallel plates with the droplet sandwiched in-between. The top electrode is one whole piece which remains grounded at all time, while the two disjointed square-shaped electrodes at the bottom can be switched ‘ON’ and ‘OFF’ independently as needed. There are two hydrophobic Teflon layers one each on the top and bottom plates which separate the droplet from the electrodes. The dielectric layer on the bottom plate is an insulating film which sustains the high electric field at the interface and allows a larger contact angle change upon the application of electrical voltage compared with the conventional electrowetting device without this layer (Moon et al. 2002).

Fig. 1
figure 1

Top (a) and cross-sectional (b) views of the parallel-plate EWOD device

Full size image

When a droplet is placed on a plane surface, the contact angle θ at the three-phase contact line can be modified by applying electrical potential at the droplet boundary according to the Young–Lippmann’s equation as

$$\cos \theta (V) = { \cos }\theta_{0} + \frac{{\varepsilon_{0} \varepsilon }}{{2\sigma_{\text{LG}} d}}V^{2}$$
(1)

where θ is the contact angle at the triple contact line with nonzero electrical potential, θ 0 the equilibrium contact angle with zero potential, ε 0 the permittivity of vacuum, ε the dielectric constant of dielectric layer, \(\sigma_{\text{LG}}\) the surface tension at the liquid–gas interface, d the thickness of dielectric layer, and V the magnitude of applied voltage. The Young–Lippmann equation is reasonably accurate in predicting the contact angle at low voltage. However, it has been discovered that the equation fails after the voltage reaches a certain threshold beyond which the contact angle θ only displays slight variation. This effect is referred to as contact angle saturation and has been addressed in the literature (Cho et al. 2003; Mugele and Baret 2005).

Since the contact angle at the triple contact line can be modified by applying electrical potential at the droplet boundary, this will alter droplet surface curvature and consequently surface tension-induced pressure at the liquid–gas interface according to the Young–Laplace equation (Batchelor 2000):

$$\Delta p = \sigma_{\text{LG}} (\kappa_{xy} + \kappa_{z} )$$
(2)

where Δp is the surface tension-induced pressure at the liquid–gas interface, κ xy and κ z the mean curvatures in the x–y plane and along the z-direction, respectively. Since the channel height is very small compared with the device dimension and the capillary number is much smaller than unity for the current study, the liquid–gas interface in the z-direction can be approximated as circular which yields

$$\kappa_{z} = \frac{{( - \cos \theta_{\text{t}} - cos\theta_{\text{b}} )}}{H}$$
(3)

where θ t and θ b are the contact angles at the top and bottom plates, respectively, and H the channel height between two parallel plates. See Fig. 1. Note that θ t is always constant since the top electrode is grounded, but θ b varies according to Eq. (1). Combination of Eqs. (2) and (3) gives the pressure difference at the droplet boundary across the ‘ON’ and ‘OFF’ regions as,

$$p_{\text{OFF}} - p_{\text{ON}} = \sigma_{\text{LG}} \left( {\frac{{\cos \theta_{{{\text{b}},{\text{ON}}}} - \cos \theta_{{{\text{b}},{\text{OFF}}}} }}{H} + \kappa_{{xy,{\text{OFF}}}} - \kappa_{{xy,{\text{ON}}}} } \right)$$
(4)

As shown in Fig. 2, when electrical charges are applied, the surface tension at the interface is reduced due to the decreased contact angle \(\theta_{{{\text{b}},{\text{ON}}}}\). This reduced surface tension on the electrowetted side leads to an imbalanced pressure force which moves the droplet from the ‘OFF’ to the ‘ON’ side. This mechanism is another plausible explanation of microfluidic droplet motion induced by the electrowetting effect apart from the well-known theory that the electrostatic force serves as the driving force for droplet movement (Pollack et al. 2002; Mugele and Baret 2005).

Fig. 2
figure 2

Pressure difference induced by electrical actuation

Full size image

An essential element in EWOD modeling is contact angle hysteresis, which refers to the difference in contact angles between the advancing and receding ends when the droplet is in motion (Mugele and Baret 2005; Walker and Shapiro 2006; Walker et al. 2009). When the droplet is stationary on a flat plate, a unique contact angle, referred to as the static contact angle, is formed at the triple contact line. As the droplet moves, the contact angle on the advancing side increases while that on the receding side decreases and are referred to as advancing and receding contact angles, respectively. It should be noted that the hysteresis phenomenon has a retarding effect on fluid motion (Walker and Shapiro 2006).

3 Numerical formulations

3.1 Governing equations

For incompressible flows with constant properties, the continuity and momentum equations are given by

$$\nabla \cdot \vec{\varvec{u}} = 0$$
(5)
$$\frac{{\partial \vec{\varvec{u}}}}{\partial t} + \vec{\varvec{u}} \cdot \nabla \vec{\varvec{u}} = - \frac{1}{\rho }\nabla P + \frac{1}{\rho }\nabla \cdot\varvec{\tau}+ \vec{\varvec{g}} + \frac{{\overrightarrow {{\varvec{F}_{{\mathbf{b}}} }} }}{\rho }$$
(6)

where \(\vec{\varvec{u}}\) is the velocity, \(\rho\) the density, P the pressure, \(\varvec{\tau}\) the viscous stress tensor, \(\vec{\varvec{g}}\) the gravitational acceleration, and \(\overrightarrow {{\varvec{F}_{{\mathbf{b}}} }}\) the body force. It should be noted that a free surface flow model is adopted in this study in which the dynamic effect of the air is neglected. For Newtonian fluids, the viscous stress tensor \(\varvec{\tau}\) can be written as:

$$\varvec{\tau}= 2\mu \varvec{S}\quad \varvec{S} = \frac{1}{2}\left[ {(\nabla \vec{\varvec{u}}) + (\nabla \vec{\varvec{u}})^{T} } \right]$$
(7)

where S is the rate-of-strain tensor. Equation (6) is approximated in the finite-difference form as:

$$\frac{{\vec{\varvec{u}}^{n + 1} - \vec{\varvec{u}}^{n} }}{\delta t} = - \vec{\varvec{u}}^{n} \cdot \nabla \vec{\varvec{u}}^{n} - \frac{1}{{\rho^{n} }}\nabla P^{n + 1} + \frac{1}{{\rho^{n} }}\nabla \cdot\varvec{\tau}^{n} + \vec{\varvec{g}}^{n} + \frac{1}{{\rho^{n} }}\overrightarrow {{\varvec{F}_{{\mathbf{b}}} }}^{n}$$
(8)

A two-step projection algorithm is used where Eq. (8) is decomposed into the following two equations:

$$\frac{{\vec{\varvec{u}}^{ *} - \vec{\varvec{u}}^{n} }}{\delta t} = - \vec{\varvec{u}}^{n} \cdot \nabla \vec{\varvec{u}}^{n} + \frac{1}{{\rho^{n} }}\nabla \cdot\varvec{\tau}^{n} + \vec{\varvec{g}}^{n} + \frac{1}{{\rho^{n} }}\overrightarrow {{\varvec{F}_{{\mathbf{b}}} }}^{n}$$
(9)

and

$$\frac{{\vec{\varvec{u}}^{n + 1} - \vec{\varvec{u}}^{ *} }}{\delta t} = - \frac{1}{{\rho^{n} }}\nabla P^{n + 1}$$
(10)

where \(\vec{\varvec{u}}^{ *}\) represents an intermediate velocity. In the first step, \(\vec{\varvec{u}}^{ *}\) is computed from Eq. (9) which accounts for incremental changes resulting from viscosity, advection, gravity, and body forces. The second step involves taking the divergence of Eq. (10) while projecting the velocity field, \(\vec{\varvec{u}}^{n + 1}\), to a zero-divergence vector field for mass conservation. This results in a single Poisson equation for the pressure field given by

$$\nabla \cdot \left[ {\frac{1}{{\rho^{n} }}\nabla P^{n + 1} } \right] = \frac{{\nabla \cdot \vec{\varvec{u}}^{ *} }}{\delta t}$$
(11)

which is used to obtain \(\vec{\varvec{u}}^{n + 1}\) from Eq. (10).

3.2 Interface tracking methods

The main complexity of the numerical simulation is the dynamics of a rapidly moving free surface, the location of which is unknown and is needed as part of the solution. As the flow is surface tension driven, modeling of the surface tension force with a high degree of accuracy is critical. In recent years, a number of methods have been developed for modeling free surface flows (Hirt and Nichols 1981; Rudman 1998; Sussman et al. 1994; Scardovelli and Zaleski 1999), among which the volume-of-fluid (VOF) method and the level set (LS) method are two Eulerian-based methods that have been widely used. One of the advantages offered by these methods is the ease in which flow problems with large topological changes and interface deformations can be handled. These include droplet elongation and breakup, bubble merging and bursting, and microfluidic droplet operations. The VOF method has the desirable property of mass conservation. However, it lacks accuracy on the normal and curvature calculations due to the discontinuous spatial derivatives of the VOF function near the interface. This may lead to convergence problems (Meier et al. 2002; Renardy and Renardy 2002; Scardovelli and Zaleski 1999; Tong and Wang 2007) especially in the surface tension force-dominant problems. As for the LS method, the normal and curvature can be calculated accurately from the continuous and smooth distance functions. However, one serious drawback of this method is the frequent violation of the mass conservation. To overcome such weaknesses of the LS and VOF methods, a coupled level set and volume-of-fluid (CLSVOF) method has recently been reported (Son and Hur 2002; Sussman 2003; Sussman and Puckett 2000; Yang et al. 2006). The coupled method offers improved accuracy on the surface curvature and normal calculations while maintaining mass conservation. A CLSVOF method is used in the present study with the interface reconstructed via a piecewise linear interface construction (PLIC) scheme on the VOF function (Rudman 1997) and the interface normal computed from the LS function. A brief overview of the CLSVOF scheme is given here.

The LS function, ϕ, is defined as a distance function given by

$$\phi (\vec{\varvec{x}},t) = \left\{ {\begin{array}{*{20}l} { >}0 \hfill & \quad {{\text{outside}}\,{\text{of}}\,{\text{the}}\,{\text{interface}}} \hfill \\ 0 \hfill &\quad {{\text{at}}\,{\text{the}}\,{\text{interface}}} \hfill \\ {<}0 \hfill &\quad {{\text{inside}}\,{\text{of}}\,{\text{the}}\,{\text{interface}}} \hfill \\ \end{array} } \right.$$
(12)

i.e., negative in the liquid, positive in the air, and zero at the interface. The VOF function, F, is defined as the liquid volume fraction in a cell with its value in between zero and one in a surface cell, and zero and one in air and liquid, respectively, i.e.,

$$F(\vec{\varvec{x}},t) = \left\{ {\begin{array}{*{20}l} 1 \hfill &\quad {{\text{in}}\,{\text{the}}\,{\text{fluid}}} \hfill \\ {0 < F < 1} \hfill &\quad {{\text{at}}\,{\text{the}}\,{\text{interface}}} \hfill \\ 0 \hfill &\quad {{\text{external}}\,{\text{to}}\,{\text{fluid}}} \hfill \\ \end{array} } \right.$$
(13)

The VOF and LS functions are advanced by the following equations, respectively:

$$\frac{DF}{Dt} = \frac{\partial F}{\partial t} + \left( {\vec{\varvec{u}} \cdot \nabla } \right)F = 0$$
(14)
$$\frac{D\phi }{Dt} = \frac{\partial \phi }{\partial t} + \left( {\vec{\varvec{u}} \cdot \nabla } \right)\phi = 0$$
(15)

It should be noted that since the VOF function is not smoothly distributed at the free surface, an interface reconstruction procedure is required to evaluate the VOF flux across a surface cell. In this study, the interface is reconstructed via a PLIC scheme (Rudman 1997) and the interface unit normal is calculated from the LS function given by

$$\vec{\varvec{n}} = \frac{\nabla \phi }{{\left| {\nabla \phi } \right|}} = \nabla \phi$$
(16)

The LS function would fail to be a distance function after being advanced by Eq. (15), and a reinitialization (Sussman et al. 1994) process is needed for its return to a distance function. This can be achieved by obtaining a steady-state solution of the following reinitialization equation:

$$\frac{\partial \phi }{\partial \tau } = \frac{{\phi_{0} }}{{\sqrt {\phi_{0}^{2} + h^{2} } }}(1 - |\nabla \phi |)$$
(17)

where ϕ 0 is the LS function at the previous time step, τ the artificial time, and h the grid spacing. Finally, in order to achieve mass conservation, the LS functions have to be redistanced (Son and Hur 2002) prior to being used. The curvature, computed directly from the LS function, is given by

$$\kappa = \nabla \cdot \left( {\frac{\nabla \phi }{{\left| {\nabla \phi } \right|}}} \right)$$
(18)

A flow chart for the CLSVOF algorithm is shown in Fig. 3. Details of the numerical formulation can be found in here (Tong and Wang 2007; Wang and Tong 2010).

Fig. 3
figure 3

Flowchart of the CLSVOF scheme: coupling process in the dashed box

Full size image

3.3 Surface tension modeling scheme

The continuum surface force (CSF) method (Brackbill et al. 1992) is used to model the surface tension in which the surface tension force is treated as a body force given by

$$\overrightarrow {{\varvec{F}_{{\mathbf{b}}} }} = \sigma \delta (x)\kappa \vec{\varvec{n}}$$
(19)

where σ is the surface tension coefficient, δ(x) a delta function concentrated on the interface, κ the mean curvature and \(\vec{\varvec{n}}\) the unit vector normal to the free surface. The body force \(\overrightarrow {{\varvec{F}_{{\mathbf{b}}} }}\) is distributed within a transition region near the free surface across which the fluid properties are assumed to change continuously from one grid to another. The discontinuous jump of fluid properties across the free surface is thus eliminated. By incorporating Eqs. (2) and (3), Eq. (19) becomes:

$$\overrightarrow {{\varvec{F}_{{\mathbf{b}}} }} = \sigma \delta (x)\left( {\kappa_{xy} + \frac{{ - \cos \theta_{\text{t}} - cos\theta_{\text{b}} }}{H}} \right)\vec{\varvec{n}}$$
(20)

3.4 Viscous stress exerted by the parallel plates

Considering the fact that the channel height between the parallel plates is very narrow compared with the dimensions of the device in the x–y plane, the electrowetting-induced pressure is expected to be uniform in the z-direction and the velocity component in the z-direction is negligible (Kirby 2010). The microfluidic flow can be approximated as a plane flow in the x–y plane, and the Couette flow model can be used for analyzing the variation of velocities u and v in the z-direction if the flow were fully developed. However, since the dispensing process involves time-varying movement of the fluid and the flow is by no means steady, the viscous stress from the Couette flow model are modified with the incorporation of a multiplication factor λ vs , which are given by

$$\tau_{zx} = \lambda_{vs} *\mu *\frac{u}{H}$$
(21)
$$\tau_{zy} = \lambda_{vs} *\mu *\frac{v}{H}$$
(22)

where μ is the dynamic viscosity, u and v the average velocities in the x- and y-direction, respectively.

3.5 Contact angle hysteresis

As mentioned earlier, contact angle hysteresis has an overall effect of reducing the droplet speed and its physics is still not completely understood. The fact that dynamic contact angles are not only influenced by the plate material (Gupta et al. 2011), but also by other factors such as temperature, ambient pressure, plate surface smoothness, and droplet speed and physical properties makes prediction of dynamic contact angles very challenging. In the current study, the following scheme is used to determine whether the interface is advancing or receding at each time step before the dynamic contact angles are applied,

$$\vec{\varvec{u}} \cdot \varvec{\vec{n} = }\left\{ {\begin{array}{*{20}l} {<}0 \hfill & {{\text{Receding}}\,{\text{interface}}} \hfill \\ { >}0 \hfill & {{\text{Advancing}}\,{\text{interface}}} \hfill \\ \end{array} } \right.$$
(23)

Once the direction is determined, the dynamic contact angles are computed by the following equations as:

$${\text{top}}\,{\text{receding}}\,{\text{angle}}\quad \theta_{{{\text{t}},{\text{R}}}} = \theta_{\text{t}} -\Delta _{\text{R}}$$
(24)
$${\text{bottom}}\,{\text{receding}}\,{\text{angle}}\quad \theta_{{{\text{b}},{\text{R}}}} = \theta_{\text{b}} -\Delta _{\text{R}}$$
(25)
$${\text{top}}\,{\text{advancing}}\,{\text{angle}}\quad \theta_{{{\text{t}},{\text{A}}}} = \theta_{\text{t}} +\Delta _{\text{A}}$$
(26)
$${\text{bottom}}\,{\text{advancing}}\,{\text{angle}}\quad \theta_{{{\text{b}},{\text{A}}}} = \theta_{\text{b}} +\Delta _{\text{A}}$$
(27)

where \(\Delta _{\text{R}}\) and \(\Delta _{\text{A}}\) are the deflections of the receding and advancing contact angles from the static contact angle, respectively. By replacing θ t and θ b in Eq. (20) with the above dynamic contact angles, the hysteresis effect is properly implemented into the current numerical model (Walker and Shapiro 2006). Due to lack of information on contact angle hysteresis in the experiment, \(\Delta _{\text{R}}\) and \(\Delta _{\text{A}}\) are assumed to have the same value. It has been found from the present numerical study that hysteresis has slight effects on both the time scale of dispensing process and the volume of generated droplet. The optimum values which best match the experiments are reported in Table 1.

Table 1 Parameters used in the current study
Full size table

4 Results and discussion

4.1 Numerical simulations

Numerical simulations of micro droplet dispensing in parallel-plate EWOD devices with three different reservoir designs, namely ‘conventional reservoir’ (Fig. 4), ‘stripped reservoir’ (Fig. 5), and ‘TC reservoir’ (Fig. 6) designs have been performed alongside an experimental study (Yaddessalage 2013). The EWOD devices for the experiments were fabricated in the Cleanroom Research Laboratory at the University of Texas at Arlington. The applied voltage is 150 V AC for all three designs and the generation frequencies are set as 4.425 Hz, 4.386 Hz, and 2.762 Hz for the conventional, stripped, and TC reservoirs, respectively. More details of the experiments can be obtained from elsewhere (Wijethunga et al. 2011; Yaddessalage 2013) and will be provided in a forthcoming paper focusing on the experimental work. For each design, fifty droplets are consecutively dispensed from the reservoir. The ‘conventional reservoir’ design has been used in many microfluidic droplet dispensing experiments in which the reservoir site consists of one single electrode of rectangular or square shape (Berthier et al. 2006; Gong and Kim 2008; Jang et al. 2007; Wang et al. 2011). The electrical voltage is applied throughout the reservoir whenever the reservoir electrode is activated. Two electrodes with square shape and much smaller sizes are located on one side of the reservoir, which serve as droplet generating and cutting sites. Each of these three electrodes can be switched ‘ON’ and ‘OFF’ independently. The ‘stripped reservoir’ design is similar to the ‘conventional reservoir’ design except that the reservoir electrode is divided into ten strips of equal size. Each of these ten strips can be switched ‘ON’ and ‘OFF’ independently as needed. The ‘TC reservoir’ design consists of a T-shape electrode as the cutting site and several C-shape electrodes as the reservoir. Note that the number of C-shape electrodes is determined by the initial volume of reservoir drop. Each electrode can also be switched ‘ON’ and ‘OFF’ independently to move the droplet toward the cutting and generating sites step by step and complete the dispensing process. For the ‘TC reservoir’ design, a much shorter cutting length can be achieved with a much narrower range of pinch-off locations.

Fig. 4
figure 4

‘Conventional reservoir’ design: the schematic (a); four steps of the dispensing process: filling stage (b); cutting stage (c); relocating stage (d, e)

Full size image
Fig. 5
figure 5

‘Stripped reservoir’ design: the schematic (a); five steps of the dispensing process: filling stage (b, c); cutting stage (d); relocating stage (e, f)

Full size image
Fig. 6
figure 6

‘TC reservoir’ design: the schematic (a); five steps of the dispensing process: filling stage (b–d); cutting stage (e); relocating stage (f)

Full size image

Deionized (DI) water is used as the working liquid for the current study with relevant data given in Table 1. The channel height between the two parallel plates is 0.1 mm and the size of the generating electrode is 2 × 2 mm2 for all three designs. Note that a typical dispensing process consists of three essential stages: (1) filling stage: liquid in the reservoir flows into the generating and cutting electrodes until the two electrodes are filled up; (2) cutting stage: the gas–liquid interface shrinks toward the center of the cutting electrode until the neck pinches off with a small droplet created on the generating electrode. (3) Relocating stage: the droplet produced on the generating electrode is relocated by the EWOD device for further actions. Note that the cutting and relocating stages can also be regarded as droplet splitting and transport processes, respectively. Since it is rather difficult to ascertain that the filling stage has reached the steady state by simply observing the motion of liquid interface, the duration for the filling stage is set to 1000 ms in the numerical simulations in order to minimize the interference on the dispensing process due to insufficient filling time.

The computational domain used for the dispensing process in the ‘conventional reservoir’ design is shown in Fig. 7. In order to conserve computational resources, symmetry is assumed and only half of the drop is modeled with computations performed on a domain of dimensions 30 × 12 mm2. Uniform square mesh with grid spacing of 0.2 mm is used based on the results of a grid convergence study which is reported in the ‘Appendix.’ Similar computational domains are used for the ‘stripped reservoir’ and ‘TC reservoir’ designs as well. Free-slip boundary conditions are implemented at all sides of the domain except for the left side where a continuative outflow boundary condition is used for droplet relocation. It should be noted that since the liquid is, by design, not expected to reach the top and right sides of the computational domain, the nature of the boundary condition is of no consequence. The bottom side is a symmetric axis where the free-slip boundary condition is also applied. The time step for the numerical computations is automatically adjusted during the course of calculations, which is taken as the minimum of the time step constraints for numerical stability of capillarity, viscosity and the courant condition (Brackbill et al. 1992; Harlow and Amsden 1971; Kothe et al. 1991). Due to lack of static contact angle values in the experimental results, 117° and 90° are used for \(\theta_{{{\text{b}},{\text{OFF}}}}\) and \(\theta_{{{\text{b}},{\text{ON}}}}\), respectively, following a previous numerical electrowetting-based micro droplet splitting study (Guan and Tong 2015a).

Fig. 7
figure 7

Computational domain for the ‘conventional reservoir’ design

Full size image

For the dispensing process in the ‘conventional reservoir’ design, a large drop of irregular shape is initially placed in the reservoir with the liquid boundary marginally touching the cutting electrode in the experiment (Fig. 4a). Droplets are then dispensed consecutively from the reservoir by running the cycles of filling, cutting, and relocating stages repeatedly (Fig. 4b–e) until all fifty droplets have been generated. It should be mentioned that this irregular shape is difficult to prescribe as the initial condition in the numerical simulation. Instead, a drop of circular shape is used with the size comparable to the experiment. It is believed that the effect of initial condition on the dispensing process is negligible.

The numerical and experimental results of a typical dispensing process for the ‘conventional reservoir’ design are shown in Fig. 8. As given by Eq. (4), a pressure difference is created across the liquid boundary when the cutting and generating electrodes are switched ‘ON’ with the reservoir electrode switched ‘OFF’ simultaneously. Liquid in the reservoir then flows into the two activated electrodes until they are filled up (a, b). When the cutting electrode is switched ‘OFF’ as the reservoir electrode is turned back ‘ON’ simultaneously, the menisci at the exterior corners of the cutting electrode shrink toward the center with a small neck developed due to the pressure gradient within the liquid (c). As more liquid in the neck flows back to the reservoir, the neck finally pinches off with a small droplet produced on the generating electrode (d).

Fig. 8
figure 8

Dispensing process for the ‘conventional reservoir’ design: numerical (top present study): filling stage (a–b); cutting stage (c–d); experimental (middle and bottom)

Full size image

As shown in Fig. 8, liquid interface on the generating and cutting electrodes appears to have excellent agreement between the numerical and experimental results. However, there are two noticeable distinctions in the dispensing process. First, the liquid in the reservoir has a rounded shape in the experiment while the shape is non-circular in the numerical simulation. It has been found that this non-circular shape is inherent in the numerical device and is already formed at the end of the filling stage of the first droplet. Since the generating and cutting electrodes have much smaller sizes compared with the reservoir where a large drop of circular shape is situated as the initial condition, as soon as the filling stage takes place, the pressure contours within the drop rapidly develop into a radial distribution as shown in Fig. 9. It is of great significance to mention that the difference between curvatures \(\kappa_{{z,{\text{OFF}}}}\) and \(\kappa_{{z,{\text{ON}}}}\) not only creates an internal pressure gradient which drives the liquid from the ‘OFF’ to the ‘ON’ regions, but also results in a pressure jump at the points where the liquid interface cuts the border of the ‘ON’ and ‘OFF’ electrodes. This pressure jump leads to the formation of some localized areas where a much larger pressure gradient is induced than the rest areas, which directly determines the direction and speed of the fluid flow as well as the deformation of the liquid in the reservoir. This interesting phenomenon involved in electrowetting-based microfluidic droplet motions can also be found in other droplet operations including splitting, merging, and transport (Guan and Tong 2015a, b). As indicated by the pressure gradient, liquid close to the cutting electrode has a larger moving speed toward the activated areas while the speed is much smaller elsewhere. As a consequence, the interface in the localized areas shrinks toward the reservoir center during the filling stage and deforms from a smooth curve into a flat line. Simultaneously, the liquid at the drop trailing edge flows toward the top area as demonstrated by the pressure and flow fields, which results in the flat interface at the northeast corner of the reservoir drop. It has been found that the radial distribution of pressure contours sustains the entire filling stage which eventually results in the non-circular shape of the liquid in the reservoir.

Fig. 9
figure 9

Pressure and velocity fields at the beginning of the filling stage of the first droplet for the ‘conventional reservoir’ design (Note that the velocity fields for the two magnified areas are not plotted in the same scale. The flow has a much larger speed near the cutting electrode as indicated by the pressure fields.)

Full size image

The second distinction is the additional volume accumulated at the exterior corners of the cutting electrode at the end of the filling stage in the numerical simulation (Fig. 8b), which is absent in the experiment. This distinction appears to be a combined result of plate surface smoothness and contact angle hysteresis effect. It is known that surface smoothness and hysteresis angle are non-uniform and dependent on the time and location in the experiment, which affects liquid shape and can be illustrated by the unsmooth droplet contour shown in Fig. 8. In the numerical simulation, on the other hand, surface smoothness is uniform and the hysteresis angle is constant and equal for \(\Delta _{\text{R}}\) and \(\Delta _{\text{A}}\). After the generating and cutting electrodes are filled up, the effect of \(\Delta \kappa_{z}\) is greatly reduced while κ xy takes over the filling stage instead. Due to the concave shape of liquid interface at the exterior corners of the cutting electrode where the magnitude of κ xy is smaller than the rest areas, the liquid accumulates there to flatten the concave interface and compensate the imbalanced pressure force within the liquid.

The five steps of droplet dispensing for the ‘stripped reservoir’ design are given in Fig. 5b–f, and the numerical and experimental results are shown in Fig. 10. Similar to the ‘conventional reservoir’ design, a drop of irregular shape is placed in the reservoir initially. Prior to the start of filling stage for the first droplet, a few stripped electrodes on the cutting electrode side are activated, which enables liquid to fill the left side of reservoir (Fig. 5a). This special arrangement is a crucial step for the ‘stripped reservoir’ design which needs to be performed before every filling stage (Fig. 5b). After the liquid fills the first few stripped electrodes (Fig. 10a), the filling stage is initiated by activating the generating, cutting, and first stripped electrode while keeping the rest electrodes deactivated. As a result, a long liquid–gas interface is created at the left reservoir boundary which sustains the entire filling stage (Fig. 10b). After the generating and cutting electrodes are filled with liquid, the cutting electrode is then turned ‘OFF’ and the entire ten stripped electrodes are turned ‘ON’ simultaneously. The liquid on the cutting electrode then flows back to the reservoir with a neck of the same shape as in the ‘conventional reservoir’ design formed (Fig. 10c). The neck finally pinches off with a small droplet produced on the generating electrode (Fig. 10d). Good agreement has been achieved between the numerical and experimental results except for the liquid accumulated at the exterior corners of the cutting electrode for the same reason explained previously.

Fig. 10
figure 10

Dispensing process for the ‘stripped reservoir’ design: numerical (top present study): filling stage (a, b); cutting stage (c, d); experimental (middle and bottom)

Full size image

The five steps of droplet dispensing for the ‘TC reservoir’ design are given in Fig. 6b–f and the numerical and experimental results are shown in Fig. 11. Excellent agreement has been achieved between the numerical and experimental results except for the liquid shape in the reservoir, which results from the same reason explained for the ‘conventional reservoir’ design.

Fig. 11
figure 11

Dispensing process for the ‘TC reservoir’ design: numerical (top present study): filling stage (a); cutting stage (b–d); experimental (middle and bottom)

Full size image

Certain key non-dimensional groups have been evaluated with the values listed in Table 1. U R is the reference velocity which makes the maximum non-dimensional velocity close to unity. The dimensionless parameters are defined as: Ca = μU R/σ, Re = ρU R H/μ, We = ρU 2R H/σ, and \(Oh = \mu /\sqrt {\rho \sigma H}\). It is understood that certain aspects of microfluidic droplet motion induced by the electrowetting effect can be characterized by these non-dimensional numbers. There are three adjustable parameters in the numerical model: \(\Delta _{\text{R}}\), \(\Delta _{\text{A}}\), and λ vs . It has been observed that varying λ vs only changes the time scale of dispensing process with negligible effects on liquid shape. Optimum λ vs is subsequently determined by matching the time scale of numerical simulations with the corresponding experiments.

4.2 Droplet volume inconsistency

Volume inconsistency of generated droplets has been examined for all three designs. In the numerical study, droplet size was measured by a MATLAB program which calculates the total area of numerical cells within the interface. For the experiment, the volume was computed from the droplet footprint area on the generating electrode, which was determined by a MATLAB image processing code. As shown in Fig. 12, the ‘conventional reservoir’ design offers decent volume consistency with volume inconsistencies of 0.744 and 0.740 % for the experimental and numerical results, respectively. However, all volumes are in the range of 0.52–0.55 mm3, which are at least 30 % larger than the volume occupied by the generating electrode (0.4 mm3). This additional volume primarily comes from the neck formed in the cutting stage.

Fig. 12
figure 12

Volumes of droplet generated from the ‘conventional reservoir’ design

Full size image

Different from the findings in some literature that the pinch-off location was responsible for the volume variation (Cho et al. 2003; Wang et al. 2011; Yaddessalage 2013), it has been found from the current numerical results that the pinch-off locations are fairly stable among droplets (Fig. 13a). Instead, the section of liquid interface which cuts the left reservoir boundary at the end of the filling stage varies and appears to play a significant role in volume variation (Fig. 13b). As the droplet being dispensed, the liquid in the reservoir is accumulated at the left side since the pressure gradient close to the cutting electrode is much larger than the rest areas in the cutting stage (Fig. 14). As a result, the intercept of the liquid interface at the left reservoir boundary at the end of filling stage is found to move up for the first thirty-five droplets as the slope of the interface increases progressively. The intercept then moves down for the last fifteen droplets due to the liquid in the reservoir getting depleted (Fig. 13b). The variation of the intercept locations alters the pressure fields on the cutting electrode at the beginning of the cutting stage among droplets. Given the pressure fields on the generating electrode is relatively stable in the cutting stage, the pressure gradient on the cutting electrode is actually in charge of the deformation of the neck and eventually determines the amount of liquid adding to the generated droplet after the pinch-off. Therefore, the pressure fields on the cutting electrode at the beginning of the cutting stage are extremely crucial for the volume of generated droplet.

Fig. 13
figure 13

Pinch-off locations (a) and intercepts (b) versus droplet volumes for the ‘conventional reservoir’ design

Full size image
Fig. 14
figure 14

Pressure field at the beginning of the cutting stage of the first droplet for the ‘conventional reservoir’ design

Full size image

To substantiate this point, the numerical results of a larger (11th) and a smaller droplet volume (31st) are shown in Fig. 15. It is found that the intercepts are located at different places at the end of the filling stage due to the different slopes of interface section as discussed earlier. As soon as the cutting stage takes place, a larger pressure gradient is created on the cutting electrode for the eleventh droplet since the intercept is closer to the cutting electrode and squeezes the pressure contours (b, c). The larger pressure gradient for the eleventh droplet results in a slightly different neck right before the pinch-off (g) and eventually produces a droplet with a slightly larger volume than the thirty-first droplet (h). In summary, when the intercept location at the end of the filing stage is closer to the cutting electrode, a larger pressure gradient will be formed on the cutting electrode at the beginning of the cutting stage, which leads to the generation of a droplet with slightly larger volume and vice versa. Note that the intercept location is not the sole factor controlling droplet volume which can also be affected by some other elements such as pinch-off location and liquid volume remaining in the reservoir. The variation of droplet volume does not necessarily have an exactly inverse relationship with intercept location as shown in Fig. 13b.

Fig. 15
figure 15

Numerical results of the eleventh and thirty-first droplet for the ‘conventional reservoir’ design: liquid shape at the end of the filling stage: eleventh droplet (a); thirty-first droplet (d); liquid shape at the beginning of the cutting stage: eleventh droplet (b); thirty-first droplet (e); pressure fields at the beginning of the cutting stage: eleventh droplet (c); thirty-first droplet (f); liquid contour right before the pinch-off (g); droplet contour right after the pinch-off (h)

Full size image

As for the ‘stripped reservoir’ design, the volume inconsistency is 0.437 % for the experiment versus 0.426 % for the numerical results (Fig. 16). The improvement of volume inconsistency is mainly contributed from the long liquid–gas interface at the left reservoir boundary sustaining the entire filling and cutting stages. This liquid–gas interface eliminates the intercept in the ‘conventional reservoir’ design and stabilizes the curvatures at the exterior corners of the cutting electrode at the end of the filling stage. Consequently, the pressure fields on the cutting electrode at the beginning of the cutting stage become steady among droplets which greatly reduce volume inconsistency. The numerical results of the eleventh and thirty-first droplets are shown in Fig. 17. It has been found that the pressure fields on the cutting electrode at the beginning of the cutting stage are very similar (c, f), which results in overlapping liquid contours before the pinch-off (g) and eventually similar droplet volumes (h).

Fig. 16
figure 16

Volumes of droplet generated from the ‘stripped reservoir’ design

Full size image
Fig. 17
figure 17

Numerical results of the eleventh and thirty-first droplet for the ‘stripped reservoir’ design: liquid shape at the end of the filling stage: eleventh droplet (a); thirty-first droplet (d); liquid shape at the beginning of the cutting stage: eleventh droplet (b); thirty-first droplet (e); pressure fields at the beginning of the cutting stage: eleventh droplet (c); thirty-first droplet (f); liquid contour right before the pinch-off (g); droplet contour right after the pinch-off (h)

Full size image

A very interesting phenomenon found in both the experimental and numerical results is that the volumes demonstrate a noticeable increase in the last few droplets (Fig. 16). It has been discovered that the liquid in the reservoir is almost depleted for the last few droplets and the liquid–gas interface becomes very close to the left reservoir boundary, which squeezes the pressure contours on the cutting electrode. Consequently, the pressure gradient becomes slightly greater for the last few droplets and eventually leads to the increase in droplet volumes for the same mechanism given for the ‘conventional reservoir’ design.

To substantiate this point, another dispensing case has been numerically performed for the ‘stripped reservoir’ design in which the initial liquid volume is increased by 12 %. As shown in Fig. 16, the new case has a smaller inconsistency of 0.326 % without the noticeable increase in the last few droplets. It has been found that the pressure gradients on the cutting electrode display very similar patterns for the last few droplets, which suggests that the liquid in the reservoir has negligible effect on the droplet volume as long as the reservoir is sufficiently filled.

As shown in Fig. 18, the volume inconsistencies for the ‘TC reservoir’ design are 0.333 and 0.331 % for the experimental and numerical results, respectively. The pressure fields on the cutting electrode, shown in Fig. 19, are very similar for the eleventh and thirty-first droplet (c, f), which results in their similar volumes. It has been discovered that the reservoir is also almost depleted for the last few droplets, but the pressure fields still display almost the same patterns, which suggests that the volume is hardly affected by the liquid in the reservoir. Another notable difference between the ‘TC reservoir’ and the other two designs is that all volumes are within the range of 0.40–0.42 mm3, less than 5 % over the volume occupied by the generating electrode (0.4 mm3), which is primarily contributed from the reduced sizes of the cutting length and liquid neck formed in the cutting stage. The results appear to fully demonstrate the advantages of ‘TC reservoir’ design over the other two designs, which are especially favorable for the biomedical applications in which both volume consistency and accuracy are of paramount importance.

Fig. 18
figure 18

Volumes of droplet generated from the ‘TC reservoir’ design

Full size image
Fig. 19
figure 19

Numerical results of the eleventh and thirty-first droplet for the ‘TC reservoir’ design: liquid shape at the end of the filling stage: eleventh droplet (a); thirty-first droplet (d); liquid shape at the beginning of the cutting stage: eleventh droplet (b); thirty-first droplet (e); pressure fields at the beginning of the cutting stage: eleventh droplet (c); thirty-first droplet (f) liquid contour right before the pinch-off (g); droplet contour right after the pinch-off (h)

Full size image

5 Conclusion

The dynamics of micro water droplet dispensing in parallel-plate EWOD devices with three different reservoir designs have been investigated numerically. The transient governing equations for the microfluidic flow are solved by a finite-volume scheme with a two-step projection method on a fixed computational domain. The interface between liquid and gas is tracked by a CLSVOF method. A CSF model is employed to model the surface tension at the interface. Contact angle hysteresis, which is a crucial element in EWOD modeling, has been implemented together with a simplified model for the viscous stresses exerted by the two plates. The numerical results obtained from the current study are in good agreement with the corresponding experiments. The physics involved in the droplet dispensing process has been studied and the volume inconsistency of generated droplets has been examined for all three designs. It has been discovered that the pressure distribution on the cutting electrode at the beginning of the cutting stage is of considerable significance for the inconsistency of droplet volumes, which can be improved by stabilizing the intercept of liquid interface at the reservoir boundary at the end of the filling stage. Smaller volume inconsistency can also be achieved by shortening the liquid cutting length, which reduces the size of the neck as well as the volume added to the generated droplet after the pinch-off. It has been found that the ‘stripped reservoir’ design has smaller volume inconsistency than the ‘conventional reservoir’ design due to the elimination of the intercept at the reservoir boundary. However, the ‘stripped reservoir’ design becomes unreliable when the liquid in the reservoir is near depletion. The ‘TC reservoir’ design is the best among the three designs since the volume displays excellent consistency and is close to the size of the generating electrode due to a much shorter neck formed in the cutting stage.