1 Introduction

Electrokinetic phenomena arise from the interaction of an external force with an electrical double layer (EDL), which is formed when an electrically charged surface is in contact with a liquid containing mobile charges such as ions. The ions of opposite charge to that of the surface (counterions) are attracted toward the surface, while ions of equal charge (co-ions) are repelled. The EDL is defined as the domain in which, due to the excess of counterions over co-ions, the electrical neutrality of the liquid is violated. Different electrokinetic phenomena can arise depending on the interaction of the external force and the EDL. When we apply a tangential electric field to the EDL, the counterions migrate and drag the surrounding solvent molecules by viscous interactions. This establishes a (bulk) flow which is termed electroosmosis, electrokinetic flow or electroosmotic flow (EOF). Comprehensive review on EDLs and various electrokinetic phenomena is available in the literature as, e.g., in Refs. Delgado et al. (2007) and Hunter (1981).

Typically, electroosmotic (net) flow is only observed in pores/channels with openings of less than around 1 mm since the flow generating force occurs in the nano-scopic EDL and the much larger volume of the bulk liquid is only dragged. In other words, EOF is a microscale phenomenon and only observed when the surface-to-liquid volume ratio is sufficiently large. Consequently, we can expect that EOF is especially prominent if it takes place in porous substrates. Indeed, electroosmosis was initially observed in clay structures by Reuss (1809) more than 200 years ago.

In the recent years, research on EOF has experienced a renaissance since it can be employed in microfluidic systems. Typical applications include the (single channel) transport of samples for analytical purposes (Barz and Ehrhard 2005; Dong and Young-Ho 2007; Waters et al. 1998), flow focussing (Jacobson and Ramsey 1997) or to generate secondary flow patterns to improve mixing (Barz et al. 2011; Bockelmann et al. 2012; Chang and Yang 2007). Microfluidic pumps, which are based on EOF, offer several advantages such as the absence of mechanical parts, pulse-free flows and that the flow rate and direction are conveniently controlled by the electrical field. Additionally, these electroosmotic pumps (EOPs) can be fabricated using standard microfabrication technologies, and thus, they can be readily incorporated on microdevices. In this regard, chip-integrated micropumps can simply consist of single (Hu and Chao 2007) or arrays of open channels (Glawdel et al. 2009; Lazar and Karger 2002; Pu and Liu 2004). Other electroosmotic pumps utilize bas-relief structures on the channel floors (Jahanshahi et al. 2012) or integrate gas separators to remove electrolysis products (Heuck and Staufer 2011). However, the more favorable design incorporates porous structures with large surface-to-volume ratios to generate high flow rates along with high pump pressures. Such incorporated (on-chip) porous structures usually comprise packed beds of micron-sized spherical particles (Borowsky et al. 2008a, b). Review on EOPs for microfluidic applications is available from Ref. Wang et al. (2009).

The application of EOF is also beneficial for several chromatography techniques where pressure losses in the separation columns can be up to 600 bar, which has demanding requirements for the design and the materials of mechanical pumps. There are some fundamental differences where the EOF is produced though, depending on the type of chromatography technique. Capillary electrochromatography, the EOP also acts as a separation column; review on capillary electrochromatography is available in Refs. Cikalo et al. (1998) and Simal-Gándara (2004). For other methods, such as high-performance liquid chromatography, the flow through the separation column is generated with an external EOP. Hence, a multitude of different external EOP concepts can be found in the literature. Generally, the active porous materials of external EOPs can be classified into two different structures. On the one hand, the EOP is designed as a (consolidated) packed bed which has been realized using silica particles (Kang et al. 2007; Reichmuth et al. 2003; Shin et al. 2011; Zeng et al. 2001, 2002) or sintered borosilicate particles (Barz et al. 2009; Kim et al. 2008; Yao et al. 2003). Additionally, there are further fabrication methods which produce packed bed-like structures including monoliths made from silica (Wang et al. 2006) or from monomers (Gu et al. 2012; Tripp et al. 2004), as well as membranes from mixed cellulose ester and nylon (Kwon et al. 2012). On the other hand, there are pumping substrates which can be considered a large array of more or less identical capillary pores. These structures have been realized by membranes made from anodic aluminum oxide (Ai et al. 2010; Leese and Mattia 2014), glass (Cao et al. 2012) and from (track-etch) polymeric materials such as polycarbonate and polyethylene terephthalate (Wang et al. 2012). Both kind of structures, the capillary- and the packed bed-type, create large surface-to-volume ratios. However, there are some fundamental differences. According to Niven (2002), packed beds feature a much more complex network of interconnected pore conduits, consisting of both tetrahedral and octahedral pockets between solid particles, joined by narrower pore necks. The pore conduits themselves are of a complex cross-sectional form, including three-pointed stars, four-pointed stars and a variety of shapes in between (Niven 2002).

In order to describe the nature of flows through porous structures, two main approaches are widely used. On the one hand, it is possible to engage a deterministic approach to model the flow on a microscopic level based on the governing equations of mass and momentum continuity. Deterministic models give a detailed insight within the flow, but their application still suffers from some considerable disadvantages. The detailed geometry of the porous substrate is usually not known, and the costly numerical simulation is limited to rather small domains. Hence, we do not consider deterministic approaches in this work since they cannot easily be used for engineering and design purposes.

On the other hand, phenomenological models based on averaged (macroscopic) parameters are a useful semiempirical approach to obtain design guidelines for technical systems. This approach does not intend to resolve the flow field in detail but to correlate macroscopic parameters such as flow rate and pressure drop to the properties of the porous substrate. Some experiments are required, but the resulting correlations are usually simple mathematical expressions; well known examples are Darcy’s Law, (Carman) Blake–Kozeny and the Ergun equation (see any text, e.g., Bird et al. 2007). The phenomenological models for EOF in porous materials that can be found in the literature assume capillary-type structures. Mazur and Overbeek (1951) modeled a porous diaphragm as an idealized arrangement of a large number of parallel and identical capillary pores. The same idealization has been adapted by Vallano and Remco (2000) to packed beds of macro-porous particles and by Yao and Santiago (2003) to porous glass frits. A generalized volume-averaged model for pressure-driven and electroosmotic flows based on the assumption of an array of tortuous capillaries was proposed by Scales and Tait (2006). The model is based upon a scaling of the Navier–Stokes equations extended by Coulomb and Forchheimer forces. Analytical solutions which are derived for several (simple) cases result in extensive expressions. While such capillary-type models may be appropriate for cellular materials, such as consolidated foams and membranes, they have limited relevance for packed beds of granular materials. That is, the models do not capture the inter-pore connectivity and geometrical characteristics such as strongly varying cross sections with concave rather than convex boundaries.

Consequently, the motivation for this work is the lack of a simple but sufficiently accurate model for EOF in packed beds of granular materials. Hence, we continue this article with a theory section where we examine the underlying physics based on dimensional reasoning. Then, the experimental methodology and materials used for this work are discussed. Subsequently, we proceed with the presentation of the results of defined experiments which are employed to derive a phenomenological correlation of comparable simplicity to Blake–Kozeny law. Finally, the article is summarized with some concluding remarks.

2 Theory

In this section, EOF through packed beds of granular material is analyzed based on dimensional reasoning. Additionally, we derive a dynamic model for the center-of-mass motion of the fluidic parts of the experimental setup. This model is used to reveal the influence of different phenomena such as Joule heating in our experiment.

2.1 Dimensional analysis of electroosmotic flow through packed beds

In our previous work (Barz and Steen 2013), we developed a model for the EOF in a porous frit based on dimensional reasoning. Here we use in principle the same methodology, but deviate in some important aspects which results in an improved averaging of the microscale to obtain a more accurate macroscale behavior.

Generally, Smoluchowski observed that the electroosmotic velocity \({v}_\mathrm{{eof}}\) through a single pore scales linearly with the electric field \(E\) which exerts a Coulomb force in the EDL, the zeta potential \(\zeta\) of the substrate in contact with the liquid, and the liquid’s dynamic viscosity \(\mu\) and permittivity \(\varepsilon\) (Smoluchowski 1903); it is

$${v}_\mathrm{{eof}} \propto \frac{-\varepsilon \zeta }{\mu }E.$$
(1)

It can be assumed that the superficial EO velocity \(\bar{v}_\mathrm{eof}\) through a packed bed scales similarly and can be correlated with the relevant independent quantities: zeta potential of the bed particles, permittivity and viscosity of the liquid, Debye length, electric field, effective hydraulic diameter and the wetted surface area (per bed length) according to

$$\bar{v}_\mathrm{{eof}} = f( \zeta ,\varepsilon , \mu , l_\mathrm{D}, E, d_\mathrm{h}, S_\mathrm{L}),$$
(2)

where \(f\) is a functional relationship to be derived by the rules of dimensional analysis. The physicochemical liquid parameters of viscosity and permittivity along with the electric field do not require any further explanation. Other relevant quantities can have multiple definitions, and we discuss our assumptions in the following:

The zeta potential \(\zeta\) is an indirect measure of the electrical charge of a surface in contact with a liquid. It is defined as the electrical potential at the shear plane, which is a sub-layer of the EDL. The zeta potential depends on various factors such as the kind of substrate, the ion species and concentration as well as the pH value of the liquid (Kirby and Hasselbrink 2004). Usually, the magnitude of the zeta potential is high for low ion content in the liquid, but there is no general theory which allows for its prediction. Nevertheless, since the zeta potential is an important parameter for many disciplines, various empirical correlations for different substrates can be found in the literature as, e.g., in Refs. Barz et al. (2009), Falahati et al. (2014) and Kirby and Hasselbrink (2004). In this work, we perform streaming current experiments to obtain an empirical correlation for the zeta potential of borosilicate as a function of the pH value and the ionic strength of an aqueous NaCl electrolyte. The ionic strength \(I\) captures the influence of the overall ion content. It can be calculated from \(I = \frac{1}{2}\sum _{i} \bar{z}_i^2 c_i\) where \(\bar{z}_i\) and \(c_i\) are the valency and the concentration of the ion species \(i\), respectively.

The Debye length \(l_\mathrm{D}\) is the physicochemical property which approximately describes the thickness of the EDL. That is, it gives an estimation of how far the electrostatic effect of the surface charges ranges into the liquid. Interestingly, the Debye length depends only on the liquid parameters and is independent of the surface properties; it is

$$l_D = \sqrt{\frac{\varepsilon R_\mathrm{g} T_{0}}{2IF^2}},$$
(3)

where \(R_\mathrm{g}\) is the universal gas constant, \(T_{0}\) is the absolute temperature and \(F\) is the Faraday constant. In terms of electroosmosis, the Debye length indicates the thickness of the volume where the Coulomb force induces electroosmosis. Additionally, for cases where the Debye length is on the same order as the pore diameter, the pore-scale electroosmotic velocity (cf. Eq. 1) is a complex function of the ratio of Debye length to pore diameter.

The effective hydraulic diameter \(d_\mathrm{h}\) can be interpreted in terms of EOF as a measure for the liquid volume which is pumped due to the EDL flow; further discussion is made in conjunction with the specific surface area of the packed bed below. In terms of pressure-driven flows, an ensemble of various non-circular pores can be replaced by an array of uniform circular pores, with a certain effective hydraulic diameter, which features the same pressure loss for a given flow rate. The use of the hydraulic diameter concept for laminar flows can introduce significant errors since the concept stems from turbulent flows, where the pressure loss depends primarily on the shear in the (wall) boundary layer and thus scales with the wall surface area. For laminar flows, friction also occurs within the bulk fluid and the concept of hydraulic diameter is not recommended (Bird et al. 2007; Niven 2002). However, since the EOF is generated in a wall boundary layer as well, i.e., the EDL, the concept of hydraulic diameter appears adequate for our purposes. The hydraulic diameter is defined for straight pores as four times the ratio of the cross-sectional area to the wetted perimeter \(d_\mathrm{h} = 4A_\mathrm{c}/P_\mathrm{c}\) (see any text, e.g., Bird et al. 2007). In terms of packed beds of granular materials, there is another problem related to this definition since the varying cross sections result in a variable hydraulic diameter along the flow direction. A more appropriate hydraulic diameter, or characteristic dimension of the porous medium, is the ratio of four times the volume of voids to their surface area (Bird et al. 2007). We choose the modified definition of Mehta and Hawley (1969) which accounts for the influence of the (outer) packed bed wall on the flow by introducing an additional \(M\) factor. This approach appears suitable in our work since the packed bed wall can contribute to electroosmosis as well, and the \(M\) factor allows for an assessment of the influence. Hence, the hydraulic diameter in the current work is given as

$$d_\mathrm{h}=\frac{2}{3}\frac{\psi }{(1-\psi )}\frac{d_\mathrm{p}}{M}\quad \text {where}\quad M=1+\frac{2d_\mathrm{p}}{3d_\mathrm{pb}(1-\psi )}.$$
(4)

Here, \(\psi\) is the porosity of the packed bed, \(d_\mathrm{p}\) is the effective particle diameter, and \(d_\mathrm{pb}\) denotes the diameter of the packed bed. If there is no influence of the packed bed wall, the \(M\) factor goes toward one and the hydraulic diameter is computed in the standard way. The \(M\) factor contains the ratio \(d_\mathrm{p}/d_\mathrm{pb}\) which is also an important criterion for the packing structure. A homogeneous packing structure is only achieved for \(d_\mathrm{p}/d_\mathrm{pb} <0.1\) (Dias et al. 2004); i.e., the \(M\) factor has to be smaller than \(M\lessapprox 1.1\). Note that the effective particle diameter is a function of particle size and its distribution. We use binary mixtures of borosilicate microspheres to prepare packed beds of different porosities. The effective particle diameter of a mixture of particles, with a number fraction \(x_i\) and mean diameter \(d_i\) for the particle species \(i\), can be calculated according to \(d_\mathrm{p} =\sqrt{\sum _{i} x_id_{i}^2} \quad where \sum _{i} x_i = 1\).

The wetted surface area \(S_L\) is another important packed bed parameter since it determines (along with \(l_\mathrm{D}\)) the volume where the EOF is induced. Here, several considerations from the knowledge of EOF in a single pore should be considered. For increasing size of channel cross sections, the surface-to-volume ratio decreases and all boundary effects become less important. That is, the EOF in the tiny EDL is not sufficient to drag the liquid bulk by viscous forces if the hydraulic diameter of the pore is too large. Typically, EOF is only observed in pores with diameters of less than several hundred micrometers. Consequently, the EOF only scales with the pore cross-sectional area up to a certain degree. To increase the electroosmotic flow rate effectively, rather more pores than larger pores are needed. Additionally, the length of a (homogenous) pore does not contribute to the flow rate but rather to the pressure which can be generated. Hence, to account for the active area where electroosmosis is generated, we consider the wetted surface area of the packed bed normalized with bed length as the relevant quantity. We use the specific surface area \(S_v\) per unit volume of a packed bed, made from a spherical particle mixture and according to the coordination number theory (cf. Ouchiyama and Tanaka 1981), to arrive at

$$S_L = \frac{\pi d_\mathrm{pb}^2 }{4}S_v= \pi r_\mathrm{pb}^2 \frac{6\sum _{i=1}^{n} x_i d_{i}^2}{\sum _{i=1}^{n} x_i d_{i}^3}.$$
(5)

We proceed with our dimensional analysis by applying the Buckingham \(\Pi\) theorem (cf. Buckingham 1914). The number of relevant physical quantities in Eq. (2) corresponds to \(n=7\), while the physical dimensions—mass, time, length and charge—correspond to \(m=4\). The Buckingham \(\Pi\) theorem gives \(k=(n+1)-m = 4\) preliminary dimensionless groups \(\Pi _k\) to develop a functional correlation between the physical quantities. We rearrange the preliminary dimensionless groups and choose

$$Sm \equiv \Pi _1 = \frac{\bar{v}_\mathrm{{eof}}}{\frac{\zeta \varepsilon }{\mu }E}, \quad \textit{RW} \equiv \frac{\Pi _3}{\Pi _4}=\frac{l_D}{d_h}, \quad \textit{PB} \equiv \frac{\Pi _2}{\Pi _4}=\frac{S_L}{d_h}$$
(6)

to obtain three dimensionless groups which comprise the physicochemical characteristics of the liquid as well as microscopic and macroscopic packed bed parameters. In detail, the first dimensionless group is the ratio of superficial packed bed to pore-scale electroosmotic velocity. This group incorporates the physicochemical characteristics of liquid and substrate and follows the general Smoluchowski observation Eq. (1). Hence, we dedicate this dimensionless group to Marian von Smoluchowski and name it the electroosmotic Smoluchowski number \(Sm\). The second group reflects the microscopic structure by the ratio of Debye length to the hydraulic diameter. It allows for two kinds of interpretations, a viscous and an electrical one. On the one hand, it indicates the ratio of the length scales of the liquid domains which are “active” and “passive.” That is, the EDL where electroosmosis is induced and the liquid bulk which is dragged by viscous interactions. For small ratios, a plug flow profile can be assumed in the pore. However, if the ratio is too small, the EDL flow is not sufficient to drag the bulk liquid. On the other hand, there is an electrical interpretation. For \(l_\mathrm{D}/d_\mathrm{h} \gtrsim 0.1\), the overlap of the EDL results in a diminished electroosmotic pore-scale flow. The first paper on this effect in cylindrical capillaries was published by Rice and Whitehead (1965). Thus, we name this dimensionless group the Rice–Whitehead number \(RW\). Finally, the third number correlates macroscopic and microscopic packed bed parameters and can be best explained by a simple example considering a capillary-type structure. For a constant specific wetted surface area, the electroosmotic flow increases with a decreasing hydraulic diameter since this corresponds to a larger number of pores. We name this dimensionless group the packed bed number \(PB\) from now on. Finally, the functional relationship \(\Pi _1=\phi (\Pi _2,\Pi _3,\Pi _4)\) can be rewritten as

$$\textit{Sm}=\Phi (\textit{RW},\textit{PB}),$$
(7)

where the form of the function \(\Phi\) has to be determined by a series of experiments.

2.2 Center-of-mass model of the fluidic experimental setup

We utilize a capillary interface tracking method to measure the EOF rate in the packed bed. To do so, a capillary tube with a known diameter is connected to the packed bed and the electroosmotic flow moves the air/liquid interface in the capillary. This method was utilized by several researchers including Refs. Kang et al. (2007) and Zeng et al. (2001) who assumed that the capillary flow rate is equal to the EOF rate. However, this approach neglects the fact that the capillary flow can impact the EOF. Therefore, we develop a center-of-mass model of the fluidic parts of the experimental setup to study its dynamic behavior. Another motivation comes from Joule heating; a term which describes the heat production related to the electrical current in the liquid. Research on this effect has been generally performed for single microchannels/capillaries. Here, axial and lateral temperature profiles have been simulated which can have a profound influence on most liquid properties such as density and viscosity (Tang et al. 2004; Xuan 2008). We realize a considerable influence of Joule heating in some of our experiments. In detail, we observe constant capillary flow rates, even for longer times, instead of a decrease which is expected due to the increasing counter-pressure induced by the rising liquid column in the capillary. Since the measurement of the temperature in our setup is difficult, we utilize our model to extract important information on the influence of Joule heating from the experimentally observed flow rates.

Fig. 1
figure 1

a Experimental setup for capillary interface tracking to measure the EOF velocity; b Schematic of the fluidic experimental setup used for the translational center-of-mass model

Full size image

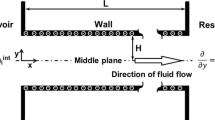
Figure 1a illustrates the fluidic experimental setup which is used to measure the EOF through the packed bed. The setup consists of a liquid reservoir, packed bed, T-connection and an elbow connection which contains the capillary. The electric field, induced by electrodes in the reservoir and the T-junction, pumps the liquid from the reservoir into the capillary. Figure 1b shows a corresponding principle sketch where we simplify the setup to be one-dimensional in order to track the translational center of mass of the liquid. That is, we divide the setup into the single compartments: liquid reservoir (rv), reservoir connection (rc), packed bed (pb), T-connection (tc), elbow connection (ec) and capillary (cp), each with certain height \(l_j\) and volume \(V_j\); the respective index for \(j\) is given in the brackets. The 1D \(z\)-coordinate system with the origin at the bottom of the reservoir is used to track the positions of the segments’ center of mass which are indicated by solid circles. Additionally, we introduce another \(z_\mathrm{if}\)-coordinate system for the position of the capillary interface since this is the quantity which is measured in the experiments. Both coordinate systems are coupled to each other.

Newton’s law states that the momentum change of the system’s center-of-mass equals the sum of the forces which act on it. We introduce the position of the system’s center of mass \(z_c=1/V_T(z_\mathrm{rv}V_\mathrm{rv}+z_\mathrm{rc}V_\mathrm{rc}+{z_\mathrm{pb}\psi }V_\mathrm{pb}+z_\mathrm{tc}V_\mathrm{tc}+z_\mathrm{ec}V_\mathrm{ec}+z_\mathrm{cp}V_\mathrm{cp})\), where \(V_{T}=V_\mathrm{rv}+V_\mathrm{rc}+{\psi }V_\mathrm{pb}+V_\mathrm{tc}+V_\mathrm{ec}+V_\mathrm{cp}\) is the total liquid volume of all compartments, to obtain

$$\frac{\mathrm{d}}{\mathrm{{d}}t} \left( \rho V_T \frac{\mathrm{d}z_c}{\mathrm{d}t}\right) = \sum _{j} F_j.$$
(8)

Here, \(t\) is the time, \(\rho\) is the liquid density, and \(F_j\) denotes the forces to be defined. In order to formulate Newton’s Law in terms of \(z_\mathrm{if}\), we consider that the volumes of all compartments but the capillary are constant. This assumption even holds for the reservoir since its volume is large and the EOF is rather small. Also, the positions of the center of mass of all single compartments, but the capillary, are constant. The capillary volume can be expressed using its cross section (radius) according to \(V_\mathrm{cp}=A_\mathrm{cp} z_\mathrm{if} =\pi r_\mathrm{cp}^2 z_\mathrm{if}\). The center-of-mass position of the capillary can be written in terms of the capillary interface position as \(z_\mathrm{cp}=l_\mathrm{rv}+l_\mathrm{rc}+l_\mathrm{pb}+l_\mathrm{tc}+l_\mathrm{ec}+\frac{z_\mathrm{if}}{2} \equiv l_{T}+\frac{z_\mathrm{if}}{2}\). Finally, if we further consider that \(\frac{\mathrm{d}z_\mathrm{cp}}{\mathrm{d}t}=\frac{\mathrm{d}z_\mathrm{if}}{\mathrm{d}t}\), we can rewrite Newton’s Law (8) according to

$$\frac{\rm d}{{\rm d}t}\left( \rho V_T \frac{{\rm d}z_c}{{\rm d}t}\right) \approx \ \rho A_{\rm cp} \bigg (2 \left( \frac{{\rm d}z_{if}}{{\rm d}t}\right) ^2+\left( l_{T}+\frac{3}{2} z_{\rm if}\right) \frac{{\rm d}^2z_{\rm if}}{{\rm d}t^2}\bigg )=\sum _{j} F_j.$$
(9)

For a further treatment, we identify the following forces \(F_j\) which act on the system’s center-of-mass:

The electroosmotic force \(F_\mathrm{EOF}\) is induced when an electric field is applied to the packed bed. The resulting EOF causes only minor viscous losses to good approximation and the packed bed can be rather considered as a pump. Hence, the product of EOF and an appropriate viscous resistance \(R_{\mu }\) of the packed bed can be interpreted as an electroosmotic pressure rise as defined by \(\Delta p_\mathrm{{eof}}\equiv \ R_\mu \dot{V}_\mathrm{{eof}}\); just opposite to the pressure drop that would be observed if a viscous flow of the same flow rate as the EOF passed through the bed. We use the Blake–Kozeny equation for the modeling of \(R_{\mu }\) and arrive in

$$F_\mathrm{{eof}} = A_\mathrm{pb} \Delta p_\mathrm{{eof}} =A_\mathrm{pb}\, K_1\frac{l_\mathrm{pb}\mu }{d_\mathrm{p}^2}\frac{(1-\psi )^2 }{\psi ^3}\bar{v}_\mathrm{{eof}}.$$
(10)

The proportionality constant \(K_1\) depends on the packed bed structure; a range of 72 to 150 for consolidated porous media is given in the literature (Bird et al. 2007). However, the determination of \(K_1\) values was generally done for packed beds of homogenous spheres of sizes on the order of 1 mm to 1 cm as well as for pressure-driven flows. In contrast, particles as small as 6 \(\mu m\) are used in the current work resulting in much larger surface-to-volume ratios. Additionally, the pore-scale plug-like velocity profile of the EOF is considerably different to the parabolic profile of a pressure-driven flow. Hence, we consider \(K_1\) as a fitting parameter which is determined from the instantaneous EOF that we measure as described below. We find the proportionality constant to be \(K_{1}=3.66\pm 1.03\) for all packed beds and experimental conditions used in this work, which confirms the assumed significant differences to the pressure-driven flow. The variation of the electroosmotic proportionality constant is with roughly \(\pm 30\%\) rather small compared to the range of constants which is reported in the literature for pressure-driven packed bed flows as mentioned above.

The viscous force \(F_\mathrm{vis}\) is related to the pressure drop that arises from the viscous losses of the liquid flow through the capillary. We use a Hagen–Poiseuille approach which is a good approximation for laminar flows. We relate the flow rate to the motion of the capillary interface and obtain

$$\begin{aligned} F_\mathrm{vis} = -A_\mathrm{cp} \Delta p_\mathrm{cp}= -A_\mathrm{cp}\frac{8\mu }{r_\mathrm{cp}^2} z_\mathrm{if}\left( \frac{\mathrm{d}z_\mathrm{if}}{\mathrm{d} t}\right) . \end{aligned}$$
(11)

The hydrostatic force \(F_\mathrm{g}\) arises due to the hydrostatic pressure which is induced by the rise of the liquid column in the capillary. The resulting force can be written as

$$F_\mathrm{g} =\ -A_\mathrm{cp} \rho g z_\mathrm{if},$$
(12)

where \(g\) is the gravitational constant. Note that there is an equilibrium height of the capillary interface \(z_\mathrm{if}(t=0)\) before the EOF is induced. We cancel the gravitational force related to the initial height by the static part of the capillary force as described below.

The capillary force \(F_\mathrm{cp}\) reflects the influence of capillarity, which is twofold in our system. On the one hand, the surface tension between liquid and air along with the adhesive force between liquid and capillary results in capillary action. That is, the liquid moves in the capillary (independent of electroosmosis) until an equilibrium state with the gravitational force is achieved. On the other hand, the contact angle of a dynamic interface also depends on the interface velocity and therefore deviates from its equilibrium value. For the current work, we adopt a model based on the molecular kinetic theory as proposed by Blake and Haynes (1969) which give the dynamic contact angle \(\theta _{\rm D}\) as

$$\cos \left( \theta _{\rm D}\right) = \cos \left( \theta _{\rm e} \right) - \frac{\sigma '}{\sigma _o}\sin h ^{-1} \left( \frac{v}{v'}\right) ,$$
(13)

where \(\sigma _o=0.072\) N/m is the surface tension of water and air, \(v=\mathrm{d}z_\mathrm{if}/\mathrm{d}t\) is the velocity of the interface and \(\theta _\mathrm{e}\) is the (static) equilibrium contact angle. We measure the equilibrium height in the capillary before each experiment to be \(z_\mathrm{if}(t=0)=11.7\, \pm 0.2\) mm which corresponds to \(\theta _\mathrm{e} =62\pm 1^{\circ }\). This is in very good agreement to the value of \(61.9\pm 1.3^{\circ }\) that we infer from direct measurements of the contact angle using a high resolution camera.

The parameter \(\sigma '\) is proportional to the thermal energy and has units of surface tension, while the parameter \(v'\) is a velocity which is determined by molecular quantities. We use \(\sigma '=0.0172\) N/m, \(v' = 5\cdot 10^{-3}\) m/s as proposed by Popescu et al. (2008) for smooth glass capillaries, air and aqueous electrolytes. Furthermore, we linearize the inverse hyperbolic sine according to \(\sin h ^{-1} \left( \frac{v}{v'}\right) \approx {v}/{v'}\) which is a valid approximation for low interface velocities. Finally, the capillary force is formulated the standard way, however, with the assumptions made above to be

$$F_\mathrm{cp}=A_\mathrm{cp} \frac{2\sigma }{r_\mathrm{cp}} \left( \cos \theta _\mathrm{e} - \frac{\sigma '}{\sigma _o v'} \frac{\mathrm{d}z_\mathrm{if}}{\mathrm{d}t} \right) .$$
(14)

Finally, there is recent research by Das et al. (2014) who found that capillary filling is subjected to so-called electroviscous effects. That is, the observed flow rates are lower than the predicted ones due to the generation of a streaming potential, which triggers electroosmosis in opposite direction to the main flow. However, the magnitude of the streaming potential in a conduit scales with the reciprocal square of the hydraulic diameter (cf., e.g., Saini et al. 2014). Since the capillary diameter in our setup is \(1.2\) mm, all electroviscous effects can be neglected. We now insert the forces into Eq. (9) and pass to a non-dimensionalized system for the sake of convenience. The length coordinate is scaled with the radius of the packed bed to obtain the dimensionless coordinate \(Z_\mathrm{if}=z_\mathrm{if}/r_\mathrm{pb}\). The velocity is scaled with a characteristic electroosmotic pore-scale velocity \(v_0=\frac{\zeta _0\varepsilon }{\mu }E_0\) to obtain the dimensionless velocity \(V_\mathrm{{eof}}=\bar{v}_\mathrm{{eof}}/v_0\). The time is scaled with a characteristic convective scale to obtain the dimensionless time \(T={t}v_0/{r_\mathrm{pb}}\). We use the non-dimensional variables just as defined and also normalize all terms with a hydrostatic pressure to obtain after some rearrangements

$$\begin{aligned}&Z_\mathrm{if}+\left( 2\Omega _0 + 8\Omega _1 Z_\mathrm{if} \right) \frac{\mathrm{d}Z_\mathrm{if}}{\mathrm{d} T}+2\Omega _2\left( \frac{\mathrm{d}Z_\mathrm{if}}{\mathrm{d} T}\right) ^2 +\Omega _2\left( \frac{l_T{}}{r_\mathrm{pb}}+\frac{3}{2}Z_\mathrm{if}\right) \frac{\mathrm{d}^2 Z_\mathrm{if}}{\mathrm{d} T^2}\nonumber \\&\quad =3.66\Omega _3+2\Omega _4. \end{aligned}$$
(15)

Here, the non-dimensional groups

$$\begin{aligned} \Omega _0\equiv & {} \frac{\sigma ' v_0}{g\rho r_\mathrm{cp}r_\mathrm{pb} v'}, \quad \Omega _1 \equiv \frac{\mu v_0}{g\rho r_\mathrm{cp}^2},\quad \Omega _2\equiv \frac{v_0^2}{gr_\mathrm{pb}},\quad \Omega _3\equiv \frac{\mu v_0(1-\psi )^2}{\rho g \psi ^3}\frac{r_\mathrm{pb} l_\mathrm{pb}}{d_\mathrm{p}^2 r_\mathrm{cp}^2}V_\mathrm{eof },\nonumber \\&\Omega _4\equiv \frac{\sigma _o\cos \theta _e}{g\rho r_\mathrm{cp}r_\mathrm{pb}} \end{aligned}$$
(16)

arise from the non-dimensionalization and allow for an evaluation of the significance of the different terms. The dimensionless groups \(\Omega _0\) and \(\Omega _4\) indicate the ratio of the dynamic and the static capillary force to the hydrostatic force, respectively. Both groups can be interpreted as inverted Bond numbers. The dimensionless group \(\Omega _1\) is the ratio of viscous to hydrostatic force and is comparable to an inverted Archimedes number. The dimensionless group \(\Omega _2\) is the ratio of inertial to hydrostatic force, which is equivalent to an inverted Richardson number. Finally, \(\Omega _3\) indicates the significance of the electroosmotic force relative to the hydrostatic force. Note that, unlike the other dimensionless groups, we have to extract \(\Omega _3\) from the experimental observation of the capillary interface position \(Z_\mathrm{if}(T)\) over time to infer the superficial electroosmotic velocity in the packed bed. Unfortunately, there is no analytical solution of this second-order nonlinear ODE readily available. A magnitude of order analysis reveals that the influence of inertia is rather negligible so that we can assume \(\Omega _2\approx 0\). However, the analytical solution of this simplified version of Eq. (15) involves the complex Lambert-W function which cannot be expressed in terms of elementary functions. Finally, we choose a feasible solution which comprises of the regression of a third-order polynomial to the measured \(Z_\mathrm{if}(T)\) data. The polynomial, its first- and second-order derivatives, and the dimensionless groups \(\Omega _0, \Omega _1,\Omega _2,\Omega _4\) are inserted in Eq. (15) to determine \(\Omega _3\) and thus \(V_\mathrm{EOF}\) over the measurement time.

Finally, we would like to point out that another interesting capillary flow model was developed by Waghmare and Mitra (2010). The authors applied an integral momentum balance to model the penetration length of the liquid/gas interface driven by a combined electroosmotic and pressure-driven flow through a horizontal capillary of rectangular cross section. It is worth noting that the condensed dimensionless correlation that they derived has essentially the same mathematical form as Eq. (15). However, there are considerable differences to the current work, such as a the presence of a pressure-driven flow, a scaling with capillary forces, an EOF which is generated within the capillary and its consideration as an integral Coulomb force. Hence, the pre-factors in their model consist of very complex time-dependent correlations of constants along with Bond, Ohnesorge and an electroosmotic number.

3 Experimental methodology

Here, we give the details of the experimental setups, methods and materials that we employ for the measurement of the EOF in the packed bed as well as for the streaming current that is used to infer the zeta potential of the particulate material.

Fig. 2
figure 2

a Sketch of the streaming current setup; b design of the streaming current measurement cell

Full size image

3.1 Streaming current

We employ the streaming current method to infer an empirical correlation for the zeta potential of borosilicate in contact with an aqueous NaCl electrolyte of defined ionic strength and pH value. The streaming current—another electrokinetic phenomenon—is a convective charge transport which is induced if a pressure gradient generates a flow in the EDL. More comprehensive information is available, e.g., in Delgado et al. (2007). The streaming current measurements are usually conducted in very defined geometries. We use a microchannel formed by two parallel flat borosilicate wafers. The measured streaming current \(I_\mathrm{sc}\) can then be related to the zeta potential according to the Helmholtz–Smoluchowski formula

$$\zeta = \frac{\mu }{\varepsilon } \frac{L_\mathrm{c}}{A_\mathrm{c}}\frac{-I_\mathrm{sc}}{\Delta p},$$
(17)

where \(A_\mathrm{c}\) is the area of the microchannel’s cross section, \(L_\mathrm{c}\) its length and \(\Delta p\) is the pressure difference which is applied between the channel’s inlet and outlet. In practice, streaming currents are measured for various pressure differences and the respective slope \(\mathrm{d}I_\mathrm{SC}/\mathrm{d}\Delta p\) is used in Eq. (17).

3.1.1 Experimental setup

Figure 2a shows a schematic sketch of the experimental setup that is used for the streaming current experiments. The setup consists of the measurement (electrokinetic) cell and further fluidic and electrical components. Within the cell, there is a shallow microchannel where the wetted surface is made from borosilicate glass. The cell is connected to a polyethylene vessel containing the aqueous electrolyte. This vessel can be charged with a controlled pressure by a nitrogen gas cylinder (Ultra High Purity 99.999 %, MEGS, Canada) to pump the aqueous solution through the cell. The pressure drop across the cell is indicated by two incorporated pressure gauges. The cell also contains two Ag/AgCl electrodes which are connected to a precise potentiostat (PGSTAT302N, Metrohm Autolab B.V., the Netherlands) which measures various electrical signals. Figure 2b gives a detailed insight into the cell design. The cell is made from two \(\hbox {Teflon}^{\circledR }\) (PTFE) blocks and allows for the incorporation of two test wafers of dimensions \(70\,{\text{ mm }}\times 30\,{\text{ mm }} \times 1.5\,{\text{ mm }}\) to form the microchannel. Any material can be tested as long as it features the specified wafer dimensions. We use borosilicate wafers of similar chemical composition as the granular material of the packed bed for the sake of comparability. The blocks are assembled with two gasket in between. The inner rigid (spacer) gasket is made of PTFE and maintains a 175-μm gap between the wafers to adjust the height of the microchannel. The outer soft gasket is made of latex rubber and is required for sealing purposes.

3.1.2 Experimental protocol

The streaming current measurements are taken according to the following procedure: First, borosilicate wafers are cleaned using a cleaning protocol as described in Barz et al. (2009). Wafers and gaskets are assembled in the cell which is then installed in the setup. We prepare the same aqueous electrolyte solutions as it is done for the EOF measurements described below. The vessel is filled with electrolyte solution which is then pressurized with nitrogen gas. The electrolyte solution is pumped through the cell for around 30 min at \(\Delta p = 25\) kPa. Then, the actual experiment is undertaken by adjusting to 5 pressure differences in the range of \(10\) to \(75\) kPa. The respective streaming current is measured for 60 s at a constant pressure, and we use the corresponding time-averaged value for data evaluation. A total of 60 experiments are performed to obtain a wide applicability and high accuracy of the empirical correlation for the zeta potential of borosilicate.

3.2 Electroosmosis

3.2.1 Experimental setup

The experimental setup for the EOF measurements consists of several fluidic components, electrical instruments as well as electronic equipment for data processing as sketched in Fig. 3. In detail, the setup consists of an electrolyte beaker which is connected to a glass tube which contains the packed bed. From the other end, a capillary made from borosilicate glass (\(r_\mathrm{cp}=0.6\) mm, \(t=1.5\) mm, \(l_\mathrm{cp}=30.48\) cm, McMaster-Carr, Aurora, OH, USA) is connected via a T-connection (\(r_\mathrm{tc}= 4.15\) mm, Cole-Parmer, Montreal, QC, Canada) and an elbow connection (\(r_\mathrm{ec} =4\) mm, glass, custom made) to the glass tube. Platinum wire electrodes (LabSmith Inc., CA, USA) are inserted into the beaker and the T-connection and electrically connected to a high-voltage power supply (Bertan Model 105-03R, Equiptek Labs Inc., CA, USA). The motion of the capillary interface is tracked by using a CMOS camera (DFK 23UM021, The Imaging Source, NC, USA). These data are analyzed by using the LabView Vision Builder software (National Instruments, Austin, TX, USA). To obtain insight into the influence of Joule heating, two PFA insulated thermocouples (5TC-TT-K-20-36, Omega Engineering, QC, Canada) are attached to the ends of the packed bed. Note that these temperature sensors contact the glass outside of the packed bed since it is not possible to immerse electrically based temperature sensors into the liquid due to the large electric fields. Hence, we receive a rather vague insight into the temperature distribution in the packed bed.

Fig. 3
figure 3

Schematic of the experimental setup utilized for the electroosmotic flow experiments

Full size image

3.2.2 Experimental procedure

First, we prepare packed beds using consolidated binary particle mixtures in order to obtain a wide range of porosities, wetted surface areas and effective hydraulic diameters. In detail, we utilize borosilicate microspheres with mean diameters of 6 and 18 \(\upmu\)m (Microspheres-Nanospheres, NY, USA) and of 50, 140, 230 and 1000 \(\upmu\)m (Mo-Sci Specialty Products, L.L.C, MO, USA). All packed beds are prepared in borosilicate glass tubes (Pegasus-Glass, ON, Canada) with an inner radius of \(r_\mathrm{pb}=4.75\) mm, and the thickness of the glass wall is \(1\) mm. Different techniques are described in the literature for the consolidation of granular materials. We adopt the method used by van den Bosch et al. (1996), where particles are sintered in a way that creates two permeable retention frits at each end of the packed bed. This method appears especially suitable since the retention frits are made from the same material as the packed bed. First, a small part of the glass tube is filled with the designated particle mixture. These particles are consolidated, immersed in an aqueous solution of sodium silicate and then sintered using a butane torch. The concentration of sodium silicate in solution, sintering time and temperature are optimized so that the frits maintain a porosity similar to the rest of the packed bed. Thereafter, the glass tube is filled with the particle mixture until the desired packed bed length is achieved. The particle bed is compacted using a Teflon rod, and its top is sintered in the same way as the lower retention frit. After the fabrication, the packed beds are chemically treated to remove any contamination using a procedure as described in Barz et al. (2009). The porosity is measured by weighing the bed in a dry and a water-saturated state with a precise scale (AZ3102, Sartorius AG, Germany).

Before each EOF experiment, the packed beds are equilibrated in an electrolyte solution with defined pH value for at least \(48\) hours. The aqueous electrolyte solutions of desired ionic strength are prepared using sodium chloride (NaCl, \(\ge\)99.0 %, ACS reagent, Sigma-Aldrich, CA) dissolved in a DI water matrix (\(\sigma \le\) 1 \(\upmu\)S/cm). The pH value of the aqueous electrolyte is adjusted with the addition of either sodium hydroxide (NaOH, \(\ge\)97 %, ACS reagent, Sigma-Aldrich, CA) or hydrochloric acid (HCl, 32 % in water, ACS reagent, Fisher Scientific, CA). Conductivity and pH testings are performed before and after an electroosmosis experiment using a modular pH and conductivity meter (Mettler-Toledo, SevenMulti, Switzerland). We observe that the change in pH and conductivity is always less than \(1\) %.

To perform an EOF experiment, the packed beds are assembled in the experimental setup as shown in Fig. 2. The aqueous electrolyte is filled in the reservoir along with the other compartments. To remove any gas bubbles inside the setup, the electrolyte solution is pumped through the fluidic parts and the packed bed by utilizing a syringe pump. The experiment is initialized by applying a voltage between the electrodes. This moves the electrolyte solution from the reservoir through the packed bed, the T- and elbow connection and into the capillary. Finally, a comprehensive set of experiments based on a full factorial design is performed to obtain the correlation \(\Phi\) among the dimensionless groups as given in Eq. (7). The range of the experimental parameters is listed in Table 1 in the Appendix.

4 Results and discussion

In this section, we first give the results of the streaming current experiment. Then, we present the characterization of the packed beds to show the relationships between different packed bed parameters. Finally, selected results of the electroosmosis experiments are shown and the correlation \(\Phi\) between the dimensional groups is derived.

Fig. 4
figure 4

Zeta potential normalized with the negative logarithm of the ionic strength as a function of the pH

Full size image

4.1 Streaming current

Figure 4 gives the zeta potentials of a borosilicate surface that are inferred from streaming current measurements for various ionic strengths and pH values of the aqueous electrolyte. We choose a presentation of the results where we normalize the zeta potentials with the respective negative logarithm of the ionic strength and plot them versus the pH value of the aqueous electrolyte. This often leads to a collapse of various data points onto a single curve as shown in many works as reviewed in Kirby and Hasselbrink (2004). The symbols indicate the average normalized values compiled from various ionic strength measurements at a constant pH value. The resulting small standard deviations (for an electrokinetic experiment) underline the high validity of the normalization approach. In detail, there is a rather linear decrease in the normalized zeta potential between the pH values of 3–7. For larger pH values, the slope decreases and the normalized zeta potential approaches a limiting value (plateau). This behavior is in good agreement with the work of Scales et al. who investigated potassium chloride electrolytes in contact with fused-silica surfaces (Scales et al. 1992). The authors claim that the plateau at pH value of around 8 can be related to the full deprotonation of the silanol surface sites so that a maximum of negatively charged sites is obtained. We perform a second-order regression of the collapsed data which results in

$$\frac{\zeta (\mathrm pH)}{-\mathrm{log}(I)} =\left( 0.532 \, \mathrm{pH}^2-10.80\,\mathrm{pH}+18.04\right) \mathrm{mV},$$
(18)

which can be used with good accuracy for the phenomenological model that we propose. The regression has a coefficient of determination value of 0.965 and is given in Fig. 4 as a solid line.

4.2 Packed bed parameters

The properties of the packed beds made from binary particle mixtures depend on several factors such as the mixture composition, the size ratio of the spheres as well as the mixing procedure. Different models have been developed to predict the porosity of heterogenous particle beds. In terms of regular packing structures, a practicability of the models is not given when dealing with microparticles. Furthermore, the random packing of binary particle mixtures results in highly unpredictable packing densities (Dias et al. 2004). Hence, we discuss the resulting packed bed parameters in this work solely on the definitions given in Sect. 2.1 along with the measured porosities.

Fig. 5
figure 5

Porosity of the packed bed versus the effective particle diameter of the particle mixtures

Full size image

Figure 5 shows the relationship between the effective particle diameter and the measured porosities for the different beds that we prepare in this work. Recall that for a randomly packed bed of homogenous spherical particles, with a small ratio of particle to packed bed diameter, the porosity hardly depends on the particle diameter. Typical literature values for dense random packing vary between \(\psi = 0.36\) to 0.38 (de Klerk 2003). In contrast, we find three different intervals I, II, III for our binary mixtures where, evidently, different packing mechanisms/structures prevail. Note that the following interpretation is a pure qualitative approach and there are rather smooth transitions between the intervals than stringent boarders. In interval I, we observe that the porosity decreases with an increasing effective particle diameter. The situation changes completely for the interval II, and we observe an increase in the porosity as the effective particle diameter increases. Subsequently, the trend changes again in interval III where the porosity decreases as the effective particle diameter increases further. The categorization into intervals also allows for a better interpretation of the underlying mechanisms. To do so, we assign the particle mixtures of an interval to a corresponding group as given in Table 2 in the Appendix and characterize them by the ratio of small to large particle diameter \(\delta = \frac{d}{D}\) along with the volume fraction \(v_d\) of the small particles. We realize that the packed beds in group 1 are prepared using particle mixtures with a significant difference in particle size (\(\delta \simeq 0.1\) ) along with a low volume fraction of small particles (\(v_d \simeq 0.1\)). Hence, we assume that these mixtures promote the formation of a “skeleton” in the packed bed. The term skeleton is used to indicate the presence of a overarching structure which consists solely of large particles. The skeleton’s void volume provides a space where small particles can accumulate (Dias et al. 2004). Indeed, we find that the group 1 mixtures with higher volume ratios of small particles feature lower porosities.

Group 2 consists of particle mixtures with either a very low particle size ratio (\(\delta \simeq \ 0.05\)) along with a high volume fraction of small particles (\(v_{d} \simeq\) 0.4–0.5) or with a medium particle size ratio (\(\delta \simeq\) 0.13–0.36) and a low volume fraction of small particles ( \(v_{d} \simeq\) 0.02–0.1). The first combination should promote skeleton formation, and we assume that the high volume fraction of small particles considerably fills the void volume of the skeleton. The other combination may promote a skeleton formation in the packed bed as well. However, the very low volume fraction of small size particles occupies only a small part of the void volume. The increase and decrease in porosity that we observe for this group cannot be easily explained, and we assume that these mixtures create complex packed bed structures. The mixtures which are categorized in group 3 have the highest size ratio of the particles ( \(\delta \simeq\) 0.2–0.5 ) along with the highest fractions of small particles ( \(v_{d} \simeq\) 0.2–0.5). We assume that no significant skeletal formation takes place due to comparable particle sizes and concentrations of small and large particles. This assumption is supported by the relatively high porosity values which are close to those of (dense) randomly packed beds of homogenous particles. Note that the \(M\) factors of our packed beds are between 1 and 1.1 so that we can assume a homogenous packing structure and exclude a significant influence of the packed bed wall on electroosmosis.

Fig. 6
figure 6

Specific surface area versus the effective particle diameter of the packed beds

Full size image

Figure 6 illustrates the relation between the (calculated) wetted specific surface area and the effective particle diameter. If we used homogenous particles, the specific surface area would decrease as the particle diameter increases. It is obvious that the usage of binary particle mixtures leads to more complex dependencies. As expected, we find the highest specific surface areas for small effective particle diameters. Then, the specific surface area considerably decreases until the effective particle diameter approaches a value of around 40 \(\upmu\)m. That is, the group 1 and some of the group 2 mixtures, where we assume skeleton formation and/or we have a large volume fraction of small particles, behave like a packed bed of homogenous particle. For larger effective particle diameters than around 40 \(\upmu\)m, the specific surface area remains more or less constant. Here, we assume that the influence of effective particle diameter is compensated by the simultaneous increase in porosity (cf. Fig. 5). This happens for mixtures with either no skeleton formation or for those with a low volume fraction of small particles.

Fig. 7
figure 7

Hydraulic diameter versus effective particle diameter of the packed beds

Full size image

Figure 7 shows the correlation between (calculated) hydraulic diameter and the effective particle diameter. For a randomly packed bed of homogeneous particles, with a more or less constant porosity, there should be an increase in the hydraulic diameter as the particle diameter increases (cf. Eq. 4). In terms of our binary mixtures, we see that the hydraulic diameter remains more or less constant until the effective particle diameter approaches a size of roughly 40 \(\upmu\)m, i.e., for group 1 mixtures with skeleton formation and group 2 mixtures with a high fraction of small particles. We assume that the simultaneous decrease in porosity (cf. Fig. 5) compensates the influence of the effective particle diameter. For group 2 mixtures with low volume fraction of small particles and effective particle diameters larger than around 40 \(\upmu\)m and group 3 mixtures without skeleton formation, the hydraulic diameter increases with increasing particle diameter.

Fig. 8
figure 8

Typical outcome of an EOF experiment for two different electric field strengths. The dimensionless superficial EO velocities are inferred based on a continuity approach with the capillary flow (CF) as well as based on center-of-mass model of the fluidic setup (ODE)

Full size image

4.3 Electroosmosis

Figure 8 shows the results of two exemplarily EOF measurements, incorporating a packed bed with a porosity of \(\psi =0.241\), an electrolyte of ionic strength \(I=0.01\) mM and pH = 6 and for two electric fields of strength 2 and 20 kV/m. The dimensionless superficial electroosmotic velocities are inferred using two different evaluation methods. For the first method, we assume that the EOF is not influenced by the presence of the capillary. That is, we use the capillary flow rate, computed from the measured track of the capillary interface over time and apply a continuity assumption, i.e., \(V_\mathrm{{eof}}\equiv (\mathrm{d}Z/\mathrm{d}t )A_\mathrm{cp}/A_\mathrm{pb}\). The second method involves the center-of-mass model as described in Sect. 2.2 and accounts for the influence of the rising column, the moving contact line, as well as inertial and viscous effects. Recall that we fitted the proportionality constant \(K_1\) such that we achieve identical initial values of \(V_\mathrm{{eof}}\) for both evaluation methods. However, this fitting does not influence the trend over time which can be, as we discuss below, very different for both methods. In terms of the low electric field strengths, we find that the capillary flow-based method (dotted line) results in a rather constant superficial velocity over time. The comparison with the ODE-based superficial velocity reveals a slight increase over the observation time. For such low electric field strengths, the observed difference is mainly related to the correction for the hydrostatic force and the moving contact line. The situation changes considerably if an electric field of high strength is applied at the packed bed. Here, we find that the capillary flow-based \(V_\mathrm{{eof}}\) (dashed line) slightly increases over time. However, the value of the ODE-based \(V_\mathrm{{eof}}\) (dashed-dotted line) considerably increases over time and we find almost the triple of the initial value at the end of the time interval. A more detailed inspection reveals that the influence of the forces which are induced by the capillary flow is here more significant than for the case of the low electric field strength. That is, the real flow rate in the packed bed would be considerably higher if it were not slowed down by the phenomena related to the presence of the capillary, i.e., mainly the rising hydrostatic pressure and the moving contact line. However, the observed massive increase in \(V_\mathrm{{eof}}\) can only be explained by Joule heating which induces a considerable temperature gradient along the packed bed. The temperature gradient, in turn, induces a density gradient which triggers a flow additionally to the EOF. Indeed, we measure a rise in temperature at the outside wall of the packed bed in case of high voltages (≥2 kV) and high electrolyte conductivities (ionic strength ≥10 mM) about 5 s after the voltage has been applied. For lower ionic strengths, the times before a temperature gradient is observed are considerably longer. Again, the wall temperature measurements give only a rough insight into the time-dependent temperature distribution in the liquid due to the heat capacity of the packed bed tube and the convective and conductive heat transfer in the system. Nevertheless, the utilization of the center-of-mass model clarifies the influence of Joule heating, if present, with the correct time scale. Hence, we use the insight that we gain from the center-of-mass model to evaluate the experimental data in a range which excludes Joule heating effects. That is, for relatively low electric field strength, we use a superficial velocity which is averaged over the evaluation interval. For high electric field strengths, the initial value is used for further processing.

Fig. 9
figure 9

Electroosmotic Smoluchowski No. versus the Packed Bed No. for constant values of the Rice–Whitehead No

Full size image

Finally, the superficial EO velocity is used along with the physicochemical and the geometrical parameters to calculate the dimensionless groups as defined in Eq. (6). The results are given in form of mean values and their standard deviations based on six replicates. Figure 9 shows results of the EOF experiments plotted as a functional relationship between the magnitude of the Smoluchowski number Sm and the Packed Bed number PB for constant values of the Rice–Whitehead number RW. The connections between the data points are for the sake of a better illustration, and we realize that the track of the curves appears similar. Note that, due to the nature of our experiments, it is difficult to keep RW strictly constant while varying the other groups. Hence, we group the \(RW\) data such that the average values still span over several magnitudes while maintaining a relatively narrow range of variation. We find that for all given RW, Sm decreases as PB increases. The correlations, despite being plotted on a logarithm scale, do not appear linear. We rather find different intervals with different behaviors. For PB ~ 105–106, the correlation between the logarithmic values appears rather linear. Then, Sm remains more or less constant with increasing PB before it decreases again at the upper limit that we investigate. Additionally, all curves show a regular behavior in terms of the RW groups, i.e., the lower RW and the higher Sm for a given PB. In terms of interpretation of the correlations, the observed behavior appears intuitive if we interpret \(PB\) in terms of the porosity and for a bed of homogenous particles. Then, PB is proportional to the reciprocal porosity and we can assume that the higher the porosity (the lower PB), the higher the EOF. In terms of the different scaling behavior that we observe, we should recall that \(Sm\) is the ratio of superficial to pore-scale electroosmotic velocity and the scaling of the groups is not necessarily the same as the scaling of the single phenomena. That is, if we increase the pore-scale velocity in a packed bed, we cannot expect that the superficial velocity scales in the same fashion due to the complex flow and electric field path.

Fig. 10
figure 10

Electroosmotic Smoluchowski No. versus the Rice–Whitehead No. for constant values of the Packed Bed No

Full size image

Figure 10 illustrates the correlation between Sm and RW for different values of PB. The connections between the data points are for the sake of a better illustration. Generally, we observe that Sm decreases if RW increases. The correlation between the logarithmic values appears linear, to good approximation. We also find a regular behavior of the curves with different values of PB; the lower PB, the higher the Sm values which are observed for a given RW. It is interesting that we find a decrease in Sm—i.e., the EOF—with increasing RW even though the Debye length is only on the order of ~1 % of the hydraulic diameter. However, we should emphasize once more that a packed bed of spherical particles features pore conduits of a complex cross-sectional form which size also varies in flow direction. In other words, we can assume that there is always a fraction of the complex pore network where an EDL overlap occurs even though the (averaged) hydraulic diameter does not indicate this. Hence, when we increase the EDL thickness or lower the hydraulic diameter, this fraction increases.

Fig. 11
figure 11

Electroosmotic Smoluchowski No. versus the product of the Rice–Whitehead and the Packed Bed No

Full size image

Finally, we try different combinations of the dimensionless groups to derive a correlation which gives a quantitative expression that involves all investigated physicochemical phenomena. It turns out that, if we plot the magnitude of \(Sm\) against the product of \(RW\) and \(PB\) on a logarithmic scale, all data points collapse to good approximation on a single curve as given in Fig. 11. A linear regression results in

$$\begin{aligned} Sm \approx -3.10 \left( PB\cdot RW\right) ^{-2/3}, \end{aligned}$$
(19)

with a good value of 0.94 for the coefficient of determination. Alternatively, we insert the definitions of the dimensionless groups to obtain an expression in terms of the measurable porosity and (known) particle size and composition according to

$$\bar{v}_\mathrm{{eof}} \approx -\frac{1}{4} \left( \frac{\psi }{(1-\psi )} \sqrt{\sum \nolimits _{i=1}^{n} x_i d_{i}^2} \right) ^{\frac{4}{3}} \left( l_{D}r_{pb}^2 \frac{\sum _{i=1}^{n} x_i d_{i}^2}{\sum _{i=1}^{n} x_i d_{i}^3} \right) ^{-\frac{2}{3}} \frac{\zeta \varepsilon }{\mu }E,$$
(20)

which is only valid for a \(M\) factor similar to one and isothermal conditions.

5 Concluding remarks

In the current research, we derive a phenomenological correlation for the electroosmotic flow through packed beds of granular material based on dimensional reasoning, in the spirit of the Blake–Kozeny correlation for pressure-driven flows. At first, we identify the relevant quantities which can be used for the qualitative description of the related phenomena. Then, we apply Buckingham \(\Pi\) theorem to establish a functional relationship between three relevant dimensionless group.

Numerous experiments are performed to infer the correlation between the dimensionless groups. In details, we use streaming current measurements to obtain an empirical expression for the zeta potential of borosilicate in contact with an aqueous electrolyte of defined ionic strength and pH value. A variety of packed beds are made from binary mixtures of borosilicate microspheres. The ratio of the particle diameter to the packed bed diameter is kept sufficiently low so that the influence of the packed bed wall on the electroosmotic flow can be neglected. The packed bed characterization reveals that the binary particle mixtures feature a different behavior than packed beds which are made from homogenous particles. We utilize the motion of a capillary interface to measure the electroosmotic superficial velocity in the packed beds. Here, we derive a dynamic model based on Newton’s law for the translational center-of-mass motion of the fluidic system. The model allows for the interpretation of the experimental results in terms of an influence of Joule heating which cannot easily be achieved in terms of temperature measurements. Hence, we consider only results which are not or hardly influenced by Joule heating. Finally, a phenomenological correlation between the dimensionless groups is derived which has sufficient accuracy for many engineering applications such as the design of electroosmotic pumps for chromatography or microfluidic applications. It should be noted that the correlation that we propose is not dependent on the substrate. The packed bed can be made of any granular matter which has a more or less spherical shape, though some of the packed bed parameters have to be known or experimentally derived. Also, the material’s zeta potential in contact with the liquid has to be experimentally determined if this information is not available in the literature. The main limitations of our correlation are that it does not account for Joule heating and the influence of the packed bed wall. Nevertheless, electroosmotic pumps can be designed such that these factors have no major relevance. This should be even easier for microchannels where there is increased heat dissipation due to enhanced heat transfer over the channel walls which is another scaling effect of the high surface-to-volume ratio. Here, the problem of a high particle to channel diameter (wall influence) could be mitigated by considering nano-size granular materials. In future works, the correlation could be expanded so that it accounts for the non-isothermal conditions arising from Joule heating as well as the influence of the packed bed wall on the electroosmotic flow, though the incorporation of these parameters would increase the number of required experiments tremendously.