Introduction

In delay-and-sum (DAS) beamforming, which is the standard beamforming technique for medical ultrasound imaging, signal components from undesired positions remain because of sidelobe components. These unnecessary signals cause artifacts and contrast degradation in B-mode images. Apodization, which weights a preset window function to the received signals of individual elements, is applied as a general method to reduce the sidelobe components at the expense of lateral resolution and signal-to-noise ratio (SNR) [1]. Generally, apodization is not applied (set the weights of all elements to 1) in the deep region to prevent SNR degradation.

Numerous adaptive beamforming techniques have been proposed to reduce the unnecessary signals contained in received signals [2,3,4]. Coherence-based beamforming (CBB) [5,6,7,8,9,10,11,12], which is one of the techniques, is effective in reducing unnecessary signals caused by sidelobes with low computational complexity. In CBB, the coherence factor (CF) [5, 13, 14], which represents the coherence among the received signals, is weighted to the signal after DAS to reduce the brightness value of the pixel where the unnecessary signal is dominant.

Speckle noises [15, 16] are generated in B-mode images of the human body owing to the interference of sound waves from many scatterers. Speckle noise is a variation of the brightness value that is not directly related to the structure in the human body. In ultrasound diagnosis, lesions are often observed from minute changes in brightness, and the speckle noises interfere with diagnosis by lowering the contrast-to-noise ratio (CNR) [17]. When applying CBB, it is necessary to focus on the CNR as well as the effect of reducing unnecessary signals. The generalized coherence factor (GCF) [6, 7, 18], which is one of the factors used for CBB, focuses on the depiction of diffused scattering media, and has a significantly better CNR than other factors [19].

Recently, high-performance beamforming techniques including CBB have been realized in real time by improving the performance of field-programmable gate arrays (FPGA), central processing units (CPUs), and graphics processing units (GPUs) [20, 21]. The synthetic transmit aperture (STA) [22,23,24,25,26,27] technique, which realizes dynamic-transmit focusing, can also be realized with commercial ultrasonic diagnostic equipment. However, the STA technique requires dozens of times more DAS processing for each transmission. Therefore, a technology with a lower computational complexity is required to incorporate CBB into the STA. In contrast, ultrasonic diagnostic equipment has been made smaller and more portable. To achieve high image quality with limited computing power for such a model, it is necessary to reduce the computational complexity of CBB, making it possible to expand the image quality with a wider range of models.

The aim of this study is to reduce the computational complexity of the GCF [6], which has better CNR than other factors used in CBB. With the GCF, it is necessary to generate an analytic signal for the received signal of each element and perform a discrete Fourier transform (DFT) in the element direction at each sample point. Therefore, the computational complexity is high compared to the standard DAS beamformer. We have shown in a previous study [28] that generation of the analytic signals can be omitted, and the GCF value can be calculated from real signals. In the present study, we propose a method that further reduces the computational complexity of the GCF value calculation by binarizing the real input signals. Moreover, the performance difference between the proposed method and conventional GCF is verified, and the validity of the proposed method is evaluated.

Conventional methods

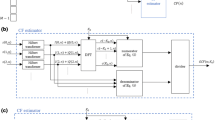
Figure 1a shows the system block diagram for CBB using GCF. The focused beam is generated from received signals in the number of channels connected to the ultrasound diagnostic apparatus. The received signals in the channels are converted to digital signals discretized in the time direction by analog-to-digital converters (ADC) and delayed to in phase for waves from the focus point. The GCF is calculated from the received signals after delay processing and before summation, and then used as a weighting value for the signal \({x}_{\mathrm{in}}(n,l)\) after applying DAS [6]. Here, \(n\) is the sample number in the time direction and \(l\) is the scan line number. By weighting the GCF value to the signal \({x}_{\mathrm{in}}(n,l)\), \({x}_{\mathrm{in}}(n,l)\) including unnecessary signals is suppressed and output as a signal \({x}_{\mathrm{out}}(n,l)\). This process is applied at each focus point corresponding to \((n,l)\) and repeated at all positions. However, as the GCF decreases to a very small value around the strong scatterer, the brightness of the surrounding diffused scattering medium is significantly reduced, and a dark region artifact (DRA) is generated [29]. Therefore, to apply GCF to a B-mode image, it is necessary to adjust the reduction effect. In the present study, similar to the sign coherence factor (SCF) [8], the index \(p\) in Eq. (1) was used as the weight:

$$x_{{{\text{out}}}} \left( {n,l} \right) = \left[ {GCF\left( {n,l} \right)} \right]^{p} x_{\text{in}} \left( {n,l} \right).$$
(1)
Fig. 1
figure 1

a System block diagram for coherence-based beamforming and b input/output of the LUT

Full size image

Adjustment by the power \(p\) is implemented using a look-up table (LUT), as outlined in Fig. 1a. If \(p<1\) is set to weaken the reduction effect in DRA, the relationship between \(GCF(n,l)\) and \({\left[GCF(n,l)\right]}^{p}\) is as shown in Fig. 1b.

Calculation of the GCF value is described next. When the analytic signal generated from the received signal of the channel number \(m (m=0, 1, \cdots , M-1)\) is represented by \(I\left(m,n,l\right)+\mathrm{j}Q(m,n,l)\), the GCF is calculated from Eq. (2) using the Fourier coefficient \({S}_{\mathrm{IQ}}\left(k,n,l\right)\) obtained by the DFT of \(I\left(m,n,l\right)+\mathrm{j}Q(m,n,l)\) in the \(m\)-th direction [6]:

$$GCF\left(n,l; {K}_{0}\right)=\frac{\sum_{k=-{K}_{0}}^{{K}_{0}}{\left|{S}_{\mathrm{IQ}}\left(k,n,l\right)\right|}^{2}}{M\cdot \sum_{m=0}^{M-1}{\left|I\left(m,n,l\right)+\mathrm{j}Q\left(m,n,l\right)\right|}^{2}} ,$$
(2)

where \(k\) is the frequency index in the \(m\)-th direction, and \(k=-K,-K+1,\dots ,0,\dots ,K-1, \left(K=M/2\right)\) for an even number \(M\). The GCF value is the ratio of the power value of all frequency components (denominator) to that of the DC vicinity components represented by \([-{K}_{0}, {K}_{0}] (\mathrm{numerator})\). Figure 2a shows the block diagram for calculating the GCF value using Eq. (2). Generation of the analytic signal in each channel requires processing such as mixers and filters at a high sampling frequency in the \(n\)-th direction. Therefore, when these processes are applied to all the channel signals, the computational complexity increases significantly. Therefore, we proposed a method for calculating the GCF value from real signals without generating analytic signals [28]. When generation of the analytic signal is omitted and the GCF value is calculated from the real signals, a frequency component that is twice the frequency of the received signal is generated in the \(n\)-th direction. It was demonstrated that GCFreal obtained by removing this component using a low-pass filter (LPF) was equivalent to the GCF in Eq. (2). In Eq. (2), replacing the analytic signal \(I\left(m,n,l\right)+\mathrm{j}Q(m,n,l)\) with the real signal \(s\left(m,n,l\right)\), and \({S}_{\mathrm{IQ}}\left(k,n,l\right)\) with \(S\left(k,n,l\right)\), then adding LPFs to the numerator and denominator in the \(n\)-th direction, GCFreal is expressed as

Fig. 2
figure 2

System block diagram for a conventional GCF and b GCFB estimators

Full size image
$${GCF}_{\mathrm{real}}\left(n,l; {K}_{0}\right) =\frac{{\sum }_{h=-{N}_{\mathrm{f}}}^{{N}_{\mathrm{f}}}\left[{f}_{\mathrm{LPF}}\left(h\right)\cdot \left\{\sum_{k=-{K}_{0}}^{{K}_{0}}{\left|\left.S(k,n-h,l\right)\right|}^{2}\right\}\right]}{{\sum }_{h=-{N}_{\mathrm{f}}}^{{N}_{\mathrm{f}}}\left[{f}_{\mathrm{LPF}}\left(h\right)\cdot \left\{M\sum_{m=0}^{M-1}{\left|\left.s(m,n-h,l\right)\right|}^{2}\right\}\right]}.$$
(3)

Equation (3) shows the case where a finite impulse response low-pass filter (FIR-LPF) with coefficients \({f}_{\mathrm{LPF}}\left(h\right), (h=-{N}_{\mathrm{f}}\dots {N}_{\mathrm{f}})\) is used as the LPF.

Generalized coherence factor estimated from binarized signals (GCFB)

In the present study, we propose a method that further reduces the computational complexity of Eq. (3), which calculates the GCF value without the generation of analytic signals. The input real signal \(s\left(m,n,l\right)\) is binarized as

$$u\left(m,n,l\right)=\left\{\begin{array}{c}-1\,\text{ if }\,s (m, n,l)<0,\\ +1\,\text{ if }\,s (m,n,l)\ge 0,\end{array}\right.$$
(4)

and the DFT for \(u (m,n,l)\) in the \(m\)-th direction is given by

$$U\left(k,n,l\right)=\sum_{m=0}^{M-1}u \left(m,n,l\right)\mathrm{exp}\left[-\mathrm{j}\frac{2mk\uppi }{M}\right].$$
(5)

Because \(u(m,n,l)\) is 1 or − 1, Eq. (5) can be calculated by adding and subtracting complex exponential functions. Replacing the real signal \(s\left(m,n,l\right)\) with the binary signal \(u\left(m,n,l\right)\), and \(S\left(k,n,l\right)\) with \(U\left(k,n,l\right)\), Eq. (3) is expressed as

$$GCFB\left(n,l; {K}_{0}\right) =\frac{{\sum }_{h=-{N}_{f}}^{{N}_{f}}\left[{f}_{\mathrm{LPF}}\left(h\right)\cdot \left\{\sum_{k=-{K}_{0}}^{{K}_{0}}{\left|\left.U(k,n-h,l\right)\right|}^{2}\right\}\right]}{{\sum }_{h=-{N}_{f}}^{{N}_{f}}\left[{f}_{\mathrm{LPF}}\left(h\right)\cdot \left\{M\sum_{m=0}^{M-1}{\left|\left.u(m,n-h,l\right)\right|}^{2}\right\}\right]}.$$
(6)

The denominator is a fixed value because \({\left|\left.u(m,n,l\right)\right|}^{2}=1\), so LPF can be omitted, and Eq. (6) becomes

$$GCFB\left(n,l; {K}_{0}\right) =\frac{{\sum }_{h=-{N}_{f}}^{{N}_{f}}\left[{f}_{\mathrm{LPF}}\left(h\right)\cdot \left\{\sum_{k=-{K}_{0}}^{{K}_{0}}{\left|\left.U(k,n-h,l\right)\right|}^{2}\right\}\right]}{{M}^{2}}.$$
(7)

The computational complexity of GCFB can be reduced compared to GCFreal because (1) the DFT of Eq. (5) can be calculated only by addition and subtraction, (2) the addition and LPF of the denominator in Eq. (6) can be omitted, and (3) the division of Eq. (7) can be replaced with multiplication of the fixed value \(1/{M}^{2}\). The configuration for calculating the GCFB from Eq. (7) is shown in Fig. 2b, which is simpler than the configuration of the conventional GCF shown in Fig. 2a.

Comparison of computational load of conventional GCF, GCFreal, and GCFB

Table 1 shows the number of multiplications and additions required to calculate the GCF, GCFreal, and GCFB values for each spatial sample. Here, it is assumed that the order \(2{N}_{\mathrm{f}}\) of the Hilbert transform filter required in the conventional GCF is similar to the order of the LPF used in Eq. (3) or Eq. (7). For GCFreal and GCFB, the frequency components were calculated only on the positive side because the frequency spectrum of a real signal is positive–negative symmetric. To demonstrate the calculation complexity of each method, an example where the channel number \(M=96\), DC vicinity range \({K}_{0}=1\), and Hilbert transform or LPF order \(2{N}_{\mathrm{f}}=20\) is shown. For GCFreal, the number of multiplications and additions is approximately 1/6 of those for GCF. Furthermore, for GCFB, the number of multiplications is 1/20 or less of those for GCFreal. For GCFB, the calculation complexity can be further reduced by replacing the division in Eq. (7) with multiplication of \(1/{M}^{2}\). Especially in ASICs and FPGAs, the circuit scale can be condensed by reducing the number of such operations. However, reduction of the calculation depends on the algorithm of the compiler and configuration of the processor.

Table 1 Computational load in conventional GCF, GCFreal, and GCFB
Full size table

In apodization, which is generally used to reduce the sidelobe components, the signal of each channel is weighted using a window function; therefore, multiplications by the number of channels are required. GCFB can be realized with a smaller number of multiplications.

When baseband demodulation is used to generate the analytic signals in GCF instead of the Hilbert transform, multiplication of the mixers and LPFs for both the real (I) and imaginary (Q) parts is required, and the calculation complexity in this part increases. Instead, the calculation complexity can be reduced by lowering the sampling rate of the subsequent processing. However, regardless of whether the Hilbert transform or baseband demodulation is used, the number of calculations becomes large compared to the subsequent processing. Therefore, the total number of calculations is smaller when the analytic signal generation is omitted [28]. Second-order sampling can be used to generate approximate analytic signals with a low number of calculations, but it is not considered in the present study because it limits the sampling rate of the ADC and causes serious errors in wideband transmission [30].

Evaluation methods

Comparison of GCFreal and GCFB values

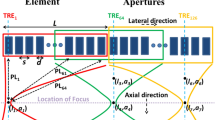
Because the signal binarization in the proposed method is a special process, it is difficult to express the general relationship between \(S (k,n,l)\) and \(U (k,n,l)\). Consequently, it is difficult to theoretically predict how the binarization process will affect the weighting of the received signal. Therefore, we focus on the effect of reducing unnecessary signals caused by sidelobes, and the ability to visualize diffused scattering media. As shown in Fig. 3, the GCFreal and GCFB values were compared for the following two cases using the received signal of each channel generated by simulation and acquired from a phantom using an ultrasonic diagnostic apparatus.

Fig. 3
figure 3

Geometry for generating received signals in the simulation. a Receiving focus region for one scatterer. b Receiving focus point in a diffused scattering medium

Full size image

(a) A receiving focus region around one scatterer.

(b) A receiving focus point in a diffused scattering medium.

We evaluated the effect of binarization by comparing GCFreal. We used a convex probe, which is mainly used for observing the abdomen, where there are many regions of diffused scattering media.

Evaluation of B-mode images weighted by GCFreal and GCFB

The contrast performances of B-mode images obtained with GCFreal and GCFB were evaluated using the following contrast and CNR values:

$$Contrast=20{\mathrm{log}}_{10}\left(\frac{{\mu }_{1}}{{\mu }_{2}}\right) ,$$
(8)
$$CNR=\frac{\left|{\mu }_{1}-{\mu }_{2}\right|}{\sqrt{{{\sigma }_{1}}^{2}+{{\sigma }_{2}}^{2}}} ,$$
(9)

where \({\mu }_{i}\) and \({\sigma }_{i}\) are the mean value and standard deviation of the envelope signal in region \(i\), respectively. As shown in Eq. (1), when the GCF value is weighted to the signal after DAS, the weighting effect is adjusted by the power of \(p\). The \(p\)-values for GCFreal and GCFB are defined as \({p}_{\mathrm{GCFreal}}\) and \({p}_{\mathrm{GCFB}}\), respectively. \({p}_{\mathrm{GCFreal}}\) is determined so that DRA does not occur near a strong scatterer. Moreover, \({p}_{\mathrm{GCFB}}\) is determined in the same region so that the mean value of GCFreal with \({p}_{\mathrm{GCFreal}}\) and that of GCFB with \({p}_{\mathrm{GCFB}}\) are equal. The contrast and CNR values are calculated from the signals of both methods adjusted by these coefficients.

Simulations and experimental setup

RF data generation by simulation

The signal change in the channel direction that occurs based on the scatterer and receiving focus positions is generated simply. As shown in Fig. 3a, b polar coordinate system \((R+r,\theta )\) is set based on the center of the curvature of the convex probe surface; here, \(R\) is the radius of the curvature of the convex probe, \(r\) is the distance from the probe surface, and \(\theta\) is 0° in the vertical direction of the probe. The position of the scatterer with number \(q\) is represented by \(({R+r}_{q},{\theta }_{q})\). Considering the receiving focus point \((R+{r}_{\mathrm{f}}(n),{\theta }_{\mathrm{f}}(l))\), where \({r}_{\mathrm{f}}(n)\) is the receiving focus distance and \({\theta }_{\mathrm{f}}(l)\) is the azimuth angle of the \(l\)-th scanning line,\({r}_{\mathrm{f}}(n)\) is represented by

$${r}_{\mathrm{f}}\left(n\right)=n/{f}_{\mathrm{s}}\cdot c/2,$$
(10)

where \(n\) is the sample number in the time direction, \({f}_{\mathrm{s}}\) is the sampling frequency of the receiving signal, and \(c\) is the sound velocity. To consider the propagation and delay times, we converted to the Cartesian coordinate system in which the origin was set on the probe surface, the \(\theta =0^\circ\) direction was the \(z\) axis, and the azimuth direction was the \(x\) axis, as shown in Fig. 3a. The coordinates of the scatterer \(({x}_{q}, {z}_{q})\) and receiving focus \(\left({x}_{\mathrm{f}}, {z}_{\mathrm{f}}\right)\) are represented by

$$\begin{gathered} x_{q} = \left( {R + r_{q} } \right)\sin \theta_{q} , \hfill \\ z_{q} = \left( {R + r_{q} } \right)\cos \theta_{q} - R , \hfill \\ \end{gathered}$$
(11)
$$\begin{gathered} x_{\mathrm{f}} \left( {n,l} \right) = \left( {R + r_{\mathrm{f}} \left( n \right)} \right)\sin \theta_{\mathrm{f}} \left( l \right), \hfill \\ z_{\mathrm{f}} \left( {n,l} \right) = \left( {R + r_{\mathrm{f}} \left( n \right)} \right)\cos \theta_{\mathrm{f}} \left( l \right) - R. \hfill \\ \end{gathered}$$
(12)

The signal obtained by delaying the received signal from the scatterer \(({x}_{q}, {z}_{q})\) is represented by

$$\begin{gathered} s^{\prime} \left( {m,n,l,x_{q} ,z_{q} } \right) \hfill \\ = \sum\limits_{{m_{\mathrm{T}} = M_{s} }}^{{M_{e} }} {G\left( { - \tau \left( {m_{\mathrm{T}} ,m,x_{q} ,z_{q} } \right) + \tau_{d} \left( {m_{\mathrm{T}} ,m,x_{\mathrm{fTx}} \left( l \right),z_{\mathrm{fTx}} \left( l \right),x_{\mathrm{f}} \left( {n,l} \right),z_{\mathrm{f}} \left( {n,l} \right)} \right)} \right)}, \hfill \\ \end{gathered}$$
(13)

where

$$\left.G(t\right)=\mathrm{exp}\left[-{2\left\{\uppi \sigma t\right\}}^{2}\right]\cdot \mathrm{cos}\left[2\uppi {f}_{0}t\right]$$
(14)

is a Gaussian pulse with center frequency \({f}_{0}\) and − 6 dB bandwidth \(\sigma\).

$$\begin{gathered} \tau \left( {m_{\mathrm{T}} ,m,x_{q} ,z_{q} } \right) = \sqrt {\left( {x_{\mathrm{e}} \left( {m_{\mathrm{T}} } \right) - x_{q} } \right)^{2} + \left( {z_{\mathrm{e}} \left( {m_{\mathrm{T}} } \right) - z_{q} } \right)^{2} } /c + \hfill \\ \sqrt {\left( {x_{\mathrm{e}} \left( m \right) - x_{q} } \right)^{2} + \left( {z_{\mathrm{e}} \left( m \right) - z_{q} } \right)^{2} } /c \hfill \\ \end{gathered}$$
(15)

is the propagation time until the sound wave transmitted from the element with a number \({m}_{\mathrm{T}}(={M}_{s},{M}_{s}+1,\dots ,{M}_{e})\) is reflected by the scatterer \(({x}_{q},{z}_{q})\) and received by the receiving element with number \(m\).

$$\begin{gathered} \tau_{d} \left( {m_{\mathrm{T}} ,m,x_{\mathrm{fTx}} \left( l \right),z_{\mathrm{fTx}} \left( l \right)} ,x_{\mathrm{f}} \left( n,l \right) ,z_{\mathrm{f}}\left( n,l \right) \right) \hfill \\ =\sqrt {\left( {x_{\mathrm{e}} \left( m_{\mathrm{T}} \right) - x_{\mathrm{fTx}} \left( l \right) } \right)^{2} + \left( {z_{\mathrm{e}} \left( m_{\mathrm{T}} \right) - z_{\mathrm{fTx}} \left( l \right) } \right)^{2}} /c - {r_{\mathrm{fTx}} \mathord{\left/ {\vphantom {{r_{f} \left( n \right)} c}} \right. \kern-\nulldelimiterspace} c} +{r_{\mathrm{f}}\left( n \right)}/c +\sqrt {\left( {x_{\mathrm{e}} \left( m \right) - x_{\mathrm{f}} \left( n,l \right) } \right)^{2} + \left( {z_{\mathrm{e}} \left( m \right) - z_{\mathrm{f}} \left( n,l \right) } \right)^{2}} /c \\ \end{gathered}$$
(16)

represents the sum of the transmitting delay time given to the element with the number \({m}_{\mathrm{T}}\) and the receiving delay time given to the element with number \(m\).\({(x}_{\mathrm{e}}\left(m\right){, z}_{\mathrm{e}}\left(m\right))\) represents the element position with number \(m\).\({r}_{\mathrm{fTx}}\) represents the transmission focus distance, and the azimuth angle of the transmission focus is \({\theta }_{\mathrm{f}}(l)\), which is the same as the receiving focus. The transmission focus coordinate \(\left({x}_{\mathrm{fT}x}, {z}_{\mathrm{fT}x}\right)\) in the Cartesian coordinate system is

$$\begin{gathered} x_{\mathrm{fTx}} \left( l \right) = \left( {r_{\mathrm{fTx}} + R} \right)\sin \theta_{\mathrm{f}} \left( l \right), \hfill \\ z_{\mathrm{fTx}} \left( l \right) = \left( {r_{\mathrm{fTx}} + R} \right)\cos \theta_{\mathrm{f}} \left( l \right) - R. \hfill \\ \end{gathered}$$
(17)

As shown in Fig. 3b, when focusing on a diffused scattering medium, the delayed signals are generated by superimposing the received signals from \(Q\) scatterers at different positions as follows:

$$s_{{{\text{sim}}}} \left( {m,n,l} \right) = \sum\limits_{q=1}^{Q} {{s^{\prime}} } \left( {m,n,l,x_{q} ,z_{q} } \right).$$
(18)

The GCFreal value is calculated by substituting the real signal \({s}_{\mathrm{sim}}\left(m,n,l\right)\) into \(s(m,n,l)\) in Eq. (3). The GCFB value is calculated from Eq. (7) after substituting \({s}_{\mathrm{sim}}\left(m,n,l\right)\) into \(s(m,n,l)\) in Eq. (4). In the simulation, the amplitude values of the received signals from the anechoic region are all zero. In this case, because the signal values are all + 1 according to Eq. (4), the GCFreal and GCFB values are 1. To avoid this, random noise with a maximum of − 40 dB relative to the amplitude of the Gaussian pulse in Eq. (14) was added to the signal for each channel. In the simulation, the same conditions were used as the experimental data acquisition conditions presented later (Table 2). The center frequency \({f}_{0}\) and − 6 dB bandwidth \(\sigma\) of the Gaussian pulse were set to 3 MHz and 1.5 MHz, respectively, according to the experimental data.

Table 2 Input data conditions in the simulations and the experiments
Full size table

Experimental RF data acquisition

The experimental RF data were acquired using the ultrasonic diagnostic system ProSound α10 (Hitachi, Tokyo, Japan) with ultrasonic multipurpose phantom 403GS-LE (Gammex, WI, USA) as the measurement object. A convex probe (UST-9130, center frequency 3.5 MHz, radius of curvature 60 mm, element pitch 0.38°) was used, and the number of channels was \(M=96\). In this measurement, an image was formed from 312 received scan lines in the range of a 60° viewing angle. Both the transmitting and receiving apertures for forming the scan line were set with the scan line as the center. Table 2 lists the transmitting and receiving conditions.

Results

Comparison of GCFreal and GCFB values for one scatterer

In the present study, all the verifications were performed under the condition of \({K}_{0}=1\), which was suitable for reducing unnecessary signals in a previous study [28]. Figure 4 shows the simulation data. Figure 4a–c show the values of DAS, GCFreal, and GCFB, respectively, where the vertical axis is the depth \({r}_{\mathrm{f}}(n)\) and the horizontal axis is the angle \({\theta }_{\mathrm{f}}(l)\) of the receiving focus point, when there is one scatterer at (\({r}_{q},{\theta }_{q}\)) = (46.2 mm, 0°). For \({\theta }_{\mathrm{f}}(l)\), only the positive side is shown because the result is positive–negative symmetric. For DAS, the amplitude value of the envelope is displayed in decibels. Similarly, Fig. 4d–f show the values of DAS, GCFreal, and GCFB, respectively, when there is one scatterer at (\({r}_{q},{\theta }_{q}\)) = (65.8 mm, 0°), and Fig. 4g–i show those when there is one scatterer at (\({r}_{q},{\theta }_{q}\)) = (85.3 mm, 0°). Since GCFreal and GCFB are evaluation values of coherence, they are large over a wider range in the depth direction than DAS, which represents the amplitude value. In Fig. 4a, b, it can be observed that in the region where the DAS value increased because of the sidelobe, the GCFreal value also increased. However, this sidelobe influence was hardly observed in Fig. 4c. Similar tendencies were observed at all depths (Fig. 4d–i). These results suggest that GCFB is more effective at reducing the unnecessary signals caused by the sidelobe components than GCFreal.

Fig. 4
figure 4

Comparison of GCFreal and GCFB values around scatterers in the simulation data. a DAS, b GCFreal, and c GCFB values for the scatterer at \(r\) = 46.2 mm. d DAS, e GCFreal, and f GCFB values for the scatterer at \(r\) = 65.8 mm. g DAS, h GCFreal, and i GCFB values for the scatterer at \(r\) = 85.3 mm. GCFreal and GCFB values at j dashed line 1 and k dashed line 2 in b. l \(s(m,n,l)\) and \(u(m,n,l)\) at the position indicated by the arrow in b

Full size image

Figure 4j shows the values of GCFreal and GCFB at the scatterer depth indicated by dashed line 1 in Fig. 4b. When \(\theta_{\mathrm{f}} \left( l \right) < 0.5^{^\circ }\), the phases among the channels were roughly aligned or changed slowly, so that the GCFreal and GCFB values were both close to 1. However, there was a region where the GCFB value was approximately 0.2 lower than that of GCFreal. This is because high-frequency components in the channel direction are generated in binarized signals in the case of GCFB. In addition, GCFreal and GCFB increase again around \(\theta_{\mathrm{f}} \left( l \right) = 0.4^{^\circ }\), because the signal is concentrated on the component of \(k=1\). Moreover, when \(\theta_{\mathrm{f}} \left( l \right) > 1^{^\circ }\), while GCFreal was approximately 0, GCFB fluctuated by a small value because of the influence of binarization. Figure 4k shows the GCFreal and GCFB values at the depth indicated by dashed line 2 in Fig. 4b. GCFreal exhibited a higher value than GCFB when \({\theta }_{\mathrm{f}}(l)\) was in the range of 0.5 to 2.0° because of the influence of the sidelobes. Figure 4l shows the real \(s(m,n,l)\) and binarized \(u(m,n,l)\) signals in the channel direction at the position affected by the sidelobe indicated by the arrow in Fig. 4b. Here, the amplitude values of \(u(m,n,l)\) were normalized so that the power values of both signals were equal. In \(s(m,n,l)\) used to calculate GCFreal, the received signal from the scatterer was dominant in the channel of \(m>60\). The GCFreal value increased because of this signal, and the sidelobe component was not sufficiently reduced.

Figure 5a is a B-mode image constructed from the obtained experimental data. The GCFreal and GCFB values around the three wires surrounded by yellow squares are shown in Fig. 5b–g. The vertical axis is the depth \({r}_{\mathrm{f}}(n)\), and the horizontal axis is \(\theta_{\mathrm{f}}^{^{\prime}} \left( l \right)\), where the azimuth angle relative to the scanning line passing through each wire (0°) is shown as \(\theta_{\mathrm{f}}^{^{\prime}} \left( l \right)\). Figure 5b, c show the GCFreal and GCFB values around the wire at \(r\) = 46.2 mm, Fig. 5d, e show the values at \(r\) = 65.8 mm, and Fig. 5f, g show the values at \(r\) = 85.3 mm.

Fig. 5
figure 5

Comparison of GCFreal and GCFB values around wire targets in the experimental data. a B-mode image of the data. b GCFreal and c GCFB values for the wire at \(r\) = 46.2 mm. d GCFreal and e GCFB values for the wire at \(r\) = 65.8 mm. f GCFreal and g GCFB values for the wire at \(r\) = 85.3 mm. GCFreal and GCFB values at h dashed line 1 and i dashed line 2 in b. j \(s(m,n,l)\) and \(u(m,n,l)\) at the position indicated by the arrow in b

Full size image

Figure 5h shows the GCFreal and GCFB values at dashed line 1 shown in Fig. 5b. Similar to the simulation results, GCFB was slightly lower than GCF at \(\theta_{\mathrm{f}}^{^{\prime}} \left( l \right) < 0.5^{^\circ }\), where the signal coherence was high. GCFreal was approximately 0 at \(1^\circ <\theta_{\mathrm{f}}^{^{\prime}} (l)<3^\circ\). When the signal after DAS is weighted using this value, the amplitude is significantly reduced and a DRA occurs. However, the value of GCFB was slightly larger than that of GCFreal in this region, which suppressed the occurrence of DRA. Figure 5i shows the GCFreal and GCFB values at dashed line 2 in Fig. 5b. Similar to the simulation results, it can be confirmed that GCFreal was large because of the influence of the sidelobe components at \(0.5^\circ <\theta_{\mathrm{f}}^{^{\prime}} (l)<1^\circ\). Figure 5j shows the real \(s(m,n,l)\) and binarized \(u(m,n,l)\) signals at the positions affected by the sidelobe indicated by the arrows in Fig. 5b. Similar to Fig. 4l, the amplitude values of \(u(m,n,l)\) were normalized so that the power values of both signals were equal. Similar to the simulation results, in the case of GCFreal, the received signal from the wire was dominant in the channel at the end \((m>70)\).

Comparison of GCFreal and GCFB values for diffused scattering media

Figure 6a shows the GCFreal and GCFB values at the receiving focus points in the diffused scattering media in the simulation data. The scatterer density was set to 100/mm2 to generate sufficiently dense scatterers with respect to the wavelength (0.5 mm). The mean value after repeating the simulation 100 times by changing the arrangement of the scatterers at each depth is shown. The GCFreal and GCFB values changed depending on the depth and increased near the transmission focus depth (105 mm). This is because the influence of the signals from the scatterers near the focus point was more dominant as the transmission beam width became narrower, and the coherence of the signals among the channels increased. The GCFB values were smaller than the GCFreal values, and when they were used as the weight values, the brightness of the diffused scattering media was lower than that of GCFreal.

Fig. 6
figure 6

Comparison of GCFreal and GCFB at diffused scattering medium. a GCFreal and GCFB values in the diffused scattering medium for the simulation data. b Changes in GCFreal and GCFB values relative to the noise level. c Regions for estimating GCFreal and GCFB values for the experimental data. d GCFreal and GCFB values in diffused scattering media shown in c

Full size image

Figure 6b shows the GCFreal and GCFB values when the noise level given to each channel was changed at \({r}_{\mathrm{f}}(n)\) = 100 mm in a diffused scattering medium. The noise level is expressed as the mean value of DAS in the absence of noise as 0 dB. The values of GCFreal and GCFB decreased with the increase in noise level, making the difference between the two small.

The results of the experimental data are shown in Fig. 6c, d. Figure 6c is a B-mode image constructed by DAS. The mean GCFreal and GCFB values calculated for each region indicated by the yellow circles are shown in Fig. 6d. Similar to the simulation results, the GCFB values were smaller than the GCFreal values. It can also be confirmed that the difference between the GCFreal and GCFB values decreased as the values decreased. In the experimental data, because the SNR decreased as a result of attenuation with depth, the GCFreal and GCFB values were smaller than the simulation results in Fig. 6a, and were highest at 85 mm shallower than the transmission focus.

B-mode images and CNR values by CBB

Figure 7a–c show the B-mode images yielded by DAS and CBB using GCFreal and GCFB, obtained from the acquired experimental data. The dynamic range of the display was 80 dB. For GCFreal, \({p}_{\mathrm{GCFreal}}\) was set to 0.2 to avoid the occurrence of DRA around the wire indicated by the arrow in Fig. 7a. As a result of adjusting \({p}_{\mathrm{GCFB}}\) so that the mean value of GCFB in the region near the wire was similar to that of GCFreal, \({p}_{\mathrm{GCFB}}\) was set to 0.26. Figure 7b, c show the images adjusted using these \(p\)-values. Moreover, Fig. 7d shows the azimuth brightness profile of each image averaged in the depth direction for the region shown by the yellow square in Fig. 7b. In the case of GCFreal and GCFB, the brightness of the diffused scattering medium was lower than that of DAS, but more than that, the brightness of the anechoic region was significantly reduced owing to the unnecessary signal reduction effect. Table 3 shows the contrast and CNR values of each image calculated from Eqs. (8) and (9), with the red and yellow squares shown in Fig. 7a as regions 1 and 2, and with the green and yellow squares shown in Fig. 7a as regions 1 and 2, respectively. In the case of GCFreal and GCFB, both the contrast and CNR were superior to DAS, and the same degree of contrast improvement was observed.

Fig. 7
figure 7

B-mode images generated by a DAS and those weighted by b GCFreal and c GCFB. d Lateral profiles of the anechoic region shown by the square in b

Full size image
Table 3 Contrast and CNR values of the B-mode image generated using each method
Full size table

Discussion

The advantages of GCFB over GCFreal are discussed below. For signals such as those shown in Figs. 4l and 5j, positive signals near \(m=90\), which are considered to be signals from the strong scatterer around the receiving focus point, are dominant. Consequently, the DAS value increases even though there is no scatterer at the focus point. This is the influence of the sidelobe component. In this case, because the DC component increases, the numerator of Eq. (3) also increases, making the GCFreal value large and similar to that of DAS. However, in the case of GCFB calculated from the binarized signal \(u(m,n,l)\), the amplitude value of the signal is not considered, and the signal received by more channels becomes dominant. For example, for the signal shown in Fig. 4l, because there is no scatterer at the receiving focus point, all signals at \(m<60\), which are not signals from the scatterer, are noise. Because the GCFB uses binarization, these noise signals become dominant. The effect is relatively weak because the number of receiving channels is small for signals near \(m=90\). Consequently, the GCFB value is smaller than that of GCFreal, which considers the amplitude, at the position where the sidelobe component is generated in DAS. As shown in Fig. 5j, when the focus point is in a diffused scattering medium, the signals from the diffused scattering medium are received by all channels. However, some channels receive signals from the wire located at a position different from the focus point. Therefore, the calculated GCFB value is significantly influenced by the diffused scattering medium, and the influence of the sidelobe component can be relatively suppressed. From the above, when the signal caused by the sidelobe is larger than the original signal of the receiving focus point and becomes an unnecessary signal, GCFB has an excellent reduction effect compared to GCFreal.

Similarly, even in the vicinity of a strong scatterer where DRA is likely to occur, the influence of the signal from the focus point is stronger than that from the strong scatterer at a position different from the focus point in GCFB. Therefore, the value does not decrease as significantly as GCFreal, and GCFB suppresses the occurrence of DRA more than GCFreal.

From the above, GCFB is superior to GCFreal in reducing unnecessary signals and can suppress the occurrence of DRA. The wider the bandwidth, the fewer the channels that receive the signal from the strong scatterer, and the stronger this tendency becomes. This feature generally holds regardless of the measurement target.

The disadvantages of GCFB versus GCFreal are discussed below. As can be observed in Figs. 4j and 5h, both GCFB and GCFreal have values close to 1 near \({\theta }_{\mathrm{f}}\left(l\right)=0^\circ\), where the receiving focus and scatterer position match. However, in the vicinity of \({\theta }_{\mathrm{f}}\left(l\right)=0.3^\circ\), where the receiving focus is slightly shifted from the scatterer, a slight phase change occurs in the signal in the channel direction. High-frequency components are generated in the frequency spectrum in the channel direction by binarizing the signal, such that GCFB has a smaller value than GCFreal. The advantage of GCF is that it becomes a large value and the brightness can be maintained even when there is a slight phase change, whereas GCFB may reduce such signals. However, if \(p<1\) is adjusted so that DRA does not occur in GCF, a larger GCF value leads to a smaller change in \({\left[GCF(n,l)\right]}^{p}\) with regards to the change in the GCF value, as shown in Fig. 1b. Therefore, for a signal with high coherence, even if there is a slight difference between the GCFB and GCFreal values, the difference between the two after adjustment with the \(p\)-values \((<1)\) is small, having a slight effect on the image quality.

Similarly, for a signal from the diffused scattering medium, as a result of the scattered waves interfering with each other, a phase change occurs in the channel direction [6], and high-frequency components increase because of binarization. Therefore, as shown in Fig. 6a, d, GCFB has smaller values than GCFreal, which may reduce the brightness. Because the GCFB value in the diffused scattering medium is not as large as the GCFB value at the strong scatterer, the brightness value decreases, as shown in Fig. 7d, even if it is adjusted by the \(p\)-value.

As mentioned above, GCFB is superior to GCFreal in terms of its ability to reduce unnecessary signals generated by sidelobes; however, the brightness value of the diffused scattering medium is also reduced. Consequently, the contrast and CNR calculated from the diffused scattering medium and the hypoechoic regions are equivalent to those of GCFreal, as shown in Table 3. However, because the contrast and CNR depend on the degree of reduction in brightness in the diffused scattering medium and the degree of reduction in unnecessary signals, the performances of GCFB and GCFreal are considered to depend on the observation target.

Additionally, since GCF is a process that reduces the brightness of unnecessary signals, the resolution of an image generated using GCF is not inferior to that of DAS. However, since the noise component is also reduced, it may give the impression that spatial high-frequency components are suppressed.

In the present study, to evaluate the effect of binarization, GCFB was verified with GCFreal as a comparator. Because GCF and GCFreal have equivalent values [28], it is considered that the same results can be obtained by comparing GCF and GCFB. In the case of the sign coherence factor (SCF) [8], which is one of the coherence factors, the phase of the signal is binarized to 0° and 180° in calculating the phase coherence factor (PCF) [8], which indicates the variance value of the phase in the channel direction. Similar to the proposed method, the phase variance value is calculated using the mean value of the binarized signals. It is considered that SCF and GCFB \(({K}_{0}=0)\) are similar because the process of calculating the variance value from the mean value of binarized signals is considered to be similar to adjusting the effect (a conversion such as the \(p\)-value). Table 4 summarizes these relationships, and SCF using binarized signals is a special case of GCFB \(({K}_{0}=0)\). By evaluating up to the DC vicinity component \(({K}_{0}>0)\) in GCF, the variation in values can be suppressed in diffused scattering media, and CNR values superior to CF and SCF can be obtained. This effect can also be achieved with GCFB.

Table 4 Relationship between coherence factors
Full size table

Conclusions

In the present study, we proposed a GCFB that binarizes the input real signals to reduce the number of GCF computations. Focusing on the effect of reducing unnecessary signals and the ability to visualize diffused scattering media, the validity of the proposed method was verified using simulation and experimental data. From the results, the contrast performance was superior to DAS in the case of both the conventional method and GCFB. The performance of both methods for improving the CNR may depend on the observation target. Under the conditions in the present study, comparable performance was achieved with both methods. Because GCFB can significantly reduce the computational complexity by binarization, it is potentially applicable for clinical diagnostic equipment.