Generalized coherence factor estimated from real signals in ultrasound beamforming

Abstract

Purpose

The generalized coherence factor (GCF), an adaptive beamforming technique, can reduce unnecessary signals from an unfocused position without reducing the contrast-to-noise ratio. However, the computational complexity of this method is large compared to the conventional delay-and-sum (DAS) beamformer. In the present paper, we propose a novel method to achieve the same reduction effect of unnecessary signals with a smaller computational load than that of the conventional GCF approach.

Methods

One of the factors increasing the computational complexity of the GCF-based beamformer compared with DAS is the generation of analytic signals at receiving elements. We clarified the mechanism of generating unnecessary signal components to enable the calculation of the GCF value directly from real signals without generating analytic signals. Furthermore, we proposed a method to filter out these components without generating analytic signals.

Results

The GCF values obtained using the proposed and conventional methods were compared and verified using the actual data acquired from a phantom with an ultrasound diagnostic system. We also compared the B-mode images. As a result, equivalent GCF values and similar B-mode image quality were achieved with the proposed method with reduced computational complexity.

Conclusion

With the proposed method, generation of analytic signals at receiving elements can be omitted, and as a result, the computational load of the GCF method can be greatly reduced, while preserving the effect of reducing unnecessary signals like with the conventional method.

Introduction

Ultrasound imaging is widely used for medical diagnosis purposes as it provides real-time cross-sectional images of the human body noninvasively. In conventional ultrasound diagnostic systems, the received signals are focused at any position in the B-mode image using delay-and-sum (DAS) beamforming. However, even with the use of DAS beamforming, reflected signals from positions other than the desired one, such as, for example, a signal generated by the sidelobe, cannot be completely removed. Due to such unnecessary signals, artifacts are generated on a B-mode image, and the image quality deteriorates. In ultrasound image diagnosis, the examiner often diagnoses the lesion based on a slight change in brightness. Consequently, the deterioration in the image quality affects the diagnosis and might lead to misdiagnosis and stress on the examiner.

Many adaptive beamformers have been proposed to improve image quality by reducing unnecessary signals contained in received signals. For example, minimum variance beamforming (MVB), which adaptively calculates the weight values of the signals in receiving elements, has been actively studied [1,2,3]. However, the computational complexity of MVB is large, and it is difficult to implement in general ultrasound systems. Coherence-based beamforming (CBB) using the coherence factor (CF) [4, 5] has been proposed as an adaptive beamforming technique with relatively small computational complexity. CF is a factor representing the coherence of the received signals after the delay compensation of individual elements. In CBB, by weighting the CF value to the received signal after DAS, the brightness value of the pixel where the unnecessary signal is dominant is reduced. Moreover, various factors other than CF have been proposed in the literature [6,7,8,9].

Speckle noises [10, 11] are generated in B-mode images as scatterers are uniformly distributed in most parts of the human body. Speckle noise is caused by the interference of sound waves from many scatterers and is a variation of a brightness value that is not directly related to the structure in the human body. In such a region, the phases of the received signals are not completely aligned with each other, and minor phase fluctuations occur. If CF is applied to such a region, it can result in a problem where the average brightness in the region of the diffuse scattering medium is lowered, and speckle noise is emphasized [6, 12]. Although there have been studies seeking to clinically obtain useful information from the characteristics of the speckle noise [13] on B-mode images, enhancement of the speckle noise generally causes degradation of the contrast-to-noise ratio (CNR), which hinders making a correct diagnosis. Therefore, speckle reduction methods, such as spatial compound [14], frequency compound [15], or image processing [16, 17], have been studied and developed. Therefore, when using CBB for imaging of a diffuse scattering medium, it is important not to emphasize speckle noises. The generalized coherence factor (GCF) [6], which is one of the factors used for CBB, can reduce unnecessary signals without emphasizing speckle noise and has CNR higher than that of other factors [12]. As another approach that focuses on the imaging ability in diffuse scattering media, a phase coherence factor (PCF), in which phase variation is suppressed by applying DAS in each divided sub-aperture, has been proposed [18].

Recently, with the improvement in graphical processing units (GPU), high-performance beamforming including CBB can be realized in real time [19, 20]. On the other hand, miniaturization and portability of ultrasonic diagnostic apparatuses have been progressing as well. In such small models and low-end models, it is important to achieve high image quality with limited computing power. Therefore, there is a need for a method with low computational complexity when applying CBB, so that CBB can be expanded to a wider range of models using this technique.

In the present study, we aimed to reduce the computational complexity of the GCF [6], which has CNR higher than that of other factors. The computational complexity of the GCF is higher than that of the DAS beamformer as it requires generation of analytic signals for individual elements and calculation of the discrete Fourier transform (DFT) of the element direction for each pixel. The generation of analytic signals for individual elements is required in many adaptive beamformers including the PCF. To omit the calculation of the DFT of the element direction, a method has been proposed in which the GCF value is estimated from autocorrelation [21]. In the present paper, we propose a method to calculate the GCF values from real signals, omitting generation of analytic signals. It has been reported that the correct GCF value cannot be calculated using real signals due to the presence of the carrier frequency [7]. However, the specific problems related to the presence of the carrier frequency have not been reported in detail. In the present paper, this problem is clarified by theoretically comparing cases where the GCF values are calculated from real signals and where the GCF values are calculated from analytic signals following the conventional method. Then, we propose a method to calculate the value equivalent to the conventional GCF using real signals. To conclude on the applicability of the proposed method, we evaluated the GCF values obtained using the channel data acquired from a phantom with the ultrasonic diagnostic equipment and the B-mode images calculated by the conventional and the proposed methods.

Conventional methods

Coherence-based beamforming [4, 6–9]

Figure 1a shows the system block diagram for CBB using CF. The focused beam is generated from received signals in the number of channels connected to the ultrasound diagnostic apparatus. The received signals in channels are converted to digital signals discretized in the time direction by analog-to-digital converters (ADC) and delayed to be in phase for waves coming from the focus point. The focused signal $x_{{{\text{in}}}} (n)$ is obtained by the sum of delayed signals $s(m,n)$, where $m(m = 0, 1, \ldots , M - 1)$ represents the channel number corresponding to the element, $M$ represents the number of received channels, and $n$ is the sampling number in the time direction. CF is calculated from $s(m,n)$ and then used as a weighting factor for $x_{{{\text{in}}}} (n)$, as described below. As shown in Fig. 1, the calculated CF value can be adjusted using a look-up table (LUT).

Fig. 1

a System block diagram for coherence-based imaging. b GCF estimator. c The proposed method (GCF_real)

Coherence factor (CF) [4]

The CF value $CF(n)$ [4, 5] is obtained as follows:

$$ CF(n) = \frac{{\left| {\mathop \sum \nolimits_{m = 0}^{M - 1} s(m,n)} \right|^{2} }}{{M \cdot \mathop \sum \nolimits_{m = 0}^{M - 1} \left| {s(m,n)} \right|^{2} }}. $$

(1)

The denominator is the total power value (incoherent sum) of the received signals in the channel direction, and the numerator represents the power value of the DC component (coherent sum). As the difference between phases of the received signals among channels is small, the CF value increases because the numerator, which corresponds to the power of the DC component, becomes large. If the received signals are completely in phase and their amplitudes are equal for all channels, the CF value gets the maximum value of 1. However, when the difference between phases of the received signals among channels is large, the CF value decreases, because the power of the DC component becomes small. CF is large when a reflected or scattered wave is received only from the focus point. Therefore, by weighting CF to the signal $x_{{{\text{in}}}} (n)$ after applying DAS, $x_{{{\text{in}}}} (n)$ including unnecessary signals is suppressed. However, as CF becomes too small around the strong scatterer, the signals from the surrounding diffuse scattering medium are excessively reduced, and a dark region artifact is generated [22]. Therefore, to apply CF to a B-mode image, it is necessary to adjust the reduction effect. In the present paper, similarly to the sign coherence factor (SCF) [8], the index $p$ in Eq. (2) was used as a weight:

$$ x_{{{\text{out}}}} (n) = \left[ {CF(n)} \right]^{p} x_{{{\text{in}}}} (n). $$

(2)

The adjustment by the power $p$ is implemented using LUT, as outlined in Fig. 1a.

Generalized coherence factor (GCF) [6]

In a signal received from the diffuse scattering medium, the incoherent components are included due to the interference of ultrasonic waves from many scatterers. Therefore, the CF value decreases, and weighting of CF reduces the brightness value in the region of the diffuse scattering medium accordingly. To deal with this problem, GCF, which is an improvement of CF, has been proposed. Figure 1b shows the configuration, where the CF estimator unit in Fig. 1a is changed to that of GCF. GCF is calculated from the following equation using the power value of the Fourier coefficient $c(k,n)$ obtained using DFT of the analytic signal $I(m,n) + {\text{j}}Q(m,n)$ in the channel direction:

$$ GCF(n;\,K_{0} ) = \frac{{\mathop \sum \nolimits_{{k = - K_{0} }}^{{K_{0} }} \left| {c(k,n)} \right|^{2} }}{{\mathop \sum \nolimits_{k = - K}^{K - 1} \left| {c(k, n)} \right|^{2} }}, $$

(3)

where $k$ is the frequency index in the channel direction, and $k = - K, - K + 1, \ldots ,0, \ldots ,K - 1, \left( {K = M/2} \right)$ for an even number $M$. Here, the CF value is calculated from the GCF value as $CF(n) = GCF(n; 0)$. While CF is calculated from the power value of the DC component $c(0,n)$, GCF is calculated from the power value of the frequency components in the range of $\left[ { - K_{0} , K_{0} } \right]$. Therefore, the decrease in GCF caused by the phase fluctuation due to the diffuse scattering media is suppressed. The effect on GCF can be adjusted by $K_{0}$. The GCF value approaches the maximum value of 1 if the frequency component around DC determined by $K_{0}$ is dominant over the entire power spectrum in the channel direction. As GCF aims to reduce unnecessary signals, it is necessary to set an appropriate value $K_{0}$ to avoid inclusion of frequency components of signals outside of the focal point. As $K_{0}$ becomes larger, unnecessary signal components far from DC are included in the numerator of Eq. (3). As a result, the GCF value increases, and unnecessary signals cannot be suppressed.

For example, the GCF value can be obtained from Eq. (3) after calculating $c(k,n)$ for analytic signals in the channel direction using the fast Fourier transform (FFT). However, as the value of $K_{0}$ is generally a small number, the computational complexity can be reduced by DFT only for necessary components. Also, there is no need to calculate DFT for the denominator, because the value can be calculated from the squared sum of the received analytic signals in the channel direction based on Parseval’s theorem as follows:

$$ \mathop \sum \limits_{k = - K}^{K - 1} \left| {c(k,n)} \right|^{2} = M \cdot \mathop \sum \limits_{m = 0}^{M - 1} \left| {I(m,n) + {\text{j}}Q(m,n)} \right|^{2} , $$

(4)

where $I(m,n)$ and $Q(m,n)$ are the real and imaginary parts of the analytic signal, respectively. Substituting Eq. (4) into Eq. (3) provides the follows:

$$ GCF(n;\,K_{0} ) = \frac{{\mathop \sum \nolimits_{{k = - K_{0} }}^{{K_{0} }} \left| {c(k,n)} \right|^{2} }}{{M \cdot \mathop \sum \nolimits_{m = 0}^{M - 1} \left| {I(m,n) + {\text{j}}Q(m,n)} \right|^{2} }}. $$

(5)

As in the case of CF, the signal $x_{{{\text{in}}}} (n)$ after applying DAS is weighted using the GCF value.

Proposed method

Generalized coherence factor estimated from real signal (GCF_real)

According to the conventional formula, GCF is calculated using analytic signals generated from the received signals in individual channels. However, as multipliers such as mixers and low pass filters are required at a high sampling frequency, the computational complexity becomes significantly large when generation of the analytic signal is applied to the signal in each element. Therefore, we propose a method to calculate GCF based on real signals to omit the generation of analytic signals.

First, let us consider the conventional GCF calculation. Although we derive analytic signals by Hilbert transform here, the same approach can also be applied to the case of baseband demodulation. For the delayed signal in channel $m$, the analytic signal calculated by the Hilbert transform in the $n$th direction is expressed as follows:

$$ I(m,n) + {\text{j}}Q(m,n) = A(m,n){\exp}\left[ {{\text{j}}2\pi fnT} \right], $$

(6)

where $A(m,n)$ is the complex amplitude including the phase change in the channel direction, and its absolute value represents the signal envelope. Here, $f$ represents the carrier frequency of the received signal, and $T$ represents the reception sampling period. When DFT is applied to the analytic signal in the channel direction, the Fourier coefficient $c(k,n)$ is expressed as follows:

$$ \begin{aligned} c(k,n) & = \frac{1}{M}\mathop \sum \limits_{m = 0}^{M - 1} \left\{ {I(m,n) + {\text{j}}Q(m,n)} \right\}\exp \left[ { - {\text{j}}\frac{2mk\pi }{M}} \right] \\ & = \frac{1}{M}\mathop \sum \limits_{m = 0}^{M - 1} A(m,n)\exp \left[ {{\text{j}}2\pi fnT} \right]\exp \left[ { - {\text{j}}\frac{2mk\pi }{M}} \right] \\ & = \frac{1}{M}\exp \left[ {{\text{j}}2\pi fnT} \right]\mathop \sum \limits_{m = 0}^{M - 1} A(m,n)\exp \left[ { - {\text{j}}\frac{2mk\pi }{M}} \right]. \\ \end{aligned} $$

(7)

Consequently, the power value of $c(k,n)$ is calculated by

$$ \left| {c(k,n)} \right|^{2} = \frac{1}{{M^{2} }}\left| {\mathop \sum \limits_{m = 0}^{M - 1} A(m,n){\exp}\left[ { - {\text{j}}\frac{{2mk{\uppi }}}{M}} \right]} \right|^{2} , $$

(8)

where it has no terms depending on $f$. Then, GCF is calculated by substituting Eq. (8) into Eq. (3) or Eq. (5). The term that changes in the $n$th direction in Eq. (8) is only $A(m,n)$. As $A(m,n)$ is the complex amplitude of the envelope, the change is gradual compared to $f$. In the case of baseband demodulation, there is no carrier frequency component in Eq. (6), and as a result, the power value of $c(k,n)$ is the same as in Eq. (8).

Next, let us consider the case when GCF is calculated from the Fourier coefficients obtained by DFT for the real signal $I(m,n)$. As the real signal is represented by

$$ I(m,n) = \frac{1}{2}\left[ {\left\{ {I(m,n) + {\text{j}}Q(m,n)} \right\} + \left\{ {I(m,n) + {\text{j}}Q(m,n)} \right\}^{*} } \right], $$

(9)

the Fourier coefficient $d(k,n)$ of $I(m,n)$ is represented by

$$ d(k,n) = \frac{1}{2}\left\{ {c(k,n) + c^{*} ( - k,n)} \right\}. $$

(10)

Therefore, the power value of $d(k,n)$ is expressed as follows:

$$ \begin{aligned} \left| {d(k,n)} \right|^{2} & = \frac{1}{4}\left| {c(k,n) + c^{*} ( - k,n)} \right|^{2} \\ & = \frac{1}{4}\left\{ {\left| {c(k,n)} \right|^{2} + c(k,n)c( - k,n) + c^{*} (k,n)c^{*} ( - k,n) + \left| {c^{*} ( - k,n)} \right|^{2} } \right\}. \\ \end{aligned} $$

(11)

Substituting $d(k,n)$ instead of $c(k,n)$ in Eq. (3) provides the following:

$$ GCF_{{\text{I}}} (n;\,K_{0} ) = \frac{{\mathop \sum \nolimits_{{k = - K_{0} }}^{{K_{0} }} \left| {d(k,n)} \right|^{2} }}{{\mathop \sum \nolimits_{k = - K}^{K - 1} \left| {d(k, n)} \right|^{2} }} = \frac{{\mathop \sum \nolimits_{{k = - K_{0} }}^{{K_{0} }} \left| {d(k,n)} \right|^{2} }}{{M \cdot \mathop \sum \nolimits_{m = 0}^{M - 1} \left| {s(m,n)} \right|^{2} }}, $$

(12)

where notation $GCF_{{\text{I}}} (n; K_{0} )$ is used to distinguish from the conventional GCF calculated from the analytic signals. The right hand side of Eq. (12) shows the case when the denominator is calculated from the real signal $s(m,n)$ similarly as in Eq. (5). Substituting Eq. (11) into Eq. (12) gives the following:

$$ GCF_{{\text{I}}} (n;\,K_{0} ) = \frac{{\mathop \sum \nolimits_{{k = - K_{0} }}^{{K_{0} }} \left\{ {\left| {c(k,n)} \right|^{2} + c(k,n)c( - k,n) + c^{*} (k,n)c^{*} ( - k,n) + \left| {c^{*} ( - k,n)} \right|^{2} } \right\}}}{{\mathop \sum \nolimits_{k = - K}^{K - 1} \left\{ {\left| {c(k,n)} \right|^{2} + c(k,n)c( - k,n) + c^{*} (k,n)c^{*} ( - k,n) + \left| {c^{*} ( - k,n)} \right|^{2} } \right\}}}. $$

(13)

As

$$ \mathop \sum \limits_{{k = - K_{0} }}^{{K_{0} }} \left| {c(k,n)} \right|^{2} = \mathop \sum \limits_{{k = - K_{0} }}^{{K_{0} }} \left| {c^{*} ( - k,n)} \right|^{2} $$

(14)

and

$$ \mathop \sum \limits_{{k = - K_{0} }}^{{K_{0} }} \left\{ {c(k,n)c( - k,n) + c^{*} (k,n)c^{*} ( - k,n)} \right\} = 2\mathop \sum \limits_{{k = - K_{0} }}^{{K_{0} }} {\text{Re}}\left\{ {c(k,n)c( - k,n)} \right\}, $$

(15)

Equation (13) can be rewritten as follows:

$$ \begin{aligned} GCF_{{\text{I}}} (n;\,K_{0} ) & = \frac{{\mathop \sum \nolimits_{{k = - K_{0} }}^{{K_{0} }} \left| {c(k,n)} \right|^{2} + \mathop \sum \nolimits_{{k = - K_{0} }}^{{K_{0} }} {\text{Re}}\left[ {c(k,n)c( - k,n)} \right]}}{{\mathop \sum \nolimits_{k = - K}^{K - 1} \left| {c(k,n)} \right|^{2} + \mathop \sum \nolimits_{k = - K}^{K - 1} {\text{Re}}\left[ {c(k,n)c( - k,n)} \right]}} \\ & = \frac{{p( - K_{0} ,K_{0} ,n) + x( - K_{0} ,K_{0} ,n)}}{p( - K,K - 1,n) + x( - K,K - 1,n)}, \\ \end{aligned} $$

(16)

where

$$ p(k_{1} ,k_{2} ,n) = \mathop \sum \limits_{{k = k_{1} }}^{{k_{2} }} \left| {c(k,n)} \right|^{2} , $$

(17)

$$ x(k_{1} ,k_{2} ,n) = \mathop \sum \limits_{{k = k_{1} }}^{{k_{2} }} {\text{Re}}\left[ {c(k,n)c( - k,n)} \right]. $$

(18)

In Eq. (16), the cross term represented by Eq. (18) is added to the denominator and numerator in Eq. (3). As the term in Eq. (17) is equivalent to the denominator and numerator in Eq. (3), it is expressed as a GCF term in the present paper. The term $c(k,n)c( - k,n)$ in Eq. (18) is calculated by

$$ c(k,n)c( - k,n) = \frac{1}{{M^{2} }}{\exp}\left[ {{\text{j}}4\pi fnT} \right]\mathop \sum \limits_{m = 0}^{M - 1} A(m,n){\exp}\left[ { - {\text{j}}\frac{{2mk{\uppi }}}{M}} \right]\mathop \sum \limits_{m = 0}^{M - 1} A(m,n){\exp}\left[ {{\text{j}}\frac{{2mk{\uppi }}}{M}} \right], $$

(19)

where there is a component of frequency $2f$ in the time ($n$th) direction. Due to this component, $GCF_{{\text{I}}} (n)$ has oscillation of $2f$, which does not appear in the GCF value calculated from the analytic signals. To calculate GCF_real equivalent to GCF by removing this unnecessary cross term, we used the finite impulse response low pass filter (FIR-LPF) with the coefficient $f_{{{\text{LPF}}}} (l), (l = - L, \ldots ,L)$ for the $n$th direction, as in the following equation:

$$ \begin{aligned} GCF_{{{\text{real}}}} (n;\,K_{0} ) & = \frac{{\mathop \sum \nolimits_{l = - L}^{L} \left[ {f_{{{\text{LPF}}}} (l) \cdot \left\{ {\mathop \sum \nolimits_{{k = - K_{0} }}^{{K_{0} }} \left| {\left. {d(k,n - l} \right)} \right|^{2} } \right\}} \right]}}{{\mathop \sum \nolimits_{l = - L}^{L} \left[ {f_{{{\text{LPF}}}} (l) \cdot \left\{ {\mathop \sum \nolimits_{k = - K}^{K} \left| {\left. {d(k,n - l} \right)} \right|^{2} } \right\}} \right]}} \\ & = \frac{{\mathop \sum \nolimits_{l = - L}^{L} \left[ {f_{{{\text{LPF}}}} (l) \cdot \left\{ {\mathop \sum \nolimits_{{k = - K_{0} }}^{{K_{0} }} \left| {\left. {d(k,n - l} \right)} \right|^{2} } \right\}} \right]}}{{\mathop \sum \nolimits_{l = - L}^{L} \left[ {f_{{{\text{LPF}}}} (l) \cdot \left\{ {M\mathop \sum \nolimits_{m = 0}^{M - 1} \left| {\left. {s(m,n - l} \right)} \right|^{2} } \right\}} \right]}}. \\ \end{aligned} $$

(20)

Figure 1c shows a block diagram for estimating GCF_real in the CF estimator unit presented in Fig. 1a. Compared to Fig. 1b, the Hilbert transformer at each channel is eliminated, and LPF is added after the denominator and numerator calculations. As LPF is the processing after which the channel signals are delayed and summed, the number of calculations can be reduced to approximately 2/(channel number) when the computational load of the Hilbert transform for one channel is comparable to LPF.

Results and discussion

Experimental setup

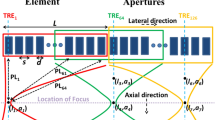
To verify the proposed method, the RF data were acquired from 96 channels using the ultrasound diagnostic system ProSound α10 (Hitachi, Tokyo, Japan). The measurement object was a multipurpose phantom 403 GS-LE (Gammex, WI, USA). In this experiment, we set $M = 96$ and $K = 48$. The GCF and GCF_real values were calculated offline using the acquired RF data and compared to each other, and B-mode images weighted according to the obtained values were also constructed. As GCF has better CNR than other factors in the case of uniform scattering media [12], a 60R convex probe (UST-9130, 3.5 MHz, element pitch 0.38°) mainly used for observation of the abdomen, where there are many regions of diffuse scattering media, was employed in the experiment. The transmitting center frequency was 5 MHz, and the depth of the transmitting focus position was 105 mm from the probe surface. The sampling frequency of the RF data was 20 MHz. Figure 2a shows a B-mode image obtained by the conventional DAS. The image consists of 312 received scanning lines in the range of a viewing angle of 60°. We analyzed the signals of the scanning lines in the three regions of interest (ROI) shown in the B-mode image. Region A contained a wire target. Region B was shifted by six scanning lines (about 2 mm (1.1°) from the wire target) in the azimuth direction with respect to region A. Region C contained a diffuse scattering medium. All three ROIs were set at the same depth (42–52 mm). As shown in Fig. 2b, the transmitting and receiving aperture used for measuring each ROI were set such that the lateral position of each ROI was located in the center of the aperture.

Fig. 2

a Original B-mode image (delay and sum). The blue line A shows the ROI containing the wire target. The red line B shows the ROI shifted about 2 mm (1.1°) in the azimuth direction with respect to the wire target. The yellow line C shows the ROI of the diffuse scattering medium. b Schematic diagram showing the transmit and receive aperture used in each ROI

Channel data and power spectrum in each ROI

In this section, we discuss the channel data $s(m,n)$ and the power spectrum $\left| {c\left( {k,n} \right)} \right|^{2}$ used for the GCF estimation in each ROI. Figure 3a–c show the channel data $s(m,n)$ in ROIs A, B, and C after delayed processing. Figure 3d–f show the absolute values of the analytic signal $I(m,n) + {\text{j}}Q(m,n)$ obtained by the Hilbert transform of $s(m,n)$ for each $m$ in the $n$th direction, and their phases are shown in Fig. 3g–i. Figure 3j–l show the power spectra obtained by DFT of the analytic signals in the $m$th direction for each $n$, and the DC component ($k = 0$) is shown by the white dashed lines. The display range ([MIN, MAX]) differs depending on the ROI, except for Fig. 3g–i. The GCF values were calculated from $\left| {c(k,n)} \right|^{2}$ in Fig. 3j–l using Eq. (3). In Fig. 3a, d, g for ROI A, after the signals from the wire target were received and delayed, they were aligned in the $m$th direction as the position of the receiving focus matched the position of the wire target. Therefore, the power value from the wire target was concentrated on the DC component, and the other frequency components were minor, as shown in Fig. 3j. In Fig. 3b, e, h for ROI B, the position of the wire target and the receiving focus position do not coincide. Therefore, after delayed processing, the reception time of the reflected waves from the wire target was shifted for $m$, and the phases in the $m$th direction changed. Received signals in ROI C shown in Fig. 3c, f, i tended to be in phase in the $m$th direction. However, as the scattered waves from many scatterers interfere, the phases fluctuated, as can be seen in comparison to Fig. 3g. Therefore, the power spectrum in Fig. 3l was distributed around DC and was observed to have a wider bandwidth than that presented in Fig. 3j.

Fig. 3

Delayed RF signals and their analytic signals in each ROI. a–c show RF signals in ROIs A, B, and C. d–f show amplitude values of analytic signals generated from (a)–(c). g–i show phases of analytic signals generated from (a)–(c). j–l show power spectra obtained by DFT in the $m$-th direction on analytic signals generated from (a)–(c)

Characteristic of cross term

Once the Fourier coefficient $c(k,n)$ is obtained, the cross term $x(k_{1} , k_{2} , n)$ in Eq. (18), which has to be removed in Eq. (16), can be calculated. To confirm the necessity of the cross term reduction by LPF and its effect, we compared magnitudes of the cross term and the GCF term. As mentioned above, when reducing unnecessary signals by GCF, $K_{0}$ should be set to an appropriate value. Here, to investigate the cross term, two cases of $K_{0}$ = 1 and $K_{0}$ = 5 were examined. Figure 4Ia–c show the GCF term $p( - 1, 1, n)$ and the cross term $x( - 1, 1, n)$ values calculated for $K_{0}$ = 1 in ROIs A, B, and C. If GCF is calculated from real signals, the sum of GCF and cross terms are calculated as shown in Eq. (16). Also, the power spectra by DFT in the $n$th direction for the signals are shown in Fig. 4IIa–c. In ROI A, the peak of the cross term was about − 10 dB with respect to the peak value of the GCF term (i.e., power of the DC component), while it was as small as about − 20 dB in ROIs B and C. To illustrate this difference quantitatively, the ratio of the squared sum of the cross term to the GCF term was calculated from the following equation in each ROI:

$$ r(k_{1} ,k_{2} ) = \frac{{\mathop \sum \nolimits_{{n = N_{1} }}^{{N_{2} }} \left| {x(k_{1} ,k_{2} ,n)} \right|^{2} }}{{\mathop \sum \nolimits_{{n = N_{1} }}^{{N_{2} }} \left| {p(k_{1} ,k_{2} ,n)} \right|^{2} }}, $$

(21)

Fig. 4

GCF term $p( - 1, 1, n)$ and cross term $x( - 1, 1, n)$ values in ROIs Ia A, Ib B, and Ic C. Power spectra obtained by DFT in the $n$-th direction with respect to ROIs IIa A, IIb B, and IIc C

where $N_{1}$ and $N_{2}$ represent the sample numbers at the top and bottom in each ROI, respectively. The cross term of the numerator oscillates at $2f$, while there is less fluctuation in the GCF term of the denominator, which is the power value of the envelope. Therefore, even if the cross term of the numerator and the GCF term of the denominator have the same amplitude, the power value of the cross term is half of that of the GCF term. Thereby, the maximum value of $r(k_{1} ,k_{2} )$ is 0.5. The value of $r( - 1, 1)$ in each ROI is shown in Table 1. As it was close to the maximum value of 0.5 in ROI A, the amplitude value of the cross term was almost the same as that of the GCF term. $r( - 1, 1)$ in ROIs B and C were close to each other. Figure 5 shows the GCF term $p( - 5, 5, n)$ and the cross term $x( - 5, 5, n)$, and those of power spectra for $K_{0}$ = 5 in ROIs A, B, and C. The ratio $r( - 5, 5)$ is also presented in Table 1. For ROI A, both amplitudes of the GCF term and the cross term were equivalent in the case of $K_{0}$ = 1. However, in ROI B, the peak value of the cross term in the power spectrum was about − 30 dB with respect to the GCF term, as shown in Fig. 5IIb, and it can be seen that $r( - 5, 5)$ is considerably smaller than those corresponding to the other ROIs. In ROI C, $r( - 5, 5)$ is slightly smaller than $r( - 1, 1)$.

Table 1 Ratio of the squared sum of the cross term to the GCF term $r(k_{1} , k_{2} )$

Fig. 5

GCF term $p( - 5, 5, n)$ and cross term $x( - 5, 5, n)$ values in ROIs Ia A, Ib B, and Ic C. Power spectra obtained by DFT in the $n$-th direction with respect to ROIs IIa A, IIb B, and IIc C

Considering the above results, we can conclude on the difference between $K_{0}$ = 1 and $K_{0}$ = 5 in each ROI. As can be seen in Fig. 3j, the power value of the signal in ROI A, where the wire target was included, is concentrated at DC ($k = 0$) in the power spectrum. Therefore, changing the value of $K_{0}$ from 1 to 5 does not lead to significant changes in either the GCF term or the cross term. Moreover, assuming that the signal component at $k = 0$ is dominant, the GCF term in Eq. (8) and the envelope of the cross term in Eq. (19) have the same amplitude despite the fact that the cross term oscillates at $2f$. In ROI B (Fig. 3k), as the signal component from the wire target hardly exists in the narrow range of $K_{0}$ = 1, the signal from the diffuse scattering medium on the focal point is dominant. Therefore, $r( - 1, 1)$ in ROI B was equivalent to that in ROI C. In the case of $K_{0}$ = 5, the frequency component, which was biased to the positive side by the reflected wave from the wire target, was included in the range of [$- K_{0} , K_{0} ]$, as shown in Fig. 3k. Therefore, the cross term calculated from multiplication of the positive and negative frequency components was smaller compared to that of the GCF term. In ROI C, $r( - 5, 5)$ was lower than $r( - 1, 1)$. This is because the observation range of the power spectrum at $K_{0}$ = 1 is narrower than the one at $K_{0}$ = 5, and the influence of the DC component ($k = 0$), where the GCF term and the envelope of the cross term have the same amplitude, became dominant.

As mentioned above, the GCF value becomes smaller in the case of setting $K_{0}$ in such way that the component of the unnecessary signal is not included in the range of [$- K_{0} , K_{0} ]$. Therefore, in the case of ROI B, $K_{0}$ should be set to avoid inclusion of the signal from the wire target. For this reason, $K_{0}$ = 1 is preferable in this experimental data. Furthermore, there are few situations where only a strong reflector like a wire target exists in a human body. In general, due to the presence of similar scatterers around it, the spectrum has a bandwidth similar to that shown in ROI C (Fig. 3l). Therefore, within a narrow range such as $K_{0}$ = 1, the frequency component is less biased to positive or negative sides. Consequently, there are few regions where the cross term becomes smaller, as shown in Fig. 5Ib and IIb. In most of the data obtained from the biological object, the cross terms cannot be ignored, and their reduction by LPF is essential. If the cross term remains, the GCF_real value differs from that of the conventional GCF, and there is a possibility that speckle noise may be emphasized by the presence of high-frequency components.

Cross term reduction by FIR-LPF

Here, the effect of reducing the cross term by applying FIR-LPF in Eq. (20) is discussed, considering the case of $K_{0} = 1$, which is effective for reducing unnecessary signals. As shown in Eq. (8), the GCF term has only low-frequency components in the $n$th direction, because it has no carrier frequency component. As the center frequency of the acquired data was approximately 3 MHz, that of the cross term is considered to be distributed around 6 MHz according to Eq. (19). For all of the power spectra shown in Figs. 4 and 5, it was confirmed that the GCF term was distributed around the DC component, and the cross term was distributed around 6 MHz. Therefore, the cross term was reduced using an 8th-order FIR-LPF with a cutoff frequency of 3 MHz. Figure 6Ia–c show the results of applying LPF to the numerator values $p( - 1, 1, n) + x( - 1, 1, n)$ in Eq. (16) in ROIs A, B, and C. The value of $p( - 1, 1, n)$ obtained by the conventional GCF and that of $LPF\left[ {p( - 1, 1, n) + x( - 1, 1, n)} \right]$ obtained by the proposed method were in agreement for all ROIs. Although the reduction effect of the cross term was different depending on the frequency characteristics of LPF, the differences were minor, and the correlation coefficients of $p( - 1, 1, n)$ and $LPF\left[ {p( - 1, 1, n) + x( - 1, 1, n)} \right]$ were sufficiently high (0.99 or more in each ROI) in the 8th-order FIR-LPF. Figure 6IIa–c show the power spectra obtained by DFT in the $n$th direction in Fig. 6Ia–c. In addition, the power spectra of the signal $p( - 1, 1, n) + x( - 1, 1, n)$ before LPF and the frequency characteristic of the 8th-order FIR-LPF are shown in Fig. 6IIa–c. It can be confirmed that the frequency component of the cross terms was reduced, and the GCF term became dominant after applying LPF.

Fig. 6

Ia–Ic Signals and IIa–IIc power spectra in which cross terms have been reduced by low-pass filtering for signals of $p( - 1, 1, n) + x( - 1, 1, n)$. Ia and IIa show results for ROI A, Ib and IIb show results for ROI B, and Ic and IIc show results for ROI C

Comparison of GCF_real and GCF

Figure 7a, b, c show the values of the proposed GCF_real obtained from Eq. (20) and the conventional GCF obtained from Eq. (5) at $K_{0} = 1$ adopted as outlined in Fig. 6. GCF_real and GCF were close to each other, and the correlation coefficient of them showed 0.99 or more in each ROI. The vicinity of $nT = 60 {{\mu s}}$. corresponds to the time, where the signals from the wire target were received. In ROI B, the value became almost 0 around $nT = 60 {{\mu s}}$, and it can be concluded that the output signal including the signal received from outside of the focus point was suppressed by weighting of GCF_real. However, as the GCF_real values were too small, the use of these values as the weight values resulted in the dark region artifact [22]. Therefore, adjustment of the GCF values by the power $p$ in Eq. (2) is required to apply weighting. Figure 7d shows a B-mode image obtained by DAS, and Fig. 7e, f show B-mode images weighted by GCF_real and GCF at $p = 0.2$. The dynamic range of each image is 80 dB. Sidelobes were generated in the azimuth direction for wire targets in Fig. 7d; however, they were reduced in Fig. 7e, f. As a representative example, the intensity profiles in the azimuth direction at the depth of the wire target surrounded by the green square in Fig. 7d are shown in Fig. 7g. Regarding GCF_real and GCF, it can be confirmed that the sidelobe generated around the wire target was reduced, while the brightness of the wire target was at the same level as in the DAS. The CNR values were calculated from the following equation [23] using the brightness values after log compression in the yellow ROI as region 1, and the red ROI as region 2, as shown in Fig. 7d:

$$ CNR = \frac{{\left| {\mu_{1} - \mu_{2} } \right|}}{{\sqrt {\sigma_{1}^{2} + \sigma_{2}^{2} } }}, $$

(22)

Fig. 7

GCF_real and GCF values calculated in ROIs a A, b B, and c C. B-mode images generated by d DAS and those weighted by e GCF_real and f GCF. The dynamic range of each image is 80 dB. g Lateral amplitude profiles in the depth of the wire target are shown by the green square in (d)

where $\mu_{1}$ and $\sigma_{1}$ are the average brightness and the standard deviation of region 1, respectively, and $\mu_{2}$ and $\sigma_{2}$ are those of region 2. The CNR values in the respective images are 2.29, 2.65, and 2.64 for DAS, GCF_real, and GCF, respectively. Therefore, the CNR improvement effect of the proposed method was equivalent to that of the conventional GCF. It was confirmed that the computational complexity for applying FIR-LPF in the proposed GCF_real calculation was approximately 1/50 compared with that for generating the analytic signals in all channels in the conventional GCF calculation so that the computational complexity can be drastically reduced by the proposed method. The quality of the B-mode image weighted by the proposed GCF_real was equivalent to that weighted by the conventional GCF. Here, the computational complexity indicates the number of calculations for generating the analytic signals in all channels, which is only used in the conventional method, or applying FIR-LPF, which is only used in the proposed method.

The conventional GCF has the advantage of reducing the sampling frequency when using baseband demodulators. Reducing the sampling frequency is equivalent to reducing the number of subsequent GCF value calculations. The conventional GCF is composed of analytic signal generation and GCF value calculation, whereas the proposed method only needs GCF_real value calculation. The analytic signal generation needs to filter the signals in the time ($n$th) direction for all channels. Therefore, the number of multiplications required per pixel is $L_{f} M$, where $L_{f}$ is the number of filter coefficients and $M$ is the number of received channels. On the other hand, the processing for the channel signals in the GCF_real value calculation is DFT and power value calculation in the channel ($m$th) direction. Therefore, the number of multiplications required per pixel is $\left( {2K_{0} + 1} \right)M + M = 2\left( {K_{0} + 1} \right)M$, where $K_{0} = 1$ was used in the present paper. In general, since $L_{f}$ is larger than $2\left( {K_{0} + 1} \right)$, the number of calculations is smaller in the GCF_real value calculation than in the analytic signal generation. Therefore, the number of calculations in the proposed method is small even when compared with the conventional GCF, in which the sampling frequency is reduced by baseband demodulation.

Conclusions

Adaptive beamforming based on GCF can reduce unnecessary signals without reducing CNR. However, in this method, it is necessary to generate analytic signals for the received signals in individual channels, and, therefore, the computational complexity increases compared to the conventional DAS beamforming. In the present paper, we proposed a method to calculate the values equivalent to that of the conventional GCF method using only real signals. The proposed method can omit the generation of analytic signals without deteriorating the accuracy of the GCF value. Additional processing is required in terms of applying only FIR-LPF after DAS. Regarding this part, the computational complexity can be reduced to approximately 2/(receive channel number) as compared to the conventional GCF method. The proposed method can improve the feasibility of small and low-end models of ultrasonic diagnostic apparatuses. There are two factors that increase the computational complexity of conventional GCF compared to DAS. One is the generation of analytic signal in each channel, and the other is the part that calculates the GCF value by DFT in the channel direction for each pixel. In the present paper, we focused on the former and succeeded to omit the generation of analytic signals. In future research, we will consider the latter by developing a method to further reduce the computational complexity of the GCF calculation units.