Introduction

Submarine landslides are a major natural geohazard commonly occurring in offshore continental slopes. They present significant threats to offshore infrastructure, in particular in the North Sea (Bryn et al. 2005), the Gulf of Mexico (Jeanjean et al. 2005), the Nankai Trough (Yamamoto et al. 2015), the offshore Northwest Australia (Hengesh et al. 2013) and the Caspian Sea (Hill et al. 2015) where offshore resource explorations are active. Some significant historical events have been reported to have triggered disastrous tsunamis, for example the giant Storegga landslide that occurred 8200 years ago, the case off Papua New Guinea in 1998 (Synolakis et al. 2002) and the latest Sulawesi landslide in 2018 that might have caused the deadly Palu tsunami (Liu et al. 2020).

A local failure zone triggered by e.g. excess water pressure accumulation may evolve into a catastrophe covering a series of successive failures with strength reduction during shearing in sensitive clays (e.g. Puzrin et al. 2004; Zhang et al. 2015). Marine clay sediments are typical sensitive clays mainly because of the surface charge under seawater conditions, with the soil sensitivity (the ratio between the peak and residual strengths) normally ranging from 2 to 6 (Randolph and Gourvenec 2011). Another important characteristic of submarine landslide is the flowing rheology of sliding materials that acts between the flow and the bed (Khaldoun et al. 2009; Grue 2015). Evaluations of slope stability, post-failure flow dynamics and consequences are key elements of risk assessment of submarine landslides, which need proper considerations of strain softening and rheology attainted to the failed sensitive soils.

Many numerical studies have been carried out with the focus mainly on replications of the run-out features such as the travel distance and velocity during the past two decades (Gauer et al. 2005; Pastor et al. 2014; Issler et al. 2015; Dey et al. 2016; Dong et al. 2017; Zhang et al. 2019). Among them, mesh free methods such as the smoothed particle hydrodynamics and the material point method, the Eulerian-based computational fluid dynamics and the arbitrary Lagrangian-Eulerian methods have become increasingly popular because of their advantages in dealing with large deformation. In spite of them, the simple depth-integrated method based on the shallow water condition is still the most widely used numerical method for the debris flow dynamics modelling especially for practical engineering applications (Dong et al. 2020). Until now, a dozen of commercial packages, e.g. DAN (Hungr 1995), Debris2D (Liu and Huang 2006), MassMov2D (Beguería et al. 2009), RAMMS (Christen et al. 2010) and EDDA (Chen and Zhang 2015), along with many in-house numerical programmes such as the BingClaw (Kim et al. 2018), have been emerging and developed with the implementations of different depth-integrated models. They can simulate the debris flow dynamics well enough with considerations of various rheological models. However, almost all these programmes need input information about the volume and initial velocity of the failed mass, which are usually difficult to determine without proper consideration of the initiation mechanism for submarine landslides. Moreover, a one-off input makes these programmes unable to reflect post-failure patterns, such as retrogressive failure and gradual ploughing common in submarine landslides. Attempt has to be made to integrate the pre-failure initiation and post-failure mechanisms into the favoured depth average method for more accurate as well as time-efficient modelling of flow dynamics in submarine landslides.

Uphill retrogressive failure in sensitive clays was firstly supposed to be formed by a series of rotational slip surfaces (Bjerrum 1955), and hence the volume of initial failure can be determined according to the limit equilibrium or limit analysis and forwarded to any depth-integrated debris flow package. However, it has no simple way to deal with progressive rotational failure with the limit equilibrium or limit analysis, let alone the translational failure mechanism that has been increasingly recognised from recent site investigations of submarine landslides (Kvalstad et al. 2005, L’Heureux et al. 2012, Quinn et al. 2012). The latter, however, can be well explained by the shear band propagation (SBP) theory developed by Puzrin and Germanovich (2005) and followed by many other studies (Viesca and Rice 2012; Puzrin et al. 2010, 2016; Zhang et al. 2017, 2019; Buss et al. 2019). The SBP approach assumes the shear band initiates and propagates within a favoured (weak) layer depending on the pre-conditioning sedimentary history and triggering conditions, potentially followed by active and passive slab failure at uphill and downhill, respectively. Criteria for catastrophic shear band propagation and slab failure with specific geometry and loading conditions have been recently developed and applied into back analyses of several historical events (Stoecklin 2019; Zhang et al. 2020). In addition, large deformation numerical modellings of progressive failure have extended the SBP analysis from shear band propagation to complex post-failure behaviours (Dey et al. 2016; Zhang et al. 2019; Stoecklin et al. 2020). However, these large deformation numerical methods largely rely on heavy programmes and expert users in addition to the low computational efficiency, which hence limit their practical applications.

This study mainly aims to introduce an original package for modelling the submarine landslides by numerically solving the SBP governing equations with the simple depth-integrated method. The proposed package is able to cover the whole process of the landslide from shear band initiation and propagation to complex post-failure behaviours such as the retrogressive failure, ploughing and run-out. The solutions of flow dynamics are obtained from a simple finite difference scheme by considering materials of strain softening and rate dependency. For its simplicity and efficiency, the depth-integrated-based SBP package is rather promising for practical applications. In addition, the package can be easily implemented, with light coding, into any existing debris flow software and in-house programmes using the depth average approximation.

Theory and governing equation

The approach is based on the classical flow dynamics equations with considerations of mass and momentum conservations, analogy to the well-known Savage–Hutter model (Savage and Hutter 1989). The depth integration (or averaging) approximation was used, which assumes the length of the sliding mass is much greater than the depth, satisfying the shallow water condition (or Saint Venant condition). The depth integration method has become the most widely used approach for debris flow modelling, due to its easy implementation and efficiency. In a traditional depth-integrated debris flow modelling, a debris flow can be divided into two layers: a plug layer and a shear layer, with the friction taking place in the shear layer only. Variations of the kinematic properties along the depth are neglected and flow dynamics parameters such as the velocity and pressure are averaged in the plug layer. Figure 1 a gives a schematic model for the traditional depth-integrated debris flow modelling.

Fig. 1
figure 1

a Depth-integrated analysis for traditional debris flow. b Depth-integrated analysis for slides with shear band propagation in weak layer

Full size image

Although the depth integration approximation is originated for debris flow modelling, it is also applicable to simulate the failure initiation and progressive failure with SBP in weak layers, as shown in Fig. 1b. Soils within a weak layer undergo strain softening during shearing, leading to strain localisation and hence shear band propagation along the weak layer. Upon sufficient magnitude of shear band propagation, catastrophic failure might occur with the SBP in the weak layer limited either by slope flattening or upon active/passive failure in the sliding layer. Within the SBP model, the weak layer (or shear surface) and sliding layer are, respectively, similar to the shear layer and plug layer in the traditional debris flow modelling using the depth integration method. Observed from finite element modelling, soils below the weak layer remained intact during shear band propagation and post-failure stages (Zhang et al. 2015) and were hence assumed rigid in the depth-integrated modelling.

A great advantage of the depth-integrated modelling of shear band propagation compared to the conventional one is that it is capable of modelling the full process of a landslide in sensitive clays covering initiation, slab failure, post-failure and deposition behaviours. Rather than essential inputs in the conventional depth integration methods, in the proposed method the volume and velocity of the initially failed mass are automatically calculated through the modelling. Furthermore, some complex and realistic post-failure behaviours relevant to submarine landslides, such as retrogression, ploughing and run-out, can also be simulated within the proposed numerical scheme.

Figure 2 shows the mass and momentum conservations in an infinitesimal block in the sliding layer. In each slice, conservation of angular momentum with respect to the intersection of two bounding radii, R and R + dR, from the local centre of rotation is expressed by

$$ P\left(R-\frac{s}{2}\right)+\tau \left(R+\frac{dR}{2}\right) dl+{\tau}_{drag} Rdl+d{I}_a=\left(P+ dP\right)\left(R+ dR-\frac{s+ ds}{2}\right)+{\tau}_g\left(R+\frac{dR}{2}\right) dl $$
(1)
Fig. 2
figure 2

a Mass conservation of each soil block. b Momentum conservation of each soil block

Full size image

where P is the slope parallel force per unit thickness (N/m), s is the thickness of the sliding layer (m), τ is the shear resistance and τg is the gravity shear stress at the shear surface (Pa), τdrag is the drag by the ambient water acting on the seabed surface (Pa), dl is the infinitesimal slice length (m) and dIa is the rate of change of angular momentum in each slice (kg m2 s−2). The gravity shear stress is given by

$$ {\tau}_g={\gamma}^{\prime}\left(s+\frac{ds}{2}\right)\mathit{\sin}\theta $$
(2)

where γ′ is the submerged unit weight of soil (N/m3) and θ is the slope angle; while the rate of change of angular momentum is expressed by

$$ {dI}_a=\rho \left(s+\frac{ds}{2}\right)\left(R+\frac{dR}{2}-\frac{s}{2}-\frac{ds}{4}\right)\frac{\partial^2u}{\partial {t}^2} dl $$
(3)

where ρ is the saturated density of soil (kg/m3), u is the displacement (m) and t is the time (s). Generally, change in slope angle in a submarine slope is not significant, i.e. the curvature is small, and thus one may assume s ≪ R and dR ≪ R. Hence, Eq. (1) becomes

$$ \frac{dP}{dl}-\left(\tau +{\tau}_{drag}-{\tau}_g\right)=\rho s\frac{\partial^2u}{\partial {t}^2}=\rho s\frac{\partial v}{\partial t} $$
(4)

where v is the velocity (m/s). Note that soil constitutive models relate values of P and τ to the displacement u and its gradient du, which will be detailed later. A rheology model from fluid mechanics was used similar to previous debris flow modelling (e.g. in Liu and Huang 2006, Christen et al. 2010, Dong et al. 2017, Kim et al. 2018), in addition to the soil mechanics-based strain softening.

Shear resistance in the weak layer

Within the weak layer (shear surface), soils are subjected to simple shear whereby the shear stress is limited to the shear strength and, considering a linear degradation and the Herschel-Bulkley rheological rule (Coussot 1997; Zhang et al. 2019), is given by

$$ \tau ={s}_{u,w}=\mathit{\max}\left[{\tau}_{p,w}+\left({\tau}_{r,w}-{\tau}_{p,w}\right)\frac{\delta^p}{\delta_r^p},{\tau}_{r,w}\right]\cdotp \left[1+\eta {\left(\frac{v}{v_{ref}}\right)}^n\right] $$
(5)

where τp, w and τr, w are peak and residual shear strengths in the weak layer, respectively (Pa); δp is the plastic shear displacement across the weak layer (m), \( {\delta}_r^p \) is the value of δp to soften the shear strength to the residual (m), vref is the reference velocity (m/s), η is the dimensionless viscous parameter (consistency coefficient) and n is the flow index. Though the current study used the linear degradation and Herschel-Bulkley rheological model, one may easily adapt the method with implementations of non-linear strength degradations (e.g. the exponential degradation by Einav and Randolph (2005)) and other rheological rules (e.g. the Bingham model). Figure 3 gives examples of strain softening and rheology rules in soils.

Fig. 3
figure 3

a Strain softening in soils. b Rate effect in soils

Full size image

Within the elasticity regime, the shear stress is calculated as

$$ \tau =\overline{G}{\delta}^e $$
(6)

where \( \overline{G} \) is the elastic shear stiffness (Pa/m) and δe is the elastic shear displacement across the weak layer (m). Ignoring any shear deformation in the sliding layer, the shear displacement across the weak layer δ equals the sliding displacement u, i.e.

$$ u=\delta ={\delta}^e+{\delta}^p $$
(7)

Drag forces from ambient water

The hydrodynamic drag on submarine landslides by ambient water can be approximated by (Elverhoi et al. 2005)

$$ {\tau}_{drag}=\frac{1}{2}{C}_d{\rho}_w{v}^2;{C}_d={C}_f+{C}_p $$
(8)

where Cd is the drag coefficient with Cf and Cp being its frictional and pressure components respectively, and ρw is the seawater density (kg/m3). The hydrodynamic pressure drag of water generally acts on the frontal upwind face of the sliding mass, while the skin friction caused by viscous shearing acts on the surfaces parallel to the sliding mass travel direction. The skin frictional drag is dominant compared to the pressure drag for streamlined bodies like a submarine sliding mass, and thus Cd = Cf is assumed in the present study. In case that submarine landslides are of bluff bodies, Cd ≈ Cp. The skin friction drag coefficient, Cf, depends on the Reynolds number and the flow type and varies at different positions of the sliding mass. The averaged friction drag coefficient over the submarine sliding mass can be simplified by (Schlichting 1980; Norem et al. 1990; Elverhoi et al. 2010)

$$ {C}_f={\left(1.89+1.62\mathit{\log}\frac{L}{k}\right)}^{-2.5} $$
(9)

where L is the sliding mass length (m) and k is the roughness length of the sliding mass surface in the range of 0.01–0.1 m. For the length of the sliding mass varying between 10 and 1000 m, the friction drag coefficient by Eq. (9) falls in the range of 0.005–0.016. Such a small drag force is usually insignificant compared to the shear resistance in the weak layer. Entrainment of water into the sliding mass is not considered in the current numerical scheme. The hydrodynamic pressure acting on the frontal upwind face may cause a thicker front, which, in turn, gradually increases the frontal drag force. Therefore, for flows exhibiting significant slide ploughing patterns, it is essential to keep the pressure drag term.

Lateral earth pressure in the sliding layer

Within the sliding layer, soils undergo extension upslope and compression downslope during SBP along the weak layer. Correspondingly, slope parallel (lateral) earth pressure, σh, gradually decreases and increases towards the active (upslope) and passive (downslope) failure limits, respectively. Within the elastic regime, it is expressed by

$$ {\sigma}_h={E}_{ps}{\varepsilon}^e $$
(10)

where Eps is the plane strain modulus (Pa) and εe is the elastic normal strain. The earth pressure coefficient is given by the ratio between the lateral and vertical (σv, Pa) stresses i.e.

$$ K=\frac{\upsigma_h}{\upsigma_v} $$
(11)

which should be bounded by two limits at active and passive failure states. The averaged vertical stress in the sliding layer is given by

$$ {\sigma}_v=\frac{1}{2}{\gamma}^{\prime }s $$
(12)

With an undrained condition for cohesive material, the limits of the lateral earth pressure coefficient can be approximated by

$$ {K}_a=1-2\chi\ \mathrm{and}\ {K}_p=1+2\chi $$
(13)

where Ka and Kp are the earth pressure coefficients at the active and passive failure states respectively, χ = su,s/σv represents the current strength ratio with su, s being the current shear strength of soils in the sliding layer. Considering the strain softening and rate effect, the current shear strength su, s can be expressed by

$$ {s}_{u,s}=\mathit{\max}\left[{\tau}_{p,s}+\left({\tau}_{r,s}-{\tau}_{p,s}\right)\frac{\gamma^p}{\gamma_r^p},{\tau}_{r,s}\right]\cdotp \left[1+\eta {\left(\frac{\dot{\gamma}}{{\dot{\gamma}}_{ref}}\right)}^n\right] $$
(14)

where τp, s and τr, s are the peak and residual shear strengths in the sliding layer respectively, γp is the plastic shear strain across the weak layer, \( {\gamma}_r^p \) is the value of γp to soften the shear strength to the residual, \( \dot{\gamma} \) is the shear strain rate and \( {\dot{\gamma}}_{ref} \) is the reference shear strain rate (1/s).

Depth-integrated finite difference scheme

The finite difference (FD) method was used to numerically solve the governing equation (4). The solution domain should be chosen as covering all potential failure regions, usually bounded by flat terrains. A rough estimation of shear band propagation limit can be made according to Zhang et al. (2019). The solution domain is then discretised into a series of infinitesimal blocks (i.e. one-dimensional meshes). Figure 4 shows a schematic set of numerical meshes (or soil blocks bounded by dashes) in both space and time domains. The material point, where displacement u, horizontal coordinate x, block height h, block length ∆l, slope angle θ, gravity shear stress τg and current soil strength in the weak layer su, w are stored, is initially located at the centre of each soil block and marked as a solid circle in the figure. Other parameters, such as lateral earth pressure σh, slope parallel force P, earth pressure coefficient K, inter-block normal strain ε and current soil strength in the sliding layer su, s are stored at the boundary points (see black hollow circles in the figure). Intermediate time intervals (see red hollow circles in the figure) are used to calculate velocities.

Fig. 4
figure 4

An example of numerical meshes and material points

Full size image

An explicit FD scheme, coded in Python, was developed with a Lagrangian framework whereby the numerical meshes move with the sliding mass. Such that, the mass conservation is apparent by maintaining the constant area in each soil block, i.e. s∆l = cons. Using the central difference and mesh scheme in Fig. 4, Eq. (4) is discretised as

$$ {P}_{i+\frac{1}{2}}^j-{P}_{i-\frac{1}{2}}^j-\left({\tau}_i^j+{\tau}_{drag,i}^j-{\tau}_{g,i}^j\right)\Delta {l}_i^j=\rho {h}_i^j\frac{\Delta {l}_i^j}{\Delta t}\left({v}_i^{j+\frac{1}{2}}-{v}_i^{j-\frac{1}{2}}\right) $$
(15)

where the counters i ∈ [0, Nx] and j ∈ [0, Nt] refer to points in space and time domains respectively, with ∆t representing the time step (s). It is convenient to set i = 0 and Nx at flat areas where shear band propagation should be restricted. Therefore, the Dirichlet boundary conditions were set, i.e. \( {v}_0={v}_{N_x}=0 \). For the initial step, the forward difference is used whereby Eq. (4) is discretised as

$$ {P}_{i+\frac{1}{2}}^0-{P}_{i-\frac{1}{2}}^0-\left({\tau}_i^0-{\tau}_{g,i}^0\right)\Delta {l}_i^0=\rho {h}_i^0\frac{\Delta {l}_i^0}{\Delta t}2{v}_i^{\frac{1}{2}} $$
(16)

assuming the initial velocity is nil everywhere (i.e. the Dirichlet initial condition).

Incremental displacement of each material point is calculated using the central difference as

$$ \Delta {u}_i^j=\Delta {u}_i^{j-1}+{v}_i^{j-\frac{1}{2}}\Delta t $$
(17)

and hence the position of each material point is updated as

$$ {x}_i^{j+1}={x}_i^j+\Delta {u}_i^j\mathit{\cos}{\theta}_i^j $$
(18)

The new slope angle is then calculated according to the new position of the material point. The new length of each soil block is calculated as

$$ \Delta {l}_i^{j+1}=\Delta {l}_i^j+\frac{\Delta {u}_{i+1}^j-\Delta {u}_{i-1}^j}{2} $$
(19)

and its new height can be estimated accordingly based on the constant area (mass conservation). A detailed FD algorithm is illustrated in Fig. 5a. The elastic and plastic components (with superscripts of ‘e’ and ‘p’ respectively) of \( \Delta {u}_i^j \) can be worked out by comparing the trial mobilised shear stress (\( =\overline{G}\Delta {u}_i^j \)) to the current shear strength in the weak layer su, w. The shear strength for the next step is then updated with an explicit manner according to the solved plastic shear displacement and softening rule. The flowchart for updating su, w is shown in Fig. 5b.

Fig. 5
figure 5

a Overall numerical scheme. b Numerical scheme for shear stress calculation in weak layer and slope parallel earth pressure calculation in sliding layer

Full size image

In the sliding layer, the incremental axial strain is given by

$$ \Delta {\varepsilon}_{i+\frac{1}{2}}^j=-2\frac{\Delta {u}_{i+1}^j-\Delta {u}_i^j}{\Delta {l}_{i+1}^j+\Delta {l}_i^j} $$
(20)

where compression is taken as positive. The vertical strain is the opposite to the axial strain as the volume change is nil. Elastic and plastic components (with superscripts of ‘e’ and ‘p’ respectively) of \( \Delta {\varepsilon}_{i+\frac{1}{2}}^j \) in the sliding layer can be figured out comparing the slope parallel earth pressure to the limits (active and passive earth pressures) as also shown in Fig. 5b. Similarly, the plastic component of the incremental shear stain \( \Delta {\gamma}_{i+\frac{1}{2}}^j \) is calculated and thus the current shear strength in the sliding layer, su, s, is updated based on Eq. (14).

The updated gravity shear stress and slope parallel force are given by

$$ {\tau}_{g,i}^{j+1}={\gamma}^{\prime }{s}_i^{j+1}\mathit{\sin}{\theta}_i^{j+1}\kern0.5em and\kern0.5em {P}_{i+\frac{1}{2}}^{j+1}={\sigma}_{h,i+\frac{1}{2}}^{j+1}{s}_{i+\frac{1}{2}}^{j+1} $$
(21)

where \( {s}_{i+\frac{1}{2}}^j \) is calculated using a central difference, i.e. \( {s}_{i+\frac{1}{2}}^j=0.5\left({s}_{i+1}^j+{s}_i^j\right) \).

The mesh size and time step are chosen based on the following criteria.

  • The mesh size should be sufficiently small so that it may fully capture the evolution of the process zone, where the shear strength reduces from the peak to the residual, in the weak layer. The process zone length is slightly larger than the characteristic length lu (m) (Zhang et al. 2015), which is given by (Puzrin and Germanovich 2005)

$$ {l}_u=\sqrt{\frac{\delta_r^p{E}_{ps}h}{\tau_{p,w}-{\tau}_{r,w}}} $$
(22)

The mesh size is then suggested to satisfy

$$ \Delta l<\frac{l_u}{20} $$
(23)

  • The time step should be small sufficiently so that the numerical ‘wave’ would not pass through a mesh in every step, that is

$$ \frac{\Delta l}{\Delta t}>c $$
(24)

where c is the ‘wave’ speed (m/s) with its maximum being \( \sqrt{E_{ps}/\rho } \) in the study.

  • The mesh size may turn large or small upon extension or compression and thus need remesh upon over distortion, in spirit of the arbitrary Lagrangian-Eulerian method. The upper limit is governed by (23) while the lower limit is governed by (24).

A trial analysis has shown that numerical results are accurate sufficiently as long as both criteria (23) and (24) are met.

Treatment of the failure initiation

The initiation history for submarine landslides varies according to the type of external factor that might trigger a failure, for example whether the trigger is a gradual increase in loading condition until a limiting shear stress is reached, or alternatively failure is initiated by shear strength reduction in the critical layer.

If the gradual increase in loading is assumed to occur uniformly along the whole weak layer, the shear band will initiate from the most critical point. In this case, the strength reduction during shearing and SBP in the weak layer and global failure in the sliding layer are self-driven and inherently reflected in the constitutive model. This type of initiation may occur in nature due to external factors such as seismic shaking, volcanic eruption, rapid sedimentation and diapirism. The pseudostatic seismic shaking force, if relevant, has to be considered as a driving force in addition to the gravity force, whereby Eq. (15) becomes

$$ {P}_{i+\frac{1}{2}}^j-{P}_{i-\frac{1}{2}}^j-\left({\tau}_i^j+{\tau}_{drag,i}^j-{\tau}_{g,i}^j-{\tau}_{h,i}^j\right)\Delta {l}_i^j=\rho {h}_i^j\frac{\Delta {l}_i^j}{\Delta t}\left({v}_i^{j+\frac{1}{2}}-{v}_i^{j-\frac{1}{2}}\right) $$
(25)

where τh = ραhscosθ is the pseudostatic shear stress (Pa) with ah being the horizontal pseudostatic acceleration (Pa).

A different initiation history might comprise an initial softened zone where the sediment strength is smaller (relative to the ambient shear stress) than surrounding material within the weak layer. Catastrophic SBP occurs with sufficient driving force from the pre-softened zone. Initial reduced strength within the pre-softened zone has to be assigned in the numerical modelling to consider this type of failure initiation history, which is given by

$$ {s}_{u,w}={\tau}_0,x\in \left({x}_a,{x}_b\right) $$
(26)

where τ0 is the current shear strength in the pre-softened zone (Pa) and xa and xb are the two ends of the pre-softened zone.

Treatment of the slab failure and the post-failure landslide evolution

After catastrophic propagation, the overlying sliding layer may undergo active and passive failure during unloading and loading at uphill and downhill slope portions, respectively (Puzrin et al. 2016; Zhang et al. 2019). This failure mechanism for landslides in sensitive clays has been identified and discussed by many studies (e.g. Bernander 2000, Puzrin et al. 2004, Puzrin and Germanovich 2005, Locat et al. (2011), Zhang et al. 2015, Buss et al. 2019), and is able to explain the large scale of submarine landslide (Kvalstad et al. 2005). Analytical criteria for initiation of shear band propagation and active/passive failure under the quasi-static condition have been presented in Zhang et al. (2019); however, the post-failure dynamics needs numerical investigation. Different post-failure mechanisms can be recognised as shown in Fig. 6. At the uphill slope portion, failure might be extended as a form of retrogression with the downward transport of sliding mass; while at the downhill slope portion, depending on whether or not the sliding mass can be confined by the front intact soil blocks, two types of failure mechanisms, i.e. frontally confined (or ploughing) and frontally emergent (or run-out), can be identified.

Fig. 6
figure 6

Different post-failure mechanisms in submarine landslides: a Frontally confined (ploughing) and b Frontally emergent (run-out)

Full size image

The retrogression and frontally confined mechanisms can be automatically reflected by the current numerical scheme as both limit the shear band propagation within the weak layer. The frontally emergent mechanism, however, needs special treatment as the shear surface might develop through the sliding layer to the seabed surface. Puzrin et al. (2016) have thoroughly discussed the morphology evolution and criteria for the two mechanisms. In this study, a simple criterion for static conditions proposed in their study was used to distinguish the frontally emergent from the confined mechanism, which is

$$ \Delta h>4\frac{{\overline{s}}_{u,s}}{\gamma^{\prime }} $$
(27)

where ∆h is the heave of the confined sliding mass (m) and \( {\overline{s}}_{u,s} \) is the average undrained shear strength in the sliding layer (Pa). Once criterion (27) is satisfied, the shear surface is altered in the numerical scheme from the weak layer to the seabed with the shear band segment in the sliding layer 45° inclined with respect to the slope parallel direction, which is consistent with the conventional failure plane under undrained conditions.

Numerical modelling and verifications

In this section, the above depth-integrated numerical scheme is adopted to model large-scale submarine landslides, with the results compared with the large deformation finite element (LDFE) modelling. The dynamic large deformation finite element analysis was conducted based on the approach termed remeshing and interpolation technique with small strain (RITSS: Hu and Randolph 1998). The analysis divides the whole process into a series of small strain increments, each having sufficiently small time step to avoid mesh distortion, followed by remeshing and interpolation of field variables from old to new meshes. The updated Lagrangian calculation is undertaken by the commercial package Abaqus/Standard (Dassault Systems 2014) in each increment, and more details about the finite element modelling can be found in Zhang et al. (2019).

Numerical details

A curvilinear model used here comprises an upper sliding layer and an intermediate weak layer, as shown in Fig. 7. The weak layer, providing locus for shear surface, is assumed to be parallel to the ground surface which is antisymmetric about the slope centre and described by an exponential function (as documented in the Appendix) for base cases. Effect of the geometry function is also addressed later. In Fig. 7, θc is the maximum slope angle at the centre, H is the half-height of the slope (m), h is the depth of the weak layer (m) and s (=hcosθ) is the thickness of the sliding layer (m). The length of the model was set to 8000 m so that the slope angles at two ends approach zero. Base geometry and soil properties are the same with those in Zhang et al. (2019) and listed in Table 1. A total of 40 cases were conducted with various soil properties and geometries given in Table 2. The soil sensitivity in the weak layer was adopted as 5 which is typical for offshore environments, while much less softening with St = 1 was assumed in the sliding layer which was kept consistent with Zhang et al. (2019) for comparison. Cases were considered either with or without rate effects, with the former representing the quasi-static condition and the latter the dynamic condition.

Fig. 7
figure 7

Numerical model used for landslides with shear band propagation

Full size image
Table 1 Base parameters for numerical analyses
Full size table
Table 2 Parameters and results for parametric study
Full size table

Shear band initiation and propagation

Figure 8 a and b show the distributions of the mobilised shear stress during shear band initiation due to two types of triggering (gradual increase of loading or decrease of strength) respectively, for the case S05 (as shown in Table 2) without rate effects. Note that the origin of the coordinate system was set at the slope centre.

Fig. 8
figure 8

Shear stress distributions during shear band initiation and propagation by a increasing weak layer depth and b decreasing shear strength in weak layer

Full size image

The peak mobilised shear stress at the slope centre is smaller than the peak shear strength of τp = 10 kPa when the weak layer depth is h = 8 m. With increasing h, the shear band initiates when the maximum shear stress exceeds the shear strength. When h = 9 m, the progressive shear band propagation is apparent though the slope is still stable after maintaining the loading condition for 100 s, as shown in Fig. 8a. When h is increased to 10 m, catastrophic shear band propagation occurs where the shear band length grows rapidly to near 200 m within 2 s.

The criterion for catastrophic SBP is given by (Zhang et al. 2017)

$$ \frac{\tau_{p,w}}{\gamma^{\prime }h}<\mathit{\tan}{\overline{\theta}}_{l_u} $$
(28)

where \( \mathit{\tan}{\overline{\theta}}_{l_u} \) is a tangent slope gradient with measured distance of lu from the steepest point. With the properties listed in Table 1, the critical depth is about hcri = 9.2 m, which is well between the numerical results i.e. between 9 and 10 m. h = 10 m was chosen in the following such that the value is around 10% higher than the critical ensuring the failure initiation. Similar evolution of mobilised shear stress relative to the shear strength can be observed during the decrease of the shear strength as shown in Fig. 8b. Shear band propagates progressively when τp = 11 kPa but catastrophically when τp = 10 kPa, between which the critical value of τp = 10.7 kPa given by (28) falls in.

Figure 9 shows the shear band growth and distributions of mobilised shear stress during the catastrophic shear band propagation. At t = 5 s, the length of the fully softened zone is less than 100 m and the process zone, where the shear stress ranges between the peak and residual strengths, at each end of the fully softened zone is slightly shorter. The shear band covering both the fully softened and process zones is still limited at this stage with the mobilised shear stresses at far fields the same with the gravity shear stresses. The shear band propagates quickly with a maximum rate of 35 m/s which approaches the compression wave velocity \( \sqrt{E_{ps}/\rho }=37 \) m/s and can be much larger than the transport velocity of the sliding mass. The results in terms of the shear band length from the DAM analysis compare well with the results from the LDFE analysis. After t = 10 s, the fully softened zone is dominant compared to the process zone within the shear band whereby the contribution from the process zone is negligible. Therefore, considering that the shear resistance in the shear band is constant at the residual, the force equilibrium between the shear resistance and the gravity shear stress gives

$$ {\int}_{-\frac{l}{2}}^{\frac{l}{2}}\left({\tau}_g-{\tau}_r\right)=0\to {\int}_{-\frac{l}{2}}^{\frac{l}{2}}r=0\to \overline{r}=0 $$
(29)
Fig. 9
figure 9

a Shear band growth and b shear stress distributions with catastrophic shear band propagation for the case S05 without slab failure

Full size image

where l is the shear band length (m) and \( \overline{r} \) is the average shear stress ratio within the shear band. Equation (29) gives the final shear band length of l = 1644 m under the quasi-static condition (Puzrin et al. 2016). According to Zhang et al. (2019), Eq. (29) is a conservative estimation and a more accurate prediction considering the contribution of the process zone generates the critical shear band length of l = 1482 m which is around 10% smaller than that from Eq. (29). The final shear band length with consideration of the rate effect is 1514 m, as listed in Table 2, which is slightly larger than the accurate prediction in Zhang et al. (2019) but smaller than the simple prediction from Eq. (29). The final shear band length without consideration of the rate effect, however, can propagate much further to l = 2356 m.

Post-failure behaviour

Figure 10 presents the shapes of shear band and ground surface, with contours of degree of softening SD = (su − τp)/(τp − τr) where su is the current shear strength, at different post-failure stages for the case S01 without rate effects. The results from the depth-integrated analysis are compared to the LDFE analysis with velocity contours. The downslope and upslope segments of shear band are denoted by lds and lus, respectively, with the total length l = lds + lus. It is observed from both the depth-integrated and LDFE analyses that slab failure is obvious at t ≥ 20s with passive failure downslope and active failure upslope. The propagation rate of shear band is faster downslope than upslope due to the significant increase of soil volume downslope. The configurations resulted from the depth-integrated analysis are quite comparable to the LDFE analysis.

Fig. 10
figure 10

Configurations of shear band and post-failure surface at different stages for the case S01

Full size image

In summary, the results from the depth-integrated analysis, in terms of the critical condition for shear band propagation and arrest, and post-failure behaviour, have good agreement with the results from the LDFE analysis and analytical solutions, validating the numerical scheme proposed in the study.

Frontally confined vs frontally emergent mechanisms

To verify the ability of the numerical scheme in simulating the frontally emergent behaviour, the case S02 was modified by setting a higher strength to the downslope flat basin at x > 300 m (Fig. 11). The undrained shear strength in the stronger basin is increased from 10 to 40 kPa, such that the ploughing mechanism in this region is effectively supressed, giving way to the frontally emergent mechanism (i.e. run-out). Other parameters were kept the same as in S02 without rate effects. The numerical model used for the frontally emergent analysis is shown in Fig. 11.

Fig. 11
figure 11

Numerical model used for frontally emergent analysis

Full size image

Figure 12 shows the evolution of SBP in the weak layer and post-failure configurations of the sliding mass surface for the analysed case. For t < 10 s, the SBP in the weak layer dominates the failure; when t = 10 s, the slab failure initiates upslope followed by a retrogression. After the passive failure occurs downslope, the sliding mass gradually accumulates confined at x = 300 m, increasing the frontal heave. When the criterion for frontally emergent mechanism (27) gets satisfied, the confined sliding mass runs out over the seabed, serving as the new shear surface. The emergent sliding mass finally settles at t = 150 s, with the front of the mass transport deposit at around x = 750 m.

Fig. 12
figure 12

Numerical results of frontally emergent behaviours

Full size image

Discussion

To further explore the ability of the depth-integrated numerical scheme for modelling submarine landslides with shear band propagation, parametric studies with respect to the effects of the peak strength in the sliding layer, τp,s, the weak layer depth, h, the half-height of the slope, H, the maximum slope angle, θc, and the geometry function were conducted, as presented in this section.

Effects of the peak strength in the sliding layer τ p, s

The shear band fronts and slab failure fronts for cases (S01-S05) with various peak strengths in the sliding layer and without rate effects are given in Fig. 13 and Table 2. The distance between the two slab failure fronts is defined as global length of the seafloor affected by the slope failure (including retrogression, ploughing and run-out; hereafter called global failure length), L, as labelled in Fig. 1b. Similar to the shear band length, the downslope and upslope segments of the global failure length are denoted as Lds and Lus, respectively, with the total length L = Lds + Lus. Except for the case S05 where slab failure is not relevant, the downslope segments of the shear band length (lds) and the global failure length (Lds) are much larger than their upslope counterparts (lus and Lus, respectively), due to the increase of soil volume downslope. This can be further verified by the fact that the downslope shear band and global failure lengths grow firstly and then level off, after which they start growing again because of the accumulation of downward moving sliding mass. For the upslope segment, continued growth of the shear band and global failure lengths can be observed until their maximums are reached. The shear band length increases while the global failure length decreases with the increase of the shear strength in the sliding layer. In cases where the shear strength in the sliding layer is comparable to or less than the weak layer, the shear band fronts are close to the slab failure fronts.

Fig. 13
figure 13

a Shear band fronts, b slab failure fronts, and c shear band length and global failure length versus time for cases S01-05 without rate effects

Full size image

Figure 14 shows the shear band and slab failure fronts, shear band length and global failure length for the cases S01-05 with the consideration of the rate effect. Shear band and global failure lengths for different cases are also summarised in Table 2. With rate effects, the shear band length and global failure length are much smaller than that without rate effects as a considerable amount of energy has been dissipated through material damping in the former. For the case S05, the upslope segment of shear band is close to the downslope segment, which is in alignment with the case of no rate effect.

Fig. 14
figure 14

a Shear band fronts, b slab failure fronts, and c shear band length and global failure length versus time for cases S01-05 with rate effects

Full size image

Figure 15 shows final configurations of the sliding mass deposit for cases S02-S04 without rate effects, compared with the LDFE results. With the increase of the strength in the sliding layer, the retrogressive failure upslope is gradually limited and the sliding layer breaks off leaving a scar. Generally, most post-failure features can be well replicated by the depth-integrated analysis. The main shortcoming is that it is unable to simulate the formation of horsts and grabens in the sliding layer as identified in the LDFE analysis. This does not demerit the practical application of the method for assessing the main features of landslides, such as global failure length, velocity and configuration of sliding mass deposit.

Fig. 15
figure 15

Final configurations of shear band and post-failure surface for cases a S02, b S03, and c S04 without rate effects

Full size image

Effects of the weak layer depth h

Table 2 summarises the shear band and global failure lengths for cases S06-S10 characterised by different weak layer depths, with and without rate effects. Note that the shear strength ratio (which is the shear strength over the effective overburden pressure) is assumed as 0.117 in the weak layer and as 0.234 (averaged) in the sliding layer. It can be observed that the shear band length increases with the increase of the weak layer depth, implying a greater propagation in the deep-seated weak layer. The slab failure occurs upslope only for the case of h = 50 m and does not occur at all for the case of h = 100 m.

Effects of the half-height of the slope H

In cases S10 to S12 in Table 2, the half-height of the slope varies from 10 to 100 m. The shear band and global failure lengths increase by almost a factor of 5 with the increase of the half-height of the slope H from 10 to 100 m.

Effects of the maximum slope angle θ c

The maximum slope angle θc varies between cases S12-S15 from 6° to 16°. The shear band and global failure lengths dramatically increase with the decrease of the maximum slope angle, implying that shear band propagation can be more dangerous in milder slopes. This explains the enormous volume of some submarine landslides observed in very gentle slopes.

Effects of the geometry function

Different geometry functions were tested in examples S16 to S20, with and without accounting for rate effects. In addition to the exponential function, the hyperbolic function and logarithmic functions were used as documented in the Appendix. In particular, a family of logarithmic functions (Puzrin and Burland 1996) can cover a wide spectrum of geometries by adjusting the value of \( {\overset{\sim }{X}}_u \) (Zhang et al. 2019). It is found that, provided the same H and θc, the results with the hyperbolic geometry are very close to that with the exponential geometry, with the difference of around 5%. For the cases with a logarithmic geometry, the shear band and global failure lengths vary with the value of \( {\overset{\sim }{X}}_u \). With the increase of \( {\overset{\sim }{X}}_u \) from 2 to 15, the shear band and global failure lengths have almost doubled.

Modelling of St. Niklausen slide

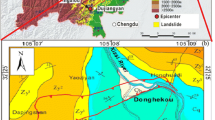
St. Niklausen slide is a subaqueous mass movement at the bottom of the perialpine Lake Lucerne in Central Switzerland (Fig. 16a). It covers around 1.5 × 106 m3 of postglacial sediments affecting an area of 0.8 km2 from the main scar to the mass flow deposits (Fig. 16a, Schnellmann et al. 2005). It was dated back to 2420 cal yr BP and triggered by a major northern alpine earthquake of Mw > 6.5 (Strasser et al. 2007). The travel distance of the failed mass (from the main scar to the mass transport deposit limit) is up to 1500 m and the width of main scar is about 1200 m (Schnellmann et al. 2002, 2005). Such scale of subaqueous failure event was considered to trigger a tsunami hazard with the run-up height up to 4 m, and thus has received considerable attention (Schnellmann et al. 2002, 2005; Stegmann et al. 2007; Strasser 2007, 2011), including a comprehensive large deformation numerical analysis using the Coupled Eulerian-Lagrangian (CEL) method (Stoecklin et al. 2020). The post-failure morphology of the event has been documented using a high-resolution seismic system (Schnellmann et al. 2005) and the soil properties of the intact and failed mass have been investigated through both in situ and lab geotechnical testings (Strasser et al. 2007). The wealth of available information allows for the St. Niklausen slide to be used as a case study for illustrating the application of the proposed numerical framework considering the SBP mechanism.

Fig. 16
figure 16

Illustration of St. Niklausen slide. a Bathymetry map with outline of the slide (after Schnellmann et al. 2005). b Pre-failure slope geometry (after Strasser et al. 2011)

Full size image

The focus is on a two-dimensional section with the furthest travel distance as shown in Fig. 16a. Figure 16 b provides the initial geometry of the sectional model used in the numerical analysis, where the pre-failure lake bottom was reconstructed assuming the initial surface was parallel to the identified slide surface (Strasser et al. 2011; Stoecklin et al. 2020). The peak undrained strength profile of the site near the scar was obtained by Strasser et al. (2007) as replotted in Fig. 17, with the averaged value in the sliding layer and weak layer being 6.1 kPa and 6.0 kPa, respectively. Soil sensitivity, which is the ratio between the peak and residual undrained shear strengths, is between 1.9 and 2.1 (Stoecklin et al. 2020) with the averaged value 2.0 used in present study. The shear displacement required for the sensitive soils fall to the steady state typically ranges between 0.1 and 0.5 m (Skempton 1985) and was set to 0.15 m in this analysis. Elastic deformation of soils is considered with the shear modulus in the slide plane adopted as 150 times the undrained shear strength (= 900 kPa) and the plane strain Young’s modulus in the sliding layer as 600 times the undrained shear strength (= 3660 kPa). The pre-failure lateral earth pressure coefficient was set to 0.6, considering normally consolidated conditions. The initial failure was assumed to be triggered by an earthquake of horizontal pseudostatic acceleration of 0.2 m/s2 lasting for 2 s, which is consistent with the setting in Stoecklin et al. (2020). Considering the sliding mass length of ~ 500 m and its surface roughness of 0.01–0.1 m, the skin friction drag coefficient is averaged at around 0.005 according to Eq. (9). Other parameters are listed in Table 3 in accordance with Stoecklin et al. (2020).

Fig. 17
figure 17

Peak undrained shear strength profile of St. Niklausen slide mass (after Strasser et al. 2007)

Full size image
Table 3 Parameters for the numerical analysis of the St. Niklausen slide
Full size table

Figure 18 shows the numerical modelling of the St. Niklausen slide post-failure evolution using the proposed method, with the red solid line and the black solid line and representing the shear band in the weak layer and the apparent seabed surface, respectively. The dash lines denote the initial configurations of the lake bottom and the weak layer. With the seismic shaking (< 2 s), the shear band first initiates within the steepest part of the slope, i.e. near the toe. The shear band then continues to propagate along the weak layer, also after the seismic action is terminated, reaching the slope toe downslope and the sufficiently flat area upslope. Thereafter, the sliding layer experiences active failure upslope and passive failure downslope resulting in the global slab failure. The failed mass moves downwards thrusting the basin sediments and triggering further shear band propagation downslope with a main headwall formed upslope. No retrogressive failure is observed in the numerical modelling of the St. Niklausen slide. Figure 19 compares the final post-failure configuration using the proposed method with the CEL numerical result (Stoecklin et al. 2020) and the measured seismic reflection profile. Those results agree well with each other in terms of configuration of the stacked mass transport deposits, main scar and global failure length.

Fig. 18
figure 18

Numerical modelling of the St. Niklausen slide evolution

Full size image
Fig. 19
figure 19

Post-failure mass transport deposit of St. Niklausen slide from a seismic reflection profile, b current depth-integrated modelling, and c CEL modelling (Stoecklin et al. 2020)

Full size image

Conclusions

The study has proposed a numerical method that can simulate the whole evolution of submarine landslides, including the failure initiation, shear band propagation, slab failure and post-failure dynamics. Diverse post-failure mechanisms, such as retrogression upslope and ploughing and run-out downslope, can also be recorded through the proposed numerical scheme. Conventional debris flow numerical methods solve flow dynamics using the depth-integrated method, which however needs input information such as the volume and initial velocity of the failed mass. They might be roughly estimated in back analyses of historical events but can be hardly determined for carrying out failure prediction and recurrence. The proposed numerical scheme has combined the shear band propagation theory and the depth-integrated method with the former able to naturally reflect failure initiation and propagation. The governing equations have been established based on the conservation of mass and the conservation of momentum and solved using an explicit finite difference scheme. The drag force from the ambient water is simplified and formulated into the governing equations. Shear band propagation in the weak layer and slab failure in the sliding layer are controlled by the strain softening and rate dependency of the corresponding undrained strength parameters. The soil parameters and flow dynamics in the sliding layer are averaged over the depth.

The results obtained through the proposed numerical scheme are in good agreement with the analytical solutions and large deformation finite element analyses, in terms of the critical conditions for failure initiation as well as the post-failure dynamics. Upon failure initiation, the failure extends further into the downslope segment of the slope than into the upslope one. The shear band length increases while the global length of the seafloor affected by the slope failure (global failure length) decreases with the increase of the shear strength in the sliding layer. Meanwhile, the shear band length and global failure length dramatically increase with the decrease of the maximum slope angle, implying upon shear band propagation the failure in less inclined slope can be more dangerous. This explains the enormous volumes of some submarine landslides observed in very gentle slopes.

The St. Niklausen slide at the floor of the perialpine Lake Lucerne in Central Switzerland has been simulated using the proposed DAM framework considering the shear band propagation mechanism. The numerical results from the current numerical method agree well with the large deformation finite element analysis and the measured seismic reflection profile in terms of the shape of the stacked mass transport deposits, the position of the main scar and the global failure length.

The main shortcomings of the numerical method are (a) it is neither able to simulate the formation of horsts and grabens in the sliding layer, (b) nor to reflect the lubrication and hydroplaning caused by water entrainment and entrapment. Nevertheless, the simplicity and time efficiency of the proposed numerical scheme seem promising for assessing the main features of submarine landslides, such as the travel distance, flow dynamics and configuration of sliding mass deposit.