Introduction

The mass flows treated in this paper consist of rocks or poorly sorted sediments and water, rapidly moving across a steep-slope region and mainly driven by gravity force. It is a kind of natural hazard induced by rainfalls, earthquakes and some other factors. Solid and fluid forces act in concert and both vitally influence the motion of these flows, contributing to their high mobility and unique destructive power (Iverson 1997). They are one of the most catastrophic types of natural hazards due to their extremely high velocity and impact forces. To study and quantify the flow-like behaviour of geophysical flows, governing equations are derived from the principles of mass and momentum conservation, based on the framework of continuum mechanics. Significant advancements have occurred during the last several decades, with development of more and more sophisticated models. Single-phase dry granular avalanches (Savage and Hutter 1989), single-phase debris flows (Chen 1988), two-fluid debris flows (Pitman and Le 2005) and two-layer flows (Fernández-Nieto et al. 2008; Meng et al. 2017) have given gradually more detailed descriptions of the debris flows complexity.

On the basis of the work by Savage and Hutter (1989), most of the current mass flow models use a set of depth-averaged non-linear equations to describe their evolution including shock wave formation. They play an increasingly important role in the risk assessment of natural hazards, including floods, landslides, debris flows and other ‘flow’ movements that can be described by a shallow water-like model with different rheology laws (Hungr and McDougall 2009). To obtain sufficiently accurate and stable computations with shock capturing, various numerical schemes have been developed, including Lagrangian or Eulerian techniques, mesh-based or mesh-free (e.g. Mangeney et al. 2003; Pastor et al. 2009; Savage and Hutter 1989; Tai et al. 2002).

In this paper, we present a mass-flow model based on a second-order central difference scheme (NT) that was originally proposed by Nessyahu and Tadmor (1990) and we apply it to study a catastrophic historical landslide that occurred in Italy in 1783. To test the accuracy and robustness of the code, numerical results are compared with analytical solutions, which exist only for ideal cases, and with experimental data. The analytical solutions we use as benchmark cases are the solution of a typical dam break problem given by Stoker (1957) and the solution for simplified granular flows provided by Faccanoni and Mangeney (2013). The results of the 2D dam-break problem we treat numerically are compared with published data obtained by other numerical approaches, i.e. with results by Fagherazzi et al. (2004) and by Ouyang et al. (2013). As for the experimental data, we use data from a hydraulic laboratory experiment performed by the EU CADAM (European Union Concerted Action on Dam Break Modelling) where a dam-break over a triangular hump was reproduced (e.g. Brufau et al. 2002; Liang and Marche 2009; Liu et al. 2016; Mao et al. 2016). According to the benchmark results, we can consider our code as totally validated since it performs very well for all tested cases (including analytical solutions and experiment data).

The catastrophic event we analyse in this paper is the tsunamigenic landslide that occurred in 1783 in Scilla, southern Italy, which6 is a very important case for the assessment of risk in the Tyrrhenian Calabria and northern Sicily. It was already investigated by Mazzanti and Bozzano (2011) and Zaniboni et al. (2016). It is simulated here with our code, solving a modified flow-like model proposed by Xia and Liang (2018) to treat complicated topographies based on a global Cartesian coordinate system. Our numerical investigations mainly focus on the dynamic evolution and on the deposit region of the landslide. We test the performance of a linear and a quadratic drag law and conclude that the latter provides a better description of the deposit distribution.

Governing equations

Based on the conservation law of mass and momentum, different numerical models have been developed over years (e.g. George and Iverson 2011; Iverson and Denlinger 2001; Meng and Wang 2016; Pudasaini 2012; Savage and Hutter 1989), which can be given the form of the classical SWEs (shallow water equations) and can be expressed in vector notation as follows:

$$ \frac{\partial \overrightarrow{U}}{\partial t}+\frac{\partial \overrightarrow{F}}{\partial x}+\frac{\partial \overrightarrow{G}}{\partial y}=\overrightarrow{S} $$
(1)

In the LHS of Eq. (1), \( \overrightarrow{U} \) is the vector of the conservative variables and \( \overrightarrow{F} \) and \( \overrightarrow{G} \) represent down-slope and cross-slope momentum flux respectively. Further, t, x and y denote time, down-slope direction and cross-slope direction respectively. As for the RHS, \( \overrightarrow{S} \) is the vector of the source terms. For a traditional shallow water model, the conservative vector \( \overrightarrow{U} \) includes the depth-averaged height h and the fluxes along x and y directions. The momentum flux vectors \( \overrightarrow{F} \) and \( \overrightarrow{G} \) contain fluxes and gravity effects. Basal topography and friction terms are included in the source term \( \overrightarrow{S} \). More details are explained by formulas in the next sections.

Numerical scheme

Combining a first-order Lax–Friedrichs scheme (Lax 1954) with a piecewise linear reconstruction, the central Nessyahu–Tadmor (NT) scheme (Nessyahu and Tadmor 1990) we adopt here computes the staggered cell averages at the interfacing break-points and has the advantage of the simplicity of a Riemann-solver-free approach. In this section, we explain the cell average and the linear reconstruction techniques of the NT scheme that is written in a conservative form to automatically satisfy the conservation properties of the original equations. Integrating the conservation law of Eq. (1) on a cell in both space and time provides the full set of discrete equations for the numerical code. A staggered grid algorithm is adopted since it provides an automatic mechanism to control spurious oscillations, which are further reduced by means of a suitable flux limiter method. The scheme is a so-called shock capturing scheme, solving the Eq. (1) on a fixed Cartesian grid (Eulerian approach) and identifying the shocks by the regions with large gradients. For more details, one can refer to Tai et al. (2002).

Cell average

In order to explain our numerical scheme better, we use a 1D case first, where the governing equations take the following form:

$$ {u}_t\left(x,t\right)+{f}_x\left(u\left(x,t\right)\right)=s\left(u\left(x,t\right)\right) $$
(2)

Here u is the conservative variable, f is the momentum flux along x direction and s is the source term. Hereafter, the subscripts t, x represent derivatives with respect to the time and x directions. To solve this problem, the idea of cell average is applied on a staggered grid.

$$ {\displaystyle \begin{array}{l}{U}_i^n=\frac{1}{\varDelta x}{\int}_{{\mathrm{x}}_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}u\left(x,{t}^n\right) dx,\\ {}{U}_{i+\frac{1}{2}}^n=\frac{1}{\varDelta x}{\int}_{x_i}^{x_{i+1}}u\left(x,{t}^n\right) dx\end{array}} $$
(3)

Here, U denotes cell-average values. The subscript i and the superscript n represent at the ith node and at the current state respectively. The center of the interval (xi − 1/2, xi + 1/2) is xi, and the interval is named as cell Ii. Thus, the interval (xi, xi + 1) is naturally denoted as cell Ii + 1/2. Taking the cell Ii as an example and integrating the hyperbolic equations in time over the interval (tn, tn + 1) and in space over the interval (\( {x}_{i-\frac{1}{2}},{x}_{i+\frac{1}{2}} \)), one obtains the following:

$$ {\displaystyle \begin{array}{ll}& {\int}_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}{\int}_{t^n}^{t^{n+1}}{u}_t\left(x,t\right) dxdt=\\ {}& -{\int}_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}{\int}_{t^n}^{t^{n+1}}{f}_x\left(u\left(x,t\right)\right) dxdt\\ {}& +{\int}_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}{\int}_{t^n}^{t^{n+1}}s\left(u\left(x,t\right)\right) dxdt\end{array}} $$
(4)

that can be easily written as follows:

$$ {\displaystyle \begin{array}{ll}& {\int}_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}u\left(x,{t}^{n+1}\right) dx={\int}_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}u\left(x,{t}^n\right) dx\\ {}& -{\int}_{t^n}^{t^{n+1}}\left(f\left(u\left({x}_{i+\frac{1}{2}},t\right)\right)-f\left(u\left({x}_{i-\frac{1}{2}},t\right)\right)\right) dt\\ {}& +{\int}_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}{\int}_{t^n}^{t^{n+1}}s\left(u\left(x,t\right)\right) dx dt\end{array}} $$
(5)

The LHS and the first term of the RHS of the above equation can be further manipulated by the cell average technique:

$$ {\displaystyle \begin{array}{ll}& {\int}_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}u\left(x,{t}^{n+1}\right) dx=\Delta x{U}_i^{n+1}\\ {}& {\int}_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}u\left(x,{t}^n\right) dx=\frac{\varDelta x}{2}{U}_{i-\frac{1}{4}}^n+\frac{\varDelta x}{2}{U}_{i+\frac{1}{4}}^n\end{array}} $$
(6)

As for the other terms in the RHS, they similarly can be transformed to the following:

$$ {\displaystyle \begin{array}{ll}& {\int}_{t^n}^{t^{n+1}}\left(f\left(u\left({x}_{i+\frac{1}{2}},t\right)\right)-f\left(u\right({x}_{i-\frac{1}{2}},t\left)\right)\right) dt\\ {}& =\Delta t\left(f\left({u}_{i+\frac{1}{2}}^{n+\frac{1}{2}}\right)-f\left({u}_{i-\frac{1}{2}}^{n+\frac{1}{2}}\right)\right)\end{array}} $$
(7)
$$ {\displaystyle \begin{array}{ll}& {\int}_{x_{i-\frac{1}{2}}}^{x_{i+\frac{1}{2}}}{\int}_{t^n}^{t^{n+1}}s\left(u\left(x,t\right)\right) dxdt\\ {}& =\frac{\varDelta t\varDelta x}{2}\left(s\left({U}_{i+\frac{1}{4}}^{n+\frac{1}{2}}\right)+s\left({U}_{i-\frac{1}{4}}^{n+\frac{1}{2}}\right)\right)\end{array}} $$
(8)

where \( {u}_i^n \) is used to denote u(xi, tn).

By a piecewise linear approximation, we can assume the following:

$$ {U}_{i\pm \frac{1}{4}}^n={u}_{i\pm \frac{1}{2}}^n\mp \frac{\varDelta x}{4}{\left({u}_x\right)}_{i\pm \frac{1}{2}}^n $$
(9)

Further, the values at half-time step can be similarly predicted by Taylor’s expansion and the original equation Eq. (2):

$$ {\displaystyle \begin{array}{ll}& {u}_{i\pm \frac{1}{2}}^{n+\frac{1}{2}}={u}_{i\pm \frac{1}{2}}^n+\frac{\varDelta t}{2}{\left({u}_t\right)}_{i\pm \frac{1}{2}}^n\\ {}& ={u}_{i\pm \frac{1}{2}}^n-\frac{\varDelta t}{2}{\left({f}_x\right)}_{i\pm \frac{1}{2}}^n+\frac{\varDelta t}{2}{(s)}_{i\pm \frac{1}{2}}^n\end{array}} $$
(10)
$$ {U}_{i\pm \frac{1}{4}}^{n+\frac{1}{2}}={u}_{i\pm \frac{1}{2}}^{n+\frac{1}{2}}\mp \frac{\varDelta x}{4}{\left({u}_x\right)}_{i\pm \frac{1}{2}}^{n+\frac{1}{2}} $$
(11)

Therefore the cell average values \( {U}_i^{n+1} \) can be obtained from the original values at the previous time step at the nodes \( {x}_{i-\frac{1}{2}},{x}_{i+\frac{1}{2}} \) denoted as \( {u}_{i\mp \frac{1}{2}}^n \). Based on the present scheme, on integrating values in the intervals Ii + 1/2 and Ii, the values of the original nodes can be updated after two time steps. Figure 1 explains the procedure of the time advance process.

Fig. 1
figure 1

Stencil for 1D cases. Assume that the initial computational domain includes three values \( {u}_{i-1}^n \), \( {u}_i^n \) and \( {u}_{i+1}^n \), denoted as black-filled circles. With the information at a ghost node \( {u}_{i+2}^n \) shown as a black-filled rectangle, the values of middle points \( {u}_{i-1/2}^{n+1} \), \( {u}_{i+1/2}^{n+1} \) and \( {u}_{i+3/2}^{n+1} \), marked as unfilled circles can be obtained by the mentioned strategy. Moreover, with the values at another ghost node \( {u}_{i-3/2}^{n+1} \) marked as an unfilled rectangle, the values at original domain are obtained at the next time step, which are denoted as \( {u}_{i-1}^{n+2} \), \( {u}_i^{n+2} \) and \( {u}_{i+1}^{n+2} \). Therefore, the time advance process of the conservative variable is achieved

Full size image

Flux limiter

To attenuate possible spurious oscillations in the numerical solution, a flux limiter method is applied to conduct the second-order piecewise linear reconstructions. To satisfy the non-oscillatory property, the cell average derivative is determined by a generalized minmod-like limiter involving a parameter θ (Kurganov and Tadmor 2000).

$$ {\left({u}_x\right)}_i^n= MM\left(\theta \frac{u_i^n-{u}_{i-1}^n}{\varDelta x},\frac{u_{i+1}^n-{u}_{i-1}^n}{2\varDelta x},\theta \frac{u_{i+1}^n-{u}_i^n}{\varDelta x}\right) $$
(12)

where θ is a predefined parameter and 1 ≤ θ ≤ 2. MM denotes the function of the minmod limiter expression. For the present flux limiter involving three values, i.e. MM(z1, z2, z3):

$$ \mathrm{minmod}\kern.2em \left({z}_1,{z}_2,{z}_3\right)=\left\{\begin{array}{ll}\min \left\{{z}_1,{z}_2,{z}_3\right\},& \kern1em \mathrm{if}\ {z}_{1,2,3}>0\\ {}\max \left\{{z}_1,{z}_2,{z}_3\right\},& \kern1em \mathrm{if}\ {z}_{1,2,3}<0\\ {}0,& \kern1em \mathrm{otherwise}.\end{array}\right. $$

Stability condition

The CFL (Courant–Friedrichs–Lewy) stability condition is used to ensure that the maximum phase velocity cmax is always smaller than the speed associated with the grid, i.e. Δx/Δt, and gives the expression of the adaptive time step for solving the governing equations:

$$ \Delta t\le k\frac{\varDelta x}{c_{\mathrm{max}}} $$
(13)
$$ {c}_{\mathrm{max}}=\underset{\forall i}{\max}\left(|{\lambda}_i^{\left(\min \right)}|,|{\lambda}_i^{\left(\max \right)}|\right) $$
(14)

where \( {\lambda}_i^{\left(\min \right)} \) and \( {\lambda}_i^{\left(\max \right)} \) are the minimum and maximum eigenvalues of the Jacobian matrix \( {\left(\partial \overrightarrow{F}/\partial \overrightarrow{U}\right)}_i^n \). The parameter k is usually taken less than 1/0.5 for the NT scheme applied to 1D/2D cases, and k = 0.475 for 2D simulations is suggested by the numerical experiments conducted by Jiang and Tadmor ( 1998).

Extension to two-dimensional cases

With a 2D cell, the formulas given in the previous section have to be adapted to cover both space directions. Each loop of calculation is divided into two time steps. In the first time step, the values of cell average, denoted as \( {U}_{i+1/2,j+1/2}^{n+1} \) are updated from the original nodal values, denoted as \( {u}_{i,j}^n \). In the second time step, the values of cell average \( {U}_{i,j}^{n+2} \) are updated from the values \( {u}_{i+1/2,j+1/2}^{n+1} \) obtained from the first time step. Thus, the values atthe original nodes are updated every two time-steps calculations. Figure 2 illustrates this procedure. The operation is carried out on a matrix with the same size, which is friendly for programming.

Fig. 2
figure 2

Stencil for 2D cases. The values at the original nodes \( {u}_{i,j}^n \) are shown as orange points, and the region defined by orange solid lines is the computational domain. By means of the mentioned numerical scheme, cell average values at \( {U}_{i+1/2,j+1/2}^{n+1} \) (green nodes) can be obtained with the help of ghost nodes for the first time step. Let values at the nodes be equal to the obtained cell average values, that is \( {u}_{i+1/2,j+1/2}^{n+1}={U}_{i+1/2,j+1/2}^{n+1} \). By one more time step, all the values at original nodes \( {u}_{i,j}^{n+2} \) can be successfully updated (shown as blue nodes). Naturally, the information of the displayed ghost nodes are used

Full size image

Benchmarks

Classical ‘dam-break’ problem

The dam-break problem is a classical benchmark for shock-capturing numerical schemes and has been widely used for mass flow models validation. The analytical solution of this kind of Saint-Venant equations is reviewed in Faccanoni and Mangeney (2013). The governing equations can be given the following form:

$$ \overrightarrow{U}=\left[\begin{array}{c}h\\ {} hu\end{array}\right];\kern1em \overrightarrow{F}=\left[\begin{array}{c} hu\\ {}h{u}^2+\frac{1}{2}g{h}^2;\end{array}\right];\kern1em \overrightarrow{G}=0;\kern1em \overrightarrow{S}=0 $$
(15)

where h is the height of water, g = 9.81 m/s2 is the gravity acceleration, u is the x direction velocity. The initial condition is that the water is still, and its level has an abrupt jump from the higher constant value h1 to the lower constant value h2. We ran very many experiments that all gave very satisfactory results. What we show here refers to the same configuration treated by Louaked and Hanich (1998), i.e. the initial upstream depth is set to h1 = 1.0 m and the downstream depth is set as h2 = 10−6 m. The adopted fixed space step is Δx = 0.01 m. The numerical and analytical solutions for a specific time t = 0.1 s are compared in Fig. 3 to show that the shock wave is well captured by the present method.

Fig. 3
figure 3

Comparison between numerical simulation and analytical solution of the dam break problem for t = 0.1 s

Full size image

Another typical benchmark for mass flows is the debris mixture flowing over a rough slope inclined at an angle α, described by the following equations:

$$ {\displaystyle \begin{array}{ll}& \overrightarrow{U}=\left[\begin{array}{c}h\\ {} hu\end{array}\right];\kern1em \overrightarrow{F}=\left[\begin{array}{c} hu\\ {}h{u}^2+\frac{1}{2}{\beta}_x{h}^2;\end{array}\right];\\ {}& \overrightarrow{G}=0;\kern1em \overrightarrow{S}=\left[\begin{array}{c}0\\ {} hg\cos \alpha \left(\tan \alpha -\tan \delta \right)\end{array}\right]\end{array}} $$
(16)

where βx = g cos α and δ are the basal friction angles. If lateral Earth pressure is taken into consideration, we have βx = Kxg cos α, where Kx is the lateral Earth pressure coefficient (Savage and Hutter 1989) along the x direction. The model adopted hereafter assumes that lateral Earth pressure coefficient is equal to 1. Here we use the initial configuration of the ‘dry bed’ test case (the downstream water level h2 = 0.0 m) provided by Faccanoni and Mangeney (2013), where α = 22∘, δ = 21∘ and the upstream water level is h1 = 0.1446 m. The mesh density of Δx = 0.01 m is used. The results obtained from this numerical scheme at t = 0.5 s are seen in Fig. 4.

Fig. 4
figure 4

Comparison between numerical simulation and analytical solution for a mixture flow over a rough inclined slope for t = 0.5 s

Full size image

Two-dimensional ‘dam-break’ problem

The geometry of this problem is first used by Fennema and Chaudhry (1990) and has been widely adopted for testing numerical codes or new approaches, such as by Fagherazzi et al. (2004), Ouyang et al. (2013) and La Rocca et al. (2015). The computational domain is a 200-m-long and 200-m-wide channel with a thin dam that is located at the position of (x, y) = (100 m, 0 − 200 m) along the y direction. Water depths of the upstream and downstream regions are 10 m and 5 m respectively. Assuming that a part of the dam, that is (x, y) = (100 m, 95 − 170 m), breaks instantaneously, the water upstream crashes into the reservoir with lower water depth. The wall condition is enforced at the boundary of the channel and at the non-breaking sector of the dam, where the velocities normal to the wall are set to zero. Contour and height profiles of water are given at t = 7.2s in Figs. 5 and 6. Using coarse grids with a resolution of 2.5 m, the results obtained with the presenting scheme agree well with the published results that can be found in Fagherazzi et al. (2004) and in the other aforementioned papers.

Fig. 5
figure 5

Contour plot of the break at t = 7.2 s. Resolution for the simulation is set to 2.5 m for both x and y directions

Full size image
Fig. 6
figure 6

Height profile of the water break t = 7.2 s

Full size image

Dam break over a triangular hump

The European project EU CADAM (European Union Concerted Action on Dam Break Modelling) provides a laboratory experiment for testing the capability of numerical schemes applied to a practical case. The set-up is a 38 m long horizontal domain with a dam located at x = 15.5 m. Seven gauges named G2, G4, G8, G10, G11, G13 and G20, located at x = 17.5, 19.5, 23.5, 25.5, 26.5, 28.5 and 35.5 m, were set to measure the time history of the water depth. The configuration is illustrated in Fig. 7.

Fig. 7
figure 7

Sketch of the set-up of the dam break experiment over a triangular hump

Full size image

In the numerical simulation, the node separation is set to Δx = 0.05 m and the Manning coefficient n = 0.0125 s/m1/3 is adopted throughout the entire domain. On the left end, a rigid wall condition is imposed, while on the right end, the condition is a free flow. The duration of the computed time record is 90 s, according to the experimental data handed over by Prof. Lanhao Zhao of the Hohai University in China. After the sudden opening of the gate, the water in the reservoir rushes out and inundates the downstream domain. The water wave propagates along the domain over the basal topography. Due to gravity and friction, the direction of water motion changes with time, causing several surges observed at gauges. In Fig. 8, it can be seen that the laboratory test is reproduced by the current numerical scheme with high accuracy and resolution. The prediction of arriving time and water depth of the various water pulses nearly coincide, which is a quite remarkable result.

Fig. 8
figure 8

Time histories of the water elevation at the seven gauges

Full size image

Investigation of the 1783 Scilla landslide

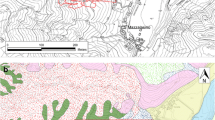
The narrow Messina Strait, between the eastern tip of Scilly and the southern end of Calabria, connecting the Tyrrhenian Sea to the north with the Ionian Sea to the south, as shown in Fig. 9a, is one of the most seismically active areas of southern Italy. Tectonically, it is dominated by the development of the Siculo-Calabrian Rift Zone and is the northernmost sector of the high level seismic belt including the largest earthquakes that occurred in southern Italy in the last four centuries, such as the 1693 SE Sicily earthquakes, the 1783 Calabrian seismic sequence, the 1905 Monteleone earthquake and the Messina earthquake of 1908 (Catalano et al. 2008). The 1783 seismic crisis started with a sequence of strong earthquakes from February to March, exceeding magnitude Mw 7 (Rovida et al. 2011) and lasted for at least 3 years (1783–1785). It caused more than 30,000 casualties, destroyed 200 localities (Porfido et al. 2011) and triggered a further series of secondary disasters including numerous mass failures, river dams with temporary lake formation and tsunamis. The most catastrophic episode of this crisis in terms of death toll was the Scilla tsunami event, which was generated by an earthquake-induced landslide and that killed more than 1500 people on 6 February 1783. The landslide occurred south of the coastal village of Scilla. The earthquake regarded as the trigger of the landslide happened offshore in the Messina Strait and was a Mw = 5.9 aftershock of a strong shock occurred the day before. The mass failure took place about 30 min later, and a huge tsunami generated by the landslide crashing into the sea was observed soon after the mass collapse (Minasi 1785). Available historical reports and studies provide the tsunami run-up heights and inundation distances, as summarized in Graziani et al. (2006). On the basis of recent field surveys of subaerial and submarine scars, the total volume involved in the failure was postulated to be 8 Mm3 and the deposit was estimated at 5–6 Mm3 (Bozzano et al. 2006; Bozzano et al. 2011).

Fig. 9
figure 9

a Geographical location of Scilla (red rectangle). Solid blue circles represent the 1783 seismic sequence with size increasing with earthquake magnitude. b Area of the Scilla landslide (modified from Zaniboni et al. (2016))

Full size image

Previous studies of the Scilla event were carried out by Avolio et al. (2009), Mazzanti and Bozzano (2011) and Zaniboni et al. (2016). The Scilla landslide in the first two papers was simulated by the cellular automata technique and by the DAN3D code (Hungr and McDougall 2009). The last paper used a 1D Lagrangian block model (Tinti et al. 1997). The reconstruction by Avolio et al. (2009) merely provides the area of deposits. DAN3D is the developed code that uses a Lagrangian numerical method to solve the aforementioned depth-averaged governing equations and where a variety of basal rheological relationships, material entrainment and other features can be included. The DAN3D simulations, where underwater drag and friction were accounted through a turbulence coefficient, revealed that the Scilla landslide accelerated to 45 m/s after 20 s and decelerated to rest after 80 s. The DAN3D computed deposits agree acceptably with the observed data, but the dynamic evolution of the mass was not provided in the published papers. As for the 1D Lagrangian block model, the total mass is discretized into blocks that interact with each other. Forces including gravity, friction, drag and block–block interaction act on blocks, which are allowed to change shape, but not volume. The numerical investigations by Zaniboni et al. (2016) provide reasonable results in both landslide dynamics and tsunami generation. However, it is worth noting that for the 1D block model the mass motion path has to be predefined, which implies that the topography effects have to be studied before applying the model.

In this section, the landslide is represented as a mixture flow, and the motion is calculated by means of the present numerical approach. We remark that we adopt a flow model that is capable of fully handling topography and of computing the mass motion path. Two drag models, obeying a linear and a quadratic law, are implemented to investigate the time evolution of the mass. Consequently, two kinds of landslide dynamics are obtained from the simulation. We anticipate that the time history obtained by means of the linear drag assumption provides a motion mechanism similar to that from the 1D block model (Zaniboni et al. 2016). A sketch of the Scilla landslide body and of the deposit area is given in Fig. 9b.

Mixture model with topography modifications

To investigate the dynamic evolution of the Scilla landslide, a grain–water mixture model with topography modification is used here. As shown in ‘Classical ‘dam-break’ problem’, the mixture model can be simply regarded as the extension of the shallow water equations, with additional lateral pressure coefficient and friction terms. For more technical details, such as the assumptions, simplification and depth-average theory, one can refer to other works (Gray et al. 1999; Iverson and Denlinger 2001; Savage and Hutter 1989). Topography, that is the driving factor for geophysical mass flows, can be treated in a Cartesian coordinate system but also in a curvilinear coordinate system (Gray et al. 1999). For the numerical application of shallow water models to real cases, an additional topography-linked coordinate system (i.e. Kelfoun and Druitt 2005) or more complicated Boussinesq-like models (e.g. Castro-Orgaz et al. 2015; Denlinger and Iverson 2004) are required for ensuring the accuracy and the stability of numerical schemes. Here we use a global Cartesian coordinate system, using a model (Xia and Liang 2018) that, considering vertical acceleration and curvature effects, has been proven to be successful in both theoretical studies and applications. The vector form of the equations is given as follows:

$$ {\displaystyle \begin{array}{ll}& \overrightarrow{U}=\left[\begin{array}{c}h\\ {} hu\\ {} hv\end{array}\right];\kern1em \overrightarrow{F}=\left[\begin{array}{c} hu\\ {}h{u}^2+\frac{1}{2}g{\phi}^{-2}{h}^2\\ {} hu v\end{array}\right];\kern1em \\ {}& \overrightarrow{G}=\left[\begin{array}{c} hv\\ {} hu v\\ {}h{v}^2+\frac{1}{2}g{\phi}^{-2}{h}^2\end{array}\right];\kern1em \overrightarrow{S}={\overrightarrow{S}}_b+{\overrightarrow{S}}_f\end{array}} $$
(17)
$$ {\displaystyle \begin{array}{ll}& {\overrightarrow{S}}_b=\left[\begin{array}{c}0\\ {}- ah{b}_x+\frac{1}{2}g{h}^2\frac{\partial \left({\phi}^{-2}\right)}{\partial x}\\ {}- ah{b}_y+\frac{1}{2}g{h}^2\frac{\partial \left({\phi}^{-2}\right)}{\partial y}\end{array}\right];\\ {}& {\overrightarrow{S}}_f=\left[\begin{array}{c}0\\ {}-\frac{\mu ahu\phi}{\sqrt{u^2+{v}^2+{\left(u{b}_x+v{b}_y\right)}^2}}\\ {}-\frac{\mu ahv\phi}{\sqrt{u^2+{v}^2+{\left(u{b}_x+v{b}_y\right)}^2}}\end{array}\right]\end{array}} $$
(18)
$$ {\displaystyle \begin{array}{ll}& a={\phi}^{-2}\left(g+{\overrightarrow{v}}^T\overrightarrow{H}\overrightarrow{v}\right),\kern1em \overrightarrow{v}={\left(u,v\right)}^T;\\ {}& \overrightarrow{H}=\left[\begin{array}{cc}{b}_{xx}& {b}_{xy}\\ {}{b}_{xy}& {b}_{yy}\end{array}\right];\kern1em \phi ={\left({b}_x^2+{b}_y^2+1\right)}^{1/2}\end{array}} $$
(19)

where \( {\overrightarrow{S}}_b \) is the basal topography term and \( {\overrightarrow{S}}_f \) is the friction term. The factor ϕ−2 merely related to basal topography is theoretically important for the governing equations considering complex topography in a Cartesian coordinate system. The term \( {\overrightarrow{v}}^T\overrightarrow{H}\overrightarrow{v} \) accounts for the effect of the centrifugal force. \( \overrightarrow{v} \) is the velocity vector including velocity components along x and y directions. μ is the basal friction coefficient, and b(x, y) is the basal surface of the landslide. bx(y) and bxx, bxy, byy represent the first-order and the second-order derivatives. In this case, we have assumed that the lateral Earth pressure coefficients Kx and Ky are equal to 1.

Buoyancy and drag force terms

In the study conducted by Mazzanti and Bozzano (2011), using the DAN3D model, the motion of the mass underwater is computed by applying a turbulence coefficient, which is rarely used in mass flow models. In our simulation, the whole event is restricted to the motion of the slide, and the complicated interactions between mass and water are simplified as buoyancy and drag forces acting on the mass itself. The effective gravity acceleration for the submarine motion of the slide is reduced to (1 − γ)g, where γ is the ratio between the fluid and debris densities, i.e. γ = ρf/ρs, with ρf = 1000 kg/m3 and ρs = 1700 kg/m3 adopted for the simulations. The drag force is the effect of a rather complicated process difficult to describe. In mass flow modeling, it can be expressed as a linear or quadratic function of the relative mass–water velocity (Meng and Wang 2016; Pudasaini 2012). However, the quantification of the drag force coefficient is not easy and it is usually determined by empirical formulas based on experiments data. Additionally, some proposed models (i.e. Pudasaini 2012) involving several parameters that are hard to evaluate, are scarcely adequate for practical applications. Here, we focus on the performance of two different drag force relationships. In our model the drag force is given as an additional source term:

$$ {\displaystyle \begin{array}{ll}& \overrightarrow{S}={\overrightarrow{S}}_b+{\overrightarrow{S}}_f+{\overrightarrow{S}}_{\mathrm{drag}};\\ {}& {\overrightarrow{S}}_{l\mathrm{drag}}=\left[\begin{array}{c}0\\ {}-{C}_d hu\\ {}-{C}_d hv\end{array}\right];\kern1em {\overrightarrow{S}}_{q\mathrm{drag}}=\left[\begin{array}{c}0\\ {}-{C}_d hu\sqrt{u^2+{v}^2}\\ {}-{C}_d hv\sqrt{u^2+{v}^2}\end{array}\right]\end{array}} $$
(20)

where Cd is the drag force coefficient that has dimensions of inverse time for linear model and dimensions of inverse length for quadratic model. The drag force term is denoted as \( {\overrightarrow{S}}_{\mathrm{drag}} \), which is implemented as linear drag forces \( {\overrightarrow{S}}_{l\mathrm{drag}} \) or quadratic drag forces \( {\overrightarrow{S}}_{q\mathrm{drag}} \) into the model. A constant drag coefficient is used in the simulations, choosing Cd = 0.05 s−1 for linear drag and the Cd = 0.015 m−1 for quadratic drag forces.

Dynamic evolution of the Scilla landslide

After the triggering, the falling mass moves over the basal topography acted by driving and resisting forces and finally deposits at a certain distance. The triggering mechanism of the landslide is not contained in the model, and the mass is released without initial velocity. To account for the dynamic evolution of the landslide, the average velocity, calculated by the total momentum and total height, is used to capture the overall dynamic state of the landslide. At each time step, the code detects the boundary of the region that contains the mass material, so determining the computational domain. The choice of friction coefficients depends on the back analysis, according to the observed data (Zaniboni et al. 2016) and differentiates between subaerial and submarine sliding. The notations of μSA and μSM are used to represent the basal friction coefficient for subaerial sliding and submarine sliding respectively. For the simulation adopting the linear drag model, μSA = 0.25 and μSM = 0.05, while μSA = 0.25 and μSM = 0.03 are chosen for the quadratic drag model.

The average velocity time histories shown in Fig. 10 clearly provide two distinct dynamics obtained from two adopted different drag functions. As for the linear-law case, one may observe that the curve we obtain here is similar to the one computed by Zaniboni et al. (2016) with their 1D block model, where they used however a quadratic law for the drag. Indeed, in both cases, the landslide experiences a rapid acceleration stage followed by a slightly less rapid deceleration stage. The only difference is that the velocity peak appears at slightly different times. The curve we obtain for the quadratic law model however is quite different. The acceleration phase is shorter, the peak velocity is much less (24 m/s vs. circa 32 m/s) and the deceleration phase lasts several minutes, much longer than for the linear drag case.

Fig. 10
figure 10

Time evolution of the mean velocity of the landslide. The dynamics obtained from the linear drag model is quite similar to the motion depicted by the 1D quadratic-drag block model (Zaniboni et al. 2016), with slightly different accelerations. The landslide accelerates, reaching a peak value at 32 m/s and then starts slowing down. Instead, the curve from the quadratic law provides a much longer duration of the landslide motion. The landslide is strongly decelerated by the water when it crashes into the sea with high velocity and then moves slowly to the final still position. The peak velocity of the present simulations is smaller than the value exceeding 40 m/s obtained by Mazzanti and Bozzano (2011), but the deposit region is successfully reproduced by the model

Full size image

Propagation and deposition

The field surveys of subaerial and submarine scars reveal the initial and final position of the landslide, while the heights of the offshore deposits are not known from the literature. We present the snapshots of the landslide height at different times in Figs. 11 and 12. The snapshots are shown at 10 s time intervals for the linear drag model simulation, whereas different time intervals are used for the quadratic drag model. As shown by the snapshots, the mass moves along a reasonable direction, which validates the goodness of the mixture-flow model with topographical modifications (Xia and Liang 2018).

Fig. 11
figure 11

Snapshots of the landslide mass taken at 10-s intervals (from t = 10 s to t = 90 s) obtained through the linear drag model. The observed landslide subaerial scar area is bounded by a solid blue line, and the observed landslide deposit area is bounded by a dashed red line. The coastline is denoted by the black line. The movement can be separated into two stages: the acceleration stage (t = 0–30 s) and the following deceleration stage. Easting and Northing are implemented as x and y directions in the simulation

Full size image
Fig. 12
figure 12

Snapshots of the landslide mass (from t = 10 s to t = 300 s) obtained through the quadratic drag model. The blue line depicts the boundary of the initial region of the landslide. The observed landslide deposit is bounded by a dashed redline with the black line denoting the coastline. The movement can be separated into three stages: an acceleration stage and two deceleration phases. The mass is mainly driven by gravity forces in the first 15 s and then experiences a strong deceleration until 30s and then a gradual slow down until the rest. Easting and Northing are implemented as x and y directions in the simulation

Full size image

Figure 11 is the set of snapshots regarding the linear drag model. After the landslide front crashes into water, the rest of the mass enters the sea and is affected by a relatively low resistance that does not heavily impede the motion of the landslide. This dynamic is depicted by the behaviour of the front body. In the first 30 s, the main body concentrates on the middle and the rear of the landslide. Later, mainly as the effect of the drag force, the main mass moves to the front and the middle, as can be seen in the snapshot at t = 40 s. During the deceleration stage, most mass deposits within the observed region (delimited by the dashed red line, see the t = 70 s snapshot), and the motion is practically over after 90 s.

Figure 12 displays the simulations concerning the quadratic drag case. Impacted by a very large drag when the mass front crashes into water, the landslide moves slowly and tightly during the underwater propagation. In contrast to what is shown in Fig. 11, the main mass concentrates on the front and the middle of the body during the acceleration stage. The lateral spreading behaviour shown in Fig. 11 is restricted in Fig. 12. After 160 s, the main body arrives at the observed deposit region and then slowly decelerates until it stops. Note that the deposit shapes resulting from the two laws are similar, though reached at quite different times (see the t = 90 s image of Fig. 11).

We observe that the deposits from our simulations are located inside the region defined by the observed data, and therefore, we can state that both kinds of simulations successfully reconstruct the landslide event from the run-out perspective. The main difference between the two simulations is that the landslide moves more slowly and remains more concentrated at least during most of the motion when the quadratic drag model is implemented, while a linear drag accounts for a larger spreading.

Conclusions

A second-order central scheme with a general minmod-like limiter has been proposed to solve the system of hyperbolic partial differential equations that represent geophysical-flow like problems. Several typical benchmarks used in mass flow simulations have been carried out and compared against analytical solutions and experimental data to validate the model. As regards both accuracy and resolution, the scheme has been proven to perform very adequately, which enabled us to apply it to cases of practical geophysical and societal interest.

In this paper, we have selected as an application the historical catastrophic landslide occurred in Scilla, Calabria (South Italy) in 1783, already investigated through field surveys and other numerical approaches. A mixture flow model, considering topography modifications based on a global Cartesian coordinates (Xia and Liang 2018), has been solved, providing a reasonable motion pattern for the landslide. For the underwater motion, buoyancy forces and drag forces have been taken into account, and the landslide dynamics has been numerically investigated by two different drag models. For the linear drag law, the computed landslide dynamic is similar to the 1D block-model simulation carried out by Zaniboni et al. (2016), describing a landslide that experiences a 30-s-long acceleration and a 60-s-long deceleration stage, reaching a peak velocity slightly larger than 30 m/s. Instead, by using a quadratic drag model, the simulated landslide dynamics is different since the landslide rapidly decelerates when it crashes into the sea and then moves slowly until it stops. The deposits of both numerical simulations locate at a reasonable region compared with the observed data.

We remark that the accurate reconstruction of historical landslide events is a tough task, depending on factors including physical parameters, model assumptions, numerical methods and field surveys. We showed that our mass flow model provides reasonable results in good agreement with available observations. However, more complicated mechanisms considering erosion, soil–water interaction and various material-behaviour need to be figured out in the future.