1 Introduction

Structural deformation monitoring is one of the key topics in the field of structural health monitoring. It can provide important reference information for structural health monitoring systems, control systems and fault diagnosis systems to ensure a safe operation. What's more, it can realize conditional maintenance and reduce maintenance cost. Therefore, there are several studies on shape sensing thus far. Among them, three methods have been proven to be more effective and successful, including Ko’s displacement theory, the modal method, and the inverse finite element method (iFEM). Compared with the other two methods, the iFEM has attracted extensive attention since it was proposed.

The iFEM was originally developed by Tessler et al. [1], and a three-node triangular inverse-shell element iMIN3 [2] was firstly demonstrated by a least-squares functional minimization between measured strain and theoretical strain. It is noteworthy that this technique only makes use of a set of strain measurements and strain–displacement relations to compute displacements on the entire structure. Most important of all, any material properties and load information are unnecessary. At present, the widespread application of the iFEM offered several benefits in terms of structural deformation monitoring. Concurrently, a variety of inverse element models have already been developed successively to enrich the iFEM capability to solve the inversion algorithm problem of different types of structures.

Cerracchio et al. [3] established a three-node triangular inverse finite element iRZT3 based on the iFEM and the improved zigzag theory for shape and stress monitoring of sandwich structures. Gherlone et al. [4,5,6,7] put forward the shape sensing of some three-dimensional frame structures by a least-squares variational principle considering the section strain, involving tension, torsion, bending and transverse shear of the Timoshenko theory. Kefal et al. [8, 9] proposed a quadrilateral inverse shell element iQS4 to extend the inverse shell element library and improve some deficiencies of iMIN3. It is applied to the deformation monitoring of large ship hull and other marine structures [10, 11] to obtain accurate information about structural safety status in real time. Papa et al. [12] developed a triangular flat shell element iTRIA3 and validated experimentally the method on an equivalent plate model. Mooij [13] applied an inverse hexahedral solid element and a new standard set of benchmark problems of iFEM algorithm. Kefal [14] employed an efficient curved inverse-shell element iCS8 with curved geometry to monitor the displacement and stress of cylindrical offshore structures. To further compare the performance of different inverse elements, a detailed investigation was carried out on iMIN3, iQS4 and iCS8 elements for structural shape and stress monitoring [15]. In addition, a two-dimensional deformation monitoring method was proposed by the iFEM of an iBeam3 element [16] for the pipeline in the process of soil freezing and thawing. There are a few comparative studies involving common shape reconstruction methods. Esposito et al. [17, 18] discussed the modal method, Ko’s displacement theory and the iFEM. The comparison of deformation reconstruction results was performed on a composite wing box. Additionally, there are a few studies on structural damage identification exploiting the unique advantages of the iFEM. Some damage detection techniques with the iFEM were applied for damage localization [19,20,21,22,23,24,25] and damage quantification [26].

To summarize, the iFEM catches researchers’ attention in recent years and has been proven to be successful in various fields. Recently, the above studies mainly consider small-displacement assumptions because the iFEM was originally based on the linear theory. However, there are plenty of flexible structures in practical engineering, such as solar arrays, tensional domes, suspension bridges, and so on, and the deformations of such flexible structures generally have geometrically nonlinear characteristics. Thus, it is inappropriate to still use the linear hypothesis for analyzing, and the errors will far exceed the controllable range. At this time, it should be discussed by the nonlinear theory. It seems that few applications of the iFEM to structural large-displacement problems have been reported in the literature. Tessler et al. [27] briefly introduced the range of applicability of the iFEM formulation. It is important to point out that nonlinear strain–displacement relations can replace linear relations, or an incremental linear analysis method can be applied to the simulation of large displacement for geometrically nonlinear deformation problems. An inverse finite element strategy was implemented to recover large displacements of a cantilever beam, which extended linear iFEM formulation in some sense. However, only a two-dimensional plane model was considered [28]. Tessler et al. [29] proposed an iFEM incremental algorithm for nonlinear deformations of a clamped square plate based on the iMIN3 element.

This work aims to further study the shape reconstruction of large displacement problems based on the iFEM. This paper proposes a nonlinear iFEM strategy based on the basic principle of linearized iFEM theory and iterative algorithm. The iterative method is a classical algorithm to solve nonlinear problems. That is, the nonlinear responses are treated by linearization approximation. The paper is structured as follows. In Sect. 2, the general framework of the nonlinear iFEM based on the iQS4 element is briefly described. Section 3 provides information on the application examples with large-displacement problems. The results regarding the deformation calculation results are reported in Sect. 4. Finally, some concluding remarks and recommendations are stated for future research in Sect. 5.

2 Nonlinear Inverse Finite Element Method Review

As previously mentioned, some deformation analysis can be applied by a small-displacement assumption, namely it can be approximately linearized in the calculation process, which, however, is improper for some structures with strong nonlinear characteristics such as large displacement. Therefore, it should be discussed using the geometrically nonlinear theory. Herein, a brief description of the nonlinear iFEM is reported. The proposed method is presented based on the theoretical framework of linear iFEM in this work.

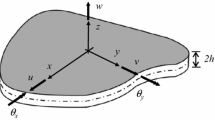
As one of the most important methods to reconstruct displacement of structures at present, some advantages of the iFEM are more favored. There are different inverse elements and the described iFEM approaches are valid for different types of structures. This work focuses on a four-node inverse quadrilateral shell element iQS4 as shown in Fig. 1. Because of the inclusion of drilling rotations θzi, it has less tendency toward shear locking. It is assumed that the iQS4 element has a thickness of 2 h and that z ∈ (-h, h) defines the thickness coordinate system. ui and vi are the positive x and y translations, respectively. Consequently, the elemental degrees-of-freedom vector u ei is formulated as follows.

$$ \begin{gathered} {\varvec{u}}_{i}^{e} = \left\{ {\begin{array}{*{20}c} {u_{i} } & {v_{i} } & {w_{i} } & {\theta_{xi} } & {\theta_{yi} } & {\theta_{zi} } \\ \end{array} } \right\}^{{\text{T}}} \left( {i = 1,2,3,4} \right) \hfill \\ {\varvec{u}}^{e} = \left\{ {\begin{array}{*{20}c} {{\varvec{u}}_{1}^{e} } & {{\varvec{u}}_{2}^{e} } & {{\varvec{u}}_{3}^{e} } & {{\varvec{u}}_{4}^{e} } \\ \end{array} } \right\}^{{\text{T}}} \hfill \\ \end{gathered} $$
(1)
Fig. 1
figure 1

The iQS4 element in global coordinates

Full size image

The (x, y) coordinate in the reference plane of the iQS4 element is defined as a function of the bilinear shape function Ni (s, t) with (s, t) ∈ [−1, 1]. The mapping functions are defined in Eq. (2), where (xi, yi) (i = 1, 2, 3, 4) are the element’s local nodal coordinates, and (s, t) is the isoparametric dimensionless coordinate.

$$ \begin{gathered} x\left( {s,t} \right) \equiv x = \sum\limits_{i = 1}^{4} {N_{i} } x_{i} \hfill \\ y\left( {s,t} \right) \equiv y = \sum\limits_{i = 1}^{4} {N_{i} } y_{i} \hfill \\ \end{gathered} $$
(2)

The \(u\) and \(v\) membrane displacements are defined by

$$ \begin{gathered} u\left( {x,y} \right) \equiv u = \sum\limits_{i = 1}^{4} {N_{i} } u_{i} + \sum\limits_{i = 1}^{4} {L_{i} } \theta_{zi} \hfill \\ v\left( {x,y} \right) \equiv v = \sum\limits_{i = 1}^{4} {N_{i} } v_{i} + \sum\limits_{i = 1}^{4} {M_{i} } \theta_{zi} \hfill \\ \end{gathered} $$
(3)

where Li and Mi are shape functions that define the relationship between drilling rotation and membrane displacement [9], respectively. The transverse displacement w and the bending rotations θx, θy are defined by the positive z translation wi and positive anticlockwise rotations θxi, θyi.

$$ \begin{gathered} w\left( {x,y} \right) \equiv w = \sum\limits_{i = 1}^{4} {N_{i} } w_{i} - \sum\limits_{i = 1}^{4} {L_{i} } \theta_{xi} - \sum\limits_{i = 1}^{4} {M_{i} } \theta_{yi} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} \theta_{x} \left( {x,y} \right) \equiv \theta_{x} = \sum\limits_{i = 1}^{4} {N_{i} } \theta_{xi} \hfill \\ \begin{array}{*{20}c} {\begin{array}{*{20}c} {} & {} \\ \end{array} } & {} \\ \end{array} \theta_{y} \left( {x,y} \right) \equiv \theta_{y} = \sum\limits_{i = 1}^{4} {N_{i} } \theta_{yi} \hfill \\ \end{gathered} $$
(4)

Based on the strain–displacement relations of linear elastic constitutive theory, the kinematic relations of iQS4 element are established based on the first-order shear deformation theory (FSDT). The strain components consist of membrane section strains, bending section strains and transverse-shear strains. These can be expressed in terms of the nodal degrees of freedom.

$$ \left\{ {\begin{array}{*{20}c} {\varepsilon_{xx} } \\ {\varepsilon_{yy} } \\ {\gamma_{xy} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {u_{,x} } \\ {v_{,y} } \\ {u_{,y} + v_{,x} } \\ \end{array} } \right\} + z\left\{ {\begin{array}{*{20}c} {\theta_{y,x} } \\ { - \theta_{x,y} } \\ {\theta_{y,y} - \theta_{x,x} } \\ \end{array} } \right\} = {\varvec{e}}\left( {{\varvec{u}}^{e} } \right) + z{\varvec{k}}\left( {{\varvec{u}}^{e} } \right) = {\varvec{B}}^{m} {\varvec{u}}^{e} + z{\varvec{B}}^{k} {\varvec{u}}^{e} $$
(5)
$$ \left\{ {\begin{array}{*{20}c} {\gamma_{xz} } \\ {\gamma_{yz} } \\ \end{array} } \right\} = \left\{ {\begin{array}{*{20}c} {w_{,x} + \theta_{y} } \\ {w_{,y} - \theta_{x} } \\ \end{array} } \right\} = {\varvec{g}}\left( {{\varvec{u}}^{e} } \right) = {\varvec{B}}^{g} {\varvec{u}}^{e}$$
(6)

where ue is the nodal displacement vector. The matrices of Bm, Bk and Bg consist of derivatives of shape functions concerning the membrane, bending and shear response, respectively.

As described before, the experimental strain measurements are required as input strain and can be evaluated from measured surface strains at n discrete locations. The strain sensors are placed on the top and bottom surfaces of the plate, as shown in Fig. 2. Furthermore, the membrane and bending strain components at ± h from the middle of the element is written as:

$$ {\varvec{e}}_{i}^{\varepsilon } = \frac{1}{2}\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{ + } + \varepsilon_{xx}^{ - } } \\ {\varepsilon_{yy}^{ + } + \varepsilon_{yy}^{ - } } \\ {\gamma_{xy}^{ + } + \gamma_{xy}^{ - } } \\ \end{array} } \right\}_{i} \begin{array}{*{20}c} {} & {} \\ \end{array}, {\varvec{k}}_{i}^{\varepsilon } = \frac{1}{2h}\left\{ {\begin{array}{*{20}c} {\varepsilon_{xx}^{ + } - \varepsilon_{xx}^{ - } } \\ {\varepsilon_{yy}^{ + } - \varepsilon_{yy}^{ - } } \\ {\gamma_{xy}^{ + } - \gamma_{xy}^{ - } } \\ \end{array} } \right\}_{i} $$
(7)

where the superscripts ‘ + ’ and ‘−’ denote the strain measurements on the top and bottom surfaces, respectively. For the deformation of thin shells, g εi can be neglected in the subsequent calculation when compared with other terms.

Fig. 2
figure 2

Discrete surface strains measured at location xi = (x, y)

Full size image

The core formulas of the iFEM are derived from the extreme value of the least-squares function in terms of numerical strains and measured strains. It minimizes a weighted least-squares function concerning the unknown displacement degrees of freedom. Thus, the function for each element is expressed as:

$$ \Phi_{e}^{\lambda } \left( {{\varvec{u}}^{e} } \right) = \omega_{m} \left\| {{\varvec{e}}({\varvec{u}}^{e} ) - {\varvec{e}}^{\varepsilon } } \right\|^{2} + \omega_{k} \left\| {{\varvec{k}}({\varvec{u}}^{e} ) - {\varvec{k}}^{\varepsilon } } \right\|^{2} + \omega_{g} \left\| {{\varvec{g}}({\varvec{u}}^{e} ) - {\varvec{g}}^{\varepsilon } } \right\|^{2} $$
(8)
$$ \left\| {{\varvec{e}}({\varvec{u}}^{e} ) - {\varvec{e}}^{\varepsilon } } \right\|^{2} = \frac{1}{n}\iint_{{A^{e} }} {\sum\limits_{i = 1}^{n} {\left( {{\varvec{e}}({\varvec{u}}^{e} )_{i} - {\varvec{e}}_{i}^{\varepsilon } } \right)^{2} {\text{d}}x{\text{d}}y} } $$
(9a)
$$ \left\| {{\varvec{k}}({\varvec{u}}^{e} ) - {\varvec{k}}^{\varepsilon } } \right\|^{2} = \frac{{\left( {2h} \right)^{2} }}{n}\iint_{{A^{e} }} {\sum\limits_{i = 1}^{n} {\left( {{\varvec{k}}({\varvec{u}}^{e} )_{i} - {\varvec{k}}_{i}^{\varepsilon } } \right)^{2} {\text{d}}x{\text{d}}y} } $$
(9b)
$$ \left\| {{\varvec{g}}({\varvec{u}}^{e} ) - {\varvec{g}}^{\varepsilon } } \right\|^{2} = \frac{1}{n}\iint_{{A^{e} }} {\sum\limits_{i = 1}^{n} {\left( {{\varvec{g}}({\varvec{u}}^{e} )_{i} - {\varvec{g}}_{i}^{\varepsilon } } \right)^{2} {\text{d}}x{\text{d}}y} } $$
(9c)

where ωm, ωk, and ωg are the positive weighting values associated with a given element. These weighting coefficients determine the extent to each theoretical strain component constrained by measured values in the element. Moreover, these coefficients ensure stable performance even when strain values are not obtained from every finite element of the structure. If every inverse element has a specific measured value, ωm = ωk = ωg = 1. Meanwhile, a value of 10–4 is given to each weighting coefficient when no strain values are taken for elements.

The unknown variable of the minimum error functional is the element node displacement in Eq. (8). According to the variational principle, the condition for the minimum value of the function is defined as

$$ \frac{{\partial \Phi_{e}^{\lambda } }}{{\partial {\varvec{u}}^{e} }} = {\varvec{k}}^{e} {\varvec{u}}^{e} - {\varvec{p}}^{e} = 0\begin{array}{*{20}c} {} \\ \end{array} \Rightarrow \begin{array}{*{20}c} {} \\ \end{array} {\varvec{k}}^{e} {\varvec{u}}^{e} = {\varvec{p}}^{e} $$
(10)
$$ {\varvec{k}}^{e} = \iint_{{A^{e} }} {\left( {\omega_{m} ({\varvec{B}}^{m} )^{{\text{T}}} {\varvec{B}}^{m} + \omega_{k} (2h)^{2} ({\varvec{B}}^{k} )^{{\text{T}}} {\varvec{B}}^{k} + \omega_{g} ({\varvec{B}}^{g} )^{{\text{T}}} {\varvec{B}}^{g} } \right)}{\text{d}}x{\text{d}}y $$
(11a)
$$ {\varvec{p}}^{e} = \frac{1}{n}\iint_{{A^{e} }} {\sum\limits_{i = 1}^{n} {\left( {\omega_{m} ({\varvec{B}}^{m} )^{{\text{T}}} {\varvec{e}}_{i}^{\varepsilon } + \omega_{k} (2h)^{2} ({\varvec{B}}^{k} )^{{\text{T}}} {\varvec{k}}_{i}^{\varepsilon } + \omega_{g} ({\varvec{B}}^{g} )^{{\text{T}}} {\varvec{g}}_{i}^{\varepsilon } } \right){\text{d}}x{\text{d}}y} } $$
(11b)

Equation (11) contains the local iFEM matrix–vector equations, which can be assembled for the complete iFEM/iQS4 discretization like the classical finite-element assembly procedure. Considering the conversion of the displacement vector from the local coordinate to the global coordinate, the element matrix of a discrete structure is assembled into the linear equation system. Synthesizing the above formula leads to the global solution for the nodal displacements of the whole structure (refer to Eq. (12)).

$$ {\varvec{KU}}_{i} = {\varvec{P}}_{i} \begin{array}{*{20}c} {} \\ \end{array} \Rightarrow \begin{array}{*{20}c} {} \\ \end{array} {\varvec{U}}_{i} = \left( {\varvec{K}} \right)^{ - 1} {\varvec{P}}_{i} $$
(12)

where Ui is the displacement at the ith step within the total incremental step used in the nonlinear shape-sensing calculation. K is called a time-independent global pseudo stiffness matrix. The matrix is inverted (or calculated) only once, which only depends on the given sensor network and mesh distribution of the inverse model. Pi is a function of the values of the measured strain, which needs to be updated at each iteration step during the nonlinear iFEM program.

In the following, a schematic of the nonlinear iFEM framework is depicted in Fig. 3a, and the iterative process is observed in Fig. 3b.

Fig. 3
figure 3

The nonlinear iFEM-based large displacement reconstruction scheme: a the schematic of the computational process of nonlinear iFEM; b the iterative calculation

Full size image

The basic computing process of the nonlinear iFEM method is illustrated as follows.

  1. (1)

    Firstly, the displacement components of inverse element iQS4 are formulated in Eqs. (3) and (4). The relevant matrices are formed by Eqs. (5) and (6). The FE model and inverse finite element model are established. Thus, the required parameters of the calculated structure are also determined. In this work, two models adopt the same mesh configuration.

  2. (2)

    Secondly, a nonlinear FE calculation is carried out. The strain measurements are obtained in Eq. (7) at each incremental step. It should be pointed out that the strain is a total strain treated as the measured value in practical applications. In this work, the iFEM can still exert its merits although the linear and nonlinear strain components are not separated in the case of large displacement analysis.

  3. (3)

    Then, a finite number of strain measurements from Step (2) are taken as the input data in Eq. 11(b) to execute the iFEM. As a result, the deformations Ui based on Eq. (12) at this time are reconstructed.

  4. (4)

    Finally, Steps (2) and (3) are repeated until all iterative calculations are completed. The final overall deformation shape can be obtained from Fig. 3a.

In this paper, the linear iFEM theory is further modified. The algorithm model of the nonlinear iFEM is established by linearizing the nonlinear response analysis. For a nonlinear FE analysis, the load value Pi is determined when the iterative calculation of each incremental step is completed (in an equilibrium convergence state). Concurrently, a set of corresponding strain data can be obtained. Then the strain data from each step are inputted to execute the nonlinear iFEM program. Meanwhile, the deformation is reconstructed at each incremental step by Eq. (12). Until all iterative calculations are finished, all the shape information is finally summarized and the real deflections of the structure are presented. Finally, the performance of this algorithm about linear iFEM and nonlinear iFEM can be evaluated by comparing the final deflection results.

3 Numerical Examples

The effectiveness of the proposed method is numerically demonstrated on a cantilever plate model and a stiffened plate. Herein, it needs to point out that the iFEM mesh adopts the same mesh configuration as the FE model mesh in this study.

Fig. 4
figure 4

A cantilever plate model: a geometric dimensions and boundary conditions of a cantilever plate; b a high-fidelity FE model as reference

Full size image
Fig. 5
figure 5

A cantilever-stiffened plate subjected to a uniformly distributed load

Full size image
Fig. 6
figure 6

Two mesh division schemes of a stiffened plate model: a a direct FE model with a fine mesh; b a direct FE model with a coarse mesh

Full size image

3.1 A Cantilever Plate Subjected to a Uniformly Distributed Load

A cantilever plate is considered and the overall dimension is 0.7 m × 0.3 m with a thickness of 12.5 mm. The elastic modulus and Poisson's ratio of the plate are shown in Fig. 4a. The top surface of the cantilever plate is subjected to a uniformly distributed load (3 MPa) and the left edge is clamped. In this section, the required measured strain values as input to the program are all extracted from the FE model. As a consequence, a high-fidelity FE model is established with 800 S4R elements and 5166 DOFs, as shown in Fig. 4b.

3.2 A Stiffened Plate (SP) Subjected to a Uniformly Distributed Load

Figure 5 shows a stiffened cantilever plate subjected to a uniformly distributed load (1 MPa) which is clamped along the left edge. The stiffened plate with a thickness of 12.5 mm is composed of four ribs with a height of 0.03 m and a thickness of 12.5 mm. To further validate this method, two different schemes of mesh are selected as the reference model for discussion, including a dense mesh and a coarse mesh. The model in Fig. 6a is named SP1152, which consists of 1152 S4R elements and 7326 DOFs. Likewise, the model in Fig. 6b is defined as SP126, which is composed of 126 S4R elements and 900 DOFs.

Fig. 7
figure 7

Displacement contours corresponding to direct FEM of a cantilever plate

Full size image
Fig. 8
figure 8

The z-direction displacement results at the center of the cantilever plate under the nonlinear FEM, nonlinear iFEM with different noises and linear iFEM: a deflection results under different cases; b reconstruction error distribution

Full size image

4 Results

As anticipated in Sect. 3, the measured strains are both computed from the centroid of each element of direct FE analysis. Meanwhile, there are several different configurations of measuring points to be calculated, including full distribution points and partial distribution points. Besides, this work firstly discusses the influence of different levels of noises on the reconstruction accuracy of large displacement problems. It is used to simulate the effect of some inevitable errors in practical applications, and the generality of this method is further discussed. Herein, the definition of relative error is introduced to validate the method, and it is calculated from the percent difference between iFEM and direct FEM analyses.

4.1 Discussion of the Results of the Cantilever Plate

In Fig. 7, the displacement field of the plate is simulated with direct FEM. To investigate the accuracy of the proposed method, what is discussed is the z-direction displacement of the reference point marked in Fig. 4a at the central position of the plate. Figure 8a shows reconstruction of the z-direction displacement. It can be concluded that the large displacement can be effectively reconstructed based on the nonlinear iFEM. Referring to Fig. 8b, the relative errors are zero between the reconstruction results with free noise and nonlinear FE results in previous steps. Because there are some errors in the displacement reconstruction calculation of each substep, the errors will accumulate with the continuous iteration. The error reaches the maximum value in the last substep. The maximum error is 4.7% by a preliminary comparison and the change in the curve is consistent. Contaminated by 3% random noise, the errors are below 0.5% and the maximum error is about 4.8%. As the noise level increases, the z-direction displacement curves are still in good agreement. Figure 8b shows that due to different noise pollution, the errors fluctuate around 1%.

As shown in Fig. 9a, the θy rotation reconstruction is evaluated by the nonlinear iFEM. As previously noted, the nonlinear iFEM can effectively reconstruct the rotation of the cantilever plate and update the angle value at each step. Furthermore, based on the curve of y-direction rotation, it can be judged that the cantilever plate has undergone a large displacement and the geometric nonlinearity is prominent. Compared with the reconstruction results of the degrees of freedom of all nodes, the reconstruction accuracy of θy rotation is higher than that of the displacement. Referring to Eqs. (2–12), the w displacement has a larger prediction error than the rotation because the former is derived from the latter by comparing Fig. 8 and Fig. 9. Similarly, after adding three different noises of 3%, 5% and 10%, the reconstruction performance of the θy rotation is more ideal than that of the displacement w. It can be seen from Fig. 9b that although polluted by different levels of noise, the overall reconstruction accuracy is high, that is, the relative errors are less than 1.4%. The corresponding error curves exhibit a large fluctuation range when the noise level increases (Fig. 9).

Fig. 9
figure 9

Maximum y-axis rotation corresponding to the nonlinear FEM, nonlinear iFEM and linear iFEM: a maximum y-axis rotation; b reconstruction error distribution

Full size image
Fig. 10
figure 10

Different schemes of distribution points of iFEM model with a fine mesh: a an iFEM model named SP1152-1; b an iFEM model named SP1152-2; c an iFEM model named SP1152-3; d an iFEM model named SP1152-4

Full size image

4.2 Discussion of the Results for the Stiffened Plate

The predicted displacement results of the reference point (refer to Fig. 5) are computed with the nonlinear iFEM and linear iFEM. The influence of sensor layout (see Fig. 10) on the accuracy of shape reconstruction is briefly investigated for the stiffened plate, as highlighted in Figs. 11 and 12. Specifically, the large displacement is effectively restructured based on the nonlinear iFEM and the results agree well with the nonlinear FE solution. The deformation shape reconstructed by the linear iFEM is a straight line from the initial point to the endpoint. There is a sharp contrast with the reconstruction results of nonlinear iFEM. Additionally, the results calculated by the linear iFEM differ greatly from the actual deformation, that is, the reconstruction error is large. On the other hand, the deformed shape by using the linear iFEM exhibits no nonlinear characteristics. To further estimate the generality of this method, strain data of measuring points are polluted by different random noises to simulate some inevitable errors in practical applications. Herein, three different levels of noises of 3%, 5% and 10% are mainly considered.

Fig. 11
figure 11

Results of the z-direction displacement w at the center of the stiffened plate by the linear iFEM, nonlinear iFEM and FE calculation when polluted by different noises: a the deflections of SP1152-1; b the deflections of SP1152-2; c the deflections of SP1152-3; d the deflections of SP1152-4

Full size image
Fig. 12
figure 12

Comparison of errors under different conditions between the nonlinear FEM and the nonlinear iFEM with different noises: a relative errors of SP1152-1; b relative errors of SP1152-2; c relative errors of SP1152-3; d relative errors of SP1152-4

Full size image

As described in Sect. 4.1, it can be found that the nonlinear iFEM allows obtaining a good reconstruction of the displacement, and these results agree well with the nonlinear FE results in previous steps. It is demonstrated that even if contaminated by different noises, the estimation capability still reaches an optimal level. Concurrently, Fig. 12 reports the relative errors of calculation results of the nonlinear iFEM in different scenarios. The best accuracy is obtained under free noise conditions. With the progress of iterative calculation, the maximum error is about 6.2%. Polluted by different noises, the relative error curves of most of the previous steps fluctuate obviously. Under the condition of 3% noise, the fluctuation of error curve is relatively small, which is below 1%. The fluctuation range increases significantly with 5% and 10% noise, but both remain below 4%. It is the same as the case with no noise, the error reaches the maximum at the end of an iteration. For example, the maximum reconstruction error is approximately 7.8% when polluted by 10% noise.

In the following, four different schemes of distribution points of the coarse mesh configuration (Fig. 13) are taken into consideration to further validate the proposed method. The subplots in Fig. 14 show the reconstruction results of z-direction displacement under different sensor networks. Compared with the dense mesh (refer to Fig. 10), the deformation curves by the nonlinear iFEM and nonlinear FE results have the same behavior even though with a coarse mesh. While accurately reconstructing the deformation shape of the stiffened plate, more importantly, it can exhibit the geometrically nonlinear characteristics. The linear iFEM presents a straight line between the initial point and the endpoint. In fact, it seriously lacks effective information of true deformation. What deserves attention is that the final reconstruction results are not affected by the roughness of meshing based on the nonlinear iFEM. Contaminated by different noises, the reconstructed shape curves have a great fluctuation, but the geometrically nonlinear information is still discovered from the displacement diagrams. Polluted by 3% noise, the reconstruction errors are less than 3% and the maximum error is about 5.1%. When the noise level is up to 10%, some errors slightly below 5% are observed and the maximum error reaches about 5.4%. The aforementioned errors are within the controllable range. It is concluded that despite the pollution of noise, the nonlinear iFEM can still effectively restructure the large displacement.

Fig. 13
figure 13

Different schemes of distribution points of iFEM model with a coarse mesh: a an iFEM model named SP126-1; b an iFEM model named SP126-2; c an iFEM model named SP126-3; d an iFEM model named SP126-4

Full size image
Fig. 14
figure 14

Results of the z-direction displacement w at the center of the stiffened plate by the linear iFEM, nonlinear iFEM and FE calculation when polluted by different noises: a the deflections of SP126-1; b the deflections of SP126-2; c the deflections of SP126-3; d the deflections of SP126-4

Full size image
Fig. 15
figure 15

Comparison of errors of different conditions between the nonlinear FEM and nonlinear iFEM with different noises: a relative errors of SP126-1; b relative errors of SP126-2; c relative errors of SP126-3; d relative errors of SP126-4

Full size image

Secondly, the reconstruction results of the distribution of measuring points of two iFEM models SP126-3 and SP126-4 are depicted in Fig. 14c and Fig. 14d. The influence of noise pollution on the calculation results is checked simultaneously. It is demonstrated that large displacements are reconstructed by the nonlinear iFEM. The above figures depict that the deformed shape is effectively predicted by the nonlinear iFEM and the geometrically nonlinear characteristics are displayed. Additionally, compared with a fine mesh of Fig. 10a and a coarse mesh of Fig. 13a, the results are similar in the case of no noise, that is, most errors are close. However, the deflection curve of the coarse mesh scheme has larger amplitude of fluctuation than that of the fine mesh under the same noise level when affected by random noises. The calculation accuracy of the scheme of partial distribution points could not reach the level of the full distribution points, that is, the relative errors of the former are larger than the latter. From Fig. 14, when relatively sparse measured points are selected, the displacement reconstruction results can be effectively obtained by using the nonlinear iFEM. It is noticed that the distribution of measuring points at the boundary position has a great impact on reconstruction accuracy. It has the same performance as the results of the model in Fig. 10. In conclusion, the large displacement can be effectively reconstructed by a few measured strains and the errors are below 10%.

Table 1 reports the estimation capability of the final deflection results of different stiffened plate model schemes. The effectiveness of the proposed method is verified by comparing the results of linear iFEM, nonlinear iFEM and nonlinear FE calculation. It can be noticed that there is a large error between the calculation based on linear iFEM and nonlinear FE results. There is an error of about higher than 10% because of the differences. Nevertheless, the accuracy of displacement reconstruction is relatively high by the nonlinear iFEM. An error of within 10% is acceptable. Referring to Table 1, SP1152 and SP126 can both achieve ideal accuracy based on the nonlinear iFEM. Even if a coarse meshing of the iFEM model is selected, better reconstruction results can be estimated. Thus, it is concluded that large displacement reconstruction can be realized with fewer strain data. More than that, these results are closer to the true deformation of the model when geometric nonlinearity needs to be taken into consideration.

Table 1 Comparison of final deformation between the iFEM and FEM results
Full size table

5 Conclusions

In this work, a nonlinear inverse finite element method based on the linear iFEM is investigated to realize the shape reconstruction of structures with large displacement. Herein, the validity of this method is demonstrated by carrying out two numerical simulations, including a cantilever plate and a stiffened plate. Moreover, there are different configurations of iFEM model selected for discussion to validate the method, including a fine mesh and a coarse mesh. This method makes full use of the unique advantages of the iFEM. On one hand, the change of structural shape can be restructured in real-time calculation with only a small amount of measured strains. On the other hand, the method does not require any a priori knowledge of the load or material properties of the structure. Moreover, there is no need to distinguish between the linear elastic part of the strain and the part of geometric nonlinearity caused by large displacement. Despite all this, the nonlinear iFEM still maintains the characteristics of the iFEM. Consequently, the method not only reconstructs the displacement fields with the help of the iterative method, but also simultaneously presents the geometrically nonlinear characteristics.

The validity of this method is confirmed by the results. This work firstly discusses the influence of different levels of noise on shape reconstruction by the nonlinear iFEM. The results show that the large displacement problems of structures are effectively addressed. Compared with previous studies, the method has been successfully applied to the deformation reconstruction of plate structures by using the iQS4. Importantly, when dealing with nonlinear problems, the solution accuracy of this method is in close agreement with the actual situation. It can reach an acceptable precision even though polluted by different levels of noise. Further comparative studies will focus on exploring the effect of meshing schemes of the iFEM model and noises on the large displacement reconstruction. Furthermore, an exhaustive investigation on the influence of sensor layout concerning the capability of this approach will be assessed in realistic applications.