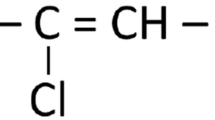1 Introduction

Filled rubber materials, such as carbon black or silica, are widely used in automobiles, machines, and buildings owing to their superior elastic and damping properties [1,2,3,4,5,6]. These materials exhibit mechanical properties such as hyperelasticity and viscoelasticity. Similar to the Mullins effect [7,8,9], reversible softening was observed with an increase in strain amplitude, known as the Payne effect [10]. The Payne effect is related to filler–filler and filler–rubber interactions, and can be described as the breakage and recovery of the network during cyclic loading. Among the specifically developed models, the Kraus model [11] is based on microstructural destruction and reorganization rates of the carbon black network. The modeling results fit the test data without any time-domain formulation, while the material parameters need reidentification if the frequency changes. Luo [12] further extended the Kraus model and used it to model frequency- and amplitude-dependent dynamic modulus and hysteresis loss. Lion [13,14,15] developed a time-domain formulation valid for arbitrary deformation and employed a constitutive model using a series of nonlinear Maxwell elements. Youn [16] extended the Kraus model to consider a large static pre-strain. Tomita [17] further proposed a visco–hyperelastic eight-chain network model that incorporates a nonlinear dashpot with Langevin springs.

As a standard experimental approach, the dynamic mechanical analysis (DMA) is very helpful for studying these effects. In DMA, an oscillating elongation is applied to the sample and the response of the material is analyzed as a force signal, which includes all material nonlinearities. The processing of these signals allows computing new dynamic measures known as the dynamic modulus. Further, considering time signals is very helpful for investigating transient effects in the time domain directly.

This paper first builds a nonlinear constitutive model of chloroprene rubber considering the strain amplitude effect, which is specified by the Mooney–Rivlin model and Prony series under uniaxial tension. Second, with the DMA test results, an empirical formula of the loss modulus is obtained from the hysteresis loop to predict the strain amplitude effect. Finally, the storage modulus is fitted by the same expression as that for the loss modulus. The proposed empirical formula has certain accuracy in predicting the dynamic modulus under different strain amplitudes for both the storage modulus and the loss modulus, and it can be further expressed in a simple form.

2 Dynamic Characteristics

2.1 General Theory

The time-dependent vector function \({x}=\chi ({X},t)\) is defined as the time-dependent mapping between the position vector X(P) of the reference configuration and the position vector x(P) of the current configuration. The deformation gradient F(t) at the current time t is written as

$$\begin{aligned} F(t)=\mathrm{Grad}(\chi (X,t))=\frac{\partial x}{\partial X} \end{aligned}$$
(1)

The relative deformation gradient in Cartesian coordinates is defined as

$$\begin{aligned} F_t (s)=F(s)F^{-1}(t){ }0\le s\le t \end{aligned}$$
(2)

The deformation gradient tensor F(t) maps the material tangent vectors from the current configuration at time t to the tangent vectors at previous time s. The right and left Cauchy–Green deformation tensors C and B are separately defined as

$$\begin{aligned} C=F^{T}F,\,\,B=FF^{T} \end{aligned}$$
(3)

Further, the Piola and Green–Lagrange strain tensors e and E are defined as

$$\begin{aligned} e=\frac{1}{2}(C^{-1}-I),\quad E=\frac{1}{2}(C-I) \end{aligned}$$
(4)

Using Eq. (2), the relative right Cauchy–Green deformation tensor is expressed as

$$\begin{aligned} C_t (s)=F_t^T (s)F_t (s)=F^{-T}(t)C(s)F^{-1}(t) \end{aligned}$$
(5)

and the relative Piola and Cauchy–Green strain tensors are

$$\begin{aligned} e_t (s)=\frac{1}{2}(C_t^{-1} (s)-\hbox {I}),\,\,\hbox {E}_t (s)=\frac{1}{2}(\hbox {C}_t (s)-\hbox {I}) \end{aligned}$$
(6)

Equations (5) and (6) have the properties

$$\begin{aligned} E_t (s)=e_t (s)=0,\quad \hbox {d}/\hbox {d}s(E_t (s)\cdot 1)={E}'(s)\cdot C^{-1}(t) \hbox { and } \hbox {d}/\hbox {d}s(e_t (s)\cdot 1)={e}'(s)\cdot C(t) \end{aligned}$$
(7)

As rubber-like materials exhibit mechanical properties such as hyperelasticity and viscoelasticity, the Helmholtz free energy per unit reference volume W depends not only on the Cauchy–Green deformation tensor C, but also on the rate of Cauchy–Green strain tensor \(\dot{E}\), which is the sum of two parts

$$\begin{aligned} W= & {} W(C,\dot{E})=W_e (C)+W_v (C,\dot{E},\eta _i ) \nonumber \\= & {} W_e (I_1 ,I_2 ,I_3 , C_{j} ){+}\frac{1}{2}(E_L (\eta _i ,t)*\dot{E}):C \nonumber \\= & {} W_e (I_1 ,I_2 ,I_3 ,C_j ){+}\frac{1}{2}\left[ {\int _0^t {E_L (\eta _i ,t-\tau )} \dot{E}(\tau )\mathrm{d}\tau } \right] :C \end{aligned}$$
(8)

where \(W_e\) represents the elastic strain energy density corresponding to the equilibrium state; \(W_e (C)\) is obtained from hyperelastic parameters \(C_j\) and three independent invariants \(I_1, I_2\), and \(I_{3}\) of the right Cauchy–Green deformation tensor C; \(W_v (C, \dot{E})\) is the viscous dissipation of the solid during the mechanical response; \(E_L \) is the relaxation function; the notation “:” denotes the contraction over two tensors A and B (\(A:B=A_{ij} B_{ij}\)); and the symbol “*” represents the convolution integral between two functions f(t) and g(t) (i.e., \(f*{g}=\int _0^t {f(t-\tau )g(\tau )\mathrm{d}\tau }\)).

As the rubber-like material is considered incompressible, the independent invariant \(I_3\) equals 1; thus, Eq. (8) becomes

$$\begin{aligned} W= & {} W(C, \dot{E})=W_e (C)+W_v (C, \dot{E},\eta _i ) \nonumber \\= & {} W_e (I_1 ,I_2 ,C_{\mathrm{j}} ){+}\frac{1}{2}\left[ {E_L (\eta _i ,t)*\dot{E}} \right] :C \end{aligned}$$
(9)

Then, the Clausius–Duhem inequality is written in the alternative form

$$\begin{aligned} \frac{{1}}{{2}}T:\dot{C}-\dot{W}-{s}\dot{T}-\frac{q}{T}\cdot \nabla T\ge 0 \end{aligned}$$
(10)

where T is the second Piola–Kirchhoff stress tensor, and s and q are the entropy and heat flux flowing outside the material, respectively.

Substituting Eq. (9) into Eq. (10), and considering the isothermal process, the total energy dissipation rate \(\dot{D}\) can be derived as

$$\begin{aligned} \dot{D}= & {} \left( {T+pC^{-1}-2\left( {\frac{\partial W_e }{\partial I_1 }+I_1 \frac{\partial W_e }{\partial I_2 }} \right) I+2\frac{\partial W_e }{\partial I_2 }C-E_L *\dot{E}} \right) :\frac{\dot{C}}{2}-\frac{1}{2}\left( {\frac{\partial E_L }{\partial t}*\dot{E}+E_L (\eta _i ,0)\dot{E}(t)} \right) :C \nonumber \\&-\sum _{j=1}^m {\frac{\partial W_e }{\partial C_j }} \dot{C}_j -\sum _{i=1}^n {\frac{\eta _i }{2}\left( {\frac{\partial E_L }{\partial \eta _i }*\dot{E}} \right) } :C\ge 0 \end{aligned}$$
(11)

where p is a multiplier representing hydrostatic pressure that could be determined from the boundary conditions.

When the current stretch does not exceed the maximum reached in the loading, \(\dot{C}_j\) and \(\dot{\eta }_i\) equal to zero, i.e., the third and fourth terms of Eq. (11) vanish. The first term of \(\dot{D}\) vanishes if an instantaneous mechanical balance is assumed for any arbitrary \(\dot{C}\), and then, the second Piola–Kirchhoff stress tensor is written as

$$\begin{aligned} T=-pC^{-1}+2\left( {\frac{\partial W_e }{\partial I_1 }+I_1 \frac{\partial W_e }{\partial I_2 }} \right) I-2\frac{\partial W_e }{\partial I_2 }C+E_L *\dot{E} \end{aligned}$$
(12)

Considering the relationship between Cauchy stress and the second Piola–Kirchhoff stress, Eq. (12) can be expressed as

$$\begin{aligned} \sigma =-pI+2\left( {\frac{\partial W_e }{\partial I_1 }+I_1 \frac{\partial W_e }{\partial I_2 }} \right) B-2\frac{\partial W_e }{\partial I_2 }B^{2}+F(E_L *\dot{E})F^{T}. \end{aligned}$$
(13)

The second term represents the energy loss rate caused by the viscosity of the rubber-like materials.

$$\begin{aligned} \dot{D}_v =-\frac{1}{2}\left( {\frac{\partial E_L }{\partial t}*\dot{E}+E_L (\eta _i ,0)\dot{E}(t)} \right) :C. \end{aligned}$$
(14)

2.2 Dynamic Modulus under Tension

In the DMA test, the material is subjected to a harmonic strain \(\varepsilon _{1} \sin \omega t\) with a given pre-strain \(\varepsilon _0\); thus, the deformation gradient F, the left Cauchy–Green strain tensor B, and the rate of the Green–Lagrange strain tensor \(\dot{E}\) are given as

$$\begin{aligned} \left[ F \right] =\left[ {{\begin{array}{ccc} \lambda &{}\quad 0&{}\quad 0 \\ 0&{}\quad {1/{\sqrt{\lambda }}}&{}\quad 0 \\ 0&{}\quad 0&{}\quad {1/{\sqrt{\lambda }}} \\ \end{array} }} \right] \,\left[ B \right] =\left[ {{\begin{array}{ccc} {\lambda ^{2}}&{} 0&{} 0 \\ 0&{}\quad {1/\lambda }&{}\quad 0 \\ 0&{}\quad 0&{}\quad {1/\lambda } \\ \end{array} }} \right] \,\left[ {\dot{E}} \right] =\left[ {{\begin{array}{ccc} {\lambda \dot{\lambda }}&{}\quad 0&{}\quad 0 \\ 0&{}\quad {-\frac{{1}}{{2}}\lambda ^{-2}\dot{\lambda }}&{} 0 \\ 0&{}\quad 0&{}\quad {-\frac{{1}}{{2}}\lambda ^{-2}\dot{\lambda }} \\ \end{array} }} \right] \end{aligned}$$
(15)

Using the Mooney–Rivlin and the generalized Maxwell models to describe the hyperelastic and viscoelastic characteristics separately, \(W_e\) and \(W_v\) are expressed as

$$\begin{aligned} W_e= & {} C_1 (I_1 -3)+C_2 (I_2 -3) \end{aligned}$$
(16)
$$\begin{aligned} W_v= & {} \frac{1}{2}\left[ {\sum _{i=1}^n {E_i \hbox {e}^{-t/{\tau _i }}} *\dot{E}(t)} \right] :C \end{aligned}$$
(17)

Substituting Eqs. (15), (16), and (17) into Eq. (13), the constitutive relationship between the stresses and the stretch are

$$\begin{aligned} \sigma _{11}= & {} -p+2\left[ {C_1 +(\lambda ^{2}+2\lambda ^{-1})C_2 } \right] \lambda ^{2}-2C_2 \lambda ^{4}+\lambda ^{2}\left[ {\sum _{i=1}^n {E_i \hbox {e}^{{-t}/{\tau _i }}*(\lambda \dot{\lambda })} } \right] \end{aligned}$$
(18)
$$\begin{aligned} \sigma _{22}= & {} -p+2\left[ {C_1 +(\lambda ^{2}+2\lambda ^{-1})C_2 } \right] \lambda ^{-1}-2C_2 \lambda ^{-2}-\frac{\lambda ^{-1}}{2}\left[ {\sum _{i=1}^n {E_i \hbox {e}^{{-t}/{\tau _i }}*(\lambda ^{-2}\dot{\lambda })} } \right] \end{aligned}$$
(19)

Since the tension experiments are adopted, and the boundary conditions \(\sigma _{22} =0\) are considered, the hydrostatic pressure is obtained as

$$\begin{aligned} p=2\left[ {C_1 +(\lambda ^{2}+2\lambda ^{-1})C_2 } \right] \lambda ^{-1}-2C_2 \lambda ^{-2}-\frac{\lambda ^{-1}}{2}\left[ {\sum _{i=1}^n {E_i \hbox {e}^{{-t}/{\tau _i }}*(\lambda ^{-2}\dot{\lambda })} } \right] \end{aligned}$$
(20)

Thus, the uniaxial stress can be written as

$$\begin{aligned} \sigma _{11} =2(\lambda ^{2}-\lambda ^{-1})C_1 +2(\lambda +\lambda ^{-2})C_2 +\lambda ^{2}\left[ {\sum _{i=1}^n {E_i \hbox {e}^{{-t}/{\tau _i }}*(\lambda \dot{\lambda })} } \right] +\frac{\lambda ^{-1}}{2}\left[ {\sum _{i=1}^n {E_i \hbox {e}^{{-t}/{\tau _i }}*(\lambda ^{-2}\dot{\lambda })} } \right] \nonumber \\ \end{aligned}$$
(21)

The relationship between the stretch and the strain is given as

$$\begin{aligned} \lambda =1+\varepsilon _0 +\varepsilon _1 \sin \omega t=\lambda _0 (1+\hat{{\varepsilon }}\sin \omega t) \end{aligned}$$
(22)

with

$$\begin{aligned} \hat{{\varepsilon }}=\frac{\varepsilon _1 }{1+\varepsilon _0} \end{aligned}$$
(23)

As the dynamic strain is usually small to be regarded as \(\varepsilon _1 \ll 1\), which means \(\hat{\varepsilon }\ll 1\) as well. Neglecting the transient and higher-order terms, Eq. (21) becomes

$$\begin{aligned} \sigma _{11} =2(\lambda _0^2 -\lambda _0^{-1} )C_1 +2(\lambda _0 +\lambda _0^{-2} )C_2 +{E}'\hat{{\varepsilon }}\sin \omega t+{E}''\hat{{\varepsilon }}\cos \omega t \end{aligned}$$
(24)

The storage modulus and loss modulus are, respectively, given as

$$\begin{aligned} {E}'= & {} E_{0} +\sum _{i=1}^n {E_i \frac{(1+2\lambda _0^6 )\omega ^{2}\tau _i^2 }{2\lambda _0^2 (1+\omega ^{2}\tau _i^2 )}} \nonumber \\= & {} 2(2\lambda _0^2 +\lambda _0^{-1} )C_1 +2(\lambda _0 +2\lambda _0^{-2} )C_2 +\sum _{i=1}^n {E_i \frac{(1+2\lambda _0^6 )\omega ^{2}\tau _i^2 }{2\lambda _0^2 (1+\omega ^{2}\tau _i^2 )}} \end{aligned}$$
(25)
$$\begin{aligned} E''= & {} \sum _{i=1}^n {E_i \frac{(1+2\lambda _0^6 )\omega \tau _i }{2\lambda _0^2 (1+\omega ^{2}\tau _i^2 )}}. \end{aligned}$$
(26)

2.3 Hysteresis Loss and Energy Dissipation

When a viscoelastic material is subjected to a sinusoidal excitation under tension, the mechanical energy absorbed per unit volume of the material in the deformation up to time t is given by

$$\begin{aligned} W(t)=\int _0^t {\sigma _{11} (\tau )\dot{\varepsilon }_{11} (\tau )\mathrm{d}\tau } \end{aligned}$$
(27)

The amount of energy dissipated [18,19,20,21] in a full cycle of oscillatory straining can be calculated by integrating Eq. (27) over the cycle.

$$\begin{aligned} D_v =\int _0^{\frac{2\pi }{\omega }} {\sigma _{11} (\tau )\dot{\varepsilon }(\tau )\mathrm{d}\tau } =\pi \varepsilon _1^2 {E}'' \end{aligned}$$
(28)

3 Experiment, Results, and Discussion

3.1 Experiment

Rectangular specimens with dimensions of \(5~\hbox {mm} \times 25~\hbox {mm} \times 2~\hbox {mm}\) were selected for the test. These specimens were provided by the Dongxin rubber company in Hengshui, Hebei, China. The amplitude sweep experiment of chloroprene rubber was measured using a dynamic mechanical analyzer (DMA, Gabo Eplexor 500 N), as shown in Fig. 1.

Fig. 1
figure 1

DMA, Gabo Eplexor 500 N

Full size image

Repeated cyclic stretching was carried out on specimens before the experiment to ensure that the stress was within the range of linear viscoelasticity during the experiment, and the Mullins effect was removed. The specimens were sinusoidally stretched under a pre-strain of 5% at various frequencies (1, 5, 10, 20, and 30 Hz); the dynamic strain amplitude ranges from 0.1% to 3% and is linearly distributed in logarithmic coordinates. The stress responses to the strain excitations were recorded automatically; the tensile storage modulus and the loss modulus were calculated from these measurements; and the mechanical hysteresis loop in a full strain cycle was also constructed.

3.2 Results

Fig. 2
figure 2

Storage modulus under amplitude sweep

Full size image
Fig. 3
figure 3

Loss modulus under amplitude sweep

Full size image

The test results are shown in Figs. 2 and 3, where the storage and loss moduli are shown as a function of the applied frequency and strain amplitude. The results indicate that the storage modulus decreases with an increase in strain amplitude, while the loss modulus does not show a peak value, which are similar to the experimental results in [22]. These results are attributed to the filler–filler and filler–rubber interactions.

Fig. 4
figure 4

Hysteresis loops under different frequencies and strain amplitudes

Full size image

Figure 4 shows the hysteresis loops of the material under different frequencies and strain amplitudes. The area of the hysteresis loop represents the energy dissipated in a full deformation cycle, each of which is obtained by numerical integration.

Fig. 5
figure 5

Hysteresis loss of strain amplitude at specified frequency and strain amplitude

Full size image

Figure 5 shows the integration results at the specified frequency and strain amplitude. It can be easily determined that hysteresis increases with an increase in the strain amplitude, and it has weak dependency on the frequency. Compared with the test results, the calculation results of Eq. (28) are relatively close.

3.3 Discussion

Figure 5a indicates that in the double logarithmic coordinate system, there is a linear relationship between the hysteresis loss and the strain amplitude, implying that the hysteresis loss and strain amplitude have a power-law relationship. The \(\log D_v \sim \log \varepsilon _1\) curves are parallel and linear, which overlap after a vertical shift. Therefore, there is a vertical shift factor, which satisfies the shift relation,

$$\begin{aligned} D_v (f,\varepsilon _1)=\varphi _f D_v (f_0 ,\varepsilon _1 )=\varphi _f (a\varepsilon _1^b) \end{aligned}$$
(29)

To simplify Eq. (29), we regard parameter b as a constant value, i.e., \(b=1.934\). The specific relationship between \(D_v\) and \(\varepsilon _1\), and the values of \(\varphi _f\) at each frequency (reference frequency \(f_0 =1\,Hz\)) are summarized in Table 1.

Considering the strain amplitude \(\varepsilon _r =0.1\%\) as a reference to normalize the hysteresis loop for other strain amplitudes, \(D_v/D_{vr}\) is plotted in Fig. 6. The figure indicates that the hysteresis loss ratio is weakly dependent on frequency, but strongly dependent on \(\varepsilon _r /\varepsilon _{1}\), which is similar to the data in [12]. Assuming that the hysteresis loss ratio is only related to the strain amplitude ratio \(\varepsilon _r /\varepsilon _{1}\), we can express the hysteresis loop \(D_v\) as Eq. (30), which is also applicable to [12].

$$\begin{aligned} D_v (f,\varepsilon _1)=a\left( {\frac{\varepsilon _r }{\varepsilon _1 }} \right) ^{k}D_{vr} (f,\varepsilon _r) \end{aligned}$$
(30)

Substituting Eq. (28) into Eq. (30), the loss modulus can be derived as

$$\begin{aligned} {E}''(f,\varepsilon _1 )=a\left( {\frac{\varepsilon _r }{\varepsilon _1 }} \right) ^{k+2}{E}''(f,\varepsilon _r) \end{aligned}$$
(31)
Table 1 Function of \(D_v \) and \(\varphi _f\) at each frequency
Full size table
Fig. 6
figure 6

Experimental data of \(D_v/D_{vr}\) (a Test data; b Literature [12])

Full size image
Table 2 Parameters of Eq. (30)
Full size table

The method of least squares is used for the nonlinear fitting of data in Fig. 6, and the parameters are listed in Table 2. Using Eq. (31), the loss modulus \(E^{\prime \prime }\) can be predicted when the reference loss modulus is provided, which is often obtained from the frequency sweep test. The reference strain amplitude is selected as \(\varepsilon _r =0.1\%\); and the predicted data at the strain amplitudes of 0.2%, 0.3%, 0.5%, and 1% are displayed in Fig.  7. In comparison with the experimental data of the loss modulus versus frequency, a good agreement can be seen between the results, indicating that the empirical formula achieves a good prediction at different strain amplitudes.

Fig. 7
figure 7

Fitting results of loss modulus \(E''\) (solid: Prediction; hollow: Test data)

Full size image

In order to determine the accuracy of the predicted results and the experimental data, the variance formula is used.

$$\begin{aligned} R^{{2}}{=1-}\frac{\sum _{n=1}^N {({E}^{''2}_\mathrm{{pre}} -{E}^{''2}_{\exp })} }{\sum _{n=1}^N {({E}^{''2}_{\exp } -\bar{E}^{''2}_{\exp })} } \end{aligned}$$
(32)

The predicted data and the experimental data are substituted into Eq. (32), and the variance of each strain amplitude is listed in Table 3.

Table 3 R-square between the predicted and experimental results of loss modulus
Full size table

At last, the storage modulus \(E^{\prime }\) is predicted as well. It is not difficult to see from Eq. (27) that the right side is only a polynomial when moving \(E_0\) to the left side. Similarly, we take \(\varepsilon _r /\varepsilon \) as the x-axis and \({E}'{-}E_{0} /{E}'_r {-}{E}'_{r{0}}\) as the y-axis, and the expression takes the form similar to that of Eq. (31).

$$\begin{aligned} \frac{{E}'(f,\varepsilon _1 ){-}E_0 }{{E}'(f,\varepsilon _r ){-}E_{r0} }=\hbox {b}\left( {\frac{\varepsilon _r }{\varepsilon _1 }} \right) ^{p} \end{aligned}$$
(33)

By fitting the experimentally measured data of storage modulus \({E}'\) through the method of least squares, the parameters are determined as \(b=1.1415, p=0.3163\).

Fig. 8
figure 8

Fitting results of storage modulus \(E^{\prime }\) (a This paper; b Literature [12]; solid: Prediction; hollow: Test data)

Full size image

The predicted data for the strain amplitudes \(\varepsilon =0.2\%, 0.3\%, 0.5\%\) and 1% are displayed in Fig. 8a in comparison with the original data of storage modulus \(E^{\prime }\) versus frequency. The variances between the predicted and experimental values of storage modulus are listed in Table 4. The results indicate a good agreement, implying that the empirical formula is effective. Further, Eq. (32) is used to fit the data of storage modulus in [12], which shows a good agreement, as shown in Fig. 8b.

Table 4 R-square between the predicted and experimental results of storage modulus
Full size table

4 Conclusion

To consider the strain amplitude effect, the superposition of a hyperelastic model and a viscoelastic model was established. The storage modulus and loss modulus were obtained under uniaxial tension, and the model was specified based on the Mooney–Rivlin model and Prony series. An empirical expression was established using the hysteresis loop. A good agreement was observed in comparison with the experimental data of the loss modulus. In addition, the same type of empirical expression was designed, and the fitting results were found to be satisfactory. Moreover, the empirical formula was used to fit the data in the literature, and it proved to be effective. Thus, the empirical formula proposed in this paper, with a simple expression, has certain accuracy in predicting the dynamic modulus under different strain amplitudes.