Hardening–Softening Constitutive Model of Hard Brittle Rocks Considering Dilatant Effects and Safety Evaluation Index

Abstract

The damage and even failure of hard brittle rocks has been the most important challenge facing the safety of construction of deep engineering works, so the key to solving this problem is the recognition of the strength characteristics and description of the mechanical behavior of hard brittle rocks. Therefore, in view of this problem, in this study, we first analyzed the strength and mechanical response characteristics revealed in tests of, and site excavation in, hard brittle rocks. Second, by analyzing rock-strength envelopes on meridional and deviatoric planes, the generalized polyaxial strain energy (GPSE) strength criterion was applied. This allows description of the effects of the minimum principal stress, intermediate principal stress, hydrostatic pressure, and Lode’s angle of stress on the strength of hard rocks. By establishing evolutionary relationships of strength parameters and dilation parameters with plastic volumetric strain in rock failure, we established an elasto-plastic mechanical constitutive model for hard brittle rocks based on the GPSE criterion. In addition, through use of the failure approach index theory and the dilatancy safety factor, an evaluation index for degree of damage considering dilatant effects of rocks was proposed. Finally, the constitutive model established in this study and the proposed evaluation index were integrated into the numerical simulation method to simulate triaxial tests on rocks and numerical simulation of deformation and fracture of the rocks surrounding the deep-buried auxiliary tunnels in China’s Jinping II Hydropower Station. In this way, the reasonableness of the model and the index was verified. The strength theory and the constitutive model established in this research are applicable to the analysis of high-stress deformation and fracture of hard brittle rock masses, which supports the theoretical work related to deep engineering operations.

1 Introduction

Hard brittle rocks are geological bodies most commonly seen in the construction of deep underground engineering works. Under high in situ stress in deep areas, the most important challenge in the safe construction of engineering works is fracture and even failure of hard brittle rocks [1]. The key solution to this problem is recognition of their strength characteristics and the description of their mechanical behavior; a strength criterion, mechanical constitutive model, and evaluation on degree of damage (DOD) of hard brittle rocks are thus important topics in the current field of rock mechanics.

Over the years, many relevant research results related to rock-strength theories have been acquired and some representative strength criteria, such as the Mohr–Coulomb criterion, Hoek–Brown criterion, and Drucker–Prager criterion, have been widely used in rock engineering. These criteria were proposed based on a general stress state or conventional triaxial test results. However, Handin et al. [2], Mogi [3], Takahashi and Koide [4], Chang and Haimson [5], and Haimson and Chang [6] proved that rock strength is affected by the intermediate principal stress in true triaxial tests, and that this characteristic cannot be represented through the above strength criteria. Based on this, Mogi [3, 7], Wiebols and Cook [8], Lade and Duncan [9], Zhou [10], Aubertin et al. [11], Ewy [12], and Yu [13] successively proposed strength criteria that can show the effect of intermediate principal stress on rocks. The existing strength criteria have their own characteristics, separately focusing on some aspects of rock-strength characteristics or the strength characteristics of a certain type of rock. However, it is still difficult for them to describe all the effects of minimum principal stress, intermediate principal stress, hydrostatic pressure, and Lode’s angle of stress (will be discussed in detail in the next section) presented by rocks in such test conditions [14]. Actually, for brittle rocks, the failure process is the process of crack propagation; that is, the failure mechanism in brittle rock is closely related to the development of micro-cracks. Opening and closing of micro-cracks, generation and development of new cracks, and interconnection of original cracks result in the final failure modes of brittle rocks including shear failure, tensile failure, or a composite failure, while these cannot be fully demonstrated through the existing criteria.

The generation and development of cracks in the loading process of brittle rocks also lead to nonlinear mechanical behaviors. In view of this problem, many constitutive models have been proposed, such as the elasto-plastic constitutive model, the constitutive model for damage, and fracture or coupled constitutive models of rocks based on various strength criteria. Representative results include the ideal elasto-plastic constitutive models established on the basis of traditional strength criteria (such as the Mohr–Coulomb criterion, Drucker–Prager criterion, and Hoek–Brown criterion). Because these models do not take real changes in the yield surface into account, they are only applicable to describing the behavior of soft rocks or broken rock masses, but not the post-peak strain-softening behavior of brittle rocks. Lately, internal variables have been introduced to show strain-hardening/-softening behaviors, and elasto-plastic strain-softening models were proposed, such as the strain-softening models considering sudden or gradual changes of cohesion c and internal friction angle $\phi$ with internal variables based on the Mohr–Coulomb criterion. Research by Pelli et al. [15], Martin [16], Hajiabdolmajid [17], and Hajiabdolmajid et al. [18] demonstrates that these constitutive models are not ideal in simulating the range and depth of brittle failure of hard rocks under high in situ stress. The reason is that they cannot reflect brittle fracture mechanisms and their evolution in hard brittle rocks under high in situ stress. To solve this problem, based on the Mohr–Coulomb criterion, Hajiabdolmajid [17] and Hajiabdolmajid et al. [18] proposed a constitutive model of hard rocks considering cohesion weakening and friction strengthening (CWFS). In addition, to express the evolution of changes in the elastic parameters of rocks upon plastic deformation, Bazant et al. [19] built an endochronic constitutive model by replacing the traditional plastic potential theory with endochronic theory. Moreover, Desai and Toth [20] and Desai [21] devised the disturbing dynamic plasticity theory to solve such problems. Han and Chen [22] proposed the use of plastic-fracture theory to simulate irreversible deformation and reductions in the rigidity of rock materials. The loading and deformation processes in rocks are accompanied by the rupture process. Therefore, the theory of damage and fracture mechanics is introduced to rock mechanics to establish the corresponding constitutive model, so as to understand the entire process of rock deformation and failure based on the understanding of a failure mechanism [23]. These models, like the fictitious crack model of Hillerborg et al. [24], the damage model for jointed rocks of Kawamoto et al. [25], the microscopic damage model of Shao and Rudnicki [26], and the continuum damage model of Krajcinovic [27], are representative. The aforementioned ground-breaking work has laid a solid foundation for studying the constitutive models of rock behavior, especially for brittle rock. During excavation in deep underground engineering projects, with the development of fracture process, mechanical properties of hard brittle rock masses deteriorate and mechanical parameters change accordingly. Meanwhile, rock masses on tunnel walls show obvious bulging deformation; that is, fracture and dilatant effect of rock masses. However, satisfactory results pertaining to the evolution of mechanical parameters and volume dilatant effects in rock fracture cannot be obtained by using the existing models.

Owing to rock-strength theory being the basis of a constitutive model, both of them have to reflect development and evolution processes, and mechanisms, of rock fracture and consider strength and mechanical response characteristics of hard brittle rocks. Therefore, aiming at the aforementioned problem, in this research, we first analyzed the strength and mechanical response characteristics revealed in tests on hard brittle rocks and in situ excavation. Second, the generalized polyaxial strain energy strength criterion (GPSE) was applied by analyzing rock-strength envelopes on the meridional and deviatoric planes. Based on such a criterion and analysis of the evolution of mechanical parameters, an elasto-plastic mechanical constitutive model of hard brittle rocks was established. Furthermore, the evaluation index for degree of damage (DOD) showing dilatant effects of rocks was proposed based on the failure approach index (FAI) theory proposed by Zhang et al. [28]. Finally, the constitutive model built in the research and evaluation index were integrated into a numerical simulation of triaxial tests on rocks and numerical simulation of the excavation of deep-buried auxiliary tunnels in China’s Jinping II Hydropower Station, so as to verify the reasonableness of the model and the index.

2 Strength Characteristics and Mechanical Behavior of Hard Brittle Rocks

2.1 Strength Characteristics

The strength and failure behaviors of most brittle rocks show a common characteristic, namely that they are closely correlated with the stress state, and such a conclusion has been verified through a large number of test results [7, 29]. The main reason for this can be attributed to the dependence of the development of micro-fractures in rocks on the stress state. These micro-fractures initiate and propagate under stress, then connect and accumulate to form macro-cracks, thus resulting in overall failure of the rock. For different kinds of brittle rocks, the degrees of dependence of strength and failure mode on stress differ. On the whole, the strength of hard brittle rocks manifests the effects of the minimum principal stress, intermediate principal stress, hydrostatic pressure, and Lode’s angle of stress. The effect of the minimum principal stress refers to the characteristic whereby rock strength increases nonlinearly with the minimum principal stress. As the minimum principal stress increases to a certain value, the strength of the rock increases in a quasi-linear manner, and the conventional triaxial test results show the effect of confining pressure on strength.

Under conventional triaxial test conditions, strength of hard brittle rocks rises monotonically with the increase of confining pressure, while the vast majority of rock masses on site are in a true triaxial stress state and show differences in all three-dimensional principal stresses. Under true triaxial conditions, the strength of hard brittle rocks first increases and then decreases with the intermediate principal stress $\sigma _{2}$; and the greater is the minimum principal stress $\sigma _{3}$, the higher is the strength, which is known as the effect of intermediate principal stress on rock strength [6, 29].

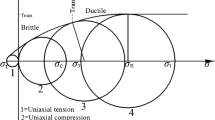
While discussing the applicability of rock-strength criteria, Colmenares and Zoback [29] gave four strength criteria: failure envelopes in circular form, regular hexagonal form, irregular hexagonal form, and curved hexagon form on the deviatoric plane. However, the test results (Fig. 1) show that, with increasing hydrostatic pressure, the shape of the failure envelope of brittle rocks on the deviatoric plane is not fixed, but gradually tends to a circle. Meanwhile, the rock-strength envelope on the meridional plane changes from one exhibiting a nonlinear increase to one showing a linear increase. The characteristics in these two cases exemplify the effect of hydrostatic pressures on rock strength. Unequal tension and compression of rock strength determines that the effect of Lode’s angle of stress on strength exists. Such an effect is demonstrated in the true triaxial test results shown in Fig. 2.

Fig. 1

Shapes of failure envelope on the deviatoric plane of Vosges sandstones under different octahedral normal stresses: a$\sigma _{\mathrm{oct}}= 50$ MPa; b$\sigma _{\mathrm{oct}} = 210$ MPa [30, 31]

Fig. 2

Relationship between strength of Soignies limestone and Lode’s angle of stress [30, 31]

2.2 Mechanical Behavior Characteristics

High strength and brittleness, brittle-to-ductile transition, and volumetric expansion are typical for hard brittle rocks [32, 33]. Figure 3 shows the stress–strain curves from conventional triaxial tests on $\hbox {T}_{2\mathrm{b}}$ marble from the Baishan formation at Jinping Hydropower Station. In the figure, $\varepsilon _{\mathrm{v}}$ represents the volumetric strain in the samples and a positive strain indicates shrinkage, while a negative strain denotes dilation. Jinping marble shows the characteristics of brittle failure under low confining pressure, and with increasing confining pressure, the degree of brittleness gradually decreases while the degree of plasticity rises. When the confining pressure reaches 40 MPa, the curve in the post-peak area presents ideal plasticity in the transition of deformation behavior with confining pressure. This is related to the magnitude of confining pressure and the lithology of rocks.

Fig. 3

Conventional triaxial stress–strain curves of $\hbox {T}_{2\mathrm{b}}$ marble at Jinping Hydropower Station

The essence of the brittle-to-ductile transition is a change in the failure mode of rocks with increasing confining pressure [33]. As displayed in Fig. 4, under low confining pressures, brittle fracture dominated by tensile micro-cracks mainly occurs in the rocks and the fracture plane is uneven and mainly extends along the axial direction without frictional sliding. Under high confining pressures, cracks are closed and mainly demonstrate ductile failure dominated by frictional sliding. Fracture planes act as inclined shear planes and generate rock flour under frictional sliding. Moreover, with increasing confining pressure, the irregular and uneven fracture plane becomes regular and even. After the confining pressure rises to a certain extent, the samples undergo barreling failure without showing macro-fracture planes. Densely and uniformly distributed conjugate slip lines are found in the middle of the rock samples and the stress–strain curve evinces hardening.

Fig. 4

Typical failure modes of deep marble samples under conventional triaxial confining pressure (the numbers in the figure represent the confining pressures)

Figure 3 shows the lateral and volumetric deformation curves of Jinping marble. The volumetric deformation of this marble begins to change from compression to expansion at the onset of damage. With the development of fracturing, both the lateral deformation and volumetric deformation increase rapidly and volumetric expansion becomes significant. During the excavation of tunnels, tangential stress around the tunnel wall increases, while radial stress decreases. The tangential and radial stresses correspond to the axial stress $\sigma _{\mathrm{a}}$ and confining pressure $\sigma _{\mathrm{p}}$ in the conventional triaxial testing of rock or the axial stress $\sigma _{\mathrm{a}}$ and the minimum lateral stress $\sigma _{\mathrm{lat1}}$ in a true triaxial test. When surrounding rock masses are damaged, the tunnel walls mainly show radial outward deformation under tangential stress. Therefore, volumetric expansion of the tunnel walls is more significant in the fracture of hard brittle surrounding rock mass on site, as shown in Fig. 5.

Fig. 5

Fracture and bulging of side wall F in first-phase test tunnel in Jinping Underground Laboratory

The rock strength determines the extent of failure depth in surrounding rock mass, while the volumetric expansion of rocks governs the development of deformation in surrounding rock mass; therefore, the strength criteria for hard brittle rocks can reveal the aforementioned four effects of strength, while the constitutive model is required to reflect the brittle-to-ductile transition and volumetric expansion therein.

3 GPSE Strength Criterion

Although rock-strength criteria have various expressions, the octahedral stress can always be used [4, 13], i.e.,

$$\begin{aligned} \tau _\mathrm{oct} =F_\mathrm{mp} \left( {\sigma _\mathrm{oct} } \right) F_\mathrm{octp} \left( {\theta _\sigma } \right) \end{aligned}$$

(1)

To facilitate dimensionless expression, Eq. (1) can be rewritten as

$$\begin{aligned}&\frac{\tau _\mathrm{oct} }{f_c }-F_\mathrm{mp} \left( {\frac{\sigma _\mathrm{oct} }{f_\mathrm{c} }} \right) F_\mathrm{octp} \left( {\theta _\sigma } \right) =0 \end{aligned}$$

(2)

$$\begin{aligned}&\tau _\mathrm{oct} =\sqrt{\left( {\sigma _1 -\sigma _2 } \right) ^{2}+\left( {\sigma _2 -\sigma _3 } \right) ^{2}+\left( {\sigma _3 -\sigma _1 } \right) ^{2}}/3 \end{aligned}$$

(3)

$$\begin{aligned}&\sigma _\mathrm{oct} =\left( {\sigma _1 +\sigma _2 +\sigma _3 } \right) /3 \end{aligned}$$

(4)

$$\begin{aligned}&\theta _\sigma = -\frac{1}{3}\sin ^{-1}\left( {\frac{3\sqrt{3}J_3 }{2J_2^{\frac{3}{2}} }} \right) \end{aligned}$$

(5)

where $\tau _{\mathrm{oct}}$, $\sigma _{\mathrm{oct}}$, and $\theta _{\sigma }$ indicate the octahedral shear stress, the octahedral normal stress (representing hydrostatic pressure), and Lode’s angle of stress, respectively; $\sigma _{1}, \sigma _{2}$, and $\sigma _{3}$ denote the maximum principal stress, the intermediate principal stress, and the minimum principal stress, respectively; $J_{2}$ and $J_{3}$ denote, respectively, the second and the third invariants of the component $S_{ij}$ of the deviatoric stress tensor; $F_{\mathrm{mp}}$ ($\sigma _{\mathrm{oct}})$ shows the shape and position of failure function on the meridian plane ($\tau _{\mathrm{oct}}$–$\sigma _{\mathrm{oct}}$ plane); and $F_{\mathrm{octp}}(\theta _{\sigma })$ is the failure function on the deviatoric plane.

In strength criteria in unified form, the effects of hydrostatic pressure and Lode’s angle of stress can be expressed explicitly, while the effects of the minimum principal stress and intermediate principal stress are implicit. In fact, the effects of minimum principal stress and intermediate principal stress are mainly shown as failure functions on the meridional and deviatoric planes, and their influences on the strength of brittle rock are the results of the combined effects of these two functions.

It is assumed that rock is damaged as long as the stored strain energy reaches a certain critical value. Therefore, based on the Wiebols–Cook polyaxial energy criterion [8], the yield function on the meridional plane is defined as

$$\begin{aligned} F_\mathrm{mp} \left( {\frac{\sigma _\mathrm{oct} }{f_\mathrm{c} }} \right) =\left( {a^{2}\left( {\frac{\sigma _\mathrm{oct} }{f_\mathrm{c} }} \right) ^{2}+b\frac{\sigma _\mathrm{oct} }{f_\mathrm{c} }+c} \right) ^{n} \end{aligned}$$

(6)

where a, b, and c are parameters related to the rock material; n represents the index of the effects of hydrostatic pressure ($0 \le n \le 1$). By analyzing the test results on brittle rock samples [2,3,4,5,6], it is found that $n= 0.5$; therefore, the failure function of brittle rocks on the meridional plane is

$$\begin{aligned} F_\mathrm{mp} \left( {\frac{\sigma _\mathrm{oct} }{f_\mathrm{c} }} \right) =\left( {a^{2}\left( {\frac{\sigma _\mathrm{oct} }{f_\mathrm{c} }} \right) ^{2}+b\frac{\sigma _\mathrm{oct} }{f_\mathrm{c} }+c} \right) ^{0.5} \end{aligned}$$

(7)

On the deviatoric plane, the rock-strength envelope must be a continuous convex curve, and the smooth ridge model recommended by Yu [13] is used:

$$\begin{aligned} F_{\mathrm{octp}} \left( {\theta _\sigma } \right)= & {} \frac{2\left( {1-\gamma ^{2}} \right) +\left( {\gamma -2} \right) \sqrt{4\left( {\gamma ^{2}-1} \right) +\left( {5-4\gamma } \right) f_{\theta _\sigma }^2 }}{4\left( {1-\gamma ^{2}} \right) -\left( {\gamma -2} \right) ^{2}f_{\theta _\sigma }^2 }\gamma f_{\theta _\sigma } \end{aligned}$$

(8)

$$\begin{aligned} f_{\theta _\sigma }= & {} \sec \left( {\frac{\pi }{6}-\theta _\sigma } \right) , \quad -\frac{\pi }{6}\le \theta _\sigma \le \frac{\pi }{6} \end{aligned}$$

(9)

where $\gamma$ represents the triaxial tensile–compressive strength ratio that controls the shape of the failure function on the deviatoric plane and is related to $\sigma _\mathrm{oct}$. According to the analysis of the above test results, $\gamma$ is correlated with hydrostatic pressure and is given by

$$\begin{aligned} \gamma= & {} \gamma _0^\rho \end{aligned}$$

(10)

$$\begin{aligned} \rho= & {} \exp \left( {-\beta \frac{\sigma _\mathrm{oct} }{f_\mathrm{c} }} \right) \end{aligned}$$

(11)

$$\begin{aligned} \gamma _0= & {} \frac{3-\sin \phi }{3+\sin \phi } \end{aligned}$$

(12)

where $\gamma _{0}$ represents the triaxial tensile–compressive strength ratio; $\rho$ indicates the influence of hydrostatic pressure and reflects the effects of hydrostatic pressure on the triaxial tensile–comprehensive strength ratio, which can generally be ignored; that is, $\beta = 0$ and $\rho = 1$. In theory, the rate of change of $\gamma _{0}$ is $0.5 \le \gamma _{0} \le 1$ [13].

A rock-strength criterion should be able to demonstrate the changes in strength of brittle rocks and pass through the six stress points in the stress spaces that correspond to the strengths obtained based on tension and compression tests. Meanwhile, under triaxial compressive stress, when $\sigma _{\mathrm{oct}}$ is much greater than zero, the failure function on the meridional plane gradually tends to the Mohr–Coulomb envelope; thus,

$$\begin{aligned} \frac{\partial \tau _{\mathrm{oct}} }{\partial \sigma _\mathrm{oct} }=\frac{\mathrm{d}\tau _\mathrm{oct} }{\mathrm{d}\sigma _\mathrm{oct} }=\frac{2\sqrt{2}\sin \phi }{3-\sin \phi } \end{aligned}$$

(13)

where $\phi$ denotes the internal friction angle of rocks, and therefore, based on the above three conditions, i.e., uniaxial compression, uniaxial tension, and triaxial compression, the expressions of the three parameters, a, b, and c are obtained, namely

$$\begin{aligned} a= & {} \frac{2\sqrt{2}\sin \phi }{3-\sin \phi } \end{aligned}$$

(14)

$$\begin{aligned} b= & {} \frac{1}{3}\left[ {\frac{2\left( {\gamma ^{2}-\alpha ^{2}} \right) }{\gamma ^{2}\left( {1+\alpha } \right) }-a^{2}\left( {1-\alpha } \right) } \right] \end{aligned}$$

(15)

$$\begin{aligned} c= & {} \left( {2-3b-a^{2}} \right) /9 \end{aligned}$$

(16)

$$\begin{aligned} \alpha= & {} \frac{f_t }{f_c } \end{aligned}$$

(17)

where $\alpha$ denotes the uniaxial tensile–comprehensive strength ratio. By substituting a, b, and c into Eq. (7), the failure function on the meridional plane is obtained before being substituted into Eq. (2) together with Eq. (8), so as to obtain the GPSE strength criterion. Furthermore, it can be found from the above expressions of the three parameters that these three parameters are dimensionless. Of them, parameter a is related to the internal friction angle, while b and c are related to not only the internal friction angle, but also the uniaxial tensile–compressive strength ratio $\alpha$ and the triaxial tensile–compressive strength ratio $\gamma$. Therefore, the three parameters have physical meaning.

All parameters in this criterion can be obtained through three conventional tests, i.e., uniaxial compression, tension, and triaxial compression, dispensing with the need for true triaxial testing in these circumstances, thus facilitating the application of the criterion in engineering practice [34].

Huang et al. [34] presented the failure curves in the meridian and deviatoric planes, as shown in Figs. 6, 7. Under low hydrostatic pressures, the failure function on the meridional plane is in the form of a hyperbolic curve, which can constantly realize natural coupling of compressive and tensile strength. This criterion is an extension of the Griffith–Murrell criterion in the state of polyaxial stress (it becomes the Griffith–Murrell criterion when $a=0$, $c=0$, and $F_{\mathrm{octp}}=1$), which can present significant differences in tension–compression strength and brittle failure behavior as controlled by tensile micro-cracks. Under high hydrostatic pressures, the envelope of this criterion connects to that of the Mohr–Coulomb criterion on the meridional plane. In other words, this criterion can be transformed into the generalized Mises criterion ($F_{\mathrm{octp}}=1$) at this time, which shows ductile failure controlled by frictional sliding of brittle rocks under high hydrostatic pressures. At intermediate hydrostatic pressures, this criterion is in the transitional stage between the above two criteria and the failure of brittle rocks changes from one controlled by tensile micro-cracks to that controlled by frictional sliding. At this time, the failure of brittle rocks is under compound control, demonstrating the transition from brittle failure to ductile failure of brittle rocks under high hydrostatic pressures.

Fig. 6

Failure curve of GPSE criterion in meridian plane with $\theta _{\sigma }=30{^{\circ }}$ [31]

Fig. 7

Envelope of GPSE criterion on deviatoric planes under different octahedral stresses [31]

For this criterion, the shape of the failure envelope in the deviatoric plane changes. As shown in Fig. 7, at low hydrostatic pressures, the shape of failure envelope on the deviatoric plane approximates to a curved triangle and is circumscribed by the six angular points of the Mohr–Coulomb criterion and internally tangential to the generalized twin-shear criterion. With increasing hydrostatic pressure, the failure envelope on the deviatoric plane gradually tends to be circular.

By comparing the true triaxial test results of different categories of hard brittle rocks, such as coarse marble, KTB amphibolites, Western granite, Jinping marble, and Laxiwa granite with the results predicted by using the GPSE criterion, Huang et al. [34] verified that this criterion is reasonable. Furthermore, this demonstrates that this criterion can reasonably describe the effects of the minimum principal stress, intermediate principal stress, hydrostatic pressure, and Lode’s angle of stress and reflect the significant differences in nonlinear strength characteristics and tension–compression strength of brittle rocks on both meridional and deviatoric planes, as shown in Fig. 8.

Fig. 8

Comparison between test strengths and theoretical values based on GPSE criterion: a in $\sigma _{1}$-$\sigma _{2}$ space; b in $\tau _{\mathrm{oct}}$-$\sigma _{\mathrm{oct}}$ space; c in the deviatoric plane of this figure, the solid lines are strength envelopes and the data points are tested values [31]

4 Elastic-Plastic Hardening–Softening Constitutive Model for Hard Brittle Rock

In the construction of deep underground engineering works, hard brittle rocks show significant strain softening, dilatancy, and a brittle-to-ductile transition. The accurate description thereof is the key to predicting the deformation and failure response of a rock mass and preventing the failure of surrounding rock mass and the development of volumetric expansion and deformation. Based on the test results of Jinping marble samples and the aforementioned GPSE strength criterion, in this section, we propose an elastic-plastic hardening–softening constitutive model of hard brittle rocks considering dilatant effects; moreover, we present a yield criterion, plastic potential function, and hardening–softening rule, and discuss the evolution of the mechanical parameters involved in this model. The formula used to calculate the increment in the model can be deduced through the finite-element or finite-difference theory and is beyond the scope of this work.

4.1 Yield Criterion

It is assumed that the shape of yield surface keeps unchanged and only the size changes in the reduction of rock strength after yielding. By introducing hardening parameter $\kappa$ into Eq. (2), the yield function is obtained:

$$\begin{aligned}&f\left( {\sigma _{ij} ,\kappa } \right) =\tau _\mathrm{oct} /f_\mathrm{c} -F_\mathrm{octp} \left( {\theta _\sigma } \right) F_\mathrm{mp} \left( {\sigma _\mathrm{oct} /f_\mathrm{c} ,\kappa } \right) \end{aligned}$$

(18)

$$\begin{aligned}&F_\mathrm{mp} \left( {\sigma _\mathrm{oct} /f_\mathrm{c} ,\kappa } \right) =\left[ {A\left( \kappa \right) \left( {\sigma _\mathrm{oct} /f_\mathrm{c} } \right) ^{2}+B\left( \kappa \right) \left( {\sigma _\mathrm{oct} /f_\mathrm{c} } \right) +C\left( \kappa \right) } \right] ^{0.5} \end{aligned}$$

(19)

$$\begin{aligned}&A\left( \kappa \right) =\frac{8\sin ^{2}\phi \left( \kappa \right) }{\left( {3-\sin \phi \left( \kappa \right) } \right) ^{2}} \end{aligned}$$

(20)

$$\begin{aligned}&B\left( \kappa \right) =-\frac{4c\left( \kappa \right) \sin 2\phi \left( \kappa \right) \left( {3+2\sin \phi \left( \kappa \right) +4\sin ^{2}\phi \left( \kappa \right) } \right) }{3\left( {3-\sin \phi \left( \kappa \right) } \right) ^{2}\left( {1-\sin ^{2}\phi \left( \kappa \right) } \right) } \end{aligned}$$

(21)

$$\begin{aligned}&C\left( \kappa \right) =4c\left( \kappa \right) ^{2}\cos ^{2}\phi \left( \kappa \right) \nonumber \\&\quad \left[ {\frac{2}{\left( {3-\sin \phi \left( \kappa \right) } \right) ^{2}\left( {1-\sin \phi \left( \kappa \right) } \right) ^{2}}-\frac{10\sin ^{2}\phi \left( \kappa \right) }{9\left( {3-\sin \phi \left( \kappa \right) } \right) ^{2}\left( {1-\sin ^{2}\phi \left( \kappa \right) } \right) }} \right] \end{aligned}$$

(22)

where $\kappa$ represents the hardening parameter and describes the hardening–softening behavior of the yield surface.

4.2 Plastic Potential Function

By utilizing a non-associated flow rule, the plastic potential function is defined as follows:

$$\begin{aligned} g\left( {\sigma _{ij} ,\kappa } \right) =\tau _\mathrm{oct} +F_\mathrm{octp} \left( {\theta _\sigma } \right) {K}_\psi \left( \kappa \right) \sigma _\mathrm{oct} +\zeta \end{aligned}$$

(23)

where $\xi$ is a constant and $K_{\uppsi }$ represents a parameter describing the dilatant effects. Dilation is closely related to the deformation and failure of rocks and is an important property used in characterizing the mechanical response of rocks. Based on the research of Alejano and Alonso [35], the dilation angle $\psi$ is used as a material parameter to represent the dilation of the rock. Here, for convenience, when defining the plastic potential function, the dilation parameter $K_{\psi }$ is defined according to Eq. (13):

$$\begin{aligned} K_\psi =\frac{2\sqrt{2}\sin \psi }{3-\sin \psi } \end{aligned}$$

(24)

The loading and unloading conditions for this constitutive model are derived with reference to the results obtained by Shao and Rudnicki [26].

4.3 Hardening–Softening Rule

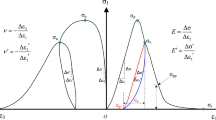
To consider the dilatant effects on rock failure, in this study, we select the plastic volumetric strain $\varepsilon _{v}^{p}$ as the hardening–softening parameter to characterize accumulated damage to the rock [36]. To derive the relationships linking cohesion C, internal friction angle $\phi$, and dilation parameter $K_{\psi }$ with $\varepsilon _{v}^{p}$, damage-controlled loading and unloading tests were conducted on Jinping marble samples. Using the method recommended by Martin [37] to analyze the test data, the relationships linking C and $\phi$ with $\varepsilon _{v}^{p}$ are obtained:

$$\begin{aligned}&C=C_\mathrm{res} +\left( {C_\mathrm{pea} -C_\mathrm{res} } \right) \left[ {\exp \left( {-\frac{\varepsilon _v^p }{\varepsilon _{v,c}^p }} \right) } \right] ^{2} \end{aligned}$$

(25)

$$\begin{aligned}&\left\{ {\begin{array}{ll} \phi =\phi _\mathrm{pea} \left( {\frac{\varepsilon _v^p }{\varepsilon _{v,\phi 1}^p }} \right) ^{0.5} &{} \big (0 \le \varepsilon _v^p <\varepsilon _{v,\phi 1}^p \big ) \\ \phi =\phi _\mathrm{res} +\left( {\phi _\mathrm{pea} -\phi _\mathrm{res} } \right) \left[ {\exp \left( {-\frac{\varepsilon _\varepsilon ^p -\varepsilon _{v,\phi 1}^p }{\varepsilon _{v,\phi 2}^p }} \right) } \right] ^{2}&{}( \varepsilon _v^p \ge \varepsilon _{v,\phi 1}^p) \\ \end{array}} \right. \end{aligned}$$

(26)

Figures 9, 10 show that the recommended expressions provide a good fit to the experimental values of C and $\phi$ and their relationship to $\varepsilon _{v}^{p}$.

Fig. 9

Theoretical and experimental values in relationship between C and $\varepsilon _{v}^{p}$ ($\varepsilon _{v,c}^{p} =0.15\%$)

Fig. 10

Theoretical and experimental values in relationship between $\upvarphi$ and $\varepsilon _{v}^{p}$ ($\varepsilon _{v,\phi 1}^{p}=0.15\%$ and $\varepsilon _{v,\phi 2}^{p} =0.3\%$)

The relationship between the dilation parameter $K_{\psi }$ and $\varepsilon _{v}^{p}$ is as follows:

$$\begin{aligned} K_\psi =K_{\psi , \mathrm{pea}} \left[ {\exp \left( {-\frac{\varepsilon _v^p }{\varepsilon _{v,\psi }^p }} \right) } \right] ^{2} \end{aligned}$$

(27)

where $\varepsilon _{v,\psi }^{p}$ indicates the material parameter reflecting the dilatant effects, and $K_{\psi ,\mathrm{pea}}$ represents the peak dilation parameter. According to Eq. (24), the latter is defined as

$$\begin{aligned} K_{\psi , \mathrm{pea}} =\frac{2\sqrt{2}\sin \psi _\mathrm{pea} }{3-\sin \psi _\mathrm{pea}} \end{aligned}$$

(28)

where $\psi _{\mathrm{pea}}$ represents the peak dilation angle. Considering the influence of confining pressure, in accordance with the research of Alejano and Alonso [35], the relationship between $\psi _{\mathrm{pea}}$ and the confining pressure is

$$\begin{aligned} \psi _\mathrm{pea} =\frac{\phi _\mathrm{pea} }{1+\log _{10} \sigma _c }\log _{10} \frac{\sigma _c }{\left| {\sigma _3 } \right| +0.1} \end{aligned}$$

(29)

where $\phi _\mathrm{pea}$ and $\sigma _{{c}}$ denote the initial friction angle and uniaxial compressive strength of intact rock blocks, respectively.

Figure 11 shows the theoretically calculated and experimental values governing the relationship between $K_{\psi }$ and $\varepsilon _{v}^{p}$ and the good fit therein.

Fig. 11

Theoretical and experimental values in relationship between $K_\psi$ and $\varepsilon _{v}^{p}$ ($\varepsilon _{v,\uppsi }^p =5.1\%$)

5 Safety Evaluation Index for Surrounding Rock Mass

In underground engineering, excavation can lead to the loss of equilibrium of in situ stress, and stress concentration occurs in near-field surrounding rock mass due to the secondary adjustment of the global stress field. When the concentrated stress does not exceed the damage threshold of rock masses, no new damage is generated in surrounding rock mass. At this time, surrounding rock masses are in a stable state. However, when the concentrated stress exceeds the strength of the rock mass, surrounding rock masses are fractured and damaged, thus causing failure and obvious dilation. Therefore, the excavation damage zone (EDZ) and failure zone appear in the surrounding rock mass after excavation of deep tunnels. In this study, to emphasize the dilatant effect, the EDZ was called the excavation dilatant damaged zone (EDDZ), while the failure zone was known as the dilatant fault zone (DFZ). The accurate understanding of the range, depth, and evolution of these zones is important when optimizing staged excavation work and formulating stability-control strategies for the surrounding rock mass.

To analyze the rock mass during excavation and carry out the safe division thereof, Zhang et al. [28] put forward the FAI to describe the DOD of surrounding rock mass in excavations under complex stress states. In addition, work was conducted on surrounding rock mass according to different DODs. This index includes a yield approach index (YAI) and the degree of failure (DF). Based on this theory, we proposed the YAI based on the GPSE criterion and then defined a dilation degree index considering dilatant effects. Then, the dilation safety factor (DSF) considering dilatant effects was proposed.

5.1 YAI Based on GPSE Criterion

Based on the theory of Zhang et al. [28], in the principal stress space, the shortest distance from a stress point to the GPSE yield surface was calculated, and then the point at which the isocline on the same deviatoric plane of the stress point intersecting the deviatoric plane was obtained. The minimum distance from this point to the GPSE yield surface was calculated, and then, the ratio of these two distances was obtained, thus acquiring the YAI based on the GPSE criterion. The GPSE criterion is expressed in terms of the normal and shear stresses on the $\pi$-plane:

$$\begin{aligned} f\left( {\tau _\pi , \sigma _\pi , \theta _\sigma } \right) =\frac{\tau _\pi }{\sqrt{3}}-A\left( {\theta _\sigma } \right) B\left( {\sigma _\pi } \right) \end{aligned}$$

(30)

where $A\left( {\theta _\sigma } \right) =\frac{2C\cos \phi }{1-\sin \phi }F_\mathrm{octp} \left( {\theta _\sigma } \right)$ and $B\left( {\sigma _\pi } \right) =\left( {\frac{a_\phi ^2 }{3}\bullet \left( {\frac{1-\sin \phi }{2C\cos \phi }} \right) ^{2}\sigma _\pi ^2 +\frac{b}{\sqrt{3}}\bullet \frac{1-\sin \phi }{2C\cos \phi }\sigma _\pi +c} \right) ^{0.5}(\tau _\pi =\sqrt{3}\tau _\mathrm{oct}$ and $\sigma _\pi =\sqrt{3}\sigma _\mathrm{oct} )$.

In Fig. 12, points $P_{0}(\sigma _\pi , 0), P_{1}$ ($\sigma _\pi ,\tau _\pi )$, and C ($\sigma _\pi ,\tau _\pi ^{\prime })$ lie in the same deviatoric plane. The lengths of line segments $P_{0}P_{1}$ and $P_{0}C$ are $\tau _\pi$ and $\tau _\pi ^{\prime }$, respectively; and line segments $P_{1}A_{1}$ and $P_{0}A_{0}$ have lengths dand D, respectively.

Fig. 12

Relationship between stress points and yield surface in principal stress space

Owing to point C sitting on the yield surface, the coordinates of point C meet the yield function based on the GPSE criterion, thus obtaining the following formula, according to Eq. (30):

$$\begin{aligned} f\left( {\tau _\pi ^{\prime } ,\sigma _\pi ,\theta _\sigma } \right) =\frac{\tau _\pi ^{\prime } }{\sqrt{3}}-A\left( {\theta _\sigma } \right) B\left( {\sigma _\pi } \right) =0 \end{aligned}$$

(31)

Thus,

$$\begin{aligned} \tau _\pi ^{\prime } =\sqrt{3}A\left( {\theta _\sigma } \right) B\left( {\sigma _\pi } \right) \end{aligned}$$

(32)

The yield line on the meridional plane is curved, so triangles $\Delta P_{1}A_{1}C$ and $\Delta P_{0}A_{0}C$ are approximately similar; therefore, according to the definition of the YAI,

$$\begin{aligned} \mathrm{YAI}=\frac{d}{D}\approx \frac{L_{P_1 C} }{L_{P_0 C} }=\frac{\tau _\pi ^{\prime } -\tau _\pi }{\tau _\pi ^{\prime } }=1-\frac{\tau _\pi }{\tau _\pi ^{\prime } } \end{aligned}$$

(33)

Substituting Eq. (32) into Eq. (33) gives

$$\begin{aligned} \mathrm{YAI}=\frac{\sqrt{3}A\left( {\theta _\sigma } \right) B\left( {\sigma _\pi } \right) -\tau _\pi }{\sqrt{3}A\left( {\theta _\sigma } \right) B\left( {\sigma _\pi } \right) } \end{aligned}$$

(34)

Other parameters are as defined above.

In accordance with the above analysis, the YAI function is used for evaluating the safe stress in materials undergoing elastic deformation. On the yield surface, the YAI is 0, while it is 1 on the isoclinal axis.

5.2 Dilation Factor and DSF

Under high stress, brittle rocks show an obvious dilation phenomenon while being damaged, so it is necessary to establish an evaluation index reflecting such dilatant effects in rocks. At yield point, because the stress state of brittle rock is non-unique, there exist certain difficulties in defining rock failure in the stress space. Owing to plastic strain monotonically increasing and being irreversible, we utilized the plastic volumetric strain $\varepsilon _{v}^{p}$ to describe plastic volumetric dilation, so as to evaluate the DOD in the material itself. When it reaches a certain value, the materials are deemed to have been damaged. It is supposed that there is a critical plastic volumetric strain $\varepsilon _{v,cri}^{p}$ suitable for being used as a criterion for defining failure of brittle rocks, and such a criterion is a material parameter. Based on this, a plastic dilatation factor (PDF) is proposed:

$$\begin{aligned} \mathrm{PDF}=\frac{\varepsilon _v^p }{\varepsilon _{v,cri}^p } \end{aligned}$$

(35)

When $\varepsilon _v^p =\varepsilon _{v,cri}^p$, $\mathrm{PDF}_{cri} =1$.

By combining the YAI in an elastic state with the PDF in a plastic state, a new evaluation index, namely the DSF, is proposed:

$$\begin{aligned} \mathrm{DSF}=\left\{ {\begin{array}{ll} 1-\mathrm{YAI} &{} \quad 0<YAI<1 \\ 1+\mathrm{PDF} &{}\quad \mathrm{YAI} = 0, \mathrm{PDF}>0 \\ \end{array} } \right. \end{aligned}$$

(36)

In accordance with Eq. (36), although the YAI in an elastic state and the PDF in a plastic state are established in two different types of space, they are dimensionless parameters used to indicate hazards and can be re-combined to express risk of a given hazard arising in brittle rocks at different deformation states (or stages). In addition, Eq. (36) shows that the smaller is the DSF value, the safer is the rock; while the larger is the value, the greater are the hazards caused by dilation of the rock mass.

Based on the DSF, the EDDZ can be defined as the zone in which stress exceeds the strength of the rock mass. In this zone, cracks propagate, cluster, and connect. Moreover, surrounding rock masses are damaged significantly and dilation appears after volumetric deformation, thus reducing the wave velocity therein. In this zone, $\lambda _{\sigma cd} \le \mathrm{DSF}<1+\mathrm{PDF}_\mathrm{cri} =2$. $\lambda _{\sigma cd}$ represents the damage strength ratio of rocks, namely the ratio of damage strength to peak strength. After surrounding rock masses are damaged, rock masses become unstable and suffer damage, such as collapse, spalling, and rockburst. At this time, rock blocks are separated from the parent rock mass. If the surrounding rock mass can reach a steady state again, the zone between contour lines of the fracture surface after self-stabilization is defined as the DFZ, and the initial excavation contour line $\hbox {DSF}{>}2$.

6 Verification of Constitutive Model and Evaluation Index

To verify the capacity of the model established in this study for describing the mechanical behavior and properties of hard brittle rocks, we obtained conventional triaxial compression stress–strain curves of rocks under different confining pressures by numerical simulation and compared them with the experimental data. For the applicability of the proposed DSF evaluation index based on the GPSE criterion, it was verified by simulating the mechanical response to the excavation of the rocks surrounding the deeply buried auxiliary tunnels in Jinping II Hydropower Station and comparing it with the test results obtained on site.

6.1 Model Verification

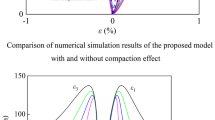
FLAC3D software (Itasca Consulting Group, Inc., USA) was used to simulate the conventional triaxial compression tests on marble samples, and the mechanical parameters therein are listed in Table 1. The samples in the simulation and test had the same shapes and dimensions, and uniformly distributed normal loads were applied around the samples to simulate the confining pressure. Two axial end faces were constrained by applying normal displacement, and the loading was conducted at a constant displacement rate during the compression process. Figure 13 shows the stress–strain curves obtained through simulation. By comparing Fig. 13 with Fig. 1, the constitutive model presented here can be deemed to be capable of simulating the brittle behavior and strain-softening characteristics with increasing confining pressure on brittle rocks under low confining pressures and the brittle-to-ductile transition characteristics of brittle rocks under high confining pressures. According to the volumetric strain curve shown in Fig. 14, the constitutive model here can also simulate the dilatant effects and effects of confining pressure when brittle rocks are damaged. These simulation tests can demonstrate the main characteristics, such as brittleness, brittle-to-ductile transition, and volumetric expansion in damage shown in the laboratory tests on brittle rocks.

Table 1 Mechanical parameters of marble samples used in the numerical simulation test

Fig. 13

Stress–strain curves obtained in conventional tests simulated using the proposed constitutive model

Fig. 14

Volumetric strain–axial strain curves in conventional tests simulated using the constitutive model presented here

The mechanical behavior described by the constitutive model suggested here depends on the evolution curve of the strength and the dilation parameters with the plastic internal variable, and the morphology of these evolution curves depends on the physical and mechanical constants in Eqs. (25)–(27). That is to say, although the mechanical behaviors of different types of hard brittle rocks are different, they can be accurately described based on the obtained physical and mechanical constants.

6.2 Verification of Evaluation Index

An auxiliary tunnel in Jinping II Hydropower Station, as the key construction project in the early stage of Jinping I and II Hydropower Stations, provides the transportation route connecting the east and west branches of the Ya-lung River. Furthermore, it serves as the auxiliary tunnel for constructing the headrace tunnel and plays a role as an advanced exploratory tunnel. The auxiliary tunnel in Jinping II Hydropower Station comprises two single-lane tunnels, with the entrance in the upstream around 150 m from the Jingfeng Bridge on the western Ya-lung River, and the exit lying downstream and 400 m from Dashuigou on the eastern Ya-lung River. The tunnel passes through the Jinping Mountain in the approximately east-west direction. Auxiliary tunnel #A in the south, with a total length of 17.5 km, is designed with a net height of 6.95 m and width of 5.70 m. Auxiliary tunnel #B in the north, with a total length of 17.5 km, is designed to be 7.54 m high and 6.20 m wide. Horizontal adits are designed at intervals of 500–800 m between the two tunnels.

To assess the DOD of surrounding rock mass during construction and excavation, an acoustic wave test was conducted in 6-1# horizontal adit at the east end of the auxiliary tunnel. The centerline of the tunnel corresponds to pile BK13+845 m in tunnel #B and the burial depth is approximately 1673 m, as shown in Fig. 15. The figure presents the depth of the low-wave-velocity zone obtained through the acoustic wave tests in each borehole. The low-wave-velocity zone refers to the zone in which wave velocity decreases, resulting from fracture and damage of surrounding rock mass after excavation; and this zone corresponds to the EDDZ. Stratum $\hbox {T}_{2\mathrm{y}}6$ is found in the tested section, involving ash black to black medium-thin layers of limestone, ash black to black medium-thick layers of limestone, and fresh rock. The mechanical parameters of rock masses used in the numerical simulation on this tunnel section are listed in Table 2, and the in situ stresses corresponding to the 6-1# horizontal adit are presented in Table 3 (see the coordinates in Fig. 16).

Fig. 15

Schematic of the layout of tested section in relaxation zone in the $6\hbox {-}1^{\#}$ horizontal adit of auxiliary tunnel in the east of diversion tunnel in Jinping II Hydropower Station: a location of tested section in relaxation zone; b test results from relaxation zone (the numbers in brackets represent the depth of the relaxation zone)

Table 2 Mechanical parameters of rock masses

Table 3 In situ stress around 6-1# horizontal adit, auxiliary tunnel #B, Jinping II Hydropower Station

Fig. 16

DSF distributions in rocks surrounding 6-1# horizontal adit in auxiliary tunnel #B in Jinping II Hydropower Station (the numbers in figure represent the distance from the damage zone to the tunnel boundary)

Figure 16 shows the nephogram of the DSF distribution: the shape and dimensions of the EDDZ revealed in the numerical simulation match those of the low-wave-velocity zone obtained experimentally and the DODs of different parts of the EDDZ are presented, which provides a direct basis for the selection of support parameters for this tunnel.

6.3 Engineering Verification of Constitutive Model

In the excavation of the auxiliary tunnel, the convergence and deformation were monitored at chainage BK14+599 m in tunnel #B in the east of the auxiliary tunnel (Fig. 17). The burial depth of the tunnel section is approximately 1538 m. The test section comprises marbles in the Yantang formation, belonging to type-II surrounding rock mass. The mechanical parameters of rock masses used in the numerical simulation of this section are listed in Table 4. The In situ stresses corresponding to section BK14+599 m in auxiliary tunnel #B are listed in Table 5 (see Fig. 17 for coordinates). Table 6 lists the monitored deformation of the rock surrounding tunnel section BK14+599 m, and sections BA, ED, BC, and AC are four measuring lines for convergence and deformation measurement (Fig. 17).

Fig. 17

Schematic showing dimensions of section BK14+599 m and layout of measuring lines (units: cm) (Sections BA, ED, BC, and AC are measuring lines)

Table 4 Mechanical parameters of rock masses

Table 5 In situ stresses at Section BK14+599 m, auxiliary tunnel #B, Jinping II Hydropower Station

Table 6 Comparisons of final monitored and calculated values of convergence and deformation of surrounding rock mass at chainage BK14+599 m

Figure 18 shows a comparison of the final monitored and calculated values of convergence and deformation of surrounding rock mass. By combining these data with those in Table 6, the numerical simulation results of convergence and deformation of surrounding rock mass given by the recommended constitutive model match those obtained in situ. In addition, the deformation of surrounding rock mass calculated using the recommended constitutive model is greater than that calculated by utilizing the model without considering dilation, so the former can better reflect the deformation induced by fracture and bulging of hard brittle rocks under high stresses. This provides a direct basis for evaluating stability of the rocks surrounding this tunnel.

Fig. 18

Comparisons of final monitored and calculated values of convergence and deformation of surrounding rock mass at chainage BK14+599 m

The simulation results of conventional triaxial tests on rock samples and the numerical simulation results of tunnel excavation show that the hardening–softening constitutive model of hard brittle rocks proposed based on the GPSE criterion can accurately describe the mechanical behavior of such rocks. The DSF evaluation index proposed on the basis of the GPSE criterion can offer reasonable evaluations of the hazards and DODs of surrounding rock mass in different parts and depths of such tunnels. The model and the evaluation index provide reliable theoretical support for damage evolution and evaluation in the rock surrounding such a deep underground excavation.

7 Conclusions

Existing strength theories cannot reveal the fracture development mechanisms or failure modes of hard brittle rocks and cannot comprehensively reflect the effects of intermediate principal stress, minimum principal stress, hydrostatic pressure, and Lode’s angle of stress on rock strength. For these reasons, we introduced a GPSE strength criterion based on the Wiebols–Cook polyaxial energy criterion. The parameters of this criterion can be obtained through conventional triaxial testing without the help of complex true triaxial tests, which is favorable for widening its application.

In view of the defects in the constitutive model of hard brittle rocks in their inability to reflect dilatant effects and characteristics of nonlinear mechanical behavior during fracturing of rocks, we proposed the corresponding yield criterion based on the proposed GPSE criterion. By using plastic volumetric strain as the hardening parameter, the hardening–softening rule showing the evolution of mechanical parameters of hard brittle rocks was established based on laboratory data.

Based on the proposed strength criterion and constitutive model, we proposed an evaluation index for DOD and dilation of hard brittle rocks, namely the DSF. Through calculation and verification on site, the proposed evaluation index can evaluate the DODs of deeply buried hard brittle rock masses.