Introduction

Global navigation satellite system (GNSS) has been widely used in the field of real-time high-precision positioning, especially for Real-Time Kinematic (RTK) positioning. Under the desired observation conditions, RTK technology can achieve millimeter-level positioning accuracy (Xi et al. 2018). Although some common error terms, including the satellite clock error, receiver clock error and satellite orbit error, can be eliminated or corrected by the Double-Difference (DD) observation technology, there are some errors, for example, multipath, which can be neither eliminated nor precisely modelled but affects positioning accuracy to a certain extent (Zhang et al. 2022).

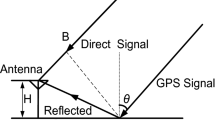
Multipath effect refers to the direct and indirect signals received by GNSS antennas, where indirect signals are caused by reflection and diffraction from objects around the station. The strategies of multipath error mitigation mainly focus on the observation environment, GNSS receiver antennas and data processing algorithm. For high-precision GNSS positioning, an open sky environment is usually chosen to avoid multipath effects. However, it is not easy to completely free of the multipath effects in the field of deformation monitoring. Although hardware technology of GNSS antennas can effectively suppress multipath effects, it will bring a cost burden to GNSS receiving equipment (Yang et al. 2016). The algorithm of multipath errors mitigation is widely investigated, such as a data filter, named the Vondrak filter with cross-validation for separating signal and noise from GPS observations(Zheng et al. 2005; Zhong et al. 2008); a ray tracing method is introduced to estimate the multipath error based on a priori information about the satellite-reflector-antenna geometry, reflector material, and antenna characteristics (Lau & Cross 2007); a 3-D map and ray-tracing method are used to estimate the indirect and direct signal paths from satellite to receiver (Miura et al. 2015); the combined observation of pseudo-range and carrier phase observables is used to reflect pseudo-range multipath, named Code Minus Carrier phase (CMC) (Hilla & Cline 2004; G. Wang et al. 2015). Since carrier phase multipath is directly related to the signal-to-noise ratio (SNR) in GNSS observations, SNR can be used to reflect the distribution of multipath errors. (Comp & Axelrad 1998; Bilich & Larson 2007; Zhang et al. 2019). When the surrounding environment of the station remains unchanged, GNSS multipath effects are the temporal repeatability, so Sidereal Filtering (SF) is popular and suitable for real-time multipath error mitigation.

The temporal repeatability is based on the factor that GNSS signal transmitted from the same satellite position to the same station have the same multipath effect if the station environment does not change. The period of the repeatability is the exact orbit repetition period (ORP) of each individual satellite. The SF model based on temporal repeatability mainly relies on the method of estimating the ORP and the model of extracting multipath errors. In order to better match the multipath errors of the two days before and after, the strategy of ORP estimation has been widely studied, such as a nominal sidereal day (Genrich & Bock 1992), the Orbital Repeat Time Method (ORTM) (Choi et al. 2004), the Aspect Repeat Time Adjustment (ARTM) (Axelrad et al. 2005; Agnew & Larson 2007), the Residual Correlation Method (RCM) (Ragheb et al. 2007), time series window matching (Shen et al. 2020) and the satellite orbit maneuver detection method (Zhou et al. 2023). For multipath model extraction, since wavelet technique can provide both time and frequency information of a signal, the Wavelet Transform (WT) is widely used in GNSS denoising and multipath errors extraction. Souza & Monico (2004) applied wavelet shrinkage method to reduce high frequency noise in DD residuals and verified that the wavelet basis function (SYM12) with the hard threshold has better positioning performance. Azarbad & Mosavi (2014) used stationary wavelet transform (SWT), soft threshold function and universal threshold to identify the multipath interference in DD residual. Lau (2017) applied three-level wavelet packets, the universal threshold and hard threshold function to retrieve the carrier phase multipath errors in DD residuals. Su et al. (2018) used the universal threshold and modified threshold function (Chen et al. 2017) to extract multipath errors in Single Difference (SD) residual. The SD SF model considers the ORP of each satellite rather than the satellite pair of DD observations, so multipath errors from observations in each satellite can be mitigated individually. Su et al. (2021) proposed an adaptive layer selection strategy and bootstrap search strategy based on carrier-power-to-noise density ratio (C/N0) constraints to enhance multipath extraction and mitigation in SD residual. However, considering the efficiency and accuracy of wavelet denoising, the number of decomposition layers is adaptively selected between 1 and 4. Srivastava et al. (Srivastava et al. 2016) analyzed low-frequency and high-frequency components of a continuous wave electron spin resonance (cw-ESR) spectrum after the WT and believed that the number of wavelet decomposition layers should be 5.

From the above analysis, most researchers in the GNSS community used WT as a tool for noise reduction and multipath error extraction in DD residuals or SD residuals. In practice, the process of the WT is related to wavelet decomposition levels, threshold functions and thresholds. Improper selection of the number of decomposition levels, threshold functions, and thresholds may result in the loss of useful signal or the introduction of significant noise in the reconstructed signal. However, no study has systematically assessed the performance of multipath effect mitigation in DD and SD residuals based on wavelet decomposition levels, wavelet thresholds and wavelet threshold functions. Up to now, there are still four main issues worth studying in the WT. (1) Multipath errors can be extracted by the WT from DD or SD residuals. Among DD and SD residuals, which one is more advantages for extracting and mitigating multipath errors. (2) It is well known that the higher the number of wavelet decomposition levels is set, the more obvious the WT denoising effect will be. However, if the number of wavelet decomposition layers is set too high, it will cause signal distortion. Thus, the choice of the number of wavelet decomposition levels is a trade-off between noise reduction and signal distortion. (3) There are four wavelet thresholds in the WT, namely sqtwolog, rigrsure, heursure and minimax. Which threshold provides the best denoising performance. (4) There are two commonly used threshold functions for quantized wavelet coefficients, namely hard and soft threshold function. Which one is more suitable for denoise and multipath error extraction. In this study, multipath errors in DD and SD residuals are extracted by the WT, and the multipath error mitigation effects of different wavelet decomposition levels, thresholds, and threshold functions are systematically studied.

The structure of this article is described as follows: firstly, the base principle of SF, the transformation model from DD residual to SD residual, WT, wavelet decomposition level, wavelet threshold and wavelet threshold function are introduced. Secondly, experimental analysis is conducted on multipath error extraction and mitigation at different wavelet decomposition levels, threshold functions and thresholds are presented. Finally, the conclusions are summarized.

Method

The principle of sidereal filtering

The principle of SF is to extract low-frequency components from the previous residual time series and use low-frequency components to establish a multipath correction model. The correction values from the multipath correction model are then subtracted from the residual time series for subsequent days. Finally, the residual time series after multipath error correction is obtained. The SF model in this study only handles Global Positioning System (GPS) observations. The processing steps of SF are shown in Fig. 1.

  1. 1.

    GPS observations on the first day are processed in static relative positioning mode. The post-fit DD pseudo-range and carrier phase residuals can be calculated by fixed integer ambiguities and baseline vectors.

  2. 2.

    Transform DD residuals to SD residuals using Eq. (7).

  3. 3.

    The multipath error in the SD residual time series is extracted by WT with different wavelet decomposition levels, wavelet thresholds and wavelet threshold functions, and a multipath correction model is constructed.

  4. 4.

    The ORP is estimated by the ORTM.

  5. 5.

    The values of the multipath model are subtracted from the SD residual time series for subsequent days.

  6. 6.

    The corrected SD residuals are converted into DD residuals and the baseline vector of the rover station for subsequent days is estimated in kinematic positioning mode which can reflect very slow displacements in the field of deformation monitoring.

Fig. 1
figure 1

Flowchart of sidereal filtering

Full size image

Obtaining SD residuals from DD residuals

The GNSS pseudo-range and carrier phase observation can be expressed as follows:

$$P_{k}^{s} \left( t \right) = \rho_{k}^{s} + c\left[ {dtr_{k} \left( t \right) - dts^{s} \left( t \right)} \right] + trop_{k}^{s} \left( t \right) + ion_{k}^{s} \left( t \right) + TGD_{P}^{s} + TGD_{k,P} + M_{k,P}^{s} \left( t \right) + \varepsilon_{k,P}^{s} \left( t \right)$$
(1)
$$\Phi_{k}^{s} \left( t \right) = \rho_{k}^{s} + c\left[ {dtr_{k} \left( t \right) - dts^{s} \left( t \right)} \right] + trop_{k}^{s} \left( t \right) - ion_{k}^{s} \left( t \right) + \lambda N_{k}^{s} + TGD_{\phi }^{s} + TGD_{k,\phi } + M_{k,\phi }^{s} \left( t \right) + \varepsilon_{k,\phi }^{s} \left( t \right)$$
(2)

wre, the superscript \(s\) denotes satellites; subscripts \(k\), \(P\) and \(\phi\) represent receiver, pseudo-range and carrier phase, respectively; \(t\) is the observed epoch. \(P_{k}^{s} \left( t \right)\). and \(\Phi_{k}^{s} \left( t \right)\) are pseudo-rang and carrier phase observations;\(\rho_{k}^{s}\) is the satellite-receiver geometric distance; \(c\) is the speed of light in vacuum; \(dtr_{k} \left( t \right)\) and \(dts^{s} \left( t \right)\) the receiver clock offset and satellite clock offset; \(trop_{k}^{s} \left( t \right)\) and \(ion_{k}^{s} \left( t \right)\) are the tropospheric delay and ionosphere delay; \(TGD^{s}\) and \(TGD_{k}\) are the time group delay (TGD) of satellite and receiver, respectively; \(\lambda\). and \(N_{k}^{s}\) are wavelength and integer aiguities, respectively; \(M_{k}^{s} \left( t \right)\) and \(\varepsilon_{k}^{s} \left( t \right)\) are multipath errors and random noise.

The DD technique is widely used to remove some common error terms, such as orbit error, satellite, receiver clock error, receiver and satellite hardware error etc. Since the short baseline is generally within 10 km, and the baseline between receivers A and B in our exment is less than 10 m, DD can also eliminate ionospheric and troposphericerrors. The DD observation equation can be simplified as follows:

$$d_{AB,P}^{ij} \left( t \right) = \nabla \Delta M_{AB,P}^{ij} \left( t \right) + \nabla \Delta \varepsilon_{AB,P}^{ij} \left( t \right)$$
(3)
$$d_{AB,\phi }^{ij} \left( t \right) = \nabla \Delta M_{AB,\phi }^{ij} \left( t \right) + \nabla \Delta \varepsilon_{AB,\phi }^{ij} \left( t \right)$$
(4)

where, \(d_{AB,P}^{ij} \left( t \right) = \nabla \Delta P_{AB}^{ij} \left( t \right) - \nabla \Delta \rho_{AB}^{ij}\) and \(d_{AB,\phi }^{ij} \left( t \right) = \nabla \Delta \Phi_{AB}^{ij} \left( t \right) - \nabla \Delta \rho_{AB}^{ij} - \lambda \nabla \Delta N_{AB}^{ij}\) are DD pseudo-range residual and carrier phase residual, respectively. The integer ambiguities \(\nabla \Delta N_{AB}^{ij}\) is fixed by the LAMBDA (Leastsquares AMBiguity Decorrelation) (Teunissen 1995). The DD observation residuals only include multipath errors and random noise. At this time, we can use wavelet transform to extract multipath errors, which can be used to correct the residual time series of subsequent days.

In order to simply describe the relationship between DD and SD observation residuals, the \(d_{AB,P}^{ij} \left( t \right)\) and \(d_{AB,\phi }^{ij} \left( t \right)\) are instead of \(d_{AB}^{ij}\) are uniformly represented by:

$$d_{AB}^{ij} = s_{A}^{ij} - s_{B}^{ij} = \left( {\Phi_{A}^{i} - \Phi_{A}^{j} } \right) - \left( {\Phi_{B}^{i} - \Phi_{B}^{j} } \right)$$
(5)

where, superscripts \(i\) and \(j\) denote Pseudo-Random Noise code (PRN); subscripts \(A\) and \(B\) represents receivers; \(d_{*}^{*}\) and \(s_{*}^{*}\) are DD and SD observations in meters (m), respectively; \(\Phi_{*}^{*}\) are pseudo-range and carrier phase observations in meters (m).

Equation (5) can be simplified to:

$$d = Ds$$
(6)

where, \(D\) is the differencing operator matrix which maps SD to DD observations.

Because DD technique needs to select a reference satellite with a higher elevation angle, if there are \(n\) SD observations, only \(n - 1\) linearly independent DD observations can be formed in Eq. (6). Therefore, the coefficient matrix \(D\) rank-defect. In order to have a \(D\) matrix with the inverse property, an additional constraint on SD observations needs to be added (Alber et al. 2000).

$$\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {w^{1} } \\ 1 \\ {\begin{array}{*{20}c} 1 \\ {\begin{array}{*{20}c} \cdots \\ 1 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {w^{2} } \\ { - 1} \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} \cdots \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {w^{3} } \\ 0 \\ {\begin{array}{*{20}c} { - 1} \\ {\begin{array}{*{20}c} \cdots \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \cdots \\ \cdots \\ {\begin{array}{*{20}c} \cdots \\ {\begin{array}{*{20}c} \cdots \\ \cdots \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {w^{n} } \\ 0 \\ {\begin{array}{*{20}c} 0 \\ {\begin{array}{*{20}c} \cdots \\ { - 1} \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {s_{{AB}}^{1} } \\ {s_{{AB}}^{2} } \\ {\begin{array}{*{20}c} {s_{{AB}}^{3} } \\ \cdots \\ {s_{{AB}}^{n} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\sum\nolimits_{{j = 1}}^{n} {w^{j} s_{{AB}}^{j} } } \\ {d_{{AB}}^{{12}} } \\ {\begin{array}{*{20}c} {d_{{AB}}^{{13}} } \\ {\begin{array}{*{20}c} \ldots \\ {d_{{AB}}^{{1n}} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]$$
(7)

where, \(\sum\nolimits_{{j = 1}}^{n} {w^{j} } s_{{AB}}^{j} = 0\) denotes the zero mean assumption of SD observations; \(w^{j}\) is the weighting factor determined using the elevation angle (Zhong et al. 2010).

$$w^{j} = sin^{2} \left( {\theta^{j} } \right)$$
(8)

where \(\theta^{j}\) denotes satellite elevation angle.

Orbit repeat time method

The ORTM based on broadcast parameters is the simplest method to estimate sidereal shifts (Axelrad et al. 2005). According to Kepler’s third law, the orbit period can be given by:

$$T = \frac{{2\pi r^{3/2} }}{{\sqrt {GM} }}$$
(9)

where \(T\) and \(r\) are the orbit period and the semi-major axis of the satellite orbit, respectively; \(GM = 3.986004418 \times 10^{14} m^{3} /s^{2}\) is the gravitational constant.

The ORP of a GPS satellite is twice its orbit period (Agnew & Larson 2007). Introducing the correction to the mean motion, the ORP can be expressed as:

$$T_{0} = 2T = \frac{4\pi }{{n_{0} + n_{c} }} = \frac{4\pi }{{\sqrt {GM} r^{ - 3/2} + n_{c} }}$$
(10)

where, \(T_{0}\) is the ORP; \(n_{0}\) and \(n_{c}\) are the mean motion and the correction to the mean motion, respectively.

The daily advance time or shift can be given by:

$$T_{a} = 86400 - T_{0}$$
(11)

where, \(T_{a}\) and \(86400\) are daily advance and a GPS day, respectively.

Wavelet denoise

The essence of wavelet denoising is to suppress the useless parts of the signal and enhance the useful parts. The principle of wavelet denoising mainly includes three steps. First, the signal is decomposed by wavelet orthogonal basis; then, the threshold is set to remove high-frequency components; finally, wavelet coefficients can used to reconstruct the signal. In detail, the processing steps of wavelet denoising are listed in the Fig. 2 as following:

  1. 1.

    Decomposition: Choose a wavelet basis function and \(N\) levels to decompose the signal.

  2. 2.

    Threshold processing: After decomposition, select an appropriate threshold and use the threshold function to modify the wavelet coefficients of each level.

  3. 3.

    Wavelet reconstruction: Reconstruct the signal by processing the modified wavelet coefficients to obtain a denoised signal.

Fig. 2
figure 2

The Wavelet denoising process

Full size image

Wavelet transform

The continuous WT is an inner product of the signal and the wavelet basis functions. The continuous WT of the signal can be calculated as (Daubechies 1992):

$$W_{j} \left( {a,b} \right) = \langle x,\Psi _{{a,b}} \rangle = \frac{1}{{\sqrt a }}\int_{{ - \infty }}^{{ + \infty }} x \left( t \right)\Psi \left( {\frac{{t - b}}{a}} \right)dt$$
(12)

where subscript \(j\) denotes the decomposition level of signal; \(W_{j} \left( {a,b} \right)\) is wavelet coefficients, \(x\left( t \right)\) is the signal; \(\Psi \left( {\frac{t - b}{a}} \right)\) is the wavelet basis function; \(a\) and \(b\) are dilation and translation parameters \(\left( {a,b \in R,{ }a \ne 0} \right)\), respectively; \(\langle *,*\rangle\) represents inner product operation.

In practical signal processing, the signal is sampled at a limited number of epoch points, so continuous WT needs to be discretized. Considering the computational efficiency, choices of dilation and translation parameters are \(a = 2^{ - i}\) and \(b = k2^{ - i}\). The discrete WT can be defined as the following form (Mallat 1999).

$$\Psi_{i,k} \left( t \right) = 2^{i/2} \Psi \left( {2^{i} t - k} \right)$$
(13)

where, \(i\) and \(k\) are integers greater than 0.

Wavelet decomposition level

In the WT, the number of decomposition levels is a key factor affecting the performance of wavelet denoising. The number of decomposition levels determines how denoised the signal is. In general, when the WT is performed, the signal is subjected to multiple iterations of low-pass filtering and high-pass filtering. The low frequency components are used as input for the next iteration. Each iteration produces both low- and high-frequency components, as shown in Fig. 3.

Fig. 3
figure 3

The process of WT, X denotes signal; cA* and cD* denote the approximation coefficient vector (low-frequency) and detailed coefficient vector (high-frequency) of the *-th decomposition level, respectively

Full size image

Wavelet threshold function

A threshold function is used to correct the wavelet coefficients at each decomposition level. In the process of wavelet denoising, different threshold functions reflect different processing strategies for wavelet coefficients. There are two common threshold functions, namely hard and soft threshold.

Hard thresholding refers to setting the coefficients to zero when the absolute value of the wavelet coefficients is lower than the threshold. The hard threshold can be written as follows:

$$\hat{W} = \left\{ {\begin{array}{*{20}c} {W,\left| W \right| \ge \lambda } \\ {0,\left| W \right| < \lambda } \\ \end{array} } \right.$$
(14)

Soft threshold is refined based on hard threshold. When the absolute value of the wavelet coefficients is greater than the threshold, these coefficients should shrink towards zero. Soft threshold can be expressed as (Donoho 1995):

$$\hat{W} = \left\{ {\begin{array}{*{20}c} {\left[ {sign\left( W \right)} \right]\left( {\left| W \right| - \lambda } \right),{ }\left| W \right| \ge \lambda } \\ {0,\left| W \right| < \lambda } \\ \end{array} } \right.$$
(15)

where, \(\hat{W}\) and \(\lambda\) are the quantized wavelet coefficients and wavelet threshold, respectively; \(sign\) is signum function.

Wavelet threshold

The choice of wavelet threshold is crucial to the effect of signal denoising. There are four well-known threshold estimation methods based on noise models. Here is a brief introduction to these threshold estimation methods.

Sqtwolog

Donoho & Johnstone (1994) proposed the sqtwolog threshold method, also known as the universal threshold. The threshold method is proportional to the standard deviation of the noise. The universal threshold can be expressed as:

$$\lambda_{j} = \sigma_{j} \sqrt {2\log \left( {N_{j} } \right)}$$
(16)

where, superscript \(j\) denotes the decomposition level of signal; \(\sigma_{j}\) and \(N_{j}\) are the standard deviation of noise and signal length, respectively.

In practical GNSS positioning applications, a priori knowledge of the standard deviation of noise in the GNSS station environment is not available. Since WT can separate low-frequency and high-frequency components from the residual time series, the standard deviation of noise can be estimated by the wavelet coefficients in each decomposition level. The method for estimating the standard deviation of noise can be written as:

$$\sigma_{j} = \frac{{MAD_{j} }}{0.6745} = \frac{{median\left\{ {\left| {W_{j} } \right|} \right\}}}{0.6745}$$
(17)

where, \(MAD_{j}\) denotes the median absolute deviation of the wavelet coefficients.

Rigrsure

This threshold selection is based on Stein’s unbiased risk estimate. In this threshold method, the risk vector can be estimated as follows (Donoho & Johnstone 1995):

$$Risk_{j}^{k} = \frac{{N_{j} - 2k + \mathop \sum \nolimits_{i = 1}^{k} S_{j}^{i} + \left( {N_{j} - k} \right)S_{j}^{k} }}{{N_{j} }}$$
(18)
$$m = min\left\{ {Risk_{j}^{1} \cdots Risk_{j}^{k} \cdots Risk_{j}^{{N_{j} }} } \right\}$$
(19)
$$\lambda_{j} = \sqrt {S_{j}^{m} }$$
(20)

where, \(Risk_{k}^{j}\) denotes the \(k\) th \(\left( {k = 1 \cdots N_{j} } \right)\) risk vector; \(S_{k}^{j}\) is the square of the wavelet coefficient, sorted from small to large; the subscript \(m\) corresponds to the minimum value of the risk vector.

Heursure

The heursure threshold selection is a combined threshold of the sqtwolog and rigrsure thresholds. The heursure threshold rule determines whether to select a sqtwolog or rigrsure threshold by comparing the values of the variables \(\beta\) and \(\gamma\) (Mallat et al. 1992).

$$\beta = \frac{{\mathop \sum \nolimits_{i = 1}^{{N^{j} }} \left| {W_{i} } \right|^{2} - N^{j} }}{{N^{j} }}$$
(21)
$$\gamma = \sqrt {\frac{1}{{N^{j} }}\left( {\frac{{lnN^{j} }}{ln2}} \right)^{3} }$$
(22)
$$\lambda ^{j} = \left\{ {\begin{array}{*{20}l} {Sqtwolog,} \hfill & {\beta < \gamma } \hfill \\ {min\left( {Sqtwolog,Rigrsure} \right),} \hfill & {\beta \ge \gamma } \hfill \\ \end{array} } \right.$$
(23)

If \(\beta\). is less than \(\gamma\), the threshold takes the sqtwolog value, otherwise the threshold takes the smaller one of the rigrsure threshold and the sqtwolog threshold.

Minimax

This thresholding method is used in statistics to design estimators. The minmax estimator can obtain the minimum mean square error given a set of maximum mean square error functions. In other words, this threshold can produce the minimum variance (Verma & Verma 2012). This threshold can be expressed as (Johnstone & Silverman 1997):

$$\lambda ^{j} = \left\{ {\begin{array}{*{20}l} {0,{\text{ }}N^{{j \le }} 32} \hfill \\ {\sigma ^{j} \left( {0.3936 + 0.1829\frac{{\ln N^{j} }}{{\ln 2}}} \right),N^{j} > 32} \hfill \\ \end{array} } \right.$$
(24)

Experiment and analysis

DD residual and SD residual analysis

In order to further analyze the transform relationship between DD residuals and SD residuals, the GNSS dual-frequency (L1 and L2) datasets of Curtin University rooftop stations CUT0 and CUTA are recorded into Receiver Independent Exchange Format (RINEX) files. GPS datasets from Days Of Year (DOY) 16–17 in 2018 is used in the experiment, with a sampling interval of 1 Hz. The CUT0 is reference station, and the baseline length between stations CUT0 and CUTA is approximately 8.42 m, which is an ultra-short baseline. The reference station and rover station are equipped with TRIMBLE NETR9 receivers, which can obtain unfiltered and unsmoothed measurement data. Since the surrounding environment of stations of CUT0 and CUTA remains unchanged and atmospheric errors can be considered to be eliminated by DD observations, the SF can be used to mitigate the multipath errors.

To ensure that this study is convincing, observation data are processed in single-epoch kinematic mode using RTK technology. The cutoff elevation angle of the satellites is set to 10°. In order to illustrate the relationship between DD residuals, SD residuals and satellite elevation angles, the residual time series of a high-elevation angle satellite and a low-elevation angle satellite are shown in Fig. 4, respectively. It is seen from Fig. 4 that the trend change of SD residual is consistent with that of DD residual. Within the elevation angle range of 40°–50° for the satellite PRN27, SD residuals are significantly smaller than DD residuals, as shown in Fig. 4(a). However, within the elevation angle range of 10°–20°, the changes in SD residuals are almost consistent with those in DD residuals. The maximum elevation angle of satellite PRN31 is only about 40°, and difference between the SD residual and DD residual of satellite PRN31 is not obvious. The main reason is to convert DD residuals into SD residuals using the elevation angle dependent weighting model in Eq. (8). Since the elevation angle of satellite PRN27 reaches the maximum value of all visible satellites between 10,000 and 14,000 epochs, the satellite PRN27 is selected as the reference satellite. It is worth pointing out that RTK technology selects the highest elevation angle as the reference satellite in each observation epoch to minimize the effect of multipath errors on positioning. Therefore, DD residual of satellite PRN27 does not exist between 10,000 and 14,000 epochs. Figure 5 shows that the Root Mean Square (RMS) of DD residuals and SD residuals for each satellite. It can be seen from Fig. 5 that the RMS of SD residuals is significantly better than DD residuals. This also indirectly illustrates the reliability of transforming DD residuals into SD residuals model and the feasibility of multipath mitigation based on SD residuals.

Fig. 4
figure 4

Relationship between SD and DD residual time series, a satellite PRN27 L1 frequency and b satellite PRN31 L1 frequency

Full size image
Fig. 5
figure 5

The RMS of DD residuals and SD residuals for each satellite

Full size image

Wavelet denoising analysis

In order to demonstrate the effect of wavelet denoising, the WT is performed on the SD residual time series of satellites PRN27 and PRN31. The parameters of common WT are given in Table 1. Figure 6 shows that the SD residual time series before and after wavelet denoising processing. As can be seen from Fig. 6, the WT separates the high-frequency components and low-frequency components in the SD residual time series, which can achieve perfect denoising effect. The value range of the low-frequency component is − 15 mm to 15 mm, which is less than the theoretical value of the multipath error (1/4 wavelength). This phenomenon is consistent with the analysis results of Zhang et al. (2023). The essence of wavelet transform indeed could extract all time-related signals. Besides multipath errors studied in this paper, our method could also extract other time-correlated signals exist in short-baseline double-differenced observation residuals. However, the other time-correlated signals can be effectively eliminated if they repeat according to the orbital period. If the other time-related signals are occurred by chance, they will be introduced into the next day’s multipath error correction. When the data from consecutive days is processed by the wavelet transform, the influence of the chanced other time-correlated signals could be reduced. Therefore, what we extract mainly belongs to the multipath effect. In this study, we do not further discuss the performance of the WT in extracting multipath errors from the SD residual time series. Multipath effects in the residual time series actually depend on various GNSS signals and receiver parameters, such as signal type, modulation mode, pre-correlation bandwidth and filter characteristics, relative power levels of multipath signals, chipping rate of code, geometric path delay (short-delay or long-delay multipath), actual number of multipath signals, type of discriminator and chip spacing between correlators (Irsigler et al. 2004).

Table 1 Detailed common WT parameters
Full size table
Fig. 6
figure 6

Residual time series before and after the wavelet transform processing, a PRN27 L1 frequency b PRN31 L1 frequency

Full size image

The estimation of orbital repeat period

Since satellite orbital parameters in broadcast ephemeris are spaced two hours apart (sometimes slightly less than two hours for individual satellites), the ORP is estimated every two hours on the first day. These estimated ORPs are averaged as the final ORP for each satellite. In order to illustrate the ORP difference for each satellite, the mean sidereal shift for each day over 10 consecutive days is calculated, as shown in Fig. 7. The mean sidereal shift of satellite PRN21 is approximately 240 s which is the smallest of all satellites. The mean sidereal shift of satellite PRN6 is the largest, reaching about 250 s. Although the maximum and minimum values differ by 10 s, the mean sidereal shift of satellites PRN6 and PRN21 does not exceed the normal range of 235–255 s. It should be noted that the normal range of the ORP is 86,145–86165 s (M. Wang et al. 2018). Figure 8 presents the mean difference in sidereal shift of GPS satellite for two consecutive days from DOY 10 to 19, 2018. The mean absolute difference in sidereal shift for all satellites for two consecutive days is less than 0.6 s. These results indicate that there is no satellite maneuver during DOY 10 to 19, 2018, which makes sidereal filtering feasible for multipath mitigation.

Fig. 7
figure 7

The mean sidereal shift for each GPS satellite from DOY 10–19, 2018

Full size image
Fig. 8
figure 8

The mean difference in sidereal shift of GPS satellite for two consecutive days from DOY

Full size image

The performance analysis of the DD SF and SD SF

In order to further compare the superiority of DD residuals and SD residuals in mitigating multipath errors, the SF is performed on the data of visible GPS satellites on DOY 17, 2018. Figure 9 shows the positioning results of the original, DD SF and SD SF in the east, north, and up directions. It can be clearly seen that the positioning performance of the DD SF and SD SF is significantly better than the original. In particular, due to the serious multipath error in residuals from epochs 1334 s to 1391 s in the east direction, the GPS ambiguity cannot be successfully fixed and the positioning error even reaches about 28 mm. Fortunately, the DD SF and SD SF can effectively mitigate multipath errors, so the receiver position can achieve a fixed ambiguity solution from epoch 1334 s to 1391 s in the east direction and the positioning error is only about 9 mm. The power spectrum analysis of the residual time series of the original, DD SF and SD SF is shown in Fig. 10. The power spectrum results show that the multipath error of the low-frequency components of the DD SF and SD SF is significantly reduced. In the high-frequency components, the power spectral densities of the original, DD SF and SD SF almost maintain similar fluctuation levels.

Fig. 9
figure 9

Residual time series before and after sidereal filtering

Full size image
Fig. 10
figure 10

Power spectrum density of residual time series before and after sidereal filtering.10–19, 2018

Full size image

The RMS of positioning errors of the original, DD SF and SD SF is listed in Table 2. The RMS of the DD SF in the east, north and up direction are improved by about 29.46%, 7.85% and 12.20% respectively, but are slightly lower than SD SF, which is consistent with the analysis results of Zhong et al. (2010). Table 3 lists ambiguity success rates of the original, DD SF and SD SF. We can see from Table 3 that the ambiguity success rate of the DD SF and SD SF is increased by about 1.24%, among which the success rate of the SD SF is slightly higher than that of DD SF. The ambiguity success rate of SD SF is as high as 99.51%.

Table 2 RMS statistics of positioning results of the original, DD SF and SD SF
Full size table
Table 3 Fixed rates of ambiguity resolution of the original, DD SF and SD SF at station CUTA
Full size table

The performance analysis of wavelet decomposition levels, threshold functions and thresholds

Based on the above experimental analysis, the results show that the positioning performance of the SD SF is better than that of DD SF. Therefore, in the following experiments, the analysis of the multipath error extraction effect of the WT at different decomposition levels, threshold functions and thresholds is based on the SD SF model. GPS dual-frequency observations from CUT0, CUTA, CUTB and CUTC stations on the roof of Curtin University are used to analyze the multipath mitigation impact of the WT at different decomposition levels, threshold functions and thresholds. The dataset from DOY16 to 17 in 2018 was recorded at a sampling interval of 1 Hz. The satellite elevation cutoff angle is set to 10°. The CUT0 is reference station and the other stations are rover stations. The baseline lengths of CUT0 to CUTA, CUTB and CUTC are approximately 8.42 m, 4.27 m and 7.99 m, respectively.

In order to describe the relationship between the selection of the number of wavelet decomposition levels and the effect of multipath error extraction, the SD residual time series of satellite PRN2 is subjected to WT processing at 1–10 decomposition levels, as shown in Fig. 11. It can be seen from Fig. 11 that as the number of wavelet decomposition levels is increased, the noise of SD residual is significantly reduced. When the wavelet is decomposed into levels 1 to 6, the WT only performs denoising, and the low-frequency multipath error does not change significantly. However, when the number of wavelet decomposition levels is reached 7, the low frequency multipath error has been slightly distorted at about epoch 2000s. When the number of wavelet decomposition levels is greater than 7, the distortion of the low frequency multipath error is serious. This phenomenon is consistent with the characteristics of wavelet decomposition. Therefore, the number of optimal decomposition level for the WT of SD residual time series may be 6. Table 4 lists the explanations of different types of abbreviations and.

Fig. 11
figure 11

The residual time series of satellite PRN2 after WT at different decomposition levels, a Level 1–5 b Level 6–10, unit(mm)

Full size image
Table 4 Description of different types of acronyms
Full size table

Table 5 represents the RMS of satellite PRN2 after WT at different decomposition levels. In Table 5, the positioning accuracy of wavelet decomposition at level 6 is 17.83% higher than that of traditional decomposition level (level 3). Due to space limitations, the SD residual time series of other satellites after WT processing of levels 1–10 are not presented here.

Table 5 Statistics of the RMS of satellite PRN2 after WT at different decomposition levels, unit(mm)
Full size table

In order to further investigate the impact of wavelet decomposition levels on multipath error extraction and mitigation, Fig. 12 shows the RMS of positioning error of the WT at decomposition levels from 1 to 10 for each wavelet threshold. As the number of wavelet decomposition levels increases, the RMS of the heursure, sqtwolog and minimax thresholds in the hard threshold function first decreases and then increases, but this change trend of rigrsure threshold is not obvious, as shown in Fig. 12(a). As can be seen from Fig. 12(b), the RMS change trend of the four thresholds in the soft threshold function is more significant than that in the hard threshold function. In hard and soft threshold function, the RMS of rigrsure, heursure, sqtwolog and minimax thresholds at level 6 is the smallest among levels 1 to 10 of wavelet decomposition. This result is consistent with the previous analysis.

Fig. 12
figure 12

The RMS of positioning error of the WT at decomposition levels from 1–10 for each wavelet threshold, a hard threshold function, b soft threshold function

Full size image

In order to further investigate the impact of wavelet thresholds on multipath error extraction and mitigation, Fig. 13 shows the RMS of the positioning error for four thresholds of the WT at each decomposition level. In Fig. 13, in the east direction of CUTA and CUTC stations, it can be clearly seen that the RMS of the positioning error of the four wavelet thresholds in the hard and soft function is significantly reduced compared with the original positioning. This is because there are walls to the south and east, so the multipath effect is significant. However, in the east direction of CUTB station, the positioning accuracy of the rigrsure threshold in the hard threshold function is slightly better than the original positioning, as shown in Fig. 13(a). In the north direction of CUTA station, the RMS of the positioning error of the rigrsure threshold in the soft function is smaller than the original positioning, while the RMS in the hard function is larger than the original positioning. This may indicate that the rigrsure threshold is more suitable for soft threshold function. When the wavelet decomposition level is 1, in the north and up direction of three stations, the positioning accuracy of four thresholds in the hard and soft threshold is almost not improved compared with the original positioning. This is because the number of decomposition levels is too small, resulting in an insignificant effect of wavelet denoising. The positioning performance of the heursure and sqtwolog thresholds is better that that of the rigrsure and minimax thresholds. This is because all wavelet coefficients need to be processed in the heursure and sqtwolog thresholds to achieve a more ideal denoising effect. However, the rigrsure and minimax thresholds only handle a few coefficients, which is a compromised approach.

Fig. 13
figure 13

The RMS of the positioning error for four thresholds of the WT at each decomposition level a hard threshold function, b soft threshold function

Full size image

Figure 14 shows the improvement rate of the positioning performance for four wavelet thresholds at each decomposition level. When the number of wavelet decomposition levels is between 1 and 6, as the wavelet decomposition level is increased, the improvement rate of the positioning performance of four thresholds is also gradually increased. Especially, in the east direction of CUTA station, when the wavelet decomposition level reach 6, the improvement rates of the positioning performance of the rigrsure, heursure, sqtwolog and minimax thresholds in thehard threshold function are 20.92%, 31.20%, 31.41% and 29.75% compared with the original positioning. The corresponding improvement rates of the positioning performance in the soft threshold function are 29.72%, 32.37%, 32.36% and 26.19%, respectively. When the number of wavelet decomposition level in the soft threshold function reaches 10, the improvement rates of the positioning performance of the rigrsure threshold is significantly better than other thresholds. This shows that the ability of the rigrsure threshold to suppress waveform distortion is better than other thresholds, which is consistent with the results of Luo et al. (2021). In the soft threshold function, when the number of wavelet decomposition level is less than 6, the improvement rate of the positioning performance of the sqtwolog threshold is almost the same as that of the heursure threshold. However, when the number of wavelet decomposition levels is greater than 6, the positioning performance of the heursure threshold is better than that of the sqtwolog threshold. This is because the heursure threshold inherits the properties of the rigrsure threshold. Table 6 and Table 7 respectively list the average improvement rate of the four thresholds in the hard threshold function and soft threshold function of the three stations. In the north direction, the positioning performance of the rigrsure threshold in the hard threshold function is worse than the original positioning. As can be seen from Table 6 and Table 7, except for rigrsue threshold in hard threshold function, the average improvement rate of other threshold in the optimal decomposition level ( 6th level) is increased about 2% compared with that in traditional decomposition level (3th level).

Fig. 14
figure 14

The improvement rate of positioning performance of the WT for four wavelet thresholds at each decomposition level, a hard threshold function, b soft threshold function

Full size image
Table 6 the average improvement rate of four thresholds in the hard threshold function
Full size table
Table 7 the average improvement rate of four thresholds in the soft threshold function
Full size table

From the previous experimental analysis, we can know that the positioning performance of heursure and sqtwolog thresholds is better than rigrsure and minimax thresholds. In order to further study the impact of the wavelet threshold function on multipath error extraction and mitigation, the RMS of the positioning error for heursure and sqtwolog thresholds is analyzed, as shown in Fig. 15. It is obvious that the positioning performance of heursure and sqtwolog thresholds in the soft threshold function is slightly better than that in the hard threshold function. This is because the soft threshold function is refined based on the hard threshold function, making the soft threshold function more suitable for extracting GNSS multipath errors.

Fig. 15
figure 15

The RMS of positioning error of WT with different threshold function in each decomposition level, a Sqtwolog threshold, b Heursure threshold

Full size image

Conclusion

In complex urban environments, the multipath effect is the bottleneck for GNSS to achieve millimeter-level high-precision positioning. The SF based on the temporal repeatability can effectively mitigate multipath errors. The SF mainly includes two parts: ORP estimation and multipath error extraction. For estimating ORP, ORTM is the simplest and easiest to implement method. Since wavelet technology can denoise on signals, it is widely used in GPS multipath error extraction.

In order to extract multipath errors more accurately, we systematically analyzed the performance of multipath error mitigation in DD and SD residuals based on different wavelet decomposition levels, thresholds and threshold functions. GPS dual-frequency observation data from CUT0, CUTA, CUTA and CUTC stations on the roof of Curtin University were used for experimental analysis. The experimental results are summarized below.

  1. 1.

    In order to further compare the superiority of DD residuals and SD residuals in mitigating multipath errors, the SF was performed on the GPS observations of CUTA station on DOY 17, 2018. The result shows that the DD SF and SD SF can effectively mitigate multipath errors. The RMS of the DD SF in the east, north and up direction is improved by about 29.46%, 7.85% and 12.20% respectively, but are slightly lower than SD SF. The ambiguity fixed success rate of the DD SF and SD SF is increased by about 1.24%, among which the success rate of the SD SF is slightly higher than that of DD SF.

  2. 2.

    GPS dual-frequency observations from CUT0, CUTA, CUTB and CUTC stations on the roof of Curtin University are used to analyze the multipath mitigation impact of the WT at different decomposition levels, threshold functions and thresholds. (1) For wavelet decomposition levels, in hard and soft threshold function, the RMS of rigrsure, heursure, sqtwolog and minimax thresholds at level 6 is the smallest among levels 1 to 10 of wavelet decomposition. Especially, in the east direction of CUTA station, when the wavelet decomposition level reach 6, the improvement rates of the positioning performance of the rigrsure, heursure, sqtwolog and minimax thresholds in the hard threshold function are 20.92%, 31.20%, 31.41% and 29.75%, respectively. The corresponding improvement rates of the positioning performance in the soft threshold function are 29.72%, 32.37%, 32.36% and 26.19%, respectively. (2) For wavelet threshold, the positioning performance of the heursure and sqtwolog thresholds is better that that of the rigrsure and minimax thresholds. In the soft threshold function, when the number of wavelet decomposition level is less than 6, the improvement rate of the positioning performance of the sqtwolog threshold is almost the same as that of the heursure threshold. However, when the number of wavelet decomposition levels is greater than 6, the positioning performance of the heursure threshold is better than that of the sqtwolog threshold. (3) For threshold function, in order to further study the impact of the wavelet threshold function on multipath error extraction and mitigation, the RMS of the positioning error for heursure and sqtwolog thresholds is analyzed. The positioning performance of heursure and sqtwolog thresholds in the soft threshold function is slightly better than that in the hard threshold function.