Introduction

With the development of industries such as autonomous driving and the Internet of Things, there is increasing demand from the general public for high-precision GNSS location services (Jingnan et al. 2020; Yang et al. 2020). However, affected by electromagnetic signal interference, multipath effects, low signal-to-noise ratio, etc. Especially for dynamic low-cost single-frequency mass users, frequent cycle slips are prone to occur. If not handled properly, these slips will have an unpredictable impact on user positioning performance (Leick et al. 2015; Li et al. 2019; Li et al. 2022; Zhang et al. 2023).

The research on cycle slip detection and repair algorithms can be traced back to the 1980s (Bastos and Landau 1988) and remains a hot topic in the field of GNSS today. It can be broadly divided into three categories: single-frequency, dual-frequency, and triple-frequency cycle slip detection algorithms. In terms of cycle slip detection and repair of low-cost single station single frequency receivers, traditional methods include the between-epoch high-order phase difference method, polynomial fitting method, Doppler-aided method, pseudorange and phase combination method, posterior gross error detection method, and odomter aided time-differenced and satellite-differenced method. The between-epoch high-order phase difference method uses the difference between adjacent epochs in carrier phase data to detect cycle slips, but it also amplifies random noise. This method has weak detection capabilities for small and continuous cycle slips and has a time delay, which is not conducive to real-time application (Hofmann-Wellenhof et al. 2007). The polynomial fitting method evaluates discrepancies between the polynomial and carrier phase time series, making it less susceptible to noise compared to the between-epoch high-order phase difference method. However, this method requires normal historical observations within a fitting window, and determining the appropriate window length and polynomial order can be challenging. Additionally, it cannot reliably detect small cycle slips (de Lacy et al. 2008; Xu 2007). The Doppler method utilizes the relationship between Doppler observations and phase observations to construct cycle slip detection terms, but the ability to detect small cycle slips is also weak (Carcanague 2012; Lee et al. 2003; Zhao et al. 2020). The pseudorange phase combination method utilizes pseudorange and phase observations to construct a cycle slip term, eliminating the influence of a large number of errors. However, it is not sensitive to small cycle slips due to the influence of pseudorange noise (Collin and Warnant 1995; Habrich 2000). The posterior gross error detection method considers phase observations with cycle slips as gross errors, but when there are multi-dimensional gross errors, it is easy for gross error transfer to occur, leading to detection failure (Kirkko-Jaakkola et al. 2009; Li et al. 2022; Odijk and Verhagen 2007; Soon et al. 2008; Teunissen 1998; Yang et al. 2014). The between-epoch and between-satellite differenced method leverages INS for position constraints, utilizes satellite-differenced to eliminate clock error term, and constructs a cycle slip detection term based on time-differenced carrier phase (TDCP) equation (Feng 2022; Kim et al. 2015). However, selecting an appropriate reference satellite presents a challenge, especially in environments prone to frequent partial occlusion. Designing reliable algorithms for detecting and repairing small and continuous cycle slips in single-station single-frequency GNSS data with strong detection capabilities and unaffected by multi-dimensional gross errors is still challenging.

Compared to extensive research on cycle slip detection, there has been limited research on the clock speed characteristics of GNSS receivers, and some scholars model the clock speed as a first-order Gauss-Markov process (Wu 2010; Yu et al. 2014) or a random walk process (Brown and Hwang 1997). For different receivers, their clock speed characteristics are inconsistent. Therefore, it is necessary to assess their clock speed characteristics before applying them to ensure their suitability for use.

At the same time, autonomous vehicles have entered the stage of mass production. They are equipped with GNSS receivers for global positioning and other sensors for local positioning, including wheel Odometry sensors, low-cost cameras, inertial navigation equipment, and so on (Qin et al. 2021). Recently, local positioning methods have been developed (Campos et al. 2021; Mourikis and Roumeliotis 2007; Qin et al. 2018) and various low-cost odometry have achieved impressive dead reckoning accuracy of about 1%, i.e., a divergence error of about 1 m for a 100-m journey (Geiger et al. 2012). With the maturity and widespread application of the odometry software and hardware, the cost of obtaining high-precision vehicle position increments between epochs has become lower.

In this study, we propose a cycle slip detection and repair method that uses additional position increment (Delta_POS) and clock error increment (Delta_CLK) constraints. The method relies on eliminating or modeling time-related terms in the GNSS observation equation. After solving the traditional Time Difference Carrier Phase (TDCP) equation, Delta_POS and Delta_CLK are considered respectively. Delta_POS is provided by odometry, while Delta_CLK is predicted using a random walk process. The proposed method adds Delta_POS and Delta_CLK constraints to the TDCP equation to better detect cycle slips in complex environment and maintain the continuity of cycle slip detection. By doing so, the performance of cycle slip detection will only depend on the relationship between cycle slip level and other unmodeled noise levels.

In “Methodology”, section we introduce the cycle slip detection method and technical flow. In “Experiments and results”, section we conduct experiments using three sets of public datasets and three sets of self-collected datasets to comprehensively evaluate the cycle slip detection algorithm proposed in this study. Finally, the research contributions are summarized in “Conclusion” section.

Methodology

The technical flow chart is presented in Fig. 1. Initially, we employ the traditional TDCP algorithm to calculate the Delta_POS and Delta_CLK. The accumulated Delta_POS are aligned with the odometer’s trajectory to complete initialization. Next, a cycle slip detection term (DT) is constructed by combining the predicted Delta_CLK and the Delta_POS provided by the odometer, and the theoretical accuracy of the DT is also derived. Finally, a TDCP method with additional Delta_POS and Delta_CLK constraints was proposed.

Fig. 1
figure 1

Technical flow chart of cycle slip detection

Full size image

Initialization

A carrier phase observation in the cycles can be expressed as:

$$\begin{gathered} \phi = \frac{1}{\lambda }[\rho - I + T] + \frac{1}{\lambda }(dt_r - dt^s ) + N + \varepsilon_\phi \hfill \\ \, \hfill \\ \end{gathered}$$
(1)

where \(\phi\) is the phase observation, \(\varepsilon_\phi\) is its corresponding random noises. \(\rho\), \(I\) and \(T\) are the satellite-receiver geometric range, the ionospheric delay, and the tropospheric delay. \(dt_r\) and \(dt^s\) are the clock errors of the receiver and satellite. \(N\) is the ambiguity with wavelength \(\lambda\).

By subtracting the phase observations between two adjacent epochs \(t_{k + 1}\) and \(t_k\), the TDCP measurement (in cycles) can be formulated as follows (Soon et al. 2008; Sun et al. 2020):

$$\begin{aligned} \Delta \phi & = \phi_{t_{k + 1} } - \phi_{t_k } \\ & = \left[ {\frac{1}{\lambda }[\rho - I + T] + \frac{1}{\lambda }(dt_r - dt^s ) + N + \varepsilon_\phi } \right]_{t_{k + 1} } - \left[ {\frac{1}{\lambda }[\rho - I + T] + \frac{1}{\lambda }(dt_r - dt^s ) + N + \varepsilon_\phi } \right]_{t_k } \\ & = \frac{1}{\lambda }(\rho_{t_{k + 1} } - \rho_{t_k } ) + \frac{1}{\lambda }(dt_{r,t_{k + 1} } - dt_{r,t_k } ) + \varepsilon_{\Delta \phi } = \frac{1}{\lambda }\Delta \rho_{t_{k + 1} } + \frac{1}{\lambda }\Delta dt_{r,t_{k + 1} } + \varepsilon_{\Delta \phi } \\ \end{aligned}$$
(2)

where the symbol \(\Delta\) denotes the between-epoch difference operator, \(\Delta \phi\) denotes the change in phase observation, \(\Delta dt_{r,t_{k + 1} }\) is the change in \(dt_r\), \(\Delta \rho_{t_{k + 1} }\) is the change in \(\rho\), and \(\varepsilon_{\Delta \phi }\) represents the residual error due to changes in errors in the satellite clock, satellite position, ionospheric, tropospheric, multipath, and receiver noise between epochs and are considered to be negligible within a short time. Furthermore, \(\Delta \rho_{t_{k + 1} }\) can be expressed as follows:

$$\begin{aligned} \Delta \rho_{t_{k + 1} } & = \rho_{t_{k + 1} } - \rho_{t_k } = \left| {{\bf{p}}_{s_{k + 1} }^e - {\bf{p}}_{r_{k + 1} }^e } \right| - \left| {{\bf{p}}_{s_k }^e - {\bf{p}}_{r_k }^e } \right| \\ \, & = {{\varvec{e}}}_{k + 1}^{\,} \cdot ({\bf{p}}_{s_{k + 1} }^e - {\bf{p}}_{r_{k + 1} }^e ) - {{\varvec{e}}}_k^{\,} \cdot ({\bf{p}}_{s_k }^e - {\bf{p}}_{r_k }^e ) \\ \, & = {{\varvec{e}}}_{k + 1}^{\,} \cdot ({\bf{p}}_{s_k }^e + \Delta {\bf{p}}_{s_{k + 1} }^e - {\bf{p}}_{r_k }^e - \Delta {\bf{p}}_{r_{k + 1} }^e ) - {{\varvec{e}}}_k^{\,} \cdot ({\bf{p}}_{s_k }^e - {\bf{p}}_{r_k }^e ) \\ \, & = ({{\varvec{e}}}_{k + 1}^{\,} - {{\varvec{e}}}_k^{\,} ) \cdot ({\bf{p}}_{s_k }^e - {\bf{p}}_{r_k }^e ) + {{\varvec{e}}}_{k + 1}^{\,} \cdot ( - \Delta {\bf{p}}_{r_{k + 1} }^e + \Delta {\bf{p}}_{s_{k + 1} }^e ) \\ \end{aligned}$$
(3)

where the superscript \(e\) denotes Earth-Centered Earth-Fixed (ECEF) coordinate system. \({\bf{p}}_{s_{k + 1} }^e\) and \({\bf{p}}_{s_k }^e\) are the satellite position vectors in ECEF at time \(t_{k + 1}\) and \(t_k\). \({\bf{p}}_{r_{k + 1} }^e\) and \({\bf{p}}_{r_k }^e\) are the receiver position vectors in ECEF at time \(t_{k + 1}\) and \(t_k\). \({{\varvec{e}}}_{k + 1}^{\,}\) and \({{\varvec{e}}}_k^{\,}\) are the unit line of sight vectors at time \(t_{k + 1}\) and \(t_k\), respectively. \(\Delta {\bf{p}}_{s_{k + 1} }^e\) and \(\Delta {\bf{p}}_{r_{k + 1} }^e\) are the receiver and satellite position increment vectors in ECEF between time \(t_{k + 1}\) and \(t_k\).

In (3), the magnitude of \(({{\varvec{e}}}_{k + 1}^{\,} - {{\varvec{e}}}_k^{\,} )\) is typically quite small, usually below \(10^{ - 6}\). Even if the user’s absolute position error reaches several hundred meters, it still has a minimal impact on value \(\Delta \rho_{t_{k + 1} }\), which is usually below millimeters. Therefore, the accuracy of \(\Delta \rho_{t_{k + 1} }\) is primarily determined by the increments in the user’s position and the satellite’s position.

Substituting (3) into (2) yields:

$$\begin{aligned} \Delta \phi & = \frac{1}{\lambda }\Delta \rho_{t_{k + 1} } + \frac{1}{\lambda }\Delta dt_{r,t_{k + 1} } + \varepsilon_{\Delta \phi } \\ & = \frac{1}{\lambda }\left[ {({{\varvec{e}}}_{k + 1}^{\,} - {{\varvec{e}}}_k^{\,} ) \cdot ({\bf{p}}_{s_k }^e - {\bf{p}}_{r_k }^e ) + {{\varvec{e}}}_{k + 1}^{\,} \cdot ( - \Delta {\bf{p}}_{r_{k + 1} }^e + \Delta {\bf{p}}_{s_{k + 1} }^e )} \right] + \frac{1}{\lambda }\Delta dt_{r,t_{k + 1} } + \varepsilon_{\Delta \phi } \\ \end{aligned}$$
(4)

we can reformulate (4) as follows:

$$\left[ {{{\varvec{e}}}_{k + 1} - {1}} \right]\left[ \begin{gathered} \Delta {\bf{p}}_{r_{k + 1} }^e \hfill \\ \Delta dt_{r,t_{k + 1} } \hfill \\ \end{gathered} \right] = {{\varvec{e}}}_{k + 1} \cdot \Delta {\bf{p}}_{s_{k + 1} }^e + ({{\varvec{e}}}_{k + 1} - {{\varvec{e}}}_k ) \cdot ({\bf{p}}_{s_k }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi + \lambda \varepsilon_{\Delta \phi }$$
(5)

when there are more than three satellite observations available, it becomes possible to solve the following equation:

$$\left[ \begin{gathered} {{\varvec{e}}}_{k + 1}^1 { - 1} \\ {{\varvec{e}}}_{k + 1}^2 { - 1} \\ \cdots \\ {{\varvec{e}}}_{k + 1}^n { - 1} \\ \end{gathered} \right]\left[ \begin{gathered} \Delta {\bf{p}}_{r_{k + 1} }^e \hfill \\ \Delta dt_{r,t_{k + 1} } \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {{\varvec{e}}}_{k + 1}^1 \cdot \Delta {\bf{p}}_{s_{k + 1}^1 }^e + ({{\varvec{e}}}_{k + 1}^1 - {{\varvec{e}}}_k^1 ) \cdot ({\bf{p}}_{s_k^1 }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi^1 \\ {{\varvec{e}}}_{k + 1}^2 \cdot \Delta {\bf{p}}_{s_{k + 1}^2 }^e + ({{\varvec{e}}}_{k + 1}^2 - {{\varvec{e}}}_k^2 ) \cdot ({\bf{p}}_{s_k^2 }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi^2 \\ \cdots \\ {{\varvec{e}}}_{k + 1}^n \cdot \Delta {\bf{p}}_{s_{k + 1}^n }^e + ({{\varvec{e}}}_{k + 1}^n - {{\varvec{e}}}_k^n ) \cdot ({\bf{p}}_{s_k^n }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi^n \\ \end{gathered} \right] + \lambda \left[ \begin{gathered} \varepsilon_{\Delta \phi }^1 \\ \varepsilon_{\Delta \phi }^2 \\ \cdots \\ \varepsilon_{\Delta \phi }^n \\ \end{gathered} \right]$$
(6)

Let \({{\varvec{B}}} = \left[ \begin{gathered} {{\varvec{e}}}_{k + 1}^1 { - 1} \\ {{\varvec{e}}}_{k + 1}^2 { - 1} \\ \cdots \\ {{\varvec{e}}}_{k + 1}^n { - 1} \\ \end{gathered} \right],\) \({{\varvec{l}}} = \left[ \begin{gathered} {{\varvec{e}}}_{k + 1}^1 \cdot \Delta {\bf{p}}_{s_{k + 1}^1 }^e + ({{\varvec{e}}}_{k + 1}^1 - {{\varvec{e}}}_k^1 ) \cdot ({\bf{p}}_{s_k^1 }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi^1 \\ {{\varvec{e}}}_{k + 1}^2 \cdot \Delta {\bf{p}}_{s_{k + 1}^2 }^e + ({{\varvec{e}}}_{k + 1}^2 - {{\varvec{e}}}_k^2 ) \cdot ({\bf{p}}_{s_k^2 }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi^2 \\ \cdots \\ {{\varvec{e}}}_{k + 1}^n \cdot \Delta {\bf{p}}_{s_{k + 1}^n }^e + ({{\varvec{e}}}_{k + 1}^n - {{\varvec{e}}}_k^n ) \cdot ({\bf{p}}_{s_k^n }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi^n \\ \end{gathered} \right],\) and \(\delta {{\varvec{x}}} = \left[ \begin{gathered} \Delta {\bf{p}}_{r_{k + 1} }^e \hfill \\ \Delta dt_{r,t_{k + 1} } \hfill \\ \end{gathered} \right],\) We can utilize the least squares method to solve for \(\delta {{\varvec{x}}}\) as:

$$\delta {{\varvec{x}}} = ({{\varvec{B}}}^T {{\varvec{B}}})^{ - 1} {{\varvec{B}}}^T {{\varvec{l}}}$$
(7)

By (7), the user Delta_POS \(\Delta {\bf{p}}_{r_{k + 1} }^e\) and Delta_CLK \(\Delta dt_{r,t_{k + 1} }\) at the time \(t_{k + 1}\) can be obtained. The iterative nearest point algorithm (Besl and McKay 1992) is then used to align the accumulated user position increment from several epochs with the trajectory of the odometer. So far, we have completed the alignment of GNSS and odometer, as well as the initialization of Delta_CLK. This serves as the basis for predicting \(\Delta dt_{r,t_{k + 1} }\) in subsequent epochs and constructing the cycle slip detection term.

Construction of cycle slip detection term

If we can determine the characteristics of the Delta_CLK of the receiver, and with the aid of the user Delta_POS of the odometer, we can predict the phase observation of the next epoch:

$$\begin{aligned} \phi_{t_{k + 1} }^{forcast} & = \phi_{t_k } + \left( {\frac{1}{\lambda }\Delta \rho_{t_{k + 1} }^{Odometer} + \frac{1}{\lambda }(\Delta dt_{r,t_{k + 1} } )^{forcast} + \varepsilon_{\Delta \phi } } \right) \\ \, & { = }\frac{1}{\lambda }\left( { - {{\varvec{e}}}_{k + 1}^{\,} \cdot (\Delta {\bf{p}}_{r_{k + 1} }^e )^{Odometer} + (\Delta dt_{r,t_{k + 1} } )^{forcast} } \right) + \phi_{t_k } + \frac{1}{\lambda }\left( {({{\varvec{e}}}_{k + 1}^{\,} - {{\varvec{e}}}_k^{\,} ) \cdot ({\bf{p}}_{s_k }^e - {\bf{p}}_{r_k }^e ) + {{\varvec{e}}}_{k + 1}^{\,} \cdot \Delta {\bf{p}}_{s_{k + 1} }^e } \right) + \varepsilon_{\Delta \phi } \\ \, & { = }{{\varvec{F}}} \cdot \left[ {\begin{array}{*{20}c} {(\Delta {\bf{p}}_{r_{k + 1} }^e )^{Odometer} } \\ {(\Delta dt_{r,t_{k + 1} } )^{forcast} } \\ \end{array} } \right] + C \\ \end{aligned}$$
(8)

where \({{\varvec{F}}} = \frac{1}{\lambda }[ - {{\varvec{e}}}_{k + 1} \;1],\) \(C = \phi_{t_k } + \frac{1}{\lambda }(({{\varvec{e}}}_{k + 1}^{\,} - {{\varvec{e}}}_k^{\,} ) \cdot ({\bf{p}}_{s_k }^e - {\bf{p}}_{r_k }^e ) + {{\varvec{e}}}_{k + 1}^{\,} \cdot \Delta {\bf{p}}_{s_{k + 1} }^e ) + \varepsilon_{\Delta \phi }.\) \(\Delta dt_{r,t_{k + 1} }\) is modeled as a random walk (RW) with process noise \(\sigma_{prn\_\Delta dt_r }^{\,}\) that is either pre-calibrated or modeled within a short period of time. The prediction model can be expressed as follows:

$$(\Delta dt_{r,t_{k + 1} } )^{forcast} = \Delta dt_{r,t_k } + \sigma_{prn\_\Delta dt_r }^{\,}$$
(9)

substituting (9) into (8) yields:

$$\phi_{t_{k + 1} }^{forcast} = {{\varvec{F}}} \cdot \left[ {\begin{array}{*{20}c} {(\Delta {\bf{p}}_{r_{k + 1} }^e )^{Odometer} } \\ {(\Delta dt_{r,t_{k + 1} } )^{forcast} } \\ \end{array} } \right] + C = {{\varvec{F}}}_1 \cdot \left[ \begin{gathered} \begin{array}{*{20}c} {(\Delta {\bf{p}}_{r_{k + 1} }^e )^{Odometer} } \\ {\Delta dt_{r,t_k } } \\ \end{array} \\ \sigma_{prn\_\Delta dt_r }^{\,} \\ \end{gathered} \right] + C = {{\varvec{F}}}_1 \cdot \delta {{\varvec{x}}}_1 + C$$
(10)

where \({{\varvec{F}}}_1 = \frac{1}{\lambda }[ - {{\varvec{e}}}_{k + 1} \;1\;1],\) \(\delta {{\varvec{x}}}_1 = \left[ \begin{gathered} \begin{array}{*{20}c} {(\Delta {\bf{p}}_{r_{k + 1} }^e )^{Odometer} } \\ {\Delta dt_{r,t_k } } \\ \end{array} \\ \sigma_{prn\_\Delta dt_r }^{\,} \\ \end{gathered} \right],\) the theoretical accuracy of \(\phi_{t_{k + 1} }^{forcast}\) can be obtained using the law of covariance propagation:

$$\sigma_{\phi_{t_{k + 1} }^{forcast} } = \sqrt {{{{\varvec{F}}}_1 {{\varvec{Q}}}_{{{\varvec{x}}}_1 {{\varvec{x}}}_1 } {{\varvec{F}}}_1^T }}$$
(11)

where \({{\varvec{Q}}}_{{{\varvec{x}}}_1 {{\varvec{x}}}_1 }\) is:

$${{\varvec{Q}}}_{{{\varvec{x}}}_1 {{\varvec{x}}}_1 } = \left[ {\begin{array}{*{20}c} {\sigma_{(\Delta {\bf{p}}_{r_{k + 1} }^e )^{Odometer} }^2 } & {\bf{0}} & {\bf{0}} \\ {\bf{0}} & {\sigma_{\Delta dt_{r,k} }^2 } & 0 \\ {\bf{0}} & 0 & {\sigma_{prn\_\Delta dt_r }^2 } \\ \end{array} } \right]$$
(12)

where \(\sigma_{(\Delta {\bf{p}}_{r_{k + 1} }^e )^{Odometer} }^2\) represents the incremental accuracy of the odometer’s relative position, and \(\sigma_{\Delta dt_{r,k} }^2\) represents the posterior Delta_CLK accuracy of the TDCP equation. Ignoring the impact of phase measurement noise at the millimeter level, we construct the DT with the aid of Delta_POS and Delta_CLK and its theoretical accuracy is as follows:

$$DT = \phi_{t_{k + 1} } - \phi_{t_{k + 1} }^{forcast} = \phi_{t_{k + 1} } - {{\varvec{F}}}_1 \cdot \delta {{\varvec{x}}}_1 - C, \, \sigma_{DT}^2 = \sigma_{\phi_{t_{k + 1} }^{forcast} }^2$$
(13)

By setting an appropriate threshold for DT, we can detect and repair cycle slip on phase observation satellite-by-satellite.

TDCP Equation with Delta_POS and Delta_CLK Constraints

After using (13) for cycle slip detection, we utilized prior observations of Delta_POS and Delta_CLK to construct a TDCP equation with corresponding constraints:

$$\left[ \begin{gathered} {{\varvec{e}}}_{k + 1}^1\; { - 1} \\ {{\varvec{e}}}_{k + 1}^2\; { - 1} \\ \cdots \\ {{\varvec{e}}}_{k + 1}^n\; { - 1} \\ {{\varvec{I}}}\quad{ 0} \\ {0 \quad 1} \\ \end{gathered} \right]\left[ \begin{gathered} \Delta {\bf{p}}_{r_{k + 1} }^e \hfill \\ \Delta dt_{r,t_{k + 1} } \hfill \\ \end{gathered} \right] = \left[ \begin{gathered} {{\varvec{e}}}_{k + 1}^1 \cdot \Delta {\bf{p}}_{s_{k + 1}^1 }^e + ({{\varvec{e}}}_{k + 1}^1 - {{\varvec{e}}}_k^1 ) \cdot ({\bf{p}}_{s_k^1 }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi^1 \\ {{\varvec{e}}}_{k + 1}^2 \cdot \Delta {\bf{p}}_{s_{k + 1}^2 }^e + ({{\varvec{e}}}_{k + 1}^2 - {{\varvec{e}}}_k^2 ) \cdot ({\bf{p}}_{s_k^2 }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi^2 \\ \cdots \\ {{\varvec{e}}}_{k + 1}^n \cdot \Delta {\bf{p}}_{s_{k + 1}^n }^e + ({{\varvec{e}}}_{k + 1}^n - {{\varvec{e}}}_k^n ) \cdot ({\bf{p}}_{s_k^n }^e - {\bf{p}}_{r_k }^e ) - \lambda \Delta \phi^n \\ (\Delta {\bf{p}}_{r_{k + 1} }^e )^{Odometer} \\ (\Delta dt_{r,t_{k + 1} } )^{forcast} \\ \end{gathered} \right] + \lambda \left[ \begin{gathered} \varepsilon_{\Delta \phi }^1 \\ \varepsilon_{\Delta \phi }^2 \\ \cdots \\ \varepsilon_{\Delta \phi }^n \\ \varepsilon_{(\Delta {\bf{p}}_{r_{k + 1} }^e )^{Odometer} }^{\,} \\ \varepsilon_{(\Delta dt_{r,t_{k + 1} } )^{forcast} }^{\,} \\ \end{gathered} \right]$$
(14)

Even if there are less than four visible satellites, it is still possible to accurately calculate the Delta_POS and Delta_CLK by applying additional constraints. This enables continuous calculation and prediction of Delta_CLK, resulting in a continuous construction of DT. As a result, this method is suitable for positioning tasks in complex situations.

Experiments and results

In “The influence of Delta_POS and Delta_CLK with different prior accuracies on the DT”, section we have verified the theoretical relationship between the DT with the Delta_POS and Delta_CLK using public dataset. In “Positioning performance of various odometry” section evaluated the accuracy of the Delta_POS provided by the odometer. In “The characteristics of receiver Delta_CLK”, section we have demonstrated the stability of most receiver Delta_CLK between epochs, providing a strong foundation for prediction. Section “Validation of static and dynamic data” has verified the accuracy of the cycle slip detection method under two static and two dynamic datasets, while section “TDCP with Delta_POS and Delta_CLK constraints under 1–3 visible satellite” explores the maintenance of Delta_CLK accuracy by only 1–3 satellites in complex environments. We validated the new method by positioning experiment in “Positioning performance with the proposed technique” section.

The influence of Delta_POS and Delta_CLK with different prior accuracies on the DT

Equation (13) provides a theoretical approach for calculating the prediction accuracy of the DT. This section explores how different prior accuracy values, specifically Delta_CLK and Delta_POS, influence cycle slip detection using real-world measured data. Employing the low dynamic Sports Field sequence (Cao et al. 2022) as a case study, we adopt Delta_POS and Delta_CLK obtained from the single-frequency GPS, Galileo, and BDS TDCP solution as ground truth. Subsequently, we introduce varying levels of white noise to these ground truth and analyze the resulting error fluctuations in the DT.

Figure 2 indicates that the Delta_POS and Delta_CLK noise have a consistent numerical impact on the DT. Specifically, a noise of 2 cm in Delta_POS or Delta_CLK will result in a DT error of approximately 0.1 cycles at the L1 frequency, as expected theoretically. This result suggests that TDCP eliminates almost all other errors, leaving only the noise inherent to the phase itself. This means that the accuracy of determining epoch-to-epoch Delta_CLK is ideal and reflects the actual clock characteristic of the receiver. Together with the analysis in “The characteristics of receiver Delta_CLK,” section we can establish corresponding standards, choose receivers with favorable clock characteristics, and use the method presented in this sduty for cycle slip detection.

Fig. 2
figure 2

Relationship between DT error with Delta_POS and Delta_CLK noise

Full size image

Positioning performance of various odometry

This section compares different odometry methods regarding positioning performance and selects the most effective ones based on their ranking on the KITTI odometry datasets (Geiger et al. 2012). Table 1 shows that the accuracy of stereo visual odometry and the three types of LiDAR odometry are all within 0.69%. The visual-inertial odometry (VIO) we used has the lowest dead reckoning (DR) accuracy, approximately 1%.

Table 1 The highest performance of different odometry methods on the KITTI odometry datasets
Full size table

From the upper right of Fig. 3, it can be seen that the divergence of the VIO remains stable at around 1% at a speed of up to 70 km/h. The GNSS sampling rate for dynamic vehicle users is generally above 10 Hz, meaning the DR error between epochs remains within 2 cm. This high precision of DR can help assist GNSS data preprocessing.

Fig. 3
figure 3

Divergence of different odometry methods

Full size image

Subsequently, we will explore the impact of Delta_POS noise on cycle slip detection. For static stations, the relative position accuracy is very high, and the process noise in the position propagation can be considered as zero. At this point, only the discussion of dynamic situations remains. For our research, we chose the low-cost Visual Inertial Odometer (VIO) from the Sports Field sequence, the testing environment was set in a low-speed (0–2 m/s) playground with partial obstructed by tree canopy, which affected GNSS signals. We compared VIO’s Delta_POS with that of RTK in each epoch, as shown in Fig. 4. The accuracy of the VIO’s Delta_POS is comparable to that of RTK. The noise in all three dimensions is less than 1cm, resulting in less than 0.05 cycles of cycle slip detection. So far, we only need to conduct further investigation to confirm the prediction accuracy of Delta_CLK.

Fig. 4
figure 4

Consistency of TDCP, VIO, and RTK Delta_POS. The first line depicts the consistency between the TDCP Delta_POS and the RTK Delta_POS, while the second line illustrates the consistency between the VIO Delta_POS and the RTK Delta_POS. RTK’s Delta_POS serves as the reference for comparison

Full size image

The characteristics of receiver Delta_CLK

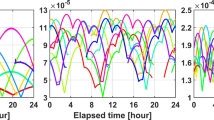
In order to enhance our comprehension of the Delta_CLK characteristics of various receivers, this section conducted a detailed statistical analysis of the between-epoch Delta_CLK for three high-frequency (≥ 1 Hz) GNSS public datasets and three self-collected datasets. The specific data is shown in Table 2. The item “Station” in the table represents the static base station name, and “Sequence” represents the dynamic data sequence name. The statistical results indicate that the Delta_CLK of the receiver mainly presents two types of characteristics: white noise (WN) and random walk (RW). The item Standard Deviation (STD) represents the noise level of the second-order difference or first-order difference in clock error. In this study, we consider it as the noise level of RW or WN. We selected some data and further plotted Figs. 5 and 6 to better illustrate these characteristics.

Table 2 Statistical analysis of Delta_CLK between epochs
Full size table
Fig. 5
figure 5

Random walk characteristics of Delta_CLK between epochs. To enhance clarity in showcasing the variations among different receiver types, sequences in the top-left and bottom-right graphs have undergone a shifting process. The naming convention of the legend is: Dataset Name (or Station/Sequence name) + Receiver + Sampling rate, for example: IGS_Javad_1Hz or Sports_F9p_1Hz

Full size image
Fig. 6
figure 6

White noise characteristics of Delta_CLK between epochs

Full size image

The first line of Fig. 5 displays the time series of Delta_CLK at different sampling rates for six types of receivers, along with the corresponding autocorrelation coefficient (AC) sequences. It is evident from the figure that there is a strong correlation between Delta_CLK at different epochs. Subsequently, we perform differencing on Delta_CLK sequence to obtain the second-order clock error sequence. The probability density function and the corresponding autocorrelation function of the new sequence are depicted in the second line. The results indicate that the second-order clock error sequence presents significant white noise characteristics. Hence, we consider modeling Delta_CLK as a random walk process, where the process noise is determined by the white noise of the second-order differenced sequence. This model provides a satisfying explanation and prediction for the Delta_CLK.

Figure 6 displays the time series of Delta_CLK for three types of receivers, along with the corresponding AC sequences. The graph illustrates that there is almost no correlation between Delta_CLK at different epochs, indicating a white noise characteristic. Based on this observation, we contemplate utilizing Delta_CLK with lower white noise for cycle slip detection, as they demonstrate better predictability. Conversely, Delta_CLK with higher white noise are deemed less effective for prediction and fall outside the scope of this study.

In theory, modeling Delta_CLK as a first-order Gauss-Markov process would provide a better integration of random walk and white noise characteristics. However, considering that the correlation time in a first-order Gauss-Markov process needs to be calibrated in advance and may vary for the same receiver in different situations (as evident in the Sports Field and Urban Driving sequences in Fig. 5), even with calibration, it can only determine an approximate magnitude. As seen in Fig. 5, for the 1Hz Xiaomi-8 cellphone dataset with the shortest correlation time \(T\) of 60.1 s. This study specifically focuses on forecasting Delta_CLK over short periods (typically not exceeding 1 s, \(\Delta t \le 1 \, s\)). At such intervals, \(- \Delta t/T\) approaches 0, resembling a random walk process (Shin 2005). When Delta_CLK presents white noise characteristics with a small magnitude, it indicates slight variations between consecutive epochs. This can also be represented in the form of a random walk.Taking above considerations into account, we model the Delta_CLK as a random walk to forecast the next epoch.

After conducting a qualitative assessment, we proceed to a quantitative analysis of Table 2 and found that.

  1. 1.

    The stability of clock speed is not closely related to the cost of the receiver. For example, the clock speed (equals to Delta_CLK/sampling_interval) stability of the low-cost single-frequency receiver Ublox M8t (Demo5 Rover1 1 Hz) is better than that of the geodetic receiver Sept Polarx5 (IGS QUAD 1 Hz).

  2. 2.

    The accuracy of Delta_CLK prediction is primarily related to the sampling rate, with higher sampling rates correlating to higher prediction accuracy. For instance, the Delta_CLK prediction accuracy of low-cost receiver Ublox F9p (APM Base1 20 Hz) is 0.37 cm/epoch, while for three types of geodetic receivers from the International GNSS Service (IGS)—Trimble-Alloy (IGS JFNG 1 Hz), Javad-Delta (IGS LEIJ 1 Hz), and Sept-Polarx5 (IGS QUAD 1 Hz)—the Delta_CLK prediction accuracies are 1.37 cm/epoch, 0.98 cm/epoch, and 7 cm/epoch respectively.

  3. 3.

    Utilizing three times the STD as the criterion, at a sampling rate of 1 Hz, the geodetic receivers Trimble-Alloy (JFNG), Javad-Delta (LEIJ) and Net-R9 (HUANGPI) present Delta_CLK process noise within half a wavelength, whereas other types of receivers extend beyond half a wavelength. It is noteworthy that, at 5 Hz and 10 Hz sampling rates, the process noise also remains within half a wavelength.

Based on these analyses, the proposed method is particularly suitable for cycle slip detection in low-cost receivers with sampling rates above 5 Hz and geodetic receivers above 1 Hz sampling rate.

This section contributes to a more comprehensive understanding of the characteristics of receiver Delta_CLK, providing empirical data support for our cycle slip detection method. This has great significance for optimizing the performance of GNSS receivers and making informed choices for receivers in various application situations.

Validation of static and dynamic data

In this section, we aim to evaluate the impact of predicting Delta_CLK on cycle slip detection. To do so, we selected the 20 Hz data from APM and 1Hz data from LEIJ for static station verification. Figure 7 illustrates the DT performance of APM under different forecast interval Delta_CLK aids. The black dashed line in the figure represents the range in which 99.74% (\(3 \, \sigma\)) of the data falls. The results indicate that even when using low-cost F9p receivers and 80-s interval prediction Delta_CLK, the cycle slip detection performance of APM stations remains significant.

Fig. 7
figure 7

The 20 Hz sampling data from APM station Ublox-F9p. The data shows DT with different time delays, aided by Delta_CLK prediction. The scatter points indicate the DT of different satellites, and the black dashed line represents 99.74% of the data within this range

Full size image

In Fig. 8, we can see the relationship between the forecast interval and the DT at the APM and LEIJ static stations. As the forecast interval increases for APM stations, the range of cycle slip detection also increases, but it remains below 0.2 cycles overall. The range of cycle slip detection term for LEIJ station hardly changes with the increase of the forecast interval, and it stays at a level below 0.25 cycles. When we combine this information with Fig. 5, we can see that the Delta_CLK of APM station and LEIJ station are considerable stable. Therefore, even under the forecast of 80 s, the overall performance remains satisfying.

Fig. 8
figure 8

Relationship between DT and forecast interval under static conditions

Full size image

Subsequently, we selected the low-speed Sports Field sequence and high-speed Urban Driving sequence to verify the cycle slip detection performance of additional Delta_POS and Delta_CLK aid under dynamic conditions. Considering that small cycle slips of more than 0.5 cycles can easily affect the ambiguity to get fixed, we set cycle slips detection threshold of 0.5 cycles to judge DT, as the red dashed line shown in Fig. 9. In a low-speed dynamic environment, the prediction of Delta_CLK within 3 s hardly causes misjudgment of phase observations without cycle slips. When combined with Fig. 10, we can see that a standard deviation of 3 times is within 0.3 cycles. Therefore, in low-speed dynamic environments, we can use this information as a reference to set strict threshold values for cycle slip detection and the upper time limits for Delta_CLK prediction.

Fig. 9
figure 9

Low dynamic Sports Field sequence 10 Hz, Delta_CLK prediction with different time delays to aid in cycle slip detection. The scatter points on the graph represent the DT of various satellites. The red dashed line corresponds to the boundary line of 0.5 cycles, while the black dashed line represents 99.74% of the data within this range

Full size image
Fig. 10
figure 10

Relationship between DT and forecast interval under dynamic conditions

Full size image

Figure 10 indicates that Delta_CLK forecasts within five seconds can successfully detect small cycle slips over 0.5 cycles, although there may be some misjudgments. The above analysis indicates the lower limit of this method. However, in practical applications, the predicted value of Delta_CLK can usually be obtained directly from the previous epoch. By referring to Figs. 8 and 10, we can observe that regardless of whether the circumstance is dynamic or static, the three times standard deviation of the cycle slip detection is within the range of 0.2 cycles.

The method proposed in this study is particularly suitable for receivers with stable clock performance and situations that require high-frequency sampling, enabling them to successfully conduct cycle slip detection.

TDCP with Delta_POS and Delta_CLK constraints under 1–3 visible satellites

In a dynamic environment, GNSS users may encounter with a situation where they receive a large number of satellite observations in one epoch, but in the next epoch, due to frequent shading and partial occlusion, there are less than four available observable satellites. In this situation, the Dleta_CLK can only be predicted based on the previous epoch. As time goes on, the accuracy of Dleta_CLK will diverge to an unpredictable level, which can lead to the failure of cycle slip detection. This, in turn, can cause gross error transfer when tightly coulping GNSS observations with other observations. This is extremely detrimental to the robust estimation of parameters.To address this issue, we explore the accuracy maintenance of Dleta_CLK by introducing Dleta_POS and Dleta_CLK constraints when the number of satellites is less than 4. We use the Sports Field sequence to illustrate this problem, and the satellite distribution is shown in Fig. 11.

Fig. 11
figure 11

Satellite sky plot of Sports Field sequence

Full size image

First, three satellites with the same side distribution, G06, E13, and E26, were selected and added to the equation to solve the Dleta_CLK. The results indicate that the observations of multiple satellites on the same side had little gain in calculating the Dleta_CLK, and all of them would cause the estimated Dleta_CLK to deviate from the ground truth, as shown in the first line of Fig. 12.

Fig. 12
figure 12

Maintenance of Dleta_CLK Accuracy with 1–3 satellites using Dleta_POS and Dleta_CLK constraint. Top: Satellites on the same side of the station. Bottom: Uniform satellite distribution around the station. The blue legend represents the accuracy of the Delta_CLK directly predicted from the previous epoch, while orange, green, and red respectively represent the constraints of adding 1, 2, and 3 satellites

Full size image

Then we selected three uniformly distributed satellites, G02, G15, and G29, and added constraints of 1–3 satellites in gradually. The second line of Fig. 12 and Table 3 show that after adding constraints of 2–3 uniformly distributed satellites, the accuracy was significantly higher than the accuracy of direct prediction from the previous epoch, increasing by 28.09% and 65.17%, respectively. Conversely, the imposition of constraints from a single satellite yielded a less desirable result, leading to a decrease in accuracy. Essentially, when a satellite constraint is added, it is equivalent to the constraint of the same side satellite, so the accuracy of Dleta_CLK under the constraint of one satellite is lower than the accuracy of prediction.

Table 3 Accuracy of Dleta_CLK with less than 4 satellites under various constraint conditions. (unit: m)
Full size table

We further investigate another extreme but frequently encountered GNSS observational condition: the situation where a GNSS user terminal transitions from an GNSS-denied environment, lacking a priori observations for Dleta_CLK and relying solely on Dleta_POS constraints provided by the odometer. Further analysis focuses on the case where only Dleta_POS serve as constraints for Dleta_CLK solutions, detailed in Table 3 and Fig. 13. The results demonstrate that, with constraints from two or more uniformly distributed satellites combined with Dleta_POS from the odometer, a high-precision solution for Dleta_CLK can be maintained. Building upon the preceding discussion, and with the selection of an appropriate receiver, accurate forecasting of Dleta_CLK for the next epoch becomes feasible. This capability facilitates cycle slip detection tasks, enabling GNSS user terminals obtain phase observations without cycle slips to the utmost possible in dynamic environments.

Fig. 13
figure 13

Maintenance of Dleta_CLK Accuracy with less than 4 satellites using only Dleta_POS constraint. Top: Satellites on the same side of the station. Bottom: Uniform satellite distribution around the station

Full size image

Positioning performance with the proposed technique

For the static station validation, We selected the stations CUT0 and CUTB GNSS data from Curtin University, sampled during January 1st, 2023, from 00:00 to 01:00. We used GPS L1 single-frequency data for ultra-short baseline simulated kinematic positioning. We calculated the Delta_CLK random walk process noise for CUT0 and CUTB, which turned out to be 1.9 cm/s and 1.7 cm/s, respectively. These values are within 0.1 cycles and provide a good basis for our cycle slip detection method.

In Fig. 14 and Table 4, we adopt different strategies for handling cycle slips in GPS data. The first strategy, represented by (a), assumes that single-frequency GPS cannot detect and repair cycle slips. Therefore, the ambiguity is not propagated between epochs. This corresponds to the "instantaneous" mode (INST). On the other hand, strategies (b) to (e) assume that no cycle slips occur and directly propagate them. These strategies correspond to the "continuous" mode (CONT). Lastly, strategy (f) assumes that cycle slips may occur anytime. It employs our method for cycle slip estimation satellite-by-satellite, with the ambiguity estimation strategy set to CONT mode.

Fig. 14
figure 14

Effect of cycle slip detection strategies on RTK positioning accuracy for static station validation. a A single epoch solution for ambiguity. b–e None of them adopt cycle slip detection methods, and it is considered that there is no cycle slip occurrence. The CONT mode is adopted. f Assumes that cycle slips may occur anytime. It employs our method for cycle slip estimation satellite-by-satellite. The CONT mode is adopted

Full size image
Table 4 Ambiguity success fixed rate and positioning error statistics for static station validation
Full size table

Considering the data quality of the static base station was good and only a small number of cycle slips were present. After 1200 s, we manually introduced cycle slips ranging from 0.2 to 10 cycles to explore their impact on positioning accuracy and to validate the effectiveness of our method in detecting cycle slips of varying magnitudes. For (a), the positioning results remain the same with additions of 0.2 to 10 cycles, with an ambiguity success fixed-rate (epochs where the positioning accuracy in the E/N/U directions within 5 cm are considered correctly fixed epochs; success fixed rate = number of correctly fixed epochs / total epochs) of 82.3%. The positioning accuracies in the E/N/U directions are 0.30 m/0.39 m/0.71 m, respectively. When introducing cycle slips of 10, 2, 0.5, and 0.2 cycles to (b)–(e), respectively, it can be observed that small cycle slips of 0.2 cycles have little impact on the short baseline RTK positioning accuracy and ambiguity success fixed rate. However, cycle slips of 0.5 cycles and above introduce significant errors in positioning. For (f), the positioning results remain the same with additions of 0.2 to 10 cycles, with a success fixed rate of 100% and positioning accuracies in the E/N/U directions of 0.003 m/0.008 m/0.009 m, respectively. This result demonstrates the obvious role of our method in GNSS data preprocessing.

For the field test validation, we further selected GNSS/VIO data from the Sports Field sequence. We chose HKKS from the Hong Kong Satellite Positioning Reference Station Network as the reference station and conducted short baseline RTK positioning experiments using GPS and BDS dual-system L1 single-frequency data. The ground truth was provided by RTK fixed solution using dual-frequency data from GPS and BDS.

In Fig. 15 and Table 5, (a) represents the single-epoch ambiguity resolution. This strategy assumes that single-frequency GPS and BDS cannot detect and repair cycle slips, so the ambiguity is not propagated between epochs. This strategy uses INST mode, with an ambiguity fixing rate of 87.62%. Assuming no cycle slips occur, (b) propagates cycle slips directly using the CONT mode. However, this strategy has a low ambiguity fixing rate of only 11.37%. Therefore, if cycle slips are not handled correctly and are directly propagated, positioning accuracy can be significantly degraded. (c) assumes that cycle slips are likely to happen at any time during GNSS positioning and adopts the method proposed in this study to detect and repair cycle slips satellite by satellite. The ambiguity estimation strategy is set to the CONT mode. The results indicate that our method can help propagate ambiguities accurately, leading to the expected accuracy of GNSS positioning.

Fig. 15
figure 15

Effect of cycle slip detection strategies on RTK positioning accuracy for filed test validation. a A single epoch solution for ambiguity. b It is considered that there is no cycle slip occurrence. The CONT mode is adopted. c It assumes that cycle slips may occur anytime. It employs our method for cycle slip estimation satellite-by-satellite. The CONT mode is adopted

Full size image
Table 5 Ambiguity success fixed rate and positioning error statistics for field test
Full size table

Conclusion

This study leverages the traditional TDCP model to separately consider the estimable parameters, namely Dleta_POS and Dleta_CLK. The Dleta_POS are obtained through odometer predictions, while Dleta_CLK are modeled as random walk process, forecasted from previous epoch. Subsequently, a cycle slip detection term is established. Both dynamic and static experiments conclusively demonstrate the efficacy of the developed Cycle Slip Detection Term in successfully identifying small cycle slips. The positioning experiment validated the new technology.

Furthermore, an analysis of Dleta_CLK characteristics for various receivers of different costs reveals that most receivers present favorable between-epoch stability in both white noise and random walk characteristics. This stability provides a robust foundation for isolating Dleta_CLK errors in our model. It is important to note that this method is applicable only to receivers with a sampling rate of 1 Hz or higher. While sampling rates below 1 Hz may limit certain applications, the consideration of receiver Dleta_CLK white noise or random walk characteristics serves as a valuable criterion for the selection of GNSS receiver for popularized application.

Additionally, with the constraint of odometer, our method maintains Dleta_CLK solution accuracy even in complex environments with only 2–3 uniformly distributed satellites, which provides reliable prior information for successive epoch-by-epoch and satellite-by-satellite cycle slip detection, contributing to the proper utilization of high-precision GNSS phase observations. Our cycle slip detection algorithm holds promise for robust GNSS applications in complex, tightly coupled multi-sensor navigation situations.