Introduction

Water vapor plays a crucial role in the dynamics and spatial distribution of the atmosphere, exerting significant influences on climate and weather patterns. The continuous and stable monitoring of water vapor is of great significance for meteorological applications including severe weather forecasting and warnings (Liu et al. 2005; Yang et al. 2021). With the development of the global navigation satellite system (GNSS) constellation and the establishment of a comprehensive ground-based observation network, GNSS has been considered as a powerful technique to retrieve water vapor and the research of GNSS meteorology has gained considerable attention from both the GNSS and meteorological communities (Wan et al. 2016; Yao et al. 2017; Zhang et al. 2022).

In GNSS meteorology, it has been widely validated that the conversion of GNSS zenith tropospheric delay into precipitable water vapor (PWV) can achieve a high level of accuracy in the millimeter (Duan et al. 1996). Since the potential of tomography was proposed to apply in GNSS meteorology by Bevis et al. (1992), GNSS water vapor tomography has become a promising method to achieve the three-dimensional distribution of water vapor using the GNSS satellite signals as scanning rays in the research area (Nilsson and Gardinarsky, 2004; Perler et al. 2011; Xia et al. 2018; Zhang et al. 2021). In GNSS water vapor tomography, the research area covered by ground-based GNSS receivers is discretized into finite cubic closed voxels based on latitude, longitude and altitude, and each voxel has a fixed amount of water vapor during a specified time period. The GNSS-derived slant water vapor (SWV), which propagates through the troposphere from the top of the study area, serves as the observation. Subsequently, the tomographic observation equation is formulated by considering the intercept of the signal as it traverses through the voxels (Zhao et al. 2020a; Yang et al. 2023).

Using the GPS data from the Kilauea network in Hawaii, Flores et al. (2000) first realized the application of water vapor tomography, and then the least-squares method has been widely employed for estimating unknown parameters in the water vapor tomography (Guo et al. 2016; Zhang et al. 2017; Zhao et al. 2019). This process needs to construct a variety of constraints such as vertical, horizontal and top constraints, which are based on empirical knowledge, and the inversion of sparse matrices often leads to deviations and instability in the tomographic results (Yang et al. 2020). On this basis, regularization methods such as the singular value decomposition (SVD), the damped least squares and the regularization method have been adopted to solve the water vapor tomographic equations. In these methods, the fluctuation of small singular value, the change of damping coefficient and the selection of regularization parameters affect the accuracy and stability of the tomographic results (Benevides et al. 2016; Shafei and Hossainali 2020; Zhao et al. 2020b). Moreover, Bender et al. (2011) proposed an iterative algorithm based on algebraic reconstruction technique (ART) and introduced other reconstruction algorithms within ART family, e.g., multiplicative algebraic reconstruction techniques (MART) and the simultaneous iterations reconstruction technique (SIRT). The comparison and analysis of these iterative algorithms and their applicability in water vapor tomography have been discussed in detail (He et al. 2015). Improved iterative algorithms, such as the parallel ART and the adaptive simultaneous ART, have also been developed (Zhang et al. 2020; Sa et al. 2021). These algorithms update the water vapor information for only a subset of the voxels within the tomographic area, and the accuracy of the tomographic results strongly relies on the exact initial values, the relaxation parameter and the termination criterion for the iteration.

Gradinarsky and Jarlemark (2004) introduced the Kalman filter algorithm for water vapor tomography, benefiting from its ability to estimate dynamically changing parameters effectively. Then the Kalman filter was widely adopted in water vapor tomography, which proves that the correlation between the tomographic epoch can be well considered and the restrictions of the additional constraints can be avoided to a certain extent by using this algorithm (Bi et al. 2010; Jiang et al. 2013). In this technique, the accurate estimation of the noise covariance matrix plays a crucial role in determining the quality of the tomographic results (Zhang et al. 2008; Rohm et al. 2014). Existing methods empirically construct the state noise covariance matrix based on the voxel distances and establish the observation noise covariance matrix using statistical information from the observations, which is difficult to provide accurate noise covariance information for the tomographic solution. Therefore, we propose a method to construct the optimized noise covariance matrix, in which the state noise covariance matrix is established using historical water vapor information derived from the atmospheric reanalysis data for each voxel, and the observation noise covariance matrix is constructed by considering the elevation angle and signal intercept.

We describe in detail the theory of the water vapor tomography and the proposed method in the methodology section. The water vapor tomographic experiment in Hong Kong is introduced in the section on experiment. The comparisons between the proposed method and the traditional method are conducted using slant water vapor, radiosonde and ERA5 data as references in the next two sections. Finally, the conclusion is given.

Methodology

The SWV is utilized as the observation in the water vapor tomography. It can be converted from slant wet delay (SWD) as follows (Bevis et al. 1992):

$${\text{SWV}} = {\text{SWD}} \times \frac{{10^{6} }}{{\rho_{w} \times \frac{R}{{m_{w} }}\left( {\frac{{k_{3} }}{{T_{m} }} + k_{2}^{\prime} } \right)}}$$
(1)

where \(\rho_{w}\) denotes the liquid water density (gm−3), R refers to the universal gas constant, and \({\text{m}}_{w}\) and \(m_{d}\) represent the molar mass of water and dry atmosphere, respectively. \(k_{1}\), \(k_{2}\) and \(k_{3}\) are the empirical physical constants. Tm represents the weighted mean temperature, which can be calculated using an empirical formula with surface temperature (Bevis et al. 1992; Yang et al. 2022). To achieve SWD, the zenith wet delay (ZWD) and the wet delay gradients need to be mapped into the elevation direction as below:

$$\begin{gathered} {\text{SWD}} = f_{w} \left( {ele} \right) \times {\text{ZWD}} + \hfill \\ \begin{array}{*{20}c} {} & {} & {} \\ \end{array} f_{w} \left( {ele} \right) \times \cot \left( {ele} \right) \times \left( {G_{\rm NS}^{w} \times \cos \left( {azi} \right) + G_{\rm WE}^{w} \times \sin \left( {azi} \right)} \right) + R_{e} \hfill \\ \end{gathered}$$
(2)

where ele and azi indicate the satellite elevation and azimuth angles, respectively, and \(f_{w}\) refers to the wet mapping function. \(G_{\rm NS}^{w}\) and \(G_{\rm WE}^{w}\) denote the wet delay gradient parameters in the north–south and east–west directions, respectively. Re is the unmodeled tropospheric slant delay, which is included in the undifferenced residuals. As the wet component of the zenith total delay (ZTD), ZWD can be obtained by subtracting the zenith hydrostatic delay (ZHD) from ZTD. The ZTD is the primary parameter retrieved from the GNSS observations, and the ZHD can be accurately calculated by the Saastamoinen model as below (Saastamoinen 1972):

$${\text{ZHD}} = \frac{{0.002277 \times P_{s} }}{{1 - 0.00266 \times \cos \left( {2\varphi } \right) - 0.00028 \times H}}$$
(3)

where \(\varphi\) and H are the latitude and geodetic height of the site, respectively, and \(P_{s}\) indicates the surface pressure.

In water vapor tomography, the research area is discretized into finite voxels and the distance of signal rays passing through the divided voxel can be obtained by ray tracing its path from receiver to satellite. Then, the basic equation of GNSS water vapor tomography can be expressed as below:

$${\text{SWV}} = \sum\limits_{i = 1}^{n} {d_{i} \cdot x_{i} }$$
(4)

where n denotes the total number of the voxels in the tomographic region and di refers to the intercepted distance of the signal inside voxel i, which can be achieved by the coordinates of the corresponding GNSS satellite and station. \(x_{i}\) is the unknown parameter, namely the water vapor density of voxel i. Then the SWV observations during a certain epoch are used to form the tomographic observation equation as follows:

$${\varvec{L}}_{k} = {\varvec{A}}_{k} {\varvec{X}}_{k} + {\varvec{e}}_{k}$$
(5)

where k denotes the tomographic epoch, \(\varvec{L}_{k}\) is the column vector of the SWV observations, \(\varvec{A}_{k}\) refers to the corresponding design matrix, \(\varvec{X}_{k}\) represents the column vector of the unknown parameters, and ek is the observation noise. Assuming that the water vapor density of each voxel conforms to the Gauss–Markov stationary stochastic process within a certain period, the state equation of the tomography is expressed as follows:

$${\varvec{X}}_{k} ={\varvec{\varPhi}}_{k - 1} {\varvec{X}}_{k - 1} + {\varvec{w}}_{k}$$
(6)

where \(\varvec{\Phi }\) refers to the state transition matrix, which is an identity matrix, \({\varvec{w}}_{k}\) denotes the state noise of epoch k, \(\varvec{X}_{k}\) is the same as (5).

In the Kalman filter (Kalman 1960), the prediction of the covariance matrix of the estimated state at epoch k (\({\varvec{P}}_{k}^{o}\)) is calculated as follows:

$${\varvec{P}}_{k}^{o} = {\varvec{P}}_{k - 1} + {\varvec{Q}}_{k}$$
(7)

where Pk-1 denotes the correction of the covariance matrix of the estimated state at epoch k-1. Qk is the covariance matrix of the state noise at epoch k. The Kalman gain matrix at epoch k (Hk) is expressed as below:

$${\varvec{H}}_{k} = \frac{{{\varvec{P}}_{k}^{o} {\varvec{A}}_{k}^{T} }}{{{\varvec{R}}_{k} + {\varvec{A}}_{k} {\varvec{P}}_{k}^{o} {\varvec{A}}_{k}^{T} }}$$
(8)

where superscript T denotes the matrix transpose. Rk is the covariance matrix of the observation noise at epoch k. \({\varvec{A}}_{k}\) and \({\varvec{P}}_{k}^{o}\) are the same as (5) and (7), respectively. The corrected estimates of water vapor in the voxels at epoch k (\({\varvec{X}}_{k}^{ + }\)) and the corresponding corrected covariance matrix (Pk) are updated as follows:

$${\varvec{X}}_{k}^{ + } = {\varvec{X}}_{k} + {\varvec{H}}_{k} \left( {{\varvec{L}}_{k} - {\varvec{A}}_{k} {\varvec{X}}_{k} } \right)$$
(9)
$${\varvec{P}}_{k} = \left( {{\varvec{I}} - {\varvec{H}}_{k} {\varvec{A}}_{k} } \right){\varvec{P}}_{k}^{o}$$
(10)

where I represents the identity matrix. \({\varvec{L}}_{k}\) and \({\varvec{A}}_{k}\) are the same as (5), and \({\varvec{H}}_{k}\) is the same as (8). After completing the above update, the iteration of epoch k + 1 is carried out, and the above steps iterate until the final water vapor tomography results are obtained.

In the process mentioned above, determining the noise covariance matrix plays a critical role in the filter solution. For the traditional methods, the observation noise covariance matrix is obtained with respect to the statistics of the observations, and the values of the state noise covariance are determined based on an empirical formula that incorporates the distance between two voxels as below:

$$Q_{ij} = \left[ {\frac{{\left( {l_{4d} } \right)^{2/3} }}{{1 + \left( {l_{4d} /L} \right)^{{{2 \mathord{\left/ {\vphantom {2 {3}}} \right. \kern-0pt} {3}}}} }}{ - }\frac{{\left( {l_{3d} } \right)^{2/3} }}{{1 + \left( {l_{3d} /L} \right)^{2/3} }}} \right] \cdot C^{2} e^{{ - \frac{{h_{i} + h_{j} }}{{h_{sc} }}}}$$
(11)

where C and L are empirical coefficients and l3d and l4d are the distances of each two voxels at the same and different epochs, respectively. hi, hj and hsc are the height of the voxel i, the voxel j and the tomographic region, respectively.

To optimize the state noise covariance matrix, we focused on the spatial structure function of water vapor density in two voxels (Gradinarsky and Jarlemark 2004), which is defined as follows:

$${\varvec{D}}_{X} \left( {i,l} \right) = E\left\{ {\left[ {{\varvec{X}}_{i + l} - {\varvec{X}}_{i} } \right]^{2} } \right\}$$
(12)

where l is the distance between each two voxels, i represents the position vector of the corresponding voxel, and Xi is its water vapor density. DX represents the covariance matrix of the two epochs, and E refers to the mathematical expectation. Then the historical water vapor information derived from the reanalysis data could be utilized to improve the state noise covariance values. In practice, the ERA5 (Hersbach et al. 2020), which is the fifth-generation atmospheric reanalysis provided by European Centre for Medium-Range Weather Forecasts (ECMWF), was selected to calculate the historical water vapor density of the voxels as follows:

$$X = \frac{{6.11 \times 10^{{\left( {\frac{7.5 \times T}{{237.3 + T}}} \right)}} \times RH}}{{R_{v} T}}$$
(13)

where T and RH are the air temperature in Kelvin (K) and the relative humidity in kg kg−1, respectively. Rv is a constant with the value of \(461.5\;{\text{J}} \cdot {\text{kg}}^{ - 1} \cdot {\text{K}}^{ - 1}\). Then the state noise covariance value of the two voxels can be expressed as follows:

$$Q_{ij} = E\left[ {\left( {{\varvec{X}}_{i} \left( {k + 1} \right) - {\varvec{X}}_{i} \left( k \right)} \right)\left( {{\varvec{X}}_{j} \left( {k + 1} \right) - {\varvec{X}}_{j} \left( k \right)} \right)} \right]\left( {k = 1,2 \cdots } \right)$$
(14)

where \({\varvec{X}}_{i} \left( k \right)\) denotes the water vapor density of voxel i at historical epoch k.

To optimize the observation noise covariance matrix, the elevation angles of the satellite signal and its intercept across the tomographic region were utilized to determine the weights of the available SWV observations, as below:

$$W_{i}^{e} = \sin^{2} \left( {ele} \right)$$
(15)
$$W_{i}^{d} = 1/\left( {1 + Dis} \right)$$
(16)
$$W_{i} = W_{i}^{e} \cdot W_{i}^{d}$$
(17)

where ele and Dis are the corresponding elevation angle and the intercept of voxel i, respectively. \(W_{i}^{e}\) and \(W_{i}^{d}\) refer to the weight based on elevation angle and intercept in voxel i, respectively. \(W_{i}\) represents the weight of ith SWV observation used in the tomographic model. Accordingly, the diagonal elements of the observation noise covariance matrix are the inverse of the weights mentioned above.

Experiment

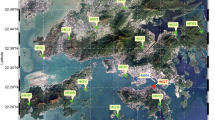
To evaluate the performance of the optimized noise covariance matrix in water vapor tomography, we selected Hong Kong as the research area to experiment. This region was chosen due to its classification as a marine subtropical monsoon climate, characterized by relatively high levels of water vapor and precipitation throughout the year. The Hong Kong Satellite Positioning Reference Station Network (SatRef) also consists of a dense network of GNSS sites, providing ample GNSS observation data for analysis. The horizontal boundary of the research area in west–east and south–north directions was 113.87ºE to 114.35ºE and 22.19ºN to 22.54ºN, with horizontal resolutions of 0.06º and 0.05º for longitudinal and latitudinal directions, respectively. In the vertical direction, the study area extended from the earth's surface to 8 km, with a resolution of 800 m, covering a total of 560 voxels. Figure 1 illustrates the location of thirteen GNSS stations, represented by red pentagons, which provided the slant water vapor (SWV) observations for the tomographic model. Additionally, the GNSS station named HKQT and the radiosonde station were utilized as references to assess the accuracy of the tomographic results.

Fig. 1
figure 1

Distribution of GNSS stations, radiosonde sites and the horizontal structure of the voxels in the study region

Full size image

One month of GNSS observation data from DOY 121 to 151 of 2022, during which the number of rainy and rainless days in Hong Kong was relatively average, were processed using the GAMIT 10.71 software (Herring et al. 2018). The data included GPS, BDS, GLONASS and Galileo constellations observations. The processing was based on a double-differenced model and aimed to obtain tropospheric parameters, including ZTD and gradients. In processing, a cutoff elevation angle of 15º and a sampling rate of 30 s were set for the observations. The LC_AUTCLN and BASELINE modes were adopted as the processing strategies. LC_AUTCLN represents the ionospheric-free linear combination of the GNSS observations, while BASELINE mode indicates that the orbital parameters were fixed. To reduce the strong correlation among tropospheric parameters due to the short baseline, three IGS sites, namely JFNG (30.5ºN, 114.5ºE), LHAZ (29.7ºN, 91.1ºE) and URUM (43.8ºN, 87.6ºE), were incorporated into the data processing. The ZHD values were achieved using the measured pressure from the meteorological sensor; then, the SWV observations used for the tomographic model were calculated using (1) and (2). In the experiment, two types of noise covariance matrix provided by the traditional method and the proposed method were utilized in the Kalman filter solution for the tomography and the estimated water vapor density obtained from both methods was compared and analyzed.

Validation of the slant water vapor

Using the estimated water vapor densities obtained from tomography and the distance of the signal rays crossing each voxel, the SWV values at the HKQT site can be computed by (4). That is, the parameters on the right side of (4) are taken as known quantities and the left side is unknown; thus, the estimated SWV is called as tomography-computed SWV. Figure 2 shows the scatter plots of the tomography-computed SWV of the two methods and the corresponding GAMIT-estimated SWV during the experimental period. In this figure, the red line refers to a linear fit line between the tomography-computed SWV and the GAMIT-estimated SWV and the black dashed line corresponds to a straight line with an angle of 45º. It can be seen that the proposed method outperforms the traditional method, as more points are concentrated near the fitted line. Specifically, the slope of the linear fitting for the proposed method is 0.9985, whereas it is 0.9786 for the traditional method.

Fig. 2
figure 2

Scatter plots of the tomography-computed SWV against the reference SWV for the traditional and proposed methods

Full size image

Figure 3 shows how the differences of the tomography-computed and GAMIT-estimated SWV changes with elevation angle. The blue and red dots in this figure refer to the traditional and our proposed methods, respectively. Both methods show the same trend, that is, the SWV differences increase as the elevation angle decreases. The largest absolute difference values are 12.7 mm for the traditional method and 9.0 mm for the proposed method. For the traditional method, the root-mean-square error (RMSE) is 2.42 mm and the mean absolute error (MAE) is 1.72 mm. Also, RMSE and MAE values for the proposed method are 1.48 and 1.12 mm with approximately 38.8% and 34.9% improvements, respectively. More than 84.1% of the SWV differences are located in the range of − 2.0 to 2.0 mm for the proposed method, while the percentage was 71.0% for the traditional method. When the range is expanded to − 5.0 to 5.0 mm, these percentages are 99.4% and 94.7% for the proposed and traditional methods, respectively.

Fig. 3
figure 3

Scatter plots of the changes of SWV residuals with elevation angle for the evaluated methods

Full size image

The SWV differences were further grouped into individual elevation bins of 5 degrees, where each bin represents a range of elevation angles (e.g., 15º to 20º). The RMSE of each elevation bin of both methods was calculated, and their changes with the elevation angle are shown in Fig. 4. This figure indicates the RMSE reduction as the increasing elevation angle for the both evaluated methods, which is consistent with their trend in Fig. 3. According to the figure, in all elevation bins, the RMSE values of the proposed method are better than 4 mm, especially for the elevation angles less than 35º. The maximum and minimum improvements of the SWV differences are 22.05 and 0.41 mm for the proposed method, respectively, appearing in the range of 20º to 25º and greater than 80º.

Fig. 4
figure 4

RMSE of each elevation bin for the two evaluated methods

Full size image

Comparison of the obtained results with radiosonde and ERA5 data

The water vapor density profiles derived from radiosonde data are considered as the reference to validate the tomographic results. Figure 5 compares the estimated water vapor density by the investigated methods and radiosonde data at different altitudes on UTC 11:45–12:15, DOY 121, 135 and 151 of 2022. These three days are the beginning, middle and end of the month with precipitation of 32.4, 26.2 and 0 mm. According to the figure, the water vapor density increased with decreasing height. The estimated water vapor density obtained by the proposed method, represented by the red lines, exhibits better agreement with the radiosonde-derived data, particularly in the lower atmosphere near the earth surface.

Fig. 5
figure 5

Water vapor density comparison between radiosonde data and the two evaluated methods

Full size image

To further assess the tomographic results using the radiosonde data, the residuals between the tomographic water vapor density and that derived from radiosonde data were counted for each day of the experimental period, and their RMSE was also calculated. Figure 6 represents boxplots illustrating the statistical characteristics of these residuals and RMSE. In the boxplots, Q1 and Q3 represent the first and third quartiles, respectively, while Q2 refers to the second quartile located within the box. The quartiles divide a set of residuals into four sections, each representing 25% of the residuals. According to the figure, it can be observed that the proposed method exhibits a smaller range of bounds and box length (the range from Q1 to Q3) compared to the traditional method in both panels. This suggests that the proposed method yields more favorable WVD residuals and RMSE distributions than the traditional method. The values of Q1, Q2 and Q3 for the residual comparison are − 0.23, 0.57 and 1.44 g/m3 for the traditional method and − 0.24, 0.35 and1.14 g/m3 for the proposed method, respectively. In the RMSE comparison, the quartiles show that 50% of the RMSE is concentrated in the range of 1.15 to 2.17 g/m3 for the traditional method and 0.96 to 1.56 g/m3 in the proposed method. The average RMSE and median for the proposed method are 1.26 and 1.27 g/m3, outperforming the traditional method with approximately 23.2% and 27.4% improvement. In addition, the differences in the water vapor density at different layers were computed for both evaluated methods using the radiosonde data as references, and their statistics are listed in Table 1. It is observed that the proposed method outperforms the traditional method in each height layer, exhibiting lower RMSE and MAE values. The mean RMSE and MAE values for the proposed method are 1.26 g/m3 and 0.99 g/m3, respectively, while for the traditional method, the corresponding values are 1.58 g/m3 and 1.30 g/m3.

Fig. 6
figure 6

Boxplot of the residuals and RMSE between the radiosonde data and the two evaluated methods

Full size image
Table 1 RMSE and MAE values of the water vapor density from the investigated methods at different layers using radiosonde as references (values in g/m3)
Full size table

Figure 7 indicates the three-dimensional distribution of SWD derived from the two investigated methods along with the computed water vapor density from the ERA5 reanalysis data as a reference at UTC 12:00, DOY 135 of 2022, through the troposphere. According to the tomographic results, both evaluated methods can describe the spatial distribution of water vapor. However, the proposed method demonstrates closer agreement with the ERA5 data in certain voxels than the traditional method. Moreover, the water vapor density derived from both methods at different layers was compared to the computed values from ERA5 data, and the corresponding statistics are listed in Table 2. It can be seen that the accuracy of the water vapor density derived from both methods is improved by moving upward. This can be attributed to the decreasing amount of water vapor with the increasing height of the atmosphere. The proposed method outperformed the traditional one in each layer with better RMSE and MAE values. Specifically, the mean RMSE and MAE values have been decreased from 1.56 and 1.06 g/m3 to 1.13 and 0.59 g/m3, with an approximate improvement of 27.6% and 44.3%, respectively.

Fig. 7
figure 7

Three-dimensional distribution of water vapor density computed from the evaluated methods and ERA5 data

Full size image
Table 2 RMSE and MAE values of the water vapor density from the investigated methods at different layers (values in g/m3)
Full size table

Conclusion

We proposed a new water vapor tomography method based on a Kalman filter with an optimized noise covariance matrix to estimate the three-dimensional water vapor density accurately. The proposed method establishes the state noise covariance matrix based on the historical water vapor information derived from the atmospheric reanalysis data. It constructs the observation noise covariance matrix considering the elevation angle and the intercept crossing the voxels by the signal rays.

The proposed method is validated by water vapor tomographic experiments using the GNSS data collected over HONG KONG from DOY 121 to 151 of 2022. In a comparison between the GAMIT-estimated SWV and tomography-computed SWV at HKQT site, the RMSE and MAE of the proposed method are 1.48 and 1.12 mm, outperforming the traditional method with an improvement of 38.8% and 34.9%, respectively. In addition, the tomographic results obtained using the proposed method exhibited better agreement with both radiosonde and ERA5 data compared to the traditional method. When compared to radiosonde data, the proposed method achieved an average RMSE and MAE of 1.26 g/m3 and 1.00 g/m3, respectively, while against ERA5 data, the corresponding values were 1.13 g/m3 and 0.59 g/m3, indicating improvements of approximately 23.2% and 24.8%, as well as 27.6% and 44.3%, respectively, compared to the traditional method. Future studies should consider additional influencing factors such as different weather conditions, the number of available satellite systems, and the density and distribution of GNSS sites to further enhance the accuracy and applicability of the water vapor tomography.