Introduction

Troposphere delay can be divided into vertical and horizontal component in safety–critical civil aviation precision approach supported by ground-based augmentation system (GBAS). Under the normal tropospheric activity, the vertical differential troposphere delay can be corrected using the standard model based on the empirical tropospheric refractivity index recommended by DO-253C (RTCA 2008). The horizontal differential troposphere delay can be eliminated due to the spatial correlation between the horizontal tropospheric gradients. Therefore, the troposphere delay can be mitigated sufficiently by the dual-correction processing.

Under the abnormal tropospheric activity due to the dramatic changes in local meteorological parameters, the horizontal differential troposphere delay caused by horizontal tropospheric gradient between ground facility and aircraft is relatively large and may induce hazardous misleading position error. The abnormal horizontal differential troposphere delay measured in range domain is defined as the non-nominal troposphere in this contribution (Zhang et al. 2018). With the development of global navigation satellite system (GNSS) meteorology, various non-nominal troposphere events have been observed in local atmospheric abnormal activities (Lawrence et al. 2006; Huang and Graas 2007; Yu and Liu 2021). For example, an extreme non-nominal troposphere of approximately 0.4 m caused by the hazardous horizontal tropospheric gradients is observed at the baseline of 5 km in Ohio (Huang et al. 2008), which is unacceptable for high-precision navigation. With the rapid development of GNSS modernization, the dual-frequency multi-constellation corrections have been designated to support GBAS approach service types-F (Circiu et al. 2017). The navigation and integrity performance benefits from more measurement redundancy because the increased number of visible satellites and the available dual-frequency signals. Specifically, ionospheric-free combination can be used to eliminate the first order of ionospheric effect. Unfortunately, the non-nominal troposphere remains an integrity risk for future GBAS approach service type-F, because troposphere delay is independent with the frequency. Consequentially, the non-nominal troposphere is non-negligible for the demanding integrity requirement of GBAS.

To evaluate the impact of the non-nominal troposphere on GBAS integrity, the protection level of the position domain is used for bounding the potential positioning errors. Guilbert et al. (2015) have proven that the non-nominal troposphere can be effectively bounded by a conservative inflation of Vertical Protection Level (VPL) based on the empirical model. However, sufficient experiments have demonstrated that the average increment of VPL caused by the non-nominal troposphere is larger than 2.32 m, which means the availability of GBAS will be significantly impacted (Wang et al. 2017). Furthermore, the empirical models based on the historical meteorological data collected at fixed locations may not adequately represent the potential non-nominal troposphere, which will increase the integrity risks of GBAS (Walpersdorf et al. 2007; Chen et al. 2011). In general, it is challenging to satisfy the integrity and availability requirements of GBAS simultaneously by bounding the non-nominal troposphere. Therefore, the ground facility should take more responsibility for detecting the non-nominal troposphere to improve the integrity and the availability of GBAS.

The international civil aviation organization-navigation systems panel (ICAO-NSP) shows an unexpected atmospheric behavior using Honeywell’s GAST D ionospheric gradient monitor, which has been confirmed by Federal Aviation Administration (FAA) and Boeing to be associated with the non-nominal troposphere rather than the anomalous ionospheric gradient (Alexander 2014). It is no doubt that the non-nominal troposphere can be detected efficiently by the carrier phase-based ground monitor when the ambiguity is correctly fixed (Jing et al. 2014). The failure modes of the carrier phase-based ground monitor are the collection of the non-nominal troposphere and ambiguity resolution failure, when the anomalous ionospheric gradient is assumed to be correctly detected and excluded. To enhance the false alarm and the missed detection performance of the non-nominal troposphere monitoring, the overall false alarm and missed detection rate have to be allocated among the complete failure modes. Without independent ambiguity resolution, one solution is to directly treat the ambiguity and the non-nominal troposphere as a combined quantity in the monitoring model, which simplifies the complex failure modes by sacrificing the continuity of effective monitoring range (Khanafseh et al. 2012). Patel et al. (2020) proposed the fixed allocation method with the theoretical ambiguity resolution success rate to simultaneously detect the non-nominal troposphere and ambiguity resolution failure. The multi-detection thresholds were used for constraining the false alarm and missed detection errors to compensate for the unacceptable theoretical ambiguity resolution success rate. However, when the ambiguity is correctly fixed, but its theoretical ambiguity resolution success rate is not satisfactory, the over-conservative multi-detection thresholds will limit the detection sensitivity. Consequently, it can be concluded that the dynamic allocation of the false alarm and missed detection rate according to the real-time situation of ambiguity resolution is crucial for the detection sensitivity of the non-nominal troposphere monitoring.

To isolate the impact of the ambiguity resolution failure on the non-nominal troposphere monitoring, a two-step monitoring method is proposed based on the multiple short-baseline reference receivers. Specifically, the ambiguity resolution monitoring (ARM) is carried out in the first step. The non-nominal troposphere monitoring (NTM) is carried out in the second step. The ARM result is considered as the driving factor for allocating the overall false alarm and missed detection rate between the two-step monitoring of the ambiguity resolution and the non-nominal troposphere. By dynamically adjusting the false alarm and missed detection allocation coefficients, the detection sensitivity of the NTM can be significantly improved, which is the main motivation of this research.

The non-nominal troposphere threat model and the ground facility configuration are introduced first. Next, we construct the test statistics for two-step monitoring-based multiple short-baseline reference receivers, respectively. Then, the dynamic allocation concept of the proposed two-step monitoring method is derived by constraining the false alarm and missed detection errors, simultaneously. Finally, the real BDS dual-frequency data are utilized to evaluate the improvement of non-nominal troposphere monitoring performance and summarize the research findings.

Non-nominal troposphere threat model

The hazardous horizontal tropospheric gradient is closely related to the drastic changes of local meteorological parameters such as temperature, pressure and specific humidity (Huang et al. 2007). Under the abnormal tropospheric activity, the maximum changing rate of temperature, pressure, and specific humidity can be up to 10 °C/h, 5 hPa/h and 0.003/h, respectively (Zhang et al. 2018). To investigate the impact of the hazardous horizontal tropospheric gradient on differential measurements, the classical weather wall model is used for characterizing the non-nominal troposphere, as shown in Fig. 1 (Huang et al. 2008; Graas and Zhu 2011). When the satellite signal to the ground facility leaves the common troposphere layer, it faces the different meteorological conditions (Path 1) than the satellite signal to the aircraft that continues in the weather wall (Path 2). The differential measurement across spatially separated reference receivers can be used for detecting the non-nominal troposphere. In addition, it can be induced that the detection sensitivity of the ground monitoring facility is immune to the baseline length between the spatially separated reference antennas, because the non-nominal troposphere based on the classic weather wall model is independent with the baseline length.

Fig. 1
figure 1

Weather wall non-nominal troposphere model

Full size image

Multiple antenna configuration

The ground facility of GBAS contains multiple spatially separated reference receivers and antennas, which provide the hardware basis for the NTM. Li et al. (2020) have verified that the use of multiple spatially separated antennas is conducive to improving the integrity monitoring performance. Another advantage is that the multiple short-baseline antennas can be used for the ARM, which will reduce the threats of ambiguity resolution failure for the NTM (Khanafseh et al. 2006). Figure 2 shows the multiple antennas configuration used for the proposed two-step monitoring method. Antenna a1 and a2 form the baseline b1, and antenna a3 and a4 form the baseline b2. Under the optimal conditions, b1 and b2 are parallel to the centerline of the runway to improve the detection sensitivity ultimately. It should be noted that this optimal antenna configuration imposes high requirements on the airport which may limit the applicability. In general, the detected differential troposphere delay in the b1 direction (T) can be converted to the runway direction (\(\overline{T}\)) by projecting the tropospheric mapping function as (Douša 2010; Belabbas et al. 2011; Guilbert et al. 2017),

$$ \begin{gathered} \Delta \nabla \bar{T}_{{b_{1} }}^{{s - s^{\prime } }} = \left[ {m\left( {\theta _{{a_{1} }}^{s} ,\psi _{{a_{1} }}^{s} } \right) - m\left( {\theta _{{a_{1} }}^{{s^{\prime } }} ,\psi _{{a_{1} }}^{{s^{\prime } }} } \right)} \right] \times \cos \beta \times ZTD_{{a_{1} }} \hfill \\ \quad \quad \quad \quad - \left[ {m\left( {\theta _{{a_{2} }}^{s} ,\psi _{{a_{2} }}^{s} } \right) - m\left( {\theta _{{a_{2} }}^{{s^{\prime } }} ,\psi _{{a_{2} }}^{{s^{\prime } }} } \right)} \right] \times \cos \beta \times ZTD_{{a_{2} }} \hfill \\ \quad \quad \quad \quad = \Delta \nabla T_{{b_{1} }}^{{s - s^{\prime } }} \times \cos \beta \hfill \\ \end{gathered} $$
(1)

where \(\Delta \nabla\) indicates the double-difference (DD) operation between antennas and satellites, m expresses the relation between a troposphere delay in any elevation and zenith, \(\theta\) and \(\psi\) indicate the elevation and azimuth angle, respectively. The superscript s and \(s^{\prime}\) indicate the faulty-free satellite and the faulty satellite affected by the non-nominal troposphere, ZTD indicates the zenith total delays above each antenna, \(\beta\) indicates an angle between the baseline b1 and the runway centerline. It can be found that the non-nominal troposphere detection sensitivity along the runway direction will decrease with the increasing of \(\beta\). Therefore, the parallel baseline geometry is recommended as the optimal multiple antenna configuration for the proposed monitoring method.

Fig. 2
figure 2

Optimal configuration of multiple short-baseline receivers

Full size image

Ambiguity resolution monitoring

Since the stringent requirement of the ambiguity resolution reliability can hardly be satisfied by applying the ambiguity validation methods such as the ratio test and the success rate evaluation, an ambiguity resolution correctness monitoring method is carried out in the first step. Considering the geometric range can be corrected with the precise location of antennas and the orbit ephemerides, the test statistics t1 for the ARM can be constructed as,

$$ \begin{aligned} t_{1,f} &= \Delta \nabla \phi_{{f,b_{1} }}^{{s - s^{\prime}}} - \Delta \nabla \phi_{{f,b_{2} }}^{{s - s^{\prime}}} \\ & = \left( {\Delta \nabla \overline{T}_{{b_{1} }}^{{s - s^{\prime}}} - \Delta \nabla \overline{T}_{{b_{2} }}^{{s - s^{\prime}}} } \right) - \alpha_{f} \left( {\Delta \nabla I_{{b_{1} }}^{{s - s^{\prime}}} - \Delta \nabla I_{{b_{2} }}^{{s - s^{\prime}}} } \right) \\ & \quad + \lambda_{f}^{{}} \left( {\Delta \nabla {\mathbf{N}}_{{f,b_{1} }}^{{s - s^{\prime}}} - \Delta \nabla {\mathbf{N}}_{{f,b_{2} }}^{{s - s^{\prime}}} } \right) + \varepsilon_{{t_{1} }} \\ \end{aligned} $$
(2)

where \(\phi\) indicates the carrier phase measurements in meters, the subscript f is the frequency of carrier phase, I indicates the ionosphere delay, \(\alpha_{f}\) is the ratio of the ionosphere delay at f frequency to the delay at L1 frequency, Nf is the integer ambiguity with the corresponding wavelength of \(\lambda_{f}\), \(\varepsilon_{{t_{1} }}\) is the Gaussian-distributed noise of the test statistic t1. It can be found from (2) that when baseline b1 and b2 are closely spaced, it is feasible to ignore the residual troposphere delay and ionosphere delay in test statistic t1 due to the strong correlation of atmosphere delay. Thus, the ambiguity becomes the primary error source which dominates the distribution characteristics of test statistics.

Although the ionosphere is assumed to be quiet, the typical geometry-based ambiguity estimate model will be impacted by the non-nominal troposphere and ionosphere delay. Therefore, the dual-frequency ionospheric-restricted and geometry-free model are used for ambiguity estimating. It should be noted that the subscript of the reference receiver and the superscript of the satellite will be ignored to ensure concise expression.

We first estimate the wide lane ambiguity (NWL) by the Melbourne–Wübbena (MW) combination as,

$$ \Delta \nabla N_{WL} = \frac{{\Delta \nabla \phi_{WL} - \Delta \nabla P_{WL} }}{{\lambda_{WL} }} = \left[ {\frac{{\left( {\frac{{f_{1} \Delta \nabla \phi_{1} - f_{2} \Delta \nabla \phi_{2} }}{{f_{1} - f_{2} }}} \right) - \left( {\frac{{f_{1} \Delta \nabla P_{1} + f_{2} \Delta \nabla P_{2} }}{{f_{1} + f_{2} }}} \right)}}{{\frac{c}{{f_{1} - f_{2} }}}}} \right] $$
(3)

where P is the code measurements, \(\left[ \cdot \right]\) indicates the rounding estimator. Although the LAMBDA algorithm has better ambiguity resolution performance, the rounding estimator is selected to accurately obtain the ambiguity resolution success rate with the analytical probability density distributions, which is beneficial for the allocation of false alarm and missed detection rate (Teunissen 2001; Li et al. 2018; Cheng et al. 2020). Moreover, in order to improve the reliability of ambiguity resolution, the multiple epochs moving average method is adopted to suppress the combined noise. The number of accumulated epochs is defined as the averaging length.

When the wide lane ambiguity is correctly fixed, the narrow lane ambiguity (N1 and N2) can be fixed as,

$$ \begin{gathered} \Delta \nabla N_{1} = \left[ {\frac{{\Delta \nabla \phi _{1} - \Delta \nabla \phi _{2} - \lambda _{2} \Delta \nabla N_{{{\text{WL}}}} }}{{\lambda _{1} - \lambda _{2} }}} \right]\Delta \nabla N_{2} \hfill \\ \quad \quad \;\;\;\;\; = \Delta \nabla N_{1} - \Delta \nabla N_{{{\text{WL}}}} \hfill \\ \end{gathered} $$
(4)

After the narrow lane ambiguity is correctly fixed, it can be induced that the test statistic t1 follows the zero-mean Gaussian distribution. Thus, the false alarm error of the ARM can be expressed when the test statistics exceed the detection threshold,

$$ P_{fa1} = P\left\{ {\left| {t_{1} } \right| > T_{1} \left| {CF} \right.} \right\} = \int_{ - \infty }^{{ - T_{1} }} {\frac{1}{{\sqrt {2\pi } \sigma_{{t_{1} }} }}} \exp \left\{ { - \frac{{x^{2} }}{{2\sigma_{{t_{1} }}^{2} }}} \right\}dx + \int_{{T_{1} }}^{\infty } {\frac{1}{{\sqrt {2\pi } \sigma_{{t_{1} }} }}} \exp \left\{ { - \frac{{x^{2} }}{{2\sigma_{{t_{1} }}^{2} }}} \right\}dx $$
(5)

where Pfa1 indicate the required false alarm rate of the ARM; CF indicates the correct ambiguity fixing; \(\sigma_{{t_{1} }}\) is the standard deviation of test statistic t1; T1 is the detection threshold of the ARM which can be calculated as,

$$ T_{1} = k_{fa1} \sigma_{{t_{1} }} = - \Phi^{ - 1} \left( {\frac{{P_{fa1} }}{2}} \right)\sigma_{{t_{1} }} $$
(6)

where \(\Phi \left( x \right) = \int_{ - \infty }^{x} {\frac{1}{{\sqrt {2\pi } }}\exp \left( { - \frac{1}{2}v^{2} } \right)} \;dv\) is the Gaussian cumulative probability function. By comparing the test statistics t1 with the detection threshold T1, the incorrect ambiguity can be effectively detected. Once the ARM triggers an alert, the ambiguity needs to be re-fixed by extending the averaging length until it is passed. In other words, for the newly acquired and re-acquired satellites, the float ambiguity requires a period of averaging length for fixing, which will cause the time to alert (TTA) fail to meet the requirement of precision approach. In general, the averaging length is less than 100 epochs to reduce the loss of TTA performance.

When the test statistics t1 is less than the detection threshold T1, the resulting missed detection rate Pmd1 of the ARM should be evaluated under the ambiguity resolution failure hypothesis,

$$ P_{{md1\left| {IF_{i} } \right.}} = P\left\{ {\left| {t_{1} } \right| < T_{1} \left| {IF_{i} } \right.} \right\} = \int_{{ - T_{1} }}^{{T_{1} }} {\frac{1}{{\sqrt {2\pi } \sigma_{{t_{1} }} }}} \exp \left\{ { - \frac{{\left( {x - i\lambda } \right)^{2} }}{{2\sigma_{{t_{1} }}^{2} }}} \right\}dx = \Phi \left( {\frac{{T_{1} - i\lambda }}{{\sigma_{{t_{1} }} }}} \right) - \Phi \left( {\frac{{ - T_{1} - i\lambda }}{{\sigma_{{t_{1} }} }}} \right) $$
(7)

where IF indicates the incorrect ambiguity fixing. \(i \in Z\) indicates the different ambiguity resolution failure modes. If the incorrect ambiguity fixing is not detected by the ARM, it will increase the false alarm and missed detection error of the NTM. Thus, the integrity risk of the ARM caused by ambiguity resolution failures is crucial for the NTM which can be evaluated as,

$$ P_{{{\text{md1}}\left| {{\text{IF}}_{{\text{i}}} } \right.}} P_{{{\text{IF}}_{i} }} = P_{{md1\left| {\left( {{\text{CFIIF}}_{i} } \right)} \right.}} P_{{{\text{CF}}_{{b_{1} }} }} P_{{{\text{IF}}_{{i,b_{2} }} }} + P_{{{\text{md}}1\left| {\left( {{\text{IF}}_{i} \cap {\text{CF}}} \right)} \right.}} P_{{{\text{IF}}_{{i,b_{1} }} }} P_{{{\text{CF}}_{{b_{2} }} }} + P_{{{\text{md}}1\left| {\left( {{\text{IF}}_{i} \cap {\text{IF}}_{i} } \right)} \right.}} P_{{{\text{IF}}_{{i,b_{1} }} }} P_{{{\text{IF}}_{{i,b_{2} }} }} $$
(8)

where PCF and PIF can be calculated by the normal cumulative probability function (Teunissen 1998; Li et al. 2017). Since the ambiguity resolution success and failure rate are equal between b1 and b2, the baseline subscripts are ignored for simplicity. In addition, the conservative assumption that PCF = 1 is adopted because PIF is much smaller than PCF after multi-epoch averaging. Furthermore, if the incorrect fixing event is present for b1 and b2, simultaneously, the ARM will be invalidated due to the neutralization of integer biases. Thus, a conservative assumption, i.e., \(P\left\{ {\left| {t_{1} } \right| < T_{1} \left| {{\text{IF}}_{{i,b_{1} }} \cap {\text{IF}}_{{i,b_{2} }} } \right.} \right\} = 1\), is adopted to describe the upper bound of (8) as,

$$ P_{{{\text{md}}1\left| {{\text{IF}}_{{\text{i}}} } \right.}} P_{{{\text{IF}}_{i} }} < 2P_{{{\text{IF}}_{i} }} P_{{{\text{md}}1\left| {\left( {{\text{CF}} \cap {\text{IF}}_{i} } \right)} \right.}} { + }P_{{{\text{IF}}_{i} }}^{2} $$
(9)

Since the detection threshold T1 is determined from the false alarm constraint, the resulting missed detection rate for different ambiguity failure modes is constant without changing the required Pfa1. Thus, the integrity risk of the ARM is impacted by the ambiguity resolution reliability, which can be further expressed as a function of averaging length. This provides a basis for the dynamic allocation of false alarm and missed detection rates between the ARM and the NTM. When the ARM raises no alarms, the NTM will be performed.

Non-nominal troposphere monitoring

With the fixed narrow lane ambiguity, the high-accuracy DD carrier phase residuals can be expressed as,

$$ \Delta \nabla r_{{f,b_{n} }}^{{s - s^{\prime}}} = \Delta \nabla \phi_{{f,b_{n} }}^{{s - s^{\prime}}} - \left( {\nabla {\mathbf{e}}^{{s - s^{\prime}}} } \right)^{T} {\mathbf{b}}_{n} - \lambda_{f}^{{}} \Delta \nabla {\mathbf{N}}_{{f,b_{n} }}^{{s - s^{\prime}}} = \Delta \nabla \overline{T}_{{b_{n} }}^{{s - s^{\prime}}} - \alpha_{f} \Delta \nabla I_{{b_{n} }}^{{s - s^{\prime}}} + \varepsilon_{\Delta \nabla \phi } $$
(10)

where es indicate the line-of-sight unit vector from ground facility to satellite s, b indicate the baseline vector, n indicate the number of baselines, \(\varepsilon_{\Delta \nabla \phi }\) indicate the noise of DD carrier phase. The ionospheric-free (first-order) test statistic t2 is used for the NTM,

$$ t_{2} = \frac{{f_{1}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}r_{{1,b_{n} }}^{{s - s^{\prime}}} - \frac{{f_{2}^{2} }}{{f_{1}^{2} - f_{2}^{2} }}r_{{2,b_{n} }}^{{s - s^{\prime}}} = \Delta \nabla \overline{T}_{{b_{n} }}^{{s - s^{\prime}}} + \varepsilon_{{t_{2} }} $$
(11)

where \(\varepsilon_{{t_{2} }}\) is the test statistic noise whose standard deviation is approximately three times larger than that of ionosphere-based test statistics proposed by Yu and Liu (2021). From (11), we know that the test statistic t2 trades the decorrelation monitoring ability by losing part of the measurement accuracy. Nonetheless, the test statistic t2 is still sensitive to the non-nominal troposphere due to the high precision of the carrier phase.

For the non-nominal troposphere monitoring, we defined two mutually exclusive hypotheses, i.e., the fault-free hypothesis H0: troposphere is healthy, and the alternative hypothesis H1: troposphere is faulty. The false alarm and the missed detection errors must be constrained simultaneously to satisfy the integrity requirement of safety–critical civil aviation precision approach applications.

Under the H0 hypothesis, the false alarm errors will occur when both of the following constraints are satisfied simultaneously, i.e., 1) the test statistic t1 is smaller than the detection threshold T1; 2) the test statistic t2 is larger than the detection threshold T2. Therefore, depending on the monitoring result of the ARM, the overall false alarm rate Pfa has two component sources which can be expressed as,

$$ \begin{aligned} P_{fa} = & P\left\{ {\left| {t_{1} } \right| < T_{1} \cap \left| {t_{2} } \right| > T_{2} \left| {H_{0} } \right.} \right\} \\ & \quad = \left( {P\left\{ {\left| {t_{1} } \right| < T_{1} \left| {CF} \right.} \right\}P_{CF} + \sum\limits_{i \in Z}^{{}} {P\left\{ {\left| {t_{1} } \right| < T_{1} \left| {IF_{i} } \right.} \right\}P_{{IF_{i} }} } } \right)P\left\{ {\left| {t_{2} } \right| > T_{2} \left| {H_{0} } \right.} \right\} \\ & \quad = (1 - P_{fa1} )P_{CF} P_{{fa2\left| {CF} \right.}} + \sum\limits_{i \in Z}^{{}} {P_{{md1\left| {IF_{i} } \right.}} P_{{IF_{i} }} P_{{fa2\left| {IF_{i} } \right.}} } \\ \end{aligned} $$
(12)

where T2 is the detection threshold of the NTM. Pfa2 is the allocated false alarm rate of the NTM, which can be calculated as,

$$ \begin{array}{*{20}l} {P_{{fa2\left| {CF} \right.}} = P\left\{ {\left| {t_{2} } \right| > T_{2} \left| {H_{0} ,CF} \right.} \right\} = \Phi \left( {\frac{{ - T_{2} }}{{\sigma_{{t_{2} }} }}} \right) + 1 - \Phi \left( {\frac{{T_{2} }}{{\sigma_{{t_{2} }} }}} \right)} \hfill \\ {P_{{fa2\left| {IF_{i} } \right.}} = P\left\{ {\left| {t_{2} } \right| > T_{2} \left| {H_{0} ,IF_{i} } \right.} \right\} = \Phi \left( {\frac{{ - T_{2} - \tau_{i} }}{{\sigma_{{t_{2} }} }}} \right) + 1 - \Phi \left( {\frac{{T_{2} - \tau_{i} }}{{\sigma_{{t_{2} }} }}} \right)} \hfill \\ \end{array} $$
(13)

where \(\tau_{i}\) indicates the ionospheric-free combined bias caused by the ambiguity resolution failure mode I; \(\sigma_{{t_{2} }}\) is the standard deviation of test statistic t2. We conservatively assume that all the incorrect ambiguity fixing events will trigger an alert in the NTM, i.e., \(P_{{{\text{fa2}}\left| {{\text{IF}}_{i} } \right.}} = 1\). By substituting (9) into (12), the upper bound of (12) can be obtained as,

$$ P_{fa} < (1 - P_{fa1} )P_{CF} P_{{fa2\left| {CF} \right.}} + \sum\limits_{i \in Z} {\left[ {2P_{{IF_{i} }} P_{{md1\left| {\left( {CF \cap IF_{i} } \right)} \right.}} + P_{{IF_{i} }}^{2} } \right]} $$
(14)

thus, the false alarm error can be constrained when the upper bound of (12) is less than or equal to the required overall false alarm rate Pfa. It is desirable to adjust the allocation coefficient \(\alpha\) according to the contribution of each term of (14) to the overall false alarm rate to achieve the optimal false alarm performance. Since the last term of (14), i.e.,\(\sum\limits_{i \in Z} {2P_{{{\text{IF}}_{i} }} P_{{{\text{md1}}\left| {\left( {{\text{CF}} \cap {\text{IF}}_{i} } \right)} \right.}} { + }P_{{{\text{IF}}_{i} }}^{2} }\) is only related to the integrity risk of the ARM, the allocation coefficient \(\alpha\) can be determined as,

$$ \alpha P_{{{\text{fa}}}} = \sum\limits_{i \in Z} {\left[ {2P_{{{\text{IF}}_{i} }} P_{{{\text{md1}}\left| {\left( {{\text{CF}} \cap {\text{IF}}_{i} } \right)} \right.}} { + }P_{{{\text{IF}}_{i} }}^{2} } \right]} $$
(15)

from (15), we know that the allocation coefficient \(\alpha\) will be dynamically adjusted to satisfy the requirements with the change of the real-time averaging length, which is positive to compensate for the overly conservative performance caused by the fixed allocation method. After determining the allocation coefficient \(\alpha\), the false alarm error of the NTM should be controlled to satisfy the requirement of the allocated false alarm rate Pfa2|CF. Therefore, the detection threshold T2 can be obtained as,

$$ \, T_{2} = - \Phi^{ - 1} \left( {\frac{{P_{{fa2\left| {CF} \right.}} }}{2}} \right)\sigma_{{t_{2} }} = - \Phi^{ - 1} \left( {\frac{{\left( {1 - \alpha } \right)P_{fa} }}{{2\left( {1 - P_{fa1} } \right)P_{CF} }}} \right)\sigma_{{t_{2} }} $$
(16)

when the test statistic t2 is larger than the detection threshold T2, the ground facility must alert users and isolate the faulty satellite. Otherwise, we need to evaluate the missed detection error to avoid the availability loss of the NTM.

Under the H1 hypothesis, the missed detection errors will occur when the test statistics t1 and t2 are both within the protection of the detection thresholds. There are two cases contributing the probability of missed detection. The first case is the failure of the NTM in detecting the non-nominal troposphere, i.e., the ambiguity is correctly fixed and the ARM is alarm-free. The other case is the missed detection from the ARM and the NTM. Thus, the overall probability of missed detection Pmd can be expressed as,

$$ \begin{gathered} P_{{{\text{md}}}} = P\left\{ {\left| {t_{1} } \right| < T_{1} \cap \left| {t_{2} } \right| < T_{2} \left| {H_{1} } \right.} \right\} \hfill \\ \, = \left( {P\left\{ {\left| {t_{1} } \right| < T_{1} \left| {{\text{CF}}} \right.} \right\}P_{{{\text{CF}}}} + \sum\limits_{i \in Z} {P\left\{ {\left| {t_{1} } \right| < T_{1} \left| {{\text{IF}}_{i} } \right.} \right\}P_{{{\text{IF}}_{i} }} } } \right)P\left\{ {\left| {t_{2} } \right| < T_{2} \left| {H_{1} } \right.} \right\} \hfill \\ \, = (1 - P_{{{\text{fa1}}}} )P_{{{\text{CF}}}} P_{{{\text{md2}}\left| {{\text{CF}}} \right.}} + \sum\limits_{i \in Z}^{{}} {P_{{{\text{md1}}\left| {{\text{IF}}_{i} } \right.}} P_{{{\text{IF}}_{i} }} } P_{{{\text{md2}}\left| {{\text{IF}}_{i} } \right.}} \hfill \\ \end{gathered} $$
(17)

where Pmd2 is the allocated missed detection rate of the NTM which can be calculated as,

$$ \begin{array}{*{20}l} {P_{{{\text{md2}}\left| {{\text{CF}}} \right.}} = P\left\{ {\left| {t_{2} } \right| < T_{2} \left| {H_{1} ,{\text{CF}}} \right.} \right\} = \Phi \left( {\frac{{T_{2} - T_{{{\text{non}}}} }}{{\sigma_{{t_{2} }} }}} \right) - \Phi \left( {\frac{{ - T_{2} - T_{{{\text{non}}}} }}{{\sigma_{{t_{2} }} }}} \right)} \hfill \\ {P_{{{\text{md2}}\left| {{\text{IF}}_{i} } \right.}} = P\left\{ {\left| {t_{2} } \right| < T_{2} \left| {H_{1} ,{\text{IF}}_{i} } \right.} \right\} = \Phi \left( {\frac{{T_{2} - \left( {T_{non} + \tau_{i} } \right)}}{{\sigma_{{t_{2} }} }}} \right) - \Phi \left( {\frac{{ - T_{2} - \left( {T_{{{\text{non}}}} + \tau_{i} } \right)}}{{\sigma_{{t_{2} }} }}} \right)} \hfill \\ \end{array} $$
(18)

where Tnon indicates the unknown bias caused by the non-nominal troposphere. Similarly, we conservatively assume that the actual non-nominal troposphere will be masked by the wrong ambiguity, resulting in the missed detection, i.e., \(P_{{{\text{md2}}\left| {{\text{IF}}_{i} } \right.}} = 1\). Thus, the upper bound of (17) can be simplified as,

$$ P_{{{\text{md}}}} < (1 - P_{{{\text{fa1}}}} )P_{{{\text{CF}}}} P_{{{\text{md2}}\left| {{\text{CF}}} \right.}} + \sum\limits_{i \in Z} {\left[ {2P_{{{\text{IF}}_{i} }} P_{{{\text{md1}}\left| {\left( {{\text{CF}} \cap {\text{IF}}_{i} } \right)} \right.}} { + }P_{{{\text{IF}}_{i} }}^{{2}} } \right]} $$
(19)

Similarly, the overall missed detection rate Pmd should be allocated with the allocation coefficient \(\beta\) to ensure that the upper bound of (17) is less than or equal to the required overall missed detection rate Pmd. By comparing (14) and (19), it can be found that the integrity risk of the ARM will affect the allocation of the overall false alarm and missed detection rate, simultaneously. In general, the overall false alarm rate is much smaller than the overall missed detection rate due to the existence of a priori probability of non-nominal troposphere. Therefore, when the overall false alarm rate allocation requirement of (15) is satisfied, the overall missed detection rate allocation requirement can also be satisfied. Specifically, given a required overall missed detection rate, the allocation coefficient \(\beta\) can be calculated as,

$$ \beta = \frac{{\alpha P_{{{\text{fa}}}} }}{{P_{{{\text{md}}}} }} $$
(20)

Then, the allocated missed detection rate of NTM can be expressed as,

$$ P_{{md2\left| {CF} \right.}} = \frac{{\left( {1 - \beta } \right)P_{{{\text{md}}}} }}{{(1 - P_{{{\text{fa1}}}} )P_{{{\text{CF}}}} }} $$
(21)

When the resulting missed detection rate of the NTM is less than the allocated missed detection rate, it can be determined that the overall missed detection error can be constrained so that the ground facility can provide real-time protection for civil aviation precision approach against the non-nominal troposphere.

The proposed non-nominal troposphere monitoring method can be implemented in two steps by adopting the measurements from multiple short-baseline reference receivers. Specifically, we first detect whether the ambiguity is correctly or incorrectly fixed because the ambiguity resolution performance plays an important role in the detection sensitivity of the non-nominal troposphere. When the ARM is alarm-free, the ionospheric-free test statistics is used for the NTM in the second step. Through the two-step sequential monitoring, the contribution of ambiguity resolution failure to the non-nominal troposphere monitoring is accurately characterized and controlled. Moreover, the overall probabilities of false alarm and missed detection between the two steps are dynamically allocated so that the false alarm and missed detection error can be constrained, simultaneously. Thus, the superior performance of the non-nominal troposphere monitoring can be anticipated.

Experiment and discussion

We conducted the experiments based on the real GPS/BDS dual-frequency data to evaluate the proposed two-step sequential monitoring method. First, the real hazardous horizontal tropospheric gradients were used to analyze the characteristics of the non-nominal troposphere. Then, the dynamic allocation results of false alarm and missed detection rates were analyzed according to the performance of the ARM. Finally, the benefits of the proposed two-step sequential monitoring method were evaluated. The required overall probability of false alarm and missed detection were conservatively set as 10–8 and 10–6, respectively. The cut-off elevation was set as 10 deg. The elevation-dependent weighting model \(\sigma \left( \theta \right) = \sigma_{0} \left( {1 + 1/\sin \theta } \right)\) was adopted to describe measurements accuracy, and \(\sigma_{0}\) is set as 3 mm and 30 cm in dual-frequency undifferenced carrier phase and code measurements, respectively.

Analysis of non-nominal troposphere characteristics

The typical hazardous horizontal tropospheric gradients are observed for three different areas, Stennis (30.2°N, 89.4°W), Raleigh (35.5°N, 78.3°W), and Hong Kong (22.1°N, 113.5°E) (Lawrence et al. 2006; Huang and Graas 2007; Yu and Liu 2021). A detailed description of the data is given in Table 1.

Table 1 Data information
Full size table

Figure 3 shows the processing results of each hazardous horizontal tropospheric gradients. As shown in the left panel of the figure, all the DD residuals of three baselines share similar significant fluctuations when the non-nominal troposphere occurs. Since the hazardous horizontal tropospheric gradient is present at the lower layer of the atmosphere, there are multiple satellites affected by the non-nominal troposphere, simultaneously, which means that even a small non-nominal troposphere can cause large positioning errors.

Fig. 3
figure 3

Post-processing results of different hazardous horizontal tropospheric gradient. The panels from top to bottom represent the MSSC-NDBC, the NCRD-RALR, and the HKKT-HKLT

Full size image

To accurately characterize the non-nominal troposphere, the decorrelation analysis results of the DD residuals are shown in the right panel of Fig. 3. Since the troposphere delay is frequency independent and ionosphere delay is frequency dependent, a fixed ratio can be derived to account for the contribution of the troposphere delay with respect to the L1 and L2 DD carrier phase residuals, respectively. Specifically, on a plot where the x-axis represents the L1 DD carrier phase residuals and the y-axis represents the L2 DD carrier phase residuals, the troposphere delay contribution is a vector with a slope of \({{\lambda_{1} } \mathord{\left/ {\vphantom {{\lambda_{1} } {\lambda_{2} }}} \right. \kern-0pt} {\lambda_{2} }}\). Similarly, the ionosphere delay with respect to the L1 and L2 DD carrier phase residuals is a vector with a slope of \({{\lambda_{2} } \mathord{\left/ {\vphantom {{\lambda_{2} } {\lambda_{1} }}} \right. \kern-0pt} {\lambda_{1} }}\). It can be found that the signature of the residuals clearly follows the tropospheric trendline rather than the ionospheric trendline. In addition, the non-nominal troposphere of 0.3 cycles can be observed at Stennis, which indicates the non-nominal troposphere can be effectively detected by the carrier phase-based monitor.

Dynamic allocation results of false alarm and missed detection error

Since the dynamic allocation result is closely related to the integrity risk of the ARM, the real BDS dual-frequency data from Hong Kong continuously operating reference stations are used for testing the integrity performance of the ARM. Four adjacent stations HKPC, HKMW, HKCL and HKNP are selected to construct approximately parallel baselines (\(\beta \approx 3.5\deg\)). Specifically, HKPC-HKMW constitutes b1 and HKCL-HKNP constitutes b2. The location of multi-reference stations is shown in Fig. 4. A detailed description of the data is given in Table 2. In addition, the IGS products include the final precise GNSS satellite ephemeris and ionospheric vertical total electron content maps were used to demonstrate that the collected data are immune to the ephemeris fault and the anomalous ionospheric gradient. Moreover, the image of radar echoes of the Hong Kong observatory is used to verify that the troposphere is healthy.

Fig. 4
figure 4

Location of selected Hong Kong SatRef GPS stations

Full size image
Table 2 Data information
Full size table

Figure 5 shows the test statistics for the proposed ARM. The detection thresholds are given with the gray dotted line. When the ambiguity is correctly fixed, it can be found that the test statistics are less than the detection threshold and gradually converge to 0.2 cycle. However, when the ambiguity is fixed to a wrong integer, the test statistics will respond quickly, i.e., exceed the protection of the detection threshold. Therefore, it can be verified that the ARM can effectively detect ambiguity resolution failure.

Fig. 5
figure 5

Test statistics and detection thresholds of the ARM

Full size image

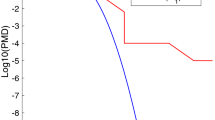
Figure 6 shows the calculated missed detection rate of the ARM with different ambiguity resolution failure modes. According to the characteristics of the rounding estimator, the minimum bias caused by incorrect fixing is ± 1 cycle. Thus, the maximum resulting missed detection rate can be obtained at ± 1 cycle, which is approximately 10–8, because the small bias is more challenging to be monitored. Furthermore, since the resulting missed detection rate of ± 2 cycle failure modes is far less than the requirements of the overall false alarm and missed detection rate, it is acceptable to consider only the ambiguity resolution failure mode of ± 1 cycle and ± 2 cycle during the allocation process.

Fig. 6
figure 6

Calculated missed detection rate of the ARM

Full size image

With the integrity risk of the ARM, the dynamic allocation coefficient corresponding to different averaging lengths is shown in Fig. 7. It can be found from the figure that the averaging length is beneficial for reducing the integrity risk of the ARM. In addition, even if the conservative measurement accuracy is adopted (\(\sigma_{0} = 12mm\)), both the allocation coefficient of false alarm and missed detection rate can be adjusted to be less than 10–5 when the averaging length is larger than 120 epochs, which means that the contribution of ambiguity resolution failure to the NTM can be effectively limited. It should be noted that the numerical allocation results can be saved in the offline database so that the corresponding allocation coefficients can be selected according to the real-time averaging length and measurement standard deviation during the monitoring process.

Fig. 7
figure 7

Dynamic allocation results of false alarm and missed detection errors

Full size image

Benefits of two-step sequential monitoring

To evaluate the benefits of the proposed two-step sequential monitoring method based on the dynamic allocation of the probabilities of false alarm and missed detection, the traditional single-step monitoring method based on the fixed allocation was selected to be compared with the proposed method. The traditional single-step monitoring method based on the fixed allocation comes from Patel et al. (2020) and Jing et al. (2014). The minimum averaging length was selected as 120 epochs to improve the ambiguity resolution reliability. The ambiguity resolution failure modes of ± 1 cycles were used to allocate false alarm and missed detection rates. It should be noted that shorter averaging times (about 10 min) can be achieved with higher rate data (typically 2 Hz). However, the actual accumulated epochs would increase because the correlation among higher rate measurements impairs the averaging efficiency.

Figure 8 shows two groups of test statistics and detection thresholds constructed by the fault-free data in Table 2. It can be found that the test statistics of the proposed method have more uncertainty than the traditional fixed allocation method due to the ionospheric-free combination expands the measurement noise. Moreover, it can be observed that limited by the conservative fixed allocation, the multi-detection thresholds corresponding to the correct fixing and the incorrect fixing with the bias of ± 1 cycle are utilized to control the false alarm errors. No alarm will be triggered when the test statistics lies inside the threshold regions corresponding to the ambiguity correct fixing or the threshold regions corresponding to ± 1 incorrect fixings. By counting the number of test statistics exceeding the detection threshold protection, it can be found that the test statistics of both the proposed method and the traditional method are less than the detection threshold protection, which means the comparable false alarm performance can be achieved by the proposed method with a stricter detection threshold.

Fig. 8
figure 8

Test statistics and detection thresholds for the NTM. Left panel: The fixed allocation method; Right panel: The dynamic allocation method

Full size image

In order to evaluate the improvement of missed detection performance of the proposed method, we test the sensitivity of fault detection under the H1 hypothesis. In order to avoid the counter-balance between the non-nominal troposphere of the reference satellite and the non-reference satellite, the simulated tropospheric fault is injected into the code and phase measurements to affect the DD measurements of all satellites except the reference satellite C01. The weather wall model based on historical meteorological statistics data was utilized to simulate the tropospheric fault (Guilbert et al. 2017). The fitting function of the weather wall model can be expressed as,

$$ T_{\max } \left( i \right) = A \times \exp \left( { - \frac{\theta \left( i \right)}{B}} \right) + C $$
(22)

where the \(T_{\max } \left( s \right)\) indicate the maximum troposphere delay in satellite s, \(\theta \left( s \right)\) is the elevation angle of satellite s. The unknown parameters A, B and C represent fitting parameters, respectively. Table 3 shows the weather wall model parameters fitted with different numerical weather models. We conservatively selected the Ohio wall model to simulate the tropospheric fault because the Ohio wall model can bound the worst-case troposphere delay.

Table 3 Fitting parameters of the weather wall model
Full size table

The tropospheric fault injection status is shown in Fig. 9. There are 11 satellites involved in tropospheric fault during the experiment, and a total of 23,294 test statistics can be generated. Moreover, since the simulated tropospheric fault is inversely proportional to the elevation, the maximum tropospheric fault bias reaches 0.93 m when the elevation is 10 degree. It can be induced that the simulated tropospheric fault will damage the navigation accuracy and the integrity of GBAS without effective monitoring.

Fig. 9
figure 9

Process of tropospheric fault injection. Left panel indicates fault state; Right panel indicates tropospheric fault bias

Full size image

The integrity monitoring results of the non-nominal troposphere are shown in Fig. 10. It can be found that both the test statistics constructed by the fixed allocation method and the proposed dynamic allocation method can quickly respond to the tropospheric fault, when the simulated tropospheric fault is injected. However, some test statistics are still less than the detection threshold for the conservative multi-detection thresholds. In contrast, the proposed dynamic allocation method performs better in detecting the simulated tropospheric fault, indicating the proposed method has higher detection sensitivity to the non-nominal troposphere.

Fig. 10
figure 10

Non-nominal troposphere monitoring results. Left panel: The fixed allocation method; Right panel: The dynamic allocation method

Full size image

Table 4 shows the numerical results of the NTM. It should be noted that the numerical missed detection rate is defined as the ratio of the number of test statistics that are still less than the detection threshold protection level to the total number of test statistic when the tropospheric fault is injected. It can be found that the missed detection rate of both the fixed allocation and the dynamic allocation method reduces along with the increased tropospheric fault bias. The fixed allocation method can effectively detect the non-nominal troposphere when the fault bias is larger than 0.74 m. In contrast, the proposed dynamic allocation method can effectively detect the non-nominal troposphere when the fault bias is larger than 0.39 m, which has a 40.5% improvement in detection sensitivity. The comparison of detection results indicates that the proposed monitoring method is beneficial for improving the missed detection performance of the non-nominal troposphere monitoring.

Table 4 Numerical missed detection rate results
Full size table

In order to reveal the efficiency of the proposed monitoring method, we compared the positioning performance with and without the non-nominal troposphere monitoring. HKPC and HKMW were simulated as reference station and rover station, respectively. Baseline b1 and baseline b2 were used for the non-nominal troposphere monitoring. The number of visible BDS satellites and the simulated azimuth of the weather wall are shown in Fig. 11. Note that the satellites whose signal pass through the weather wall (azimuth of 30°–150°) were injected with the simulated tropospheric fault.

Fig. 11
figure 11

Sky plot and the azimuth of the weather wall at HKMW, 2021/4/8

Full size image

The pseudorange differential positioning results of different monitoring conditions are shown in Fig. 12. It can be found that there are significant biases in both horizontal and vertical positioning results without the non-nominal troposphere monitoring. When the satellite geometry is poor, the vertical positioning error can be up to 4 m, which undermines the accuracy and integrity of the precision approach supported by GBAS. The quantitative statistics of root mean squares (RMS) of the positioning errors are shown in Table 5. It can be found that by applying the proposed monitoring method, the horizontal and vertical positioning errors can be reduced by 0.85 m and 1.05 m, respectively. It can be inferred that the proposed monitoring method is of significance to provide protection for civil aviation precision approach against the non-nominal troposphere.

Fig. 12
figure 12

Positioning results of different monitoring conditions. Left panel: East and North direction positioning result; Right panel: Vertical direction positioning result

Full size image
Table 5 Positioning error comparisons with different monitoring conditions
Full size table

Concluding remarks

High sensitivity non-nominal troposphere monitoring is a challenge for carrier phase-based monitors. This is because the ambiguity resolution failure deteriorates the false alarm and missed detection performance of the NTM. Thus, a two-step monitoring method based on multiple short-baseline receivers is developed. The contribution of ambiguity resolution failure to the non-nominal troposphere monitoring is sufficiently controlled by using the ARM. The overall false alarm and missed detection rate are dynamically allocated based on the real-time averaging length to isolate the impact of ambiguity resolution failure, so that the detection sensitivity of the non-nominal troposphere can be improved.

The proposed ARM can detect ambiguity resolution failures with an acceptable probability of missed detection. The dynamic allocation results of the probabilities of false alarm and missed detection indicate that the contribution of ambiguity resolution failure to the NTM can be sufficiently mitigated. The comparative experiments with the simulated tropospheric fault were conducted to verify the improvement of integrity monitoring performance. The results have shown that the false alarm and missed detection errors of the proposed monitoring method can be constrained simultaneously when the simulated tropospheric fault bias is larger than 0.39 m. The detection sensitivity of the proposed two-step sequential monitoring method is improved by 40.5% when compared with the traditional single-step monitoring method. The positioning results show that the horizontal and vertical positioning errors can be significantly reduced with the non-nominal troposphere monitoring when the simulated tropospheric fault is injected. Therefore, the developed two-step sequential non-nominal troposphere monitoring method is applicable for improving the integrity and continuity of safety–critical navigation services. Future work includes assessing the impact of non-nominal troposphere and establishing a set of monitoring indicators for high-precision navigation services.