Keywords

1 Introduction

Nowadays navigation system is indispensable for civil air transportation. Navigation system allows aircraft to determine its location and to fly on a predetermined route. This can avoid many hazardous aviation accidents. For instance, when aircraft drifts off course, pilot is able to correct the error of position with navigation system. To build a robust navigation system, several work has been made in the past century. Before 1970s, the research of aircrafts navigation system focused on Radio Navigation System (RNS) and Inertial Navigation System (INS). But these two systems both have drawbacks such as limited system coverage and increasing navigation errors over time [1]. After 1970s, satellite-based positioning system which provides users with global coverage and lower positioning error began to flourish [2].

From the 1970s up to the present, many countries and regions have established their own satellite-based positioning systems such as Global Navigation System (GPS, USA), GLONASS (Russia), BeiDou Navigation Satellite System (BDS, China), and Galileo (Europe). At the same period, some augmentation systems, like Ground-Based Augmentation System (GBAS) and Satellite-Based Augmentation Systems (SBAS), have been built to improve the navigation performance. The combination of these satellite-based positioning systems (GPS, BDS, GLONASS, and Galileo) is referred to as Global Navigation Satellite System (GNSS), and each individual satellite-based positioning system is termed as constellation [3].

For civil aviation, navigation system which meets stringent requirements is critical to guarantee the safety during the flight. The International Civil Aviation Organization (ICAO) put forward some metrics for satellite-based positioning system [4]. Two of the most challenging requirements for civil aviation are integrity and continuity [5]. Integrity is a measure of trust, which is used to determine whether the positioning solution provided by the navigation system is correct. Continuity measures navigation system’s ability to operate without unplanned interruptions [4]. Receiver Autonomous Integrity Monitoring (RAIM) is a system that can provide users with real-time integrity monitoring results [6]. When satellite fault occurs during the flight, timely warning can be sent by RAIM to users. After mid-1990s, by using single frequency signal and single constellation, RAIM has become a backup navigation tool and it can be applied to en-route flight [5]. But previous research has found the drawbacks of RAIM. One of the major drawbacks is occasional lack of availability [7].

With the great development of satellite-based positioning system, single frequency signal and single constellation positioning are gradually replaced by dual-frequency signal and multi-constellation positioning because it possesses two advantages. (a) Dual-frequency signal can cancel the ionosphere delay [8]. (b) Multi-constellation positioning with increased number of satellites improves user’s geometry [9].

Due to these two advantages, dual-frequency signal and multi-constellation positioning can significantly improve the accuracy and stability of positioning [10]. The superiority and greater redundancy of dual-frequency multi-constellation positioning lead to consider making up the shortcomings of RAIM. So Advanced Receive Autonomous Monitoring (ARAIM) has been put forward to overcome these shortcomings. Many researchers have made great contributions to this. For instance, Professor Juan Blanch from Stanford University and Professor Boris Pervan from Illinois Institute of Technology have already built a solid theoretical foundation for ARAIM Multiple Hypothesis Solution Separation (MHSS) algorithm. Some institutions, take Stanford GPS Lab as an example, have devised ARAIM prototype that can be equipped on aircraft. Though dual-frequency signal and multi-constellation positioning have better accuracy and greater redundancy for integrity monitoring, it also brings the higher probability of having faulted satellites which can severely affect the positioning solution.

Since the current augmentation systems, SBAS and GBAS, cannot cover every region of the world [11, 12], it is urgent to develop ARAIM MHSS algorithm for the place with poor navigation performance. ARAIM MHSS algorithm enables aircraft to detect navigation fault and to correct positioning result by excluding some faulty satellites or constellations. Meanwhile, today’s ARAIM MHSS algorithm also has some weaknesses, and one of them is that the probability bound of ARAIM algorithm is not tight enough, which can significantly affect navigation performance especially when there exists exclusion function in ARAIM algorithm. To avoid this weakness, we propose a new approach of calculating the probability bound and establish multi-constellation ARAIM test platform to validate the theory.

The second part of this paper will introduce the basic principles of ARAIM. The third part of this paper focuses on introducing the new approach. In this chapter, the probability bound will be rewritten mathematically and new Probability of Hazardous Misleading Information (PHMI) equation will be introduced. The fourth part of this paper explains the working principles of multi-constellation ARAIM test platform. The fifth part of this paper shows the navigation performance under different conditions (MHSS algorithm and new approach).

2 ARIAM Overview

2.1 ARAIM Background

Based on linearized pseudorange equations, GNSS receiver can compute the user’s location by solving linear algebraic equation, which can be expressed as:

$$\begin{aligned} \varvec{\mathrm{y}}=\varvec{\mathrm{Hx}}+\varvec{\epsilon }+\varvec{\mathrm{f}} \end{aligned}$$
(1)

where \(\varvec{\mathrm{y}}\) is a \(n \times 1\) measurement vector, and this vector represents the corrected pseudorange of satellites. \(\varvec{\mathrm{H}}\) is a \(n \times (3+N)\) matrix in which n and N are the number of satellites and constellations, respectively. \(\varvec{\mathrm{x}}\) is a \((3+N)\times 1\) vector, which includes the user’s location and the clock error of different constellations. \(\varvec{\epsilon }\) is the noise, which comes from clock error, ephemeris error, tropospheric error, multipath, and receiver noise, and it follows normal distribution. \(\varvec{\mathrm{b}}\) and \(\varvec{\mathrm{V}}\) are defined as bias vector and covariance matrix of \(\varvec{\epsilon }\), respectively. \(\varvec{\mathrm{f}}\) is a \(n \times 1\) vector, which indicates the fault magnitude of navigation system. The solution of equation Eq. (1) is all-in-view estimation positioning solution, and it can be written as:

$$\begin{aligned} \varvec{{\hat{\mathrm{x}}}}_0={(\varvec{\mathrm{H}}^{T} \varvec{\mathrm{V}}^{-1}\varvec{\mathrm{H}})^{-1}} \varvec{\mathrm{H}}^T \varvec{\mathrm{V}}^{-1} \varvec{\mathrm{y}} \end{aligned}$$
(2)

When one satellite or more satellites that corresponds to the \(i \)th fault model was excluded, satellite-removed positioning solution \(\varvec{{\hat{\mathrm{x}}_i}}\) can be written as:

$$\begin{aligned} \varvec{{\hat{\mathrm{x}}}}_i={(\varvec{\mathrm{H}}^{T} \varvec{\mathrm{V}}^{-1}_i\varvec{\mathrm{H}})}^{-1} \varvec{\mathrm{H}}^T \varvec{\mathrm{V}}_i^{-1} \varvec{\mathrm{y}} \end{aligned}$$
(3)

\(\varvec{\mathrm{V}}_i\) in Eq. (3) is the covariance matrix which excludes the faulty satellite or satellites corresponding to ith fault model. For ith fault model, we assume that pth satellite is in ith fault model and qth satellite is faultless. Based on this assumption, we can compute covariance matrix \(\varvec{\mathrm{V}}_i\) below:

$$\begin{aligned} \varvec{\mathrm{V}}_i(p,p)=0,\quad \varvec{\mathrm{V}}_i(q,q)=\varvec{\mathrm{V}}(g,g) \end{aligned}$$
(4)
$$\begin{aligned} \varvec{\hat{\mathrm{x}}}_{ex,k}=(\varvec{\mathrm{H}}^{T}\varvec{\mathrm{V}}^{-1}_{ex,k}\varvec{\mathrm{H}})^{-1}\varvec{\mathrm{H}}^{T}\varvec{\mathrm{V}}^{-1}_{ex,k}\varvec{\mathrm{y}} \end{aligned}$$
(5)

When considering MHSS ARAIM exclusion function, we introduce \(\varvec{\mathrm{V}}_{ex,k}\), which excludes the kth subset fault model, under the exth fault model. For fault model ex and the subset fault model k, we assume that the pth satellite is in the exth fault model or the kth subset fault model and qth satellite is faultless. Based on this assumption, we can compute covariance matrix \(\varvec{\mathrm{V}}_{ex,k}\) below:

$$\begin{aligned} \varvec{\mathrm{V}}_{ex,k}(p,p)=0, \quad \varvec{\mathrm{V}}_{ex,k}(q,q)=\varvec{\mathrm{V}}(q,q) \end{aligned}$$
(6)

If fault model ex and subset fault mode k have been excluded, the estimation positioning solution can be written as:

$$\begin{aligned} \varvec{\hat{\mathrm{x}}}_{ex,k}=(\varvec{\mathrm{H}}^{T}\varvec{\mathrm{V}}^{-1}_{ex,k}\varvec{\mathrm{H}})^{-1}\varvec{\mathrm{H}}^{T}\varvec{\mathrm{V}}^{-1}_{ex,k}\varvec{\mathrm{y}} \end{aligned}$$
(7)

By using Eqs. (1), (2) and (4), error test statistic \({\epsilon }_0\) and detection test statistic \({\varDelta }_i\) can be defined as:

$$\begin{aligned} {\epsilon }_0=\varvec{{\hat{\mathrm{x}}_0}}-\varvec{\mathrm{x}}, \quad {\epsilon }_0\sim \left( {{\mu }}_{HI,0},\quad \varvec{\mathrm{P}}_0\right) \end{aligned}$$
(8)

where \({{\mu }}_{HI,0}\) and \(\varvec{\mathrm{P}}_0\) are equal to \(\varvec{\mathrm{S}}_0\varvec{\mathrm{f}}+\varvec{\mathrm{S}}_0\varvec{\mathrm{b}}\) and \({(\varvec{\mathrm{H}}^{T} \varvec{\mathrm{V} }^{-1}\varvec{\mathrm{H}})^{-1}}\), respectively.

$$\begin{aligned} {\varDelta }_i=\varvec{{\hat{\mathrm{x}}}}_0-\varvec{{\hat{\mathrm{x}}}}_i, \quad {\varDelta }_i \sim ({{\mu }}_{HI,i},\quad \varvec{\mathrm{P}}_i) \end{aligned}$$
(9)

where \({{\mu }}_{ND,i}\) and \(\varvec{\mathrm{P}}_i\) are equal to \(\varvec{\mathrm{S}}_0\varvec{\mathrm{f}}+\varvec{\mathrm{S}}_0\varvec{\mathrm{b}}-\varvec{\mathrm{S}}_i\varvec{\mathrm{b}}\) and \((\varvec{\mathrm{H}}^{T} \varvec{\mathrm{V}}_i^{-1}\varvec{\mathrm{H}})^{-1}-{(\varvec{\mathrm{H}}^{T} \varvec{\mathrm{V} }^{-1}\varvec{\mathrm{H}})^{-1}}\), respectively.

\(\varvec{\mathrm{S}}_0\) and \(\varvec{\mathrm{S}}_i\) are equal to \((\varvec{\mathrm{H}}^T \varvec{\mathrm{V}}^{-1} \varvec{\mathrm{H}})^{-1} \varvec{\mathrm{H}}^T \varvec{\mathrm{V}}^{-1}\) and \((\varvec{\mathrm{H}}^T \varvec{\mathrm{V}}_i^{-1} \varvec{\mathrm{H}} )^{-1} \varvec{\mathrm{H}}^T \varvec{\mathrm{V}}_i^{-1}\), respectively. By using Eqs. (1), (3), and (5), for the second layer detection of MHSS ARIAM, error test statistic \({\epsilon }_{ex}\) and detection test statistic \({\varDelta }_{ex,k}\) can be defined as:

$$\begin{aligned} {\epsilon }_{ex}=\varvec{{\hat{\mathrm{x}}}}_{ex}-\varvec{\mathrm{x}},\quad {\epsilon }_{ex}\sim \left( {{\mu }}_{HI,ex},\quad \varvec{\mathrm{P}}_{ex}\right) \end{aligned}$$
(10)

where \({{\mu }}_{HI,ex}\) and \(\varvec{\mathrm{P}}_{ex}\) are equal to \(\varvec{\mathrm{S}}_{ex}\varvec{\mathrm{b}}\) and \({(\varvec{\mathrm{H}}^{T} \varvec{\mathrm{V} }_{ex}^{-1}\varvec{\mathrm{H}})^{-1}}\), respectively.

$$\begin{aligned} {\varDelta }_{ex,k}=\varvec{{\hat{\mathrm{x}}}}_{ex,k}-\varvec{{\hat{\mathrm{x}}}}_{ex}, \ {\varDelta }_{ex,k} \sim ({{\mu }}_{ND,ex},\ \varvec{\mathrm{P}}_{ex,k}) \end{aligned}$$
(11)

where \({{\mu }}_{ND,ex}\) and \(\varvec{\mathrm{P}}_{ex,k}\) are equal to \(\varvec{\mathrm{S}}_{ex}\varvec{\mathrm{b}}\) and \({(\varvec{\mathrm{H}}^{T} \varvec{\mathrm{V} }_{ex}^{-1}\varvec{\mathrm{H}})^{-1}}\), respectively.

\(\varvec{\mathrm{S}}_{ex,k}\) are equal to \((\varvec{\mathrm{H}}^T \varvec{\mathrm{V}}_{ex,k}^{-1} \varvec{\mathrm{H}})^{-1} \varvec{\mathrm{H}}^T \varvec{\mathrm{V}}_{ex,k}^{-1}\), respectively.

In the following paper, ARAIM is referred to as MHSS ARAIM.

2.2 ARAIM User Algorithm

ARAIM user algorithm consists of five functions:

  1. (1)

    Analyzing the fault models

In practice, the number of fault models increases sharply with the number of satellites and constellations. To reduce computational burden, ARAIM user algorithm does not need to monitor all the fault models. Based on required threshold \(P_{thresh}\) (\(8 \times 10^{-8}\)) [13,14,15], the sum of unmonitored fault models should meet the following requirement:

$$\begin{aligned} \sum _{j=1}^h P_j <= P_{thresh} \end{aligned}$$
(12)

where \(P_j\) is the probability of the jth unmonitored fault model occurring in navigation system, and h is the number of unmonitored fault models.

  1. (2)

    Determining detection and exclusion threshold

Detection threshold \(T_i\) can be derived from the allocated probability \(P_{FA\_NE}\), which represents the probability that test statistic \({\varDelta }_i\) exceeds their threshold under fault-free hypothesis [13, 14].

To calculate the exclusion threshold \(T_{ex,k}\), we use the allocated probability \(P_{FD\_{NE}}\), which represents the probability that test statistic \({\varDelta }_{ex,k}\) exceeds its threshold under second layer fault-free hypothesis [13, 14].

  1. (3)

    Evaluating ARAIM user algorithms availability

Before conducting the fault detection and exclusion function, the availability of ARAIM algorithm needs to be evaluated. If ARAIM user algorithm is not available, the algorithm will skip the fault detection and exclusion functions. The requirement of ARAIM availability depends on different application scenarios. LPV-200 is a stringent requirement for ARAIM in approach phase. LPV-200 requirements of availability are as follows: (a) Vertical protection level (VPL) is lesser than vertical alert limit (VAL) (VPL \(\le \) 35 m), (b) Effective monitor threshold (EMT) \(\le \) 15 m, (c) \(95\%\) of the time, vertical accuracy \(\le \) 4 m, (d) \(99.99999\%\) of the time, fault-free vertical accuracy \(\le \) 10 m. The method of calculating VPL can derive from the equation of PHMI.

  1. (4)

    Fault detection

When ARAIM algorithm is available, fault detection function can be conducted. The result of fault detection function depends on the equation below:

$$\begin{aligned} \varDelta _{i,d}=|\varvec{\mathrm{x}}_{0,d}-\varvec{\mathrm{x}}_{k,d}|\quad \quad (d=1,2,3) \end{aligned}$$
(13)

where the subscript d represents the horizontal \((d=1,2)\) and vertical \((d=3)\) direction. If \(\varDelta _{i,d}\) is larger than detection threshold \(T_{i,d}\), it shows that the fault is detected by ARIAM user algorithm and fault exclusion function is about to exclude the fault. Otherwise, the algorithm skips the fault exclusion function.

  1. (5)

    Fault exclusion

If fault has been detected, exclusion function attempts to correct the navigation solution by excluding some satellites or constellations [16]. To determine the correctness of exclusion, we introduce \(\varDelta _{ex,k,d}\), which can be expressed by the following:

$$\begin{aligned} \varDelta _{ex,k,d}=|\varvec{\mathrm{x}}_{ex,d}-\varvec{\mathrm{x}}_{ex,k,d}|\quad \quad (d=1,2,3) \end{aligned}$$
(14)

when \( \varDelta _{ex,k,d}\) is larger than exclusion threshold \(T_{ex,k,d}\), it shows that the fault cannot be eliminated by ARAIM algorithm and the user needs to be alerted.

3 Optimized ARAIM Algorithm

3.1 Tighter Bound of PHMI

PHMI evaluation is of great importance in ARAIM user algorithm. This evaluation can monitor the efficiency of algorithm. But the current evaluation of PHMI accumulates errors in summation process. This may lead to safety problems.

To calculate PHMI more precisely, we use the independence of \(\epsilon _0\) and \(\varDelta _i\), \(\epsilon _{ex}\), and \(\varDelta _{ex,k}\) [17] to simplify the current PHMI equation. The simplified form can be given by:

$$\begin{aligned} \begin{aligned}&P_{HMI}\le P(|\epsilon _0|>l|H_0)P_{H0}\\ {}&+\sum _{i=1}^{m}\max \limits _{\varvec{\mathrm{f}}_i}\bigg (P(|\epsilon _0 |>l|H_i,\varvec{ \mathrm{f}}_i)\varvec{\cdot }P(|\varDelta _i |<T_i|H_i,\varvec{\mathrm{f}}_i)\bigg )P_{H_i}\\ {}&+\sum _{ex=1}^{m}(P(|\epsilon _{ex}|>l|H_0)P_{H_0}+ P(|\epsilon _{ex}|>l|H_{ex})P_{H_{ex}}\\ {}&+\sum _{\begin{array}{c} k=1\\ k\ne ex \end{array}}^{m_1} \max \limits _{\varvec{\mathrm{f}}_k}\bigg (P(|\epsilon _{ex}|>l|H_k,\varvec{ \mathrm{f}}_k) \varvec{\cdot }\\ {}&\quad \quad \quad \quad \quad \quad \quad \quad \quad \quad P(|\varDelta _{ex,k}|<T_{ex,k}|H_k,\varvec{ \mathrm{f}}_k))\bigg )P_{H_k} \end{aligned} \end{aligned}$$
(15)

where \(\max \limits _{\varvec{\mathrm{f}}_i}\) and \(\max \limits _{\varvec{\mathrm{f}}_k}\) represent the function of calculating the maximum value under fault model i and subset fault model k. \(\varvec{\mathrm{f}}_i\) and \(\varvec{\mathrm{f}}_k\) are the fault magnitude corresponding to the fault model i and subset fault model k. m and \(m_1\) are the number of fault models that need to be monitored in detection function and exclusion function.

The first term of Eq. (15) is PHMI of detection function under fault-free condition, so fault magnitude does not exist in this term.

For the second term of Eq. (15), it indicates a condition that the fault has existed in navigation system but detection function fails to detect the fault. We denote \(P_{HI,i,d}\) and \(P_{ND,i,d}\) as \(P(|\epsilon _0|>l|H_i,\varvec{ \mathrm{f}}_i)\) and \(P(|\varDelta _i|<T_i|H_i,\varvec{ \mathrm{f}}_i)\), respectively. In Chapter “Ultra-Rapid Direct Satellite Selection Algorithm for Multi-GNSS”, we explained the bias and variance of random variable \(\epsilon _0\) and \(\varDelta _i\). These numerical characteristics can rewrite the second term of Eq. (15) mathematically.

As for \(P_{HI,i,d}\), it can be rewritten as:

$$\begin{aligned} P_{HI,0,d}=1-\int _{-l_d}^{l_d} \frac{1}{\sqrt{2\pi \varvec{\mathrm{P}}_0(d,d)}} exp\left( \frac{(x-\mu _{HI,0,d})^2}{2\varvec{\mathrm{P}}_0(d,d)}\right) dx \end{aligned}$$
(16)

where \(\varvec{\mathrm{P}}_0\) is covariance matrix of \(\epsilon _0\) and \(\mu _{HI,i,d}\) can be written as:

$$\begin{aligned} \mu _{HI,0,d}=\sum _{e=1}^{n}|\varvec{\mathrm{S}}_0(d,e)|\varvec{\mathrm{b}}(e,d)+\sum _{e=1}^{n}|\varvec{\mathrm{S}}_0(d,e)|\varvec{\mathrm{f}}_{i}(e,1) \end{aligned}$$
(17)

For \(P_{ND,i,d}\), it can be written as:

$$\begin{aligned} P_{ND,i,d}=\int _{-T_{\varDelta _d}}^{T_{\varDelta _d}} \frac{1}{\sqrt{2\pi \varvec{\mathrm{P}}_i(d,d)}} exp\left( \frac{(y-\mu _{ND,i,d})^2}{2\varvec{\mathrm{P}}_i(d,d)}\right) dy \end{aligned}$$
(18)

where \(\varvec{\mathrm{P}}_i\) is covariance matrix of \(\varDelta _i\) and \(\mu _{ND,i,d}\) can be written as:

$$\begin{aligned} \begin{aligned} \mu _{ND,i,d}=&-\sum _{e=1}^{n}|\varvec{\mathrm{S}}_0(d,e)-\varvec{\mathrm{S}}_i(d,e)|\varvec{\mathrm{b}}(e,d)\\&+\sum _{e=1 }^{n}|\varvec{\mathrm{S}}_0(d,e)|\varvec{\mathrm{f}}_{i}(e,1) \end{aligned} \end{aligned}$$
(19)

Since the only variable in Eqs. (17) and (19) is \(\varvec{\mathrm{f}}_i\), we can rewrite \(P_{HI,i,d} \cdot P_{ND,i,d}\) as:

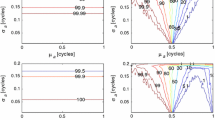
$$\begin{aligned} \begin{aligned} P_{HMI,2}&=P_{HI,i,d}\cdot P_{ND,i,d}\\&=k_i\int _{-T_{\varDelta _d}}^{T_{\varDelta _d}}\exp \left( \frac{(y-M+b_i)^2}{ 2\varvec{\mathrm{P}}_i(d,d)}\right) dy\\ {}&\quad -k_i k_0 \int _{-l_d}^{l_d}\int _{-T_{\varDelta _d}}^{T_{\varDelta _d}}\exp \left( - \frac{(y-M+b_i)^2}{ 2\varvec{\mathrm{P}}_i(d,d)}\right) \\ {}&\quad \exp \left( -\frac{(x-M-b_0)^2}{ 2\varvec{\mathrm{P}}_0(d,d)} \right) dxdy \end{aligned} \end{aligned}$$
(20)

where \(k_i=\frac{1}{\sqrt{2\pi \varvec{\mathrm{P}}_i(d,d)}}\), \(k_0=\frac{1}{\sqrt{2\pi \varvec{\mathrm{P}}_0(d,d)}}\), \(y-M+b_i=y-\mu _{ND,i,d}\), and \(x-M-b_0=x-\mu _{HI,0,d}\). The subscript 2 in \(P_{HMI,2}\) represents the second term of Eq. (15). Figure 1 shows the image function of Eqs. (15), (17), and (19).

In Eqs. (16) and (18), \(b_0\) and \(b_i\) are defined as positive and negative values, respectively. This definition takes into account the worst-case scenario. Under this definition, the maximum value of PHMI can be obtained. In Figs. 2 and 3, we discuss four conditions of \(b_0\) and \(b_i\) \((b_0>0, b_0<0, b_i>0, b_i<0)\). Figure 2 shows the function image of \(P_{HI,0,d}\) and \(P_{ND,0,d}\).

Fig. 1
figure 1

Function image (logarithmic form) of \(P_{HI,0,d}\) \(P_{ND,i,d}\) and \(P_{HI,0,d}\cdot P_{ND,i,d}\)

Full size image
Fig. 2
figure 2

Function image (logarithmic form) of \(P_{HI,0,d}\) and \(P_{ND,i,d}\) with different biases

Full size image
Fig. 3
figure 3

Function image (logarithmic form) of \(P_{HI,0,d}\cdot P_{ND,i,d}\) with different biases

Full size image

In Fig. 2 , the function images of \(b_0>0\) and \(b_i<0\) are above the other function images, so their product is lager than other conditions. Figure 3 is the function image of \(P_{HMI,2}\) under different conditions. It shows that the product of \(P_{HI,0,d} (b_0>0)\) and \(P_{ND,i,d} (b_i<0)\) is above other function images. So we draw the conclusion that the product of \(b_0>0\) and \(b_i<0\) can be used in calculating the maximum value of PHMI.

The third and the fourth terms in Eq. (16) are the PHMI of exclusion function which are under fault-free condition and right exclusion condition, respectively. So fault magnitude does not exist in these two terms.

For the fifth term of Eq. (15), it indicates a condition that even exclusion function has excluded some satellites but the fault still exists in navigation system and the second layer detection fail to detect the fault. We denote \(P_{HI,ex,d}\) and \(P_{ND,ex,d}\) as \(P(|\epsilon _{ex}|>l|H_k,\varvec{ \mathrm{f}}_k)\) and \(P(|\varDelta _{ex,k}|<T_{ex,k}|H_k,\varvec{ \mathrm{f}}_k)\), respectively. In Chapter 2, we explained the bias and variance of random variable \(\epsilon _{ex}\) and \(\varDelta _{ex,k}\). Similar to the derivation of formula Eq. (20), these numerical characteristics can rewrite the fifth term of Eq. (15) mathematically.

For \(P_{HI,ex,d}\), it can be rewritten as:

$$\begin{aligned} \begin{aligned} P_{HI,ex,d}&=1-\frac{1}{\sqrt{2\pi \varvec{\mathrm{P}}_{ex}(d,d)}}\varvec{\cdot } \\&\quad \int _{-l_d}^{l_d} \exp \left( \frac{(x-\mu _{HI,ex,d})^2}{2\varvec{\mathrm{P}}_{ex}(d,d)}\right) dx \end{aligned} \end{aligned}$$
(21)

where \(\varvec{\mathrm{P}}_{ex}\) is covariance matrix of \(\epsilon _{ex}\) and \(\mu _{HI,ex,d}\) can be written as:

$$\begin{aligned} \mu _{HI,ex,d}=\sum _{e=1}^{n}|\varvec{\mathrm{S}}_{ex}(d,e)|\varvec{\mathrm{b}}(e,d)+\sum _{e=1}^{n}|\varvec{\mathrm{S}}_{ex}(d,e)|\varvec{\mathrm{f}}_{k}(e,1) \end{aligned}$$
(22)

For \(P_{ND,ex,d}\), it can be written as:

$$\begin{aligned} \begin{aligned} P_{ND,ex,d}&=\frac{1}{\sqrt{2\pi \varvec{\mathrm{P}}_{ex,k}(d,d)}}\varvec{\cdot }\\ {}&\quad \int _{-T_{\varDelta _{ex,k,d}}}^{T_{\varDelta _{ex,k,d}}} \exp \left( \frac{(y-\mu _{ND,ex,d})^2}{2\varvec{\mathrm{P}}_{ex,k}(d,d)}\right) dy \end{aligned} \end{aligned}$$
(23)

where \(\varvec{\mathrm{P}}_{ex,k}\) is covariance matrix of \(\varDelta _{ex,k}\) and \(\mu _{ND,ex,d}\) can be written as:

$$\begin{aligned} \begin{aligned} \mu _{ND,ex,d}=&-\sum _{e=1}^{n}|\varvec{\mathrm{S}}_{ex}(d,e)-\varvec{\mathrm{S}}_{ex,k}(d,e)|\varvec{\mathrm{b}}(e,d)\\ {}&+\sum _{e=1 }^{n}|\varvec{\mathrm{S}}_{ex}(d,e)|\varvec{\mathrm{f}}_{k}(e,1) \end{aligned} \end{aligned}$$
(24)

we can rewrite \(P_{HI,ex,d} \cdot P_{ND,ex,d}\) as:

$$\begin{aligned} \begin{aligned} P_{HMI,5}&=P_{HI,ex,d}\cdot P_{ND,ex,d}\\ {}&=k_{ex,k}\int _{-T_{\varDelta _{ex,k,d}}}^{T_{\varDelta _{ex, k,d}}}\exp \left( \frac{(y-M+b_{ex,k})^2}{ 2\varvec{\mathrm{P}}_{ex,k}(d,d)}\right) dy\\ {}&\quad -k_{ex,k} k_{ex} \int _{-l_d}^{l_d}\int _{-T_{\varDelta _{ex,k,d}}}^{T_{\varDelta _{ex,k,d}}}\exp \left( - \frac{(y-M+b_{ex,k})^2}{ 2\varvec{\mathrm{P}}_{ex,k}(d,d)}\right) \\ {}&\quad \exp \left( -\frac{(x-M+b_{ex})^2}{ 2\varvec{\mathrm{P}}_{ex}(d,d)} \right) dxdy \end{aligned} \end{aligned}$$
(25)

where \(k_{ex,k}=\frac{1}{\sqrt{2\pi \varvec{\mathrm{P}}_{ex,k}(d,d)}}\), \(k_{ex}=\frac{1}{\sqrt{2\pi \varvec{\mathrm{P}}_{ex}(d,d)}}\), \(y-M+b_{ex,k}=y-\mu _{ND,ex,d}\), and \(x-M+b_{ex}=x-\mu _{HI,ex,d}\). The derivation of \(P_{HMI,5}\) is similar to \(P_{HMI,2}\), so the function image of \(P_{HMI,5}\) is similar to Fig. 1. As for \(b_{ex,k}\) and \(b_{ex}\), the definition is same as \(b_i\) and \(b_0\).

In order to evaluate navigation performance, we need to derive the equation of calculating VPL. When the integrity risk requirement \(I_{req}\) is specified, VPL can be derived from Eq. (15). Corresponding to Eq. (15), \(I_{req}\) is divided into five terms.

$$\begin{aligned} I_{req}\le I_1+I_2+I_3+I_4+I_5 \end{aligned}$$
(26)

Based on the first term in Eq. (15), the first term of Eq. (26) can be expressed as:

$$\begin{aligned} I_{1}=\left[ \bar{Q}\left( \frac{-{ {VPL}}-b_{0,3}}{\sigma _{0,3}}\right) +Q\left( \frac{{ {VPL}}-b_{0,3}}{\sigma _{0,3}}\right) \right] P_{H_0} \end{aligned}$$
(27)

where function Q and \(\bar{Q}\) are defined as:

$$\begin{aligned} Q(x)=\frac{1}{2\pi }\int _x^\infty \exp (-\frac{t^2}{2})dt, \quad \bar{Q}(x)=1-Q(x) \end{aligned}$$
(28)

In Eq. (15), the second term represents the system contains a specific fault \(H_{i}\) and the magnitude \(\varvec{\mathrm{f}}_i\) of this fault model. \(I_2\) in Eq. (26) is under this condition, and it can be expressed as:

$$\begin{aligned} \begin{aligned} I_2&=\sum _{i=1}^{m}{\max \limits _{\varvec{\mathrm{f}}_i}\bigg (P(|\epsilon _0 |>l|H_i,\varvec{ \mathrm{f}}_i)\varvec{\cdot }P(|\varDelta _i |<T_i|H_i,\varvec{\mathrm{f}}_i)\bigg )P_{H_i}} \\&=\sum _{i=1}^{m}\left[ \bar{Q}\left( \frac{-{ {VPL}}-\mu _{HI,i,3}}{\varvec{\mathrm{P}}_{0}(3,3)}\right) +Q\left( \frac{{ {VPL}}-\mu _{HI,i,3}}{\varvec{\mathrm{P}}_{0}(3,3)}\right) \right] \\&\quad \varvec{\cdot } \left[ Q\left( \frac{-T_{\varDelta _{i,3}}-\mu _{ND,i,3}}{\varvec{\mathrm{P}}_{i}(3,3)}\right) -Q\left( \frac{T_{\varDelta _{i,3}}-\mu _{ND,i,3}}{\varvec{\mathrm{P}}_{i}(3,3)}\right) \right] P_{H_i} \end{aligned} \end{aligned}$$
(29)

where \(\mu _{HI,i,3}\), \({\varvec{\mathrm{P}}_{0}(3,3)}\) and \(\mu _{ND,i,3}\), \({\varvec{\mathrm{P}}_{i}(3,3)}\) in Eq. (29) are bias and covariance corresponding to the maximum value of \(P(|\epsilon _0 |>l|H_i,\varvec{ \mathrm{f}}_i)\varvec{\cdot }P(|\varDelta _i |<T_i|H_i,\varvec{\mathrm{f}}_i)\).

As for the third and the fourth terms of Eq. (26), these two terms represent the fault-free model in exclusion function. The third term \(I_3\) can be written as:

$$\begin{aligned} I_3=\sum _{ex=0}^{m}\left[ \bar{Q}\left( \frac{-{ {VPL}}-b_{ex,3}}{\sigma _{ex,3}}\right) +Q\left( \frac{{ {VPL}}-b_{ex,3}}{\sigma _{ex,3}}\right) \right] P_{H_0} \end{aligned}$$
(30)

and the fourth term can be written as:

$$\begin{aligned} \begin{aligned} I_4&=\sum _{ex=0}^{m}\left[ \bar{Q}\left( \frac{-{ {VPL}}-b_{ex,3}}{\sigma _{ex,3}}\right) +\right. \\&\left. \quad Q\left( \frac{{ {VPL}}-b_{ex,3}}{\sigma _{ex,3}}\right) \right] P_{H_{ex}} \end{aligned} \end{aligned}$$
(31)

The last term \(I_5\) of Eq. (26) still exist the fault, and its magnitude can affect the value of PHMI. This term can be calculated as:

$$\begin{aligned} \begin{aligned} I_5&=\sum _{ex=0}^{m}\sum _{\begin{array}{c} k=1\\ k\ne ex \end{array}}^{m_1}\max \limits {\varvec{\mathrm{f}}_k}\bigg (P(|\epsilon _{ex}|>l|H_k,\varvec{ \mathrm{f}}_k) \varvec{\cdot }\\ {}&\quad P(|\varDelta _{ex,k}|<T_{ex,k}|H_k,\varvec{ \mathrm{f}}_k)\bigg )P_{H_k} \\&=\sum _{ex=0}^{m}\sum _{\begin{array}{c} k=1 \\ k\ne ex \end{array}}^{m_1}\left[ \bar{Q}\left( \frac{-{ {VPL}}-\mu _{HI,ex,3}}{\varvec{\mathrm{P}}_{ex}(3,3)}\right) \right. \\&\left. \quad +Q\left( \frac{{ {VPL}}-\mu _{HI,ex,3}}{\varvec{\mathrm{P}}_{ex}(3,3)}\right) \right] \\&\varvec{\cdot } \left[ Q\left( \frac{-T_{\varDelta _{ex,k,3}}-\mu _{ND,ex,3}}{\varvec{\mathrm{P}}_{ex,k}(3,3)}\right) \right. \\&\left. \quad -Q\left( \frac{T_{\varDelta _{ex,k,3}}-\mu _{ND,ex,3}}{\varvec{\mathrm{P}}_{ex,k}(3,3)}\right) \right] P_{H_k} \end{aligned} \end{aligned}$$
(32)

where \(\mu _{HI,ex,3}\), \({\varvec{\mathrm{P}}_{ex}(3,3)}\), and \(\mu _{ND,ex,3}\), \({\varvec{\mathrm{P}}_{ex,k}(3,3)}\) in Eq. (32) are bias and covariance corresponding to the maximum value of \(P(|\epsilon _{ex}|>l|H_k,\varvec{ \mathrm{f}}_k) \varvec{\cdot }P(|\varDelta _{ex,k}|<T_{ex,k}|H_k,\varvec{ \mathrm{f}}_k)P_{H_k}\).

From Eqs. (27)–(32), the only variable is \({ {VPL}}\). So we can derive the value of VPL by using the numerical method in APPENDIX E of [14]. In order to compute the maximum value in Eqs. (29) and (32), we introduce a numerical method in the following section and it could seek the maximum value.

3.2 Numerical Method and Test Example

To calculate the maximum value in Fig. 3, we introduce a numerical method: optimization method (Fig. 4).

Fig. 4
figure 4

Flowchart of optimization method

Full size image

Before we introduce the method in detail, we denote \(f\left( x(k)\right) \) as the maximum value of the function. At the beginning of optimization method, we first need to determine the interval where the extremum is located. Based on the properties of probability density function (PDF) of normal distribution, the initial searching interval is set to [0, \({\text {T}}+37\)], where T is the threshold for test statistic. If we assume the extremum locates within [a, b], then the method chooses two point \(x\left( 1\right) \) and \(x\left( 2\right) \) in [a, b] where \(x\left( 1\right) =(1-0.618)\times (b-a)\) and \(x\left( 2\right) =0.618\times (b-a)\). If \(f\left( x(1)\right) > f\left( x(2)\right) \), the searching interval is changed to \([x\left( 1\right) , b]\). If \(f\left( x(1)\right) < f\left( x(2)\right) \), the searching interval is changed to \([a, x\left( 2\right) ]\). Especially, when \(f\left( x(1)\right) = f\left( x(2)\right) \), the searching interval is changed to \([x\left( 1\right) , x\left( 2\right) ]\). When \(x\left( 1\right) \) and \(x\left( 2\right) \) are close enough (\(|x(1)-x(2)|<0.01\)), the search will be terminated.

Take \(Z=-(x-5)^2+70\) as an example, the maximum value of Z is 70 and the corresponding point is 5. In order to find this maximum value, the initial interval is set to [4, 7]. Table 1 shows the result of optimization method with different termination conditions.

Table 1 Test example result
Full size table
Fig. 5
figure 5

Hardware of ARAIM test platform

Full size image
Fig. 6
figure 6

ComNav GNSS receiver

Full size image

4 ARIAM Test Platform

4.1 Hardware Description

Figure 5 shows the three important hardware parts of ARAIM test platform: GNSS antenna, GNSS receiver, and user’s computer. When we operating ARAIM test platform, we first use chock ring antenna which located on the top of SJTU GNC Lab (31.026105436 N, 121.442347327 E, 36.836202 m) to receive GPS, BDS, and GLONASS signals. Then analog signals will be processed by multi-frequency GNSS receiver, which is able to convert the analog signals to digital signals and to provide users with the message of ephemeris and pseudorange. Next, digital signals will be transmitted to computer by serial communication. Figures 6 and 7 shows the chock ring antenna and GNSS receiver (from ComNav, China) that is used to build ARAIM test platform.

Fig. 7
figure 7

Chock ring antenna

Full size image

4.2 Software Description

The software of ARAIM test platform consists of two parts: online version and offline version. For online version, when binary input stream is transmitted by serial communication from GNSS receiver to user’s computer, the computer first decodes the binary input stream based on IEEE 754 protocol. After we acquiring the message of ephemeris and pseudorange from decoded binary input stream, local computer is able to calculate user’s location and implement ARIAM algorithm. Figure 8 shows the structure of online version ARAIM test platform. For offline version, it is designed for some harsh circumstance that local computer is malfunctioning and serial communication is interrupted. Due to GNSS receiver has 100 megabytes of memory, the lost data processed by GNSS receiver can be stored in the receiver as RENIX format. Then, by using RENIX file, we can calculate the user’s location and start running the ARAIM algorithm. Figure 9 shows the structure of offline version ARAIM test platform.

Fig. 8
figure 8

Online ARAIM test platform

Full size image
Fig. 9
figure 9

Offline ARAIM test platform

Full size image

5 Result

5.1 Global Almanac Data Result

We use 6-h almanac data from International GNSS Service (IGS) to calculate the worldwide VPL and 99.5% coverage. For ARAIM Fault Detection (FD) algorithm and ARAIM Fault Detection and Exclusion (FDE) algorithm, based on the requirement of continuity [5], we analyze the VPL and 99.5% coverage. The computational burden of ARAIM algorithm and our new method is also listed below.

Table 2 Computational burden of different method
Full size table
Table 3 VPL for ARAIM FD algorithm
Full size table
Table 4 Coverage for ARAIM FD algorithm
Full size table
Table 5 VPL for ARAIM FDE algorithm
Full size table
Table 6 Coverage for ARAIM FDE algorithm
Full size table

The results which are listed in Tables 2, 3, 4, 5, and 6 show tighter bound ARIAM algorithm can lower the protection level and improve the coverage worldwide without increasing too much computational burden for real-time capability.

5.2 ARAIM Test Platform Result

Using ARAIM test platform, we collect 6-h, three constellations’ (GPS, BDS, GLONASS) real-time data to verify the effect of our new method on navigation performance. The total time of processing 6-h real-time data using MHSS algorithm and tighter bound algorithm is 392 and 443 min. For each epoch, the time of MHSS algorithm and tighter bound algorithm 1.09 and 1.23 s, respectively. Figure 10 shows the 6-h positioning error. The average errors in east, north, and up direction are 1.12 m, 1.99 m, and 3.00 m, respectively.

Fig. 10
figure 10

6-h positioning error

Full size image

Figure 11 shows the 6-h VPL by using ARAIM FD algorithm. The blue line, red line, and yellow line in Fig. 11 represent the VPL of single constellation, dual constellation, and three constellation. Navigation performance increases with the number of constellations. Three constellation can provide the best navigation performance for user.

Fig. 11
figure 11

VPL using different constellations

Full size image

Figure 12 shows the 6-h VPL by using MHSS ARAIM FD algorithm and tighter bound ARAIM algorithm. When the test platform applies three constellations, VPL can be declined by our tighter bound ARAIM algorithm. The blue line and red line in Fig. 12 represent the VPL of MHSS algorithm and tighter bound ARAIM algorithm.

Fig. 12
figure 12

VPL of different methods (URA = 1, b = 0.75)

Full size image

6 Conclusion

In this paper, there are three main contributions. Firstly, we build ARIAM test platform which supports real-time integrity monitoring and post-processing integrity monitoring. Secondly, we find the bound of PHMI in ARAIM user algorithm is not tight enough and propose a new method to overcome this drawback. At last, by using real-time data and IGS data, we prove that our new method is able to improve the navigation performance without affecting real-time capability.