Introduction

Autonomous driving has become a popular topic and gains much attention. GNSS is the most utilized navigation system for the self-perception of moving vehicles. However, its performance is strongly influenced by the inconsecutive signals and multipath effects, particularly in some typical conditions such as the city canyon and tunnel. So, fusing augmented sensors may be an effective solution to ensure navigation performance during GNSS outages.

The GNSS/INS-integrated system has been widely applied to tackle the interrupt problems of GNSS signals. Shin (2005) has demonstrated that the integrated DGPS/INS system could realize a sub-meter level positioning in GPS-denied conditions, but the error accumulation of IMU still confines its performance. In order to suppress the divergence of INS errors during GPS outages, Klein (2010) verified the availability of motion constraints and used the knowledge of vehicle behaviors to aid the estimation process. In recent years, the development of multi-GNSS also promotes the progress of the GNSS/INS system. Gao et al. (2016) showed that augmentation with multi-GNSS could help the integrated system have a better performance compared to the GPS-only integrated system. However, GNSS is still dominant in the integration system. In GNSS long outages, the GNSS/INS integration will lose the advantage due to the rapid time-increasing INS errors.

Fortunately, visual-inertial odometry (VIO) has an excellent performance in the local pose estimation. A remarkable measurement model of filter methods was proposed by Mourikis and Roumeliotis (2007). In their algorithm, 3D feature positions are removed from the state vector, and geometric constraints are added to relative frames to reduce computational costs. Based on this model, the filter-based approaches have been developed rapidly for its high efficiency. Huang et al (2010), Li and Mourikis (2013) and Hesch et al (2017) proved and corrected the inconsistent of EKF filter methods, which improved the accuracy of the filter framework. To increase the robustness of the system in the low-texture environment, He et al (2018) and Zheng et al (2018) added line features, and Zhang and Ye (2020) extracted plane features to aid point features in detecting and tracking. With the development of computer technology, real-time optimization-based VIO methods become possible and proliferate rapidly. The raw measurements of IMU are constructed as a pre-integration item and added to factor graphs to improve the accuracy of optimization frameworks in Forster et al. (2017). Leutenegger et al. (2015) first adopted the keyframe strategy and maintained a bounded-sized optimization window to reduce the computation complexity of optimization-based approaches. Qin et al. (2018) constructed a high-precision monocular visual-inertial optimization system and added online extrinsic calibration, re-localization, and global optimization to increase the robustness and universality. In order to resist the influence of low-texture and illumination changes, the motion of the camera is directly estimated by minimizing a photometric error based on pixels with large enough intensity gradients instead of sparse feature points in Usenko et al. (2018). Generally, the property of re-linearization at each iteration makes optimization-based approaches more accurate. However, these iterations also lead to a high computational cost. By contrast, Sun et al. (2018) and Bloesch et al. (2015) demonstrated that filter-based methods have a more efficient way to achieve comparable accuracy, which is more critical for the sensor fusion.

VIO has an impressive performance in the local pose estimation, and GNSS can provide global high-precision positioning results. For the sake of realizing a local accurate and global drift-free pose estimation, it is advisable to fuse VIO and GNSS. A general EKF-based integrated framework is designed by Lynen et al. (2013) to fuse both relative and absolute form measurements from different sensors. Mascaro et al. (2018) regarded the sensor fusion problem as an alignment problem. The transformation between the local frame and the global frame is estimated and updated frequently to correct the drift of VIO in a smooth way. Won et al. (2014) and Vu et al. (2012) demonstrated that the vision/vision-inertial system can provide highly available and lane-level vehicle navigation by fusing GNSS pseudorange measurements. Although the integration of the GNSS/IMU/Vision has been discussed in several studies, they mainly focus on the fusion of vision and the low-cost micro-electro-mechanical system (MEMS) IMU, and only pseudorange observations or GPS position were mainly used in these frameworks. In the experiment, these methods were only verified with the simulated data or small-scale data under the open-sky condition.

In this situation, we intend to develop an integrated framework of GNSS/INS/Vision to provide robust and continuous navigation results for moving vehicles facing the GNSS-challenged environment. The vision information is integrated with high-grade IMU, and multi-GNSS observation of the double-frequency pseudorange and carrier phase and Doppler observation are all available in our integrated system. A new feature tracking method is provided in the feature tracking for the vehicle image acquisition, which can significantly improve the performance of feature matching and tracking in the long camera baseline condition. In order to comprehensively assess the performance of our solution, both the simulation experiment of GNSS outages and vehicular field experiments were conducted. The field experiments cover different GNSS observation conditions and consist of variable large-scale scenes.

Algorithm formulation

We discuss the algorithm details of the integrated system in this section. First, the system overview is introduced for a clear explanation of the integrated framework. Then, we present the definition of the system states in the error state vector section. The main parts of the algorithm are the process model and the measurement model. The process model mainly expounds on the filter propagation equations of the INS error state model and the augmentation of the camera state. In the measurement model, we discuss the multi-GNSS measurement model and the visual measurement model. In addition, the design of the vision processing front end is also presented in this part.

System overview

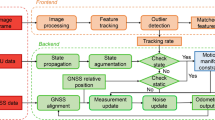
Figure 1 shows the architecture of the proposed GNSS/INS/Vision integrated system, and the measurements come from three different parts. Whereas GNSS receivers provide the multi-frequency and multi-system pseudorange, carrier phase, and Doppler observations, the high-frequency acceleration and angular velocity during the vehicle motion can be collected by IMU. The stereo camera captures the variation of the surroundings.

Fig. 1
figure 1

Implementation of EKF-based stereo camera, IMU and multi-GNSS integration system

Full size image

The designed integrated system is based on the EKF method. It starts with system initialization, which sets the parameters and configurations of the system and gets the initial attitude by an initial alignment procedure. After that, the high-rate angular velocity and acceleration measurements are processed by the INS mechanization, and the results are used to update the prediction of the currently integrated system states and the corresponding covariance.

Raw GNSS observations from the base and rover stations are used to construct DD code and phase observations. After passing the quality checking, the available multi-GNSS results can be used by the integrated EKF engine for measurement updates. As for the visual part, once the new image sequences are recorded, the feature extracting and tracking procedure is proceeded by the front end. Once the current image is identified as a keyframe, the corresponding error state and covariance will be added to the system state vector by state augmentation and maintained by a sliding window mechanism. When a feature fails to be tracked or the sliding window is full, a visual measurement update will be performed for the vehicle state estimation. Finally, the estimated biases of gyroscope and accelerometer are fed back to compensate the corresponding raw observations for next update procedures.

Error state vector

There are two different variables in the state vector of the integrated system. One is the INS state, which represents the current navigation information of the vehicle. The other one is the camera states, which store the information on historical camera poses. In the algorithm, we adopted the error state vector instead of the original state vector to avoid the additional constraint of the rotation. The entire error state vector at time step \(k\) can be expressed as:

$$\delta x_{k} { = }\left[ {\begin{array}{*{20}c} {\delta x_{{_{{_{INS} }} }}^{T} } & {\delta x_{{_{{_{{C_{1} }} }} }}^{T} } & \cdots & {\delta x_{{_{{_{{C_{k} }} }} }}^{T} } \\ \end{array} } \right]^{T}$$
(1)

where \(\delta x_{INS}\) is the INS error state at the current time step \(k\). \(\delta x_{{C_{i} }}\) is the historical camera error state at time step \(i\) (\(i = 1,2,3, \cdots ,k\)). The INS error state is derived as:

$$\delta x_{{_{INS} }} = \left[ {\begin{array}{*{20}c} {\left( {\delta \theta_{b}^{n} } \right)^{T} } & {\left( {\delta b_{g} } \right)^{T} } & {\left( {\delta v_{b}^{n} } \right)^{T} } & {\left( {\delta b_{a} } \right)^{T} } & {\left( {\delta r_{b}^{n} } \right)^{T} } \\ \end{array} } \right]^{T}$$
(2)

where \(\delta v_{b}^{n}\) and \(\delta r_{b}^{n}\) represent the velocity and position error state vector of INS in \(n\)-frame (i.e., navigation frame, north-east-down), respectively. \(\delta \theta_{b}^{n}\) denotes the error state vector of INS attitude in \(n\)-frame. \(\delta b_{g}\) and \(\delta b_{a}\) are the gyroscope bias vector and accelerometer bias vector. The camera error state at time step \(i\) is defined as:

$$\delta x_{{_{{C_{i} }} }} = \left[ {\begin{array}{*{20}c} {\left( {\delta \theta_{{c_{i} }}^{l} } \right)^{T} } & {\left( {\delta r_{{c_{i} }}^{l} } \right)^{T} } \\ \end{array} } \right]^{T}$$
(3)

where \(\delta \theta_{{c_{i} }}^{l}\) and \(\delta r_{{c_{i} }}^{l}\) are the error state vector of the camera pose in \(l\)-frame at time step \(i\). The definition of the \(l\)-frame can be found in augmentation of camera state section. For the stereo camera, the attitude and position of the right camera can be obtained with the extrinsic parameters, so only the left camera pose is included in the error state vector.

Process model

The process model of the integration system is discussed in this section. We acquire the discrete-time implementation for the state propagation in the EKF by the discretization of the continuous-time INS error state model. In addition, the INS error state is augmented with a new camera state once a new image is passing the keyframe screening.

INS error state model

The initial states of the inertial system are determined from the alignment process. According to the different states of the vehicle and grades of IMU, the stationary alignment, the position vector matching method, and the velocity matching method can be adopted in the alignment process based on (Liu et al. 2017). The following states of the inertial system are processed by mechanization. The inertial system is mechanized in the \(n\)-frame and its error dynamics equations are based on the Psi-angle error model (Shin 2005). The Psi-angle error is a rotation vector between the computer frame (c-frame) and the true navigation frame (Savage 2000). The error dynamics equations can be expressed as:

$$\left[ {\begin{array}{*{20}c} {\delta \dot{r}^{n} } \\ {\delta \dot{v}^{n} } \\ {\delta \dot{\theta }^{n} } \\ \end{array} } \right]{ = }\left[ {\begin{array}{*{20}c} { - \omega_{en}^{n} \times \delta r^{n} { + }\delta v^{n} } \\ {C_{b}^{n} \delta f^{b} - \left( {2\omega_{ie}^{n} + \omega_{en}^{n} } \right) \times \delta v^{n} + f^{n} \times \delta \theta^{n} + \delta g^{n} } \\ {(\omega_{ie}^{n} + \omega_{en}^{n} ) \times \delta \theta^{n} - C_{b}^{n} \delta \omega_{ib}^{b} } \\ \end{array} } \right]$$
(4)

where \(\delta \dot{r}^{n}\), \(\delta \dot{v}^{n}\), and \(\delta \dot{\theta }^{n}\) represent the derivative of position, velocity, and attitude error in \(n\)-frame, respectively. \(f^{n}\) denotes the specific force in \(n\)-frame, which describes the difference between the true acceleration and the acceleration due to gravity. \(C_{b}^{n}\) denotes the rotation matrix from \(b\)-frame (i.e., body frame) to \(n\)-frame. \(\omega_{en}^{n}\) denotes the turn rate of \(n\)-frame relative to \(e\)-frame, projected in \(n\)-frame. \(\omega_{ie}^{n}\) is the angular velocity of \(e\)-frame (i.e., earth-centered earth-fixed, ECEF frame) relative to inertial \(i\)-frame, projected in \(n\)-frame. \(\delta g^{n}\) represents the gravity error vector. The symbol \(\left( \times \right)\) denotes the cross-product. The \(\delta f^{b}\) and \(\delta \omega_{ib}^{b}\) are the summation error of the accelerometer and gyroscope measurement in \(b\)-frame, which are defined as:

$$\begin{gathered} \delta f^{b} { = }b_{a} + n_{a} \hfill \\ \delta \omega_{ib}^{b} = b_{g} + n_{g} \hfill \\ \end{gathered}$$
(5)

where \(n_{a}\) and \(n_{g}\) are the noise of accelerometer and gyroscope measurements, which are modeled as the Gaussian white noise, \(n_{a} \sim N(0,\sigma_{a}^{2} )\), \(n_{g} \sim N(0,\sigma_{g}^{2} )\). \(b_{a}\) and \(b_{g}\) represent the biases of the accelerometer and gyroscope, and they are modeled as the random walk. The derivatives of the biases are the Gaussian white noise:

$$\begin{gathered} \dot{b}_{a} \left( t \right) = n_{{b_{a} }} \left( t \right) \hfill \\ \dot{b}_{g} \left( t \right) = n_{{b_{g} }} \left( t \right) \hfill \\ \end{gathered}$$
(6)

where \(n_{{b_{a} }}\) and \(n_{{b_{g} }}\) are the Gaussian white noise of the accelerometer and gyroscope biases, \(n_{{b_{a} }} \sim N(0,\sigma_{a}^{2} )\), \(n_{{b_{g} }} \sim N(0,\sigma_{g}^{2} )\). Based on (4) and (5), the linearized continuous-time dynamic error model is described as:

$$\delta \dot{x}_{INS} = F\delta x_{INS} + Gn_{INS}$$
(7)

where \(n_{INS}\) represents the noise of the inertial system, \(n_{INS}^{T} = \left[ {\left( {n_{g} } \right)^{T} ,\left( {n_{bg} } \right)^{T} ,\left( {n_{a} } \right)^{T} ,\left( {n_{{b_{a} }} } \right)^{T} } \right]^{T}\), \(F\) is a dynamic matrix, and \(G\) is a design matrix. The close form of \(F\) and \(G\) can be found in Chatfield (1997).

The mechanization of the inertial system can update the INS state. The propagation of INS error state uncertainty can be obtained from the discretization of (7). First, the process noise covariance matrix can be computed as:

$$Q_{k} { = }\int_{{t_{k} }}^{{t_{k + 1} }} {\Phi \left( {k + 1,\tau } \right)G(\tau )QG^{T} (\tau )\Phi \left( {k + 1,\tau } \right)^{T} d\tau }$$
(8)

with

$$\Phi_{k} { = }\Phi \left( {k + 1,k} \right){ = }\exp \left( {\int_{{t_{k} }}^{{t_{k + 1} }} {F\left( \tau \right)d\tau } } \right)$$
(9)

where \(Q = E[n_{INS} n_{INS}^{T} ]\) is the covariance matrix of the INS error state noise. \(\Phi\) represents the state transition matrix. While the interval of the sampling time is small enough, \(\Phi_{k}\) can be approximated with the First-order Taylor expansion as:

$$\Phi_{k} \approx \exp \left( {F\left( {t_{k} } \right)\Delta t} \right) \approx I + F\left( {t_{k} } \right)\Delta t$$
(10)

Then, the propagation of the whole INS error state uncertainty can be computed as:

$$P_{{II_{{k + 1,k}} }} = \Phi _{k} P_{{II_{k} }} \Phi _{k}^{T} + Q_{k}$$
(11)

where \(P_{{II_{K} }}\) is the covariance matrix of the INS error state at time step \(k\). Once the state vector contains the historical camera states, the covariance matrix is updated as:

$$P_{{k + 1,k}} = \left( {\frac{{P_{{II_{{k + 1,k}} }} }}{{P_{{IC_{k} }}^{T} \Phi _{k}^{T} }}\frac{{\Phi _{k} P_{{IC_{k} }} }}{{P_{{CC_{K} }} }}} \right)$$
(12)

where \(P_{k + 1,k}\) presents the covariance matrix of the error state vector. \(P_{{CC_{K} }}\) represents the covariance matrix of the camera error state at time step \(k\). \(P_{{IC_{K} }}\) indicates the covariance matrix between the camera error state and the INS error state.

Augmentation of camera state

The initial pose of the new camera in \(e\)-frame at time step \(k\) can be obtained with the latest INS state as:

$$\hat{C}_{{c_{k} }}^{e} = C_{{n_{k} }}^{e} \cdot \hat{C}_{{b_{k} }}^{{n_{k} }} \cdot C_{c}^{b}$$
(13)
$$\hat{r}_{{c_{k} }}^{e} = D^{ - 1} \hat{r}_{{b_{k} }}^{{n_{k} }} + C_{{n_{k} }}^{e} \hat{C}_{{b_{k} }}^{{n_{k} }} r_{c}^{b}$$
(14)

where \(C_{n}^{e}\) is the rotation matrix from \(n\)-frame to \(e\)-frame, which can be computed from the geographical location. \(C_{c}^{b}\) and \(r_{c}^{b}\) represent the rotation and translation from \(c\)-frame (i.e., camera frame, right-down-forward) to \(b\)-frame, which can be obtained with the IMU-camera extrinsic parameter calibration. \(D^{ - 1}\) is a transfer matrix from the geodetic coordinate to the \(e\)-frame.

The estimated pose of the new camera is projected from the \(e\)-frame to local frame for the numerical stability. The local frame (\(l\)-frame) is defined with the reference of the first camera pose in the \(e\)-frame (\(C_{{c_{0} }}^{e}\),\(r_{{c_{0} }}^{e}\)). The estimated pose of the new camera in \(l\)-frame can be derived as:

$$\hat{C}_{{c_{k} }}^{l} = \left( {C_{{c_{0} }}^{e} } \right)^{T} \hat{C}_{{c_{k} }}^{e}$$
(15)
$$\hat{r}_{{c_{k} }}^{l} = \left( {C_{{c_{0} }}^{e} } \right)^{T} \left( {\hat{r}_{{c_{k} }}^{e} - r_{{c_{0} }}^{e} } \right)$$
(16)

The augmented covariance matrix is computed as:

$$P_{k,k} = \left( {\begin{array}{*{20}c} {I_{15 + 6N} } \\ J \\ \end{array} } \right)P_{k,k} \left( {\begin{array}{*{20}c} {I_{15 + 6N} } \\ J \\ \end{array} } \right)^{T}$$
(17)

with

$$J = \left( {\begin{array}{*{20}c} { - \left( {C_{{c_{0} }}^{e} } \right)^{T} C_{b}^{c} \left( {\hat{C}_{b}^{n} } \right)^{T} } & {0_{3 \times 3} } & {0_{3 \times 3} } & {0_{3 \times 3} } & {0_{3 \times 3} } \\ {\left( {C_{{c_{0} }}^{e} } \right)^{T} C_{n}^{e} \left( {\hat{C}_{b}^{n} r_{c}^{b} \times } \right)} & {0_{3 \times 3} } & {0_{3 \times 3} } & {0_{3 \times 3} } & H \\ \end{array} } \right)$$
(18)

where \(H\) is a differential equation between the geodetic coordinate system and the \(e\)-frame, which can be computed as:

$$H = \left[ {\begin{array}{*{20}c} {A\cos B\cos L - \left( {N + h} \right)\sin B\cos L} & { - \left( {N + h} \right)\cos B{\text{sin}}L} & {\cos B\cos L} \\ {A\cos B\sin L - \left( {N + h} \right)\sin B\sin L} & {\left( {N + h} \right)\cos B{\text{cos}}L} & {\cos B\sin L} \\ {A\left( {1 - e^{2} } \right)\sin B + \left( {N\left( {1 - e^{2} } \right) + H} \right)\cos B} & 0 & {\sin B} \\ \end{array} } \right]$$
(19)

with

$$A = \frac{{ae^{2} \sin B\cos B}}{{\sqrt {\left( {1 - e^{2} \sin B\sin B} \right)^{3} } }}$$
(20)

where \(B\) and \(L\) indicate the geodetic latitude and the geodetic longitude, respectively. \(h\) is the ellipsoidal height. \(a\) denotes the semimajor axis of the reference ellipsoid. \(e\) denotes the linear eccentricity of the reference ellipsoid. \(N\) is the radii of curvature in the prime vertical.

Measurement model

The measurement model of the integrated system consists of two parts. The multi-GNSS measurement model is employed to process the raw GNSS observations, and the quality control methods are also applied to eliminate outliers. The final results of GNSS with actual uncertainties will be used for the EKF updating. The frond-end of vision processes feature tracking and matching. The matched features will be used to construct the re-projection error equations and the EKF state estimation in the visual measurement model.

Double-difference multi-GNSS measurement model

The observation equations of the GNSS pseudorange, carrier phase, and Doppler from the base and rover stations can be presented as (Li et al. 2015):

$$P_{i} = \rho + c\left( {t_{r} - t^{s} } \right) + T_{r}^{s} + I_{r,i}^{s} + c\left( {d_{r,i} - d_{i}^{s} } \right) + \Delta \rho + \varepsilon_{P}$$
(21)
$$L_{i} = \rho + c\left( {t_{r} - t^{s} } \right) + T_{r}^{s} - I_{r,i}^{s} + \lambda_{i} N_{i} + \lambda_{i} \left( {b_{r,i} - b_{i}^{s} } \right) + PH_{r,i}^{s} + \Delta \rho + \varepsilon_{L}$$
(22)
$$D_{i} = \dot{\rho } + c\left( {\dot{t}_{r} - \dot{t}^{s} } \right) + \dot{T}_{r}^{s} + \dot{I}_{r,i}^{s} + c\left( {\dot{d}_{r,i} - \dot{d}_{i}^{s} } \right) + \Delta \dot{\rho } + \varepsilon_{D}$$
(23)

where and \(s\) represent for the receiver and satellite, and \(i\) is the GNSS carrier phase frequency. \(P_{i}\), \(L_{i}\), and \(D_{i}\) denote the pseudorange, carrier phase, and Doppler observations from receivers. \(\rho\) depicts the geometric distance between the receiver antenna phase center and the satellite antenna phase center. \(t_{r}\) and \(t^{s}\) are the offsets of the receiver clock and satellite clock. \(c\) is the speed of light. \(T_{r}^{s}\) and \(I_{r,i}^{s}\) are the tropospheric and ionospheric delays along the signal path at \(i\) frequency. \(\lambda\) and \(N\) are the carrier phase wavelength and integer ambiguity. \(d_{r,i}\) and \(d_{i}^{s}\) are the differential code biases (DCB) of the receiver and satellite at \(i\) frequency. \(b_{r,i}\) and \(b_{i}^{s}\) are the un-calibrated phase delay (UPD) of the receiver and satellite at \(i\) frequency. \(PH_{r,i}^{s}\) is the carrier phase wind-up effect. \(\Delta \rho\) represents other corrections. \(\varepsilon_{P}\), \(\varepsilon_{L}\) and \(\varepsilon_{D}\) denote the measurement noises of the pseudorange, carrier phase, and Doppler, respectively. The DD is adopted between the stations and satellites. After that, the observation equations of the pseudorange and carrier phase are described as:

$$\nabla \Delta P_{i} = \nabla \Delta \rho + \nabla \Delta T + \nabla \Delta I_{i} + \nabla \Delta \varepsilon_{P}$$
(24)
$$\nabla \Delta L_{i} = \nabla \Delta \rho + \nabla \Delta T - \nabla \Delta I_{i} + \lambda_{i} \nabla \Delta N_{i} + \nabla \Delta \varepsilon_{L}$$
(25)

where \(\nabla \Delta \left( \cdot \right)\) represents the DD operator. For the DD equations, the offsets of the receiver clock and satellite clock, the DCB and the UPD of the satellite end and the ground receiver are eliminated. In our research, the baseline is usually less than 5 km. When using the DD equations for this short baseline, the residuals of the ionospheric and tropospheric delays are negligible. The geometric ranges and the ambiguities are the only estimated parameters as:

$$\nabla \Delta P_{i} = \nabla \Delta \rho + \nabla \Delta \varepsilon_{P}$$
(26)
$$\nabla \Delta L_{i} = \nabla \Delta \rho + \lambda_{i} \nabla \Delta N{}_{i} + \nabla \Delta \varepsilon_{L}$$
(27)

where the parameters in this equation are the same as in (24) and (25).

The quality of GNSS observations is checked by the signal–noise ratio, satellite number and elevation. The variances of GNSS observations are determined by the satellite elevation-dependent weight model following (Ge et al. 2008). In order to further eliminate the influence of the outliers in the process of GNSS measurement updates, we adopted a robust estimation based on bifactor equivalent weight (Yang et al. 2002).

In the GNSS module, the EKF method is applied to perform data processing. When the GNSS results are available and passed the position check based on the INS or INS/Vision prediction, the integrated system can conduct the measurement update procedure through the EKF engine. Generally, there is an offset between the IMU center and the GNSS receiver antenna reference point (ARP); it is necessary to compensate for the lever-arm effect for data fusion. The lever-arm corrections of the position and velocity in \(n\)-frame are expressed as:

$$r_{GNSS}^{n} { = }r_{b}^{n} + D^{ - 1} C_{b}^{n} l^{b} { + }n_{GNSS}^{r}$$
(28)
$$v_{GNSS}^{n} = v_{b}^{n} - \left( {\left( {\omega_{ie}^{n} + \omega_{en}^{n} } \right) \times } \right)C_{b}^{n} l^{b} - C_{b}^{n} \left( {l^{b} \times } \right)\omega_{ib}^{b} + n_{GNSS}^{v}$$
(29)

where \(r_{GNSS}^{n}\) and \(v_{GNSS}^{n}\) indicate the GNSS position and velocity results from the GNSS module in the \(n\)-frame. \(r_{b}^{n}\) and \(v_{b}^{n}\) denote the position and velocity of IMU center solved by the INS mechanization. \(l^{b}\) is the lever-arm offset in the \(b\)-frame. \(n_{GNSS}^{r}\) and \(n_{GNSS}^{v}\) are the covariance matrixes of the GNSS position and velocity results. After the linearization of the measurement model (28, 29), the residuals at time step \(k\) can be expressed as:

$$r_{k} = \left[ {\begin{array}{*{20}c} {r_{GNSS,k}^{n} - \hat{r}_{INS,k}^{n} } \\ {v_{GNSS,k}^{n} - \hat{v}_{INS,k}^{n} } \\ \end{array} } \right] = H_{GNSS,k} \delta x_{k}$$
(30)

where \(\hat{r}_{INS}^{n}\) and \(\hat{v}_{INS}^{n}\) are the position and velocity of the GNSS antenna phase center predicted by INS, considering the lever-arm effect. The design matrix \(H_{GNSS,k}\) can be derived as:

$$H_{GNSS,k} = \left( {\begin{array}{*{20}c} {D^{ - 1} (C_{b}^{n} l^{b} \times )} & {0_{3 \times 3} } & {0_{3 \times 3} } & {0_{3 \times 3} } & {I_{3 \times 3} } & {0_{N \times 3} } \\ { - \left( {\omega_{in}^{n} \times } \right)C_{b}^{n} \left( {l^{b} \times } \right) - C_{b}^{n} \left( {l^{b} \times \omega_{ib}^{b} } \right)} & {0_{3 \times 3} } & {I_{3 \times 3} } & {0_{3 \times 3} } & {0_{3 \times 3} } & {0_{N \times 3} } \\ \end{array} } \right)$$
(31)

where \(N\) is the quantity of the camera error states left in the error state vector at time step \(k\).

Vision processing front end

In our implementation, the baseline between the left and right camera can reach 505 mm, which makes the illumination and viewpoint between the left and the right image vary slightly. So, a feature tracking method combining the rotated binary robust independent elementary features (BRIEF) descriptor (Rublee et al. 2011) and the Kanade-Lucas-Tomasi (KLT) sparse optical flow algorithm (Lucas and Kanade 1981) is proposed in the front end. For the first image, the features from the accelerated segment test (FAST) keypoint detector (Trajkovic and Hedley 1998) with a rotated BRIEF descriptor is used to extract image features, and they are matched between left and right images based on their rotated BRIEF descriptors. For the next sequences of the stereo images, the KLT tracking algorithm is used for the feature tracking between two consecutive images, and the INS mechanization can predict the initial pose of the current image. A random sample consensus (RANSAC) method with a fundamental matrix model (Hartley and Zisserman 2003) is adopted to remove outliers in the tracking process. After the RANSAC checking, the rotated BRIEF descriptors of the tracked features in the current image are extracted. In addition, the feature matching between the current left and right images is to proceed to maintain the accuracy of feature tracking.

The matching results between the left and right cameras are depicted in Fig. 2, while Fig. 3 reveals the condition of tracking between the previous image and the current image. From both results, we can find that more mismatching features exist in the KLT-only method, which demonstrates our method can clearly improve feature matching and tracking in the long baseline condition.

Fig. 2
figure 2

Comparison of the KLT-based method (top) and our method (bottom) in terms of the feature matching performance between left and right images

Full size image
Fig. 3
figure 3

Comparison of the KLT-based method (left) and our method (right) in terms of the feature tracking performance between pre-frame and cur-frame images

Full size image

To further verify the reliability of our algorithm from the statistical perspective, 100 left frames and right frames images and 100 per-frame and cur-frame images are selected as test data. The ORB descriptor distances between matched features are used to describe the accuracy of matching. The experimental result is shown in Figs. 4 and 5. In these figures, the X-axis represents descriptor distances between matching feature points and ranges from 0 to 255. The Y-axis describes the frequency of the occurrence of different ORB descriptor distances in 100 images. From the results, we can find out that the frequency of matching points with smaller descriptor distance is significantly increased by our method. In Fig. 4, the average descriptor distances based on KLT method and our method are 54.64 and 40.10, respectively. In Fig. 5, the average descriptor distances are 22.90 in KLT method and 11.03 in our method. All of these results show that our method performs better than the KLT-based method in the long-baseline feature matching.

Fig. 4
figure 4

Depiction of the oriented FAST and rotated BRIEF (ORB) descriptor distance between matched features in 100 left and right images by the KLT based method and our method

Full size image
Fig. 5
figure 5

Depiction of the ORB descriptor distance between matched features in 100 pre-frame and cur-frame images by the KLT based method and our method

Full size image

Besides the feature tracking, the keyframe strategy is also applied in the visual front-end to bound the computation cost. The selection of keyframes follows three criteria. The first criterion is the average parallax of continuously tracked features apart from the previous keyframe (Qin et al. 2018). Once its value exceeds the pre-set line, the current frame will be chosen as a keyframe. The average parallax can be calculated as:

$$p = \frac{{\sum\limits_{k = 1}^{N} {\sqrt {(du_{k} )^{2} + (dv_{k} )^{2} } } }}{N}$$
(32)

where \(N\) is the number of tracked features. \(k\) is the feature ID. \(du_{k} = u_{jk} - u_{ik}\), \(dv_{k} = v_{jk} - v_{ik}\), \(u\) and \(v\) represent the pixel coordinates in the image. \(i\) and \(j\) present the previous keyframe and the current frame, respectively.

The second strategy is used to guarantee the quality of tracking. When the number of tracked features in the new frame is lower than 50 percent of the number of tracked points in the previous frame, the keyframe needs to be inserted. The last criterion is a complementary mechanism. When the number of non-keyframe reaches a pre-set threshold, we compulsively insert a keyframe. The threshold is set to 10 in our experiment.

Visual measurement model

The estimated stereo camera measurements of a single feature \(f_{j}\) at time step \(i\) is represented as:

$$\hat{z}_{i}^{j} { = }\left[ {\begin{array}{*{20}c} {\hat{X}_{j}^{{C_{i,1} }} /\hat{Z}_{j}^{{C_{i,1} }} } \\ {\hat{X}_{j}^{{C_{i,1} }} /\hat{Z}_{j}^{{C_{i,1} }} } \\ {\hat{X}_{j}^{{C_{{i,{2}}} }} /\hat{Z}_{j}^{{C_{{i,{2}}} }} } \\ {\hat{X}_{j}^{{C_{{i,{2}}} }} /\hat{Z}_{j}^{{C_{{i,{2}}} }} } \\ \end{array} } \right] + n_{i}^{j}$$
(33)

where \(n_{i}^{j}\) is the measurement noise vector. \(\left( {\hat{X}_{j}^{{C_{i,k} }} ,\hat{Y}_{j}^{{C_{i,k} }} ,\hat{Z}_{j}^{{C_{i,k} }} } \right)^{T}\) \(k \in \left\{ {1,2} \right\}\) indicates the feature positions in the left camera frame \(C_{i,1}\) and the right camera frame \(C_{{i,{2}}}\), which can be computed with the equation as:

$$\left[ {\begin{array}{*{20}c} {\hat{X}_{j}^{{C_{i,1} }} } & {\hat{Y}_{j}^{{C_{i,1} }} } & {\hat{Z}_{j}^{{C_{i,1} }} } \\ \end{array} } \right]^{T} = \left( {\hat{C}_{{C_{i,1} }}^{l} } \right)^{T} \left( {\hat{r}_{j}^{l} - \hat{r}_{{C_{i,1} }}^{l} } \right)$$
(34)
$$\left[ {\begin{array}{*{20}c} {\hat{X}_{j}^{{C_{i,2} }} } & {\hat{Y}_{j}^{{C_{i,2} }} } & {\hat{Z}_{j}^{{C_{i,2} }} } \\ \end{array} } \right]^{T} {\text{ = C}}_{{C_{i,1} }}^{{C_{i,2} }} \left( {\hat{r}_{j}^{{C_{i,1} }} - r_{{_{{C_{i,1} }} }}^{{C_{i,2} }} } \right)$$
(35)

where \(\left( {C_{{c_{i,1} }}^{l} r_{{c_{i,1} }}^{l} } \right)\) represents the pose of the left camera in \(l\)-frame. \(C_{{C_{i,1} }}^{{C_{i,2} }}\) and \(r_{{_{{C_{i,1} }} }}^{{C_{i,2} }}\) are the transformation from the left camera to the right camera. \(r_{j}^{l}\) is the feature position in the \(l\)-frame, which is computed by the least square method given in Montiel and Civera (2006) based on current camera pose. After the linearization of the measurement model, the residual can be expressed by:

$$r_{i}^{j} = z_{i}^{j} - \hat{z}_{i}^{j} = H_{{C_{i} }}^{j} \delta x_{{C_{i} }} + H_{{f_{i} }}^{j} \delta p_{{f_{j} }}^{l} + n^{j}$$
(36)

where \(n^{j}\) denotes the measurement noise vector. \(H_{{C_{i} }}^{j}\) and \(H_{{f_{i} }}^{j}\) represent the Jacobians of the camera error state and the feature position error state. \(\delta x_{{C_{i} }}\) and \(\delta p_{{f_{j} }}^{l}\) are the camera error state and feature position error state. The corresponding Jacobians can be computed as:

$$H_{{C_{i} }}^{j} { = }\left( {\begin{array}{*{20}c} {J_{1} \left( {\hat{r}_{j}^{{C_{i,1} }} \times } \right)} & { - J_{1} \left( {\hat{C}_{{C_{i,1} }}^{l} } \right)^{T} } \\ {\left( {J_{2} \cdot C_{{C_{i,1} }}^{{C_{i,2} }} } \right)\left( {\hat{r}_{j}^{{C_{i,1} }} \times } \right)} & { - \left( {J_{2} \cdot C_{{C_{i,1} }}^{{C_{i,2} }} } \right)\left( {\hat{C}_{{C_{i,1} }}^{l} } \right)^{T} } \\ \end{array} } \right)$$
(37)
$$H_{{f_{i} }}^{j} { = }\left( {\begin{array}{*{20}c} {J_{1} \left( {\hat{C}_{{C_{i,1} }}^{l} } \right)^{T} } \\ {J_{2} C_{{C_{i,1} }}^{{C_{i,2} }} \left( {\hat{C}_{{C_{i,1} }}^{l} } \right)^{T} } \\ \end{array} } \right)$$
(38)

with.

$$J_{1} = \frac{{\partial z_{i}^{j} }}{{\partial r_{j}^{{C_{i,1} }} }}{ = }\frac{1}{{\hat{Z}_{j}^{{C_{i,1} }} }}\left( {\begin{array}{*{20}r} \hfill 1 & \hfill 0 & \hfill { - \frac{{\hat{X}_{j}^{{C_{i,1} }} }}{{\hat{Z}_{j}^{{C_{i,1} }} }}} \\ \hfill 0 & \hfill {1} & \hfill { - \frac{{\hat{Y}_{j}^{{C_{i,1} }} }}{{\hat{Z}_{j}^{{C_{i,1} }} }}} \\ \hfill {0} & \hfill {0} & \hfill {0} \\ \hfill {0} & \hfill {0} & \hfill {0} \\ \end{array} } \right), \quad J_{2} = \frac{{\partial z_{i}^{j} }}{{\partial r_{j}^{{C_{i,2} }} }}{ = }\frac{1}{{\hat{Z}_{j}^{{C_{i,2} }} }}\left( {\begin{array}{*{20}r} \hfill {0} & \hfill {0} & \hfill {0} \\ \hfill {0} & \hfill {0} & \hfill {0} \\ \hfill {1} & \hfill {0} & \hfill { - \frac{{\hat{X}_{j}^{{C_{i,2} }} }}{{\hat{Z}_{j}^{{C_{i,2} }} }}} \\ \hfill 0 & \hfill {1} & \hfill { - \frac{{\hat{Y}_{j}^{{C_{i,2} }} }}{{\hat{Z}_{j}^{{C_{i,2} }} }}} \\ \end{array} } \right)$$
(39)

Usually, the same feature \(f_{j}\) can be observed by the stereo camera at different time steps. The residuals from all of the features’ measurements can be expressed as:

$$r^{j} = H_{x}^{j} \delta x + H_{f}^{j} \delta p_{{f_{j} }}^{l} + n^{j}$$
(40)

where \(\delta x\) is the error state vector, which contains the multiple camera error states. In the implementation, the feature position error state \(\delta p_{{f_{j} }}^{l}\) is not in the error state vector because of the consideration of system robustness and the boundary of computational complexity. For this problem, as pointed out in Mourikis and Roumeliotis (2007), the residual in (40) is projected to the left null space of \(H_{f}^{j}\). The new formulation of the residual can be derived as:

$$r_{o}^{j} = V^{T} r^{j} = V^{T} H_{x}^{j} \delta x + V^{T} H_{f}^{j} \delta p_{{f_{j} }}^{l} + V^{T} n^{j} { = }H_{{x,{\text{o}}}}^{j} \delta x + n_{o}^{j}$$
(41)

where \(V^{T} H_{f}^{j} { = }0\). The \(r_{o}^{j}\) and \(H_{x,o}^{j}\) are also computed following Mourikis and Roumeliotis (2007).

The sliding window algorithm is used to maintain the quantity of the camera error states for efficiency. The size of the window is set to 10. The updates of the visual measurements are executed following two kinds of conditions. For feature tracking, once the font-end no longer tracks a feature, all measurements are used for measurement updates. For keyframes, once the number of camera poses in the sliding window reaches the limitation, two keyframes are selected by the parallax following Sun et al. (2018) and marginalized from the error state vector.

Experiment

Both simulation and field experiments were adopted to validate the performance of the proposed GNSS/INS/Vision integrated system. The experiment data involved the most common ground vehicle motions, such as acceleration, deceleration, stationary, and turning. The vehicle-borne mobile system was used to collect the experiment data. It was equipped with A Septentrio PolaRx5 GNSS receiver (Septentrio Corporation 2019) together with a NovAtel GPS-703-GGG-HV antenna (NovAtel Corporation 2014), two Blackfly S cameras (FLIR Corporation 2019) and a tactical IMU-FSAS (NovAtel Corporation 2015). The GPS (L1, L2, L5), GLONASS (L1, L2, L3), Galileo (E1,E5ab,E6) and BDS (B1, B2, B3) signals are supported by Septentrio receiver. The Blackfly S camera is a global shutter industry CMOS camera. It can provide 1920 × 1200 resolution images at the maximum frequency of 53 Hz. The specification information of IMU sensor is provided in Table 1. The experiment data are collected with sampling rates of 1 Hz, 200 Hz and 10 Hz for GNSS, IMU, and cameras, respectively.

Table 1 Technical specifications of the IMU sensor
Full size table

The structure of the platform and the connections between the equipment can be seen in Fig. 6. The GNSS antenna was linked to a GNSS receiver and an IMU device through a signal power divider. Two cameras were tightly mounted on the front of the platform with a 505 mm baseline. For time synchronization, the GNSS receiver generates pulses per second (PPS) to trigger camera exposures, and the feedback signal is recorded. By this means, the time synchronization is realized at the hardware level, and timestamps of sensors are united to GPS time. As for extrinsic parameters between different sensors, the shift between IMU center and GNSS ARP was measured precisely to compensate for the lever-arm effect. The extrinsic parameters of stereo camera and camera-IMU are acquired, respectively, through offline calibration following (Furgale et al. 2013).

Fig. 6
figure 6

Illustration of the experimental equipment including the hardware platform (top) and the data acquisition vehicle (bottom)

Full size image

The GNSS base station was set up near the experiment field and within 5 km to the rover station. The vehicle remained stationary about 5 min in the beginning and end of each trajectory for the initial alignment and the backward smoothing procedure in post-processing. The corresponding data were deliberately removed in the results for a more direct display. In the experiment, the tactical IMU-FSAS is used to verify the performance of GNSS/IMU/Vision fusion. Compared with MEMS IMU, the tactical IMU can maintain a certain accuracy of position and attitude output without external correction information for a relatively long time, which makes it more sensitive to the noise and errors of visual observation and can better evaluate the performance of the integration system. Besides, based on our knowledge, few studies have verified the effect of visual information to the high-end GNSS/IMU integration algorithm, which is very important for the development of visual-based HD maps in autonomous driving. We employed commercial Inertial Explorer 8.7 software (NovAtel Corporation 2018) to calculate the smoothed solution of multi-GNSS/INS tight integration and the multi-GNSS/INS loosely coupled solution. The former is considered a reference, and the latter is used as a contrast to assess the integrated system performance. The position accuracy of the reference value can reach the dm level; the velocity accuracy can reach the cm/s level, and the attitude accuracy is less than 1 degree.

GNSS outage simulation experiment

To validate the capacity of the INS/Vision integrated system in the GNSS outage condition, we selected two trajectories from a vehicle experiment in the open-sky condition. The selected data is based on the real vehicle collection data, and the outage of the GNSS signal can be achieved by directly blocking the GNSS measurement in data processing. Each trajectory is divided into five segments and each segment lasts for 50 s. To prevent the correlation between different segments, there is about a 100 s gap between segments. The average numbers of available satellites of GPS, BDS, Galileo, GLONASS and GPS + BDS + Galileo + GLONASS in experiment are 9.565, 4.494, 6.336, 3.995, and 24.390, respectively. The average value of PDOP is 0.979. The GNSS measurements remain available until each segment begins to make them have the same observation condition.

Figure 7 shows the RMSs of the position with two solutions. For GNSS outage time from 5 to 50 s, the position RMSs of INS solution are degraded from 0.046, 0.024 and 0.007 m to 3.116, 3.042 and 0.152 m in east, north and vertical directions, respectively. While using the INS/Vision solution, the values drop from 0.047, 0.047 and 0.035 m to 1.509, 1.817 and 1.047 m in east, north and vertical directions. The INS/Vision solution achieves better accuracy in contrast with the INS-only solution, despite that the position accuracy of both solutions becomes worse with the increase of GNSS break off time.

Fig. 7
figure 7

Depiction of RMSs of position drifts from INS/Vision and INS-only solutions during GNSS outages on different scales

Full size image

Figure 8 shows the RMSs of the velocity with two solutions. For INS-only solution, the velocity RMSs increase from 0.019, 0.012 and 0.004 m/s to 0.165, 0.184, and 0.009 m/s in east, north and up directions. However, the RMSs drop from 0.020, 0.023 and 0.005 m/s to 0.117, 0.137 and 0.036 m/s in the INS/Vision solution along with the outage time. The statistics indicate that the INS/Vision solution could realize a higher accuracy of velocity than the INS-only solution in the horizontal direction, and the divergence of the velocity is effectively suppressed with the assist of vision.

Fig. 8
figure 8

Depiction of RMSs of velocity drifts from INS/Vision and INS-only solutions during GNSS outages on different scales

Full size image

Figure 9 shows the RMSs of the attitude with two solutions. The INS/Vision solution has a better estimation in attitude than the INS-only solution, especially in the heading direction. According to the statistics, when the outage time of GNSS increases from 5 to 50 s, the attitude RMSs of the INS/Vision solution degrade from \(0.422^{ \circ }\), \(0.054^{ \circ }\), and \({0}{\text{.041}}^{ \circ }\) to \(0.464^{ \circ }\), \(0.062^{ \circ }\), and \({0}{\text{.052}}^{ \circ }\) in yaw, pitch and roll directions, respectively. Relatively, the RMSs of the INS-only solution drop from \(0.553^{ \circ }\), \(0.067^{ \circ }\), and \({0}{\text{.028}}^{ \circ }\) to \(0.896^{ \circ }\), \(0.069^{ \circ }\), and \({0}{\text{.056}}^{ \circ }\) in the same conditions.

Fig. 9
figure 9

Depiction of RMSs of attitude drifts from INS/Vision and INS-only solutions during GNSS outages on different scales

Full size image

The result indicates that the additional visual information can significantly enhance the capacity of INS during GNSS outages. The error corrections from the visual measurement updates can make a positive contribution to the state estimation, which helps the vision-aided method maintain a more accurate and stable navigation output during GNSS outages than the INS-only method.

GNSS partly blocked condition experiment

The experimental data were collected at the Wuhan University campus, including both the GNSS blocked area and the open-sky area. In GNSS blocked area, trees with dense forest canopies are planted on both sides of the road, making the tracking of the GNSS signal difficult and aggravating the multipath effect. The total distance of the trajectory is about 1563 m, and the whole experiment lasts for 7 min. The typical situations of the trajectory are displayed in Fig. 10

Fig. 10
figure 10

Typical situations (bottom) in the GNSS partly blocked condition

Full size image

The observability of GNSS is evaluated by the continuity of satellite signal tracking, the number of available satellites and the position dilution of precision (PDOP). In our experiments, the value of the cutoff elevation angle for available satellites is set to \(10^{ \circ }\). The top of Fig. 11 indicates the number of available GNSS satellites. The GLONASS satellites were removed during the DD process due to the low elevation angle and sparse observable satellites. The average numbers of available satellites of GPS, BDS, Galileo and GPS + BDS + Galileo are 4.757, 4.195, 4.878 and 13.830, respectively. The number of visible satellites has a rapid drop, especially in the tree-lined roads. The middle of Fig. 11 describes the time series of the elevation angle and the signal tracking information of GNSS satellites. The breakpoint indicates that the observation of satellite is not available. For satellites with elevation angle under \(40^{^\circ }\), the interruption during the tracking period is frequent. The impact is also reflected in the PDOP value, which is shown at the bottom of Fig. 11. The average value of PDOP is 4.169 and reaches 45.310 at the worst. On account of the signal blocking, the observation quantity of captured satellites reduces significantly, and the signal tracking becomes discontinuous, which is a challenge to GNSS positioning.

Fig. 11
figure 11

Depiction of the satellite visibility consists of the quantity of multi-GNSS available satellites (top), the elevation angle time series of GNSS satellites (middle) and the PDOP (bottom) in the partly blocked condition

Full size image

Figure 12 shows the trajectories overview of three different solutions. Because of the frequent interruptions of the GNSS signal, the GNSS-only solution cannot achieve reliable and continuous positioning results. The other two solutions can provide a continuous navigation output. However, the result of the GNSS/INS solution would drift gradually over time for the time-increasing INS error in GNSS gaps.

Fig. 12
figure 12

Trajectory of the ground truth, the GNSS/INS solution, the GNSS/INS/Vision solution (top) and the multi-GNSS Result (bottom)

Full size image

Figure 13 depicts the position errors of the GNSS/INS solution and GNSS/INS/Vision solution compared to the ground-truth, and Table 2 shows the RMSs of position error. From statistical analysis, compared to the GNSS/INS solution, the GNSS/INS/Vision position error RMSs reduce from 7.438 and 2.219 m to 0.939 and 0.646 m in east and north directions, with improvements of 87.4% and 70.9%, respectively. In vertical directions, the GNSS/INS/Vision solution does not acquire an improvement. The maximum position errors of GNSS/INS solution arrive at 27.413, −6.110 and 0.828 m in the east, north and up directions, respectively, and the absolute position error is 28.098 m. Comparing with the position error of the GNSS/INS method, the maximum position errors of the GNSS/INS/Vision solution are −2.706, −1.067 and −3.411 m in the east, north and up directions, respectively, and the absolute position error is 4.483 m. This indicates that visual information can significantly suppress the accumulation of IMU errors in position estimation.

Fig. 13
figure 13

Accuracy comparison of the GNSS/INS/Vision solution and the GNSS/INS solution about the position in the GNSS partly blocked condition

Full size image
Table 2 RMSs of position errors, velocity errors and attitude errors of the GNSS/INS/Vision solution and the GNSS/INS solution in the GNSS partly blocked condition
Full size table

Figure 14 shows the velocity errors of the two methods. According to Table 2, the velocity RMSs of GNSS/INS solution are 0.177, 0.127 and 0.006 m/s in the east, north and up directions, respectively. The precision of velocity in the horizontal direction of the GNSS/INS/Vision solution is much better. The velocity error RMSs of GNSS/INS/Vision solution are 0.051, 0.060 and 0.028 m/s in the east, north and up directions with improvements of 71.2% and 52.8% in the horizontal direction than that of GNSS/INS solution.

Fig. 14
figure 14

Accuracy comparison of the GNSS/INS/Vision solution and the GNSS/INS solution about velocity in the GNSS partly blocked condition

Full size image

Figure 15 describes the attitude errors of the two methods. Both methods achieve high accuracy in roll and pitch estimation, and the attitude error RMSs of them are close. As for yaw angle estimation, the GNSS/INS/Vision method achieves a better performance, which has a 23.7% improvement compared to the GNSS/INS method.

Fig. 15
figure 15

Accuracy comparison of the GNSS/INS/Vision solution and the GNSS/INS solution about attitude in the GNSS partly blocked condition

Full size image

GNSS difficult condition experiment.

The experimental data were also collected near the Wuhan University campus. The length of the route is about 2221 m and takes about 10 min. Figure 16 displays the top view of the trajectory and typical situations of surroundings. Compared to the GNSS partly blocked condition experiment, the road is narrower with trees and buildings on both sides. As a result, the GNSS signal is seriously blocked for a longer time.

Fig. 16
figure 16

Typical situations (bottom) in the GNSS difficult condition

Full size image

The top of Fig. 17 reflects the number of satellites during the experiment. Similar to the partly blocked experiment, there is also no available GLONASS satellite during this period. It is easy to find that the number of available satellites fluctuates greatly, and the average numbers of GPS, BDS, Galileo and GPS + BDS + Galileo satellites are 5.862, 5.506, 4.728 and 16.096. The middle of Fig. 17 shows the signal tracking continuity of satellites. Compared with the partly blocked condition, the signal interruption is more severe during the entire process. Besides, large jumps also appear in the PDOP values based on the bottom of Fig. 17. The average value and maximum value of PDOP are 6.242, 57.170, respectively, compared to 4.169, 45.310 in the partly blocked condition.

Fig. 17
figure 17

Depiction of the satellite visibility consists of the quantity of multi-GNSS available satellites (top), the elevation angle’s time series of GNSS satellites (middle) and the PDOP (bottom) in the GNSS difficult condition

Full size image

The trajectories overview of the GNSS-only solution, the GNSS/INS solution and the GNSS/INS/Vision solution are shown together in Fig. 18. In contrast with the GNSS partly blocked condition, the GNSS outage time lasted longer.

Fig. 18
figure 18

Trajectory of the ground truth, the GNSS/INS solution, the GNSS/INS/Vision solution (top) and the multi-GNSS Result (bottom)

Full size image

The position errors of the GNSS/INS solution and the GNSS/INS/Vision solution are depicted in Fig. 19. The position error RMSs of the GNSS/INS solution in Table 3 are 8.006, 4.022 and 1.397 m compared to 0.694, 0.843 and 1.103 m of the GNSS/INS/Vision solution in east, north and up directions. The specific values of improvement are 91.3%, 79% and 21%. The maximum position errors of the GNSS/INS solution arrive at 39.875, 16.435 and −4.829 m in the east, north and up directions, respectively, and the absolute position error is 43.399 m. By contrast, the maximum position errors of the GNSS/INS/Vision solution are only 2.269, −3.773 and −0.952 m in the east, north and up directions, respectively, and the absolute position error is 4.504 m. A conclusion can be reached that the fusion of visual data can dramatically improve the positioning performance of the system, which is the same as the partly blocked condition.

Fig. 19
figure 19

Accuracy comparison of the GNSS/INS/Vision solution and the GNSS/INS solution about position in the GNSS difficult condition

Full size image
Table 3 RMSs of position errors, velocity errors and attitude errors of the GNSS/INS/Vision solution and the GNSS/INS solution in the GNSS difficult condition
Full size table

Figure 20 shows the velocity errors of two methods. Table 3 indicates the velocity error RMSs of the GNSS/INS solution are 0.211, 0.124 and 0.016 m/s in the east, north and up directions, respectively. By contrast, the velocity errors RMSs of GNSS /INS/Vision solution are 0.041, 0.041 and 0.029 m/s in the east, north and up directions, respectively. The vision-aided solution has a remarkable improvement in east and north directions, and the specific values are 80.6% and 66.9%. However, the vertical direction velocity errors are similar, which is the same result as the partly blocked condition.

Fig. 20
figure 20

Accuracy comparison of the GNSS/INS/Vision solution and the GNSS/INS solution about velocity in the GNSS difficult condition

Full size image

Figure 21 describes the attitude errors of two methods, and both methods achieve a high accuracy pose estimation in the pitch and the roll angle. For the yaw angle estimation, the RMS of the GNSS/INS solution is \(0.155^{ \circ }\), which is better than \(0.410^{ \circ }\) in the GNSS /INS/Vision solution. The main reason may be related to the feature mismatches caused by the repeating texture of trees and dynamic objects.

Fig. 21
figure 21

Accuracy comparison of the GNSS/INS/Vision solution and the GNSS/INS solution about attitude in the GNSS difficult condition

Full size image

Table 4 shows the average processing-time required by the visual part of the GNSS /INS/Vision integrated system. The experimental data are processed on the laptop with a quad-core i7-7700HQ CPU at 2.80 GHz, and a 32 GB of RAM. Table 5 describes that the most time-consuming part of visual processing is the construction of the visual measurement equation. The selection of keyframe, the calculation of the feature points location, the selection of the feature points involved in measurement update and the construction of the observation equation are all included in this part. The average time cost for the visual measurements of the two sets of experimental data is 33.76 ms and 36.50 ms, which demonstrates our filter-based vision framework is very efficient and can be used for real-time data processing.

Table 4 Average processing-time of the visual part of the GNSS /INS/Vision integrated system
Full size table

Conclusions

We presented a robust GNSS/INS/Vision integrated system and validated it with both simulation and vehicular field experiments. The experiment results demonstrate that the adding visual information can help the system maintain a more accurate and stable navigation output than the INS-only method during GNSS outages. In the GNSS-degraded environment, the statistical results indicated that the RMSs of position estimation have a maximum 91.3%, 79.0% and 21.0% improvements in east, north and vertical directions, respectively, comparing to the GNSS/INS solution. Moreover, the stability of positioning can be significantly enhanced. The promotion of the velocity estimation can reach to 80.6% and 66.9% in east and north directions, respectively. As for attitude estimation, both solutions can realize high-precision estimation in the pitch and the roll angle. The GNSS/INS/Vision solution has a 23.7% improvement in the yaw angle estimation under the GNSS partly blocked condition. However, it gets worse in the GNSS difficult condition because of feature mismatches and dynamic objects in complex driving situations. In this condition, the next step of our work is to reduce the instability of the integrated system caused by the visual vulnerability in the real driving condition.