Introduction

Global Navigation Satellite System (GNSS) signals are affected by the earth’s atmosphere. The delayed signals limit the high-precision positioning and navigation applications, but the error can be exploited to study different parts of the atmosphere, including the water vapor. Monitoring the atmospheric water vapor is important since it is a major atmospheric greenhouse gas with significant impact on the earth’s radiative balance (Sinha and Harries 1997). It can generally act as a warming amplifier so that the cycling rate of water vapor reduces with the warming climate (Schneider et al. 2010). High-temporal resolution observations and an increasing number of satellites have turned GNSS into a promising measuring tool for investigating the variability of the water vapor, especially in the presence of a dense network of permanent stations.

Owing to the high temporal resolution, the accuracy of products, and the capability of making measurements even in severe weather conditions, the retrieved water vapor content of the atmosphere from ground-based GNSS observations has been identified as one of the reference data for GCOS (Global Climate Observing System) Reference Upper Air Network (GRUAN, Ning et al. 2016). Precipitable water vapor (PWV) from GNSS has increasingly been used for climate research (Gradinarsky et al. 2002; Nilsson and Elgered 2008; Wang et al. 2016; Alshawaf et al. 2017). The accuracy of the estimated climatic trends using GNSS PWV depends on the homogeneity of the analyzed time series (Alshawaf et al. 2018; Klos et al. 2018). For different reasons such as hardware or software changes, the data might contain inhomogeneities (temporal jumps or offsets). Such artifacts should be detected and eliminated through a delicate homogenization process without affecting climatic abrupt changes.

By definition, a homogeneous climate time series can only contain the variations caused by weather and climate (Venema et al. 2012). The main sources of inhomogeneity in GNSS-derived PWV data are instrumental changes or software settings of the GNSS station, e.g., antenna change, radome installation or removal, and cut-off angle setting (Vey et al. 2009). Most of the changes stem from the technological advancements, which make it unavoidable to update the hardware in GNSS stations. Therefore, GNSS-derived PWV time series are likely to have inhomogeneities, especially in the longer time series that would be used for climate studies. The changes are usually documented in the stations’ log files, but the documentation might be incomplete or missing for some of them. Change in the measurement conditions and the surrounding area of the station such as urbanization and growth or removal of vegetation might also affect the homogeneity of the time series. In the case of not using a reprocessed dataset, the change of processing software or procedure is another possible source of inhomogeneity. The external measurements that are used to obtain PWV from GNSS data processing, such as air pressure and temperature can pass their heterogeneity to the derived PWV time series. It should be noted that the mentioned reasons of inhomogeneity are generally not documented in the station’s log file. Therefore, finding a pragmatic solution for detection and verification of undocumented changes during the homogenization process is inevitable.

Different approaches have been introduced to check the homogeneity of GNSS products. For instance, Rodionov (2004) proposed a sequential algorithm which introduced a statistic entitled the Regime Shift Index (RSI) coupled with the Student’s t test to enhance detection of a regime shift. The Penalized maximal t test has widely been used for data homogenization (Jarušková 1996; Wang et al. 2007; Ning et al. 2016; Balidakis et al. 2018). Wang (2008), Ning et al. (2016), Klos et al. (2017), and Van Malderen et al. (2017), considered lag-1 autocorrelation in time series of first-order autoregressive noise. To support the detection of multiple change points in a time series, Wang (2008) proposed an empirical approach based on a stepwise testing algorithm. Ning et al. (2016) applied an iterative adapted version of penalized maximal t test to the monthly PWV time series, which helps in avoiding the difficulty of change point detection in the presence of high temporal variations and noise in the daily PWV data.

The “Data homogenization” activity of the sub-working group WG3 of COST ES1206 Action has assessed various statistical tools for homogenization using a synthetic benchmark dataset. The simulated dataset was based on the difference between GNSS-derived PWV time series and the European Centre for Medium-Range Weather Forecasts (ECMWF) reanalysis data (ERA-Interim) (Van Malderen et al. 2017). Using the difference time series can facilitate the detection of slight changes, but it is difficult to interpret the origin of the detected changes. Ning et al. (2016) validated detected change points using more than one reference dataset (e.g., VLBI, DORIS). Therefore, the verification process is left inconclusive in the case of not having another reference data set for a station. The latter study shows the possibility of the presence of inhomogeneities in the ERA-Interim dataset. The study reveals the need for having an independent verification procedure of any reference data. Van Malderen et al. (2017) preferred not to consider absolute statistical homogenization methods as practical approaches, owing to the problem of reliability, even though they confirm that ERA-interim might have its own inhomogeneities.

We develop and apply an approach to detect abrupt changes in an undifferenced time series. GNSS-derived PWV time series, in addition to the probable inconsistencies, contain the effects of climate or meteorological variabilities. Therefore, at least one reference dataset is required, e.g., ERA-Interim, to distinguish whether the offsets are caused by climate or meteorological effects or by inhomogeneities. We developed a method of offset detection in PWV time series, which is independently applicable to GNSS and ERA-Interim PWV data as well as their difference. This is performed by analyzing the time series variations with respect to a representative model. For this purpose, we exploit the singular spectrum analysis (SSA) as a subspace-based technique, which makes use of empirical functions derived from the data to model the time series in a pre-specified level of details. SSA is a non-parametric method that does not need any statistical assumptions such as stationarity of the series or normality of the residuals (Hassani and Thomakos 2010). Even in the presence of periodicity and noise, SSA can offer an adequate estimation of the time series based on setting a few arguments (such as window length). It can be used for trend extraction and extrapolation (Alexandrov 2008; Modiri et al. 2018), periodicity detection, seasonal adjustment, smoothing, noise reduction (Ghil et al. 2001; Golyandina et al. 2001) as well as change point detection (Escott-Price and Zhigljavsky 2003).

After a brief description of the datasets in the next section, we sketch out the SSA technique at the beginning of the methodology section, which continues by introducing our approach for homogenization. That section also comprises details of the offset detection method, as well as preprocessing and verification procedures. The performance assessment based on applying the method to simulated data is followed by a real GNSS dataset homogenization in the results section. A summary of the conclusions of this study is provided in the last section.

Dataset

We use a PWV near real-time dataset produced by the German Research Centre for Geosciences (GFZ). The dataset has a temporal resolution of 15 min with a delay of about 30 min and an accuracy of 1–2 mm (Li et al. 2014). The PWV time series are calculated from the Zenith Total Delay (ZTD) derived at GNSS stations of the German SAPOS network in PPP mode.

The GNSS-derived PWV can be obtained from the wet part of the ZTD, the Zenith Wet Delay (ZWD), via the conversion factor Q:

$${\text{ZWD }} = {\text{ ZTD }} - {\text{ ZHD}}$$
(1)
$${\text{PWV}} = \frac{\text{ZWD}}{Q}$$
(2)

where the ZHD is the Zenith Hydrostatic Delay (ZHD) estimated by the Saastamoinen model (Saastamoinen 1972) using measurements of surface pressure. The conversion factor is computed using (Askne and Nordius 1987):

$$Q = 10^{ - 6} \rho_{\text{w}} R_{\text{w}} \left( {k^{\prime}_{2} + \frac{{k_{3} }}{{T_{\text{m}} }}} \right)$$
(3)

where \(\rho_{\text{w}}\) and \(R_{\text{w}}\) are the density of liquid water and the specific gas constant for water vapor. The \(k^{\prime}_{2}\) and \(k_{3}\) are constants estimated from laboratory experiments (Bevis et al. 1994) and \(T_{\text{m}}\) is the water vapor weighted mean temperature in Kelvin.

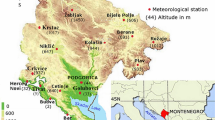
Near real-time GNSS tropospheric time series are likely to contain more cases of inconsistencies compared to the time series from a post-processed dataset that utilizes a consistent strategy and settings for the processing. Therefore, choosing the near real-time dataset gives us the opportunity of encountering and addressing more cases of inhomogeneities. We apply our homogenization approach to a selected dataset of near real-time GNSS-derived PWV time series at 214 permanent GNSS stations from 2010 to 2016. See Fig. 10 for the location of the stations.

The proposed homogenization method utilizes a reference dataset which contains a priori information about abrupt changes that are not inhomogeneities. Here we use ERA-Interim PWV time series as the reference to provide the required information about climatic and meteorological effects. The ERA-Interim dataset, released by ECMWF, is a global atmospheric reanalysis product covering a time span of about 40 years from 1979 onwards. It provides gridded data products with a spatial resolution of approximately 79 km including a wealth of 3-hourly information of surface parameters describing weather, ocean-wave and land-surface conditions, as well as 6-hourly upper-air parameters covering the troposphere and stratosphere. The vertical resolution includes 60 model layers with the top of the atmosphere located at 0.1 hPa (Dee et al. 2011). For verification of the detected inhomogeneities as well as performance assessment of the proposed method, we will also simulate a test dataset based on the ERA-Interim time series.

The undifferenced PWV datasets, i.e. GNSS and ERA-Interim, compared to their difference exhibit different noise characteristics. Figure 1 depicts the pattern of natural variability of PWV from GNSS, ERA-Interim, and the difference time series at a station in Berlin, Germany. For each day of this annual pattern, the standard deviation of PWV is calculated using the values of the same day in 15 years of GNSS, ERA-Interim, and the difference time series. As expected, during hot months the variations reach the maxima while lowest variations happen in the cold season. We have higher variability in the undifferenced time series compared to significantly lower variability in the difference time series. We will consider these aspects of the time series for selecting appropriate sensitivity threshold during offset detection.

Fig. 1
figure 1

PWV yearly variation pattern at a GNSS station in Berlin, Germany

Full size image

Singular spectrum analysis

In our homogenization approach, filling data gaps and method of change point detection are based on SSA. This technique is a general time series analysis tool, which has been used for a wide range of applications such as trend extraction, noise mitigation, forecasting and change-point detection (Alexandrov 2008). For more information about SSA and its main steps, readers are referred to, e.g., Golyandina et al. (2001) and Ghil et al. (2001).

To model the variations of a time series into a representative trend, we use the SSA technique. By the term trend, we mean a smoothed slowly-varying version of a time series that comprises long-term variations and periodicities. SSA builds a specific matrix using the time series entries, then decomposes the matrix to its principal components and finally reconstructs the time series using the most important principal components of the matrix.

Assuming the time series \(F = (f_{1} ,f_{2} , \ldots ,f_{N} ),\;f_{i} \in {\mathbb{R}},\;i = 1,2, \ldots ,N\), SSA at the first step which is called the embedding step forms a trajectory matrix (\({\mathbf{X}}\)) by moving a window over the entries of the time series, as follows:

$$\mathop {\boxed{f_{1} ,f_{2} , \ldots ,f_{L} }}\limits_{{}}^{window \to } ,f_{L + 1} ,f_{L + 2} , \ldots ,f_{N}$$
$${\mathbf{X}} = \left( {x_{ij} } \right)_{i,j = 1}^{L,K} = \left[ {\begin{array}{*{20}c} {f_{1} } & {f_{2} } & {f_{3} } & \cdots & {f_{K} } \\ {f_{2} } & {f_{3} } & {f_{4} } & \cdots & {f_{K + 1} } \\ {f_{3} } & {f_{4} } & {f_{5} } & \cdots & {f_{K + 2} } \\ \vdots & \vdots & \vdots & \ddots & \vdots \\ {f_{L} } & {f_{L + 1} } & {f_{L + 2} } & \cdots & {f_{N} } \\ \end{array} } \right]$$
(4)

where \(L\) is the window length, \(K = N - L + 1\) and \(1 < L < K\). Next, the singular value decomposition (SVD) is applied to the trajectory matrix, i.e.,

$${\mathbf{X}} = {\mathbf{U\varSigma V}}^{{\mathbf{T}}}$$
(5)

with the superscript T being the transpose operator. \({\mathbf{U}}\) and \({\mathbf{V}}\) contain left and right singular vectors, respectively, and \({\varvec{\Sigma}}\) is a diagonal matrix containing the singular values (\(\sigma_{i}\)) of \({\mathbf{X}}\). Now, the trajectory matrix can be written as the sum of its uncorrelated components (\({\mathbf{X}}_{{\mathbf{i}}}\)):

$${\mathbf{X}} = {\mathbf{X}}_{{\mathbf{1}}} + {\mathbf{X}}_{{\mathbf{2}}} + \cdots + {\mathbf{X}}_{{\mathbf{d}}} ,\;{\mathbf{X}}_{i} = \sigma_{i} {\mathbf{U}}_{{\mathbf{i}}} {\mathbf{V}}_{{\mathbf{i}}}^{{\mathbf{T}}}$$
(6)

By selecting a proper group of \(\{ {\mathbf{X}}_{{\mathbf{1}}} ,{\mathbf{X}}_{{\mathbf{2}}} , \ldots ,{\mathbf{X}}_{{\mathbf{d}}} \}\), which is called the grouping step, we can create a representative estimation of the original trajectory matrix (\({\mathbf{X}}\)) that will finally be used for the trend extraction:

$$\left\{ {\begin{array}{*{20}l} {{\mathbf{X}}_{{{\mathbf{trend}}}} {\mathbf{ = X}}_{{\mathbf{1}}} + {\mathbf{X}}_{{\mathbf{2}}} + \cdots + {\mathbf{X}}_{{\mathbf{I}}} {\mathbf{ = }} (\hat{x}_{ij} )_{i,j = 1}^{L,K} } \hfill \\ {{\mathbf{X}}_{{{\mathbf{residual}}}} {\mathbf{ = X}}_{{{\mathbf{I + 1}}}} + {\mathbf{X}}_{{{\mathbf{I + 2}}}} + \cdots + {\mathbf{X}}_{{\mathbf{d}}} } \hfill \\ \end{array} } \right.$$
(7)

The trend values are calculated by averaging the anti-diagonal entries of \({\mathbf{X}}_{{{\mathbf{trend}}}}\). Let \(L < K\), then the trend of time series \(G = (g_{1} ,g_{2} , \ldots ,g_{N} )\) is:

$$g_{i} = \left\{ {\begin{array}{*{20}l} {\frac{1}{i}\sum\limits_{m = 1}^{i} {\hat{x}_{m,i - m + 1} } } \hfill & {\quad 1 \le i < L} \hfill \\ {\frac{1}{L}\sum\limits_{m = 1}^{L} {\hat{x}_{m,i - m + 1} } } \hfill & {\quad L \le i \le K} \hfill \\ {\frac{1}{N - i + 1}\sum\limits_{m = i - K + 1}^{N - K + 1} {\hat{x}_{m,i - m + 1} } } \hfill & {\quad K \le i \le N} \hfill \\ \end{array} } \right.$$
(8)

where \(\hat{x}_{i,j}\) is an estimation of the element \(f_{i + j - 1}\) of the original time series.

Homogeneity check

GNSS-derived tropospheric time series, e.g., PWV or ZTD, can generally be considered as a linear combination of different components. Assuming the time series \(F = (f_{1} ,f_{2} , \ldots ,f_{N} ),\;f_{i} \in {\mathbb{R}},\;i = 1,2, \ldots ,N\) is given by the sum of five components, i.e.

$$\left\{ {\begin{array}{*{20}l} {F = F_{t} + F_{i} + F_{c} + F_{s} + F_{n} } \hfill \\ {\varepsilon = F_{t} + F_{i} + F_{c} + F_{s} - F_{\text{SSA}} } \hfill \\ \end{array} } \right.$$
(9)

where \(F_{t}\), \(F_{i}\), \(F_{c}\), \(F_{s}\), and \(F_{n}\) represent the group of low to high-frequency components comprising secular trend, inhomogeneities (mean shifts), cyclic, seasonal, and noise components, respectively. The cyclic part involves fluctuations, e.g. due to extreme meteorological events, which might be repeated but cannot be called periodic. \(F_{\text{SSA}}\), the extracted SSA trend, estimates the sum of the first four components and leaves the residuals \(\varepsilon\). We focus on detecting mean shifts stored in \(F_{i}\). Based on the occurrence rate of the documented changes in the log files of the GNSS stations, we consider \(F_{i}\) to be a non-periodic step function. Encountering periodic inhomogeneities with approximately similar magnitudes is considered as an unlikely situation and is not focused on in this study. The SSA trend, owing to its smoothing feature, would not perfectly model the step function in the immediate vicinity of jumps. We assume that by choosing an appropriate window length, singular values and corresponding singular vectors, the SSA can capture almost all the information stored in the first four components, except \(F_{i}\) in close proximity to the abrupt changes. We will use this assumption for detecting the position of change points.

Figure 2 shows a flowchart of the homogenization approach we have developed to detect change points and correct the GNSS tropospheric time series. It mainly comprises three stages. The first stage, the preprocessing, starts with identifying and eliminating outliers followed by applying SSA to fill the gaps, and modeling and removing the seasonal component. In the next stage, we use the SSA-based method to detect change points. The last stage is devoted to the verification of detected change points and correcting the GNSS time series.

Fig. 2
figure 2

Homogenization workflow

Full size image

Preprocessing

Addressing data gaps is also performed using the SSA technique. The first step in applying SSA is the choice of the window length. According to Golyandina and Zhigljavsky (2013), the largest window length that would provide the most detailed decomposition is \(L \simeq {N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2}\). For periodic time series with a dominant period of \(T\), the smallest choice for the window length would be \(L = T\). Selecting such a window length would maximize the correlation between the columns of the trajectory matrix. This, in turn, leads to a more efficient decomposition. For the window lengths larger than \(T\), they suggest to choose \(L\) so that it is close to \({N \mathord{\left/ {\vphantom {N 2}} \right. \kern-0pt} 2}\), and \({L \mathord{\left/ {\vphantom {L T}} \right. \kern-0pt} T}\) is an integer, although it dramatically increases the processing time. In the PWV time series with a dominant annual component, we use a 365-day window length that produces the maximum average correlation between columns of the trajectory matrix.

Finding the change points is based on the assessment of variations with respect to the representative trend of the time series. Missing data might lead to an erroneous analysis of the variations. Figure 3, using a real PWV time series, gives an idea about how data gaps can make the estimated SSA trend unrepresentative. The time series shown in the figure contain a data gap of about 1 year. The top panel is produced just by taking out the missed values and applying SSA to the remaining data. It can clearly be seen that the trend of the time series around the gap area is wrong. The bottom panel is the result of filling the data gaps in the same PWV time series. To generate such a trend, we chose a 365-day window length in the embedding step and five singular values (and vectors) in the grouping step. The reasons for selecting this setting for the grouping step is discussed in the next section.

Fig. 3
figure 3

Effect of data gaps on the SSA trend extraction. The trend extraction ignoring data gaps (top), trend extraction after applying gap filling (bottom). The black line shows the Fourier series estimation of the time series, which is used as initial values for iterative SSA gap filling

Full size image

We apply SSA iteratively to predict missing values based on the temporal correlation present in the data. Kondrashov and Ghil (2006) and Golyandina and Zhigljavsky (2013) provide more details about the application of SSA to gap filling. Before starting the iteration, the missing values are replaced by initial values calculated using a Fourier series containing bias, linear trend, annual and semi-annual terms which are shown in black line in Fig. 3 (bottom). Having the initial values calculated, we apply SSA to compute the trend from which new estimates of the missing values for the next iteration are extracted. In GNSS tropospheric products, the seasonal component dominates the behavior of the time series. Therefore, for detecting slight changes in the time series, dominant periodicities should be modeled and eliminated.

Detecting change points

The reconstructed trajectory matrix in the grouping step contains useful entries that can indicate abrupt changes in the time series. Considering the chosen window length, up to \(L\)-adjacent columns of the trajectory matrix directly contribute to the calculation of the trend values. Figure 4 (top) schematically highlights involving elements of \({\mathbf{X}}_{{{\mathbf{trend}}}}\) in calculation of the i-th trend value.

Fig. 4
figure 4

Involving elements of the reconstructed trajectory matrix in the calculation of the i-th trend value (top) and worsening estimation precision of the anti-diagonals of \({\mathbf{X}}_{{{\mathbf{trend}}}}\) in the vicinity of a change point at time index = 400 (bottom)

Full size image

The dispersion of the anti-diagonal elements of \({\mathbf{X}}_{{{\mathbf{trend}}}}\) can reveal the fluctuations of the time series around the trend. Therefore, we define the change point as a point at which the original distribution of the time series with respect to the trend in its vicinity is being changed. For this reason, a quantity is needed by which we can observe how the spread of anti-diagonal elements is being squeezed or stretched. The impact of a change on the anti-diagonal elements can be seen in Fig. 4 (bottom). Each anti-diagonal element is an estimation for the trend values. Therefore, more dispersion corresponds to more error in the estimation of the trend by each column of \({\mathbf{X}}_{{{\mathbf{trend}}}}\). Consequently, while the averages of anti-diagonals produce the trend values, \(g_{i}\) in (8), their standard deviations quantify the perturbations of the time series with respect to the trend and could be used as an indicator of a change point.

We define the Change Magnitude Estimator (CME) index, represented by \(\xi\), to evaluate the amount of change at every single epoch of the time series. Therefore, the local maxima of the CME diagram indicate the change points and their significance. The CME index is calculated using the entries of each anti-diagonal of \({\mathbf{X}}_{{{\mathbf{trend}}}}\) as:

$$\xi_i^{2} = \left\{ {\begin{array}{*{20}l} 0 \hfill & {\quad i \in \left\{ {1,N} \right\}} \hfill \\ {\frac{1}{i - 1}\sum\limits_{m = 1}^{i} {\left( {\hat{x}_{m,i - m + 1} - g_{i} } \right)^{2} } } \hfill & {\quad 1 < i < L} \hfill \\ {\frac{1}{L - 1}\sum\limits_{m = 1}^{L} {\left( {\hat{x}_{m,i - m + 1} - g_{i} } \right)^{2} } } \hfill & {\quad L \le i \le K} \hfill \\ {\frac{1}{N - i}\sum\limits_{m = i - K + 1}^{N - K + 1} {\left( {\hat{x}_{m,i - m + 1} - g_{i} } \right)^{2} } } \hfill & {\quad K < i < N} \hfill \\ \end{array} } \right.$$
(10)

To define a change point, we need the magnitude of change and the time index, i.e., the temporal location in the time series. Our first aim is to find the temporal location of the change points. It should be noted that properly timing the offsets is important. The timing uncertainty may affect the long-term linear trend determination. Particularly, shifts at the beginning and end of the time series will have more weight on the linear trend estimation (Williams 2003).

The grouping step or selecting proper singular values and vectors for trend extraction has a significant impact on the results of change point detection. Including more singular values and vectors in the reconstruction of the trajectory matrix corresponds to more sensitivity to slight local variations of the time series and will result in false alarms, i.e. a point is reported as a change point by mistake. Including fewer singular values, however, would reduce the accuracy of finding the temporal location of change points. Therefore, we complete the procedure of selecting singular values in two steps. The first step is finding the region of maximum curvature in the singular values spectrum and the second step is selecting the singular values with a minimum \(\xi_{T}\) value, defined as follows:

$$\xi_{T} = {\text{sd}}({\mathbf{X}}_{{\varvec{\Delta}}} )$$
(11)
$${\mathbf{X}}_{{\varvec{\Delta}}} = \left[ {\begin{array}{*{20}c} {\hat{x}_{1,1} - g_{1} } & {\hat{x}_{1,2} - g_{2} } & \cdots & {\hat{x}_{1,K} - g_{K} } \\ {\hat{x}_{2,1} - g_{2} } & {\hat{x}_{2,2} - g_{3} } & \cdots & {\hat{x}_{2,K} - g_{K + 1} } \\ {\hat{x}_{3,1} - g_{3} } & {\hat{x}_{3,2} - g_{4} } & \cdots & {\hat{x}_{3,K} - g_{K + 2} } \\ \vdots & \vdots & \ddots & \vdots \\ {\hat{x}_{L,1} - g_{L} } & {\hat{x}_{L,2} - g_{L + 1} } & \cdots & {\hat{x}_{L,K} - g_{N} } \\ \end{array} } \right]$$
(12)

where \(\xi_{T}\) is the overall CME calculable using the residual trajectory matrix, \({\mathbf{X}}_{{\varvec{\Delta}}}\), and \({\text{sd}}\) is the standard deviation of all entries of the matrix. The matrix \({\mathbf{X}}_{{\varvec{\Delta}}}\) is formed by subtracting trend values (\(g_{i}\)) from the corresponding anti-diagonals of \({\mathbf{X}}_{{{\mathbf{trend}}}}\). We use \(\xi_{T}\) to select a proper set of singular values and vectors. Figure 5 illustrates the behavior of the CME index with and without having a change (mean shift) in a synthetic time series. Application of \(\xi_{T}\) as a threshold is shown in the figure. Its application in selecting singular values can be seen in Fig. 6.

Fig. 5
figure 5

Behavior of CME (\(\xi\)) index for a synthetic time series: without any mean shift (top), with an artificial offset at time index = 400 (bottom)

Full size image
Fig. 6
figure 6

Selecting singular values for change point detection using the synthetic time series from Fig. 5. Finding the maximum curvature region on the singular values spectrum (top), minimizing the overall CME that makes the extracted SSA trend representative (middle), the effect of selected singular values on the accuracy of detection and the number of false alarms (bottom)

Full size image

The residuals after the trend estimation might contain autoregressive noise, which in turn might affect the CME values. False alarms induced by this effect can be reduced by setting \(\xi_{T}\) as a threshold. We then justify and enhance the estimated positions of our detected offsets by applying a t test to symmetric intervals around the time index of the candidate change points.

Verification and correction

After detecting the position of mean shifts (jumps), we estimate the magnitude of the offsets in the three time series of each station, i.e., ERA-Interim, GNSS, and the difference time series. The magnitude of each offset is calculated using the difference between the mean values of the left and right sides of the offset. After manual verification of the detected offsets, we correct the verified offsets within the GNSS time series by constructing and then subtracting the step function \(F_{i}\) in (9). It should be noted that the step function does not change the overall mean value of the GNSS time series after the correction.

The procedure of finding and verifying inhomogeneities is demonstrated using the real data of the station in Saarbrücken, Germany (Fig. 7). Data gaps, seasonality and outliers have been addressed in the three time series, and then we applied our SSA-based offset detection method to find the position of change points.

Fig. 7
figure 7

Sample result of change detection in the difference (top), ERA-Interim (middle) and real GNSS (bottom) PWV time series for the station in Saarbrücken, Germany (latitude = 49.22°, longitude = 7.01°). The range of vertical axis for the difference time series (ΔPWV) is reduced to improve the visibility

Full size image

As can be seen in Fig. 7, the time series contain three different cases of change points. The first case consists of the offsets, which are seen in the GNSS and the difference time series within a six-month time window with almost the same magnitude. If there is no shift in the ERA-Interim time series; we correct the GNSS time series using the time index and mean shift obtained from the difference time series.

The second case includes the mean shifts, which are seen in GNSS and ERA-Interim with almost the same time index and magnitude. These shifts might be due to a phenomenon sensed by both datasets, e.g., climatic or meteorological effects. In this case, even if due to different sensitivities some slight changes are transferred to the difference time series, the GNSS data are left uncorrected.

The third case is the changes which happen in all three time series (difference, GNSS and ERA-Interim) at approximately the same epochs with quite different mean shifts. If the sum of the mean shifts in the GNSS and ERA-Interim data equals to the shift in the difference time series, the GNSS time series is corrected using the mean shift obtained from the GNSS. As a special case in this station, we have an antenna and radome change and, at the same time, a non-systematic event (maybe a climatic signal) has happened. In this case, we search for the same signal in the nearby stations. If we find the same signal, we correct the GNSS data using the shift obtained from the difference time series.

Results

We use a test and a real dataset to evaluate the developed method for detecting possible inconsistencies and homogenizing tropospheric products. The impact of homogenization of GNSS data is shown through a comparison of linear trends and internal consistency of datasets.

Test dataset

We performed a Monte Carlo simulation to evaluate the performance of our method. This simulation is based on the ERA-Interim dataset at 400 points distributed over Germany from 2002 to 2017. This choice assumed that the ERA-Interim time series are less likely to contain inhomogeneities. We randomly inserted \(2.1 \times 10^{5}\) offsets in \(7 \times 10^{4}\) time series. To create new cases in each iteration, the time series were altered by adding newly generated random offsets. However, these time series contain possible abrupt changes due to climatic or meteorological conditions. In every iteration process, about 200 time series out of 400 were randomly selected for imposing synthetic offsets and the remaining were left unchanged. We added in average 6 offsets with a maximum of 10 offsets (upper limit) that randomly have different magnitudes between 0.5 and 3 mm with a negative or positive sign in every time series. The distribution of the inserted changes into the time series is done randomly such that separation between two successive changes is at least 1 year. Different classes are considered for summarizing the results. Based on these classes, the test results are arranged in Table 1. For each case, the Mean Absolute Error (MAE) of detection for the time index, \({\text{MAE}}_{\tau }\), and the mean shift, \({\text{MAE}}_{\delta }\), are estimated as follows:

$$\left\{ {\begin{array}{*{20}l} {e_{i}^{\tau } = \hat{\tau }_{i} - \tau_{i} ,} \hfill & {\quad {\text{MAE}}_{\tau } = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {e_{i}^{\tau } } \right|} } \hfill \\ {e_{i}^{\delta } = \hat{\delta }_{i} - \delta_{i} } \hfill & {\quad {\text{MAE}}_{\delta } = \frac{1}{n}\sum\limits_{i = 1}^{n} {\left| {e_{i}^{\delta } } \right|} } \hfill \\ \end{array} } \right.$$
(13)

where \(\tau_{i}\) and \(\delta_{i}\) are the true values, \(\hat{\tau }_{i}\) and \(\hat{\delta }_{i}\) are the estimated values of the time index and the magnitude of mean shift, respectively. \(e_{i}^{\tau }\) and \(e_{i}^{\delta }\) denote the detection errors in terms of the time index and the magnitude, respectively, and n is the total number of successfully detected offsets.

Table 1 Success rate of the proposed method based on different thresholds of detection
Full size table

The left side of Table 1 explains how successful the method is in finding the time index of change points. Three criteria of 182, 91, and 30 days are chosen for the time index to calculate the number of successful detections. Beyond each chosen criterion, e.g. \(\left| {e_{{}}^{\tau } } \right| > 30^{\text{days}}\) for the detection criterion of 30 days, we define the method to be unsuccessful. It should be noted that the simulation study could not be carried out using the difference data. The difference time series contain much less background noise, which leads to higher accuracy in detecting mean shifts. Our goal for applying the method to the original dataset (ERA-Interim or GNSS) is to justify the detected mean shifts in the differenced time series. Table 1 shows a success rate of 81.1% with MAE of about 28 days in detecting time index and 0.26 mm for estimating mean shift.

The right side of Table 1 shows how successful the method performs in estimating the magnitude of offsets. The method successfully detected most of the offsets bigger than 1 mm while about half of the inserted changes with a magnitude of 0.5–1 mm are retrieved. Figure 8 depicts a performance overview of the change detection method in terms of the magnitude and the time index of offsets.

Fig. 8
figure 8

Overview of the detection performance of the SSA-based method for detecting change points in PWV time series based on a Monte Carlo simulation. The mean absolute errors of the time index and the magnitude of the detected offsets are marked with red dots on the axes and are associated with a success rate of 81.1%. The prominent peak of the histogram indicates the highest occurrence frequency of the simulation results with \(\left| {e_{{}}^{\delta } } \right| \approx 0.05\;{\text{mm}}\) and \(\left| {e_{{}}^{\tau } } \right| \approx 13\;{\text{days}}\)

Full size image

Real GNSS-derived PWV data

We applied our homogenization method to a GNSS PWV dataset consisting of 214 stations in Germany over a 7-year timespan (2010–2016). We did not use a reprocessed dataset since we aimed to detect all possible different changes in the dataset. A sensitivity threshold for the detection procedure, which is the slightest change detectable by the method, can be chosen based on the time series characteristics discussed in the dataset section. The sensitivity of detection has been set to 0.2 mm for the difference PWV time series and 0.5 mm for both ERA-Interim and GNSS PWV time series.

We first applied the method to identify all possible mean shifts in the GNSS, ERA-Interim, and the difference time series (ERA-Interim minus GNSS) without considering stations log files. Then, the log files of the GNSS stations were checked to find any support for the detected changes. Next, we manually inspected the detected offsets and corrected GNSS time series using the verified offsets. As mentioned earlier, climatic or meteorological effects can also induce changes in the time series. This type of changes must be left uncorrected. If changes are detected at more than one station in the same sub-region, only those having a documented event in the log file, e.g., hardware change, are corrected.

The detected change points and corresponding mean shifts are listed in the supplementary material. In total, 140 change points were detected of which 134 were related to the mean shifts in the GNSS time series and 6 shifts were more likely to be originating from ERA-Interim data. Amongst all detected changes in the GNSS dataset, 45 of them (~ 34%) are not supported by the documented changes in the station log files. The detection accuracy,\({\text{MAE}}_{\tau }\), based on the documented changes in the GNSS dataset is approximately 30 days.

Linear trends

We apply linear regression to PWV time series of GNSS stations to evaluate the impact of homogenization on the trend value. It should be noted that the scope of this research is not the trends themselves; therefore, the readers are referred to e.g. Alshawaf et al. (2018) and Klos et al. (2018) for detailed discussion about trend estimation in GPS tropospheric time series. Estimations of the linear trends were carried out for homogenized and not-homogenized GNSS time series. Figure 9 shows the trends before and after correction of mean shifts together with trends obtained from the ERA-Interim data. Note that no correction was implemented on the ERA-Interim dataset. The figure highlights a clear improvement in the consistency between the GNSS and ERA-Interim datasets after homogenization. The lower part of the figure shows the standard error of the linear regression. Lower improvements at some stations, e.g. station Hamburg with the index 154 (latitude = 53.55°, longitude = 9.98°), can be related to the remaining unverified changes specially at the beginning or the end of the time series or at vicinity of a gap interval. The unverified changes are the offsets that are detected in the difference time series but could not be attributed to either of the GNSS or the reference time series.

Fig. 9
figure 9

Impact of homogenization on the fitting linear trends of the ERA-Interim and the GNSS PWV time series (before and after homogenization)

Full size image

Regional correlations of the stations were defined and calculated to be used for evaluating the internal consistency of the GNSS dataset after homogenization. The value of the regional correlation for each station is a weighted average of all the correlations with other stations. We used Inverse Distance Weighting (IDW) for calculating the correlations. Figure 10 reflects an improved internal consistency after the GNSS data is corrected for the mean shifts. A noticeable regional improvement can be seen over the southwest of Germany (the right panel of Fig. 10). It should be noted that the upgrade or maintenance procedure of adjacent stations in a GNSS network might be scheduled and performed consecutively within a short period. Thus, similar inhomogeneities might be introduced to the time series of nearby stations which could be misinterpreted as non-systematic events if they are not documented. The zero-difference approach introduced in this study can avoid such a misinterpretation.

Fig. 10
figure 10

Regional correlation of PWV time series for the ERA-Interim and the GNSS datasets before and after homogenization (left), regional correlation improvement for each GNSS station (right)

Full size image

Conclusion

A homogenization method based on singular spectrum analysis (SSA) for detecting and correcting temporal mean shifts (inhomogeneities) in GNSS-derived tropospheric time series was introduced. To assess the performance of the method, a Monte Carlo simulation was performed based on the ERA-Interim dataset. The result of the Monte Carlo process suggests an overall success rate of 81.1%. The simulation study estimates the precision of 28 days and 0.26 mm for detecting the position of changes and the mean shifts in the undifferenced time series, respectively.

We used the method to investigate the possible shifts in the precipitable water vapor (PWV) time series of 214 GNSS stations in Germany. The data was obtained from near real-time PPP processing over a 7-year timespan (2010–2016). The method was independently applied to the GNSS, ERA-Interim and the difference (ERA-Interim minus GNSS) daily time series of each station to find and verify inconsistencies. In total, 96 GNSS stations were identified as inhomogeneous containing 134 mean shifts from which 45 changes (~ 34%) were undocumented in the stations’ log files.

The comparison between the retrieved linear trends from GNSS and ERA-Interim dataset indicates a significant improvement after homogenization. An increase in correlation of 39% is seen for the trends after correcting the mean shifts in the GNSS time series.

The proposed method can successfully detect changes with and without reference dataset. Since using a reference dataset for homogeneity checking tries to make datasets look like each other, it might contaminate the target time series. Therefore, the homogenization approach discussed here would mitigate major inconsistencies and provide a more homogenized GNSS time series. The homogenized GNSS datasets would be a promising data source for climatic applications. The capability of the method to find changes in the undifferenced time series would also make it a useful tool to detect climatic and meteorological signals. The proposed method can be applied to other regions and for other meteorological parameters such as pressure, temperature as well as GNSS coordinate time series.