Introduction

Real-time precise point positioning has drawn increasing attention over the past years and has been widely applied in various fields, such as geoscience research and engineering surveying (Malys and Jensen 1990; Zumberge et al. 1997; Bar-Sever et al. 1997; Kouba and Héroux 2001; Kouba 2005; Chen 2004). Reliable precise orbit determination (POD) of satellites with low latency is a crucial prerequisite to achieving high positioning accuracy at the centimeter or millimeter level. Thus, the IGS has been providing real-time precise orbit products in recent years.

Currently, the IGS (http://www.igs.org/library) ultra-rapid products (IGU) are used extensively in real-time service (Dow et al. 2009). Products of 48-h span are available with a latency of 3 h, in which the first half are estimated orbits and clock corrections from GNSS network observations, while the second half are predicted orbits and clock corrections to support real-time utilization. Their performances in real time have been analyzed by many scholars. Experiments by Montenbruck et al. (2017) and Kazmierski et al. (2018) showed that the accuracy of these products relates to the arc length of the observed orbits and the prediction time span, and they show better performance only when the dynamic model and the earth orientation parameters are accurate. However, Choi et al. (2013), Rodriguez-Solano et al. (2012, 2013) and Li et al. (2015) have found that once the dynamic model changes, e.g., when a sudden variation of the force on the satellite occurs, such as a satellite in a sun–earth eclipse season or during maneuver (Arnold et al. 2015), the accuracy of the predicted orbit products will decrease significantly. This has also been proved by Prange et al. (2017) and Laurichesse et al. 2013).

To overcome these problems and provide real-time orbit products, many scholars have adopted a sequential estimation filter. In contrast to batch processing, Tapley et al. (2004) demonstrated that processing with a sequential filter updates the orbit state and dynamic model parameters epoch by epoch instead of estimating the initial condition parameters. Therefore, this process can more flexibly adjust the process noise of the orbit parameters to balance the contribution of the dynamic model and the observations in case the dynamic models are less accurate. In addition, this process can detect maneuver satellites in real time as verified by Xu et al. (2012). It can avoid redundant computation, large historical data storage and potential numerical inaccuracy and instability, which is essential and of great importance for real-time orbit determination with high efficiency.

In recent years, ambiguity resolution techniques for the undifferenced processing model have been successfully developed to improve positioning and orbit accuracy. Blewitt (1998) has pointed out that the major problem of these techniques is that the undifferenced ambiguity of a satellite–receiver pair is naturally not an integer value, due to the existence of uncalibrated phase delays (UPDs) originating in the receiver and the satellite. To overcome this problem, Ge et al. (2005) proposed to first fix double-differenced ambiguities in the network, because the UPDs will cancel and then transformed back into the four original undifferenced ambiguities when imposing the constraints. This was mainly applied to network and post-processing. For real-time and PPP applications, Ge et al. (2008) first separated the UPDs and then enabled PPP users to retrieve the integer properties of the undifferenced ambiguities with the UPDs. In addition, Bertiger et al. (1997) delivered all the undifferenced ambiguity estimates that contained the UPDs to users for PPP ambiguity resolution. By contrast, Laurichesse et al. (2009) and Collins (2008) assimilated the UPDs into the receiver and satellite clock estimates of a GPS network solution, and PPP users then used these satellite clocks to directly obtain the undifferenced ambiguity estimates with integer property. Furthermore, Teunissen and Verhagen (2010) assimilated the UPDs, as well as the atmospheric delays, into the clock estimates to achieve rapid ambiguity resolution in a real-time PPP, augmented by a dense network of reference stations. Geng et al. (2017) have deduced that the three methods above are equivalent in theory and that they perform comparably in practice.

Integer ambiguity resolution is necessary to improve the accuracy of real-time orbit products, but correctly fixed ambiguities should be ensured because they are used as constraints in the current epoch and influence the follow-up epochs in the real-time filter. If some incorrectly fixed ambiguities are used, the sequential estimation will be polluted and irreparable. Thus, we will focus our research on real-time ambiguity resolution using the square-root information filter (SRIF) algorithm.

The development of real-time POD with a sequential estimation filter and its current challenges are introduced and clarified first. Then, the realization procedure of real-time ambiguity resolution using the SRIF method for simulated real-time POD is presented, and the respective strategies are recommended. Later, experiments are conducted to verify the proposed algorithm, and its effects on accuracy improvements are analyzed. In the final section, some significant conclusions are drawn.

Methods

The fundamentals of data processing in orbit determination using the SRIF method followed by the ambiguity resolution strategy are first addressed in detail. After integer ambiguities are successfully resolved, virtual observation equations are added to constrain the floating ambiguities to the integer value. Finally, the constraints from the previous epoch to the current epoch are presented in its entirety in a flow chart.

Function models for real-time POD

Usually, the ionospheric-free combinations of the pseudorange and carrier phase observables are used in orbit determination in order to eliminate the first-order ionospheric delays. Hence, the linearized undifferenced measurement equations between the receiver r and the satellite s at epoch \(k\) can be written as:

$$\left\{ {\begin{array}{*{20}c} {V_{{P_{k,r,if}^{s} }} = - l_{k,r}^{s} \cdot x_{k,r} + l_{k,r}^{s} \cdot x_{k}^{s} + c \cdot \left( {t_{k,r} - t_{k}^{s} } \right) + M_{k,r}^{s} \cdot T_{k,r} } \\ {V_{{L_{k,r,if}^{s} }} = - l_{k,r}^{s} \cdot x_{k,r} + l_{k,r}^{s} \cdot x_{k}^{s} + c \cdot \left( {t_{k,r} - t_{k}^{s} } \right) + \lambda_{1} N_{k,r,if}^{s} + M_{k,r}^{s} \cdot T_{k,r} } \\ \end{array} } \right.$$
(1)

where \(V_{{P_{k,r,if}^{s} }}\) and \(V_{{L_{k,r,if}^{s} }}\) denote the observed minus computed ionospheric-free measurements for the pseudorange and the carrier phase, respectively, \(l_{k,r}^{s}\) contains the cosine vector from receiver k to satellite s direction, and xk,r represents the correction values of the station coordinate, while \(x_{k}^{s}\) represents the correction values relative to the reference orbit derived from orbit integration. c denotes the speed of light, tk,r and \(t_{k}^{s}\) are the receiver clock and the satellite clocks, respectively, Tk,r denotes the zenith tropospheric delay, whose mapping function is denoted as \(M_{k,r}^{s}\), \(N_{k,r,if}^{s}\) is the float ambiguity of the ionospheric-free observables, and λ1 is the L1 wavelength. Among the errors in (1), the pseudorange hardware delays can be absorbed into the receiver and satellite clocks, while the phase hardware delay can be absorbed into float ambiguity parameters (Laurichesse et al. 2009).

As mentioned above, the SRIF algorithm not only has an inherently lower storage requirement but also has better stability and numerical accuracy, which is essential to providing a real-time precise satellite navigation and positioning service. Therefore, herein we adopt the SRIF method to estimate the unknown parameters in (1). In the function model of the SRIF algorithm, the prediction of the estimated parameters between epochs can be described by a state equation. The prediction of the orbital state parameters from the previous epoch k −1 to the current epoch k can be expressed as:

$$x_{k}^{s} = \varPhi^{\text{s}} (k,k - 1) \cdot x_{k}^{s}$$
(2)

where \(x_{k}^{s}\) represents the state parameters at epoch k and \(\varPhi^{\text{s}} (k,k - 1)\) denotes the state transition matrix. The effects of phase center offsets (PCOs) and phase center variations (PCVs) at satellite and receiver antenna, as well as phase windup, can be corrected with the current models. Other estimated parameters, such as zenith tropospheric wet delay and ambiguities, are time-updated with their corresponding coefficients and process noise, which are presented in Table 1 in the following section in detail. Together with (1) and (2), the real-time precise orbit can be obtained epoch by epoch.

Table 1 Observation, force models and parameter estimations strategy in GPS precise orbit determination
Full size table

Ambiguity resolution strategy for filter processing

The float ambiguity of the ionospheric-free observables is a well-known combination of wide lane and a narrow lane for ambiguities:

$$N_{k,r,if}^{s} = \frac{{f_{1} \cdot f_{2} }}{{f_{1}^{2} - f_{2}^{2} }} \cdot N_{w} + \frac{{f_{1} }}{{f_{1} + f_{2} }} \cdot N_{n}$$
(3)

where \(f_{1}\) and \(f_{2}\) denote the nominal frequencies. \(N_{w}\) and \(N_{n}\) are the wide-lane and narrow-lane ambiguities in units of cycles, respectively.

We adopt the ambiguity resolution method proposed by Ge et al. (2005, 2008). To resolve as many integer ambiguities as possible, all double-differenced ambiguities in the network are defined, which eliminates the uncalibrated phase delays that destroy the integer characteristics of undifferenced ambiguities (Blewitt 1989; Gabor 1999). The method in Ge et al. (2005, 2008) has both a baseline level and a network level.

Independent baselines are first selected according to their lengths, starting with the shortest ones (Dong and Bock 1989; Mervart 1995). Then, all possible double-differenced ambiguities without selecting a reference satellite are fixed, and finally independent double-differenced integer ambiguities are selected. For each baseline, the double-differenced wide-lane ambiguity is first calculated from the average value of the corresponding carrier phase and pseudorange Hatch–Melbourne–Wübbena combination (HMW) in a continuous arc (Hatch 1982; Melbourne 1985; Wübbena 1985). After its successful fixing, the corresponding double-differenced narrow-lane ambiguity and its related standard deviation are derived from (3) and tested to determine whether they are fixable or not. An ionospheric-free ambiguity is fixed only when both its wide lane and narrow lane are fixed. The fixing probability is derived from the formula of Dong and Bock (1989), which is similar to that used by Blewitt (1998):

$$P_{0} = 1 - \sum\limits_{n = 1}^{\infty } {\left[ {erfc\left( {\frac{n - (N - I)}{\sqrt 2 \sigma }} \right) - erfc\left( {\frac{n + (N - I)}{\sqrt 2 \sigma }} \right)} \right]}$$
(4)

with

$$erfc(x) = \frac{2}{\sqrt \pi }\int\limits_{x}^{\infty } {e^{{ - t^{2} }} {\text{d}}t}$$
(5)

where \(N\) and \(\sigma^{2}\) are the wide-lane or narrow-lane estimates and their variances, and \(I\) is the nearest integer of \(N\). According to the calculated fixing probability for the wide lane and narrow lane described above, we sort all double-differenced ambiguities, with ambiguities that are easier to fix having priority. After all the defined ambiguities are ordered, we resolve ambiguities and search for independent ambiguities with the Gram–Schmidt procedure (Ge et al. 2005; Cohen 1993). On the network level, all the selected double-differenced ambiguity candidates over all baselines are arranged in the same way as each of the baselines. Meanwhile, the required invertible mapping matrix, used to transform the double-differenced ambiguities back into undifferenced ambiguities, is established.

Usually, for an original observation equation with undifferenced ambiguity parameters, resolving a double-differenced ambiguity is equivalent to imposing the following constraints on the four related undifferenced ambiguities (Ge et al. 2005, 2008).

$$\begin{aligned} \nabla \Delta N_{\text{LC}} & = \frac{{f_{1} \cdot f_{2} }}{{f_{1}^{2} - f_{2}^{2} }} \cdot \nabla \Delta \bar{N}_{w} + \frac{{f_{1} }}{{f_{1} + f_{2} }} \cdot \nabla \Delta \bar{N}_{n} \quad P = 10^{8} \\ \nabla \Delta N_{\text{LC}} & = N_{i,if}^{p} - N_{j,if}^{p} - N_{i,if}^{q} + N_{j,if}^{q} \\ \end{aligned}$$
(6)

where \(\nabla \Delta \bar{N}_{w}\) and \(\nabla \Delta \bar{N}_{n}\) are the resolved integer double-differenced wide-lane and narrow-lane ambiguities. The subscripts \(i\) and \(j\) represent two stations, and the superscripts \(p\) and \(q\) represent two satellites. \(N_{i,if}^{p}\) denotes the undifferenced ambiguity for ionospheric-free observables from station \(i\) to satellite \(p\). \(P\) is the weight of the constraint equation. This equation, treated as a virtual observation equation, can be incorporated together with the original observation equations in the measurement update. In this way, the constraints are delivered epoch by epoch. The procedures of the measurement update and the time update using the SRIF method, both with and without ambiguity resolution, are presented in Fig. 1.

Fig. 1
figure 1

Procedures of the measurement update and time update using the SRIF algorithm both with and without ambiguity resolution

Full size image

In the SRIF algorithm, the a priori information together with all the observation equations for the current epoch is transformed into an upper triangular matrix, which will be treated as the a priori information at the next epoch (Bierman 1977). As presented in Fig. 1, there are differences between the transformed coefficient matrixes in the left panel and the right panel, because additional constraints are involved after introducing the ambiguity resolution. Thus, successful ambiguity resolution should be guaranteed to avoid polluting the results of the current epoch, which also means the a priori information of the following epochs. Additionally, it should be emphasized that all the estimated ambiguities and their variances during and before the current epoch \(t_{k}\) are extracted from the SRIF after the time and measurement updates and then are used to recover integer ambiguity. This means that all recovered integer ambiguities are dependent on the historical information before the current epoch, while the constraints start to work at the current time. Thus, these two aspects should be considered before imposing constraints.

It is necessary to judge whether a cycle slip occurs for the fixed double difference at the current epoch. Once a cycle slip occurs for one of the four undifferenced ambiguities corresponding to the double-differenced ambiguity, the fixed ambiguities should not be used as constraints at the current epoch. Otherwise, the integer ambiguities are applied to impose constraints because the ambiguity parameter keeps unchanged during the continuous arc.

It should be mentioned that we check whether the fixed ambiguities at the current epoch are already fixed and used to impose constraints at previous epochs. The initial value plus its estimated correction at the previous epoch are considered the initial ambiguity value at the current epoch. Assuming one double-differenced ambiguity is fixed to an integer and used to impose a constraint at the previous epoch, its filtered value after time and measurement update will already contain the constraints, which can easily be fixed at the current epoch. Theoretically, the filtered value, as the initial value at the current epoch, is close to an integer. There is no need to impose more constraints at the current epoch.

Implementation of the algorithm

The implementation flowchart of the proposed algorithm is illustrated in Fig. 2. It consists of steps carried out within two modules. (1) In the SRIF module, the time update, observation reduction, and measurement update are done epoch by epoch. Wide-lane and narrow-lane ambiguities are extracted per epoch after the measurement update and stored in the data pool. (2) In the ambiguity-fixing module, all double-differenced ambiguities are sorted according to their calculated fixing probabilities and then independent ambiguities are searched. The ambiguity resolution strategy and the interaction of the two modules should be carefully studied.

Fig. 2
figure 2

Flowchart of orbit determination with ambiguity resolution based on the SRIF algorithm

Full size image

It is worth noting that stricter thresholds and quality controls are adopted in real-time sequential ambiguity resolution, in contrast to batch processing. First, the standard deviation of the float ambiguity is monitored filtering forward with a decreasing trend using an empirical threshold of 0.20 cycles. Inaccurate ambiguity parameters, e.g., the parameters that resulted from a satellite during eclipse season, are excluded from ambiguity resolution. Then, the minimum common observation time and the maximum decimal fractional offset are set as 1200 s and 0.15 cycles. Meanwhile, only the double-differenced ambiguities over baselines shorter than 4000 km are resolved. Finally, we start to recover integer ambiguities after the filter convergence, for efficiency.

Data collection and processing strategy

To evaluate the above algorithm, a network of 100 globally distributed stations from IGS is used to determine the GPS satellite orbits in a simulated real-time situation. The distribution of the 100 stations is shown in Fig. 3. The Positioning And Navigation Data Analysis (PANDA) software developed by GNSS Research Centre of Wuhan University (Liu and Ge 2003; Shi et al. 2008), which has been widely used for high-precision GNSS data processing including the POD of GNSS and LEO satellites and Precise Point Positioning (PPP), is adapted to implement our algorithm in this study. Six days of GPS pseudorange (P1 and P2) and carrier phase observations (L1 and L2) collected from January 1–6, 2016, are processed at a sampling rate of 30 s. For receivers that only support GPS C1 and P2 observables, the P1–C1 DCB product from the Center for Orbit Determination in Europe (CODE) is used for correction (ftp.aiub.unibe.ch/CODE/2016). The first-order ionosphere delay is eliminated by ionospheric-free combination, while the higher-order ionospheric delays are ignored. Specifically, the important errors and force models considered in the real-time POD are listed in Table 1.

Fig. 3
figure 3

Distribution of 100 stations selected for simulated real-time POD

Full size image

All parameters are estimated using the SRIF method. Cycle slips are detected and gross errors are removed before parameter estimation. Among all stated parameters, the receiver coordinates are estimated as constant and strongly constrained to the values from the IGS weekly solutions. The ambiguities are also estimated as constant with a priori precision of 10 m. The a priori precision and process noise for receiver clock are set as 9000 m and 900 m/s, respectively, while for satellite clock, we use the a priori precision and process noise of 2000 m and 5 m/s, respectively. The satellite position and velocity parameters are constrained to the a priori precision of 0.05 m and 10−4 m/s, respectively, with the same process noise 10−12 m/s. Moreover, the zenith tropospheric wet delays are estimated in the stochastic process using the a priori precision of 0.2 m and process noise of 10−5 m/s.

Result and analysis

We first investigate the effectiveness of the ambiguity resolution for all independent baselines in terms of the fixing rate. Then, the performance of the convergence time and the filtered GPS orbits with and without ambiguity resolution are compared with the IGS final orbit products. Finally, the impact of the ambiguity resolution on the orbital accuracy of different satellites is evaluated in detail, and the orbital accuracy is compared to the ultra-rapid products, including the IGS combination products IGU, COU (from CODE) and ESU (from ESA) products.

Convergence time analysis

As mentioned above, SRIF algorithm is employed to determine the simulated real-time GPS satellite orbits. Due to the precision of the orbital a priori values, the dynamic model accuracy, the geometry dilution of precision (DOP), the filtering algorithms usually have a convergence time (Zhang et al. 2007). During this period, it is risky to impose the constraints because correct fixing of ambiguities cannot be ensured. Once the wrong constraint equations are introduced, the filtered orbits will be polluted, and this pollution is irreparable. Therefore, experiments were carried out without ambiguity resolution or with application of ambiguity resolution from 3 h, 5 h and 7 h after start of the filter, to analyze the convergence time and determine whether a positive effect could be achieved by introducing constraints during and after the convergence period. Usually, the convergence performance is analyzed for the same satellite type instead of for each satellite separately, because satellites of the same type usually have a similar convergence performance (Qing et al. 2018). Usually, the orbit convergence criterion is constructed empirically (Laurichesse et al. 2013). The criterion adopted in our study is that the differences of simulated real-time estimated orbits and the IGS final orbits are in the defined range of accuracy, less than 20 cm in three orbital directions for all GPS satellites. The time series of filtered orbits without and with ambiguity resolution from the acceptable moment are shown in Fig. 4.

Fig. 4
figure 4

Time series of filtered orbits without ambiguity resolution (top panel) and orbits with ambiguity resolution starting at 7 h (bottom panel), in DOY 001, 2016

Full size image

The top panel is the time series of the estimated orbits without ambiguity resolution over 24 h in DOY 001, 2016, and the bottom panel is the time series of the estimated orbits with ambiguity resolution starting at 7 h. The along-track, cross-track and radial directions are shown from left to right. Each dotted line represents one satellite, and the thick red line represents the average value of all satellites in the same direction. We can see from the top panel it takes several hours to converge to the final accuracy in three directions. The radial direction takes the longest time to converge, in contrast to the cross-track and along-track directions. The moments after which the filtered orbits are within ± 20 cm are 2.75 h, 3.25 h and 4.5 h for the along-track, cross-track and radial directions, respectively. However, the convergence performance and the orbital accuracy become worse if ambiguities are used to recover to integer values at 3 h and 5 h. The negative effect disappears if ambiguity resolution is started at 7 h, as shown in Fig. 4. It is suggested that ambiguity resolution should be started after a long enough convergence time. Thus, the proposed method does not accelerate the convergence time in the experiment. We focus on starting the ambiguity resolution properly so that better orbit accuracy can be achieved.

Ambiguity resolution performance

Figure 5 shows the number of independent double-differenced ambiguities and the percentage of fixed double-differenced ambiguities on DOY 003, 2016 according to the baseline length. An average fixing percentage of more than 90% can be obtained for baselines with lengths below 1000 km. The fixing percentage gradually decreases as the length of the baseline increases. For baselines longer than 2000 km, a fixing rate of 82.5% can be achieved. Overall, the real-time ambiguity resolution of the SRIF algorithm has fixed 89.4% of the independent ambiguities, which is lower than the fixing percentage of the batch processing, which has a fixing percentage of more than 97% (Ge et al. 2005). We also analyze the time-to-first-fix through the performance of the ambiguity resolution from the filter start. Under the premise of starting the ambiguity resolution after the convergence period of about 7 h as mentioned above, the averaged times-to-first-fix are 7.35 h, 7.5 h and 7.7 h for baselines with lengths below 1000 km, between 1000 km and 2000 km, and above 2000 km, respectively.

Fig. 5
figure 5

Number of independent double-differenced ambiguities and fixing rates in DOY 003, 2016

Full size image

Orbit precision evaluation

The IGS final products with a 3D accuracy of 2.5 cm (Griffiths and Ray 2009; http://acc.igs.org/media/) are chosen as “truth” to assess the accuracy of the real-time filtered orbits. Orbits over six days are determined with and without ambiguity resolution using the SRIF method, and comparisons are made every 15 min in accordance with the interval of the IGS final products. Considering the convergence performance, we start the ambiguity resolution 7 h after start of the filter and assess the orbit accuracy of 5 days over DOY 002-006 in 2016, in order to demonstrate the performance of the proposed method. The accuracy of the filtered orbits is evaluated based on the RMS values in the along-track, cross-track, and radial directions, and in three dimensions.

Daily RMS values and mean RMS values for each satellite are presented in Figs. 6 and 7, respectively. Each subgraph in Fig. 6 illustrates the performance of one satellite in three directions. Different colors denote different directions, while solid and dotted lines of the same color denote whether integer ambiguities are resolved or not.

Fig. 6
figure 6

Daily RMS values of the orbit differences between the IGS final products and the real-time filtered orbits based on SRIF algorithm for each satellite. Each subgraph represents one satellite in the along-track (the blue), cross-track (the cyan) and radial directions (the magenta). The solid lines denote orbits with ambiguity resolution, while the dotted lines denote orbits without ambiguity resolution

Full size image
Fig. 7
figure 7

Multi-day (DOY 002-006, 2016) average RMS values of the orbit differences between the IGS final products and the real-time filtered orbits for each satellite. The top three panels represent the along-track, cross-track and radial directions, while the bottom panel represents the 3D results. The blue and red bars denote orbits without and with ambiguity resolution, respectively

Full size image

As shown in Figs. 6 and 7, the daily RMS values of all satellites are better than 10, 7 and 5 in the along-track, cross-track and radial directions, respectively. The accuracy in the radial direction is noticeably better than the accuracies in the along-track and cross-track directions, in accordance with results in Loyer et al. (2012) and Hadas and Bosy (2014). The reason is the error in radial direction which can be absorbed into clocks (Laurichesse et al. 2013). In particular, Fig. 6 shows that daily filtered orbits with ambiguity resolution are improved compared to those without ambiguity resolution, for every satellite in all three directions. This fully illustrates the effectiveness of the proposed method. Moreover, two conclusions can be drawn from Figs. 6 and 7. There are different improvements in each of the three directions. The along-track and cross-track directions show greater improvement than the radial direction. However, similar improvement can be found among different days in the same direction. Comparisons between different satellites reveal various accuracy improvements that may result from the geometric structure and the satellite dynamic model.

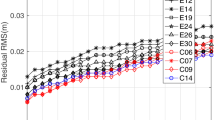
The daily RMS values of the filtered orbits for all satellites with and without ambiguity resolution in the along-track, cross-track, radial and 3D directions are shown in Fig. 8, together with the corresponding statistical accuracy of the IGU, COU and ESU products. It should be noted that the daily RMS values of the IGU, COU and ESU products are the statistical values for the predicted orbit, which consists of four parts with a prediction time span of 6 h in each arc.

Fig. 8
figure 8

Daily average RMS values for all satellites over five days, for orbits with and without ambiguity resolution in the along-track, cross-track, radial and 3D directions over DOY 002-006, 2016

Full size image

As shown in Fig. 8 from the nearly parallel lines for float and fix in each subgraph, we can see that after application of the proposed ambiguity resolution method, the orbit accuracy improves from (5.9, 3.4, 2.3) cm to (4.7, 2.6, 2.2) cm in the along-track, cross-track and radial directions, respectively. This means that approximately 20, 22 and 6% improvements can be achieved for the three directions. Better improvements in the along-track and cross-track directions are achieved than in the radial direction. This is reasonable because ambiguity resolution mainly gives information in the horizontal directions and barely does not constrain the radial direction due to the correlation between radial direction and clock parameters (Laurichesse et al. 2013).

In contrast, the precision of filtered orbits with ambiguity resolution is almost at the same level as the COU products, but slight lower than the ESU and IGU products. Since the advantage of the filtering algorithm is mainly reflected in the estimated orbits of satellite during an eclipse period or an orbital maneuver, we further individually analyze the orbital accuracy of those satellites that are going through an eclipse period. There are five satellites including G07, G11, G24, G30 and G31 in such situations. Their daily RMS values from filtered orbits with ambiguity resolution as well as their IGU, COU and ESU products are shown in Fig. 9. Each row represents one satellite in the along-track, cross-track and radial directions. We can see that the filtered orbits for some satellites achieve better accuracy than the ultra-rapid products in the along-track and cross-track directions, especially for satellite G11 and satellite G24. The largest RMS value of more than 10 cm is from the ultra-rapid orbit for satellite G24 in the along-track direction, indicating that the predicted orbit is not reliable when the satellite is in an eclipse period. This is because the satellite models, e.g., the solar radiation model, are less accurate for the satellite during the eclipse period (Arnold et al. 2015), which would affect the predicted orbit. In contrast, the filtered orbit can compensate for the inaccurate dynamical models to some extent.

Fig. 9
figure 9

Daily average RMS values for all satellites experiencing eclipse or orbital maneuver over five days for orbits with ambiguity resolution and for IGU products in the along-track, cross-track, radial directions over DOY 002-006, 2016

Full size image

Summary and conclusion

This study has proposed an efficient approach for ambiguity resolution based on the SRIF algorithm. The integer ambiguity constraints are imposed sequentially. The experiment shows that significant improvements can be achieved in the real-time orbit determination with the proposed method, especially in the along-track and cross-track directions. Based on the experimental results, the following conclusions can be summarized:

  1. (1)

    The convergence times for orbital accuracy to be better than 20 cm for the along-track, cross-track and radial directions are approximately 2.75 h, 3.25 h and 4.5 h, respectively. Successful ambiguity resolution can be ensured 7 h after start of the filter. Almost 90% of the double-differenced ambiguities are fixed correctly after the convergence time for baselines shorter than 1000 km.

  2. (2)

    Better orbit precision can be achieved with the proposed method. Compared with the IGS final products, the orbital difference RMS values for the along-track, cross-track and radial directions can be reduced from (6.1, 3.5, 3.3) cm to (4.8, 2.7, 3.1) cm on average, respectively.

  3. (3)

    Different satellites obtain different improvement percentages in the same direction. Meanwhile, different directions obtain different improvements. Obvious improvements occur in the along-track and cross-track directions, while relatively slight improvement can be seen in the radial direction. Statistical results indicate that an approximately 22% improvement can be achieved in both the along-track and cross-track directions, and nearly 6% improvement can be achieved in the radial direction.

  4. (4)

    Simulated real-time filtered orbits with the proposed method can obtain almost the same accuracy as the COU products. Moreover, for satellites in the eclipse period, the filtered orbits show better accuracy compared with the ultra-rapid products, especially in the along-track and cross-track directions, indicating that the filtering method can compensate for the dynamic model error well.

We focused on the real-time ambiguity resolution using SRIF method and its impact on accuracy of GPS satellite orbit. However, more studies need to be done. Potential further studies include the judgment of successful ambiguity fixing, a better fixing rate, higher ambiguity resolution efficiency, and acceleration of the filter convergence. Moreover, the impact of the proposed method on multi-GNSS satellites, e.g., GLONASS ambiguity resolution (Liu et al. 2016) and BeiDou ambiguity resolution (Lou et al. 2017), can be further analyzed as well.