Model comparison for GLONASS RTK with low-cost receivers

Abstract

GLONASS ambiguity resolution in differential real-time kinematic (RTK) processing is affected by inter-frequency phase biases (IFPBs). Previous studies empirically determined that IFPBs are linearly dependent on the frequency channel number and calibration values have been derived to mitigate these biases for geodetic receivers. The corresponding IFPB-constrained model is currently the de facto approach in RTK, but the growing market of GNSS receivers, and especially low-cost receivers, makes calibration and proper handling of metadata a complex endeavor. Since IFPBs originate from timing offsets occurring between the carrier phase and the code measurements, we confirm other studies that show that IFPBs are not exactly linearly dependent on the frequency channel number, but rather linearly dependent on the channel wavelength, which calls for a modification in the GLONASS functional model. As an alternative to calibration, we revisit a calibration-free method for GLONASS ambiguity resolution and provide new insights into its applicability. A practical experiment illustrates that the calibration-free approach can offer better ambiguity fixing performance when the uncertainty on the IFPB parameter is large, unless partial ambiguity resolution is performed.

Introduction

With the modernization of the GLONASS constellation, satellites of the GLONASS-M+ and GLONASS-K1 types broadcast signals on a third frequency using code division multiple access (CDMA) (Urlichich et al. 2011). However, the current constellation composed mainly of the GLONASS-M satellites still relies on frequency division multiple access (FDMA). This method of satellite identification ensures that all GLONASS satellites in view transmit signals at a slightly different frequency.

Timing inconsistencies in GNSS signals have long been a concern for GNSS applications. It was recognized early that signals tracked at different frequencies are subject to inter-frequency biases affecting ionospheric studies (Lanyi and Roth 1988). Timing variations between carrier phase and code observations were also found to impact receiver clock estimates for time transfer and cause day-boundary jumps (Defraigne and Bruyninx 2007). By defining clock estimates relying solely on phase measurements, Collins et al. (2010) could demonstrate significant intra-day and longer-term variations in clock estimates involving code measurements. Apart from these timing fluctuations between signals, Sleewaegen et al. (2012) explained that a constant offset between carrier phase and code observations could occur within the digital signal processing section of a GNSS receiver. This timing discrepancy manifests itself as a linear bias in GLONASS carrier phase ambiguities due to the different wavelengths of each satellite and leads to inter-frequency phase biases (IFPBs). Geng et al. (2017) coined the term differential code-phase bias (DCPB) for this timing error and emphasized that the concepts of IFPB and DCPB are not equivalent. This distinction is the key point underlying our derivations of the functional models.

The satellite-dependent wavelengths associated with GLONASS satellites were also found to be problematic for ambiguity resolution (Wang et al. 2001). Due to FDMA, forming double-differenced observations in units of meters between pairs of receivers and satellites does not cancel the ambiguity of the reference satellite. A common approach for eliminating this extra unknown from the system of equations is to compute its value based on a combination of carrier phase and code measurements (Mader et al. 1995). However, due to a misalignment of the phase and code observables within receivers, this procedure leads to IFPBs. From zero-length baseline tests, it was determined empirically that IFPBs between receivers of different manufacturers have a linear dependency with respect to the frequency channel number (Wanninger and Wallstab-Freitag 2007; Al-Shaery et al. 2013). Wanninger (2012) also analyzed a larger sample of receivers running various firmware versions and equipped with different antenna models. That study played a key role in GLONASS RTK by proposing manufacturer-specific calibration values to be used as a priori corrections to the carrier phase observables and recommended estimating a residual IFPB parameter to absorb unit-specific discrepancies from these ensemble means. Providing a priori calibration values for the code-phase bias is now an accepted solution in the high-precision GNSS industry, and the Radio Technical Commission on Maritime (RTCM) Services has defined message type 1230 to exchange such information when available.

With the rapid growth in low-cost GNSS receivers, it is a reasonable assumption that not all GLONASS-enabled receivers have calibrated IFPBs and there is no guarantee that the exchange of metadata will remain consistent. Therefore, Banville et al. (2013) proposed a method for GLONASS ambiguity resolution of mixed receiver types that does not require any external calibration. The approach requires a re-parameterization that allows for the ambiguity of the reference satellite to be explicitly estimated in the positioning filter. This is achieved by selecting two reference satellites that, preferably, have adjacent frequency channel numbers. Recently, Odijk and Wanninger (2017) claimed that this model is only applicable for identical receiver pairs. We will demonstrate that the claim is unfounded in practice.

To demonstrate the applicability of the calibration-free model, the GLONASS functional model for short-baseline RTK processing is first introduced. Two methods for removing the inherent rank deficiency of this system are described: The first one is the IFPB-constrained model with an emphasis on the distinction between the IFPB and DCPB representations. The calibration-free approach of Banville et al. (2013) is then revisited to explicitly show how IFPBs between receivers are absorbed by the model parameters, regardless of receiver type. Numerical and field examples show how each model recovers integer GLONASS ambiguities in practice.

GLONASS functional model

Since our focus is on short-baseline differential positioning, atmospheric effects induced by the troposphere and the ionosphere are neglected in subsequent derivations. For simplification purposes, the baseline components are not included in the model, although it can be shown that this omission has no impact on the conclusions. Under these assumptions, the GLONASS functional model for carrier phase (L) and code (C) observations to satellite j reduces to a simple timing-equation form only and reads:

$$L_{AB}^{j} = dT_{AB,L} + \lambda^{j} N_{AB}^{j} ;$$

(1)

$$C_{AB}^{j} = dT_{AB,C} + {\text{IFCB}}_{AB}^{j} ,$$

(2)

where subscript $AB$ represents the single-differenced operator $\left( \cdot \right)_{AB} = \left( \cdot \right)_{B} - \left( \cdot \right)_{A}$ between two stations (A and B). The receiver clock offset is denoted as $dT$, and the integer carrier phase ambiguity is represented by $N$ and is multiplied by the wavelength $\lambda$. Since GLONASS uses FDMA to identify satellites, the wavelength of the carrier differs for every satellite in view and can be expressed as:

$$\lambda^{j} = \frac{c}{{f + k^{j} \Delta f}},$$

(3)

where $c$ is the speed of light, $f$ is the frequency of the carrier (1602 MHz for the L1 link), $k$ is the frequency channel number, and $\Delta f$ is the frequency variation per channel (0.5625 MHz for L1).

Different clock parameters are specified for the phase and code observables in (1) and (2), as indicated by the parameter subscripts L and C, respectively. This distinction is necessary primarily to model the DCPB, i.e., the timing delays induced by the digital signal processing (DSP) component of GNSS receivers (Sleewaegen et al. 2012). Different timing references for the carrier and code observable can, therefore, be modeled as:

$$dT_{AB,L} = dT_{AB,C} + {\text{DCPB}}_{AB} .$$

(4)

Equation (2) also contains receiver- and satellite-specific hardware delays referred to as inter-frequency code biases (IFCBs). These biases are significant and can reach the meter level (Felhauer 1997; Yamada et al. 2010). While similar timing delays theoretically exist for carrier phase measurements as well, their magnitude has been shown to be at the sub-millimeter level, at least for Septentrio receivers (Sleewaegen et al. 2012). Empirical tests using data from non-Septentrio receivers, presented in subsequent sections, confirm that this assumption is a reasonable one.

The system of (1) and (2) is rank deficient for both carrier phase and code observables. Since IFCBs are physical quantities contained within a predefined interval of a few meters, a priori constraints can be applied to each IFCB parameter to remove the singularity of (2). Another rank deficiency occurs in (1) due to the linear dependency between the phase clock and the ambiguities. A common approach for solving this issue for CDMA-based systems consists of redefining the phase-clock parameter as:

$$\overline{dT}_{AB,L} = dT_{AB,L} + \lambda^{1} N_{AB}^{1} ,$$

(5)

where superscript “1” refers to a selected reference satellite. Introducing (5) into the observation equation of satellite $n > 1$ yields,

$$L_{AB}^{n} = \overline{dT}_{AB,L} + \lambda^{n} N_{AB}^{n} - \lambda^{1} N_{AB}^{1} = \overline{dT}_{AB,L} - \left( {\lambda^{1} - \lambda^{n} } \right)N_{AB}^{1} + \lambda^{n} N_{AB}^{1n}$$

(6)

with

$$N_{AB}^{1n} = N_{AB}^{n} - N_{AB}^{1} .$$

(7)

As a consequence of FDMA, this re-parameterization did not eliminate the rank deficiency of the system because the single-differenced ambiguity of the reference satellite $\left( {N_{AB}^{1} } \right)$ is still present in (6). The following sections present two methods for dealing with this singularity.

The IFPB-constrained model

A common approach for removing the FDMA singularity is to compute an approximate value for $N_{AB}^{1}$ using carrier phase and code observations (Mader et al. 1995):

$$\tilde{N}_{AB}^{1} = \frac{{L_{AB}^{1} - C_{AB}^{1} }}{{\lambda^{1} }} = N_{AB}^{1} + \frac{{{\text{DCPB}}_{AB} - {\text{IFCB}}_{AB}^{1} }}{{\lambda^{1} }}.$$

(8)

When using receivers from the same manufacturer, the single-differenced DCPB and IFCB terms typically vanish and residual errors are negligible. However, when mixing receiver types, no assumptions can be made, so that these terms remain in the functional model when introducing (8) into (6):

$$\tilde{L}_{AB}^{n} = L_{AB}^{n} + \left( {\lambda^{1} - \lambda^{n} } \right)\tilde{N}_{AB}^{1} = \overline{dT}_{AB,L} + \frac{{\left( {\lambda^{1} - \lambda^{n} } \right)}}{{\lambda^{1} }}\left( {{\text{DCPB}}_{AB} - {\text{IFCB}}_{AB}^{1} } \right) + \lambda^{n} N_{AB}^{1n} .$$

(9)

The magnitude of ${\text{IFCB}}_{AB}^{1}$ is typically below 10 m (Shi et al. 2013; Aggrey and Bisnath 2016), while DCPBs could exceed 100 m (Sleewaegen et al. 2012). Equation (9) can be simplified to:

$$\tilde{L}_{AB}^{n} = \overline{dT}_{AB,L} + \lambda^{n} \cdot \left( {k^{n} - k^{1} } \right) \cdot \frac{\Delta f}{c} \cdot \left( {{\text{DCPB}}_{AB} - {\text{IFCB}}_{AB}^{1} } \right) + \lambda^{n} N_{AB}^{1n}$$

(10)

by using

$$\frac{{\left( {\lambda^{1} - \lambda^{n} } \right)}}{{\lambda^{1} }} = \frac{{\left( {k^{n} - k^{1} } \right) \cdot \Delta f}}{{f + k^{n} \Delta f}}.$$

(11)

Since $\Delta f$ is constant, ${\text{DCPB}}_{AB}$ is satellite independent, and ${\text{IFCB}}_{AB}^{1}$ is introduced in the functional model of all satellites, these terms can be grouped together as a parameter that is typically referred to as the IFPB:

$$\delta_{AB} = \frac{\Delta f}{c} \cdot \left( {{\text{DCPB}}_{AB} - {\text{IFCB}}_{AB}^{1} } \right).$$

(12)

Substituting (12) into (10) gives the functional model used as the basis for the IFPB-constrained model:

$$\tilde{L}_{AB}^{n} = \overline{dT}_{AB,L} + \lambda^{n} \cdot \left( {k^{n} - k^{1} } \right) \cdot \delta_{AB} + \lambda^{n} N_{AB}^{1n} .$$

(13)

A common approximation, derived from empirical studies, consists of setting:

$$\delta_{AB}^{{\prime }} \approx \lambda^{1} \cdot \delta_{AB} .$$

(14)

Factoring the approximation of (14) into the rigorous model of (13), we obtain the widely used functional model for GLONASS modeling IFPBs as a linear function of the frequency channel number:

$$\tilde{L}_{AB}^{n} = d\bar{T}_{AB,L} + \left( {k^{n} - k^{1} } \right) \cdot \delta_{AB}^{\prime } + \lambda^{n} N_{AB}^{1n} + \varepsilon_{\text{IFPB}} ,$$

(15)

where

$$\varepsilon_{\text{IFPB}} = \left( {\lambda^{n} - \lambda^{1} } \right) \cdot \left( {k^{n} - k^{1} } \right) \cdot \delta_{AB} .$$

(16)

As also discussed by Geng et al. (2017), the formulation of (15) using $\left( {k^{n} - k^{1} } \right)$ as a partial derivative for the IFPB parameter is incorrect, although the impact of this approximation is negligible in practical terms. We note here that the GLONASS RTK model of Odijk and Wanninger (2017) assumes the IFPB parameter is inherent to the observable. However, there is no justification for introducing this parameter a priori, that is before computing the reference ambiguity with code observations.

The a priori values for $\delta_{AB}^{\prime }$ derived from a dense network of receivers (Wanninger 2012), zero-length baselines (Al-Shaery et al. 2013), or even global networks of receivers (Tian et al. 2015; Geng et al. 2017) serve the purpose of removing the bulk of the IFPB error. Even though this quantity is quite repeatable from unit to unit of the same manufacturer, variations in the order of a few millimeters per channel were noticed. These slight deviations do not prevent the tightly constraining of this parameter in the positioning filter and achieving fast ambiguity resolution.

If no a priori calibration values are available for a given receiver type, a looser initial constraint must be applied to the IFPB parameter. Since this parameter is not directly observable without fixing at least one double-differenced ambiguity, the IFPBs will propagate into the estimated ambiguities and will corrupt their integer nature (Takac 2009). When the rover position is precisely determined, as in case of long observation sessions, Habrich et al. (1999) showed that it is often possible to fix a first GLONASS ambiguity whose channel separation with respect to the reference satellite $\left( {k^{n} - k^{1} } \right)$ is small, preferably ± 1. In this case, the standard deviation of $\delta_{AB}^{\prime }$ drops significantly and the integer nature of other ambiguities is revealed. The same principle can be applied when the precise position is obtained from a GPS ambiguity-fixed solution (Yao et al. 2017). Since the uncertainty in the IFPB parameter is reflected in the ambiguity covariance matrix, fixing ambiguities using integer least squares with an ambiguity decorrelation procedure, e.g., LAMBDA (Teunissen 1993), still allows for fast ambiguity resolution when the IFPB is loosely constrained. However, we will show that this approach is not necessarily optimal.

The calibration-free model

The main drawback of the previous model is that it is inherently rank deficient. The first-order system of equations is singular unless a second-order a priori constraint is applied to the IFPB parameter. To solve this issue and avoid the need for external calibration, Banville et al. (2013) proposed a re-parameterized functional model using a second reference satellite to remove the rank deficiency of the system. The first reference satellite provides a timing datum for the phase-clock parameter, see (5). A second reference satellite, where no double-differenced ambiguity parameter is estimated, allows for the explicit estimation of the reference satellite ambiguity, such that (6) becomes:

$$L_{AB}^{2} = \overline{dT}_{AB,L} - \left( {\lambda^{1} - \lambda^{2} } \right)\bar{N}_{AB}^{1}$$

(17)

with

$$\bar{N}_{AB}^{1} = N_{AB}^{1} - \frac{{\lambda^{2} }}{{\lambda^{1} - \lambda^{2} }}N_{AB}^{12} .$$

(18)

Introducing (5) and (18) into (6) for satellite $n > 2$ leads to:

$$L_{AB}^{n} = \overline{dT}_{AB,L} - \left( {\lambda^{1} - \lambda^{n} } \right)\bar{N}_{AB}^{1} + \lambda^{n} \bar{N}_{AB}^{1n} ,$$

(19)

where

$$\bar{N}_{AB}^{1n} = N_{AB}^{1n} - \left[ {\frac{{k^{1} - k^{n} }}{{k^{1} - k^{2} }}} \right]N_{AB}^{12} .$$

(20)

The double-differenced ambiguities of (20) will necessarily be integers when $\left| {k^{1} - k^{2} } \right| = 1$. This condition implies that reference satellites should not be selected arbitrarily, but should preferably have adjacent frequency channel numbers. With a clear sky view, this condition is satisfied in most cases. This condition is, however, not a prerequisite for the method to be applicable. For instance, multiplying each side of (20) by $\left( {k^{1} - k^{2} } \right)$ gives:

$$\bar{\bar{N}}_{AB}^{1n} = \left( {k^{1} - k^{2} } \right)\bar{N}_{AB}^{1n} = \left( {k^{1} - k^{2} } \right)N_{AB}^{1n} - \left( {k^{1} - k^{n} } \right)N_{AB}^{12} .$$

(21)

Introducing (21) into (19) leads to:

$$L_{AB}^{n} = \overline{dT}_{AB} - \left( {\lambda^{1} - \lambda^{n} } \right)\bar{N}_{AB}^{1} + \frac{{\lambda^{n} }}{{\left( {k^{1} - k^{2} } \right)}}\bar{\bar{N}}_{AB}^{1n} .$$

(22)

This equation shows that, although the wavelength of the estimated ambiguities is divided by the channel spacing between the two reference satellites, the integer nature of the ambiguities is not affected. When the channel separation is large, the short wavelengths will result in large ambiguity variances which should be taken into consideration by the ambiguity validation step.

It should be noted that since:

$$\frac{{\lambda^{2} }}{{\lambda^{1} - \lambda^{2} }} = \frac{{f/\Delta f + k^{1} }}{{k^{2} - k^{1} }}$$

(23)

with $f/\Delta f = 2848$ for both L1 and L2, the parameter $\bar{N}_{AB}^{1}$ also has, in principle, an integer nature. The denominator $\left( {k^{2} - k^{1} } \right)$ could again be factored out to preserve the integer nature when the channel numbers for the reference satellites are not adjacent. However, in practice, since the partial derivative for this parameter is very small, it is not possible to confidently fix its value to an integer; hence, it is considered to be real-valued.

It is important to stress that the derivations for the calibration-free model do not require code measurements to remove the rank deficiency of the system. Therefore, contrary to the IFPB-constrained model, the calibration-free approach is not affected by IFPBs originating from the DCPB. While inter-frequency carrier phase biases from other sources could impact the validity of the approach, no study has demonstrated their existence so far. For the sake of completeness, “Appendix” shows that the calibration-free model can still provide integer ambiguities in the presence of phase biases as long as they can be modeled as a function of $\lambda^{n} k^{n}.$

To summarize, the system of equations for this model is:

$$L_{AB}^{1} = \overline{dT}_{AB,L}$$

(24)

$$L_{AB}^{2} = \overline{dT}_{AB,L} - \left( {\lambda^{1} - \lambda^{2} } \right)\bar{N}_{AB}^{1}$$

(25)

$$L_{AB}^{n} = \overline{dT}_{AB,L} - \left( {\lambda^{1} - \lambda^{n} } \right)\bar{N}_{AB}^{1} + \lambda^{n} \bar{N}_{AB}^{1n} .$$

(26)

The calibration-free model differs from the IFPB-constrained model in that no a priori calibration values are required for the estimated ambiguities to converge to integers, which makes it particularly well suited for low-cost receivers.

Connection between models

The calibration-free model yields estimable double-differenced ambiguities that are linear combinations of ambiguities. In this section, we show that these linear combinations cancel the effects of $\delta_{AB}$ when applied to the IFPB-constrained model. Let us recall the IFPB-constrained model as defined in (13):

$$\tilde{L}_{AB}^{n} = \overline{dT}_{AB,L} + \lambda^{n} \cdot \left( {k^{n} - k^{1} } \right) \cdot \delta_{AB} + \lambda^{n} N_{AB}^{1n} .$$

(27)

Since the IFPB parameter is not estimable before a first double-differenced ambiguity is fixed to an integer, the satellite-specific contribution of the IFPB parameter propagates into the estimated ambiguities. The resulting biased ambiguities, denoted by the hat symbol, are:

$$\hat{N}_{AB}^{1n} = N_{AB}^{1n} + \left( {k^{n} - k^{1} } \right) \cdot \delta_{AB} .$$

(28)

For example, the estimated double-differenced ambiguities for satellites 2 and 3 are:

$$\hat{N}_{AB}^{12} = N_{AB}^{12} + \left( {k^{2} - k^{1} } \right) \cdot \delta_{AB}$$

(29a)

$$\hat{N}_{AB}^{13} = N_{AB}^{13} + \left( {k^{3} - k^{1} } \right) \cdot \delta_{AB} .$$

(29b)

Multiplying (29a) by $\left( {k^{3} - k^{1} } \right)$ and (29b) by $\left( {k^{2} - k^{1} } \right)$ will nullify the IFPB when differencing the equations yielding a bias-free ambiguity:

$$N_{AB}^{123} = \left( {k^{3} - k^{1} } \right)\hat{N}_{AB}^{12} - \left( {k^{2} - k^{1} } \right)\hat{N}_{AB}^{13} = \left( {k^{3} - k^{1} } \right)N_{AB}^{12} - \left( {k^{2} - k^{1} } \right)N_{AB}^{13} .$$

(30)

The transformation of (30) can be represented in matrix form as:

$$\bar{\varvec{n}} = \varvec{T\hat{n}},$$

(31)

where $\hat{\varvec{n}}$ is the vector of estimated non-integer ambiguities and $\varvec{T}$ is a $\left( {n - 1,n} \right)$ matrix, where $n$ is the number of double-differenced ambiguities. The matrix $\varvec{T}$ contains the coefficients defining the linear combinations of ambiguities required to cancel any frequency-dependent effects. Through variance propagation, the covariance matrix ($\varvec{Q}$) of the ambiguities can be defined as:

$$\varvec{Q}_{{\bar{\varvec{n}}}} = \varvec{TQ}_{{\hat{\varvec{n}}}} \varvec{T}^{T} .$$

(32)

Matrix $\varvec{T}$ is the transformation matrix that converts real-valued double-differenced ambiguities from the IFPB-constrained model to the integer-valued ambiguities of the calibration-free model. It plays a similar role as the decorrelation transformation of LAMBDA, although it is not an admissible ambiguity transformation since it is not invertible (Teunissen 1995). This is because it is possible to go from the IFPB-constrained model to the calibration-free model, but not the opposite since the transformation cancels IFPBs which cannot be recovered. This is directly analogous to the double-differenced observation transformation that cancels the station and satellite clock parameters.

Since the ambiguity covariance matrix contains the correlation information associated with the uncertainty of the IFPB parameter, the decorrelation procedure of LAMBDA typically forms IFPB-canceling linear combinations. However, since only $n - 1$ independent bias-free ambiguities can be formed, partial ambiguity resolution should be performed when the uncertainty on the IFPB parameter is large.

Numerical examples

The application of the two models introduced above is presented using GLONASS data from both geodetic-quality receivers and low-cost single-frequency receivers. Data from geodetic receivers are analyzed first. A dataset collected on January 1, 2012, at the University of New Brunswick (UNB) campus in Fredericton, Canada, used NovAtel OEMV3 (UNBN) and Trimble NetR5 (UNB3) receivers connected to the same antenna. Therefore, differencing measurements between the two receivers cancel all error sources, except timing offsets (clocks and biases) and carrier phase ambiguities. From previous calibration sessions, the inter-frequency phase biases between these receiver types have been determined to be 30 mm/channel (Wanninger 2012).

To better demonstrate the intricacies of each model, a single epoch of data, 00:00:00 GPST, is analyzed and only four satellites are selected. Table 1 shows the single-differenced carrier phase ($L_{AB}^{j}$) on L1 converted to meters using the wavelength ($\lambda^{j}$) as well as the single-differenced code measurements ($C_{AB}^{j}$). These values were computed directly from observations contained in the RINEX files. The frequency channel number of each satellite ($k^{j}$) is also provided.

Table 1 Information regarding selected GLONASS satellites from the UNBN-UNB3 baseline on January 1, 2012

The IFPB-constrained model

In the IFPB-constrained model, the ambiguity of the reference satellite is computed following (8):

$$\tilde{N}_{AB}^{1} = \frac{{L_{AB}^{1} - C_{AB}^{1} }}{{\lambda^{1} }} = - \,4.194.$$

(33)

The functional model follows from (13), where carrier phase measurements are first corrected using the ambiguity value computed for the reference satellite:

$$\left[ {\begin{array}{*{20}c} {L_{AB}^{1} } \\ {L_{AB}^{2} } \\ {L_{AB}^{3} } \\ {L_{AB}^{4} } \\ {\delta_{0} = 0} \\ \end{array} } \right] + \left[ {\begin{array}{*{20}c} 0 \\ {\left( {\lambda^{1} - \lambda^{2} } \right)\tilde{N}_{AB}^{1} } \\ {\left( {\lambda^{1} - \lambda^{3} } \right)\tilde{N}_{AB}^{1} } \\ {\left( {\lambda^{1} - \lambda^{4} } \right)\tilde{N}_{AB}^{1} } \\ 0 \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 & 0 \\ 1 & {\lambda^{2} \left( {k^{2} - k^{1} } \right)} & {\lambda^{2} } & 0 & 0 \\ 1 & {\lambda^{3} \left( {k^{3} - k^{1} } \right)} & 0 & {\lambda^{3} } & 0 \\ 1 & {\lambda^{4} \left( {k^{4} - k^{1} } \right)} & 0 & 0 & {\lambda^{4} } \\ 0 & 1 & 0 & 0 & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\overline{dT}_{AB,L} } \\ {\delta_{AB} } \\ {N_{AB}^{12} } \\ {N_{AB}^{13} } \\ {N_{AB}^{14} } \\ \end{array} } \right] ,$$

(34)

where $\delta_{0}$ is an a priori constraint with a null value added to remove the singularity of the system. The following parameter estimates are obtained:

$$\left[ {\begin{array}{*{20}c} {\overline{dT}_{AB,L} } \\ {\delta_{AB} } \\ {N_{AB}^{12} } \\ {N_{AB}^{13} } \\ {N_{AB}^{14} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {14.400} \\ {0.000} \\ {20.833} \\ { - \,135.309} \\ {914.186} \\ \end{array} } \right].$$

(35)

An important characteristic of (35) is that the ambiguities are not close to integer values. This discrepancy can be attributed to the IFPBs between receiver types because applying the calibration value of $\delta_{AB}^{{\prime }} = 30\,{\text{mm}}$/channel to the ambiguities leads to:

$$\left[ {\begin{array}{*{20}c} {N_{AB}^{12} } \\ {N_{AB}^{13} } \\ {N_{AB}^{14} } \\ \end{array} } \right] - \left[ {\begin{array}{*{20}c} {0.03 \cdot \left( {k^{2} - k^{1} } \right)/\lambda^{2} } \\ {0.03 \cdot \left( {k^{3} - k^{1} } \right)/\lambda^{3} } \\ {0.03 \cdot \left( {k^{4} - k^{1} } \right)/\lambda^{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {20.994} \\ { - \,134.989} \\ {914.025} \\ \end{array} } \right].$$

(36)

Hence, when precise a priori calibration values are available, the ambiguity estimates better approximate to integers. As stated previously, these calibration values are available for geodetic receivers, but not necessarily for mass-market receivers.

The calibration-free model

The calibration-free model, using multiple reference satellites, relies solely on carrier phase measurements. Based on (24)–(26), the functional model is:

$$\left[ {\begin{array}{*{20}c} {L_{AB}^{1} } \\ {L_{AB}^{2} } \\ {L_{AB}^{3} } \\ {L_{AB}^{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 1 & { - \,\left( {\lambda^{1} - \lambda^{2} } \right)} & 0 & 0 \\ 1 & { - \,\left( {\lambda^{1} - \lambda^{3} } \right)} & {\lambda^{3} } & 0 \\ 1 & { - \,\left( {\lambda^{1} - \lambda^{4} } \right)} & 0 & {\lambda^{4} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\overline{dT}_{AB} } \\ {\bar{N}_{AB}^{1} } \\ {\bar{N}_{AB}^{13} } \\ {\bar{N}_{AB}^{14} } \\ \end{array} } \right].$$

(37)

For the first two satellites, no double-differenced ambiguity parameters are set up to allow the estimation of the receiver clock offset and the ambiguity of the reference satellite. These two satellites have adjacent frequency channel number, i.e., $k^{1} - k^{2} = 1$, ensuring that ambiguities are estimated with the full wavelength. The estimated parameters for this system are:

$$\left[ {\begin{array}{*{20}c} {\overline{dT}_{AB,L} } \\ {\bar{N}_{AB}^{1} } \\ {\bar{N}_{AB}^{13} } \\ {\bar{N}_{AB}^{14} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {14.400} \\ { - \,59,329.590} \\ { - \,176.976} \\ {935.019} \\ \end{array} } \right].$$

(38)

Unlike the IFPB-constrained model, code observations do not play a role in removing the system’s rank deficiency. Therefore, carrier phase measurements are not affected by IFPBs and no a priori correction needs to be applied to the measurements for the double-differenced ambiguities to converge to integers. Note that the ambiguity of the reference satellite $\left( {\bar{N}_{AB}^{1} } \right)$ is not expected to converge to an integer value due to its short wavelength.

If we select two reference satellites with a channel spacing of 2, such as satellites R11 and R13, the partial derivatives for the double-differenced ambiguities need to be adjusted accordingly by dividing the wavelength by the channel spacing:

$$\left[ {\begin{array}{*{20}c} {L_{AB}^{1} } \\ {L_{AB}^{2} } \\ {L_{AB}^{3} } \\ {L_{AB}^{4} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} 1 & 0 & 0 & 0 \\ 1 & { - \left( {\lambda^{1} - \lambda^{2} } \right)} & {\frac{{\lambda^{2} }}{{k^{1} - k^{3} }} } & 0 \\ 1 & { - \left( {\lambda^{1} - \lambda^{3} } \right)} & 0 & 0 \\ 1 & { - \left( {\lambda^{1} - \lambda^{4} } \right)} & 0 & {\frac{{\lambda^{4} }}{{k^{1} - k^{3} }}} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {\overline{dT}_{AB} } \\ {\bar{N}_{AB}^{1} } \\ {\bar{N}_{AB}^{12} } \\ {\bar{N}_{AB}^{14} } \\ \end{array} } \right].$$

(39)

The estimated parameters following this change of reference satellites are:

$$\left[ {\begin{array}{*{20}c} {\overline{dT}_{AB,L} } \\ {\bar{N}_{AB}^{1} } \\ {\bar{N}_{AB}^{12} } \\ {\bar{N}_{AB}^{14} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {14.400} \\ {192,684.234} \\ {176.976} \\ {1693.062} \\ \end{array} } \right].$$

(40)

The above results show that the integer property of the ambiguities is not impacted by a change in the reference satellites, although the wavelengths have been reduced.

Connection between models

Since the double-differenced ambiguities of the IFPB-constrained model can be transformed into the re-parameterized ambiguities of the calibration-free model, we apply the appropriate transformation matrix to the ambiguity estimates of the IFPB-constrained model obtained in (35):

$$\left[ {\begin{array}{*{20}c} {N_{AB}^{123} } \\ {N_{AB}^{124} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\left( {k^{3} - k^{1} } \right)} & { - \left( {k^{2} - k^{1} } \right)} & 0 \\ {\left( {k^{4} - k^{1} } \right)} & 0 & { - \,\left( {k^{2} - k^{1} } \right)} \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {N_{AB}^{12} } \\ {N_{AB}^{13} } \\ {N_{AB}^{14} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} { - \,176.976} \\ {935.019} \\ \end{array} } \right].$$

(41)

With satellites 1 and 2 being involved in the linear combinations of both transformed ambiguities, the values obtained are identical to the ones from (38) computed from the calibration-free model. This equality is expected since the linear combinations are simply a different representation of the calibration-free model.

The same principle can be achieved using LAMBDA. By assigning a carrier phase standard deviation of 6 mm and with $\sigma_{{\delta_{0} }} = 5 \,{\text{cm}}$, we obtain from (34) the estimated ambiguities and their covariance matrix:

$$\hat{\varvec{n}} = \left[ {\begin{array}{*{20}c} {20.833} \\ { - \,135.309} \\ {914.186} \\ \end{array} } \right]$$

(42)

$$\varvec{Q}_{{\hat{\varvec{n}}}} = \left[ {\begin{array}{*{20}c} {0.073} & {0.144} & { - \,0.070} \\ {0.144} & {0.287} & { - \,0.142} \\ { - \,0.070} & { - \,0.142} & {0.073} \\ \end{array} } \right].$$

(43)

The decorrelation matrix of LAMBDA is:

$$\varvec{Z} = \left[ {\begin{array}{*{20}c} 1 & { - \,1} & 0 \\ 2 & { - \,1} & 0 \\ 1 & { - \,1} & { - \,1} \\ \end{array} } \right].$$

(44)

Applying (44) to the ambiguities of (42) and their covariance matrix gives:

$$\hat{\varvec{z}} = \varvec{Z\hat{n}} = \left[ {\begin{array}{*{20}c} {156.143} \\ {176.976} \\ { - \,758.043} \\ \end{array} } \right]$$

(45)

$$\varvec{Q}_{{\hat{\varvec{z}}}} = \varvec{ZQ}_{{\hat{\varvec{n}}}} \varvec{Z}^{\varvec{T}} = \left[ {\begin{array}{*{20}c} {0.073} & {0.003} & {0.002} \\ {0.003} & {0.006} & {0.002} \\ {0.002} & {0.002} & {0.004} \\ \end{array} } \right].$$

(46)

The first decorrelated ambiguity is significantly less precise and is further from an integer value. This result can be understood by applying the linear combinations contained in the decorrelation matrix to the frequency channel numbers:

$$\Delta k^{2} - \Delta k^{3} = 1$$

(47)

$$2\Delta k^{2} - \Delta k^{1} = 0$$

(48)

$$\Delta k^{2} - \Delta k^{3} - \Delta k^{4} = 0,$$

(49)

where $\Delta k^{i} = k^{i} - k^{1}$ which is due to the definition of the reference satellite. While the last two decorrelated ambiguities cancel the IFPB, the first one is still affected by this error source. This outcome is justified by the fact that only $n - 1$ independent bias-free ambiguities can be formed. Hence, partial ambiguity resolution should be performed to ensure that poorly defined ambiguities do not affect ambiguity validation.

Field experiment

The ambiguity fixing performance of the IFPB-constrained and calibration-free models are assessed using data from a u-blox M8T EVK receiver and antenna collected on top of the Netherlands Measurement Institute (NMi) building in Delft (de Bakker 2017; de Bakker and Tiberius 2017). IGS station DLF1 is located approximately 13 m away and is used as the base station. DLF1 runs a Trimble NetR9 receiver and supplies data at 1 Hz sampling interval allowing between-station single-differenced measurements with the u-blox receiver. For the purpose of our demonstration, 1 h of GPS + GLONASS data were selected starting at 00:00:00 GPST on August 10, 2016, and this data set was divided into 12 independent 5-min sessions.

Two post-processed kinematic (PPK) solutions were obtained with identical processing settings, except for the handling of the IFPBs. The first solution implements the IFPB-constrained model of (15): Since no IFPB calibration values are available for the u-blox receiver, an a priori constraint of zero with an uncertainty of 5 cm was applied to the $\delta_{AB}^{'}$ parameter. The second solution is based on the calibration-free model of (24)–(26). Since the system is of full rank, no additional constraint is needed. In both of these models, ambiguity resolution was attempted for both GPS and GLONASS simultaneously. Code measurements were included in the system with a system-specific code-clock parameter as in (2), and satellite-specific IFCBs were estimated for GLONASS with a priori constraints of 10 m.

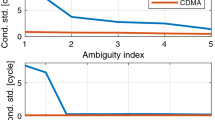
The first aspect analyzed is the volume of the ambiguity search space, characterized by the ambiguity dilution of precision (ADOP) (Teunissen and Odijk 1997), as shown in Fig. 1. Although the ADOP values for the IFPB-constrained and calibration-free solutions are quite similar, it can be noticed that slightly smaller values are obtained for the calibration-free model as the solution converges. Since ADOP can be computed from the product of the sequential conditional variances from the ${\text{LDL}}^{T}$ decomposition of the ambiguity covariance matrix, more insight can be obtained by examining the largest decorrelated conditional standard deviation for each model (see Fig. 2). The striking conclusion is that, for the IFPB-constrained model, this conditional standard deviation does not converge as well as it does for the calibration-free model. This can be explained by the fact that the IFPB parameter is not observable without fixing at least one double-differenced ambiguity and that, if $n$ GLONASS ambiguities are estimated, only $n - 1$ bias-free linear combinations can be formed as explained in the section on connection between models above. Therefore, with a loose initial constraint on the IFPB parameter, one ambiguity remains poorly defined. The calibration-free model is not affected by this issue since all parameters are observable.

Fig. 1

Ambiguity dilution of precision (ADOP) for independent 5-min PPK solutions

Fig. 2

Largest sequential conditional standard deviation for independent 5-min PPK solutions

A common method for validating the selected vector of integer ambiguities is to use the ratio test, i.e., the ratio of the smallest over the second-smallest ambiguity residual norms (Landau and Euler 1992). The smaller the ratio value, the better the discrimination between ambiguity vectors and the more confidence one should have in the fixed solution. Figure 3 presents the ratio test values for both models with the critical value 1/3 displayed as a horizontal green line. For the calibration-free model, the value for the ratio test typically decreases as the PPK filter converges, showing that the float ambiguities converge to integer values. Jumps in the ratio test occur when a new satellite rises or when ambiguities are reset. For the IFPB-constrained model, it is expected that the float ambiguities do not converge to integers since the IFPB propagates into these parameters, although the ambiguity covariance matrix contains the correlation information needed to properly identify the correct integer vector. However, instead of decreasing over time, the ratio test for the IFPB-constrained model converges to a value close to 1. This behavior is likely due to the largest conditional ambiguity variance discussed in the previous paragraph. Since this ambiguity is poorly defined, the incorrect integer candidate does not significantly increase the ambiguity residual norm. As this norm increases over time, the ratio of the best and second-best candidates, therefore, tends toward 1. Hence, when considering the full vector of ambiguities, the IFPB-constrained model could lead to failures in ambiguity validation based on the ratio test which would negatively impact position estimates.

Fig. 3

Ratio test values for ambiguity validation for independent 5-min PPK solutions

Since only $n - 1$ independent bias-free ambiguities can be formed using LAMBDA, partial ambiguity resolution can mitigate validation issues associated with the IFPB-constrained model. Figure 4 shows the estimated position errors for both cases using the following strategy: First, a subset of ambiguities, whose lower-bound on their probability of successful fixing is greater than 0.99, is selected (Teunissen 1998). Then, the ratio test is applied on this subset with a critical value of 1/3. Ambiguity validation is performed on an epoch-by-epoch basis while always keeping the underlying float solution in the filter. The output solution at a given epoch is the fixed solution when ambiguities are successfully validated, or the float solution otherwise. Figure 4 demonstrates that the IFPB-constrained solution with partial ambiguity resolution and the calibration-free solution are practically identical. Partial ambiguity resolution discards any poorly defined ambiguities, such as the conditional ambiguities referred to in Fig. 2. In such a case, it is only possible to fix all ambiguities with the calibration-free model, whereas the IFPB-constrained model needs one float ambiguity to absorb any calibration error. In general, the IFPB-constrained model is only equivalent to the calibration-free model when combined with partial ambiguity resolution.

Fig. 4

3D position error with epoch-by-epoch partial ambiguity resolution for independent 5-min PPK solutions

Conclusion

Our derivations confirmed the discussion of Geng et al. (2017) showing that IFPBs originating from timing offsets between GLONASS carrier phase and code measurements do not follow the empirically derived linear relationship with respect to the frequency channel number. This concept has been extended by proposing a more rigorous partial derivative for the IFPB-constrained model which considers the product of the wavelength and channel number. It was also emphasized that IFPBs are not inherent to the phase observables, but only appear in the carrier phase functional model when introducing code observations.

The calibration-free model of Banville et al. (2013) removes singularities in the GLONASS functional model by selecting two reference satellites allowing for an explicit estimation of the reference satellite ambiguity. Such a formulation remains unaffected by IFPBs originating from the DCPB since it is independent from code observations. While inter-frequency carrier phase biases from other sources could impact the validity of the approach, no study has demonstrated their existence so far. A numerical example and a field experiment further confirm the validity of the model and demonstrate that the claim made by Odijk and Wanninger (2017) that the calibration-free model is not applicable to different receiver types is unfounded.

The calibration-free model requires two reference satellites to define a system of full rank. Extending the model of Banville et al. (2013), the constraint that these two reference satellites require adjacent frequency channel numbers can be relaxed, although the wavelength of the estimated ambiguities is reduced by their channel spacing. When using this model, the estimated ambiguities are shown to be linear combinations canceling IFPBs, thereby preserving their integer nature. A connection between the IFPB-constrained and calibration-free models can, therefore, be defined by an appropriate, unidirectional, transformation. Similarly, the decorrelation procedure of LAMBDA cannot cancel IFPB effects in all linear combinations, and partial ambiguity resolution is recommended for successful ambiguity validation when the uncertainty on the IFPB parameter is large.

Both the IFPB-constrained and calibration-free models can achieve fast ambiguity resolution. However, GLONASS ambiguities only maintain their integer nature with the full-rank calibration-free model and, in practice, this provides for a stronger and more robust solution, especially where IFPB calibration values are unknown or of poor quality as for low-cost receivers.

Appendix

The derivations for the calibration-free model presented in previous sections are based on the assumption that IFPBs originate from the DCPB. This appendix presents an alternate derivation showing that the method can also cancel IFPBs present in carrier phase observations, provided that they can be modeled with a partial derivative taking the form of $\lambda^{n} k^{n}$, such that:

$$L_{AB}^{n} = dT_{AB,L} + \lambda^{n} N_{AB}^{n} + \lambda^{n} k^{n} \delta_{AB} .$$

(50)

Selecting a first reference satellite allows for the definition of the biased receiver clock:

$$\overline{dT}_{AB,L} = dT_{AB,L} + \lambda^{1} N_{AB}^{1} + \lambda^{1} k^{1} \delta_{AB} .$$

(51)

The second reference satellite enables the estimation of the biased ambiguity of the reference satellite such that:

$$L_{AB}^{2} = d\bar{T}_{AB,L} - \left( {\lambda^{1} - \lambda^{2} } \right)\bar{N}_{AB}^{1}$$

(52)

with

$$\bar{N}_{AB}^{1} = N_{AB}^{1} - \frac{{\lambda^{2} }}{{\lambda^{1} - \lambda^{2} }}N_{AB}^{12} + \frac{{\left( {k^{1} \lambda^{1} - k^{2} \lambda^{2} } \right)}}{{\lambda^{1} - \lambda^{2} }}\delta_{AB} .$$

(53)

Inserting (51) and (53) into (50) leads to:

$$L_{AB}^{n} = \overline{dT}_{AB,L} - \left( {\lambda^{1} - \lambda^{n} } \right)\left[ {\bar{N}_{AB}^{1} + \omega \delta_{Ab} } \right] + \lambda^{n} \bar{N}_{AB}^{1n} ,$$

(54)

where $\bar{N}_{AB}^{1n}$ has the same definition as (20) and:

$$\omega = \frac{{\lambda^{1} k^{1} - \lambda^{n} k^{n} }}{{\lambda^{1} - \lambda^{n} }} - \frac{{\lambda^{1} k^{1} - \lambda^{2} k^{2} }}{{\lambda^{1} - \lambda^{2} }}.$$

(55)

By recognizing that:

$$\frac{{\lambda^{1} k^{1} - \lambda^{n} k^{n} }}{{\lambda^{1} - \lambda^{n} }} = \frac{{\lambda^{1} k^{1} - \lambda^{2} k^{2} }}{{\lambda^{1} - \lambda^{2} }} = - \frac{f}{\Delta f};$$

(56)

the term $\omega$ cancels from (54) and leads to a consistent system similar to (24)–(26). The only differences are the definition of the estimable receiver clock and reference ambiguity parameters, as shown by (51) and (53), respectively, while the definition of the estimable integer ambiguities remains unchanged.