Design and implementation of a model predictive observer for AHRS

Abstract

A GPS-aided Inertial Navigation System (GAINS) is used to determine the orientation‚ position and velocity of ground and aerial vehicles. The data measured by Inertial Navigation System (INS) and GPS are commonly integrated through an Extended Kalman Filter (EKF). Since the EKF requires linearized models and complete knowledge of predefined stochastic noises‚ the estimation performance of this filter is attenuated by unmodeled nonlinearity and bias uncertainties of MEMS inertial sensors. The Attitude Heading Reference System (AHRS) is applied based on the quaternion and Euler angles methods. A moving horizon-based estimator such as Model Predictive Observer (MPO) enables us to approximate and estimate linear systems affected by unknown uncertainties. The main objective of this research is to present a new MPO method based on the duality principle between controller and observer of dynamic systems and its implementation in AHRS mode of a low-cost INS aided by a GPS. Asymptotic stability of the proposed MPO is proven by applying Lyapunov’s direct method. The field test of a GAINS is performed by a ground vehicle to assess the long-time performance of the MPO method compared with the EKF. Both the EKF and MPO estimators are applied in AHRS mode of the MEMS GAINS for the purpose of real-time performance comparison. Furthermore‚ we use flight test data of the GAINS for evaluation of the estimation filters. The proposed MPO based on both the Euler angles and quaternion methods yields better estimation performances compared to the classic EKF.

Introduction

The aim of navigation is recognition of one way from the other ways when there exist different options (Anderson 1966). Strapdown Inertial Navigation System (INS) and satellite-based GPS are two commonly used techniques for vehicle positioning. Since both systems suffer from different drawbacks‚ superior navigation performances can be obtained by combining these two techniques. In the INS‚ triple sets of accelerometers and gyroscopes are considered in three orthogonal directions to construct an Inertial Measurement Unit (IMU). The data of IMU sensors are fed into attitude and navigation computers‚ which in turn perform the tasks of integration and other computations to produce navigation outputs including position‚ velocity and orientation components. First‚ the rotational angles of the vehicle body with respect to a pre-defined reference frame are obtained based on gyroscopes data and earlier known angles. Next‚ these angles are applied to transfer the measurement vector of accelerometers to the navigation reference frame. By twice integration of the transferred data of accelerometers‚ both the position and velocity vectors are updated in the navigation reference frame. Owing to uncertainties of inertial sensors comprising stochastic noise‚ accelerometer bias instability‚ gyroscope drift, and computational errors of microprocessor‚ the navigation errors of INS accumulate with time. On the other hand, a GPS receiver requires locking onto at least four satellites to determine 3-dimensional positioning data. The GPS signals could be interrupted by other sources of radio signals‚ electromagnetic fields‚ and especially signal blockage by high buildings and natural barriers. Also‚ 1 Hz (up to 20 Hz) update rate of low-cost receivers together with few-seconds start-up time encourage the navigation experts to integrate the GPS data with high-update-rate data of INS. Hence‚ long-time errors of INS could be decreased by high accuracy positioning data of GPS receivers. We design an optimal integration filter to enhance the reliability and accuracy of a manufactured MEMS GPS-aided Inertial Navigation System (GAINS). Therefore‚ optimally integrated navigation data will be obtained through the GAINS‚ which includes high-frequency MEMS inertial sensors and a low-cost 1 Hz GPS receiver.

Since the appearance of state-space theory and the estimation of state variables in 1950 (Simon 2006)‚ INS has benefited by the state estimation filters. The optimal filters including Extended Kalman Filter (EKF) play the main role of integration in combined navigation systems (Faruqi and Turner 2000). According to NøRgaard et al. (2000)‚ there are several methods to generate optimal estimations in nonlinear system without any considerable advantages of one over the others. Requirements of estimation in nonlinear systems have led to the development of nonlinear estimation theories such as EKF (Zhang and Zhao 2011; Hide et al. 2003)‚ moving horizon estimation (Robertson et al. 1996)‚ Bayesian estimation (Bishop and Welch 2001)‚ unscented Kalman filter (Wang et al. 2006), and particle filter (Fang and Gong 2010). The filter introduced by Kalman and Bucy (Bucy 1970) has been widely used in aerospace industry as the first optimal recursive estimator. This filter assumes the exact linear model of the system and Gaussian statistical information of the input disturbances and noises. However, due to unknown statistical characteristics and modeling uncertainties of practical systems‚ limited suboptimal solutions of the filter are obtained. Despite the difficulties and lack of motivation of using the other estimators‚ the EKF is used as a good solution for complex systems. The disadvantage of this filter is the raising difficulties in practical implementations according to Wilson et al. (1998). Artificial neural networks and fuzzy logic-based methods are also applicable for estimation of nonlinearities and uncertainties in practical systems (Musavi and Keighobadi 2015).

Some major issues arise from the inability of accurate inclusion of physical aspects in software models and computational algorithms. To overcome these difficulties‚ we propose the Model Predictive Observer (MPO) solution of the nonlinear state estimation problem. The designed MPO filter could be properly used in the online optimal estimation of nonlinear models. Furthermore‚ the MPO technique incorporates probable physical constraints into the optimization solution with high accuracy. As the main innovation‚ the new MPO, comprising orthogonal Laguerre functions, is designed for merging data of the low-cost MEMS GAINS. By applying the orthogonal Laguerre terms‚ the propagation of computational errors in the designed MPO components is removed.

Moving horizon estimation has acquired attention in connection with the application of optimal Model Predictive Control (MPC) method as an estimation technique. Most research works in the control systems field are being carried out on the design of controllers. Optimal controller and estimator/observer are dual in the Linear Quadratic Regulator (LQR) setting. Hence‚ by applying this duality‚ the observer design process is shortened by use of its present dual controller. Compared with a directly designed observer‚ a dual-based observer can be more reliable due to the removal of probable drawbacks and difficulties in the design of the earlier dual controller. To obtain algorithm of the proposed MPO, we apply the duality principle into the MPC optimization cost function. To achieve an observer from the common direct method (Doostdar and Keighobadi 2012)‚ a stochastic optimization problem should be solved. However, by use of the equivalence and duality in estimation and control as well as the duality of stochastic and deterministic problems‚ the observer of the stochastic problem is identically obtained by its dual controller in the deterministic problem. Here‚ an H₂ objective function including the orthogonal Laguerre functions is considered in the design of dual MPO. Configuration by the Laguerre functions leads to simple scaling, tuning and software programming of the MPO system in low-cost microcontroller chipsets.

For hardware implementation purpose, a calibrated MEMS IMU as well as a 1 Hz Garmin GPS receiver has been considered. Regarding the MEMS-grade IMU and low-cost commercial GPS and vehicular application‚ the local level geographical frame with North-East-Down (NED) axes is considered as the navigation reference coordinate system. Therefore‚ the rotation rate of the earth‚ which is not measurable by the MEMS sensors‚ and the related negligible accelerations are removed from navigation algorithms. Due to the physical insight‚ the minimal Euler attitude-heading angles are commonly preferred in practical orientation representations. Additionally, the quaternions vector is introduced to decrease the linearization errors and avoid the singularity of Euler angles dynamics near to ± 90° pitch angles. The affine dynamics of quaternions related to gyroscope data deals well with the structure of EKF. Strapdown 3-axis magnetometers are applied to measure the heading/yaw angle‚ since the ground-tracking angle by GPS would not be valid under 3 km/h forward velocities. To this end‚ a complete magnetic calibration algorithm is applied to remove hard- and soft-iron magnetic fields of the vehicle body and its other steel-made parts. To assemble a complete MEMS GAINS, a low-cost ADIS16407 IMU-magnetometer with SPI output‚ a Garmin 35 GPS receiver with standard NMEA output and a serial RS-232 communication port are gathered with an F28335 micro-controller of Texas Instruments. Therefore‚ the software codes of the MPO and the magnetic calibration process could be executed real time. We use a high-quality 50 Hz Companav-2 INS/GPS of Teknol to produce correct reference trajectories for assessment of the implemented MPO in Attitude Heading Reference System (AHRS) mode of the GAINS. The real test of a ground vehicle is performed in different road conditions and maneuvering. Furthermore, the flight test data of a small commercial Unmanned Air Vehicle (UAV) are used for better validations. During the tests‚ the AHRS system is affected by gradual and abrupt changes in inertial sensors inputs‚ velocities and orientation angles. Based on the statistical properties of the tests results‚ the proposed MPO shows a better performance with respect to the EKF.

In the following sections‚ the strapdown AHRS‚ duality between control and estimation‚ proposed MPO‚ stability analysis‚ implementation‚ calibration of 3-axis magnetometers‚ real test results‚ conclusion and references are presented‚ respectively.

Strapdown AHRS system

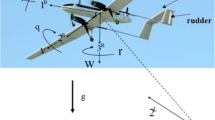
An AHRS computes the attitude-heading angles using the measurements of IMU and probable aiding sensors. Referring to Fig. 1‚ the orthogonal axes $x_{b}, y_{b}$ and $z_{b}$ of the right-handed body coordinate frame (b-frame), respectively, coincide to the N‚ E and D axes of local-level navigation frame (n-frame). The setup where these axes are perfectly aligned provides the zero roll‚ pitch and yaw angles. In the local level plane‚ the horizontal axes $X_{L}$ and $Y_{L}$ make the magnetic heading angle‚ $\psi_{\text{Mag}}$ with N and E axes‚ respectively. Thereby‚ the heading angle $\psi$ about $z_{b}$-axis‚ the pitch angle $\theta$ about the rotated $y_{b}$-axis by $\psi$, and the roll angle $\varphi$ about the rotated $x_{b}$-axis by $\psi$ and $\theta$ constitute 3-successive rotations of transformation from reference n-frame to b-frame. The direction cosine matrix (DCM) to transfer from the n-frame to the b-frame is obtained as (Titterton and Weston 2004):

$$ C_{n}^{b} = \left[ {\begin{array}{*{20}c} {\cos \theta \cos \psi } & { - \cos \varphi \sin \psi + \sin \varphi \sin \theta \cos \psi } & {\sin \varphi \sin \psi + \cos \varphi \sin \theta \cos \psi } \\ {\cos \theta \sin \psi } & {\cos \varphi \cos \psi + \sin \varphi \sin \theta \sin \psi } & { - \sin \varphi \cos \psi + \cos \varphi \sin \theta \sin \psi } \\ { - \sin \theta } & {\sin \varphi \cos \theta } & {\cos \varphi \cos \theta } \\ \end{array} } \right] $$

(1)

Figure 1 shows that the strapdown gyroscopes of the IMU measure the angular velocity vector of b-frame with respect to inertial frame‚ $\omega_{ib}^{b}$, where the superscript b stands for the expression of vector $\omega_{ib}$ in b-frame. Since the rotation rate of the earth is much slower than the noise level of MEMS gyroscopes‚ the vector $\omega_{ib}^{b}$ is approximated to the rotation rate of b-frame with respect to n-frame‚ $\omega_{nb}^{b}$. Therefore‚ the dynamics of the Euler angles can be used to update the rotation of body axes with respect to reference n-frame (Titterton and Weston 2004):

$$ \begin{aligned} & \dot{\varphi } = \left( {\omega_{y} \sin \varphi + \omega_{z} \cos \varphi } \right)\tan \theta + \omega_{x} \\ & \dot{\theta } = \omega_{y} \cos \varphi - \omega_{z} \sin \varphi \\ & \dot{\psi } = \left( {\omega_{y} \sin \varphi + \omega_{z} \cos \varphi } \right)\sec \theta \\ \end{aligned} $$

(2)

$$ \omega_{nb}^{b} = \left[ {\begin{array}{*{20}c} {\omega_{x} } & {\omega_{y} } & {\omega_{z} } \\ \end{array} } \right]^{\text{T}} $$

(3)

where the measured turn rates by gyroscopes are included in the vector $\omega_{nb}^{b}$ and the superscript T stands for the transpose of a vector or matrix. The application of Euler angles is limited by the singularity of the first and third equations of (2) at pitch angles close to ± 90°.

Fig. 1

Representation of body‚ inertial‚ earth-fixed and local level coordinate frames

The quaternions vector, $q$, defines the orientation as a single rotation of magnitude $\eta$ around the direction vector‚ $\underline{\eta }$, in the reference frame:

$$ q = \left( {\begin{array}{*{20}c} {q_{1} } \\ {q_{2} } \\ {\begin{array}{*{20}c} {q_{3} } \\ {q_{4} } \\ \end{array} } \\ \end{array} } \right) = \left( {\begin{array}{*{20}c} {\cos \left( {\eta /2} \right)} \\ {\left( {\eta_{x} /\eta } \right)\sin \left( {\eta /2} \right)} \\ {\begin{array}{*{20}c} {\left( {\eta_{y} /\eta } \right)\sin \left( {\eta /2} \right)} \\ {\left( {\eta_{z} /\eta } \right)\sin \left( {\eta /2} \right)} \\ \end{array} } \\ \end{array} } \right) $$

(4)

$$ \begin{array}{*{20}l} {\underline{\eta } = \left[ {\begin{array}{*{20}c} {\eta_{x} } & {\eta_{y} } & {\eta_{z} } \\ \end{array} } \right]^{\text{T}} } \\ {\eta = \left( {\eta_{x}^{2} + \eta_{y}^{2} + \eta_{z}^{2} } \right)^{1/2} } \\ \end{array} $$

(5)

The unit magnitude of quaternions yields the following kinematic constraint‚

$$ q_{1}^{2} + q_{2}^{2} + q_{3}^{2} + q_{4}^{2} = 1 $$

(6)

Hence‚ the computational error of quaternions can be simply decreased through normalization as,

$$ q \simeq q/\sqrt {q^{\text{T}} q} $$

(7)

The dynamics of quaternions is obtained according to Titterton and Weston (2004):

$$ \dot{q} = \frac{1}{2}\left[ {\begin{array}{*{20}c} 0 & { - \omega_{nb}^{\text{T}} } \\ {\omega_{nb} } & { - \left[ \omega \right]} \\ \end{array} } \right]q = \frac{1}{2}\left[ {\begin{array}{*{20}c} 0 & { - \omega_{x} } & {\begin{array}{*{20}c} { - \omega_{y} } & { - \omega_{z} } \\ \end{array} } \\ {\omega_{x} } & 0 & {\begin{array}{*{20}c} {\omega_{z} } & { - } \\ \end{array} \omega_{y} } \\ {\begin{array}{*{20}c} {\omega_{y} } \\ {\omega_{z} } \\ \end{array} } & {\begin{array}{*{20}c} { - \omega_{z} } \\ {\omega_{y} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ { - \omega_{x} } \\ \end{array} } & {\begin{array}{*{20}c} {\omega_{x} } \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]q $$

(8)

$$ \left[ \omega \right] = \left[ {\begin{array}{*{20}c} 0 & { - \omega_{z} } & {\omega_{y} } \\ {\omega_{z} } & 0 & { - \omega_{x} } \\ { - \omega_{y} } & {\omega_{x} } & 0 \\ \end{array} } \right] $$

(9)

The transposed DCM (1)‚ which is used to transform vectors from b-frame to n-frame‚ may be expressed regarding quaternions as (Rogers 2003):

$$ C_{n}^{{b^{\text{T}} }} = C_{b}^{n} = \left[ {\begin{array}{*{20}c} {\left( {q_{1}^{2} + q_{2}^{2} - q_{3}^{2} - q_{4}^{2} } \right)} & {2\left( {q_{2} q_{3} - q_{1} q_{4} } \right)} & {2\left( {q_{2} q_{4} + q_{1} q_{3} } \right)} \\ {2\left( {q_{2} q_{3} + q_{1} q_{4} } \right)} & {\left( {q_{1}^{2} - q_{2}^{2} + q_{3}^{2} - q_{4}^{2} } \right)} & {2\left( {q_{3} q_{4} - q_{1} q_{2} } \right)} \\ {2\left( {q_{2} q_{4} - q_{1} q_{3} } \right)} & {2\left( {q_{3} q_{4} + q_{1} q_{2} } \right)} & {\left( {q_{1}^{2} - q_{2}^{2} - q_{3}^{2} + q_{4}^{2} } \right)} \\ \end{array} } \right] $$

(10)

The components $c_{ij}$ of $C_{b}^{n}$ are related to quaternions as (Titterton and Weston 2004):

$$ \begin{aligned} & q_{1} = \frac{1}{2}\left( {1 + c_{11} + c_{22} + c_{33} } \right)^{1/2} \\ & q_{2} = \frac{1}{{4q_{1} }}\left( {c_{32} - c_{23} } \right) \\ & q_{3} = \frac{1}{{4q_{1} }}\left( {c_{13} - c_{31} } \right) \\ & q_{4} = \frac{1}{{4q_{1} }}\left( {c_{21} - c_{12} } \right) \\ \end{aligned} $$

(11)

Similarly, the quaternions can be expressed in terms of Euler angles as:

$$ \begin{array}{*{20}c} {q_{1} = \cos \frac{\varphi }{2}\cos \frac{\theta }{2}\cos \frac{\psi }{2} + \sin \frac{\varphi }{2}\sin \frac{\theta }{2}\sin \frac{\psi }{2}} \\ {q_{2} = \sin \frac{\varphi }{2}\cos \frac{\theta }{2}\cos \frac{\psi }{2} - \cos \frac{\varphi }{2}\sin \frac{\theta }{2}\sin \frac{\psi }{2}} \\ {\begin{array}{*{20}c} {q_{3} = \cos \frac{\varphi }{2}\sin \frac{\theta }{2}\cos \frac{\psi }{2} + \sin \frac{\varphi }{2}\cos \frac{\theta }{2}\sin \frac{\psi }{2}} \\ {q_{4} = \cos \frac{\varphi }{2}\cos \frac{\theta }{2}\sin \frac{\psi }{2} + \sin \frac{\varphi }{2}\sin \frac{\theta }{2}\cos \frac{\psi }{2}} \\ \end{array} } \\ \end{array} $$

(12)

At nonsingular situations, when $\theta$ is not close to ± 90°, the Euler angles are determined regarding DCM (1):

$$ \begin{aligned} & \theta = - \sin^{ - 1} \left( {c_{31} } \right) \\ & \varphi = \tan^{ - 1} \left( {\frac{{c_{32} }}{{c_{33} }}} \right) \\ & \psi = \tan^{ - 1} \left( {\frac{{c_{21} }}{{c_{11} }}} \right) \\ \end{aligned} $$

(13)

However, in singular cases of (13), we should use the sum and difference of $\varphi$ and $\psi$ as:

$$ \begin{array}{*{20}l} { \psi - \varphi = \tan^{- 1} \left({\frac{{c_{23} - c_{12}}}{{c_{13} + c_{22}}}} \right) \;{\text{for}}\;\theta \,{\text{near}}\,{\text{to}}\, + \,90^\circ} \\ {\psi + \varphi = \tan^{- 1} \left({\frac{{c_{23} + c_{12}}}{{c_{13} - c_{22}}}} \right)\;{\text{for}}\;\theta \,{\text{near}}\,{\text{to}}\, - \,90^\circ} \\ \end{array} $$

(14)

Since $\varphi$ and $\psi$ could not be obtained separately, we freeze the angle $\varphi$ at its current value and then update the value of $\psi$ according to (14). At the next process time, $\psi$ would be frozen, and $\varphi$ is determined by (14). This process of updating $\varphi$ or $\psi$ alone would continue until $\theta$ is no longer in the region of $\pm \,90^\circ$ (Titterton and Weston 2004).

Output vector

The measurement vector of AHRS consists of the 3-axis accelerometers outputs‚ $\left[ {\begin{array}{*{20}c} {f_{x}^{b} } & {f_{y}^{b} } & {f_{z}^{b} } \\ \end{array} } \right]^{\text{T}}$ and the GPS heading angle‚ $\psi_{\text{GPS}}$:

$$ m = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {f_{x}^{b} } & {f_{y}^{b} } & {f_{z}^{b} } \\ \end{array} } & {\psi_{\text{GPS}} } \\ \end{array} } \right]^{\text{T}} $$

(15)

$$ \left[ {\begin{array}{*{20}c} {f_{x}^{b} } & {f_{y}^{b} } & {f_{z}^{b} } \\ \end{array} } \right]^{\text{T}} = \frac{{{\text{d}}V^{b} }}{{{\text{d}}t}} + \left[ \omega \right]V^{b} + C_{n}^{b} \left( q \right)\left[ {\begin{array}{*{20}c} 0 & 0 & { - g} \\ \end{array} } \right]^{\text{T}} $$

(16)

$$ V^{b} = [\begin{array}{*{20}c} {V_{x} } & {V_{y} } & {V_{z} } \\ \end{array} ]^{\text{T}} = C_{n}^{b} V_{\text{GPS}}^{n} $$

(17)

where by neglecting the small changes of $V^{b}$ in short-time processing intervals‚ the matching of gravity vector between b-frame and n-frame (16) is simplified to:

$$ \left[ {\begin{array}{*{20}c} {f_{x}^{b} } & {f_{y}^{b} } & {f_{z}^{b} } \\ \end{array} } \right]^{\text{T}} = \left[ \omega \right]C_{n}^{b} \left( q \right)V_{\text{GPS}}^{n} + C_{n}^{b} \left( q \right)\left[ {\begin{array}{*{20}c} 0 & 0 & { - g} \\ \end{array} } \right]^{\text{T}} $$

(18)

$\psi_{\text{GPS}}$ is replaced by the magnetic heading angle‚ $\psi_{\text{Mag}}$, at forward velocity under 3 km/h. Furthermore, $g$ and $V_{\text{GPS}}^{n}$ stand for the local gravity acceleration and the velocity vector of GPS resolved in n-frame‚ respectively. Considering the uncertainty and noise vector $v$ on $\varphi_{\text{acc}} \;{\text{and}}\;\theta_{\text{acc}}$ obtained by (18), and on $\psi_{\text{GPS/Mag}}$ or their equivalent quaternion vector q, the standard output equation of AHRS is obtained as:

$$ y = h\left( x \right) + v $$

(19)

where the measured Euler angles or the equivalent quaternions are included in the vector $x$.

Duality and equivalence in estimation and control

We design the proposed observer based on the duality of estimation and control systems. Therefore‚ first the duality and equivalence method is developed according to Kailath et al. (2000). A set of linearly independent vectors are considered as $\left\{{z, y} \right\}$:

$$ \begin{array}{*{20}l} { z \triangleq {\text{col}}\left\{{z_{0}, \ldots, z_{m}} \right\} } \\ {y \triangleq {\text{col}}\left\{{y_{0}, \ldots, y_{n}} \right\}} \\ \end{array} $$

(20)

In general, the vectors of a dual system are not required to be linearly independent. However, to estimate the set $\left\{ {z_{i} } \right\}$ based on the visible set $\left\{ {y_{i} } \right\}$, this condition should be satisfied. The corresponding Gramian for this set of vectors is studied by the inner product $\left\langle { \cdot , \cdot } \right\rangle$ as (Kailath et al. 2000):

$$ \left\langle {\left[{\begin{array}{*{20}c} z \\ y \\ \end{array}} \right], \left[{\begin{array}{*{20}c} z \\ y \\ \end{array}} \right]} \right\rangle = \left[{\begin{array}{*{20}c} {\left\langle {z,z} \right\rangle} & {\left\langle {z,y} \right\rangle} \\ {\left\langle {y,z} \right\rangle} & {\left\langle {y,y} \right\rangle} \\ \end{array}} \right] = \left[{\begin{array}{*{20}c} {R_{z}} & {R_{zy}} \\ {R_{yz}} & {R_{y}} \\ \end{array}} \right] $$

(21)

Regarding the nonsingular set $\left\{{z,y} \right\}$, both the matrices $R_{z}$ and $R_{y}$ are nonsingular. The linear space ${\mathcal{L}}\left\{{z,y} \right\}$ of all the vectors is defined as:

$$ a_{0} z_{0} + \cdots + a_{m} z_{m} + b_{0} y_{0} + \cdots + b_{n} y_{n} $$

(22)

where $a_{i}, b_{i} \in S$ the ring of complex numbers. Linearly independent vectors $\left\{{z_{0}, \ldots, z_{m}, y_{0}, \ldots, y_{n}} \right\}$ constitute a base of ${\mathcal{L}}\left\{{z,y} \right\}$. Dual of the base $\left\{{z,y} \right\}$ is defined as the pair $\left\{{z^{d}, y^{d}} \right\}$ with the following two properties:

$$ \begin{aligned} & {\mathcal{L}}\left\{ {z^{d} ,y^{d} } \right\} = {\mathcal{L}}\left\{ {z,y} \right\} \\ & \left\langle {\left[ {\begin{array}{*{20}c} {z^{d} } \\ {y^{d} } \\ \end{array} } \right], \left[ {\begin{array}{*{20}c} z \\ y \\ \end{array} } \right]} \right\rangle = \left[ {\begin{array}{*{20}c} {\left\langle {z^{d} ,z} \right\rangle } & {\left\langle {z^{d} ,y} \right\rangle } \\ {\left\langle {y^{d} ,z} \right\rangle } & {\left\langle {y^{d} ,y} \right\rangle } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} I & 0 \\ 0 & I \\ \end{array} } \right] \\ \end{aligned} $$

(23)

The normalized vectors‚ $z^{d}$ and $y^{d}$ are orthogonal to y and z‚ respectively:

$$ \begin{array}{*{20}c} {\left\langle {z^{d}, z} \right\rangle = I} \\ {\left\langle {y^{d}, y} \right\rangle = I} \\ \end{array} $$

(24)

The aforementioned properties are referred as the bi-orthogonality condition. The dual foundation is interpreted in two algebraic and geometric methods. In the algebraic configuration‚ $\left\{{z,y} \right\}$ and $\left\{{z^{d}, y^{d}} \right\}$ span the same linear space for some nonsingular block matrix $\left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]$ as (Kailath et al. 2000):

$$ \left[ {\begin{array}{*{20}c} {z^{d} } \\ {y^{d} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} A & B \\ C & D \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} z \\ y \\ \end{array} } \right] $$

(25)

Hence:

$$ \left[ {\begin{array}{*{20}c} {z^{d} } \\ {y^{d} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {R_{z} } & {R_{zy} } \\ {R_{yz} } & {R_{y} } \\ \end{array} } \right]^{ - 1} \left[ {\begin{array}{*{20}c} z \\ y \\ \end{array} } \right] $$

(26)

this yields the Gramian as:

$$ \left[{\begin{array}{*{20}c} {R_{{z^{d}}}} & {R_{{z^{d} y^{d}}}} \\ {R_{{y^{d} z^{d}}}} & {R_{{y^{d}}}} \\ \end{array}} \right] = \left\langle {\left[{\begin{array}{*{20}c} {z^{d}} \\ {y^{d}} \\ \end{array}} \right],\left[{\begin{array}{*{20}c} {z^{d}} \\ {y^{d}} \\ \end{array}} \right]} \right\rangle = \left[{\begin{array}{*{20}c} {R_{z}} & {R_{zy}} \\ {R_{yz}} & {R_{y}} \\ \end{array}} \right]^{- 1} $$

(27)

As the first step in the geometric description of the dual basis‚ the projections of vectors on a plane are defined as:

• $\left( {\hat{z} |y} \right) \triangleq$ the projection of z onto ${\mathcal{L}}\left\{ y \right\}$

• $\left( {\hat{y} |z} \right) \triangleq$ the projection of y onto ${\mathcal{L}}\left\{ z \right\}$

Accordingly, the corresponding errors are computed as:

$$ \begin{aligned} & \tilde{z} \triangleq \tilde{z}\left| y \right. = z - \hat{z}\left| y \right. \\ & \tilde{y} \triangleq \tilde{y}\left| z \right. = y - \hat{y}\left| z \right. \\ \end{aligned} $$

(28)

The orthogonality principle of least-mean-square estimation leads to $\left\langle {\tilde{z},y} \right\rangle = 0$ and $\left\langle {z^{d}, y } \right\rangle= 0$. Combination of these two properties yields that $\tilde{z}$ and $z^{d}$ must span the same linear space. Thus‚ $z^{d} = M\tilde{z}$ for some nonsingular matrix‚ $M = R_{{\tilde{z}}}^{ - 1}$. Using the geometric characterizations of dual basis (28) in the algebraic one (27) results in:

$$ \left\langle {\left[{\begin{array}{*{20}c} {\tilde{z}\left| y \right.} \\ {\tilde{y}\left| z \right.} \\ \end{array}} \right], \left[{\begin{array}{*{20}c} {z^{d}} \\ {y^{d}} \\ \end{array}} \right]} \right\rangle = \left[{\begin{array}{*{20}c} {R_{{\tilde{z}}}} & 0 \\ 0 & {R_{{\tilde{y}}}} \\ \end{array}} \right]\left\langle {\left[{\begin{array}{*{20}c} {z^{d}} \\ {y^{d}} \\ \end{array}} \right],\left[{\begin{array}{*{20}c} {z^{d}} \\ {y^{d}} \\ \end{array}} \right]} \right\rangle = \left[{\begin{array}{*{20}c} {R_{{\tilde{z}}}} & 0 \\ 0 & {R_{{\tilde{y}}}} \\ \end{array}} \right]\left[{\begin{array}{*{20}c} {R_{z}} & {R_{zy}} \\ {R_{yz}} & {R_{y}} \\ \end{array}} \right]^{- 1} $$

(29)

$$ \left[{\begin{array}{*{20}c} {R_{z}} & {R_{zy}} \\ {R_{yz}} & {R_{y}} \\ \end{array}} \right]^{- 1} = \left[{\begin{array}{*{20}c} {R_{\tilde{z}}^{- 1}} & 0 \\ 0 & {R_{{\tilde{y}}}^{- 1}} \\ \end{array}} \right]\left[{\begin{array}{*{20}c} I & {- R_{zy} R_{y}^{- 1}} \\ {- R_{yz} R_{z}^{- 1}} & I \\ \end{array}} \right] $$

(30)

Comparison of (27) and (30) implies that:

$$ \begin{aligned} & R_{{z^{d} }} = R_{{\tilde{z}}}^{ - 1} \\ & R_{{y^{d} }} = R_{{\tilde{y}}}^{ - 1} \\ & R_{zy} R_{y}^{ - 1} = - R_{{\tilde{z}}} R_{{z^{d} y^{d} }} = - R_{{z^{d} }}^{ - 1} R_{{z^{d} y^{d} }} = - \left( {R_{{y^{d} z^{d} }} R_{{z^{d} }}^{ - 1} } \right)^{*} \\ & \left\| {\left. {\tilde{z}} \right| y } \right\|^{2} = R_{{\tilde{z}}} \\ \end{aligned} $$

(31)

As an important result‚ in linear systems, the gain matrix for estimation of z based on observations y is the negative conjugate transpose of the gain matrix for estimation of $y^{d}$ from $z^{d}$. Now‚ the obtained results are specialized to state-space models with dual basis. The standard linear model affected by noise term‚ $v$, is considered as:

$$ y = Hz + v = \left[ {\begin{array}{*{20}c} H & I \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} z \\ v \\ \end{array} } \right] $$

(32)

The dual system of (32) is:

$$ z^{d} = - H^{*} y^{d} + v^{d} $$

(33)

where * stands for complex conjugate.

Dual of a state-space model

The elements‚ $\left\{{z_{i}, y_{i}} \right\}$ of $\left\{{z,y} \right\}$ are assumed to satisfy a forward-time state-space model of the general discrete system as:

$$ \left\{ {\begin{array}{*{20}l} {x_{i + 1} = F_{i} x_{i} + G_{i} z_{i} } \\ {y_{i} = H_{i} x_{i} + D_{i} z_{i} + v_{i}} \\ \end{array}\quad i \ge 0} \right. $$

(34)

for some matrices $\left\{{F_{i}, G_{i}, H_{i}, D_{i}} \right\}$, the state information $x_{i}$ with zero-initial condition as $x_{0} = 0$, the input signal $z_{i}$, the output signal $y_{i}$ and the uncorrelated white noise $v_{i}$ of variance $R_{i}$. Universally‚ any equation in the state-space form (34) is a linear relationship between the aggregate output and input vectors $\left\{{y, z ,v} \right\}$ as:

$$ y \triangleq {\text{col}}\left\{{y_{0}, \ldots, y_{N}} \right\},\; z \triangleq {\text{col}}\left\{{z_{0}, \ldots, z_{N}} \right\},\;v \triangleq {\text{col}}\left\{{v_{0}, \ldots, v_{N}} \right\} $$

Also:

$$ \begin{aligned} & y = Az + v \\ & R_{v} = \left\| {v^{2} } \right\| = {\text{diag}}\left\{ {R_{0} ,R_{1} , \ldots ,R_{N} } \right\} \\ \end{aligned} $$

(35)

where A is a block lower triangular matrix of (34) as (Kailath et al. 2000):

$$ A = \left[{\begin{array}{*{20}c} {D_{0}} & 0 & {\begin{array}{*{20}c} {0} & {0} & {0} \\ \end{array}} \\ {H_{1} G_{0}} & {D_{1}} & {\begin{array}{*{20}c} {0} & {0} & {0} \\ \end{array}} \\ {\begin{array}{*{20}c} {H_{2} F_{1} G_{0}} \\ \vdots \\ {H_{N} \varPhi \left({N, 1} \right)G_{0}} \\ \end{array}} & {\begin{array}{*{20}c} {H_{2} G_{1}} \\ \vdots \\ {H_{N} \varPhi \left({N, 2} \right)G_{1}} \\ \end{array}} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {D_{2}} \\ \vdots \\ \ldots \\ \end{array}} & {\begin{array}{*{20}c} {0} \\ {\ddots} \\ {H_{N} G_{N - 1}} \\ \end{array}} & {\begin{array}{*{20}c} {0} \\ {0} \\ {D_{N}} \\ \end{array}} \\ \end{array}} \\ \end{array}} \right] $$

(36)

as usual, $\varPhi \left({N, i} \right) = F_{N - 1} F_{N - 2} \ldots F_{i}$. The vectors $\left\{{z^{d}, y^{d}} \right\}$ which have been defined as the dual basis for‚ ${\mathcal{L}} = \left\{{z,y} \right\}$ satisfy:

$$ z^{d} = - A^{*} y^{d} + v^{d} $$

(37)

A complete block-diagram of control and estimation systems in Fig. 2 shows that the dual model can be obtained simply by reversing the direction of time in the original control model and making the following substitutions:

$$ F_{i} \leftrightarrow F_{i}^{*}, \; H_{i} \leftrightarrow G_{i}^{*}, \; G_{i} \leftrightarrow - \, H_{i}^{*}, \; D_{i} \leftrightarrow - \, D_{i}^{*} $$

(38)

where for example, A and − A* in (35) through (37) are the realization of the original model and its dual‚ respectively.

Fig. 2

Duality of control and observer in state-space model

Equivalent stochastic and deterministic problems

For the linear model (32), the projection of z onto ${\mathcal{L}}\left\{ y \right\}$ is denoted by $\left. {\hat{z}} \right|y$ and is computed as $\hat{z}y = K_{o} y$; where the optimal gain matrix $K_{o}$ is obtained through the following stochastic minimization problem:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{K} \left\| {z - Ky} \right\|^{2} \\ & K_{o} = R_{z} H^{*} \left( {R_{v} + HR_{z} H^{*} } \right)^{ - 1} \\ \end{aligned} $$

(39)

Now‚ by determining the vector $\hat{z}$, the solution of (39) is also obtained by the following deterministic optimization problem:

$$\begin{aligned} & \mathop {{\text{min}}}\limits_{z} \left[ {z^{*} R_{Z}^{{ - 1}} z + \left\| {y - Hz} \right\|_{{R_{v}^{{ - 1}} }}^{2} } \right] \\ & \hat{z} = \left( {R_{z}^{{ - 1}} + H^{*} R_{v}^{{ - 1}} H} \right)^{{ - 1}} H^{*} R_{v}^{{ - 1}} y \triangleq K_{o} y \\ \end{aligned}$$

(40)

In other words, the solutions of both (39) and (40) result in the subjected gain matrix‚ $K_{o}$, which shows the equivalence of the stochastic problem (39) and the deterministic problem (40). For the linear dual model (37), $K_{o}^{d}$ is obtained through the following minimum-mean-square-error optimization problem:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{K^{d} }} \left\| {y^{d} - K^{d} z^{d} } \right\|^{2} \\ & K_{o}^{d} = - R_{y}^{d} H\left( {R_{v}^{d} + H^{*} R_{y}^{d} H} \right)^{ - 1} = - R_{v}^{ - 1} H\left( {R_{z}^{ - 1} + H^{*} R_{v}^{ - 1} H} \right)^{ - 1} \\ \end{aligned} $$

(41)

Then‚ the problem of determining vector $\hat{y}^{d}$ is considered as:

$$ \begin{aligned} & \mathop {\hbox{min} }\limits_{{y^{d} }} \left[ {y^{d*} R_{v} y^{d} + \left\| {z^{d} + H^{*} y^{d} } \right\|_{{R_{z} }}^{2} } \right] \\ & \hat{y}^{d} = - \left( {R_{v} + HR_{z} H^{*} } \right)^{ - 1} HR_{z} z^{d} \triangleq K_{O}^{d} z^{d} \\ \end{aligned} $$

(42)

Comparison of (40) and (42) shows that $K_{o}^{d} = - \,K_{o}^{*}$. Therefore‚ expression (39) is dual with (41) and (40) is dual with (42) because the corresponding gain matrices are the negative conjugate transpose of each other. The gain matrix‚ $K_{o}^{d}$ could be obtained through the solution of either (41) or (42). Furthermore‚ the deterministic system (42) is dual to the original stochastic system (39).

The discrete-time LQR optimization problem is considered as (Kailath et al. 2000):

$$ \mathop {\min}\limits_{{\left\{{z_{0}, \ldots, z_{N}} \right\}}} \left[{x_{N + 1}^{*} P_{N + 1}^{d} x_{N + 1} + \mathop \sum \limits_{i = 0}^{N} \left({y_{i} - H_{i} x_{i}} \right)^{*} R_{i}^{d} \left({y_{i} - H_{i} x_{i}} \right) + \mathop \sum \limits_{i = 0}^{N} z_{i}^{*} Q_{i}^{d} z_{i}} \right] $$

(43)

subjected to the state-space model constraint (34), $x_{i + 1} = F_{i} x_{i} + G_{i} z_{i},\; x_{i} = 0$, where $P_{N + 1}^{d} \ge 0,\; R_{i}^{d} \ge 0$ and $Q_{i}^{d} \ge 0$ are design/weighting matrices corresponding to initial state vector‚ measurement residual and input vector‚ respectively. The state-space process is considered with a zero-initial state vector, and a large matrix P. Since the cost function (43) can be written as (40), its solution is obtained via the dual stochastic problem. For this purpose‚ by introducing the vectors $z \triangleq {\text{col}}\left\{{z_{0}, \ldots, z_{N}} \right\}$ and $S = {\text{col}}\left\{{H_{0} x_{0}, H_{1} x_{1}, \ldots, H_{N} x_{N}} \right\}$ the following block lower triangular matrix is considered (Kailath et al. 2000):

$$ B = \left[{\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varPhi \left({N + 1, 1} \right)G_{0}} \\ 0 \\ {\begin{array}{*{20}c} {H_{1} G_{0}} \\ {H_{2} \varPhi \left({2, 1} \right)G_{0}} \\ {\begin{array}{*{20}c} \vdots \\ {H_{N} \varPhi \left({N, 1} \right)G_{0}} \\ \end{array}} \\ \end{array}} \\ \end{array}} & {\begin{array}{*{20}c} {\varPhi \left({N + 1, 2} \right)G_{1}} \\ {} \\ {\begin{array}{*{20}c} 0 \\ {H_{2} G_{1}} \\ {\begin{array}{*{20}c} \vdots \\ {H_{N} \varPhi \left({N, 2} \right)G_{1}} \\ \end{array}} \\ \end{array}} \\ \end{array}} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} \ldots \\ {} \\ {\begin{array}{*{20}c} {} \\ 0 \\ {\begin{array}{*{20}c} \ddots \\ \ldots \\ \end{array}} \\ \end{array}} \\ \end{array}} & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\varPhi \left({N + 1, N} \right)G_{N - 1}} \\ {} \\ {\begin{array}{*{20}c} {} \\ {} \\ {\begin{array}{*{20}c} 0 \\ {H_{N} G_{N - 1}} \\ \end{array}} \\ \end{array}} \\ \end{array}} & {\begin{array}{*{20}c} {G_{N}} \\ {} \\ {\begin{array}{*{20}c} {} \\ {} \\ {\begin{array}{*{20}c} {} \\ 0 \\ \end{array}} \\ \end{array}} \\ \end{array}} \\ \end{array}} \\ \end{array}} \\ \end{array}} \right] $$

(44)

It could be simply verified by direct computation that‚ $\left[ {\begin{array}{*{20}c} {x_{N + 1} } \\ S \\ \end{array} } \right] = Bz$. Equation (43) can be equivalently rewritten as:

$$ \begin{aligned} & y = A\mathop {\hbox{min} }\limits_{z} \left[ {z^{*} Q^{d} z + \left\| {\left[ {\begin{array}{*{20}c} 0 \\ { - y} \\ \end{array} } \right] + Bz} \right\|_{{W^{d} }}^{2} } \right] + v \\ & Q^{d} \triangleq {\text{diag}}\left\{ {Q_{0}^{d} , \ldots ,Q_{N}^{d} } \right\} \\ & W^{d} \triangleq {\text{diag}}\left\{ {P_{N + 1}^{d} ,R_{0}^{d} , \ldots ,R_{N}^{d} } \right\} \\ \end{aligned} $$

(45)

Moreover‚ the solution is‚

$$ \hat{z} = K_{o} \left[ {\begin{array}{*{20}c} 0 \\ { - y} \\ \end{array} } \right] $$

(46)

Equation (46) is the estimation of z based on observations y.

Design of MPO

To achieve an observer from the common direct method (Doostdar and Keighobadi 2012)‚ the stochastic optimization problem (39) for linear model (35) should be solved. However, by use of the equivalence and duality in estimation and control as well as the duality of stochastic and deterministic problems‚ the stochastic problem (39) and its deterministic equal (40) are dual with the deterministic problem (42). The gain matrices determine both the observer and the controller of stochastic (39) and deterministic (40) problems‚ respectively. Therefore‚ the observer of stochastic problem (39) is identically obtained by its dual controller in the deterministic problem (42). According to Fig. 2 and (34), a dual predictive state-space model at m future sampling time is introduced:

$$ \begin{aligned} & x\left( {k_{i} + m\left| {k_{i} } \right.} \right) = F^{m} x\left( {k_{i} } \right) + \mathop \sum \limits_{i = 0}^{m - 1} F^{m - i - 1} Gz\left( {k_{i} + i} \right) \\ & y\left( {k_{i} + m\left| {k_{i} } \right.} \right) = HF^{m} x\left( {k_{i} } \right) + \mathop \sum \limits_{i = 0}^{m - 1} HF^{m - i - 1} Gz\left( {k_{i} + i} \right) + \mathop \sum \limits_{i = 0}^{m - 1} F^{m - i - 1} Dz\left( {k_{i} + i} \right) + v_{i} \\ \end{aligned} $$

(47)

where $x\left( {k_{i} + m\left| {k_{i} } \right.} \right)$ stands for the predicted state at future time‚ $k_{i} + m$, based on the current state $x\left( {k_{i} } \right)$. A discrete orthogonal Laguerre network can be made through discretization of a continuous-time Laguerre network (Wang 2009). To include the orthogonal characteristics‚ Laguerre functions are considered in the deterministic problem (42) which simply avoid the modeling difficulties of the stochastic cost function (39). The Laguerre functions are incorporated in the predicted input vector of (47) as:

$$ z\left( {k_{i} + i} \right) = L\left( i \right)^{\text{T}} \eta $$

(48)

where the Laguerre terms $l_{0} \left(k \right), l_{1} \left(k \right), \ldots, l_{N} \left(k \right)$ of $L\left( k \right)$ are together with Laguerre coefficients in vector form as‚ $\eta = \left[ {C_{1} \; C_{2} \ldots C_{N} } \right]^{\text{T}}$. The orthonormal Laguerre functions are included in the discrete-time LQR with a sufficiently large prediction horizon $N_{p}$ as (Wang 2009):

$$ J = \mathop \sum \limits_{m = 1}^{{N_{p} }} x\left( {k_{i} + m\left| {k_{i} } \right.} \right)^{\text{T}} Qx\left( {k_{i} + m\left| {k_{i} } \right.} \right) + \eta^{\text{T}} R_{L} \eta $$

(49)

where the objective is to find the coefficient vector $\eta$ with the weighting matrices $Q > 0$ and $R_{L} > 0$. Now‚ applying (47) into the cost function (49) gives:

$$ J =\, \eta^{\text{T}} \left( {\mathop \sum \limits_{m = 1}^{{N_{p} }} \sigma \left( m \right)Q\sigma \left( m \right)^{\text{T}} + R_{L} } \right)\eta + 2\eta^{\text{T}} \left( {\mathop \sum \limits_{m = 1}^{{N_{p} }} \sigma \left( m \right)QF^{m} } \right)x\left( {k_{i} } \right) + \mathop \sum \limits_{m = 1}^{{N_{p} }} x\left( {k_{i} } \right)^{\text{T}} (F^{\text{T}} )^{m} QF^{m} x\left( {k_{i} } \right) $$

(50)

For an optimal solution without constraints‚ the partial derivative of (50) with respect to $\eta$ yields:

$$ \begin{aligned} & \eta = - \left({\mathop \sum \limits_{m = 1}^{{N_{p}}} \sigma \left(m \right)Q\sigma \left(m \right)^{\text{T}} + R_{L}} \right)^{- 1} \left({\mathop \sum \limits_{m = 1}^{{N_{p}}} \sigma \left(m \right)QF^{m}} \right)x\left({k_{i}} \right) \hfill \\ & \sigma \left(m \right) = \mathop \sum \limits_{i = 0}^{m - 1} F^{m - i - 1} GL\left(i \right)^{\text{T}}, \quad \left({\mathop \sum \limits_{m = 1}^{{N_{p}}} \sigma \left(m \right)Q\sigma \left(m \right)^{\text{T}} + R_{L}} \right)^{- 1} \ne 0 \hfill \\ \end{aligned} $$

(51)

considering‚

$$ \begin{aligned} & {\varvec{\Psi}} = \left( {\mathop \sum \limits_{m = 1}^{{N_{p} }} \sigma \left( m \right)QF^{m} } \right) \\ & \varOmega = \left( {\mathop \sum \limits_{m = 1}^{{N_{p} }} \sigma \left( m \right)Q\sigma \left( m \right)^{\text{T}} + R_{L} } \right) \\ \end{aligned} $$

(52)

leads to:

$$ \eta = - \varOmega^{ - 1} {\varvec{\Psi}}x\left( {k_{i} } \right) $$

(53)

$$ z\left( {k_{i} } \right) = L\left( 0 \right)^{\text{T}} \eta $$

(54)

where for a given N and a:

$$ L\left( 0 \right)^{\text{T}} = \sqrt {1 - a^{2} } \left[ {\begin{array}{*{20}c} 1 & { - a} & {\begin{array}{*{20}c} {a^{2} } & { - a^{3} } & {\begin{array}{*{20}c} \cdots & {\left( { - 1} \right)^{N - 1} a^{N - 1} }\\ \end{array}}\\ \end{array}}\\ \end{array}}\right] $$

(55)

$$ K_{o}^{d} = L\left( 0 \right)^{\text{T}} \varOmega^{ - 1} {\varvec{\Psi}} $$

(56)

the dual controller $K_{o}^{d}$ of the dual model (38) or the observer of the original state-space model (34) is obtained.

Stability analysis

The Lyapunov function $V\left({x\left(k \right), k} \right)$ is considered as the minimum of the finite horizon cost function (49):

$$ \begin{array}{*{20}l} {V\left({x\left(k \right), k} \right) = \mathop \sum \limits_{m = 1}^{{N_{p}}} x\left({k + m\left| k \right.} \right)^{\text{T}} Qx\left({k + m\left| k \right.} \right) + \mathop \sum \limits_{m = 0}^{{N_{p} - 1}} z\left({k + m} \right)^{\text{T}} Rz\left({k + m} \right)} \\ {x\left({k + m\left| k \right.} \right) = F^{m} x\left(k \right) + \mathop \sum \limits_{i = 0}^{m - 1} F^{m - i - 1} GL\left(i \right)^{\text{T}} \eta^{k}} \\ \end{array} $$

(57)

where the equality constraint on terminal state‚ $x\left( {k + N_{p} \left| k \right.} \right) = 0$ will lead to the closed-loop stability. There exists a solution of $\eta$ in minimization of $J$ (49) with the inequality constraints and the terminal equality constraint. The positive definite‚ $V\left({x\left(k \right), k} \right)$ (57), is radially unbounded. At sample time $k + 1$, the Lyapunov function (57) becomes (Wang 2009):

$$ \begin{aligned} & V\left({x\left({k + 1} \right), k + 1} \right) = \mathop \sum \limits_{m = 1}^{{N_{p}}} x\left({k + 1 + m\left| {k + 1} \right.} \right)^{\text{T}} Qx\left({k + 1 + m\left| {k + 1} \right.} \right) + \mathop \sum \limits_{m = 0}^{{N_{p} - 1}} z\left({k + 1 + m} \right)^{\text{T}} Rz\left({k + 1 + m} \right) \hfill \\ & x\left({k + 1 + m\left| {k + 1} \right.} \right) = F^{m} x\left({k + 1} \right) + \mathop \sum \limits_{i = 0}^{m - 1} F^{m - i - 1} GL\left(i \right)^{\text{T}} \eta^{k + 1} \hfill \\ \end{aligned} $$

(58)

where $\eta^{k + 1}$ and $\eta^{k}$ stand for the solution of Laguerre’s coefficient vector at $k + 1$ and $k$ sample times‚ respectively. The difference of Lyapunov function between two consequent sample times k + 1 and k should be computed. A feasible solution of $\eta^{k + 1}$ for the initial state variable $x\left( {k + 1} \right)$ in the receding horizon is $\eta^{k}$ assuming $x\left( {k + 1} \right)$ as the one step ahead response of $x\left( k \right)$ related to $z\left( k \right)$; that is $x\left( {k + 1} \right) = Fx\left( k \right) + Gz\left( k \right)$. The feasible control sequence at $k + 1$ is obtained by shifting the terms $L\left(0 \right)^{\text{T}} \eta^{k}, L\left(1 \right)^{\text{T}} \eta^{k}, L\left(2 \right)^{\text{T}} \eta^{k}, \ldots, L\left({N_{p} - 1} \right)^{\text{T}} \eta^{k}$ one time-step forward and replacing the last term by zero as‚ $L\left(1 \right)^{\text{T}} \eta^{k}, L\left(2 \right)^{\text{T}} \eta^{k}, \ldots, L\left({N_{p} - 1} \right)^{\text{T}} \eta^{k},\; 0$. Using the last sequence in (58) gives the upper bound‚ $\bar{V}\left({x\left({k + 1} \right), k + 1} \right)$ because of the optimal solution of $\eta^{k + 1}$ as:

$$ V\left({x\left({k + 1} \right), k + 1} \right) \le \bar{V}\left({x\left({k + 1} \right), k + 1} \right) $$

(59)

By satisfying the aforementioned terminal state constraint at sample time $k + 1$, $\bar{V}\left({x\left({k + 1} \right), k + 1} \right)$ coincides to $V\left({x\left({k + 1} \right), k + 1} \right)$. The difference between $V\left({x\left({k + 1} \right), k + 1} \right)$ and $V\left({x\left(k \right), k} \right)$ could be bounded as:

$$ V\left({x\left({k + 1} \right), k + 1} \right) - V\left({x\left(k \right), k} \right) \le \bar{V}\left({x\left({k + 1} \right), k + 1} \right) - V\left({x\left(k \right), k} \right) $$

(60)

Since $\bar{V}\left({x\left({k + 1} \right), k + 1} \right)$ shares the same control and the same state sequences with $V\left({x\left(k \right), k} \right)$ in sample times‚ $k + 1$, $k + 2$, …‚ $k + N_{p} - 1$, the right hand of (60) yields:

$$ \bar{V}\left({x\left({k + 1} \right), k + 1} \right) - V\left({x\left(k \right), k} \right) = x(k + N_{p} \left| {k)} \right.^{\text{T}} Qx(k + N_{p} \left| {k)} \right. - x\left({k + 1} \right)^{\text{T}} Qx\left({k + 1} \right) - z(k)^{\text{T}} Rz\left(k \right) $$

(61)

By imposing the above-mentioned equality constraint on the terminal state:

$$ \bar{V}\left({x\left({k + 1} \right), k + 1} \right) - V\left({x\left(k \right), k} \right) = - x\left({k + 1} \right)^{\text{T}} Qx\left({k + 1} \right) - z(k)^{\text{T}} Rz\left(k \right) $$

(62)

Comparing (60) and (62) results in:

$$ V\left({x\left({k + 1} \right), k + 1} \right) - V\left({x\left(k \right), k} \right) \le - x\left({k + 1} \right)^{\text{T}} Qx\left({k + 1} \right) - z(k)^{\text{T}} Rz\left(k \right) < 0 $$

(63)

Hence‚ the negative difference of Lyapunov function (57) indicates the asymptotic stability of the MPO.

Implementation

In the AHRS mode of an integrated INS and GPS, the unknown uncertainties affect the output data of inertial sensors. To this end‚ a precise model of sensors and system is hard to be captured which attenuates the estimation quality of the EKF. To achieve accurate outputs containing attitude and heading angles‚ the MPO method is implemented. Based on the capability of Laguerre network set in dealing with the terms of nonlinearity and uncertainty‚ the MPO estimator is a suitable solution for data merging problem of the MEMS GAINS. The commercial grade 1 Hz GPS receiver and 3-axis accelerometers‚ magnetometers and gyroscopes of MEMS-grade 50 Hz ADIS16407 IMU are gathered, and therefore‚ the output and input data set during ground/flight test by a vehicle and a small UAV are completely produced. The observation matrix‚ $H = \frac{\partial h\left( q \right)}{\partial q} = I_{4 \times 4}$ (19) and the following matrices of quaternions dynamics (8) are used in the implementation of both EKF and MPO algorithms in the AHRS:

$$ \begin{array}{*{20}c} {F = \frac{1}{2}\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\begin{array}{*{20}c} 0 \\ {\omega_{x} } \\ {\begin{array}{*{20}c} {\omega_{y} } \\ {\omega_{z} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} { - \omega_{x} } \\ 0 \\ {\begin{array}{*{20}c} { - \omega_{z} } \\ {\omega_{y} } \\ \end{array} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} { - \omega_{y} } \\ {\omega_{z} } \\ {\begin{array}{*{20}c} 0 \\ { - \omega_{x} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} { - \omega_{z} } \\ { - \omega_{y} } \\ {\begin{array}{*{20}c} {\omega_{x} } \\ 0 \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]} \\ {G = \frac{1}{2}\left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} { - q_{2} } \\ { q_{1} } \\ {\begin{array}{*{20}c} { q_{4} } \\ { - q_{3} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} { - q_{3} } \\ { - q_{4} } \\ {\begin{array}{*{20}c} { q_{1} } \\ { q_{2} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} { - q_{4} } \\ { q_{3} } \\ {\begin{array}{*{20}c} { - q_{2} } \\ { q_{1} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] } \\ \end{array} $$

(64)

Using (18), when the vehicle is at rest‚ the initial alignment of AHRS is performed as:

$$ \theta_{0} = - { \sin }^{ - 1} \left( {\frac{{f_{x} }}{g}} \right) $$

(65)

$$ \varphi_{0} = \sin^{ - 1} \left( {\frac{{f_{y} }}{{g\cos \left( {\theta_{0} } \right)}}} \right) $$

(66)

$$ \psi_{0} = \psi_{\text{Mag}} $$

(67)

noting that the singularity of (66) at $\theta_{0} = 90^\circ$ does not occur in the on-ground alignment. Therefore‚ the initial quaternions are obtained by imposing (12) to the angles calculated by (65) through (67). The EKF covariance matrices are set to the values given in Doostdar and Keighobadi (2012). In the implementation of MPO for AHRS with quaternions dynamics (8), the Laguerre pole places for each input a and the number of Laguerre terms for each input N are considered as:

$$ \begin{array}{*{20}l} {a = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {a_{1} } & {a_{2} } & {a_{3} } \\ \end{array} } & {a_{4} } \\ \end{array} } \right]} \\ {N = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} {N_{1} } & {N_{2} } & {N_{3} } \\ \end{array} } & {N_{4} } \\ \end{array} } \right]} \\ \end{array} $$

(68)

where the prediction horizon length $N_{P}$ together with a and N are selected by the designer. The covariance matrices of the EKF and the weighting diagonal matrices of the system dynamics Q and the measurement vector R are assigned using the specifications of Table 1.

Table 1 Specifications of inertial sensors (Keighobadi et al. 2011; Mahapatra et al. 2001)

In the implementation of MPO for AHRS using Euler dynamics (2), the 3-dimensional Q and R as well as the Laguerre parameters $a$ and N should be considered as‚

$$ \begin{array}{*{20}l} {a = \left[ {\begin{array}{*{20}c} {a_{1} } & {a_{2} } & {a_{3} } \\ \end{array} } \right]} \\ {N = \left[ {\begin{array}{*{20}c} {N_{1} } & {N_{2} } & {N_{3} } \\ \end{array} } \right]} \\ \end{array} $$

(69)

To simplify the implementation of AHRS with Euler angles dynamics (2) in which $x = \left[ {\begin{array}{*{20}c} \varphi & \theta & \psi \\ \end{array} } \right]^{\text{T}}$, the two attitude angles obtained from accelerometers data are gathered with the heading angle‚ $\psi_{\text{GPS/Mag}}$, in the measurement vector y as:

$$ \varphi_{\text{acc}} = { \tan }^{ - 1} \left( {\frac{{ - f_{y} }}{{ - f_{z} }}} \right) $$

(70)

$$ \theta_{\text{acc}} = { \sin }^{ - 1} \left( {\frac{{f_{x} }}{{\left( {f_{x}^{2} + f_{y}^{2} + f_{z}^{2} } \right)^{0.5} }}} \right) $$

(71)

$$ y = \left[ {\begin{array}{*{20}c} {\varphi_{\text{acc}} } & {\theta_{\text{acc}} } & {\psi_{\text{GPS/Mag}} } \\ \end{array} } \right]^{\text{T}} $$

(72)

$$ z = \left[ {\begin{array}{*{20}c} {\omega_{x} } & {\omega_{y} } & {\omega_{z} } \\ \end{array} } \right]^{T} $$

(73)

where the subscripts acc and Mag stand for accelerometer and magnetometer‚ respectively. The system and measurement matrices regarding Euler angles dynamics are obtained as:

$$ \begin{aligned} & F = \left[{\begin{array}{*{20}c} {\omega_{y} \cos \varphi \tan \theta - \omega_{z} \sin \varphi \tan \theta} & {\left({\omega_{y} \sin \varphi + \omega_{z} \cos \varphi} \right)\left({1 + \tan \theta} \right)^{2}} & 0 \\ {- \omega_{y} \sin \varphi - \omega_{z} \cos \varphi} & 0 & 0 \\ {\omega_{y} \cos \varphi/\cos \theta - \omega_{z} \sin \varphi/\cos \theta} & {\omega_{y} \sin \varphi \sin \theta/\cos^{2} \theta + \omega_{z} \cos \varphi \sin \theta/\cos^{2} \theta} & 0 \\ \end{array}} \right] \hfill \\ & G = \left[{\begin{array}{*{20}c} 1 & {\sin \varphi \tan \theta} & {\cos \varphi \tan \theta} \\ 0 & {\cos \varphi} & {- \sin \varphi} \\ 0 & {\sin \varphi \sec \theta} & {\cos \varphi \sec \theta} \\ \end{array}} \right] \hfill \\ & H = \left[{1\; 0\; 0, 0\; 1\; 0, 0\; 0\; 1} \right]^{\text{T}} \hfill \\ \end{aligned} $$

(74)

The implementation algorithm of both the MPO and the EKF with quaternions dynamics is represented in Fig. 3.

Fig. 3

Implementation block-diagram of quaternion-based AHRS

Calibration of three-axial magnetometers

Since the heading angle of GPS‚ $\psi_{\text{GPS}}$, is not valid at velocities under about 3 km/h and in particular during on-ground alignment process‚ the uncalibrated magnetic heading angle $\hat{\psi}_{\text{Mag}}$ is obtained by the 3-Axis Magnetometers (TAM) as:

$$ \hat{\psi}_{\text{Mag}} = - \tan^{- 1} \left({\frac{{M_{y}^{h}}}{{M_{x}^{h}}}} \right) $$

(75)

Along the ${\text{X}}_{L}$-${\text{Y}}_{\text{L}}$ axes in local level plane‚ which make the magnetic heading angle with respect to N-E axes‚ the measured magnetic field by TAM is resolved to $M_{x}^{h}$ and $M_{y}^{h}$ components:

$$ \left[ {\begin{array}{*{20}c} {M_{x}^{h} } \\ {M_{y}^{h} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\cos \theta } & {\sin \theta \sin \varphi } & {\cos \varphi \sin \theta } \\ 0 & {\cos \varphi } & { - \sin \varphi } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {M_{x}^{b} } \\ {M_{y}^{b} } \\ {M_{z}^{b} } \\ \end{array} } \right] $$

(76)

where $\left[ {\begin{array}{*{20}c} {M_{x}^{b} } & {M_{y}^{b} } & {M_{z}^{b} } \\ \end{array} } \right]^{\text{T}}$ denotes the measured magnetic field vector by TAM in b-frame coordinates. The complete version of (75) gives the magnetic North angle at range 0° through 360° as:

$$ \hat{\psi}_{\text{Mag}} = \left\{{\begin{array}{*{20}l} {90} \hfill & {M_{x}^{h} = 0, M_{y}^{h} < 0} \hfill \\ {270} \hfill & {M_{x}^{h} = 0, M_{y}^{h} > 0} \hfill \\ {180 - \tan^{- 1} \left({\frac{{M_{y}^{h}}}{{M_{x}^{h}}}} \right) \times \frac{180}{\pi}} \hfill & {M_{x}^{h} < 0} \hfill \\ {- \tan^{- 1} \left({\frac{{M_{y}^{h}}}{{M_{x}^{h}}}} \right) \times \frac{180}{\pi}} \hfill & {M_{x}^{h} > 0, M_{y}^{h} < 0} \hfill \\ {360 - \tan^{- 1} \left({\frac{{M_{y}^{h}}}{{M_{x}^{h}}}} \right) \times \frac{180}{\pi}} \hfill & {M_{x}^{h} > 0, M_{y}^{h} > 0} \hfill \\ \end{array}} \right. $$

(77)

The magnetic heading angle is affected by hard- and soft-iron local magnetic fields mostly produced by the vehicle steel parts and its electromechanical driving parts. Therefore‚ the following swinging calibration process is carried out (Keighobadi et al. 2011):

$$ \delta \psi = A + B\sin \left( {\hat{\psi }} \right) + C\cos \left( {\hat{\psi }} \right) + D\sin \left( {2\hat{\psi }} \right) + E\cos \left( {2\hat{\psi }} \right) $$

(78)

$$ \delta \psi = \psi_{\text{ref}} - \hat{\psi } $$

(79)

where $\hat{\psi }$ and $\psi_{\text{ref}}$ stand for the affected heading angle by magnetic disturbances and the reference heading angle of calibration‚ respectively. The calibration coefficients A to E are computed in the following regression form by the least-square algorithm:

$$ \left[ {\begin{array}{*{20}c} {\delta \psi_{1} } \\ {\delta \psi_{2} } \\ {\begin{array}{*{20}c} \vdots \\ {\delta \psi_{N} } \\ \end{array} } \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\begin{array}{*{20}c} 1 \\ 1 \\ {\begin{array}{*{20}c} \vdots \\ 1 \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\sin \hat{\psi }_{1} } \\ {\sin \hat{\psi }_{2} } \\ {\begin{array}{*{20}c} \vdots \\ {\sin \hat{\psi }_{N} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\begin{array}{*{20}c} {\cos \hat{\psi }_{1} } \\ {\cos \hat{\psi }_{2} } \\ {\begin{array}{*{20}c} \vdots \\ {\cos \hat{\psi }_{N} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\sin 2\hat{\psi }_{1} } \\ {\sin 2\hat{\psi }_{2} } \\ {\begin{array}{*{20}c} \vdots \\ {\sin 2\hat{\psi }_{N} } \\ \end{array} } \\ \end{array} } & {\begin{array}{*{20}c} {\cos 2\hat{\psi }_{1} } \\ {\cos 2\hat{\psi }_{2} } \\ {\begin{array}{*{20}c} \vdots \\ {\cos 2\hat{\psi }_{N} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} A \\ B \\ {\begin{array}{*{20}c} C \\ {\begin{array}{*{20}c} D \\ E \\ \end{array} } \\ \end{array} } \\ \end{array} } \right] $$

(80)

The reference heading angle‚ $\psi_{\text{ref}}$, is rendered either by a rotating calibration table or by the course angle of GPS at velocities above 3 km/h. The calibrated magnetic heading angle is obtained as:

$$ \psi_{\text{c}} = A + B\sin \left( {\hat{\psi }} \right) + C\cos \left( {\hat{\psi }} \right) + D\sin \left( {2\hat{\psi }} \right) + E\cos \left( {2\hat{\psi }} \right) + \hat{\psi } $$

(81)

where $\psi_{\text{c}}$ stands for the calibrated heading angle.

Test results

For experimental evaluation purpose, we perform long-time road and flight tests considering a Companav-2 INS/GPS as the reference system. Companav-2 is a high-efficiency navigation system developed by Teknol Ltd for both ground and flight applications (Teknol 2009). Barometric altimeter‚ accelerometers‚ magnetometers‚ sensors of angular rate and a temperature sensor for thermal calibration of IMU have been gathered in the Companav-2 system. The reliability and accuracy of the Companav-2 system were illustrated in long-time operations and several ground/flight tests (Teknol 2009). To assess the tracking accuracy of attitude angles‚ the precise reference attitude data are supplied by the Companav-2 system. The data set of Garmin-35 receiver and ADIS16407 IMU has been used as measurement data and process input data of AHRS. The main statistical features of both the Companav-2 INS/GPS and ADIS16407 inertial sensors are given in Table 1 (Keighobadi et al. 2011; Mahapatra et al. 2001). Since we do not have direct access to the internal software of Companav-2 system‚ its magnetic sensors could not be calibrated concerning hard-iron and soft-iron magnetic fields of the test vehicle. Therefore‚ the Companav-2 equipment must be placed out of the vehicle. For this reason, the sensors of Companav-2 system‚ the GPS receiver and the ADIS16407 IMU all are mounted on a rigid aluminum frame fixed to the vehicle body as depicted in Fig. 4. The raw measurements of IMU together with the orientation‚ velocity and position of INS are provided at the same rate‚ 50 Hz. Online data monitoring is executed through a serial RS-232 port on a personal computer as shown in Fig. 5.

Fig. 4

AHRS and reference INS/GPS hardware together with test vehicle

Fig. 5

ADIS16407 IMU and GPS data logger

Due to government restrictions for flight test, we preferred to request this test from a company that has commercial fixed-wing UAVs, flight test permission and a test field. Owing to the use of pure kinematical equations of quaternion‚ position and velocity vectors‚ both the GAINS and the reference Companav-2 are independent of the dynamical and aero-dynamical behavior of the test vehicles. Therefore‚ every test vehicle of the ground or flying type merely produces input trajectory data to IMU‚ INS and GPS. According to Figs. 6 and 7‚ during the flight test the reference Companav-2‚ ADIS16407 IMU‚ GPS and other test equipment were under different conditions of trajectory and maneuvers. The UAV begins its fly at point p₁ with a high forward velocity during takeoff and then follows the trajectory with some maneuvers to p₂ and returns on the trajectory to p₃. Next‚ it continues along the given return trajectory and consequently performs the landing in point p₄.

Fig. 6

Reference geographical latitude–longitude trajectory

Fig. 7

Reference altitude trajectory

The final calibrated magnetic heading angle based on online GPS course angle is obtained as:

$$ \psi_{\text{Mag}} = \, \hat{\psi }_{\text{Mag}} + 0.215264 + 0.100083\sin \left( {\hat{\psi }_{\text{Mag}} } \right) - 0.261611\cos \left( {\hat{\psi }_{\text{Mag}} } \right) + 0.072486\sin \left( {2\hat{\psi }_{\text{Mag}} } \right) + 0.071829\cos \left( {2\hat{\psi }_{\text{Mag}} } \right) $$

(82)

The calibration effects on the heading angle and the tracking errors are presented in Figs. 8 and 9, respectively. By looking at Fig. 8, one can find that following the calibration process‚ the magnetic heading angle approximately coincides with the GPS heading angle. The tracking error of calibration process in Fig. 9 confirms considerable removal of bias, scale-factor, and other uncertain alignment errors.

Fig. 8

Heading angle trajectories by GPS‚ uncalibrated and calibrated magnetometers

Fig. 9

Tracking errors of magnetometer calibration process

The estimated attitude and heading trajectories through the MPO and the EKF methods are compared with the reference trajectories of Companav-2 INS/GPS during the long-time flight test in Fig. 10. The test has been carried out about 1800 s in an urban area to assess both the Euler and quaternion methods‚ simultaneously. Figure 11 represents the attitude-heading angles obtained by the quaternions system. Both Figs. 10 and 11 illustrate better tracking of all reference attitude-heading angles by the MPO compared with the EKF. The values of MPO parameters‚ $a_{1 \times 4}, N_{1 \times 4}$ $a_{1 \times 3}, \;N_{1 \times 3}$ in Table 2 as well as $N_{P} = 1$ are used corresponding to quaternion and Euler angles techniques.

Fig. 10

Estimated $\varphi$, $\theta$ and $\psi$ angles through MPO and EKF of Euler dynamics compared with reference values of Companav-2 in flight test#1

Fig. 11

Estimated $\varphi$, $\theta$ and $\psi$ angles through MPO and EKF of quaternions dynamics compared with reference values of Companav-2 in test#1

Table 2 The values of vectors‚ a and N for quaternions and Euler angles in UAV test

Using Table 1 and the referred sensors datasheet‚ the weighting diagonal matrices of process‚ $Q_{3 \times 3}$, and measurements‚ $R_{4 \times 4}$, $R_{3 \times 3}$ for both quaternion and Euler based AHRS are designated as:

$$ \begin{aligned} & Q_{3 \times 3} = {\text{diag}}\left[ {\begin{array}{*{20}c} {10^{ - 4} } & {10^{ - 4} } & {10^{ - 2} } \\ \end{array} } \right] \\ & R_{4 \times 4} = {\text{diag}}\left[ {\begin{array}{*{20}c} {10^{ - 3} } & {10^{ - 2} } & {\begin{array}{*{20}c} {10^{ - 2} } & {10^{ - 2} } \\ \end{array} } \\ \end{array} } \right] \\ & R_{3 \times 3} = {\text{diag}}\left[ {\begin{array}{*{20}c} {0.09} & {0.99} & {0.99} \\ \end{array} } \right] \\ \end{aligned} $$

(83)

For better evaluation of the proposed MPO method concerning the EKF, the estimation errors of heading and attitude components with respect to the reference values of Companav-2 are compared in Figs. 12 and 13. Besides‚ the statistical mean and standard deviation (SD) of attitude and heading errors are released in Table 3. By Figs. 12 and 13‚ owing to uncompensated uncertainties and bias term of inertial MEMS sensors‚ the EKF estimations are together with more bias, drift, and noisy fluctuations. Furthermore‚ regarding Tables 3 and 4‚ the statistical mean and SD of attitude and heading errors in both Euler and quaternion systems of MPO decreased compared to the EKF. Therefore‚ owing to adaptation regarding nonlinear terms and the prediction of long-term behavior of uncertainties‚ the implementation of MPO technique yields a better low-cost AHRS for UAV applications.

Fig. 12

Estimation errors of $\varphi$, $\theta$ and $\psi$ angles through MPO and EKF of Euler angles dynamics in test#1

Fig. 13

Estimation errors of $\varphi$, $\theta$ and $\psi$ angles through MPO and EKF of quaternions in test#1

Table 3 Statistical mean and SD of estimation errors using Euler angles dynamics in test#1

Table 4 Statistical mean and SD of estimation errors by quaternions dynamics in test#1

The fixed alignment error of the EKF heading angle $\psi$ at the beginning of Fig. 13 is removed by the increase in the vehicle velocity above 3 km/h. According to Tables 3 and 4‚ compared with the EKF, the MPO method results in a better performance based on both the Euler angles and quaternions. To this end‚ due to affine dynamics of quaternions‚ the estimation accuracy of the EKF is affected by less nonlinearity and uncertainty compared with the Euler angles method. Therefore‚ in the sense of the mean values of estimation errors‚ setting the EKF with the quaternions vector yields better results compared with the Euler angles. The close results of quaternions and Euler angles through the MPO show the capability of the proposed method in filtering unknown uncertainties and nonlinearities.

In Figs. 14 and 15, the estimated attitude and heading angles by the applied MPO and EKF in both the Euler angles and quaternion methods are compared with the reference values of Companav-2 during the 1200 s test#2 of the ground vehicle in an urban area. The design parameters $a_{1 \times 4}$, $N_{1 \times 4}$, $a_{1 \times 3}$, $N_{1 \times 3}$ in Table 5 as well as $N_{P} = 1$ are used corresponding to quaternion and Euler techniques for ground vehicle test purpose.

Fig. 14

Estimated $\varphi$, $\theta$ and $\psi$ angles through MPO and EKF of Euler dynamics compared with reference values of Companav-2 in test#2

Fig. 15

Estimated $\varphi$, $\theta$ and $\psi$ angles through MPO and EKF of quaternions system compared with reference values of Companav-2 in test#2

Table 5 Values of components of a and N for quaternions and Euler angles dynamics in test#2

The weighting diagonal matrices of the system dynamics‚ $Q_{3 \times 3}$, and the measurement vector $R_{4 \times 4}$ and $R_{3 \times 3}$ for both the quaternion and Euler angles methods of test#2 are the same as test#1 (83). According to Figs. 14 and 15‚ compared with the EKF‚ the implementation of MPO for AHRS mode of low-cost GAINS results in a better accuracy of attitude and heading angles in the ground vehicle test.

Regarding the reference values of Companav-2 system‚ the estimation errors by both MPO and EKF along the attitude and heading angles are compared in Figs. 16 and 17‚ respectively. Furthermore‚ the statistical mean and SD of these errors are represented in Tables 6 and 7 for both the Euler and quaternion systems‚ respectively. Small range maneuvers and smooth movements of the ground vehicle can interpret the small errors in Table 6. Since the design matrices, $Q$ and $R$ of both the EKF and the MPO have been tuned for flight test#1‚ larger errors occur in quaternion method of the ground vehicle test in Table 7. A separate tuning of the design parameters for the vehicular application may decrease these errors. However, an AHRS system that uses a unique set of design parameters for all applications is preferred. In other words, through manipulating the covariance matrices of process and measurement equations‚ we may obtain closer results by both the quaternion and the Euler angles systems in Tables 6 and 7. However‚ keeping the standard parameters of estimation algorithms based on the specifications in Table 1 and the AHRS dynamics yields the optimal solutions of MPO and EKF.

Fig. 16

Estimation errors of $\varphi$, $\theta$ and $\psi$ angles through MPO and EKF of Euler angles method in test#2

Fig. 17

Estimation errors of $\varphi$, $\theta$ and $\psi$ angles through MPO and EKF of quaternion method in test#2

Table 6 Statistical mean and SD of estimation errors by Euler angles in test#2

Table 7 Statistical mean and SD of estimation errors by quaternions in test#2

Conclusion

For MEMS AHRS purpose‚ we designed a new MPO method based on the duality principle between observer and controller systems. Based on the available dual controller‚ the design process of the MPO was considerably shortened. The optimal and robust behavior of the proposed MPO adapts to the MEMS AHRS affected by unknown uncertainties of low-cost sensors. Applying the Laguerre network of orthonormal basis functions in the MPO system led to further attenuation of the uncertainty effects in the AHRS. Additionally, the propagation of computational errors due to the correlation of AHRS dynamic equations was decreased. Practical tests of the AHRS mode of a GAINS with aerial and ground vehicles were used to assess the performance of the proposed MPO in comparison with the classic EKF. During the tests‚ the AHRS sensors were affected by acceleration and angular velocity changes of the carrying vehicle. In addition to visually improved tracking along the reference trajectories of attitude and heading angles‚ the statistical SD and mean of estimation errors emphasized on the better performance of MPO with respect to the EKF. The small mean values of navigation errors at the scale of a low-cost AHRS confirmed the capability of the designed MPO method in compensation of uncertainties of MEMS sensors. Furthermore‚ the predictive structure of the MPO renders a better dealing with nonlinear dynamics of the AHRS‚ which leads to higher precisions compared to the classic EKF.