Introduction

In the analysis of global navigation satellite system (GNSS) data, atmospheric propagation effects due to the troposphere and the ionosphere must be taken into account. Tropospheric models become increasingly complex, e.g., they are based on pressure, temperature and humidity fields from numerical weather models (NWMs) (Boehm et al. 2015), while the ionospheric models are comparatively simple.

In fact, in many positioning applications there is no need for an ionospheric model; the ionospheric propagation effects are almost completely eliminated by a suitable linear combination of dual-frequency observables. However, in precise positioning applications an advanced ionospheric model is required to mitigate the remaining higher-order ionospheric errors (Hoque and Jakowski 2008). Typically, the assumption is that the electron density field is spherically symmetric. Only recently, Kashcheyev et al. (2012) used a realistic electron density field based on the NeQuick-2 model (Nava et al. 2008) to investigate higher-order ionospheric errors.

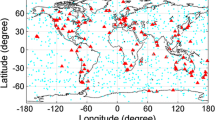
In atmospheric remote sensing applications, i.e., retrieving the total electron content (TEC) from the observables (Komjathy 1997), some ionospheric model is required as well. This ionospheric model aims to relate the slant TEC, which is hidden in the observables together with instrumental biases (Jin et al. 2012), and the vertical TEC. The ratio between the slant and vertical TEC is called the mapping function (MF). The most commonly used MF is the so-called single-layer model (SLM) MF (Schaer 1999). Again, the assumption is that the electron density field is spherically symmetric. The single thin-layer altitude of the ionosphere is either chosen to be constant or it is adjusted for a given location and time. Typically, the thin-layer altitude of the ionosphere is chosen to be 450 km. This value is reasonable for mid-latitude and day-time conditions, but it can induce significant errors elsewhere. For example, Hernandez-Pajares et al. (2005) showed that deviations from the 450 km reference value reach up to ±200 km and larger during geomagnetic storms. Therefore, instead of the constant value, Palamartchouk (2010) used the height of the electron density peak from the international reference ionosphere (IRI) model (Bilitza, 2001) for the thin-layer altitude of the ionosphere. In this case, the SLM MF depends on the time, location and elevation angle. Figure 1 shows the height of the electron density peak from the IRI model for specific station locations for the year 2012, day of year 75 at 12 UTC. The 783 stations with global coverage belong to the Tide Gauge Benchmark Monitoring Project (TIGA) network (Deng et al. 2014). The variability of the height of the electron density peak is obvious. However, the variability of the height of the electron density peak, or to be more specific the variability of the height of the electron density peak in the vicinity of the stations, indicates that an improved MF can be obtained if not only the time, location and elevation angle but also the azimuth angle is taken into account.

Fig. 1
figure 1

Height of the electron density peak (km) from the IRI model for specific station locations (Year 2012, DOY 75, 12 UTC). The 783 stations belong to the TIGA network. The height of the electron density peak corresponds to the electron density maximum of the electron density profile

Full size image

For a comprehensive overview on both the higher-order ionospheric effects and the MF, the reader is referred to Petrie et al. (2011). In their concluding remarks, they mention that in future it will become feasible to determine the electron density field at global scale and in great detail thanks to large constellations of GNSS receivers on board low earth orbit satellites and this will allow further investigations into higher-order ionospheric errors and MF errors in particular around the distinctly non-spherical equatorial anomaly. The GNSS data from low earth orbit satellites can be combined with GNSS data from ground-based stations in a multisource data assimilation approach in order to further improve the retrieved electron density field (Yue et al. 2012). By taking into account that the GNSS data are assimilated into a priori electron density fields we start our investigations with the available a priori electron density fields and will continue our investigations with the analysis electron density fields in future. The primary purpose of the present study is the development of a new MF concept.

We develop a ready-to-use MF which is based on the electron density field derived from the IRI. This station specific MF utilizes a look-up table which contains a set of ray-traced ionospheric phase advances and code delays. Therefore, the proposed MF differs from the SLM MF in several respects. At first, the MF depends on the time, location, elevation and azimuth angle. Second, the MF depends on the considered carrier frequency. In order to explain the reason behind the frequency dependency, we begin by deriving the relevant expressions for the ionospheric phase advances and code delays. In the subsequent section, we define the MF and describe the computation of ray-integrals. This is followed by a discussion on how the frequency dependency of the MF can be used to mitigate higher-order ionospheric errors, a comparison of the proposed MF and the SLM MF, and a summary.

Ionospheric phase advance and code delay

The phase and code observation equation is written as

$${\begin{aligned} l_{i} = r + T + L_{i} \\ p_{i} = r + T + P_{i} \\ \end{aligned} }$$
(1)

where r denotes the geometric distance between the station and the satellite, T denotes the tropospheric delay, L i denotes the ionospheric phase advance and P i denotes the ionospheric code delay. The index i refers to the band number of the carrier frequency. The observation equation given above does take into account atmospheric effects only. It does not take into account other effects such as instrument biases and multipath effects (Larson and Nievinski 2013; Jin et al. 2016a, 2016b; Vergados et al. 2016). The tropospheric delay T is defined as

$${T = \int {n_{\infty } {\text{d}}s_{\infty } - r} }$$
(2)

with

$${n_{\infty } = 1+ 1 0^{ - 6} N}$$
(3)

where N denotes the refractivity of the neutral atmosphere, n ∞ denotes the refractive index in the absence of the ionosphere and ds ∞ denotes the ray-path element in the absence of the ionosphere. The ray-path follows from Fermat’s principle. The application of the principle of least time at this point must be understood as a convention. This convention is useful insofar as a suitable linear combination of dual-frequency observables allows one to treat the combined observable as if the ionosphere is absent. For details see also section about higher-order ionospheric effects below. The atmospheric induced excess phase δl i and the atmospheric induced excess range δp i read as (Wee and Kuo 2015)

$${\begin{aligned} \delta l_{i} = \int {n_{i} {\text{d}}s_{i} - r} \\ \delta p_{i} = \int {g_{i} {\text{d}}s_{i} - r} \\ \end{aligned} }$$
(4)

with

$${\begin{aligned} n_{i} = 1+ 1 0^{ - 6} N - \frac{C}{{f_{i}^{ 2} }}Ne \\ g_{i} = 1+ 1 0^{ - 6} N + \frac{C}{{f_{i}^{ 2} }}Ne \\ \end{aligned} }$$
(5)

where n i denotes the refractive index experienced by the phase of the signal, g i denotes the refractive index experienced by the group of the signal, ds i denotes the ray-path element, f i denotes the carrier frequency, Ne denotes the electron density, and C denotes a constant. Note that higher-order terms, i.e., the second- and third-order term (Hoque and Jakowski 2008), in the refractive index for the phase and the group of the signal are neglected. Again, the ray-path follows from Fermat’s principle. However, the application of the principle of least time at this point is a necessity and not a convention. Note that

$${\begin{aligned} l_{i} = r + \delta l_{i} \\ p_{i} = r + \delta p_{i} \\ \end{aligned} }$$
(6)

and therefore

$${\begin{aligned} L_{i} = \delta l_{i} - T \\ P_{i} = \delta p_{i} - T \\ \end{aligned} }$$
(7)

The ionospheric phase advance and code delay explicitly read as

$${\begin{aligned} L_{i} = \int {\left( { 1+ 1 0^{ - 6} N - \frac{C}{{f_{i}^{ 2} }}Ne} \right)} {\text{d}}s_{i} - \int {\left( { 1+ 1 0^{ - 6} N} \right){\text{d}}s_{\infty } } \\ P_{i} = \int {\left( { 1+ 1 0^{ - 6} N + \frac{C}{{f_{i}^{ 2} }}Ne} \right)} {\text{d}}s_{i} - \int {\left( { 1+ 1 0^{ - 6} N} \right){\text{d}}s_{\infty } } \\ \end{aligned} }$$
(8)

or

$${\begin{aligned} L_{i} = \frac{ - C}{{f_{i}^{ 2} }}\int {Ne\,{\text{d}}s_{i} } + \int {\left( { 1+ 1 0^{ - 6} N} \right)} {\text{d}}s_{i} - \int {\left( { 1+ 1 0^{ - 6} N} \right)} {\text{d}}s_{\infty } \\ P_{i} = \frac{C}{{f_{i}^{ 2} }}\int {Ne\,{\text{d}}s_{i} } + \int {\left( { 1+ 1 0^{ - 6} N} \right)} {\text{d}}s_{i} - \int {\left( { 1+ 1 0^{ - 6} N} \right)} {\text{d}}s_{\infty } \\ \end{aligned} }$$
(9)

We call the difference between the second and third integral in (9) the bending term. Note that the bending term is additive in the ionospheric code delay expression whereas it is subtractive in the ionospheric phase advance expression. The proposed MF will be based on these expressions for the ionospheric phase advance and the code delay.

Before we define the MF, it is convenient to derive simplified expressions for the ionospheric phase advance and code delay and introduce a simple MF. In order to do so, two simplifying assumptions are necessary. At first, let us assume that the ionospheric phase advance and code delay are not sensitive to the refractivity of the neutral atmosphere. Specifically, in the absence of the troposphere n ∞  = 1 which implies ds ∞  = dr and therefore

$${\begin{aligned} L_{i} = \frac{ - C}{{f_{i}^{ 2} }}\int {Ne\,{\text{d}}\sigma_{i} } + \int {{\text{d}}\sigma_{i} - r} \\ P_{i} = \frac{C}{{f_{i}^{ 2} }}\int {Ne\,{\text{d}}\sigma_{i} } + \int {{\text{d}}\sigma_{i} - r} \\ \end{aligned} }$$
(10)

where dσ i denotes the ray-path element in the absence of the troposphere. Still, due to the bending term the difference between the ionospheric phase advance and code delay is not solely an opposite sign. Second, let us assume that ray-bending is negligible, dσ i  = dr, then

$${\begin{aligned} L_{i} = \frac{ - C}{{f_{i}^{ 2} }}\int {Ne{\text{d}}r} \\ P_{i} = \frac{C}{{f_{i}^{ 2} }}\int {Ne{\text{d}}r} \\ \end{aligned} }$$
(11)

Next, we define the line of sight (LoS) slant total electron content STEC through

$${{\text{STEC}} = \int {Ne\,{\text{d}}r} }$$
(12)

and the Vertical Total Electron Content VTEC through

$${{\text{VTEC}} = \int {Ne\,{\text{d}}h} }$$
(13)

where h denotes the altitude. The ionospheric phase advance and code delay read as

$${\begin{aligned} L_{i} = - \frac{C}{{f_{i}^{ 2} }} \cdot M \cdot {\text{VTEC}} \\ P_{i} = \frac{C}{{f_{i}^{ 2} }} \cdot M \cdot {\text{VTEC}} \\ \end{aligned} }$$
(14)

where the mapping function M is defined as

$${M = \frac{\text{STEC}}{\text{VTEC}}}$$
(15)

The VTEC can be defined at an arbitrary point. The STEC remains unchanged. Once this point is specified, the MF is defined for this specific point as well. Typically, the MF is defined for the point where the LoS path reaches a certain altitude. A simple MF is the SLM MF which is based on the thin-shell approximation of the ionosphere (Schaer 1999). The SLM MF reads as

$${M\left( z \right) = \frac{ 1}{{{ \cos }\left( {z^{{\prime }} } \right)}}}$$
(16)

where z denotes the zenith angle and

$${{ \sin }\left( {z^{{\prime }} } \right) = \frac{R}{R + H} \cdot { \sin }\left( z \right)}$$
(17)

with H = 450 km and R = 6371 km. The point where the LoS path reaches the altitude 450 km is called the Ionospheric Pierce Point (IPP). The projection of the IPP on surface of the earth is called the sub-IPP. The proposed MF will be based on the electron density field of the ionosphere. Still, we will call the point where the LoS path reaches the altitude 450 km the IPP and we will call the projection of the IPP on earth’s surface the sub-IPP.

Ionospheric mapping function

We make use of the expressions for the ionospheric phase advance and the code delay which do not rely on the two aforementioned simplifying assumptions. Hence, for some station location and time, we use (9) and define the MF as follows

$${\begin{aligned} M_{L,i} (z,a) = - \frac{{f_{i}^{ 2} }}{C}\frac{{L_{i} (z,a)}}{{{\text{VTEC}}(z,a)}} \\ M_{P,i} (z,a) = \frac{{f_{i}^{ 2} }}{C}\frac{{P_{i} (z,a)}}{{{\text{VTEC}}(z,a)}} \\ \end{aligned} }$$
(18)

Due to the ray-bending, the MF differs for the ionospheric phase advance and the code delay. In addition, since the ray-bending depends on the frequency, the MF depends on the frequency as well. The MF depends on the zenith angle z and the azimuth angle a because the ionospheric phase advance and code delay, which stem from the electron density field, depend on the zenith angle and azimuth angle. Note that the VTEC depends on the zenith angle and azimuth angle as well because the VTEC is defined at the point where the LoS path reaches a certain altitude. The MF is consistent with the phase and code observation equation since

$${\begin{aligned} l_{i} (z,a) = r(z,a) + T(z,a) - \frac{C}{{f_{i}^{ 2} }} \cdot M_{L,i} (z,a) \cdot {\text{VTEC}}(z,a) \\ p_{i} (z,a) = r(z,a) + T(z,a) + \frac{C}{{f_{i}^{ 2} }} \cdot M_{P,i} (z,a) \cdot {\text{VTEC}}(z,a) \\ \end{aligned} }$$
(19)

The ionospheric model together with a tropospheric model provides a complete atmospheric model.

Ray-integral computation

In order to determine the ionospheric phase advances and code delays, the ray-integrals must be computed. The ray-paths follow from Fermat’s principle. Let n denote the refractive index field and let [x,y(x)] denote the coordinates of the ray-path. The Euler–Lagrange equation can be manipulated to yield the following differential equation for the ray-path

$${\frac{{{\text{d}}^{ 2} y}}{{{\text{d}}x^{2} }} = \frac{ 1}{n}\left[ {\frac{\partial n}{\partial y} - \frac{\partial n}{\partial x}\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right]\left[ { 1+ \left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)^{ 2} } \right]}$$
(20)

Given the position of the satellite [x t , y t ] and the position of the station [x s , y s ], this represents a nonlinear two-point boundary value problem (BVP). We do take into account the flattening of the earth by using an osculating sphere with the Gaussian curvature radius, but as already indicated by the equation above, we ignore out-of-plane bending. In essence, we do not allow the ray-path to leave the plane of constant azimuth. This approximation is justified if we consider the troposphere only (n = n ∞ ). To what extend this approximation is justified if the ionosphere is added on top of the troposphere (n = n i ) remains to be analyzed. The nonlinear two-point BVP is solved by a finite difference scheme (Zus et al. 2014). This finite difference scheme was originally developed for the troposphere and modified to include the ionosphere. Once the ray-paths are computed, the ray-integrals are computed by numerical integration. The ionospheric phase advance and code delay are computed with high speed and millimeter-level precision for any elevation angle down to 3°. This precision estimate refers to the numerical accuracy with which the ray-integrals are computed (Zus et al. 2014). This precision estimate does not refer to the absolute accuracy of the computed ray-integrals.

The absolute accuracy of the computed ionospheric phase advance and code delay depends mainly on the accuracy of the underlying electron density field. In this study, the electron density field stems from the IRI model. The 2012 version of the IRI is used in this study. The FORTRAN code is available from http://iri.gsfc.nasa.gov/. We use the default settings and extract a grid every 3 h with a horizontal resolution of 2° by 2° on 97 equidistant altitude levels between 80 and 2000 km. Below and above the IRI model, the electron density is obtained by log-linear extrapolation. The IRI is an empirical model, the validity of which has been proven for different conditions using various TEC measurements. For example, Ping et al. (2004) report that the statistical difference between Jason-1 measurements and the IRI model is about 1 ± 10 TEC units (TECU). For the present study, this deviation between measured and modeled VTEC values is not regarded as problematic for two reasons. At first, we are mainly interested in the MF and therefore we expect that common errors in the computed ionospheric phase advance, code delay and the VTEC cancel. Second, we will solely compare the MF, which is based on an electron density field, with the SLM MF. The ionospheric phase advance and code delay and hence the MF is not very sensitive to the underlying refractivity field of the neutral atmosphere. We may choose a simple refractivity field, and none of the main features of the MF discussed in this study are seriously affected. Nevertheless, we decided to choose the refractivity field from a NWM. The rationale behind this choice is that the tropospheric delays, which are computed in parallel, are used to generate our tropospheric model. The tropospheric model consists of hydrostatic and non-hydrostatic zenith delays, the hydrostatic and non-hydrostatic MF (Zus et al. 2015a) and the horizontal delay gradients (Zus et al. 2015b). We use Global Forecast System (GFS) data of the National Centers for Environmental Prediction (NCEP) (www.ncep.noaa.gov) provided with a horizontal resolution of 1° by 1° on 26 pressure levels between 10 and 1000 hPa. In post-processing mode, we use the GFS analysis whereas in real-time mode we use GFS short-range forecasts.

Implementation

We generate station specific MFs. The stations belong to the TIGA network. For each station, 144 ratios of the ionospheric phase advance and the VTEC, and 144 ratios of the ionospheric code delay and the VTEC, i.e., mapping factors, are computed; the elevation angles are 3°, 5°, 7°, 10°, 15°, 20°, 25°, 30°, 40°, 50°, 70°, 90°, and the azimuth angles are 0°, 30°, 60°, 90°, 120°, 150°, 180°, 210°, 240°, 270°, 300°, 330°. The orbital altitude is chosen to be 20,200 km. The VTEC is computed at the point where the LoS path reaches an altitude of 450 km. We note again that we will call this point the IPP and we will call the projection of the IPP on earth’s surface the sub-IPP. We consider three GNSS carrier frequencies f 1 = 1575.42 MHz, f 2 = 1227.60 MHz and f 5 = 1176.45 MHz. For any elevation and azimuth angle pair, the six mapping factors plus the VTEC are computed and used as a look-up table. The MF must be available for any elevation and azimuth angle. The following easy-to-use algorithm is proposed for this purpose. Given some azimuth angle a and zenith angle z, we search for the nearest azimuth angle a n , zenith angle z n , mapping factor m n , and VTEC value VTEC n in the look-up table and then determine the required mapping factor m through

$${m = \frac{ 1}{{\sqrt { 1- b^{ 2} } }}}$$
(21)

where

$${b = \frac{{{ \sin }\left( z \right)}}{{{ \sin }\left( {z_{n} } \right)}}\sqrt {\frac{{m_{n}^{ 2} - 1}}{{m_{n}^{ 2} }}} }$$
(22)

This expression follows from the SLM MF where H is tuned for the specific mapping factor m n . In other words, the proposed MF differs from the SLM MF in that H is not a constant but depends on time, location, elevation and azimuth angle. In fact, H depends on the frequency as well. The MF is valid at the sub-IPP 450 km only. However, it is worth mentioning that the look-up table can be used to approximate the MF at a different sub-IPP.

Results and discussion

We focus on one epoch corresponding to moderate ionospheric conditions: year 2012, day of year 75 at 12 UTC. The MFs and the VTEC values are computed with the method described in the previous section. Figure 2 shows the scatter plot of the VTEC at the sub-IPP 450 km. The elevation angle is 3°, and the azimuth angle is 180°. Note that the VTEC at the sub-IPP is plotted at the location of the station. Such a scatter plot of the VTEC at the sub-IPP strongly depends on the elevation and azimuth angle. The typical features of the ionosphere are present; high and low VTEC values at day and night time, respectively, and high VTEC values around the ‘apparent’ geomagnetic equator.

Fig. 2
figure 2

Scatter plot showing the VTEC [TECU] at the sub-IPP 450 km. The elevation angle is 3°, and the azimuth angle is 180° (Year 2012, DOY 75, 12 UTC). The VTEC at the sub-IPP is plotted at the location of the station

Full size image

Higher-order ionospheric effects

The MF depends on the time, location, elevation and azimuth angle. In addition, the MF depends on the frequency. This frequency dependency of the MF can be readily used to estimate the higher-order ionospheric effect due to ray-bending. The higher-order ionospheric effects due to higher-order terms in the refractive index cannot be examined. For example, the standard linear combination of dual-frequency phase (code) observables for the frequencies f 1 and f 2 read as

$${\begin{aligned} l_{\text{c}} = \frac{{f_{ 1}^{ 2} }}{{f_{ 1}^{ 2} - f_{ 2}^{ 2} }} \cdot l_{ 1} - \frac{{f_{ 2}^{ 2} }}{{f_{ 1}^{ 2} - f_{ 2}^{ 2} }} \cdot l_{ 2} \\ p_{\text{c}} = \frac{{f_{ 1}^{ 2} }}{{f_{ 1}^{ 2} - f_{ 2}^{ 2} }} \cdot p_{ 1} - \frac{{f_{ 2}^{ 2} }}{{f_{ 1}^{ 2} - f_{ 2}^{ 2} }} \cdot p_{ 2} \\ \end{aligned} }$$
(23)

This standard linear combination of dual-frequency phase and code observables does not remove the higher-order ionospheric effect due to the ray-bending. In terms of the MF and VTEC, the standard linear combination of dual-frequency phase and code observables read as

$${\begin{aligned} l_{\text{c}} = r + T - \frac{{M_{L1} - M_{L2} }}{{f_{ 1}^{ 2} - f_{ 2}^{ 2} }} \cdot C \cdot {\text{VTEC}} \\ p_{\text{c}} = r + T + \frac{{M_{P1} - M_{P2} }}{{f_{ 1}^{ 2} - f_{ 2}^{ 2} }} \cdot C \cdot {\text{VTEC}} \\ \end{aligned} }$$
(24)

Thus, the higher-order ionospheric residual, which is the last term in the expression above, is related to the frequency dependency of the MF. In terms of the MF and VTEC, the ionospheric-free combination of dual-frequency phase and code observables read as

$${\begin{aligned} l_{\text{f}} = l_{\text{c}} + \frac{{M_{L1} - M_{L2} }}{{f_{ 1}^{ 2} - f_{ 2}^{ 2} }} \cdot C \cdot {\text{VTEC}} \\ p_{\text{f}} = p_{\text{c}} - \frac{{M_{P1} - M_{P2} }}{{f_{ 1}^{ 2} - f_{ 2}^{ 2} }} \cdot C \cdot {\text{VTEC}} \\ \end{aligned} }$$
(25)

This expression can be used to mitigate the higher-order ionospheric effect due to ray-bending. In such application, the required VTEC values can be taken from the Global Ionosphere Map (GIM) estimates (Mannucci et al. 1998).

Figures 3 and 4 show the scatter plot of the higher-order ionospheric residual for the phase and the code, respectively. The elevation angle is 3°, and the azimuth angle is 180°. At first, we note that the residual for the phase and the code has opposite sign. Second, we note that the magnitude of the residual for the phase is smaller than the magnitude of the residual for the code. This is in good agreement with Hoque and Jakowski (2008) and can be traced back to the bending term which is additive in the ionospheric code delay expression whereas it is subtractive in the ionospheric phase advance expression. We want to emphasize again that the higher-order ionospheric effects due to higher-order terms in the refractive index, which are linked to earth’s magnetic field, can yet not be examined.

Fig. 3
figure 3

Scatter plot showing the residual (mm) of the l 1 and l 2 linear combination. This higher-order ionospheric effect is due to the frequency dependency of ray-paths. The elevation angle is 3°, and the azimuth angle is 180° (Year 2012, DOY 75, 12 UTC)

Full size image
Fig. 4
figure 4

Scatter plot showing the residual (mm) of the p 1 and p 2 linear combination. This higher-order ionospheric effect is due to the frequency dependency of ray-paths. The elevation angle is 3°, and the azimuth angle is 180° (Year 2012, DOY 75, 12 UTC)

Full size image

MF comparison

In the following discussion, we consider the frequency f 1. We also restrict the discussion to the ionospheric phase advance because similar conclusions can be drawn for the ionospheric code delay. Figure 5 shows the error of the VTEC at the sub-IPP 450 km due to the error of the SLM MF. This is defined through

Fig. 5
figure 5

Scatter plot showing the error of the VTEC [TECU] at the sub-IPP 450 km due to the error of the SLM MF. The elevation angle is 3°, and the azimuth angle is 180° (Year 2012, DOY 75, 12 UTC). For this specific elevation and azimuth angle, the global map shows the deviation between the SLM MF and the MF measured in terms of the VTEC at the sub-IPP. The VTEC deviation at the sub-IPP is plotted at the location of the station

Full size image
$${\Delta {\text{VTEC}} = - \frac{{f^{ 2} }}{C}\frac{L}{M} - {\text{VTEC}}}$$
(26)

In essence we compute the ionospheric phase advance, with the elevation angle being 3° and the azimuth angle 180°, divide the ionospheric phase advance by the SLM MF, and then subtract the computed VTEC at the sub-IPP. Note that for the elevation angle 3° and the azimuth angle 180° the MF is error free because the MF is tuned for this specific elevation and azimuth angle. Therefore, Fig. 5 represents the deviation between the SLM MF and the MF. The deviation is seen largest around the ‘apparent’ geomagnetic equator. This can be explained by the fact that, in addition to a number of other simplifying assumptions, the SLM MF is based on a spherically symmetric electron density field while the MF is based on the asymmetric electron density field. The deviations between the SLM MF and the MF reach about ± 10 TECU. For the considered frequency f 1, a deviation of 1 TECU translates into a range deviation of about 16 cm.

Next we examine the elevation and azimuth angle dependency of the SLM MF and the MF. For each station, 144 ionospheric phase advances and VTEC values at the sub-IPP 450 km are computed; the elevation angles are 4°, 6°, 8°, 12°, 17°, 22°, 27°, 35°, 45°, 60°, 80°, 90°, and the azimuth angles are 15°, 45°, 75°, 105°, 135°, 165°, 195°, 225°, 255°, 285°, 315°, 345°. The rationale behind this set of elevation and azimuth angles is that both the SLM MF and the MF are not error free. This specific choice of elevation and azimuth angles is used to estimate the upper bound for the error of the MF.

The scatter plot in Fig. 6 shows the error of the VTEC at the sub-IPP 450 km that is due to the error of the SLM MF as a function of the elevation angle. The scatter plot corresponds to all TIGA stations, and all elevation and azimuth angles listed above. As to be expected, the errors show a strong elevation angle dependency; the lower the elevation angles the larger the errors. At the lowest elevation angle, the errors exceed ± 10 TECU. The blue line, which represents the mean deviation as a function of the elevation angle, indicates that there is no bias close to the zenith but a bias of several TECU for the lowest elevation angle. Figure 1 provides a rough explanation for the random and mean deviation. The random deviation is related to the variability of the height of the electron density peak, and the mean deviation is related to the average height of the electron density peak. The average height of the electron density peak must not be directly compared to the single thin-layer altitude of 450 km. The reason is that the height of the electron density peak corresponds to the electron density maximum of the electron density profile. For example, provided that the height of the electron density peak is 350 km, then, depending on the scale height of the electron density profile and the elevation angle, the corresponding thin-layer altitude must be chosen somewhere in between 400 and 450 km (Schaer, 1999). The average height of the electron density peak in Fig. 1 is 300 km. Therefore, we expect that the corresponding thin-layer altitude must be chosen somewhere in between 350 and 400 km. The scatter plot in Fig. 7 shows the result when the single thin-layer altitude of 450 km is replaced by the single thin-layer altitude of 400 km in the SLM MF. As expected, the mean deviation is reduced by the proper choice for the single thin-layer altitude. Conversely, if the average height of the electron density peak in the IRI does not match the true average height of the electron density peak, then the MF which is based on the IRI will be biased. In fact, the model for the electron density peak height in the IRI is an area of active research. For example, with the 2016 version of IRI, two new options for the electron density peak heights are available which are based on measurements by ionosondes (Altadill et al., 2013) and radio occultation (Shubin, 2015), respectively.

Fig. 6
figure 6

Error of the VTEC [TECU] at the sub-IPP 450 km due to the error of the SLM MF as a function of the elevation angle (Year 2012, DOY 75, 12 UTC). The blue line indicates the mean deviation as a function of the elevation angle

Full size image
Fig. 7
figure 7

Error of the VTEC [TECU] at the sub-IPP 450 km due to the error of the SLM MF as a function of the elevation angle (Year 2012, DOY 75, 12 UTC). The blue line indicates the mean deviation as a function of the elevation angle. The single thin-layer altitude of 450 km is replaced by the altitude of 400 km

Full size image

For comparison, the scatter plot in Fig. 8 shows the error of the VTEC at the sub-IPP 450 km due to the error of the MF as a function of the elevation angle. The scatter plot corresponds to all TIGA stations and all elevation and azimuth angles listed above. Since the MF is tuned for a different set of elevation and azimuth angles, the MF is not error free. Again, the errors show a strong elevation angle dependency but at the lowest elevation angle the errors are well below ±10 TECU. The blue line, which represents the mean deviation as a function of the elevation angle, indicates that there is no bias for any elevation angle.

Fig. 8
figure 8

Error of the VTEC [TECU] at the sub-IPP 450 km due to the error of the MF as a function of the elevation angle (Year 2012, DOY 75, 12 UTC). The blue line indicates the mean deviation as a function of the elevation angle

Full size image

The comparison in Fig. 9 shows the Root-Mean-Square Error (RMSE) of the VTEC at the sub-IPP 450 km for the SLM MF (black line) and the MF (red line) as a function of the elevation angle. The MF outperforms the SLM MF. For example, the RMSE for the SLM MF exceeds 1 TECU already at an elevation angle of 20° while the RMSE for the MF is below 1 TECU for any elevation angle. A final remark concerns the RMSE of the MF. If the number of azimuth and elevation angle pairs in the look-up table increases, the RMSE decreases. Conversely, if the number of azimuth and elevation angle pairs in the look-up table decreases, the RMSE increases.

Fig. 9
figure 9

RMSE of the VTEC [TECU] at the sub-IPP 450 km due to the error of the SLM MF (black line) and the MF (red line) as a function of the elevation angle (Year 2012, DOY 75, 12 UTC)

Full size image

So far we considered stations with good global coverage but a single epoch. The ionosphere is highly variable in both space and time. The maps from the Real-Time IRI (Galkin et al. 2012) available at http://giro.uml.edu/IRTAM/illustrate this. From the perspective of a station, the ionosphere strongly depends on the time of day while the day-to-day variability is comparable weak. An example is given below. Clearly, the seasonal variability and the solar cycle must not be ignored. In essence, scatter plots such as those in Figs. 1, 2, 3, 4, 5 are substantially different for the times 0, 3, 6, 9, 12, 15, 18 and 21 UTC. However, scatter plots such as those in Figs. 6, 7, 8, 9 and the derived statistics are not substantially different for the different hours due to the fact that the data stem from stations with good global coverage. In order to gain some insight into the time dependency of the MF, we pick out a single station. The station is located in Potsdam (Germany), and we focus on three months, day of year 1–91 of 2012. Figures 10 and 11 show the time dependency of the VTEC at the sub-IPP 450 km (top panel), the MF (middle panel) and the higher-order ionospheric residual for the phase (lower panel) for the azimuth angle 0° and 180°, respectively. The elevation angle is 3°. For all considered quantities, the plots show a strong diurnal cycle. The day-to-day variability is comparable weak. The comparison of Figs. 10 and 11 also reveals that the considered quantities are significantly different for different azimuth angles. For comparison, the red line in the middle panels shows the SLM MF. In fact, for the considered station, time period and the azimuth angle 180° there is almost no bias between the SLM MF and the MF. However, for the considered station, the time period and the azimuth angle 0° there is a negative bias between the SLM MF and the MF. Again, Fig. 1 provides a rough explanation for the azimuth dependent deviation between the SLM MF and the MF. For the considered elevation angle of 3°, the height of the electron density peak at the station is not relevant. Instead, for azimuth angles 0° and 180° the electron density peak heights to the north of the station and the electron density peak heights to the south of the station are relevant. For the considered station, a station at mid-latitudes, the electron density peak heights to the north of the station are smaller than the electron density peak heights to the south of the station. Therefore, the corresponding thin-layer altitude to the north of the station is smaller than the corresponding thin-layer altitude to the south of the station. Hence, the MF for an azimuth angle of 0° is larger than the MF for an azimuth angle of 180°.

Fig. 10
figure 10

VTEC [TECU] at the sub-IPP 450 km (top panel), MF (middle panel) and the higher-order ionospheric residual for the phase (mm) (lower panel) as a function of the time (Year 2012, DOY 1-91) for the station Potsdam (Germany). The elevation angle is 3°, and the azimuth angle is 0°. The red line in the middle panel shows the SLM MF

Full size image
Fig. 11
figure 11

VTEC [TECU] at the sub-IPP 450 km (top panel), MF (middle panel) and the higher-order ionospheric residual for the phase (mm) (lower panel) as a function of the time (Year 2012, DOY 1-91) for the station Potsdam (Germany). The elevation angle is 3°, and the azimuth angle is 180°. The red line in the middle panel shows the SLM MF

Full size image

Practical considerations

The current choice of azimuth and elevation angle pairs is a tradeoff between the accuracy and the data volume. The computational time to generate the station specific MFs is not an issue; for one epoch, the look-up table for the TIGA stations is generated in less than 5 min. This computational time is based on a FORTRAN implementation, the Intel FORTRAN compiler and an ordinary PC using a single core. In an open multiprocessing environment, the computational time scales linearly with the number of cores. For example, if we generate MFs for a global grid with a horizontal resolution of 2° by 2°, the look-up table for this grid is generated in about 25 min utilizing four cores. The data volume of this look-up table is about eight times the data volume of the IRI electron density field. Hence, it is impractical from the perspective of the data volume to handle this task. Still, the grid specific MF can be very useful to investigate globally and in great detail the higher-order ionospheric effect due to ray-bending for example. Figures 12 and 13 show the global map of the higher-order ionospheric residual for the phase for azimuth angle 180° and 0°, respectively. The elevation angle is 3°. The strong azimuth angle dependency of the higher-order ionospheric residual for the phase around the equatorial anomaly is obvious. We conclude that if the purpose of an ionospheric model is to mitigate the higher-order ionospheric effect due to ray-bending then this ionospheric model must take into account its strong azimuth angle dependency. This is consistent with Kashcheyev et al. (2012) who investigated two meridian cross sections. The global maps can also be compared to those maps recently published by Hernández-Pajares et al. (2014). By taking into account the different settings, i.e., medium solar activity and elevation angle 3° versus high solar activity and elevation angle 10°, an overall good agreement can be stated.

Fig. 12
figure 12

Global map showing the residual (mm) of the l 1 and l 2 linear combination. This higher-order ionospheric effect is due to the frequency dependency of ray-paths. The elevation angle is 3°, and the azimuth angle is 180° (Year 2012, DOY 75,12 UTC)

Full size image
Fig. 13
figure 13

Global map showing the residual (mm) of the l 1 and l 2 linear combination. This higher-order ionospheric effect is due to the frequency dependency of ray-paths. The elevation angle is 3°, and the azimuth angle is 0° (Year 2012, DOY 75,12 UTC)

Full size image

In order to show that the MF concept can also be used to investigate higher-order ionospheric effects due to the higher-order terms in the refractive index, we consider the following refractive index for the phase and the group of the signal

$${\begin{aligned} \tilde{n}_{i} = 1 + 10^{ - 6} N - \frac{C}{{f_{i}^{ 2} }}Ne - \frac{Q}{{2f_{i}^{ 3} }}Ne \cdot B\cos (\varphi ) \\ \tilde{g}_{i} = 1 + 10^{ - 6} N + \frac{C}{{f_{i}^{ 2} }}Ne + \frac{Q}{{f_{i}^{ 3} }}Ne \cdot B\cos (\varphi ) \\ \end{aligned} }$$
(27)

Here ϕ is the angle between earth’s magnetic field vector B and the wave normal vector and Q denotes a constant (Moore and Morton 2011). For the considered carrier frequencies, the wave normal vector can be approximated by the ray-propagation direction (Moore and Morton 2011). Then the ionospheric phase advance and code delay explicitly read as

$${\begin{aligned} L_{i} = \int {\left( { 1+ 1 0^{ - 6} N - \frac{C}{{f_{i}^{ 2} }}Ne - \frac{Q}{{2f_{i}^{ 3} }}Ne \cdot B\cos (\varphi )} \right)} d\eta_{i} - \int {\left( { 1+ 1 0^{ - 6} N} \right){\text{d}}s_{\infty } } \\ P_{i} = \int {\left( { 1+ 1 0^{ - 6} N + \frac{C}{{f_{i}^{ 2} }}Ne + \frac{Q}{{f_{i}^{ 3} }}Ne \cdot B\cos (\varphi )} \right)} d\eta_{i} - \int {\left( { 1+ 1 0^{ - 6} N} \right){\text{d}}s_{\infty } } \\ \end{aligned} }$$
(28)

where dη i denotes the ray-path element. The ray-path follows from Fermat’s principle. Again, we do not allow the ray-path to leave the plane of constant azimuth. The Euler–Lagrange equation can be manipulated to yield the following differential equation for the ray-path

$${\frac{{{\text{d}}^{ 2} y}}{{{\text{d}}x^{2} }} = \frac{ 1}{{n_{i} }}\left[ {\frac{{\partial n_{i} }}{\partial y} - \frac{{\partial n_{i} }}{\partial x}\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right]\left[ { 1+ \left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)^{ 2} } \right] + \frac{Q}{{2f_{i}^{ 3} n_{i} }}}\left[ {\frac{{\partial \left( {Ne \cdot B_{x} } \right)}}{\partial y} - \frac{{\partial \left( {Ne \cdot B_{y} } \right)}}{\partial x}} \right]\left[ {1 + \left( {\frac{{{\text{d}}y}}{{{\text{d}}x}}} \right)^{2} } \right]^{3/2}$$
(29)

where B x and B y denote the x- and y-coordinate of the projection of the earth’s magnetic field vector into the plane of constant azimuth. From this equation, we deduce that the curvature term due to earth’s magnetic field is negligible small and thus we ignore it. In other words, the ray-paths are not altered by including earth's magnetic field. The ray-integrals are altered by including earth’s magnetic field. In our calculations, the magnetic field stems from the International Geomagnetic Reference Field (IGRF) (Matteo and Morton 2011). Once the ray-integrals are computed, the MF is defined according to (18). The MF is consistent with the phase and code observation Eq. (19), and the expression for the higher-order ionospheric residual (24) remains unchanged. For example, Figs. 14 and 15 show the global map of the higher-order ionospheric residual for the phase for the azimuth angle 180° and 0°, respectively. The elevation angle is 3°. The global maps show the composite of both effects, the higher-order ionospheric effect due to the ray-bending and the higher-order ionospheric effect due to the higher-order term in the refractive index and are therefore different from the global maps shown in Figs. 12 and 13.

Fig. 14
figure 14

Global map showing the residual (mm) of the l 1 and l 2 linear combination. The elevation angle is 3°, and the azimuth angle is 180° (Year 2012, DOY 75, 12 UTC)

Full size image
Fig. 15
figure 15

Global map showing the residual (mm) of the l 1 and l 2 linear combination. The elevation angle is 3°, and the azimuth angle is 0° (Year 2012, DOY 75, 12 UTC)

Full size image

Finally, we show how the higher-order ionospheric corrections leak into estimated station coordinates and tropospheric parameters in epoch-wise precise point positioning. We utilize the linearized observation equation

$${{\frac{{M_{L1} (z,a) - M_{L2} (z,a)}}{{f_{ 1}^{ 2} - f_{ 2}^{ 2} }}C \cdot {\text{VTEC}}(z,a) = }} - \varvec{u}(z,a){\text{d}}\varvec{X} + m_{\text{w}} (z){\text{d}}Z + m_{\text{g}} (z)\left[ {{\text{d}}N\cos (a) + {\text{d}}E\sin (a)} \right]$$
(30)

and estimate by a least-square fit the station coordinate residual dX, the tropospheric north gradient residual dN, the tropospheric east gradient residual dE and the tropospheric zenith delay residual dZ. Here u denotes the tangent unit vector of the station-satellite link, m w denotes the non-hydrostatic MF and m g denotes the tropospheric gradient MF. The standard zenith angle-dependent weighting 1/cos(z) is applied in the least-square fit. Station coordinates correspond to the TIGA network. For any station, the elevation angles are 3°, 5°, 7°, 10°, 15°, 20°, 30°, 50°, 70°, 90° and the spacing in azimuth is 30°. The scatter plot in Fig. 16 shows the residuals in the positioning and tropospheric parameter domain. The results agree qualitatively and quantitatively with previous studies (Kedar et al. 2003), i.e., the application of higher-order ionospheric corrections in precise point positioning leads to a southward shift of the stations. The previous studies did not pay attention to the tropospheric gradients. We predict a significant effect on the tropospheric gradients, in particular on the tropospheric north gradient component. The effect, which is significant insofar as the root-mean-square deviation between GNSS and NWM tropospheric gradients is typically about 0.5 mm (Li et al. 2015), can be explained by the strong correlation of the horizontal station position and the tropospheric gradient components. The detailed analysis of this effect deserves a future study. For the present study, the important conclusion is that the MF concept can be used to mitigate all higher-order ionospheric effects.

Fig. 16
figure 16

Scatter plots showing the station coordinate residuals (mm) (left panels) and the tropospheric parameter residuals (mm) (right panels) due to the higher-order ionospheric corrections (Year 2012, DOY 75, 12 UTC). The station east, north and up component residual is shown in the top, middle and bottom panel, respectively. The tropospheric east gradient, north gradient and zenith delay residual is shown in the top, middle and bottom panel, respectively

Full size image

Conclusion

We developed a MF which is based on an electron density field. This MF depends on the time, location, elevation and azimuth angle. In addition, the ray-bending effects are taken into account which means that the MF is different for different frequencies.

In a practical application, the frequency dependency of the MF can be readily used to mitigate the higher-order ionospheric effects. We developed an expression for this purpose. In such application, the required VTEC values can be taken from the GIM estimates. This brings us to another application of the MF the generation of the GIM estimates. In this study, we only compare the SLM MF with the proposed MF. From this comparison, we expect to find differences in the estimated VTEC of up to ± 10 TECU under moderate ionospheric conditions. We expect to find such significant differences around the equatorial anomaly when low elevation observations are included in the analysis. The primary purpose of this study is the development of a new MF concept. The validation of such MF using independent data, e.g., ionosonde and radio occultation data, is necessary and will be subject to a future study.

We generate the MF look-up table for the TIGA stations in less than five minutes on an ordinary PC using a single core. The ionospheric model and the tropospheric model for the TIGA stations are available with no latency. It takes about 25 min utilizing four cores to generate the MF look-up table for a global grid with a horizontal resolution of say 2° by 2°. While from the perspective of computing time this is not regarded as impractical, from the perspective of the data volume to handle this is impractical. A suitable parameterization in order to reduce the data volume in order to ease the access is under development.