Introduction

Tropospheric mapping functions (MFs) are known to be an important error source for precise positioning with the Global Navigation Satellite System (GNSS) (Vey et al. 2006). The most commonly used MFs to date include the Niell mapping function (NMF) (Niell 1996), the Global mapping function (GMF) (Boehm et al. 2006a), and its successor the so-called GPT2 (Lagler et al. 2013). The drawback of these functions is that they are based on climatology, and therefore, they are limited in their capability to predict short-term and anomalistic atmosphere behavior. In contrast, the numerical weather models (NWM) capture the short-term variability of the atmosphere and thus are considered a valuable atmospheric data source for MFs (Niell 2001). To date, the most accurate MF is the Vienna mapping function 1 (VMF1) (Tesmer et al. 2007). Its excellent performance can be explained by the fact that it is based on an accurate functional formulation and an accurate underlying atmospheric data source, namely the operational analysis from the Integrated Forecast System of the European Centre of Medium-range Weather Forecast (Boehm et al. 2006b). The VMF1 and the routines to generate a MF based on the VMF1 concept are available at http://ggosatm.hg.tuwien.ac.at/DELAY/.

The German Research Center for Geosciences (GFZ) generated a MF that is based on the VMF1 concept. This MF, called GFZ-VMF1, utilizes short-range forecasts from the global forecast system (GFS) of the National Centers for Environmental Prediction available at http://www.ftp.ncep.noaa.gov/data/nccf/com/gfs/prod/ and GFZs in-house point-to-point ray-trace software (Zus et al. 2012). When deriving GFZ-VMF1, we encountered three issues, namely a MF based on the VMF1 concept is tuned for (1) a specific elevation angle, (2) specific station height, and (3) specific orbital altitudes. The latter issue is typically ignored by assuming that a MF is independent of the orbital altitude (Boehm et al. 2006b). In this study, we analyze systematic errors introduced by the tuning for the month of March 2013. To do so, we compare the GFZ-VMF1 with the Potsdam mapping factors (PMFs) (Zus et al. 2014). The PMFs are obtained by a concept known as direct mapping (Rocken et al. 2001). According to this concept, for any required station–satellite link, the ratio of the tropospheric delay in the slant and zenith direction is computed directly. Since the PMFs are obtained by direct mapping, they are error-free when compared to parameterized mapping. Both the GFZ-VMF1 by definition and the PMFs used in this study approximate the earth as a sphere with the Gaussian curvature radius and assume that the atmosphere is spherically layered. In addition, both the GFZ-VMF1 and PMFs utilize the same NWM data. Therefore, differences caused by different NWM data do not show up in such comparison. Any difference between the GFZ-VMF1 and the PMFs is an error of the VMF1 concept.

We begin by describing how the GFZ-VMF1 is generated. In the subsequent section, we reveal the systematic errors of the GFZ-VMF1. This is followed by a discussion about strategies to avoid these errors and a summary.

Generation of a MF based on the VMF1 concept

The generation of a MF requires an atmospheric data source and a ray-trace algorithm (Davis et al. 1985). A detailed description of our point-to-point ray-trace algorithm is provided in Zus et al. (2012). This algorithm computes the signal travel time delay induced by the neutral atmosphere, referred to as tropospheric delay expressed in units of meters, between a GNSS satellite and a station given a NWM refractivity field. In essence, the tropospheric delay ∆L reads as

$$\Delta L = \int {n \cdot ds - g}$$
(1)

where n denotes the index of refraction, ds denotes the line element of the ray-trajectory, and g denotes the geometric distance between the satellite and the station. The tropospheric delay is separated into the hydrostatic and non-hydrostatic delays. The mapping factors are the ratios of the slant delays and zenith delays. The formal precision in terms of the tropospheric delay is estimated to be 1 mm. We also compared our approach with other state-of-the-art algorithms, e.g., those developed at the Department of Geodesy and Geomatics Engineering, University of New Brunswick, Canada (UNB) (Nievinski and Santos 2010). The comparisons showed an excellent agreement, i.e., if GFZ and UNB utilize the same NWM data and if GFZ and UNB agree on the space geodetic technique, then both predict the same tropospheric delay for any elevation and azimuth angle (Zus et al. 2014).

An excellent description of how a MF based on the VMF1 concept is generated can be found at http://unb-vmf1.gge.unb.ca/. The same link also provides access to the UNB-VMF1, a MF provided by UNB (Urquhart et al. 2013). The routines to generate the MF are available at http://ggosatm.hg.tuwien.ac.at/DELAY/SOURCE/. The GFZ-VMF1 is tuned for the elevation angle of 3°, the station heights correspond to the orography available at http://ggosatm.hg.tuwien.ac.at/DELAY/GRID/, and satellite orbital altitudes correspond to those of the global positioning system (GPS). The latter means that the satellite altitude above the osculating sphere is 20,200 km. To date, the GFZ-VMF1 is the only available MF, which is tuned for GPS. Therefore, the GFZ-VMF1 can be regarded as the GPS solution. The underlying 6-h forecast of the GFS is provided with the grid resolution of 1° by 1° on 26 pressure levels. The GFZ-VMF1 is prepared with the grid resolution of 1° by 1°, and it is available for 0, 6, 12, and 18 UTC with no latency. Note that the model orography is initially available with a grid resolution of 2° by 2.5°. The desired grid resolution of 1° by 1° is obtained by a bilinear interpolation. Clearly, due to the limited grid resolution of the model orography, differences between the model orography and the actual orography exist. For example, the differences between the model orography and the international GNSS service (IGS) station heights (http://www.igs.org/network/list.html) are shown in Fig. 1. According to this figure, height differences reach up to ±2 km in complex terrain.

Fig. 1
figure 1

Differences between the GFZ-VMF1 model orography and IGS station heights. The GFZ-VMF1 model orography at the location of the IGS station is obtained by bilinear interpolation. The units are meter

Full size image

Systematic errors in MF parameterization

We compare MFs in terms of tropospheric delays, i.e., we compute the zenith hydrostatic and non-hydrostatic delays, apply the hydrostatic and non-hydrostatic MFs, respectively, and combine both to obtain the tropospheric delay. The tropospheric delay difference can be translated into a station height difference in GPS processing. According to the rule of thumb by Boehm et al. (2006b), the station height difference is equal to one-fifth of the tropospheric delay difference at the lowest elevation angle included in the GPS processing. For example, if the elevation cutoff angle is 3° and the tropospheric delay difference at this elevation cutoff angle is 5 mm, then the station height difference is 1 mm. Therefore, since a station height difference of 1 mm is regarded significant, a tropospheric delay difference of 5 mm is regarded significant as well.

The mean deviation between the GFZ-VMF1 and the PMFs (GFZ-VMF1 minus PMFs) for March 2013 is shown in Fig. 2. In this comparison, it is not surprising that the GFZ-VMF1 is free of any error since we computed the MFs for the elevation angle of 3°, the station heights correspond to the orography, and the orbital altitudes correspond to the GPS. The GFZ-VMF1 is tuned for such settings. The numerical noise, which is independent of the geographical region, is insignificant. Next, we perform three experiments to reveal the errors of the GFZ-VMF1 separately; we alter separately the elevation angle, the station height, or the orbital altitude. At first, we compute MFs for the elevation angle of 5°. Second, we compute MFs for station heights 2 km above the orography. Third, we compute MFs for a different space geodetic technique, namely very long baseline interferometry (VLBI). The mean deviation between the GFZ-VMF1 and the PMF is shown in Figs. 3, 4, and 5, respectively.

Fig. 2
figure 2

Systematic errors of GFZ-VMF1 tropospheric delays for March 2013. The elevation angle is 3°, the station heights correspond to the orography, and the orbital altitudes correspond to the GPS. The units are mm

Full size image
Fig. 3
figure 3

Systematic errors of GFZ-VMF1 tropospheric delays for March 2013. The elevation angle is 5°, the station heights correspond to the orography, and the orbital altitudes correspond to the GPS. The units are mm

Full size image
Fig. 4
figure 4

Systematic errors of GFZ-VMF1 tropospheric delays for March 2013. The elevation angle is 3°, the station heights correspond to the orography plus 2 km, and the orbital altitudes correspond to the GPS. The units are mm. The station height dependency (Niell 1996) is included in the GFZ-VMF1

Full size image
Fig. 5
figure 5

Systematic errors of GFZ-VMF1 tropospheric delays for March 2013. The elevation angle is 3°, the station heights correspond to the orography, and an infinite height for the radio source like in case of VLBI is used. The units are mm. The differences correspond to the differences between GPS and VLBI tropospheric delays

Full size image

Elevation tuning

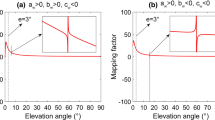
In order to understand the systematic errors, consider the elevation angle dependency of the MF which is based on the continued fraction form proposed by Marini (1972) and normalized by Herring (1992) to yield unity at zenith,

$$m(e) = \frac{{1 + \frac{a}{{1 + \frac{b}{1 + c}}}}}{{\sin \,(e) + \frac{a}{{\sin \,(e) + \frac{b}{\sin \,(e) + c}}}}}$$
(2)

Here, e denotes the elevation angle, and the coefficients a, b, and c must be estimated. This is done separately for the hydrostatic and non-hydrostatic MFs. Typically, for some elevation angles, the mapping factors are computed, and a, b, and c are estimated by a least square fit. If however the MF is based on the VMF1 concept, the coefficients b and c are not estimated but obtained from a climatology, and a is determined by inverting the continued fraction form for a single mapping factor. The approach of estimating all coefficients is referred to as the rigorous VMF concept (Boehm and Schuh 2004), and it is clear that this concept mitigates the systematic errors shown in Fig. 3. The drawback of the rigorous VMF concept is the computational cost and the additional parameters to disseminate (Urquhart et al. 2013). On the other hand, Fig. 3 supports to some extent the VMF1 concept; the tropospheric delay error is about ±6 mm corresponding to a station height error of ±1 mm only.

Station height dependence

Equation (2) is not complete. A MF based on the VMF1 concept also includes the station height dependency proposed by Niell (1996). In essence, the MF based on the VMF1 concept reads as

$$m(e) = \frac{{1 + \frac{a}{{1 \,+\, \frac{b}{1 \,+\, c}}}}}{{\sin \,(e) + \frac{a}{{\sin \,(e) \,+\, \frac{b}{\sin \,(e) \,+\, c}}}}} + h \cdot \left( {\frac{1}{\sin \,(e)} - \frac{{1 + \frac{{a_{h} }}{{1 \,+\, \frac{{b_{h} }}{{1 \,+\, c_{h} }}}}}}{{\sin \,(e) + \frac{{a_{h} }}{{\sin \,(e) \,+\, \frac{{b_{h} }}{{\sin \,(e) \,+\, c_{h} }}}}}}} \right)$$
(3)

where h denotes the station height in kilometers. The coefficients a h , b h and c h are adopted from Niell (1996) who used a climatology for their estimation. For this reason, a single mapping factor is still sufficient to determine the MF; the mapping factor is computed for a specific station height; the station height dependency is subtracted; and a is determined by inverting the continued fraction. Note that a h , b h , and c h equal zero for the non-hydrostatic MF. In other words, it is assumed that the non-hydrostatic MF is independent of the station height. Compared to systematic errors shown in Fig. 3, those shown in Fig. 4 are larger by about one order of magnitude. For example, for an airplane flying 2 km above mean sea level along the west coast of South America from 20°S to 20°N, the GPS-derived airplane altitude error is ±10 mm. Likewise, for an airplane flying 2 km above Antarctica, the GPS-derived airplane altitude error is 10 mm. Taking into account the height differences between the model orography and the actual orography (Fig. 1), comparable GPS-derived station height errors can be expected in complex terrain.

Orbital altitude dependence

Equation (3) now includes the elevation angle and station height dependency. The orbital altitude dependency is ignored. It is assumed that the MF is the same for GPS and VLBI (Boehm et al. 2006b). This is not true, although the tropospheric delay is indeed not very sensitive to the actual GPS satellite altitude. For example, if the GPS satellite altitude is altered by ±100 km, the tropospheric delay difference is at the submillimeter level. If the GPS satellite altitude is altered by ±1,000 km, i.e., this corresponds to Galileo or GLONASS satellite altitudes, the tropospheric delay difference is still negligible. However, if a different space geodetic technique such as VLBI is considered, the tropospheric delay difference is no longer negligible. Recall that the GFZ-VMF1 is free of any error if the elevation angle is 3°, the station altitudes correspond to the orography, and the orbital altitudes correspond to the GPS (Fig. 2). Hence, Fig. 5 shows the differences between GPS and VLBI tropospheric delays. Consider a collocated GPS and VLBI station in the tropics near mean sea level. The estimated station heights will differ by 1 mm if the same MF is applied for the GPS and VLBI station. The systematic differences between GPS and VLBI tropospheric delays are caused by the ray-bending. The larger the ray-bending, the larger the tropospheric delay difference. The ray-bending is caused by refractivity gradients. Since the refractivity gradients are the largest near mean sea level in the tropics, the tropospheric delay differences are the largest there. It is also clear that the tropospheric delay differences increase (decrease) with decreasing (increasing) elevation angles. For example, the tropospheric delay difference is about 25 mm for a 1° elevation. For an elevation of 5°, the tropospheric delay difference is only 1 mm.

Discussion

At first, we put the systematic errors of the MF shown in Figs. 3, 4, and 5 into general perspective. Figure 6 shows the mean deviation between the UNB-VMF1 and the GFZ-VMF1. We use the UNB-VMF1 in lieu of the original VMF1 due to the known issue regarding the assumption of a constant radius of the earth in the original VMF1 (Urquhart et al. 2013). Note that the UNB-VMF1 is based on the Canadian Meteorological Center’s Global Environment Mesoscale analysis. Again, we computed MFs for the elevation angle of 3°, the station heights correspond to the orography, and the orbital altitudes correspond to the GPS. The differences in Fig. 6 are to a small extent attributed to the differences between VLBI and GPS tropospheric delays, but they are mainly due to the different NWM data sets.

Fig. 6
figure 6

Mean deviation between UNB-VMF1 and GFZ-VMF1 tropospheric delays for March 2013. The elevation angle is 3°, the station heights correspond to the orography, and the orbital altitudes correspond to the GPS. The units are mm

Full size image

The comparison of Figs. 4 and 6 reveals that the systematic errors caused by the station height dependency and the systematic differences caused by different NWM data source have a comparable magnitude. In this sense, the imperfect station height dependency of the MF is regarded a significant error source. Figure 7 shows the systematic errors due to the station height of Fig. 4, but separately for the hydrostatic (top) and non-hydrostatic (bottom) MFs. Such a comparison, or the comparison of the MFs themselves, can be used to improve the station height dependency of the hydrostatic and non-hydrostatic MFs. The two components should be distinguished mainly due to their different variability in space and differences in the effective heights; the hydrostatic part depends on the total pressure while the non-hydrostatic part depends mainly on the water vapor pressure. By some new empirical models and parameter estimates, we may succeed in mitigating the systematic errors of the MF. However, another possibility is obvious; replace the MF by the PMFs in GPS processing.

Fig. 7
figure 7

Systematic error of GFZ-VMF1 hydrostatic (top) and non-hydrostatic (bottom) delays for March 2013. The elevation angle is 3°, the station heights correspond to the orography plus 2 km, and the orbital altitudes correspond to the GPS. The units are mm. The station height dependency (Niell 1996) is included in the GFZ-VMF1

Full size image

Current thinking is that the direct mapping is impractical due to the large computational burden as well as additional large data volume to handle (Urquhart et al. 2012). We only agree in part when considering the data throughput of the PMFs; irrespectively of the elevation angle, about 2,000 hydrostatic and non-hydrostatic mapping factors are computed per second. Note that if we consider slant factors (Urquhart et al. 2012) instead of mapping factors, i.e., if tropospheric asymmetry is accounted for, our data throughput reduces by about 25 % only. The rapid data throughput is a strong argument for the PMFs. Clearly, this estimate for the data throughput must be viewed with some caution as well because it depends on the programming language, the compiler, and the computer platform. Our estimate for the data throughput is based on a FORTRAN implementation, the Intel FORTRAN compiler, and an ordinary PC (Core2Quad Intel processor, 2.5 GHz, 2 GB RAM) using a single core. In an open multiprocessing environment, the data throughput scales linearly with the number of cores. For example, given 800 stations and ten station–satellite links per station, i.e., 8,000 station–satellite links per epoch, then all mapping factors are produced within one second utilizing four cores. However, the key behind the rapid data throughput is not the computer power but the underlying algorithm; there are possibilities to further increase the speed.

In fact, the data throughput can be easily doubled. To understand this, some details of the underlying algorithm are required. The hydrostatic and non-hydrostatic delays are computed by numerical integration once the ray-trajectory of the radio signal between the satellite and the station is determined. The ray-trajectory [x, y(x)] is obtained by solving the Euler–Lagrange equation corresponding to Fermat’s principle

$$\frac{{{\text{d}}^{2} y(x)}}{{{\text{d}}x^{2} }} - \left[ {\frac{{n_{y} (x,y)}}{n(x,y)} - \frac{{n_{x} (x,y)}}{n(x,y)} \cdot \frac{{{\text{d}}y(x)}}{{{\text{d}}x}}} \right] \cdot \left[ {1 + \left( {\frac{{{\text{d}}y(x)}}{{{\text{d}}x}}} \right)^{2} } \right] = 0$$
(4)

Here, the subscripts x and y denote partial derivatives. Given the position of the satellite [x s , y s ] and the position of the station [x g , y g ], Eq. (4) represents a two-point boundary value problem. The basic idea of our algorithm is to define a node sequence X = [x 1 ,…,x n ] and to replace for this node sequence the derivatives of y with respect to x by finite differences (Lagrange interpolating polynomials of degree two). This leads to a nonlinear system of equations

$$F(Y) = 0$$
(5)

where Y = [y 1 ,…,y n ] denotes the solution vector. The nonlinear system of equations is solved by Newton’s method. Let Y r denote the solution vector at the iteration step r. The solution vector Y r+1 at the iteration step r + 1 is obtained by solving the system of linear equations

$$J[Y_{r} ] \cdot (Y_{r+1} - Y_{r} ) = - F(Y_{r} )$$
(6)

where J denotes the Jacobian matrix. The Jacobian matrix is determined analytically. In each Newton–Raphson iteration, the linear system of equations is solved by a lower upper (LU) decomposition. The first guess vector Y 0 corresponds to the straight line between the satellite and the station. It turns out that a single Newton–Raphson iteration, i.e., a single LU decomposition, is sufficient for elevation angles ≥3°. On a coding level, this means that the computation of the hydrostatic and non-hydrostatic delay can be reduced to two loops. In the first loop, we compute the main, lower, and upper diagonal of the Jacobian; the right-hand side of the system of equations; and perform the forward substitution. In the second loop, we perform the backward substitution to obtain the ray-trajectory and simultaneously compute the hydrostatic and non-hydrostatic delays by numerical integration. In addition, we halve the number of nodes for which the ray-trajectory is determined. We call this procedure the ultra-rapid PMFs and show in Fig. 8 the root mean square (RMS) difference between the ultra-rapid PMFs and the PMFs in case the elevation angle is 3°, and the station altitudes correspond to the orography, and the orbital altitudes correspond to the GPS. The RMS differences shown in this figure are caused by the lower resolution of the ray-trajectory that is used in the numerical integration. In particular, in the tropics where the variability of the refractivity is largest, the lower resolution of the ray-trajectory reduces precision. However, Fig. 8 justifies our approach; the RMS differences do not exceed 1 mm.

Fig. 8
figure 8

RMS difference between ultra-rapid PMFs and PMFs for March 2013. The elevation angle is 3°, the station heights correspond to the orography, and the orbital altitudes correspond to the GPS. The units are mm

Full size image

In summary, the ultra-rapid PMFs have negligible errors provided that the elevation angle is ≥3°; about 4,000 hydrostatic and non-hydrostatic mapping factors are produced per second. From this perspective, replacing a parameterized mapping approach by a rapid direct mapping approach in GPS processing can no longer be regarded impractical. The large NWM data volume to handle is still regarded a drawback of the direct mapping approach. In any case, whether direct mapping is preferred or not, the PMFs have an important practical application; the mapping factors which are needed in the generation of the GFZ-VMF1 are PMFs. Hence, the ultra-rapid PMFs allow us to generate the GFZ-VMF1 for one epoch in less than 15 s.

Conclusion

A MF which is based on the VMF1 concept has systematic errors because it is tuned for specific elevation angles, station heights, and orbital altitudes. We introduced a MF, called GFZ-VMF1, and compared it with a direct mapping approach, so-called PMFs, to quantify the systematic errors on a global scale. We found that in particular the parameterization of the station height dependency is a concern in regard to applications in complex terrain or in airborne applications. For example, if a station is located 2 km above the MF model orography and if low-elevation observations are included in the GPS processing, our analysis suggests that the GPS-derived station height error can reach up to 1 cm. It is important to note that low-elevation observations are affected by a variety of error sources, e.g., poor or missing antenna phase center models, multipath, and increased measurement noise, such that low-elevation observations are often discarded. In this case, the GPS-derived station height will be hardly affected by any of the systematic errors of the MF. If however low-elevation observations are included, we see three options. At first, we may try to improve the station height dependency of the MF. Second, we may provide a site-specific rigorous MF. Third, we note that the PMFs are both precise and fast. In fact, it appears that parameterized mapping is superfluous in GPS processing. For a real-time application, however, we are currently not in the position to provide an alternative to the GFZ-VMF1, which is available at ftp://gfz-potsdam.de/home/kg/zusflo/PMFa.

Finally, it is important to note that we did not study another aspect in favor of direct mapping, i.e., tropospheric asymmetry. To some extend, the effect of tropospheric asymmetry was analyzed in recent studies (Urquhart et al. 2012, 2013). A more detailed global analysis with a reasonable amount of computing time is possible and foreseen with the rapid point-to-point ray-trace algorithm outlined in this study.