An exact algorithm for the minimum quartet tree cost problem

Abstract

The minimum quartet tree cost (MQTC) problem is a graph combinatorial optimization problem where, given a set of $n \ge 4$ data objects and their pairwise costs (or distances), one wants to construct an optimal tree from the $3 \cdot {n \atopwithdelims ()4}$ quartet topologies on n, where optimality means that the sum of the costs of the embedded (or consistent) quartet topologies is minimal. The MQTC problem is the foundation of the quartet method of hierarchical clustering, a novel hierarchical clustering method for non tree-like (non-phylogeny) data in various domains, or for heterogeneous data across domains. The MQTC problem is NP-complete and some heuristics have been already proposed in the literature. The aim of this paper is to present a first exact solution approach for the MQTC problem. Although the algorithm is able to get exact solutions only for relatively small problem instances, due to the high problem complexity, it can be used as a benchmark for validating the performance of any heuristic proposed for the MQTC problem.

1 Introduction

The minimum quartet tree cost (MQTC) problem is a graph combinatorial optimization problem having strong implications in hierarchical clustering contexts. Hierarchical clustering methods are generally represented by a two dimensional diagram known as dendrogram (Diestel 2000), which illustrates the fusions or divisions made at each successive stage of analysis. A dendrogram, or tree diagram, is a mathematical way to represent a complete clustering process by means of a tree structure. A dendrogram has the objects attached as leaves (i.e. nodes at the bottom-most level of the tree; they are connected with only one other node), the internal nodes (i.e. nodes at the inner level of the tree; they are connected with more than one other node) representing the structure of the clusters, and the length of the stems (i.e. path lengths) representing the distances among the clusters. The arrangement of leaves, internal nodes, and stems determines the topology of the dendrogram, whose branches show the relationships among the clustered objects. The clustering level of an object with respect to another is determined by the number of stems between the corresponding leaves. There are many different types of dendrograms (Diestel 2000). In some there are limits placed on the degrees of the internal nodes. In others, additions are made to the structure, by labelling the nodes, or by orienting, ordering or assigning lengths to the edges. In particular, unordered trees are of dominant interest in clustering contexts because edge orderings have no effect on the path lengths between the nodes in the tree.

Given a set N of $n\ge 4$ objects, the MQTC problem deals with a full unrooted binary tree with n leaves, a special topology dendrogram having all internal nodes connected exactly with three other nodes, the objects of N assigned to the leaf nodes, and without any distinction between parent and child nodes (Furnas 1984). A full unrooted binary tree with $n\ge 4$ leaves has exactly $n-2$ internal nodes, and consequently it has a total of $2n-2$ nodes. This dendrogram is sometimes called boron tree (or ternary tree), since such a tree, with $2n-2$ total nodes, has $n-2$ nodes connected with other three nodes (corresponding to boron atoms) and n nodes connected with only one other node (corresponding to hydrogen atoms).

A full unrooted binary tree with exactly $n = 4$ leaves is also referred to as simple quartet topology, or just as quartet (Furnas 1984; Diestel 2000). Given a set N of $n\ge 4$ objects, the number of sets of four objects from the set N is given by:

$$\begin{aligned} {n \atopwithdelims ()4} = \frac{n!}{4!(n-4)!}=\frac{n(n-1)(n-2)(n-3)}{24}. \end{aligned}$$

(1)

Given four generic objects $\{a,b,c,d\} \in N$, there exist exactly three different quartets: ab|cd, ac|bd, ad|bc, where the vertical bar divides the two pairs of leaves, with each pair labelled by the corresponding objects and attached to the same internal node (Fig. 1).

Fig. 1

The three different simple quartet topologies of the generic set $\{a,b,c,d\}$ of objects

Thus, considering the set N of $n\ge 4$ objects, the total number of possible simple quartet topologies is:

$$\begin{aligned} 3 \cdot {n \atopwithdelims ()4} = \frac{n(n-1)(n-2)(n-3)}{8}. \end{aligned}$$

(2)

Definition 1

(Consistency) A full unrooted binary tree is said to be “consistent” with respect to a simple quartet topology, say ab|cd, if and only if the path from a to b does not cross the path from c to d (Felsenstein 1981). This quartet ab|cd is also said to be “embedded” in the given full unrooted binary tree.

In order to visually represent the distances among the set N of $n\ge 4$ objects as well as possible, the MQTC problem considers all $3 \cdot {n \atopwithdelims ()4}$ possible quartet topologies, each with a given cost (as it will be formally defined in Sect. 3), and looks for the full unrooted binary tree such that the summed costs of the embedded (or consistent) quartet topologies is minimal.

Cilibrasi and Vitányi (2011) proved that the MQTC problem is an NP-hard combinatorial optimization problem by reduction from the more general maximum quartet consistency (MQC) problem (Steel 1992). In (Cilibrasi and Vitányi 2011) it is also demonstrated that a polynomial time approximation scheme for the MQTC problem is not possible.

The aim of this paper is to present the details of an exact solution algorithm for the MQTC problem. As it will be shown, this algorithm is able to provide the first gold standard for the MQTC problem which can be used as a benchmark for validating the performance of any heuristic proposed for the problem. In addition, the proposed algorithm contains some very interesting insights which may be useful, e.g., to hybridize (Consoli and Moreno-Pérez 2012) and enhance the MQTC heuristics to date in the literature (Cilibrasi and Vitányi 2005, 2011; Consoli et al. 2010), or in general to foster further research on the subject. The rest of the paper is organized as follows. In Sect. 2, the literature related to the MQTC problem and to the quartet method of hierarchical clustering is described. The MQTC problem is then formulated in Sect. 3. In Sect. 4, we present the details of the exact solution approach that we propose for the MQTC problem. Section 5 includes our computational experience related to the creation of a gold standard for the problem, and finally the paper ends with some conclusions and suggestions for possible future research (Sect. 7).

2 Related literature

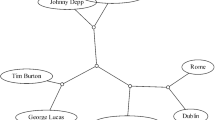
The MQTC problem was originally proposed in (Cilibrasi et al. 2004; Cilibrasi and Vitányi 2005). There the main focus was on compression-based distances, but the authors visually presented the tree reconstruction results by full unrooted binary trees deriving by their MQTC problem formulation. Hence, they developed the quartet method for hierarchical clustering, a new approach aimed at general hierarchical clustering of data from different domains, not necessarily biological phylogenies.

Several practical applications of the quartet method have been explored so far in the literature. In particular, Cilibrasi et al. (2004) proposed a robust automatic music classification procedure consisting of two steps. The first step consisted of extracting the Normalized Compression Distances (NCD) (Li and Vitányi 1997) among some considered pieces of music. The Normalized Compression Distance is a similarity metric based on string compression which mimics the ideal performance of Kolmogorov complexity (Li and Vitányi 1997). The second step consisted of creating an efficient visualization of the extracted pairwise distances by means of the quartet method of hierarchical clustering. To substantiate the claims of universality and robustness of this automatic classification method, evidence of other successful applications in areas as diverse as genomics, virology, languages, literature, handwriting, astronomy and combinations of objects from completely different domains, were reported in (Cilibrasi and Vitányi 2005). In addition, Cilibrasi and Vitányi (2007) reported an interesting application of this theory, consisting of the automatic extraction of similarities among words and phrases from the WWW using Google page counts. Granados et al. (2011) studied the impact of several kinds of information distortion on compression-based text clustering, showing their results as ternary trees by means of the quartet method of hierarchical clustering. In a recent application, a quartet method based on variable neighborhood search was used for biomedical literature extraction and clustering (Consoli and Stilianakis 2015, 2017).

In (Cilibrasi and Vitányi 2011), the authors presented the MQTC problem in a more formal way. They showed the main concepts, components, advantages and disadvantages of the quartet method of hierarchical clustering, particularly underlining the similarities and differences with respect to other methods from biological phylogeny. Cilibrasi and Vitányi (2011) also showed that the MQTC problem is NP-hard by reduction from the MQC problem, and provided a Randomized Hill Climbing heuristic to obtain approximate problem solutions. Several other efficient metaheuristics (Greedy Randomized Adaptive Search Procedure, Simulated Annealing, and Variable Neighbourhood Search) were proposed and compared for the MQTC problem in (Consoli et al. 2010). These metaheuristics performed well for the problem, although a proper solution quality evaluation was not possible as no benchmarks on the exact solutions of the MQTC problem exist. In this paper we propose an exact algorithm for the MQTC problem.

3 Problem formulation

Considering a set N of $n\ge 4$ objects, the MQTC problem accepts as input a distance matrix, $\varvec{D}$, which is a matrix containing the distances (or, in general, costs, or dissimilarities), taken pairwise, among the n objects. It is therefore a symmetric $n \times n$ matrix containing non-negative rationals, normalized between 0 and 1, as entries. The value 1 represents the largest distance between two objects; the closer to 1 the distance between two objects is, the further the objects will be apart. Obviously, all the elements in the diagonal of the distance matrix are equal to 0.

To extract a hierarchy of clusters from the distance matrix, the MQTC problem determines a full unrooted binary tree with n leaves that visually represents the symmetric $n \times n$ distance matrix as well as possible according to a cost measure. This representation allows useful information to be extracted from the data and clusters of data to be related to each other (Cilibrasi and Vitányi 2005). Considering the set N of $n\ge 4$ objects, and the set Q of all possible $3 \cdot {n \atopwithdelims ()4}$ quartets, let $C: Q \rightarrow {\mathbb {Q}}^+$ be a cost function assigning a positive rational valued cost C(ab|cd) to each quartet topology $ab|cd \in Q$. The cost assigned to each simple quartet topology is defined as the sum of the distances (taken from the distance matrix) between each pair of neighbouring leaves (Cilibrasi and Vitányi 2011). For example, the cost associated with the quartet ab|cd is $C(ab|cd) = D_{(a,~b)} + D_{(c,~d)},$ where $D_{(a,~b)}$ and $D_{(c,~d)}$ indicate, respectively, the distances between the two neighbouring objects (a and b) and (c and d), obtained from the distance matrix.

Consider the set $\varGamma$ of all full unrooted binary trees with $2n-2$ nodes (i.e. n leaves and $n-2$ internal nodes), obtained by placing the n objects to cluster as leaf nodes of the trees. For each full unrooted binary tree $t \in \varGamma$, precisely one of the three possible simple quartet topologies for any set of four leaves is consistent (Cilibrasi and Vitányi 2005). Thus, for each $t \in \varGamma$, there exist precisely ${n \atopwithdelims ()4}$ consistent quartet topologies (one for each set of four objects) embedded in t. Then, the cost associated with a full unrooted binary tree$t \in \varGamma$ is defined as the sum of the costs of its ${n \atopwithdelims ()4}$ consistent quartet topologies, that is

$$\begin{aligned} C(t)=\sum _{\forall ab|cd \in Q_t}{C(ab|cd)}, \end{aligned}$$

(3)

where $Q_t$ is the set of such ${n \atopwithdelims ()4}$ quartet topologies embedded in t. In most cases, it is not possible to create a full unrooted binary tree which embeds all the simple quartet topologies with the minimum cost for all the sets of four objects (especially for a large number of objects n), due to inconsistency. Thus, it is a matter of making the most balanced choice of the quartet topologies to embed. This is the goal of the MQTC problem: trying to find (or approximate as closely as possible) the full unrooted binary tree $t \in \varGamma$ with the minimum total cost. The MQTC optimization problem can be formally defined as follows (Cilibrasi and Vitányi 2005, 2011). Given a set N of $n\ge 4$ objects, a symmetric distance matrix $n \times n$ containing their pairwise distances, and a cost function $C: Q \rightarrow {\mathbb {Q}}^+$ assigning a positive rational valued cost to each quartet topology, find the full unrooted binary tree $t \in \varGamma$ with the minimum total cost C(t), i.e. $C(t) = \text {min}( \sum _{\forall ab|cd \in Q_t}{C(ab|cd)}).$

4 Exact solution approach

Although several heuristics for the MQTC problem have been proposed in the literature (Cilibrasi and Vitányi 2005, 2011; Consoli et al. 2010), an exact solution approach for the problem does not exist yet. Despite the high complexity of the problem, in this paper it is presented an exact algorithm, which is able to get exact solutions for relatively small instances of the MQTC problem.

The exact algorithm consists of enumerating all possible solutions of the MQTC problem, and then extracting the solution with the overall minimum cost. The approach can be dissected into the following two main tasks:

T1.:

Given n objects, generate all different full binary trees topologies with n leaves ($n- 2$ internal nodes);

T2.:

For each different full binary tree topology, perform all possible different permutations of its leaves, and find the solution with the minimum cost for each considered topology.

The global optimum solution is then the solution with the minimum cost among the set of best solutions of all full binary trees topologies.

While the second algorithm’s task can be intuitively obtained by enumerating and comparing all permutations of leaves for a given topology, the first task is quite complex. The first enumeration of boron trees, or ternary trees, has been given by Cyvin et al. (1995). Successively Cameron (2000a, b) provided the generating formula of this enumeration, whose growth rate is exponential (Rains and Sloane 1999). This sequence is referred in Sloane and Plouffe (1995)’s Encyclopedia of Integer Sequences to as A000672. In particular, given n objects, the growth rate of item T1 is singly exponential, and more precisely of the form $2^{{\mathcal {O}}(n)}$, whereas the asymptotic growth of item T2 rises up to ${\mathcal {O}}(n!)= 2^{O(n \log n)}$.

In order to generate all different boron trees topologies of n objects attached as leaves, and to meet then the first task of our algorithm, we use a new methodology which allows to easily compare boron trees topologies, and to discard a topology already evaluated. This procedure is possible by associating to each dendrogram a particular matrix representation, as it will described next, and it allows a uniform random generation of the different boron trees topologies of n objects, i.e. in an equiprobable way (Furnas 1984).

When all boron trees topologies are generated, all different permutations of the leaves for each topology are evaluated and the relative minimum cost solution is extracted. After evaluating all boron trees topologies along with their permutations of leaves, it will be possible to produce the solution with the minimum cost among the set of stored best solutions. This is the global best solution for the MQTC problem.

Before examining the details of our proposed algorithm, it is useful to specify some notations related to full unrooted binary treew which will be used next.

Definition 2

(Degree of an internal node) The “degree of an internal node” of a full unrooted binary tree is defined as the number of connections of the node with other internal nodes.

As by definition a full unrooted binary tree has each internal node connected exactly with three other nodes, therefore the degree of each internal node is bounded to lie in the interval (1, 3).

Definition 3

(Classification of internal nodes) Given a full unrooted binary tree, its internal nodes can be classified as:

• “terminal nodes”: connected to two leaves and another internal node (degree = 1));

• “transition nodes”: connected to one leaf node and two other internal nodes (degree = 2);

• “cross nodes”: connected to three other internal nodes (degree = 3).

Definition 4

(Boron degree) The “boron degree” of a full unrooted binary tree is defined as its number of cross nodes.

Fig. 2

The six different boron trees topologies with nine leaves. The nodes labelled with the notation $k_i$ are the seven internal nodes

Definition 5

(Flat structure) The “flat structure” of a full unrooted binary tree is its structural topology having no cross node (i.e., having boron degree equal to zero).

Definition 6

(Branch) A “branch” of a full unrooted binary tree is any of its subgraphs containing at most transition nodes and delimited either

• by two terminal nodes (in case of boron degree $= 0$, i.e. the flat structure);

• or by one terminal node and one cross node, or by two different cross nodes (case boron degree $> 0$).

For example, Fig. 2 contains the six different boron tree topologies having nine leaves. In particular, Fig. 2a shows the flat structure, which has boron degree $= 0$, and just one branch; Fig. 2b shows the three topologies with boron degree $= 1$, and each having exactly three branches; finally Fig. 2c shows the two topologies with boron degree $= 2$, and each having exactly five branches.

4.1 Description of the algorithm

The building blocks of the proposed exact algorithm for the MQTC problem may be summarized as the following:

• 1. definition of the initial topology structure (Sect. 4.1.1);

• 2. data representation (Sect. 4.1.2);

• 3. mechanism to compute efficiently the cost function value (Sect. 4.1.3);

• 4. procedure to evaluate all permutations of the leaves (Sect. 4.1.4);

• 5. way to generate all the different structural boron tree topologies (Sect. 4.1.5).

The overall algorithm which assembles all these fundamental parts is discussed in Sect. 4.1.6, where a pseudo-code description is also given.

4.1.1 Initial topology structure

Given n objects and their pairwise distances stored in the $n \times n$ symmetric distance matrix $\varvec{D}$, the algorithm starts by computing from the easiest possible full unrooted binary tree topology, that is the flat structure (see Definition 5). This structure has boron degree equal to zero, i.e. it does not contain any cross node but only transition nodes and two terminal nodes. As an example consider the flat structure topology for the case with nine leaves reported Fig. 2a. Proceeding with the computations, our algorithm will increase the complexity of the topology structure in terms of boron degree, discarding the topologies already evaluated. In this way the algorithm will be able to generate all the possible full unrooted binary tree structural topologies for n objects.

4.1.2 Data representation

Given n objects, each solution is represented by a $(2n-2) \times (2n-2)$ matrix that we refer to as Complete Pseudo-Adjacency matrix, $\varvec{A}=[A_{(i,~j)}]$ where $i,j=1,\ldots ,(2n-2)$. Similarly to an usual adjacency matrix [see e.g. Diestel (2000)], in $\varvec{A}$ we have $A_{(i,~j)} = 0$ for each non-diagonal entry $A_{(i,~j)}$, $i \ne j$, where the two nodes i and j are not directly connected each other. Conversely, when two nodes i and j are directly connected we have $A_{(i,~j)} > 0$, but not the value 1 as in the usual adjacency matrix representation (Diestel 2000). As it will be shown next, we use a different convention also for the diagonal entries, which are used to store important information to speed-up the computations.

The Complete Pseudo-Adjacency matrix can be also partitioned as

where $\varvec{K}$, referred to as Structure sub-matrix, is a $(n-2) \times (n-2)$ pseudo-adjacency matrix for the internal nodes and it represents the structural topology of the given solution; $\varvec{L}$, referred to as Leaves sub-matrix, is a $(n-2) \times n$ adjacency matrix representing the connections of the leaves with the internal nodes; $\varvec{C}$, called Coefficients sub-matrix, is sized ${n \times n}$ and contains some useful coefficients used to compute the cost associated to the given solution.

We can broaden the partitions of the Complete Pseudo-Adjacency matrix by labelling its rows and columns as following:

where $k_1, \ldots , k_{n-2}$ are the internal nodes, and $l_1, \ldots , l_n$ are the leaves. In particular, for the Structure sub-matrix $\varvec{K}$, in the diagonal are stored the degrees of the corresponding internal nodes; for each non-diagonal entry $A_{(i,~j)}$, $i \ne j$, $i, j \le (n-2)$, we have $A_{(i,~j)} = 0$ if nodes i and j are not directly connected each other; conversely, if the nodes are directly connected, $A_{(i,~j)} > 0$, and in particular $A_{(i,~j)}$ is equal to to the number of leaves attached to the subgraph obtained by removing edge (i, j) from the boron tree, and containing node j. For the Leaves sub-matrix $\varvec{L}$, we have $A_{(i,~j)} = 0$, with $i \le (n-2)$ and $j > (n-2)$, if the node j (i.e. leaf $l_{j-(n-2)}$) is not connected to the node i (i.e. internal node $k_i$), otherwise $A_{(i,~j)} = 1$. The entries $A_{(i,~j)}$, $i,j=n-1,\ldots ,2n-2$ in the Coefficients submatrix $\varvec{C}$ have to be derived as specified in the paragraph that comes next.

For the example with nine leaves (i.e. seven internal node) the Complete Pseudo-Adjacency matrix of the initial flat structure (Fig. 2a) has the following aspect:

Fig. 3

Flat structure with nine leaves

where the leaves have been assigned as in Fig. 3. As we may see from the figure, each edge connecting every pair of internal nodes is labelled with two weights at its extremities (in red), which represent the number of leaves contained in the two subgraphs obtained by removing that edge from the boron tree (which are the non-diagonal entries $A_{(i,~j)}$, $i \ne j$, $i, j \le (n-2)$, of the Structure sub-matrix $\varvec{K}$, also depicted in the matrix in red). These weights will be useful in the determination of the coefficients $A_{(i,~j)}$, $i,j=n-1,\ldots ,2n-2$, of submatrix $\varvec{C}^{n \times n}$, as it will be explained in the next paragraph.

4.1.3 Computation of the cost function value

Given a full unrooted binary tree t with leaves assigned, to evaluate the cost of t we should evaluate first all the ${n \atopwithdelims ()4} = \frac{n!}{4!(n-4)!}$ consistent quartet topologies embedded in its configuration, and then summing the costs of all these quartets, which are taken from the distance matrix $\varvec{D}$. That is, for the example of the flat structure with nine leaves given in Fig. 3, we would need to enumerate first all the quartets embedded in t:

$$\begin{aligned}&(l_1 l_2 | l_3 l_4), (l_1 l_2 | l_3 l_5), (l_1 l_2 | l_3 l_6), \ldots , (l_1 l_2 | l_3 l_9), \\&(l_1 l_2 | l_4 l_5), (l_1 l_2 | l_4 l_6), \dots , (l_1 l_2 | l_4 l_9), \ldots , \\&(l_2 l_3 | l_4 l_5), (l_2 l_3 | l_4 l_6), \dots , (l_1 l_2 | l_4 l_9), \ldots , \ldots , \\&(l_6 l_7 | l_8 l_9) . \end{aligned}$$

Then, to get C(t), we should sum the costs of all these embedded quartets (as expressed in compact form in Eq. 3):

$$\begin{aligned} C(t)&= C(l_1 l_2 | l_3 l_4) + C(l_1 l_2 | l_3 l_5) + C(l_1 l_2 | l_3 l_6) +\cdots + C(l_1 l_2 | l_3 l_9) \\&\quad + C(l_1 l_2 | l_4 l_5) + C(l_1 l_2 | l_4 l_6) + \dots + C(l_1 l_2 | l_4 l_9) + \dots \\&\quad + C(l_2 l_3 | l_4 l_5) + C(l_2 l_3 | l_4 l_6) +\cdots + C(l_1 l_2 | l_4 l_9) +\cdots +\cdots \\&\quad + C(l_6 l_7 | l_8 l_9) \end{aligned}$$

that is, taking the costs from the distance matrix D:

$$\begin{aligned} C(t)&= (D_{(l_1,~l_2 )} + D_{( l_3,~l_4)}) + (D_{(l_1,~l_2)} + D_{(l_3,~l_5)}) + (D_{(l_1,~l_2)} + D_{(l_3,~l_6)}) +\cdots \\&\quad +\,(D_{(l_1,~l_2)} + D_{(l_3,~l_9)})+ (D_{(l_1,~l_2)} + D_{(l_4,~l_5)}) + (D_{(l_1,~l_2)}+ D_{(l_4,~l_6)}) \\&\quad + \dots + (D_{(l_1,~l_2)} + D_{(l_4,~l_9)}) +\cdots + (D_{(l_2,~l_3)} + D_{(l_4,~l_5)})+ (D_{(l_2,~l_3)} \\&\quad +D_{(l_4,~l_6)}) +\cdots + (D_{(l_1,~l_2)} + D_{(l_4,~l_9)}) +\cdots +\cdots + (D_{(l_6,~l_7)} + D_{(l_8,~l_9)}). \end{aligned}$$

Summing all the common terms, for the particular case of the flat structure topology with nine leaves, we would end up in something like:

$$\begin{aligned} C(t)&= 21 \cdot D_{(l_1,~l_2 )} + 15 \cdot D_{( l_1,~l_3)} + 10 \cdot D_{(l_1,~l_4)} +\cdots \\&\quad + 10 \cdot D_{(l_6,~l_9)} + 15 \cdot D_{(l_7,~l_9)} + 21 \cdot D_{(l_8,~l_9)}, \end{aligned}$$

that is:

$$\begin{aligned} C(t) = \frac{1}{2} \sum _{ a,b=1 }^{ n}{ coef{(a,b)} \cdot D_{( l_a,~l_b)} } , \end{aligned}$$

(4)

with coef(a, b) denoting the coefficient multiplying the distance $D_{( l_a,~l_b)}$. Note that the 1 / 2 factor is included to the final result since the terms $D_{( l_a,~l_b)}$ and $D_{( l_b,~l_a)}$ are equal, due to the symmetry of the distance matrix $\varvec{D}$, and thus the terms in the sum are counted two times; therefore the result must be divided by two. We can store the $coef{(\cdot ,\cdot )}$ factors in the Coefficients submatrix $\varvec{C}$, in particular they are set to $A_{(i,~j)}$, with $i,j=n-1,\ldots ,2n-2$; coefficient values in the diagonal are set instead simply to one (they are irrelevant because they are always multiplied by zero, since $D_{( i,i)} = 0$ by definition of dissimilarity matrix). The Complete Pseudo-Adjacency matrix takes the form of:

(5)

where in green are depicted the evaluated coefficients of $\varvec{C}$. In this way, the cost of the full unrooted binary tree t can be simply obtained in compact form by multiplying the transpose of the Coefficients submatrix $\varvec{C}$ by the distance matrix $\varvec{D}$:

$$\begin{aligned} C(t) = \frac{1}{2} \cdot \varvec{C}^T \cdot \varvec{D} . \end{aligned}$$

(6)

But the nicest thing is that, in addition, we have found an efficient and automatic way to calculate the coefficients of $\varvec{C}$ avoiding the burdensome procedure just illustrated, i.e. without the need of evaluating each time all the ${n \atopwithdelims ()4} = \frac{n!}{4!(n-4)!}$ consistent quartet topologies embedded in the boron tree t, and then summing the costs of all these quartets. We discovered that the coefficient factors $coef{(\cdot ,\cdot )}$ stored in $\varvec{C}$ (in green) depend directly from the weights stored in the Structure sub-matrix $\varvec{K}$ (in red) by means of the formula of triangular numbers (Deza and Deza 2012). Triangular numbers are those numbers which can be arranged in a compact triangular pattern, that is they count the objects that can form an equilateral triangle (Deza and Deza 2012). The triangular number of n, referred to as T(n), where n is any natural number, is the sum of the n natural numbers from 1 to n, i.e. $1+2+3+4+5+6+7+\cdots +n$. It can be obtained by means of the following explicit formulas:

$$\begin{aligned} T(n) = \sum _{ i=1 }^{n}{ i} = \frac{n (n+1)}{2} = {n+1 \atopwithdelims ()2} , \end{aligned}$$

(7)

e.g., $T(1) = \mathbf{1 }; T(2) = 1 + 2 = \mathbf{3 }; T(3) = 1 + 2 + 3 = \mathbf{6 }; T(4) = 1 + 2 + 3 + 4 = \mathbf{10 }$.

In other words, the sequence of triangular numbers (sequence A000217 in Sloane and Plouffe (1995)’s Encyclopedia of Integer Sequences), starting at the 0th triangular number, is: 0, 1, 3, 6, 10, 15, 21, 28, 36, 45, 55, 66, 78, 91, 105, 120, 136, 153,  $171, 190, 210, 231, 253, 276, 300, 325, 351, 378, 406, \ldots$.

The properties of such numbers were first studied by ancient Greek mathematicians, particularly the Pythagoreans. Flocks of birds often fly in this triangular formation. Even several airplanes when flying together constitute this fascinating swarm sequence (Deza and Deza 2012).

We found a particular relation between the coefficients stored in $\varvec{C}$ and the weights of the Structure sub-matrix $\varvec{K}$. The coefficient multiplying $D_{(l_a,~l_b)}$, namely coef(a, b), is equal to the sum of the triangular numbers of the weights, subtracted by one, of the outgoing edges linked to internal nodes which are excluded from the subgraph obtained by connecting nodes a and b.¹

We explain this statement with an example. Consider the full unrooted binary tree with nine leaves depicted in Fig. 3. To get the coefficient multiplying $D_{( l_1,~l_4)}$, i.e. $coef{(l_1,l_4)}$, stored in position $A_{(8,~11)}$ in the Coefficients submatrix $\varvec{C}$, evaluate first the path between $l_1$ and $l_4$; the resulting subgraph has the following nodes: $\{k_1, k_2, k_3\}$. Consider now the outgoing edges, linked to internal nodes only, which are excluded from this subgraph; this set is composed in this case by edge $(k_3,k_4)$ only. The outgoing weight $(k_3,k_4)$ is 5 [see Fig. 3 and the corresponding entry within the Structure sub-matrix $\varvec{K}$ given in (5)]. Consider now the triangular number of this weight minus one (i.e. of 4); the resulting coefficient is 10, as you can see stored in $\varvec{C}$. To show another instance, let’s consider the coefficient multiplying $D_{( l_5,~l_6)}$, i.e. $coef{(l_5,l_6)}$, stored in position $A_{(12,~13)}$ in the Coefficients submatrix $\varvec{C}$. The path between $l_5$ and $l_6$ is formed by the nodes: $\{k_4,k_5\}$. The outgoing edges excluded from this subgraph, and linked to internal nodes only, are the following edges: $(k_4,k_3)$ and $(k_5,k_6)$. The corresponding outgoing weights are, respectively, 4 and 3. The triangular numbers of these weights minus one (i.e. 3 and 2) are, respectively, 6 and 3. The sum of these triangular numbers is 9, which is the resulting coefficient $coef{(l_5,l_6)}$ (i.e. $A_{(12,~13)}$) stored in $\varvec{C}$.

This procedure can be easily automated for all coefficients, allowing to find them in polynomial time, and avoiding the burdensome calculations of all the costs of the consistent quartet topologies embedded in t. Then the overall cost of t is simply obtained by Eq. 6. But this cost is that given by the particular assignment of the leaves as illustrated in Fig. 3. To evaluate all the costs of a fixed full unrooted binary tree topology, i.e. the flat structure topology in our example, we need to perform all the permutations of its assigned leaves and, for each performed leaves permutation, evaluate the correspondent tree cost. This will be explained in more detail in the next section.

4.1.4 Evaluation of all permutations of the leaves

This section explains how to address the algorithm task T2 stated in Sect. 4. Given a full unrooted binary tree topology, to find its minimal possible cost we need to evaluate the costs of all the possible combinations of the leaves attached to that specific considered topology. The combination which will give the minimum amongst these costs will be the best possible solution for that specific topology.

To consider all the possible combinations of attached leaves, we need to perform all the permutations of the leaves. Given a distance matrix $\varvec{D}$ with n objects, considering all the possible permutations of the leaves attached to a specific full unrooted binary tree topology takes a factorial time with respect to n:

$$\begin{aligned} \frac{n!}{2^{n\_term}}, \end{aligned}$$

where $n\_term$ stands for the number of terminal nodes of the considered topology. The factorial term n! is divided by $2^{n\_term}$ because we do not need to evaluate the permutations of two leaves attached to the same terminal node, since this permutation will not bring a change in the cost value; therefore we need to evaluate only one of the two possibilities for each terminal node.

The factorial growth of this phase of the algorithm further confirms the high computational complexity of the considered problem. To some extent the adopted representation of data through the Complete Pseudo-Adjacency matrix provides us some help. Indeed, to consider all these combinations we can work directly on $\varvec{A}$ and perform all the possible permutations of rows and columns with $i,j=(n-1),\ldots ,(2n-2)$, i.e. rows and columns of the Leaves sub-matrix, $\varvec{L}$. The permutations will involve also commuting the elements of the Coefficients sub-matrix, providing us automatically the corrected coefficient values for the new configuration, thus avoiding any additional calculation at this purpose. For example, consider the case of the flat structure topology with nine leaves, whose initial Complete Pseudo-Adjacency matrix is given in (5). For instance, in order to perform the permutation of leaves $l_3$ and $l_5$, we need to swap the rows and columns corresponding to those leaves, i.e. rows $A_{(:,~10)}$ and $A_{(:,~12)}$, and columns $A_{(10,~:)}$ and $A_{(12,~:)}$. The resulting matrix $\varvec{A}$ is the following:

where in yellow are depicted the swapped rows and columns.

To evaluate the cost associated to this new configuration we need just to multiply the transpose of the new Coefficients submatrix $\varvec{C}$ by the distance matrix $\varvec{D}$ (Eq. 6). After evaluated all the possible permutations, and calculated the correspondent cost values, the configuration providing the minimal overall cost will provide us the best possible solution obtained by the considered full unrooted binary tree topology.

The global optimum solution of the MQTC problem is then the solution with the minimum cost among the set of best solutions of all different full binary trees topologies. Given a distance matrix $\varvec{D}$ among n objects, we need therefore a generation mechanism of all the different boron tree topologies having n objects. This generation procedure will be explained in the next section.

4.1.5 Generation of all different structural boron tree topologies

This section shows how to address the algorithm task T1 stated in Sect. 4, which consists on the generation of all different boron trees topologies having n leaves. The enumeration of non-isomorphic boron trees, see generating formula A000672 in Sloane and Plouffe (1995)’s Encyclopedia of Integer Sequences, has exponentialgrowth rate (Rains and Sloane 1999), as shown in Fig. 4 and Table 1.

Fig. 4

Plot of sequence A000672

The procedure which we illustrate here is able to enumerate and to generate all non-isomorphic boron tree topologies with n leaves, and to discard topologies already evaluated, avoiding useless repetitions. To this aim we will work with the Structure sub-matrix $\varvec{K}$ only, since we do not require any information on the particular connections order of the attached leaves. Indeed $\varvec{K}$ is a $(n-2) \times (n-2)$ pseudo-adjacency matrix for the internal nodes and it represents itself the structural topology of the corresponding boron tree. To discard topologies already evaluated, we will make use of isomorphism invariants of graphs. That is, given two graphs $G_1$ and $G_2$, with adjacency matrices $A_1$ and $A_2$, these are isomorphic if and only if there exists a permutation matrix P such that $P \cdot A_1 \cdot P^{-1}=A_2$. In particular $A_1$ and $A_2$ are similar and therefore have the same minimal polynomial, characteristic polynomial, spectrum (i.e., the set of its eigenvalues), determinant, and trace, which serve as isomorphic invariants of the graphs. Following this concept, it is possible to discard incumbent full unrooted binary tree topologies if their isomorphic invariants coincide with those of the boron tree topologies already evaluated before. In this way repetitions of topologies are excluded.

Table 1 Enumeration of non-isomorphic boron trees given by the generating formula A000672 in Sloane and Plouffe (1995)’s Encyclopedia of Integer Sequences

The procedure used to generate all non-isomorphic full unrooted binary tree topologies with n leaves (i.e. $n-2$ internal nodes) is illustrated in Algorithm 1. The algorithm starts by generating the initial topology structure (Line 1), which, as already specified before, is chosen to be the flat structure (see Definition 5). This is indeed the simplest possible full unrooted binary tree topology, having boron degree equal to zero (see Fig. 2a). This first topology is stored in $\varTheta$ (Line 3.1), which represents the set of non-isomorphic full unrooted binary tree topologies already evaluated. To keep track of this structure, its isomorphic invariants are calculated and stored in the Box set, as shown in Line 3.2. Then another full unrooted binary tree topology is selected from $t_{struct}$ by using the generation function referred to as ${Next-struct(t_{struct})}$ (Line 3.3.1). The function is aimed at increasing by one the degree of the incumbent boron tree topology; for every branch of the incumbent tree, iteratively if there are two transition nodes in the same branch, they are transformed into one cross node and one leaf node, by modifying consequently the corresponding Structure sub-matrix. For example, considering the initial flat structure of Fig. 2a, the function would compute one branch only; from this branch, it will select the first two consecutive transition nodes, namely $k_2$ and $k_3$, and transform them into one cross node and one leaf node, yielding to the first graph depicted in Fig. 2b which has a boron degree increased by one with respect to the previous boron tree topology. This new topology will be is stored in $\varTheta$, along with its isomorphic invariants in Box. The procedure is iterated also for the other successive internal nodes, and eventually for other branches of the incumbent topology structure, discarding each time isomorphic topologies ($Invar(t_{struct}) \in Box$, see Line 3.3), while storing the new non-isomorphic topologies and the corresponding isomorphic invariants. The functions breaks when all full unrooted binary tree topologies have been evaluated (i.e. $t_{struct}$ is null, Line 3.3), giving in output the set of non-isomorphic full unrooted binary tree topologies $\varTheta$ with n leaves (Line 4).

At this point it is now possible to find the global optimum solution of the MQTC problem. For each different full binary tree topology produced, we need performing all possible permutations of its leaves, as specified in Sect. 4.1.4, and then finding the solution with the minimum cost for each considered topology. Finally, the minimal cost solution among this obtained set will provide the global MQTC best solution, as described in more detail in the next section.

4.1.6 Resulting exact algorithm

The overall solution approach that we propose for the MQTC problem results from the combination of the basic building blocks just described in the previous paragraphs. It has been been implemented by using the C++ programming language under the Microsoft Visual Studio .NET framework, version 4.6. The executables and source codes of the algorithm are available to download upon request from the authors. The details of our exact method are summarized in pseudo-code in the following Algorithm 2.

Given $n\ge 4$ objects to cluster, and an appropriate distance metric determining the dissimilarities among those objects, the algorithm starts from a symmetric distance matrix $\varvec{D}$ containing the $n \times n$ pairwise distances, normalized between 0 and 1, among the n objects. As explained in Sect. 4.1.1, the initial flat boron tree topology, $t_{struct}$, is generated by the Initialization($\cdot$) procedure; successively we will generate and evaluate all the other different boron tree topologies of n objects by following Algorithm 1, already explained in Sect. 4.1.5. We store the topology structure $t_{struct}$ under evaluation in $\varTheta$ (Line 2.1), and its isomorphic invariants in the Box set (Line 2.2). Next, the n objects are randomly placed to leaves of $t_{struct}$ by means of the Assign-leaves($\cdot ,\cdot$) procedure, producing the incumbent solution t (Line 2.3). Considering all the objects dissimilarities in $\varvec{D}$, the cost function value of this solution is evaluated as thoroughly explained in Sect. 4.1.3 and, being this the first considered solution, it is saved as the best solution to date, $t_{best}$ (Lines 2.5–2.5.1).

Now we need to evaluate all the leaves permutations in order to get the best solution for the specific full unrooted binary topology that is considered. This involves exchanging the position of each pair of leaves (procedure ${Swap-leaves(t,i,j)}$, $\forall i,j \in [1,n]$), and saving the solution with the lowest cost function value as best solution to date $t_{best}$ (Lines 2.6.3a–2.6.3b). Note that useless repetitions at this step are avoided as explained in Sect. 4.1.4.

Afterwards another full unrooted binary tree topology $t_{struct}$ is iteratively constructed, following the generation routine already illustrated in Algorithm 1 (Sect. 4.1.5), and repeating the previous steps (Lines 2.1–2.6.3). The overall procedure is iterated and throughout the execution of the algorithm, the best solution to date is stored as the binary tree $t_{best}$. The algorithm will stop when all full unrooted binary tree topologies and their permutations have been evaluated (i.e. $t_{struct}$ is null, Line 2.7) producing as output the minimal cost solution $t_{best}$ (Line 3), that represents the global optimum for the MQTC problem.

5 Gold standard foundation

Table 2 provides the gold standard for the MQTC problem. To create the gold standard, we have randomly generated 10 problem instances for each configuration of the number of internal nodes, n. In particular, given a specific n value, ten different dissimilarity matrices $\varvec{D}$ have been randomly generated, thus providing ten different problem instances for each n configuration. Each matrix $\varvec{D}$ contains the pairwise distances among the n objects. The dissimilarities are positive rational values which have been taken randomly in [0,  1], with the dissimilarity value 1 representing the largest distance between two objects. Note that in the process of generation of the distance matrices it has been imposed both the symmetry constraint of each $\varvec{D}$, and the triangle inequality (Diestel 2000), i.e.: $\forall i,j, i\ne j < n$, $D_{(i,~j)} \le D_{(i,~k)} + D_{(k,~j)}$, for any $k\ne i,j$. All the elements in the diagonal of each $\varvec{D}$ have been set equal to 0. Although we impose symmetry of $\varvec{D}$ and holding of triangle inequality to refer to Euclidean distances for the process of generation of the problem instances of the gold standard, the algorithm is in principle generalizable to other kind of distances for which these properties might not be valid or applicable.

Table 2 The table shows the exact solutions obtained by our algorithm on the considered MQTC problem instances

After generating the problem instances, we executed the exact algorithm to solve them, starting with the instances with the lowest number of internal nodes $n=4$, and then increasing it. The results are reported in Table 2, which shows the exact solutions obtained by our algorithm on the considered MQTC problem instances. On top are reported the computational results in terms of cost function values C(t) and on bottom the running times in seconds. The first column specifies the number of internal nodes n, the second column the number of different structural boron tree topologies for the given n, and the third one the number of permutations n! to consider for each of the boron tree topologies. The columns $\#1$ ...$\#10$ provide the results for each of the ten problem instances generated for each n. Our computational experiments were conducted on an Intel Quad-Core i5 5300U CPU (2.3 GHz) with 16 GB of RAM.

The instances with a low n value, e.g. $n=4$–8 were easily solved within few seconds. However increasing n the computational time started to increase considerable, becoming in the order of magnitude of minutes for $n=9$–10. Afterwards, even with a small increase of n, the computational time exploded confirming the high computational complexity of the problem, and for each instance the exact method required hours of computations. Instances with $n=12$, which required the evaluations of millions of different candidate solutions, produced by $479\cdot 10^6$ for each of the 37 different boron tree topologies, were solved in around 24 hours of computation for each problem instance. Therefore we stopped our computations with this value of n, producing an overall gold standard of 90 different problem instances.

Despite the factorial complexity growth on the number of candidate solutions to evaluate, these results represent the first known gold standard for the MQTC problem. It can be freely downloaded from https://sites.google.com/site/quartetmethod/GoldStandard.zip. This is a useful resource for any researcher in the field interested in the MQTC problem and it allows the validation of the performance of any quartet tree heuristic proposed for the MQTC problem.

6 Discussion

The implementation of the proposed exact algorithm contains some very interesting insights and still few open questions, which we depict in the following.

• To represent the topology structure of each solution we use a particular Pseudo-adjacency matrix representation, $\varvec{A}$, as explained in Sect. 4.1.2. This data representation allows us to embed important information within $\varvec{A}$ itself, avoiding the cumbersome recalculation of its coefficients at every iteration, and speeding up the overall algorithm computation. This data representation, for example, permits the quick evaluation of the cost function value of a full unrooted binary tree t simply by multiplying the transpose of its Coefficients submatrix $\varvec{C}$ in $\varvec{A}$ by the distance matrix $\varvec{D}$ given in input, as in Eq. 6.

• The particular relation that we discovered between the coefficient factors $coef{(\cdot ,\cdot )}$ stored in $\varvec{C}$ and the weights stored in the Structure sub-matrix $\varvec{K}$, expressed by means of the formula of triangular numbers (Eq. 7) is very handful. We found that the coefficient multiplying $D_{(l_a,~l_b)}$, namely coef(a, b), is equal to the sum of the triangular numbers of the weights, subtracted by one, of the outgoing edges linked to internal nodes which are excluded from the subgraph obtained by connecting nodes a and b. As explained is Sect. 4.1.3, this fascinating relationship permits the calculation of the coefficients of $\varvec{C}$ in a fast and automatic way, avoiding at each iteration the burdensome enumeration procedure of the ${n \atopwithdelims ()4} = \frac{n!}{4!(n-4)!}$ consistent quartet topologies embedded in a boron tree t, and the sum of the costs of all these quartets.

• The adopted data representation through $\varvec{A}$ provides us a shortcut in the evaluation of all permutations of the leaves, which by default has an high factorial computational complexity with respect to the number of leaves. Indeed, to consider all the leaves combinations we work directly on $\varvec{A}$ and perform all the possible permutations of rows and columns with $i,j=(n-1),\ldots ,(2n-2)$, i.e. rows and columns of the Leaves sub-matrix, $\varvec{L}$. These permutations involve also commuting the elements of the Coefficients sub-matrix, providing us automatically the corrected coefficient values for the new configuration, thus avoiding any additional calculation at this purpose.

• In addition, as explained in Sect. 4.1.4, given a boron tree t and its number of terminal nodes, $n\_term$, the factorial n! related to the evaluation of all the permutations of the leaves of t is soften by the factor $2^{n\_term}$, since we can skip the computation of the permutations of two leaves attached to the same terminal node, because this does not provide any change in the cost function value.

• We also found out experimentally that the traces, say $tr_k(n)$, of all the possible Structure sub-matrices $\varvec{K}$ for a given number of nodes n are always equal. In addition $tr_k(n)$ linearly increases by a coefficient 2 with the respect to the number of nodes n , i.e. $tr_k (n+1)= tr_k (n) + 2$ with $n>4$ and $tr_k (4)=2$, as shown in Fig. 5.

• Similarly, we found out experimentally that the smallest eigenvalues, say $min\_\lambda _k(n)$, of all the possible Structure sub-matrices $\varvec{K}$ for a given number of nodes n are always equal. In addition $min\_\lambda _k(n)$ linearly decreases by a coefficient 1 with respect to the number of nodes n , i.e. $min\_\lambda _k(n+1)= min\_\lambda _k(n) - 1$ with $n>4$ and $min\_\lambda _k(4)=-1$, as shown in Fig. 6.

Fig. 5

Plot of traces $tr_k(n)$ of the Structure sub-matrices $\varvec{K}$ which increase linearly with the number of nodes n by a coefficient 2

Fig. 6

Plot of smallest eigenvalues $min\_\lambda _k(n)$ of the Structure sub-matrices $\varvec{K}$ which decrease linearly with the number of nodes n by a coefficient 1

7 Conclusion

In this paper we considered the minimum quartet tree cost (MQTC) problem, a graph combinatorial optimization problem suited for general hierarchical clustering. Given a set of $n \ge 4$ data objects and their pairwise costs (or distances), the goal of the MQTC problem consists of finding the full unrooted binary tree having the n objects as leaves and minimal sum of the costs of the ${n \atopwithdelims ()4}$ embedded (or consistent) quartet topologies. The MQTC problem is NP-complete and in the literature some heuristics have been proposed in order to get approximate solutions to the problem.

This paper has presented an exact solution approach for the MQTC problem. The algorithm is able to get exact solutions for relatively small problem instances, due to the high problem complexity. These solutions represent the first known gold standard for the MQTC problem, which represents a meaningful resource to be used as a benchmark for validating the performance of any approximate solution approach proposed for the problem. In addition, the algorithm contains some very interesting concepts and insights which may be useful for the construction of more efficient heuristics, obtained either by improving the MQTC heuristics to date, or by hybridization of the exact method with some other heuristic producing some advanced mat-heuristics.