Abstract
Virtualization technology allows service providers to operate data centers in a cost-effective and scalable manner. The data center network (substrate network) and the applications executed in the data center (virtual networks) are often modeled as graphs. The nodes of the graphs represent (physical or virtual) servers and switches, and the edges represent communication links. Nodes and links are annotated with the provided and required resources (e.g., memory and bandwidth). The NP-hard virtual network embedding (VNE) problem deals with the embedding of a set of virtual networks to the substrate network such that (i) all (resource) constraints of the substrate network are fulfilled, and (ii) an objective is optimized (e.g., minimizing the communication costs). The existing two-step highly customizable model-driven virtual network embedding (MdVNE) approach combines model transformation (MT) and integer linear programming (ILP) techniques to solve the VNE problem based on a declarative specification. MdVNE generates element mapping candidates from an MT specification and identifies an optimal and correct embeddings using an ILP solver. In the past, developers created the MT and ILP specifications manually and needed to ensure carefully that both are compatible and respect the problem description. In this article, we present a novel construction methodology for synthesizing the MT and ILP specification from a given declarative model-based VNE problem description. This problem description consists of a metamodel for substrate and virtual networks, additional OCL constraints, and an objective function that assigns costs to a given model. This methodology ensures that the derived embeddings are correct w.r.t. the metamodel and the OCL constraints, and optimal w.r.t. the optimization goal. The novel model-based VNE specification is applicable to different network domains, environments, and constraints. Thus, the construction methodology allows to automate most of the steps to realize a correct and optimal VNE algorithm compared to a hand-crafted VNE implementation. Furthermore, the simulative evaluation confirms that using MT techniques reduces the time for solving the VNE problem considerably in comparison with a purely ILP-based approach.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
Today, online services such as social networking and e-commerce are ubiquitous and place high demands on service providers in terms of availability and scalability. The enormous amount of data involved in the analysis, processing, and storage tasks pushes traditional network topologies and management techniques to their limits [9]. Cloud computing is a leading technology in this area and allows users to meet the high demands on availability, scalability, and flexibility. Data centers provide the required large number of data and storage servers. While operating these complex environments, hardware virtualization decouples the underlying hardware infrastructure from the running applications. This allows operators to provide new services automatically and to migrate these services to other physical servers flexibly, scalably, and economically. The achieved high utilization of the physical network and hardware resources leads to a reduced energy consumption. The configuration of these virtual networks and servers is standardized and, often, managed centrally. This allows a service provider to operate a data center in a hardware- and vendor-independent way.
The embedding of virtual networks in data centers is a complex task. The virtual network embedding (VNE) problem describes a general optimization problem for embedding a set of virtual networks into a substrate network (e.g., a data center) [17]. Common optimization goals are the minimization of communication or monetary costs, or used hardware resources [57]. Besides, structural, functional, and non-functional constraints must be fulfilled during the embedding. Structural constraints affect the resources of the physical servers and links, which must be respected (e.g., computing capacity of servers and bandwidth of links). The functional and non-functional constraints are defined as service-level agreements, security policies, or hardware-specific functionalities (e.g., firewalls). The abundance of possible combinations of (non-)functional constraints with different network topologies, application scenarios, and optimization goals makes the development, adaptation, simulation, and comparison of VNE algorithms challenging.
Due to the increasing importance of cloud computing and network virtualization, research to solve the VNE problem in data centers has been intensified [9, 17]. In addition to embedding one virtual network after another, several virtual networks can also be embedded simultaneously (e.g., to improve the utilization of the data center). In general, VNE is an NP-hard optimization problem with a large search space [5]. Therefore, various algorithms have been proposed to reduce the search space and, thus, the runtime to solve the VNE problem. Surveys on VNE (e.g., [5, 17]) focus on two major types of approaches: approaches based on heuristics (e.g., [8, 20, 60]) and approaches based on integer linear programming (ILP) (e.g., [56, 60]). Heuristics-based approaches are tailored to particular infrastructures and application scenarios. These approaches tend to reduce the search space drastically to achieve an approximation of the optimal solution of the VNE problem within an acceptable amount of time even for large data centers. For example, Guo et al. [20] introduce a heuristics-based algorithm to map virtual networks in the smallest possible subset of a tree-based data center (with server as leaves and switches as inner nodes), only taking bandwidth constraints into account. Zeng et al. [60] additionally consider the traffic between virtual machines and minimize the total communication costs between them but without taking the bandwidth of the links into account. However, both algorithms lack optimality guarantees regarding the compliance with all basic constraints. Also, adapting these algorithms to other usage scenarios and network topologies is difficult. In contrast, ILP-based approaches support a wide range of applications, ensuring compliance with constraints and requirements, and achieving optimal results. Thus, not only (hard) constraints, like in heuristics-based algorithms, can be integrated into the ILP program, but also all kinds of constraints and requirements in addition to the optimization goal. Due to the large search space, the applicability is limited to small data centers [56].
To close the gap between hand-crafted highly adapted heuristics-based and purely ILP-based solutions, we proposed an iterative working model-driven virtual network embedding (MdVNE) approach for tackling the VNE problem using a combination of model transformation (MT) and ILP techniques [49]. Figure 1 shows a schematic view of MdVNE. An MdVNE configuration (in the middle of Fig. 1) represents the problem specification for MdVNE and consists of two parts: MT rules and an ILP formulation including an objective function. The MT rules define possible element mappings from virtual to substrate elements  and are used to generate possible element mapping candidates
and are used to generate possible element mapping candidates  . An element mapping candidate corresponds to a potentially possible element mapping between a virtual and substrate element. From the set of element mapping candidates
. An element mapping candidate corresponds to a potentially possible element mapping between a virtual and substrate element. From the set of element mapping candidates  , the candidate selection step
, the candidate selection step  chooses a correct and optimal element mapping
chooses a correct and optimal element mapping  by solving the ILP problem. The MT-based candidate generation reduces the number of potential element mappings for the candidate selection step compared to an ILP-only candidate selection. Importantly, the candidate generation step does not generate all combinations of possible embeddings of a virtual network into a substrate network. Instead, potentially allowed individual element mappings of virtual nodes and links to substrate nodes and links are generated. These element mappings are then combined with additional constraints to reduce the number of possible embeddings. After executing the MT rules, the set of element mapping candidates still contains an optimal solution that fulfills all specified constraints (i.e., is correct). Here, an optimal solution achieves the global maximum (minimum) of the objective function for the VNE problem. The MdVNE approach allows developers to create novel VNE algorithms in a declarative manner (thanks to the MT-based specification) while considering optimization goals and constraints of the VNE problem description. This adaptability and the ensured optimality of the resulting embeddings make it possible to compare different VNE algorithms (e.g., heuristics) with their specific constraints and network topologies. Deviations from an optimal solution can be assessed quantitatively and qualitatively. Therefore, MdVNE also fosters the creation of benchmarks for VNE algorithms.
by solving the ILP problem. The MT-based candidate generation reduces the number of potential element mappings for the candidate selection step compared to an ILP-only candidate selection. Importantly, the candidate generation step does not generate all combinations of possible embeddings of a virtual network into a substrate network. Instead, potentially allowed individual element mappings of virtual nodes and links to substrate nodes and links are generated. These element mappings are then combined with additional constraints to reduce the number of possible embeddings. After executing the MT rules, the set of element mapping candidates still contains an optimal solution that fulfills all specified constraints (i.e., is correct). Here, an optimal solution achieves the global maximum (minimum) of the objective function for the VNE problem. The MdVNE approach allows developers to create novel VNE algorithms in a declarative manner (thanks to the MT-based specification) while considering optimization goals and constraints of the VNE problem description. This adaptability and the ensured optimality of the resulting embeddings make it possible to compare different VNE algorithms (e.g., heuristics) with their specific constraints and network topologies. Deviations from an optimal solution can be assessed quantitatively and qualitatively. Therefore, MdVNE also fosters the creation of benchmarks for VNE algorithms.
The top part of Fig. 1 sketches the major contribution of the article: a novel methodology for deriving an MdVNE configuration systematically based on a declarative model-based specification of the VNE problem description. The model-based VNE problem description consists of
-
a metamodel, which specifies structural properties of valid virtual networks, substrate networks, and embeddings of virtual to substrate networks,
-
additional OCL constraints, which ensure that all network-, resource-, and use-case-specific constraints are fulfilled,
-
an objective function, which specifies the optimization goal for the VNE problem.
The construction step transforms this model-based specification into an MdVNE configuration and ensures that each candidate selected in step  is correct w.r.t. the metamodel and the OCL constraints, and optimal w.r.t. the optimization goal. This construction step ensures a strong optimality (search for a global optimum) and further extends the MdVNE approach presented in [49].
is correct w.r.t. the metamodel and the OCL constraints, and optimal w.r.t. the optimization goal. This construction step ensures a strong optimality (search for a global optimum) and further extends the MdVNE approach presented in [49].
The following four major contributions of this article extend our previous work [48] considerably:
-
(i) We define the VNE problem in data centers using model-based techniques, such as class diagrams and OCL constraints, which are complemented by a specification of the optimization goal (see Sect. 2). This declarative representation is formal and human-readable at the same time.
-
(ii) We show how to derive an MdVNE configuration systematically from a model-based specification using results on the synthesis of model construction rules [26] and the refinement of MT rules based on OCL constraints [24, 41] (see Sect. 3). This allows for automating most of the steps to realize a correct and optimal VNE algorithm.
-
(iii) We show that an MdVNE configuration resulting from the construction step is correct w.r.t. the metamodel including the OCL constraints and optimal w.r.t. the optimization goal (see Sect. 4). Thereby, we prove that any embedding algorithm developed using MdVNE return optimal and correct embeddings.
-
(iv) We present and discuss results of a simulative evaluation of MdVNE in comparison with a purely ILP-based approach w.r.t. scalability, optimality, and correctness (see Sect. 6). Thereby, we investigate the question if the time for solving the VNE problem can be reduced by using MT techniques.
In relation to our previous work [48], the set-theoretical aspects of the search spaces introduced in [48] are used and significantly extended to prove the correctness and optimality of the new construction methodology. In the evaluation section, the setup from [48] is reused and extended by a data set that reflects the characteristics of real-world scenarios more precisely. The research questions are considered and discussed more intensively, so that RQ2 from [48] is represented by RQ1 and 2, and RQ3 reappears within the discussion of threats to validity. To maintain continuity between this article and [48], the introduction and basic ILP-based VNE problem description have only been adjusted slightly.
This article is structured as follows along the steps and artifacts in Fig. 1. In Sect. 2, we present an established VNE problem description based on ILP and introduce our novel model-based problem approach. In Sect. 3, we present the novel construction methodology for generating the MT rules and the ILP formulation from the model-based VNE problem description. After that, we prove correctness and optimality for the novel construction methodology in Sect. 4. Then, we present in Sect. 5 the tool support to simulate the derived algorithms. In Sect. 6, we present evaluation results and a discussion regarding the scalability, correctness, and optimality of the MdVNE implementation. After a discussion of related work in Sect. 7, we conclude this article in Sect. 8.
2 VNE problem description
In this section, we define the VNE problem for data centers formally. The VNE problem description is divided into three parts: (i) the substrate and virtual network models, (ii) the constraints, and (iii) the objective of the optimization problem. The problem description considers the embedding of one or more virtual networks into a substrate network and is an NP-hard problem [5]. In general, a substrate network can also be a virtual network. Therefore, the general VNE problem considers nested networks and different abstraction layers [17]. In the following, we focus on the VNE problem for data centers [9]. In this setting, a substrate network represents a physical data center.
The presented problem description consists of a model-based and an ILP-based part. The model-based specification in Sect. 2.1 (Fig. 1) is a novel VNE problem description and one major contribution of this article. It consists of a metamodel (represented by a class diagram) as detailed in Sect. 2.1.1, a set of OCL constraints in Sect. 2.1.2, and an objective function in Sect. 2.1.3. The ILP formulation in Sect. 2.2 is inspired by Sahhaf et al. [43]. It consists of three parts: substrate and virtual network model (Sect. 2.2.1), decision variables (Sect. 2.2.2), linear equations and inequalities (ILP constraints, Sect. 2.2.3), and an objective function (Sect. 2.2.4).
2.1 Model-based problem description
The model-based specification (see also Fig. 1) for the VNE problem description is divided into the following three parts: (i) substrate and virtual network models, (ii) constraints, and (iii) the optimization goal. In the following, we provide details on each of these parts.
2.1.1 Metamodel
We employ metamodeling as a technique for specifying the structural properties of valid virtual networks, substrate networks, and embeddings of virtual networks to substrate networks. A metamodel MM characterizes a set of valid model instances \(\mathfrak {L}(MM) \) that conform to this metamodel. It consists of classes, attributes, and associations with multiplicities. We use class diagrams [18] as concrete syntax for metamodels. Figure 2 shows the joint metamodel for (i) virtual networks on the left-hand side (VirtualNetwork), (ii) substrate networks on the right-hand side (SubstrateNetwork), and (iii) element mappings from virtual to substrate network elements as annotated associations in the center.
The Virtual and Substrate prefixes indicate to which network each class belongs. A substrate network, modeled as an undirected weighted graph, consists of nodes (SubstrateNode), links (SubstrateLink), and paths (SubstratePath). Additionally, a substrate node can either be a server or a switch. The condition that each substrate node is either a server or a switch is represented by the two subtypes SubstrateServer and SubstrateSwitch of the abstract type SubstrateNode. Substrate nodes and links provide resources. For example, we consider the following resources in this article: A server has integer-valued computing capacity (cpu), memory (memory), storage (storage), a substrate link has an integer-valued bandwidth (bandwidth), and a switch has no associated resources. A path has a source and a target node, and is composed of substrate links. The acyclicity of paths cannot be expressed graphically in the metamodel. We ensure this property by generating all substrate paths during the creation of the substrate links. Whenever a substrate link is created, the corresponding paths are also generated up to a fixed number of hops (e.g., depending on the network topology). Therefore, the generation of all paths is only done once during the initialization of the substrate network. A substrate link has source and target associations to specify the source and target node.
The structure of the metamodel part for virtual networks, also, modeled as an undirected weighted graph, is similar to the one for substrate networks. In contrast to the substrate network, virtual node and link resources are interpreted as required instead of provided resources. Another major difference is that a virtual node implements exactly one service. This means, a virtual node is either a virtual server or a virtual switch and a substrate server can host a virtual server or switch. Additionally, a virtual server has at most one fail-over server. A fail-over server operates as backup or standby server. If the master server fails, its applications are migrated to the fail-over server. To represent the use-case-specific constraint that a virtual server may have at most one fail-over server, the metamodel contains a self-association of the VirtualNode class.

The element mappings of virtual nodes and links are represented as associations between virtual and substrate elements (e.g., VirtualServer.substrateServer). The multiplicities (i.e., 0..1) at the association ends of the substrate elements indicate that each virtual element has at most one corresponding substrate element.

2.1.2 OCL constraints
The metamodel in Fig. 2 does not encode all constraints that a valid solution for the VNE problem must fulfill. To ensure that all network-, resource-, and use-case-specific constraints are fulfilled, we complement the metamodel with a set of constraints formulated in the Object Constraint Language (OCL) [19]. Since the full scope of OCL is not required to describe common constraints from the VNE domain, we limit ourselves in this article to a subset of OCL invariants. This subset consists of the Essential OCL (EOCL) [19, 41], the two-valued, first-order logic fragment of OCL, and the iterate() operation [19], which is restricted to the summation of the individual elements in the set to be iterated (analogous to the sum() operation). Since the iterate() operation is required for the summation of resources (CPU, memory, storage, and bandwidth), we define auxiliary functions for each resource type. As an example, the auxiliary function for summing up the CPU resources over a set of elements (e.g., virtual servers) is presented below. The other auxiliary functions for memory, storage, and bandwidth are defined analogously.
Modeling Node Constraints
The node constraints ensure that (1) all virtual nodes are mapped to exactly one substrate node, (2) a substrate server can host a virtual server or switch and a substrate switch only a virtual switch, and (3) the resources of a substrate node are not overbooked by the resource demands of the virtual nodes mapped to it. The first constraint is ensured by the metamodel (Fig. 2) because the multiplicities of the associations between VirtualServer and SubstrateServer as well as between VirtualSwitch and SubstrateSwitch only permit to connect a virtual element to exactly one substrate element. The second constraint is also ensured by the metamodel because a virtual server (switch, resp.) can only be mapped to a substrate server (switch, resp.). The only node constraints that are not covered by the metamodel are the resource constraints for the computing capacity, memory, storage, and bandwidth. These constraints require that the aggregated required resources of all virtual nodes that are mapped to a substrate node do not exceed the available resources of this substrate node. Therefore, we represent this requirement using three additional OCL constraints. As an example for these constraints, we present the constraint for the CPU resource \(C_{\text {cpu}}\). The other constraints can be found in Appendix A.1.


Modeling Link Constraints The link constraints ensure that (1) a virtual link is mapped to exactly one substrate path, (2) the source and target nodes of a virtual link are mapped to the source and target nodes of the substrate path, and (3) the resources of the links in a substrate path are not overbooked by the virtual links mapped to this substrate path.
The first link constraint demands that a virtual link is mapped to exactly one substrate path. This constraint is ensured by the multiplicity (i.e., \(0\dots 1\)) of the association VirtualLink.substratePath. The second link constraint require that the source and target node of a virtual link are mapped to the source and target nodes of the substrate path. This is reflected by the following OCL constraint \(C_{\text {src}}\) , whereas \(C_{\text {trg}}\) is presented in Appendix A.1.

The third link constraint ensures that the bandwidth of the substrate path is not overbooked by the bandwidth of the mapped virtual links and is similar to the node resource constraints (e.g., \(C_{\text {cpu}}\)). In our running example, we use the following OCL constraint \(C_{\text {bw}}\).

Modeling Use-Case-Specific Constraints A use-case-specific constraint is a functional or non-functional constraints that depends on the use case and may be specified in service-level agreements, business models, or security policies [12]. As an example of a use-case-specific constraint, we integrate the fail-over constraint into the set of OCL constraints. One condition of the fail-over constraint is that a virtual server has at most one fail-over server. This condition is ensured by the metamodel due to the 0..1-multiplicity of the VirtualNode.failover association. The remaining two conditions need to be encoded using OCL. First, a virtual server shall not be its own fail-over server \(C_{\text {fo1}}\). Second, the substrate servers of a master and its fail-over server shall be distinct \(C_{\text {fo2}}\).



2.1.3 Objective function
The objective function of a VNE problem varies depending on the application scenario, service provider, or business model (like infrastructure as a service [10]). A common optimization goal is to minimize the aggregated communication costs for the virtual servers in the substrate network as in [60]. We assume that the optimization function can be represented as a linear combination of constant values multiplied by the respective mapping variables. Furthermore, we assume that this cost function is defined by the network operator. Possible reference points for a cost calculation in practice include required resources of virtual links and provides resources of the substrate network, as well as, operating cost, delay, or the substrate network structure. For common data center topologies, cost matrices and an optimization function can be found in [33]. To calculate the communication costs, we use the cost matrix \(cost^{l}_{p}\), which is constant at runtime and defines the communication costs for each possible element mapping of a virtual link l to a substrate path p. In this article, we use the cost function from [33] for a 2-tier network with a VL2 topology, which is defined as follows:
For the model-based specification we are using an extension of the OCL language proposed in [29] to specify the optimization function. This extension allows us to integrate the objective function into the OCL expressions. The optimization goal is to minimize the aggregated communication costs of all virtual links. To calculate the total communication costs, the costs of all possible element mappings of virtual links on substrate paths must be summarized. The post conditions ensure that all virtual links are mapped to substrate paths and virtual servers (switches) to substrate servers (servers or switches). This results in the following objective function:

2.2 ILP-based problem description
In this subsection, we introduce the substrate and virtual network model (Sect. 2.2.1), the decision variables (Sect. 2.2.2), linear equations and inequalities (ILP constraints, Sect. 2.2.3), and an objective (Sect. 2.2.4) as ILP for the VNE problem.
2.2.1 Network model
Substrate Network Model We model the substrate network as an undirected weighted graph \(G^S=(N^S, L^S)\) containing a set of typed substrate nodes \(N^S\) and links \(l_{uv} \in L^S\). A path \(p_{uv} \in P^S\) in the substrate network consists of a sequence of acyclic connected links that connect nodes u and v (see ILPsPath).

Every node provides the following resource types: computing capacity (\(C^S_u\)), memory (\(M^S_u\)), storage (\(S^S_u\)), a substrate link a bandwidth (\(B_{l_{uv}}^S\)), and a switch has no associated resource type (see ILPsRes).

A substrate node exposes a set of service types (Sr, Sw) to define which services (server, switch) may run on this node (see ILPsTyp). The service type Sr includes the service type Sw because a substrate server can also host a virtual switch.

Table 1 summarizes the introduced notation for substrate networks.
Virtual Network Model Similar to the substrate network, we model a virtual network as an undirected weighted graph \(G^V=(N^V, L^V)\). The resources and services of the virtual nodes \(N^V\) and virtual links \(l_{ij} \in L^V\) are defined similarly to the substrate network as follows.

Equation (ILPvFo) encodes the relationship between a fail-over and a master server.

Table 2 summarizes the notations for virtual networks.
2.2.2 Mapping model and decision variables
The mapping model summarized in Table 3 determines the set of decision variables of the ILP problem and specifies the mapping of virtual elements to substrate elements. A node-mapping variable \(x_u^i \in X\) indicates whether a virtual node i is mapped to a substrate node u. If \(x_u^i = 1\), virtual node i is mapped to substrate node u. For each pair of substrate and virtual node, a node-mapping variable exists.

Analogously, a link-mapping variable \(y_{uv}^{ij} \in Y\) indicates whether a virtual link \(l_{ij}\) is mapped to a substrate path \(p_{uv}\). If \(y_{uv}^{ij} = 1\), the virtual link \(l_{ij}\) is mapped to the substrate path \(p_{uv}\).


2.2.3 ILP constraints
In the following, we specify all technical, functional, and non-functional requirements for embedding a virtual network to a substrate network as ILP constraints. We divide these requirements into node, link, and use-case-specific constraints. A valid embedding of a virtual network fulfills all constraints.
Node Constraints The first constraint ILPnc states that every virtual node is mapped to exactly one substrate node. Therefore, if an element mapping for a virtual node \(i \in N^V\) and substrate node \(u \in N^S\) is chosen (\(x_{u}^i = 1\)), then all other element mappings \(x_{v}^i\) for a substrate node \(v \ne u \in N^S\) must be rejected (\(x_{v}^i = 0\)). Given \(N^S~=~\{u_1,\ldots ,u_n\}\), \(\sum _{u \in N^S} x_{u}^i\) denotes the sum over all variables \(x_1^i,\dotsc ,x_n^i\).

The second constraint ILPnTyp requires that a substrate node u is capable of hosting the service types of all virtual nodes i mapped to u. A substrate server can host a virtual server or switch and a substrate switch only a virtual switch. We use the \(\le \)-operator to encode this logical implication [23, 31]. For example, choosing an element mapping \(x_u^i = 1\) with \(i^{Sr}=1\) implies that \(u^{Sr}=1\), that is, \(i^{Sr} x_u^i \le u^{Sr}\). Note that \(i^{Sr}\) and \(i^{Sw}\) are constants and not decision variables to ensure a linear inequality. The variables \(i^{Sr}\) and \(i^{Sw}\) are equal to 1 iff the virtual node i hosts a server and switch, respectively. In contrast, \(x_u^i\) is the decision variable for the element mapping.

The last three similarly structured node constraints ILPcpu, ILPmem, and ILPsto (ILPmem, and ILPsto can be found in Appendix A.1) ensure that the resources of a substrate node u are not overbooked by the resource demands of the virtual nodes mapped to u. The required resources (e.g., computing capacity \(C_i\)) are coefficients of the corresponding mapping variable \(x_u^i\) and contribute to the sum if the mapping variable is set (i.e., \(x_u^i = 1\)).


Link Constraints The link constraint ILPlc ensures that a virtual link is mapped to exactly one substrate path.

The next similarly structured link constraint ILPsrc (ILPtrg can be found in Appendix A.1) ensures that the source and target nodes of a virtual link are mapped to the source and target nodes of the substrate path, respectively. As before, we encode the logical implication using the \(\le \)-operator.

The last constraint ILPbw ensures that the resources of the links e in the substrate path \(p_{uv}\) are not overbooked by the virtual links \(l_{ij}\) mapped to \(p_{uv}\). The used bandwidth resources are coefficients (\(B_{l_{ij}}\)) for the mapping variables \(y_{uv}^{ij}\) and contribute to the sum only if the respective mapping variable is selected (i.e., \(y_{uv}^{ij}=1\)).

Use-Case-Specific Constraints ILPfo illustrates the idea of use-case-specific constraints. It shows constraints that ensure that a master node and its fail-over node must be different and not placed on the same substrate node. Also, every master must have at most one fail-over node.


2.2.4 ILP objective function
The following objective function minimizes the aggregated cost over all link mappings.


3 Model-driven virtual network embedding
In this section, we first present our approach for deriving correct and optimality-preserving MdVNE configurations. In Sect. 3.1, we describe the original MdVNE approach [49], which automatically derives optimal embedding decisions based on a given MdVNE configuration, consisting of a MT specification for candidate generation and an ILP specification for candidate selection. Previously, the developer was responsible for deriving these two specifications and for ensuring that both specifications were compatible (e.g., that the MT specification does not neglect optimal candidates). To overcome this manual step, we present a systematic construction methodology in Sect. 3.2. Using the methodology, we derive the MT and ILP specifications from a common model-based problem specification in a correct and optimality-preserving manner. This construction methodology is one major contribution of this article.
3.1 The MdVNE approach
The original MdVNE approach is illustrated in the lower part of Fig. 1. Before MdVNE can be applied, an MdVNE configuration is created consisting of the two parts: (i) a set of MT rules for candidate generation, and (ii) an ILP formulation for candidate selection. This configuration encodes domain knowledge (e.g., about allowed element mapping relations and resource constraints), is independent of the actual sequence of virtual network requests (VNRs), and the actual substrate network instance.
At runtime, the user first creates one or more VNRs, which represent the virtual networks that shall be embedded into the substrate network (Fig. 1 ). In general, the substrate network already contains embedded virtual networks (indicated by gray rectangles) and possesses free resources (indicated by white rectangles). A VNR that still needs to be processed is decorated with a red
). In general, the substrate network already contains embedded virtual networks (indicated by gray rectangles) and possesses free resources (indicated by white rectangles). A VNR that still needs to be processed is decorated with a red  -symbol.
-symbol.
The MdVNE approach works iteratively. In each iteration, one or more pending VNRs are selected (here: \(\text {VNR}_{1}\)), and all possible element mapping candidates for these requests are generated using the MT rules of the MdVNE configuration (see  in Fig. 1). The MT rules filter out candidates that violate structural or resource constraints expressible by the MT specification. Conversely, the MT rules in the MdVNE configuration have to guarantee that the result set of the candidate generation step contains at least one correct and optimal element mapping candidate if a solution exists.
in Fig. 1). The MT rules filter out candidates that violate structural or resource constraints expressible by the MT specification. Conversely, the MT rules in the MdVNE configuration have to guarantee that the result set of the candidate generation step contains at least one correct and optimal element mapping candidate if a solution exists.
In MdVNE, the user specifies the MT rules for candidate generation as a triple graph grammar. A triple graph grammar (TGG) [45] describes possible element mappings between two graphs (here, a virtual and a substrate network) together with a third correspondence graph (here, the element mapping between virtual and substrate networks) in a declarative manner. The declarative TGG rules can be operationalized in multiple ways. In the context of MdVNE, the two involved graphs (i.e., virtual and substrate network) are given, and the correspondence graph is missing. This type of operationalization is called consistency checking [31]. MdVNE builds on the MT tool eMoflon [30] for automating the candidate generation step.
The candidate generation step results in a set of possible element mapping candidates, as shown in Fig. 1 . This set may still contain element mapping candidates that are: (i) incorrect (i.e., violate the metamodel or an OCL constraint not expressible by the MT rules) or (ii) fulfill all domain constraints but are suboptimal w.r.t. the optimization goal. Therefore, in the candidate filtering step
. This set may still contain element mapping candidates that are: (i) incorrect (i.e., violate the metamodel or an OCL constraint not expressible by the MT rules) or (ii) fulfill all domain constraints but are suboptimal w.r.t. the optimization goal. Therefore, in the candidate filtering step  , correct and optimal element mappings are composed of the set of optimal element mapping candidates resulting from step
, correct and optimal element mappings are composed of the set of optimal element mapping candidates resulting from step  . This selection step is performed based on the ILP constraints that are part of the MdVNE configuration, and an ILP encoding of the set of element mapping candidates. An ILP solver is then used to determine an embedding for the VNR that is correct w.r.t. the constraints and optimal w.r.t. the optimization goal.
. This selection step is performed based on the ILP constraints that are part of the MdVNE configuration, and an ILP encoding of the set of element mapping candidates. An ILP solver is then used to determine an embedding for the VNR that is correct w.r.t. the constraints and optimal w.r.t. the optimization goal.
Finally, the determined optimal embedding calculated by the ILP solver is deployed to the substrate network, as shown in Fig. 1 . Afterward, the embedding of the virtual network is finished (indicated by a green check mark
. Afterward, the embedding of the virtual network is finished (indicated by a green check mark  ) and (if it exists) the next VNR is processed.
) and (if it exists) the next VNR is processed.
The description of the MdVNE approach reveals that, on the one hand, it is crucial that the candidate generation step does not neglect correct element mappings and, therefore, at least one optimal candidate exists. On the other hand, it is desirable to reduce the size of the set of element mapping candidates as much as possible.
3.2 From model-based specification to MdVNE configuration
In [48, 49], the developer was responsible for ensuring that the consistency specification (for the candidate generation step  ) covers all valid element mappings and that the additional ILP constraints and objective function (for the candidate selection step
) covers all valid element mappings and that the additional ILP constraints and objective function (for the candidate selection step  ) ensure that the selected candidate is correct w.r.t. all constraints and additionally optimal w.r.t. the optimization goal. Thus, the task of deriving an MdVNE configuration requires deep expertise in VNE, is error prone and time-consuming, and entails a correctness proof for the required properties.
) ensure that the selected candidate is correct w.r.t. all constraints and additionally optimal w.r.t. the optimization goal. Thus, the task of deriving an MdVNE configuration requires deep expertise in VNE, is error prone and time-consuming, and entails a correctness proof for the required properties.
One major contribution of this article is that we propose a systematic correct-by-construction approach to derive the MdVNE configuration consisting of MT rules and an ILP formulation from a declarative model-based specification of the domain (highlighted as dashed frame in the upper part of Fig. 1). This approach also ensures that only incorrect candidates are excluded by the MT rules and that at least one optimal solution is found if exists.
3.2.1 Overview of construction methodology
Our approach starts with a model-based problem description (see also Sect. 2.1) consisting of three parts. First, the metamodel characterizes the superset of all structurally valid substrate and virtual networks. Second, declarative OCL constraints encode additional structural consistency properties that cannot be expressed in the metamodel (e.g., regarding the aggregated resources of nodes and links), and element mapping consistency properties that a valid embedding fulfills. Third, an optimization goal, also specified in OCL, determines which objective function to apply (e.g., minimizing communication costs or energy consumption).
Our approach transforms the declarative model-based problem description into a correct and optimality-preserving MdVNE configuration. The MdVNE configuration is correct w.r.t. the model-based specification if the candidate selection step only returns element mapping candidates that are allowed according to the metamodel and the OCL constraints. The MdVNE configuration is optimality-preserving w.r.t. the model-based specification if it is correct and each embedding returned by the candidate selection step fulfills the optimization goal. Our correct-by-construction transformation approach operates in three major steps ( ,
,  , and
, and  ), as shown in Fig. 1. These steps split and transform the metamodel, OCL constraints, and optimization goal into MdVNE configuration artifacts for the candidate generation step (green top-down arrows) and the candidate filtering step (blue top-down arrows).
), as shown in Fig. 1. These steps split and transform the metamodel, OCL constraints, and optimization goal into MdVNE configuration artifacts for the candidate generation step (green top-down arrows) and the candidate filtering step (blue top-down arrows).
First, we derive a set of basic TGG rules to cover the metamodel  . Following the approach by Kehrer et al. [26], we ensure constructively that any possible pair of related virtual and substrate network models that conforms to the metamodel can be constructed by a sequence of applications of the basic TGG rules. Section 3.2.2 contains a detailed description of this construction step. Second, we split the OCL constraints into EOCL [41], a first-order logic subset of OCL, and complementary OCL (COCL), a second-order logic subset of OCL, constraints
. Following the approach by Kehrer et al. [26], we ensure constructively that any possible pair of related virtual and substrate network models that conforms to the metamodel can be constructed by a sequence of applications of the basic TGG rules. Section 3.2.2 contains a detailed description of this construction step. Second, we split the OCL constraints into EOCL [41], a first-order logic subset of OCL, and complementary OCL (COCL), a second-order logic subset of OCL, constraints  . EOCL constraints can be translated into additional preconditions of the basic TGG rules that ensure that any application of the modified TGG rules preserves the original EOCL constraints. In other words, the candidate generation step may only exclude element mapping candidates that violate at least one EOCL constraint. For this step, we rely on the constructive approach originally proposed by Heckel and Wagner [24] and extended by Radke et al. for accepting EOCL constraints as input [41]. Radke’s adoption of the constructive approach works by transforming each EOCL constraint first into a nested graph constraint [22]. This graph constraint is then specialized into a weakest precondition [16] of each TGG rule. This weakest precondition is necessary and sufficient to ensure that the refined TGG rule preserves the graph constraint. The resulting refined TGG rules constitute the MT part of the derived MdVNE configuration. Section 3.2.3 contains a detailed description of this construction step. Third, we translate the optimization goal and the COCL constraints into the ILP part of the derived MdVNE configuration
. EOCL constraints can be translated into additional preconditions of the basic TGG rules that ensure that any application of the modified TGG rules preserves the original EOCL constraints. In other words, the candidate generation step may only exclude element mapping candidates that violate at least one EOCL constraint. For this step, we rely on the constructive approach originally proposed by Heckel and Wagner [24] and extended by Radke et al. for accepting EOCL constraints as input [41]. Radke’s adoption of the constructive approach works by transforming each EOCL constraint first into a nested graph constraint [22]. This graph constraint is then specialized into a weakest precondition [16] of each TGG rule. This weakest precondition is necessary and sufficient to ensure that the refined TGG rule preserves the graph constraint. The resulting refined TGG rules constitute the MT part of the derived MdVNE configuration. Section 3.2.3 contains a detailed description of this construction step. Third, we translate the optimization goal and the COCL constraints into the ILP part of the derived MdVNE configuration  . Each COCL is translated into a set of side constraints of the ILP problem. The transformation of the optimization goal is straightforward because it is usually formulated in terms of the ILP variables. Section 3.2.4 contains a detailed description of this construction step. After executing the three construction steps, the created MdVNE configuration can be used as input of the MdVNE approach (see also Sect. 3.1).
. Each COCL is translated into a set of side constraints of the ILP problem. The transformation of the optimization goal is straightforward because it is usually formulated in terms of the ILP variables. Section 3.2.4 contains a detailed description of this construction step. After executing the three construction steps, the created MdVNE configuration can be used as input of the MdVNE approach (see also Sect. 3.1).
3.2.2 Construction of basic TGG rules
The first part of an MdVNE configuration is the specification of element mapping candidates formulated as a TGG. Therefore, in the following, we describe how to obtain a set of basic TGG rules from a given metamodel such that any model that conforms to the metamodel can be constructed by a sequence of rule applications.
Fundamentals of TGGs We begin with a short introduction to TGGs [45] based on the TGG rules shown in Fig. 10. A TGG consists of a set of TGG rules and is defined in the context of a left-hand side, right-hand side, and correspondence metamodel. In this article, the left-hand side metamodel is the metamodel consisting of all virtual network classes (see classes with prefix Virtual in Fig. 2), the right-hand side metamodel is the metamodel for substrate networks (see classes with prefix Substrate in Fig. 2), and the correspondence metamodel is induced by all associations that connect virtual and a substrate network metamodel elements (see the four hexagons in the center of Fig. 2). A correspondence class always has exactly two associations to a left-hand side and a right-hand side class, respectively. The left-hand side association corresponds to the virtual* association end, and the right-hand side association corresponds to the substrate* association end in the metamodel.
A TGG rule consists of object variables (e.g., SubstrateNetwork in Fig. 10a), link variables (e.g., from SubstrateNetwork to SubstrateSwitch in Fig. 10b), and relational attribute constraints. The object and link variables are placeholders for objects and links in one of the three metamodels of the TGG. A variable either describes the required context that is necessary for the rule to be applicable (shown in black), or a model element created by the TGG rule (shown in green, and decorated with a ++ symbol) by a TGG rule. For example, the TGG rule in Fig. 10b is only applicable if a SubstrateNetwork exists and creates a SubstrateSwitch and a connection to the SubstrateSwitch. A relational attribute constraint consists of a binary operator (e.g., \(\texttt {<} \) or =) and references to the attribute values of two object variables.
A TGG is a grammar, which describes in our case the language of all allowed substrate networks and embeddings of virtual networks in substrate networks. From the multiple possible operationalizations of a TGG, we are interested in establishing consistency between existing left-hand side and right-hand side models. This means that only the correspondence model (i.e., the substrate-virtual associations in Fig. 2) is missing [31]. In the context of consistency checking, an application of a TGG rule is interpreted as follows. Let us assume that we have existing substrate and virtual network models. Then, each element in these models is unmarked initially. The application of a TGG rule while checking consistency consists of the following steps. First, we have to find for each black variable of the TGG rule a suitable marked model element, and for each green left-hand side or right-hand side variable an unmarked model element. Throughout this article, we assume that distinct variables are mapped to distinct model elements (i.e., injective pattern matching [24]). Second, for each green left-hand side or right-hand side variable, we mark the respective model elements. Third, for each green correspondence variable, we create a new correspondence model element.
For example, all TGG rules in Fig. 10 have variables that belong to the right-hand side metamodel. This means that any application of these rules serves to mark elements in the substrate network model. The only TGG rule that is applicable initially is the rule shown in Fig. 10a because it requires no context (also called axiom rule [6]). After applying the aforementioned rule, we can mark a SubstrateSwitch using the TGG rule in Fig. 10b. In contrast to the substrate network rules (Fig. 10), the virtual network rules in Fig. 11 also contain correspondence variables. The rule in Fig. 11c requires a marked SubstrateNetwork and an unmarked VirtualNetwork and creates an new NtN correspondence object (along with the necessary left-hand side and right-hand side associations).
Deriving Basic TGG Rules In [26], Kehrer et al. propose a technique for deriving a set of edit operations that is capable of creating all valid instances \(\mathfrak {L}(MM) \) of a given metamodel MM. We use the same technique for deriving the set of basic TGG rules (\(R_{MM} \)). Due to the monotonic nature of the VNE problem, we only need to consider object-creating rules and neglect object-deleting, -moving or -changing transformation rules. While the substrate network can be created independently of the virtual networks and their embeddings, we first construct a rule set for creating a complete substrate network. Second, the virtual network and their element mapping candidates are created, whereas the substrate network serves as context in the TGG rules.
In the following, we present the two sets of resulting basic TGG rules. Figure 10 shows the six basic TGG rules that are used to cover the substrate network in isolation (i.e., without virtual networks or the correspondence model). In Fig. 10a, a substrate network is created, which serves as context element for all other rules. In Fig. 10b, c, a substrate switch and server, respectively, are created and attached to the substrate network. In Fig. 10d, a path of length zero with identical source and target substrate node is created. In Fig. 10e, f, paths with lengths of one and two hops are created, respectively. Depending on the topology (e.g., tree-based) of the substrate network, the developer specifies analogous rules for creating paths of length three, four, and more hops. In common data center networks, a path with three hops is sufficient to solve the VNE problem [9].
The second set of basic TGG rules creates virtual elements along with their corresponding element mappings into an existing substrate network (Fig. 11 on the left-hand side). This joint mapping is necessary to ensure that the multiplicity constraint of the substrate* association ends in Fig. 2 are fulfilled. The instantiation of a correspondence class corresponds to the creation of the respective virtual* or substrate* associations (see hexagons in Fig. 2). Rule MTnet (Fig. 11a) maps a virtual network to the existing substrate network. The rules MTsw (Fig. 11b) and MTsr (Fig. 11c) create a virtual switch and server, respectively, and map them to an (abstract) substrate node and substrate server, respectively. Rule MTlink (Fig. 11e) maps a virtual link to a substrate path.

3.2.3 Construction of MT specification
The basic TGG rules (Figs. 10 and 11 on the left-hand side) constructed in the previous section can be used to cover all substrate and virtual network models and all possible element mappings according to the metamodel in Fig. 2. Still, the resulting models may violate the specified OCL constraints (Sect. 2.1.2). For example, the TGG rule MTsr (Fig. 11c, left-hand side) may map a virtual server to a substrate server whose computing capacity is insufficient (i.e., VirtualServer.cpu> SubstrateServer.cpu, which violates \(C_{\text {cpu}}\)).
Therefore, the basic TGG rules are further refined to reduce the number of element mapping candidates by ensuring as many OCL constraints as possible from the set of all OCL constraints. For this purpose, we use an existing static analysis technique that transforms OCL constraints into application conditions of graph transformation rules [14, 24, 41]. These application conditions prevent the application of the refined TGG rule in contexts where the rule application would violate the OCL constraints. The approach in [41] only supports the transformation of EOCL, a subset of the complete OCL [19]. Generally speaking, EOCL comprises all elements of the OCL that correspond to arithmetic first-order logic (e.g., set expression, existential and all-quantification, relational operators, arithmetic expressions of variables, and Boolean equations). A comprehensive overview of EOCL can be found in [41]. During the refinement of the TGG rules, we only consider EOCL constraints and defer the handling of COCL constraints to transformation step  in Fig. 1.
in Fig. 1.
Thus, we distinguish between the languages OCL, EOCL, and COCL, where EOCL and COCL are both disjunctive subsets of OCL. Similarly, \(\mathfrak {L}(OCL)\), \(\mathfrak {L}(EOCL)\), and \(\mathfrak {L}(COCL)\) represent sets of constraints that can be expressed in OCL, EOCL, or COCL, as follows:
Constraint sets are represented by \(C_{\text {Suffix}}\), a subset of \(\mathfrak {L}(OCL)\) (\(C_{\text {Suffix}} \subseteq \mathfrak {L}(OCL) \)). Thus, we define the following constraint sets:
In this context, \(\mathfrak {L}(C_{\text {OCL}})\), \(\mathfrak {L}(C_{\text {EOCL}})\), and \(\mathfrak {L}(C_{\text {COCL}})\) are the sets of models that respect the constraint sets \(C_{\text {OCL}}\), \(C_{\text {EOCL}}\), and \(C_{\text {COCL}}\), respectively. The following applies:
Relaxation of OCL Constraints From the set of OCL constraints specified in Sect. 2.1.2, the constraints \(C_{\text {src}}\), \(C_{\text {trg}}\), \(C_{\text {fo1}}\), and \(C_{\text {fo2}}\) are EOCL constraints. The remaining four OCL constraints \(C_{\text {cpu}}\), \(C_{\text {mem}}\), \(C_{\text {sto}}\), and \(C_{\text {bw}}\), which all relate to server and link resources, are COCL constraints. For these constraints, we propose to derive relaxed EOCL (ROCL) constraints, which form the set \(C_{\text {ROCL}}\).
An OCL constraint \(C_{\text {B}}\) relaxes an OCL constraint \(C_{\text {A}}\) if each model that fulfills \(C_{\text {A}}\) also fulfills \(C_{\text {B}}\). Conversely, any model that violates \(C_{\text {A}}\) also violates \(C_{\text {B}}\). This means that if the candidate generation step uses relaxed variants of the COCL constraints to filter out mapping candidates, no feasible candidate is removed. Based on this definition, we distinguish between three cases for handling an OCL constraint \(C_{\text {A}}\) in the model-based specification:
-
(i) If \(C_{\text {A}}\) is an EOCL constraint, we refine the TGG rules for the candidate generation
 based on \(C_{\text {A}}\) and may neglect \(C_{\text {A}}\) during the candidate selection
based on \(C_{\text {A}}\) and may neglect \(C_{\text {A}}\) during the candidate selection  .
. -
(ii) If \(C_{\text {A}}\) is a COCL constraint and we find a non-trivial relaxation \(C_{\text {B}}\) of \(C_{\text {A}}\) that is an EOCL constraint, we use \(C_{\text {B}}\) for the candidate generation
 and the original constraint \(C_{\text {A}}\) for the candidate filtering in step
and the original constraint \(C_{\text {A}}\) for the candidate filtering in step  .
. -
(iii) If \(C_{\text {A}}\) is a COCL constraint for which we cannot derive an EOCL relaxation, we only consider \(C_{\text {A}}\) during candidate filtering in step
 .
.
In our scenario, we relax the four COCL constraints \(C_{\text {cpu}}\), \(C_{\text {mem}}\), \(C_{\text {sto}}\), and \(C_{\text {bw}}\) to the following constraints \(C_{\text {cpuR}}\), \(C_{\text {memR}}\), \(C_{\text {stoR}}\), and \(C_{\text {bwR}}\), respectively. Since all constraints are structured similarly, we present \(C_{\text {cpu}}\) in the following and list the other constraints in Appendix A.2.

The corresponding ILP formulations are similar to ILPcpu, ILPmem, ILPsto, and ILPbw, respectively. We explain the underlying idea of this relaxation based on the OCL constraint \(C_{\text {cpuR}}\). For a given substrate server and several virtual servers that are mapped to this substrate server, the sum of the required computing capacity (cpu) of all virtual servers can only be smaller than the available computing capacity of the substrate server. This can only be valid if the computing capacity of each individual virtual server is smaller than the available computing capacity. Table 4 summarizes the original OCL constraints and their relaxations (if necessary).
Transformation into Preconditions In the following, we describe how the set of EOCL constraints can be translated into a set of application conditions for the basic TGG rules using the constructive approach [24, 41].
Our goal is to derive a set of TGG rules that preserve consistency w.r.t. all eight EOCL constraints (see second column in Table 4). This means that we exclude all COCL constraints from the following construction step. A TGG rule is consistency preserving if a model that fulfills the specified constraints is transformed into a model that still preserves these constraints. Focusing on consistency preservation allows us to analyze in how far an individual TGG rule application can lead to inconsistencies. Consistency preservation is only applicable if the initial network model is consistent. This is the case in our scenario because the initial network model contains no element mappings (i.e., \(C_{\text {cpu}}\), \(C_{\text {sto}}\), \(C_{\text {mem}}\), \(C_{\text {bw}}\), \(C_{\text {src}}\), \(C_{\text {trg}}\), \(C_{\text {fo2}}\) do not apply) and we can assume that each VNR is well formed (i.e., \(C_{\text {fo1}}\) is fulfilled).
We first translate the EOCL constraints into nested graph constraints [22] following the approach by Radke et al. [41]. For the running example of this article, nested graph constraints with a nesting depth of one are sufficient. We represent this subtype of nested graph constraints using premise–conclusion constraints [24], as defined in the following. Figure 21 illustrates the following definitions. A graph constraint consists of one premise pattern and a (possibly empty) set of conclusion patterns. A pattern consists of a pattern graph, with object and link variables as nodes and edges, and relational attribute constraints. A match of a pattern in a model maps the variables represented by the pattern graph into the model such that all attribute constraints are fulfilled. Each conclusion pattern of a graph constraint extends the premise pattern. A pattern pA extends a pattern pB if the pattern graph of pA is a subgraph of the pattern graph of pB and if the attribute constraints of pA imply the attribute constraints of pB. A positive graph constraint has at least one conclusion pattern, and a negative graph constraint has zero conclusion patterns. For example, the graph constraint GCcpuR in Fig. 12 is a positive graph constraint and has one premise and one conclusion pattern. The premise pattern represents a virtual server (vs) that is mapped to a substrate server (self). The conclusion pattern extends the premise pattern by an additional attribute constraint to ensure that the required computing capacity of the virtual server vs is not larger than the available computing capacity of the substrate server self.
A model fulfills a graph constraint if each match of the premise pattern of the graph constraint can be extended to a match of at least one conclusion pattern. For example, a model fulfills GCcpuR if and only if each virtual server that is mapped to a substrate server does not exceed the computing capacity of the substrate server.
In [41], Radke et al. present rules for transforming an arbitrary EOCL constraint into a nested graph constraint. In our scenario, we consider graph constraints that represent the eight EOCL constraints in Table 4.
These EOCL constraints correspond to the ten graph constraints discussed in the following. Where possible, we reuse the OCL variable names in the graph constraints to establish traceability between OCL and graph constraints. For instance, the object variable that corresponds to the context of the OCL constraint is always called self. The graph constraint GCcpuR shown in Fig. 12 correspond to the relaxed EOCL constraints \(C_{\text {cpuR}}\). The other three graph constraints GCmemR, GCstoR, and GCbwR (shown in Appendix A.2) are similar to GCcpuR and correspond to \(C_{\text {memR}}\), \(C_{\text {stoR}}\), and \(C_{\text {bwR}}\). Each constraint has one premise pattern and one conclusion, which are identical except for the additional attribute constraint in the conclusion pattern.
The two graph constraints in Fig. 13 correspond to the EOCL constraint \(C_{\text {src}}\), which require that the virtual source and target node of a virtual link are compatible with the substrate source and target nodes of the substrate path that corresponds to the virtual link. The reason for the increased number of graph constraints is that the EOCL constraints contain a condition based on the concrete type of the virtual source and target node of the virtual link (self). The graph constraints GCsrc1 and GCtrg1 cover the situation that the source and target virtual node (vs) are virtual switches, respectively. Conversely, the graph constraints GCsrc2 and GCtrg2 cover the analogous situation for virtual servers as source and target nodes.
Since the other constraints for \(C_{\text {trg}}\) are very similar to \(C_{\text {src}}\), we present them in Appendix A.2.
Finally, the two graph constraints GCfo1 and GCfo2 in Fig. 14 correspond to the EOCL constraints \(C_{\text {fo1}}\) and \(C_{\text {fo2}}\), respectively. These graph constraints are the only negative graph constraints in our case study. The constraint GCfo1 requires that no virtual server has a looping master-failover association. The constraint GCfo2 requires that there is no virtual server (self) whose fail-over server (vs) is mapped to the same substrate server as self.
The graph constraints that we obtain from the EOCL constraints can be used to evaluate whether a given model fulfills the graph constraints. The second step in the constructive approach is to refine each TGG rule based on each graph constraint resulting in the rule set \(R_{EOCL+ROCL} \). A single refinement iteration is independent of other refinement iterations. Therefore, given the five TGG rules and ten graph constraints, we need to conduct 50 refinement iterations of the constructive approach. Table 5 provides an overview of the results of the constructive approach that we discuss in the following. The table shows that 10 of the 50 refinement operations lead to modifications of TGG rules indicated by the + markers. The iterations for GCsrc2 and GCsrc1 as well as GCtrg2 and GCtrg1 are combined in the columns for \(C_{\text {src}}\) and \(C_{\text {trg}}\), respectively. Therefore, Table 5 contains only \(5 \times 8 = 40\) entries.
The fundamental idea of the constructive approach is to identify, for a given rule–constraint pair, all situations in which the unmodified rule violates the constraint. Each situation is transformed into a weakest precondition [16] of the rule, which ensures that the rule is applicable if and only if the rule application does not violate the currently considered constraint if the model fulfilled the constraint before. The set of all generated preconditions is necessary and sufficient to ensure that the refined TGG rules preserve the EOCL constraints. We refrain from presenting details of the constructive approach here and refer to [24, 41] instead.
Figure 11 shows how three of the five basic TGG rules are refined using the constructive approach. The basic TGG rules are shown to the left of the block arrows, and the resulting refined TGG rules are shown on the right-hand side. The TGG rules MTnet and MTsw are missing from the figure because they are not modified during the rule refinement. Figure 11c shows the basic and refined variants of the TGG rule MTsr for mapping a virtual server to a substrate server. During the rule refinement, MTsr is modified three times by adding attribute constraints for ensuring that the virtual server does not exceed either the computing capacity (GCcpuR, \(C_{\text {cpuR}}\)), memory (GCmemR, \(C_{\text {memR}}\)), or storage (GCstoR, \(C_{\text {stoR}}\)) of the substrate server.
Figure 11d shows the basic and refined variants of MTfoSr, which maps a fail-over server of an already embedded virtual master server to a substrate node. In total, this TGG rule is modified four times during the refinement. During the refinement, the three graph constraints GCcpuR, GCmemR, and GCstoR cause three new attribute constraints to be added to MTfoSr. Furthermore, the second fail-over constraint GCfo2 causes the insertion of a negative application condition indicated by the crossed-out hexagon. A negative application condition restricts the applicability of a TGG rule. In this case, the fail-over virtual server may only be mapped to a substrate node if its master server has not been mapped to the same substrate server before. In contrast to GCfo2, this rule already preserves GCfo1 because we apply injective pattern matching, which maps the two distinct virtual server variables to distinct virtual servers in the network.
Figure 11e shows the basic and refined variant of the TGG rule MTlink, which maps a virtual link to a substrate path. We represent the eight additional application conditions as eight refined TGG rule variants, as shown in Table 6. We obtain eight variants for the following reasons. The reason is that the involved source and target virtual nodes can each be either a virtual switch or a virtual server. Considering only this distinction results in four variants (see unique combinations of Var1, Var2, and Var3 in Table 6). Still, we also have to consider the distinction between substrate paths of length zero, whose source and target nodes are identical, and paths having a length of at least one, whose source and target nodes are distinct (due to injective pattern matching). The former case is shown in the bottom-right corner and the latter case is shown in the top right corner of Fig. 11e. The types of the correspondence variables Var5 and Var6 can be derived from the types of Var1 and Var2. If Var1 (Var6, resp.) is of type VirtualSwitch, Var5 (Var6, resp.) is of type StN and, otherwise, of type StS. Finally, each variant is further refined based on GCbwR. This refinement results in the additional attribute constraint that ensures that the required bandwidth of the virtual link does not exceed the available bandwidth on the substrate path. A special case is the TGG rule for paths of length zero, which begin and end at the same substrate server. Their bandwidth is usually set to a large, but finite value to indicate that the communication between virtual servers that are mapped to the same substrate server is usually very fast.

3.2.4 Construction of ILP specification
The candidates generated based on the MT specification of the MdVNE configuration that we derived in Sect. 3.2.3 fulfill all EOCL constraints. This means that the ILP specification of the MdVNE configuration must (only) ensure that both the MT specification and the COCL constraints are fullfilled and only optimal element mapping candidates are preserved. Therefore, the generation of ILP formulations (at runtime) is divided into two steps: (i) based on the MT specification and (ii) based on the COCL constraints. Further information about this generation process can be found in [49].
ILP node-mapping variables based on Fig. 7
ILP generation based on the MT specification Based on the MT specification, ILP formulations must be created to ensure the grammatical properties of TGGs. To ensure this, we use a general approach for consistency checking using TGGs [31], which is integrated in the tool eMoflon [30]. The main idea is that for each set of element mapping candidate (StN, StS, and LtP) created by MT, unique ILP variables and necessary ILP constraints are generated at runtime and added to comply with the TGG specification. The different mapping options (mapping a virtual switch, server, or link) are explained in more detail below. Table 7 summarizes the created ILP constraints.
Mapping a Virtual Switch The TGG rule in Fig. 11 generates an element mapping candidate \(stn_{(i,u)}\) for each element mapping of a virtual switch \(i \in N^V (i^{Sw} = 1)\) to a substrate node \(u \in N^S\). For every element mapping candidate, we generate an ILP node-mapping variable \(x^{i}_{u}\), so that exactly one unique ILP variable \(x^{i}_{u}\) exists for each element mapping candidate \(stn_{(i,u)}\) (\(StN \rightarrow X\)). To ensure that for each virtual switch i, exactly one element mapping candidate from the set of all possible candidates \(stn_{(i,v)}, v \in N^V\) exists, the following inequalities are required.

Mapping a Virtual Server The creation of the ILP variables \(x^{i}_{u}\) and the ILP constraints for the virtual servers using the TGG rule in Fig. 11c is done analogously to the creation of the ILP variables for the virtual switches. Thus, for each possible element mapping of a virtual server \(i \in N^V (i^{Sr} = 1)\) to a substrate server \(u \in N^S (u^{Sr} = 1)\) an element mapping candidate \(sts_{(i,u)}\) exists, created by MT (\(StS \rightarrow X\)). Afterward, the ILP variables \(x^{i}_{u}\) are generated based on these element mapping candidates and, again, it must be ensured that only one element mapping candidate \(sts_{(i,v)}\) can be selected from the set of all possible candidates for a virtual server i.

Mapping a Virtual Link The generation of the link-mapping ILP variables \(y^{ij}_{uv}\) for mapping a virtual link \(l_{ij}\) to a substrate path \(p_{uv}\) is also done analogously to the generation of the node-mapping ILP variables \(x^{i}_{u}\). However, link-mapping ILP variables \(y^{ij}_{uv}\) are generated for all element mapping candidates \(ltp_{(l_{ij},p_{uv})}\), which are generated by using MT for each virtual link \(l_{ij} \in L^V\) to each substrate path \(p_{uv} \in P^S\) (\(LtP \rightarrow Y\)). Again, it must be ensured that each virtual link is mapped exactly once to a substrate path.
ILP generation based on the COCL constraints After creating the ILP node- and link-mapping variables \(x^{i}_{u}\) and \(y^{ij}_{uv}\) from the element mapping candidates and the necessary ILP constraints to comply with the TGG specifications, the COCL constraints must now be integrated into the ILP problem. These COCL constraints have the following structure:
These constraints can be translated into ILP constraints in a semantics-preserving way of the following form:
This concerns the constraints \(C_{\text {cpu}}\), \(C_{\text {mem}}\), \(C_{\text {sto}}\), and \(C_{\text {bw}}\), so that the substrate resources CPU, memory, storage, and bandwidth capacity are not overbooked. For this purpose, the ILP constraints ILPcpu, ILPmem, ILPsto, and ILPbw from the problem description are generated at runtime and integrated into the ILP formulation.

ILP Objective Function The objective function for the ILP problem is synthesized according to \(C_{\text {obj}}\) defined in OCL. We iterate over every virtual link l (self.links) in the respective virtual network (self) and sum up all costs according to the cost matrix \(cost^{l}_{p}\) for every substrate path p in the set of the element mapping candidates \(ltp_{(l,p)}\) (l.substratePath) for this virtual link l. Since all ILP link-mapping variables \(y^{l}_{p}\) were created in advance for each element mapping candidate \(ltp_{(l,p)}\), we iterate over all virtual links (\(self.links = L^V\)) in this virtual network (self) and all substrate paths (\(P^S\)) and multiply the link-mapping variables \(y^{l}_{p}\) with the cost matrix \(cost^{l}_{p}\). This results in the following ILP formulation:
The post-conditions from \(C_{\text {obj}}\) for the links are already synthesized by Eq. (8), for the virtual servers by Eq. (7), and for the virtual switches by Eq. (6).
4 Correctness results
In this section, we show that applying the proposed construction methodology results in a MdVNE configuration that produces correct and optimal solutions w.r.t. the model-based specification. The related concepts introduced in Sects. 2.1 and 3 are further formalized in this section. For this purpose, we present in Definition 1 the sets of models characterized by the metamodel, the language and the set of OCL constraints in Definition 2, the sets and the language of the construction methodology for MdVNE in Definition 3, and the sets related to the optimization function in Definition 4. After that, we prove in Theorem 1 that the set of optimal and correct embeddings of the model-based specification is equal to the result set of the MdVNE approach using the provided construction methodology (after step  ).
).
Figure 16 sketches the idea of the proof of Theorem 1 providing the sets of optimal and correct solutions from the model-based specification \(\mathcal {O} \) on the left-hand side and the solutions of the MdVNE approach using the proposed construction methodology \(\mathcal {O}' \) on the right-hand side. We prove that, starting from the model-based specification, we can derive a MT rule set for creating all necessary network model instances described be the metamodel. After that, we integrate application conditions derived from EOCL and ROCL constraints into this rule set. Using this rule set and the remaining COCL constraints in combination with the optimization function, we get the same set of optimal and correct embeddings compared to solving the VNE problem for the model-based specification directly.
Sketch for the correctness and optimality results in Theorem 1
To have a correctly working MdVNE implementation, the following conditions must be fulfilled:
-
The derivation of the ILP formulations from the COCL constraints (\(C_{\text {COCL}}\)) must be performed in a semantics-preserving manner.
-
The ILP solver used must work correctly. It must calculate the correct results and it must be granted enough resources (e.g., computing time) to find an optimal solution if one exists.
-
The MT tool used must work correctly. That means it must find all element mapping candidates that fulfill the considered ECOL (\(C_{\text {EOCL}}\)) and ROCL (\(C_{\text {ROCL}}\)) constraints. Furthermore, it must be granted sufficient resources (e.g., memory and computing time) to find these candidates.
Definition 1
(Language of a metamodel) Given a metamodel MM, the language \(\mathfrak {L}(MM) \) is the set of all valid models that conform to MM.
Definition 2
(Languages of constraint-fulfilling models) In this definition, we characterize subsets of \(\mathfrak {L}(MM) \) based on whether the models in these subsets fulfill certain types of OCL constraints. The language \(\mathfrak {L}(C_{\text {OCL}})\) is the set of all models in \(\mathfrak {L}(MM) \) respecting the given set \(C_{\text {OCL}}\) of OCL constraints defined in the model-based specification; more formally: \(\mathfrak {L}(C_{\text {OCL}}):= \{m \in \mathfrak {L}(MM) \mid m \models C_{\text {OCL}} \}\), where \(m \models C_{\text {OCL}} \) represents a semantic consequence, such that \(C_{\text {OCL}}\) is fulfilled in m. The set \(\mathfrak {L}(C_{\text {OCL}}) = \mathfrak {L}(C_{\text {EOCL}} \cup C_{\text {COCL}}) = \{m \in \mathfrak {L}(MM) \mid m \models C_{\text {EOCL}} \wedge \text { } m \models C_{\text {COCL}} \} = \mathfrak {L}(C_{\text {EOCL}}) \cap \mathfrak {L}(C_{\text {COCL}}) \) with \(C_{\text {EOCL}} = C_{\text {OCL}} \cap \mathfrak {L}(EOCL) \), \(C_{\text {COCL}} = C_{\text {OCL}} \cap \mathfrak {L}(COCL) \), and \(C_{\text {OCL}} \subseteq \mathfrak {L}(OCL) \) contains all models that satisfy both the EOCL and the COCL constraints. The languages \(\mathfrak {L}(OCL)\), \(\mathfrak {L}(EOCL)\), and \(\mathfrak {L}(COCL)\) represent sets of constraints that can be expressed in OCL, EOCL, or COCL, as follows: \(\mathfrak {L}(OCL) = \mathfrak {L}(EOCL) \cup \mathfrak {L}(COCL) \). The set \(C_{\text {ROCL}} \subseteq \mathfrak {L}(EOCL) \) is a set of relaxed constraints for the set of constraints \(C_{\text {COCL}} \subseteq \mathfrak {L}(COCL) \). The set of constraints \(C_{\text {ROCL}}\) relaxes the set of constraints \(C_{\text {COCL}}\) if the following condition is fulfilled: {\(\forall m \in \mathfrak {L}(MM) \mid m \models \) \( C_{\text {COCL}} \Rightarrow \) \( m \models C_{\text {ROCL}} \)}. Therefore, \(\mathfrak {L}(C_{\text {ROCL}})\), a superset of \(\mathfrak {L}(C_{\text {COCL}}) \), contains all models respecting the relaxed COCL constraints.
Definition 3
(Languages of MdVNE-generated rule sets) We define the language \(\mathfrak {L}(R_{MM})\) as the language of the rule set \(R_{MM} \) for all models in \(\mathfrak {L}(MM) \). \(R_{MM} \) is a set of rules constructed using the methodology introduced in [26] such that \(\mathfrak {L}(R_{MM}) = \mathfrak {L}(MM) \). That is, the language generated by the constructed set of rules \(R_{MM} \) generates all model instances that conform to the metamodel MM.
\(R_{EOCL} \) is a set of rules derived from the combination of \(R_{MM} \) with a given set \(C_{\text {EOCL}}\) of EOCL constraints (see Sect. 3.2.3). The derivation process enriches the given set of rules \(R_{MM} \) with application conditions using the methodology introduced in [24, 41] such that \(\mathfrak {L}(R_{EOCL}) = \{m \in \mathfrak {L}(R_{MM}) \mid m \models C_{\text {EOCL}} \} \overset{[26]}{=} \{m \in \mathfrak {L}(MM) \mid m \models C_{\text {EOCL}} \} = \mathfrak {L}(C_{\text {EOCL}}) \). Analogously, we add the set of relaxed constraints \(C_{\text {ROCL}}\) to the set of \(C_{\text {EOCL}}\) constraints to derive a set of rules \(R_{EOCL+ROCL}\) such that \(\mathfrak {L}(R_{EOCL+ROCL}) = \mathfrak {L}(C_{\text {EOCL}} \cup C_{\text {ROCL}}) \) (see Proposition 1).
Definition 4
(Objective function) The set \({{\,\mathrm{opt}\,}}(C_{\text {COCL}}, \text {fg})\) contains the optimal solutions of the objective function fg for a given set of models that respect the set of constraints \(C_{\text {COCL}}\). Therefore, the set \(\mathcal {O}':= {{\,\mathrm{opt}\,}}(C_{\text {COCL}}, \text {fg})\) for \(\mathfrak {L}(R_{EOCL+ROCL})\) contains the optimal solutions created by MdVNE. The set of the optimal solutions for the model-based specification is \(\mathcal {O}:= {{\,\mathrm{opt}\,}}(C_{\text {OCL}}, \text {fg})\) for \(\mathfrak {L}(MM)\).
Proposition 1
In the subsequent Theorem 1, we prove that the MdVNE approach calculates optimal and correct solutions after step  in Fig. 1 when the proposed construction methodology is used to translate a model-based specification into an MdVNE configuration.
in Fig. 1 when the proposed construction methodology is used to translate a model-based specification into an MdVNE configuration.
Theorem 1
(Correctness and optimality for the construction methodology) The set \(\mathcal {O}' \) representing the solutions of MdVNE (after step  in Fig. 1) is equal to \(\mathcal {O} \), the set of optimal and correct solutions for the model-based specification. To show that \(\mathcal {O} = \mathcal {O}' \), we have to prove the following equality (see Definition 2 and 3).
in Fig. 1) is equal to \(\mathcal {O} \), the set of optimal and correct solutions for the model-based specification. To show that \(\mathcal {O} = \mathcal {O}' \), we have to prove the following equality (see Definition 2 and 3).
Proof
We prove Theorem 1 by reformulating the characterization of the set \(\mathcal {O}' \).
This means that the set of optimal solutions based on the model-based specification is equal to the solution set created by MdVNE using the presented construction methodology. \(\square \)
The ILP formulation used in  from Fig. 1 is derived from \(\mathfrak {L}(R_{EOCL+ROCL})\) and the COCL constraints (\(C_{\text {COCL}}\)). Since only iterative operations with summations of the individual elements beside EOCL are allowed in the problem definition (see Sect. 2.1.2), we can transform every iterative operation in \(C_{\text {COCL}}\) into an ILP formulation. Thus, \(C_{\text {COCL}}\) can be realized as sums of constant values with or without ILP variables. The ILP formulation from \(\mathfrak {L}(R_{EOCL+ROCL})\) is created with a generic methodology for consistency checking using TGGs [31].
from Fig. 1 is derived from \(\mathfrak {L}(R_{EOCL+ROCL})\) and the COCL constraints (\(C_{\text {COCL}}\)). Since only iterative operations with summations of the individual elements beside EOCL are allowed in the problem definition (see Sect. 2.1.2), we can transform every iterative operation in \(C_{\text {COCL}}\) into an ILP formulation. Thus, \(C_{\text {COCL}}\) can be realized as sums of constant values with or without ILP variables. The ILP formulation from \(\mathfrak {L}(R_{EOCL+ROCL})\) is created with a generic methodology for consistency checking using TGGs [31].
In this section, we proved that the MdVNE approach, using the proposed construction methodology, only can generate optimal and correct solutions for the VNE problem. We have shown, that the result set after executing the MdVNE approach is equal to the result set of an ILP-based approach. Therefore, MdVNE always guarantees optimal and correct solutions.
5 Tool support
In this section, we present an overview of the tool support to derive MdVNE configurations and simulate these algorithms using MT and ILP technologies. Using MT technology, we can derive executable code from a declarative MT configuration (e.g., a TGG rule set) and pass an ILP formulation to an ILP solver via interfaces for solving the optimization problem.
In Fig. 17, an overview of the transformation of the model-based specification into executable code is presented in order to use MdVNE to solve real-world VNE problems. The first step is to create a model-based specification, which consists of a UML class diagram, OCL constraints, and an optimization goal, also encoded in OCL. This specification can now be transformed into an MdVNE configuration using the presented construction methodology. This step is currently performed manually. The resulting MT rule set can be directly and automatically transformed into executable source code by an MT tool (e.g., eMoflon [30] or Viatra [50]).
At runtime, these MT rules are executed and, with the help of an MT–ILP converter, ILP variables and ILP inequalities are automatically derived from the found or modified matches. For MdVNE, an existing and generic MT–ILP converter as part of eMoflon can be used (see [31]). Now that the necessary ILP variables and inequalities have been derived from the (MT) matches, the additional ILP variables, inequalities, and the target function must be created using the mathematical formulation. In the first step, an ILP converter is used to adapt the (existing) ILP variables, inequalities and the target function based on the changes in the model. The configuration of this ILP converter based on the mathematical formulation has to be carried out manually for the realization of a new VNE algorithm. Promising approaches for a (partial) automation are available in the literature and will also be discussed in the outlook [35, 36, 52, 53].
The ILP converter can now derive the final ILP variables and inequalities to solve the VNE problem. As soon as the final ILP variables are known, the ILP converter can also generate the ILP target function. Together with the ILP inequalities from the MT–ILP converter, these data are transferred to a generic ILP API (e.g., Cardygan ILP–API [44]). This generic ILP–API now realizes the connection to different ILP solvers (e.g., Gurobi [21] or Cplex [13]), whereby the ILP problem can be solved and the result can be translated into a concrete embedding. Together with the virtual networks and the substrate network, a concrete VNE problem can be solved in a simulation environment, the identified embeddings can be applied into the model and thus an evaluation of this VNE algorithm can be performed.
6 Evaluation
This section evaluates the MdVNE approach against an ILP-only baseline approach. The evaluation focuses on scalability, as correctness and optimality of the approach are already addressed in Sect. 4 and are also considered again in Sect. 6.5. The setup is similar to the setup described in [48]. In contrast to [48], the virtual networks are created on the basis of real data (instead of uniform random distributions) and comprise use-case-specific requirements in the form of fail-over server constraints. To investigate scalability, we focus on the size of the substrate network and the batch size. The batch size is the number of simultaneously embedded VNRs. The generation of the VNRs remains the same across all experiments. The complete runtime that is required to solve the VNE problem and the ILP solving time serve as performance metrics. Furthermore, we investigate the influence of the batch size on the complete runtime of the results. We discuss the following research questions:
- RQ: 1:
-
How does varying the substrate network size influence the complete runtime and ILP solving time?
- RQ: 2:
-
How does varying the batch size influence the complete runtime and ILP solving time?
6.1 Setup
The evaluation setup consists of a small and a large 2-tier substrate network. Each network has 2 core switches, which are connected to the rack switches via a bandwidth of 10 Gbit/s. Each rack contains 10 servers each with 32 CPU cores, 512 GB of memory, and 1 TB of storage. The bandwidth between the servers and the rack switch is set to 1 Gbit/s. The smaller 2-tier network has 4 racks (i.e., in total 40 servers), and the larger 2-tier network has 12 racks (i.e., in total 120 servers).
Each VNR is a star topology with 2 to 10 evenly distributed virtual servers (similar to [55]). The resources of the servers and links are calculated using the realistic values from the Bitbrains data set [46]. For each virtual server, the number of CPU cores is between 1 and 32 and for the memory between 1 and 511 GB. The required bandwidth ranges from 0.1 to 1 GB/s . The Bitbrains data set lacks information about requested storage for the virtual machines. Therefore, we use equally distributed values in the range from 50 to 300GB. For the exact probability distributions of the CPU, memory, and bandwidth, we refer the reader to the paper by Shen et al. [46]. To evaluate the use-case-specific constraints, we randomly define between 0 and 2 virtual fail-over servers, equally distributed, and their corresponding masters. The total number of VNRs is 30 in the small setup and 100 in the large setup to ensure that every VNR can be embedded.
To calculate the objective for the 2-tier substrate network, we use the cost functions for the VL2 topology from [33]. Therefore, the cost function is defined as follows (\(p_{uv}\): substrate path, \(l_{ij}\): virtual link):
To investigate the scalability and the research questions RQ 1 and RQ 2, we use the same setup and experiments. These experiments have two degrees of freedom: (i) the substrate network size and (ii) the batch size. The size of the substrate network is determined by the two setups (small and large). The batch size represents the number of VNRs embedded simultaneously. An embedding of a batch can only be done if a solution for all VNRs in this batch including all constraints is found. The batch sizes here are 1 and 5. The time for the ILP solver to find the solution is limited to 2 h (7200 s). All experiments were executed on a machine with an Intel Xeon E5-2630 v3 CPU having 2.4 GHz. The operating system was Windows Server 2016. We used a Java SE Development Kit 8 and the ILP solver Gurobi 7.52 [21]. In the following, each data point is the median of three repeated experiments.
6.2 RQ 1: Efficiency versus substrate network size
Figure 18 shows the complete runtime for solving the VNE problem (including all pre- and postprocessing steps, as well as the ILP solving time) for the small (Fig. 18a) and large setup (Fig. 18b). The x-axis shows the total number of virtual networks embedded in the substrate network. The y-axis (logarithmic scale) shows the complete runtime in seconds. The solid lines represent the MdVNE and the dashed lines the ILP-only approach. The timeout of the ILP solver is visualized in Fig. 18b as a horizontal solid gray line. Tables 8a and b provides details on the mean values, the inter-quartile range (IQR, difference of 25-percentile and 75-percentile), the range (difference of minimum and maximum), and the number of timeouts of the ILP solver for the two diagrams (Fig. 18a, b).
In addition, Fig. 19 shows the percentage of the ILP solving time compared to the complete runtime for the small (Fig. 19a) and the large setup (Fig. 19b). The x-axis also shows the number of virtual networks embedded in the substrate network and the y-axis shows the percentage for the MdVNE configuration with a batch size of 1 and 5.
6.2.1 Results
For the small setup in Fig. 18a, we see that the fluctuations of embedding a VNR for MdVNE are lower than for the ILP-only approach. This is also apparent in the IQR and the range values in Table 8a. The IQR for a batch size of 1 is approx. 3 times smaller for MdVNE (1.4 s for MdVNE and 4.0 for ILP-only) and for a batch size of 5 it is even approx. 20 times smaller (6.7 s for MdVNE and 153.2 s for ILP-only). But also for the range, the considerable range of 28.0 s for ILP-only for batch size 1 (452.3 s for batch size 5) in contrast to 4.9 s for MdVNE (11.7 s for batch size 5) are evident. The average complete runtime for the MdVNE approach is up to 18 times smaller for a batch size of 5 (301.6 s for ILP-only and 11.7 s for MdVNE). Even with a batch size of 1, the average complete runtime for solving the VNE problem is approx. 25% smaller.
In the large setup and with a batch size of 5, the ILP-only approach experiences a timeout in 19 of 20 iterations (95%). This is reflected both by the small IQR and by the average mean value of 6900 s, which is very close to the timeout of 7200 s. Although the ILP-only approach ran into the timeout, the results for the embeddings were still optimal. With MdVNE, a timeout occurred in 4 of 20 iterations (20%). To investigate how long the ILP solver runs to solve the VNE problem, we re-ran the large setup with the first 15 VNRs and an increased timeout of 10 h. The ILP-only approach required approx. 2.5 h for the embedding of the VNRs 6 to 10 and reached the timeout of 10 h for embedding the VNRs 11 to 15. The MdVNE approach solved the problem for the VNRs 11 to 15 in about 4.5 h. With a batch size of 1, as in the small setup, a smaller range for MdVNE can also be seen from the IQR (141.5 s for ILP-only and 132.8 s for MdVNE). The range for MdVNE is larger by a factor of 2 than the range of the ILP-only approach (1422.1 s MdVNE and 623.3 s ILP-only). The average complete runtime for solving the VNE problem is approx. 3 times larger for MdVNE for batch size 1 and 2 times smaller for batch size 5 compared to the ILP-only approach.
When comparing the complete runtime values for varying substrate network sizes and a fixed batch size, the ILP-only approach grows by a factor of about 23 regardless of the batch size. For MdVNE, the complete runtime for batch size 1 increases by a factor of 84 and for batch size 5 by a factor of 191. For a fixed setup, the complete runtime for the ILP-only approach and a batch size of 5 is approx. 70 to 75 larger compared to a batch size of 1. The corresponding increase for MdVNE is 5 to 12.
6.2.2 Discussion
For a fixed setup and varying batch sizes, the ILP-only approach shows that the complete runtime increases by a factor of 70 to 75. For MdVNE, the construction of the substrate network has a large impact on the complete runtime. The complete runtime increase is 5 for the small setup and 12 for the large setup. The different factors can be explained by considerably more pattern matches (especially those that involve path objects) that are found in the larger substrate network. In the case of enlarging the substrate network with a constant batch size, the data shows that ILP-only scales better here (factor for ILP-only: approx. 23, factor for MdVNE: 84 to 191). This can be explained by the fact that, in MdVNE, the complete substrate network is also constructed using TGG rules, with considerably more (path) elements being present in the large setup. In addition, the number of pattern matches also increases. Nevertheless, the complete runtime of MdVNE is at least 2 times smaller than the ILP-only approach for the large setup and a batch size of 5 with less timeouts. If a timeout occurs, no guarantee on the optimality of the returned result can be given. Therefore, MdVNE performs considerably more robustly compared to the ILP-only baseline (MdVNE: 20% timeouts, ILP-only: I95% timeouts).
A comparison of the percentages of the ILP solving time to the complete runtime in Fig. 19a, b reveals that, for batch size 1, the percentages vary between approx. 2% and 80%. With the batch size of 5, the fractions varies between approx. 42 to 68% in the small scenario, whereas in the large scenario the ILP percentages varies between 22 and 94%. The mean value for a batch size of 1 is approximately the same for both the small and the large scenario with approx. 24%. With a batch size of 5, the ILP fraction is 57% on average for the small scenario and 70% for the large scenario.
Answer to RQ1: How does varying the substrate network size influence the complete runtime and ILP solving time? The measurements show that, by enlarging the substrate network, the complete runtime increases by a factor of approx. 23 (batch size 1 and 5) for the ILP-only approach and by 84 to 191 (batch size 1 and 5) for the MdVNE approach. However, MdVNE is 18 times faster in the small setup and 2 times faster in the large setup in solving the VNE problem than the ILP-only approach for a batch size of 5. Also, MdVNE returned optimal results considerably more reliably than the baseline approach (in terms of timeouts). The ILP solving time contributes on average 24% to the complete runtime for a batch size of 1 and 57–70% for a batch size of 5.
6.3 RQ 2: Batch size
Figure 20 shows runtime measurements for the small setup and varying batch sizes. The plots shows three data series for the complete runtime for MdVNE and the ILP-only baseline as well as the ILP solving time for MdVNE. The x-axis shows the batch size and the y-axis (logarithmic scale) the runtime in seconds. The MdVNE measurements are again displayed as solid lines and the ILP-only approach as dashed lines.
Results All runtime values increase monotonously with the batch size. For MdVNE, the ratio of complete runtime and ILP solving time remains stable for batch sizes above 5. The average ILP solving time ratio for MdVNE is approx. 24% for a batch size of 1 and stabilizes in the range of 60–70% for batch sizes of 5 or larger. The plots show that the MdVNE approach solves the ILP problem more than one order of magnitude faster than the ILP-only approach.
Discussion The preceding results show that the ILP solving time ratio for MdVNE increases while the ratio of the runtime for generating the candidate (Fig. 1 ) decreases in the same way for larger batch sizes. MdVNE reduces the complete runtime by more than one order of magnitude for large batch sizes compared to the ILP-only baseline.
) decreases in the same way for larger batch sizes. MdVNE reduces the complete runtime by more than one order of magnitude for large batch sizes compared to the ILP-only baseline.
Answer to RQ2: How does varying the batch size influence the complete runtime and ILP solving time? The measurements show that by increasing the batch size MdVNE is more than one order of magnitude faster than the ILP-only approach and that generating the candidates in MdVNE is reduced to approx. 30–40% on average starting from a batch size of 5.
6.4 Summary of evaluation
In this evaluation, we investigated the scalability of the MdVNE implementation based on two realistic data sets. The ILP-only approach was used as baseline for the performance measurements and for checking the correctness and optimality of the results in our experiments. Compared to the baseline, MdVNE solved the VNE problem up to 18 times faster for the small setup and more than twice as fast for the large setup (with a batch size of 5). In the large setup, MdVNE experienced approx. 5 times less timeouts compared to the baseline. We showed that the candidate selection (Fig. 1 step  ) of MdVNE solved the ILP problem up to 30 times faster than the ILP-only baseline. In addition, the complete runtime of MdVNE is more homogeneous, which is apparent in smaller IQR and range values. The ratio of the ILP part compared to the complete runtime for MdVNE was on average 24 % for a batch size of 1 and between 57 and 70% for a batch size of 5. The investigation of different batch sizes showed that the fraction of the candidate generation (Fig. 1 step
) of MdVNE solved the ILP problem up to 30 times faster than the ILP-only baseline. In addition, the complete runtime of MdVNE is more homogeneous, which is apparent in smaller IQR and range values. The ratio of the ILP part compared to the complete runtime for MdVNE was on average 24 % for a batch size of 1 and between 57 and 70% for a batch size of 5. The investigation of different batch sizes showed that the fraction of the candidate generation (Fig. 1 step  ) of MdVNE (for a batch size of 5) is between 30 and 40% and that the ILP part dominates the behavior.
) of MdVNE (for a batch size of 5) is between 30 and 40% and that the ILP part dominates the behavior.
6.5 Threats to validity
In this section we examine the threats to validity for the results of the evaluation for the MdVNE approach using the categories from [54]: conclusion validity, internal validity, construct validity, and external validity.
Conclusion validity The networks (substrate network and virtual networks) and their resource distributions (CPU, memory, storage, and bandwidth) are constructed based on probability distributions from [46]. To reduce the influence of the randomly selected values, all experiments were repeated three times and the median was calculated from the resulting data. The number of repetitions was limited to three due to the long runtime of individual experiments. All experiments were performed on the same hardware with the same operating system and software environment.
Internal validity In the evaluation, we consider a purely ILP-based approach as a comparison algorithm in addition to the MdVNE approach. To ensure that these two approaches act very similarly and, thus, deliver largely comparable results, we have made sure that (i) large parts of the code base are identical between these two approaches, (ii) the same ILP solver is used, (iii) consistency checks of the found results are performed at runtime, and (iv) the same unit tests are used.
For the consistency checks (iii) the embedding decisions were executed and verified after each solution of the VNE problem. This means that all available substrate resources are reduced depending on the resource requirements of the mapped servers and links. The MdVNE tool verifies automatically that all constraints regarding element types are met, available resources are not overbooked, and master and fail-over servers are placed on different substrate servers. These consistency checks provide additional assurance that the identified solutions are correct w.r.t. the problem specification.
Construct validity To avoid further sources of errors, we used the same unit tests for MdVNE and the ILP-based approach to check the correctness of the embedding of sample networks. These unit tests were created manually, using one- and two-tier networks, as well as a Google Fattree network [3]. Thus, different VNE scenarios were determined systematically and solved manually afterward to obtain pairs of input-output data for the unit tests. These unit tests were then used for both the ILP-based and the MdVNE implementation. In total, we created 330 unit tests to check the correctness and optimality of the embeddings. Additionally, the values of the objective function for both approaches were compared and common metrics (runtime to solve the problem) were used.
External validity To create the application scenario for this evaluation, comparable evaluations from other publications and real probability distributions of applications from data centers were examined and taken into account in the selection process. Thus, we decided to use a 2-tier network as substrate network, which is a widely used network for mostly smaller data centers and a star topology for the virtual networks. To make the resource requirements for the virtual elements as realistic as possible, we oriented ourselves on the statistical data set for applications in a data center, which provides probability functions of real measured values for the requested and actually used resources like CPU cores, memory and bandwidth [46].
Apart from ILP, other technologies can be employed to describe and solve the VNE problem (e.g., SAT and SMT solvers). However, the ILP formulation used here is established [43] and is improved by an ongoing collaboration with experts. Since the runtime for solving the ILP strongly depends on the choice of the ILP solver and the respective version, we have chosen Gurobi, an established, state-of-the-art ILP solver used in the industry and in various publications (e.g., [31, 38, 52, 60]).
7 Related work
This section surveys related work regarding generating mode instances from a metamodel, VNE algorithms for data centers, developing network applications using model-driven development, and combining MT and optimization techniques.
7.1 Generating model instances from a metamodel
The generation of model instances from a metamodel is the basis for the simulation of concrete VNE problems, whereby various methods and technologies are available in the literature. For example, Alanen et al. [4] present an algorithm to derive a context-free grammar from a metamodel, which enables the generation of model instances. Since this algorithm only represents tree-like metamodels and only a subset of possible associations, these limitations make this method difficult to apply to VNE problems. Also, formal methods like Alloy [25] can be used to generate instances. For this purpose, a class diagram is transformed to Alloy and, then, the instance generation of Alloy is applied to generate the respective model instances. Since SAT solvers are used to generate all instances, the use of model transformations has the advantage of using a grammar and a declarative visual language. Also, the integration into the presented construction methodology can be simplified by using MT methods and technologies.
7.2 VNE algorithms for data centers
The virtualization of data center networks and the VNE problem have been investigated extensively, and an overview of these areas can be found in [9, 17]. As a result, many algorithms for VNE in data centers have been developed to reduce the search space of this NP-hard problem [5]. For example, Guo et al. [20] present SecondNet, a heuristics-based approach for embedding a subset of virtualized data centers into a tree-based data center. The authors consider only the bandwidth and number of virtual machines per physical server to reduce the search space and, thus, the time needed to solve the problem. Zeng et al. [60] additionally consider the data traffic between the individual virtual machines and specify the minimization of the resulting communication costs as an optimization goal. The authors present an ILP-based formulation for small data centers and a heuristics-based algorithm for larger data centers. In [39], the relationships between switches and links are also taken into account and the optimization goal minimizes the communication costs and server fragmentation by avoiding network bottlenecks. Compared to the previously mentioned algorithms, MdVNE enables developers to consider different network topologies, resource constraints, requirements, and optimization goals by modifying the metamodel and MT rules of MdVNE and transforming the generated models into sets of ILP formulas as needed. Depending on the scenario, developers can reduce the search space and seamlessly adapt embedding decisions to changing boundary conditions while all constraints are met by the design.
7.3 Model-driven development of network applications
Model-driven software development is a promising method for developing applications independently of a concrete platform. The partly automatic verification of the specification and code generation also play an important role in numerous applications. For example, brake-by-wire in the automotive industry requires allocating software components on networked electronic control units. Pohlmann et al. [37] describe a model-driven allocation approach specifying the problem in an OCL-based language, transformed into an ILP formulation and solved the optimization problem afterward. In the area of Software-defined Networking, Lopes et al. [32] describe a method for creating application, controller, and network independent code for Software-defined Networking applications by modeling the physical network and its functionalities. Kluge et al. [28] present an approach for the development of topology control algorithms by graph transformations taking into account global and local consistency constraints (e.g., preservation of connectivity). The aforementioned approaches indicate that model-driven development is a promising method for specifying algorithms in various network domains. Still, the focus of these models and approaches is not the simultaneous support for network resources and limitations or specifying VNE algorithms for data center environments.
7.4 Combining search-based techniques and MT
The combination of MT, optimization techniques, and other search-based techniques is used in other areas. The paper by Zschaler et al. [61] provides a good overview and classification of state-of-the-art approaches including research challenges in this area. They also presents a prototype for a model-based optimization technique. Denil et al. [15] present an approach for integrating search-based optimizations into the model-driven development process. Using an example from the creation of electrical circuits, different optimization techniques such as randomized search or hill climbing are used to solve the problem. Strüber et al. [47] present an approach and implementation for the optimization of a model using a fitness function to create mutation operators for generic algorithms efficiently. The mutation operators are trained using a higher-order model transformation to improve performance and quality. Fleck et al. [11] describe how MT technologies and search-based algorithms are used to search for an optimal sequence of rule applications. By evaluating fitness values after each (arbitrarily performed) rule application, the approach reduces the search space on the fly but might fail in finding a global optimum. Another approach of optimization techniques in model-driven development is learning model transformations by examples [27], where the applicability to large models is the limiting aspect. In [1], a multi-objective optimization problem is solved by using a non-dominated sorting genetic algorithm. They find promising candidates based on a sequence of rule applications and presented an automated tooling for this approach.
7.5 Approaches for ensuring correctness
In the following, we survey approaches for ensuring the correctness of a system based on correctness by construction, verification, and testing. A prominent correct-by-construction approach in systems engineering is Event-B [2], which works by stepwise refinement. In [24], Heckel and Wagner laid the foundation for correct-by-construction approaches in the MT community based on generating weakest preconditions [16]. They represent graph constraints as premise-conclusion structure and propose a constructive algorithm that transforms a graph constraint into a weakest precondition of a model transformation rule. This weakest precondition is necessary and sufficient for preserving correctness w.r.t. the graph constraint. Nested graph constraints are an extension of premise-conclusion constraints and as expressive as first-order logic [22]. In this article, we formalize consistency properties using OCL constraints and possible element mapping operations using TGG rules. Then, we rely on [41] for transforming EOCL constraints into nested graph constraints. Using [22], we refine the TGG rules such that the refined TGG rules are correct w.r.t. EOCL constraints. Recently, with OCL2AC [35], tool support for automating the entire refinement step has been proposed. OCL2AC builds on the model transformation tool Henshin [7], whereas we use the model transformation tool eMoflon for the candidate generation step. In future work, we will explore how to transform eMoflon TGG rules automatically to and from Henshin rules to be able to employ OCL2AC. In [14], Deckwerth and Varró propose how to handle complex attribute constraints of premise-conclusion graph constraints during the constructive approach. Support for handling complex attribute constraints in nested graph constraints is still missing. In [40], Radke and Habel propose \(HR^{*}\) graph constraints that allow to encode path expressions. They also show that \(HR^{*}\) graph constraints can be translated into weakest preconditions in the spirit of the constructive approach. It is worthwhile to investigate in how far their results can be used in our scenario.
Verification-based approaches evaluate the required consistency properties a posteriori [42]. The constructive approach [24] is also suitable for static verification. If the generated preconditions are implied by the original preconditions of a rule, no modification is necessary because the rule already preserves consistency. Similar to correct-by-construction approaches, static verification allows for examining correctness properties independent of the system size. Still, a major reason for employing verification is that a system has not been realized using techniques that support the integration of consistency properties during the development. This necessitates dynamic verification using model checkers. A model checker constructs the state space of a system up to a threshold (e.g., based on time budget or model size). Afterward, it investigates the state space w.r.t. the desired consistency properties. For example, in [58, 59], Zave identifies critical flaws in the prominent network protocols SIP and Chord using model checkers The major drawback of dynamic verification is that the analyzed state space is finite and, typically, small.
Test-based approaches exercise a given system based on a set of input data and check whether the resulting behavior (e.g., the output data or the performance) conforms to the expectations [34]. Similar to dynamic verification, a test-based approach cannot prove that a system is correct. Instead, testing allows us to evaluate the behavior of the system in certain (corner) cases and to avoid regression by deriving test cases from errors that have been fixed. For the evaluation of this article, we employed unit testing to ensure that the code generated from the TGG specification behaves as expected in a number of representative scenarios.
8 Conclusion
In this article, we present a novel construction methodology to produce a suitable configuration for the model-driven virtual network embedding approach, which synthesizes the model transformation and integer linear programming specification from a given declarative model-based problem description. This provides correct and optimal solutions for the virtual network embedding problem, an optimization problem for embedding virtual networks in a substrate network. This methodology uses a novel model-based problem description for the VNE problem. It supports various types of resources, requirements, and constraints that are described by a metamodel, OCL constraints, and an optimization goal. The methodology is used to generate MT rules and ILP formulations that ensure all identified solutions respect the constraints and are optimal w.r.t. the optimization goal. Thus, our methodology enables developers to create a set of VNE algorithms for scenarios on an declarative level, to derive a prototypical implementation from a given specification semiautomatically.
Our evaluation results indicate that MdVNE is considerably faster than the ILP-only baseline in solving the VNE problem in particular for larger batch sizes. We validated the optimality by comparing the objective values of the outputs of the MdVNE and ILP-only approaches. Furthermore, we assured the quality of our implementation by using a redundant ILP-only implementation, consistency checks at runtime, and unit tests. The runtime of the MdVNE approach fluctuates less than the ILP-only baseline.
As a next step, we plan to support a larger subset of OCL to generalize the derivation process of ILP formulations for OCL. Furthermore, we will build a tool chain that covers the complete construction process using the model-based specification as a starting point and integrates it with the MdVNE approach. In this tool chain, a systematic derivation of OCL constraints in ILP formulations can take place using Clafer as an intermediate language [52, 53]. In addition, the derivation of OCL constraints can be done according to MT rule application conditions via graph constraints [35, 36]. To support dynamic VNE scenarios, changes in the networks (e.g., removing a virtual server) at runtime as well as migrations and costs for migrations have to be taken into account. These dynamic system changes will trigger migration and error protection strategies to achieve the permanent fulfillment of hardware and software constraints. In addition to updating the generated candidates, the ILP problem must also be adapted based on the incremental changes. Incremental pattern matching techniques [51] are a promising approach to address these dynamic scenarios and reduce the runtime for solving these problems. Finally, we will extend the MdVNE simulation framework to investigate further network types, VNE algorithms, and transition between different VNE algorithms.
References
Abdeen, H., Varró, D., Sahraoui, H.A., Nagy, A.S., Debreceni, C., Hegedüs, Á., Horváth, Á.: Multi-objective optimization in rule-based design space exploration. In: Crnkovic, I., Chechik, M., Grünbacher, P. (eds.) International Conference on Automated Software Engineering (ASE). ACM, pp. 289–300 (2014)
Abrial, J.R., Hallerstede, S.: Refinement, decomposition, and instantiation of discrete models: application to Event-B. Fundam. Inform. 77(1–2), 1–28 (2007)
Al-Fares, M., Loukissas, A., Vahdat, A.: A scalable, commodity data center network architecture. In: ACM SIGCOMM Conference on Applications, Technologies, Architectures, and Protocols for Computer Communications, pp. 63–74 (2008)
Alanen, M., Porres, I., Centre, T., Science, C.: A relation between context-free grammars and meta object facility metamodels. Technical report (2003)
Amaldi, E., Coniglio, S., Koster, A.M.C.A., Tieves, M.: On the computational complexity of the virtual network embedding problem. Electron. Notes Discrete Math. 52, 213–220 (2016)
Anjorin, A., Leblebici, E., Kluge, R., Schürr, A., Stevens, P.: A systematic approach and guidelines to developing a triple graph grammar. In: International Workshop on Bidirectional Transformations, CEUR vol. 1396, pp. 81–95 (2015)
Arendt, T., Biermann, E., Jurack, S., Krause, C., Taentzer, G.: Henshin: advanced concepts and tools for in-place EMF model transformations. In: International Conference on Model Driven Engineering Languages and Systems (MODELS), vol. 6394. Springer, pp. 121–135 (2010)
Ballani, H., Costa, P., Karagiannis, T., Rowstron, A.I.T.: Towards predictable datacenter networks. In: Conference on Applications, pp. 242–253 (2011)
Bari, M.F., Boutaba, R., Esteves, R.P., Granville, L.Z., Podlesny, M., Rabbani, M.G., Zhang, Q., Zhani, M.F.: Data center network virtualization: a survey. Commun. Surv. Tutor. 15(2), 909–928 (2013)
Bhardwaj, S., Jain, L., Jain, S.: Cloud computing: a study of infrastructure as a service (IaaS). Int. J. Eng. Inf. Technol. 2(1), 60–63 (2010)
Bill, R., Fleck, M., Troya, J., Mayerhofer, T., Wimmer, M.: A local and global tour on momot. Softw. Syst. Model. 18(2), 1017–1046 (2019)
Böhm, M., Leimeister, S., Riedl, C., Krcmar, H.: Cloud computing–outsourcing 2.0 or a new business model for it provisioning? In: Application Management. Springer, pp. 31–56 (2011)
Cplex, I.I.: 12.2 user’s manual. Book 12.2 User’s Manual, Series 12.2 User’s Manual (2010)
Deckwerth, F., Varró, G.: Attribute handling for generating preconditions from graph constraints. In: International Conference on Graph Transformation (ICGT), pp. 81–96 (2014)
Denil, J., Jukss, M., Verbrugge, C., Vangheluwe, H.: Search-based model optimization using model transformations. In: System Analysis and Modeling: Models and Reusabilit (SAM), pp. 80–95 (2014)
Dijkstra, E.W.: A Discipline of Programming, vol. 1. Prentice Hall, Upper Saddle River (1976)
Fischer, A., Botero, J.F., Beck, M.T., de Meer, H., Hesselbach, X.: Virtual network embedding: a survey. Commun. Surv. Tutor. 15(4), 1888–1906 (2013)
Fowler, M.: UML Distilled: A Brief Guide to the Standard Object Modeling Language. Addison-Wesley Professional, Boston (2004)
Group, O.M.: Object constraint language 2.0. OMG (2003)
Guo, C., Lu, G., Wang, H.J., Yang, S., Kong, C., Sun, P., Wu, W., Zhang, Y.: Secondnet: a data center network virtualization architecture with bandwidth guarantees. In: Conference on emerging Networking EXperiments and Technologies (CoNEXT), pp. 15:1–15:12 (2010)
Gurobi Optimization, I.: Gurobi optimizer reference manual. https://www.gurobi.com/ (2016). Accessed 17 Jan 2018
Habel, A., Pennemann, K.: Correctness of high-level transformation systems relative to nested conditions. Math. Struct. Comput. Sci. 19(2), 245–296 (2009)
Hadjiconstantinou, E.: Transformation of propositional calculus statements into integer and mixed integer programs: an approach towards automatic reformulation. Brunel University, Technical report (1990)
Heckel, R., Wagner, A.: Ensuring consistency of conditional graph grammars—a constructive approach. ENTCS 2, 118–126 (1995)
Jackson, D.: Alloy: a lightweight object modelling notation. ACM Trans. Softw. Eng. Methodol. 11(2), 256–290 (2002)
Kehrer, T., Taentzer, G., Rindt, M., Kelter, U.: Automatically deriving the specification of model editing operations from meta-models. In: International Conference on Model Transformation (ICMT), pp. 173–188 (2016)
Kessentini, M., Sahraoui, H., Boukadoum, M.: Model transformation as an optimization problem. In: International Conference on Model Driven Engineering Languages and Systems (MODELS). Springer, Berlin, pp. 159–173 (2008)
Kluge, R., Stein, M., Varró, G., Schürr, A., Hollick, M., Mühlhäuser, M.: A systematic approach to constructing incremental topology control algorithms using graph transformation. JVLC 38, 47–83 (2017)
Krieger, M.P., Brucker, A.D.: Extending OCL operation contracts with objective functions. ECEASST 4. https://journal.ub.tu-berlin.de/eceasst/article/view/662, (2011)
Leblebici, E., Anjorin, A., Schürr, A.: Developing eMoflon with eMoflon. ICMT 8568, 138–145 (2014)
Leblebici, E., Anjorin, A., Schürr, A.: Inter-model consistency checking using triple graph grammars and linear optimization techniques. In: Fundamental Approaches to Software Engineering (FASE), pp. 191–207 (2017)
Lopes, F.A., Lima, L., Santos, M., Fidalgo, R., Fernandes, S.: High-level modeling and application validation for SDN. In: Network Operations and Management Symposium, pp. 197–205 (2016)
Meng, X., Pappas, V., Zhang, L.: Improving the scalability of data center networks with traffic-aware virtual machine placement. In: IEEE International Conference on Computer Communications (INFOCOM), pp. 1154–1162 (2010)
Myers, G.J., Sandler, C., Badgett, T.: The Art of Software Testing. Wiley, Hoboken (2011)
Nassar, N., Kosiol, J., Arendt, T., Taentzer, G.: OCL2AC: automatic translation of OCL constraints to graph constraints and application conditions for transformation rules. In: International Conference on Graph Transformation (ICGT), pp. 171–177 (2018)
Nassar, N., Kosiol, J., Arendt, T., Taentzer, G.: Constructing optimized validity-preserving application conditions for graph transformation rules. In: International Conference on Graph Transformation (ICGT), pp. 177–194 (2019)
Pohlmann, U., Hüwe, M.: Model-driven allocation engineering (t). In: International Conference on Automated Software Engineering (ASE), pp. 374–384 (2015)
Pohlmann, U., Hüwe, M.: Model-driven allocation engineering: specifying and solving constraints based on the example of automotive systems. Autom. Softw. Eng. 26(2), 315–378 (2019)
Rabbani, M.G., Esteves, R.P., Podlesny, M., Simon, G., Granville, L.Z., Boutaba, R.: On tackling virtual data center embedding problem. In: IFIP/IEEE International Symposium on Integrated Network Management, pp. 177–184 (2013)
Radke, H.: Weakest liberal preconditions relative to HR* graph conditions. In: International Workshop on Graph Computation Models (GCM), pp. 165–178 (2010)
Radke, H., Arendt, T., Becker, J.S., Habel, A., Taentzer, G.: Translating essential OCL invariants to nested graph constraints for generating instances of meta-models. Sci. Comput. Program. 152, 38–62 (2018)
Rensink, A., Schmidt, A., Varró, D.: Model checking graph transformations: a comparison of two approaches. In: International Conference on Graph Transformation (ICGT), vol. 3256. Springer, pp. 226–241 (2004)
Sahhaf, S., Tavernier, W., Rost, M., Schmid, S., Colle, D., Pickavet, M., Demeester, P.: Network service chaining with optimized network function embedding supporting service decompositions. Comput. Netw. 93, 492–505 (2015)
Schnabel, T., Weckesser, M., Kluge, R., Lochau, M., Schürr, A.: Cardygan: tool support for cardinality-based feature models. In: International Workshop on Variability Modelling of Software-Intensive Systems. ACM, pp. 33–40 (2016)
Schürr, A.: Specification of graph translators with triple graph grammars. In: Graph–Theoretic Concepts in Computer Science, pp. 151–163 (1994)
Shen, S., van Beek, V., Iosup, A.: Statistical characterization of business-critical workloads hosted in cloud datacenters. In: International Symposium on Cluster, Cloud and Grid Computing (CCGrid), pp. 465–474 (2015)
Strüber, D.: Generating efficient mutation operators for search-based model-driven engineering. In: International Conference on Model Transformation (ICMT), pp. 121–137 (2017)
Tomaszek, S., Leblebici, E., Wang, L., Schürr, A.: Virtual network embedding: reducing the search space by model transformation techniques. In: International Conference on Model Transformation (ICMT), pp. 59–75 (2018)
Tomaszek, S., Leblebici, E., Wang, L., Schürr, A.: Model-driven development of virtual network embedding algorithms with model transformation and linear optimization techniques. Modellierung 2018, 39–54 (2018)
Varró, D., Bergmann, G., Hegedüs, Á., Horváth, Á., Ráth, I., Ujhelyi, Z.: Road to a reactive and incremental model transformation platform: three generations of the VIATRA framework. Softw. Syst. Model. 15(3), 609–629 (2016)
Varró, G., Varró, D., Schürr, A.: Incremental graph pattern matching: Data structures and initial experiments. ECEASST 4. https://doi.org/10.14279/tuj.eceasst.4.12 (2006)
Weckesser, M.: Automatisierte analyse integrierter software-produktlinien-spezifikationen. Ph.D. thesis, Darmstadt University of Technology, Germany (2019)
Weckesser, M., Lochau, M., Ries, M., Schürr, A.: Towards complete consistency checks of clafer models. In: International Workshop on Feature-Oriented Software Development (SIGPLAN), pp. 11–20 (2017)
Wohlin, C., Runeson, P., Höst, M., Ohlsson, M.C., Regnell, B.: Experimentation in Software Engineering. Springer, Berlin (2012)
Yang, Y., Chang, X., Liu, J., Li, L.: Towards robust green virtual cloud data center provisioning. IEEE Trans. Cloud Comput. 5(2), 168–181 (2017)
Yang, Z., Guo, Y.: An exact virtual network embedding algorithm based on integer linear programming for virtual network request with location constraint. China Commun. 13(8), 177–183 (2016)
Yu, M., Yi, Y., Rexford, J., Chiang, M.: Rethinking virtual network embedding: substrate support for path splitting and migration. SIGCOMM Comput. Commun. Rev. 38(2), 17–29 (2008)
Zave, P.: Understanding SIP through Model-Checking. In: Principles, Systems and Applications of IP Telecommunications. Services and Security for Next Generation Networks, vol. 5310. Springer, pp. 256–279 (2008)
Zave, P.: Using lightweight modeling to understand chord. SIGCOMM Comput. Commun. Rev. 42(2), 49–57 (2012)
Zeng, D., Guo, S., Huang, H., Yu, S., Leung, V.C.: Optimal VM placement in data centers with architectural and resource constraints. Int. J. Autonom. Adapt. Commun. Syst. 8(4), 392–406 (2015)
Zschaler, S., Mandow, L.: Towards model-based optimisation: using domain knowledge explicitly. In: Software Technologies: Applications and Foundations (STAF), Collocated Workshops, pp. 317–329 (2016)
Acknowledgements
This work was funded by the German Research Foundation (DFG) as part of project A1 within the Collaborative Research Center (CRC) 1053 – MAKI.
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Davide Di Ruscio.
Publisher's Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Appendix
Appendix
In the appendix we present the restrictions that are not necessary for understanding the work. In Appendix A.1, we present all further restrictions from Sect. 2.1.2. Afterward, we present in Appendix A.2 the constraints and graph constraints from Sect. 3.2.3 (Figs. 21, 22).
1.1 VNE problem description
In this section, we present all node and link constraints relating to Sects. 2.1.2 and 2.2.3





Further ILP node constraints


Further ILP link constraints

1.2 Construction of MT specification
In this section, we present the additional relaxed and graph constraints related to Sect. 3.2.3.




Rights and permissions
About this article
Cite this article
Tomaszek, S., Speith, R. & Schürr, A. Virtual network embedding: ensuring correctness and optimality by construction using model transformation and integer linear programming techniques. Softw Syst Model 20, 1299–1332 (2021). https://doi.org/10.1007/s10270-020-00852-z
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-020-00852-z




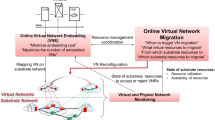











 based on
based on  .
. and the original constraint
and the original constraint  .
. .
.









