Abstract
Managing temporal process constraints in a suitable way is crucial for long-running business processes in many application domains. However, proper support of time-aware processes is still missing in contemporary information systems. This paper tackles a particular challenge existing in this context, namely the handling of temporal constraints for modularized processes (i.e., processes comprising subprocesses), which shall enable both the reuse of process knowledge and the modular design of complex processes. In detail, this paper focuses on the representation and support of time-aware modularized processes in process-aware information systems. To this end, we present a sound and complete method to derive the duration restrictions of a time-aware (sub-)process in such a way that its temporal properties are completely specified. We then show how this characterization of a process can be utilized when reusing it as a subprocess within a modularized process. As a motivating example, we consider a compound process from healthcare. Altogether the proper handling of temporal constraints for modularized processes is crucial for the enhancement of time- and process-aware information systems.
Similar content being viewed by others
Avoid common mistakes on your manuscript.
1 Introduction
It is widely acknowledged that the capability to modularly design process schemas constitutes an important requirement for creating comprehensible and reusable process schemas [31, 33]. Thus, the support of complex processes, which may comprise subprocesses at different levels, is essential for process-aware information systems (PAIS) as it allows for the reuse of existing process knowledge from a process repository as well as the modular design of such processes.
On the other hand, temporal process constraints, such as deadlines and maximum allowable delays between task executions, must be suitably handled in many application domains. Even tough this topic has received increasing attention in the research community during the last years [2, 6, 11, 17, 24], a complete support of time-aware processes is still missing in contemporary PAIS.
At first glance, temporal process constraints and process modularity seem to be orthogonal features that may be managed in an independent way. However, when getting to the heart of these two features, it turns out that modularity in combination with the reuse of time-aware processes requires the ability to represent the overall temporal behavior of a process [19]. Only then, it becomes possible to evaluate the temporal constraints of a process containing time-aware subprocesses in a truly modular way, i.e., without replacing the subprocess tasks with their (temporal) components. Moreover, one may then attach temporal information to the process schema when storing it in a central process repository. This knowledge can, for example, be essential in the context of business process analysis and optimization [32].
In [19], the issue of representing the temporal properties of a process has been considered. This paper extends and completes the approach for the representation and support of time-aware modularized processes, which we presented in [19]. In particular, we introduce and prove a sound and complete method to derive the duration restrictions of a time-aware process in such a way that its temporal properties are completely described. Then, we show how this characterization of a process can be merged with other temporal constraints when reusing it as a subprocess of a modularized process. In accordance with recent research contributions, we focus on the issue of dynamic controllability (DC) of time-aware processes [6, 17]. In general, DC corresponds to the capability of a PAIS to execute a process schema in a way such that all allowed durations of all tasks are possible, while still satisfying all temporal constraints; i.e., DC ensures that it is possible to execute a process schema without any need to restrict the allowed durations of a task for satisfying all temporal constraints. In this context, task durations are called contingent as they are not under the control of the PAIS (i.e., its process engine).
The two main research questions addressed in this paper are:
-
1.
How can the overall temporal behavior of a process be represented (cf. Sect. 5)? Addressing this issue constitutes a fundamental prerequisite for providing some kind of modularity from the temporal perspective as well. Note that without such characterization, it would be necessary to recompute the temporal features of a subprocess schema each time it is used in a modularized process. More particularly, this paper focuses on providing a formal description of how to represent and derive temporal constraints for modularized processes. As will be shown, a process duration can be represented as a kind of range composed of two parts. One part represents all possible durations, while the second one, which often constitutes a restriction of the first part, represents the core of durations the PAIS cannot restrict at runtime. On the one hand, the duration of the subprocess can be controlled to some extent due to the nature of the contained temporal constraints; on the other hand, it cannot be fully controlled as the contingent durations of the contained tasks cannot be controlled by the PAIS and must be guaranteed.
With respect to the informal proposal made in [19], this paper provides a formal and complete description of how to represent and derive the overall temporal behavior of a process.
-
2.
How to apply knowledge about the temporal behavior of a process when reusing its schema as a subprocess inside a modularized process in order to avoid having to re-analyze the internal constraints of the subprocess (cf. Sect. 6)? This will, for example, enable us to store time-aware processes including their overall temporal properties in a process repository and to reuse them in a truly modular fashion.
In addition to our preliminary work on managing time-awareness in modularized processes [19], this paper presents all proofs related to the formal part of the approach. Moreover, we reorganize the structure applied in [19] to provide a more insightful and detailed discussion of each relevant aspect and we describe the design and implementation of a proof-of-concept prototype of the approach (cf. Sect. 7). In detail, the remainder of this work is organized as follows: Sect. 2 introduces a clinical guideline dealing with the management of osteoarthritis of the hand, hip and knee as an example of a process schema with subprocesses and temporal properties. We use this clinical example for illustration purposes throughout the paper. Section 3 extends the discussion of existing work related to the management of temporal constraints in business processes. In Sect. 4, we present, in an extended way, the Simple Temporal Network with Partially Shrinkable Uncertainty (STNPSU) model. In particular, this model is used for temporal reasoning on subprocesses. In turn, Sect. 5 constitutes the core of the paper. It discusses how to characterize time-aware processes by mapping them to corresponding STNPSUs extended with the concept of contingency span. In this context, all relevant concepts are formally described and formal statements are proven. Section 6 then discusses how the temporal properties of a (sub-)process can be utilized in order to check the controllability of the overall process without unfolding its subprocesses. As another novel contribution, Sect. 7 presents the architecture of ATAPIS, which is an open framework for the design, verification and enactment of modularized temporal processes. Finally, Sect. 8 summarizes the main results of our work and gives an outlook on future work.
2 Motivating example
As a motivating scenario, we consider a high-level specification of an excerpt of a clinical guideline related to the management of osteoarthritis of the hand, hip and knee [16]. A possible schema of this process is depicted in Fig. 1.
After completing the initial Patient Evaluation (task \(T_0\): \(\mathtt {PatEv}\)), two parallel branches become activated. The first one is composed of process Non-Pharmacologic Recommendation (\(P_0\): \(\mathtt {NonPharmR}\)) followed by process Specification of Physical Exercises (\(P_1\): \(\mathtt {PhysEx}\)). The second one consists of process Pharmacologic Recommendation (\(P_2\): \(\mathtt {PharmR}\)) followed by a Treatment Explanation to the patient (task \(T_8\): \(\mathtt {TrExp}\)). As depicted in Fig. 1, \(P_0\), \(P_1\) and \(P_2\) correspond to subprocesses (from a process repository) that comprise other tasks and may be reused in the context of other clinical processes (e.g., related to other pathologies). In detail, Non-Pharmacologic Recommendation\(P_0\) consists of two parallel branches. The first branch evaluates the patient’s ability to perform activities of daily live (task \(T_1\): \(\mathtt {ADLsEv}\)) followed by the identification of needed assistive devices (task \(T_2\): \(\mathtt {DevId}\)). The second branch consists of giving instructions to the patient related to the use of thermal modalities (task \(T_3\): \(\mathtt {ThermMod}\)). In turn, the Specification of Physical Exercises (i.e., \(P_1\)) consists of the specification of aquatic exercises (task \(T_4\): \(\mathtt {AqEx}\)) followed by the specification of land exercises (task \(T_5\): \(\mathtt {LndEx}\)). Finally, Pharmacologic Recommendation (i.e., \(P_2\)) consists of the evaluation of contraindications (task \(T_6\): \(\mathtt {CntrEval}\)) followed by a drug specification (task \(T_7\): \(\mathtt {DrgSp}\)).
We enrich the process schemas with temporal constraints that need to be obeyed in order to guarantee the clinically successful completion of each step of the therapy. Furthermore, such temporal constraints will help practitioners (e.g., doctors and nurses) in planning their daily work as they can anticipate how long previous steps will take and how much freedom they have for performing their tasks. The temporal constraints allow for the temporal characterization of tasks, edges and gateways according to the concepts introduced in [18]. Note that the durations of tasks are not completely under the control of the PAIS as these tasks are carried out by practitioners.
Therefore, task durations are represented as guarded ranges. Such a duration range may be partially restricted by the system during process execution in order to ensure successful completion of the processes. For example, task \(T_6\) has temporal constraint  meaning that prior to the execution of the task, its duration may be restricted, but in any case, the minimum required duration must not exceed 2 time units and the maximum duration cannot be constrained below 4 (e.g., a duration of [3, 5] or [1, 2] would be disallowed). As another example consider task \(T_7\) with temporal constraint
meaning that prior to the execution of the task, its duration may be restricted, but in any case, the minimum required duration must not exceed 2 time units and the maximum duration cannot be constrained below 4 (e.g., a duration of [3, 5] or [1, 2] would be disallowed). As another example consider task \(T_7\) with temporal constraint  . The latter expresses that this task may last 1 to 7 time units, and all possible durations shall be allowed during process execution. This ensures that the user executing the task has sufficient flexibility to successfully complete the task. Constraints on gateways and edges constitute standard temporal constraints, specifying the possible durations (within a range), which are under the control of the PAIS (i.e., its process engine).
. The latter expresses that this task may last 1 to 7 time units, and all possible durations shall be allowed during process execution. This ensures that the user executing the task has sufficient flexibility to successfully complete the task. Constraints on gateways and edges constitute standard temporal constraints, specifying the possible durations (within a range), which are under the control of the PAIS (i.e., its process engine).
As already discussed, two challenges emerge in this context.
-
The first challenge concerns the representation of the overall temporal behavior of (sub-)processes. One must be able to describe how a subprocess like, for example, \(\mathtt {PhysEx}\) behaves temporally if it shall be reusable inside any time-aware processes. Note that \(\mathtt {PhysEx}\) involves physical therapists and is usually required in the context of many other healthcare processes. For example, the activities of this (sub-)process with the same internal temporal constraints might be also required when managing patients that suffer from multiple sclerosis [15] or sarcopenia (loss of muscular mass and decline in associated muscular function occurring with aging [8]). Furthermore, the subprocess is relevant for managing patients with osteogenesis imperfecta (a pathology caused by a mutation in a gene that affects bone formation, bone strength, and the structure of other tissues [26]) often undergoing multiple rehabilitation periods after bone fractures. These three clinical scenarios only constitute few examples of real-world clinical processes whose definition could make use of subprocess \(\mathtt {PhysEx}\). In general, the designers of a clinical process schema would benefit from the establishment of a clinical process library that collects reusable, suitably defined clinical subprocesses. To allow for the proper reuse of such subprocesses, in turn, their temporal behavior needs to be part of their overall description. Note that similar considerations can be made for other subprocesses as well. For example, subprocess \(\mathtt {PharmR}\) is common to many decision-based care processes.
-
The second challenge is related to the efficient temporal analysis of the top-level (i.e., main) process. Ideally, this analysis can be accomplished without need for unfolding all used subprocesses \(P_0, P_1,\) and \(P_2\). Only then, the temporal analysis can be accomplished effectively and quickly. In general, the provision of modularized clinical (sub-)processes will allow checking temporal properties of the main process, while only considering a reduced number of constraints and tasks/subprocesses. Regarding the running example, for instance, it should be possible to verify the temporal properties of the process for managing osteoarthritis patients without need to consider the internal structure and constraints of \(\mathtt {PharmR}\), \(\mathtt {NonPharmR}\), and \(\mathtt {PhysEx}\).
3 Related work
In the literature, there is considerable work on the management of temporal constraints in PAIS [1, 2, 7, 10,11,12, 17, 23, 25]. Issues these approaches are focusing on include the modeling and verification of time-aware processes.
For each process exhibiting temporal constraints, a time-aware process schema needs to be defined [17]. In the context of this work, a process schema corresponds to a directed graph that comprises a set of nodes—representing tasks and gateways (e.g., AND-Split/Join)—as well as a set of control edges linking these nodes and specifying precedence relations between them. Each process schema contains unique start and end nodes, and may be composed of control flow patterns like sequence, parallel split, and synchronization.
Lanz et al. [22, 24] introduced 10 time patterns representing common temporal constraints of time-aware processes (cf. Table 1). In particular, time patterns facilitate the comparison of existing approaches based on a universal set of notions with well-defined semantics. While [24] introduced the empirically evidenced time patterns informally, [22] additionally provided a formal semantics for them. Moreover, the need for a sophisticated runtime support for the time patterns was elaborated in [24].
Marjanovic et al. [25] defined a conceptual model for temporal constraints on a process schema, which is tailored to check for temporal consistency. Considering the time pattern classification (cf. Table 1), [25] dealt with time lags between activities (TP1), activity and process durations (TP2), and fixed date elements (TP4). Furthermore, [25] proposed a set of rules for verifying time-aware process schemas, whereas no runtime support was considered.
Eder et al. [10] presented an extended version of the Critical Path Method, which is known from the project planning domain. In detail, [10] proposed the use of Timed Workflow Graphs (TWG) for representing the temporal properties of activities and their control flow relations. Regarding the time patterns, [10] considered time lags between activities (TP1), activity durations (TP2), fixed date elements (TP4), and schedule restricted elements (TP5). Note that [10] presumes that activity durations are deterministic, i.e., activity durations are the same for all process instances. As for activity durations, in [13, 14], authors discussed a probabilistic approach based on duration histograms to deal with temporal information about tasks.
Bettini et al. [1] proposed an approach based on Simple Temporal Network (STN) [9]. In particular, this differs significantly from the aforementioned ones. In an STN, nodes represent timepoints, whereas each directed edge \(a {\mathop {\longrightarrow }\limits ^{v}} b\) between timepoints a and b represents a temporal constraint \(b-a\le v\) with v being a real value. If \(v\ge 0\) holds, the constraint represents the maximum allowable delay between b and a; otherwise (i.e., \(v<0\)), it represents the minimum time span to be elapsed after b before a may occur. In [1], each process activity is represented by two nodes of the respective STN, which correspond to the starting and ending timepoint of the activity. In turn, the edges of the STN represent temporal constraints and precedence relations between the corresponding nodes. Finally, [1] considered time lags between activities (TP1), activity durations (TP2), and fixed date elements (TP4).
Combi et al. [2, 3] proposed a temporal conceptual model for specifying time-aware process schemas. In this conceptual model, time lags between activities (TP1), activity durations (TP2), fixed date elements (TP4), schedule restricted elements (TP5), and periodicity (TP10) are considered. First of all, [3] shows how to check consistency of time-aware processes at design time, Furthermore, [3] argues that different strategies for ensuring consistency of a process instance during runtime may be applied, depending on the considered kind of consistency of a process schema. In [2], in turn, the authors extended their work considering also tasks for which the execution time cannot be decided, but only observed, analyzing the computational complexity of the dynamic controllability problem (cf. Sect. 1) and proposing a general algorithm to check for the dynamic controllability of a time-aware process schema.
Zhang et al. [35] addressed the issue of determining whether a business activity is eligible for relocation in a business process in order to optimize overall execution performance. Note that even in this case, it is crucial to characterize the temporal behavior of each activity.
The concept of temporal controllability has been mainly investigated in the AI area in connection with temporal constraint networks. In [30], Morris et al. proposed an STN [9] extension, the Simple Temporal Network With Uncertainty (STNU). Regarding STNUS, it is also possible to specify a new kind of constraint, the contingent links. The latter are not under the control of the system and, hence, the concept of consistency is extended to the concept of dynamic controllability.
Finally, Combi et al. [6] transferred the concept of dynamic controllability to time-aware process schemas. Recently, in [4, 5], authors extended STNU to Conditional Simple Temporal Network with Uncertainty (CSTNU), which additionally consider alternative execution paths.
4 Backgrounds
This work relies on Simple Temporal Network with Partially Shrinkable Uncertainty (STNPSU), an extension of STNU that enlarges contingent links to enable a more flexible management of temporal constraints [18]. This section provides a detailed discussion on STNPSU. Moreover, it presents the definitions required to understand the formal proofs given in the following sections.
An STNPSU [18] is a directed weighted graph (cf. Fig. 2a) whose nodes represent time-point variables (timepoints), usually corresponding to the start or end of activities, and whose edges  , called requirement links, represent a lower and an upper bound constraint on the distance between the two timepoints it connects; e.g.,
, called requirement links, represent a lower and an upper bound constraint on the distance between the two timepoints it connects; e.g.,  represents a constraint expressing that timepoint B must occur between x and y time units after the occurrence of A (i.e., \(x\le B-\!A\le y\)). For an STNPSU, it is possible to characterize certain timepoints as contingent timepoints, meaning that their value cannot be decided by the system executing the STNPSU; instead, the value is decided by the environment during runtime. Each contingent timepoint has one incoming edge, which is called guarded link and drawn as a double line, e.g.,
represents a constraint expressing that timepoint B must occur between x and y time units after the occurrence of A (i.e., \(x\le B-\!A\le y\)). For an STNPSU, it is possible to characterize certain timepoints as contingent timepoints, meaning that their value cannot be decided by the system executing the STNPSU; instead, the value is decided by the environment during runtime. Each contingent timepoint has one incoming edge, which is called guarded link and drawn as a double line, e.g.,  . A guarded link
. A guarded link  consists of a pseudo-contingent duration range [x, y] augmented with two guards, the lower guard\(x'\) and the upper guard\(y'\) [18]. A is called the activation timepoint. Before executing a guarded link, its duration range [x, y] may be modified. However, any modification must be accomplished in a way respecting the corresponding guards, i.e., \(x\le x'\) and \(y\ge y'\). When activating a guarded link
consists of a pseudo-contingent duration range [x, y] augmented with two guards, the lower guard\(x'\) and the upper guard\(y'\) [18]. A is called the activation timepoint. Before executing a guarded link, its duration range [x, y] may be modified. However, any modification must be accomplished in a way respecting the corresponding guards, i.e., \(x\le x'\) and \(y\ge y'\). When activating a guarded link  (i.e., when executing timepoint A), the current value \([x^*,y^*]\) of the duration range becomes a fully contingent range, which is then made available to the environment for executing timepoint C. That means, once A is executed, C is guaranteed to be executed such that \(C-A \in [x^*,y^*]\) holds. Note that the specific time at which C is executed is uncontrollable since it is decided by the environment; i.e., it can be only observed when it happens.
(i.e., when executing timepoint A), the current value \([x^*,y^*]\) of the duration range becomes a fully contingent range, which is then made available to the environment for executing timepoint C. That means, once A is executed, C is guaranteed to be executed such that \(C-A \in [x^*,y^*]\) holds. Note that the specific time at which C is executed is uncontrollable since it is decided by the environment; i.e., it can be only observed when it happens.
More formally, an STNPSU is a triple \(\left( \mathcal {T},\mathcal {C},\mathcal {G}\right) \), where
-
\(\mathcal {T}\) is a set of timepoints;
-
\(\mathcal {C}\) is a set of requirement links
 , and
, and -
\(\mathcal {G}\) is a set of guarded links each having the form
 , where A and C correspond to timepoints, and \(0<x\le y\!<\infty , x\le x', 0<\! y'\le y\).
, where A and C correspond to timepoints, and \(0<x\le y\!<\infty , x\le x', 0<\! y'\le y\).
Moreover, if  as well as
as well as  are distinct guarded links in \(\mathcal {G}\), \(C_1\) and \(C_2\) will be distinct timepoints. It is noteworthy that guarded links may be used to represent two different types of constraints: If \(x' < y'\) holds, a guarded link represents a temporal constraint with a partially contingent range. Particularly, the guarded link then represents a constraint with a contingent (i.e., unshrinkable) core\([x', y'] \subseteq [x, y]\). In turn, if \(x' \ge y'\) holds, a guarded link represents a temporal constraint with a partially shrinkable range with a guarded core\([y', x']\).
are distinct guarded links in \(\mathcal {G}\), \(C_1\) and \(C_2\) will be distinct timepoints. It is noteworthy that guarded links may be used to represent two different types of constraints: If \(x' < y'\) holds, a guarded link represents a temporal constraint with a partially contingent range. Particularly, the guarded link then represents a constraint with a contingent (i.e., unshrinkable) core\([x', y'] \subseteq [x, y]\). In turn, if \(x' \ge y'\) holds, a guarded link represents a temporal constraint with a partially shrinkable range with a guarded core\([y', x']\).
Furthermore, each STNPSU is associated with a distance graph\(\mathcal {D}= (\mathcal {T}, \mathcal {E})\), derived from the upper and lower bound constraints [18, 29]. In the distance graph (cf. Fig. 2b), each link between a pair of timepoints A and B is represented as two ordinary edges in \(\mathcal {E}\):  , representing constraint \(B\le A+y\), and
, representing constraint \(B\le A+y\), and  for representing constraint \(B\ge A+x\), \(x,y\in \mathbb {R} \). Moreover, for each guarded link between a pair of timepoints A and C, \(\mathcal {E}\) contains two other labeled edges, called lower and upper-case labeled values. A lower-case labeled value,
for representing constraint \(B\ge A+x\), \(x,y\in \mathbb {R} \). Moreover, for each guarded link between a pair of timepoints A and C, \(\mathcal {E}\) contains two other labeled edges, called lower and upper-case labeled values. A lower-case labeled value,  , expresses that C cannot be forced to be executed at a time greater than \(x'\) after A, i.e., , it is not possible to add a constraint
, expresses that C cannot be forced to be executed at a time greater than \(x'\) after A, i.e., , it is not possible to add a constraint  to the network. In turn, an upper-case labeled value,
to the network. In turn, an upper-case labeled value,  , expresses that C cannot be forced to be executed at a time less than \(y'\) after A, i.e., it is not possible to add a constraint
, expresses that C cannot be forced to be executed at a time less than \(y'\) after A, i.e., it is not possible to add a constraint  to the network.
to the network.
These two kinds of labels are fundamental for determining the dynamic controllability of the network as explained in the following. Note that these two representations of an STNPSU can be used interchangeably.
An STNPSU is denoted as dynamically controllable (DC), if there exists a strategy for executing its timepoints in such a way that: i) all constraints in the network can be satisfied, no matter how the execution of any guarded link turns out, and ii) for any other guarded link  , the lower bound x must not be increased beyond its lower guard \(x'\) and the upper bound y must not be decreased below its upper guard \(y'\) [18].
, the lower bound x must not be increased beyond its lower guard \(x'\) and the upper bound y must not be decreased below its upper guard \(y'\) [18].
In [18], it was shown how one can adapt and extend the edge-generation rules and algorithm proposed by Morris et al. for checking the dynamic controllability (DC) of STNU [29] in order to check the DC of an STNPSU in polynomial time (cf. Algorithm 1).

The checking algorithm works by recursively generating new edges in the STNPSU distance graph according to the rules from Table 2 and by checking whether newly added edges result in so-called negative semi-reducible cycles in the graph [27]. For each rule, existing edges are represented as solid arrows and newly added ones as dashed arrows. Each of the first four rules takes two existing edges as input and generates a single edge as output. Finally, notation \(R \not \equiv S\) expresses that R and S must be distinct time-point variables, but does not represent a constraint on the values of those variables. A path in an STNPSU distance graph is called semi-reducible if, through the subsequent application of the edge-generation rules (cf. Table 2), it can be transformed into a path solely consisting of ordinary or upper-case edges [27]. A semi-reducible cycle with negative unlabeled length is called a negative semi-reducible cycle. To detect negative semi-reducible cycles, Algorithm 1 uses the AllMax-Projection of the STNPSU. The AllMax-Projection is the distance matrix for the Simple Temporal Network (STN) [9] formed by all of the original and generated ordinary and upper-case edges (without their alphabetic labels) and represents the occurrence when all guarded links in the original network assume their upper guard value.
Example 1
(Negative Semi-Reducible Cycle) Consider the distance graph depicted in Fig. 2b corresponding to the STNPSU from Fig. 2a. It is a matter of applying the edge-generation rules from Table 2 to verify that Fig. 3 depicts the derived distance graph of Fig. 2b (dashed lines are the generated ones) containing the semi-reducible cycle \(A-C-A\). Moreover, as the unlabeled length of this semi-reducible cycle is negative, the respective STNPSU cannot be dynamically controllable. In particular, let us consider the scenario where D is executed 4 time units after C and B is executed 2 time units after A. Then, due to the fact that D may be executed at most 2 time units after B, C has to be executed at most 0 time units after A (i.e., at the same item as A). In turn, in the scenario where D is executed 2 time units after C and B is executed 4 time units after A, C has to be executed at least 1 time unit after A in order to be able to satisfy the requirement link between B and D. However, it is not possible to satisfy both conditions at the same time. Thus, the STNPSU is not DC.
New generated edges in distance graph of Fig. 2b
We observe that the edge-generation rules from Table 2 only generate ordinary or upper-case edges. The upper-case edges generated by respective rules represent conditional constraints, called waits [29]. In particular, an upper-case edge  represents the following constraint: as long as contingent timepoint C remains unexecuted, timepoint B must wait at least v units after the execution of A, the activation timepoint for C. Note that [27] and [28] presented two optimizations of the original algorithm, which are not further discussed in this paper.
represents the following constraint: as long as contingent timepoint C remains unexecuted, timepoint B must wait at least v units after the execution of A, the activation timepoint for C. Note that [27] and [28] presented two optimizations of the original algorithm, which are not further discussed in this paper.
5 Characterization of time-aware processes
This section shows how to determine a proper representation for the duration of a process. For this purpose, we consider a process schema P with a single start and a single end node. In this paper, we do not consider the choices pattern, but we are currently extending STNPSU to support choices as well. However, our preliminary analysis has shown that the results presented in this paper will be also applicable to this extended kind of STNPSU.
First, we show how to verify the dynamic controllability (DC) of process schema P and, if P is DC, how to derive its minimal constraints. Second, we discuss how to determine the guards for a guarded link representing the duration of a process. Finally, we propose to extend the concept of guarded range in order to completely represent the overall temporal properties of a process.
5.1 STNPSU representation of a process schema
In order to verify the dynamic controllability of a process schema P, it is transformed into an STNPSU S using the transformation rules depicted in Table 3. The resulting STNPSU has a single initial timepoint that occurs before any other one—called Z—and a single ending timepoint—called E—that occurs after any other timepoint. This STNPSU is then checked for DC by applying the standard algorithm for DC checking [18] to it. Given the above transformation, one can easily show that the original process is DC if and only if the corresponding STNPSU is DC. In turn, this results in the following theorem.
Theorem 1
Given a time-aware process schema P, which uses the process modeling elements from Table 3, there exists an STNPSU \(S_P\) such that P is dynamically controllable if and only if \(S_P\) is DC.
Proof
Table 3 depicts the mapping of the elements available for modeling a time-aware process (i.e., tasks, control edges, AND gateways, and temporal constraints) to the associated STNPSU fragments.
-
Task. Given a process schema, each task node A is transformed into two STNPSU timepoints, \(A_S\) and \(A_E\), representing its start and end instants. The duration attribute of A, \([[x,x'][y',y]]\), is converted to the guarded link
 .
. -
ANDjoin/ANDsplit gateways. The conversion process is analogous to the one of a task. However, duration attribute [x, y] is converted to a requirement link
 as control connectors are executed by the process engine of the PAIS.
as control connectors are executed by the process engine of the PAIS. -
Control Edge. A control edge from task A to task B is converted to a requirement link
 with duration range \([0,\infty ]\) in order to guarantee the correct execution order of the original process.
with duration range \([0,\infty ]\) in order to guarantee the correct execution order of the original process. -
Time Lags. Consider a time lag \(\mathsf {\langle I_F\rangle [t, u]\langle I_S\rangle }\), where \(I_F\) and \(I_S\) represent the kind of instants to be considered, i.e., ‘S’ for the start instant and ‘E’ for the end instant. If the considered time lag is between tasks A and B, it is converted to a requirement link between the timepoints associated with instants \(A_{I_F}\) and \(B_{I_S}\) of the two tasks A and B. The resulting requirement link then has the same duration range [t, u] as the time lag.
Let P be a time-aware process schema. Applying the above transformation to P and to the possible time lags, one can simply verify that the obtained STNPSU represents all precedence relations and temporal constraints of the original process schema P.
As introduced in Sect. 1, a time-aware process schema is dynamically controllable if it is possible to execute it for all required durations of all activities, while still satisfying all temporal constraints. Furthermore, recall that an STNPSU is dynamically controllable if it is possible to execute it in a way such that, no matter how the execution of any guarded link turns out, for any other guarded link  , the lower bound x must never be increased beyond its guard \(x'\) and the upper bound y must never be decreased below its guard \(y'\) in order to ensure controllability of the network.
, the lower bound x must never be increased beyond its guard \(x'\) and the upper bound y must never be decreased below its guard \(y'\) in order to ensure controllability of the network.
Therefore, it is a matter of definition to verify that the dynamic controllability of a process schema implies dynamic controllability of the corresponding STNPSU and vice versa. \(\square \)
5.2 Lower and upper guard
Assuming that the process is DC, it is noteworthy that the DC checking algorithm also derives the minimum and maximum duration between timepoints Z and E, i.e., the minimum and maximum durations of the process. However, these bounds are not sufficient for characterizing the temporal behavior of the process as they do not represent its possible non-restrictable duration ranges. As an example consider the STNPSU depicted in Fig. 4c, which corresponds to process \(P_2\) of Fig. 1. One can easily show that the duration range between Z and E corresponds to [5, 19]. However, this range cannot be reduced to [5, 10], for example, since internal task \(T_7\) has a contingent duration of 1 to 7, which cannot be controlled (i.e., restricted) by the PAIS. In particular, if \(T_7\) lasts exactly 7 time units, process \(P_2\) will last at least 11 time units. On the other hand, representing a subprocess by considering the duration range between Z and E to be contingent would make the overall process over-constrained and thus limit the overall temporal flexibility of the modularized process.
STNPSUs corresponding to subprocesses \(P_0, P_1\) and \(P_2\) from Fig. 1a STNPSU corresponding to \(P_0\)b STNPSU corresponding to \(P_1\)c STNPSU corresponding to \(P_2\)
We, therefore, suggest representing the duration of a process by a guarded range with proper guards in order to prevent unacceptable restrictions of the duration range of the process. In the following, we propose a method to determine the lower and upper guard of such a guarded range based on the STNPSU representation of the process schema. In this context, the upper guard for the duration range of a process P represents the lowest value the maximum duration of the process may be decreased to. In other words, considering the STNPSU S corresponding to P, the upper guard corresponds to the lowest value the upper bound of the requirement link, which is derived between Z and E by the DC checking algorithm, may be decreased to. It can be determined by considering the maximum guards of any guarded link and the lower bounds of any requirement link in S as outlined in Ex. 2.
Example 2
(Upper Guard) Consider the STNPSU depicted in Fig. 4c. While the upper bounds of the internal requirement links may be restricted to their lower bounds (i.e., 1) by the process engine, the upper bounds of the two guarded links cannot be restricted below their upper guards (i.e., 4 and 7, respectively). Therefore, the value we obtain when summing the lower bound values of the requirement links and the upper guards of the guarded links, i.e., \(1+4+1+7+1= {14}\), represents the minimal value the upper bound of the link between Z and E may be restricted to.
In turn, the lower guard for the duration range of a process P represents the greatest value the minimum duration of the process may be increased to. Regarding the STNPSU S, therefore, the lower guard corresponds to the greatest value the lower bound of the requirement link between Z and E may be increased to.
If there are several paths leading from Z to E, it becomes necessary to consider the maximum/minimum value considering all paths. Therefore, Definitions 1 and 2 specify the concept of lower/upper guard for any timepoint of an STNPSU.
Definition 1
(Upper Guard) Let S be a dynamically controllable STNPSU with distance graph \(\mathcal {D}= (\mathcal {T}, \mathcal {E})\) and let C be a timepoint. Then: The minimum value that may be set for the upper bound v of a requirement link  is called the upper guard of C:
is called the upper guard of C:

Definition 2
(Lower Guard) Let S be a dynamically controllable STNPSU with distance graph \(\mathcal {D}= (\mathcal {T}, \mathcal {E})\) and let C be a timepoint. Then: The maximum value that may be set for the lower bound u of a requirement link  is called the lower guard of C:
is called the lower guard of C:

Considering Definition 1 and 2 it is easy to verify that
-
when there is a requirement link
 in STNPSU S, the upper guard of C is \(\ge x\);
in STNPSU S, the upper guard of C is \(\ge x\); -
when there is a guarded link
 in STNPSU S, the upper guard of C is in \([y', y]\);
in STNPSU S, the upper guard of C is in \([y', y]\); -
when there is a requirement link
 in STNPSU S, the lower guard of C is \(\le y\);
in STNPSU S, the lower guard of C is \(\le y\); -
when there is a guarded link
 in STNPSU S, the lower guard of C is in \([x, x']\);
in STNPSU S, the lower guard of C is in \([x, x']\); -
in general, for any timepoints A and C with
 derived by the DC checking algorithm, it holds upper guard of C is \(\ge \mathrm{upperGuard}(A) + c\) and the lower guard of C is \(\le {{\mathrm{lowerGuard}}}(A) + d\).
derived by the DC checking algorithm, it holds upper guard of C is \(\ge \mathrm{upperGuard}(A) + c\) and the lower guard of C is \(\le {{\mathrm{lowerGuard}}}(A) + d\).
Example 3
Regarding the STNPSUs from Fig. 4, one can verify that the values of \({{\mathrm{lowerGuard}}}\) and \({{\mathrm{upperGuard}}}\) between Z and E correspond to
-
\({{\mathrm{lowerGuard}}}_{P_0}(E) = {15}\) and \({{\mathrm{upperGuard}}}_{P_0}(E)= {15}\),
-
\({{\mathrm{lowerGuard}}}_{P_1}(E) = {13}\) and \({{\mathrm{upperGuard}}}_{P_1}(E)= {11}\), and
-
\({{\mathrm{lowerGuard}}}_{P_2}(E) = {10}\) and \({{\mathrm{upperGuard}}}_{P_2}(E)= {14}\).
Definitions 1 and 2 allow determining to which extent the upper/lower bound of the derived requirement link between Z and a timepoint C in an STNPSU S may be reduced/increased without affecting the DC of S (cf. Lemmas 1 and 2).
Lemma 1
(Upper Guard) Let S be a dynamically controllable STNPSU, Z be the initial timepoint, and C be a timepoint in S. Then: The upper bound v of the distance  between Z and C may be reduced to at most \({{\mathrm{upperGuard}}}_S(C)\), preserving the DC of S.
between Z and C may be reduced to at most \({{\mathrm{upperGuard}}}_S(C)\), preserving the DC of S.
Proof
First, we show that if v is set to a value less than \({{\mathrm{upperGuard}}}_S(C)\), the network cannot be DC. Let \(B_1 \ldots B_k\) be the path from Z to C in the distance graph \(\mathcal {D}\) that determines the value for \({{\mathrm{upperGuard}}}(C)\), i.e.,

where \(\alpha _i\) is either an ordinary or upper-case edge and \(- \sum _{i \in \{0,\ldots ,k\}} {\tilde{\alpha _i}} = {{\mathrm{upperGuard}}}(C)\) with \(\tilde{\alpha _i}\) corresponding to the value of \(\alpha _i\) ignoring any label. Given such path, in the AllMax-Projection \(\mathcal {D}'\), any upper-case edge \(\alpha _i = \{{D_i}:{-y'_i}\}\) is replaced by \(\tilde{\alpha _i} = -y'_i\). Thus, it is easy to verify that by the standard STN propagation rules in the AllMax-Projection, an ordinary edge  is derived. At the same time, if we add a requirement edge
is derived. At the same time, if we add a requirement edge  with \(v^* < {{\mathrm{upperGuard}}}(C)\) to the distance graph \(\mathcal {D}\) of the original STNPSU S, the same edge will also be added to the AllMax-Projection \(\mathcal {D}'\), resulting in a negative cycle
with \(v^* < {{\mathrm{upperGuard}}}(C)\) to the distance graph \(\mathcal {D}\) of the original STNPSU S, the same edge will also be added to the AllMax-Projection \(\mathcal {D}'\), resulting in a negative cycle  , i.e., the STNPSU cannot be DC.
, i.e., the STNPSU cannot be DC.
Second, we show that if S is DC and v is reduced to a value \(v'\ge {{\mathrm{upperGuard}}}_S(C)\), \(v'\) cannot be part of any negative semi-reducible cycle, i.e., the resulting network must be DC as well. Let us assume that  is restricted to
is restricted to  with \({{\mathrm{upperGuard}}}(C) \le v' \le v\) and that the resulting network is not DC. This implies that there exists a negative semi-reducible cycle
with \({{\mathrm{upperGuard}}}(C) \le v' \le v\) and that the resulting network is not DC. This implies that there exists a negative semi-reducible cycle  in the distance graph \(\mathcal {D}\) consisting only of ordinary or upper-case edges \(\alpha _i\) such that \(\sum _{i \in \{0, \ldots , l\}} \tilde{\alpha _i} + v^* < 0\), i.e., \(v^* < - \sum _{i \in \{0, \ldots , l\}} \tilde{\alpha _i}\). Based on Definition 1, it follows that for any such path \(E_1, \ldots , E_l\) from Z to C it holds \({{\mathrm{upperGuard}}}(C) \ge -\sum _{i \in \{0,\ldots ,l\}} \tilde{\alpha _i}\) and, thus, \({{\mathrm{upperGuard}}}(C) \le v^* < -\sum _{i \in \{0,\ldots ,l\}} \tilde{\alpha _i} \le {{\mathrm{upperGuard}}}(C)\). This, in turn, contradicts the assumption. \(\square \)
in the distance graph \(\mathcal {D}\) consisting only of ordinary or upper-case edges \(\alpha _i\) such that \(\sum _{i \in \{0, \ldots , l\}} \tilde{\alpha _i} + v^* < 0\), i.e., \(v^* < - \sum _{i \in \{0, \ldots , l\}} \tilde{\alpha _i}\). Based on Definition 1, it follows that for any such path \(E_1, \ldots , E_l\) from Z to C it holds \({{\mathrm{upperGuard}}}(C) \ge -\sum _{i \in \{0,\ldots ,l\}} \tilde{\alpha _i}\) and, thus, \({{\mathrm{upperGuard}}}(C) \le v^* < -\sum _{i \in \{0,\ldots ,l\}} \tilde{\alpha _i} \le {{\mathrm{upperGuard}}}(C)\). This, in turn, contradicts the assumption. \(\square \)
Lemma 2
(Lower Guard) Let S be a dynamically controllable STNPSU, Z be the initial timepoint, and C be a timepoint in S. Then: The lower bound u of distance  between Z and C may be increased to at most \({{\mathrm{lowerGuard}}}_S(S)\), preserving the DC of S.
between Z and C may be increased to at most \({{\mathrm{lowerGuard}}}_S(S)\), preserving the DC of S.
Proof
The proof is analogous to the one of Lemma 1 using the AllMin-Projection and applying a similar reasoning. The AllMin-Projection is similar to the AllMax-Projection, but considers solely ordinary and lower-case edges. \(\square \)
Using Definition 1 and 2, it becomes possible to determine to which extent the lower/upper bound of the duration range of a process can be restricted, while preserving its DC. This is illustrated by Example 4.
Example 4
The minimum and maximum durations of the processes from Fig. 1 are determined by the DC checking algorithm as \(P_0\): \([10, 20]\), \(P_1\): \([5, 19]\), and \(P_2\): \([5, 19]\). Using Definitions 1 and 2, it now becomes possible to determine to which extent these duration ranges may be restricted:
-
the minimum duration of \(P_0\) may be restricted to \({{\mathrm{lowerGuard}}}_{P_0}(E) = {15}\) at most, whereas its maximum duration may be restricted to \({{\mathrm{upperGuard}}}_{P_0}(E)= {15}\);
-
the duration of \(P_1\) may be restricted to \({{\mathrm{lowerGuard}}}_{P_1}(E) = {13}\) and \({{\mathrm{upperGuard}}}_{P_1}(E)={11}\), respectively, and
-
the duration of \(P_2\) may be restricted to \({{\mathrm{lowerGuard}}}_{P_2}(E) = {10}\) and \({{\mathrm{upperGuard}}}_{P_2}(E)={14}\), respectively.
Therefore, the guarded range representing the duration of the three subprocesses \(P_0, P_1,\) and \(P_2\) are  , and
, and  , respectively.
, respectively.
Based on the definitions of \({{\mathrm{lowerGuard}}}\) and \({{\mathrm{upperGuard}}}\), one can easily verify that their value is always non-negative. Moreover, it becomes easy to show that the \({{\mathrm{upperGuard}}}(C)\) value is given by value u of edge  in the AllMax-Projection graph of the network, whereas the \({{\mathrm{lowerGuard}}}(C)\) value is given by value v of edge
in the AllMax-Projection graph of the network, whereas the \({{\mathrm{lowerGuard}}}(C)\) value is given by value v of edge  in the AllMin-Projection graph. Using standard STN algorithms [9], therefore, the computational cost of determining \({{\mathrm{lowerGuard}}}(C)\) and \({{\mathrm{upperGuard}}}(C)\) is at most \(O(n^3)\), with n being the number of timepoints in the considered STNPSU.
in the AllMin-Projection graph. Using standard STN algorithms [9], therefore, the computational cost of determining \({{\mathrm{lowerGuard}}}(C)\) and \({{\mathrm{upperGuard}}}(C)\) is at most \(O(n^3)\), with n being the number of timepoints in the considered STNPSU.
5.3 Contingency span
Given a range [u, v] that represents the overall duration of a DC process, Definitions 1 and 2 assure that it is always possible to reduce one of the two bounds of the respective duration range to the corresponding guard (i.e., \({{\mathrm{upperGuard}}}(E)\) or \({{\mathrm{lowerGuard}}}(E)\)) without affecting the DC of the process. However, it is not possible to restrict both bounds simultaneously since the restriction of one bound may change the guard of the other bound as shown by Example 5.
Example 5
Consider the STNPSU from Fig. 4c, which corresponds to subprocess \(P_2\). One can easily show that \({{\mathrm{lowerGuard}}}_{P_2}(E) = {10}\) and \({{\mathrm{upperGuard}}}_{P_2}(E) = {14}\) hold. Moreover, the duration range of the process corresponds to \([5,19]\) as determined by the DC checking algorithm. Considering Lemmas 1 and 2, it then can be easily shown that the minimum duration of the process may be increased to \({10}\) or its maximum duration may be restricted to \({14}\). However, for process \(P_2\) it is not possible to increase the minimum duration to \({10}\) while, at the same time, restricting the maximum duration to \({14}\). In particular, if the minimum duration is increased to \({10}\), due to the partially contingent guarded link between timepoints \(T_{7_S}\) and \(T_{7_E}\) (representing task \(T_7\)), the maximum duration must not be decreased below 16 to further guarantee DC of the process. On the other hand, the maximum duration may be decreased to \({14}\). In this case, the minimum duration must not be increased beyond 8. In detail, a span of at least \({6}\) must be ensured for the final duration range of the process.
To fully represent the overall temporal properties of a process, we suggest considering an additional value that represents the minimal span to be guaranteed for the duration range. We denote this value as the contingency span of the process. It can be defined using the link contingency span and path contingency span of the corresponding STNPSU.
Definition 3
(Link Contingency Span) A positive link contingency span \(\varDelta \) corresponds to the span that needs to be guaranteed for a link in order to ensure the DC of an STNPSU. In turn, a negative link contingency span corresponds to the maximum span provided by a link that can be used to reduce the contingency span of previous guarded link.
-
a)
For a guarded link
 , the link contingency span \(\varDelta _{AB}\) is defined as \(\varDelta _{AB} = b' - a'\).
, the link contingency span \(\varDelta _{AB}\) is defined as \(\varDelta _{AB} = b' - a'\). -
b)
For a requirement link
 , the link contingency span \(\varDelta _{AB}\) is defined as \(\varDelta _{AB} = a - b\).
, the link contingency span \(\varDelta _{AB}\) is defined as \(\varDelta _{AB} = a - b\).
Taking Definition 3 it is easy to verify that, respectively
-
the link contingency span of a requirement link is less than or equal to zero, i.e.,
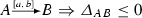 ;
; -
the link contingency span of a partially shrinkable guarded link is less than or equal to zero, i.e.,
 ;
; -
the link contingency span of a partially contingent guarded link is greater than zero, i.e.,
 .
.
Next, we need to find a way to determine the contingency span of a path based on the link contingency span of its links. First, let us consider a guarded link  followed by a requirement link
followed by a requirement link  . In this case, the contingency span required by the guarded link can be partially or fully compensated by the subsequent requirement link, as the duration of the latter can be decided based on the actual duration of the former. Thus, the contingency of the path from A to C is given by \(\varDelta _{AB} + \varDelta _{BC}\). In turn, for a requirement link
. In this case, the contingency span required by the guarded link can be partially or fully compensated by the subsequent requirement link, as the duration of the latter can be decided based on the actual duration of the former. Thus, the contingency of the path from A to C is given by \(\varDelta _{AB} + \varDelta _{BC}\). In turn, for a requirement link  followed by a guarded link
followed by a guarded link  , we must differentiate two subcases: If the guarded link is partially contingent (i.e., \(c' < d'\)), the previous requirement link cannot be used to compensate its contingency span as the duration of the requirement link must be decided before executing the guarded link. Therefore, the contingency span of the path from A to C is given by \(\varDelta _{BC}\). However, if the guarded link is partially shrinkable (i.e., \(d' \le c'\)), its link contingency \(\varDelta _{BC}\) is negative. In this case, the contingency span of the path from A to C is again given by \(\varDelta _{AB} + \varDelta _{BC}\) as both links could be used to reduce the contingency of a previous guarded link. Finally, the combination of two requirement links (guarded links) is similar to the above cases. When considering a path that consists of more than two links, the link contingency spans need to be combined in an incremental way starting from the initial timepoint Z. When considering two or more parallel paths, in turn, it becomes necessary to consider the most demanding case, i.e., the path with the largest contingency span. This leads to the following recursive approach for calculating the contingency span of a path.
, we must differentiate two subcases: If the guarded link is partially contingent (i.e., \(c' < d'\)), the previous requirement link cannot be used to compensate its contingency span as the duration of the requirement link must be decided before executing the guarded link. Therefore, the contingency span of the path from A to C is given by \(\varDelta _{BC}\). However, if the guarded link is partially shrinkable (i.e., \(d' \le c'\)), its link contingency \(\varDelta _{BC}\) is negative. In this case, the contingency span of the path from A to C is again given by \(\varDelta _{AB} + \varDelta _{BC}\) as both links could be used to reduce the contingency of a previous guarded link. Finally, the combination of two requirement links (guarded links) is similar to the above cases. When considering a path that consists of more than two links, the link contingency spans need to be combined in an incremental way starting from the initial timepoint Z. When considering two or more parallel paths, in turn, it becomes necessary to consider the most demanding case, i.e., the path with the largest contingency span. This leads to the following recursive approach for calculating the contingency span of a path.
Definition 4
(Path Contingency Span) Let S be a dynamically controllable STNPSU and let Z be its initial timepoint. By definition, the path contingency span of Z is \({{\mathrm{cont}}}_S(Z) = 0\). Then: The path contingency span\(cont_S(C)\) of any other timepoint C is given by
It is noteworthy that the path contingency span of any timepoint is always greater or equal to zero, i.e., \({{\mathrm{cont}}}_S(C) \ge 0\). Moreover, the problem of determining the value of \({{\mathrm{cont}}}_S(C)\), i.e., the maximum contingency span among all possible paths from Z to C, can be reduced to the problem of finding the minimal distance between Z and C in a suitable weighted graph whose construction considered the link contingency spans as edge values.
Definition 5
(Contingency Graph) Let \(S = \left( \mathcal {T},\mathcal {C},\mathcal {G}\right) \) be an STNPSU to which the DC checking algorithm has been applied (cf. Algorithm 1). The corresponding contingency graph for S has the form \(\mathcal {CO} = (\mathcal {T}, \mathcal {E}_{\mathcal {CO}})\). Thereby, each timepoint in \(\mathcal {T}\) serves as a node in the graph; \(\mathcal {E}_{\mathcal {CO}}\) is a set of weighted edges:
-
a)
For each guarded link
 , there exists a single edge
, there exists a single edge  .
. -
b)
For each requirement link
 , there exist two edges
, there exist two edges  ,
,  .
. -
c)
For each timepoint \(T \in \mathcal {T}\), there exists an edge
 .
.
Based on Definition 4, one can easily verify that the path contingency span of any timepoint \(C\in \mathcal {T}\) corresponds to the negative value of the shortest path from initial timepoint Z to C in the corresponding contingency graph (cf. Definition 5).
Two comments are noteworthy with respect to Definition 4 and Definition 5. First, as a requirement link may connect two-non sequential timepoints, its link contingency span can be used in combination with the contingency coming from any of its endpoints. Definition 5 considers these two mutually exclusive options by adding two edges  . Second, edges
. Second, edges  added by Step c) in Definition 5 guarantee that the length of any path in the graph starting at timepoint Z is always less than or equal to 0, i.e., the corresponding path contingency is always positive as requested by the definition.
added by Step c) in Definition 5 guarantee that the length of any path in the graph starting at timepoint Z is always less than or equal to 0, i.e., the corresponding path contingency is always positive as requested by the definition.
Moreover, as S is DC, the contingency graph \(\mathcal {CO}\) cannot contain any negative cycles. In particular, the only edges with a negative edge value are the ones resulting from a partially contingent guarded link  . Then, for any path \(B = E_0,\ldots ,E_k = A\) it must hold \(-\sum _{i = 1\ldots k-1} \varDelta _{E_{i}E_{i+1}} \ge \varDelta _{AB}\), otherwise S cannot be DC. Using the Bellman–Ford algorithm, the computational cost of determining \({{\mathrm{cont}}}_S(C)\) is at most \(O(n^3)\), with n being the number of timepoints in the STNPSU.
. Then, for any path \(B = E_0,\ldots ,E_k = A\) it must hold \(-\sum _{i = 1\ldots k-1} \varDelta _{E_{i}E_{i+1}} \ge \varDelta _{AB}\), otherwise S cannot be DC. Using the Bellman–Ford algorithm, the computational cost of determining \({{\mathrm{cont}}}_S(C)\) is at most \(O(n^3)\), with n being the number of timepoints in the STNPSU.
Example 6
The path contingency graph corresponding to the STNPSU depicted in Fig. 4a is shown in Fig. 5. Note that insignificant edges determined by the DC checking algorithm have been omitted for the sake of readability. Applying the Bellman–Ford algorithm to this graph, the grayed values in bracket are determined (insignificant edges are re-omitted). In particular, edge ZE is derived as  . Moreover, by applying Definition 4 to Fig. 4a, it can be easily verified that \({{\mathrm{cont}}}_{P_0}(E)={2}\) holds.
. Moreover, by applying Definition 4 to Fig. 4a, it can be easily verified that \({{\mathrm{cont}}}_{P_0}(E)={2}\) holds.
Contingency Graph of the STNPSU in Fig. 4a showing values determined by the Bellman–Ford algorithm (grayed bracketed values)
Regarding the other STNPSUs from Fig. 4, the path contingency span of timepoints E are as follows:
-
\({{\mathrm{cont}}}_{P_1}(E)={2}\), and
-
\({{\mathrm{cont}}}_{P_2}(E)={6}\).
Based on Definition 4, it becomes possible to describe the admissible duration ranges between two timepoints in an STNPSU.
Lemma 3
Let S be a dynamically controllable STNPSU, Z be its initial timepoint, and C be any other timepoint. Then: In order to preserve the DC of S, any restriction  (\(u\!\le \!u^*\!\le \!{{\mathrm{lowerGuard}}}_S(C)\), \({{\mathrm{upperGuard}}}_S(C) \le v^*\le v\)) of the distance between Z and C must be set in such a way that \(v^*-u^* \ge {{\mathrm{cont}}}_S(C)\) holds.
(\(u\!\le \!u^*\!\le \!{{\mathrm{lowerGuard}}}_S(C)\), \({{\mathrm{upperGuard}}}_S(C) \le v^*\le v\)) of the distance between Z and C must be set in such a way that \(v^*-u^* \ge {{\mathrm{cont}}}_S(C)\) holds.
Proof
We solely consider timepoints C with a positive path contingency span \({{\mathrm{cont}}}_S(C) > 0\) and \({{\mathrm{upperGuard}}}_S(C) - {{\mathrm{lowerGuard}}}_S(C) < {{\mathrm{cont}}}_S(C)\); otherwise it is already ensured that \(v^*-u^* \ge {{\mathrm{cont}}}_S(C)\) holds (either by the fact that \(v^*-u^* \ge 0\) holds or by the guards).
First of all, let us consider the definition of \({{\mathrm{cont}}}_S(C)\). Note that a positive path contingency span can only occur when there is at least one partially contingent guarded link inside S. Moreover, taking the definition of \({{\mathrm{cont}}}_S()\), it is always possible to find a sequence of timepoints \(B_0,\ldots ,B_k\) with \(B_k \equiv C\) for which it holds
with
-
1.
\({{\mathrm{cont}}}_S(B_0) = 0\),
-
2.
\(\forall j \in \{1,\ldots ,k\} \sum _{i \in \{1,\ldots ,j\}} \varDelta _{B_{i-1}, B_i} > 0\),
i.e., \(\forall j \in \{1,\ldots ,k\} {{\mathrm{cont}}}_{S}(B_j) > 0\)
Then, by definition, link \(B_0B_1\) is a partially contingent guarded link:  .
.
If path \(B_0,\ldots ,B_k\) contains a sequence of requirement links  , there also exists an equivalent single requirement link
, there also exists an equivalent single requirement link  resulting in the same value of \({{\mathrm{cont}}}_S(B_{i+1})\). Moreover, if path \(B_0,\ldots ,B_k\) contains a sequence of guarded links
resulting in the same value of \({{\mathrm{cont}}}_S(B_{i+1})\). Moreover, if path \(B_0,\ldots ,B_k\) contains a sequence of guarded links  , it is always possible to split timepoint \(B_{i}\) into two timepoints \(B'_{i}\) and \(B''_{i}\) connected by a requirement link with value [0, 0] without changing the properties of the network (particularly \({{\mathrm{cont}}}_S(B_{i+1})\)), i.e.,
, it is always possible to split timepoint \(B_{i}\) into two timepoints \(B'_{i}\) and \(B''_{i}\) connected by a requirement link with value [0, 0] without changing the properties of the network (particularly \({{\mathrm{cont}}}_S(B_{i+1})\)), i.e.,  .
.
In summary, without loss of generality, we can assume that the sequence of timepoints \(B_0,\ldots ,B_k\) always has the following pattern:

where  is the requirement link derived by the DC checking algorithm.
is the requirement link derived by the DC checking algorithm.
We can now show by induction that it is not possible to restrict  to \([u^*, v^*]\) such that \(v^*-u^* < {{\mathrm{cont}}}_S(B_k)\) holds. Particularly, assuming that \(v^* - u^* = {{\mathrm{cont}}}_S(B_k) - \epsilon \), \(\epsilon > 0\) holds, we show that at least one link inside path \(Z, B_0,\ldots ,B_k\) has to be restricted beyond its bounds/guards.
to \([u^*, v^*]\) such that \(v^*-u^* < {{\mathrm{cont}}}_S(B_k)\) holds. Particularly, assuming that \(v^* - u^* = {{\mathrm{cont}}}_S(B_k) - \epsilon \), \(\epsilon > 0\) holds, we show that at least one link inside path \(Z, B_0,\ldots ,B_k\) has to be restricted beyond its bounds/guards.
First, consider a path consisting of 3 timepoints \(B_0, B_1\), and \(B_2\), i.e.,  (Note that the case of two timepoints follows by assuming \(y_2 = x_2 = 0\) and the case of one timepoints is given by definition as \(b-a \le {{\mathrm{cont}}}_S(B_0) - \epsilon = < 0\) holds then). In this case, \({{\mathrm{cont}}}_S(B_2)\) is given by \({{\mathrm{cont}}}_S(B_2) = {{\mathrm{cont}}}_S(B_0) + (y'_1 - x'_1) + (x_2 - y_2)\) with \({{\mathrm{cont}}}_S(B_0) = 0\). Assume
(Note that the case of two timepoints follows by assuming \(y_2 = x_2 = 0\) and the case of one timepoints is given by definition as \(b-a \le {{\mathrm{cont}}}_S(B_0) - \epsilon = < 0\) holds then). In this case, \({{\mathrm{cont}}}_S(B_2)\) is given by \({{\mathrm{cont}}}_S(B_2) = {{\mathrm{cont}}}_S(B_0) + (y'_1 - x'_1) + (x_2 - y_2)\) with \({{\mathrm{cont}}}_S(B_0) = 0\). Assume  is restricted to
is restricted to  with \(v^* - u^* = {{\mathrm{cont}}}_S(B_2) - \epsilon = (y'_1 - x'_1) + (x_2 - y_2) - \epsilon \), \(\epsilon > 0\). Then, by applying the No-Case Rule (cf. Table 2), a requirement link
with \(v^* - u^* = {{\mathrm{cont}}}_S(B_2) - \epsilon = (y'_1 - x'_1) + (x_2 - y_2) - \epsilon \), \(\epsilon > 0\). Then, by applying the No-Case Rule (cf. Table 2), a requirement link  between Z and \(B_1\) is derived. Moreover, the Lower-Case Rule (cf. Table 2) derives an ordinary edge
between Z and \(B_1\) is derived. Moreover, the Lower-Case Rule (cf. Table 2) derives an ordinary edge  . In turn, the Upper Case Rule (cf. Table 2) derives a wait
. In turn, the Upper Case Rule (cf. Table 2) derives a wait  . This wait is then transformed into the ordinary edge
. This wait is then transformed into the ordinary edge  by the Label Removal Rule (cf. Table 2). Note that \((v^*-x_{2})-y'_{1} \ge - x'_{1}\) holds as \(v^* \ge y'_{1} + x_{2} \ge y'_{1} - x'_{1} + x_{2}\) must hold for the original network to be DC. In summary, a requirement link
by the Label Removal Rule (cf. Table 2). Note that \((v^*-x_{2})-y'_{1} \ge - x'_{1}\) holds as \(v^* \ge y'_{1} + x_{2} \ge y'_{1} - x'_{1} + x_{2}\) must hold for the original network to be DC. In summary, a requirement link  is derived. Hence, it must hold \(b \le (v^*-x_{2})-y'_{1}\) and \(a \ge (u^*-y_{2}) - x'_{1}\) and, therefore, it must also hold:
is derived. Hence, it must hold \(b \le (v^*-x_{2})-y'_{1}\) and \(a \ge (u^*-y_{2}) - x'_{1}\) and, therefore, it must also hold:
which shows that the network can no longer be DC as the requirement link \(ZB_0\) is restricted too much.
Now let us consider a path consisting of \(k+3\) timepoints \(B_0,\ldots ,B_{k+2}\) as depicted below (Again, the case of \(k+2\) timepoints follows by assuming \(y_{k+2} = x_{k+2} = 0\)).

Let us assume that  is restricted to
is restricted to  with \(v^* - u^* = {{\mathrm{cont}}}_S(B_{k+2}) - \epsilon \), \(\epsilon > 0\). Then, by the No-Case Rule (cf. Table 2), a requirement link
with \(v^* - u^* = {{\mathrm{cont}}}_S(B_{k+2}) - \epsilon \), \(\epsilon > 0\). Then, by the No-Case Rule (cf. Table 2), a requirement link  is derived. Moreover, the Lower-Case Rule derives an ordinary edge
is derived. Moreover, the Lower-Case Rule derives an ordinary edge  . In turn, the Upper Case Rule derives a wait
. In turn, the Upper Case Rule derives a wait  . This wait is transformed into ordinary edge
. This wait is transformed into ordinary edge  by the Label Removal Rule because \((v^*-x_{k+2})-y'_{k+1} \ge - x'_{k+1}\) holds, as \(v^* \ge y'_{k+1} + x_{k+2} \ge y'_{k+1} - x'_{k+1} + x_{k+2}\) must hold for the original network to be DC. In summary, a requirement link
by the Label Removal Rule because \((v^*-x_{k+2})-y'_{k+1} \ge - x'_{k+1}\) holds, as \(v^* \ge y'_{k+1} + x_{k+2} \ge y'_{k+1} - x'_{k+1} + x_{k+2}\) must hold for the original network to be DC. In summary, a requirement link  is derived.
is derived.
Thus, for the span of the requirement link  between Z and \(B_k\) derived by the DC checking algorithm, it holds:
between Z and \(B_k\) derived by the DC checking algorithm, it holds:
Hence, the range of the requirement link  is restricted such that \(q - p \le {{\mathrm{cont}}}_S(B_k) - \epsilon < {{\mathrm{cont}}}_S(B_k)\) holds. By subsequent application of the same steps (i.e., by induction), it follows that for
is restricted such that \(q - p \le {{\mathrm{cont}}}_S(B_k) - \epsilon < {{\mathrm{cont}}}_S(B_k)\) holds. By subsequent application of the same steps (i.e., by induction), it follows that for  it holds \(b - a < {{\mathrm{cont}}}_S(B_2)\). However, as previously shown, this implies that the network can no longer be DC. \(\square \)
it holds \(b - a < {{\mathrm{cont}}}_S(B_2)\). However, as previously shown, this implies that the network can no longer be DC. \(\square \)
From the previous observations, we can derive important relationships between \({{\mathrm{lowerGuard}}}(C)\), \({{\mathrm{upperGuard}}}(C)\), and \({{\mathrm{cont}}}(C)\) values:
Lemma 4
Let S be a dynamically controllable STNPSU, Z be its initial timepoint, and C be any other timepoint. If T is the network derived from S by restricting upper bound v of the distance  between Z and C to \(v^*\), with \({{\mathrm{upperGuard}}}_S(C) \le v^* \le v\), for T it holds:
between Z and C to \(v^*\), with \({{\mathrm{upperGuard}}}_S(C) \le v^* \le v\), for T it holds:
Lemma 5
Let S be a dynamically controllable STNPSU, Z be its initial timepoint, and C be any other timepoint. If T is the network derived from S by restricting the lower bound u of the distance  between Z and C to \(u^*\), with \(u \le u^* \le {{\mathrm{lowerGuard}}}_S(C)\), for T it holds:
between Z and C to \(u^*\), with \(u \le u^* \le {{\mathrm{lowerGuard}}}_S(C)\), for T it holds:
Proof
The proofs of Lemmas 4 and 5 are very similar. For the sake of brevity, we only prove Lemma 4.
First, let us assume that \({{\mathrm{lowerGuard}}}_T(C) > v^* - {{\mathrm{cont}}}_S(C)\) holds. When applying Definition 2 and Lemma 2, we obtain that u may be increased to \(u^* = {{\mathrm{lowerGuard}}}_T(C) > v^* - {{\mathrm{cont}}}_S(C)\). According to Lemma 3, however, then the resulting network cannot be DC.
Second, let us assume that u is increased to \(u^* = v^* - {{\mathrm{cont}}}_S(C)\) with \(u^* \le {{\mathrm{lowerGuard}}}_S(C)\) in T and that the resulting network is not DC. This implies that there exists a negative semi-reducible cycle

in the distance graph \(\mathcal {D}_T\) of T such that \(\sum _{i \in \{1,\ldots ,l\}} \tilde{\alpha _i} - (v^* - {{\mathrm{cont}}}_S(C) ) < 0\) holds, i.e., \({{\mathrm{cont}}}_S(C) < v^* - \sum _{i \in \{1,\ldots ,l\}} \tilde{\alpha _i}\). Moreover, it holds that \(v^* \le v \le \sum _{i \in \{1,\ldots ,l\}} \tilde{\alpha _i}\) and thus \({{\mathrm{cont}}}_S(C) < v^* - \sum _{i \in \{1,\ldots ,l\}} \tilde{\alpha _i} \le 0\), which contradicts the basic property that \({{\mathrm{cont}}}_S(C) \ge 0\) holds.
Third, let us assume that u is increased to \(u^* = {{\mathrm{lowerGuard}}}_S(C)\) with \(u^* \le v^* - {{\mathrm{cont}}}_S(C)\) and that the resulting network is not DC. Again, this implies that there exists a negative semi-reducible cycle

in the distance graph \(\mathcal {D}_T\) of T such that \(\sum _{i \in \{1,\ldots ,l\}} \tilde{\alpha _i} -{{\mathrm{lowerGuard}}}_S(C) < 0\) holds, i.e., \(\sum _{i \in \{1,\ldots ,l\}} \tilde{\alpha _i} < {{\mathrm{lowerGuard}}}_S(C)\). Consequently, it also holds \(\sum _{i \in \{1,\ldots ,l\}} \tilde{\alpha _i} < {{\mathrm{lowerGuard}}}_S(C) \le v^* - {{\mathrm{cont}}}_S(C) \le v^* \le v\), i.e., \(\sum _{i \in \{1,\ldots ,l\}} \tilde{\alpha _i} < v\), which contradicts the basic assumption that v has been restricted to \(v^*\). \(\square \)
5.4 Overall temporal properties of a process
The previous results give rise to the following theorem that enables a complete description of the overall temporal properties of a process.
Theorem 2
(Overall Temporal Properties of a Process) Considering a process P and its corresponding STNPSU S, let Z and E be the single start and single end timepoints of S. Then: The overall temporal properties of P can be described by a guarded range with contingency , where
, where
-
x and y are the bounds of the requirement link
 between initial timepoint Z and ending timepoint E in S, as derived by the DC checking algorithm,
between initial timepoint Z and ending timepoint E in S, as derived by the DC checking algorithm, -
\(x' = {{\mathrm{lowerGuard}}}_S(E)\) and \(y' = {{\mathrm{upperGuard}}}_S(E)\), and
-
\(c = {{\mathrm{cont}}}_S(E)\).
Proof
Definitions 1 and 2 show how to use the values of \({{\mathrm{lowerGuard}}}_S(E) = x'\) and \({{\mathrm{upperGuard}}}_S(E) = y'\) to specify the possible restrictions regarding the lower and upper bounds of the duration range [x, y] of a process (i.e., its minimum and maximum duration). This way, we can fully represent the possible duration ranges of the process as a guarded range  . Moreover, Lemmas 3–5 show how to use the path contingency span \({{\mathrm{cont}}}_S(E) = c\) in order to ensure that any possible restriction of the duration range
. Moreover, Lemmas 3–5 show how to use the path contingency span \({{\mathrm{cont}}}_S(E) = c\) in order to ensure that any possible restriction of the duration range  of the process preserves its DC. \(\square \)
of the process preserves its DC. \(\square \)
Based on Theorem 2, it becomes possible to represent the overall temporal properties of a process using a single guarded range with contingency. This is illustrated by Example 7.
Example 7
First, consider process \(P_1\) (cf. Fig. 1) and its corresponding STNPSU (cf. Fig. 4). The overall temporal properties of this process may be described by guarded range with contingency  . Since the contingency span of this process corresponds to 2, it is possible to restrict the overall duration range of the process to \([{13}, 15]\) or \([9, {11}]\), while still preserving its DC. In turn, the overall temporal properties of process \(P_2\) (cf. Figs. 1 and 4) can be described by a guarded range with contingency
. Since the contingency span of this process corresponds to 2, it is possible to restrict the overall duration range of the process to \([{13}, 15]\) or \([9, {11}]\), while still preserving its DC. In turn, the overall temporal properties of process \(P_2\) (cf. Figs. 1 and 4) can be described by a guarded range with contingency  . For example, therefore, the duration range of the process can be restricted to \([6, {14}]\), \([{10}, 17]\), or \([8, {14}]\). However, due to the required contingency span of \({6}\), it must not be restricted to, for example, \([{10}, {14}]\), or \([{10}, 15]\).
. For example, therefore, the duration range of the process can be restricted to \([6, {14}]\), \([{10}, 17]\), or \([8, {14}]\). However, due to the required contingency span of \({6}\), it must not be restricted to, for example, \([{10}, {14}]\), or \([{10}, 15]\).
Such kind of compact representation of the overall temporal properties of a process schema is crucial for reusing it as part of a modularized process. In particular, when adding a subprocess task to a process schema, a duration range must be specified. Based on the guarded range with contingency determined for the subprocess, it now becomes possible to determine a proper duration range for it, when adding it to the main process. Without any need to re-analyze the subprocess schema, this duration range ensures that any restriction of the duration of the subprocess task in the main (i.e., top-level) process will be made in such a way that the subprocess remains dynamically controllable.
6 Checking the dynamic controllability of modularized time-aware processes
As shown in the previous section, for each time-aware process, one can derive a guarded range with contingency that fully describes the overall temporal properties of the process. In particular, this guarded range with contingency specifies the possible durations of the process as well as the permissible restrictions that may be applied to its duration range without violating the DC of the process. This section shows how such a knowledge can be utilized to enable a sophisticated PAIS support for modularized time-aware processes.
In a PAIS, in general, the available process schemas are stored in a central process model repository [34]. Based on the results presented in Sect. 5, it now becomes possible to enhance the repository information about a process schema with its overall temporal properties represented as a guarded range with contingency. Such information can then be utilized when reusing a process schema as part of a modularized time-aware process. In particular, during design time, a process designer may select a process schema from the repository and reuse it as a subprocess task. Similar to an atomic task, the designer then has to configure the subprocess task in the process schema; i.e., he must specify the duration range of the particular subprocess task. In this context, it must be ensured that the temporal constraints of the modularized process as well as the ones of the subprocess can be satisfied. In order to ensure the executability of the modularized process the designer must guarantee that the duration range set for the subprocess task is compliant with the overall temporal properties of the (sub-)process schema. In this context, the repository information about the overall temporal properties of the (sub-)process schema can be used to support the process designer in choosing a proper duration range for the respective subprocess task. In other words, the designer must select a guarded range as duration range of the subprocess task, which satisfies the guards as well as the contingency of the guarded range with contingency representing the overall temporal properties of the (sub-)process schema as stored in the repository.
In general, the duration range  of a subprocess task needs to be selected with respect to the overall temporal properties of the respective (sub-)process schema
of a subprocess task needs to be selected with respect to the overall temporal properties of the respective (sub-)process schema  such that \(u\le x \le x' \le u'\) and \(v\ge y \ge y' \ge v'\) hold. Moreover, if \(c > 0\) holds, \(y' - x' \ge c\) must hold as well. When observing these constraints, it is guaranteed that, during the execution of a subprocess task of a modularized process, the respective subprocess instance may be completed without violating any of its temporal constraints (i.e., the subprocess is DC).
such that \(u\le x \le x' \le u'\) and \(v\ge y \ge y' \ge v'\) hold. Moreover, if \(c > 0\) holds, \(y' - x' \ge c\) must hold as well. When observing these constraints, it is guaranteed that, during the execution of a subprocess task of a modularized process, the respective subprocess instance may be completed without violating any of its temporal constraints (i.e., the subprocess is DC).
Example 8
Figure 6 depicts the modularized process from Fig. 1. Proper duration ranges have been selected for the three subprocess tasks \(P_0\), \(P_1\) and \(P_2\), which are related to (sub-)process schemas NonPharmR, PhysEx and PharmR. For example, for subprocess task \(P_0\), duration range  is used. This range has the same outer bounds as the overall temporal properties of the respective process schema, i.e.,
is used. This range has the same outer bounds as the overall temporal properties of the respective process schema, i.e.,  . Moreover, the lower and upper guard of the duration range ensure that the guards as well as the contingency value determined for the process schema are observed. In turn, for subprocess task \(P_1\), the designer decides to further restrict the upper bound of the duration range to 11 (thus also decreasing the lower guard to 9 due to the contingency of \({2}\)). Note that this still guarantees the DC of subprocess schema \(\texttt {PhysEx}\) as the new constraints comply with the respective guards and contingency. Finally, for subprocess \(P_2\), the designer increases the lower bound to 8 and the upper guard to 17, thus providing a possible contingency of 7 instead of the required contingency of 6.
. Moreover, the lower and upper guard of the duration range ensure that the guards as well as the contingency value determined for the process schema are observed. In turn, for subprocess task \(P_1\), the designer decides to further restrict the upper bound of the duration range to 11 (thus also decreasing the lower guard to 9 due to the contingency of \({2}\)). Note that this still guarantees the DC of subprocess schema \(\texttt {PhysEx}\) as the new constraints comply with the respective guards and contingency. Finally, for subprocess \(P_2\), the designer increases the lower bound to 8 and the upper guard to 17, thus providing a possible contingency of 7 instead of the required contingency of 6.
After completing the design of the modularized process schema, the dynamic controllability of the parent process schema itself needs to be verified. Then, the overall temporal properties of the modularized process schema may be determined based of the approach presented in Sect. 5.
Finally, the modularized process itself may be added to the process repository. It may then be reused as a subprocess in the context of another modularized process. This enables the definition of hierarchically structured modularized time-aware process schemas comprising multiple levels.
7 Architecture and implementation of the proof-of-concept prototype
The presented approach was implemented as a proof-of-concept prototype in the ATAPIS Toolset [20, 21], which, in turn, is based on the AristaFlow BPM Suite [31].
Due to its Open API as well as its strict modular and service-oriented design, AristaFlow can be easily applied and adapted to different application domains. This way, it allows for the integration of advanced process support functions into domain-specific PAIS as well as the provision of domain-specific client, service and activity implementations.
In our case, we extended the original AristaFlow architecture by modifying the time-aware modules, Design Toolset, ChangeOperations, and ProcessManager, to consider temporal aspects of tasks and (sub-)processes. Moreover, we introduced a new module, called TimeManager, that provides the runtime support for all the temporal features discussed in this paper. We denoted this extended framework as ATAPIS Toolset. Figure 7 depicts the architecture of the ATAPIS Toolset, where the extended/new modules are displayed with a gray background. ATAPIS Toolset supports the designer in specifying a time-aware process, verifying its properties, and enacting it.
In particular, the design toolset, called Process Template Editor, and the underlying modules enable designers to create time-aware process schemas and to automatically transform them to a corresponding STNPSU. The STNPSU, in turn, can then be checked for dynamic controllability. Moreover, the overall temporal properties of the process can be determined. The screenshot from Fig. 8 shows the Process Template Editor.Footnote 1
At the top of Fig. 8, frame A depicts the common options available for opening, editing and viewing time-aware process schemas. Moreover, there are the main options for creating the corresponding STNPSU of the loaded process schema, checking the temporal features of the STNPSU, and enacting the time-aware process schema. Frame B, in turn, depicts the panel where the process schema is designed. In Fig. 8, the process schema from Fig. 1c is shown. At the bottom, the automatically generated STNPSU, frame E, and the STNPSU after the DC check, frame D, are depicted. Finally, the dialog in the middle, frame C, shows the overall temporal properties of the process schema, which have been determined based on the STNPSU.
Using the ATAPIS prototype, it becomes possible to create modularized time-aware processes and to assign a proper duration range to each subprocess task based on the overall temporal properties of the respective (sub-)process schema. The resulting modularized time-aware process schema can then be checked for dynamic controllability, and its overall temporal properties be determined. It is then possible to reuse this modularized time-aware process schema for any subprocess task in another modularized process.
First, simulations based on the ATAPIS prototype show a significantly improved performance of our modularization-based approach compared to the “classical approach”, where each subprocess task has to be replaced by its respective (temporal) components. Overall, the prototype demonstrates the applicability of our approach.
8 Summary and outlook
Time and modular design constitute two fundamental aspects for properly supporting business processes by PAIS. So far, these aspects have only been considered in isolation, although the overall temporal behavior of a (sub-)process significantly differs from the one of simple tasks.
This paper closes this gap by considering modularization and time-awareness of processes in conjunction with each other. In particular, we propose a novel approach for determining and representing the overall temporal behavior of a process, called guarded range with contingency. Using this representation, we can specify the possible durations of a (sub-)process as well as any permissible restriction that may be applied to it, while still ensuring the executability of the process. Moreover, we show how this may be used in the context of process repositories and multilayered process hierarchies.
We are currently extending STNPSU to consider conditional aspects as well. In future work, we want to study the integration of (modularized) time-aware processes in PAISs, specifically focusing on aspects like scalability and usability. Finally, we would like to explore the concept of modularization in the context of temporal networks in order to improve the performance of controllability checking of such network.
Notes
A screencast demonstrating the toolset is available at http://dbis.info/atapis.
References
Bettini, C., Wang, X.S., Jajodia, S.: Temporal reasoning in workflow systems. Distrib. Parallel Databases 11(3), 269–306 (2002). https://doi.org/10.1023/A:1014048800604
Combi, C., Gambini, M., Migliorini, S., Posenato, R.: Representing business processes through a temporal data-centric workflow modeling language: an application to the management of clinical pathways. IEEE Trans. Syst. Man Cybern. Syst. 44(9), 1182–1203 (2014). https://doi.org/10.1109/TSMC.2014.2300055
Combi, C., Gozzi, M., Posenato, R., Pozzi, G.: Conceptual modeling of flexible temporal workflows. ACM Trans. Auton. Adapt. Syst. (TAAS) 7(2), 19:1–19:29 (2012). https://doi.org/10.1145/2240166.2240169
Combi, C., Hunsberger, L., Posenato, R.: An algorithm for checking the dynamic controllability of a conditional simple temporal network with uncertainty. In: ICAART 2013—Proceeding of the 5th international conference on agents and artificial intelligence, vol. 2, pp. 144–156. SciTePress (2013). https://doi.org/10.5220/0004256101440156
Combi, C., Hunsberger, L., Posenato, R.: An algorithm for checking the dynamic controllability of a conditional simple temporal network with uncertainty - revisited. In: Filipe, J., Fred, A.L.N. (eds.) Agents and artificial intelligence—5th international conference, ICAART 2013, Barcelona, Spain, February 15–18, 2013. Revised Selected Papers, Communications in Computer and Information Science, vol. 449, pp. 314–331. Springer (2013). https://doi.org/10.1007/978-3-662-44440-5_19
Combi, C., Posenato, R.: Controllability in temporal conceptual workflow schemata. In: Business process management, 7th international conference, BPM 2009, Ulm, Germany, September 8–10, 2009. Proceedings, LNCS, vol. 5701, pp. 64–79. Springer (2009). https://doi.org/10.1007/978-3-642-03848-8_6
Combi, C., Posenato, R.: Towards temporal controllabilities for workflow schemata. In: Markey, N., Wijsen, J. (eds.) 17th international symposium on temporal representation and reasoning (TIME 2010), pp. 129–136. IEEE Computer Society (2010). https://doi.org/10.1109/TIME.2010.17
Cruz-Jentoft, A., Baeyens, J., Bauer, J., et al.: Sarcopenia: European consensus on definition and diagnosis. Age Ageing 39(4), 412–423 (2010). https://doi.org/10.1093/ageing/afq034
Dechter, R., Meiri, I., Pearl, J.: Temporal constraint networks. Artif. Intell. 49(1–3), 61–95 (1991)
Eder, J., Gruber, W., Panagos, E.: Temporal modeling of workflows with conditional execution paths. In: Proceedings of DEXA’00, pp. 243–253. Springer (2000)
Eder, J., Panagos, E., Rabinovich, M.: Time Constraints in Workflow Systems, pp. 191–205. Springer, Berlin (2013). https://doi.org/10.1007/978-3-642-36926-1_15
Eder, J., Panagos, E., Rabinovich, M.: Workflow time management revisited. In: Seminal contributions to information systems engineering, pp. 207–213. Springer, Berlin (2013). https://doi.org/10.1007/978-3-642-36926-1_16
Eder, J., Pichler, H.: Duration histograms for workflow systems. In: Rolland, C., Brinkkemper, S., Saeki, M. (eds.) Proceedings of the working conference on engineering information systems in the internet context (IFIP TC8/WG8.1), IFIP conference proceedings, vol. 231, pp. 239–253. Kluwer, B.V. (2002)
Eder, J., Pichler, H., Gruber, W., Ninaus, M.: Personal schedules for workflow systems. In: van der Aalst, W.M.P., ter Hofstede, A.H.M., Weske, M. (eds.) Proceedings of the 1st international conference on business process management (BPM’03), Lecture Notes in Computer Science, vol. 2678, pp. 216–231. Springer (2003). https://doi.org/10.1007/3-540-44895-0
Haselkorn, J., Hughes, C., Rae-Grant, A., et al.: Summary of comprehensive systematic review: rehabilitation in multiple sclerosis. Neurology 85(21), 1896–1903 (2015). https://doi.org/10.1212/WNL.0000000000002146
Hochberg, M.C., et al.: American college of rheumatology 2012 recommendations for the use of nonpharmacologic and pharmacologic therapies in osteoarthritis of the hand, hip, and knee. Arthritis Care Res. 64(4), 465–474 (2012)
Lanz, A., Posenato, R., Combi, C., Reichert, M.: Controllability of time-aware processes at run time. In: Meersman, R., Panetto, H., Dillon, T.S., Eder, J., Bellahsene, Z., Ritter, N., Leenheer, P.D., Dou, D. (eds.) On the move to meaningful internet systems: OTM 2013 conference-confederated international conference: CoopIS, DOA-Trusted Cloud, and ODBASE, Lecture Notes in Computer Science, vol. 8185, pp. 39–56. Springer (2013). https://doi.org/10.1007/978-3-642-41030-7_4
Lanz, A., Posenato, R., Combi, C., Reichert, M.: Simple temporal networks with partially shrinkable uncertainty. In: Loiseau, S., Filipe, J., Duval, B., van den Herik, H.J. (eds.) ICAART 2015—Proceedings of the international conference on agents and artificial intelligence, vol. 2, Lisbon, Portugal, 10–12 January, 2015., pp. 370–381. SciTePress (2015). https://doi.org/10.5220/0005200903700381
Lanz, A., Posenato, R., Combi, C., Reichert, M.: Controlling Time-Awareness in Modularized Processes. In: Enterprise, Business-Process and Information Systems Modeling - 17th International conference, BPMDS 2016, 21st international conference, EMMSAD 2016, Lecture Notes in Business Information Processing, vol. 248, pp. 157–172 (2016). https://doi.org/10.1007/978-3-319-39429-9_11
Lanz, A., Reichert, M.: Dealing with changes of time-aware processes. In: Proceedings of BPM’14, LNCS, vol. 8659, pp. 217–233 (2014)
Lanz, A., Reichert, M.: Enabling time-aware process support with the atapis toolset. In: Proceedings of BPM’14 demo track (2014)
Lanz, A., Reichert, M., Weber, B.: A formal semantics of time patterns for process-aware information systems. Technical Represents UIB-2013-02, University of Ulm (2013)
Lanz, A., Reichert, M., Weber, B.: Process time patterns: a formal foundation. Inf. Syst. 57, 38–68 (2016). https://doi.org/10.1016/j.is.2015.10.002
Lanz, A., Weber, B., Reichert, M.: Time patterns for process-aware information systems. Requir. Eng. 19(2), 113–141 (2014). https://doi.org/10.1007/s00766-012-0162-3
Marjanovic, O., Orlowska, M.E.: On modeling and verification of temporal constraints in production workflows. Knowl. Inf. Syst. 1(2), 157–192 (1999)
Monti, E., Mottes, M., Fraschini, P., Brunelli, P., Forlino, A., Venturi, G., Doro, F., Perlini, S., Cavarzere, P., Antoniazzi, F.: Current and emerging treatments for the management of osteogenesis imperfecta. Ther. Clin. Risk Manag. 6, 367 (2010)
Morris, P.: A structural characterization of temporal dynamic controllability. In: F. Benhamou (ed.) International conference on principles and practices of constraint programming (CP’06), pp. 375–389. Springer (2006)
Morris, P.: Dynamic controllability and dispatchability relationships. In: Simonis, H. (ed.) International conference on integration of AI and OR techniques in constraint programming (CPAIOR’14), LNCS, vol. 8451, pp. 464–479. Springer (2014)
Morris, P.H., Muscettola, N.: Temporal dynamic controllability revisited. In: National conference on artificial intelligence (AAAI’05), pp. 1193–1198 (2005)
Morris, P.H., Muscettola, N., Vidal, T.: Dynamic control of plans with temporal uncertainty. In: International joint conference on artificial intelligence (IJCAI’01), pp. 494–502. Morgan Kaufmann (2001)
Reichert, M., Weber, B.: Enabling Flexibility in Process-Aware Information Systems—Challenges, Methods, Technologies. Springer, Berlin (2012). https://doi.org/10.1007/978-3-642-30409-5
Reijers, H.A.: Design and Control of Workflow Processes. Springer, Berlin (2003)
Vanhatalo, J., Völzer, H., Koehler, J.: The refined process structure tree. Data Knowl. Eng. 68(9), 793–818 (2009). https://doi.org/10.1016/j.datak.2009.02.015
Weber, B., Reichert, M., Mendling, J., Reijers, H.A.: Refactoring large process model repositories. Comput. Ind. 62(5), 467–486 (2011). https://doi.org/10.1016/j.compind.2010.12.012
Zhang, Y., Perry, D.E.: A Data-Centric Approach to Optimize Time in Workflow-Based Business Process. In: 2014 IEEE international conference on services computing, pp. 709–716. IEEE (2014). https://doi.org/10.1109/SCC.2014.129
Author information
Authors and Affiliations
Corresponding author
Additional information
Communicated by Dr. Ilia Bider and Rainer Schmidt.
Rights and permissions
About this article
Cite this article
Posenato, R., Lanz, A., Combi, C. et al. Managing time-awareness in modularized processes. Softw Syst Model 18, 1135–1154 (2019). https://doi.org/10.1007/s10270-017-0643-4
Received:
Revised:
Accepted:
Published:
Issue Date:
DOI: https://doi.org/10.1007/s10270-017-0643-4







 , and
, and , where A and C correspond to timepoints, and
, where A and C correspond to timepoints, and 
 .
. as control connectors are executed by the process engine of the PAIS.
as control connectors are executed by the process engine of the PAIS. with duration range
with duration range 
 in STNPSU S, the upper guard of C is
in STNPSU S, the upper guard of C is  in STNPSU S, the upper guard of C is in
in STNPSU S, the upper guard of C is in  in STNPSU S, the lower guard of C is
in STNPSU S, the lower guard of C is  in STNPSU S, the lower guard of C is in
in STNPSU S, the lower guard of C is in  derived by the DC checking algorithm, it holds upper guard of C is
derived by the DC checking algorithm, it holds upper guard of C is  , the link contingency span
, the link contingency span  , the link contingency span
, the link contingency span 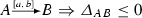 ;
; ;
; .
. , there exists a single edge
, there exists a single edge  .
. , there exist two edges
, there exist two edges  ,
,  .
. .
.
 between initial timepoint Z and ending timepoint E in S, as derived by the DC checking algorithm,
between initial timepoint Z and ending timepoint E in S, as derived by the DC checking algorithm,

