Distributions of powers of the central beta matrix variates and applications

Abstract

We consider the central Beta matrix variates of both kinds, and establish the expressions of the densities of integral powers of these variates, for all their three types of distributions encountered in the statistical literature: entries, determinant, and latent roots distributions. Applications and computation of credible intervals are presented.

1 Introduction

For a positive random variable X, its power ${{X}^{c}}$, with c positive or negative, is often encountered in applications. “Weibullized” distribution is a particular application of this approach (see Bekker et al. 2009; Nadarajah and Kotz 2004; Pauw et al. 2010).

Distributions with matrices as arguments have acquired increasing importance since Wishart (1928) established the distribution bearing his name in 1928, on the covariance matrix of a normal sample. The matrix Gamma, matrix Beta are derived from the Wishart, similarly to the univariate case, where we obtain the Beta from the univariate Normal through the Chi-square. But while there is only one distribution in the univariate case, there are at least three in ${{\mathbb {R}}^{p}}, p\ge 2$, as explained in Sect. 3. To test hypotheses in multivariate analysis we have to use tools based on determinants, or latent roots, of certain matrices, among them the Betas, which are the subjects of this article.

We consider first the univariate random variable U having central Beta distribution of the first kind, $U \sim Bet{{a}_{1}^{I}}\left( a,b \right)$, where $a,b>0$, with the probability density function (PDF):

$$\begin{aligned} f\left( u \right) =\frac{{{u}^{a-1}}{{\left( 1-u \right) }^{b-1}}}{B\left( a,b \right) } \text {, for} \,\,{0<u<1,}\,\, \end{aligned}$$

(1)

where $B\left( a,b \right) =\frac{\Gamma \left( a \right) \Gamma \left( b \right) }{\Gamma \left( a+b \right) }$, and the random variable V having central Beta distribution of the second kind, $V \sim Beta_{1}^{II}\left( a,b \right)$, where $a,b>0$, with PDF:

$$\begin{aligned} g\left( v \right) =\frac{{{v}^{a-1}}{{\left( 1+v \right) }^{-a-b}}}{B\left( a,b \right) } \text {, for} \,\, {v>0.}\,\, \end{aligned}$$

(2)

More generally, for some types of integral equations of Wilks type, Mathai (1984) has pointed out that the solutions involve some powers of Beta variables, as considered here.

In the case of matrix variates, two types of Betas are also defined and play very important roles in Multivariate Statistics, where they provide numerous tests through the distributions of their determinants (Wilks 1932) and their latent roots (Lawley 1938; Roy 1953; Pillai 1954). A fairly detailed study of both matrix Betas is given in Chapter 5 of Gupta and Nagar (2000). It is then natural to consider the powers ${{U}^{c}}$ and ${{V}^{c}}$ as being the matrix generalizations of the above univariate cases. Besides, the case of powers of the determinant, ${{\left| \mathbf {U} \right| }^{c}}$ or ${{\left| \mathbf {V} \right| }^{c}}$, is well-known in applications as powers of Wilks’s statistics, related to the likelihood ratio statistic used in multivariate analysis of variance (MANOVA). We will see that, while the univariate case is fairly simple, the matrix case is much more complex, and is worth investigating under all its three types of distributions. Furthermore, using our approach we can carry out some computation and graphing, making matrix variates quite operational in Applied Statistics.

The rest of the article is organized as follows. In Sect. 2 we start with the univariate case and give explicit solutions to these distributions. In Sect. 3 we first find the characteristic function and the moment generating function of both matrix Beta variates. Results show how the process can be transferred from the univariate to the matrix variate case. Then we find the expressions for the densities of the powers of the central Beta matrix variate, for both the first and second kinds, and in three types of distributions. Hence, there are two kinds of matrix variate Betas (first kind, denoted $\mathbf {U}$, second kind, denoted $\mathbf {V}$), each having three types of distributions (entries, determinant and latent roots), resulting in six separate sets of results. In Sect. 4 we give some applications of those results, including an interval estimation of the product of the latent roots and of its geometric mean.

Note 1

Since this article emphasizes applications we will not present here a general theory of ${{\mathbf {U}}^{m}}$, $\mathbf {U}\sim Beta_{p}^{I}\left( a,b \right)$ and of ${{\mathbf {V}}^{m}}$, $\mathbf {V}\sim Beta_{p}^{II}\left( a,b \right)$. These topics will be addressed later, in a separate lengthy paper of a rather theoretical nature.

2 The univariate case

The univariate case is usually simpler to understand and serves as guide to the matrix case which is much more complicated.

a) Let us start with the univariate Beta of the first kind, $U \sim Beta_{1}^{I}\left( a,b \right)$. Let $X={{U}^{m}}$ and $Y={{U}^{-m}}$, where $m>0$. Using the classical technique to transform a random variable, we have the PDF of X as

$$\begin{aligned} f\left( x \right) =\frac{{{x}^{\frac{a-m}{m}}}{{\left( 1-{{x}^{\frac{1}{m}}} \right) }^{b-1}}}{mB\left( a,b \right) }, \quad \text {for}\,\,{0<x<1.}\,\, \end{aligned}$$

(3)

And we have the PDF of $Y={{U}^{-m}}$ as

$$\begin{aligned} f\left( y \right) =\frac{{{y}^{\frac{-\left( a+b+m-1 \right) }{m}}}{{\left( {{y}^{\frac{1}{m}}}-1 \right) }^{b-1}}}{mB\left( a,b \right) },\quad \text {for}\,\,{y>1.}\,\, \end{aligned}$$

(4)

b) For the univariate Beta of the second kind, $V \sim Beta_{1}^{II}\left( a,b \right)$. The PDF of $Z={{V}^{m}}$, where $m>0$, is given by

$$\begin{aligned} f\left( z \right) =\frac{{{z}^{\frac{a-m}{m}}}{{\left( 1+{{z}^{\frac{1}{m}}} \right) }^{-\left( a+b \right) }}}{mB\left( a,b \right) }, \quad \text {for}\,\,{z>0.}\,\, \end{aligned}$$

(5)

Again, using the classical approach based on change of variable, we can establish the PDF of $T={{V}^{-1}}$ as $Beta_{1}^{II}\left( b,a \right)$, and the PDFs of ${{T}^{m}}={{V}^{-m}}$, with $m>0$, as (5) with a, b interchanged.

Remark 1

Concerning some new random variables frequently encountered in the literature, e.g. the generalized beta distribution used in Economics by McDonald and Xu (1995), it can be seen that it has properties similar to those of the powers ${{U}^{c}}$ and ${{V}^{c}}$ of our variables.

3 Case of the matrix variate distribution

To completely study the powers of the two central Beta matrix variates we distinguish first between three types of distributions that come with each, as done in Pham-Gia and Turkkan (2011a): (a) Entries distribution distribution of its entries (or variables), or a mathematical relation relating all the entries, but for convenience, their determinant is generally used, (b) determinant distribution distribution of its determinant, considered as variable, and (c) latent roots distribution the distribution of its latent roots. Naturally, these distributions are intimately related to each other, and fuse into a single one, given by (1) and (2), when $p=1$. But each of them has its own use in statistical studies, the first one provides the mathematical relationship between the matrix entries, while the second one gives the distribution of an univariate measure of the matrix, and the third one gives a multivariate joint density of these latent roots.

3.1 Entries distributions

Definition 1

The random symmetric positive definite matrix $\mathbf {U}$ is said to be a central Beta matrix variate of the first kind with parameters $a,b>\tfrac{p-1}{2}$, noted $\mathbf {U} \sim Beta_{p}^{I}\left( a,b \right)$, if its PDF is given by

$$\begin{aligned} f\left( \mathbf {U} \right) =\frac{{{\left| \mathbf {U} \right| }^{a-\frac{p+1}{2}}}{{\left| {{\mathbf {I}}_{p}}-\mathbf {U} \right| }^{b-\frac{p+1}{2}}}}{{{B}_{p}}\left( a,b \right) },\quad {for} \,\, \mathbf {0}<\mathbf {U}<{{\mathbf {I}}_{p},}\, \end{aligned}$$

(6)

where ${{B}_{p}}\left( a,b \right)$ is the multivariate Beta function in ${{\mathbb {R}}^{p}}$, i.e. ${{B}_{p}}\left( a,b \right) =\frac{{{\Gamma }_{p}}\left( a \right) {{\Gamma }_{p}}\left( b \right) }{{{\Gamma }_{p}}\left( a+b \right) }$, with ${{\Gamma }_{p}}\left( a \right) ={{\pi }^{\frac{p\left( p-1 \right) }{4}}}\prod \limits _{j=1}^{p}{\Gamma \left( a-\frac{j-1}{2} \right) }$. The random symmetric positive definite matrix $\mathbf {V}$ is said to be a central Beta matrix variate of the second kind with parameters $a,b>\tfrac{p-1}{2}$, noted $\mathbf {V} \sim Beta_{p}^{II}\left( a,b \right)$, if its PDF is given by

$$\begin{aligned} g\left( \mathbf {V} \right) =\frac{{{\left| \mathbf {V} \right| }^{a-\frac{p+1}{2}}}{{\left| {{\mathbf {I}}_{p}}+\mathbf {V} \right| }^{-\left( a+b \right) }}}{{{B}_{p}}\left( a,b \right) },\quad {for} \,\, \mathbf {0}<\mathbf {V}.\, \end{aligned}$$

(7)

We refer to Chapter 5 of Gupta and Nagar (2000) for the basic properties of these two matrix variates.

3.1.1 The Moment generating functions of the two central matrix betas

Characteristic and Moment generating functions of a random variable have always played important roles in the study of its distribution. For the two univariate Betas they are expressed as confluent hypergeometric functions of first and second kinds. To have similar expressions for the matrix Betas we have to generalize first these hypergeometric functions, from scalar argument to matrix argument, and then find their integral representations. Pham-Gia and Thanh (2016) can provide some information on this topic. The final results bear some similarities with the univariate case, as can be seen below.

I. Scalar case

a) Kummer confluent hypergeometric function of the first kind, in the scalar case,

$$\begin{aligned} _{1}{{F}_{1}}\left( \alpha ,\beta ;z \right) =\sum \limits _{j=0}^{\infty }{\frac{\left( \alpha ,j \right) }{\left( \beta ,j \right) }}\frac{{{z}^{j}}}{j!}, \end{aligned}$$

with $\left( a,j \right) =\Gamma \left( a+j \right) /\Gamma \left( a \right)$, and $\left( a,0 \right) =1$. Its integral representation is

$$\begin{aligned} _{1}{{F}_{1}}\left( \alpha ,\beta ;z \right) =\frac{\Gamma \left( \beta \right) }{\Gamma \left( \alpha \right) \Gamma \left( \beta -\alpha \right) }\int \limits _{0}^{1}{{{e}^{zt}}}{{t}^{\alpha -1}}{{\left( 1-t \right) }^{\beta -\alpha -1}}dt. \end{aligned}$$

b) Kummer confluent hypergeometric function of the second kind, in the scalar case,

$$\begin{aligned} \psi \left( \alpha ,\beta ;z \right) =\frac{\Gamma \left( 1-\beta \right) }{\Gamma \left( 1+\alpha -\beta \right) }{}_{1}{{F}_{1}}\left( \alpha ,\beta ;z \right) +\frac{\Gamma \left( \beta -1 \right) }{\Gamma \left( \alpha \right) }{{z}^{1-\beta }}_{1}{{F}_{1}}\left( 1+\alpha -\beta ,2-\beta ;z \right) . \end{aligned}$$

Its integral representation is

$$\begin{aligned} \psi \left( \alpha ,\beta ;z \right) =\frac{1}{\Gamma \left( \alpha \right) }\int \limits _{0}^{\infty }{{{e}^{-zt}}}{{t}^{\alpha -1}}{{\left( 1+t \right) }^{\beta -\alpha -1}}dt. \end{aligned}$$

Using the above two relations, we have for U, the univariate Beta of the first kind, its characteristic function

$$\begin{aligned} {{\varphi }_{U}}\left( t \right) =\mathbb {E}\left[ \exp \left( itU \right) \right] ={}_{1}{{F}_{1}}\left( \alpha ,\alpha +\beta ;it \right) , \end{aligned}$$

where $i=\sqrt{-1}$, and its moment generating function

$$\begin{aligned} {{M}_{U}}\left( t \right) =\mathbb {E}\left[ \exp \left( tU \right) \right] ={}_{1}{{F}_{1}}\left( \alpha ,\alpha +\beta ;t \right) . \end{aligned}$$

Similarly, we have, for V, the univariate Beta of the second kind

$$\begin{aligned} {{M}_{V}}\left( t \right) =\mathbb {E}\left[ \exp \left( tV \right) \right] =\psi \left( \alpha ,\alpha +\beta ;t \right) . \end{aligned}$$

II. Matrix case

When the variable is a matrix, there are several ways to define the hypergeometric function. One way is using zonal polynomials (see Muirhead 1982), which, unfortunately, are very difficult to compute, except in simple cases.

We have Kummer hypergeometric function of the first kind, for the symmetric matrix $\mathbf {R}$,

$$\begin{aligned}&_{1}{{F}_{1}}\left( \alpha ,\beta ;\mathbf {R} \right) =\frac{{{\Gamma }_{p}}\left( \beta \right) }{{{\Gamma }_{p}}\left( \alpha \right) {{\Gamma }_{p}}\left( \beta -\alpha \right) }\\&\quad \int \limits _{\mathbf {0}<\mathbf {S}<{{\mathbf {I}}_{p}}}^{{}}{etr\left( \mathbf {RS} \right) {{\left| \mathbf {S} \right| }^{\alpha -\left( p+1 \right) /2}}}{{\left| {{\mathbf {I}}_{p}}-\mathbf {S} \right| }^{\beta -\alpha -\left( p+1 \right) /2}}d\mathbf {S}, \end{aligned}$$

where $etr\left( \mathbf {X}\right) =\exp \left( trace\mathbf {X}\right)$, and for the Kummer hypergeometric matrix function of the second kind

$$\begin{aligned} \psi \left( \alpha ,\beta ;\mathbf {R} \right) =\frac{1}{{{\Gamma }_{p}}\left( \alpha \right) }\int \limits _{\mathbf {0}<\mathbf {S}}^{{}}{etr\left( -\mathbf {RS} \right) {{\left| \mathbf {S} \right| }^{\alpha -\left( p+1 \right) /2}}}{{\left| {{\mathbf {I}}_{p}}+\mathbf {S} \right| }^{\beta -\alpha -\left( p+1 \right) /2}}d\mathbf {S}. \end{aligned}$$

The characteristic function of the matrix Beta variate of the first kind $\mathbf {U}$ is then

$$\begin{aligned} {{\varphi }_{\mathbf {U}}}\left( \mathbf {Z} \right) ={}_{1}{{F}_{1}}\left( \alpha ,\alpha +\beta ;i\mathbf {Z} \right) , \end{aligned}$$

where $\mathbf {Z}$ is a symmetric ${{\left( p\times p \right) }}$ matrix of scalars, with form $\mathbf {Z}=\left( \frac{1}{2}\left( 1+{{\delta }_{ij}} \right) {{z}_{ij}} \right)$, where ${{\delta }_{ij}}$ is the Kronecker symbol. Its moment generating function is

$$\begin{aligned} {{M}_{\mathbf {U}}}\left( \mathbf {Z} \right) {{=}_{1}}{{F}_{1}}\left( \alpha ,\alpha +\beta ;\mathbf {Z} \right) . \end{aligned}$$

The characteristic function for the matrix Beta variate of the second kind $\mathbf {V}$ is then

$$\begin{aligned} {{\varphi }_{\mathbf {V}}}\left( \mathbf {Z} \right) ={{\frac{{{\Gamma }_{p}}\left( \alpha +\beta \right) }{{{\Gamma }_{p}}\left( \beta \right) }}}\psi \left( \alpha ;-\beta +\left( p+1 \right) /2;-i\mathbf {Z} \right) . \end{aligned}$$

Its moment generating function is

$$\begin{aligned} {{M}_{\mathbf {V}}}\left( \mathbf {Z} \right) ={{\frac{{{\Gamma }_{p}}\left( \alpha +\beta \right) }{{{\Gamma }_{p}}\left( \beta \right) }}}\psi \left( \alpha ;-\beta +\left( p+1 \right) /2;-\mathbf {Z} \right) . \end{aligned}$$

See Gupta and Nagar (2000) for some of the arguments used here.

3.1.2 Distributions of powers of $\mathbf {U}$ and $\mathbf {V}$

For the integral positive and negative powers of the two types of central Beta matrix variates we have:

Theorem 1

Let $\mathbf {U} \sim Beta_{p}^{I}\left( a,b \right)$, $\mathbf {V} \sim Beta_{p}^{II}\left( a,b \right)$ with distinct latent roots and positive integer m. We have

• (a) The PDF of $\mathbf {X}={{\mathbf {U}}^{m}}$ is given by, for $\mathbf {0}<\mathbf {X}<{\mathbf {I}}_{p}$,

  $$\begin{aligned} {{f}_{\mathbf {X}}}\left( \mathbf {X} \right) =\frac{{{\left| \mathbf {X} \right| }^{\frac{a-m-\frac{p-1}{2}}{m}}}{{\left| {{\mathbf {I}}_{p}}-{{\mathbf {X}}^{\tfrac{1}{m}}} \right| }^{b-\frac{p+1}{2}}}}{{{m}^{p}}{{B}_{p}}\left( a,b \right) }\prod \limits _{i<j}{\left| \frac{\eta _{i}^{\tfrac{1}{m}}-\eta _{j}^{\tfrac{1}{m}}}{{{\eta }_{i}}-{{\eta }_{j}}} \right| }, \end{aligned}$$

  (8)

  where ${{\eta }_{1}},\,{{\eta }_{2}},\dots ,\,{{\eta }_{p}}$ are the latent roots of $\mathbf {X}$ and ${{\mathbf {X}}^{\tfrac{1}{m}}}$ denotes the m-th symmetric positive definite root of $\mathbf {X}$, i.e. ${{\left( {{\mathbf {X}}^{\frac{1}{m}}} \right) }^{m}}=\mathbf {X}$.

• (b) The PDF of $\mathbf {Y}={{\mathbf {U}}^{-m}}$ is given by, for $\mathbf {Y}>{\mathbf {I}}_{p}$,

  $$\begin{aligned} {{f}_{\mathbf {Y}}}\left( \mathbf {Y} \right) =\frac{{{\left| \mathbf {Y} \right| }^{\frac{-\left( a+b+m-1 \right) }{m}}}{{\left| {{\mathbf {Y}}^{\tfrac{1}{m}}}-{{\mathbf {I}}_{p}} \right| }^{b-\frac{p+1}{2}}}}{{{m}^{p}}{{B}_{p}}\left( a,b \right) }\prod \limits _{i<j}^{{}}{\left| \frac{{{\xi }_{i}}^{\frac{1}{m}}-{{\xi }_{j}}^{\frac{1}{m}}}{{{\xi }_{i}}-{{\xi }_{j}}} \right| }, \end{aligned}$$

  (9)

  where ${{\xi }_{1}},\,{{\xi }_{2}},\dots ,\,{{\xi }_{p}}$ are the latent roots of $\mathbf {Y}$.

• (c) The PDF of $\mathbf {Z}={{\mathbf {V}}^{m}}$ is given by, for $\mathbf {Z}>\mathbf {0}$,

  $$\begin{aligned} {{f}_{\mathbf {Z}}}\left( \mathbf {Z} \right) =\frac{{{\left| \mathbf {Z} \right| }^{\frac{a-m-\frac{p-1}{2}}{m}}}{{\left| {{\mathbf {I}}_{p}}+{{\mathbf {Z}}^{\tfrac{1}{m}}} \right| }^{-\left( a+b \right) }}}{{{m}^{p}}{{B}_{p}}\left( a,b \right) }\prod \limits _{i<j}^{{}}{\left| \frac{\theta _{i}^{\tfrac{1}{m}}-\theta _{j}^{\tfrac{1}{m}}}{{{\theta }_{i}}-{{\theta }_{j}}} \right| }, \end{aligned}$$

  (10)

  where ${{\theta }_{1}},\,{{\theta }_{2}},\dots ,\,{{\theta }_{p}}$ are the latent roots of $\mathbf {Z}$.

• (d) The PDF of ${{\mathbf {V}}^{-m}}$ has the same expression as the PDF of ${{\mathbf {V}}^{m}}$, with a and b interchanged.

Proof

(a) The Jacobian of transformation $\mathbf {U}\rightarrow X={{\mathbf {U}}^{m}}$ is (Mathai 1997)

$$\begin{aligned} {{m}^{p}}{{\left| \mathbf {U} \right| }^{m-1}}\prod \limits _{i<j}^{{}}{\left| \frac{\lambda _{i}^{m}-\lambda _{j}^{m}}{{{\lambda }_{i}}-{{\lambda }_{j}}} \right| } \end{aligned}$$

for a positive definite symmetric matrix $\mathbf {U}$ with real distinct and positive latent roots ${{\lambda }_{1}},\dots ,{{\lambda }_{p}}$. We have ${{\eta }_{i}}=\lambda _{i}^{m}$, where ${{\eta }_{i}}$ is the latent root of $\mathbf {X}$ because $\mathbf {X}={{\mathbf {U}}^{m}}$. Using (6), we have the above (8) for the PDF of $\mathbf {X}={{\mathbf {U}}^{m}}$.

(b) For $\mathbf {U} \sim Beta_{p}^{I}\left( a,b \right)$, we have the PDF of $\mathbf {W}={{\mathbf {U}}^{-1}}$ as follows (Gupta and Nagar 2000)

$$\begin{aligned} \frac{{{\left| \mathbf {W} \right| }^{-\left( a+b \right) }}{{\left| \mathbf {W}-{{\mathbf {I}}_{p}} \right| }^{b-\frac{p+1}{2}}}}{{{B}_{p}}\left( a,b \right) } \text {, for} \,\, \mathbf {W}>{{\mathbf {I}}_{p}.} \end{aligned}$$

Setting $\mathbf {Y}={{\mathbf {U}}^{-m}}={{\mathbf {W}}^{m}}$, applying the same approach as part (a) we have the PDF of ${{\mathbf {U}}^{-m}}$.

(c) The proof here is similar to part (a).

(d) Moreover, for $\mathbf {V} \sim Beta_{p}^{II}\left( a,b \right)$, we have ${{\mathbf {V}}^{-1}} \sim Beta_{p}^{II}\left( b,a \right)$ (Gupta and Nagar 2000). Hence ${{\mathbf {V}}^{-m}}$, has its PDF exactly as the density of ${{\mathbf {V}}^{m}}$, but with a and b permuted. $\square$

3.2 Determinant distributions

The determinant of a Beta matrix variate can have its univariate distribution expressed as a product of independent univariate Betas, hence by a Meijer G-function distribution, as shown in Pham-Gia (2008), Pham-Gia and Turkkan (2011a), where it also shown how numerical computation of these distributions can be carried out by using Meijer G-functions. Let $\mathbf {U} \sim Beta_{p}^{I}\left( a,b \right)$, $\mathbf {V} \sim Beta_{p}^{II}\left( a,b \right)$. We have

• (a) The PDF of $\left| \mathbf {U} \right|$ is given by Pham-Gia (2008) as follows, for $0<u<1$,

  $$\begin{aligned} {{f}_{\left| \mathbf {U} \right| }}\left( u \right) =\prod \limits _{j=1}^{p}{\frac{\Gamma \left( a+b-\tfrac{j-1}{2} \right) }{\Gamma \left( a-\tfrac{j-1}{2} \right) }}{{G}{\begin{matrix} p &{}\quad 0 \\ p &{}\quad p \\ \end{matrix}}}\left[ u\left| \begin{matrix} a+b-1,a+b-\frac{3}{2},\dots ,a+b-\frac{p+1}{2} \\ a-1,a-\frac{3}{2},\dots ,a-\frac{p+1}{2} \\ \end{matrix} \right. \right] \nonumber \\ \end{aligned}$$

  (11)

  where ${{G}{\begin{matrix} m &{}\quad n \\ r &{}\quad q \\ \end{matrix}}}\left( . \right)$ is the Meijer G-function (see Mathai et al. 2010).

• (b) The PDF of $\left| \mathbf {V} \right|$ is given by Pham-Gia (2008) as follows, for $v>0$,

  $$\begin{aligned} {{f}_{\left| \mathbf {V} \right| }}\left( v \right) =\frac{1}{\prod \limits _{j=1}^{p}{\Gamma \left( a-\tfrac{j-1}{2} \right) \Gamma \left( b-\tfrac{j-1}{2} \right) }}{{G}{\begin{matrix} p &{}\quad p \\ p &{}\quad p \\ \end{matrix}}}\left[ v\left| \begin{matrix} -b,-\left( b-\frac{1}{2} \right) , \ldots , -\left( b-\frac{p-1}{2} \right) \\ a-1,a-\frac{3}{2}, \ldots , a-\tfrac{p+1}{2} \\ \end{matrix} \right. \right] . \end{aligned}$$

  (12)

For the positive and negative powers of the determinants of the two types of central Beta matrix variates we have:

Theorem 2

Let $\mathbf {U} \sim Beta_{p}^{I}\left( a,b \right)$, $\mathbf {V} \sim Beta_{p}^{II}\left( a,b \right)$, and $m>0$. We have

• (a) The PDF of ${{\left| \mathbf {U} \right| }^{m}}$ is given by, for $0<x<1$,

  $$\begin{aligned} f\left( x \right)&=\frac{1}{m}\prod \limits _{j=1}^{p}{\frac{\Gamma \left( a+b-\tfrac{j-1}{2} \right) }{\Gamma \left( a-\tfrac{j-1}{2} \right) }}\nonumber \\&\quad \times \, {{G}{\begin{matrix} p &{}\quad 0 \\ p &{}\quad p \\ \end{matrix}}}\left[ {{x}^{\frac{1}{m}}}\left| \begin{matrix} a+b-m,a+b-m-\tfrac{1}{2},\ldots ,a+b-m-\frac{p-1}{2} \\ a-m,a-m-\frac{1}{2},\dots ,a-m-\frac{p-1}{2} \\ \end{matrix} \right. \right] . \end{aligned}$$

  (13)

• (b) The PDF of ${{\left| \mathbf {U} \right| }^{-m}}$ is given by, for $y>1$,

  $$\begin{aligned} f\left( y \right)&= \frac{1}{m}\prod \limits _{j=1}^{p}{\frac{\Gamma \left( a+b-\tfrac{j-1}{2} \right) }{\Gamma \left( a-\tfrac{j-1}{2} \right) }} \nonumber \\&\quad \times \, {{G}{\begin{matrix} 0 &{}\quad p \\ p &{}\quad p \\ \end{matrix}}}\left[ {{y}^{\frac{1}{m}}}\left| \begin{matrix} -a-m+1,-a-m+\frac{3}{2},\dots ,-a-m+\frac{p+1}{2} \\ -a-b-m+1,-a-b-m+\frac{3}{2},\dots ,-a-b-m+\frac{p+1}{2} \\ \end{matrix} \right. \right] . \end{aligned}$$

  (14)

• (c) The PDF of ${{\left| \mathbf {V} \right| }^{m}}$ is given by, for $z>0$,

  $$\begin{aligned} f\left( z \right)&=\frac{1}{m\prod \limits _{j=1}^{p}{\Gamma \left( a-\tfrac{j-1}{2} \right) \Gamma \left( b-\tfrac{j-1}{2} \right) }}\nonumber \\&\quad \times \, {{G}{\begin{matrix} p &{}\quad p \\ p &{}\quad p \\ \end{matrix}}}\left[ {{z}^{\frac{1}{m}}}\left| \begin{matrix} -b-m+1,-b-m+\frac{3}{2},\dots ,-b-m+\frac{p+1}{2} \\ a-m,a-m-\frac{1}{2},\dots ,a-m-\frac{p-1}{2} \\ \end{matrix} \right. \right] . \end{aligned}$$

  (15)

• (d) And the PDF of ${{\left| \mathbf {V} \right| }^{-m}}$ is the same as (15), but with a and b interchanged.

Proof

(a) Using the classical transform technique $X={{\left| \mathbf {U} \right| }^{m}}$ and using (11) we have the PDF of $X={{\left| \mathbf {U} \right| }^{m}}$ as

$$\begin{aligned} \frac{{{x}^{\tfrac{1-m}{m}}}}{m}\prod \limits _{j=1}^{p}{\frac{\Gamma \left( a+b-\tfrac{j-1}{2} \right) }{\Gamma \left( a-\tfrac{j-1}{2} \right) }}{{G} {\begin{matrix} p &{}\quad 0 \\ p &{}\quad p \\ \end{matrix}}}\left[ {{x}^{\frac{1}{m}}}\left| \begin{matrix} a+b-1,a+b-\frac{3}{2},\dots ,a+b-\frac{p+1}{2} \\ a-1,a-\frac{3}{2},\dots ,a-\frac{p+1}{2} \\ \end{matrix} \right. \right] . \end{aligned}$$

Using the equation (1.60) in Mathai et al. (2010) we have

$$\begin{aligned}&{{x}^{\frac{1-m}{m}}}{{G}{\begin{matrix} p &{}\quad 0 \\ p &{}\quad p \\ \end{matrix}}}\left[ {{x}^{\frac{1}{m}}}\left| \begin{matrix} a+b-1,\dots ,a+b-\tfrac{p+1}{2} \\ a-1,\dots ,a-\tfrac{p+1}{2} \\ \end{matrix} \right. \right] \\&\quad ={{G}{\begin{matrix} p &{}\quad 0 \\ p &{}\quad p \\ \end{matrix}}}\left[ {{x}^{\frac{1}{m}}}\left| \begin{matrix} a+b-m,a+b-m-\frac{1}{2},\dots ,a+b-m-\frac{p-1}{2} \\ a-m,a-m-\frac{1}{2},\dots ,a-m-\frac{p-1}{2} \\ \end{matrix} \right. \right] . \end{aligned}$$

(b) Using (11) we have the PDF of $T={{\left| \mathbf {U} \right| }^{-1}}$ as

$$\begin{aligned} \prod \limits _{j=1}^{p}{\frac{\Gamma \left( a+b-\tfrac{j-1}{2} \right) }{\Gamma \left( a-\frac{j-1}{2} \right) }}{{t}^{-2}}{{G}{\begin{matrix} p &{}\quad 0 \\ p &{}\quad p \\ \end{matrix}}}\left[ {{t}^{-1}}\left| \begin{matrix} a+b-1,a+b-\frac{3}{2},\dots ,a+b-\frac{p+1}{2} \\ a-1,a-\frac{3}{2},\dots ,a-\frac{p+1}{2} \\ \end{matrix} \right. \right] . \end{aligned}$$

Using the equation (1.58) in Mathai et al. (2010) we have

$$\begin{aligned}&{{G}{\begin{matrix} p &{}\quad 0 \\ p &{}\quad p \\ \end{matrix}}}\left[ {{t}^{-1}}\left| \begin{matrix} a+b-1,a+b-\frac{3}{2},\dots ,a+b-\frac{p+1}{2} \\ a-1,a-\frac{3}{2},\dots ,a-\frac{p+1}{2} \\ \end{matrix} \right. \right] \\&\quad ={{G}{\begin{matrix} 0 &{}\quad p \\ p &{}\quad p \\ \end{matrix}}}\left[ t\left| \begin{matrix} -a+2,-a+\frac{5}{2},\dots ,-a+\frac{p+3}{2} \\ -\left( a+b \right) +2,-\left( a+b \right) +\frac{5}{2},\dots ,-\left( a+b \right) +\frac{p+3}{2} \\ \end{matrix} \right. \right] . \end{aligned}$$

Using the equation (1.60) in Mathai et al. (2010) we have

$$\begin{aligned}&{{t}^{-2}}{{G}{\begin{matrix} 0 &{}\quad p \\ p &{}\quad p \\ \end{matrix}}}\left[ t\left| \begin{matrix} -a+2,-a+\frac{5}{2},\dots ,-a+\frac{p+3}{2} \\ -\left( a+b \right) +2,-\left( a+b \right) +\frac{5}{2},\dots ,-\left( a+b \right) +\frac{p+3}{2} \\ \end{matrix} \right. \right] \\&\quad ={{G}{\begin{matrix} 0 &{}\quad p \\ p &{}\quad p \\ \end{matrix}}}\left[ t\left| \begin{matrix} -a,-a+\frac{1}{2},\dots ,-a+\frac{p-1}{2} \\ -a-b,-a-b+\frac{1}{2},\dots ,-a-b+\frac{p-1}{2} \\ \end{matrix} \right. \right] . \end{aligned}$$

Setting $X={{T}^{m}}={{\left| \mathbf {U} \right| }^{-m}}$, it is the same as (a) we have the PDF of ${{\left| \mathbf {U} \right| }^{-m}}$ as (14). (c) and (d) applying the same approach as (a) and (b). $\square$

Remark 2

If m is positive integer, we have ${{\left| \mathbf {U} \right| }^{m}}=\left| {{\mathbf {U}}^{m}} \right|$, ${{\left| \mathbf {V} \right| }^{m}}=\left| {{\mathbf {V}}^{m}} \right|$, ${{\left| \mathbf {U} \right| }^{-m}}=\left| {{\mathbf {U}}^{-m}} \right|$, ${{\left| \mathbf {V} \right| }^{-m}}=\left| {{\mathbf {V}}^{-m}} \right|$.

3.3 Latent roots distributions

The latent roots of matrix variates $\mathbf {U}$ and $\mathbf {V}$ are very much present in statistical tests in multivariate analysis. Their joint distributions have been found almost simultaneously by five well-known statisticians in the late thirties and early fifties. They have been used in hypothesis testing, in relation to the equality of two covariance matrices (Pham-Gia and Turkkan 2011b), in multivariate analysis of variance, in canonical correlation, among other topics. Lately, they play an active role in random matrix theory in theoretical Physics.

Let us recall that the PDF of the latent roots $\left\{ {{\lambda }_{1}},\dots ,{{\lambda }_{p}} \right\}$ of $\mathbf {U}$$\sim \, Beta_{p}^{I}\left( a,b \right)$ is given by

$$\begin{aligned} \frac{{{\pi }^{{{p}^{2}}/2}}}{{{\Gamma }_{p}}\left( p/2 \right) {{B}_{p}}\left( a,b \right) }\left[ \prod \limits _{j=1}^{p}{\lambda _{j}^{a-\frac{p+1}{2}}{{\left( 1-{{\lambda }_{j}} \right) }^{b-\frac{p+1}{2}}}} \right] \prod \limits _{i<j}{\left( {{\lambda }_{i}}-{{\lambda }_{j}} \right) }, \end{aligned}$$

(16)

where $1>{{\lambda }_{1}}>{{\lambda }_{2}}>\dots>{{\lambda }_{p}}>0$. The PDF of the latent roots $\left\{ {{l}_{1}},\dots ,{{l}_{p}} \right\}$ of $\mathbf {V}\,\sim \,Beta_{p}^{II}\left( a,b \right)$ is given by

$$\begin{aligned} \frac{{{\pi }^{{{p}^{2}}/2}}}{{{\Gamma }_{p}}\left( p/2 \right) {{B}_{p}}\left( a,b \right) }\left[ \prod \limits _{j=1}^{p}{l_{j}^{a-\frac{p+1}{2}}{{\left( 1+{{l}_{j}} \right) }^{-\left( a+b \right) }}} \right] \prod \limits _{i<j}{\left( {{l}_{i}}-{{l}_{j}} \right) }, \end{aligned}$$

(17)

where ${{l}_{1}}>{{l}_{2}}>\dots>{{l}_{p}}>0$.

We also have ${{l}_{j}}={{\lambda }_{j}}/\left( 1-{{\lambda }_{j}} \right)$. For the latent roots distributions of integral positive and negative powers of Beta matrix variates, we have:

Theorem 3

Let $\mathbf {U} \sim Beta_{p}^{I}\left( a,b \right)$, $\mathbf {V} \sim Beta_{p}^{II}\left( a,b \right)$, and m be a positive integer. We have

• (a) The PDF of the latent roots $\left\{ {{\eta }_{1}},{{\eta }_{2}},\dots ,{{\eta }_{p}} \right\}$ of ${{\mathbf {U}}^{m}}$ is given by

  $$\begin{aligned} h\left( {{\eta }_{1}},\dots ,{{\eta }_{p}} \right) =\frac{C}{{{m}^{p}}}\prod \limits _{j=1}^{p}{{{\eta }_{j}}^{\frac{a-m-\frac{p-1}{2}}{m}}{{\left( 1-{{\eta }_{j}}^{\tfrac{1}{m}} \right) }^{b-\frac{p+1}{2}}}}\prod \limits _{i<j}^{{}}{\left( \eta _{i}^{\tfrac{1}{m}}-\eta _{j}^{\tfrac{1}{m}} \right) }, \end{aligned}$$

  (18)

  where $1>{{\eta }_{1}}>{{\eta }_{2}}>\dots>{{\eta }_{p}}>0$ and $C=\frac{{{\pi }^{{{p}^{2}}/2}}}{{{\Gamma }_{p}}\left( p/2 \right) {{B}_{p}}\left( a,b \right) }$.

• (b) The PDF of the latent roots $\left\{ {{\xi }_{1}},{{\xi }_{2}},\dots ,{{\xi }_{p}} \right\}$ of ${{\mathbf {U}}^{-m}}$ is given by

  $$\begin{aligned} h\left( {{\xi }_{1}},\dots ,{{\xi }_{p}} \right) =\frac{C}{{{m}^{p}}}\prod \limits _{j=1}^{p}{{{\xi }_{j}}^{\frac{-(a+b+m-p)}{m}}{{\left( {{\xi }_{j}}^{\tfrac{1}{m}}-1 \right) }^{b-\frac{p+1}{2}}}}\prod \limits _{i<j}^{{}}{\frac{\left( {{\xi }_{i}}^{\tfrac{1}{m}}-{{\xi }_{j}}^{\tfrac{1}{m}} \right) }{{{\left( {{\xi }_{i}}{{\xi }_{j}} \right) }^{\tfrac{1}{m}}}}}, \end{aligned}$$

  (19)

  where ${{\xi }_{1}}>{{\xi }_{2}}>\dots>{{\xi }_{p}}>1$.

• (c) The PDF of the latent roots $\left\{ {{\theta }_{1}},{{\theta }_{2}},\dots ,{{\theta }_{p}} \right\}$ of ${{\mathbf {V}}^{m}}$ is given by

  $$\begin{aligned} h\left( {{\theta }_{1}},{{\theta }_{2}},\dots ,{{\theta }_{p}} \right) =\frac{C}{{{m}^{p}}}\left[ \prod \limits _{j=1}^{p}{\theta _{j}^{\frac{a-m-\frac{p-1}{2}}{m}}{{\left( 1+{{\theta }_{j}}^{\tfrac{1}{m}} \right) }^{-\left( a+b \right) }}} \right] \prod \limits _{i<j}{\left( \theta _{i}^{\tfrac{1}{m}}-\theta _{j}^{\tfrac{1}{m}} \right) }, \end{aligned}$$

  (20)

  where ${{\theta }_{1}}>{{\theta }_{2}}>\dots>{{\theta }_{p}}>0$.

• (d) The PDF of the latent roots of ${{\mathbf {V}}^{-m}}$ is the same as (20) with a and b interchanged.

Proof

(a) We noted that the latent roots of ${{\mathbf {U}}^{m}}$, $1>{{\eta }_{1}}>{{\eta }_{2}}>\dots>{{\eta }_{p}}>0$, are determined by the transformation $\{{\lambda }_{1}$, ${\lambda }_{2}$, $\ldots$, ${\lambda }_{p}\}$ to $\{{{\eta }_{1}}={{\lambda }_{1}}^{m}$, ${{\eta }_{2}}={{\lambda }_{2}}^{m}$, $\ldots$, ${{\eta }_{p}}={{\lambda }_{p}}^{m}\}$. The Jacobian of those transformation is ${{m}^{p}}\prod \nolimits _{j=1}^{p}{{{\lambda }_{j}}^{m-1}}$. Using (16) we have the PDF of the latent roots $\left( {{\eta }_{1}},{{\eta }_{2}},\dots ,{{\eta }_{p}} \right)$ of ${{\mathbf {U}}^{m}}$ as given by (18).

We have the proofs of (b), (c) and (d) by applying the same approach as (a). $\square$

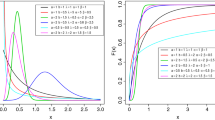
Graphical representations We give here the graphical representations of some latent roots distributions. We are limited to $p=2$ although by Theorem 3 the idea can be extended to any value of p. For example, let $\mathbf {U}\,\sim \,Beta_{2}^{I}\left( 10,8 \right)$ and $\mathbf {V}\,\sim \, Beta_{2}^{II}\left( 10,8 \right)$. The explicit expressions PDFs of latent roots of ${{\mathbf {U}}^{2}}$, ${{\mathbf {U}}^{-2}}$, ${{\mathbf {V}}^{2}}$, and ${{\mathbf {V}}^{-2}}$ are given by the Eqs. (18)–(20) where $p=m=2$, $a=10$, and $b=8$. For example, the density of latent roots of ${{\mathbf {U}}^{2}}$ is:

$$\begin{aligned} {{h}_{{{\mathbf {U}}^{2}}}}\left( {{\eta }_{1}},{{\eta }_{2}} \right) =\frac{C}{4}{{\eta }_{1}}^{\frac{15}{4}}{{\eta }_{2}}^{\frac{15}{4}}{{\left( 1-\sqrt{{{\eta }_{1}}} \right) }^{\frac{13}{2}}}{{\left( 1-\sqrt{{{\eta }_{2}}} \right) }^{\frac{13}{2}}}\left( \sqrt{{{\eta }_{1}}}-\sqrt{{{\eta }_{2}}} \right) , \end{aligned}$$

for $0<{{\eta }_{2}}<{{\eta }_{1}}<1$, where $C=\frac{{{\pi }^{2}}{{\Gamma }_{2}}\left( 18 \right) }{{{\Gamma }_{2}}\left( 1 \right) {{\Gamma }_{2}}\left( 10 \right) {{\Gamma }_{2}}\left( 8 \right) }=132237685800$. The graphs of PDFs are given by Figs. 1a, b, 2a, and b, where the vertical scales are different.

Fig. 1

The PDF of the latent roots of ${{\mathbf {U}}^{2}}$ and ${{\mathbf {U}}^{-2}}$, where $\mathbf {U}\, \sim \, Beta_{2}^{I}\left( 10,8 \right)$

Fig. 2

The PDF of the latent roots of ${{\mathbf {V}}^{2}}$ and ${{\mathbf {V}}^{-2}}$, where $\mathbf {V}\, \sim \, Beta_{2}^{II}\left( 10,8 \right)$

4 Applications

4.1 Applications in MANOVA

Both matrix beta variates have found applications in MANOVA, for testing various hypotheses there. Pham-Gia (2008) showed the use of Wilks’s statistic $\Lambda$, which is the determinant of $\mathbf {U}$, in testing ${{H}_{0}}:{{}_{{}}}{{\mu }_{1}}=\dots ={{\mu }_{k}}$ in ${{\mathbb {R}}^{p}}$, with numerical computations using Meijer functions. Other tests include: Independence between k sets of variables and test based on partitioning the total variations and error matrices. Rencher and Christensen (2012) gives an example of using $\Lambda$, to test the equal mean growths of six apple tree varieties, based on rootstock data, which consists of 48 observations of dimension 4, collected between 1918 and 1934. Several other tests are based on latent roots of the Beta matrix variates (Lawley 1938; Roy 1953; Pillai 1954 etc.).

4.2 The posterior distribution in Bayesian analysis

In the univariate case we know that the Beta of the first kind is conjugate to binomial sampling, i.e. for the proportion $\pi$ with a beta prior distribution, $\pi \sim Beta_{1}^{I}\left( a,b \right)$, with x successes out of n trials, we have the posterior distribution of $\pi$ as $Beta_{1}^{I}(a+x, b+n-x)$. The explicit expressions of the densities of ${{\pi }^{m}}$ and ${{\pi }^{-m}}$ obtained earlier, will also allow us to determine the highest posterior density (HPD) interval (see Sect. 4.3) for $W={{\pi }^{m}}$ or ${{\pi }^{-m}}$, if we start with a power of $\pi$, instead of $\pi$ itself. By using algorithm in Turkkan and Pham-Gia (1993) we can compute this interval, which cannot be determined from the HPD interval of $\pi$.

Let $W={{\pi }^{2}}$, for example, be the parameter of interest in the Bernoulli model. Suppose $\pi$ has the Beta of the first kind $Beta_{1}^{I}\left( \alpha ,\beta \right)$, here $Beta_{1}^{I}\left( 5,7 \right)$, as prior. Then by (3), W has as prior the density

$$\begin{aligned} f\left( w|data \right) =\frac{{{\left( \sqrt{w} \right) }^{3}}{{\left( 1-\sqrt{w} \right) }^{6}}}{2B\left( 5 ,7 \right) }, 0<w<1, \end{aligned}$$

a result which is difficult to obtain directly. Suppose binomial sampling gives x successes out of n trials, then the posterior distribution of $\pi$ is $Beta_{1}^{I} \left( 5 +x, 7 +n-x\right)$, and, again by (3), the posterior distribution of W is

$$\begin{aligned} f(w)=\frac{{{\left( \sqrt{w} \right) }^{3 +x}}{{\left( 1-\sqrt{w} \right) }^{6+n-x}}}{2B\left( 5+x,7+n-x\right) },0<w<1. \end{aligned}$$

Let the sampling results be $n=10,x=4$. We then have posterior distribution of $\pi$ is $Beta_{1}^{I}\left( 9,13 \right)$ and posterior density of W is $f\left( w\right) =\frac{{{\left( \sqrt{w} \right) }^{7}}{{\left( 1-\sqrt{w}\right) }^{12}}}{2B\left( 9,13 \right) },0<w<1$. Graphs of the PDFs of the priors of $\pi$ and ${{\pi }^{2}}$ and given by Fig. 3a, and those of the posteriors by Fig. 3b.

Fig. 3

The PDFs of the priors and the posteriors of $\pi$ and ${W={\pi }^{2}}$, where $\pi \,\sim \, Beta_{1}^{I}\left( 5,7 \right)$

4.3 Interval estimation of the product of latent roots and distributions of geometric means

4.3.1 Highest probability density interval

Latent roots of square random matrices have been in use in multivariate statistics for a long time and, lately, have seen an important role in theoretical physics where they represent different levels of energy. Here, we consider the product of latent roots and compute its credible interval. This interval is different from the classical confidence interval which comes from a sample of observations. Here, we consider the probability density of the parameter, or product of parameters, and search for an interval with $\left( 1-\alpha \right) 100\%$ probability in which this parameter would lie. Furthermore, the interval should have the property that any point inside it has a higher probability than any point outside it. It is called highest probability density interval (HPD) and one algorithm given to derive it is Turkkan and Pham-Gia (1993) for the univariate case. Turkkan and Pham-Gia (1997) treats the bivariate case. Computation of the HPD interval is particularly interesting in the case of multimodal densities, where the algorithm would return a set of disjoint intervals.

Let $\mathbf {U} \sim Beta_{p}^{I}\left( a,b \right)$ having p latent roots $1>{{\lambda }_{1}}>\dots>{{\lambda }_{p}}>0$ and let $\mathbf {V} \sim Beta_{p}^{II}\left( a,b \right)$ having p latent roots ${{l}_{1}}>{{l}_{2}}>\dots>{{l}_{p}}>0$. Firstly, we have $\left| \mathbf {U} \right| =\prod \nolimits _{i=1}^{p}{{{\lambda }_{i}}}$, and hence the $\left( 1-\alpha \right) 100\%$ HPD interval $\left( c,d \right)$ for the product $\prod \nolimits _{i=1}^{p}{{{\lambda }_{i}}}$ is the $\left( 1-\alpha \right) 100\%$ HPD interval for $\left| \mathbf {U} \right|$. For example, for $p=2$, $\mathbf {U} \sim Beta_{2}^{I}\left( 10,8 \right)$, the $90\%$ HPD interval of the product ${{\lambda }_{1}}{{\lambda }_{2}}$ is $\left( 0.1529914846, 0.4463566639\right)$, given by Fig. 4a, while the bivariate PDF of $\left\{ {{\lambda }_{1}},{{\lambda }_{2}} \right\}$ is the Eq. (16) where $p=2$. Similarly, for any value of p, the $\left( 1-\alpha \right) 100\%$ HPD interval for the product ${{\left( \prod \nolimits _{i=1}^{p}{{{\lambda }_{i}}} \right) }^{m}}$ of latent roots is the HPD interval for ${{\left| \mathbf {U} \right| }^{m}}$. We note that the HPD interval $\left( {c}^{\prime },{d}^{\prime } \right)$ of ${{\left( \prod \nolimits _{i=1}^{p}{{{\lambda }_{i}}} \right) }^{m}}$ cannot be determined from the HPD interval $\left( c,d \right)$ of $\prod \nolimits _{i=1}^{p}{{{\lambda }_{i}}}$ because $\left( {c}^{\prime },{d}^{\prime } \right)$ is different from $\left( {{c}^{m}},{{d}^{m}} \right)$. For example, for $\mathbf {U} \sim Beta_{2}^{I}\left( 10,8 \right)$, the $90\%$ HPD interval of ${{\left( {{\lambda }_{1}}{{\lambda }_{2}} \right) }^{2}}$, Fig. 4b, is (0.007566535046, 0.2471269211) different from

$$\begin{aligned} \left( {0.1529914846}^{2}, {0.4463566639}^{2}\right) =\left( 0.02337, 0.19918\right) . \end{aligned}$$

Similar results can be obtained for ${{\left( \prod \limits _{i=1}^{p}{{{\lambda }_{i}}} \right) }^{-m}}$, ${{\left( \prod \limits _{i=1}^{p}{{{l}_{i}}} \right) }^{m}}$, and ${{\left( \prod \limits _{i=1}^{p}{{{l}_{i}}} \right) }^{-m}}$.

Fig. 4

The $90\%$ credible interval of ${{\lambda }_{1}}{{\lambda }_{2}}$ and ${{\left( {{\lambda }_{1}}{{\lambda }_{2}} \right) }^{2}}$

4.3.2 Distributions of geometric means

Pillai (1955) suggested three test criteria to be used in MANOVA, which are based on the harmonic means: ${{H}^{\left( p \right) }}=p{{\left\{ \sum \limits _{i=1}^{p}{{{\left( 1-{{\lambda }_{i}} \right) }^{-1}}} \right\} }^{-1}}$, ${{R}^{\left( p \right) }}=p{{\left\{ \sum \limits _{i=1}^{p}{\lambda _{i}^{-1}} \right\} }^{-1}}$, and ${{T}^{\left( p \right) }}=p{{\left\{ \sum \limits _{i=1}^{p}{l_{i}^{-1}} \right\} }^{-1}}$. Here, we consider the distributions of geometric means, $G{{M}_{I}}={{\left( \prod \limits _{i=1}^{p}{{{\lambda }_{i}}} \right) }^{1/p}}$ and $G{{M}_{II}}={{\left( \prod \limits _{i=1}^{p}{{{l}_{i}}} \right) }^{1/p}}$ as two new test criteria for MANOVA. Their interval estimation can be made, as before, by relations $\left| \mathbf {U} \right| =\prod \limits _{i=1}^{p}{{{\lambda }_{i}}}$, $\left| \mathbf {V} \right| =\prod \limits _{i=1}^{p}{{{l}_{i}}}$ since we have the PDFs of $G{{M}_{I}}$ and $G{{M}_{II}}$ given by Eqs. (13) and (15) where $m=\tfrac{1}{p}$ (since we are dealing with the determinant, a real value, m can take a non-integral value here). For example, let $p=3$ and $\mathbf {U}\,\sim \,Beta_{3}^{I}\left( 10,8 \right)$. The PDFs of $\left| \mathbf {U} \right| ={{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{3}}$ and $G{{M}_{I}}={{\left( {{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{3}} \right) }^{1/3}}$ are given by Fig. 5, and similar computations of their HPD intervals can be carried out like previously. Similar computations can be carried out for $\left| \mathbf {V} \right| =\prod \limits _{i=1}^{p}{{{l}_{i}}}$ and $G{{M}_{II}}={{\left( \prod \limits _{i=1}^{p}{{{l}_{i}}} \right) }^{1/p}}$.

Fig. 5

The PDFs of $\left| \mathbf {U} \right| ={{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{3}}$ and $G{{M}_{I}}={{\left( {{\lambda }_{1}}{{\lambda }_{2}}{{\lambda }_{3}} \right) }^{1/3}}$, $\mathbf {U}\,\sim \,Beta_{3}^{I}\left( 10,8 \right)$

5 Conclusion

This article has presented the expressions of the densities associated with integral powers of the central Beta matrix variates, under three frequently considered types: entries, determinant and latent roots. Various applications to different topics in statistics: multivariate analysis, matrix variate analysis, and in random matrix theory, can be readily made from the results given here.