Multiple treatment comparisons in analysis of covariance with interaction

Abstract

When multiple treatments are analyzed together with a covariate, a treatment-covariate interaction complicates the interpretation of the treatment effects. The construction of simultaneous confidence bands for differences of the treatment specific regression lines is one option to proceed. The application of these methods is difficult because they are described as a collection of special cases and the implementation requires additional programming or relies on non-standard or proprietary software. If inferential interest can be restricted to a pre-specified set of covariate values, a flexible alternative is to compute simultaneous confidence intervals for multiple contrasts of the treatment effects over this grid. This approach is available in the R software: next to treatment differences in the linear model, approximate simultaneous confidence intervals for ratios of expected values and asymptotic extensions to generalized linear models are straightforward. The paper summarizes the available methodology and presents three case studies to illustrate the application to different models, differences and ratios, as well as different types of between treatment comparisons. Simulation studies in the general linear model, for different parameters and different types of comparisons are provided. The R code to reproduce the case studies and a hint to a related R package is provided.

1 Introduction

In linear models, the effects of a classification variable, e.g., the indicator for two or several treatments, can be modeled together with that of covariates. The presence of a significant overall treatment-covariate interaction complicates the interpretation of treatment effects: the significance, magnitude or even direction of the treatment effects depends on the value of the covariate. Nevertheless, the primary objective can be the comparison of the treatments. Often not all possible comparisons but only a special subset of treatment comparisons are of interest. A simplistic approach is to perform these multiple treatment comparisons for one fixed value of the covariate, e.g., the overall mean of the covariate. A more detailed comparison of treatments is provided by methods that yield confidence bands for differences between the treatment-specific regression lines. However, the practical application of such methods is complicated by the fact that they are described as many separate special cases. The focus of this work is on a flexible and user-friendly alternative that is computationally available in free software: simultaneous confidence intervals for multiple contrasts among treatments for a set of pre-specified values of the covariate.

A multitude of publications consider the construction of simultaneous confidence bands for (multiple) differences of regression lines, and it is difficult to review all methodological special cases completely. The methods differ in the number of treatments and the set of contrasts between treatments that can be handled; they differ in whether restrictions are imposed on the treatment specific subsets of the design matrix, the number of covariates and the considered range of the covariate. Most methods have in common that they are based on the assumptions of the general linear model. The very general and easily applicable method by Scheffe (1959) can be used to construct exact simultaneous confidence intervals for all possible contrasts. However, in many applications a restricted set of contrasts among the treatments and a restricted range of the covariates is of interest a priori, for example, all pairwise comparisons, comparisons to a control, special user-defined contrasts or one-sided comparisons. Then, the Scheffe method yields unnecessarily conservative confidence bands. Alternative solutions are provided for all contrasts but a restricted range of covariates (Spurrier 1999; Lu and Chen 2009; Jamshidian et al. 2010). Confidence bands for all pairwise differences and differences to control among several treatments have been proposed (Spurrier 2002; Bhargava and Spurrier 2004), however, under restrictive assumptions concerning the equality of the treatment specific design matrices. In a paper addressing various problems (Liu et al. 2004), a number of numerical approaches is described for all pairwise differences and differences to control with three or more treatment groups, several covariates, and, importantly, without severe restrictions on the design matrices. In a recent book (Liu 2010), a number of these approaches is described again. However, all these previous publications concerning exact simultaneous confidence bands have two practical problems: the computational methods are split up in a number of special cases, described in special publications or book chapters, and, more severely, putting the computation of the critical values into practice usually requires the additional programming of the described algorithms or relies on non-standard or proprietary software packages (Jamshidian et al. 2005).

Alternatively, one may restrict inference to a pre-specified set of covariate values and construct simultaneous confidence intervals (SCI) for multiple comparisons among the treatments for this set of values. This approach will not lead to simultaneous confidence bands for all possible covariate values. But it still allows a more detailed interpretation of the treatment effects in case of an interaction than do global tests like the ANOVA-F-test, and treatments can be compared in terms of multiple contrasts which are tailored for the particular experimental question (Bretz et al. 2001). Standard problems as all pairwise comparisons and comparisons to control are contained as special cases. Asymptotically, this approach can be used in generalized linear models (Hothorn et al. 2008), or, treatment effects may be expressed as ratios instead of differences, using approaches of Young et al. (1997) and Dilba et al. (2006). The computational methods to obtain adequate quantiles of multivariate t and multivariate normal distributions are available in the package mvtnorm (Genz et al. 2011) in the R software. For a number of special cases, this approach has been applied recently: Bretz et al. (2010, p. 111–114) and, with different computational details, Westfall et al. (2011) show the application to the comparison of two regression lines. Herberich et al. (2014) consider the comparison of differently shaped curves, fitted by splines, between several treatment groups in presence of repeated measurements from the same subject, including a simulation study customized for this special application.

This manuscript recapitulates the methods to construct simultaneous confidence intervals for multiple contrasts among the treatments for a pre-specified set of covariate values. Approximate extensions to generalized linear models multiple ratios are described. A simulation study is presented to assess the validity of the methods for differences and ratios in the general linear model. Three examples illustrate the application, including all pairwise differences, comparisons to a control in terms of ratios in a model including an interaction to the quadratic term, as well as all pairwise comparisons in log logistic model assuming a binomial response.

2 Material and methods

Consider the general linear model

$$\begin{aligned} {\varvec{y}} = \mathbf{X}{\varvec{\theta }} + {\varvec{e}}, \end{aligned}$$

(1)

where ${\varvec{y}}$ is an $(N \times 1)$ vector of observations, $\mathbf{X}$ is an $(N \times P)$ design matrix, ${\varvec{\theta }}$ is a $(P \times 1)$ parameter vector with index $p=1,\ldots , P$, and ${\varvec{e}}$ an $(N \times 1)$ vector of residuals. The residuals are assumed to be identically Gaussian distributed, $e_{n} \sim N(0, \sigma ^{2})$, independently for $n=1,\ldots ,N$. Fitting the model yields the estimate $\hat{{\varvec{\theta }}}$ and the corresponding $(P \times P)$ covariance matrix $\hat{{\varvec{\varSigma }}}$.

2.1 SCI for linear combination of parameters

Under the assumption of an independent, homogeneous Gaussian error distribution, the estimates $\hat{{\varvec{\theta }}}$ follow a multivariate normal distribution. The predictions $\hat{{\varvec{y}}}={\varvec{X}}\hat{{\varvec{\theta }}}$, linear combinations thereof, or other linear combinations of the model parameters follow a multivariate normal distribution as well. Simultaneous confidence intervals for M linear combinations of the P model parameters can be constructed using quantiles of the multivariate t distribution with degree of freedom $N-P$, or, asymptotically, using multivariate normal quantiles (Genz et al. 2011; Hothorn et al. 2008). The general methodology according to Hothorn et al. (2008) is:

Let $\mathbf{C}$ be a $(M\times P)$ matrix with elements $c_{mp}$, $m=1,\ldots ,M$, which define M linear combinations of the P model parameters, ${\varvec{\delta }}=\mathbf{C}{\varvec{\theta }}$. An estimate for ${\varvec{\delta }}$ is $\hat{{\varvec{\delta }}}=\mathbf{C}\hat{{\varvec{\theta }}}$. The $(M\times M)$ covariance matrix of $\hat{{\varvec{\delta }}}$ can be estimated by $\hat{\mathbf{V}}=\mathbf{C}\hat{{\varvec{\varSigma }}}{} \mathbf{C}^{T}$, where $^{T}$ denotes a transposed matrix. Denote the diagonal elements of $\hat{\mathbf{V}}$ by $\hat{{\varvec{v}}}=(\hat{v}_{11},\hat{v}_{22},\ldots ,\hat{v}_{MM})$. Standardizing the covariance matrix $\hat{\mathbf{V}}$ by its diagonal elements yields the correlation matrix $\hat{\mathbf{R}}$ with elements $r_{mm'}$, i.e., $r_{mm'}=\hat{v}_{mm'}\hat{v}_{mm}^{-1/2}\hat{v}_{m'm'}^{-1/2}$.

The lower and upper limits, $\hat{\delta }_{m}^{(l)},\hat{\delta }_{m}^{(u)}$, of simultaneous 95% confidence intervals for the M linear combinations can be constructed by

$$\begin{aligned} \left[ \hat{\delta }_{m}^{(l)}, \hat{\delta }_{m}^{(u)}\right] = \left[ \hat{\delta }_{m} \pm t_{0.95, \hat{\mathbf{R}}, df=N-P}\hat{v}_{mm}^{-1/2} \right] , \end{aligned}$$

where $\hat{\delta }_{m}$ is the $m\hbox {th}$ element of $\hat{{\varvec{\delta }}}$ and $t_{0.95, \hat{\mathbf{R}}, df=N-P}$ is an appropriate two-sided 0.95 quantile of the multivariate t distribution as is computable using the R–package mvtnorm (Genz et al. 2011): $P\left( \left| t_{m}\right| <t_{0.95, \hat{\mathbf{R}}, df=N-P}, \forall m=1,\ldots ,M \right) =0.95$, where ${\varvec{t}}=\left( t_{1},\ldots , t_{M}\right) ^{T}$ is a central M-variate t random vector with degree of freedom $N-P$ and correlation $\hat{\mathbf{R}}$. When interest is in one-sided intervals, a quantile $t_{0.95, \hat{\mathbf{R}}, df=N-P}$ has to be chosen such that

$$\begin{aligned} P\left( t_{m}<t_{0.95, \hat{\mathbf{R}}, df=N-P}, \forall m=1,\ldots ,M \right) =0.95. \end{aligned}$$

The methods implemented in mvtnorm can deal with complicated structures of $\hat{\mathbf{R}}$, including the case that $\hat{\mathbf{R}}$ has not full rank. This case is important for the following applications, where confidence sets are constructed for substantially more linear combinations than there are elements in the parameter vector, that is $P<M$. Note that M is bounded at 1000 in this implementation. For the computational details, see Genz and Bretz (2009). An implementation of the complete method relying on a fitted model object and a corresponding contrast matrix $\mathbf{C}$, is available in the R–package multcomp (Hothorn et al. 2008).

These intervals are simultaneous 95% confidence intervals, i.e., the probability that at least one of the M true parameters $\mathbf{\delta }$ is not included, is smaller than 5%, $P(\hat{\delta }_{m}^{(l)} \le \delta _{m}\le \hat{\delta }_{m}^{(u)}, \forall m=1,\ldots ,M) = 0.95$. Corresponding hypotheses tests for a hypothetical parameter $\delta _{m0}$, $H_{0}:\cap _{m=1}^{M} \delta _{m}=\delta _{m0}$ versus $H_{1}: \cup _{m=1}^{M} \delta _{m} \ne \delta _{m0}$ can be rejected if at least one of the hypothesized parameters is excluded by the corresponding lower or upper bounds, $\hat{\delta }_{m}^{(l)} > \delta _{m0}$ or $\delta _{m0}> \hat{\delta }_{m}^{(u)}$ for at least one m. For such tests, the familywise error rate (FWER) is controlled in the strong sense (Hothorn et al. 2008), that is, the probability of erroneously excluding at least one of the true hypothesized parameters is $= 0.05$, irrespective of which of the remaining $\delta _{m0}$ are true.

2.2 Differences on the link scale of generalized linear models

Asymptotically, the above methodology can be applied to the scale of the linear predictor in generalized linear models. Consider the systematic part of a generalized linear model,

$$\begin{aligned} g({\varvec{\mu }}) = {\varvec{\eta }} = \mathbf{X}{\varvec{\theta }}, \end{aligned}$$

(2)

where ${\varvec{\theta }}$ is parameterized as above, and g() is the link function. Relying on the asymptotic normality of $\hat{{\varvec{\theta }}}$ (McCulloch and Searle 2001; Hothorn et al. 2008), the methods described in Sect. 2.1 can be applied as well with the exception that a quantile $z_{M, 0.95, \hat{\mathbf{R}}}$ will be taken from the multivariate normal distribution with dimension M, correlation matrix $\hat{\mathbf{R}}$. The resulting intervals are constructed for differences on the scale of the linear predictor, ${\varvec{\eta }}$.

2.3 Multiple ratios in the general linear model

In the general linear model in Eq. (1), treatment effects may be expressed in terms of ratios instead of differences (Zerbe 1978; Young et al. 1997; Djira 2010). Their methods are briefly reviewed in the following: the parameters of interest are M ratios $\gamma _{m} = \left( {\varvec{c}}_{m}{\varvec{\theta }}\right) {/}\left( {\varvec{d}}_{m}{\varvec{\theta }}\right)$, $m=1,\ldots ,M$. The known coefficients in the vectors ${\varvec{c}}_{m}=\left( c_{m1},\ldots ,c_{mP}\right)$ and ${\varvec{d}}_{m}=\left( d_{m1},\ldots ,d_{mP}\right)$ define which linear combinations of ${\varvec{\theta }}$ are to be compared in the $m\hbox {th}$ ratio. They are summarized in the two $(M\times P)$ matrices $\mathbf{C}$ and $\mathbf{D}$, with elements $c_{mp}$ and $d_{mp}$, respectively. To construct simultaneous confidence intervals for $\gamma _{1},\ldots ,\gamma _{M}$, consider $W_{m} = \left( {\varvec{c}}_{m} - \gamma _{m}{\varvec{d}}_{m}\right) \hat{{\varvec{\theta }}}$. The joint distribution of $W_{m}$ is M-variate normal with covariance matrix $\mathbf{U}$, with elements $u_{mm'}$ given in Eq. (3):

$$\begin{aligned} u_{mm'}=Cov\left( W_{m}, W_{m'}\right) =\left( {\varvec{c}}_{m} - \gamma _{m}{\varvec{d}}_{m}\right) {\varvec{\varSigma }} \left( {\varvec{c}}_{m'} - \gamma _{m'}{\varvec{d}}_{m'}\right) ^{T}. \end{aligned}$$

(3)

$\mathbf{U}$ depends on the unknown ratios, an estimate, $\hat{\mathbf{U}}$, can be obtained by evaluating Eq. (3) at the estimates $\hat{\gamma }_{m} = {\varvec{c}}_{m}\hat{{\varvec{\theta }}}/{\varvec{d}}_{m} \hat{{\varvec{\theta }}}$ and $\hat{{\varvec{\varSigma }}}$ (Dilba et al. 2006; Djira 2010). The corresponding correlation matrix $\hat{\mathbf{R}}$ can be obtained by standardizing $\hat{\mathbf{U}}$ by its diagonal elements. That is, the elements $\hat{\rho }_{mm'}$ of $\hat{\mathbf{R}}$ are then: $\hat{\rho }_{mm'}=\hat{u}_{mm'} \hat{u}_{mm}^{-1/2} \hat{u}_{m'm'}^{-1/2}$. Approximate simultaneous 95% Fieller-type confidence intervals can be obtained by solving the corresponding inequalities

$$\begin{aligned} \frac{\left[ \left( {\varvec{c}}_{m} - \gamma _{m}{\varvec{d}}_{m}\right) \hat{{\varvec{\theta }}}\right] ^{2}}{\left( {\varvec{c}}_{m} - \gamma _{m}{\varvec{d}}_{m}\right) \hat{{\varvec{\varSigma }}}\left( {\varvec{c}}_{m} - \gamma _{m}{\varvec{d}}_{m}\right) ^{T}} \le t_{0.95, M, df=N-P, \hat{\mathbf{R}}}^{2} \end{aligned}$$

(4)

for $\gamma _{m}$ (Djira 2010). Note, that the resulting intervals may be unbounded, that is, there might be no solution, or solutions that are not easily interpretable. The method is approximate because the critical value for inverting the test in Eq. (4), $t_{0.95, M, df=N-P, \hat{\mathbf{R}}}^{2}$ depends on the unknown parameters of interest via the plug-in of the estimates $\hat{\gamma }_{m}$ to obtain the correlation matrix, $\hat{\mathbf{R}}$. These methods are implemented in the function gsci.ratio in the R–package mratios (Djira et al. 2011).

2.4 Simultaneous confidence intervals over a grid of covariate values: multiple differences between treatments

The above methods can be applied to compare multiple treatments over a pre-specified grid of covariate values. It is assumed that interest is only in a fixed range of the covariate, and that the grid of covariate values spans this range, i.e., the limits of the range of interest are the minimal and maximal values of the covariate grid. What remains is to formulate $\mathbf{C}$ for a given model parameter ${\varvec{\theta }}$ such that ${\varvec{\delta }}$ defines the comparison of model predictions between treatments for a number of different values of the covariate x. This involves to consider how treatment and treatment-covariate interaction are parameterized in ${\varvec{\theta }}$, the definition of a set of covariate values, and the definition of the type of treatment comparisons of interest. As a simple introduction, denote the index of I treatments with $i=1,\ldots ,I$, and denote $j=1,\ldots ,J_{i}$ as the index of replications of treatment i, such that an experimental unit is identified by ij. The observed values of the covariate and dependent variable in unit ij are denoted $x_{ij}$ and $y_{ij}$, respectively, and the model (Eq. 5) involves treatment specific intercepts $\alpha _{i}$ and slopes $\beta _{i}$,

$$\begin{aligned} y_{ij} = \alpha _{i} + \beta _{i}x_{ij} + e_{ij}, \quad e_{ij} \sim N(0, \sigma ^2), \end{aligned}$$

(5)

where the parameter vector first contains the I intercepts followed by the I slopes, ${\varvec{\theta }}=\left( \alpha _{1},\ldots ,\alpha _{I},\beta _{1},\ldots ,\beta _{I}\right) ^{T}$. Denote by Q the number of positions of x for which the treatment specific regression lines should be compared, and the actual values by $\tilde{{\varvec{x}}}=\left( \tilde{x}_{1},\ldots ,\tilde{x}_{Q}\right)$, with index $q=1,\ldots ,Q$. Lastly, let $\mathbf{A}$ define a $(K \times I)$ matrix where the rows $k=1,\ldots ,K$ define the K comparisons of interest between the I treatments. If the parameters in ${\varvec{\delta }}$ should be interpretable as differences of (weighted arithmetic means) of the treatment specific regression lines for the covariate positions $\tilde{{\varvec{x}}}$, the coefficients $a_{ki}$ should be defined under the constraints $\sum _{i=1}^{I}a_{ki}=0$ and $\sum _{i:a_{ki}>0}a_{ki}=1$ for each row $k=1,\ldots ,K$. The $M=QK$ comparisons of interest can then shortly be written as

$$\begin{aligned} \mathbf{C} = \left( \begin{array}{cc}{\varvec{1}}_{Q}&\tilde{{\varvec{x}}}\end{array}\right) \otimes \mathbf{A}, \end{aligned}$$

(6)

where $\otimes$ denotes the Kronecker product and ${\varvec{1}}_{Q}$ denotes a column vector of 1s of length Q. As an illustration, consider a case with $Q=4$ covariate values of interest, $\tilde{{\varvec{x}}}=\left( 5,10,15,20\right) ^{T}$ and the $K=2$ comparisons to the control group ($i=1$) when there are $I=3$ treatment groups:

$$\begin{aligned} \mathbf{C} = \left( \begin{array}{cc} 1 &{}\quad 5\\ 1 &{}\quad 10\\ 1 &{}\quad 15\\ 1 &{}\quad 20\\ \end{array}\right) \otimes \left( \begin{array}{ccc} -1 &{}\quad 1 &{}\quad 0 \\ -1 &{}\quad 0 &{}\quad 1 \\ \end{array}\right) = \left( \begin{array}{cccccc} -1 &{}\quad 1 &{}\quad 0 &{}\quad -5 &{}\quad 5 &{}\quad 0 \\ -1 &{}\quad 0 &{}\quad 1 &{}\quad -5 &{}\quad 0 &{}\quad 5 \\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ -1 &{}\quad 1 &{}\quad 0 &{}\quad -20 &{}\quad 20 &{}\quad 0 \\ -1 &{}\quad 0 &{} \quad 1 &{}\quad -20 &{}\quad 0 &{}\quad 20 \\ \end{array}\right) . \end{aligned}$$

(7)

2.5 Multiple ratios and odds ratios in generalized linear models

In the important case of dichotomous observations, modeled in a generalized linear model with the binomial distribution (or related assumptions) and the canonical logit link, the resulting confidence bounds can be transformed by the $\exp$ function and can then be interpreted as intervals for odds ratios between the predicted treatment specific odds at $\tilde{x}_{1},\ldots , \tilde{x}_{Q}$. Similarly, for count data modeled with the Poisson distribution or related assumptions and the canonical log link, the $\exp$ transformation of the confidence bounds leads to confidence bounds for ratios of means between the treatments at $\tilde{x}_{1},\ldots , \tilde{x}_{Q}$.

2.6 Multiple ratios of model predictions in the general linear model

The matrices of coefficients for the numerator and denominator, $\mathbf{C}$ and $\mathbf{D}$ can be defined in a similar way as described for the difference in Sect. 2.4. For the model in Eq. (5) with the parameterization ${\varvec{\theta }}=\left( \alpha _{1},\ldots ,\alpha _{I},\beta _{1},\ldots ,\beta _{I}\right) ^{T}$, the K ratios among the I treatments can be defined in two $(K \times I)$ matrices $\mathbf{A}$ and $\mathbf{B}$, for the numerator and the denominator, respectively. The $M=QK$ ratios of interest for Q positions of x can then shortly be written as

$$\begin{aligned} \mathbf{C} = \left( \begin{array}{cc}{\varvec{1}}_{Q}&\tilde{{\varvec{x}}}\end{array}\right) \otimes \mathbf{A}, \text{ and } \mathbf{D} = \left( \begin{array}{cc}{\varvec{1}}_{Q}&\tilde{{\varvec{x}}}\end{array}\right) \otimes \mathbf{B}. \end{aligned}$$

(8)

An illustration for a slightly more complicated model is given in Example 4.2.

2.7 Simulation study

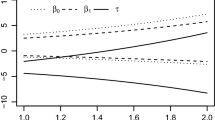
Given that only a fixed range of the covariate is of interest, and the set of covariate values $(\tilde{x}_{1},\ldots , \tilde{x}_{Q})$ spanning this range is pre-specified, the above methods will control the simultaneous coverage probability (e.g., Bretz et al. 2001; Hothorn et al. 2008; Bretz et al. 2010; Djira 2010) for the family of the resulting M parameters of interest (Fig. 1 left panel). In many applications, such a coarse grained interpretation of the treatment-covariate-interaction will be sufficient. If the number of contrasts between treatments, K, is not large, say $K<20$, even rather dense grids of $Q=50$ covariate values can be computed given the computational limitation of $KQ=M<1000$ in the package mvtnorm.

It may still be tempting to perform the computations of the multivariate t quantile for a limited number of covariate values, Q, spanning the covariate range of interest, but then to perform inference for any possible covariate value in that range. That means to interpret the simultaneous confidence intervals as if a simultaneous confidence band for all values in the pre-specified covariate range had been constructed: First, adjacent confidence limits for a given between-treatment comparison may be joined by lines (Fig. 1, middle), this will be referred to as linear interpolation. Second, one may use the quantile of the multivariate t or normal distribution that has been computed for a limited number (Q) of covariate values that span the pre-specified covariate range of interest. This ’approximated’ quantile may be used for computing a smooth confidence band over the range of interest (Fig. 1, right), for a much larger set of covariate values than has been used for computing the quantile; this will be referred to as quantile approximation. For such approximations of confidence bands and subsequent interpretations for any possible value of x in the given range of the covariate, the simultaneous coverage probability of the nominal level 0.95 is not guaranteed for all cases. However, depending on the complexity of the model, on using differences or ratios and depending on the number of grid points Q, the extent and direction of violation of the nominal coverage probability may change:

In case that the true functions of interest are straight lines depending on the covariate (e.g. differences between treatment specific regression lines in model Eq. (5) or Example 4.1), it is clear from Fig. 1, that the linear interpolation will yield simultaneous confidence bands that have slightly too much content and might be slightly conservative, if only few covariate values are used. If one uses the quantile approximation in this case, using too few equidistant values spanning the pre-specified range of the covariate when computing the quantile, will yield a liberal confidence band. However, for a large number of grid points, Q, the simultaneous coverage probability of both approaches should be close to the nominal simultaneous confidence, as suggested for discrete confidence bands for the difference of two treatments (Bretz et al. 2010).

In case that the true functions of interest are no straight lines depending on the covariate, a larger number of covariate values, Q, will be needed to yield an interpretation that is close to a simultaneous confidence band for all values in the pre-specified covariate range. Such cases are, for example, ratios of regression lines or differences of quadratic regressions per treatment (Example 4.2), or the more ambitious problem of comparing splines between several treatments as considered by Herberich et al. (2014).

Fig. 1

Point wise interpretation at $Q=6$ grid points, linear interpolation between adjacent confidence limits in the covariate range [0; 10] and construction of a confidence band over that fixed range, by using the approximate quantile for only six points. Black lines and symbols show the true difference between two predicted lines, gray shows model estimates and corresponding confidence limits

A simulation study has been performed to illustrate that with increasing Q, practically valid simultaneous confidence bands can be constructed: the model in Eq. (5), has been used to simulate data with $x_{ij}$ sampled from the uniform distribution, with number of treatment groups $I=3$ or 6, sample sizes of $n_{i}=5,10,20$ or 100 per treatment group, and parameter configurations involving intercepts and slopes equal, either slopes or intercepts differing between treatments or both intercepts and slope differing between treatments. For each simulated data sets, the methods described above have been applied for comparisons to control (referred to as Dunnett), all pairwise comparisons (referred to as Tukey) and comparisons of each treatment to the average of treatments (referred to as GrandMean), combined with a set of $Q=3,6,10,$ or 20 equidistant grid points spanning the pre-specified covariate range. For each combination of parameter setting and each method, 5000 data sets have been simulated such that the estimated simultaneous coverage probability for an exact 0.95 simultaneous confidence set can be expected to fall within [0.944; 0.956] with a probability 0.95.

More complications arise if the treatment difference of interest is not a linear function depending on the covariate, for example, when the model involves a treatment-interaction with a quadratic term, as in Example 4.2. In this situation, the point wise interpretation of between treatment differences is still exact, whereas it is obviously unwise to use the linear interpolation with only few covariate values. In this case, the quantile approximation can be supposed to be the better choice to approximate confidence bands. Yet more complications arise when using the ratio approach described in Sect. 2.3: even for the point wise interpretation, the small sample performance is not clear because the method involves the plug-in of an estimated correlation matrix that depends on the estimated ratios of interest. For this reason, the ratio approach has been simulated for model (5) and the parameter and sample size settings described above. Moreover, a model involving treatment-specific intercepts, slopes, and quadratic terms, $y_{ij} = \alpha _{i} + \beta _{1i}x_{ij} + \beta _{2i}x_{ij}^{2} + e_{ij}$ has been simulated for the sample size settings described above. The parameter settings involved cases without any treatment effect, as well as treatment interactions w.r.t to the linear and/or the quadratic term. For $Q=3, 6, 10$, and 20, ratios (middle row of Fig. 3) and differences (lower row of Fig. 3) between model predictions over a covariate grid have been considered. The full details of the simulation settings are provided as supplementary material, part A, which is also available from the GitHub repository.

2.8 Software

The methods can be applied in R (Team 2014) with a few lines of code using basic functionality of R and the add-on packages mvtnorm (Genz et al. 2011), multcomp (Hothorn et al. 2008) and mratios (Djira et al. 2011). The code for applying the above methods will involve the model fit, the definition of the treatment contrasts of interest and the grid of covariate values, their combination by the Kronecker product, and the computation of simultaneous confidence intervals. For the figures, the R package ggplot2 (Wickham 2009) has been used. The R code for the examples shown below is provided as supplementary material part B.

For even simpler application, the R package statintcov is provided on the GitHub repository: the special case of a linear model with one treatment factor and interaction to one covariate (Eq. 5) is covered in the functions scitreatcov, sciratiotreatcov, for differences and ratios, respectively. For slightly more general cases, involving generalized linear models, more than one covariate or interactions with quadratic terms as exemplified in Sect. 4.2, the functions cmiacov and cmratioiacov can be used to supply linear combinations of the parameters of a fitted model that are suitable for further use in the function glht of package multcomp or in function gsci.ratio of package mratios. The R code for the analysis of the examples using this package is provided as supplementary material part C. Recently, Lenth (2016) provided the R–package lsmeans which allows to apply the methods for differences of regression lines in a very versatile way, when combined with the multcomp package.

3 Results

For the simple model involving only treatment specific intercepts and slopes and inference in terms of differences, simulated simultaneous coverage probabilities are shown in Fig. 2: the linear interpolation provides confidence bands with adequate coverage probabilities already for small numbers of covariate values, such as $Q=3$ or 6, irrespective of the type of treatment contrast, the number of treatment groups or the sample size settings. When using the multivariate t quantile computed for only $Q=3$ or 6 equidistant values in the covariate range, constructed confidence bands (‘quantile approximation’) based on that quantile have too low simultaneous coverage probability. However, the simulation settings used here suggest that already multivariate t quantiles computed for $Q=10$ or 20 covariate values, lead to confidence bands with actual simultaneous coverage probability very close to the nominal.

Fig. 2

Simulated simultaneous coverage probabilities (5000 data sets per parameter setting) for the given set of discrete covariate values, confidence bands constructed by linear interpolation, or quantile approximation using a multivariate-t-quantile for approximation using $Q=3,6,10,20$ equidistant covariate values. Dotted lines show the range in which 95% of the simulation results can be expected for an exact 95% method

The comparison of treatment-specific regression lines in terms of ratios (Fig. 3, upper row) shows that, the point wise interpretation for a given set of covariate values yields correct simultaneous coverage probability unless being an approximative approach. The attempt to construct confidence bands using only $Q=3$ or 6 covariate values with either of the two approaches may yield liberal confidence bands, whereas $Q=20$ covariate values lead to correct confidence bands in all cases considered here. Note, that for small sample sizes and some simulation settings, up to 13% of the simulated data sets yield unbounded confidence sets and thus the methods appears conservative due to the fact that it yields uninformative confidence bands.

Fig. 3

Simulated simultaneous coverage probabilities (5000 data sets per parameter setting) for the given set of discrete covariate values, confidence bands constructed by linear interpolation, or approximation using a multivariate-t-quantile for $Q=3,6,10,20$ equidistant covariate values. Dotted lines show the range in which 95% of the simulation results can be expected for an exact 95% method. In four settings, where observed coverage probabilities fell below 0.85, the minimal coverage probability is shown in parentheses

In the quadratic model (with three parameters estimated for each treatment group), the point wise interpretation of differences between treatment-specific model predictions has observed simultaneous coverage close to the nominal level for all settings considered (Fig. 3, lower row, left panel). For either approach to construct confidence bands using only $Q=3,6$ or 10 lead to severely, or at least slightly too low coverage probabilities. When using the approximate Fieller-type intervals for ratios to compare treatment-specific predictions in the quadratic model with sample sizes as low as 5 or 10 per treatment group, the coverage probabilities appear systematically too high. This is due to the fact that for up to 50% of simulated data sets there was no finite solution for Eq. (4).

4 Examples

4.1 All pairwise comparisons with baseline as a covariate

The first data set contains weights (in lbs) of young girls before (’preweight’) and after (’postweight’) treatment for anorexia (Hand et al. 1994). The first treatment group of 26 girls is the untreated control, the second and third treatment group received a cognitive behavioral treatment (CBT) and family therapy (FT), consisting of 29 and 17 girls, respectively. Analyzing the post-weight in dependency of the treatments, including pre-weight as a possibly interacting covariate, leads to significant main effects for pre-weight and treatment ($p=0.0011$ and $p=0.0004$, respectively), as well as to a significant interaction between pre-weight and treatment ($p=0.0067$) in ANOVA.

Fig. 4

Observed post-weight and pre-weight, predicted post-weight and confidence intervals for predicted post-weight in three treatments of anorexia and pre-weight for six values in the range $\left[ 70;95\right]$

Because at least the magnitude of treatment effects depends on the pre-weight value, one may now ask, for which values of pre-weight the treatments differ significantly in post-weight, and if so, by what magnitude. Therefore, the model is fitted, parametrized as in Eq. (5), and all pairwise comparisons are specified in the $(3 \times 3)$ matrix $\mathbf{A}$ in Eq. (9), and $Q=6$ equidistant pre-weight values are chosen to cover [70; 95] (Fig. 4). The simultaneous 95% confidence intervals for the resulting $M=18$ are shown in Fig. 5.

$$\begin{aligned} \mathbf{C} = \left( \begin{array}{cccccc} -1 &{} 1 &{} 0 &{} -70 &{} 70 &{} 0 \\ -1 &{} 0 &{} 1 &{} -70 &{} 0 &{} 70 \\ \vdots &{} \vdots &{}\vdots &{} \vdots &{}\vdots &{} \vdots \\ -1 &{} 0 &{} 1 &{} -95 &{} 0 &{} 95 \\ 0 &{} -1 &{} 1 &{} 0 &{} -95 &{} 95 \\ \end{array}\right) = \left( \begin{array}{cc} 1 &{} 70\\ 1 &{} 75\\ \vdots &{} \vdots \\ 1 &{} 95\\ \end{array}\right) \otimes \left( \begin{array}{ccc} -1 &{} 1 &{} 0 \\ -1 &{} 0 &{} 1 \\ 0 &{} -1 &{} 1 \\ \end{array}\right) . \end{aligned}$$

(9)

Fig. 5

Simultaneous 95% confidence intervals for all pairwise comparisons between the three anorexia treatment groups at six equidistant values of pre-weight

As can be presumed from Fig. 4, the significant interaction between pre-weight and treatment is due to the significant difference in post-weight between the CBT and control as well as FT and control, when pre-weights are 85, 90 and 95 lbs. For none of the six pre-weight values, there is significant difference in expected post-weights between the two treatment groups CBT and FT.

The above intervals are constructed only for interpretations at the chosen $Q=6$ discrete values of the covariate, $\tilde{{\varvec{x}}}=(70,75,80,85,90,95)$. Figure 6 illustrates the effect of increasing the number of covariate values on the correlation structure (6), and consequently on the multivariate t-quantiles (7): the above all pairwise comparison problem is considered for $Q=3,6,12,24,50,100$ equidistant points in $\left[ 70; 95\right]$, resulting in total numbers of parameters of $M=9,18,36,72,150,300$. As a reference point for the critical value, the case $Q=1$, for all pairwise comparisons at the overall mean of the covariate, $\tilde{x}=\bar{x}=82.4$ is added.

Fig. 6

Correlation matrices for an increasing number Q of equidistant values $\tilde{{\varvec{x}}}$ in the range $\left[ 70;95\right]$. The rows and columns of the correlation matrices are ordered primarily by the between-treatment-comparisons (blocks), and within each between-treatment-comparison entries are ordered by increasing values of $\tilde{{\varvec{x}}}$. The entries of the correlation matrices are represented by a gray scale, where black indicates strong positive correlation

Fig. 7

Quantiles of the multivariate t distribution recomputed for an increasing number Q of equidistant values $\tilde{{\varvec{x}}}$, spanning the range $\left[ 70;95\right]$ for all $Q\ge 3$

With $Q=3$, the correlations between linear combinations with adjacent covariate values for the same treatment contrast, are below 0.5. For $Q=6$, such linear combinations have already correlations greater than 0.95, when the covariate values are close to the limits of $\left[ 70; 95\right]$, but correlations of 0.5–0.9 for covariate values in the center of the covariate range. Doubling Q from 12 to 24 yields correlations that are always higher than 0.95 for directly adjacent values of x within the same contrast. Figure 7) shows the quantiles of the multivariate t distribution with $df=72-6$ in dependence of Q, and M. For $Q=24,50$ and 100 the quantiles approach 2.88, where the slight changes in the values are mainly due to the Monte Carlo error in the computation of the quantiles. For $Q=6$ the critical value (2.84) is still slightly smaller.

4.2 Treatment interaction with a quadratic regression term

In an experiment discussed by Milliken and Johnson (2002), the yield $y_{ij}$ of a process in dependency of the amount of a substance, $x_{ij}$, was investigated. The effect of two additives (S1, S2) on that yield is compared to a control group without any additive. Among the $I=3$ treatment groups, $i=1$ denotes the control group. Milliken and Johnson (2002) assume treatment specific intercepts $\alpha _{i}$, an overall linear increase $\beta _{1}$ depending on the substance $x_{ij}$, as well as treatment specific parameters $\beta _{2i}$ for the quadratic terms $x_{ij}^{2}$ in a general linear model:

$$\begin{aligned} y_{ij} = \alpha _{i} + \beta _{1}x_{ij} + \beta _{2i}x_{ij}^{2} + e_{ij}. \end{aligned}$$

(10)

The predicted values for the yield y according to the fitted model, as well as the corresponding simultaneous 95% confidence intervals for $Q=11$ values $\tilde{{\varvec{x}}}=\left( 0,1,2,\ldots ,10\right) ^{T}$ as are shown in Fig. 8 along with the observations.

Fig. 8

Observed yield and substance x, predicted yields and confidence intervals for the predicted yield for the process data set (Example 4.2)

The parameter vector is ordered ${\varvec{\theta }} = (\alpha _{1}, \alpha _{2}, \alpha _{3}, \beta _{1}, \beta _{21}, \beta _{22}, \beta _{23})^{T}$, similar as in Eq. (1). Interest is in estimating the gain in expected yield when using one of the two additives compared to running the process without any of the additives ($K=2$ comparisons to control). Because the yields in the control group are clearly positive (except when substance x is close to 0) one could express the effect of the additives in terms of ratios. That is, expressing the increase in yield when using additive S1 or S2 as fold–change relative to the yield in the control treatment. Relying on Sect. 4.3, the matrix $\mathbf{C}$ defines the expected yield of additive S1 and S2 for $\tilde{{\varvec{x}}}$, and $\mathbf{D}$ defines the yields in the control group for $Q=9$ values of substance x, $\tilde{{\varvec{x}}}=\left( 1,2,\ldots ,9\right)$.

$$\begin{aligned} \mathbf{A}= & {} \left( \begin{array}{ccc} 0 &{}\quad 1 &{}\quad 0 \\ 0 &{}\quad 0 &{}\quad 1 \\ \end{array}\right) , \mathbf{B}=\left( \begin{array}{ccc} 1 &{}\quad 0 &{}\quad 0 \\ 1 &{}\quad 0 &{}\quad 0 \\ \end{array}\right) , \end{aligned}$$

(11)

$$\begin{aligned} \mathbf{C}= & {} \left( \begin{array}{ccccccc} 0&{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0 &{}\quad 1 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0 &{}\quad 1\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ 0 &{}\quad 1 &{}\quad 0 &{} \quad 9 &{} \quad 0 &{}\quad 81 &{}\quad 0\\ 0 &{}\quad 0 &{}\quad 1 &{} \quad 9 &{}\quad 0 &{}\quad 0 &{}\quad 81\\ \end{array}\right) = \left( \begin{array}{ccc} {\varvec{1}}_{Q \times 1} \otimes \mathbf{A}, &{} \tilde{{\varvec{x}}} \otimes {\varvec{1}}_{2 \times 1}, &{} \tilde{{\varvec{x}}}^{2} \otimes \mathbf{A} \\ \end{array} \right) , \end{aligned}$$

(12)

$$\begin{aligned} \mathbf{D}= & {} \left( \begin{array}{ccccccc} 1&{}\quad 0 &{}\quad 0 &{} \quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ 1 &{}\quad 0 &{}\quad 0 &{}\quad 1 &{}\quad 1 &{}\quad 0 &{}\quad 0\\ \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots &{}\quad \vdots \\ 1 &{}\quad 0 &{}\quad 0 &{} \quad 9 &{}\quad 81 &{}\quad 0 &{}\quad 0\\ 1 &{}\quad 0 &{}\quad 0 &{}\quad 9 &{}\quad 81 &{}\quad 0 &{}\quad 0\\ \end{array}\right) = \left( \begin{array}{ccc} {\varvec{1}}_{Q \times 1} \otimes \mathbf{B}, &{} \tilde{{\varvec{x}}} \otimes {\varvec{1}}_{2 \times 1}, &{} \tilde{{\varvec{x}}}^{2} \otimes \mathbf{B} \\ \end{array} \right) . \end{aligned}$$

(13)

Fig. 9

Simultaneous 95% confidence intervals for the ratios of expected yields between additive S1 and the control as well as additive S2 and the control

Figure 9 shows that with low concentrations of substance x, the yield is significantly increased with both additives, 1 and 2. For larger concentrations of substance x, the effect of the additives decreases and is not significantly different (at a 5% familywise error rate) for $x=8,9$ with additive 1 and $x=9$ with additive 2. With approximately 95% confidence it can be stated that the mean yield with $x=1,2,3$ using additive S1 is more than 1.96, 1.56, 1.39 times the mean yield in the control. For additive S2 and $x=1,2,3$, the mean yield is at least 2.96, 2.21, 1.89 times that of the control. Increasing the number of points in $\tilde{{\varvec{x}}}$ from $Q=10$ $(t_{0.95, M=20, df=N-P=29, \hat{\mathbf{R}}}=2.8125)$ has only small effects on the resulting quantile: for $Q=20,40,80$ equidistant values in the range $\left[ 1; 9\right]$, the corresponding quantiles are 2.8157, 2.8192, 2.8181, respectively.

4.3 All pairwise comparisons in a binomial generalized linear model

An experiment investigating the mortality of flies exposed to different concentrations of four different compounds containing Selenium is reported in Jeske et al. (2009). In the original publication, the data are analyzed by a generalized linear model assuming the binomial distribution, a probit link with a correction for baseline mortality, and compound specific intercepts and slopes in dependence on the log–concentrations. The data with non-zero concentrations are analyzed here with a simple logit link instead,

$$\begin{aligned} \begin{array}{rcl} y_{ij} &{} \sim &{} Bin(n_{ij}, \pi _{ij}), \\ \log \left[ \pi _{ij}/\left( 1-\pi _{ij}\right) \right] &{} = &{} \eta _{ij},\\ \eta _{ij} &{} = &{} \alpha _{i} + \beta _{i}x_{ij},\\ \end{array} \end{aligned}$$

(14)

where $y_{ij}$ denotes the observed number of dead flies out of $n_{ij}$ flies under observation in the ith compound and dose level j, $j=1,\ldots ,J_{i}$. The corresponding unknown mortality is denoted $\pi _{ij}$, the linear predictor $\eta _{ij}$ is modeled with $\alpha _{i}$ and $\beta _{i}$ being the compound specific intercepts and slopes on the logit scale, where $x_{ij}$ are the $\log _{10}$ of the concentrations. Fitting this model and ordering the parameter vector as in Sect. 2.2, allows to construct asymptotic 95% confidence intervals for the predicted odds at $\log _{10}$-dose levels $\tilde{{\varvec{x}}}=\left( 0.7, 0.9, 1.1, \ldots , 2.9\right) ^{T}$, i.e., $Q=12$. For this purpose, a $(48 \times 8)$ matrix $\mathbf{C}$ can be constructed by $\left( {\varvec{1}}_{Q}, \tilde{{\varvec{x}}}\right) \otimes \mathbf{A}$, where $\mathbf{A}$ is a $(4\times 4)$ identity matrix. The confidence intervals for $\mathbf{C}{\varvec{\theta }}$ are on the scale of the linear predictor and applying the inverse link $\exp (\eta )/[1+\exp (\eta )]$ on the resulting confidence bounds yields confidence bounds for the predicted mortalities shown in Fig. 10. All pairwise comparisons among the four compounds can be performed using the matrix $\mathbf{C}$ as defined in Eq. (15),

$$\begin{aligned} \mathbf{C} = \left( \begin{array}{cc} 1 &{}\quad 0.7 \\ 1 &{}\quad 0.9 \\ 1 &{}\quad 1.1 \\ \vdots &{}\quad \vdots \\ 1 &{}\quad 2.9 \\ \end{array}\right) \otimes \left( \begin{array}{cccc} -1 &{}\quad 1 &{}\quad 0 &{}\quad 0 \\ -1 &{}\quad 0 &{}\quad 1 &{}\quad 0 \\ -1 &{}\quad 0 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad -1 &{}\quad 1 &{}\quad 0 \\ 0 &{} \quad -1 &{}\quad 0 &{}\quad 1 \\ 0 &{}\quad 0 &{}\quad -1 &{}\quad 1 \\ \end{array}\right) . \end{aligned}$$

(15)

Asymptotic confidence limits for ratios among the I compounds with respect to the odds of the probability to die relative to the probability to survive,

$$\begin{aligned} \frac{\frac{\pi |i, \tilde{x}_{q}}{(1-\pi |i,\tilde{x}_{q})}}{\frac{\pi |i', \tilde{x}_{q}}{(1-\pi |i',\tilde{x}_{q})}}, \text{ for } q=1,\ldots ,Q, \text{ and } \text{ all } \text{ pairs } \{i,i'\}: i\ne i', \end{aligned}$$

(16)

can be constructed by applying the $\exp$ function to the confidence limits for the differences on the scale of the linear predictor defined by $\mathbf{C}{\varvec{\theta }}$. These intervals are shown in Fig. 11.

Fig. 10

Observed mortality for the four compounds and asymptotic simultaneous 95% confidence intervals for the predicted mortality based on the fitted model corresponding to Eq. (14)

Fig. 11

Asymptotic simultaneous 95% confidence intervals for all pairwise oddsratios among the four Selenium compounds for $Q=12$ concentration values

Figure 10 reveals a number of problems concerning pairwise comparisons among the compounds: the range of concentrations differs among the four compounds, in particular between Selenite and Selenate on the one side and Selenocysteine on the other side, with ranges only overlapping in concentration 100. If one believes in model (14), Fig. 11 may lead to the following conclusions: Selenite leads to odds(die/survive) that are roughly 80% that of Selenate for the considered high concentrations ($\tilde{{\varvec{x}}}>300$). Selenomethionine leads to increased odds (die/survive) compared to both Selenite and Selenate, for the considered high concentration values ($\tilde{{\varvec{x}}}>100$). Most striking is the 5- to 10-fold increase of this odd in Selenomethionine relative to that in Selenite for the considered high concentrations ($\tilde{{\varvec{x}}}>300$). Selenocysteine shows an about 2-fold increased odds (die/survive) compared to Selenite for the considered high concentrations ($\tilde{{\varvec{x}}}>300$) and also compared to Selenomethionine but then for the low concentration values ($\tilde{{\varvec{x}}}<10$). The two-sided 95% multivariate normal quantiles corresponding to $Q=6,12,24,48$ and 96 equidistant points in $\{0.7, 2.9\}$ for the given data are 2.9389, 2.9839, 2.9977, 2.9987 and 2.9975. That is, the intervals on the logit scale would increase in width by about 0.5% if 96 instead of the given 12 values in $\tilde{{\varvec{x}}}$ would be considered.

5 Discussion

This paper shows how a detailed interpretation of treatment-covariate interactions is possible with standard methods based on simultaneous confidence intervals for user-defined multiple contrast tests in freely available software. Different types of multiple comparisons among several treatments can be interpreted for a pre-specified set of covariate values. The case studies illustrate how to set the methods into practice for a variety of models and experimental questions.

In a strict sense, the simultaneous interpretation is valid only for the pre-specified set of covariate values which have been used for computing the quantile, and not as simultaneous confidence bands, i.e., for any covariate value over the pre-specified range of the covariate. Previously, it has been argued (Bretz et al. 2010; Westfall et al. 2011) that for a sufficiently large set of points that spans a pre-specified range of the covariate, the approach approximates the corresponding confidence bands. The informal assessment of the correlation structure and the results of simulation studies presented in this paper suggest that already a grid of 20 equidistant points in a given covariate range can be used to construct confidence bands with simultaneous coverage probabilities very close to the nominal level. However, the simulation settings used here are restricted to the general linear model and a well-behaved sampling scheme with the covariate values sampled from the uniform distribution. If model complexity increases, covariates have a skewed distribution or include extreme observations, or the covariate range differs between treatments, the recommendations for the number of covariate values may need further assessment. Also, for the application to generalized linear models an assessment of the small sample performance is needed. The findings of this paper and the need for further assessment of coverage probabilities in more complex models are supported by the simulation results of Herberich et al. (2014): their model involves repeated measurements from the same individuals and smoothing splines fitted in dependence of a covariate. The differently shaped curves are compared between several groups. In this far more complicated model only asymptotic methods are available. Though, given a sufficient sample size per group, for only slightly higher numbers of grid points (such as $Q=25$) FWER is controlled for the majority of settings in their simulation study.