Population size estimation and heterogeneity in capture–recapture data: a linear regression estimator based on the Conway–Maxwell–Poisson distribution

Abstract

The purpose of the study is to estimate the population size under a truncated count model that accounts for heterogeneity. The proposed estimator is based on the Conway–Maxwell–Poisson distribution. The benefit of using the Conway–Maxwell–Poisson distribution is that it includes the Bernoulli, the Geometric and the Poisson distributions as special cases and, furthermore, allows for heterogeneity. Parameter estimates can be obtained by exploiting the ratios of successive frequency counts in a weighted linear regression framework. The results of the comparisons with Turing’s, the maximum likelihood Poisson, Zelterman’s and Chao’s estimators reveal that our proposal can be beneficially used. Furthermore, our proposal outperforms its competitors under all heterogeneous settings. The empirical examples consider the homogeneous case and several heterogeneous cases, each with its own features, and provide interesting insights on the behavior of the estimators.

1 Introduction

Capture–recapture (CR) methods have been adopted in a wide range of applications, including ecology (Alunni-Fegatelli and Tardella 2013; Farcomeni 2011), epidemiology (Böhning et al. 2005), criminal activity (van Der Heijden et al. 2003; Farcomeni and Scacciatelli 2013), official statistics (Rocchetti et al. 2011; Gerritse et al. 2015) and, in general, in the estimation of the size of hidden populations. A recent review can be found in McCrea and Morgan (2014). CR analyses are based on the repeated sampling from a population and, consequently, on the use of recapture information to infer the number of uncaptured units. Throughout the paper, we consider the following CR setting. The target population is sampled over a certain number of capture occasions, and for each occasion, captured units are counted only once. Moreover, we consider a closed population, i.e. the unknown population size, say N, is assumed to be constant (with no births/deaths during sampling stages), missclassification is not allowed and all units act independently.

Formally, let $X_i$, $i=1,\dots ,N$ denote the number of times unit i is captured over the m sampling occasions, and let $p_x = \Pr (X_i=x)$. Also let $f_x$ denote the frequency of units captured exactly x times, $x=0,1,\dots ,m$. As $X_i=0$ is not observed, the corresponding $f_0$ is unknown and might be replaced by its expected value $Np_0$. Nevertheless, $p_0$ is usually unknown too and has to be estimated. As $X_i$ takes only non-negative integer values, the Poisson model with parameter $\lambda$ may represent a natural starting point. Clearly, this model is restrictive because it assumes a unit variance-to-mean ratio. Hence, even if the Poisson distribution can be recognized as an important tool to model count data, it may not be suitable for CR data, which are characterized by overdispersion/underdispersion, i.e. the variance is grater/lower than the corresponding sample mean, mainly due to unobserved heterogeneity (see e.g. Baksh et al. 2011).

To account for heterogeneity in the estimation of the population size, the Poisson parameter is often considered as an unobserved random variable with a latent distribution $\lambda (t)$ (Chao 1987). Accordingly, the marginal distribution is provided as

$$\begin{aligned} p_x(\lambda ) = \int _{0}^{\infty } \frac{\exp (-t)t^{x}}{x!}\lambda (t)dt \end{aligned}$$

(1)

where the mixing distribution density $\lambda (t)$ is unknown. One way to model over-dispersion is to consider the Gamma–Poisson mixture, where Poisson variables have means that follow a Gamma distribution. This yields a Negative Binomial marginal distribution. However, in the CR framework, the Negative Binomial distribution might not be appropriate as constraints on the dispersion parameter might lead to unrealistic estimates of $f_0$ and, moreover, it is limited to model over-dispersed data only, i.e. it is unable to fit under-dispersed data. Thus, to mitigate the potential bias in population size estimation due to heterogeneity, discrete (Pledger 2005; Bartolucci and Forcina 2006; Morgan and Ridout 2008) and continuous (Dorazio and Royle 2003; Niwitpong et al. 2013; Rocchetti et al. 2014) mixing distributions have been used.

We wish to contribute extending this branch of literature by proposing a more general count distribution that captures a wider range of dispersion settings than existing distributions. In detail, we look at a two-parameter generalized form of the Poisson distribution, called the Conway–Maxwell–Poisson (CMP) distribution (Shmueli et al. 2005) to account for heterogeneity as it includes as special sub-models important distributions (i.e. the Poisson, the Bernoulli and geometric distributions) and generalizes the Poisson distribution allowing for overdispersion as well as underdispersion.

In the following, we will exploit heterogeneity (in the number of times a unit is captured) through a graphical device, namely the ratio-plot (Böhning et al. 2013). The ratio-plot is a graphical method for identifying the form of the heterogeneity distribution in CR data. In particular, it assesses if the homogeneous Poisson is appropriate or whether (or not) heterogeneity arises in the observed data. Furthermore, in this work we aim at extending the usefulness of the ratio-plot beyond its descriptive nature. Indeed, we will use the ratio-plot as a tool to obtain the estimate of $p_0$ (and, accordingly, of $f_0$ and N) in a heterogeneous population. We introduce a regression estimator based on the (log) ratio-plot which provides straightforward parameter estimates and derive its asymptotic variance. Formally, we use the relationship between the (log) ratios of successive capture probabilities to estimate model parameters through a (weighted) linear regression approach.

We illustrate the proposal by a large-scale simulation study in order to investigate the empirical behaviour of the proposed distribution with respect to several factors, such as the population size, the mixing distribution and the number of occasions (modelled by varying the mean of the count variable). To show the practical usefulness of the CMP regression, we compare its performance to a few alternative estimators, widely used in the CR framework. Finally, we test the proposal by analysing several real datasets.

The outline of the paper is as follows. In Sect. 2, we specify the proposed model, along with the ratio-plot and the computational aspects of the adopted maximum likelihood regression-based algorithm. Properties of the proposed estimator are investigated in depth, and its asymptotic variance is derived. Furthermore, we summarize alternative population size estimators. In Sect. 3, we give a comparison of the performance of several model specifications under different data generation schemes by means of a simulation study. In Sect. 4, we present several real-data analyses. In Sect. 5, we point out some remarks, along with drawbacks that may arise by adopting the proposed methodology.

2 The Conway–Maxwell–Poisson distribution for capture–recapture data

2.1 The Conway–Maxwell–Poisson distribution

The CMP distribution, as an extension of the Poisson distribution, is a flexible model for analyzing count data, although it has been used less frequently as other generalizations. As discussed by Shmueli et al. (2005), the CMP distribution generalized the Poisson distribution allowing for under-dispersion as well as over-dispersion. Its probability mass function $\mathrm{CMP}(\lambda ,\nu )$ is given by

$$\begin{aligned} p_x=\frac{\lambda ^x}{(x!)^{\nu }}\frac{1}{z(\lambda ,\nu )},\quad x = 0,1,2,\dots ; \lambda > 0; \nu \ge 0 \end{aligned}$$

where the normalizing constant

$$\begin{aligned} z(\lambda ,\nu ) = \sum _{j=0}^{\infty }\frac{\lambda ^j}{(j!)^{\nu }} \end{aligned}$$

is a generalization of well-known infinite sums. The CMP distribution has been overlooked for long time due to the complexity in dealing with the infinite sum $z(\lambda ,\nu )$, that is often approximated.

The case $\nu =1$ corresponds to the Poisson distribution, as $z(\lambda ,\nu )=e^{\lambda }$. For $\nu \rightarrow \infty$, the CMP distribution approaches the Bernoulli distribution with parameter $\lambda (1+\lambda )^{-1}$. We would like to point out that, with $\nu =0$ and $0<\lambda <1$, $z(\lambda ,\nu ) = \frac{1}{1-\lambda }$ and, accordingly, the CMP distribution reduces to the geometric distribution with parameter $(1-\lambda )$. At last, note that for $\nu = 0$ and $\lambda \ge 1$, $z(\lambda ,\nu )$ does not converge, leading to an undefined distribution.

To complete the description on the CMP distribution, let us specify its moments by using an asymptotic approximation of $z(\lambda ,\nu )$, as described in Shmueli et al. (2005),

$$\begin{aligned} E(X)\approx & {} \lambda ^{1/\nu }+\frac{1}{2\nu }-\frac{1}{2}\\ V(X)\approx & {} \frac{1}{\nu }\lambda ^{1/\nu }. \end{aligned}$$

Using the Guikema and Coffelt (2008) specification, the dispersion can be written as

$$\begin{aligned} D(X) = \frac{V(X)}{E(X)} \approx \frac{\frac{\mu }{\nu }}{\mu +\frac{1}{2}\nu -\frac{1}{2}}\approx \frac{1}{\nu }, \end{aligned}$$

with $\mu = \lambda ^{1/\nu }$. When $\nu < 1$, the variance can be shown to be greater than the mean and the dispersion $>$1. This is a result of overdispersed data. When $\nu = 1$, and the mean and variance are equal, the dispersion is equal to 1 (Poisson model). When $\nu > 1$, the variance is smaller than the mean and the dispersion is ${<}$1.

2.2 The ratio-plot

In this work, we avoid classical approaches to estimation of population size (see e.g. Lindsay and Roeder 1987; Böhning et al. 2005; Bunge and Barger 2008) and propose a method based on ratios of successive probability counts, namely,

$$\begin{aligned} r_x = (x+1)\frac{p_{x+1}}{p_x} \end{aligned}$$

which is a function of the observed count x.

In CR studies, the zero counts are truncated and, hence, the observed sample frequencies $f_1,f_2,\dots$ arise from the zero-truncated distribution $\frac{p_x}{1-p_0}$. However, the ratio $r_x$ for the truncated and the untruncated distribution is identical

$$\begin{aligned} r_x = (x+1)\frac{p_{x+1}}{p_x}=(x+1)\frac{p_{x+1}/(1-p_0)}{p_x/(1-p_0)}. \end{aligned}$$

This is an important result as it makes the ratio applicable into a CR framework. The ratio for the CMP distribution has the following form

$$\begin{aligned} r_{x} = (x+1)\frac{p_{x+1}}{p_{x}} = (x+1)\frac{\frac{\lambda ^{x+1}}{\{(x+1)!\}^{\nu }} \frac{1}{z(\lambda ,\nu )}}{\frac{\lambda ^{x}}{(x!)^{\nu }} \frac{1}{z(\lambda ,\nu )}} = \lambda (x+1)^{1-\nu } \end{aligned}$$

(2)

and does not depend on the complex normalizing constant term $z(\lambda ,\nu )$. Equation (2) suggests a non-linear relation between the ratio of successive probabilities and the count x. However, if we consider the ratio on the log-scale, we achieve a linear relationship. Accordingly,

$$\begin{aligned} \log (r_{x})= & {} \log \left\{ (x+1)\frac{p_{x+1}}{p_{x}} \right\} =\log \{\lambda (x+1)^{1-\nu } \} \nonumber \\= & {} \log \lambda +(1-\nu )\log (x+1) =\beta _{0}+\beta _{1} \log (x+1). \end{aligned}$$

(3)

From (3), we have that $\lambda = \mathrm{exp}(\beta _{0})$ and $\nu =1-\beta _{1}$; however, due to $\nu \ge 0$ (or, equivalently, $1-\nu \le 1$), we must constrain $\beta _{1} \le 1$. There are no restrictions on $\beta _0$, $\lambda >0$ implies $\beta _{0} \in (-\infty ,+\infty )$.

In practice, we approximate capture probabilities by relative frequencies, therefore the ratio in (2) can be obtained by

$$\begin{aligned} r^{*}_{x} = (x+1)\frac{\hat{p}_{x+1}}{\hat{p}_{x}} = (x+1)\frac{f_{x+1}/N}{f_{x}/N} = (x+1)\frac{f_{x+1}}{f_{x}}, \end{aligned}$$

as well as the ratio in (3) can be computed as

$$\begin{aligned} \log (r^{*}_{x}) = \log \left\{ (x+1)\frac{f_{x+1}}{f_{x}} \right\} , \end{aligned}$$

where $f_{x}$ is the frequency of count x and $N= \displaystyle \sum \nolimits _{x=0}^{m}f_{x}$.

By plotting $\log (r^{*}_{x})$ against $\log (x+1)$, we derive a graphical diagnostic tool for detecting the validity of Conway–Maxwell–Poisson model. The resulting plot is known as the log-ratio plot (see Böhning et al. 2013 for further details). A log-ratio plot showing a positive slope indicates for the presence of overdispersion with respect to the Poisson distribution. On the other hand, in the case of underdispersion, the log-ratio plot displays a straight line with a negative slope. Finally, when the log-ratio plot displays a horizontal line, the equi-dispersion case is plausible, or, in other words, the Poisson distribution can be used to fit the data.

Other distributions as the Negative Binomial have been often considered to deal with heterogeneity. It has also a straight line behaviour when plotting ratios of successive capture probabilities against x, but fitting parameters has frequently boundary issues. Taking $\log (r^{*}_{x})$ helps but this destroys the linear characteristic with respect to x. Hence there are benefits of CMP distribution in comparison to the Negative Binomial as well.

2.3 Model inference

The use of the ratio in (3) goes beyond a simple graphical technique to check for under/over-dispersion in CR data. Indeed, it can be used as a tool for estimating model’s parameters. Thus, let us consider our basic Eq. (3), we fit the following model

$$\begin{aligned} \log (r_{x}^{*}) =\underbrace{ \beta _{0}+\beta _{1} \log (x+1)}_{ Systematic}+ \underbrace{ \epsilon _{x}}_{ Random}, \end{aligned}$$

(4)

where $\beta _{0}$ and and $\beta _{1}$ are the intercept and the slope parameters respectively, and $\epsilon _{x}$ is the error term.

Commonly, a least square estimation (LS) method is used to provide estimates of $\beta _{0}$ and $\beta _{1}$. However, model (4) does not satisfy the classical linear regression assumptions. In the first place, the response is discrete (although log-transformed), so we might consider a generalized linear model. However, this is inadvisable since an appropriate formulation as a generalized linear model leads to an autoregressive equation involving $\log f_x$ as an additional offset term in the linear predictor. These kinds of models experience difficulties in terms of the definition of the likelihood as well as in carrying out inference. Furthermore, CR frequencies often have $f_{1}>>f_2 > f_3 >\dots$, and, additionally, heteroskedasticity might occur in heterogeneous population due to e.g. unobserved information (see e.g. Rocchetti et al. 2014). All these issues are relevant and should be accounted for. Thus, we address them by using weighted least squares (WLS) techniques to estimate the regression parameters $\beta _{0}$ and $\beta _{1}$, and accordingly $\lambda$ and $\nu$. These are obtained by minimising

$$\begin{aligned} \sum _{x=1}^{m-1} W_{x}\left[ \log (r_{x}^{*}) -\beta _{0}-\beta _{1}\log (x+1)\right] ^{2}, \end{aligned}$$

where $W_{x}$ denotes the x-th element of an appropriate weight matrix. In other words, we take

$$\begin{aligned} \left( \begin{array}{c} \hat{\beta }_0\\ \hat{\beta }_1 \end{array}\right) = \left( \mathbf{X}'{} \mathbf{W}{} \mathbf{X}\right) ^{-1}\mathbf{X}'{} \mathbf{W}{} \mathbf{Y}, \end{aligned}$$

(5)

where

$$\begin{aligned} \mathbf{Y} = \left( \begin{array}{c} \log \frac{2f_2}{f_1}\\ \log \frac{3f_3}{f_2}\\ \vdots \\ \log \frac{mf_m}{f_{m-1}} \end{array}\right) ,\quad \mathbf{X} = \left( \begin{array}{cc} 1 &{} \log (2)\\ 1 &{} \log (3)\\ \vdots &{} \vdots \\ 1 &{} \log (m) \end{array}\right) \end{aligned}$$

and m is the maximum count used in the estimator.

The application of weighted least square requires the specification of $\mathbf{W} \approx cov(\mathbf{Y})^{-1}$ to reduce the mean square error. Following Meurant (1992) and Rocchetti et al. (2011), covariances between adjacent log-ratios do not play a large role in reducing mean square error, and thus we suggest to drop the off-diagonal terms in $cov(\mathbf{Y})$ in approximating $\mathbf{W}$, with little loss of efficiency. Accordingly

$$\begin{aligned} {\mathbf {W}}= \left[ \begin{array}{ccccc} \frac{1}{f_{1}}+\frac{1}{f_{2}} &{} 0 &{} \cdots &{} 0\\ 0 &{}\frac{1}{f_{2}}+\frac{1}{f_{3}} &{} \cdots &{} 0\\ \vdots &{}\vdots &{} \ddots &{} \vdots \\ 0&{} 0 &{} 0&{} \frac{1}{f_{m-1}}+\frac{1}{f_{m}}\end{array} \right] ^{-1}. \end{aligned}$$

(6)

To see that (6) is the right choice, let $\mathbf{W}_{x}= \left[ Var\{\log (r^{*}_{x})\} \right] ^{-1}$, we have

$$\begin{aligned} Var\left\{ \log (r_{x}^{*}) \right\}= & {} Var\left[ \log \left\{ (x+1)\frac{\hat{p}_{x+1}}{\hat{p}_x} \right\} \right] \\= & {} Var\left\{ \log (x+1)+\log (\hat{p}_{x+1})-\log (\hat{p}_{x}) \right\} \\= & {} Var\left\{ \log (\hat{p}_{x+1}) \right\} +Var\left\{ \log (\hat{p}_{x}) \right\} {-}2Cov\left\{ \log (\hat{p}_{x+1}),\log (\hat{p}_{x}) \right\} . \end{aligned}$$

Using the delta method

$$\begin{aligned} Var\left\{ \log (r_{x}^{*}) \right\}\approx & {} \frac{1}{p^{2}_{x+1}}Var(\hat{p}_{x+1}) +\frac{1}{\hat{p}^{2}_{x}}Var(\hat{p}_{x})-\frac{2Cov(\hat{p}_{x+1},\hat{p}_{x})}{\hat{p}_{x+1}\hat{p}_{x}}\\= & {} \frac{1}{p^{2}_{x+1}}\left\{ \frac{\hat{p}_{x+1} (1-\hat{p}_{x+1})}{n} \right\} +\frac{1}{\hat{p}_{x}^{2}}\left\{ \frac{\hat{p}_{x}(1-\hat{p}_{x})}{n} \right\} + \frac{\frac{2\hat{p}_{x+1}\hat{p}_{x}}{n}}{\hat{p}_{x+1}\hat{p}_{x}}\\= & {} \frac{1-\hat{p}_{x+1}}{n\hat{p}_{x+1}} +\frac{1-\hat{p}_{x}}{n\hat{p}_{x}}+\frac{2}{n}\\= & {} \frac{1}{n\hat{p}_{x+1}} -\frac{\hat{p}_{x+1}}{n\hat{p}_{x+1}}+\frac{1}{n\hat{p}_{x}}-\frac{\hat{p}_{x}}{n\hat{p}_{x}}+\frac{2}{n} \end{aligned}$$

where n is the number of observations from the target population.

Threrefore, the variance of log-ratio is given by

$$\begin{aligned} Var\left\{ \log (r_{x}^{*}) \right\} \approx \frac{1}{n\hat{p}_{x+1}}+\frac{1}{n\hat{p}_{x}}. \end{aligned}$$

In practice, $\hat{p}_{x+1}$ and $\hat{p}_{x}$ can be estimated by relative observed frequency $\frac{f_{x+1}}{n}$ and $\frac{f_{x}}{n}$, respectively. Hence

$$\begin{aligned} \widehat{Var} \left\{ \log (r_{x}^{*}) \right\} = \frac{1}{n\frac{f_{x}}{n}}+ \frac{1}{n\frac{f_{x+1}}{n}} =\frac{1}{f_{x}}+\frac{1}{f_{x+1}}. \end{aligned}$$

Thus, we get $\hat{\beta }_0$ and $\hat{\beta }_1$ from (5), in which $\mathbf{W}$ is given by (6). Accordingly, the unknown $f_0$ can be then estimated by considering that

$$\begin{aligned} \log \left( \frac{f_{1}}{f_{0}} \right)= & {} \hat{\beta _{0 }}\\ \frac{f_{1}}{ f_{0} }= & {} \exp {(\hat{\beta _{0 }} )}\\ \hat{f}_{0}= & {} f_{1} \exp {({-\hat{\beta _{0}}})}, \end{aligned}$$

where $\hat{f}_{0}$ is the unobserved frequency estimator. The linear regression estimator based on the Conway–Maxwell–Poisson distribution (LCMP) of target population size can be readily achieved as

$$\begin{aligned} \hat{N}_{LCMP}= & {} n+ \hat{f}_{0} = n+ f_{1}\exp ({-\hat{\beta _{0}}}). \end{aligned}$$

(7)

We also obtain an estimated probability of the count to be zero (unobserved) as

$$\begin{aligned} \hat{p}_0 = \hat{f}_0/\hat{N}_{LCMP}. \end{aligned}$$

We anticipate that $\hat{N}_{LCMP}$ is asymptotically unbiased in the sense

$$\begin{aligned} \frac{E(\hat{N}_{LCMP})}{N} \rightarrow _{N \rightarrow \infty } 1, \end{aligned}$$

if the sample arises from a Conway–Maxwell–Poisson distribution. The rationale for this is as follows. Suppose that $\beta _0$ would be known, then

$$\begin{aligned} \hat{N}_{LCMP} = n + f_0 = n + f_1 \exp (-\beta _0) \end{aligned}$$

(8)

is unbiased as

$$\begin{aligned} E(\hat{N}_{LCMP})= & {} N(1-p_0) + p_1 N \exp (-\beta _0) =N[(1-p_0)+ p_1/\lambda ] \\= & {} N[(1-p_0)+p_0] =N. \end{aligned}$$

For any matrix $\mathbf{W}$, the weighted least squares estimate in (5) is unbiased if $\mathbf{W}$ is non-random, as

$$\begin{aligned} E\left( \begin{array}{c} \hat{\beta }_0\\ \hat{\beta }_1 \end{array}\right) = \left( \mathbf{X}'{} \mathbf{W}{} \mathbf{X}\right) ^{-1}\mathbf{X}'{} \mathbf{W}{} \mathbf{X}\left( \begin{array}{c} {\beta }_0\\ {\beta }_1 \end{array}\right) = \left( \begin{array}{c} {\beta }_0\\ {\beta }_1 \end{array}\right) . \end{aligned}$$

However, an efficient estimator is achieved only if $\mathbf{W}={\varvec{\varSigma }}^{-1}$, where ${\varvec{\varSigma }}$ is the true variance-covariance matrix of $\mathbf{Y}$. If an estimator $\hat{{\varvec{\varSigma }}}$ of ${\varvec{\varSigma }}$ is used (as it is often the case in practice and also in our situation), efficiency is usually lost, but not asymptotic unbiasedness. For the latter, only a consistent estimate of ${\varvec{\varSigma }}$ is needed. This is the case for our situation. It is shown in Rocchetti et al. (2011) that using the weight-matrix in (6) leads to a gain in efficiency in comparison with the unweighted unbiased estimate

$$\begin{aligned} \left( \begin{array}{c} \hat{\beta }_0\\ \hat{\beta }_1 \end{array}\right) = \left( \mathbf{X}'{} \mathbf{X}\right) ^{-1}{} \mathbf{X}'{} \mathbf{Y}. \end{aligned}$$

Hence, we prefer to use (5) with weight matrix (6).

It is clear that some attention has to be paid to the fact that weights are estimated in reality and this is further addressed in the simulation study. We point out here that the Conway–Maxwell–Poisson distribution includes as a special case the geometric ($\nu =0$) so that an associated weighted least-squares estimator is available for the geometric. It has the simple form $\widehat{\log \lambda } = \left( \sum _{x=1}^{m-1} W_x\log \frac{f_{x+1}}{f_x}\right) {\big /}\left( \sum _{x=1}^{m-1} W_x \right)$, where $W_x$ is the $x-$th diagonal element of (6).

2.4 Variance estimation and confidence interval

Let $\hat{N}$ be the population size estimator, according to Böhning (2008), the variance of $\hat{N}_{LCMP}= n+ f_{1}e^{-\hat{\beta }_{0}}$ arises from two sources; these are influenced by the random variable n and the estimator $\hat{f}_{0}$. Using conditional moment techniques, a formula for the variance of population size estimator is given as:

$$\begin{aligned} Var(\hat{N}) = Var_{n}\{E (\hat{N}|n \} + E_{n} \{Var(\hat{N}|n)\}, \end{aligned}$$

(9)

where $E_{n}$ and $Var_{n}$ refer to the first and the second moment of the marginal distribution under observed data n. It is

$$\begin{aligned} E(\hat{N}|n)\approx n+\hat{f}_{0}, \end{aligned}$$

with $\hat{f}_0$ non random, so that

$$\begin{aligned} Var_{n}\{E (\hat{N}|n )\} = \widehat{ Var}_{n}\{n+\hat{f}_{0} \}= \widehat{ Var}_{n}\{n\}=N(1-p_{0})p_{0}, \end{aligned}$$

(10)

where the latter follows from the fact that $n\sim Binomial(N,1-p_0)$.

Since $E(n)=N(1-p_{0})$ and $p_{0}=E(f_{0}/N)$, leading to $\hat{p_{0}}=\frac{\hat{f}_{0}}{n+\hat{f}_{0}}$, we have that (10) can be estimated by

$$\begin{aligned} \widehat{ Var}_{n}\{E (\hat{N}|n )\} = \frac{n \hat{f}_{0}}{n+\hat{f}_{0}}=\frac{n f_{1}e^{-\hat{\beta }_{0}}}{n+ f_{1}e^{-\hat{\beta }_{0}}}. \end{aligned}$$

(11)

Also, we assume as $E_{n} \{Var(\hat{N}|n)\}$ can be estimated by $Var(\hat{N}|n)= Var(\hat{f}_{0})=Var\{f_{1}e^{ (-\hat{\beta }_{0})} \}$, hence we have that

$$\begin{aligned} E_{n} \{Var(\hat{N}|n)\} = \widehat{ Var} \{f_{1}e^{(-\hat{\beta }_{0}})\}. \end{aligned}$$

(12)

By the conditional technique,

$$\begin{aligned} Var(f_{1}e^{-\hat{\beta }_{0}}) = Var_{f_{1}}\{ E(f_{1}e^{-\hat{\beta }_{0}})|f_{1} \}+ E_{f_{1}}\{Var(f_{1}e^{-\hat{\beta }_{0}} )|f_{1} \}, \end{aligned}$$

(13)

thus

$$\begin{aligned} Var_{f_{1}}\{ E(f_{1}e^{-\hat{\beta }_{0}})|f_{1} \}\approx & {} Var(f_{1}e^{-\hat{\beta }_{0}}) =(e^{-\hat{\beta }_{0}})^{2}Var(f_{1}) \nonumber \\= & {} (e^{-\hat{\beta }_{0}})^{2} Np_{1}(1-p_{1})= (e^{-\hat{\beta }_{0}})^{2}f_{1}\left( 1-\frac{f_{1}}{N} \right) , \end{aligned}$$

(14)

as well as, $E_{f_{1}}\{Var(f_{1}e^{-\hat{\beta }_{0}} )|f_{1} \}$ can be estimated by $Var\{ (f_{1}e^{-\hat{\beta }_{0}} )|f_{1} \}$, so that

$$\begin{aligned} E_{f_{1}}\{Var(f_{1}e^{-\hat{\beta }_{0}} )|f_{1} \} \approx Var\{ (f_{1}e^{-\hat{\beta }_{0}} )|f_{1} \} = f_{1}Var(e^{-\hat{\beta }_{0}}). \end{aligned}$$

(15)

Using the delta method, we achieved that $Var(e^{-\hat{\beta }_{0}}) = (e^{-\hat{\beta }_{0}})^{2}Var(\hat{\beta }_{0})$. Hence $E_{f_{1}}\{Var(f_{1}e^{-\hat{\beta }_{0}} )|f_{1} \} \approx f_{1}^{2}(e^{-\hat{\beta }_{0}})^{2}Var(\hat{\beta }_{0})$, where $Var(\hat{\beta }_{0})$ comes from the linear regression process. The approximated expression for the variance of the new estimator $\hat{N}_{LCMP}$ is given as

$$\begin{aligned} \widehat{Var}(\hat{N}_{LCMP}) = \frac{n f_{1}e^{-\hat{\beta }_{0}}}{n+ f_{1}e^{-\hat{\beta }_{0}}} + (e^{-\hat{\beta }_{0}})^{2}f_{1}\left( 1-\frac{f_{1}}{N} \right) +f_{1}^{2}(e^{-\hat{\beta }_{0}})^{2}Var(\hat{\beta }_{0}).\quad \end{aligned}$$

(16)

Finally, when N is large, the asymptotic variance estimator of $\hat{N}_{LCMP}$ is

$$\begin{aligned} \widehat{Var}(\hat{N}_{LCMP}) = \frac{n f_{1}e^{-\hat{\beta }^{0}}}{n+ f_{1}e^{-\hat{\beta }^{0}}} + (e^{-\hat{\beta }_{0}})^{2} f_{1}[1+f_{1}Var(\hat{\beta }_{0})]. \end{aligned}$$

(17)

A confidence level refers to the percentage of all possible samples that can be expected to include the true value of population size N. We used 95 % confidence level to imply 95 % of the confidence intervals, including the true population size estimator. It is simply to construct 95 % confidence interval of N under the assumption that population distribution be approximately normal as:

$$\begin{aligned} \widehat{N} \pm z_{0.975}SE(\widehat{N}), \end{aligned}$$

(18)

where $SE(\widehat{N})$ denotes the standard error of $\widehat{N}$, approximated by the asymptotic standard error; $\widehat{SE}(\widehat{N})=\sqrt{\widehat{Var}(\widehat{N})}$, and $z_{0.975} =1.96$.

2.5 Alternative estimators

Several estimators have been applied to estimate population size in CR data. This section focuses on well-known estimators based on homogeneous Poisson and heterogeneous models. Turing’s estimator and the maximum likelihood estimator under a Poisson model are considered as estimators in the homogeneous case. Estimators for heterogeneous populations as the Zelterman’s estimator and the Chao’s lower bound estimator are considered as well. In the simulation study and in the application section, estimator performances are compared with the LCMP estimator under several settings.

2.5.1 Turing’s estimator

The application of Turing’s estimator can be used under a homogeneous Poisson distribution. Then in terms of a homogeneous Poisson distribution with parameter $\lambda$ we have

$$\begin{aligned} p_{0} = e^{-\lambda } = \frac{\lambda e^{-\lambda }}{\lambda } = \frac{p_{1}}{E(X)} = \frac{E(f_{1})/N}{E(S)/N} = \frac{E(f_{1})}{E(S)}, \end{aligned}$$

(19)

where $p_{1} = \lambda e^{-\lambda }$ and $S = \sum _{x=1}^mf_x$. Replacing these expected values by their observed quantities we have

$$\begin{aligned} \hat{p}_{0} = \frac{f_{1}}{S}. \end{aligned}$$

(20)

We achieve Turing’s estimator as

$$\begin{aligned} \hat{N}_{Turing} = \frac{n}{1-f_{1}/S}. \end{aligned}$$

(21)

The variance for Turing estimation (Lerdsuwansri 2012) is given by

$$\begin{aligned} \widehat{Var} (\hat{N}_{Turing}) = \frac{n\frac{f_{1}}{S}}{(1+\frac{f_{1}}{S})^{2}}+ \frac{n^{2}}{(1+\frac{f_{1}}{S})^{4}} \left[ \frac{f_{1}(1-\frac{f_{1}}{\hat{N}})}{S^{2}} +\frac{f_{1}^{2}}{S^{3}}\right] . \end{aligned}$$

(22)

The benefits of Turing’s estimator are that it is easy to calculate, its value can be obtained in a straightforward way, and there is no need for an iterative procedure. In addition, it uses all the information in the sample by means of S and $f_1$, the latter being usually large.

2.5.2 Maximum likelihood estimator under the zero-truncated Poisson distribution

Let us assume that the capture–recapture count data X can be modelled as a zero-truncated Poisson distribution. Thus, population size can be estimated as

$$\begin{aligned} \hat{N}_{MLE} = \frac{n}{1-\exp ({-\hat{\lambda }_{MLE}})}, \end{aligned}$$

(23)

The maximum likelihood estimator $\hat{\lambda }_{MLE}$ can be obtained by using the EM-algorithm technique under the zero-truncated Poisson distribution (see Böhning et al. 2005). A simple variance estimate of (23) is given as

$$\begin{aligned} \widehat{Var} (\hat{N}_{MLE}) = \frac{\hat{N}_{MLE}}{ \left\{ \exp \left( \frac{ \sum _{x=1}^{m} xf_x}{\hat{N}_{MLE}}\right) -\frac{ \sum ^{m}_{x=1} xf_{x}}{\hat{N}_{MLE}} -1 \right\} }. \end{aligned}$$

(24)

2.5.3 Zelterman’s estimator

Zelterman (1988) suggested an estimator under a truncated Poisson sampling estimator. This is a well-known robust estimator under potential unobserved heterogeneity. Zelterman suggests using $\hat{\lambda }_{1} = \frac{2f_{2}}{{f_{1}}}$. As Kuhnert and Böhning (2009) pointed out, there are two reasons for choosing $\hat{\lambda }_{1}$ in Zelterman’s parameter. Firstly, the majority of frequency count units are usually represented in terms of counts of once and twice $(f_{1}$ and$f_{2}$ are used), so that count data greater than two are likely to have little effect on this estimator. Secondly, $\hat{\lambda }_{1}$ is the closest neighbour of the target point of estimation $f_{0}$. The Zelterman estimator of population size is ultimately provided as

$$\begin{aligned} \hat{N}_{Zel} = \frac{n}{1-\exp \left( {-\frac{2f_{2}}{f_{1}}}\right) }. \end{aligned}$$

(25)

Zelterman’s estimator has been widely used since it is easy to understand, and it is a robust estimator because it uses only the first and second order of frequencies. However, it might be not a good estimator for long tail count data (Lanumteang 2011). Also, it can overestimate the population size under heterogeneity (Böhning and Schön 2005).

The Variance of the Zelterman’s Estimator is

$$\begin{aligned} \widehat{Var}(\hat{N}_{Zel}) = n G(\hat{\lambda )}\left[ 1+n G(\hat{\lambda })\hat{\lambda }^{2} \left( \frac{1}{f_{1}}+\frac{1}{f_{2}} \right) \right] \end{aligned}$$

(26)

where $G(\hat{\lambda }) = \frac{\exp (-\hat{\lambda })}{\{1-\exp (-\hat{\lambda })\}^{2}}$ and $\hat{\lambda }=\frac{2f_{2}}{f_{1}}$ (see Böhning 2008).

2.5.4 Chao’s lower bound estimator

Chao (1987, 1989) introduced an alternative estimator of population size under unobserved heterogeneity of the Poisson parameter. Counts are assumed to be generated from a mixed Poisson model with arbitrary mixing density $g(\lambda )$; $p_{x} = \int _{0}^{\infty }\frac{e^{-\lambda }\lambda ^{x}}{x!}g(\lambda )d\lambda$ where $x= 0,1,2,\ldots$. Based on the Cauchy-Schwarz inequality, we achieve a lower bound for $p_{0}$ as: $\frac{p_{1}^{2}}{2p_{2}} \le p_{0}$, multiplying those probabilities by N leads to $\frac{(Np_{1})^{2}}{2(Np_{2})} \le Np_{0}$. Hence replacing $Np_{1}$ and $Np_{2}$ with the observed frequencies $f_{1}$ and $f_{2}$ leads to the lower bound estimator $\frac{f_{1}^{2}}{2f_{2}}$, that is

$$\begin{aligned} \hat{f}_{0} = \frac{f_{1}^{2}}{2f_{2}} \end{aligned}$$

(27)

and

$$\begin{aligned} \hat{N}_{Chao} = n+ \frac{f_{1}^{2}}{2f_{2}} . \end{aligned}$$

(28)

Note that only $f_{1}$ and $f_{2}$ are used in Chao’s lower bound estimator. An important lower bound for estimating the population size is given.

An estimate of the variance of the Chao’s estimator is given by

$$\begin{aligned} \widehat{Var}(\hat{N}_{Chao}) = \frac{1}{4}\frac{f_{1}^{4}}{f_{2}^{3}}+ \frac{f_{1}^{3}}{f_{2}^{2}}+\frac{1}{2} \frac{f_{1}^{2}}{f_{2}}-\frac{1}{4} \frac{f_{1}^{4}}{(nf_{2}^{2})}- \frac{1}{2}\frac{f_{1}^{4}}{f_{2}(2nf_{2}+f_{1}^{2})} \end{aligned}$$

(29)

(see Böhning 2008). An extended version of the Chao’s estimator has been recently proposed in Chiu et al. (2014). It also contains a variance estimate for Chao’s estimator as well as a confidence interval construction based upon the log-normal distribution.

3 Simulation study

This section provides a comprehensive assessment of population size estimator performance. We compare the LCMP estimator proposed in this work with other well-established estimators highlighted in the previous section. We plan the simulation study to cover schemes with different underlying null models, with varying population size $N=100; 1000; 10,000$ and levels of heterogeneity.

In detail, we consider the following data generation settings

• (i) The Poisson distribution: counts are generated from the Poisson distribution with parameters

  $$\begin{aligned} \lambda \in \{ 0.5, 1.0, 1.5, 2.0, 2.5, 3.0\} \end{aligned}$$

• (ii) The geometric distribution: counts are generated from the geometric distribution with parameters

  $$\begin{aligned} \lambda \in \{0.2,0.3,0.4,0.5,0.6,0.7,0.8\} \end{aligned}$$

  where $\lambda = 1-p$, and p is a probability of success.

• (iii) The Conway–Maxwell–Poisson distribution: counts are generated from Conway–Maxwell–Poisson distribution with parameters

  $$\begin{aligned} \lambda\in & {} \{0.5,1.0,1.5,2.0,2.5,3.0 \}\\ \nu\in & {} \{0.4, 0.6, 0.8\} \end{aligned}$$

• (iv) The Negative Binomial distribution: counts are generated from a Negative Binomial distribution

  $$\begin{aligned} p_{x}= \frac{\varGamma (x+k)}{\varGamma (x+1)\varGamma (k)}(1-\lambda )^{k}\lambda ^{x}, \end{aligned}$$

  with parameters

  $$\begin{aligned} \lambda \in \{0.2, 0.4, 0.6, 0.8\}, \end{aligned}$$

  dispersion parameters

  $$\begin{aligned} k \in \{2, 4, 6\}, \end{aligned}$$

  expected value and variance given respectively by

  $$\begin{aligned} E(X) = \frac{k\lambda }{1-\lambda } = \mu \end{aligned}$$

  and

  $$\begin{aligned} Var(X) = \frac{k\lambda }{(1-\lambda )^{2}} = \mu +\frac{1}{k}\mu ^{2}. \end{aligned}$$

As the settings (i)–(ii)–(iii) covers situations where the data generation is from a special case of the CMP distribution, we include setting (iv) to investigate what happens if we leave the family, e.g. if we sample from a Negative Binomial distribution. We draw $B=1000$ samples from each null model. Any occurrences of zero counts were truncated, and five estimators of population size were compared: the Turing’s estimator (Turing), the maximum likelihood estimation under the zero-truncated Poisson model (MLEPoi), Chao’s lower bound estimator (Chao), Zelterman’s estimator (Zel) and weighted linear regression estimator under the zero-truncated Conway–Maxwell–Poisson model (LCMP).

Let $\hat{N}_{(b)}$ denotes the estimated value of the population size at replication $b\mathrm{{th}}$ where $b= 1,2,3,\ldots ,B$, we evaluate estimators performance in terms of relative bias

$$\begin{aligned} RBias(\hat{N}) = \frac{1}{N} \left[ E(\hat{N}) -N \right] = \frac{1}{N}bias(\hat{N}), \end{aligned}$$

(30)

relative variance

$$\begin{aligned} RVar(\hat{N}) = \frac{1}{N^{2}} \left\{ \frac{1}{B} \sum _{b=1}^{B} \left( \hat{N}_{b}-E[\hat{N}] \right) ^{2} \right\} \end{aligned}$$

(31)

and relative root mean square error

$$\begin{aligned} RRMSE \{\hat{N}\} = \frac{1}{N} \sqrt{Var\{ \hat{N} \} + \{bias(\hat{N})\}^{2} }. \end{aligned}$$

(32)

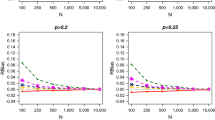
When the data generation process follows a Poisson distribution, all estimators are asymptotically unbiased with respect to the population size N (see Figs. 1, 2, 3). Sensible differences can be detected for small population sizes (e.g. $N=100$). The estimators allowing for heterogeneity (i.e. Zel and Chao) are persistently biased and show the highest RRMSE values. On the other hand, the LCMP estimator performs in line with the homogeneous, Poisson-based estimators (i.e. Turing and MLEPoi). This is an expected result, as the Poisson distribution is a special case of the CMP one, which is however more general and may be suitable under different data generation settings, far from the Poisson case.

Fig. 1

Relative bias of five estimators for counts drawn from $Poi(\lambda )$

Fig. 2

Relative variance of five estimators of seven estimators for counts drawn from $Poi(\lambda )$

Fig. 3

Relative root mean square error of five estimators for counts drawn from $Poi(\lambda )$

Fig. 4

Relative bias of five estimators for counts drawn from $Geo(\lambda )$; $\lambda = 1-p$

Indeed, by considering a geometric data generation process, the performance of all competing estimators is dramatically poor, no matter of the population size, with the exception of the LCMP estimator proposed in this work (see Figs. 4, 5, 6). The LCMP estimator provides unbiased estimates as the population size increases, at the price of a slightly higher variability, with respect to its competitors. Overall, the LCMP estimator clearly outperforms all the other estimators. Again, this is somehow expected, as the geometric distribution is a specific case nested in the CMP distribution. A comparable performance is reached by the Zelterman estimator for increasing values of $\lambda$.

Fig. 5

Relative variance of five estimators for counts drawn from $Geo(\lambda )$; $\lambda = 1-p$

Fig. 6

Relative root mean square of five estimators for counts drawn from $Geo(\lambda )$; $\lambda = 1-p$

We further test estimators performance under overdispersion and underdispersion, by generating data from a CMP distribution. We expect that the LCMP estimator, as well as Chao and Zelterman estimators, outperforms Turing and MLEPoi estimators under heterogeneous schemes. Results are displayed in Figs. 7, 8 and 9. Overall, it can be seen that the LCMP has the best performance when the population size is medium or large, whereas Turing and MLEPoi estimators underestimate the population size. Even the other heterogeneous estimators tend to underestimate the population size, providing reasonable results for $N=10,000$ only. Indeed, the CMP distribution is a very general one and accounts for many (possible) data feature, that may not be captured by existing estimators. To corroborate the simulation results on the LCMP estimator, we provide plots to show convergence to normality under the CMP data generation process for $\lambda = 0.5; 1.0$ and $\nu = 0.4,; 0.6; 0.8$ (see Fig. 10).

Fig. 7

Relative bias of five estimators for counts drawn from $CMP(\lambda ,\nu )$

Fig. 8

Relative variance of five estimators for counts drawn from $CMP(\lambda ,\nu )$

Fig. 9

Relative root mean square error of five estimators for counts drawn from $CMP(\lambda ,\nu )$

Fig. 10

Normality plot for LCMP estimator under the CMP distribution

At last, it can be said that under a Negative-Binomial the MLEPoi and Turing’s estimators show a clear underestimation of population size, as well as Chao’s, whereas Zelterman’s estimator does not have a clear path. Similar results can be found in Lanumteang and Böhning (2011). The new estimator performs much better than its competitors, although it tends to overestimate for a small population size and low values of $\lambda$. Such an effect disappears as $\lambda$ and/or k increase (see Figs. 11, 12, 13). To conclude the simulation study, the proposed LCMP estimator can be used even under a Negative Binomial data generation process.

Fig. 11

Relative bias of five estimators for counts drawn from $NB(\lambda ,k)$

Fig. 12

Relative variance of five estimators for counts drawn from $NB(\lambda ,k)$

Fig. 13

Relative root mean square error of five estimators for counts drawn from $NB(\lambda ,k)$

4 Real data examples

In this section we apply different estimators to real data examples. We consider the following benchmark datasets: the cholera data (McKendrick 1926); the golf tees data (Borchers and Buckland 2002); artificial data used by Link (2003); drug users in Bangkok (Viwatwongkasem et al. 2008). Obtained results under different estimators are also compared to provide an overview of differences in estimating population size in CR data. Furthermore, we provide results for the standard error of the population size by using the asymptotic approximation computed in Sect. 2.4. Goodness-of-fit is investigated through plots and a chi-square goodness of fit test under the null hypothesis of a homogeneous zero-truncated Poisson data is computed. The maximum likelihood estimator under the geometric distribution (Niwitpong et al. 2013) is further considered to see difference with our proposals in terms of model fitting.

4.1 Cholera epidemic in India

The example stems from Mao and Lindsay (2003) and has been discussed previously in Blumenthal et al. (1978), Scollnik (1997), and others. A cholera epidemic affected a village with 223 households in India. Originally, the data were presented by McKendrick (1926) in his paper presentation to the Edinburgh Mathematical Society. Data are provided in Table 1.

Table 2 presents the various estimates of the total number and their associated 95 % confidence intervals. For the cholera epidemic data evidence has been provided for homogeneity (see Fig. 14). Accordingly, estimates do not differ much; neither do their confidence intervals with the exception of Zelterman which has a large confidence interval. The LCMP approaches the Poisson distribution, as $\hat{\lambda } =1.01$ and $\hat{\nu }=1$, i.e. the proposed estimator can be used even if homogeneity is ensured and produces comparable results with homogeneous estimators (e.g. Turing) often used under the homogeneous population setting. This is also confirmed by the formal chi-squared test indicated that the cholera data follow homogeneity of a zero-truncated Poisson distribution with p value of 0.85. The graphical representation of estimated versus observed frequencies, provided in Fig. 18, supports this conclusion.

4.2 Golf-tees data

In a field experiment, $N=250$ groups of golf tees were placed in a survey region, either exposed above the surrounding grass or hidden by it. They were surveyed by the 1999 statistics honor class at the University of St Andrews (Scotland), see Borchers and Buckland (2002). A total of $n=162$ groups of tees were observed, but a (potentially unknown) number is missed and needs to be estimated. Table 3 shows the corresponding frequency distribution. Figure 15 provides a plot of the log-ratios of successive frequencies and the count distribution.

It is clear that the log-ratio plot displays a linear relationship between log-ratios and log-counts, with a positive slope. It is reasonable to assume that a heterogeneous model would be suited to estimate population size, such as the LCMP estimator so far proposed. The chi-squared test reject the null hypothesis that the data follow a truncated Poisson with a p value ${<}$0.001. Moreover, $f_{1}$ is greater than $f_{2}$ and so on, leading to increased variance by increasing x values. Thus, the weighted least square model might be more suitable than the least square. The estimated regression parameter estimates are $\hat{\beta }_{0} = -0.268$ and $\hat{\beta }_{1} = 1$, i.e. $\hat{\beta }_{1}$ is on the boundary of the parameter space. Accordingly, the parameters of the zero-truncated Conway–Maxwell–Poisson model are $\hat{\lambda } = 0.765$ and $\hat{\nu }=0$, i.e. the geometric distribution is obtained. Zelterman’s estimator shows the highest degree of accuracy in terms of having the smallest bias, followed by LCMP. Turing and MLEPoi provide the least accuracy since they show a very large bias, as expected as the log-ratio plot suggests to avoid any estimator based on a homogeneous model. We would remark that the imposed (and necessary) constraint on $\hat{\beta }_1$ may limit the capacity of the LCMP estimator to recover the true population size if the underlying count distribution is far from being geometrically-distributed. However, as the LCMP-based estimator allows for heterogeneity, it provides better estimates than homogeneous population-based estimators. In Fig. 18 we compare estimated frequencies under the LCMP estimator with the homogeneous MLEPoi one and, furthermore, we add estimated frequencies according the MLE under the Geometric distribution. It is even more clear from the graph that the truncated Poisson distribution is not suitable for these data (Table 4).

4.3 Link (2003) data

Her we refer to an artificial dataset considered in Link (2003), see Table 5. These data are of particular interest as they show substantial heterogeneity (see Fig. 16) with a large number of maximum recaptures. Thus, we expect that all the considered estim ators, but the LCMP one, underestimate the population size. Indeed, the long tail of the count variable may lead to biased estimates even for the Zelterman’s estimator. Population size estimates are displayed in Table 6 and provide contradictory inference about N. Homogeneous population-based estimators shows very low estimates for $\hat{N}$ with small standard errors (a similar behavior was found in the simulation study), and the corresponding 95 % confidence intervals do not overlap with those obtained accounting for heterogeneity. Chao’s estimator provides a lower bound for N in presence of heterogeneity, and Zelterman’s estimator does not differ too much, but shows a very large standard error (as expected). The LCMP-based estimator seems to fit well the data, and provides an estimate of N in line with the values obtained in Link (2003) under other parametric distributions accounting for heterogeneity. Figure 18 shows the inability of the homogeneous truncated Poisson distribution to fit the data and the close performance of the LCMP and the Geometric MLE. This is not surprising as we estimate $\nu = 0.0856$, and, as $\nu$ approaches zero, the LCMP approaches the MLE under the geometric distribution.

Table 1 Frequency distribution of the cholera epidemic data

Table 2 Cholera data: population size estimates

Fig. 14

Cholera data: the log-ratio plot of $\log \left\{ (x+1)\frac{f_{x+1}}{f_{x}} \right\}$ versus $\log (x+1)$

Fig. 15

Golf tees data: the log-ratio plot of $\log \left\{ (x+1)\frac{f_{x+1}}{f_{x}} \right\}$ versus $\log (x+1)$

Table 3 Frequency distribution of golf-tees groups detected by eight observers

Table 4 Golf tees data: population size estimates (N $=$ 250)

Table 5 Frequency distribution of Link (2003) data

Fig. 16

Link (2003) data: the log-ratio plot of $\log \left\{ (x+1)\frac{f_{x+1}}{f_{x}} \right\}$ versus $\log (x+1)$

Table 6 Link (2003) data: population size estimates

Table 7 Frequency distribution of heroin users in Bangkok

Fig. 17

Heroin users in Bangkok: the log-ratio plot of $\log \left\{ (x+1)\frac{f_{x+1}}{f_{x}} \right\}$ versus $\log (x+1)$

Table 8 Heroin users in Bangkok data: population size estimates

4.4 Heroin drug users in Bangkok

The study used all data on drug use from 61 health treatment centers in the Bangkok metropolitan region collected by the Office of the Narcotics Control Board (ONCB), Ministry of the Prime Minister, which occurred from 1, October to 31, December in 2001. Data are presented in Table 7. From Fig. 17, the log-ratio plot suggests for the use of a heterogeneous model and the LCMP approach seems to fit the data well. A formal test reject the null hypothesis of homogeneity at with a p value $<$ 0.001. Accordingly, we look at the estimates of the population size under different assumptions. Results are displayed in Table 8. As in the Golf-tees data, the geometric distribution is obtained as a special case of the LCMP, i.e $\nu = 0$. The Zelterman’s estimator does differ too much from the LCMP estimator (with almost overlapping confidence intervals), whilst all the homogeneous estimators provide smaller sample sizes. Again, the LCMP and the MLE under the geometric distributions are equivalent in terms of model fit (see Fig. 18).

Fig. 18

Real data examples: estimated versus observed frequencies

5 Conclusion

A diversity of estimators in the capture–recapture field exists, being widely applied in many areas of interest. Here, we have introduced a new method of estimating the population size under a specific form of heterogeneity based on the Conway–Maxwell–Poisson distribution. We have also been able to see how accurate and precise the method is performing when it is compared to other frequently used estimators. Overall, the proposed estimator is more accurate as well as providing small bias in the homogeneous Poisson case which asymptotically disappears. It is also found that the new estimator performs well under different heterogeneous data generation processes (i.e. Geometric, Negative Binomial); hence, it improves existing heterogeneous estimators (e.g. Chao’s and Zelterman’s estimators). Although the proposed estimator showed a better performance in terms of accuracy, it evidently gave also the largest variation; nonetheless, the variation of the new estimator considerably decreases for large population size (1000 and more), as often in real-world applications. We also provided a formula of variance approximation of the new estimator. This variance formula is not only useful to determine the efficiency of estimating, but it can be also used to construct confidence intervals. In short, the new estimator can be an alternative form of population size estimation especially for large populations and heterogeneous capturing probabilities.

The use of the ratio plot allows us to avoid computational issues related to CMP distribution. Furthermore, by using the ratio plot, formal tests can be conducted on null hypotheses of zero-truncated Poisson, i.e. $H_0:\beta _1=0$, or geometric, i.e. $H_0:\beta _1=1$, data. The proposed LCMP estimator performs equivalently as the MLE under the Poisson and the geometric distribution, supporting that the use of the ratio plot, instead of computing the MLE under the CMP distribution, does not affect estimates. We have not reported these results, but they are available upon request.