1 Introduction

Ca\(^{2+}\) is a ubiquitous ion and second messenger that regulates many cellular functions ranging from exocytosis to cell proliferation occurring on different time scales (Berridge et al. 2003). Ca\(^{2+}\) is known to directly regulate several proteins, thereby implicitly controlling many cellular functions such as gene transcription, fertilization, and arterial vasodilation (Berridge et al. 2003). The sudden rise in cytoplasmic Ca\(^{2+}\) occurs due to the release of intracellular stored Ca\(^{2+}\) from the endoplasmic reticulum (ER), which accounts for 75\(\%\) of the intracellular stored Ca\(^{2+}\) concentration (Tran et al. 2000). Ca\(^{2+}\) is released from the ER due to the action of inositol 1,4,5-trisphosphate (IP\(_3\)) on inositol trisphosphate receptors (IP\(_3\)R) present on the ER membrane. This is preceded by a sequence of events in the plasma membrane (PM) in order to transduce the extracellular information to the second messenger IP\(_3\).

We are interested here in intracellular Ca\(^{2+}\) dynamics in endothelial cells (ECs), which form the inner lining of all blood vessels. Ca\(^{2+}\) release from the ER of ECs may be triggered by different stimuli including shear stress (Shen et al. 1992), hormones (Sage et al. 1989), and extracellular adenosine triphosphate (ATP) (Carter et al. 1990). The effect of ATP released by red blood cells (RBCs) on intracellular Ca\(^{2+}\) generation is particularly important because of ATP’s crucial role in regulating blood flow and maintaining vascular tone (Xu et al. 2017). RBCs release ATP under shear stress and cell deformation. ATP released by RBCs reacts with purinergic EC receptors (P2Y\(_2\)) (a class of membrane receptors that mediates vascular reactivity) to elicit the calcium reaction cascade in ECs. Subsequently, ECs release vasodilators such as nitric oxide (NO), which maintains vascular tone by countering the effects of endothelium-derived vasoconstrictors, such as endothelin and angiotensin-II (Davignon and Ganz 2004). In addition, NO inhibits platelet adherence and aggregation, proliferation of vascular smooth muscle cells (VSMC), and leukocyte adhesion and infiltration. Thus, understanding EC Ca\(^{2+}\) kinetics is of major interest.

There is a general consensus that the calcium pathway involves three main steps: (1) reaction of a ligand with a receptor on the EC surface, (2) generation of IP\(_3\) due to ligand-receptor binding, and (3) IP\(_3\)-induced channel opening on the ER membrane to release calcium from internal stores into the cytoplasm. The three main variables are thus (besides ATP) IP\(_3\) concentration, store calcium concentration, and and cytoplasmic calcium concentration, denoted, respectively, by \({\text {IP}}_3({\text {t}})\), \({\text {Ca}}_{{\text {s}}}({\text {t}})\), \({\text {Ca}}_{{\text {c}}}({\text {t}})\), which are all time-dependent variables. Several models are available that take into account the kinetics of these three quantities (Meyer and Stryer 1988; Wiesner et al. 1996, 1997; Plank et al. 2006, 2007; Silva et al. 2007; Comerford et al. 2008; Li et al. 2015). These models have successfully accounted for several experimental features, such as cytoplasmic Ca\(^{2+}\) peak amplitude, duration of peak, and the elevated resting Ca\(^{2+}\) concentration from its initial concentration. Additionally, some of these models have introduced several new variables into the model such as cytoplasmic Ca\(^{2+}\)-calmodulin(CaM)-activated endothelial nitric oxide synthase (eNOS) (Plank et al. 2007; Comerford et al. 2008) and transmembrane potential (Silva et al. 2007) across the PM. The authors in Refs. (Plank et al. 2007; Comerford et al. 2008) have further extended their model to include inhomogeneous distribution of ATP due to advection and diffusion and have suggested that atherosclerosis development is highly dependent on cytoplasmic Ca\(^{2+}\) concentration.

A main question is how do ECs manage to achieve intracellular homeostasis in the presence of ATP in the bloodstream. The concentration of ATP in blood plasma is maintained typically at a value of a few μM. This would mean that ECs are constantly in contact with ATP with different local ATP concentration, meaning that IP\(_3\) would be constantly activated, not enabling the ER to be fully refilled by calcium. In addition, experiments have shown (Carter et al. 1990) that ECs produce a single calcium peak in the presence of ATP. When ATP is removed after the calcium response from the plasma and then reintroduced after a few minutes later, no calcium cellular response was observed; a response is only observed after a certain period of time (about 20 min is allowed to elapse). However, the same EC responds to a different agonist, histamine, immediately. This clearly highlights the fact of desensitization or inactivity of membrane receptors to ATP for a period of time. It is worthwhile to bring attention that most of ECs in that experiment responded to ATP ( 10–100 μM concentrations) with a single transient peak before returning to resting Ca\(^{2+}\) concentration. Moreover, in the same experiment, a few number of ECs have complex oscillations as well as transient peak with elevated resting Ca\(^{2+}\) concentration.

In literature (Meyer and Stryer 1988; Dupont and Goldbeter 1993; Atri et al. 1993; Shen and Larter 1995; Dupont and Erneux 1997; Borghans et al. 1997; Marhl et al. 2000; Kummer et al. 2000; Schuster et al. 2002; Politi et al. 2006), most of Ca\(^{2+}\) models have been developed to understand the mechanism behind the cytoplasmic Ca\(^{2+}\) oscillations to agonists in various cells. These Ca\(^{2+}\) oscillations are generated due to two main pathways (1) the participation of cytoplasmic Ca\(^{2+}\) in activating or deactivating the IP\(_3\)R channels in the presence of constant IP\(_3\) concentration and (2) Ca\(^{2+}\)-induced IP\(_3\) generation and degradation due to positive or negative effects of rising cytoplasmic Ca\(^{2+}\) concentration. Furthermore, certainly, another way of possible Ca\(^{2+}\) oscillation is due to the phosphorylation and dephosphorylation of surface receptors by the protein kinase C (PKC), which is either activated due to the rising of diacylglycerol (DAG) concentration (Dupont et al. 2011) or both DAG and cytoplasmic Ca\(^{2+}\) (Cuthbertson and Chay 1991; Wang et al. 2007) concentrations. Thus, the essential ingredients in these models to have oscillation must contain at least a downstream positive or negative feedback pathway which could affect the upstream biochemical reactions. Additionally, these models can be considered as a homeostatic model if all primary variables oscillate about their resting concentrations.

Calcium evolution in time is not always oscillatory in nature. For example, in most ECs a single calcium peak is observed in the presence of agonist (e.g. ATP) (Carter et al. 1990). Several attempts (Wiesner et al. 1996; Plank et al. 2006; Silva et al. 2007) have been made to understand the occurrence of a single peak of Ca\(^{2+}\).

Because of the strategic location of ECs in vascular wall and its functions to maintain vascular homeostasis, the modeling of Ca\(^{2+}\) in ECs requires much more attentions to understand the detail kinetics of the Ca\(^{2+}\) dynamics. Several attempts have been made in past years to develop and understand the single peak cytoplasmic Ca\(^{2+}\) dynamics without including the surface receptor dynamics into their model (Wiesner et al. 1996; Plank et al. 2006; Silva et al. 2007). These models have basically been focused on the cytoplasmic Ca\(^{2+}\) peak as observed in experiments, and able to reproduce the homeostasis only in the absence of agonist concentration, but not when agonist is not removed. However, when these models are tested in the presence of agonists, a major deviation from post-response homeostatic conditions is revealed for cytoplasmic Ca\(^{2+}\), as well as for store Ca\(^{2+}\), and IP\(_3\). These facts, as well as the above experimental observations according to which ECs do not respond to agonists after their immediate reintroduction (Carter et al. 1990) may point to the fact that membrane receptors activation/deactivation can play a significant role. Along this line, some authors (Lemon et al. 2003) proposed a detailed ligand-activated receptor dynamics model in which they considered a closed cell model. This model was able to produce a robust transient peak. However, the post-response plateau of Ca\(^{2+}\) is found to be higher than the resting Ca\(^{2+}\) concentration (i.e., lack of homeostasis). This is due to positive feedback of cytoplasmic Ca\(^{2+}\) on IP\(_3\) generation (see below). In addition, this model considered some simplifications (1) a closed cell model was adopted, meaning that there is no exchange of Ca2+ with the external environment. However, the refilling of store Ca\(^{2+}\) (Putney 1986; Putney et al. 2001) must be achieved thanks to Ca\(^{2+}\) coming from the extracellular environment and (2) the phosphorylated receptors, free surface receptors which are phosphorylated due to the binding of ligands, were unable to recycle to free receptors when the ligands were washed out from the plasma. It is noteworthy to mention that we are exclusively aimed to develop a robust single Ca\(^{2+}\) peak homeostatic model.

Another model (Cuthbertson and Chay 1991) also took into account the phosphorylation and dephosphorylation of G-proteins and free surface receptors (due to the negative feedback from the PKC enzyme activated by the action of both DAG and cytoplasmic calcium).

The results obtained from this model, after mimicking agonist washing out from the plasma, are as follows: (1) the Ca\(^{2+}\) response from the cell was immediate with the same magnitude when the ligands were reintroduced again just after the occurrence of the calcium peak (1–50 s). This differs from experimental observations showing that a cell takes a minimum of 5 min to several hours to express a full response (Carter et al. 1990; Garrad et al. 1998) and (2) the number of free receptors do not reach initial concentration (concentrations of free receptors prior to ligands application) even after a quite long simulation time. We expect that under physiological conditions the phosphorylated receptors must be recycled to their initial concentration when ligands are removed from the plasma. Inspired by these models, we propose a further development in order to identify how recycling of receptors can be incorporated, and how a time delay of cell response, after reintroducing agonist just after calcium peak, can be modeled. Our improved version is able to provide answers in favor of the above experimental facts. We will make several direct comparisons with experimental results, showing a reasonably good agreement with the proposed model.

2 Method and model development

2.1 Main ingredients of the model

In this section, we will develop a minimal single EC Ca\(^{2+}\) dynamics model capable of reproducing several experimental results. A major issue accounted for this model is how an ECs can maintain Ca\(^{2+}\) homeostasis in the presence of a constant ATP supply. Since ATP is constantly released by RBCs in blood, the EC might be expected to continuously produce cytoplasmic Ca\(^{2+}\) in response to this agonist. At the same time, the EC is expected to restore intracellular Ca\(^{2+}\) homeostasis in order to protect its organelles from the toxic effects of an elevated cytoplasmic Ca\(^{2+}\) concentration. Indeed, the EC develops a protective mechanism by phosphorylating ATP-bound receptors, which means that these receptors are no longer able to activate G-proteins, which are membrane ATP sensors. This thus leads to a decline in IP\(_3\) generation, allowing the EC to restore intracellular homeostasis. Inspired by the study of Lemon et al. (2003) on receptor kinetics, we develop a modified version to study membrane receptor dynamics. When coupled to Ca\(^{2+}\) and IP\(_3\) dynamics, this model accounts for several documented responses of ECs to ligands such as ATP.

2.2 G-protein cascade

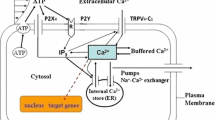
The first stage of calcium generation starts with the ATP reacting with the so-called purinergic (designated as P2Y\(_2\), see Fig. 1) receptors on the EC surface. This elicits a cascade of reactions. A key player is the G-protein (P2Y\(_2\) is a G-protein-coupled receptor), which transmits the signal from the outside to the inside of the EC. G-proteins are deactivated due to the hydrolysis of guanosine triphosphate (GTP) into guanosine diphosphate (GDP). So, the rate of change of G-protein concentration can be expressed as,

$$\begin{aligned} \frac{{\text {d}}[G]}{{\text {d}}t} = k_a \left( \delta + \rho _r\right) \left( [G_t]-[G]\right) - k_d[G], \end{aligned}$$
(1)

where [x] represents the concentration of a chemical species x, and \(k_a\) and \(k_d\) are the G-protein activation and deactivation rate constants, respectively. The ligand (ATP) concentration is denoted as [L] and that of free receptors is denoted by [R]. Once ATP reacts with receptors, it gives rise to the \({\text {LR}}\) complex whose concentration is denoted as \([{\text {LR}}]\). \([G_t]\) is the total concentration of G-protein molecules, and \(\delta\) is the G-protein intrinsic activity parameter, i.e., R can independently activate G-proteins without binding to ligands. It is reported in several experiments that G-protein is able to sense and transduce shear stress-induced signals to the cytoplasm (Chachisvilis et al. 2006; Storch et al. 2012). This explains the reason behind a non-zero basal IP\(_3\) concentration in the cytoplasm as reported by Felix et al. (1996) and Nollert et al. (1990) in the absence of ligands (ATP); see below. It is important to stress that the ATP produced by ECs due to shear stress could contribute to basal IP\(_3\) concentration. This formation of IP\(_3\) is possible only when ATP molecules bind with free receptors. The investigation of mechanisms that play a significant role in maintaining the basal IP\(_3\) concentration still remains an open area. Further experiments would be needed in order to better clarify this issue. Moreover, there is no quantitative data in literature reporting on the amount of ATP released at basal shear stress. It can be perceived from the works in Chachisvilis et al. (2006); Storch et al. (2012) that the shear induced basal IP\(_3\) plays a vital role in maintaining basal IP\(_3\) concentration without association of ligand-receptor. The ratio of receptors bound to ligands to the total number of P2Y\(_2\) receptors is \(\rho _r\) (which will be related to receptor and ligand concentration; see Subsection 2.4 for more details). This is for the moment viewed as a constant before including below the receptor dynamics into the model. We can simplify Eq. 1 by assuming that [G] activation and deactivation is governed by fast kinetics (Bennett et al. 2005), so that

$$\begin{aligned}{}[G] = [G_t]\frac{\rho _r + \delta }{\rho _r + \delta + K_g} \equiv [G_t] \lambda . \end{aligned}$$
(2)

where \(K_g = k_d/k_a\) and \(\lambda = \frac{\rho _r + \delta }{\rho _r + \delta + K_g}\)

Fig. 1
figure 1

Schematic of the Ca\(^{2+}\) homeostasis in the EC, where the abbreviations are, ATP: adensoine triphosphate, G: G-protein, PLC: phospholipase-C, PIP\(_2\): phosphatidylinositol 4,5-bisphosphate, DAG: diacylglycerol, IP\(_3\): 1,4,5-trisphosphate, IP\(_3\)R: 1,4,5-trisphosphate receptor, SOC: store-operated calcium channel, SERCA: sarco/endoplasmic reticulum Ca\(^{2+}\)-ATPase, PMCA: plasma membrane Ca\(^{2+}\)-ATPase, B: buffer proteins. Question marks (?) refer the influx of extracellular Ca\(^{2+}\) into the cytoplasm due to the action of ATP on P2X\(_4\) channel and shear stresses due to blood flow are not fully understood in experiments

Full size image

A remark is in order. Due to difference in the time scale of G-protein activation and deactivation, this approximation overestimates the IP\(_3\) peak (see supplementary information, Figure S2). However, the trend remains similar to the results of the full model, i.e. without adiabatic elimination of G-protein kinetics. This lends support to the fact that the adiabatic elimination is reasonable. Additionally, GTP bound G-protein activates the PLC-enzyme, which then forms the IP\(_3\) molecules by splitting PIP\(_2\) molecules. The rate of change of IP\(_3\) concentration, \([{\text {IP}}_3]\), can be defined as,

$$\begin{aligned} \frac{{\text {d}}\left[ IP_3\right] }{{\text {d}}t} = q_{\text {gen}}- q_{\text {deg}} , \end{aligned}$$
(3)

where \(q_{\text {gen}}\) and \(q_{\text {deg}}\) are the IP\(_3\) generation and degradation fluxes, respectively, which are defined below. There is a positive feedback from Ca\(^{2+}\) released from the ER, which triggers an increase in IP\(_3\) formation (Meyer and Stryer 1988), so that

$$\begin{aligned} q_{\text {gen}} =\gamma \lambda \frac{[{\text {Ca}}_c]}{K_1 + [{\text {Ca}}_c]}, \end{aligned}$$
(4)

with \(\gamma = {\alpha } [G_t][({\text {PIP}}_2)_t] / ( N_A {V_{\text {EC}}})\), where, the denominator containing the product of \(N_A\) and \(V_{\text {EC}}\) allows to convert IP\(_3\) generation in molar (M or mole/ltr). The entire cascade of reactions starting from G-protein activation to IP\(_3\) generation is lumped into a single flux term given by Eq. 4. The effective signal gain parameter is \(\alpha\), \(N_A\) is Avogadro number, \(V_{\text {EC}}\) is the EC volume, and \([({\text {PIP}}_2)_t]\) is the total number of phosphatidylinositol 4,5-bisphosphate (PIP\(_2\)) molecules. We here assume that there is no change in the concentration of PIP\(_2\) molecules, i.e., splitting and replenishing of PIP\(_2\) molecules is regulated by fast reactions (Bennett et al. 2005). This means that the effect of G-proteins and \([({\text {PIP}}_2)_t]\) enters as an effective multiplicative coefficient in this flux (in \(\gamma\)). The dissociation constant between the Ca\(^{2+}\) and PLC-enzyme is \(K_1\) and is considered as an important parameter for the cytoplasmic Ca\(^{2+}\) oscillations (Meyer and Stryer 1988). It turns out that keeping \(K_1\ne 0\) for ECs (single peak model) precludes return to homeostasis. Based on this observation, we will in the following set \(K_1=0\). \([{\text {Ca}}_c]\) is the cytoplasmic Ca\(^{2+}\) concentration. The rate of IP\(_3\) degradation due to the formation of IP\(_2\) or IP\(_4\) by kinases or phosphatases is given by

$$\begin{aligned} q_{\text {deg}} = k_2 \left[ {\text {IP}}_3\right] . \end{aligned}$$
(5)

where \(k_2\) is the IP\(_{3}\) degradation rate.

2.3 Intracellular calcium

The cytoplasm of an EC is a highly complex structure due to the complex shape of organelles and their arrangement with in the cytoplasm. The governing equation for the cytoplasmic Ca\(^{2+}\) concentration, \([{\text {Ca}}_c]\), is obtained by balancing the fluxes across the PM and ER membranes as shown in Fig. 2 and is given by Plank et al. (2006)

$$\begin{aligned} \frac{{\text {d}}\left[ {\text {Ca}}_c\right] }{{\text {d}}t} = \beta \left( q_{\text {rel}} - q_{\text {serca}} + q_{\text {leak}} + q_{\text {soc}} + q_{\text {in}}- q_{\text {pmca}}\right) , \end{aligned}$$
(6)
Fig. 2
figure 2

Intracellular fluxes across the plasma and ER membranes. Detailed definitions of these fluxes are given in the text

Full size image

where \(\beta\) is defined as a buffer factor for immobile buffer proteins only. The expression for \(\beta\) is obtained by assuming that the reaction between the buffer proteins and cytoplasmic Ca\(^{2+}\) is faster than the Ca\(^{2+}\) flux rates across the PM and ER membranes (detailed derivation and justification are given in supplementary information). Therefore, following (Wagner and Keizer 1994), we derive the expression for \(\beta\) as

$$\begin{aligned} \beta = \left\{ 1 + \frac{\left[ B_t\right] \frac{k_7}{k_6}}{\left( \frac{k_7}{k_6} + \left[ {\text {Ca}}_c\right] \right) ^2}\right\} ^{-1}. \end{aligned}$$
(7)

where \(k_6\) and \(k_7\) are the association and dissociation rates between the buffer proteins and cytoplasmic Ca\(^{2+}\), and \([B_t]\) is the total buffer protein concentration, a constant.

The fluxes \(q_{\text {rel}}\), \(q_{\text {serca}}\), \(q_{\text {leak}}\), \(q_{\text {soc}}\), \(q_{\text {in}}\), and \(q_{\text {pmca}}\) used in Eq. 6 are, respectively, the rates of change in the cytoplasmic Ca\(^{2+}\) concentration due to release through the IP\(_3\)R, uptake from the ER, a passive leak from the ER, ER-depleted influx from the extracellular space, a passive influx from the extracellular space, and efflux by the PM pump. The individual expressions for these fluxes are defined below. However, the expression for \(q_{\text {in}}\) is given in subsect. 2.6, and is physically interpreted as the Ca\(^{2+}\) influx required to maintain Ca\(^{2+}\) homeostasis in the absence of ATP. The IP\(_3\)-induced Ca\(^{2+}\) releasing from the ER is defined as

$$\begin{aligned} q_{\text {rel}} = k_3 \frac{\left[ {\text {IP}}_3\right] ^3}{K_2^{3} + \left[ {\text {IP}}_3\right] ^3} {\frac{ K_{i,{\text {Ca}}_c}^3}{\left[ {\text {Ca}}_c\right] ^{3} + K_{i,{\text {Ca}}_c}^{3}}} {\text {Ca}}_s , \end{aligned}$$
(8)

where \(k_3\) is the Ca\(^{2+}\) release rate from the ER, and \(K_2\) is the IP\(_3\) concentration at which half of the IP\(_3\)R sites are occupied by IP\(_3\) molecules; \(K_{i,{\text {Ca}}_c}\) is the cytoplasmic Ca\(^{2+}\) for half-maximal inhibition of IP\(_3\)R, and \(\left[ {\text {Ca}}_s\right]\) is the ER Ca\(^{2+}\) concentration. Equation 8 states that the Ca\(^{2+}\) release rate from the ER is due to binding of three IP\(_3\) molecules to the IP\(_3\)R. Moreover, several physiological IP\(_3\)R models are available in the literature in which both positive and negative effects of the cytoplasmic Ca\(^{2+}\), i.e., calcium-induced-calcium-release (CICR) and calcium-induced-calcium-inhibition on IP\(_3\)R activation, are considered (for details see (Dupont et al. 2016)). However, here we have only considered the latter because the effects of the former are not found in vascular ECs as modeled in Silva et al. (2007). In particular, we assume that the opening and closing of IP\(_3\)R channels are instantaneous. The Ca\(^{2+}\) uptake rate from the cytoplasm into the ER is defined by

$$\begin{aligned} q_{\text {serca}} = k_4 \frac{\left[ {\text {Ca}}_c\right] ^2}{K_{3}^2+ \left[ {\text {Ca}}_c\right] ^2}, \end{aligned}$$
(9)

where \(k_4\) is the Ca\(^{2+}\) uptake rate by sarco/endoplasmic reticulum Ca\(^{2+}\)-ATPase (SERCA) and \(K_3\) is the Michaelis-Menten constant. The SERCA pumps cytoplasmic Ca\(^{2+}\) into the ER by using energy from ATP. The rate of passive leak of Ca\(^{2+}\) from the ER is assumed to be due to the defects in the ER membrane or may be due to the fixed capacity of ER.

$$\begin{aligned} q_{\text {leak}} = k_5 [{\text {Ca}}_s] , \end{aligned}$$
(10)

where \(k_5\) is the Ca\(^{2+}\) leak rate from the ER. The linear dependence on \([{\text {Ca}}_s]\) have been verified, which would not be a limitation (taking for example a quadratic form, as in Plank et al. (2006), leaves our results practically unchanged; the \(k_5\) value will have a different dimension for the linear model adopted here; see Table 1).

In Putney et al. (2001), it has been reported that a channel is only activated when the ER Ca\(^{2+}\) concentration gets depleted due to IP\(_3\)-dependent Ca\(^{2+}\) release from the ER and is termed store-operated calcium channel (SOC). SOC is considered one of the important channels for ER Ca\(^{2+}\) replenishment, allowing the extracellular Ca\(^{2+}\) flux into the cytoplasm. The mechanism of SOC activation is now well understood. Due to the depletion of the ER Ca\(^{2+}\), a pathway is formed because of the interaction between the stromal interaction molecules (STIMs) and ORAIs in the ER and plasma membrane, respectively (Dupont et al. 2016). It is noteworthy to mention that these channels are switched off, STIMs and ORAIs get separated \({\text {i.e.,}}\) calcium influx is zero, when the store is completely refilled with Ca\(^{2+}\) (Thillaiappan et al. 2019; Putney 1986). We will see that this model reproduces the Ca\(^{2+}\) homeostasis both in the presence and absence of IP\(_3\). Thus, the rate of change of the cytoplasmic Ca\(^{2+}\) due to the SOC is written as Su et al. (2011)

$$\begin{aligned} q_{\text {soc}}&= k_{\text {soc}} \frac{1}{\left( 1+\frac{\left[ {\text {Ca}}_s\right] }{K_{\text {soc}}}\right) ^n}\left( \left[ {\text {Ca}}_{\text {ex}}\right] - \left[ {\text {Ca}}_c \right] \right)\times \left(\left[Ca_{s}\right](0)-\left[Ca_{s}\right]\right)\end{aligned} $$
(11)

where n is a constant, \(k_{\text {soc}}\) is the maximal Ca\(^{2+}\) influx rate through the SOC, and \(K_{\text {soc}}\) is the ER Ca\(^{2+}\) for the half-activation of the SOC. \(\left[ {\text {Ca}}_{\text {ex}}\right]\) and \(\left[ {\text {Ca}}_{s}\right] (0)\) are the external and initial ER Ca\(^{2+}\) concentrations (the homeostatic one), respectively. Equation 11 includes three important experimental observations: (1) the probability of SOC opening, (2) the fact that the amount of Ca\(^{2+}\) influx depends on the concentration gradient across the PM, and (3) the observation of no Ca\(^{2+}\) influx at resting conditions. The proposed model for SOC (Su et al. 2011) was modified by adding the last term in Eq. 11 to satisfy the third observation. \(q_{\text {in}}\) is the passive influx of Ca\(^{2+}\) due to defects in the PM, a constant whose expression is obtained in subsect. 2.6 by satisfying the EC homeostasis condition. Note that because \([{\text {Ca}}_{\text {ex}}] \gg [{\text {Ca}}_c]\) under physiological conditions, in what follows we will make the approximation that \([{\text {Ca}}_{\text {ex}}] - [{\text {Ca}}_c]\simeq [{\text {Ca}}_{\text {ex}}]\).

The cytoplasmic Ca\(^{2+}\) efflux rate from the cytoplasm into the extracellular space is defined as

$$\begin{aligned} q_{\text {pmca}} =k_8 \frac{\left[ {\text {Ca}}_c\right] ^2}{K_4^2 + \left[ {\text {Ca}}_c \right] ^2} , \end{aligned}$$
(12)

where \(k_8\) is the maximal Ca\(^{2+}\) efflux rate through plasma membrane Ca\(^{2+}\)-ATPase (PMCA), and \(K_4\) is the cytoplasmic Ca\(^{2+}\) concentration for the half-sites of PMCA. Note that the second power of [\({\text {Ca}}_c\)] is used in Eqs. 9 and 12 because both of these pumps transfer two Ca\(^{2+}\) ions from the cytoplasm to the ER and extracellular space, respectively, by consuming one ATP.

Similarly, the rate of change of Ca\(^{2+}\) in the ER, \([{\text {Ca}}_s]\), is obtained by balancing the fluxes across the ER membrane, namely

$$\begin{aligned} \frac{{\text {d}}\left[ Ca_s\right] }{{\text {d}}t} = v_r \left( q_{\text {serca}} - q_{\text {rel}} - q_{\text {leak}} \right) , \end{aligned}$$
(13)

where \(v_r\) is a volume scaling factor, i.e., the ratio between the cytoplasm and the ER volumes. Note that the three fluxes appearing above are the same fluxes that appear in Eq. 6. This results simply from mass conservation (exchange between ER and the rest of cytoplasm).

2.4 Receptor dynamics

When solving Eqs. 3, 6, and 13 (by using the different fluxes introduced above) for a constant value of \(\rho _r\), we obtained similar results for calcium pulses as in Plank et al. (2006) and other similar model (Li et al. 2015) (see Figure S1 in supplementary information). One important point is that the final steady state concentration of IP\(_3\), cytoplasmic and ER Ca\(^{2+}\) turn out to be significantly different from their physiological concentrations. In particular, the ER is not refilled, and IP\(_3\) remains at a significantly higher level than its initial value (see Figure S1 in supplementary information). In principle, one expects physiological systems to ensure homeostasis, i.e., different concentrations ultimately revert to their initial values before the application of a stimulus. By taking into account receptor dynamics, we can propose a model that can capture the essential expected physiological response of calcium kinetics. The model is based on the observation that receptors R exist in 4 different states: (1) unbound receptor, R, (2) bound receptor, LR (ligand-receptor complex), (3) phosphorylated receptor, \(R_p\), and (4) internalized receptor, \(R_I\) as shown in Fig. 3 (Lemon et al. 2003). One important assumption here is that phosphorylated receptors are no longer able to respond to the external ligands. Moreover, it is worthwhile to mention that the increase in phosphorylated receptor concentration leads to reduction in IP\(_3\) generation, thereby the release of Ca\(^{2+}\) from the ER. However, the actual reason for receptor phosphorylation (or desensitization) is still poorly understood. The rate of change of the total unphosphorylated receptor concentration, \([R_s] = [R] + [{\text {LR}}]\) becomes (this is derived using the fast kinetics approach),

$$\begin{aligned} \frac{{\text {d}}[R_s]}{{\text {d}}t} = k_r [R_t] - \left( k_r + k_p \frac{[L]}{K_r + [L]}\right) [R_s] - k_r [R_p], \end{aligned}$$
(14)

where \([R_t] = [R_s] + [R_p] + [R_I]\) is the total receptor concentration. The terms proportional to \(k_r\) sum up to \(k_r [R_I]\), implying that the internalized receptor can be recycled into membrane receptors (R or \({\text {LR}}\)). We have summed up [R] and [LR] into a single term, \([R_s]\), owing to the fact that these two unphosphorylated receptors are responsible for the activation of G-proteins and subsequently the formation of IP\(_3\) molecules. \(k_r\) and \(k_p\) are the rate constants at which \(R_I\) is recycled to R and \({\text {LR}}\) phosphorylated to \(R_p\), respectively. \(K_r = k_1^{-}/k_1^{+}\) is the unphosphorylated receptor dissociation constant, where \(k_1^{-}\) and \(k_1^{+}\) are respectively the forward and backward constants for the reversible reaction between L and R. Similarly, using the law of mass action, we can deduce the equation for the rate of change of the phosphorylated receptor concentration, \([R_p]\), i.e.,

$$\begin{aligned} \frac{{\text {d}}[R_p]}{{\text {d}}t} = k_p \frac{[L][R_s]}{K_r + [L]} - k_e[R_p]. \end{aligned}$$
(15)

This model is inspired by that of Lemon et al. (Lemon et al. 2003), which we have enriched by the fact that phosphorylated receptors \(R_p\) are converted into R in the absence of L. For that purpose, we have assumed that \({\text {LR}}\) is irreversibly phosphorylated into \(R_p\) and subsequently \(R_p\) is internalized and recycled to R at rates \(k_e\) and \(k_r\). This fact is witnessed in the second term of Eq. 15, i.e., in the absence of ligand, \([L]= 0\), the rate of change of unphosphorylated receptor, \(R_p\), is only dependent on the second term.

Fig. 3
figure 3

The red color enclosure in Fig. 1 represents the receptor and ligand binding dynamics. Free receptor, R, binds with a ligand, L, reversibly and forms a ligand-receptor complex, LR. This complex is irreversibly converted into the phosphorylated receptor, \(R_p\) and ligand, L and eventually, \(R_p\) converts into internalized receptor, \(R_I\) and then R

Full size image

In subsect. 2.2, we have assumed that \(\rho _r\) is a constant because we have implicitly assumed that the concentration of \({\text {LR}}\) remains constant. When taking into account desensitization, the concentration of \({\text {LR}}\) is no longer a constant as we know that \({\text {LR}}\) gets phosphorylated into \(R_p\) with time. The expression of \(\rho _r\) can be obtained by assuming that the formation of \({\text {LR}}\) complexes follow Michealis-Menten kinetics (rapid equilibrium approximation i.e. dissociation of \([{\text {LR}}]\) to \([L]+[R]\) is faster than the formation of \([R_p]\)) (Michaelis and Menten 1913) and using \([R_s] = [R] + [{\text {LR}}]\). This allows us to determine, \(\rho _r\), the ratio of receptors bound to ligands to the total number of P2Y\(_2\) receptors (the details are given in last section of the supplementary information)

$$\begin{aligned} \rho _r =\frac{[R_s][L]}{[R_t](K_r + [L])} \end{aligned}.$$

2.5 Summary of governing equations

Along with Eqs. 14 and 15, we present the expanded form of Eqs. 3, 6, and 13 by substituting the expressions for the fluxes mentioned in subsects. 2.2 and 2.3. These equations are

$$\begin{aligned} \frac{{\text {d}}[R_s]}{{\text {d}}t}= & {} k_r [R_t] - \left( k_r + k_p \frac{[L]}{K_r + [L]}\right) [R_s] - k_r [R_p], \end{aligned}$$
(16)
$$\begin{aligned} \frac{{\text {d}}[R_p]}{{\text {d}}t}= & {} k_p \frac{[L][R_s]}{K_r + [L]} - k_e[R_p], \end{aligned}$$
(17)
$$\begin{aligned} \frac{{\text {d}}[{\text {IP}}_3]}{{\text {d}}t}= & {} \gamma \lambda \frac{[{\text {Ca}}_c]}{K_1 + [{\text {Ca}}_c]} -k_2[{\text {IP}}_3] , \end{aligned}$$
(18)
$$\begin{aligned} \frac{{\text {d}}[{\text {Ca}}_c]}{{\text {d}}t}= & {} \left\{ 1 + \frac{\left[ B_t\right] \frac{k_7}{k_6}}{\left( \frac{k_7}{k_6} + \left[ {\text {Ca}}_c\right] \right) ^2}\right\} ^{-1} \nonumber \\&\left\{ \left( k_3 \frac{\left[ {\text {IP}}_3\right] ^3}{K_2^{3} +\left[ {\text {IP}}_3\right] ^3} \frac{ K_{i,{\text {Ca}}_c}^3}{\left[ {\text {Ca}}_c\right] ^{3} +K_{i,{\text {Ca}}_c}^{3}} + k_5\right) [{\text {Ca}}_s]\right. \nonumber \\&-k_4 \frac{\left[ {\text {Ca}}_c\right] ^2}{K_{3}^2+ \left[ {\text {Ca}}_c\right] ^2} \nonumber \\&+k_{\text {soc}} \frac{1}{\left( 1+\frac{\left[ {\text {Ca}}_s\right] }{K_{\text {soc}}}\right) ^n}\ \left[ {\text {Ca}}_{\text {ex}}\right] \left( \left[ {\text {Ca}}_{s}\right] (0)- \left[ {\text {Ca}}_s\right] \right) \nonumber \\&\left. + q_{\text {in}}-k_8 \frac{\left[ {\text {Ca}}_c\right] ^2}{K_4^2 + \left[ {\text {Ca}}_c\right] ^2} \right\} , \end{aligned}$$
(19)
$$\begin{aligned} \frac{{\text {d}}[{\text {Ca}}_s]}{{\text {d}}t}= & {} -v_r \left\{ \left( k_3 \frac{\left[ {\text {IP}}\right] ^3}{K_2^{3} + \left[ {\text {IP}}\right] ^3} \frac{ K_{i,{\text {Ca}}_c}^3}{\left[ {\text {Ca}}_c \right] ^{3} + K_{i,{\text {Ca}}_c}^{3}} + k_5\right) \right. \nonumber \\&\left. [{\text {Ca}}_s] -k_4 \frac{\left[ {\text {Ca}}_c\right] ^2}{K_{3}^2+ \left[ {\text {Ca}}_c\right] ^2}\right\} . \end{aligned}$$
(20)

Note: the right hand side of the last equation contains (with opposite signs) the same first three terms in the Eq. 19 due to mass conservation (these terms express the exchange of Ca2+ between the ER and the rest of the cytoplasm).

2.6 Homeostasis concentration

The homeostatic concentration in our simulation corresponds to the initial concentration which is maintained within the EC in the absence of ligand, \([L] = 0\). The initial concentration of the cytoplasmic Ca\(^{2+}\) (\([{\text {Ca}}_c](0)\)) and IP\(_3\), (\([{\text {IP}}_3](0)\)) are assumed to have typical values of 100 nM (Billaud et al. 2014) and 10 nM (Lemon et al. 2003), respectively. The initial ER Ca\(^{2+}\) concentration (\([{\text {Ca}}_s](0)\)) is obtained by setting Eq. 20 to zero for the given initial cytoplasmic Ca\(^{2+}\) and IP\(_3\) concentrations. Furthermore, setting Eqs. 16 and 17 to zero for \([L] = 0\), we obtain the initial concentration for the unphosphorylated receptor, \([R_s](0) = [R_t]\) and the phosphorylated receptor, \([R_p](0) = 0\). The initial concentration of all these variables are listed in Table 2. The value of the constant \(\delta\) (we have discussed the importance of \(\delta\) in subsect. 2.2) is obtained by setting Eq. 18 to zero for the given initial cytoplasmic and IP\(_3\) concentrations at \([L] = 0\), we get

$$\begin{aligned} \delta =\displaystyle {\frac{k_2 [{\text {IP}}_3](0) K_g}{\frac{[{\text {Ca}}_c](0)}{K_1 + [{\text {Ca}}_c](0)} \gamma - k_2 [{\text {IP}}_3](0)}}. \end{aligned}$$

For the constant influx, \(q_{\text {in}}\), we set Eq. 19 to zero. After rearranging the obtained expression (using conditions of initial cytoplasmic and ER Ca\(^{2+}\) and IP\(_3\)), we obtain

$$\begin{aligned} q_{\text {in}} = k_8 \frac{([{\text {Ca}}_c](0))^2}{K_4^2 + ([{\text {Ca}}_c](0))^2}. \end{aligned}$$

2.7 Parameter values

The parameter values used in this model are listed in Table 1. Most of the parameter values for the intracellular Ca\(^{2+}\) modeling are taken from Plank et al. (2006), and a few of them are slightly adjusted in order to capture the qualitative trend of the intracellular Ca\(^{2+}\) concentration observed in experiments. The parameter values for the receptor and G-protein modeling are obtained from Lemon et al. (2003), and the value of the parameter \(k_p\) is slightly changed in order to confine the ER Ca\(^{2+}\) refilling within a timescale of 500 s (according to Wiesner et al. (1996)). The importance of the parameter \(k_r\) is discussed in Sect. 3. The \(k_{\text {soc}}\) value is also slightly adjusted to ensure that the refilling of ER occurs properly and within a timescale of 500 s. Taking the value of \(k_8\) equal (or close) to that of \(k_4\) guarantees a smooth decrease of the cytoplasmic Ca\(^{2+}\) concentration curve after the transient peak occurs. Moreover, we have slightly changed the values of \(K_2\) and \(k_5\) so that we can get the initial Ca\(^{2+}\) concentration of ER closer to the physiological concentration of 500 nM (Pecze et al. 2015).

Table 1 Model parameter values
Full size table
Table 2 Model initial conditions
Full size table

3 Results and discussion

We have systematically solved the set of Eqs. 17–21 and analyzed the evolution of all the relevant variables. Inspired by several experiments (Mo et al. 1991; Carter et al. 1990; Malli et al. 2005; Colden-Stanfield et al. 1987; Jacob et al. 1988; Yang et al. 2001; Zhu and He 2005), we test our model’s ability to predict specific results such as calcium signal behavior due to a blockage of extracellular calcium and the response of calcium due to the removal of agonist at a particular moment after the calcium peak occurs.

3.1 General discussion of the outcome of the model

In this section we are going first to describe the main results implied by our model, while in the next section we will directly confront some of our predictions with existing experiments.

3.1.1 Receptor desensitization affects intracellular homeostasis

An interesting fact is that (see Fig. 4) the model shows that when an EC is stimulated with a constant ATP concentration, i.e., \([L] = 300\) nM for a long period of time, the intracellular concentration of IP\(_3\) (Fig. 4c), intracellular cytoplasmic Ca\(^{2+}\) (Fig. 4d), and ER Ca\(^{2+}\) (Fig. 4e) return naturally back to their initial concentration (homeostasis). This behavior is related to the exponential decay of unphosphorylated receptor concentration as shown in Fig. 4a, which in turn causes a decrease in IP\(_3\) generation after a transient peak at 15 s as shown in Fig. 4c. However, the transient peak time is dose-dependent; for example, the higher the ATP concentration, the faster are the EC response and IP\(_3\) transient peak. Figure 4d shows that the cytoplasmic Ca\(^{2+}\) and IP\(_3\) peak occur approximately at the same time. This is a direct consequence of the fact that a maximum of IP\(_3\) leads to a maximal release from the internal store. Another fact is that due to a prolonged presence of ligand, the concentration of unphosphorylated receptor continuously decreases to a minimal value, leading to desensitization of receptors, so that IP\(_3\) concentration is able to return to its homeostatic concentration. This also triggers a decrease in Ca\(^{2+}\) release from the ER, whereas Ca\(^{2+}\) uptake from the cytoplasm (through the SERCA, as shown in Fig. 4e) continues to operate allowing for a refilling of the internal store (ER). Moreover, as long as the ATP remains in the plasma, the unphosphorylated receptor concentration remains at its minimal concentration. Note that a higher unphosphorylated receptor concentration can be obtained by increasing the rate constants \(k_e\) and \(k_r\). These constants are responsible for the conversion of phosphorylated receptors to the unbound receptors by following two steps, i.e., \(R_p\) to \(R_I\) and \(R_I\) to R. Additionally, the phosphorylated receptors reach a transient peak (as shown in Fig. 4b) due to the availability of a minimal number of unphosphorylated receptors to bind with the external ATP in order to form phosphorylated receptors. From Fig. 4b, it is also evident that the phosphorylated receptor concentration decreases slowly due to the recycling of phosphorylated receptors to unbound receptors by undergoing an intermediate receptor state, \(R_I\).

It is worthwhile to emphasize the main difference between the present model and previous ones (Wiesner et al. 1996, 1997; Plank et al. 2006, 2007; Silva et al. 2007; Comerford et al. 2008; Li et al. 2015). One of the main criticisms is that previous models of EC Ca\(^{2+}\) do not recover the evolution with time towards intracellular homeostasis for any of the quantities at play namely, [i(t)], \([{\text {Ca}}_c(t)]\), and \([{\text {Ca}}_s(t)]\)), as shown in Figure S1 (supplementary information). Figure S1 (supplementary information) demonstrates that the intracellular cytoplasmic Ca2+ concentrations remain significantly above the initial concentration when the EC is stimulated with a constant ATP, \([L] = 300\) nM. The present model is able to recover the homeostatic conditions provided receptor desensitization is taken into account.

Fig. 4
figure 4

Variation of concentrations with time for a single EC stimulated by a constant ATP, [L] = 300 nM: a unphosphorylated receptor concentration; b phosphorylated receptor concentration; c inositol trisphosphate concentration; (d) cytoplasmic Ca\(^{2+}\) concentration; e store Ca\(^{2+}\) concentration. Normal refers to the case when an EC is stimulated for 500 s, and ATP Washed refers to the case when an EC is stimulated for 150 s

Full size image

3.1.2 Faster intracellular homeostasis in absence of ATP

Most of the experiments (Mo et al. 1991; Carter et al. 1990) have been performed by stimulating ECs for a fixed period of time with a constant ligand concentration followed by washing the stimulus away in order to investigate the trailing cytoplasmic Ca\(^{2+}\) concentration in the absence of the ligand. The trailing cytoplasmic Ca\(^{2+}\) concentration refers to the concentration after the transient peak. It has been found (Mo et al. 1991) that the cytoplasmic Ca\(^{2+}\) concentration immediately returns to its initial concentration when ATP is removed after stimulating the EC for any period of time. However, no experimental data are available for the ER Ca\(^{2+}\) and IP\(_3\) concentrations due to the experimental difficulties associated with obtaining these values. We have simulated this experimental scenario (the return of cytoplasmic Ca\(^{2+}\) to its initial concentration) by setting the ATP concentration to zero (i.e., \([L] = 0\)) after stimulating an EC for 150 s. Figure 4a (black dotted line) shows that the unphosphorylated receptor concentration increases due to the conversion of phosphorylated to unbound receptors. This increase is inevitable because of the absence of ATP and hence its inability to phosphorylate the unbound receptors. As a consequence, the IP\(_3\) concentration immediately returns to its initial level at the time when ATP is removed from the plasma, as shown in Fig. 4c. Furthermore, cytoplasmic Ca\(^{2+}\) (as shown in Fig. 4d) reverts to its initial concentration due to the pumping of cytoplasmic Ca\(^{2+}\) to the ER and the extracellular space. Additionally, Fig. 4e shows that the ER is completely refilled to its initial concentration. This is due only to Ca\(^{2+}\) uptake from the cytoplasm rather than to Ca\(^{2+}\) release from the ER to the cytoplasm in the absence of IP\(_3\). Thus, Fig. 4 clearly reveals that intracellular homeostasis is achieved faster in the absence of ATP than in the case of maintaining a constant ATP for a prolonged period, which means that EC intracellular homeostasis basically depends upon the ATP stimulation time.

3.1.3 Extracellular Ca\(^{2+}\) is responsible for ER refilling

Some Ca\(^{2+}\) dynamics models are able to explain the oscillations of intracellular Ca\(^{2+}\) concentrations without considering Ca\(^{2+}\) fluxes across the PM (Meyer and Stryer 1988; Sage et al. 1989). However, in most experiments (Carter et al. 1990; Sage et al. 1989) on ECs, a single transient peak followed by a plateau has been observed. This behavior results from the balance between Ca\(^{2+}\) fluxes across the ER membrane and the PM. In order to experimentally elucidate the role of extracellular Ca\(^{2+}\) in maintaining the cytoplasmic and ER Ca\(^{2+}\) homeostatic concentrations, as well as to understand the pathways (Lückhoff and Busse 1986; Yang et al. 2001; Malli et al. 2005) and the regulation of downstream molecules (Carter and Pearson 1992), the Ca\(^{2+}\) chelating agent EGTA (ethylene glycol-bis-N,N,N',N'- tetraacetic acid) is commonly added to the extracellular solution where it binds with the free extracellular Ca\(^{2+}\). The binding of Ca\(^{2+}\) to EGTA blocks the influx of Ca\(^{2+}\) from the extracellular environment into the cytoplasm. To understand the effect of EGTA in the simulations, we have set \(q_{\text {in}}\) and \(q_{\text {soc}}\) to zero. This has two consequences (see in Fig. 5): (1) the trailing (or steady) cytoplasmic concentration is lower than its initial concentration, and (2) the ER Ca\(^{2+}\) continues to be depleted, without any tendency of refilling towards its homeostatic concentration. Both facts are in agreement with experiments (Yamarnoto et al. 1995; Malli et al. 2007). In conclusion of this section, the inhibition of calcium entry from the extracellular space leads to undershooting of intracellular calcium, and the lack of refilling of ER Ca\(^{2+}\). In both cases, the relevant pathway is associated with the SOC; as seen in Eq. 11, the corresponding flux results from the deviation from homeostatic ER concentration, and its inhibition precludes the ER from getting back to homeostasis. We found that among the two influxes across the cytoplasmic membrane (\(q_{{\text {min}}}\) and \(q_{{\text {soc}}}\)), the SOC is dominant, in agreement with experimental findings (Malli et al. 2005, 2007).

Fig. 5
figure 5

Comparison of theoretical model variable results for a single EC stimulated by a constant ATP, [L] = 300 nM under physiological conditions (Normal) and no external Ca\(^{2+}\) (EGTA): a cytoplasmic Ca\(^{2+}\) concentration; b store Ca\(^{2+}\) concentration

Full size image

3.1.4 Variation of Ca\(^{2+}\) transient peak in ECs due to the receptor affinity

In experiments, it has been reported that a given ligand concentration can yield different amplitudes of cytoplasmic Ca\(^{2+}\) peak for individual cells originating from the same cell line (Mahama and Linderman 1994). Furthermore, when considering the same origin of ECs subjected to different agonists at the same concentration, it has been observed that the Ca\(^{2+}\) peak amplitude depends on the type of ligand, Carter et al. (1990); IJzendoorn et al. (1996). The first observation may be explained as being due to intercellular differences in the receptor concentration, the size of the cell, PLC activity or ER Ca\(^{2+}\) capacity (Mahama and Linderman 1994), whereas the second observation may attributable to variations in ligand affinity to their respective membrane receptors. This second observation (different agonists with the same EC) lends itself to a simpler interpretation as compared to the first one. Different agonists are expected to have different receptor affinity. We have thus explored this scenario by varying the dissociation constant, \(K_r\), in the range of 0.8\(-\)12.5 μM for a fixed 300 nM ligand concentration. Figure 6b displays the effect of affinity on the cytoplasmic Ca\(^{2+}\) peak. Note that increasing the receptor dissociation constant, \(K_r\), means a weaker interaction between the P2Y\(_2\) receptor and the ligand. This naturally leads to a decrease in cytoplasmic Ca\(^{2+}\) peak since this implies a slower decay of unphosphorylated receptors, resulting in fewer IP\(_3\) molecule formation as shown in Fig. 6a. The first observation (i.e., different cells of the same cell line produce different amplitudes) can be explained by randomly selecting parameter values from the Gaussian distribution around the mean parameter values (Mahama and Linderman 1994).

Fig. 6
figure 6

Theoretical model variable results for a single EC stimulated with [L] = 300 nM and by varying the P2Y\(_2\) receptor dissociation constant, \(K_r\): a unphosphorylated receptor concentration; b cytoplasmic Ca\(^{2+}\) concentration

Full size image

3.1.5 Saturation of transient peak with increasing ATP concentration

Figure 7 shows that the cytoplasmic Ca\(^{2+}\) peak concentration gets saturated with increasing of ATP concentration. The dependence of the cytoplasmic Ca\(^{2+}\) peak on ATP concentration is sigmoidal, which is commonly encountered in many biological processes. This is due to the fact that the decay of the unphosphorylated receptors is fast. As a result, IP\(_3\) formation gets saturated with the fast decay of unphosphorylated receptors. Due to the saturation of IP\(_3\) formation, a fixed quantity of Ca\(^{2+}\) is released from the ER that leads to saturation of the cytoplasmic Ca\(^{2+}\) peak.

Fig. 7
figure 7

Variation of peak cytoplasmic Ca\(^{2+}\) concentration with ATP, [L] concentration

Full size image

3.1.6 Elevated cytoplasmic Ca\(^{2+}\) depends on receptor recycling rate

Many experimental studies have reported that the steady state cytoplasmic Ca\(^{2+}\) concentration (the plateau after the peak) can sometimes be more than double that of the initial concentration (Colden-Stanfield et al. 1987; Jacob et al. 1988; Yang et al. 2001; Zhu and He 2005). This means that the cell may not return to its homeostatic condition, as one would expect in vivo. We have seen before that our model can account for homeostatic recovery, provided the phosphorylated receptor recycling rate \(k_r\) is sufficiently small enough (see Fig. 4). However, if the recycling rate is varied, our model can still capture the fact that the final Ca\(^{2+}\) concentration is higher than the homeostatic one. Figure 8a shows that an increase in \(k_r\), results in a higher steady unphosphorylated receptor concentration. This means that the phosphorylated receptors are rapidly recycled into unphosphorylated receptors in the presence of sufficiently high ATP concentration. However, the initial decaying of unphosphorylated receptors remains unchanged with changing \(k_r\). The cytoplasmic Ca\(^{2+}\) concentration change (as shown in Fig. 8b) is due to the elevated unphosphorylated concentration. As long as the unphosphorylated receptor concentration remains elevated, IP\(_3\) molecules are continuously activated, triggering further release of Ca\(^{2+}\) from the ER. However, no change in the cytoplasmic Ca\(^{2+}\) transient peak is observed upon variation of \(k_r\). In conclusion, it is tempting to speculate that the non recovery of homeostasis may be associated with an in vitro alteration of the recycling rate.

Fig. 8
figure 8

Theoretical model variable results for a single EC stimulated by a constant ATP, [L] = 300 nM as a function of the receptor recycling rate constant, \(k_r\): a unphosphorylated receptor concentration; b cytoplasmic Ca\(^{2+}\) concentration

Full size image

3.2 Direct model confrontation with experimental data

Here we confront our model with several experimental results. In order to make a comparison with the proposed model results, we have dimensionalized the cytoplasmic Ca\(^{2+}\) concentrations with their corresponding maximum cytoplasmic Ca\(^{2+}\) concentrations.

3.2.1 Calcium homeostasis recovery

In an experimental study by (Carter et al. 1990), the response (cytoplasmic Ca\(^{2+}\) concentration) of a human umbilical-vein EC (HUVEC) is analyzed by stimulating ECs with 100 μM concentrations of ATP. At the beginning of the stimulation, a rapid rise in the cytoplasmic Ca\(^{2+}\) concentration from its basal concentration is observed. This is due to the release of IP\(_3\) dependent Ca\(^{2+}\) from the ER. The cytoplasmic Ca\(^{2+}\) concentration reaches a peak at \(\sim\) 6 s and subsequently, it returns to its basal concentration. Their results are reported in Fig. 9a (symbols). We have confronted our model to this observation by taking the same ATP concentration as in the experiments. Our results are shown in Fig. 9a (solid line). Overall the model reproduces reasonably well the recovery towards homeostasis and the duration of the peak. It must be noted, however, that if the non-dimensionlized result of the cytoplasmic Ca\(^{2+}\) concentration of our model agrees with the non-dimensionalized experimental result, our model overestimates the amplitude of maximal calcium peak (see inset in Fig. 9a), when the physical value of cytoplasmic Ca\(^{2+}\) concentration is compared (instead of dimensionalized one). Certainly more systematic adaptation of model parameters is required to have a better agreement of the model and experimental results. We have tried to find the proper parameters in order to have better agreement of the physical cytoplasmic Ca\(^{2+}\) concentration of our result with the experimental result. We have attempted to vary the values of kinetic constant \(k_2\) (the IP\(_3\) degradation rate constant; Eq. 19) from 0.2 to 0.62 s\(^{-1}\). These value are within the range of values reported in the experiments, namely \(k_2\simeq\) 0.001–2 s\(^{-1}\) (Mahama and Linderman 1994). Taking for \(k_2\) =0.62 s\(^{-1}\) provides a much better agreement (Fig. 9b).

3.2.2 Homologous receptor desensitization

A central question concerns the ECs response to a second ATP stimulation after a first stimulation has been applied for a certain time and then washed out. To answer this question (Carter et al. 1990) have performed an experimental study to answer this question. For that purpose they applied ATP to ECs for a certain time, then removed it for some time, before stimulating again with ATP. Figure 9c shows that stimulating again ECs by ATP leads to no subsequent cytoplasmic Ca\(^{2+}\) response. In fact they have shown that a second calcium response due to second ATP stimulation, is seen only if the second ATP stimulation takes place after some time (from 5 to 20 min). As anticipated when building our model, this observation is a hint to the existence of some desensitization of receptors by ATP. The result from our model also reveal the absence of calcium response during second stimulation. This is to be contrasted with other models (Cuthbertson and Chay 1991; Wang et al. 2007) which predict an immediate response of the cell following the application of agonist (Figure S4, supplementary information). Note, however, that a second response of ECs requires a maximum time of 20 min to respond a second ATP stimulation, whereas our model predicts about more than 2 h (see inset Fig. 9c). Here again, we did not enforce our parameters to provide a better agreement, but have selected most of parameters from several experimental estimates. Still, we believe that further improvement will be possible in the future, by looking for best fits, as we did above for \(k_2\). We hope to dig further into this question in a future work.

3.2.3 Role of the extracellular calcium on homeostasis

In another experimental validation of the proposed model, we used the experimental result of Yamamoto et al. (2000) in which they measured the cytoplasmic Ca\(^{2+}\) concentration in the presence of exogenous EGTA (ethylene glycol-bis-N,N,N’,N’-tetraacetic acid). EGTA binds to free extracellular calcium, preventing then extracellular calcium to enter the cytoplasm. They found that the final (Fig. 9d) cytoplasmic calcium concentration is lower than the initial one (i.e. lack of homeostasis). This indicates that extracellular calcium is essential for recovery of initial cytoplasmic calcium concentration. We have simulated this experiment by setting \(q_{\text {soc}}\) and \(q_{in}\) (entering Eq. 19) to zero (further discussions about the effects of EGTA on the cytoplasmic and store Ca\(^{2+}\), has been given in subsection 3.1.3). The predicted result regarding the decrease in the dimensionless cytoplasmic Ca\(^{2+}\), after the peak of cytoplasmic Ca\(^{2+}\), has a good agreement with the experimental result (Fig. 9d).

Fig. 9
figure 9

Experimental validations of the proposed Ca\(^{2+}\) dynamics model: a the comparison of the dimensionless cytoplasmic Ca\(^{2+}\) concentration obtained from the proposed model with the experimental result is done in the presence of 100 μM of ATP concentrations for 60 s (Experimental result: Fig. 1a (Carter et al. 1990)). Inset represents the comparison of physical cytoplasmic Ca\(^{2+}\) concentration of the proposed model with the experimental result. b A better agreement result (extension of Fig. 9a) between the physical cytoplasmic Ca\(^{2+}\) concentration of the proposed model and the experimental result is acquired by setting the parameter \(k_2\) to 0.62 s\(^{-1}\) (Eq. 18); c the dimensionless cytoplasmic Ca\(^{2+}\) concentration is obtained when the EC is stimulated with 100 μM concentrations of ATP for 40 s and followed by washing out ATP from the solution and it is then applied after 60 s for 40 s (Experimental result: Fig. 2 (Carter et al. 1990)). Inset shows the time taken by the EC to respond the second dose of 100 μM concentrations of ATP (model prediction). The black bold line (below x-axis) represents the time at which ATP is injected into the solution; d the trailing dimensionless cytoplasmic Ca\(^{2+}\) concentration is obtained when the EC is stimulated with 500 nM of ATP concentrations in the presence of chelator, EGTA (ethylene glycol-bis-N,N,N’,N’-tetraacetic acid) in the extracellular space (Experimental result: Fig. 1c (Yamamoto et al. 2000))

Full size image

Finally some remarks are in order. Due to the limited availability of experimental data for the ER Ca\(^{2+}\) and IP\(_3\) concentrations, we have focused on the validation of the experimental cytoplasmic Ca\(^{2+}\) since measurement of cytoplasmic Ca\(^{2+}\) concentration with the help of fluorescence is relatively easier than the ER Ca\(^{2+}\). Owing to difficulties in loading the Ca\(^{2+}\)-sensing fluorescent dyes in the ER (Samira et al. 2013), it is rarely measured in experiments. However, several new technologies (Mark et al. 2015; Dhandapani et al. 2021) have been developed to measure the ER Ca\(^{2+}\) concentrations but it is still a matter of debate regarding the accuracy of the measured data. Similarly there are certain difficulties associated with the quantitative measurement of IP\(_3\) molecules and tracking of PIP\(_2\) molecules from where IP\(_3\) molecules are formed (Miyamoto and Mikoshiba 2017). Therefore most reported data focus on cytoplasmic Ca\(^{2+}\) concentrations. However, the complete validation of Ca\(^{2+}\) dynamics model with all the measured intracellular Ca\(^{2+}\) dynamics variables, such as \({\text {IP}}_3\), \({\text {Ca}}_c\), and \({\text {Ca}}_s\), would be an interesting topic for future research.

4 Conclusion

In this work, we have developed a homeostatic Ca\(^{2+}\) dynamics model in which the intracellular EC homeostasis depends on receptor dynamics. We have shown that the model is able to capture various experimental observations including the effect of stimulating ECs with ATP for a fixed time before washing the stimulus out, the extracellular Ca\(^{2+}\)-dependent ER Ca\(^{2+}\) refilling, the reason for varying Ca\(^{2+}\) transients in different experiments on even in the same EC, the saturation of cytoplasmic Ca\(^{2+}\) with increasing ATP concentration, and the cause of elevated cytoplasmic Ca\(^{2+}\) concentration levels.

The current Ca\(^{2+}\) model is primarily focused on how the EC is able to manage intracellular homeostatic concentrations in the presence of ATP. However, in the experiment of Carter et al. (1990), some of the ECs exhibit oscillation of cytoplasmic Ca\(^{2+}\) concentration. It would be interesting to enrich our model in order to account for oscillations. Several models in the past have successfully accounted for Ca\(^{2+}\) oscillation in the presence of agonists as discussed at the beginning of the introduction. Inspired by several models (Cuthbertson and Chay 1991; Dupont and Erneux 1997; Marhl et al. 2000; Kummer et al. 2000; Schuster et al. 2002; Politi et al. 2006; Dupont et al. 2011), leading to the oscillation, we believe that incorporating additional feedback pathways (either positive or negative or both) into the model is necessary. We have in mind certain feedback pathways which would control the dynamics of receptors. For instance, the response of the present model due to ATP is controlled by the competition between the timescales of phosphorylation of the free receptors and formation of the free receptors from the phosphorylated receptors. In order to favor oscillations, these timescales must be tuned with the feedback pathways from downstream reactions as well as with the dynamics of intracellular variables. For that purpose, a well-designed experimental protocol would be needed to gain insight into the receptor controlling feedback pathways. This would lead to an interesting future research perspective.

Finally, in a recent work, Zhang et al. (2018) have proposed a phenomenological ATP release model when RBCs are subjected to flow. The concentration of ATP in fluid, bloodstream, depends on the several factors (Gou et al. 2021) such as geometry of vascular network, flow condition, hematocrit concentration, and enzymatic reaction of enzymes present on the EC surface. These ATP molecules finally lead to activation of calcium signaling in ECs. In order to understand the effects of RBC dynamics and vascular diseases such as atherosclerosis, aneurysm, and stroke on EC response, it is indispensable to study two things together. In addition, a through study, the coupling between the RBC’s ATP release and EC Ca\(^{2+}\) signaling, is needed intending to understand the origin of EC related diseases.

In future work, we would like to study the blood flow simulation by explicitly taking into account RBCs and their ATP release as well as reaction with ECs triggering calcium for simple and complex vascular networks.