Modeling of $\hbox {TRPV}_{4}\hbox {-C}_{1}$-mediated calcium signaling in vascular endothelial cells induced by fluid shear stress and ATP

Abstract

The calcium signaling plays a vital role in flow-dependent vascular endothelial cell (VEC) physiology. Variations in fluid shear stress and ATP concentration in blood vessels can activate dynamic responses of cytosolic-free $\hbox {Ca}^{2+}$ through various calcium channels on the plasma membrane. In this paper, a novel dynamic model has been proposed for transient receptor potential vanilloid 4 $(\hbox {TRPV}_{4})\hbox {-C}_{1}$-mediated intracellular calcium dynamics in VECs induced by fluid shear stress and ATP. Our model includes $\hbox {Ca}^{2+}$ signaling pathways through P2Y receptors and $\hbox {P2X}_{4} \,\hbox {Ca}^{2+}$ channels (indirect mechanism) and captures the roles of the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ compound channels in VEC $\hbox {Ca}^{2+}$ signaling in response to fluid shear stress (direct mechanism). In particular, it takes into account that the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ compound channels are regulated by intracellular $\hbox {Ca}^{2+}$ and $\hbox {IP}_{3}$ concentrations. The simulation studies have demonstrated that the dynamic responses of calcium concentration produced by the proposed model correlate well with the existing experimental observations. We also conclude from the simulation studies that endogenously released ATP may play an insignificant role in the process of intracellular $\hbox {Ca}^{2+}$ response to shear stress.

1 Introduction

Vascular endothelial cells form a thin layer of cells that line the inner surface of blood vessels. These cells are constantly exposed to fluid shear stress generated by blood flow. This varying shear stress, either alone or along with the presence of ATP in the blood, influences the dynamics of cytosolic-free $\hbox {Ca}^{2+}$. The signaling pathways involving $\hbox {Ca}^{2+}$ play a critical role in flow-dependent VEC physiology (Ando et al. 1988, 1991; Davies 1995; Dull and Davies 1991; Mo et al. 1991; Shen et al. 1992; Yamamoto et al. 2000a; Yamamoto et al. 2000b; Yamamoto et al. 2003, 2006). However, the exact mechanism of signal transduction from shear flow and external ATP concentration, $[\hbox {ATP}]_{\mathrm{o}}$, to cytosolic $\hbox {Ca}^{2+}$ dynamics still remains elusive.

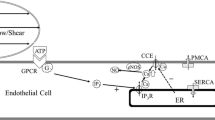
Two mechanisms of shear stress signal transduction have been proposed in the past two decades. The first one is the direct activation mechanism, which speculates that non-selective mechanosensitive cation channels on the cell membrane are directly activated by fluid shear stress, resulting in $\hbox {Ca}^{2+}$ influx across the cell membrane (Wiesner et al. 1997). The second one is the indirect activation mechanism which suggests that the $\hbox {Ca}^{2+}$ signaling pathways are indirectly mobilized by shear stress-induced ATP release from cells (Yamamoto et al. 2000a; Yamamoto et al. 2000b; Yamamoto et al. 2003, 2006). The concept of the indirect activation mechanism is illustrated in the left side of Fig. 1. Fluid shear stress induces ATP release from VECs. The released ATP binds to $\hbox {P}_{2}$Y receptors to form $\hbox {G}\upalpha$-GTP complexes that activate phospholipase C (PLC). Activated PLC (APLC) accelerates the decomposition of phosphatidylinositol (4,5)-bisphosphate ($\hbox {PIP}_{2}$) into inositol 1,4,5-trisphosphate ($\hbox {IP}_{3}$). The $\hbox {IP}_{3}$ then binds with its receptors on the endoplasmic reticulum (ER), leading to the release of $\hbox {Ca}^{2+}$ from the ER into the cytoplasm (Berridge 1995; Davies 1995; Hu et al. 2008; Munaron 2006; Plank et al. 2006). In addition to the above described $\hbox {ATP}/\hbox {P}_{2}\hbox {Y/I}\hbox {P}_{3}/\hbox {Ca}^{2+}$ pathway, another important discovery was made by Yamamoto and her colleagues that external ATP directly gates a membrane $\hbox {Ca}^{2+}$ channel, $\hbox {P2X}_{4}$, to cause $\hbox {Ca}^{2+}$ influx (Yamamoto et al. 2000a; Yamamoto et al. 2000b; Yamamoto et al. 2003, 2006).

Fig. 1

Diagram of shear stress and ATP activate cellular $\hbox {Ca}^{2+}$ signaling pathways

In line with the experimental studies, theoretical models have been developed to understand the intracellular $\hbox {Ca}^{2+}$ dynamics induced by shear stress. Wong and Klassen (1995) assumed that $\hbox {P}_{2}$Y receptors were direct transducers of shear stress signaling controlling cytosolic $\hbox {Ca}^{2+}$ dynamics in VECs. Wiesner et al. (1997) also developed a direct activation model for mechanosensitive $\hbox {Ca}^{2+}$ channels activated by shear stress. Plank et al. (2006) extended Wiesner’s model to include the indirect contribution of shear stress-induced ATP on $\hbox {P}_{2}\hbox {Y}$-mediated $\hbox {Ca}^{2+}$ dynamics. Hu et al. (2008) considered the indirect shear stress-induced $\hbox {Ca}^{2+}$ influx generated by ATP-gated $\hbox {P2X}_{4}\,\hbox {Ca}^{2+ }$ channels in VECs. These theoretical models have captured many experimental features of the intracellular $\hbox {Ca}^{2+}$ response to increases in shear stress, either alone or along with the presence of external ATP (Ando et al. 1988, 1991; Dull and Davies 1991; Mo et al. 1991; Shen et al. 1992; Yamamoto et al. 2003). However, the response to multiple stepwise increases in shear stress along with the presence of external ATP observed in experiments (Yamamoto et al. 2000a; Yamamoto et al. 2000b; Yamamoto et al. 2003, 2006) cannot be reproduced by these models.

In recent years, $\hbox {TRPV}_{4}$, a non-selective mechanosensitive cation channel in some cells, has been shown to be activated by shear flow and other physical and biochemical signals (Everaerts et al. 2010; Watanabe et al. 2003). It can also heterodimerize with $\hbox {TRPC}_{1}$, another subfamily of TRP channels, to form a complex that plays a critical role in the regulation of calcium homeostasis by $\hbox {Ca}^{2+}$ signaling in VECs (Fian et al. 2007; Filosa et al. 2013; Ma et al. 2010). The activation of $\hbox {TRPV}_{4}$ channels by shear stress is found to be regulated by intracellular $\hbox {Ca}^{2+}$ (Watanabe et al. 2003). The activation and activity of $\hbox {TRPC}_{1}$ are also modulated by intracellular $\hbox {Ca}^{2+}$ (Singh et al. 2002). In addition, the mechanical responses of $\hbox {TRPV}_{4}$ and $\hbox {TRPC}_{1}$ channels are both modulated by the binding of $\hbox {IP}_{3}$ to $\hbox {IP}_{3}\hbox {R}$ type 3 in the membrane of $\hbox {Ca}^{2+}$ stores (Fernandes et al. 2008; Rychkov and Barritt 2007). These discoveries suggest new players in intracellular $\hbox {Ca}^{2+}$ dynamics under fluid shear stress and prove the existence of direct activation mechanism as shown in Fig. 1. The contributions of $\hbox {TRPV}_{4}$ and $\hbox {TRPC}_{1}$ ($\hbox {TRPV}_{4}\hbox {-C}_{1}$ complex) channels need to be quantified to understand the detailed mechanism of $\hbox {Ca}^{2+}$ signaling.

The goal of this study is to build a dynamic model that not only includes $\hbox {Ca}^{2+}$ signaling through P2Y receptors and $\hbox {P2X}_{4}\, \hbox {Ca}^{2+}$ channels (indirect mechanism) but also captures the roles of $\hbox {TRPV}_{4}$ and/or $\hbox {TRPV}_{4}\hbox {-C}_{1}$ complex in VEC $\hbox {Ca}^{2+}$ signaling in response to fluid shear stress (direct mechanism). This novel dynamic model is not a simple integration of the previous models in the literature (Hu et al. 2008; Plank et al. 2006; Wiesner et al. 1997) that contain detailed features of VEC $\hbox {Ca}^{2+}$ signaling in response to fluid shear stress and ATP (see Fig. 1) because it also takes into account the fact that the $\hbox {TRPV}_{4}$ and/or $\hbox {TRPV}_{4}\hbox {-C}_{1}$ complex is regulated by intracellular $\hbox {Ca}^{2+}$ and $\hbox {IP}_{3}$ concentrations, which was completely missing in the previous models. Moreover, in order to precisely evaluate the contribution of shear stress-induced ATP release to intracellular $\hbox {Ca}^{2+}$ response, a recently developed dynamic ATP release model (Qin et al. 2008) is also adopted to describe the ATP release induced by shear stress, which is different from the static ATP release model (John and Barakat 2001) used in the previous models (Hu et al. 2008; Plank et al. 2006).

2 Model development

2.1 Model for extracellular ATP transport

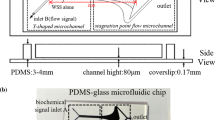
A parallel-plate flow chamber (PPFC) as shown in Fig. 2 has been widely used in experimental investigations of $\hbox {Ca}^{2+}$ signaling in the VEC response to both shear flow and ATP. VECs are cultured at the bottom of the PPFC. In this system, ATP-containing perfusate flows into the PPFC and the original ATP in the perfusate and endogenously released ATP from VECs by fluid shear stress convects and diffuses; this process follows the standard convection and diffusion equation, expressed as follows (Qin et al. 2008):

$$\begin{aligned} \frac{\partial \phi }{\partial t}+v(y,t)\frac{\partial \phi }{\partial x}=D_{\mathrm{ATP}} \left( \frac{\partial ^{2}\phi }{\partial x^{2}}+\frac{\partial ^{2}\phi }{\partial y^{2}}\right) , \end{aligned}$$

(1)

where $\phi$ is the ATP concentration, $D_{\mathrm{ATP}}$ is the diffusion coefficient of ATP, $v(y,t)$ is the flow velocity, $t$ is time, and $x$ and $y$ are the coordinates along the length direction and the height direction of the PPFC, respectively.

Fig. 2

A schematic diagram of the parallel-plate flow chamber

For steady flow, the velocity profile of the perfusate within the chamber is expressed by the famous Poiseuille formula as:

$$\begin{aligned} v(y,t)=6\overline{v} \frac{y}{h}\left( 1-\frac{y}{h}\right) , \end{aligned}$$

(2)

where $\bar{{v}}$ is the height-averaged velocity along the $x$ direction in the chamber, and $h$ is the height between the two plates. The shear stress applied to the VECs is given by:

$$\begin{aligned} \tau _\mathrm{w} =\left. \mu \frac{\partial v}{\partial y}\right| _{y=0} =\frac{6\mu \overline{v} }{h}, \end{aligned}$$

(3)

where $\tau _{\mathrm{w}}$ is the wall shear stress, and $\mu$ is the dynamic viscosity of the fluid.

The initial and boundary conditions are given as follows

$$\begin{aligned}&\phi |_{t=0,x>0} =0, \quad \phi |_{x=0} =[\hbox {ATP}]_\mathrm{o} , \end{aligned}$$

(4)

$$\begin{aligned}&\left. \frac{\partial \phi }{\partial y}\right| _{y=h} =0, \end{aligned}$$

(5)

the boundary equation of ATP flux at the surface of VECs is given as follows (John and Barakat 2001; Plank et al. 2006; Qin et al. 2008):

$$\begin{aligned} D_{\mathrm{ATP}} \left. \frac{\partial \phi }{\partial y}\right| _{y=0} =\left. \frac{V_\mathrm{m} \phi (t)}{K_\mathrm{m} +\phi (t)}\right| _{y=0} -S_{\mathrm{ATP}} (\tau _w ,t), \end{aligned}$$

(6)

where $V_\mathrm{m}$ is the maximum enzyme reaction velocity for ATP hydrolysis, and $K_\mathrm{m}$ is the Michaelis constant. $S_{\mathrm{ATP}} (\tau _\mathrm{w} ,t)$ is the ATP release rate from VECs induced by shear stress $\tau _\mathrm{w}$ applied on the VEC surface, which is described by a recently proposed dynamic model (Qin et al. 2008) instead of the static ATP release model (John and Barakat 2001) used in the previous models (Hu et al. 2008; Plank et al. 2006). For easy reference, $S_{\mathrm{ATP}} (\tau _\mathrm{w} ,t)$ is expressed as follows (Qin et al. 2008):

$$\begin{aligned} S_\mathrm{ATP} (\tau _\mathrm{w} )=s_1 s_2 , \end{aligned}$$

(7)

where $s_{1}$ ($s_{1} \in [0, 1]$) represents the effects of shear stress and open probability of all possible ATP release pathways, and $s_{2}$ ($s_{2} \in [0, 1]$) summarizes the open probability of the various ATP release pathways related to the desensitization level, which satisfy the following equations expressed as (Qin et al. 2008):

$$\begin{aligned}&\frac{\hbox {d}s_1 }{\hbox {d}t}=f(\tau _\mathrm{w} )-\frac{s_1 }{\tau _1 }, \end{aligned}$$

(8)

$$\begin{aligned}&\frac{\hbox {d}s_2 }{\hbox {d}t}=-\frac{s_2 }{\tau _2 }, \end{aligned}$$

(9)

$$\begin{aligned}&f(\tau _\mathrm{w} )=c+\frac{a\tau _\mathrm{w} }{b+\tau _\mathrm{w} }, \end{aligned}$$

(10)

where $\tau _{1}$ and $\tau _{2}$ represent the time delay constants; $a$, $b$, and $c$ are constant parameters to be determined by experimental data (Yamamoto et al. 2003). At time $t = 0$, the ATP release rate is set to be zero, and the effect of receptor desensitization does not occur; thus, the initial conditions of $s_{1}$ and $s_{2}$ can be expressed as $s_{1}(0) = 0$ and $s_{2}(0) = 1$.

2.2 Model for intracellular $\hbox {Ca}^{2+}$ dynamics

As shown in Fig. 1, intracellular calcium homeostasis is maintained by many factors, including the amount of $\hbox {Ca}^{2+}$ outflow from intracellular calcium stores into the cytosol, the amount of $\hbox {Ca}^{2+}$ inflow into calcium stores, the amount of $\hbox {Ca}^{2+}$ influx from extracellular fluid into the cytosol, the amount of $\hbox {Ca}^{2+}$ combined by soluble cytosolic proteins, and the extrusion and exchange of $\hbox {Ca}^{2+}$ to the extracellular space (Hu et al. 2008; Plank et al. 2006; Wiesner et al. 1996, 1997). The dynamics of cytosolic-free $\hbox {Ca}^{2+}$ can be expressed as follows (Hu et al. 2008; Plank et al. 2006; Wiesner et al. 1996, 1997):

$$\begin{aligned} \frac{\hbox {d}C}{\hbox {d}t}=\dot{q}_{\mathrm{rel}} -\dot{q}_{\mathrm{res}} +\dot{q}_{\mathrm{in}} -\dot{q}_{\mathrm{out}} -\dot{q}_\mathrm{b} , \end{aligned}$$

(11)

where $C$ is the intracellular $\hbox {Ca}^{2+}$ concentration, $\dot{q}_{\mathrm{rel}}$ stands for the outflow of $\hbox {Ca}^{2+}$ from calcium stores, $\dot{q}_{\mathrm{res}}$ stands for the inflow of $\hbox {Ca}^{2+}$ back into calcium stores from the cytoplasm, $\dot{q}_{\mathrm{in}}$ is the $\hbox {Ca}^{2+}$ inflow through $\hbox {Ca}^{2+}$ channels, $\dot{q}_{\mathrm{out}}$ is the rate of extrusion and exchange of $\hbox {Ca}^{2+}$ to the extracellular environment as a $\hbox {Ca}^{2+}$ clearance mechanism, and $\dot{q}_\mathrm{b}$ is the rate of buffering of $\hbox {Ca}^{2+}$ by soluble cytosolic proteins.

In Eq. (11), the expressions for $\dot{q}_{\mathrm{rel}} , \dot{q}_{\mathrm{res}}, \dot{q}_{\mathrm{out}}$, and $\dot{q}_\mathrm{b}$ are obtained from the existing models (Hu et al. 2008; Plank et al. 2006; Wiesner et al. 1996, 1997). For easy reference, these expressions are also presented as follows:

$$\begin{aligned}&\dot{q}_{\mathrm{rel}} = k_3 \frac{C}{K_{\mathrm{CICR}} +C} \left( \frac{i}{i+K_2 }\right) ^{3}, \end{aligned}$$

(12)

$$\begin{aligned}&\dot{q}_{\mathrm{res}} = k_4 \left( \frac{C}{K_3 +C}\right) ^{2}-k_5 C_s ^{2}, \end{aligned}$$

(13)

$$\begin{aligned}&\dot{q}_{\mathrm{out}} = \frac{k_8 C}{K_4 +C}, \end{aligned}$$

(14)

$$\begin{aligned}&\dot{q}_\mathrm{b} = k_6 C(B_\mathrm{T} -C_\mathrm{b} )-k_7 C_\mathrm{b} , \end{aligned}$$

(15)

where $i$ stands for the concentration of $\hbox {IP}_{3}$, $C_{\mathrm{s}}$ represents the $\hbox {Ca}^{2+}$ concentration of calcium store, and $C_{\mathrm{b}}$ denotes the concentration of cytosolic buffering $\hbox {Ca}^{2+}$. $k_{3}$ is $\hbox {Ca}^{2+}$ outflow rate constant from $\hbox {Ca}^{2+}$ stores, $k_{4}$ is the rate constant of resequestration of $\hbox {Ca}^{2+}$ back into the calcium stores, $k_{5}$ is $\hbox {Ca}^{2+}$ leak rate, $k_{6}$ and $k_{7}$ are the buffering and debuffering rate constants, respectively, $k_{8}$ is the maximal velocity of $\hbox {Ca}^{2+}$ efflux of the $\hbox {Ca}^{2+}$ clearance mechanism. $K_{\mathrm{CICR}}$ represents the sensitivity of calcium stores to the $\hbox {Ca}^{2+}$-induced $\hbox {Ca}^{2+}$ release (CICR) mechanism, $K_{2}, K_{3}, K_{4}$ are all the Michaelis–Menten constants, and $B_{\mathrm{T}}$ is the total concentration of $\hbox {Ca}^{2+}$ buffering sites on proteins in the cytosol.

The synthesis of $\hbox {IP}_{3}$ is expressed as follows (Hu et al. 2008; Plank et al. 2006):

$$\begin{aligned} \frac{\hbox {d}i}{\hbox {d}t}=k_1 \left. \frac{\phi }{K_\mathrm{c} +\phi }\right| _{y=0} \frac{C}{K_1 +C}-k_2 i, \end{aligned}$$

(16)

where $k_{1}$ and $k_{2}$ are the $\hbox {IP}_{3}$ production and degradation rate, respectively, $K_{1}$ and $K_{\mathrm{c}}$ are the Michaelis–Menten constants.

The buffered and stored $\hbox {Ca}^{2+}$ concentrations are given as follows (Hu et al. 2008; Plank et al. 2006):

$$\begin{aligned} \frac{\hbox {d}C_\mathrm{b} }{\hbox {d}t}&= \dot{q}_\mathrm{b} , \end{aligned}$$

(17)

$$\begin{aligned} \frac{\hbox {d}C_\mathrm{s} }{\hbox {d}t}&= \frac{V_\mathrm{c} }{V_\mathrm{s} } (\dot{q}_{\mathrm{res}} -\dot{q}_{\mathrm{rel}} ), \end{aligned}$$

(18)

where $V_{\mathrm{c}}/V_{\mathrm{s}}$ is the ratio of volumes of cytosol and stores. The initial conditions of $C_{\mathrm{b}}(0)$ and $C_{\mathrm{s}}(0)$ are as follows (Hu et al. 2008; Plank et al. 2006):

$$\begin{aligned} C_{\mathrm{b}}(0)=C_{\mathrm{b}0}, C_{\mathrm{s}}(0)=C_{\mathrm{s0},} \end{aligned}$$

(19)

where $C_{\mathrm{b}0}$ and $C_{\mathrm{s}0}$ are constants.

The $\hbox {Ca}^{2+}$ influx $\dot{q}_{\mathrm{in}}$ across the VEC membrane occurs mainly through mechanosensitive $\hbox {TRPV}_{4}$ and $\hbox {TRPC}_{1}$ compound channels (Ma et al. 2010; Sonkusare et al. 2012) and ATP-gated $\hbox {P2X}_{4}$ channels (Yamamoto et al. 2000a; Yamamoto et al. 2000b; Yamamoto et al. 2003, 2006). Therefore, $\dot{q}_{\mathrm{in}}$ is proposed in the following form:

$$\begin{aligned} \dot{q}_{\mathrm{in}} =\dot{q}_{\mathrm{in\_passive}} +\dot{q}_{\mathrm{in\_P2X}_4 } +\dot{q}_{\mathrm{in\_TRPV}_4 {\text {-C}}_1 } , \end{aligned}$$

(20)

where $\dot{q}_{\mathrm{in\_passive}}$ is a constant reflecting the passive influx of $\hbox {Ca}^{2+}$ in the no-load case, $\dot{q}_{\mathrm{in\_P2X}_4}$ represents the $\hbox {Ca}^{2+}$ influx through the $\hbox {P2X}_{4}$ channels directly activated by extracellular ATP (Hu et al. 2008), and $\dot{q}_{\mathrm{in\_TRPV}_4 {\text {-C}}_1}$ represents the $\hbox {Ca}^{2+}$ flux via $\hbox {TRPV}_{4}\hbox {-C}_{1}$ complex, of which the mathematical details will be given in the following Sect. 2.3.

The expression for $\dot{q}_{\mathrm{in\_P2X}_4}$ is obtained from the existing models (Hu et al. 2008). For easy reference, the expression is presented as follows (Hu et al. 2008):

$$\begin{aligned} \dot{q}_{\mathrm{in\_P2X4}} =k_{\mathrm{p2x}_4 } \left( \frac{\phi |_{{y}=0} }{K_\varphi +\phi |_{{y}=0} }\right) ^{3}(C_{\mathrm{ex}} -C), \end{aligned}$$

(21)

where $k_{\mathrm{p2x4}}$ is $\hbox {Ca}^{2+}$ flux rate, and $K_{\varphi }$ is the Michaelis–Menten constant for the interaction between ATP and $\hbox {P2X}_{4}$. $C_{\mathrm{ex}}$ is the concentration of extracellular calcium ion in the surrounding medium.

2.3 Model for $\hbox {Ca}^{2+}$ influx through the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels

The $\hbox {TRPV}_{4}$ channels and $\hbox {TRPC}_{1}$ channels are both mechanosensitive, can be directly activated by shear stress (Everaerts et al. 2010), and may sense and transduce mechanical stress (Eder and Molkentin 2011). Meanwhile, $\hbox {IP}_{3}$ binding to $\hbox {IP}_{3}$R type 3 in the membrane of the $\hbox {Ca}^{2+}$ stores may sensitize the channels to the mechanical stimuli (Boulay et al. 1999; Fernandes et al. 2008; Rychkov and Barritt (2007)). The sensitivity of $\hbox {TRPV}_{4}$ channels is decayed by increases in the intracellular $\hbox {Ca}^{2+}$ concentration (Watanabe et al. 2003), and the sensitivity of $\hbox {TRPC}_{1}$ channels is modulated by intracellular $\hbox {Ca}^{2+}$ (Singh et al. 2002). A recent study demonstrated that the depletion of $\hbox {Ca}^{2+}$ stores may enhance the vesicle trafficking of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ (Ma et al. 2011). Considering these experimental evidences, it is proposed that the expression for $\hbox {Ca}^{2+}$ influx ($\dot{q}_{\mathrm{in\_TRPV}_4 {\text {-C}}_1 }$) through $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels takes the following form:

$$\begin{aligned} \dot{q}_{\mathrm{in\_TRPV}_4 {\text {-C}}_1 } =q_{\max } \cdot {p}_1 \cdot {p}_2 \cdot {p}_3 \cdot (C_{\mathrm{s}0} -C_\mathrm{s} )(C_{\mathrm{ex}} -C), \end{aligned}$$

(22)

where $q_{\mathrm{max} }$ is the rate constant, representing the maximum of the $\hbox {Ca}^{2+}$ influx when all the channels are open; the variable $p_{1 }(p_1 \in \left[ {0,1} \right] )$ summarizes the direct effect of shear stress and the probability of the open state of the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels induced by shear stress, which is consistent with that reported by Wiesner et al. (1997) and can be expressed as follows:

$$\begin{aligned} p_1 =\frac{1}{1+\alpha \cdot \hbox {exp}\frac{-f_\mathrm{e} W(\tau _\mathrm{w} )}{8kTN}}, \end{aligned}$$

(23)

where $\alpha$ is a positive constant, $(1+\alpha )^{-1}$ is the open probability of a channel in the no-load case, $f_{\mathrm{e}} (f_{\mathrm{e}} \, \in [0, 1])$ is the fraction of the energy within the membrane that gates the shear stress-sensitive $\hbox {Ca}^{2+}$ channels, $T$ is the temperature, $N$ is the ion channel density per unit area, and $k$ is the Boltzmann constant. $W(\tau _\mathrm{w} )$ is the strain energy density in the membrane activated by shear stress expressed as follows (Wiesner et al. 1997):

$$\begin{aligned} W(\tau _\mathrm{w} )=\frac{\left( \varepsilon \tau _\mathrm{w} l+\sqrt{16\delta ^{2}+\varepsilon ^{2}\tau _\mathrm{w} ^{2}l^{2}}-4\delta \right) ^{2}}{\left( \varepsilon \tau _\mathrm{w} l+\sqrt{16\delta ^{2}+\varepsilon ^{2}\tau _\mathrm{w} ^{2}l^{2}}\right) }, \end{aligned}$$

(24)

where $\varepsilon \,(\varepsilon \in [0, 1]$) is the fraction of the applied load borne by the plasma membranes, $l$ is the length of the cell in the flow direction, and $\delta$ is the membrane shear modulus.

The variable $p_{2 }({p}_2 \in \left[ {0,1} \right] )$ describes the probability of the open state of the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channel activated by the binding of three $\hbox {IP}_{3}$ molecules to $\hbox {IP}_{3}\hbox {R}$ type 3 in the membrane of the $\hbox {Ca}^{2+}$ stores (Fernandes et al. 2008; Rychkov and Barritt (2007)), which is proposed to satisfy

$$\begin{aligned} p_2 =b_1 \left( 1+a_1 \cdot \frac{i^{3}}{(i+K_i )^{3}}\right) , \end{aligned}$$

(25)

where $K_{\mathrm{i}}$ is the Michaelis–Menten constant, and $a_{1}$ and $b_{1}$ are positive constants. Note that $b_1 (1+a_1 )$ has to be less than 1, so that $p_{2}$ is a positive number between 0 and 1.

The variable, $p_{3,}$ describes the probability of the open state of the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channel, decayed by intracellular $\hbox {Ca}^{2+}$ concentration, which satisfies the following exponential function derived from experimental data in the literature (Watanabe et al. 2003),

$$\begin{aligned} p_3 =c_1 +c_{2} \cdot \hbox {e}^{(-c_3 \cdot C)}, \end{aligned}$$

(26)

where $c_{1}, c_{2}$, and $c_{3 }$are positive constants. Note that $c_{1}+c_{2 }= 1$ such that $p_{3}$ is a positive number less than 1.

2.4 Model parameters and simulation methods

2.4.1 Model parameters

All the values for the model parameters used in the numerical simulation are listed in Table 1 (values for extracellular ATP dynamic model) and Table 2 (values for intracellular $\hbox {Ca}^{2+}$ dynamic model). Some of the parameter values are from the literature (Hu et al. 2008; Plank et al. 2006; Qin et al. 2008; Yamamoto et al. 2000b), and the others are estimated to reproduce experimental results published in the literature (Watanabe et al. 2003; Yamamoto et al. 2000b).

Table 1 Default values for extracellular ATP model parameters used in the numerical simulation

By carefully analyzing the experimental data of Watanabe and his co-workers regarding steady state inhibition of $\hbox {TRPV}_{4}$ by increased $[\hbox {Ca}^{2+}]_\mathrm{in}$ (see Fig. 4 in Watanabe et al. 2003); the ordinate value is normalized to obtain the normalized open fraction $p_3$ against increased $\hbox {Ca}^{2+}$ level (see Fig. 3). The least squares method is used to determine the $c_{1}, c_{2}$ and $c_{3}$ values in Eq. (26) to fit the experimental data.

Unless otherwise specified, these parameters are the default values used throughout the paper.

2.4.2 Simulation methods

The intracellular $\hbox {Ca}^{2+}$ dynamics in a single cell located in the center ($x=L/2$) of the bottom of the PPFC is investigated by coupling of the extracellular ATP transport and intracellular $\hbox {Ca}^{2+}$ dynamics.

Table 2 Default values for intracellular $\hbox {Ca}^{2+}$ dynamics model parameters used in the numerical simulation

Given the initial and boundary conditions (Qin et al. 2008), the convection and diffusion Eq. (1) for extracellular ATP transport could be solved numerically. The computer code developed for this purpose is based on a two-stage corrected Euler formulation with a central difference approximation in $x$ and $y$ direction and an upwind scheme in the $x$ direction, which is similar to that used in the literatures (John and Barakat 2001; Qin et al. 2008).

Given the initial conditions (Hu et al. 2008; Plank et al. 2006), the ordinary differential Eqs. (11) and (16)–(18) are solved using an adaptive step Runge–Kutta routine.

3 Simulation results

3.1 Model validation

In order to validate the dynamic model, the intracellular $\hbox {Ca}^{2+}$ responses to multiple stepwise increases in shear stress and external ATP (see Fig. 4), which have commonly been observed in experimental studies by Yamamoto et al. (2000b); Yamamoto et al. (2003, 2006), are numerically simulated based upon the proposed dynamic model. The intracellular $\hbox {Ca}^{2+}$ responses to multiple stepwise increases in shear stress under specific experimental conditions adopted by Yamamoto et al. (2000b); Yamamoto et al. (2003) are also simulated (see Fig. 5). Furthermore, the transient intracellular $\hbox {Ca}^{2+}$ responses to cessation of shear stress and washout of external ATP as adopted by Mo et al. (1991) are simulated in Fig. 6. Sustained intracellular $\hbox {Ca}^{2+}$ oscillations, which are common phenomena in many kinds of cells, are predicted by changing key parameters in the proposed dynamic model as shown in Table 3 (see Fig. 7) with a frequency within the same range of magnitude as observed experimentally (Shen et al. 1992).

3.1.1 $\hbox {Ca}^{2+}$ response to multi-step increases in shear stress and external ATP concentration

The intracellular $\hbox {Ca}^{2+}$ responses to the multistep increases in shear stress (0 Pa $\rightarrow$ 0.3 Pa $\rightarrow$ 0.8 Pa $\rightarrow$ 1.5 Pa) together with increases in external ATP concentration ($[\hbox {ATP}]_\mathrm{o} =100 \,\hbox {nM}$, 800 nM, $2\,\upmu \hbox {M}$, and $2.3 \,\upmu \hbox {M}$) are numerically simulated. Figure 4 clearly shows that with a very weak ATP stimulus, i.e., 100 nM external ATP concentration, the intracellular $\hbox {Ca}^{2+}$ concentration weakly responds to the multi-step increase in shear stress. With a moderate ATP stimulus, i.e., 800 nM external ATP, the intracellular $\hbox {Ca}^{2+ }$ concentration increases with increase in shear stress in a stepwise manner. When external ATP concentration reaches higher levels (2 or $2.3 \,\upmu \hbox {M}$), the intracellular $\hbox {Ca}^{2+ }$ concentration increases in response to shear stress, but not in a multiple stepwise increasing manner. An obvious transient peak can be observed at a low level of shear stress (0.3 or 0.8 Pa). These simulation results based upon our dynamic model show good qualitative agreement with experimental data published by Yamamoto and her colleagues (Figure 1 in Yamamoto et al. 2000b), demonstrating that our dynamic model is quite accurate from a phenomenological point of view.

3.1.2 $\hbox {Ca}^{2+}$ response to multi-step increases in shear stress under specific experimental conditions

The intracellular $\hbox {Ca}^{2+}$ responses to multi-step increases in shear stress under specific experimental conditions adopted by Yamamoto and her colleagues (Yamamoto et al. 2000b; Yamamoto et al. 2003) are simulated. Figure 5a shows the simulation of shear stress-induced $\hbox {Ca}^{2+}$ responses without external ATP as a stimulus ($[\hbox {ATP}]_{\mathrm{o}} = 0$). Shear stress-dependent increase in $\hbox {Ca}^{2+}$ concentration is inhibited by the exclusion of external ATP (solid line), but a very slight step-wise response (around the basal level) remains. A similar transient $\hbox {Ca}^{2+}$ dynamic response was experimentally observed in the VECs upon exposure to apyrase, which degrades ATP in a dose-dependent manner (Yamamoto et al. 2003).

Fig. 3

Probability of the open state of the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channel decayed by intracellular $\hbox {Ca}^{2+}$ concentration. Data from Watanabe et al. (2003) and the fitted curve obtained by the least square method

Fig. 4

Intracellular dynamic $\hbox {Ca}^{2+}$ response under the stimulus of stepwise increase in shear stress (0 Pa $\rightarrow$ 0.3 Pa$\rightarrow$ 0.8 Pa $\rightarrow$ 1.5 Pa) and external ATP concentration: top left $[\hbox {ATP}]_{\mathrm{o}} = 100$ nM; top right $[\hbox {ATP}]_{\mathrm{o}} = 800$ nM; bottom left $[\hbox {ATP}]_{\mathrm{o}}$ = 2  $\upmu \mathrm{M}$; bottom right $[\hbox {ATP}]_{\mathrm{o}} = 2.3 \, \upmu \hbox {M}$

Fig. 5

Validation diagrams of dynamic $\hbox {Ca}^{2+}$ response under certain conditions: a ablation of external ATP ($+$Apyrase), b ablation of extracellular $\hbox {Ca}^{2+}$ ($+$EGTA), c promotion of $\hbox {Ca}^{2+}$ influx through $\hbox {P2X}_{4}$ channels (+$\hbox {P2X}_{4})$

Fig. 6

a Time dependence of the $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ on cessation of shear stress at 60 s. b Time dependence of the $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ on washout of external ATP at 60 s

Fig. 7

a $\hbox {Ca}^{2+}$ oscillations under different levels of shear stress and a constant external ATP concentration ($[\hbox {ATP}]_{\mathrm{o}} = 2 \,\upmu \hbox {M}$). b $\hbox {Ca}^{2+}$ oscillations under constant shear stress (1 Pa) and various external ATP concentrations

Figure 5b shows the effect of extracellular $\hbox {Ca}^{2+}$ exclusion on the multi-step shear stress-induced $\hbox {Ca}^{2+}$ response (solid line, $+$EGTA). The absence of $\hbox {Ca}^{2+}$ in the extracellular environment leads to the absence of $\hbox {Ca}^{2+}$ inflow through any $\hbox {Ca}^{2+}$ channels, and the intracellular $\hbox {Ca}^{2+}$ response decreases at an external ATP concentration of 800 nM. However, there is an early transient increase in $\hbox {Ca}^{2+}$ response at an external ATP concentration of $2\, \upmu \hbox {M}$ or more because of the outflow of $\hbox {Ca}^{2+}$ from calcium stores. With no effect of influx through any $\hbox {Ca}^{2+}$ channels, the amplitude of the $\hbox {Ca}^{2+}$ response decreases slightly and the stepwise $\hbox {Ca}^{2+}$ response after the transient peak completely disappears since shear stress cannot induce $\hbox {Ca}^{2+}$ influx across $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels. The simulation result from our dynamic model is qualitatively in accordance with experimental evidence observed by Yamamoto et al. (2000b).

Figure 5c reproduces the experimental results of multi-step shear stress-induced $\hbox {Ca}^{2+}$ response in HEK293 cells stably expressing $\hbox {P2X}_{4}$ purinoceptors obtained by Yamamoto and her colleagues (Figure 7 in Yamamoto et al. 2000b). The external ATP concentrations are set to 0.8 and $2\,\upmu \hbox {M}$ in our model. The parameter of $\hbox {Ca}^{2+}$ flux rate caused by shear stress, $k_{\mathrm{p2x4}}$, is increased gradually (0, $4.57 \times 10^{-3}\, \hbox {s}^{-1}$ and 7.32 $\times 10^{-3}\, \hbox {s}^{-1})$ to represent different $\hbox {P2X}_{4}$ expression levels. $\hbox {P2X}_{4}$ induces shear stress-dependent $\hbox {Ca}^{2+}$ influx. The shear stress-dependent $\hbox {Ca}^{2+}$ response becomes larger as the level of $\hbox {P2X}_{4}$ expression increases.

3.1.3 Transient $\hbox {Ca}^{2+}$ response to interceptive shear stress or interceptive external ATP concentration

A sudden blocking of extracellular stimulus (shear stress or ATP) may trigger $\hbox {Ca}^{2+}$ emergency responses, which can shed new light on the understanding of the mechanism of the stimulus. The transient $\hbox {Ca}^{2+}$ response to cessation of shear stress at 60 s and the transient $\hbox {Ca}^{2+}$ response to the washout of external ATP concentration are numerically simulated (see Fig. 6). Under the mechanical stimulation of shear stress and ATP flow conditions, the model predicts a sustained $\hbox {Ca}^{2+}$ response. However, upon cessation of both stimuli, the $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ will return rapidly to basal levels. As seen in Eq. (23), shear stress can promote the activity of the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels, which plays a vital role of $\hbox {Ca}^{2+}$ inflow from the extracellular environment. With the cessation of shear stress, the calcium channels are restrained and the $\hbox {Ca}^{2+}$ response immediately returns to basal levels. Likewise, the effect of external ATP concentration is also relevant as ATP may influence the generation of $\hbox {IP}_{3}$ (see Eq. (16)) and promote the activity of the $\hbox {P2X}_{4}\, \hbox {Ca}^{2+}$ channels (see Eq. (21)). Accordingly, a similar interceptive response appears when the cessation of ATP stimulus begins, which is shown in Fig. 6b. Very similar $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ responses were experimentally obtained by Mo et al. (1991).

Table 3 Values for model parameters used in the numerical simulation of $\hbox {Ca}^{2+}$ oscillations

3.1.4 $\hbox {Ca}^{2+ }$oscillations in response to shear stress and external ATP concentration

Studies have shown that VECs may generate intracellular $\hbox {Ca}^{2+}$ oscillations upon stimulation with shear stress and ATP, and the frequency often varies depending on external conditions, particularly the concentration of stimuli. When the $\hbox {IP}_{3}$ concentration is low, the $\hbox {Ca}^{2+}$ concentration is also low, the $\hbox {Ca}^{2+}$ influx into calcium stores is low, and there is no $\hbox {Ca}^{2+}$ oscillation. The low-concentration stage and the $\hbox {Ca}^{2+}$ increase may be shortly lived. When the concentration of $\hbox {IP}_{3}$ is high, $\hbox {Ca}^{2+}$ concentration increases and there is no oscillation. In this situation, the absorption effect of calcium stores increases, which may cause a decrease in the $\hbox {Ca}^{2+}$ concentration level. Thus, within a range of agonist stimulation between the two $\hbox {Ca}^{2+}$ levels, $\hbox {Ca}^{2+}$ oscillations are obtained (Atri et al. 1993).

The model proposed above can reproduce sustained $\hbox {Ca}^{2+ }$oscillations and other phenomena observed in experiments with certain parameters (Dull and Davies 1991; Shen et al. 1992). Table 3 summarizes the values for some key parameters used to generate $\hbox {Ca}^{2+}$ oscillations. The other parameters used in the numerical simulations are the same as shown in Table 2.

Figure 7 predicts the $\hbox {Ca}^{2+}$ oscillations within a certain range of shear stress and ATP concentration. As can be readily seen from Fig. 7, the oscillation frequencies vary depending on both ATP concentration and shear stress, more specifically, enhancing the shear stress level and ATP concentration will both increase the oscillation frequency obviously, which means changes of external conditions can cause immediate changes in the oscillation frequency which are proportional to the applied stimuli (shear stress and ATP). The $\hbox {Ca}^{2+}$ oscillation and its frequency characteristic produced by the proposed dynamic model are supported by Shen et al. (1992) experimental data. However, as shown in Fig. 7, the $\hbox {Ca}^{2+}$ oscillation amplitudes decrease as the external stimuli are enhanced, which have some discrepancies with Shen and his co-workers’ observations that the $\hbox {Ca}^{2+}$ oscillation amplitudes were insensitive to shear stress. Further studies are needed to verify this point.

3.2 Understanding direct and indirect activation mechanisms

There had always been controversy regarding whether the direct role of shear stress in opening $\hbox {Ca}^{2+}$ channels (Wiesner et al. 1997) or the indirect role through endogenously released ATP is the main activation mechanism of the intracellular dynamic $\hbox {Ca}^{2+}$ response in the VECs (Yamamoto et al. 2000b; Yamamoto et al. 2003, 2006). In order to examine the role of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels, which are activated by the direct effect of shear stress and the indirect effect of ATP, and to observe the vital role of the feedback mechanism of $\hbox {IP}_{3}$ and $\hbox {Ca}^{2+}$, specific components of the model are omitted. For comparison with the baseline, which is obtained under the stimulus of increasing shear stress (0 Pa $\rightarrow$ 0.3 Pa $\rightarrow$ 0.8 Pa $\rightarrow$ 1.5 Pa) and constant external ATP concentrations of 0.8 $\upmu$M or 2 $\upmu$M, the $\hbox {Ca}^{2+}$ influx through $\hbox {TRPV}_{4}\hbox {-C}_{1 }$or the feedback regulations are ignored (see Fig. 8a, b) by setting the corresponding values to 0. In addition, the feedback regulation mechanisms of $p_{2}$ and $p_{3}$ are extracted to determine the exact promotion or inhibition effect (see Fig. 8c). When considering the indirect activation mechanism of shear stress through endogenously released ATP, the original external ATP concentration $[\hbox {ATP}]_{\mathrm{o}}$ with or without endogenously released ATP by shear stress is considered as stimulus to determine whether the indirect role of shear stress-induced increases in ATP concentration is critical (see Fig. 8d). To verify the vital role of $\hbox {P2X}_{4}$ channels, which has been observed in experimental studies by Yamamoto et al. (2000a, 2006), the closure of the channel is adopted in the proposed model (see Fig. 8e).

Fig. 8

a Transient response of $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ without consideration of the $\hbox {TRPV}_{4}-\hbox {TRPC}_{1}$ complex. b Transient response of $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ without consideration of feedback regulation of $\hbox {IP}_{3}$ and $\hbox {Ca}^{2+}$ in the $\hbox {TRPV}_{4}-\hbox {TRPC}_{1}$ complex. c ATP dose dependence of $\hbox {IP}_{3}$ feedback regulation $(p_{2})$ and calcium feedback regulation $(p_{3})$. d Time dependence of $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ with or without endogenously released ATP. e Diagram of dynamic $\hbox {Ca}^{2+}$ response without $\hbox {Ca}^{2+}$ influx through $\hbox {P2X}_{4}$ channels (-$\hbox {P2X}_{4})$

3.2.1 Role of direct activation of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ by shear stress

The $\hbox {Ca}^{2+}$ response without the effect of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels ($\dot{q}_{\mathrm{in\_TRPV}_4{\text {-C}}_1}=0)$ is simulated in Fig. 8a. Without $\hbox {TRPV}_{4}\hbox {-C}_{1}$, increasing shear stress and constant external ATP triggers a weak increase in $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ at a low ATP concentration and a large, transient $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ that slowly returns to basal value at a high ATP concentration. However, shear stress has no effect on $\hbox {Ca}^{2+}$ channels. As a result, there is no stepwise increase in $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ following the transient peak, which is in contrast to experimental data (Yamamoto et al. 2000a). It is evident that the $\hbox {TRPV}_{4}$ and $\hbox {TRPC}_{1}$ complex is indispensable for the dynamic response of $\hbox {Ca}^{2+}$ in VECs.

Figure 8b shows the impact of abrogation of feedback regulation of $\hbox {IP}_{3}$ and $\hbox {Ca}^{2+}$ in influx through the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels. This is accomplished by setting the values for $p_2$ and $p_3$ to 1. Without proper feedback regulation mechanisms, dynamic $\hbox {Ca}^{2+}$ response through $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels induced by shear stress is enhanced greatly because of the abundant number of open $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels. Higher $\hbox {Ca}^{2+}$ inflow from the channels may induce a stronger intracellular $\hbox {Ca}^{2+}$ response. The dynamic $\hbox {Ca}^{2+}$ responses noted in this situation are in contrast to Yamamoto’s experimental data (Yamamoto et al. 2000a). The feedback regulation of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ in Eq. (22), which is the main innovation point of this paper, is quite critical. It helps to regulate the mechano-sensitivity of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels to be consistent with experimental evidence (Watanabe et al. 2003; Yamamoto et al. 2000a). The feedback regulation of $p_{2 }$bridges the indirect effect of ATP stimulation on the mechano-sensitivity of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels through $\hbox {IP}_{3}$ in the intracellular $\hbox {Ca}^{2+}$ signaling pathway in Fig. 1 to adjust the step amplitudes of the stepwise $\hbox {Ca}^{2+}$ responses (different from responses to $\hbox {Ca}^{2+}$ stores). The feedback regulation of $p_{3 }$through intracellular $\hbox {Ca}^{2+}$ is obtained from experimental data (Watanabe et al. 2003). Obviously, both the $\hbox {Ca}^{2+}$ influx across the cell membrane and the $\hbox {Ca}^{2+}$ outflux from $\hbox {Ca}^{2+}$ stores participate in the feedback regulation of $p_{3}$.

Data for ATP dose dependence of $\hbox {IP}_{3}$ feedback regulation ($p_{2}$) and calcium feedback regulation ($p_{3}$) (see Eqs. (25) and (26)) are extracted for the simulation represented in Fig. 8c. It is readily seen from left of Fig. 8c that higher ATP concentration caused higher $\hbox {IP}_{3}$ feedback regulation ($p_{2}$), which means more $\hbox {Ca}^{2+}$ influx from $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channel and more intracellular $\hbox {Ca}^{2+}$; on the contrary, higher ATP concentration brought lower $\hbox {Ca}^{2+}$ feedback regulation of $\hbox {TRPV}_{4}\hbox {-C}_{1}\, (p_{3})$ resulting in less $\hbox {Ca}^{2+}$ influx (see right of Fig. 8c). So we conclude that $\hbox {IP}_{3}$ acts as a positive adjustment of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channel, while $\hbox {Ca}^{2+}$ acts as a negative one.

3.2.2 Role of indirect activation by shear stress-induced endogenously released ATP

Figure 8d shows the time dependence of $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ with or without endogenously released ATP from VECs. It is obvious that the intracellular $\hbox {Ca}^{2+}$ responses in VECs with or without endogenously released ATP are almost identical. As reported in the literature, at ATP concentration of 0.1 $\upmu$M or less, $[\hbox {Ca}^{2+}]_{\mathrm{in}}$ responded weakly to flow (Yamamoto et al. 2000a). The concentration of the ATP released by VECs in the ATP release model (Qin et al. 2008) is three times lower (i.e., $<$0.03  $\upmu \hbox {M}$) than this value. Therefore, endogenously released ATP may be insignificant in the process of inducing intracellular $\hbox {Ca}^{2+}$ dynamics.

3.2.3 Role of direct activation of $\hbox {P2X}_{4}$ by external ATP

In addition to the contribution of the direct $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels to the intracellular dynamic $\hbox {Ca}^{2+}$ response, the indirect effect of the $\hbox {P2X}_{4}$ channels is clear. As mentioned in Sect. 3.1.2, Fig. 5c, a high $\hbox {Ca}^{2+}$ flux rate may cause a larger $\hbox {Ca}^{2+}$ increase. Conversely, closure of $\hbox {P2X}_{4}$ channels, represented by setting $k_{\mathrm{p2x4}}$ to 0, may have an inhibitory effect on intracellular $\hbox {Ca}^{2+}$ concentration (see Fig. 8e). Hence, $\hbox {P2X}_{4}$ channels also play an important role in $\hbox {Ca}^{2+}$ response in VECs in the proposed dynamic model. This was observed in experimental studies by Yamamoto et al. (2000a); Yamamoto et al. (2000b); Yamamoto et al. (2003, 2006).

4 Discussion

A novel dynamic model that includes the indirect $\hbox {Ca}^{2+}$ signaling mechanism of P2Y receptors and $\hbox {P2X}_{4}$ $\hbox {Ca}^{2+}$ channels and captures the roles of the direct mechanism of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ complex in VEC $\hbox {Ca}^{2+}$ signaling in response to fluid shear stress is developed in this study. Although a number of mathematical models describing the modulation of the dynamic $\hbox {Ca}^{2+}$ response have been proposed (Hu et al. 2008; Plank et al. 2006; Wiesner et al. 1997; Wong and Klassen 1995), to the best of our knowledge, none of the existing models have incorporated all the possible direct and indirect activation mechanisms. Moreover, the fact that the $\hbox {TRPV}_{4}$ and/or $\hbox {TRPV}_{4}\hbox {-C}_{1}$ complex is modulated by intracellular $\hbox {IP}_{3}$ and $\hbox {Ca}^{2+}$ concentrations (Fernandes et al. 2008; Ma et al. 2011; Rychkov and Barritt (2007); Watanabe et al. 2003) has been completely missing in the previous models (Hu et al. 2008; Plank et al. 2006; Wiesner et al. 1997; Wong and Klassen 1995). The simulation studies have shown that the novel dynamic model developed in this paper can qualitatively reproduce the existing experimental observations quite well (Dull and Davies 1991; Mo et al. 1991; Shen et al. 1992; Yamamoto et al. 2000a; Yamamoto et al. 2000b; Yamamoto et al. 2003). This implies that our dynamic model is representative, at least from the phenomenological point of view.

As mentioned in Sect. 2.3, $\hbox {TRPV}_{4}\hbox {-C}_{1}$ has mechanosensitivity, which may be regulated by intracellular $\hbox {IP}_{3}, \hbox {Ca}^{2+}$, and the depletion of $\hbox {Ca}^{2+}$ stores (Eder and Molkentin 2011; Everaerts et al. 2010; Fernandes et al. 2008; Ma et al. 2010, 2011; Rychkov and Barritt 2007; Singh et al. 2002; Watanabe et al. 2003). Therefore, a novel model is proposed here to express the $\hbox {Ca}^{2+}$ influx ($\dot{q}_{\mathrm{in\_TRPV}_4 {\text {-C}}_1 } )$ in Eq. (22). The variable $p_{1}$ summarizes the direct activation effect of shear stress, which follows Wiesner’s model (Wiesner et al. 1997). The variable $p_{2}$ describes the open state of $\hbox {TRPV}_{4}\hbox {-C}_{1}$ activated by the binding of $\hbox {IP}_{3 }$to $\hbox {IP}_{3}$R type 3 in the membrane of the $\hbox {Ca}^{2+}$ stores, which is proposed for the first time to describe this function. The variable $p_{3}$ describes the feedback mechanism of $\hbox {Ca}^{2+}$. A model embedded with an exponential function is adopted, and a least square method is used to determine the constant parameters. Figure 3 shows that the simulation results (solid lines) fitted by the exponential function exhibit excellent agreement with experimental data (scattered squares) obtained by Watanabe et al. (2003). Since the feedback effects from $\hbox {IP}_{3}$ and $\hbox {Ca}^{2+}$ to $\hbox {TRPV}_{4}\hbox {-C}_{1}$ have never been considered in previous models in the literature, the model (see Eq. 22) together with Eqs. (25) and (26) constitutes the main contribution of this paper.

In past two decades, the mechanism for shear stress signal transduction has been a matter of controversy. Yamamoto et al. (2000a); Yamamoto et al. (2000b); Yamamoto et al. (2003, 2006) claimed that shear stress-induced ATP release from the cells indirectly activated $\hbox {P2X}_{4} \,\hbox {Ca}^{2+}$ channels on the cell membrane, which were proposed as ‘shear stress transducers’. This ‘indirect activation mechanism’ had been thought to be the primary mechanism for shear stress-activated $\hbox {Ca}^{2+}$ influx into VECs (Yamamoto et al. 2000a; Yamamoto et al. 2000b; Yamamoto et al. 2003, 2006). By carefully analyzing the simulation results from the dynamic model proposed in the current study, some important observations can be made. Figure 8a demonstrates that without the effect of the direct shear stress sensor $\hbox {TRPV}_{4}\hbox {-C}_{1}$, a multistep increase in shear stress may trigger a transient $\hbox {Ca}^{2+}$ response followed by the absence of a stepwise increase in $\hbox {Ca}^{2+}$ concentration. Obviously, the ion channels $\hbox {TRPV}_{4}\hbox {-C}_{1}$ which are directly sensitive to shear stress, are quite critical to generate the stepwise $\hbox {Ca}^{2+}$ increase. To verify this point, the intracellular $\hbox {Ca}^{2+}$ responses with the ATP-dependent $\hbox {Ca}^{2+}$ signaling pathway alone (without $\hbox {TRPV}_{4}\hbox {-C}_{1})$ by increasing the value of the kinetic parameter $a\, (\times 100, \times 200$) of the ATP release dynamic model (in Eq. 10) is shown in Fig. 9. Increase in the value of the kinetic parameter $a$ implies the increase in the amount of endogenously released ATP by shear stress. Even if the amount of endogenously released ATP increases 100 or 200 times, which is absolutely impossible in the experimental studies (Yamamoto et al. 2003), it can be readily seen from Fig. 9 that no stepwise increasing $\hbox {Ca}^{2+}$ response can be found due to the dynamic process of shear shear-induced ATP release (Yamamoto et al. 2003; Qin et al. 2008).

Fig. 9

Model-predicted $\hbox {Ca}^{2+}$ response to shear stress-induced ATP release alone (without $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels and $[\hbox {ATP}]_{\mathrm{o}} = 0$) by increasing the value of the kinetic parameter $a$ in the ATP release dynamic model (Eq. 10)

Notably, the feedback regulation mechanisms involving $\hbox {IP}_{3}$ and $\hbox {Ca}^{2+}$ also play vital roles (see Fig. 8b). Based on the indirect activation mechanism proposed by Yamamoto et al., Hu et al. (2008) proposed a dynamic model for ATP-mediated intracellular $\hbox {Ca}^{2+}$ response in VECs in response to shear stress (Hu et al. 2008). However, the simulation results of our current dynamic model demonstrate that the indirect activation mechanism alone is insufficient to describe shear stress signal transduction leading to $\hbox {Ca}^{2+}$ influx. This is evidenced by the fact that the contribution of endogenously released ATP by shear stress to the intracellular $\hbox {Ca}^{2+}$ response in VECs can be ignored, as shown in Fig. 8d. Though adjusting kinetic parameters may increase the $\hbox {Ca}^{2+}$ response to some degree, several important phenomena like the stepwise $\hbox {Ca}^{2+}$ increase cannot be generated as well (see Fig. 9). Therefore, the direct activation mechanism, which is mediated by $\hbox {TRPV}_{4}$ and/or $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels, plays a more significant role than the indirect mechanism related to shear stress-induced ATP release in $\hbox {Ca}^{2+}$ response to shear stress in VECs. However, the indirect mechanism, related to both P2Y and $\hbox {P2X}_{4}$ channels, still has an irreplaceable effect as mentioned in the Sects. 3.2.1 and 3.2.3 (see Fig. 8b, c, e) because external ATP activation on both P2Y and $\hbox {P2X}_{4}$ channels may generate feedback effect via intracellular $\hbox {IP}_{3}$ and $\hbox {Ca}^{2+}$ on the mechanosensitivity of the $\hbox {TRPV}_{4}\hbox {-C}_{1}$ channels activation by shear stress.

Based on the proposed dynamic model, the intracellular $\hbox {Ca}^{2+}$ response induced by a stepwise increase in shear stress is numerically simulated (see Fig. 4), which is in qualitative agreement with Fig. 1 in the literature (Yamamoto et al. 2000b). To further validate the dynamic model, the transient $\hbox {Ca}^{2+}$ response to cessation of shear stress and washout of external ATP are numerically simulated. The simulation results are compared with experimental evidence obtained by Mo et al. (1991). Figure 6 shows that the cessation of either stimuli may immediately pull down the intracellular $\hbox {Ca}^{2+}$ concentration to the basal level due to the closure of $\hbox {Ca}^{2+}$ channels on the membrane, which is in excellent agreement with experimental observations by Mo et al. (1991). Finally, in order to reproduce the $\hbox {Ca}^{2+}$ oscillations observed in the literature (Shen et al. 1992), some key parameters are modified, and the phenomena of $\hbox {Ca}^{2+}$ oscillations are well simulated in great accordance with frequency characteristic of the experimental results (see Fig. 7). The oscillation frequency is proportional to the applied shear stress level and ATP concentration, while the characteristic of oscillation amplitude may need to be further optimized.

The proposed model will enhance the understanding of the mechanism of $\hbox {Ca}^{2+}$ signaling in VECs in response to fluid shear stress and ATP. The model is particularly informative regarding roles of direct and indirect activation mechanism by shear stress and the nonlinear interaction among intracellular $\hbox {Ca}^{2+}$ signaling components. It will also pave the way for quantitative regulation of intracellular $\hbox {Ca}^{2+}$ signals using flow and ATP modulation. The exact mechanisms for dynamic calcium response in VECs are complex. Many issues regarding these mechanisms remain to be addressed. In the future, more theoretical and experimental studies will be needed to further clarify the mechanisms involved in shear stress-induced $\hbox {Ca}^{2+}$ signaling in VECs.

5 Conclusions

In this study, a novel dynamic model has been developed to provide a better description of shear stress-induced $\hbox {Ca}^{2+}$ signaling by considering all the possible direct and indirect mechanisms. In particular, we have taken into consideration the recent experimental evidence that $\hbox {TRPV}_{4}\hbox {-C}_{1}$ compound channels can be directly activated by shear flow, which are also modulated by both intracellular $\hbox {IP}_{3}$ and $\hbox {Ca}^{2+}$ concentrations. The dynamic behaviors of $\hbox {Ca}^{2+}$ have been investigated using numerical simulations. The simulation results show that the intracellular $\hbox {Ca}^{2+}$ response in VECs produced by the proposed dynamic model is in good accordance with experimental observations. Moreover, the direct and indirect activation mechanisms can be better understood using the current dynamic model. We also conclude from the simulation studies that endogenously released ATP may play an insignificant role in the process of intracellular $\hbox {Ca}^{2+}$ response to shear stress.