1 Introduction

Childbirth can be a psychologically and mechanically traumatic event. Despite being a natural process, it involves extensive physiologic changes in the mother to allow the passage of the fetus through the birth canal. Although a widely discussed topic, maternal birth trauma, especially in the levator ani muscle (LAM), continues to affect millions of women worldwide (Dietz et al. 2020). During vaginal delivery, the LAM stretches beyond its limits, being associated with long-term conditions such as pelvic organ prolapse and stress urinary incontinence. LAM injuries are estimated in 13–36% of women who deliver vaginally (Doumouchtsis 2016).

To facilitate the process, the mother can adopt several postures during the second stage of labor, which starts with full cervical dilation and ends with the delivery of the fetus. Maternal positions can be classified into non-flexible and flexible sacrum positions, depending on if the weight of the mother’s body is on or off the sacrum, respectively. In flexible sacrum positions, the movement of the coccyx is allowed due to the flexibility of the sacrococcygeal joint. To promote a positive birth experience, the women should be able to make an informed choice about the most comfortable birthing position (Berta et al. 2019; Zang et al. 2020).

The fetus also plays a crucial role in the birth outcome. During vaginal delivery, the fetal head molds into an elongated shape due to the pressure exerted by the birth canal and surrounding structures (Bamberg et al. 2017). This phenomenon allows the fetal head to pass through the birth canal and leads to the variation of specific fetal head diameters. The final diameters are dependent on the maternal pelvic diameters and the fetal size itself. However, excessive molding can be harmful to the fetus (Kriewall et al. 1977). Molding can occur due to the presence of sutures and fontanelles, which are dense connective tissue membranes characterized by having a viscoelastic behavior, and the ability of the skull bones to displace and overlap (Romanyk et al. 2016; Vlasyuk 2018). The described phenomenon is represented in Fig. 1.

Fig. 1
figure 1

Demonstration of the fetal head molding phenomenon during childbirth

Full size image

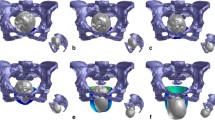
Concerning maternal complications, morbidity is generally associated with the duration of labor and mode of delivery. The position of the fetus during labor, which refers to the relationship of the fetal presenting part to the maternal pelvis, is another factor associated with pelvic floor injuries. In cephalic presentations, when the fetus is presented in the longitudinal lie, the fetal occiput is the reference, and any fetal position that is not occipito-anterior (OA) is considered to be a malposition (Kilpatrick and Garrison 2012). The most common fetal malposition is the occipito-posterior (OP) position, associated with adverse outcomes. About 50–80% of fetuses start the second stage of labor as OP but end up rotating to OA position; thus, only 5% of term fetuses are OP at time of delivery (Gimovsky 2021). The impact of this position on women and neonates is considerable, with higher rates of birth trauma associated with this type of delivery (Pilliod and Caughey 2017). According to the literature, fetuses delivered in the OP position have higher risk of acidaemia, birth trauma, admission to intensive care nursery, and longer neonatal stay in the hospital (Dahlqvist and Jonsson 2017). Figure 2 demonstrates distinct maternal (non-flexible and flexible sacrum) and fetal (OA and OP) positions that can be adopted during childbirth.

Fig. 2
figure 2

Illustration of different maternal positions considering the weight of the body on or off the sacrum. a Non-flexible sacrum with the fetus in the occipito-anterior position. b Flexible sacrum with the fetus in the occipito-posterior position

Full size image

Childbirth computational models can provide deeper insights into the mechanisms of fetal and maternal injury (Chen and Grimm 2021). Biomechanical models have been used to evaluate mechanical changes on the pelvic floor muscles (PFM) during vaginal delivery (Lien et al. 2004; Parente et al. 2008), the influence of fetal head flexion (Parente et al. 2010), the damage caused by PFM stretching (Oliveira et al. 2016b), the effect of obstetric procedures (Oliveira et al. 2016a), and the impact of labor duration on fetal head molding and PFM (Vila Pouca et al. 2017; Moura et al. 2020). Regarding mechanical characterization, hyperelastic and viscoelastic models are frequently used to characterize soft tissues, namely the PFM. The inclusion of the viscous behavior of soft tissues on a childbirth simulation allows to analyze the effect of time on the forces and stresses developed. Vila Pouca et al. (2017) implemented a visco-hyperelastic constitutive model to evaluate how the childbirth duration affects the PFM during delivery.

Previous studies have already simulated the second stage of labor with the fetus in different positions. The OP position is associated with higher stretch values on the PFM and, consequently, to a higher risk for stretch-related injuries (Parente et al. 2009a). According to Havelkovà et al. (2020), the OP position leads to an increase in the stresses measured on the levator ani muscle compared to the optimal head position. Furthermore, Borges et al. (2021) analyzed the impact of distinct maternal postures on the PFM, concluding that in non-flexible sacrum positions, the maternal pelvis, and PFM are subjected to higher efforts, being prejudicial from a biomechanical perspective.

However, the mentioned works focus only on the individual assessment of the mother or fetus, being still necessary to biomechanically analyze their interaction. Based on the described studies, the present work aims to take a step forward and investigate the impact of a persistent OP malposition on both mother and fetus, when the mother assumes a flexible-sacrum posture and the fetal head is deformable, allowing the occurrence of molding. To the best of our knowledge, this is the first study in which a finite element model composed of maternal pelvic bones and a deformable fetal head with viscous properties is used to simulate vaginal delivery considering different fetal positions.

2 Methodology

2.1 Biomechanical model

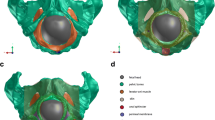
A three-dimensional (3D) finite element model of the mother and fetus was considered to simulate vaginal deliveries (Parente et al. 2008). The simulations performed in this work were conducted in Abaqus\(^\text{\textregistered }\) software. Since the labor process is a complex physiological phenomenon that includes several anatomical structures, it is important to have a representative anatomical model to perform accurate biomechanical simulations. The mother’s model, shown in Fig. 3, consists of the PFM (specifically the LAM) and their supporting structures, hip bones, sacrum, coccyx, and main pelvic ligaments.

Fig. 3
figure 3

Frontal (a) and back (b) views of the finite element model of the mother, considering the main pelvic ligaments (1—Sacroiliac ligaments. 2—Superior pubic ligament. 3—Inferior pubic ligament. 4—Sacrospinous ligament. 5—Sacrotuberous ligament), and the sacrococcygeal joint (6). (c) Pelvic floor muscles with the identification of the curve used to evaluate the stretch (path 1), the curves to analyze the maximum principal stresses (path 1 to 4), and the curve that represents the fixed nodes between the PFM and the sacrum (path 5)

Full size image

The PFM was based on geometrical data point-set acquired from a 72-year-old female cadaver measurements by Janda et al. (2003), assuming a constant thickness of 2 mm. The specimen was selected for having no pathology to the pelvic floor. The pelvic floor model also includes the supporting structures used to simulate the connections between the PFM and the coccyx, in the posterior part, and the behavior of the arcus tendinous, obturator fascia, and obturator internus, in the most anterior part. These structures were modeled recurring to hexahedral elements with hybrid formulation (C3D8H). The pelvic bones are composed of rigid triangular shell elements of type S3R and the main pelvic ligaments of truss elements of type T3D2.

Regarding the sacrum and coccyx, these structures were divided into cortical and trabecular tissue, corresponding to shell and tetrahedral elements, respectively. In the current study, the sacrococcygeal joint was included. As the sacrum is fixed, the movement of the coccyx around the joint is allowed, aiming to mimic maternal positions in which the weight of the body is off the sacrum. Further information on the anatomical structures can be found in previous works (Parente et al. 2008; Borges et al. 2021).

The maternal pelvic diameters demonstrated in Fig. 4, were adjusted according to the literature (Michel et al. 2002) and their values are presented in Table 1.

Fig. 4
figure 4

Maternal pelvic diameters, considering the frontal (a), lateral (b) and back (c) views: 1—Transverse. 2—Interspinous. 3—Obstetric conjugate. 4—Sagittal outlet. 5—Intertuberous

Full size image
Table 1 Maternal pelvic diameters considered based on Michel et al. (2002)
Full size table

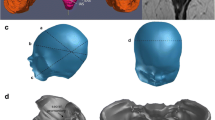
The finite element model of the fetus head, presented in Fig. 5, was modeled by Parente et al. (2008) and Silva et al. (2015). The head is at the 50th percentile for a gestational age between 36 and 40 weeks according to the fetal growth data in Kiserud et al. (2017). The model is composed of the skin, skull, and brain, modeled with solid tetrahedral elements (C3D4). The sutures and fontanelles are also included but were modeled with membrane elements (M3D3) with 1.2 mm of thickness (Coats and Margulies 2006). Since these structures allow fetal head molding to occur, their characteristics should be as close to reality as possible. Some tissues can be analyzed recurring to membrane finite elements, namely soft tissues that show a large planar extension and a smaller extension in the out-of-plane direction (plane stress state). Thus, the sutures and fontanelles were modeled with membrane elements to achieve a more realistic behavior (Moura et al. 2020).

Fig. 5
figure 5

Finite element model of the fetal head. 1—Skin. 2—Brain. 3—Skull. 4—Sutures and fontanelles

Full size image

2.2 Material models

2.2.1 Quasi-incompressible transversely isotropic hyperelastic model

The PFM was characterized by the quasi-incompressible transversely isotropic hyperelastic constitutive model proposed by Martins et al. (1998) and previously used by Parente et al. (2008). The strain energy density per unit volume is given by the following expression:

$$U_{{{\text{JM}}}} = U_{m} (\bar{I}_{1}^{C} ) + U_{f} (\bar{\lambda }_{f} ,\theta ) + U_{J} (J)$$
(1)

\(U_J\) is related to the volume change:

$$\begin{aligned} U_J = \frac{1}{D} (J - 1)^2 \end{aligned}$$
(2)

where \(J = det(\mathbf{F} )\) is the volume ratio and \(\mathbf{F}\) is the deformation gradient. D is a constant.

\(U_m\) corresponds to the isotropic strain energy stored in the isotropic matrix:

$$\begin{aligned} U_m = c \{ e^{b \big (\overline{I}_1^C - 3\big )} - 1 \} \end{aligned}$$
(3)

where c and b are constitutive constants and \(\overline{I}_1^C\) is the first invariant of the right Cauchy-Green strain tensor with the volume change eliminated.

The passive and active parts of the strain energy stored in each muscle fiber can be described as:

$$\begin{aligned} U_f = A \{ e^{[a (\overline{\lambda }_f - 1)^2]} - 1 \} + \theta ~T_0^{M} \int _{1}^{\overline{\lambda }_f} - 4 (\overline{\lambda }_f - 1)^2 + 1 ~ d\overline{\lambda }_f \end{aligned}$$
(4)

with \(0.5< \overline{\lambda }_f < 1.5\) representing the stretch ratio of the muscle fibers. For other values of \(\overline{\lambda }_f\) the muscle produces no force and, therefore, the strain energy is zero. A and a represent the constitutive constants and \(T_0^{M}\) is the maximum muscle tension produced by the muscle at resting. The level of activation is controlled by the internal variable \(\theta \in [0,1]\). In this work, it was assumed \(\theta = 0\) for all the simulations, considering that the muscles are fully relaxed due to anesthesia, which is seen in more than 60% of women who have vaginal birth according to the Centers for Disease Control (Osterman and Martin 2011).

2.2.2 Viscoelastic model

Since the viscoelastic behavior of soft tissues is essential to achieve an accurate biomechanical characterization, the viscoelastic constitutive model implemented by Vila Pouca et al. (2017) and based on Holzapfel (2000) was used to characterize the PFM and the sutures and fontanelles of the fetal head. The viscoelastic model was implemented into Abaqus\(^\text{\textregistered }\) software through a User-Defined Material Subroutine (UMAT).

To represent the viscoelastic contribution, the generalized Maxwell model was used. The implementation includes the addition of a dissipative potential to the strain energy function (Eq. 5), describing the non-equilibrium state.

$$\begin{aligned} U_M(C, \Gamma _1,\ldots , \Gamma _m) = U^\infty _{vol}(J) + U^\infty _{iso}(\overline{\mathbf{C }}) + \sum _{\alpha = 1}^{m} \gamma _\alpha (\overline{\mathbf{C }}, \varvec{\Gamma }_\alpha ) \end{aligned}$$
(5)

The configurational free energy \(\gamma _\alpha\) is a function of the modified right Cauchy-Green strain tensor, \(\overline{\mathbf{C }}\), and a set of strain-like internal variables denoted by \(\varvec{\Gamma }_\alpha\). The latter characterizes the relaxation and/or creep behavior of the material. The viscoelastic behavior is modeled by \(\alpha\)=1,...,i viscoelastic processes.

The second Piola-Kirchhoff stress can be decomposed into an equilibrium part and a non-equilibrium part characterized by the elastic response of the system and the viscoelastic response, respectively, as demonstrated in Eq. 6.

$$\begin{aligned} \mathbf{S} = \mathbf{S} ^\infty _{J} + \mathbf{S} ^\infty _{m} + \mathbf{S} ^\infty _{f} + \sum _{\alpha = 1}^{i} \mathbf{Q} _\alpha \end{aligned}$$
(6)

\(\mathbf{S} ^\infty _{J}\), \(\mathbf{S} ^\infty _{m}\) and \(\mathbf{S} ^\infty _{f}\) denote the volumetric, matrix and fiber contribution of the second Piola-Kirchhoff stress tensor. The isochoric non-equilibrium stress tensors \(\mathbf{Q} _{\alpha }\) can be defined by Eq. 7 and its solution obtained through convolutional integrals.

$$\begin{aligned} \mathbf{Q} _\alpha = \int _{t=0^+}^{t=T} exp \bigg [\frac{-(T-t)}{\tau _\alpha } \bigg ] \beta _{\alpha } \dot{\mathbf{S }}_{\alpha }~dt \end{aligned}$$
(7)

\(\tau _\alpha\) and \(\beta _\alpha\) correspond to the relaxation time and free-energy parameter, representing the viscoelastic properties derived from the Maxwell model with \(\alpha\) parallel elements.

The material elasticity tensor can also be written in a decoupled form:

$$\begin{aligned} \mathbb {C} = \mathbb {C}^\infty _{J} + \mathbb {C}^\infty _{m} + \mathbb {C}^\infty _{f} + \sum _{\alpha =1}^{m} (\mathbb {C}^\alpha _{m} + \mathbb {C}^\alpha _{f}) \end{aligned}$$
(8)

where \(\mathbb {C}^\infty _{J}\), \(\mathbb {C}^\infty _{m}\) and \(\mathbb {C}^\infty _{f}\) represent the volumetric, matrix and fiber contribution. The matrix and fiber contribution of the viscous component is defined as:

$$\begin{aligned} \mathbb {C}^{\alpha }_{m,f} = 2 \frac{\partial \mathbf{Q} ^{\alpha }_{m,f}}{\partial \mathbf{C} } \end{aligned}$$
(9)

2.2.3 Plane stress formulation

The sutures and fontanelles were modeled with membrane elements. To characterize these structures, the UMAT implemented by Moura et al. (2020) for plane stress state with the Holzapfel-Gasser-Odgen (HGO) constitutive model and the aforementioned viscoelastic contribution was used.

The strain-energy function of the HGO constitutive model is given by:

$$\begin{aligned} U_{HGO} = \frac{c_1}{2} (\overline{I}_1 - 3) + \frac{k_1}{2 k_2} \sum _{i=4,6} \big \{ e^{k_2 {\langle E_\alpha \rangle }^2}-1\} \end{aligned}$$
(10)

where \(c_1\) and \(k_1 > 0\) are stress-like material parameters and \(k_2 > 0\) is a dimensionless parameter. In membrane elements, the plane stress state can be achieved by assuming the incompressibility condition, which allows representing the strain in the out-of-plane direction as a function of the in-plane strains (Prot et al. 2007). By considering incompressibility, the component \(C_{33}\) of the right Cauchy-Green strain tensor can be formulated in terms of the in-plane components:

$$\begin{aligned} C_{33} = (C_{11} C_{22} - C^2_{12})^{-1} \end{aligned}$$
(11)

In the plane stress formulation, the second Piola-Kirchhoff stress tensor can be obtained as:

$$\begin{aligned} \mathbf{S} = 2 \sum _{\begin{array}{c} i=1 \\ i\ne 3 \end{array}}^5 \frac{\partial U}{\partial I_i} \frac{\partial I_i}{\partial \mathbf{C} } + p\mathbf{C} ^{-1} \end{aligned}$$
(12)

The scalar p can be determined assuming that the stress component \(S_{33}\) is zero for thin sheets (Eq. 13).

$$\begin{aligned} p = - 2 \sum _{\begin{array}{c} i=1 \\ i\ne 3 \end{array}}^5 \frac{\partial U}{\partial I_i} \frac{\partial I_i}{\partial C_{33}} C_{33} \end{aligned}$$
(13)

The material elasticity tensor can be calculated through the following equation:

$$\begin{aligned} \mathbb {C} = 4 \sum _{\begin{array}{c} i,j=1 \\ i,j\ne 3 \end{array}}^5 \frac{\partial ^2 U}{\partial I_i \partial I_j} \frac{\partial I_i}{\partial \mathbf{C} } \otimes \frac{\partial I_j}{\partial \mathbf{C} } + 2 \mathbf{C} ^{-1} \otimes \frac{\partial p}{\partial \mathbf{C} } + 2 p \frac{\partial \mathbf{C} ^{-1}}{\partial \mathbf{C} } \end{aligned}$$
(14)

For the implementation of a UMAT in Abaqus\(^\text{\textregistered }\), the Cauchy stress tensor and the tangent stiffness matrix have to be determined. This can be accomplished through a push-forward operation of the second Piola-Kirchhoff stress tensor and the material elasticity tensor, described in Eqs. 12 and 14, respectively. However, before performing this operation, the viscoelastic contribution described in the previous section was added. The volumetric contribution is not taken into consideration in this implementation since the plane stress condition presupposes a total incompressibility formulation.

2.3 Constitutive parameters

The PFM was modeled with a modified form of the incompressible transversely isotropic hyperelastic model proposed by Martins et al. (1998) and described in subsection 2.2.1. The hyperelastic parameters were obtained from experimental data produced by Janda (2006). In this study, passive material parameters were determined through uniaxial and equibiaxial tests performed on the pelvic floor muscles of three female fresh cadaver specimens (82, 66 and 38 years old). Based on the stress-strain curves provided, Parente et al. (2009a) performed an iterative process by varying the constitutive model constants until obtaining an adequate approximation, reaching the material parameters used in the present study. The viscoelastic parameters were retrieved from Vila Pouca et al. (2017), which iteratively determined the material properties so that the stress relaxation curve approached with a good agreement the experimental data obtained by Peña et al. (2010). The latter analyzed tissue samples from nine postmenopausal patients with a mean age of 65±10.71 years. The viscoelastic mechanical properties of vaginal tissue were investigated through tensile and relaxation tests. Moreover, the parameters used to characterize the sacrum, coccyx, and main pelvic ligaments derived from Borges et al. (2021), which used information from previous biomechanical studies that already incorporated these structures (Lei et al. 2015; Wu et al. 2018).

The skin, skull and brain of the fetal head were modeled with linear elastic models, considering the effect of geometrical nonlinearity. The elastic material properties for brain were retrieved from experimental data provided by Mehdizadeh et al. (2008). Gray matter was obtained from the parietal lobe of one-year-old bovine brain tissue. The Young modulus was calculated from the stress-strain and the material properties of gray matter were considered for the whole brain. Furthermore, the mechanical properties of the skin are based on Shergold et al. (2006), that calculated the Young modulus of the human skin based on stress-strain curves retrieved from previous studies. The skull’s characterization is based on Coats and Margulies (2006) which presents the Young modulus of the parietal bone for a newborn.

Regarding the characterization of the sutures and fontanelles, the hyperelastic parameters were obtained from a two-month-old human suture experimental curve (Coats and Margulies 2006). In the present work, a genetic algorithm was used to determine the material constants that fit the experimental curve with the HGO constitutive model, described in subsection 2.2.3, considering one family of fibers with a randomly organized orientation (Warren et al. 2008). The calibration curve is presented in Fig. 6. A R squared (\(R^2\)) of 0.9848 was obtained. Thorough research showed no results of experimental mechanical properties to characterize the viscoelasticity of these tissues, namely stress relaxation tests. Therefore, the parameters were based on those adopted for the pelvic floor muscles in Vila Pouca et al. (2017), and then adapted (Moura et al. 2020). Although these parameters were used to characterize a different tissue, the model was implemented with a similar purpose, that is, studying the effect of viscoelasticity on soft tissues.

Fig. 6
figure 6

Cauchy stress curve showing the fitting of the numerical data with the experimental data from Coats and Margulies (2006). The experimental test was performed in a human pediatric cranial bone-suture-bone specimen from a 2-month-old donor

Full size image

The material properties used for the PFM and distinct structures of the fetal head were obtained indirectly from experimental data from human or animal tissue. Regarding the main pelvic ligaments, the properties were adjusted taking into account the number of elements used and its cross-sectional area. Table 2 summarizes the material properties used to characterize the different model structures.

Table 2 Material parameters used to characterize the pelvic floor muscles, fetal head, sacrum, coccyx, and main pelvic ligaments
Full size table

2.4 Numerical simulations

The childbirth simulations were performed in Abaqus\(^\text{\textregistered }\) software to mimic the second stage of labor in a vertex presentation. Two different fetal positions were considered: occipito-anterior (OA) and occipito-posterior (OP). Both simulations were performed with a similar duration of 100 minutes, aiming to replicate the average duration of the second stage of labor in nulliparous (Quiñones et al. 2018).

To describe the fetal trajectory in the two distinct positions, all fetal movements were enforced by a reference node that allows controlling the descent (y-axis) and the movements of flexion/extension (rotation around the z-axis). For the OA position, the suboccipitobregmatic diameter (SOBD) engages the pelvis, and, for the OP position, the occipitofrontal is the presenting diameter. Therefore, the paths were defined with adjustments between the two positions so that these diameters were presented. Although the trajectory of the fetus is defined, the head can make slight adjustments in its movement to facilitate the descent. The initial configuration of the fetal head considered in both simulations is demonstrated in Fig. 7.

Fig. 7
figure 7

Demonstration of fetal engagement in the pelvic structures at the beginning of the numerical simulations for the two distinct positions. a OA position. b OP position

Full size image

Regarding boundary conditions, to mimic the maternal postures in which the weight of the mother’s body is off the sacrum, the movement of the sacrococcygeal joint was allowed and the coccyx was able to rotate. The sacrum nodes in the articular facets with the pelvic girdle bones were fixed. A tie constraint was applied between the two supporting structures of the PFM (arcus tendinous, obturator fascia, and obturator internus) and the hip bones to maintain those structures connected. The nodes of the supporting structures representing the connections between PFM and sacrum were considered fixed (defined by path 5, represented in Fig. 3c).

The standard Abaqus\(^\text{\textregistered }\) contact algorithm was used to impose the kinematic contact conditions. Contact constraints were established between the fetus head skin and the PFM, and between the fetus head skin and the pelvic bones. To create these conditions, a surface interaction with the Augmented Lagrange method was used.

The variation in the diameters of the fetal head was measured for both OA and OP fetal positions during the simulations. The diameters considered in this study are presented in Fig. 8.

Fig. 8
figure 8

Representation of the fetal head diameters. 1—Maxillo-vertical (MaVD). 2—Suboccipitobregmatic (SOBD). 3—Occipitofrontal (OFD). 4—Biparietal (BPD)

Full size image

For the OA position, the molding of the fetal head can be evaluated through the maxillo-vertical (MaVD), suboccipitobregmatic (SOBD) and biparietal (BPD) diameters. To analyze the fetal head deformations, the molding index, which represents a relation between the fetal diameters that vary during childbirth, was calculated (Eq. 15) (Sorbe and Dahlgren 1983). This index indicates the degree of deformation of the head.

$$\begin{aligned} \mathrm{MI} = \frac{\mathrm{MaVD}^2}{\mathrm{SOBD} \times \mathrm{BPD}} \end{aligned}$$
(15)

Since the occipitofrontal diameter (OFD) is the diameter that first engages the pelvis in the OP position, a new molding index was also calculated, considering the OFD instead of the SOBD (Eq. 16), aiming to analyze the molding suffered by the head when the fetus assumes an OP position.

$$\begin{aligned} MI_{new} = \frac{MaVD^2}{OFD \times BPD} \end{aligned}$$
(16)

To evaluate the behavior of the maternal pelvis during the second stage of labor, the coccyx rotation was measured. A node in the extremity of the coccyx mesh was chosen and the rotation was obtained by the analysis of variable UR3 (rotation about the z-axis, in radians), in Abaqus\(^\text{\textregistered }\) software. Regarding the PFM, the stretch caused by the passage of the fetal head and the maximum principal stresses were analyzed. To evaluate the stretch, a curve defined on the inferior part of the pelvic floor was created (designated as path 1), which is defined as the ratio between the current and the original length. By measuring the length during the simulation, the stretch values were determined relative to fetal descent. Furthermore, to analyze the stresses, different levels along the PFM were defined (paths 2, 3, and 4), according to those previously described by Parente et al. (2008). To obtain a better comparison of the results, the paths were normalized between 0 and 1, in which 0 represents one of the extremities, 0.5 the middle position, and 1 the position in the opposite extremity. The stresses were measured for the vertical displacement of the fetus corresponding to the instant of maximum stretch in each position. The distinct paths are demonstrated in Fig. 3c.

The progress of labor can be measured through the position of the presenting part of the fetus in relation to the ischial spines in the mother’s pelvis. The pelvis can be divided in stations above and below the maternal ischial spines, considering a transverse plane passing through the spines which corresponds to station 0. At the beginning of the simulation, when the vertical displacement of the fetal head corresponds to 0 mm, the fetus is at 0 station. Below the ischial spines, the presenting fetal part passes +1, +2, +3, +4 and +5 stations to delivery. After a fetal descent of 50 mm, the position of the fetus corresponds to station +5. To evaluate the labor progress, the time it took the fetus to reach station +5 in each position was registered.

3 Results

The rotation of the coccyx caused by the passage of the fetal head was analyzed for both fetal positions (Fig. 9). For the OA and OP position, a maximum rotation of 0.98\(^\circ\) and 2.17\(^\circ\) were measured, respectively. Therefore, it can be concluded that, in the OP position, the sacrum must rotate twice as much as the OA position for the fetus to pass.

Fig. 9
figure 9

Rotation of coccyx during the vertical descent of the fetal head

Full size image

The stretch suffered by the PFM during the vertical displacement of the fetal head was measured in path 1. A maximum stretch of 1.63 and 1.62 were obtained for the OP and OA positions, corresponding to a fetal descent of 60 and 65 mm, respectively. The stretch is not substantially different in the two positions since this is a geometrical factor and the fetal head follows a similar trajectory in both positions.

The maximum principal stresses were measured at the distinct paths of the PFM (defined in Fig. 3c) for both positions, as demonstrated in Fig. 10. The main differences between the two positions were observed in paths 2, 3, and 4. In path 2, the maximum stress was approximately 0.149 MPa for the OP position, consisting of an increase of 50.15% compared to 0.099 MPa in the OA position. Regarding path 3, the maximum stresses were 0.134 MPa and 0.086 MPa for the OP and OA positions, respectively, representing an increase of 55.20% from the OA to the OP position. Lastly, in path 4, the maximum stress was 0.075 MPa in the OP position and 0.055 MPa in the OA, consisting of an increase of 36.12%. Figure 11 shows the maximum principal stresses on the PFM for both positions for a vertical displacement of the fetal head of 60 mm.

During childbirth, the smallest possible diameter of the fetal head enters the pelvis first. In the OA position, the SOBD engages the maternal pelvis, while in the OP position it is the OFD that first fits the pelvis. The variation of these diameters along the vertical displacement of the fetal head for the two different fetal positions is presented in Fig. 12. The MaVD and BPD diameters were also measured, as they are necessary to calculate the molding index.

Fig. 10
figure 10

Maximum Principal Stresses obtained along the different normalized paths defined on the PFM

Full size image
Fig. 11
figure 11

Maximum principal stresses at the PFM for a OA position and b OP position corresponding to a vertical displacement of the fetal head of 60 mm

Full size image
Fig. 12
figure 12

Variation of SOBD, OFD, MaVD and BPD during the vertical displacement of the fetal head for OA and OP positions

Full size image

The molding index proposed by Sorbe and Dahlgren (1983) and the new molding index more suitable for the OP position (\(MI_{new}\)) are shown in Fig. 13. As demonstrated in Eqs. 15 and 16, the molding of the fetal head was measured considering the diameters that first present on each position under study. The molding is higher in the OA position for both indexes calculated, with maximums of MI \(= 1.87\) and \(\mathrm MI_\mathrm{new}\) = 1.56. For the OP position, maximums of MI \(= 1.81\) and \(\mathrm MI_\mathrm{new}\) = 1.53 were registered.

Fig. 13
figure 13

Variation of the molding index for the OA and OP positions along the vertical displacement of the fetal head

Full size image

The anteroposterior movement of the fetal head, which indicates its displacement along the x-axis (represented in Fig. 7), was analyzed along the fetal descent through the birth canal, given by its vertical displacement (y-axis). This relation determines the position of the head, describing its trajectory, and was compared with the Curve of Carus trajectory obtained by Jing et al. (2012), as presented in Fig. 14.

Fig. 14
figure 14

Representation of the anteroposterior movement of the fetal head during its vertical displacement and comparison with the Curve of Carus defined by Jing et al. (2012)

Full size image

Regarding the progress of labor, in the performed simulations, the fetus in the OA position took 50 min to achieve station +5, whereas in the OP position the fetus only reached this station after 54 min. The difference noted may indicate that it is more difficult for the fetus to progress in the OP position. This evidence can be corroborated by the maximum stretch instant, which is achieved at 60 mm of descent in the OP position and only at 65 mm in the OA position. With the PFM needing to reach the maximum stretch at an early stage, the second stage of labor might be prolonged since the muscles have not had enough time to adapt.

4 Discussion

Childbirth is a complex biomechanical process that can put both mother and fetus at risk of injuries and result in life-long complications (Chen and Grimm 2021). Several factors can influence the vaginal delivery outcome, namely the mode of delivery. The adaptation between the fetus and the birth canal is fundamental to a successful delivery, and the position of the mother and the fetal head can be crucial when it comes to the development of injuries on both parts. In this work, numerical simulations of vaginal delivery with the fetus in vertex presentation considering both OA and OP positions were performed, assuming a flexible sacrum birthing position. The aim of this study was to investigate the relation between fetal positioning, a specific maternal position, and the development of pelvic floor injuries. This evaluation was accomplished by measuring specific indicators in the mother’s finite element model (stretch and stresses on the PFM, rotation of the coccyx) and in the fetus (variation of diameters and molding index).

In the present study, highly similar stretch values were measured concerning the muscles’ stretching for the two positions, which can be explained by the almost identical trajectory performed by the fetus in the two simulations, demonstrated in Fig. 14. The fetal trajectory was compared in both positions with the curve of Carus (Jing et al. 2012), an imaginary arc within the pelvis which is used to describe the final course of the fetus during delivery. In the simulations performed, the head is closer to the sacrum and, when it reaches station +5, it starts to get closer to the pubic symphysis and coincident with the curve of Carus. Nevertheless, there is a discrepancy between the Carus curve and the trajectory defined for the fetus in the present simulations. Since this curve represents an anatomically ideal trajectory in the OA position, if the fetal path adopted in the simulations were even more similar to the curve, the stretch would possibly be inferior, as well as the stresses suffered.

The stretch values are lower than those obtained by Borges et al. (2021) (approximately 1.7), in which the bony structure was also used, probably due to the adoption of a deformable head in the current work. On the other hand, the stretch obtained is higher than that recorded in Moura et al. (2020), in which the deformable head was used, since the presence of the bone structure limits the trajectory of the fetus and allows obtaining more reliable results. Nonetheless, the maximum principal stresses measured in different paths of the PFM were superior in the OP position. These can be compared with those obtained in Oliveira et al. (2017), which also simulated the second stage of labor in two positions. In the mentioned study, the stresses were evaluated in different paths on the PFM, and these were substantially greater in the OP position, corroborating the results obtained. The differences observed in the range of values between the two studies can be explained by the use of a deformable head in the present work. Furthermore, similarly to the present study, Oliveira et al. (2017) also registered the maximum stretch in the OP position at an earlier stage of fetal descent. The overall results indicate that the OP position is more demanding for the PFM than the OA position, corroborated by previous numerical and clinical studies (Parente et al. 2009b; Eskandar and Shet 2009; Oliveira et al. 2017).

Concerning the maternal pelvis, the results obtained for the coccyx rotation reveal that in the OP position the coccyx needs to rotate twice as much as the OA position for the fetus to progress. In Bù (2001), the coccyx rotation was measured during PFM contraction, and it was registered an average rotation of \(15.0\pm 10.2^\circ\). During straining, the mean rotation was equal to \(12.9\pm 10.9^\circ\). Therefore, the numerical values obtained in the current study are within the physiological limits of the sacrococcygeal joint. In clinical terms, the OP position seems more demanding for the mother’s pelvis since it requires more available space for the fetus to progress. Although the clinical limits are not exceeded, there are cases in which excessive rotation of the sacrococcygeal joint can be harmful to the woman, particularly in the case of a calcified joint, which may require excessive effort and compromise the pelvis.

Fetal head deformations are also a factor that can impact the behavior of the muscles and maternal pelvis. According to the results of the numerical simulations, the OFD suffers a higher variation in the OP position in comparison with the OA. Since the OFD engages the pelvis first at the OP position, the variation that was verified in this diameter, shown in Fig. 12, was expected. Moreover, the SOBD underwent higher changes in the OA position (until 70 mm of descent), also according to the expected since this diameter engages the maternal pelvis in this position. The BPD underwent a more noticeable variation in the OA position. Regarding the MaVD, higher values are obtained for the OA position, due to the characteristic elongation of the head in this position. Literature only reports measurements of the fetal head diameters for the OA position. Nevertheless, the variations obtained in this study are within the expected, with an increase in MaVD, and a decrease in BPD and SOBD (Sorbe and Dahlgren 1983; Lapeer and Prager 2001; Pu et al. 2011).

In previous studies in which fetal malpositions were analyzed, only pelvic floor injuries were evaluated. In this study, the impact that the position has on the fetal head was also investigated. Although the OP position is generally more prone to PFM injuries, this position was found to be biomechanically favorable to the fetus, as it suffers fewer deformations in the head and has lower molding. The molding index considered for the OP position presents values noticeably lower than the one calculated for the OA position. Since fewer molding indicates a lower reduction in the BPD and SOBD, the head circumference will be greater and, consequently, increase the chance of harming the PFM. Thus, a more favorable scenario for the fetus could be more harmful to the mother. The overall conclusion is that there may be a struggle between the mother and the fetus during the second stage of labor for the existing space.

Computational biomechanics attempts to approximate as much as possible the anatomical and physiological characteristics of tissues. However, there are always limitations associated with the complexity of the models used. In the finite element model presented, the PFM were modeled with constant thickness, but the puborectal portion of the levator ani is generally thicker, which might influence stress distribution. The changes suffered by the muscles in the last weeks of pregnancy to facilitate the delivery are not considered. Regarding the characterization of the fetal head, the lack of mechanical properties to describe the viscoelastic behavior of the sutures and fontanelles can impact the results obtained. Performing relaxation tests on these structures and conducting mechanical tests on the brain, skin, and skull from the same human donor could allow obtaining more consistent properties. The fetal head also deforms during the first stage of delivery, and the fetus has already suffered modifications at the beginning of the second stage. Therefore, to further analyze the whole molding mechanism, it would be of value to simulate the vaginal delivery from the first stage of labor, including the uterus and birth canal.

Despite these limitations, the current study presents a finite element model able to simulate the second stage of labor in two different fetal positions, adopting a specific maternal configuration. The numerical results suggest that that the OP position is dangerous for the PFM and bony pelvis, with more probability of associated injuries. Also, the fetal head is more prone to mechanical injuries in the OA position. This study demonstrates that the fetal head and the PFM adapt to each other depending on the existing conditions.

As future work, the inclusion of structures to represent the birth canal and the uterus would allow performing a complete analysis of the labor process from the first stage, imposing additional restrictions on the fetus movements. The mechanical properties used to characterize the fetus head could be reassessed since more robust hyperelastic models could lead to a more realistic characterization. The inclusion of the active response of the muscles would also be interesting to analyze this event without epidural anesthesia. The simulations could also be performed for different durations to study the effect of the second stage of labor duration on the OP position.