1 Introduction

Evaluating the mechanical properties of the brain tissue is a fundamental subject in understanding intracranial brain deformation under different loading conditions. It has been shown that severe rotation of the head creates rapid angular acceleration in the brain causing brain deformations and shear strains which may lead to TBI (Holbourn 1943). TBI can also occur from blunt impacts leading to an acute subdural hematoma, diffuse axonal injury (DAI), death, or other serious disability (Faul et al. 2010; O’riordain et al. 2003; Rueda and Gilchrist 2009). To study in vivo intracranial behavior under TBI conditions, FE models have been introduced to predict the brain deformation for different applied loads (Eslaminejad et al. 2018b; Giordano et al. 2014; Goriely et al. 2015b; Hosseini-Farid et al. 2018; Ramazanian et al. 2018; Ramzanpour et al. 2018; Ratajczak et al. 2019; Raul et al. 2006). In these analyses, while creating a computational model containing detailed anatomical geometries of the human head is necessary, it is also highly important to employ accurate material properties for the intracranial organs. Modeling TBI is dynamic in nature and the brain will experience a variety of loading rates for different scenarios. Thus, for a rate-dependent material such as the brain, it is necessary to select the correct material properties corresponding to a specific simulation rate.

It has been shown that severe brain injury under blunt impact normally occurs when the brain deforms within the strain-rate range of 23–140 s−1 (Viano and Lovsund 1999; Zhang et al. 2004). Also, the recent computational studies of various impact and blast scenarios indicated that for mild to severe TBI, the brain undergoes strain rates ranging from 36 to 241 s−1 (Farid et al. 2018). It should be noticed that the effective time durations in higher-frequency loads, such as impact-induced and blast-induced TBI, are, respectively, within the order of some and less than one millisecond (Saboori and Walker 2019; Zhang et al. 2004). With such a short time duration, the rate effect is a key feature in studying the behavior of the brain in TBI-related loading. Substantial studies have focused on characterizing this viscoelastic behavior by using time-dependent stress-strain relations (de Rooij and Kuhl 2016; Hosseini-Farid et al. 2019a; Mendis et al. 1995; Miller 1999). Those studies employed the strain energy functions linearly coupled with time domain to implicitly address the strain-rate effects at large strains (Hosseini-Farid et al. 2019b; Rashid et al. 2012). Although this modeling provides effective constitutive representation for short- and long-term tissue behaviors, calibrating these linear viscoelastic models to test results from various rates is fairly challenging (Farahmand and Ahmadian 2018; Farid et al. 2017). In contrast, limited works in the literature have developed the nonlinear hyper-viscoelastic material models which were phenomenological in nature and have successfully reproduced the rate-dependent tissue responses over complex loading histories (de Rooij and Kuhl 2016). Although the hysteresis and dissipative characteristics were fully addressed by these models, their formulations are not supported in FE packages and are only useful if one is interested in self-developed numerical studies (Haldar and Pal 2018; Prevost et al. 2011).

The aim of this study is to elaborate on some key features of characterizing the brain tissue at high strain rates paving the way for investigating the injury at the central nervous system under dynamical loads. This work is going to be a preliminary step in developing a predictive model for brain tissue over a large variety of strains and strain rates. In the experimental portion of this study, unconfined tests with compression velocities of 10, 100, and 1000 mm/s were carried out on animal brain tissues for strain value of up to 30%. The nonlinear viscoelastic constitutive modeling is described, and the compatibility of the new model for implementation in FE software packages has been examined. This paper establishes an introductory step toward the development of a comprehensive experimental, theoretical, and computational framework to enhance the FE analysis being employed in a variety of biomechanical studies for traumatic brain injury.

2 Materials and methods

2.1 Experiments

Four fresh bovine brains were obtained from the Animal Science Department facilities at North Dakota State University. The animals were 2 years old, and all were healthy. The brains were carefully removed from their heads, immediately kept in phosphate-buffered saline (PBS) solution to prevent dehydration, and transported to the lab cold, but not frozen, to prevent mechanical decay. All tests were conducted within three to eight hours after the slaughtering. First, the samples from the brain were cut from the frontal and parietal lobes of each hemisphere. The procedure followed the experimental protocol by Miller and Chinzei (1997b) instructed to prepare samples for uniaxial unconfined compression tests. The actual measured diameter and height of samples before conducting the experiment were 24.8 ± 0.3 mm and 15.0 ± 0.3 mm (mean ± SD), respectively. All the extracted brain specimens consisted of a mixture of gray and white matter.

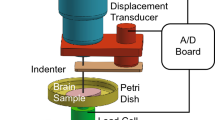
Similar to Rashid et al. (2012), the unconfined compression tests were conducted on the mixed gray and white matter specimens for up to 30% strain of each sample height. Tests were performed at room temperature (~ 22 °C) using a BOSE 3200 Electroforce machine (BOSE Corporation, Bloomington, MN, USA) designed for testing soft tissue materials. Figure 1 shows the experimental setup of the unconfined compression tests. Before each test, the surfaces of the top and lower platens were thoroughly treated with a surgical lubricant (Surgilube, Fougera Pharmaceuticals Inc.) to establish unconfined compression conditions. This procedure was essential to diminish the frictional effects and to provide a uniform expansion in the radial direction. Samples were then carefully located between the two platens. The outer surface of each brain specimen was carefully humidified with phosphate-buffered saline solution to keep the tissue hydrated, during the entire test procedure. After hydration, the upper platen was cautiously moved downward until it touched the sample. Then, all forces and reference displacement were set to zero. The tests were performed at three different deformation rates of 10 mm/s (n = 10 brain samples), 100 mm/s (n = 8), and 1000 mm/s (n = 12). These compression velocities correspond to approximate nominal strain rates of 0.67, 6.67, and 66.7 s−1. Figure 1 shows the Electroforce machine which was used for the testing. Also, the radial expansion of the cylindrical specimens captured by a high-speed camera (NanoSense MKIII, DantecDynamics) at different instances (Fig. 1) confirmed that the deformation was approximately homogeneous. It proves that employing the surgical lubricant was effective in minimizing the frictional effects between the sample and the platens.

Fig. 1
figure 1

a Electroforce machine ready for the in vitro unconfined compression test while a high-speed camera records samples deformation, and the deformation steps of brain specimen with speed of 100 mm/s in terms of time at bt = 0.00, ct = 0.021, dt = 0.033, and et = 0.045 s, corresponding to compressive strain of 0, − 0.14, − 0.21, and − 0.3

Full size image

2.2 Constitutive modeling

2.2.1 Preliminaries

The parallel rheological framework allows the introduction of a nonlinear viscoelastic material model consisting of multifold networks connected in parallel (Bergstrom 2015). As shown in Fig. 2, the mechanical response of brain tissue can be decomposed into two parallel networks: hyperelastic equilibrium network (spring), specified as network A, and a rate-dependent viscoelastic behavior (spring–dashpot), defined as network B (Farid 2019).

Fig. 2
figure 2

a Schematic representation of the proposed nonlinear viscoelastic model with two parallel networks consisted of an equilibrium network A and a viscoelastic network B, b the multiplicative decomposition of the deformation for the rheological components of this model

Full size image

Considering the parallel continuity, for each network the deformation gradient tensor can be considered to be equal:

$$\varvec{F} = \varvec{F}_{\text{A}} = \varvec{F}_{\text{B}}$$
(1)

where the deformation gradient F correlates the position of a point at deformed rate-dependent configuration x to its position at undeformed state X as:

$$\varvec{F} = \frac{{\partial \varvec{x}}}{{\partial \varvec{X}}} = \nabla \otimes \varvec{x}$$
(2)

The deformation gradient tensor introduces the right Cauchy–Green tensor C as C = FT·F. For the kinematic characterization, the deformation gradient (F) and right Cauchy–Green tensor (C) are generally decomposed into volumetric contribution, characterized through the volume change (J) and a deviatoric (isochoric), volume-preserving contribution (Laksari et al. 2012). In this regard, \(\bar{\varvec{F}}\) and \(\bar{\varvec{C}}\) denote the deviatoric part of deformation and can be written in the form of

$$\bar{\varvec{F}} = J^{{\frac{ - 1}{3}}} \varvec{F},\;\;\bar{\varvec{C}} = J^{{\frac{ - 2}{3}}} \varvec{C}$$
(3)

where J, the Jacobian tensor, represents the change in volume between the deformed and undeformed states, introduced as \(J = \det \left( \varvec{F} \right) = \lambda^{1 - 2\nu }\), with λ being the stretch ratio.

2.2.2 Elastic behavior

It is assumed that the equilibrium network response is purely elastic. Any form of strain energy function for expressing the behavior of soft materials can be employed to model the elastic (spring) response in each network. It is assumed that both networks have the same hyperelastic model (Bergstrom 2015; Goriely et al. 2015a), and the total strain energy, UT, is obtained from the weighted summation of the energies of two networks

$$U_{\text{T}} = s_{1} U\left( {\varvec{C}_{\text{A}}^{e} } \right) + s_{2} U\left( {\varvec{C}_{\text{B}}^{e} } \right)$$
(4)

where \(\varvec{C}_{\text{A}}^{e}\) and \(\varvec{C}_{\text{B}}^{e}\) are the elastic right Cauchy–Green tensor in networks A and B. The stiffness ratio of networks, si, is a dimensionless material parameter indicating the ratio of shear modulus of networks A and B and must satisfy s1 + s2 = 1.

The total Cauchy stress response, \(\varvec{\sigma}_{\text{T}}\), of the system can be derived from the strain energy function as follows:

$$\varvec{\sigma}_{\text{T}} =\varvec{\sigma}_{\text{A}} +\varvec{\sigma}_{\text{B}} = - pI + s_{1} \left\{ {2\varvec{F}_{\text{A}}^{\text{e}} \cdot \frac{{\partial U\left( {\varvec{C}_{\text{A}}^{e} } \right)}}{{\partial \varvec{C}_{\text{A}}^{e} }} \cdot \left( {\varvec{F}_{\text{A}}^{\text{e}} } \right)^{T} } \right\} + s_{2} \left\{ {2\varvec{F}_{\text{B}}^{\text{e}} \cdot \frac{{\partial U\left( {\varvec{C}_{\text{B}}^{e} } \right)}}{{\partial \varvec{C}_{\text{B}}^{e} }} \cdot \left( {\varvec{F}_{\text{B}}^{\text{e}} } \right)^{T} } \right\}$$
(5)

where p is the hydrostatic pressure that is determined by boundary conditions. In this paper, the Ogden strain energy function is used to evaluate the elastic response of both networks (Ogden 1972, 1986). The general (compressible) form of the Ogden strain energy function is:

$$U_{\text{Ogden}} = \mathop \sum \limits_{i = 1}^{N} \frac{{2\mu_{i} }}{{\alpha_{i}^{2} }}\left( {\bar{\lambda }_{1}^{{ - \alpha_{i} }} + \bar{\lambda }_{2}^{{ - \alpha_{i} }} + \bar{\lambda }_{3}^{{ - \alpha_{i} }} - 3} \right) + \mathop \sum \limits_{i = 1}^{N} \frac{1}{{D_{i} }}\left( {J - 1} \right)^{2i}$$
(6)

where \(\bar{\lambda }_{i}\) is the deviatoric principal stretch introduced as \(\bar{\lambda }_{i} = J^{{\frac{ - 1}{3}}} \lambda_{i}\), N is the material parameter number, and µi, αi, and Di are material parameters. The initial shear modulus and bulk modulus for the Ogden model are given by \(\mu_{0} = \sum\nolimits_{i = 1}^{N} {\mu_{i} }\) and \(K_{0} = \frac{2}{{D_{1} }}\), respectively. In this study, the compressible form of Ogden hyperelastic model is employed to consider the compressibility effect. For this study, the volumetric parameter (D1) was assessed by using the calculated initial shear modulus, µ0, and Poisson’s ratio, ν, as:

$$D = \frac{2}{K} = \frac{{3\left( {1 - 2v} \right)}}{{\mu_{0} \left( {1 + v} \right)}}$$
(7)

According to Eq. (7), the value for Poisson’s ratio (ν) is needed in order to determine the parameter D (Forte et al. 2017; Shojaeiarani et al. 2019). The value of ν = 0.49, reported in substantial number of studies as the Poisson’s ratio for the brain tissue (Miller et al. 2000; Tse et al. 2014), was applied to calculate the compressibility parameter of hyperelastic model.

2.2.3 Viscous behavior

The whole viscous behavior is taken into account by network B (Fig. 2a), which is modeled by assuming the multiplicative split of the deformation gradient into both elastic and viscous (inelastic) deformation (Fig. 1):

$$\varvec{F}_{\text{B}} = \varvec{F}_{\text{B}}^{e} \cdot \varvec{F}_{\text{B}}^{v}$$
(8)

where the viscous part of the deformation, \(\varvec{F}_{\text{B}}^{v }\), represents the stress-free intermediate configuration of the network B (Quintavalla and Johnson 2004). The elastic component of deformation gradient, \(\varvec{F}_{\text{B}}^{e }\), is evaluated using its classical form, and \(\varvec{F}_{\text{B}}^{v }\) is calculated via time integration of the rate of creep deformation gradient in the viscoelastic network, \(\dot{\varvec{F}}_{\text{B}}^{v}\). In this regard, the velocity gradient in network B is given by

$$\varvec{L}_{\text{B}} = \dot{\varvec{F}}_{\text{B}} \varvec{F}_{\text{B}}^{ - 1}$$
(9)

It is similarly decomposed into the elastic and inelastic components given as:

$$\varvec{L}_{\text{B}} = \left[ {\frac{\text{d}}{{{\text{d}}t}}\left( {\varvec{F}_{\text{B}}^{e} \cdot \varvec{F}_{\text{B}}^{v} } \right)} \right]\left( {\varvec{F}_{\text{B}}^{e} \cdot \varvec{F}_{\text{B}}^{v} } \right)^{ - 1} = \left[ {\dot{\varvec{F}}_{\text{B}}^{e} \cdot \varvec{F}_{\text{B}}^{v} + \varvec{F}_{\text{B}}^{e} \cdot \dot{\varvec{F}}_{\text{B}}^{v} } \right]\left( {\varvec{F}_{\text{B}}^{v} } \right)^{ - 1} \left( {\varvec{F}_{\text{B}}^{e} } \right)^{ - 1}$$
(10)

which can be written as

$$\varvec{L}_{\text{B}} = \dot{\varvec{F}}_{\text{B}}^{e} \left( {\varvec{F}_{\text{B}}^{e} } \right)^{ - 1} + \varvec{F}_{\text{B}}^{e} \cdot \dot{\varvec{F}}_{\text{B}}^{v} \left( {\varvec{F}_{\text{B}}^{v} } \right)^{ - 1} \left( {\varvec{F}_{\text{B}}^{e} } \right)^{ - 1}$$
(11)

and with respect to Eq. (9), Eq. (11) will be written in the form of

$$\varvec{L}_{\text{B}} = \varvec{L}_{\text{B}}^{e} + \varvec{F}_{\text{B}}^{e} \cdot \varvec{L}_{\text{B}}^{v} \cdot \left( {\varvec{F}_{\text{B}}^{e} } \right)^{ - 1} = \varvec{L}_{\text{B}}^{e} + \tilde{\varvec{L}}_{\text{B}}^{v}$$
(12)

where

$$\varvec{L}_{\text{B}}^{v} = \varvec{D}_{\text{B}}^{v} + \varvec{W}_{\text{B}}^{v} \;\;{\text{and}}\;\;\tilde{\varvec{L}}_{\text{B}}^{v} = \tilde{\varvec{D}}_{\text{B}}^{v} + \tilde{\varvec{W}}_{\text{B}}^{v}$$
(13)

It is assumed that the system possesses an unchanged rotation in the intermediate relaxed configuration regarding to the stress-free state (reference configuration) (Boyce et al. 1989); therefore, the viscous spin tensor becomes zero, \(\tilde{\varvec{W}}_{\text{B}}^{v} = 0\). Thus, the viscous rate of deformation in network B is constitutively represented by the symmetric part of the velocity gradient as \(\tilde{\varvec{L}}_{\text{B}}^{v} = \tilde{\varvec{D}}_{\text{B}}^{v}\). To describe the viscoelastic constitutive response of deformation gradient, the evolution of the creep part is considered (\(\tilde{\varvec{D}}_{\text{B}}^{v} \equiv \varvec{D}^{\text{cr}}\)) (Hurtado et al. 2013). Hence, through the multiplicative split of the deformation gradient for isotropic materials suggested by (Lee 1969) the rate form of creep deformation gradient is rewritten as (Dafalias 1986):

$$\dot{\varvec{F}}_{\text{B}}^{v} = (\varvec{F}_{\text{B}}^{e} )^{ - 1} \cdot \varvec{D}^{\text{cr}} \cdot \varvec{F}_{\text{B}}^{e} \cdot \varvec{F}_{\text{B}}^{v}$$
(14)

where \(\varvec{D}^{\text{cr}}\) is expressed based on creep potential, \(G^{\text{cr}} = G^{\text{cr}} \left(\varvec{\sigma}\right)\), and proportionality factor, \(\dot{\lambda }\), and the flow rule is given as:

$$\varvec{D}^{\text{cr}} = \dot{\lambda }\frac{{\partial G^{\text{cr}} \left(\varvec{\sigma}\right)}}{{\partial\varvec{\sigma}}}$$
(15)

In this model, we assume the creep potential is characterized by \(\bar{\varvec{q}}\), the equivalent deviatoric Cauchy stress, as \(G^{cr} = \bar{\varvec{q}}\), and also the proportionality factor is defined as , where is the equivalent creep strain rate. Therefore, the flow rule will be given by

(16)

where \(\bar{\varvec{\sigma }}\) is the deviatoric Cauchy stress, τ = Jσ is the Kirchhoff stress, \(\bar{\varvec{\tau }}\) is the deviatoric Kirchhoff stress, and \(\tilde{q} = J\bar{q}\). The expression of equivalent creep strain rate, , can be provided by models such as power law (Jaishankar and McKinley 2013), power-law strain hardening (Dalrymple et al. 2015; Ghoreishy and Sourki 2018), hyperbolic sine law (Hurtado et al. 2013), or either from Bergstrom–Boyce (Bergström and Boyce 2001). In this paper, is defined based on power-law strain-hardening model in the form of

(17)

where \(\overline{\varepsilon }^{\text{cr}}\) is the equivalent creep strain and A, m, and n are the material parameters.

2.3 Parameter identification

All experimental data from three different loading rates of unconfined compression tests for bovine brain tissue were simultaneously used for calibrating the material parameters. The nonlinear least-squares algorithm lsqnonlin in MATLAB was employed to identify the constitutive constants of the proposed material model. To achieve a physically meaningful amount for material constants, the shear modulus, μ1, and A were constrained to have an only positive value. Also, Eq. (7) with the value of ν = 0.49 stands as the constraints for determining the volumetric parameter, D1. At each iteration, this parameter was first calculated from the estimated shear modulus based on Eq. (7) and then employed into the optimization process. The objective function (χ2) which represents the sum of the square of the difference between experimental and numerically calculated stresses is defined as follows:

$$\chi^{2} = \mathop \sum \limits_{k = 1}^{3} \mathop \sum \limits_{i = 1}^{N} \left( {\sigma_{i}^{\text{Exp}} - \sigma_{i}^{\text{Num}} } \right)^{2}$$
(18)

where \(\sigma_{i}^{\text{Num}}\) and \(\sigma_{i}^{\text{Exp}}\) are the numerically predicted and experimentally measured true (Cauchy) stresses, respectively, for three loading rates (k = 1–3) and N is the number of data points. To accelerate the parameter identification process, it is essential to assign a restricted range for each parameter value. Therefore, in this regard the parameters m and n were set to be calculated from the range of [0.5, 10] and [− 1,0], respectively. Eventually, one set of material parameters that provided the best fit to the test results of the brain at three measured rates were obtained.

3 Results

3.1 Mechanical response of brain tissue

Based on force and displacement signals obtained directly from the testing machine, the force histories versus the compressive strains were determined and are presented in Fig. 3. To attain the stress-strain behavior of the bovine brain shown in Fig. 3d, the Lagrangian stresses were calculated by dividing the force over the initial cross-sectional area of the sample measured at its reference configuration. The averaged nominal stress-strain curves were determined by up to 30% of compressive strain, showing an inherent nonlinear mechanical behavior of tissue at each deformation rate. The brain tissue showed a stiffer response when the compression rate increased (Fig. 3d), indicating that the stress not only is a function of strain value but also depends on the loading rate.

Fig. 3
figure 3

The experimentally recorded history of forces vs. nominal compressive strain for bovine brain specimens at different compression velocities of a 10 mm/s, b 100 mm/s, and c 1000 mm/s, and d the comparison between mean nominal stresses measured at three different compression velocities

Full size image

The maximum nominal stresses at 30% compressive strain with the deformation rates of 10, 100, and 1000 mm/s are − 4.26 ± 1.26 kPa, − 8.62 ± 2.58 kPa, and − 12.74.0 ± 3.97 kPa (mean ± SD), respectively. According to one-way ANOVA (SPSS Statistics, version 24.0, IBM Corp., Armonk, NY) (Eslaminejad et al. 2018a; Jahani et al. 2018), the values of nominal stress at 30% strain showed significant statistically different (p < 0.01) over various deformation rates (Fig. 4). The apparent elastic modulus (slope of stress-strain curve) at 5%, 10%, 15%, and 20% strains for different compression velocities was determined and is compared in Fig. 4. A consistent rise in the elastic modulus was observed with increasing the strain levels and strain rates. As shown in Fig. 4, this measure of mechanical stiffness demonstrated a statistical difference and significant rate-dependent behavior for brain tissue.

Fig. 4
figure 4

a The maximum nominal stress (mean ± SD) determined at 30% compressive strain exhibits significant difference (p < 0.01) at various deformation rates. b Also, the estimated elastic moduli as a measure of apparent stiffness increased by the rise in the strain level and the strain rate. * and ** represent statistical difference using ANOVA, with the significance level set at p < 0.01 and p < 0.05, respectively

Full size image

3.2 Determined rate-dependent material parameters

Table 1 presents the summary of determined material constants of the proposed model for bovine brain tissue at three different rates. The calculated weighted factors (si) of hyperelastic stress in the first and second networks were found to be 0.273 and 0.727, respectively. Both deviatoric (µ) and volumetric (D) constitutive parameters of the Ogden hyperelastic model were evaluated. This nonlinear viscoelastic model provided excellent constitutive representation in comparison with the test data for brain tissue (R2 = 0.999). Figure 5 demonstrates the prediction of the proposed model for the mechanical response of brain tissue at three deformation rates of 10, 100, and 1000 mm/s.

Table 1 Material parameters for the nonlinear viscoelastic model, calibrated for brain tissue at different deformation rates of 10, 100, and 1000 mm/s
Full size table
Fig. 5
figure 5

The comparison between experimental data and the determined mechanical response by nonlinear viscoelastic model for brain tissue at three different rates of: a 10 mm/s, b 100 mm/s, and c 1000 mm/s

Full size image

3.3 Model verification in finite element analysis

In order to check the validity of the introduced model and the obtained material parameters for use in FE analysis, an inverse simulation of test procedure was carried out. Using ABAQUS/Standard 2016 code (ABAQUS Inc., Providence, RI), the same unconfined compression experiment was modeled by the FE technique for a brain specimen. As shown in Fig. 6a, an axisymmetric geometry with a radius of 12.5 mm and a height of 15 mm was generated resembling the brain specimen. A four-node, axisymmetric quadrilateral, reduced integration, hybrid element, which includes hourglass control, was employed. On the left rotational axis, an axisymmetric boundary condition (U1 = 0) was applied. A frictionless interaction was applied between platens and the top and bottom surfaces of the brain sample. The constitutive constants presented in Table 1 were implemented as the material properties of tissue in the FE model (see “Appendix”). The upper platen was moved in the vertical direction, compressing the specimen to 30% of its engineering strain with three deformation rates used in the experiments (i.e., 10, 100, 1000 mm/s). A uniform uniaxial deformation along with homogenous radial expansion was observed for the brain sample as depicted in Fig. 6b. That leads to fully uniaxial compression stress in vertical (“Y–Y”) direction with insignificant transverse stress in the radial direction (Fig. 6c).

Fig. 6
figure 6

a The developed FE model for unconfined compression test procedure of the brain specimen, b the homogeneous deformation configuration of tissue at 30% of compressive strain, and c) the contour of Cauchy stress in “Y–Y” (vertical) direction for the sample compressed up to ε = − 0.3 strain with velocity of 10 mm/s

Full size image

As depicted in Fig. 7, very good agreements between experimentally measured stress-strain and FE computed results were achieved for brain sample at three different tested speeds. In order to obtain the nominal stresses in the FE analysis shown in Fig. 7, the calculated reaction force for the upper platen was divided by the initial top area of the brain sample. Also, additional simulations with velocities in the range of calibrated rates (10 ~ 1000 mm/s) were chosen to further examine the validity of the model and determined material parameters. In this regard, the FE simulations were performed for the compressive speeds of 50, 250, 500, and 750 mm/s, and the computed tissue response for each rate is presented in Fig. 7. This rate-dependent model gives proper predictions of the tissue response for other intermediate rates. The calculated mechanical responses in Fig. 7 and the predicted deformed configuration in Fig. 6 were in full agreement with experimental results, verifying the validity of the proposed material model to reproduce the tissue viscoelastic behavior.

Fig. 7
figure 7

The predicted nominal stress by FE analysis of brain sample (dotted lines) with different deformation rates using the material constants presented in Table 1

Full size image

Similar to other engineering parameters, the developed strain rates in the brain specimens can be calculated by FE analysis. The results of the FE simulation show the brain has a uniform distribution of strain rates. As demonstrated in Fig. 8, at the strain value of 30% and for the compression velocity of 10, 100, and 1000 mm/s, the vertical strain rates (ER22) were found to be, respectively, − 0.94, − 9.4, and − 94 s−1. These values were negative since they are related to compressive deformations and strains. The transversal strain-rate components in “X–X” and “Z–Z” directions (ER11 and ER33) were identical and with a value of 46 s−1 at the speed of 1000 mm/s. It can be seen that the estimated strain rate associated with the highest compression velocity of this study is consistent with those reported ranges of rates at TBI (Viano and Lovsund 1999; Zhang et al. 2004). Although for constant velocity, it was expected to obtain the constant strain rate, the calculated strain rate showed some variations at different strains. These variations for both lateral and vertical strain rates (ER11 and ER22) versus the compressive strains are demonstrated and depicted in Fig. 8c, d.

Fig. 8
figure 8

The demonstration of determined strain rate: a the strain-rate contour in the direction of “Y–Y” plotted for 30% of strain, b symbol plot of strain-rate components at three directions plotted for 30% of strain, c the variation of strain rate in transversal direction versus strain, d the variation of strain rate in vertical direction versus strain

Full size image

4 Discussion

The main objective of this study was to verify and calibrate the rate-dependent model on the animal brain, and further pave the path for determining the most accurate material properties of human brain. In this regard, the rate-dependent mechanical behavior of bovine brain tissue has been investigated under unconfined compression test at intermediate to high rates. Figure 4 reveals how the peak stress and the apparent elastic modulus of the bovine brain vary as the rate changes. Based on the parallel rheological framework approach, a single-phase nonlinear viscoelastic model was developed and calibrated with the experimental result. The averaged experimental results at three different rates were employed to determine one set of material parameters. The excellent agreement between the numerically calculated and experimentally measured stresses (Fig. 5a–c) confirmed that the proposed constitutive model is fully capable of characterizing the rate-dependent behavior of brain tissue under compression deformation.

The researchers of the study presented here could not find any studies with perfectly similar deformation rates of the bovine brain tissue to compare their results with. However, good agreement was found between the results of the current study and the results provided by Laksari et al. (Laksari et al. 2012). In that study, engineering stress of 10.3 kPa (at ε = − 0.3) was reported for bovine brain samples under unconfined compression test at the nominal strain rate of 10 s−1. Pervin and Chen (2009) were able to examine the mechanical responses of the bovine brain at high rates using a modified split Hopkinson pressure bar. They obtained insignificant anisotropy behavior for white matter and showed the compressive stress at 30% strain with a nominal strain rate of 1000/s was 60 and 75 kPa for gray and white matter, respectively. Although Rashid et al. (2012) have examined porcine brain tissue, they determined the compressive stresses as 8.8, 12.8, and 16 kPa (at ε = − 0.3) corresponding to compression velocities of 150, 300, and 450 mm/s. These varying ranges were typical in the results of experimental studies. These are likely due to the fact that the samples were obtained from different animal species and ages, and prepared in different shapes and dimensions, and tested with different protocols (e.g., lubrication, preloading, etc.) (Anderson 2018; Elkin et al. 2010).

In the literature of biomechanics of the brain, some studies have been devoted to characterizing the rate-dependent mechanical properties of this tissue. Pamidi and Advani (1978) derived a nonlinear constitutive relation based on power energy function. They calibrated their model using the reported in vitro test results of Galford and McElhaney (1970) and obtained a good numerical prediction of human brain tissue under compression. Mendis et al. (1995) have developed a large-strain linear viscoelastic model to be used in finite element modeling of brain tissue. They incorporated the Prony series into the Mooney–Rivlin strain energy function and determined the time-dependent form of the hyperelastic coefficient. Miller and Chinzei (1997b) implemented a similar hyper-viscoelastic model to characterize the viscoelastic behavior of porcine brain tissue. They introduced a unique procedure to calculate the material constants over three different low to medium rates. Hrapko et al. (2006) captured the nonlinear mechanical response of brain under the shear response of tissue, using a new differential viscoelastic model that was developed based on Mooney–Rivlin viscoelastic network and included 16 material parameters. In order to capture the rate-dependent behavior at finite viscosity and deviatoric and volumetric plasticity of the brain tissue, El Sayed et al. (2008b) developed a nonlinear elastic–viscoplastic material model and verified their model with tissue response under uniaxial compression and tension test up to 50% nominal strain. Also, Prevost et al. (2011) have investigated the dynamic behavior of porcine brain tissue at nominal strain rates of 0.01, 0.1, and 1 s−1. They developed a rheology-based constitutive model to capture the effects of compressibility, hysteresis conditioning, the rate dependency, and short- and long-term viscoelastic behaviors of the tissue. Although their comprehensive model with eight parameters was proven to predict the behavior of tissue at tension, and relaxation modes as well, it has a limited ability for being used in FE software packages. Recently, Haldar and Pal (2018) developed a rate-dependent anisotropic constitutive relation and numerically modeled the brain tissue under large deformation. They have shown that their rigorous phenomenological model was able to account for the rate dependency, nonlinear viscoelasticity, anisotropy, and tension-compression asymmetry behavior of the tissue.

Although the model proposed in this study accounts for the compressibility effect of tissue deformation, it has fewer material constants to be determined in contrast to existing constitutive models which lead to a relatively faster model calibration process and less computational cost. Also, it was shown that the developed nonlinear viscoelastic model can be directly implemented in commercial FE code to perform the FE simulations with no need for writing a material subroutine. In this regard, the main features of this model in comparison with the most common viscoelastic models used to characterize the rate-dependent behavior for brain tissue are presented in Table 2.

Table 2 A summary of most well-known rate-dependent constitutive models have been introduced to characterize the brain viscoelastic behavior in comparison with the model proposed in this study
Full size table

The present study is an essential step toward the development of a constitutive model able to predict the tissue behavior during large deformation at arbitrary loading velocities. As the limitations of the current study, it should be noted that the tissue was characterized for only uniaxial deformation (unconfined compression) over a range of intermediate to high rates. If the material parameters are determined for one particular deformation mode such as compression, it may not exhibit adequate behavior for other deformation modes such as tension, shear, or other loading combinations. One other limitation of this study is the estimation of the material parameters from a mixed white and gray matter of the brain tissue. The results, therefore, are only valid for such a composite and can be useful in approximate modeling of the brain (Miller and Chinzei 1997a; Rashid et al. 2012). Also, we have assumed an isotropic structure and employed the average mechanical properties of the tissue in the determination of material parameters; however, this procedure is accepted in obtaining such parameters that are useful in evaluating an approximate behavior of the tissue. Moreover, in some studies, it was postulated that the anatomical location (Donnelly and Medige 1997; Tamura et al. 2007) and the direction (Budday et al. 2017; Pervin and Chen 2009) of extracted brain samples had an insignificant effect on the tissue response. For instance, Tamura et al. (2007) have performed several unconfined compression tests and have shown that neither the orientations nor anatomical location of the specimen do not affect the macro-mechanical behavior of porcine brain tissue.

As a suggestion for future work, further model refinement is required to address the time-dependent viscoelastic behavior associated with the biphasic inherent of brain tissue at intermediate to high deformation rate regime. This single-phase viscoelastic model provided here was a first step toward achieving this goal, and it is needed to introduce a viscoelastic biphasic constitutive model to demystify more phenomenological behavior of brain tissue. It is suggested in the next step that brain tissue is treated as a porous medium, composed of a solid matrix with interstitial fluid, and the significant role of fluid diffusion in the brain tissue is taken into account. On this subject, the future biphasic constitutive model should be able to capture the tissue rate-dependent behavior resulting from the coupled dynamical interactions between the mechanical response of the solid phase and fluid flow.

5 Conclusions

This study demonstrates the in vitro results for bovine brain tissue in unconfined compression experiments up to 30% nominal strain over three orders of deformation rate magnitudes (10–1000 mm/s). The significant effects for rate dependency of this soft biological tissue were observed. It was shown that with an increase in deformation rate, the mechanical features, i.e., the nominal stress and apparent elastic moduli, were also increased. A rate-dependent constitutive relation was introduced and simultaneously calibrated with the measured data from three various rates of deformation. The excellent correlations between the experimental, theoretical, and computational results have indicated that the proposed model is fully able to characterize brain tissue behavior and be employed in FE simulations. The outcome of this study is a promising constitutive model and a successful technique to capture the rate-dependent material properties, a complex inherent characteristic of the brain at intermediate to high strain rates.