Modeling blood flow around a thrombus using a hybrid particle–continuum approach

Abstract

A hybrid, multiscale, particle–continuum numerical method is developed for resolving the interaction of a realistic thrombus geometry with unsteady hemodynamics typically occurring within large arteries. The method is based on a discrete particle/element description of the thrombus, coupled to blood flow using a fictitious domain finite element method. The efficacy of the discrete element approach in representing thrombi with arbitrary aggregate morphology and microstructure is demonstrated. The various features of the method are illustrated using a series of numerical experiments with a model system consisting of an occlusion embedded in a channel. The results from these numerical experiments establish that this approach can resolve the complex macroscale flow structures emanating from unsteady hemodynamics interacting with a thrombus. Simultaneously, it can also resolve micromechanical features, and microscale intra-thrombus flow and perfusion. Using a staggering algorithm, the method can further capture hemodynamics around time-varying thrombus manifolds. This is established using a numerical simulation of lysis of an idealized clot. The hybrid particle–continuum description of thrombus–hemodynamics interaction mechanics, and the unified treatment of macroscale as well as microscale flow and transport, renders significant advantages to the proposed method in enabling further investigations of physiological interest in thrombosis within patient-specific settings.

1 Introduction

Thrombosis is a primary cause or complication in stroke, heart attack, and other major cardiovascular diseases. In addition, thrombosis induced by biomedical devices, or originating from vascular trauma during endovascular procedures, leads to significant impacts on patient health (Jaffer et al. 2015). Development of an in-depth understanding of thrombosis is complicated by the inherently multiscale and multiphysics nature of the underlying processes (Furie and Furie 2008; Flamm and Diamond 2012; Wang and King 2012). In particular, thrombosis has an intimate connection with blood flow and hemodynamic forces, as explored by several existing studies (Hathcock 2006; Nesbitt et al. 2009). Flow structures in the vicinity of a developing clot can determine the transport of platelets and coagulation proteins, and hemodynamic loading on the thrombus can affect thrombus size and growth, and embolization risk (Hellums 1994; Bark et al. 2012; Colace et al. 2012).

Computational models, especially based on experimental data, are becoming increasingly valuable for in-depth analysis of thrombosis biomechanics. Hemodynamic coupling with thrombosis has been computationally studied using several approaches, which include (i) coupling lattice automata-based methods with continuum description of blood flow (Xu et al. 2008; ii) mesoscale dissipative particle dynamics approaches to describe platelet aggregates in flow (Pivkin et al. 2006); and (iii) fully continuum descriptions of hemodynamics with a focus on coagulation agonist transport (Leiderman and Fogelson 2011). However, majority of these studies have primarily been limited to microscale environments or small vessels. Understanding the coupling between a thrombus, that can grow or shrink/lyse, and hemodynamics in the larger arteries has remained a challenge. A cell-based description of thrombosis becomes computationally untenable when length and time scales of arterial flow are considered. On the other hand, lattice automata and purely continuum-based descriptions used to capture macroscale dynamics often face difficulty representing the arbitrary aggregation, and microstructure, of a realistic thrombus. As unsteady pulsatile blood flow interacts with these arbitrary aggregate geometries, evaluation of flow structures around, and hemodynamic loading on, such an aggregate becomes a significant challenge. Resolving this challenge is the focus of this paper.

In order to devise a computational modeling framework that addresses the aforementioned challenges, and enables robust modeling of interaction of hemodynamic interactions in the neighborhood of a realistic macroscopic thrombus, we identify two core aspects. Firstly, an arbitrary thrombotic aggregate has to be efficiently coupled to the blood flow. Secondly, the complex morphology and intrinsic heterogeneity of the thrombus should be accounted for. Here, we propose an innovative hybrid particle–continuum approach that seeks to address these two aspects. For the former, we circumvent the complexity of explicitly resolving and meshing the thrombus and blood–thrombus interface by using a fictitious domain approach. For the latter, we propose to represent the thrombus in a mesh-free/off-lattice manner as an aggregate of discrete particles or elements.

Fictitious domain methods entail using a background computational grid devised over a simple, regular domain instead of explicitly resolving all sub-domain interfaces and complex sub-domain geometries. The solid sub-domain is assumed to be implicitly embedded within this background grid. Broadly, these belong to the family of immersed or embedded domain methods for fluid–structure interaction. The literature on this family of methods is rich and extensive; briefly, however, there are two main approaches, based on how the fluid–solid interface is handled (Hou et al. 2012). In “immersed boundary” methods the fluid flow is coupled with a forcing term that connects the immersed boundary motion to the flow, and the forcing is defined along the boundary (Peskin 2002; Boffi and Gastaldi 2003; Mittal and Iaccarino 2005). These are typically effective for modeling thin elastic structures immersed in flow and have been extensively used in a range of cardiovascular applications—most prominent being that of heart valve mechanics (Sotiropoulos and Borazjani 2009; Griffith 2012). In “immersed domain” methods on the other hand, sub-domains with finite volumes are assumed to be submerged or embedded within a background grid, and interaction terms are defined to be distributed over the domain volume using forcing terms, constraints or interpolation-based kinematic updates. Prominent variants include the fictitious domain method (Glowinski et al. 2001; Burman and Hansbo 2010; Kadapa et al. 2016) and the immersed finite element method (Zhang et al. 2004; Liu et al. 2007). Such methods have previously been used in cardiovascular applications to study, among other applications, design and deployment of stents (Gay et al. 2006), and design evaluation of mechanical heart valves (Stijnen et al. 2004). Since the interface is usually non-conforming with the computational mesh for the fluid domain, imposition or evaluation of interface tractions often requires special strategies like a cut-element Lagrange multiplier or Nitsche-type finite element formulation (Burman and Hansbo 2010, 2012), or specialized immersed interface techniques like sharp-interface immersed boundary method (Seo and Mittal 2011).

Contrary to continuum-based approaches, discrete element methods, mathematically belonging to the larger family of particle-based methods, comprise mesh-free, off-lattice particles or computational units. Physical interactions of these particles with each other, and with the background flow, govern the overall physics of the system of interest. A broad range of mathematical formulations of particle-based methods exist, with a rich literature on both mathematical and physical details as well as application areas. We refer the readers to comprehensive reviews and discussions presented in (Frenkel and Smit 2002; Li and Liu 2002; Pöschel and Schwager 2005). Particle-based methods in general have enjoyed prominence in many biological applications. Particularly in cardiovascular applications, particle-based approaches have been used to study blood flow and platelet biomechanics (Yamaguchi et al. 2010), and transport of emboli for predicting stroke risks (Mukherjee et al. 2016), among other applications. Discrete element or particle-based methods offer particular advantages in terms of representing complex geometries and micromechanical features, and handling events like fragmentation, aggregation, growth, and restructuring/remodeling. Thus, specifically for thrombosis-related applications, these methods are beneficial. In this work, we use discrete element methods as a particle-based discretized representation of the thrombus, with each individual particle or element representing a component part of the thrombus domain. Each particle is representative of a mesoscopic aggregate computational unit when macroscale large vessel clots are considered, while for microscale or cellular-level applications, they will resemble individual platelets or cells. Representing the thrombus as an aggregate of discrete particles enables modeling pore spaces as a combination of voids within the particle aggregate, and coupling the thrombus to flow is handled by coupling each discrete particle to the flow individually using an immersed domain technique.

In this paper, we outline the numerical and algorithmic details of our combined fictitious domain—discrete element method. The resultant hybrid particle–continuum description can model flow interactions at the macroscopic scales, at the same time retaining capabilities for resolving microscale flow (i.e., perfusion in clot interstitial space). We establish in this work that the proposed approach (a) can handle realistic pulsatile hemodynamics; (b) accounts for arbitrary aggregate geometries; (c) is essentially multiscale, i.e., incorporates microstructural information as well as resolves macroscale flow structures; and (d) accounts for changing thrombus geometries. We demonstrate each of these features with carefully constructed numerical experiments featuring a simplified, standard model problem of a clot embedded within a channel with a specified, physiologically realistic (wherever appropriate), inlet flow and outflow boundary condition. The objective here focuses on the challenges pertaining to resolving flow around and within realistic thrombus aggregates. Numerical techniques for thrombus deformation using a mesoscale particle approach are not the focus, and hence, we assume that the clot geometry remains rigid, although it can vary shape and grow/shrink over time. We also assume that our definition of discrete elements represents individual platelets for microscale clot models, and mesoscale coarse-grained computational elements for macroscale. Finally, additional disease considerations like diseased vessel wall at clot location are not the focus of this study. All computational framework and simulations are implemented using the open-source finite element library FEniCS (Alnæs et al. 2015), and all post-processing was done using the open-source library Visualization Toolkit (VTK) (Schroeder and Martin 1996).

2 Methods

2.1 Fictitious domain formulation

We consider an overall computational domain, denoted by $\Omega$, which encompasses both the fluid (blood) and the clot sub-domains—denoted by $\Omega _f$ and $\Omega _t$, respectively. We denote the interface between these two sub-domains as $\Gamma _{ft}$. Instead of explicitly resolving $\Gamma _{ft}$, the two sub-domains and the interface are assumed to be embedded within $\Omega$ as fictitious domains. Mathematically, $\Omega = \Omega _f \oplus \Omega _t$ and $\Omega _f \ominus \Omega _t = \Phi$, where $\Phi$ is the null set. The overall domain boundary ($\Gamma$) is decomposed into Neumann and Dirichlet components $\Gamma _n$ and $\Gamma _d$, respectively, such that $\Gamma = \Gamma _n \oplus \Gamma _d$ and $\Gamma _n \ominus \Gamma _d = \Phi$. Assuming blood to be a Newtonian fluid (density $\rho _f$; viscosity $\mu _f$), the Navier–Stokes equations and the fluid continuity equation are now discretized over the domain $\Omega$, using a Petrov–Galerkin stabilized finite element formulation. The overall variational form for this is given as follows:

$$\begin{aligned}&\rho _f \left( \mathbf {u}_t, \mathbf {w} \right) _{\Omega } + \rho _f \left( (\mathbf {u} \cdot \nabla )\mathbf {u}, \mathbf {w} \right) _{\Omega }\nonumber \\&\quad + 2\mu _f\left( \mathbf {D}(\mathbf {u}), \mathbf {D}(\mathbf {w}) \right) _{\Omega } - \rho _f \left( \mathbf {w}, \mathbf {b} \right) _{\Omega }- \left( \mathbf {w}, \mathbf {h} \right) _{\Gamma _n} \nonumber \\&\quad - \left( \nabla \cdot \mathbf {w}, p \right) _{\Omega } + \left( q, \nabla \cdot \mathbf {u} \right) _{\Omega } + a_{int}(\mathbf {u}, \mathbf {w}) \nonumber \\&\quad +\left( \tau \left( \mathbf {u}^h \cdot \nabla \right) \mathbf {w}^h , \mathcal {R}^h \right) _{\Omega ^h} +\left( \tau \nabla q^h, \mathcal {R}^h \right) _{\Omega ^h} = 0, \end{aligned}$$

(1)

where $\left( \bullet , \circ \right) _{\Omega } \equiv \int { \bullet \circ d\Omega }$, $\mathbf {u}$ and p are the flow velocity and pressure, $\mathbf {w}$ and q are the respective velocity and pressure test functions, $\mathbf {D}(\mathbf {u}) = 0.5(\nabla \mathbf {u} + \nabla \mathbf {u}^T)$, $\tau$ is the Petrov–Galerkin stabilization parameter, $\mathcal {R}^h$ is the overall residual of the momentum equation for the flow, and $\mathbf {b}$ is the placeholder for any body forces acting on the fluid. The superscript h on the two stabilization terms indicates that they are defined element-wise, consistent with the definition of Petrov–Galerkin formulation (Brooks and Hughes 1982; Franca et al. 1992; Franca and Frey 1992). The stabilization parameter $\tau$ can be chosen in different ways (Tezduyar and Osawa 2000), and for our formulation, we have employed the following form:

$$\begin{aligned} \tau = \frac{1}{\sqrt{ (2 dt)^2 + \left( \frac{2\mathbf {u}\cdot \mathbf {u}}{h}\right) ^2 + \left( \frac{4 \nu }{h} \right) ^2}}, \end{aligned}$$

(2)

where dt is the temporal discretization step, h is the element size parameter (length scale), and $\nu$ is the fluid kinematic viscosity. For this study, we employed an implicit midpoint scheme to integrate the combined variational form in Eq. (1) with respect to time.

Fig. 1

A schematic overview illustrating the various aspects of the proposed fictitious domain discrete element method

Specifically for hemodynamics, the truncated, downstream vasculature beds not included in the primary computational domain $\Omega$ are considered to be additional domains that interact with $\Omega$ via physiologically devised boundary conditions imposed at the respective interfaces. Denoting these as $\Gamma _m$, the Neumann boundary for $\Omega$ is further decomposed as: $\Gamma _n = \Gamma _m \oplus \Gamma _f$, such that $\Gamma _n \ominus \Gamma _f = \phi$ as before. The term $\Gamma _f$ corresponds to all non-multidomain coupled domain boundaries. Over $\Gamma _m$ the specified traction $\mathbf {h}$ is typically a complex function obtained from a circuit-based Windkessel model, a network-based algebraic model, or solution of a reduced-order equation system for downstream phenomena (Vignon-Clementel et al. 2006; Kim et al. 2009). Mathematically abstracting this as a function $\mathcal {L}(t)$, the Neumann contribution to Eq. (1) becomes:

$$\begin{aligned} \left( \mathbf {w}, \mathbf {h} \right) _{\Gamma _n} = \left( \mathbf {w}, \mathcal {L}(t) \right) _{\Gamma _m} + \left( \mathbf {w}, \mathbf {h}^* \right) _{\Gamma _f}. \end{aligned}$$

(3)

For example, for a multidomain boundary coupled with a single-parameter Windkessel model, which assumes pressure and total flow are connected by a resistance, the multidomain boundary function $\mathcal {L}(t)$ becomes:

$$\begin{aligned} \mathcal {L}(t) = R_m\int _{\Gamma _m}{\mathbf {u}(t)\cdot {\hat{\mathbf {n}}} d\Gamma }, \end{aligned}$$

(4)

where $R_m$ is the resistance parameter and ${\hat{\mathbf {n}}}$ is the surface normal.

The term $a_{int}(\mathbf {u}, \mathbf {w})$ in Eq. (1) is the contribution to the weak form accounting for the coupled interaction between the clot and flow. For the present method, we formulate this via a penalty-based constraint term that imposes the fluid flow velocity to take up the local velocity of the thrombus sub-domain component. This leads to the following:

$$\begin{aligned} a_{int}(\mathbf {u}, \mathbf {w}) = \left( \kappa (\mathbf {u} - \mathbf {v}_0), \mathbf {w} \right) _{\Omega _t}, \end{aligned}$$

(5)

where $\mathbf {v}_0$ is the thrombus domain velocity and $\kappa$ is the penalty parameter. We note that the implementation of this coupling implicitly assumes a definition of the thrombus sub-domain $\Omega _t$. However, owing to the fictitious domain description, this is not directly available. In addition, straightforward marking of computational nodes to be lying within or outside $\Omega _t$ is not always possible, owing to the complex geometries, and microstructure of the thrombus. Hence, we represent the thrombus domain as a collection of discrete elements $\mathcal {P}_i$, and the corresponding mathematical details are discussed in Sect. 2.2. Note here that we are assuming that the thrombus sub-domain velocity $\mathbf {v}_0$ is a known variable for the flow simulation. Thus, the interaction term does not enable a dynamic update of the thrombus sub-domain properties. We will revisit, and critique, this aspect at a later point in our discussion.

The penalty parameter $\kappa$ is chosen to vary with element size h as follows:

$$\begin{aligned} \kappa = c_1 \left( \frac{1}{h}\right) ^{c_2}. \end{aligned}$$

(6)

This choice is motivated by the form of the discretized FE basis functions as they appear in the assembled system matrices. For cases where prominent convective or diffusive regimes affect the numerics of the problem, the penalty parameter can be further modified as follows:

$$\begin{aligned} \kappa = c_1 \text {max}\left( \frac{\rho _f \parallel \mathbf {u} - \mathbf {v}_0 \parallel }{h}, \frac{\mu _f}{h^2} \right) . \end{aligned}$$

(7)

The final piece of detail lies in the description of imposing the penalty term over the fictitious domain grid, based on the definition for $\Omega _t$. Recall that the real interface $\Gamma _{ft}$ is not guaranteed to follow element edges, but may cut through elements arbitrarily (Fig. 1). Thus, the penalty term is imposed by using the sub-domain definition to identify the location of Gauss quadrature points within each element to be embedded in $\Omega _t$ or located outside of it. The corresponding “interior” contributions are integrated and assembled to provide the penalty contributions in the matrix system of equations. An alternative implementation can be realized by marking whole elements to be “interior” or “exterior” to $\Omega _t$. While this is easier to implement, it may lead to larger errors in boundary flux or traction estimates and may necessitate smaller mesh sizing requirements.

Fig. 2

An overview of discrete element geometry representation using superquadrics and their deformations. a denotes geometry variations with shape parameters, while b depicts constrained geometry change by varying shape and size parameters. c depicts geometry changes using spline coefficients, with the deformed unit-circle geometry, and the corresponding splines being placed top and bottom, respectively, for each

2.2 Discrete element representation

2.2.1 Superquadric discrete elements

The arbitrary shape and microstructure of the thrombus sub-domain are handled here by replacing the thrombus by a collection of mesh-free, off-lattice, discrete elements. Mathematically, this is represented as: $\Omega _t \approx \mathcal {P}_1 \oplus \mathcal {P}_2 \oplus \ldots \mathcal {P}_N$, where $\mathcal {P}_i$ is an individual discrete element. Each discrete element is modeled as a superquadric geometry object. Superquadrics are a family of analytically and parametrically defined geometric primitives, which enable flexible shape representation and manipulation (Barr 1981; Kindlmann 2004). Each superquadric can be mathematically represented in a standard coordinate space, and a transformed coordinate space, and is uniquely identified by three size parameters ($a_1, a_2, a_3$) and two shape (roundedness) parameters ($\epsilon _1, \epsilon _2$). Points on the superquadric, in standard space, are represented by the implicit function $\mathcal {F}$ as follows:

$$\begin{aligned} \mathcal {F}(\mathbf {x}) = \left[ \left( \frac{x_1}{a_1} \right) ^{\frac{2}{\epsilon _2}} + \left( \frac{x_2}{a_2} \right) ^{\frac{2}{\epsilon _2}} \right] ^{\frac{\epsilon _2}{\epsilon _1}} + \left( \frac{x_3}{a_3} \right) ^{\frac{2}{\epsilon _1}} \end{aligned}$$

(8)

such that $\mathcal {F}(\mathbf {x}_0) < 0 \Rightarrow$ the point $\mathbf {x}_0$ lies inside the superquadric defined by $\mathcal {F}$, $\mathcal {F}(\mathbf {x}_0) > 0 \Rightarrow$ the point $\mathbf {x}_0$ lies outside the superquadric, and $\mathcal {F}(\mathbf {x}_0) = 0 \Rightarrow$ the point $\mathbf {x}_0$ lies on the superquadric. Examples of superquadric geometry family are shown in Fig. 2a. In the transformed coordinate space, assuming a global transformation $\mathbf {T}$, the representation above is modified as follows:

$$\begin{aligned}&\mathbf {T} = \left( \begin{array}{cccc} n_1 &{} o_1 &{} a_1 &{} p_1 \\ n_2 &{} o_2 &{} a_2 &{} p_2 \\ n_3 &{} o_3 &{} a_3 &{} p_3 \\ 0 &{} 0 &{} 0 &{} 1 \end{array} \right) \end{aligned}$$

(9)

$$\begin{aligned}&\mathcal {F}(\mathbf {x}) = \left[ \left( \frac{x_1^*}{a_1} \right) ^{\frac{2}{\epsilon _2}} + \left( \frac{x_2^*}{a_2} \right) ^{\frac{2}{\epsilon _2}} \right] ^{\frac{\epsilon _2}{\epsilon _1}} + \left( \frac{x_3^*}{a_3} \right) ^{\frac{2}{\epsilon _1}} \end{aligned}$$

(10)

$$\begin{aligned}&x_1^* = n_1 x_1 + n_2 x_2 + n_3 x_3 - p_1 n_1 - p_2 n_2 - p_3 n_3 \end{aligned}$$

(11)

$$\begin{aligned}&x_2^* = o_1 x_1 + o_2 x_2 + o_3 x_3 - p_1 o_1 - p_2 o_2 - p_3 o_3 \end{aligned}$$

(12)

$$\begin{aligned}&x_3^* = a_1 x_1 + a_2 x_2 + a_3 x_3 - p_1 a_1 - p_2 a_2 - p_3 a_3. \end{aligned}$$

(13)

Thus, the marking of element nodes or Gauss quadrature points as “interior” or “exterior” to the thrombus sub-domain reduces to evaluating a composition of these implicit functions for a collection of discrete particles.

2.2.2 Parametric variations in element geometry

Superquadric representation of discrete elements also enables utilizing some advantageous mathematical properties of this family of shapes. One particular property of specific utility for the present study is that any generic superquadric volume can be expressed using a closed-form expression as follows:

$$\begin{aligned} \mathcal {V}_{\mathcal {F}} = 2 a_1 a_2 a_3 \epsilon _1 \epsilon _2 \beta \left( \frac{\epsilon _1}{2}+1, \frac{\epsilon _1}{2} \right) \beta \left( \frac{\epsilon _2}{2}, \frac{\epsilon _2}{2} \right) , \end{aligned}$$

(14)

where $\beta (\cdot , \cdot )$ is the beta function. For the discrete element representation of the sub-domain $\Omega _t \approx \mathcal {P}_1 \oplus \mathcal {P}_2 \oplus \ldots \mathcal {P}_N$, a bulk porosity estimation can be derived as: $\mathcal {V}_{\Omega _t} / \sum _{i=1}^{N}{\mathcal {V}_{\mathcal {P}_i}}$. Since, by definition herein, $\mathcal {V}_{\mathcal {P}_i} = \mathcal {V}_{\mathcal {F}_i}$, a sequence of isochoric deformations of individual discrete element shape, will enable us to capture variations in clot microstructure and morphology while still holding bulk porosity constant. By mapping a deformation into a variation of the five geometry parameters, and using Eq. (14), this leads to the following constraint on the parametric variations in discrete element shape and size:

$$\begin{aligned}&\frac{\partial \mathcal {V}_{\mathcal {F}}}{\partial a_1} \Delta a_1 + \frac{\partial \mathcal {V}_{\mathcal {F}}}{\partial a_2} \Delta a_2 + \frac{\partial \mathcal {V}_{\mathcal {F}}}{\partial a_3} \Delta a_3 + \frac{\partial \mathcal {V}_{\mathcal {F}}}{\partial \epsilon _1} \Delta \epsilon _1\nonumber \\&\quad + \frac{\partial \mathcal {V}_{\mathcal {F}}}{\partial \epsilon _2} \Delta \epsilon _2 = 0. \end{aligned}$$

(15)

An example of isochorically deformed series of element geometries using Eq. (15) is presented in Fig. 2b.

2.2.3 Extended superquadrics for arbitrary shape representation

It is evident from the form of the implicit level set function $\mathcal {F}$ in Sect. 2.2.1 that the generalized superquadric geometries have an intrinsic symmetry about their principal geometric axes. Mathematically, this arises from the fact that the coordinate exponents in Eqs. (8) and (10) are constants. Further flexibility in shape representation can be incorporated by assuming that the coordinate exponents are variable functions of the latitudinal ($\theta$) and longitudinal ($\phi$) angles—leading to an extended family of superquadric geometric primitives (Zhou and Kambhamettu 1999). Assuming that these variable exponents are represented as functions $f_1\left( \theta \right)$ and $f_2\left( \phi \right)$, the corresponding in–out function $\mathcal {F}$ can be written as:

$$\begin{aligned}&\mathcal {F}(\mathbf {x}) = \left[ \left( \frac{x_1}{a_1} \right) ^{\frac{2}{\epsilon _2^*}} + \left( \frac{x_2}{a_2} \right) ^{\frac{2}{\epsilon _2^*}} \right] ^{\frac{\epsilon _2^*}{\epsilon _1^*}} + \left( \frac{x_3}{a_3} \right) ^{\frac{2}{\epsilon _1^*}} \end{aligned}$$

(16)

$$\begin{aligned}&\epsilon _1^* = f_1\left( \text {arctan}\left( \frac{x_3}{\sqrt{x_1^2 + x_2^2}} \right) \right) \end{aligned}$$

(17)

$$\begin{aligned}&\epsilon _2^* = f_2\left( \text {arctan}\left( \frac{x_2}{x_1} \right) \right) . \end{aligned}$$

(18)

The latitudinal and longitudinal exponent functions can now be defined by using a set of control points along these two angle spans and representing the functions as Bezier curves as follows:

$$\begin{aligned} f_1(\phi )&= \sum _{i=0}^{n} P_{1,i} B_i^n\left( \frac{\phi + \pi /2}{\pi }\right) \end{aligned}$$

(19)

$$\begin{aligned} f_2(\theta )&= \sum _{i=0}^{n} P_{2,i} B_i^n\left( \frac{\theta + \pi }{2\pi } \right) , \end{aligned}$$

(20)

where $B_i^n$ are the Bernstein polynomials of degree n. Based on the choice of control points and weights, the exponent curves can be varied to either morph into desired shapes, or to fit the discrete element geometry to a specified geometry. This provides added flexibility of representing complex platelet shapes, or modeling complicated interstitial spaces in a discrete particle reconstructed thrombus. A mathematical example of this is provided via a set of deformed 2D unit-circle geometries (i.e., $a_1 = a_2 = 1, \epsilon _1 = 1$) in Fig. 2c. Note that these examples are for illustration only and are not representative of the shapes of element geometries used in simulations described later in Sect. 3.

Fig. 3

(photomicrograph courtesy of Dr. T.J. Stalker, University of Pennsylvania)

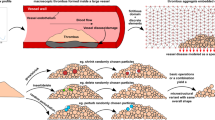
Illustration of the procedure to represent a thrombus as an aggregate of discrete particles or elements. a depicts reconstruction of an intra-luminal thrombus in an abdominal aortic aneurysm. b depicts reconstruction of a hemostatic platelet plug

2.2.4 Framework for discrete particle thrombus representation

Based on the definition of individual particle shapes, a simple computational framework was established to reconstruct a thrombus using discrete particles. For this framework, we started from acquired image data in the form of medical images (for macroscale blood clots) and fluorescent microscopy images (for microscale clots obtained from animal models and microfluidic chips). The image data were post-processed to identify thrombus manifold geometry information via image processing and segmentation, as well as platelet centroidal locations (using fluorescent signal intensity maps, for example) if available. The geometry and location information was then processed into a geometric tessellation-based algorithm to create an ensemble of discrete particles representing the thrombus. To illustrate this representation starting from image data, two specific examples are presented in Fig. 3. Panel (a) illustrates the identification of an intra-luminal thrombus in a patient with an abdominal aortic aneurysm (AAA) from computed tomography image sequences and reconstructing the thrombus using discrete elements. Panel (b) denotes a platelet aggregate reconstructed from microscopy data obtained from experiments on a mouse injury model as described in Tomaiuolo et al. (2014). The red color in the photomicrograph in panel (b) indicates all platelets, green denotes the degranulated platelets, and yellow is the merge of red and green zones. Note that for a microscale thrombus model, the detailed microscopy information on composition in terms of platelets, fibrin, and trapped blood cells can be used to devise the discretized reconstruction. For the macroscale clots, however, the discrete element reconstruction corresponds to a coarsened mesoscopic approximation of the thrombus internal domain. Hence, explicit detailed information on platelet and fibrin locations will not always be necessary to drive the macroscale discrete element reconstruction algorithm, and overall aggregate information on geometry and porosity, for example, can be used for the reconstruction.

2.2.5 Scaffold grids from discrete elements

We remark that the discrete element representation thus created can be further used to define a “scaffold grid” based off the discrete element centroidal coordinates. The scaffold grid is useful for estimation of flux and tractions for post-processing, since in the devised methodology the thrombus sub-domain and the blood–thrombus interface are not explicitly meshed. Specifically, once the grid is constructed from the particle information, the solution variables over the overall background grid are interpolated onto the scaffold grid. This is achieved by using a Galerkin $L_2$ projection method, with the solution on the scaffold grid being $\phi _s$, as follows:

$$\begin{aligned} (\phi , \theta _s)_{\Omega _t} = (\phi _s, \theta _s)_{\Omega _t} \; \text {where} \; \phi \in \left[ \mathbf {u}; p \right] , \end{aligned}$$

(21)

where $\theta _s$ are the interpolation test functions on the scaffold grid. Note that typically, the thrombus sub-domain is smaller in extent compared to the background domain, and hence, the scaffold grid can be further refined to finer grid resolutions (than permitted by the particle information alone) without adding significantly to the computational cost.

2.3 A staggered algorithm for time-varying clot shape

For applications pertaining to modeling thrombus growth or progression, and thrombolysis, the thrombus geometry is not a stationary entity. In order to account for the hemodynamic interactions with a clot manifold varying over time, additional considerations of separation of the dominant time scales need to be incorporated. While current hemodynamics simulations usually model flow over a few cardiac cycles (referred here as $T_c$), growth or lysis of a clot as a result of the underlying biomechanical and biochemical phenomena occurs over a slower time scale (referred here as $T_t$). Note that, specifically for thrombolysis, in therapeutic applications where rapid lysis occurs, such staggering and separation of time scales will not be required. To address this separation of time scales, a staggered sub-cycling algorithmic approach is devised here. The high computational complexity of a fully resolved hemodynamics computation constrains the fluid flow to be simulated over a duration $N_cT_c$, where $N_c$ is the number of cardiac cycles for the flow and pressure fields to achieve convergence from cycle to cycle. With $T_t \gg T_c$, in our framework, we assume now that the variation in thrombus sub-domain remains quasi-static at the resolution of the flow simulation time scale $N_cT_c$. Following this, the obtained spatiotemporally varying flow and pressure fields are considered to be quasi-stationary cycle to cycle, until the change in thrombus sub-domain morphology is registered and an update to the sub-domain geometry is performed. This staggered sub-cycling algorithm is illustrated in Algorithm 1. For strongly dynamically two-way coupled scenarios of flow and thrombus growth/lysis, it is beneficial to iterate between the two staggered computations to allow the solution variables to converge. This leads to iterations over the inner two loops in Algorithm 1.

Fig. 4

Benchmark problem of flow past a cylinder in a channel. Model setup described in (a), and mesh setup described in (b). c, d compare velocity and pressure solutions for explicitly meshed (top), and fictitious domain (bottom) cases for $Re_w=6.15$ and $Re_w=615$, respectively. For fictitious domain results, the cylinder is represented as a single particle for visualization purposes

3 Numerical simulations and results

3.1 Validation and benchmarking

We used the well-studied model system of a cylinder inside a channel flow in order to validate and benchmark the proposed fictitious domain approach, with the cylinder being effectively represented by a single discrete particle. As shown in Fig. 4a, the cylinder (in 2d) was placed within a rectangular channel, with a small asymmetry in the cylinder centroid with respect to the centerline along the channel width. A parabolic inlet flow was specified, along with a zero-pressure outflow and no-slip walls on the top and bottom. The flow was characterized by a Reynolds number defined using the channel width ($Re_w$), and two cases of $Re_w = 6.15$ (Case I) and $Re_w = 615$ (Case II) were simulated. For each case, flow and pressure fields obtained from the fictitious domain approach (cylinder embedded as a fictitious domain) were compared with those obtained from simulations using an explicitly meshed flow domain (cylinder excluded from the domain as a hole). The flow velocity and pressure fields are illustrated for both the cases in Fig. 4c, d. In both cases, the flow evolves through a transient development stage, following which the latter leads to the classical vortex shedding pattern in the wake of the cylinder. As shown in Fig. 4, the velocity and pressure fields, as well as the vortical structures for the higher-$Re_w$ case, for the fictitious domain and the explicitly meshed configurations, show excellent agreement. Using this model configuration, we then performed a series of simulations to characterize how mesh refinement, and strengthening the penalty constraint, influences the solution. As depicted in Fig. 4b, the mesh sizing was controlled by a global mesh sizing factor ($h_\mathrm{in}$) and a sizing ratio that refined the mesh around the fictitious domain of the cylinder ($h_\mathrm{in}/h_\mathrm{out}$). Several levels of refinement were simulated, and convergence behavior was analyzed by comparing the velocity and pressure fields at various locations, as well as integrated tractions over a scaffold grid representing the cylinder. In addition to mesh refinement, convergence behavior of these quantities was also analyzed for varying values of penalty parameter $\kappa$ (assuming a mesh with sizing ratio 3.2). A sample set of data is illustrated in Fig. 5 using final converged solutions from Case I. Panels (a) and (b) depict the influence of mesh sizing on the error in estimated velocity and pressure values (respectively) along the boundary of the cylinder; c and d depict the corresponding influence on estimated drag forces by integrating total tractions and pressure (respectively); and e and f depict the variation in solution variables, evaluated along the cylinder boundary, with penalty parameter. In general, we observe that refinement of mesh around the boundary of the fictitious domain improves solution quality. Influence of increasing penalty parameter is observably stronger for the velocity than the pressure field, mathematically owing to the way the constraint is formulated. Variations in the integrated traction along the boundary reveal that while both pressure drag and viscous drag do converge with refining mesh, the differences and the convergence rates are much slower for the viscous drag (and therefore, the full drag), as opposed to the pressure drag. This is mathematically attributed to greater errors in solution variable gradients when compared to the solution variables themselves, in the vicinity of the weakly enforced embedded interface.

Fig. 5

Illustration of mesh refinement and penalty parameter. Variation in velocity and pressure at the cylinder boundary with mesh sizing is shown in (a, b). Variation in total and pressure drag with mesh refinement is shown in (c, d). Influence of penalty parameter in velocity and pressure depicted in (e, f). Wherever appropriate, linear fits are included to show rate of convergence

Fig. 6

Illustration of results from simulations on an idealized occlusion embedded in a channel. Model setup is shown in (a). Input flow profile, with points of interest during a cardiac cycle, illustrated in (b). d The flow structures in the channel for three varying sizes of occlusions (cases 1, 2, and 3), using snapshots taken at the instants of interest (T1–T4) as indicated in (b). e depicts the flow patterns for occlusion case 3 for scenarios where the whole occlusion is removed from the flow vs where the thrombus is reconstructed as a mesoporous aggregate of discrete particles

3.2 Thrombotic occlusion within vessels

The efficacy of the proposed numerical method in capturing macroscale thrombus–hemodynamics interactions is illustrated here using detailed numerical experiments on a model system for a macroscopic arterial thrombus. The model system, depicted in Fig. 6a, consisted of a channel with width equivalent to that of the average human common carotid artery ($d_v \approx 6\,\hbox {mm}$) and length equivalent to five times the width. Background fluid was blood with density $(\rho _f) = 1.060 g/cc$ and viscosity $(\mu _f) = 4.0 cP$. A measured pulsatile inflow profile for the common carotid artery, available from the literature (Lee et al. 2008), was imposed at the inlet, and a fixed resistance boundary condition imposed at the outlet. Two specific cases of occlusions were considered. The first involved embedding an idealized, hemispherical occlusion within the channel. This occlusion was characterized by its radius $d_c$, and a set of three different occlusion radii were chosen for the simulations. Furthermore, to illustrate the differences between modeling the occlusion as a single continuum domain and as a mesoparticle aggregate, an additional set of computations were performed for this idealized case. In these simulations, the largest occlusion ($d_c=2.5$ mm) was converted into a discrete particle aggregate and embedded within the background mesh. The second case involved a more complex, realistic, clot morphology, which was derived from clotting experiments on whole blood as reported in Colace et al. (2012). The platelet aggregate profile data reported in Colace et al. (2012) for low-shear rate and high-shear rate conditions were processed using the framework discussed in Sect. 2.2.4 to create a discrete particle aggregate reconstruction of the thrombus, and the aggregate dimensions were scaled up to arterial length scales while preserving the overall bounding box aspect ratio for the geometry. These are identified as models C1 and C2, respectively, with a total of 8,576 and 8,865 particles used for their corresponding discrete element reconstruction. Note that no specific fine-tuning or calibration of microstructural information was used here. Pulsatile flow around each of these different occlusion models was simulated for a total of three cardiac cycles, starting from rest at $t=0$, and the corresponding flow fields from the final cardiac cycle for each case were compared with, and contrasted against, each other. For each of these two cases, line integral convolution (LIC) maps were employed to visualize the flow velocity magnitudes as well as the flow structures in the vicinity of the thrombus. LIC is a texture advection-based technique, which is used for visualization of dense vector field tangents (Cabral and Leedom 1993). While it does not provide vector field local direction information, it clearly demarcates local rotational or vortical regions in the field. Combined with the corresponding velocity magnitudes, this enables an effective illustration of how pulsatile flow interactions with thrombus aggregates lead to complex flow structures in the thrombus neighborhood. The model configurations as well as flow visualization for four successive instants across a cardiac cycle are presented in Fig. 6 for the hemispherical occlusion cases, and in Fig. 7 for the experimentally derived aggregate morphologies. All velocity magnitudes have been scaled to 700.0 mm/s. These results establish that our method can resolve the unsteady dynamic vortical structures spanning the domain downstream of the thrombus resulting from its interaction with the flow. Figure 6 depicts not only strong vortices and recirculation at locations distal to the clot, but also a small but noticeable recirculation region at the proximal base of the clot, occurring primarily during the decelerating phases of the cardiac cycle. Furthermore, Fig. 6e demonstrates that flow patterns around the same occlusion geometry can vary noticeably when it is considered to be a heterogeneous mesoporous aggregate. This indicates that for such heterogeneous thrombi, simply removing the clot domain and resolving the flow around the sharp blood–thrombus interface may provide less realistic information on flow patterns. Note that the particle-based aggregates for the experimentally derived morphologies were inherently associated with a porous internal microstructure through the inter-particle void spaces. This is relevant to modeling porosity/permeability effects for realistic thrombi. We remark that a detailed analysis on generating microstructures that optimally mimic real macroscopic thrombus pore microstructure and permeability, which is possible using the devised framework, was beyond the scope of the present study. However, results from the simulations using the two discrete particle aggregate reconstructions here illustrate the capability of the method in resolving intra-thrombus perfusion at the macroscale, as presented in Fig. 8. The results in this figure depict spatial distribution of perfused flow within the thrombus and are driven by the high incoming flow rates and corresponding time-varying perfusion pressure gradients at the thrombus boundary. The intra-thrombus flow velocities are observed to be at least 4 orders of magnitude smaller than the flow around the thrombus, and the estimates will be further improved if the microstructure is tuned to mimic measured data on aggregate clot porosity. A more detailed analysis of microscale flow through thrombus interstices is presented in Sect. 3.3. Particularly for the intra-thrombus flow estimation, the performance of the numerical method was analyzed by further computing the total flux around the aggregate boundary using scaffold grids as described in Sect. 2.2.5. This gave us an estimate of the numerical accuracy of maintaining flux conservation in regions of flow within complex pore microstructure. The scaled flux estimates across various instances of the final cardiac cycle are presented in Fig. 9, and absolute value of the conservation error is found to be within reasonable numerical accuracy limits, establishing additional numerical check on the model predictions.

Fig. 7

Illustration of thrombus–hemodynamics interaction using thrombus aggregates derived from experimental data. The model aggregates (as ensembles of discrete particles or elements) are shown in (a). The inlet flow profile and time points of interest are shown in (b). c The flow structures in the channel for the two models in the form of snapshots taken across T1–T8 (b)

Fig. 8

An illustration of intra-thrombus perfusion derived from the particle–continuum approach for macroscale thrombus–hemodynamics interactions. The time instants T1–T8 are identical to those in Fig. 7. Thrombus model C1 is shown on the left, and model C2 is on the right

3.3 Flow within and around a platelet plug

In order to further demonstrate the ability of the devised method in capturing microstructural and microscale flow and transport information, another set of numerical experiments were conducted on a model system comprising a thrombotic platelet plug. This was based on experimental data for a platelet plug obtained in a mouse injury model as described in Tomaiuolo et al. (2014), which was used to create a discrete particle reconstruction of the platelet plug. A total of 103 superquadric discrete elements were employed for the reconstruction. The baseline particle reconstruction employed superquadric discrete elements with planar aspect ratio of 1.0:0.6. The reconstructed platelet plug was embedded within a channel with dimensions equivalent to a small vessel, and a parabolic, non-pulsatile, inflow profile was imposed at the inlet to drive the flow. The background fluid was assumed to be plasma, with density $(\rho _f) = 1.025 g/cc$ and viscosity $(\mu _f) = 1.7 cP$, and flow around the thrombotic plug was computed for a few time steps for velocity and pressure fields to achieve convergence. The converged velocity fields characterizing flow around the thrombus, as well as microscale flow in the interior, are illustrated in Fig. 10a. The observed peak extra-thrombus flow velocity is 3.2 mm/s, and peak intra-thrombus velocity is $3.29\,\upmu \hbox {m/s}$. These observations, along with the spatial flow pattern around the plug, and within the platelet plug interstices, are in excellent agreement with reported results in Tomaiuolo et al. (2014) which were obtained from simulations with explicitly meshed platelets (that is, no fictitious/embedded domains). This comprised a direct validity check for our model predictions for flow in thrombus environment. The flexibility of a discrete particle representation, with parametrically defined geometries (Sects. 2.2.1, 2.2.2), enables rapid variations in microstructures to be modeled via parametric deformations of the individual discrete elements. This was used to create a sequence of thrombotic aggregate microstructures with the same overall aggregate morphology. First, a sequence of microstructural variations were generated without any extra constraints on the individual element deformations. This led to a family of aggregate models (e.g., M1–M4) which have differing microstructures and differing aggregate porosities. Thereafter, a sequence of isochoric (constant volume) parametric deformations as formulated via Eq. (14) were used to create aggregate models (e.g., P1–P4) with varying microstructures but (owing to same element volume and total volume fraction) same aggregate porosity. The corresponding microscale flow for four sets of microstructurally varied platelet plug models is illustrated in Fig. 10c, d, respectively. A comparison of flow between these different models reveals that microstructural variations that lead to varying aggregate porosity also have a small but noticeable influence on extra-thrombus flow. From the results in Fig. 10, this can be clearly motivated in particular by comparing models M3 and M4, which have visibly differing porosity, leading to a difference in peak extra-thrombus velocity of $70\,\upmu \hbox {m/s}$, that is likely to increase with higher incoming flow at the inlet. The distribution of flow across the interstitial spaces, as well as the peak intra-thrombus flow velocities, is, however, sensitive to microstructure and pore space network for both cases (panels c, d). Thus, resolving detailed intra-thrombus flow characteristics will require not only bulk porosity, but also information on microstructure, and our results indicate that a discrete element-based approach enables incorporating such information flexibly. Similar to Sect. 3.2, the integrated mass flux around a scaffold grid based on the platelet aggregate was compared and tracked with varying microstructures, for tracking numerical accuracy. The flux estimates, scaled with respect to total incoming flux, for the eight microstructure models are presented in Table 1.

Fig. 9

Integrated flux around the scaffold grid for experimentally derived thrombus models C1 (blue) and C2 (red), scaled with total incoming flux. This is used as an indicator for solution quality for data pertaining to intra-thrombus flow and transport

Fig. 10

Illustration of flow interactions with a platelet plug, with focus on microscale flow and microstructure effects. a, b The flow velocity around and within the platelet plug model described in Tomaiuolo et al. (2014). (c) Variations in microstructure with varying bulk porosity, and d variations with fixed porosity. Each microstructure model is labeled with peak intra-thrombus (int) and extra-thrombus (ext) velocity magnitudes

Table 1 Scaled flux estimates for intra-thrombus flow for the platelet plug model

Fig. 11

Numerical examples illustrating the capability of the proposed method in terms of handling thrombus lysis. a depicts flow structures around an idealized occlusion undergoing lysis, modeled using the staggered scheme via an algebraic size reduction rule. b, c depicts clot shrinkage due to shear loading, handled via shrinkage and removal of discrete particles from a macroscale thrombus aggregate (model C1 from Fig. 7)

3.4 Hemodynamics during thrombolysis

The fictitious domain framework with staggered sub-cycling was employed to perform numerical experiments on a modified version of the model system described in Sect. 3.2. For this, the channel dimensions and boundary conditions were kept the same as in Sect. 3.2, and two specific cases of clot shrinkage/lysis were investigated. First, an idealized hemispherical occlusion was embedded within the channel (Fig. 6a). The occlusion, characterized by its radius $d_c$, was then varied by shrinking $d_c$ over time, leading to an idealized description of lysis. A physiologically realistic macroscopic “lysis rate” was imposed by interpolating from experimental data presented by Korin et al. (2012). The normalized lysis rate ($g_l$) corresponding to a trans-plasminogen activator (tPA) treatment was used and modified to generate an algebraic macroscopic lysis rule: $d_c(t) = d_c(0)\sqrt{1.0 - g_l t}$. The derived $g_l$ value was 0.0031 s$^{-1}$. The simulation started from an initial occlusion size of $d_c = 2.5$ cm and was run for 13 staggered sub-cycles, up until a final time of 300s. The staggering parameters, as outlined in Sect. 2.3, were chosen as $N_c = 2$ and $T_g = 20$ s, with cardiac cycle being $T_c = 0.9$ s as before. Note that although this corresponds to a total of 333 cardiac cycles worth of simulation time, owing to the staggered approach a total of 26 cardiac cycles were actually computed, leading to notable computational benefits. The final lysed clot size when the simulation terminated was $\approx 0.6$ cm. The corresponding flow structures for two instances during the final cardiac cycle after 0, 6, and 12 staggering loops are presented in Fig. 11a. For the second scenario, the discrete particle reconstruction of macroscale thrombus model C1 as described in Sect. 3.2 was considered, and a hemodynamic load driven lysis scenario was modeled (see, for example, Bajd et al. 2010). Flow stresses and flow-induced shear forces were computed from the velocity and pressure fields, for each discrete particle in the thrombus. Individual discrete elements were then shrunk and ultimately removed from the thrombus, based on the lysis rate (as described above) applied on elements whose shear loading was beyond a threshold. This threshold was chosen to be at approximately $50\%$ of peak shear loading experienced across the discrete element ensemble. The computations were run for 5 staggered sub-cycles, until $\approx 12 \%$ of particles were removed. Instances of the flow pre- and post-systole, around the lysed thrombus in comparison with the original shape, are illustrated in Fig. 11b. From the overlaid final and initial thrombus geometries, we see that the lysis mainly occurred along the proximal face of the clot, while the distal face which typically faces low-shear recirculating flow saw no lysis. Note that, in both of these examples of lysis, no remeshing with changing clot shape was necessary in our proposed approach. These examples demonstrate that (a) the proposed method can resolve lysis by changing size or removing particles from the thrombus domain; (b) these modifications are easily coupled dynamically with flow and hemodynamic loading; and (c) employing the staggering scheme to separate the flow and lysis time scales, and avoiding remeshing costs, leads to key computational benefits. We emphasize that the focus here was to illustrate the essential features of the two-scale staggering algorithm. Developing a further fully resolved thrombolysis model dynamically coupled with hemodynamic loading was not the focus of the current work.

4 Discussion

4.1 Parallelization

In the proposed framework, the primary algorithmic step in coupling the fictitious domain ($\Omega _t$) to the background mesh ($\Omega$) involved resolving a penalty coupling term over the discretized domain. With a discrete element representation of $\Omega _t$, this step was abstracted out to ultimately be a series of independent inside/outside checks on a collection of analytically defined discrete particles. This step can be easily parallelized by means of a broadcast communication of the discrete particle configuration across a set of processors, over which the background mesh has been partitioned. Once this is achieved, the native parallelization capabilities of the underlying solver/library can be directly employed. Owing to the fact that the mesh is typically over a simpler, more regular domain, mesh partitioning among processes becomes less complicated as well. While a detailed analysis of parallel computing using the method presented here is beyond the scope of this paper, we present a sample illustration of the parallel performance of the method. Here, we simulate hemodynamics for one cardiac cycle using one of the experimentally derived thrombus aggregate morphologies described in Sect. 3.2 in parallel. All implementation and simulations presented here were performed using the FEniCS library, and native MPI constructs embedded within wrappers to the solver library MUMPS were utilized. The performance, for the same number of degrees of freedom distributed across varying number of processes (strong-scaling behavior), is illustrated in Fig. 12. As observed, beyond the jump from serial to parallel execution, possibly occurring due to cache effects, the scaling behavior is appreciably close to linear variation with number of processes.

Fig. 12

Sample illustration of the parallel performance of the fictitious domain, discrete element method implementation in FEniCS, using simulations of thrombus–hemodynamics interactions for model C1 in Fig. 7

4.2 Additional numerical considerations

For this paper, the fictitious domain interaction term was in the form of a penalty constraint and dynamic coupling was not the focus. However, for the sake of rigor and generalization, it is worthwhile to consider the more general scenario and discuss a more consistent definition of evaluating interface terms. Of specific interest is evaluation of gradients at the interface. Given the discrete element framework, a gradient estimate based on intrinsic discrete element properties can be defined. For this, we utilize the useful mathematical property of the underlying superquadric family of geometries (which define individual discrete elements) that surface normals can be analytically derived based on shape and size parameters as follows:

$$\begin{aligned} \mathbf {n}(\eta , \omega ) =&\left\{ \frac{1}{a_1}\cos ^{2-\epsilon _1}{\eta }\cos ^{2-\epsilon _2}{\omega }, \frac{1}{a_2}\cos ^{2-\epsilon _1}{\eta }\sin ^{2-\epsilon _2}{\omega },\right. \nonumber \\&\quad \left. \times \frac{1}{a_3}\sin ^{2-\epsilon _1}{\eta } \right\} , \end{aligned}$$

(22)

where $(\eta ,\omega )$ are surface parameters that determine location of a point on the surface of the superquadric element. Based on this definition, using a Gateaux derivative, we can now define an estimate of a scalar and vector gradient as follows:

$$\begin{aligned} \nabla \phi \cdot \mathbf {n}&= \frac{\partial \phi }{\partial \mathbf {n}} \approx \frac{\phi (\mathbf {x}^* + \alpha \mathbf {n}^*) - \phi (\mathbf {x}^* - \alpha \mathbf {n}^*)}{2\alpha } \end{aligned}$$

(23)

$$\begin{aligned} \nabla \mathbf {u} \cdot \mathbf {n}&= \frac{\partial \mathbf {u}}{\partial \mathbf {n}} \approx \frac{\mathbf {u}(\mathbf {x}^* + \alpha \mathbf {n}^*) - \mathbf {u}(\mathbf {x}^* - \alpha \mathbf {n}^*)}{2\alpha }, \end{aligned}$$

(24)

where $\mathbf {x}^*$ is a chosen point along the boundary of the discrete element and $\mathbf {n}^*$ is the corresponding normal defined by Eq. (22). This is similar in essence to the ghost-cell-based approach in sharp-interface immersed boundary methods (Seo and Mittal 2011), except that it is discrete element/particle based. Numerically, choosing $\alpha$ to be a small parameter will lead to consistent estimates. One can think of $\mathbf {x}^* = \mathbf {x}^*(\eta , \omega )$ as respective numerical quadrature points on the surface of an individual particle.

Another issue of interest is the effectiveness of the penalty term. As discussed in Sect. 3.1, increasing penalty contribution will strengthen the coupling. However, its effectiveness will depend on the slip velocity $\mathbf {u} - \mathbf {v}_0$. Therefore, for regions of larger velocity mismatch, higher penalty terms will be needed. However, assuming element basis functions $N_i(\mathbf {x})$, the penalty term will end up as diagonal contributions of the form $\kappa \int {N_i N_i}d\Omega ^h$, leading to skewing the global condition number of the matrix system if the penalty terms are increased arbitrarily. For such scenarios, alternative coupling formulations where the penalty terms are replaced by more generalized momentum source or loading terms will be required, and an iterative fluid–solid computation can be used (similar to the staggering approach described here) to numerically “push” the flow out of the solid sub-domain. This was found to be the case when simulation of thrombus growth, as opposed to lysis, was considered during the course of model development, and scenarios where the thrombus sub-domain grew into regions of high advection.

A third factor of relevance here pertains to the definition of an effective mesoscopic length scale. To describe this, we consider the discrete element models for the two arbitrary clot morphologies described in Sect. 3.2. These were generated without any constraints on element sizing, and the obtained average diameters were $\approx 0.05$ mm, which are an order of magnitude greater than the typical individual platelet size scales of $\approx 2-3\,\upmu \hbox {m}$. Thus, effectively each discrete element is representative of an aggregate of cellular entities instead of an actual cell itself, and the corresponding microstructural description is at a length scale intermediate to cellular and macroscopic length scales. Thus, the proposed discrete element approach for macroscopic large artery thrombi is representative of a mesoscopic method. This is advantageous because while a particle description is more capable of handling essentially discrete phenomena like aggregation and fragmentation (of key relevance to thrombosis), treating each cell explicitly as a particle makes a macroscopic particle-based description of a thrombus untenable and prohibitively expensive.

4.3 Remarks on underlying assumptions

We revisit here a few assumptions that were implicit in the experiments presented here to illustrate various features of the computational method. Firstly, as mentioned in Sect. 2.2.1, it was assumed that the thrombus sub-domain velocity $\mathbf {v}_0$ is a known entity, being set to 0 for all the simulations presented here. In addition, the thrombus was treated throughout as rigid. Physiologically, a thrombus, after formation and aggregation, goes through a phase of retraction and consolidation (Calaminus et al. 2007; Ono et al. 2008). This renders a stable and compact structure to the thrombus. At the level of a macroscale clot embedded in a large artery, these retracted clots can be assumed to undergo small deformations at a scale that is negligible in comparison with other dominant flow phenomena. This was the motivation for assuming the nearly rigid response of the thrombus. We remark that the consideration of deformability of the thrombus will not take away from our inferences on the capabilities of the proposed method in capturing complex flow–thrombus interactions. Additionally, the discrete element thrombus model described here can be extended by incorporating deformation mechanics at the level of individual particles. As the particles interact with each other, their collective motion will effectively describe the deformation of the thrombus. This computational extension of the method is an immediate next step that we are investigating. We remark here that there are significant modeling and numerical complexities associated with resolving this deformation, and hence this aspect needs a separate, more dedicated study by itself. Secondly, specifically for the platelet plug model system, it was assumed that platelet shapes can be generally described using regular geometry families like superquadrics. Electron microscopy images of activated platelets often reveal a distinct morphology transformation from discoid/ellipsoidal to a spiky, dendritic shape (Jagroop et al. 2000; Mangin et al. 2004). While such shapes have not been considered here, we remark that it can be easily achieved by treating each platelet as a composite particle instead of a single particle, and modifying the shape of each individual particle to mimic an overall platelet shape. In addition, in the context of a thrombus retraction, it has been observed that the dendritic shapes reduce back to more regular platelet geometries (Lam et al. 2011; Cines et al. 2014), and for such scenarios, the demonstrated examples adequately represent a realistic platelet plug microstructure. Thirdly, the portion of the vessel wall conjoined to the thrombus was throughout assumed to be a part of the no-slip and non-permeable Neumann boundary of the computational domain. In reality, this is usually an injury or a diseased part of the wall and, hence, often has a rupture, a leakage, or more permeable wall tissue (Nesbitt et al. 2009). To account for this, the boundary condition at that location needs to be correspondingly changed from the standard no-slip/non-permeable wall condition. While this was not demonstrated in the examples, it can be readily implemented based on the thrombus location, owing to the simpler background fictitious domain grid, and does not limit the applicability of the proposed framework.

4.4 Broader implications

The discrete element approach proposed here enables a unified treatment of thrombus hemodynamics interactions that can simultaneously handle macroscale as well as microscale flows. This lays out the fundamentals for continued investigation on intra-thrombus transport, thrombus perfusion, and evaluation of clot permeability, while simultaneously enabling investigations on flow, transport, and hemodynamic loading on realistic large artery clots within the paradigm of image-based large arterial/venous hemodynamics modeling. Especially for a growing or lysing thrombus, the method provides significant advantages in terms of easy modification of microstructure and avoidance of the computational/algorithmic cost of remeshing. The intrinsic advantages of discrete element methods regarding handling added complexities in microstructure also make this a suitable approach for handling further complexities like explicit fibrin mesh mechanics and trapped blood cells in the clot. In addition, the interplay of the coagulation cascade with the thrombus aggregate can potentially be handled by resolving this interaction at the level of each individual discrete element and modifying its properties in response. We note, however, that both of these aspects by themselves render substantial complications from a modeling and simulation standpoint and warrant dedicated additional investigations. Finally, while the focus here was on thrombus–hemodynamics interactions in large artery flows, the method is equally appropriate and effective for developing computational models for microfluidic assays and devices working with human whole blood. Operating pressure and flow conditions for these devices, along with device or channel geometries, can be easily incorporated as inputs, providing thus a toolkit for complementing and supplementing experimental data from microfluidic assays.

5 Concluding remarks

We have presented here a numerical method for modeling interaction of a thrombus with unsteady blood flow. The method is based on a fictitious domain approach with a discrete element framework for representing a thrombus. Detailed aspects of the method have been outlined with the primary focus of resolving hemodynamics in the neighborhood of a realistic arbitrary thrombus aggregate, along with a series of numerical experiments to demonstrate its capabilities. The validity of numerical predictions is established using a benchmark fluid dynamics problem of flow past a cylinder (Sect. 3.1) and a microscale platelet plug flow model described in the literature (Sect. 3.3). The method can incorporate complex thrombus morphology as well as microstructure information. It can resolve not only macroscale interactions of an arbitrary shaped clot with pulsatile arterial hemodynamics, but also microscale intra-thrombus flow. In addition, using a staggered algorithmic framework, it can also model interaction of flow with a time-varying thrombus manifold geometry. This is of utility in applications pertaining to thrombolysis which has been illustrated here using two numerical examples. Physiologically realistic boundary conditions can be easily incorporated, as demonstrated in the examples. Owing to using a fictitious domain approach, the complex issue of meshing and explicitly resolving the blood–thrombus interface is bypassed.