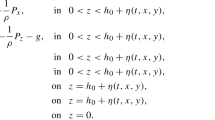1 Introduction

Long waves in an ocean rotating without friction were described by many authors (Taylor 1922; Defant 1961; Le Blond and Mysek 1978; Gill 1982; Pedlosky 1982). Long waves in an infinite ocean of a uniform depth on a beta-plane were discussed by LeBlond, Mysak (Le Blond and Mysek 1978). However, at shallows, bottom friction starts to significantly influence the propagation of long waves, and the inviscid fluid approximation becomes inappropriate. The applicability criterion of ideal fluid approximation is the Stokes’ layer thickness. If the depths are less than the Stokes’ layer thickness, the turbulent friction becomes significant and cannot be neglected (Zyryanov and Chebanova 2016; Zyryanov and Chebanova 2017a).

For the first time, a viscous damping effect in the sea current dynamics was studied by Ekman (1905), then by Welander (1957), Platzman (1963), Jelesnianski (1970), and Jordan and Baker (1980). Mofjeld (1980) also investigated the influence of vertical viscosity on the propagation of barotropic Kelvin wave.

The effect of turbulent friction on the propagation of long gravity waves was studied in detail in Kakutani (Kakutani and Matsuuchi 1975). The effect of friction is shown to largely depend on the magnitude relation between a turbulent analog of the Reynolds number ReT = HU/A and the dimensionless wave number α = H k (Н is the thickness of the unperturbed liquid layer, U is gravity wave velocity, А is the coefficient of vertical turbulent exchange, k is wave number). At O (α−5) < ReT, friction is insignificant and wave propagation can be described by Korteweg de Vries (KdV) equation. At O (α−1) < ReT ≤ O  (α−5), friction becomes significant, and it is required to pass to the KdV–Burgers equation to take it into account. An interesting case is O (α−5) ≈ ReT, when the geometric and viscous dispersions are in a balance. This case was studied in detail by Djordjevic (1980). Finally, at ReT < O (α−1), the complex phase velocity becomes purely imaginary, implying that there are no free wave motions and the dynamics of the free surface is described by a nonlinear diffusion equation of parabolic type (Djordjevic 1983). An analog of such equation was first obtained by Nakaya (1974) in a study of drop spreading over a horizontal plane.

The condition ReT < O (α−1) imposes a restriction on the depth of the liquid in the form of \( H<O\;\left(\sqrt{A/\upomega}\right) \) (ω is wave frequency). On the other hand, the propagation of wave perturbations with frequency ω in a viscous liquid is known to be accompanied by the formation at a free surface of a Stokes boundary layer with a thickness of \( {h}_{St}\sim \sqrt{A/\upomega} \). The Stokes layer is the diffusion depth of the vorticity from the free surface within the wave period (Lighthill 1978). For example, in the case of an open flow and semidiurnal tidal wave M2, the depth hSt is 12–15 m at a characteristic value A = 102 cm2/s, and for a flow with ice cover, hSt is twice as large as that. Thus, the coastal zones of seas and many reservoirs fall within the Stokes layer. At depths less than Stokes layer thickness H < hSt (supercritical depth zones) in flows with characteristic time variations T, the turbulent friction and pressure gradient are comparable accurate to O (Fr2)(\( Fr=U/\sqrt{gH} \)) (Zyryanov 1995), and the flow regime becomes gradient–viscous. In this case, the terms with turbulent friction in the momentum equation are of the order of unit: \( F{r}^2{\operatorname{Re}}_T^{-1}/\alpha \approx O\;(1) \). The evolutionary equation changes from hyperbolic to parabolic. Thus, friction itself not only manifests in viscous damping but also influences the dispersion relations.

The tidal wave propagation in shallow zones without Coriolis acceleration has been studied by Proudman (1925, 1953), Perroud (1959), Dronkers (1964), Hunt (1964), Ippen (1966), Bowden (1988), Prandle and Rahman (1980), Prandle (1985, 2009), Jay (1991), Lanzoni and Seminara (1998, 2002), Savenije (1992, 2005), Friedrichs and Aubrey (1994), Savenije and Veling (2005), and Van Rijn (2011). The following assumptions are usually made: the wavelength is greater than estuary depth; the tidal amplitude is small in comparison to the depth; the acceleration is supposed to be small; thus, the convective terms can be neglected and the equation of motion is linearized; and with a single tidal constituent predominating, tide is supposed to be a simple harmonic. To obtain a general wave picture, the frictional term can also be neglected. Great attention is given to the shape of the estuary as a factor determining the natural period of oscillations in the water basin. Classical solutions for a narrow rectangular channel without friction are described by Dronkers (1964), Hunt (1964), Ippen (1966), LeBlond (Le Blond 1978), and Prandle (2009). A frictionless channel of a variable cross-section is discussed by Proudman (1925) and Ippen (1966), and the solution presented by the authors gives an option to find a resonant oscillation period for bays of a nonrectangular shape. A necessary condition is a weak change in channel cross section, which allows neglecting it within the wavelength. Such frictionless solutions have a number of limitations. In frictionless channels, the amplitude near the vertex will increase exponentially due to Green’s law. So, it is obvious that the frictional forces play a significant role in shallow water and should be taken into account when studying estuaries. According to Le Blond (1978), the frictional force dominates the acceleration term over most of the tidal cycle. There are a number of studies (Perroud 1959; Hunt 1964; Ippen 1966; Prandle and Rahman 1980; Prandle 1985; Jay 1991; Lanzoni and Seminara 1998, 2002; Savenije 1992; Savenije and Veling 2005) in which solutions for channels of the variable shape are obtained. Perroud (1959) presented a linearized solution for variable channels with a slowly changing cross section based on the linear friction. In Ippen (1966), Harleman (1966), and Bowden (1988), the authors gave expressions for the amplitudes and velocities in a semi-enclosed rectangular channel. Proudman (1925) addressed a channel with a parabolic cross section. Prandle and Rahman (1980) gave an analytical solution for a channel with both width and depth varying with powers of distance. In Hunt (1964), Ippen (1966), Prandle (1985), Jay (1991), Savenije (1992, 2005), Lanzoni and Seminara (1998, 2002), and Savenije and Veling (2005), an analytical solution is given for an estuary with exponentially varying width and depth. Expressions for resonant channels and criteria for increasing/decreasing tidal amplitude were obtained by Hunt (1964), Ippen (1966), Prandle (1985), and Savenije (2005). Savenije (1992) introduced a quasi-nonlinear approach with the nonlinear friction term based on the envelope method. Friedrichs and Aubrey (1994) presented a first-order analytical solution for strongly convergent estuaries. They showed that the dominant effects are friction, the slope of the surface, and the rate of convergence. Van Rijn (2011) presented analytical and numerical solutions for converging tidal channels. The convergence is found to be dominant in deep converging channels, whereas bottom friction is generally dominant in shallow converging channels.

In Zyryanov and Chebanova (2016, 2017a), the hydrodynamic effects of convergence and friction on the tidal wave amplitude in the funnel-shaped estuaries were investigated for a homogeneous fluid based on the linear model with friction. Analytical solutions are given for convergent estuaries of uniform and variable depths. The estuaries are approximated by a sector of a circle. It is shown that the Stokes diffusion layer plays a significant role in the formation of the regimes of a tidal wave transformation. It is shown that the spatial modulation of the tide amplitude in bays, gulfs, and estuaries is caused by the phenomenon of the dissipative-convergent intermittency developing under competitive effects of the convergence and turbulent friction. In the inlet to an estuary, the tidal wave amplitude can initially decrease due to the effect of friction, but then, as the wave moves deeper in the estuary, the effect of the convergence begins to prevail and the tidal wave amplitude can start to increase. In the other case, it can initially increase and then decrease and increase again near the estuary head as it takes place in the Delaware estuary. This is the essence of the dissipative-convergent intermittency effect.

The effect of the dissipative-convergent intermittency is most strongly manifested in strange bays with mean water depths of the order of the Stokes layer thickness. As shown by Zyryanov and Chebanova (2017a), the spatial distribution of the tidal wave amplitude has a minimum in a convergent channel. If the minimum point lies beyond the estuary, then the effect of the convergence predominates and the wave height increases towards the vertex. If the minimum point lies in the neighborhood of an estuary head, then the effect of the turbulent friction predominates along the entire bay length and the wave height decreases towards the bay vertex. Finally, if the minimum point finds itself in the middle part of an estuary, then the case of a strange bay arises, namely, in such bays, the wave height decreases up to the minimum point and then begins to increase again after its passage. The local increase in the tidal wave amplitude can be manifested further at the mouth of the river.

In Perroud (1959), Hunt (1964), Ippen (1966), Harleman (1966), Prandle and Rahman (1980), Prandle (1985), Jay (1991), Lanzoni and Seminara (1998, 2002), Savenije and Veling (2005), Savenije (1992, 2005), Friedrichs and Aubrey (1994), van Rijn (2011), Zyryanov and Chebanova (2016), and Zyryanov and Chebanova (2017a), Earth rotation was not taken into account. In Zyryanov (1995), it is shown that the contribution of the Coriolis acceleration to the evolutionary equation for waves in supercritical depth zones is small and can be neglected. In this case, the conditions in bays open to the east or to the west will be symmetrical. But on the Earth, zonal bays are asymmetrical. A simple analysis shows that the majority of the bays with significant tides (Penzhina bay, Mezen bay, the bay of Fundy, etc.) are open to the west. A question arises as to whether the asymmetry of western and eastern bays can be connected with planetary effects: Earth rotation and sphericity. As the bays and gulfs are shallow, the viscosity, i.e., turbulent friction, should also play a significant role. The objective of this paper is to investigate the effects of the viscosity, as well as Earth rotation and sphericity on the zonal long-wave dynamics in an unbounded ocean.

2 Viscous waves

Assuming the water density constant and neglecting the nonlinear terms in the equations of momentum, the equations of motion and continuity for homogenous rotating fluid can be written as follows:

$$ \frac{\partial\;u}{\partial\;t}- fv=-\frac{1}{\rho_0}\frac{\partial P}{\partial x}+{A}_z\frac{\partial^2u}{\partial {z}^2} $$
(1)
$$ \frac{\partial\;v}{\partial\;t}+ fu=-\frac{1}{\rho_0}\frac{\partial P}{\partial y}+{A}_z\frac{\partial^2v}{\partial {z}^2} $$
(2)
$$ g{\rho}_0=\frac{\partial P}{\partial\;z} $$
(3)
$$ \frac{\partial\;u}{\partial\;x}+\frac{\partial\;v}{\partial\;y}+\frac{\partial\;w}{\partial\;z}=0 $$
(4)

where u, v are the horizontal components of flow velocity along the axes X, directed to the east along a parallel, and Y, respectively, to the north along a meridian; w is the vertical component of flow velocity; \( f=2\varOmega \sin \tilde{\phi} \) is the Coriolis parameter; Ω is the angular velocity of Earth; \( \tilde{\phi} \) is the latitude; P is the water pressure; g is the acceleration of gravity; ρ0 is the density of sea water (constant); and Az is the vertical eddy viscosity (constant). The Z axis is directed vertically downward. The origin of coordinates is located on the unperturbed surface of the water body.

The boundary conditions are specified as:

at the sea surface (z = ζ(x, y, t)) zero wind stress:

$$ \frac{\partial u}{\partial z}{\left|{}_{z=\varsigma }=\frac{\partial v}{\partial z}\right|}_{z=\varsigma }=0\kern0.24em $$
(5)

and the kinematic condition:

$$ {\left.\kern0.24em w\right|}_{z=\varsigma }=\frac{\partial \zeta }{\partial\;t}+u{\left|{}_{z=\varsigma}\frac{\partial \zeta }{\partial x}+v\right|}_{z=\varsigma}\frac{\partial \zeta }{\partial y} $$

on the seabed (z = H(x, y)), no-slip conditions:

$$ {\left.\;u\right|}_{z=H}=v{\left|{}_{z=H}=w\right|}_{z=H}=0 $$
(6)

If we have a shoreline boundary of a water body (L(x, y) = 0), then the total discharge (total flow) normal to the boundary is assumed zero on it:

$$ \left(\overrightarrow{S},\overrightarrow{n}\right)=0\kern0.5em \mathrm{where}\kern0.5em \overrightarrow{S}=\underset{\varsigma }{\overset{H}{\int }}\overrightarrow{U} dz,\overrightarrow{U}=\left(u,v\right) $$
(7)

Note that such formulation of the problem fails to allow us to specify more rigid boundary conditions for the horizontal velocity (no-slip conditions or zero normal velocity component) on the side boundaries of a water body due to the absence of horizontal derivatives of velocity components in Eqs. (1) and (2).

Integrating the hydrostatic Eq. (3) from the upper boundary of the liquid z = ζ(x, y, t) to the horizon z yields an equation for pressure in the liquid:

$$ P\left(x,y,z,t\right)={P}_a+g{\rho}_0\left(z-\zeta \right) $$
(8)

where Pa is the atmospheric pressure at the sea surface, which is constant (Pa= const) due to no wind stress. Substituting (8) into (1) and (2) yields.

$$ \frac{\partial\;u}{\partial\;t}- fv=g\frac{\partial \zeta }{\partial x}+{A}_z\frac{\partial^2u}{\partial {z}^2} $$
(9)
$$ \frac{\partial\;v}{\partial\;t}+ fu=g\frac{\partial \zeta }{\partial y}+{A}_z\frac{\partial^2v}{\partial {z}^2} $$
(10)

Wave solutions for the system of Eqs. (9) and (10) are sought for in the form

$$ u=\overline{u}{e}^{\mathrm{i}\upomega \kern0.1em \mathrm{t}},v=\overline{v}{e}^{\mathrm{i}\upomega \kern0.1em \mathrm{t}},\varsigma =\overline{\varsigma}{\mathrm{e}}^{\mathrm{i}\upomega \mathrm{t}} $$
(11)

where \( \overline{u} \), \( \overline{v} \), and \( \overline{\varsigma} \) are the amplitudes of wave variations of velocity and elevation, respectively, ω is the wave frequency, and i is the imaginary unit.

Substituting (11) into (9) and (10) yields:

$$ \mathrm{i}\upomega \overline{u}-f\;\overline{v}=g\frac{\partial \overline{\zeta}}{\partial x}+{A}_z\frac{\partial^2\overline{u}}{\partial {z}^2} $$
(12)
$$ \mathrm{i}\upomega \overline{v}+f\;\overline{u}=g\frac{\partial \overline{\varsigma}}{\partial y}+{A}_z\frac{\partial^2\overline{v}}{\partial {z}^2} $$
(13)

A particular solution to the system (12), (13), not depending on z, will satisfy the following system of equations

$$ \mathrm{i}\upomega {\overline{u}}_0-f{\overline{v}}_0=g\frac{\partial \overline{\zeta}}{\partial x} $$
(14)
$$ \mathrm{i}\upomega \overline{v}{}_0+f{\overline{u}}_0=g\frac{\partial \overline{\zeta}}{\partial y} $$
(15)

From (14) and (15), we obtain

$$ {\overline{u}}_0=\frac{g}{f^2-{\upomega}^2}\left(\mathrm{i}\upomega {\zeta}_x+f\;{\zeta}_y\right) $$
(16)
$$ {\overline{v}}_0=\frac{g}{f^2-{\upomega}^2}\left(\mathrm{i}\upomega {\zeta}_y-f\;{\zeta}_x\right) $$
(17)

Let us introduce notations \( {u}^{\prime }=\overline{u}-{\overline{u}}_0 \), \( {v}^{\prime }=\overline{v}-{\overline{v}}_0 \). In view of (14) and (15), we obtain a system of equations for \( {\overline{u}}^{\prime } \)and \( {\overline{v}}^{\prime } \):

$$ {A}_z\frac{\partial^2}{\partial {z}^2}\left(\begin{array}{l}{u}^{\prime}\\ {}{v}^{\prime}\end{array}\right)=M\;\left(\begin{array}{l}{u}^{\prime}\\ {}{v}^{\prime}\end{array}\right) $$
(18)

where M is a matrix:

$$ M=\left(\begin{array}{cc}\mathrm{i}\upomega & -f\\ {}f& \mathrm{i}\upomega \end{array}\right) $$
(19)

To find a solution to the system (18), we form a diagonal matrix from the matrix М. Let us obtain the eigenvalues and eigenvectors of the matrix М. Numbers λ1, 2 satisfying

$$ \mid M-\lambda E\mid ={\left(\mathrm{i}\upomega -\lambda \right)}^2+{f}^2=0 $$
(20)

are the eigenvalues of the matrix М.

From here, we have λ1, 2 = i(ω ± f). Form a matrix B, where the eigenvectors corresponding to each eigenvalue λ1, 2 are written as columns.

$$ \mathrm{B}=\left(\begin{array}{cc}i& 1\\ {}1& i\end{array}\right) $$
(21)

It is useful to introduce new functions u″, v″, satisfying:

$$ \left(\begin{array}{l}{u}^{\prime}\\ {}{v}^{\prime}\end{array}\right)=B\left(\begin{array}{l}{u}^{{\prime\prime}}\\ {}{v}^{{\prime\prime}}\end{array}\right) $$
(22)

Substituting (22) into (18) and taking into account the property of eigenvectors’ matrix, we obtain

$$ {A}_z\frac{\partial^2}{\partial {z}^2}\left(\begin{array}{l}{u}^{{\prime\prime}}\\ {}{v}^{{\prime\prime}}\end{array}\right)={B}^{-1} MB\left(\begin{array}{l}{u}^{{\prime\prime}}\\ {}{v}^{{\prime\prime}}\end{array}\right)=\left(\begin{array}{l}{\lambda}_1{u}^{{\prime\prime}}\\ {}{\lambda}_2{v}^{{\prime\prime}}\end{array}\right) $$
(23)

where B−1 is the inverse Hermitian self-adjoint matrix of B. The solutions of the system of Eq. (23) are the functions:

$$ {u}^{{\prime\prime} }={C}_1{e}^{\upmu_1z}+{C}_2{e}^{-{\upmu}_1z} $$
(24)
$$ {v}^{{\prime\prime} }={C}_3{e}^{\upmu_2z}+{C}_4{e}^{-{\upmu}_2z} $$
(25)

where

$$ {\mu}_1=\sqrt{\frac{\lambda_1}{A_z}}=\sqrt{\frac{i\left(\omega +f\right)}{A_z}},\kern0.36em {\mu}_2=\sqrt{\frac{\lambda_2}{A_z}}=\sqrt{\frac{i\left(\omega -f\right)}{A_z}} $$
(26)

which implies, in view of (21), that the functions \( {\overline{u}}^{\prime } \), \( {\overline{v}}^{\prime } \)are:

$$ {\overline{u}}^{\prime }=i\left({C}_1{e}^{\upmu_1z}+{C}_2{e}^{-{\upmu}_1z}\right)+\left({C}_3{e}^{\upmu_2z}+{C}_4{e}^{-{\upmu}_2z}\right) $$
(27)
$$ {\overline{v}}^{\prime }=\left({C}_1{e}^{\upmu_1z}+{C}_2{e}^{-{\upmu}_1z}\right)+i\left({C}_3{e}^{\upmu_2z}+{C}_4{e}^{-{\upmu}_2z}\right) $$
(28)

and \( \overline{u} \) and \( \overline{v} \)are:

$$ \overline{u}={\overline{u}}_0+{\overline{u}}^{\prime }=\frac{g}{f^2-{\upomega}^2}\left(\mathrm{i}\upomega {\zeta}_x+f\;{\zeta}_y\right)+i\left({C}_1{e}^{\upmu_1z}+{C}_2{e}^{-{\upmu}_1z}\right)+\left({C}_3{e}^{\upmu_2z}+{C}_4{e}^{-{\upmu}_2z}\right) $$
(29)
$$ \overline{v}={\overline{v}}_0+{\overline{v}}^{\prime }=\frac{g}{f^2-{\omega}^2}\left(\mathrm{i}\upomega {\zeta}_y-f\;{\zeta}_x\right)+\left({C}_1{e}^{\upmu_1z}+{C}_2{e}^{-{\upmu}_1z}\right)+i\left({C}_3{e}^{\upmu_2z}+{C}_4{e}^{-{\upmu}_2z}\right) $$
(30)

The constants C1, C2, C3, C4 are sought for with the use of the boundary conditions (5) and (6). Free-surface boundary conditions are linearized, i.e., satisfied at the unperturbed level z = 0. Substituting (29) and (30) into boundary conditions (5) and (6) yields

$$ \overline{u}={\overline{u}}_0+2i{C}_1\mathrm{ch}\left({\upmu}_1z\right)+2{C}_3\mathrm{ch}\left({\upmu}_2z\right) $$
(31)
$$ \overline{v}={\overline{v}}_0+2{C}_1\mathrm{ch}\left({\upmu}_1z\right)+2i{C}_3\mathrm{ch}\left({\upmu}_2z\right) $$
(32)

where

$$ {C}_1=-\frac{g}{\left(f+\omega \right)}\frac{\left({\zeta}_x+i{\zeta}_y\right)}{2\mathrm{ch}\left({\upmu}_1H\right)},{C}_3=-\frac{g}{\left(f-\omega \right)}\frac{\left({\zeta}_y+i{\zeta}_x\right)}{2\mathrm{ch}\left({\upmu}_2H\right)} $$
(33)

It follows from (31) and (32) that it is impossible to get correct boundary condition for the level \( \overline{\varsigma} \), if we use the condition of zero normal velocity components instead of zero integral discharge normal to the shoreline boundary (7).

Let us now derive a governing equation for the elevation. Integrating the continuity Eq. (4) with respect to z from z = ζ to z = H with boundary conditions and the conditions at the sea surface (5), (6), yields a continuity equation in total fluxes:

$$ \frac{\partial \zeta }{\partial \kern0.1em t}=\frac{\partial {S}_{(x)}}{\partial \kern0.1em x}+\frac{\partial {S}_{(y)}}{\partial \kern0.1em y} $$
(34)

or for amplitudes in view of (11)

$$ \mathrm{i}\upomega \overline{\zeta}=\frac{\partial {\overline{S}}_{(x)}}{\partial \kern0.1em x}+\frac{\partial {\overline{S}}_{(y)}}{\partial \kern0.1em y} $$
(35)

where

$$ {\overline{S}}_{(x)}=\underset{\zeta }{\overset{H}{\int }}\overline{u} dz,\kern1em {\overline{S}}_{(y)}=\underset{\zeta }{\overset{H}{\int }}\overline{v} dz $$
(36)

Substituting (31) and (32) into (36) and integrating, we obtain

$$ {\displaystyle \begin{array}{l}{\overline{S}}_{(x)}={\overline{\zeta}}_x\left(\frac{giH\upomega}{f^2-{\upomega}^2}+\frac{ig}{2{\upmu}_1\left(f+\upomega \right)}\mathrm{th}{\upmu}_1H-\frac{ig}{2{\upmu}_2\left(f-\upomega \right)}\mathrm{th}{\upmu}_2H\right)+\\ {}+{\overline{\zeta}}_y\left(\frac{gHf}{f^2-{\upomega}^2}-\frac{g}{2{\upmu}_1\left(f+\upomega \right)}\mathrm{th}{\upmu}_1H-\frac{g}{2{\upmu}_2\left(f-\upomega \right)}\mathrm{th}{\upmu}_2H\right)\end{array}} $$
(37)
$$ {\displaystyle \begin{array}{l}{\overline{S}}_{(y)}=-{\overline{\zeta}}_x\left(\frac{gHf}{f^2-{\upomega}^2}-\frac{g}{2{\upmu}_1\left(f+\upomega \right)}\mathrm{th}{\upmu}_1H-\frac{g}{2{\upmu}_2\left(f-\upomega \right)}\mathrm{th}{\upmu}_2H\right)+\\ {}+{\overline{\zeta}}_y\left(\frac{giH\upomega}{f^2-{\upomega}^2}+\frac{ig}{2{\upmu}_1\left(f+\upomega \right)}\mathrm{th}{\upmu}_1H-\frac{ig}{2{\upmu}_2\left(f-\upomega \right)}\mathrm{th}{\upmu}_2H\right)\end{array}} $$
(38)

It is useful to introduce:

$$ {F}_1=\frac{giH\upomega}{f^2-{\upomega}^2}+\frac{ig}{2{\upmu}_1\left(f+\upomega \right)}\mathrm{th}{\upmu}_1H-\frac{ig}{2{\upmu}_2\left(f-\upomega \right)}\mathrm{th}{\upmu}_2H $$
(39)
$$ {G}_1=\frac{gHf}{f^2-{\upomega}^2}-\frac{g}{2{\upmu}_1\left(f+\upomega \right)}\mathrm{th}{\upmu}_1H-\frac{g}{2{\upmu}_2\left(f-\upomega \right)}\mathrm{th}{\upmu}_2H $$
(40)

Then, we obtain

$$ {\overline{S}}_{(x)}={F}_1{\overline{\zeta}}_x+{G}_1{\overline{\zeta}}_y,\kern0.5em {\overline{S}}_{(y)}=-{G}_1{\overline{\zeta}}_x+{F}_1{\overline{\zeta}}_y $$
(41)

Substituting (41) into the continuity Eq. (35) yields the governing equation for the complex amplitudes of the water level elevation in the water body:

$$ \mathrm{i}\upomega \overline{\varsigma}=\frac{\partial }{\partial x}\left({F}_1{\overline{\zeta}}_x\right)+\frac{\partial }{\partial y}\left({F}_1{\overline{\zeta}}_y\right)+J\left({G}_1,\overline{\zeta}\right) $$
(42)

where \( J\left({G}_1,\overline{\zeta}\right)=\frac{\partial {G}_1}{\partial x}\frac{\partial \overline{\varsigma}}{\partial y}-\frac{\partial {G}_1}{\partial y}\frac{\partial \overline{\varsigma}}{\partial x} \) is Jacobian. In the compact form,

$$ \mathrm{i}\upomega \overline{\varsigma}=\left(\nabla, {F}_1\nabla \overline{\varsigma}\right)+J\left({G}_1,\overline{\varsigma}\right) $$
(43)

where (…, …) is the scalar product, ∇ is the Hamilton operator (gradient).

Note that the boundary condition for the level \( \overline{\varsigma} \) in a rotating fluid will be a condition with a directional derivative, as it follows from the expressions for total flows (37) and (38) and the boundary condition (7). The solvability of the boundary value problem for an elliptical equation with a directional derivative (Poincare problem (Poincare 1910)) depends on the boundary index. Depending on the boundary index, this problem can have no solutions or not a unique solution (Maz’ya 1972). In the sea current problems, the directional derivative is very close to the normal derivative; that is why the Neumann problem can replace the Poincare problem. Such a replacement is appropriate in stationary sea current problems and does not lead to the loss of effects, but in the theory of waves it can result in the loss of amphidromic systems in the basin.

With regard to G1being the function of H and f and with the use of the β-plane approximation for the Coriolis parameter, we obtain:

$$ J\left({G}_1,\zeta \right)=\frac{\partial {G}_1}{\partial H}J\left(H,\zeta \right)-\frac{\partial {G}_1}{\partial f}\upbeta {\zeta}_x $$
(44)

where \( \upbeta =\frac{\partial f}{\partial y} \) is the beta-effect.

Now the governing equation for the complex amplitudes of the water level elevation in a water body becomes:

$$ \mathrm{i}\upomega \overline{\varsigma}=\frac{\partial }{\partial x}\left({F}_1{\overline{\zeta}}_x\right)+\frac{\partial }{\partial y}\left({F}_1{\overline{\zeta}}_y\right)+\frac{\partial {G}_1}{\partial H}J\left(H,\overline{\zeta}\right)-\frac{\partial {G}_1}{\partial f}\upbeta {\overline{\zeta}}_x $$
(45)

As can be seen from (45), the longitudinal change in the water body depth and beta-effect has an impact on the zonal asymmetry.

Let us now consider a particular case of (45) without taking into account Earth rotation. Assuming f = 0 yields μ1 = μ2 = μ and

$$ {F}_1=-\frac{ig}{\upomega}\tilde{H},\kern0.5em {G}_1=0 $$
(46)

where

$$ \tilde{H}=H-\frac{1}{\upmu}\mathrm{th}\left(\upmu, H\right) $$
(47)

is the reduced depth, introduced by Zyryanov and Chebanova (2016).

Therefore, the governing equation for the complex amplitudes of the water level elevation in a water body (45) becomes:

$$ -{\omega}^2\overline{\varsigma}=\frac{\partial }{\partial x}\left(g\tilde{H}\;{\overline{\zeta}}_x\right)+\frac{\partial }{\partial y}\left(g\tilde{H}\;{\overline{\zeta}}_y\right) $$
(48)

Equation (48) has been obtained by Zyryanov and Chebanova (2016) for the waves in a water body without taking into account Earth rotation.

The parameter μ in (47) is

$$ \upmu =\sqrt{\frac{\mathrm{i}\upomega}{A_z}}=\sqrt{\frac{\upomega}{2{A}_z}}\left(1+i\right)=\alpha \left(1+i\right),\kern0.36em \alpha =\sqrt{\frac{\omega }{2{A}_z}} $$
(49)

The quantity inverse to α is the Stokes layer thickness

$$ {h}_{\mathrm{St}}=\sqrt{\frac{2{A}_z}{\upomega}} $$
(50)

To relate the frequency, the wave number and the attenuation factor, we isolate the real and imaginary parts in the expression for \( \tilde{H} \) in (47). With the use of (50), we obtain

$$ \mathrm{th}\left(\upmu H\right)=\frac{\mathrm{th}\left(\upalpha H\right)+i\;\mathrm{tg}\left(\upalpha H\right)}{1+i\;\mathrm{tg}\left(\upalpha H\right)\kern0.24em \mathrm{th}\left(\upalpha H\right)} $$
(51)

where tg is the trigonometric tangent.

Figure 1 gives plots of the real and imaginary parts of the reduced depth \( \tilde{H} \) as functions of the real depth H. The plots show that at H > 15m, the dependence of the real part \( \mathrm{Real}\left(\tilde{H}\right) \)on H is almost linear and the imaginary part \( \operatorname{Im}\left(\tilde{H}\right) \)at H > 15m asymptotically tends to a constant. The depth H~15m is equal to the Stokes layer thickness for semidiurnal tidal wave (Zyryanov 1995), and it actually separates two regimes of the tidal wave evolution: at H >  > 15 m, the regime of the wave motion is low viscosity, while at H < 15m, the turbulent friction dominates.

Fig. 1
figure 1

Plots of (1) the \( \mathrm{Real}\left(\tilde{H}\right) \) and (2) imaginary \( \operatorname{Im}\left(\tilde{H}\right) \) parts of the reduced depth \( \tilde{H} \) (47) as functions of H for the semidiurnal tidal wave at Az = 102cm2/s

Full size image

To understand the effect of the reduced depth in wave evolution, let us consider a one-dimensional analog of Eq. (48) for the case of a constant depth of a sea:

$$ \frac{\partial }{\partial \kern0.1em x}\left[\left(\mathrm{Real}\left(\tilde{H}\right)+i\operatorname{Im}\left(\tilde{H}\right)\right)\frac{\partial \overline{\varsigma}}{\partial x}\right]+\frac{\omega^2}{g}\overline{\varsigma}=0 $$
(52)

Let us find a wave solution of Eq. (52). Substituting \( \overline{\varsigma}\sim {e}^{ikx} \) into (52), we obtain a dispersion relationship

$$ {k}^2=\frac{\upomega^2}{g\left(\mathrm{Real}\left(\tilde{H}\right)+i\operatorname{Im}\left(\tilde{H}\right)\right)} $$
(53)

At the depth of the sea H >  > 15m, we have an estimate

$$ \frac{\operatorname{Im}\left(\tilde{H}\right)}{\mathrm{Real}\left(\tilde{H}\right)}<<1 $$
(54)

and, therefore, from (53) it follows

$$ k=\pm \frac{\upomega}{\sqrt{g\mathrm{Real}\left(\tilde{H}\right)}}\left(1-i\frac{\operatorname{Im}\left(\tilde{H}\right)}{2\mathrm{Real}\left(\tilde{H}\right)}\right) $$
(55)

As \( \mathrm{th}\left(\upmu \tilde{H}\right)\sim 1 \) at great depth H, an expression for the reduced depth becomes

$$ \tilde{H}\approx H-\frac{1}{\upmu}=H-\sqrt{\frac{A}{2\upomega}}+i\sqrt{\frac{A}{2\upomega}} $$
(56)

Thus, for great H, the turbulent friction also has its effect on the wave evolution through a decrease in the real depth by half of the Stokes layer thickness \( {h}_{St}\sim \sqrt{\frac{2A}{\upomega}} \). As seen from (56), at great H, an asymptote to the imaginary part of the reduced depth \( \tilde{H} \) is equal to half the Stokes layer thickness.

As seen from (26), two Stokes’ layers occur in the rotating fluid. The thickness of the first layer approaches infinity as the frequency tends to the inertial frequency. Taking into account the role of the Stokes’ layer as a criterion of the viscosity influence, we can conclude that for the waves with the near-inertial frequency, the viscosity always plays a significant role, irrespective of ocean depths. The criterion showing when we need to take into account the viscosity arises from the expression H ≤ [2Az/(f − ω)]1/2.

As can be seen from (26), the thicknesses of both Stokes’ layers tend to the Ekman layer thickness, when the frequencies are small, and to the classical Stokes’ layer for the nonrotating fluid, when the frequencies are high.

3 Zonal viscous waves on a beta-plane

In Zyryanov and Chebanova (2016), Earth rotation was not taken into account. In this case, there is no difference between the western and eastern directions for waves. Let us now investigate the influence of sphericity on the asymmetry in the long-wave dynamics.

Neglecting the surface elevation in the meridional direction along Y-axis and supposing H = const, we obtain from (45) an equation:

$$ \mathrm{i}\upomega \overline{\varsigma}=\frac{\partial }{\partial x}\left({F}_1{\overline{\varsigma}}_x\right)-\frac{\partial {G}_1}{\partial f}\upbeta {\overline{\varsigma}}_x $$
(57)

where

$$ {\displaystyle \begin{array}{l}\frac{\partial {G}_1}{\partial f}=\frac{g}{4{\left(f+\upomega \right)}^2}\left(\frac{3}{\upmu_1}\mathrm{th}{\upmu}_1H-\frac{H}{\mathrm{c}{\mathrm{h}}^2{\upmu}_1H}\right)+\\ {}+\frac{g}{4{\left(\upomega -f\right)}^2}\left(\frac{3}{\upmu_2}\mathrm{th}{\upmu}_2H-\frac{H}{\mathrm{c}{\mathrm{h}}^2{\upmu}_2H}\right)-\frac{gH\left({f}^2+{\upomega}^2\right)}{{\left({f}^2-{\upomega}^2\right)}^2}\end{array}} $$
(58)

The general solution of (57) is

$$ \overline{\zeta}(x)={C}_1\exp \left({k}_1x\right)+{C}_2\exp \left({k}_2x\right) $$
(59)

where

$$ {k}_{1,2}=\frac{\frac{\partial {G}_1}{\partial f}\upbeta \pm \sqrt{D}}{2{F}_1},\kern0.36em D={\left(-\frac{\partial {G}_1}{\partial f}\upbeta \right)}^2+4\mathrm{i}\upomega {F}_1 $$
(60)

The expression (60) gives dispersion relationships k1, 2(ω) for zonal viscous waves on the β-plane.

3.1 Extreme cases

Equation (45) can be simplified for several extreme cases.

3.1.1 Inviscid fluid

Consider an inviscid liquid on a beta-plane. Assume Az = 0, then μ1 = μ2 = ∞. Now we have

$$ {F}_1=\frac{giH\upomega}{f^2-{\upomega}^2} $$
(61)
$$ \frac{\partial {G}_1}{\partial f}=-\frac{gH\left({f}^2+{\upomega}^2\right)}{{\left({f}^2-{\upomega}^2\right)}^2} $$
(62)
$$ \frac{\partial {F}_1}{\partial f}=-\frac{2 fgiH\upomega}{{\left({f}^2-{\upomega}^2\right)}^2} $$
(63)

So that the governing Eq. (45) reduces to

$$ \mathrm{i}\upomega \overline{\zeta}=\frac{giH\upomega}{f^2-{\upomega}^2}\varDelta \overline{\zeta}-\frac{2 fgiH\upomega}{{\left({f}^2-{\upomega}^2\right)}^2}\upbeta {\overline{\zeta}}_y+\frac{gH\left({f}^2+{\upomega}^2\right)}{{\left({f}^2-{\upomega}^2\right)}^2}\upbeta {\overline{\zeta}}_x $$
(64)

Solutions to (64) are sought in the form:

$$ \overline{\zeta}={\overline{\zeta}}_0{\mathrm{e}}^{-i\left( kx+ ly\right)} $$
(65)

Substituting (65) into (64) we obtain:

$$ \upomega =-\frac{gH\upomega}{f^2-{\upomega}^2}\left({k}^2+{l}^2\right)-\frac{2 fgiH\upomega}{{\left({f}^2-{\upomega}^2\right)}^2}\upbeta l-\frac{gH\left({f}^2+{\upomega}^2\right)}{{\left({f}^2-{\upomega}^2\right)}^2}\upbeta k $$
(66)

In inviscid fluids ω, k and l have to be real, then from (66), we obtain the equation

$$ \upomega =-\frac{gH\upomega}{f^2-{\upomega}^2}\left({k}^2+{l}^2\right)-\frac{gH\left({f}^2+{\upomega}^2\right)}{{\left({f}^2-{\upomega}^2\right)}^2}\upbeta k $$
(67)

which gives us a dispersion relationship for linear waves on the β-plane. For zonal waves, we have an explicit relationship between k and ω

$$ {k}_{1,2}=\frac{-\tilde{B}\pm \sqrt{{\tilde{B}}^2+4\tilde{A}\omega }}{2\tilde{A}} $$
(68)

where

$$ \tilde{B}=-\frac{\partial {G}_1}{\partial f}\beta, \tilde{A}=i{F}_1 $$
(69)

Let us now consider the frequencies less than f (ω<<f). In this case, it follows from (67) that (Grimshaw et al. 1998)

$$ \omega =-\frac{gH\omega}{f^2}\left({k}^2+{l}^2\right)-\frac{gH}{f^2}\beta k $$
(70)

For mesoscale motions in the ocean, L is ~ 100 km, which implies that

$$ \omega <<\frac{gH\omega {k}^2}{f^2} $$
(71)

Therefore, the left part of (70) can be neglected. This leads to the dispersion relation for Rossby waves:

$$ -\omega \left({k}^2+{l}^2\right)-\beta k=0 $$
(72)

So, there is an evident zonal asymmetry for the barotropic Rossby waves (72): their phase speed is directed westward, while the group speed is directed eastward.

Let us now assume that ω>> f. From (67) it follows that

$$ {\omega}^2= gH\left({k}^2+{l}^2\right)-\frac{gH}{\omega}\beta k=0 $$
(73)

This leads to the dispersion relation for long zonal gravity waves on the β-plane.

$$ \frac{\omega }{k}=\sqrt{gH\left(1-\frac{\beta }{k\omega}\right)} $$
(74)

As can be seen from (74), the beta-effect reduces the length of short-period waves, but its influence is negligible. For example, for semidiurnal tidal waves β/kω~2.4 ⋅ 10−3, i.e., the quantity is small in comparison to 1.

The relation (74) shows that the beta-effect decreases the phase speed of long gravity waves. Therefore, Eq. (45) reduces to an equation describing gravity and Rossby waves if the turbulent exchange is neglected.

3.1.2 Viscous fluid

The expression (74) has been derived in the absence of friction (for an inviscid case). Let us now examine the role of friction and incorporate the viscous term into (74) for ω>>f. In this case, we have

$$ {\upmu}_1={\upmu}_2=\sqrt{\frac{\mathrm{i}\upomega}{A_z}}=\upmu $$
(75)

Therefore,

$$ {F}_1=-\frac{giH}{\upomega}+\frac{ig}{\upmu \upomega}\mathrm{th}\upmu H=-\frac{ig}{\upomega}\left[H-\frac{1}{\upmu}\mathrm{th}\upmu H\right],{G}_1=-\frac{gHf}{\upomega^2} $$
(76)

Similarly to (73), we have

$$ \frac{\upomega^2}{gH}=\left(1-\frac{1}{\mu H}\mathrm{th}\upmu H\right)\left({k}^2+{l}^2\right)-\frac{\beta k}{\upomega} $$
(77)

which yields the dispersion relation for zonal waves (l = 0) similar to (74) but with friction.

$$ \frac{\upomega}{k}=\sqrt{gH\left(1-\frac{1}{\upmu H}\mathrm{th}\upmu H-\frac{\upbeta}{k\upomega}\right)} $$
(78)

As can be seen from (78), viscosity leads to the introduction of a reduced depth in (78) instead of H. As the reduced depth is always less than the real depth, the viscosity always decreases the length of short-period waves.

It follows from (78) in view of (75) that in this case the wave number k becomes complex and we obtain a damping decrement in the wave evolution. In the viscid case, it is useful to consider two cases—shallow and deep water.

In deep water:

$$ \mid {\upmu}_1H\mid >>1,\mid {\upmu}_2H\mid >>1 $$
(79)

Thus, we have

$$ {F}_1=\frac{g\mathrm{i}\upomega}{f^2-{\upomega}^2}\left[H+\frac{\upmu_2\left(f-\upomega \right)-{\upmu}_1\left(f+\upomega \right)}{2{\upmu}_1{\upmu}_2\upomega}\right] $$
(80)
$$ \frac{\partial {F}_1}{\partial f}=\frac{2 fgi\upomega}{{\left({f}^2-{\upomega}^2\right)}^2}\left[H-\frac{3}{8}\frac{\upmu_2{\left(\upomega -f\right)}^2+{\upmu}_1{\left(\upomega +f\right)}^2}{f\upomega {\upmu}_1{\upmu}_2}\right] $$
(81)
$$ \frac{\partial {G}_1}{\partial f}=-\frac{g\left({f}^2+{\upomega}^2\right)}{{\left({f}^2-{\upomega}^2\right)}^2}\left[H-\frac{3}{4}\frac{\upmu_2{\left(\upomega -f\right)}^2+{\upmu}_1{\left(\upomega +f\right)}^2}{\left({f}^2+{\upomega}^2\right){\upmu}_1{\upmu}_2}\right] $$
(82)

As a result, we obtain an equation for waves similar to (66) but with complex depth correction.

In shallow water,

$$ \mid {\upmu}_1H\mid <<1,\mid {\upmu}_2H\mid <<1 $$
(83)

A second-order Taylor expansion of hyperbolic tangent yields

$$ {F}_1=\frac{g{H}^3}{3{A}_z},{G}_1=0 $$
(84)

from which it follows that the governing equation becomes

$$ \mathrm{i}\upomega \overline{\zeta}=\frac{g}{3{A}_z}\left[\frac{\partial }{\partial x}\left({H}^3{\overline{\zeta}}_x\right)+\frac{\partial }{\partial y}\left({H}^3{\overline{\zeta}}_y\right)\right] $$
(85)

or in the compact form

$$ \mathrm{i}\upomega \overline{\zeta}=\frac{g}{3{A}_z}\left(\nabla, {H}^3\nabla \overline{\zeta}\right) $$
(86)

where ∇ is the Hamilton operator (gradient), brackets ( , ) denote the scalar product.

Equation (86) is a linearized version of the nonlinear equation of the viscous flow motion at a depth less than the Stokes layer obtained by Zyryanov (1995, 2014):

$$ \frac{\partial\;\zeta }{\partial t}=\frac{g}{3{A}_z}\left(\nabla, {\left(H-\zeta \right)}^3\nabla \zeta \right) $$
(87)

3.1.3 Viscous seiches on a beta-plane

It is interesting to study seiches in view of Earth rotation and sphericity. We consider a zonal channel with a uniform depth. Let us find a wave solution of (57) in view of the Neumann boundary condition on the borders of the channel:

$$ \frac{d\overline{\zeta}}{dx}{\left|{}_{x=L}=\frac{d\overline{\zeta}}{dx}\right|}_{x=0}=0 $$
(88)

As we have seen, the boundary condition (7) with respect to (41) for the total flow will end up in the Poincare problem with the directional derivative for the level \( \overline{\zeta} \)on the channel boundary. If we use such problem setting for seiches in a channel, then a system of waves with amphidromic points can occur and it can result in additional difficulties when searching for analytical solutions. The problem can be simplified in two ways. Firstly, we can deal with water objects with frequencies of seiches being much greater than the inertial frequency f. In this case, we can use expressions (76) for F1 and G1. It is seen from (76), that if ω >  > f, than G1 <  < F1. From (41), it follows that\( {\overline{S}}_{(x)}\sim {\overline{\zeta}}_x,{\overline{S}}_{(y)}\sim {\overline{\zeta}}_y \), and the Poincare problem with the directional derivative can be approximately replaced by the Neumann problem with boundary conditions (88). Secondly, we can deal with a zonal channel with a width being less than Rossby deformation radius. In this case, Kelvin and Poincare waves transform into general zonal waves without the formation of amphidromic points (Hydrodynamics of Lakes 1984).

Wave solutions are sought for in the form \( \overline{\zeta} \)~eikx. Substituting this into (57), we derive an equation for k

$$ \mathrm{i}\upomega =-{F}_1{k}^2-\frac{\partial {G}_1}{\partial f}\upbeta ik $$
(89)

The roots of the Eq. (89) are

$$ {k}_{1,2}=A\pm B $$
(90)

where

$$ A=\left(\frac{\partial {G}_1}{\partial f}\beta \right)/2i{F}_1\kern0.5em \upbeta ={\left[{\left(\frac{\partial {G}_1}{\partial f}\upbeta \right)}^2+4i{F}_1\upomega \right]}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}/2i{F}_1 $$
(91)

Substituting a general solution \( \overline{\zeta}(x)={C}_1\exp \left(i{k}_1x\right)+{C}_2\exp \left(i{k}_2x\right) \)in the boundary conditions (88) yields

$$ \exp \left(i{k}_1L\right)-\exp \left(i{k}_2L\right)=0 $$
(92)

Thus, we obtain a dispersion relation for seiches spectrum in view of viscosity, rotating and beta-effect:

$$ L\cdot \operatorname{Re}(B)= k\pi, k=1,2,\mathrm{3...} $$
(93)

If the depths are greater than the Stokes’ layer thickness, then viscosity can be neglected and the expression (93) can be rewritten in the explicit form.

$$ {\left\{{\left[\frac{gH\left({f}^2+{\upomega}_k^2\right)\;\upbeta}{{\left({f}^2-{\upomega}_k^2\right)}^2}\right]}^2-\frac{4 gH{\upomega}_k^2}{f^2-{\upomega}_k^2}\right\}}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.}=\frac{2 k\pi gH{\upomega}_k}{\left({\upomega}_k^2-{f}^2\right)L} $$
(94)

With f = 0 and β = 0 (nonrotating fluid), we have from (94) the Merian’s formula for periods of seiches

$$ {T}_k=\frac{2L}{k\sqrt{gH}},\kern0.5em k=1,2,3 $$
(95)

From (94), we obtain the following expression for periods of seiches on the f-plane (f ≠ 0, β = 0)

$$ {T}_k=\frac{2\pi L}{\sqrt{k^2{\pi}^2 gH+{L}^2{f}^2}},\kern0.5em k=1,2,3 $$
(96)

It can be seen, that the periods of seiches depend on the latitude. Therefore, we get a correction to the Merian’s formula (95) for rotation. Rotation decreases the periods of seiches. For example, in the channel with a depth of H = 20 m and a length of L = 100 km at the latitude of 60о, the first mode of the longitudal seiche calculated by Merian’s formula is 3 h 58 m and the same mode corrected for rotation is 3 h 48 m.

The condition H<<hst yields

$$ i\omega \overline{\zeta}=\frac{g}{3{A}_z}{H}^3{\overline{\zeta}}_{xx} $$
(97)

and for periods of seiches in shallow basin, we obtain

$$ {T}_k=\frac{3{A}_z{L}^2}{\pi {k}^2g{H}^3},\kern0.5em k=1,2,3 $$
(98)

Calculation of seiches’ periods for the viscous rotating fluid by (93) gives a lesser value of the relevant mode of seiche other than calculation by the Merian’s formula for the nonviscous nonrotating fluid.

4 Zonal asymmetry of westward and eastward waves

4.1 Planetary drift

From (57), it follows that the term with the first-order derivative gives an asymmetry of eastward and westward directions. The coefficient \( \frac{\partial {G}_1}{\partial f}\upbeta \) at the first-order derivative in (57) has the dimensions of velocity. Let us introduce a notation

$$ {U}_d=-\frac{\partial G{}_1}{\partial f}\upbeta $$
(99)

It follows from (58) and (99) that Ud depends on the Coriolis parameter f(ϕ), wave frequency ω, and beta-effect.

For the limit values of Ud, we obtain

for ω>>f from (76):

$$ {U}_d=-\frac{\partial G{}_1}{\partial f}\upbeta =\frac{gH}{\omega^2}\upbeta $$
(100)

for ω<<f from (82):

$$ {U}_d=-\frac{\partial G{}_1}{\partial f}\upbeta =\frac{g}{f^2}\left(H-\frac{3}{2}{h}_E\right)\upbeta $$
(101)

where \( {h}_E={\left(\frac{A}{2f}\right)}^{\raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{$2$}\right.} \)is the Ekman layer thickness.

In deep water, when hE <  < H, from (99), we obtain

$$ {U}_d=\frac{gH}{f^2}\upbeta =R{o}^2\upbeta $$
(102)

where \( Ro=\frac{\sqrt{gH}}{f}\hbox{--} \)is the Rossby outer radius of deformation.

As it is seen from (102), the velocity Ud for long-period waves in deep water depends only on the planetary parameters f and β, therefore, let us call it the planetary drift.

Figure 2 shows the dependence of Ud on the wave frequency ω. It is shown that there are critical frequencies ω1 and ω2 for given latitude and for ω1< ω < ω2, when the planetary drift is negative. Out of this interval, the planetary drift is positive.

Fig. 2
figure 2

Planetary drift velocity Ud (m/s) for the latitude \( \upvarphi =\raisebox{1ex}{$\pi $}\!\left/ \!\raisebox{-1ex}{$3$}\right. \)and depth H = 35m

Full size image

Dispersion relation for zonal waves in the case (102) follows from (66).

$$ \omega =-\frac{R{o}^2\upbeta k}{1+R{o}^2{k}^2} $$
(103)

As seen from (103), waves move to the west, but its group velocities have the eastward direction.

$$ \frac{d\upomega}{dk}=-\frac{R{o}^2\upbeta \left(1-R{o}^2{k}^2\right)}{\left(1+R{o}^2{k}^2\right)}>0 $$
(104)

for wave numbers k > 1/Ro .

So, as seen above, Earth sphericity is a reason for an asymmetry in the tidal wave dynamics which results in the planetary drift origin. It is obvious that on the f -plane, the planetary drift does not exist and zonal waves are symmetrical.

The intervals of positive and negative values of the planetary drift depend on the latitude.

In Fig. 3, the graphs of Ud for latitudes φ =30°, 40°, 50° are given. For these latitudes, the values of \( \raisebox{1ex}{$\upomega $}\!\left/ \!\raisebox{-1ex}{$f$}\right. \)corresponding to semidiurnal tides are marked. One can see that the planetary drift for semidiurnal tides for φ < 60° is positive, i.e., it has an eastward direction. Ud approaches largest extremum around φ = 45°–55°. It is interesting that the bays with the highest tides are located at these latitudes and are open to the west. Therefore, the planetary drift for semidiurnal tides can be the reason for zonal asymmetry of western and eastern bays.

Fig. 3
figure 3

Planetary drift velocity Ud (m/s) for depth H = 35m and latitudes φ= (1) – 30°, (2) – 40°, (3) – 50°, (4) – 60°. The numbers (5) – (8) are the frequencies of semidiurnal tides for φ= (5) – 30°, (6) – 40°, (7) – 50°, (8) – 60°

Full size image

4.2 Dispersion relations for eastward and westward waves

Let us go back to the dispersion relation (60). It follows from (59) that Im(k1) and Im(k2) give dispersion relations for eastward and westward waves, and Re(k1) and Re(k2) are the corresponding decrements for these waves. For eastward waves in k1 in (60), the discriminant is taken with a sign plus, i.e., \( {k}_1=\left(\frac{\partial {G}_1}{\partial f}\upbeta +\sqrt{D}\right)/2{F}_1 \), and for westward waves, the discriminant is taken with a sign minus.

Let us introduce notations:

$$ {k}_1^i=\operatorname{Im}\left({k}_1\right),{k}_2^i=\operatorname{Im}\left({k}_2\right),{k}_1^R=\operatorname{Re}\left({k}_1\right),{k}_2^R=\operatorname{Re}\left({k}_2\right) $$
(105)

Figure 4 gives dispersion relation plots for h = 50m, A = 10−2m2/sec, φ= 60°, β=2·10−11m−1· sec1 for

$$ k={k}_1^i\left(\upomega /f\right),k={k}_2^i\left(\upomega /f\right) $$
(106)
Fig. 4
figure 4

Dispersion relations for viscous waves for h = 50m, A = 10−2m2/sec, φ = 60°, β = 2  10−11m−1 ⋅ sec−1. (1) \( {k}_1^i=\operatorname{Im}\left(\frac{g\;f\;\upbeta +\sqrt{D}}{2{F}_1}\right) \); (2) \( {k}_2^i=\operatorname{Im}\left(\frac{g\;f\;\upbeta -\sqrt{D}}{2{F}_1}\right) \); (3) k =  − β/ω (zonal Rossby waves); (4) \( k=\upomega /\sqrt{gH} \)(linear gravitational waves); (5) \( k=\pm \upomega /\sqrt{g\left(H-{h}_{St}\right)} \)

Full size image

Besides that, it also gives dispersion relation plots for Rossby waves k2 =  − β/ω, for long gravity waves without viscosity \( {k}_g=\pm \upomega /\sqrt{gH} \)and for viscosity adjusted through Stokes layer \( {k}_s=\upomega /\sqrt{g\left(H-{h}_{\mathrm{st}}\right)} \) long gravity waves for high frequencies. One can see that for high frequencies, the dispersion relations for westward waves (negative k) and for eastward waves (positive k) are symmetrical. The asymmetry occurs when the frequency approaches the critical value ωcr = f and when ω < ωcr. Moreover, the length of the wave traveling in a westward direction is larger than the length of the eastward traveling wave of the uniform frequency.

The dispersion relation for Rossby waves is in good agreement with the expression for viscous waves for \( 0.2<\raisebox{1ex}{$\upomega $}\!\left/ \!\raisebox{-1ex}{$f$}\right.<0.7 \) for given depth h = 50m, but in the area of low frequencies for \( \raisebox{1ex}{$\omega $}\!\left/ \!\raisebox{-1ex}{$f$}\right. \)< 0.2, it is just the other way round: for Rossby waves, the wave number is growing, while for viscous waves the wave number is decreasing due to the Stokes layer thickness increase and the growing role of viscosity.

Note that without sphericity, i.e., at β = 0, the dispersion curves \( {k}_1^i \) and \( {k}_2^i \) become fully symmetrical.

4.3 Damping decrement and group velocity

As it is noted in Sect. 3.2, the damping decrements are determined by functions, RE (ω) = Re (k1), RW (ω) = Re (k2), RE – for eastward waves and RW −  for westward waves, respectively.

Figure 5 gives graphs of RE (ω) and RW (ω) at latitude φ = 60° for a water object with h = 50m. The figure shows that the decrements for the eastern and western waves differ when ω < 0.5 f, and in the area of the critical frequency ωcr = f with the biggest difference between decrements.

Fig. 5
figure 5

Damping decrements of zonal viscous waves: (1) westward waves RW(ω) = Re(k2); (2) eastward waves RE(ω) = Re(k1)

Full size image

Figure 5 shows that the damping decrement of the westward waves can be 3–4 times larger than the decrement of the eastward waves for waves with similar critical frequencies. This frequency domain is 0.8 < ω < 1.2. At the latitude of 45°, waves of periods 11 h < T <16 h belong to this interval, e.g., semidiurnal tides. At the latitude of 65°, the ratio of damping decrements RЕ/RW in the area of the critical frequency is RE/RW ~ 3 ÷ 4.

From Sect. 2.1, it follows that viscous waves on the beta-plane are dispersive; therefore, the energy and mass transfer in the zonal directions has group velocity V = ∂ω/∂k. Differentiating (60) with respect to ω, we obtain reciprocal quantities \( \frac{1}{V_g^{(1)}}=\frac{\partial {k}_1^i}{\mathrm{\partial \upomega }} \)for eastward waves and \( \frac{1}{V_g^{(2)}}=\frac{\partial {k}_2^i}{\mathrm{\partial \upomega }} \)for westward waves. The graphs of \( \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${V}_g^{(1)}$}\right. \) and \( \raisebox{1ex}{$1$}\!\left/ \!\raisebox{-1ex}{${V}_g^{(2)}$}\right. \)and in Fig. 6 show the asymmetry of waves with westward and eastward group velocities. The asymmetry is particularly obvious in the area near the critical frequency ωcr = f and for frequencies ω < f. Note that positive group velocities correspond to the eastward transfer; and negative, to the westward transfer. Moreover, as seen from Fig. 6, there are areas of frequencies near f, where waves traveling both eastward and westward have only eastward group velocities, and transfer energy and mass only in the eastward direction.

Fig. 6
figure 6

Quantities reciprocal to group velocities: (1) for waves running eastward (curve 1 in Fig. 4); (2) for waves running westward (curve 2 in Fig.4)

Full size image

5 Conclusions

As seen above, viscosity plays a significant role in the long-wave dynamics. Stokes’ layer thickness is a criterion, which separates two regimes of the wave evolution: low-viscosity and viscous flows. When the depths are less than the Stokes’ layer thickness, the turbulent friction prevails for waves of given frequency. Turbulent friction also changes dispersion relations. An important result of viscosity in the long-wave dynamics is the occurrence of the reduced depth. The reduced depth is always lesser than the real depth.

The basic equation for the complex amplitudes of gravitational waves obtained in the paper also describes the extreme regimes of long-wave propagation—Rossby waves and viscous waves at the depth less than the Stokes’ layer thickness. Two Stokes’ layers occur in rotating fluid. The thickness of the first approaches infinity as the frequency tends to inertial. Considering the role of the Stokes’ layer as the criterion of the viscosity influence we can conclude that for the waves of the near-inertial frequency, the viscosity always plays a significant role irrespective of ocean depths.

It is shown that the beta-effect is the reason for the asymmetry of western and eastern directions in wave dynamics. The sphericity of the Earth, causing the planetary drift, plays a major role in the asymmetry of the eastward and westward directions in wave dynamics. The planetary drift velocity depends on the latitude, wave frequency, and ocean depth. A range of near-inertial frequencies existed for any frequency, within which the velocity of the planetary drift is directed westward. Out of this range, the velocity has an eastward direction.

Another reason for the asymmetry of the eastward and westward directions in wave dynamics is friction. Friction was found to affect eastward and westward waves through the damping decrement in different ways. For waves with the near-inertial frequencies, the damping ratio of westward waves can be 5–6 times greater than that for eastward waves.

The asymmetry of the eastward and westward waves manifests itself in the behavior of the group velocity of the wave energy transfer. In a certain range of near-inertial frequencies (in the middle latitudes, the frequency of the semidiurnal tidal wave falls within such interval) the group velocity for both westward and eastward waves is directed only eastward.

It is shown that the asymmetry of the eastward and westward directions in wave dynamics is the reason for the asymmetry of western (open to the west) and eastern bays (open to the east), which can be seen in different amplitude changes. As it follows from the theory, the amplitude of the semidiurnal tide in a western bay is greater than that in an eastern bay, other conditions being the same.

The viscosity and Earth rotation and sphericity influence seiches in enclosed water objects. The equation describing tidal-wave dynamics in a rectangular zonal channel allows getting a dispersion relation for seiches with regard to viscosity and beta-effect. If we neglect the viscosity and Earth rotation, the expression reduces to Merian’s formula. Earth rotation reduces seiches’ periods compared to a nonrotating fluid. The calculation of the seiche periods for a viscous rotating fluid gives a lesser value of the relevant seiches’ period than the calculation by the Merian’s formula. Moreover, in view of the rotation, the periods of seiches become dependable on the latitude. The viscosity, in its turn, enhances the periods due to a decrease in the length of gravity waves. The joint influence of these factors can cause an effect similar to the dissipative-convergent intermittency in the tidal wave dynamics in shallow estuaries described by Zyryanov and Chebanova (2017a).

Returning to the problem of bays with giant tides, we can make a conclusion based on the results of this paper that the asymmetry of eastern and western bays caused by the planetary drift and beta-effect exists, but at the scales of bays, it is insignificant and cannot account for the giant tides observed in some bays. The viscosity and local factors, such as the effect of the curvature of convergent bays, can have much greater influence on the asymmetry of eastern and western bays, than the planetary effects. The paper (Zyryanov and Chebanova 2017b) presents the results of laboratory modeling of the Earth rotation impact on the asymmetry of tidal wave evolution in curvilinear convergent bays with the right bend (against the earth rotation direction) and with the left bend (in the direction of the earth rotation). Comparative analysis of bays shows that the majority of all bays with significant tides have a right bend (against the earth rotation direction). The explanation given in the paper is based on the potential vorticity conservation law. Due to the conservation of the potential vorticity, a water column gets the cyclonic vorticity when entering a convergent bay. As a consequence, water column height increases. This results in the lateral shear stress growth in the right bays and its decrease in the left bays. That is why, the dissipation of a tidal energy in the right bays is lower and the amplitude of a tide is higher approximately 1.5 times than that in the left bays.

In this paper we use the “traditional approximation,” i.e., the horizontal component of the Earth’s rotation is not taken into account (Eckart 1960; Gerkema and Shrira 2005). We think it is reasonable, as, in the near-inertial range of frequencies, nontraditional effects in the stratified fluids act as a singular perturbation (Gerkema and Shrira 2005). Moreover, according to the paper (Gerkema and Shrira 2005), in a linear setting the ‘traditional approximation’ works well for waves outside the inertial range. In our case, the fluid is homogeneous and the problem is linear. A detailed review of the hydrodynamic effects in the geophysical fluid dynamics beyond the traditional approximation is given by Gerkema et al. (2008).