Highly nonlinear wind waves in Currituck Sound: dense breather turbulence in random ocean waves

Abstract

We analyze surface wave data taken in Currituck Sound, North Carolina, during a storm on 4 February 2002. Our focus is on the application of nonlinear Fourier analysis (NLFA) methods (Osborne 2010) to analyze the data set: The approach spectrally decomposes a nonlinear wave field into sine waves, Stokes waves, and phase-locked Stokes waves otherwise known as breather trains. Breathers are nonlinear beats, or packets which “breathe” up and down smoothly over cycle times of minutes to hours. The maximum amplitudes of the packets during the cycle have a largest central wave whose properties are often associated with the study of “rogue waves.” The mathematical physics of the nonlinear Schrödinger (NLS) equation is assumed and the methods of algebraic geometry are applied to give the nonlinear spectral representation. The distinguishing characteristic of the NLFA method is its ability to spectrally decompose a time series into its nonlinear coherent structures (Stokes waves and breathers) rather than just sine waves. This is done by the implementation of multidimensional, quasi-periodic Fourier series, rather than ordinary Fourier series. To determine preliminary estimates of nonlinearity, we use the significant wave height H_s, the peak period T_p, and the length of the time series T. The time series analyzed here have 8192 points and T =1677.72 s = 27.96 min. Near the peak of the storm, we find H_s ≈ 0.55 m, T_p ≈ 2.4 s so that for the wave steepness of a near Gaussian process, ${S} = \left (\pi ^{5/2}/g\right )H_{s}/{T}_{p}^{2}$, we find S ≈ 0.17, quite high for ocean waves. Likewise, we estimate the Benjamin-Feir (BF) parameter for a near Gaussian process, ${I_{BF}} = \left (\pi ^{5/2}/g \right ) H_{s} T/{T}_{p}^{3}$, and we find I_BF ≈ 119. Since the BF parameter describes the nonlinear behavior of the modulational instability, leading to the formation of breather packets in a measured wave train, we find the I_BF for these storm waves to be a surprisingly high number. This is because I_BF, as derived here, roughly estimates the number of breather trains in a near Gaussian time series. The BF parameter suggests that there are roughly 119 breather trains in a time series of length 28 min near the peak of the storm, meaning that we would have average breather packets of about 14 s each with about 5-6 waves in each packet. Can these surprising results, estimated from simple parameters, be true from the point of view of the complex nonlinear wave dynamics of the BF instability and the NLS equation? We analyze the data set with the NLFA to verify, from a nonlinear spectral point of view, the presence of large numbers of breather trains and we determine many of their properties, including the rise time for the breathers to grow to their maximum amplitudes from a quiescent initial state. Energetically, about 95% of the NLFA components are found to consist of breather trains; the remaining small amplitude components are sine and Stokes waves. The presence of a large number of densely packed breather trains suggests an interpretation of the data in terms of breather turbulence, highly nonlinear integrable turbulence theoretically predicted for the NLS equation, providing an interesting paradigm for the nonlinear wave motion, in contrast to the random phase Gaussian approximation often considered in the analysis of data.

1 Introduction

It is well known that random ocean waves are characterized to linear order by the Fourier transform for which one has a linear superposition of sine waves with random, uniformly distributed Fourier phases. The central limit theorem tells us that such a stochastic process has a Gaussian density function for the wave amplitudes. Furthermore, for a narrow-banded process, the envelope of a Gaussian process has a Rayleigh distribution, a result that led Longuet-Higgins (1952) to the conclusion that narrow-banded wave heights are approximately Rayleigh distributed. Pierson and Moskowitz (1962) gave a way to characterize ocean wave spectra by a simple formula, and later on the JONSWAP spectrum (Hasselmann et al. 1962, 1963a, b) was developed to extend their work to nonequilibrium wave motion. The use of the random phase approximation in the study of stochastic processes has been seminal to the modern understanding of random waves from both experimental and theoretical points of view (Kinsman 1965).

However, it is also well known that the Stokes wave nonlinearity is visible by eye in many random time series. Essentially, it is quite common to find time series that are up/down antisymmetric such that the crests are higher than the troughs are low (this observation has led to a very large and separate field for the statistical properties of linear and nonlinear ocean waves, see for example Goda (2010) for a modern overview). The Stokes antisymmetry contrasts with the Gaussian approximation that is up/down symmetric.

The study of randomness in nonlinear ocean waves has naturally led to the study of weak wave turbulence, an area of research that has many implications on the dynamics of wind waves (Hasselmann 1962, 1963a, b; Pushkarev et al. 2003, 2004; Resio et al. 2004, 2011; Badulin et al. 2005; Korotkevich et al. 2007; Badulin et al. 2007; Resio 2016; Ardag and Resio 2017; Zakharov et al. 2017) providing the modern basis of wind wave models (Komen et al. 1994; Young 1999; Janssen 2004; Holthuijsen 2007).

Here, however, we consider the alternative additional possibility that random ocean waves can, to leading order, be described in terms of coherent structures or coherent waveforms in the wave field, such as Stokes waves, solitons, and breather trains, which are the natural basis states of the so-called integrable, nonlinear wave equations. Integrable systems include the Korteweg-deVries and the nonlinear Schrödinger equations and their algebro-geometric solutions in terms of Riemann theta functions (a generalization of ordinary Fourier series) (Belokolos et al. 1994). The theoretical formulation for finding spectral solutions to nonlinear wave equations, typically for periodic or quasiperiodic boundary conditions, is referred to as the periodic inverse scattering transform (IST) in the USA (Ablowitz and Segur 1981) and to finite gap theory (FGT) in Russia (Belokolos et al. 1994).

In applications of integrable wave equations, one can think of studying their solutions for high nonlinearity, for which one has an approximation for turbulence that has been referred to as integrable turbulence (Zakharov 1968, 1999, 2009) (El and Kamchatnov 2005). Such a paradigm, using Riemann theta functions, requires considerable theoretical and numerical development, which we only briefly refer to herein (Osborne 1993, 2010, 2017). In the case of soliton turbulence, the statistical properties of the experimentally measured oceanic wave field are governed by a field of densely packed solitons (Costa et al. 2014).

Herein, we discuss, again from an experimental point of view, a similar highly nonlinear case where the nonlinear statistical properties of the surface wave field are described by densely distributed breather packets, a physical case that we call breather turbulence. The properties of the breather trains are described by the nonlinear modes of the measured wave field found by projecting onto the nonlinear Fourier structure of the nonlinear Schrödinger equation. This projection process is naturally referred to herein as nonlinear Fourier analysis (NLFA) and/or the nonlinear Fourier transform (NLFT). Therefore, for simplicity, we are here referring to the IST (as used in the USA) and FGT (as used in Russia) as the NLFT. A measured wave train is therefore constructible from Riemann theta functions (a kind of nonlinear superposition law) using the natural sine wave and Stokes wave basis functions, and from phase-locked Stokes waves, which are the breather trains themselves.

The problem of developing a nonlinear Fourier theory for random waves influenced by the Stokes wave nonlinearity historically required the additional focused study of the Benjamin-Feir instability (Benjamin and Feir 1967; Zakharov 1968). Given a time series of length T with a significant wave height H_s and peak period T_p one can compute a measure of the BF instability using the Benjamin-Feir parameter for a near Gaussian process in deep water (Osborne 2010) (see also Section 3.4 below):

$$ I_{BF} = \frac{\pi^{5/2}}{g} \frac{H_{s}}{{T}_{p}^{3}}T $$

(1)

An alternative form of I_BF for arbitrary depth is discussed below but it is less transparent in terms of physical wave parameters. This global form of the BF parameter (here “global” refers to an entire time series, not the individual NLFA spectral components themselves, see below) derives from the natural expression used by Yuen and Lake (1982) (see also Osborne (2010) for a discussion in terms of NLFA).

On the contrary the spectral BF parameter (sBF) (Eq. 36 below) characterizes nonlinearity in each component or mode that occurs in a nonlinear random wave train governed by the NLS equation, as seen in Table 1. Thus, the sBF parameter, provided it is small enough for each mode, reduces the NLFT to the linear superposition of sine waves in the random phase approximation, with Gaussian amplitudes. When the sBF parameter is of moderate size, but less than 1, the NLFA consists of a Stokes wave component. The surprise occurs when the sBF parameter is greater than 1: Two Stokes wave components can pair-wise phase lock with each other to form a breather packet: Such a packet is essentially a nonlinear beat. The breather packet is physically characterized by the fact that its amplitude oscillates up and down with a regular period as it propagates. This “breathing time” leads to the idea of the rise time from a quiescent initial state, or half the Fermi-Pasta-Ulam cycle time. This behavior contrasts to that of a linear beat, which is a packet that maintains constant amplitude as it propagates. Thus, the appearance of an extreme wave within a breather packet that has risen to near its maximum amplitude, generally does not remain large for a long period of time because of the breathing cycle. For example, suppose a breather has a rise time of 20 min. Then, we expect the appearance of an exceptionally large wave in a breather packet will occur for only about 3 or 4 min of this time (see examples in Figs. 11 and 12 below). This dynamical behavior thus limits ones exposure to “rogue waves.”

Table 1 There are typically four kinds of nonlinear Fourier “modes” or “components” in the NLFA Spectrum that depend on the spectral BF parameter (Eq. 36)

The formation of extreme waves in a nonlinear sea state with large global I_BF is naturally described by the nonlinear physics of densely packed, large breather states. By now, after developments during the last 20 years, there are several books and hundreds of papers in the literature on this subject (Pelinovsky and Kharif2008; Kharif et al. 2009; Osborne 2010).

A recent report from DNV-GL (Det Norske Veritas - Germanischer Lloyd) provides a recent overview of the use of breathers in offshore engineering (Bitner-Gregersen and Gramstad 2015) and a solid list of additional references: The latter paper is a pioneering work for engineering applications and an important step because it provides a first modern perspective on the application of breather train dynamics to offshore structure and ship design considerations. This report is the beginning of the first departure from the traditional design procedures using Gaussian random waves (with the design wave defined as the 1/1000 wave in the one-in-one-hundred year storm) in over 50 years.

In a previous paper, we have analyzed surface wave data in Currituck Sound and found a robust soliton spectrum that was interpreted as the first experimental evidence for soliton turbulence in low frequency oscillations in shallow water ocean waves (Costa et al. 2014). These results were based on nonlinear Fourier analysis (NLFA) methods at low frequency in the physical regime of the Korteweg-deVries equation.

Here, we use the NLFT to analyze the Currituck Sound data during a storm and in so doing we find robust breather spectra in a number of time series. The breathers are densely packed in the time series and it is thus natural that we give an interpretation in terms of a highly nonlinear dense gas of breather trains that are undergoing strong nonlinear interactions with one another. It is natural to also refer to these dense breather trains as breather turbulence. The nonlinear interactions of breathers result in mutually repulsive forces and so breathers tend to remain well separated, on the average, from one another in a measured time series. This perspective provides a natural physical motivation for designating highly nonlinear sea states as being stationary and ergodic.

The NLFA method allows us to obtain the NLFT of each of the measured time series of about 30 min in length. The wave periods are roughly in the range of 2–3 s, so that a typical time series has about 600–900 waves. The nonlinear Fourier formulation computes the following information:

• (1) Signatures for the different spectral components, including sine waves, NLS Stokes waves and breather packets

• (2) The maximum amplitudes reached by individual breather packets during their lifetimes

• (3) The rise time to maximum amplitude of each packet

• (4) The Stokes wave modulus of each wave component

• (5) The physical shape of each breather packet

• (6) The maximum steepness of each rogue wave candidate

Since the largest central waves of the breather trains at maximum amplitude are often referred to as rogue waves, we provide information about the extreme events in the time series and estimate the rogue wave amplitudes and heights that could occur in Currituck Sound.

We give a brief overview of the Currituck Sound experiment in Section 2. Section 3 is dedicated to a discussion of some important features of nonlinear Fourier analysis. We discuss details of the data set taken during the storm of 4 February 2002 in Currituck Sound in Section 4. Section 5 is dedicated to the analysis of the Currituck Sound data and its interpretation in terms of breather turbulence. Finally, Section 6 gives a summary of the results.

2 Overview of Currituck Sound experiment

The apparatus used in the Currituck Sound experiment was placed near the U. S. Army Corp of Engineers Field Research Facility as shown in the map of Fig. 1 (Long and Resio 2004, 2007). Figure 2 shows the geometry of the directional array used in making the time series measurements. The instrument has the form of two orthogonal linear arrays with a single shared gauge in the middle. Because the array is fully two dimensional, one has 360^∘ directional resolution. Thus, the instrument avoids the 180^∘ ambiguity that occurs for one-dimensional arrays. Each linear-array arm was designed using the methods of (Davis and Regier 1977). The minimum gauge spacing is 0.1 m, implying that the shortest resolvable wave has a length exceeding 0.2 m. Maximum gauge spacing along one arm of the instrument (a degenerate case for wave crests parallel to the arm) is 1.6 m. Reasonably good directional resolution is possible for waves several times this length due to the fact that directional estimates are obtained by cross-spectral phase differences computed between pairs of gauges. Thus, the array only needs to sample a large enough fraction of a wave length to detect a phase difference. Beyond roughly ten times maximum spacing (a wave length of about 16 m or a deep-water frequency of about 0.3 Hz), the resolution degrades to that of a low-resolution directional gauge, capable of estimating only a few of the low moments of a directional distribution function. However, the range of frequencies from 0.3 Hz to 2.8 Hz includes the frequencies of interest in this study, so the array geometry is adequate for our purposes. Prior to deployment, each of the wave rods was statically calibrated along its sensing length to establish a gain and offset for interpretation of its digital output. With the exception of a few tens of centimeters at the tops and bottoms of the wave rods, the response was very linear. The instrument array can be seen on location in Currituck Sound in Fig. 3. Additional details of the instrument can be found in Long and Resio (2004, 2007). A typical power spectrum measured in Currituck Sound is shown in Fig. 4.

Fig. 1

Map of Currituck Sound showing the U. S. Army Engineer Field Research Facility (FRF) pier and the location of the experiment analyzed herein (sled)

Fig. 2

Experimental design for Currituck Sound measurements. Shown are the nine wave resistance gauges (black dots) and their locations: The basic instrument forms a directional antenna

Fig. 3

Photograph of instrument array on location in Currituck Sound in 2.63 m water depth (see map in Fig. 1)

Fig. 4

Power spectrum averaged over nine simultaneous probe measurements at 21:00 of the Currituck Sound storm studied in the present paper on 4 February 2002

3 Overview of nonlinear Fourier analysis

NLFA is a Fourier (spectral) theory of ocean waves in which interacting NLS Stokes waves are the natural basis functions, rather than the traditional Fourier theory of linearly superposed sine waves. NLFA is the exact algebro-geometric solution of the nonlinear Schrödinger (NLS) equation: It is this formulation which is the theoretical basis of NLFA, i. e., “Fourier analysis with Stokes waves.” Some historical background, theoretical formulation, and data analysis methods are given in Osborne (2010) and cited references. The need for a nonlinear Fourier formulation has been recognized since the beginning of modern wave measurements when the Stokes wave nonlinearity was first seen in measured time series. The search for such a method has been long and difficult. It became clear early on (Kinsman 1965) that the paradigm for ocean waves as a linear superposition of sine waves with random phases was quite useful, and this is the approach still most used today. Here, we give an overview of the nonlinear Fourier theory and discusses some of the reasons it too is becoming useful for the study and enhancement of our understanding of nonlinear ocean waves. We now discuss NLFA and its physical and mathematical basis.

3.1 Summary of features of the NLFT

The NLFA algorithm uses nonlinearly interacting Stokes wave basis functions to construct the nonlinear Fourier spectrum of the data. The NLFA method is based on the mathematical physics and basis functions of the nonlinear Schrödinger (NLS) equation. A time series is well known to be approximated by a near-Gaussian random process with significant wave height H_s, spectral peak period T_p, and temporal length T. Deviations from an actual Gaussian process are due to nonlinearities in the physics of ocean waves. Two nonlinear physical effects are important herein: The Stokes wave nonlinearity and the Benjamin-Feir instability. The Stokes wave effect is here formulated as an “operator” that maps solutions of the NLS equation to the actual surface wave elevation. The Stokes operator thus further enhances the nonlinear physical behavior already described by the complexities of the NLS equation. NLS physics is governed by the Benjamin-Feir (BF) instability and is characterized by a global BF parameter. This global modulational parameter is based on NLFA for the NLS equation and is here extended to include near Gaussian time series:

$$I_{BF} = ({\pi^{5/2}}/g){H_{s}}T/{T}_{p}^{3} $$

Near Gaussianity implies I_BF is larger for steeper waves and for narrower bandwidth spectra. The importance of the near Gaussianity assumption is that (1) one insures the physics is near that for ocean waves and that (2) one emphasizes large amplitude modulations, rather than the historically important small-amplitude modulations. The behavior of the nonlinear Fourier components in the nonlinear spectrum depends on the size of I_BF:

• (1) NLFA reduces to the linear superposition of sine waves (a linear Gaussian random process) in the small-amplitude linear limit for I_BF << 1.

• (2) NLFA describes interacting NLS Stokes wave basis functions that are valid for small, but finite-amplitude wave motion for I_BF < 1.

• (3) For sufficiently steep and narrow-banded wave motion, such that I_BF > 1, pairs of NLS Stokes waves can phase lock with each other and form nonlinear beats or breather packets.

• (4) For I_BF >> 1, triples, quadruples and higher NLS Stokes couplings and/or phase locking can occur. These wave packets we refer to as “superbreathers.” Up to now, superbreathers have not been seen in the ocean, but improved numerical methods and remotely sensed wave fields may allow their discovery in future work.

Several observations about the NLFA method can be made:

• (1) The envelope description of ocean waves for the NLS equation, formally developed for small amplitude modulations, is here extended to the near Gaussian, large amplitude case. This means that the wave envelope of ocean waves is a near Rayleigh process and describes large amplitude modulations. This contrasts to the small amplitude modulations studied classically in modulation theory.

• (2) The breather trains are nonlinear packets that “breathe” up and down during their lifetimes, sometimes reaching amplitudes up to ∼3–4 times the carrier wave amplitudea_o of the time series (${a_{o}} = \sqrt {\pi /32} {H_{s}}$ for a Rayleigh process). Here a_o is the average of the modulation envelope of the time series as found by the Hilbert transform.

• (3) The large solutions of the NLS equation can theoretically be very high and consequently the maximum amplitudes of the breather trains must necessarily be limited by wave breaking.

• (4) The rise time or cycle time for a breather to reach the maximum amplitude varies from a few minutes to several hours. It is important to characterize the time scales of potential breather motions to help distinguish linear dispersive wave motion and Stokes wave effects from actual breather dynamics in the ocean.

It may well be that particular data sets of ocean surface waves have sufficiently small BF parameter (with small H_s and/or sufficiently large T_p) such that sine wave and/or NLS Stokes wave basis functions are sufficient to describe their nonlinear dynamics: In this case, breathers do not occur and the nonlinear Fourier decomposition is purely in terms of classical Stokes waves. In the case of the Currituck Sound data, however, we find instead that the BF parameter is typically so great that there are large numbers of breather trains in all of the time series we have analyzed. In many cases, near the peak of the storm, the number of breather trains numbers over one hundred for a time series with a length of about 28 min.

It is therefore natural to think in terms of breather turbulence to describe the nonlinear dynamics of Currituck Sound surface waves: Densely packed breather packets mixing and interacting with one another in a fashion so complex that a nonlinear stochastic description becomes useful. Such a sea state is called a rogue sea, because the large, rare extreme waves that occur at the maximum of the breather packet cycle are often referred to as rogue waves, since these extreme waves substantially exceed those for a Gaussian or Rayleigh distribution. We discuss the occurrence of rogue seas and their impact on the behavior of nonlinear ocean waves, including the determination of the risk level for extreme waves.

3.2 The nonlinear Schrödinger equation

The nonlinear Schrödinger equation can be written in two ways: (1) The “space” NLS equation (sNLS) which is an initial value problem that can be adopted for the analysis of space series and (2) The “time” NLS equation (tNLS) which is a boundary value problem that can be adopted to analyze time series (the main goal of this paper).

The “Space” NLS Equation and its Relation to Space Series Analysis

We here summarize the nonlinear Schrödinger equation, in which we use coefficients valid for arbitrary water depth (see, for example, Zakharov 1968; Hasimoto and Ono 1972; Whitham 1974; Yuen and Lake 1982 and Mei 1983). The sNLS equation is given by

$$ i(\psi_{t}+C_{g}\psi_{x})+\mu\psi_{xx}+\nu|\psi|^{2}\psi= 0 $$

(2)

The sNLS equation solves the Cauchy initial value problem: Given ψ(x,0), then (2) determines the solutions for all space and time ψ(x, t). The constant, real coefficients as a function of the water depth h of the NLS equation are given by

$$\begin{array}{@{}rcl@{}} {C_{g}} \!&=&\! \frac{\partial{\omega_{o}}}{\partial{k_{o}}} = \frac{c}{2} \left[1 + \frac{(1 - {\sigma}_{o}^{2}) k_{o} h}{\sigma_{o}} \right] \end{array} $$

(3)

$$\begin{array}{@{}rcl@{}} \mu \!&=&\! \frac{1}{2} \frac{\partial^{2} \omega_{o}}{\partial{k}_{o}^{2}} = \end{array} $$

(4)

$$\begin{array}{@{}rcl@{}} \!&=&\!- \frac{g}{8 k_{o} \sigma_{o} \omega_{o}} \left\{ \left[ \sigma_{o} - k_{o} h(1 - {\sigma}_{o}^{2}) \right]^{2} + 4 {k}_{o}^{2} h^{2} {\sigma}_{o}^{2} (1 - {\sigma}_{o}^{2}) \right\}\!\\ \nu \!&=&\! - \frac{{k}_{o}^{4}}{2 \omega_{o}} \left( \frac{c}{2\sigma_{o}} \right)^{2} \left\{\frac{1}{{C}_{g}^{2} - gh} \right. \times \\ &&\!\times \left[ 4 c^{2} + 4(1 - {\sigma}_{o}^{2})c C_{g} + gh (1 - {\sigma}_{o}^{2})^{2} \right] + \end{array} $$

(5)

$$\begin{array}{@{}rcl@{}} &&\!+ \left.\frac{(9 - 10{\sigma}_{o}^{2} + 9 {\sigma}_{o}^{4})}{2{\sigma}_{o}^{2}} \right\}\\ {\omega}_{o}^{2} \!&=&\! g k_{o} \sigma_{o} ,\sigma_{o} = \tanh ({k_{o}}h) \end{array} $$

(6)

Here, ω_o and k_o are the carrier frequency and wavenumber, described in more detail below for near Gaussian time series. Here, C_g is the linear group speed of a wave packet. The depth-dependent constant μ is the coefficient of the second-order dispersion term in the NLS (2). The depth dependent constant ν is the coefficient of the cubic nonlinear term in NLS. It is well known that μν > 0 for instabilities to be present (Whitham 1974). This idea will be exploited later to understand the formation of breather trains with regard to the spectral definition for the BF parameter (see Eq. 36 in Section 3.5 below and related text).

The linear phase speed is given by

$$ c = \frac{\omega_{o}}{k_{o}} = \left( \frac{g\sigma_{o}}{k_{o}}\right)^{2} $$

(7)

The NLS equation has the complex envelope solution

$$ \psi (x,t) = A(x,t){e^{- i\omega^{\prime}t + i\phi (x,t)}} $$

(8)

where A(x, t) is the real envelope and ϕ(x, t) is the real phase. Here, ω^′ is the nonlinear Stokes frequency correction. The associated modulated Stokes wave approximation to the free surface elevation is given to second order by

$$ \eta (x,t) = - \frac{\gamma A^{2}}{4 k_{o} \sigma_{o}} + A \left[1 + \frac{C_{g} A \phi_{x}}{\omega_{o}} \right] \cos \theta + $$

(9)

$$+ \frac{C_{g} A_{x}}{\omega_{o}} \sin \theta + \frac{\delta A^{2}}{4 k_{o} \sigma_{o}}\cos 2\theta + \ldots $$

where A = A(x, t) is the real modulation envelope and

$$ \theta = \theta (x,t) = {k_{o}}x - ({\omega_{o}} + \omega^{\prime})t + \phi (x,t) $$

(10)

is the total phase. Here,

$$ {\theta_{o}}(x,t) = {k_{o}}x - {\omega_{o}}t $$

(11)

is the carrier phase and ϕ(x, t) is the modulation phase. The real constants γ, δ are given by

$$ \gamma = \frac{2 \omega_{o} k_{o} C_{g} + (1 - {\sigma}_{o}^{2})gh {k}_{o}^{2}}{gh - {C}_{g}^{2}} $$

(12)

$$ \delta = \frac{(3 - {\sigma}_{o}^{2}){k}_{o}^{2}}{{\sigma}_{o}^{2}} $$

(13)

and the nonlinear, amplitude-dependent Stokes frequency correction is

$$ \omega^{\prime} = \nu \frac{g^{2} \bar{A}^{2}}{4{\omega}_{o}^{2}} $$

(14)

The term − γA²/4k_oσ_o in the free surface elevation (9) corresponds to slow, long wave variations referred to as radiation stress (Longuet-Higgins and Stewart 1960). Radiation stress depresses the mean sea level beneath a packet of surface waves. Note that by virtue of the fact that the dispersion parameter σ_o = σ_o(k_oh) is a function of the depth means that all of the parameters for sNLS depend on depth.

Given that Eq. 9 is a modulated Stokes wave, it is natural to ask the question: Are modulated Stokes waves stable? Will their amplitudes grow to large values after an initial small-amplitude modulation? These were the questions asked by Benjamin and Feir (1967), who found that the Stokes wave is not stable provided that kh > 1.36 (see also Whitham). Only when a Stokes wave is stable, kh < 1.36, can we speak of a wave train which propagates without change of form, maintaining the typical Stokes wave shape with high peaks and shallow troughs. In the unstable region kh > 1.36, the envelope of a Stokes wave train can grow exponentially for small times, as seen in the detailed discussions below. However, the exponential growth eventually slows, reaches a maximum and then decreases: These solutions refer to breather packet dynamics.

As noted above, ψ(x,0) is the initial value of a Cauchy solution of the sNLS equation. The important role of ψ(x,0) in this problem is also reflected by the fact that this function can be thought of as a measured space series and thus the sNLS equation is important for the NLFA of space series. Herein, however, we are primarily interested in the analysis of time series, as discussed in the next section.

The “Time” NLS Equation and its Relation to Time Series Measurements

For the analysis, herein, we seek to analyze the nonlinear Fourier structure of time series. To see how to do this first note that the leading order term for the surface wave elevation in Eq. 9 is given by

$$ \eta (x,t) = {Re} \left\{ {\psi (x,t){e^{i{k_{o}}x - i{\omega_{o}}t}}} \right\} $$

(15)

For data analysis purposes, we will use the full second-order modulated Stokes wave Eq. 64 below. As stated above, Eq. 2 solves the Cauchy initial value problem: Given ψ(x,0) compute ψ(x, t) for all space and time. Given η(x,0), we can use Eq. 9 to compute the surface elevation η(x, t) for all space and time.

But in the analysis of data, herein, we are instead confronted with a time seriesη(0, t) for which theoretically we should be able to compute η(x, t) for all space and time. This later sentence is a statement of a boundary value problem and not the initial value problem just discussed above. How can we construct the boundary value problem from the initial value problem (2) so that we can analyze time series? That is the question we now answer.

To solve this problem, we must first obtain the tNLS equation. Note that at leading order in nonlinearity in Eq. 2, we have

$$ {\psi_{t}} + {C_{g}}{\psi_{x}} \cong 0 $$

(16)

so that ψ_x≅ − ψ_t/C_g and ${\psi _{xx}} \cong {\psi _{tt}}/{C}_{g}^{2}$. When these are used in the higher order terms in (2), we obtain the “time” NLS equation (tNLS):

$$ i({\psi_{x}} + {C}_{g}^{\prime}{\psi_{t}}) + \mu '{\psi_{tt}} + \nu '{\left| \psi \right|^{2}}\psi = 0 $$

(17)

where

$$ {C}^{\prime}_{g} = \frac{1}{C_{g}} $$

(18)

$$ \mu^{\prime} = \frac{\mu}{{C}_{g}^{3}} $$

(19)

$$ \nu^{\prime} = \frac{\nu}{C_{g}} $$

(20)

The inverse scattering transform parameter used to obtain the nonlinear spectrum has the following form:

$$ \rho^{\prime} = \sqrt{\frac{\nu^{\prime}}{2\mu^{\prime}}} = {C_{g}} \sqrt{\frac{\nu}{2\mu}} = {C_{g}}\rho, \quad \rho=\sqrt{\frac{\nu}{2\mu}} $$

(21)

A measured time series η(0, t) is multiplied by ρ^′ before taking the NLFT to obtain the nonlinear spectrum as explained in Section 3.5 below. Solutions to tNLS Eq. 17 are related to solutions of sNLS (2) by the simple transformation

$$\begin{array}{@{}rcl@{}} x \to t, \qquad\quad t \to x, \qquad \rho \to \rho^{\prime}\\ C_{g} \to {C}_{g}^{\prime}, \qquad \nu \to \nu^{\prime}, \qquad \mu \to \mu^{\prime} \end{array} $$

(22)

Thus, the space (2) and time (17) NLS equations are related by a simple change of variables and parameters (22). Physically, the tNLS Eq. 17 solves a boundary value problem: Given the boundary value, ψ(0, t), the space/time dynamics of Eq. 17 determine the solutions over all space and time, ψ(x, t). Equation 17 is thus suitable for the time series analysis of measured wave trains whose assumed behavior is temporal and given by ψ(0, t). We are of course using the fact that a time series is obtained by in situ instrumentation assumed to be located at the spatial position x = 0.

One must be careful in comparing exact solutions of sNLS and tNLS because (1) the equations are only asymptotically similar and (2) the space and time coordinates have been interchanged. This means that if we call solutions of sNLS ψ_S(x, t), then we must call the solutions of tNLS ψ_T(t, x) (note the interchange of x and t). It is only in this sense that we can graphically compare solutions of sNLS and tNLS: ψ_S(x, t) ≈ ψ_T(t, x). If one forgets, for example, to interchange x and t in ψ_T then might conclude that the solutions of the two equations are not comparable.

In the remainder of the paper, we will give mathematical expressions in terms of the Cauchy problem, unless we mention otherwise. The simplicity of the transformation between sNLS and tNLS allows us to do this.

3.3 Overview of the mathematical basis of nonlinear Fourier analysis

NLFA is formally the body of mathematical methods for solving the sNLS Eq. 2 for spatially periodic boundary conditions and the tNLS (17) for temporally periodic boundary conditions. Because of the simple transformation between these two equations, the solutions to NLS are the same within a simple interchange of variables and can be adapted to both equations, with the proviso at the end of Section 3.2. Many of the mathematical methods are from the field of algebraic geometry, see for example (Belokolos et al. 1994). We only briefly note the essential features of the methods here.

The direct NLFT solves an eigenvalue problem and the inverse NLFT is constructed using Riemann theta functions. We first discuss the inverse problem and then the direct problem.

The inverse problem: the Riemann theta functions

It is well known that the NLFT (or as it is referred to in the literature the inverse scattering transform (see Osborne (2010) and references) or finite gap theory (see Belokolos et al. (1994)) solves the tNLS equation for temporally periodic boundary conditions (ψ(x, t) = ψ(x, t + T)) whose solution is given by:

$$ \psi (x,t) = {a_{o}}\frac{{\theta (x,t|\mathbf{\tau} ,{\mathbf{\phi}^ - })}}{{\theta (x,t|\mathbf{\tau} ,{\mathbf{\phi}^ + })}}{e^{i\left( {k^{\prime}x - \omega^{\prime}t} \right)}} $$

(23)

The solution is seen to be a ratio of Riemann theta functions with two different sets of phases ϕ⁻, ϕ⁺ (Kotljarov and Its 1976; Tracy and Chen 1988 and Belokolos et al. 1994). Here, k^′ and ω^′ are the physical Stokes wave corrections to the dispersion relation as computed by algebraic geometry (Osborne 2010). Their meaning is made clearer below. The theta function is defined as the particular multidimensional Fourier series:

$$ \theta(x,t) = \sum\limits_{\mathbf{n} \in \mathbf{Z}^{N}} \theta_{\mathbf{n}} e^{i{\mathbf{n}} \cdot \mathbf{k} x - i \mathbf{n} \cdot \pmb{\upomega} t + i \mathbf{n} \cdot \pmb{\upphi}} $$

(24)

where 𝜃_n = exp [iπn ⋅τn], n is an integer vector of length N, τ is the period (or Riemann) matrix, k is a vector of wavenumbers, ω is a vector of frequencies and ϕ is a vector of NLFA phases. For application purposes, these functions and their numerical computation are discussed in detail in Osborne (2010).

Why would we want to deal with multidimensional, quasiperiodic Fourier series like (24) rather than to use ordinary Fourier series? Basically for two reasons. First, because (24) can be used to solve the tNLS equation exactly for temporally periodic boundary conditions. Second, even though the mathematics is harder than that for linear Fourier series, we can actually do much more from a physical point of view. In the wave dynamics, we can explicitly account for coherent waveforms and their nonlinear interactions. This extends the traditional Fourier approach from “linear superposition of sine waves with random phases” to “nonlinear superposition of Stokes waves and breathers with random phases.”

We see that the ratio of theta functions is the spectral modulation of the solution to the tNLS equation. The dynamics of the surface wave elevation are given to leading order by

$$ \eta (x,t) = Re \left( {a_{o} \frac{{\theta (x,t|\mathbf{\tau} ,{\mathbf{\phi}^{-}})}}{{\theta (x,t|\mathbf{\tau} ,{\mathbf{\phi}^{+}})}}{e^{i\left[ {({k_{o}} + k^{\prime})x - ({\omega_{o}} + \omega^{\prime})t} \right]}}} \right) $$

(25)

The latter expression is a nonlinear superposition law for the nonlinear Fourier modes of the NLS equation. Some details of this approach are given below. Additional mathematical discussion of this spectral solution of the tNLS equation are not of great interest in this document, but can be found in the literature both theoretically (Kotljarov and Its 1976; Tracy and Chen 1988; Belokolos et al. 1994) and numerically (Osborne 2010). What we would like to do here instead is to give an overview as to how Stokes waves arise from this formulation. Consider what happens when we have no modulations in deep water:

$$ \psi (x,t) = a_{o} {e^{- \frac{i}{2}{\omega_{o}}{k}_{o}^{2} {a}_{o}^{2} t}} $$

(26)

This happens because in the absence of modulations

$$ \frac{{\theta (x,t|\mathbf{\tau} ,{\mathbf{\phi}^{-} })}}{{\theta (x,t|\mathbf{\tau} ,{\mathbf{\phi}^{+} })}} = 1 $$

(27)

This means that we have the leading order contribution to the Stokes wave:

$$ \eta (x,t) = {a_{o}}\cos \left[ {{k_{o}}x - ({\omega_{o}} + \omega^{\prime})t} \right] $$

(28)

In this simple case, for deep water, we have: k^′ = 0 and $\omega ^{\prime } = {\omega _{o}}{{k}_{o}^{2}}{{a}_{o}^{2}}/2$. This emphasizes how Stokes waves appear in this spectral formulation, even when there are no modulations. Of course, the full Stokes wave happens when we use ψ(x, t) from Eq. 26 in Eq. 9 (see also Eq. 68 below).

The direct problem: the eigenvalue problem

The spectral eigenvalue problem is the main NLFA tool in this paper and is discussed in some detail in Section 3.5 below. In NLFA we solve a Floquet eigenvalue problem to determine the nonlinear spectrum. This contrasts to the computation of the Fourier series in linear Fourier analysis, which is a simple summation. The use of the eigenvalue problem in integrable nonlinear wave equations is the standard norm and is another reason the NLFA differs from its linear counterpart. The eigenvalue problem used here is not the same as that used in many analyses in science and engineering. This is because the solutions must be temporally periodic, so that in reality, we are solving the so-called Floquet problem (refer to Section 3.5 for more details).

3.4 Linear instability analysis and the modulational dispersion relation

Yuen and Lake (1982) studied the NLS equation intensely, together with a number of other wave equations, to improve understanding of instabilities in deep-water wave trains. Their worked focused, in part, on numerical solutions of the NLS equation with spatially periodic boundary conditions. For linear instability analysis, they considered a small-amplitude modulated sine wave (a carrier) of the following form:

$$ \eta (x,t) = {a_{o}}\left[ {1 + \varepsilon \cos (Kx - {\Omega} t)} \right]\cos \left[ {{k_{o}}x - (\omega_{o}+\omega^{\prime}) t} \right] $$

(29)

The small amplitude modulation is 1 + ε cos(Kx −Ωt) for ε small. Note that the Stokes wave correction, ω^′, is often referred to as a frequency shift (14). Indeed, (28) arises from Eq. 29 for ε = 0. This is just the leading order Stokes wave (higher order terms are given in Eq. 9). Here, K is the modulation wavenumber and Ω(K) is the modulation frequency. In what follows Ω(K) will be first determined by linear instability analysis, in order to examine the small time, exponential growth of the Stokes wave train. For real modulation frequency, the Stokes wave is stable; for imaginary frequency, the Stokes wave is unstable. To determine the modulational dispersion relation Ω(K), we write the small amplitude modulation for small times as

$$\begin{array}{@{}rcl@{}} \psi (x,t) = \left\{ a_{o} + \varepsilon_{+} e^{i{\Omega} t + iK \left( x - \frac{\omega_{o}}{2 k_{o} t} \right)} \right. +\\ +\left. \varepsilon_{+} e^{- i{\Omega} t - iK \left( x - \frac{\omega_{o}}{2 k_{o}t} \right)}\right\} e^{\frac{1}{2}i \omega_{o} {k}_{o}^{2} {a}_{o}^{2} t} \end{array} $$

(30)

Inserting this last equation into the nonlinear Schrödinger Eq. 2 and linearizing gives the modulation dispersion relation, here written in deep water:

$$ {\Omega}^{2} = \frac{{\omega}_{o}^{2}}{{8{k_{o}^{2}}}}\left( {\frac{{{K^{2}}}}{{8{k_{o}^{2}}}} - {k_{o}^{2}}{a_{o}^{2}}} \right){K^{2}} $$

(31)

We see that for an initial Stokes wave train to be stable, we require $K > 2\sqrt {2{k}_{o}^{2}}{a_{o}}$. Furthermore, the expression (31) shows that an initial wave train is unstable to a small amplitude modulation provided that the modulation wavenumber K lies in the wavenumber band $0 < K < 2\sqrt {2 {k}_{o}^{2}}{a_{o}}$. This is because Eq. 31, in this range, gives a frequency which is imaginary so that $e^{- i{\Omega } t}= e^{{\Omega }_{I} t}$ grows exponentially for small time (Ω_I is the imaginary part of the frequency). The wave train is stable if it lies outside this range because the frequency is real so that ${e^{- i{\Omega }_{R} t}}$ is purely oscillatory. Thus, the modulated wave train can undergo exponential growth for early time provided we choose K in the interval $0 < K < 2\sqrt {2 {k}_{o}^{2}}{a_{o}}$ (see Fig. 6 for a graph of Eq. 31).

These results were originally very surprising (Benjamin and Feir 1967) since the authors show that the Stokes wave can be unstable because it can undergo exponential growth from an infinitesimal (arbitrarily small) initial perturbation! The idea of carrying a Stokes wave expansion out to arbitrary order is thus moot, provided that the condition $0 < K < 2\sqrt {2 {k}_{o}^{2}}{a_{o}}$ is met, because precisely computing the Stokes wave out to large order makes no sense if its real destiny is to explode exponentially. Indeed the Benjamin and Fier paper was entitled: The Disintegration of Stokes Waves on Deep Water. Such a drastic outcome for the evolution of a Stokes wave was shocking at the time, a result of linear instability analysis. However, as we see below, NLFA is effectively a kind of nonlinear instability analysis and this leads instead to breather train amplitudes which oscillate up and down in time rather than undergoing indefinite exponential growth.

3.5 The spectral eigenvalue problem

The goal in this section is to discuss the spectral eigenvalue problem for the NLS equation and some of its properties. The solution to this eigenvalue problem lies at the heart of NLFA. For the linear Fourier transform, we solve an integral (implemented as the fast Fourier transform, which is just a Fourier series). For NLFA, we solve the Floquet solution (periodic and antiperiodic boundary conditions) of an eigenvalue problem. We characterize a particular nonlinearity parameter for NLS which is the spectral Benjamin-Feir or modulational instability parameter (see Osborne (2010) for an historical overview). This parameter simultaneously tells us (1) whether the NLS Stokes wave approximation is a good one and (2) how nonlinear each NLS Stokes wave is. We now derive the BF parameter directly from the time NLS (tNLS) eigenvalue problem (Osborne 2010):

$$ {\Psi}_{t} = {\tilde{\mathbf{Q}}} \Psi, \quad {\tilde{\mathbf{Q}}} = \left[ {\begin{array}{ll} { - i\lambda }&u \\ {\sigma_{\pm} {u^{*}}}&{i\lambda } \end{array}} \right], \quad u(0,t) = \rho^{\prime} \psi (0,t) $$

(32)

Here, σ_± = ± 1 and ρ^′ is given by Eq. 21. Note that σ_± = 1 when k_oh < 1.36 and σ = − 1 when k_oh > 1.36, the latter case being applicable to the Currituck Sound data (see Figs. 4, 15–17 for the characteristic parameters of this data set). The present formulation is for the time NLS Eq. 17 (and hence is valid for time series) and as we see on right-hand side of Eq. 32, the input is the complex time series ψ(0, t), whose determination from the surface wave elevation with Hilbert transforms is given in Section 3.10 below. Now, let Ωt = T and get

$$ {\Psi}_{T} = \frac{1}{\Omega} \tilde{\mathbf{Q}} \Psi = \left[ {\begin{array}{ll} { - i\frac{\lambda }{\Omega}}&{\frac{u}{\Omega}} \\ {\sigma \frac{{{u^{*}}}}{\Omega}}&{i\frac{\lambda }{\Omega}} \end{array}} \right]\Psi $$

(33)

so that

$$ {\Psi}_{T} = \left[ {\begin{array}{ll} { - i\zeta }&{\frac{u}{\Omega}} \\ {\sigma \frac{{{u^{*}}}}{\Omega}}&{i\zeta } \end{array}} \right]{\Psi} ,\qquad \zeta = \frac{\lambda}{\Omega} $$

(34)

Now, set ψ(x, t) = 2a_oϕ(x, t) to get the rescaled time series u(0, t) = 2ρ^′a_oϕ(0, t), for which the eigenvalue problem becomes

$$ {{\Psi}_{T}} = \left[ {\begin{array}{ll} { - i\zeta }&{\frac{{2 \rho^{\prime} {a_{o}}\phi }}{\Omega}} \\ {\sigma \frac{{{2 \rho^{\prime} {a_{o}}\phi^{*}}}}{\Omega}}&{i\zeta } \end{array}} \right]{\Psi} , \quad \zeta = \frac{\lambda }{\Omega} $$

(35)

We recognize the spectral BF parameter as being given by

$$ {I_{BF}} = \frac{{2 \rho^{\prime} {a_{o}}}}{\Omega} $$

(36)

This is the BF parameter for general water depth h. Finally, the eigenvalue problem becomes

$$ {\Psi}_{T} = \left[ {\begin{array}{ll} { - i\zeta }&{{I_{BF}}\phi } \\ {\sigma {I_{BF}}{\phi^{*}}}&{i\zeta } \end{array}} \right]{\Psi} , \quad \zeta = \frac{\lambda }{\Omega} $$

(37)

So we now see how to get the spectral BF parameter from the eigenvalue problem for the tNLS equation. The spectral BF parameter I_BF (36) is seen to multiply the time series ϕ(0, t) and is the nonlinear parameter for tNLS dynamics. I_BF depends on the carrier wavenumber k_o and the carrier amplitude a_o, both assumed constant for a particular time series. I_BF also depends on the modulational frequency Ω, so that the each NLFA component has a different I_BF that depends strictly on the modulation frequency Ω. Since time x is just a parameter in the above eigenvalue problem, we might just as well set it to zero, x = 0. This means that we must study the solution to the eigenvalue problem for the input function ψ(0, t) (or equivalently ϕ(0, t)) which is what we call nonlinear time series analysis for the tNLS equation. Thus, (32) is valid for understanding the dynamics of time series. Time series are obtained from local measurements such as wave staffs, resistance gauges, and pressure recorders. Numerical methods for solving the eigenvalue problem are given in Section 3.6 below.

It is now worthwhile discussing the global spectral BF parameter for a time series beginning with Eq. 36. This happens by noting that in deep water, we have $\rho ^{\prime } = C_{g} \rho =\sqrt {2} {\omega _{o}^{3}}/(2 g)$ so that we find

$$ {I}_{BF} = \frac{\sqrt{2}}{g} \frac{{\omega}_{o}^{3} {a}_{o}}{{\Omega}} $$

(38)

This expression uses simpler notation for the data analysis given below. To obtain a global measure of an entire time series, we set Ω = 2πF, F = Δf = 1/T so that Ω = 2πΔf where T is the length of the time series. Then, we have the BF parameter in the form

$$ {I_{BF}} = \sqrt{2} \frac{k_{o} a_{o}}{{\Delta} f/ f_{o}} $$

(39)

This result is ostensibly for problems with small amplitude modulations. However, for ocean waves we can also have large amplitude modulations due to the fact that we have near Gaussian time series which has a Rayleigh envelope for narrow banded spectra. This suggests that we should use the appropriate a_o which is the mean of the envelope function of a Rayleigh distributed random variable. The mean of the envelope of the Rayleigh probability density function is given by (Osborne 2010)

$$ {a_{o}} = \sqrt{\frac{\pi}{2}} \frac{H_{s}}{4} = \sqrt{\frac{\pi}{2}} \sigma $$

(40)

Finally, we have for the BF parameter

$$ {I}_{BF} = \frac{\pi^{5/2}}{g} {f}_{o}^{3} {H_{s}}T $$

(41)

This form for the parameter is obtained by noting that the carrier frequency f_o is just the peak frequency in the spectrum and thus the peak period is T_p = 1/f_o. We prefer the simplicity of this expression (41) for the BF parameter rather than the more general form for arbitrary depth given in Eq. 36. Should one instead prefer to use (36) (together with the general dispersion relation (6) for arbitrary water depth) it is well to keep in mind that for the Currituck Sound data σ_o = tanh(k_oh) = tanh(1.36) ≈ 0.876 which is not too far from the infinite depth case for which σ_o = 1.

It is well to keep in mind that I_BF, as given here, is just a rough estimate of the number of breather trains in a time series. To obtain a precise estimate of I_BF, one must actually take the NLFT of the time series: This means numerically solving the Floquet problem for the eigenvalue problem (32) as discussed in the next section.

3.6 Computation of the nonlinear Fourier transform of a time series

In linear Fourier analysis, we compute a Fourier integral or Fourier series. In nonlinear Fourier analysis, we compute the solution to an eigenvalue problem (32). We here seek an algorithm for solving the eigenvalue problem numerically in order to determine the tNLS spectrum of a time series.

The numerical algorithm

The numerical algorithm is designed to solve the Floquet problem for Eq. 32 by replacing a time series u(0, t) by piecewise constant values u_n at temporal points t_n = nΔt where Δt = T/M, n = 1,2...M. Periodic boundary conditions are assumed so that u(0, t) = u(0, t + T) and therefore u_n = u_{n + M}. The solution of the spectral eigenfunction Ψ(t) in each interval Δt is then obtained by integrating the eigenvalue problem for a constant in a particular interval:

$$ {\Psi} ({t_{n}} + {\Delta} t) = U({u_{n}},{\Delta} t) {\Psi} ({t_{n}}) $$

(42)

where U(u_n,Δt) is the exponential of the trace-vanishing matrix:

$$\begin{array}{@{}rcl@{}} &&\!\!\!U(u) = e^{{\Delta} tQ(\lambda)} = \exp \left[ {\Delta} t\left( {\begin{array}{ll} { - i\lambda }&u \\ {\sigma u*}&{i\lambda } \end{array}} \right) \right] = \\ &&\!\!\!\left( {\begin{array}{ll} {\cosh (\omega {\Delta} t) - \frac{{i\lambda }}{\omega }\sinh (\omega {\Delta} t)}&{\frac{u}{\omega }\sinh (\omega {\Delta} t)} \\ {\frac{{\sigma u*}}{\omega }\sinh (\omega {\Delta} t)}&{\cosh (\omega {\Delta} t) + \frac{{i\lambda }}{\omega }\sinh (\omega {\Delta} t)} \end{array}} \right)\!\\ \end{array} $$

(43)

Here, ω² = σ|u|² − λ² is constant inside an interval Δt. At this point, it is convenient to introduce a four-component field consisting of Ψ and its derivative Ψ^′ with respect to λ:

$$ {\Xi} (t,\lambda ) = \left( {\begin{array}{ll} {\Psi} \\ {{\Psi}^{\prime}} \end{array}} \right) $$

(44)

where Ψ^′ = ∂Ψ/∂λ. It is clear that the field Ξ(t, λ) has a recursion relation

$$ {\Xi} ({t_{n}} + {\Delta} t) = T({u_{n}}){\Xi} ({x_{n}}) $$

(45)

where

$$ T({u_{n}}) = \left( {\begin{array}{ll} {U({u_{n}})}&0 \\ {U^{\prime}({u_{n}})}&{U({u_{n}})} \end{array}} \right) $$

(46)

is a four-by-four matrix and U^′(u_n) = ∂U(u_n)/∂λ is given by the four elements:

$$\begin{array}{@{}rcl@{}} {U^{\prime}_{11}} \!&=&\! i{\Delta} t\frac{{{\lambda^{2}}}}{{{\omega^{2}}}}\cosh (\omega {\Delta} t) - \left( {\lambda {\Delta} t + i + i\frac{{{\lambda^{2}}}}{{{\omega^{2}}}}} \right)\frac{{\sinh (\omega {\Delta} t)}}{\omega}\\ {U^{\prime}_{12}} \!&=&\! - \frac{{u\lambda }}{{{\omega^{2}}}}\left( {{\Delta} t\cosh (\omega {\Delta} t) - \frac{{\sinh (\omega {\Delta} t)}}{\omega}} \right)\\ {U^{\prime}_{21}} \!&=&\! - \frac{{\sigma {u^{*}}\lambda }}{{{\omega^{2}}}}\left( {{\Delta} t\cosh (\omega {\Delta} t) - \frac{{\sinh (\omega {\Delta} t)}}{\omega}} \right)\\ {U^{\prime}_{22}} \!&=&\! - i{\Delta} t\frac{{{\lambda^{2}}}}{{{\omega^{2}}}}\cosh (\omega {\Delta} t) - \left( {\lambda {\Delta} t - i - i\frac{{{\lambda^{2}}}}{{{\omega^{2}}}}} \right)\frac{{\sinh (\omega {\Delta} t)}}{\omega}\\&& \end{array} $$

(47)

Discretizing the field u(0, t) into M steps gives

$$ {\Xi} ({t_{n}}) = \prod\limits_{j = n - 1}^{0} {T({u_{j}}){\Xi} ({t_{o}})} $$

(48)

The monodromy matrix of Floquet theory is then given by

$$ {\mathbf{T}}({t_{o}},\lambda ) = \prod\limits_{j = M}^{0} {U({u_{j}},\lambda )} $$

(49)

The NLFT spectrum, as computed from the monodromy matrix, is now discussed.

Given the above solution of the eigenvalue problem (32) as an exercise in Floquet analysis, one can solve for the tNLS spectrum numerically, the elements of which are given by

The main spectrum

The trace of the monodromy matrix determines the main spectrum eigenvalues. Thus,

$$ \frac{1}{2}Tr{\mathbf{T}} = \frac{1}{2}({T_{11}} + {T_{22}}) = {a_{R}}({t_{o}},\lambda ) = \pm 1 $$

(50)

gives the complex eigenvalues λ_k, k = 1,2,…,2N. The complex eigenvalues are also referred to a points of simple spectrum.

The auxiliary spectrum

The auxiliary spectrum eigenvalues μ_j are found by the relation: T₁₂ = g(t_o, λ) = 0. This expression gives the complex eigenvalues μ_j(x = 0, t_o), j = 1,2,…, N. To compute both the μ_j and their complex conjugates ${\mu }_{j}^{*}$, one can of course use T₁₂ = T₂₁ = 0 to compute the spectrum.

The auxiliary spectrum of the Riemann sheet indices σ _j

The Riemann sheet indices are found from

$$ {\sigma_{k}} = {\left. {\frac{{f(\lambda )}}{{\sqrt{P(\lambda )} }}} \right|_{\lambda = {\mu_{k}}}} = {\left. {\frac{{i {Im} ({T_{11}})}}{{\sqrt{{T}_{12}^{*}{T_{21}} - {{ {Im}}^{2}}({T_{11}})} }}} \right|_{\lambda = {\mu_{k}}}} $$

(51)

These indices tell us on which of the two Riemann sheets of (32) a particular μ_j(x = 0, t_o) function lies.

Spines in the spectrum

The NLFA spectrum provides the information necessary to compute the spectral quantity known as the spines. These are curves in the complex plane with values of λ which insure that the Bloch eigenfunctions are stable, i.e., they do not blow up exponentially fast for certain values of the temporal variable, t (i.e., for arbitrary temporal translations of the Bloch eigenfunctions). The spines are defined by

$$ {Im} [Tr{\mathbf{T}}/2] = 0 \qquad - 2 \leq {Re} [Tr{\mathbf{T}}/2] \leq 2 $$

(52)

Additional analysis reveals that spines typically connect two points of simple spectrum (or even three or four, but this is the rarer case for superbreathers). When two or more points of simple spectrum are connected by a spine, the combination of spectral information is called a nonlinear mode. There are several kinds of nonlinear modes:

• (1) When two points of spectrum are connected by a spine that crosses the real axis, we have a stable sine wave or Stokes wave. One point of spectrum lies in the upper half plane and the other in the lower half plane so that the spine naturally crosses the real axis in this case.

• (2) When the two points of spectrum are connected by a spine that does not cross the real axis, we have two phase-locked unstable NLS Stokes waves referred to as a breather in the spectrum.

• (3) When three or more points of simple spectrum are connected by a spine that does not cross the real axis, we have combinations of phase locked unstable NLS Stokes waves referred to as a superbreather in the spectrum. Figure 5 show examples of spectrum for types (1) and (2) above.

Fig. 5

Inverse scattering transform lambda plane where the NLFA spectrum lives. Shown also are the types of spectrum that can occur. Eigenvalues (points of simple spectrum) are denoted by ×. Spines are lines which connect two points of simple spectrum. When the spine crosses the real (horizontal) axis the mode is a sine wave or NLS Stokes wave. When the spine does not cross the real axis the mode is a breather packet. In the analysis of data (see sections below), we do not graph the lower half plane since it is symmetric with the upper half plane

3.7 The Benjamin-Feir parameter and the physics of the modulational instability

One of the important properties of an unstable wave packet is the modulational frequency known as the growth rate. The growth rate is derived from the modulational dispersion relation by simply taking the square root of Eq. 31:

$$ {\Omega} = i{\omega_{o}}{{k}_{o}^{2}}{{a}_{o}^{2}}\left( {\frac{K}{{2\sqrt{2} {{k}_{o}^{2}}{a_{o}}}}} \right)\sqrt{1 - {{\left( {\frac{K}{{2\sqrt{2} {{k}_{o}^{2}}{{a}_{o}}}}} \right)}^{2}}} $$

(53)

Equation 53 is also the leading order approximation for the modulational dispersion relation for NLFA and this suggests that the BF parameter appropriate for use with NLFA (for the deep water Cauchy initial value problem) is given by

$$ {I_{BF}} = \frac{{2\sqrt{2} {{{k}_{o}^{2}}}{{a}_{o}}}}{{K}} =\frac{{2\sqrt{2} {k_{o}}{a_{o}}}}{{K/{k_{o}}}} = \frac{{\text{steepness}}}{{\text{bandwidth}}} $$

(54)

The wave-steepness-to-bandwidth-ratio is then proportional to I_BF. When I_BF > 1, then the frequency is imaginary in the modulational dispersion relation and the resultant exponential growth can lead to the formation of breather trains. When I_BF < 1, then the frequency is real in the modulational dispersion relation and we have sine waves and NLS Stokes waves. The Eq. 54 is just the imagery part of the modulation frequency: We graph in Fig. 6 the dimensionless form of the modulation frequency ($2{\Omega } /{\omega _{o}}{{k}_{o}^{2}}{{a}_{o}^{2}}$) as a function of the dimensionless wavenumber ($K/2{{k}_{o}^{2}}{a_{o}}$). When the dimensionless wavenumber lies under the graphed curve, the nonlinear modes of the NLS equation are unstable, leading to exponential growth for small time and “rogue waves” or “oscillatory breathers” over long times.

Fig. 6

Modulation diagram for the IST spectrum. The curve is a graph of the dimensionless modulational dispersion relation ($2{\Omega } /{\omega _{o}}{{k}_{o}^{2}}{{a}_{o}^{2}}$) as a function of dimensionless modulation wavenumber $K/2{{k}_{o}^{2}}{a_{o}}$. Any spectral components which have wavenumbers in $0 < K < 2\sqrt {2} {{k}_{o}^{2}}{a_{o}}$ (under the curve) will be modulationally unstable. The particular wavenumber K = 0 corresponds to the peak of the surface wave spectrum (see Fig. 14 below for more details)

Another important property of unstable wave packets is the maximum amplitude of the unstable breather packet with respect to the carrier amplitude (Osborne 2010):

$$ \frac{{{A_{\max}}}}{{{a_{o}}}} = 1 + 2\sqrt{1 - {{\left( {\frac{K}{{2\sqrt{2} {{k}_{o}^{2}}{a_{o}}}}} \right)}^{2}}} $$

(55)

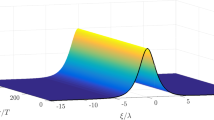
This function is graphed in Fig. 7. When the modulational wavenumber K = 0 and find A_max/a_o = 3. This is the Peregrine breather (see below with regard to Fig. 9 and accompanying text). Figure 7 shows that the largest breather packets occur near modulational wavenumber K = 0, which is near the peak of the surface wave spectrum as seen in Fig. 14. These breathers take a long time to rise up because their rise time is proportional to 1/Ω for Ω << 1.

Fig. 7

Any unstable mode, as defined in Fig. 6, will rise up to a maximum amplitude as described by this curve. We see that a zero modulational wavenumber will rise up by a factor of three. Other types of spectrum corresponding to large amplitude modulations will rise up even higher at some point in their breathing cycle. The enhancement curve in this figure decreases to zero as we move to the right and the left of the spectral peak (see Fig. 14). The enhancement is arbitrarily large for large amplitude modulations as seen in Section 3.8 below

3.8 The classical breathers

There are three classical breather formulas that have been used as convenient tools to understand breather behavior by a wide number of researchers in the field (Pelinovsky and Kharif 2008; Kharif et al. 2009; Osborne 2010). These are seen in Figs. 8, 9, and 10. In Fig. 8 is one of the first breather discovered (Akhmediev et al. 1987). From the figure, we see that the Akhmediev breather begins as a small amplitude modulation and then rises up to an amplitude of 2.414a_o. A second breather is seen in Fig. 9, that of Peregrine (1983), which is also a small amplitude modulation, that rises up to 3.0a_o. One of the more interesting classical breathers is that due to Kuznetsov and Ma [1979] (see Fig. 10). The interesting feature of this breather is that it is born from a large amplitude modulation which then rises up to 3.828a_o. The large amplitude modulations are among the most important of the breathers because they rise significantly higher than the small amplitude modulations and therefore pose greater risk for ships and offshore platforms. Details of these breathers and their formulas can be found in Osborne (2010).

Fig. 8

The space/time evolution of the Akhmediev breather. The vertical axis is the height of the modulation envelope relative to the carrier height, here set to 1. One can see that the maximum height is about 2.41 times the carrier amplitude on the graph. Note that this case is a small amplitude initial modulation, as can be seen by the shape of the surface at t = 0. This breather occurs below the carrier wave in the spectral domain (see Fig. 5)

Fig. 9

The space/time evolution of the Peregrine breather. The vertical axis is the height of the modulation envelope relative to the carrier height, here set to 1. One can see that the maximum height is 3.0 times the carrier amplitude on the graph. Note that this case is also a small amplitude initial modulation, as can be seen by the shape of the surface at t = 0. The Peregrine breather occurs at the height of the carrier wave in the spectral domain (see Fig. 5)

Fig. 10

The space/time evolution of the Kuznetsov-Ma breather. The vertical axis is the height of the modulation envelope relative to the carrier height, here set to 1. One can see that the maximum height is about 3.8 times the carrier amplitude on the graph. Note that this case is a large amplitude initial modulation, as can be seen by the shape of the surface at t = 0. The Kuznetsov-Ma breather occurs above the carrier wave in the spectral domain (see Fig. 5). This means that any wave above the carrier in the spectral domain is outside the class of small amplitude modulations usually studied as the basis of the BF instability. The not-small-initial-amplitude behavior of this breather means that it is a strong candidate for being classified as a rogue wave packet should it appear in a measured time series

From an oceanographic point of view, it is instructive to see how the time series of a breather vary along the direction of propagation as seen in Fig. 11. At the beginning of the propagation, one has a small amplitude modulation of a sine wave which, after propagating 2 km, grows from about 3 m in amplitude up to over 5 m. After 4 km, the breather has reached maximum amplitude near 8 m. Another interesting way to understand breather behavior is seen in Fig. 12 where the largest amplitude of the modulation is followed for a Peregrine breather from its small amplitude modulation near 3 m up to a 9 m maximum after a 20-min time interval. We see that the period of time that the breather is near its maximum is rather small, only 4–6 min out of the total 40-min time interval.

Fig. 11

Evolution of a typical breather packet over 4 km of propagation distance. The upper panel corresponds to a small amplitude modulation of about 3 m in amplitude. The center panel shows the influence of the modulational instability as the initial small amplitude wave train begins to focus and forms a localized packet. The lower panel corresponds to the maximum growth of the initial wave train where the central wave in the packet, after propagating 4 km, has grown from the initial 3-m wave in the upper panel to a wave of almost 8 m in the lower panel. This large wave is often referred to as a rogue wave because it has grown much larger than the initial wave by a factor 7.8/3 = 2.6. The 4-km distance traveled by the breather to rise up to the maximum crest amplitude takes about 8.5 min in the present case

Fig. 12

Time evolution of the maximum amplitude of a Peregrine breather: Initially, the wave train starts as a 3.0-m small amplitude modulation and then rises up, over a 20-min period, to a maximum height of 9 m. It can be seen that the maximum amplitude of the breather during the first 10 min never rises above 4 m. During the subsequent 5 min, the amplitude barely rises above 5 m. Only in the last 5 min does the breather rise to its maximum amplitude of 9 m. Thus, the time evolution of the breather train is such that the largest amplitude is reached for only a small fraction of the breather cycle time, here 40 min

3.9 Modulations for near Gaussian processes

We have seen that the main mathematical results for the modulational instability relate to the small amplitude modulation of a carrier wave which grows exponentially initially, but eventually reaches the maximum amplitude as a large breather state. However, the oceanic wave field is typically a near Gaussian process, not a small amplitude modulation. Furthermore, evidence of a carrier wave is not easily seen by eye as in the simple examples of Figs. 8, 9, and 10. In reality, the wave amplitudes η(0, t) are given approximately by a Gaussian distribution and the real modulational envelope (|ψ(0, t)|) is a Rayleigh distribution for a narrow-banded process (Longuet-Higgins 1952). NLFA, in its spectral structure, requires knowledge of a carrier wave, which for a near Gaussian process is the mean value of the real modulation function〈|ψ(x, t)|〉 (the brackets imply either a space or time average depending on whether we are dealing with a space or time series): This implies that we must find, approximately, the mean of the Rayleigh distribution for a narrow banded process. Given a time series, we can always compute the standard deviation σ. Then, the significant wave height is here defined by

$$ {H_{s}} = 4\sigma $$

(56)

The carrier wave amplitude, for a linear, narrow-banded sea state, is given by the mean of the Rayleigh probability density:

$$ {a_{o}} = \sqrt{\frac{\pi}{2}} \sigma= \sqrt{\frac{\pi}{2}} \frac{{{H_{s}}}}{4} \simeq 1.25331 \sigma \simeq 0.31333{H_{s}} $$

(57)

The first formula (56) is well known and the second formula (57) is based upon the narrow-bandedness and linear assumptions (Osborne 2010). The related auxiliary height is given by ${H_{o}} = 4{a_{o}} =\sqrt {8\pi } \sigma = {\sqrt {\pi /2}}{H_{s}} \simeq 5.01326\sigma \simeq 1.2533{H_{s}}$.

In the data analysis that follows, we compute a_o as the average value of the real envelope function: 〈|ψ(0, t)|〉, where ψ(0, t) is computed from the Hilbert transform of a time series (see Section 3.10).

In the absence of the Rayleigh modulation, we would typically have a small amplitude modulation of a linear/sine wave of amplitude a_o sin2πf_ot, where the frequency f_o corresponds to the peak period T_o = 1/f_o. Physically rogue wave packets rise up from small amplitude modulations, but large amplitude modulations (Section 3.10) can also occur as we now discuss.

In order to compute the ratio of the maximum wave height of a breather to the significant wave height, hear H_max/H_s, one begins with the relation (55) (Osborne 2010):

$$ \frac{{{A_{\max }}}}{{{a_{o}}}} = 1 + 2\frac{{{\lambda_{I}}}}{{{a_{o}}}} $$

(58)

Here, λ_I is the NLFA spectral signature (the mean value of two points of simple spectrum connected by a spine) associated with a breather packet. Also ${a_{o}} = \left ({\sqrt {2\pi } /8} \right ){H_{s}}$ and H_max = 2A_max and one finds

$$ \frac{{{H_{\max}}}}{{{H_{s}}}} = \sqrt{\frac{\pi}{8}} \left( {1 + 2\frac{{{\lambda_{I}}}}{{{a_{o}}}}} \right)\simeq 0.62666\left( {1 + 2\frac{{{\lambda_{I}}}}{{{a_{o}}}}} \right) $$

(59)

On this basis, we note that the Akhmediev breather has H_max = 1.513H_s ($\lambda _{I} = a_{o}/\sqrt {2}$), the Peregrine breather has H_max = 1.880H_s (λ_I = a_o) and the Kuznetsov-Ma breather has H_max = 2.399H_s ($\lambda _{I} = \sqrt 2{a_{o}}$). An interesting question is where does the ratio H_max/H_s exceed 2.0? At λ_I = 1.09576a_o (for which the wave will rise up to 2(λ_I/a_o) + 1 = 3.19152a₀). Where does the ratio H_max/H_s exceed 2.2? At λ_I = 1.25534a_o (for which the wave will rise up to 2(λ_I/a_o) + 1 = 3.51068a_o). One should compare these simple calculations with the usual definition of the design wave in the shipping and oil industries: 1.86 H_s is the 1 in 1000 wave in the 1 in 100 year storm in a linear wave field assumed to be Gaussian. This case corresponds to 2(λ_I/a_o) + 1 = 2.96812a₀. These issues are revisited with regard to the Currituck Sound data analysis in Section 5 below, particularly with regard to Fig. 28 and Table 2 below and describing text.

Table 2 Parameters of the 8 largest breathers in the NLFT spectrum of Fig. 28

At this juncture, it is worth discussing the physics and Fourier analysis of the NLFT with regard to the modulation parameter I_BF. A first observation is that the number of spectral points N in the NLFT spectrum is exactly the same as the number of points in the analyzed time series. This parallels standard Fourier analysis. However, in contrast to standard Fourier analysis, the NLFT spectral components may be sine or Stokes waves, and pairs of Stokes waves may also become phase locked with each other, resulting in breathers. Thus, each breather corresponds to two Stokes waves. The I_BF gives us the number of paired Stokes waves (breathers) in the spectrum. It may at first seem surprising that I_BF depends on the length of the time series. A simple argument tells us why. Given a time series of perhaps 20 min in length, let us suppose that we find 10 breathers. Then, for a time series of 40 min, we would on the average find 20 breathers, provided of course that the sea state meets the stationary, ergodic and homogeneous conditions. But, for a nonlinear system, we are now able to look at wave modes twice as close to the peak of the spectrum, where the really large (but slowly rising) breathers may possibly occur. So, by doubling the length of the time series, one is doubling the amount of energy under consideration and one will certainly capture extra breathers, about twice the number in the original time series.

One should not confuse the parameter I_BF used herein with the Benjamin Feir Index (BFI) in Janssen (2004), where the BFI arises by considering the modulational instability arising from narrow-banded spectra, assuming the relevant modulation period is inversely proportional to the spectral width. On the other hand, I_BF used herein resolves all nonlinear modes in a time series in order to estimate the longest modulation period which is that obtained from the length of the record T. Therefore, breathers with modulation period out to the time T can be found, but longer breathers will naturally be excluded from the analysis. Likewise, one can consider a time series much shorter than T: This means that many of the longer breathers will no longer be resolvable. Indeed a time series that is sufficiently short will be much more linear than a longer time series. How can this be? The longest modulation is that for Δf = 1/T, relative to the peak of the spectrum. A shorter time series will mean that the number of spectral points near the peak of the spectrum will be reduced as Δf = 1/T is increased, thus in effect filtering the spectrum by removing many of the longer breathers. We have not proven these statements here, but they are discussed in detail in Osborne (2010).

3.10 The nonlinear inverse Stokes transformation

We have discussed how the NLFT works: Basically, to determine the nonlinear spectrum of a time series, we need to solve the Floquet problem of the eigenvalue problem (32). But in order to solve the eigenvalue problem, we need to experimentally determine the complex function time series ψ(0, t) that is the input function to the eigenvalue problem. It is clear that ψ(0, t), as a complex function, has both real and imaginary parts, ψ(0, t) = ψ_R(0, t) + iψ_I(0, t). This means that ψ(0, t) consists of two time series, but in reality, we have at our disposal only the measured surface elevation which is a single time series: η(0, t). How are we to determine two time series ψ_R(0, t) and ψ_I(0, t) from only one time series η(0, t)? The answer lies in the expression for the surface elevation in terms of ψ(x, t):

$$ \eta (x,t) = {Re} \left( {\psi (x,t){e^{i({{k_{o}}x - {\omega_{o}} t} )}}} \right) $$

(60)

Thus, the surface elevation is the real part of ψ(x, t) times the carrier oscillation. However, we could also define the imaginary part of the surface wave elevation:

$$ \tilde \eta (x,t) = {Im} \left( {\psi (x,t){e^{i({{k_{o}}x - {\omega_{o}} t} )}}} \right) $$

(61)

We refer to this latter equation as the auxiliary surface elevation. This means that we can now construct a kind of complex surface elevation: ${\Xi }(x,t) = \eta (x,t) + i \tilde \eta (x,t)$. Provided that we could find a way to construct $\tilde \eta (x,t)$ from η, then we might think of inverting (60) and (61) to obtain ψ(x, t). By forming the complex function surface elevation time series

$$ {\Xi} (0,t) = \psi (0,t){e^{- i{\omega_{o}} t}} $$

(62)

we can invert this to give

$$ \psi (0,t) = {\Xi} (0,t){e^{i{\omega_{o}}t}} $$

(63)

This inversion procedure to determine ψ(0, t) from Ξ(0, t) is perfectly adequate provided we have a way to first compute $\tilde \eta (0,t)$ from η(0, t). It is well known that the following relation holds $\tilde \eta (0,t) = H[\eta (0,t)]$, where H[.] is the Hilbert transform (see (Osborne 2010), chapter 13 for additional details). In summary, given the surface elevation time series η(0, t), we compute its Hilbert transform to detemine $\tilde \eta (0,t)$. Then, ψ(0, t) is computed from (63). We then must solve the eigenvalue problem (32) to obtain the NLFT spectrum and it would appear that our job is done as far as defining the data analysis problem for the NLFT. However, that is not the whole story.

To see this note that the modulated Stokes wave Eq. 9, recalling that ψ(x, t) = A(x, t)exp[iϕ(x, t)], can be written for the Cauchy problem as

$$\begin{array}{@{}rcl@{}} {\Xi} &=& \psi Z + \left( {\frac{{3 - {\sigma^{2}}}}{{2{\sigma^{3}}}}} \right)\frac{{{k_{o}}}}{2}{\psi^{2} Z^{2} }+\\ &&- i\frac{1}{{2{k_{o}}}}\left[ {1 + \left( {1 - {\sigma^{2}}} \right)\frac{{{k_{o}}{h_{o}}}}{\sigma }} \right]{\psi_{x}}Z\\ &&+ \frac{{\left[ {2{\omega_{o}}V + (1 - {\sigma^{2}})g{k_{o}}h} \right]}}{{4\sigma \left( {{V^{2}} - gh} \right)}} \psi Z \psi^{*}Z^{*}+\ldots \end{array} $$

(64)

Here, Z = exp[i(k_ox − ω_ot]. Eq. 64 is the Stokes wave field for the complex surface elevation Ξ(x, t) in terms of the modulational solutionψ(x, t) of the NLS equation. The Stokes wave field Eq. 64 and the NLS Eq. 2 have been derived from the Euler equations to the same order of approximation. Equations 2 and 64 are a pair of equations that describe the nonlinear physics of unidirectional ocean waves at the order of the NLS equation. If one continues the derivation from the Euler equations to still higher order, one would determine a modulated Stokes wave at higher order and a wave equation at higher order than the NLS equation.

Note that at leading order in Eq. 64, we have Ξ = ψZ, whose inverse is ψ ≈ΞZ^− 1 which is identical with Eq. 63. If we turn off the modulation by setting $\psi (x,t)=a_{o} e^{-i \omega ^{\prime } t}$, we get the usual Stokes wave, Eq. 68 below (see for example Lamb (1916), (Kinsman 1965)). If we write the complex modulation in terms of its amplitude and phase, ψ(x, t) = A(x, t)exp[iϕ(x, t)], we get Eq. 9, equivalent to Eq. 64.

On the basis of the above discussion, the physics of the surface wave elevation therefore consists of two kinds of nonlinearities: (a) the Stokes wave field (64) and (b) the NLS Eq. 2. We are here simultaneously studying these two kinds of nonlinearity to describe ocean surface waves. It is important to recognize that both effects are to be simultaneously addressed and understood together, as the theory tells us that they are inseparable. We must now understand, in practical terms, how to do this with measured time series.

To this end, a question arises: Can we use Eq. 64 to address the Stokes wave nonlinearity and consider the possibility of removing it from the problem in order to more carefully study the NLS nonlinearity? Our perspective here is to use Eq. 64 as an approach to remove the Stokes up/down antisymmetry in the measured time series. To this end, we write a kind of Stokes operator for dealing with the physics of the Stokes wave effect:

$$ {\Xi}_{\text{NoStokes}} = \hat O^{- 1}_{\text{Stokes}} \Xi, \qquad {\Xi} = \hat O_{\text{Stokes}}{\Xi}_{\text{NoStokes}} $$

(65)

where the Stokes operator, $\hat O_{\text {Stokes}}$, and its inverse, $\hat O^{- 1}_{\text {Stokes}}$, are given by

$$\begin{array}{@{}rcl@{}} \hat{O}_{\text{Stokes}}\!&=&\! {1 + \left( {\frac{{3 - {\sigma^{2}}}}{{2{\sigma^{3}}}}} \right)\frac{{{k_{o}}}}{2}{\Xi} + }\\ &&\!- i\frac{1}{{2{k_{o}}}}\left[ {1 + \left( {1 - {\sigma^{2}}} \right)\frac{{{k_{o}}{h_{o}}}}{\sigma }} \right]\left( {\ln {{[{\Xi} ]}_{x}} - i{k_{o}}} \right) +\\ && \!+ \frac{{\left[ {2{\omega_{o}}V + (1 - {\sigma^{2}})g{k_{o}}h} \right]}}{{4\sigma \left( {{V^{2}} - gh} \right)}} {\Xi}^{*} \end{array} $$

(66)

$$\begin{array}{@{}rcl@{}} \hat{O}^{- 1}_{\text{Stokes}}&=& {1 - \left( {\frac{{3 - {\sigma^{2}}}}{{2{\sigma^{3}}}}} \right)\frac{{{k_{o}}}}{2}{\Xi} + }\\ && + i\frac{1}{{2{k_{o}}}}\left[ {1 + \left( {1 - {\sigma^{2}}} \right)\frac{{{k_{o}}{h_{o}}}}{\sigma }} \right]\left( {\ln {{[{\Xi} ]}_{x}} - i{k_{o}}} \right) +\\ &&- \frac{{\left[ {2{\omega_{o}}V + (1 - {\sigma^{2}})g{k_{o}}h} \right]}}{{4\sigma \left( {{V^{2}} - gh} \right)}} {\Xi}^{*} \end{array} $$

(67)

Note that the difference between the Stokes operator and its inverse are the differences in sign in front of the higher order terms in Eqs. 66 and 67. To leading order, we see that $\hat {O}_{\mathrm {\text {Stokes}}} \hat {O}^{- 1}_{\text {Stokes}}\sim 1$. Thus, the Stokes operator can be viewed as a kind of near identity transformation, whose inverse is found by inverting the signs of the small terms. The operator is therefore asymptotic to the order of the Stokes approximation, but is not an exact relation and can be improved only by extending the order of the modulated Stokes expansion (64) and the NLS Eq. 2 beginning with the Euler equations.

According to Eq. 65, we can remove the Stokes wave effect from the measured complex time series Ξ(t). We now have the complex surface elevation without the Stokes wave effect, ${\Xi }_{\text {NoStokes}}(t) = \hat {O}^{- 1}_{\text {Stokes}} {\Xi }(t)$, which no longer has the up/down antisymmetric form of a Stokes wave, but is now up/down symmetric and is therefore ready to be analyzed in terms of the NLS modulational spectrum by solving the eigenvalue problem (32).

We now need to obtain the complex modulational envelope ψ(0, t) without the Stokes wave effect. This is done by the relation ψ_NoStokes ≈Ξ_NoStokesZ^− 1. We are then ready to solve the eigenvalue problem (32) with ψ_NoStokes(t) as input. We simply remove the higher order Stokes terms from the measured surface wave amplitude and then compute the modulational field from this “Stokesless” surface elevation.

Is the idea of removing the Stokes wave effect from a measured time series reasonable and desirable from a physical point of view? Are indeed the solutions of the Schrödinger equation up/down symmetric? The answers are indeed “yes,” as seen by the following arguments. Let us try inverting the complex envelope: ψ(x, t) ⇒−ψ(x, t). If we insert this change of sign into the NLS equation we find, once again, the NLS equation. This says the solutions of NLS are indeed up/down symmetric and we conclude that the notion of removing the Stokes wave effect is consistent with the solutions of the NLS equation. If for some reason, the resultant wave train as computed from Eq. 65 is not up/down symmetric, then we need to use a higher order Stokes wave, say forth or fifth order, to fully remove the up/down antisymmetry of the Stokes wave from the surface elevation.

3.11 Why is NLFA a theory of Stokes waves?

We have seen that the traditional Stokes wave is a simple reduction of Eqs. 64 and 2 to the unmodulated case $\psi (x,t)=a_{o} e^{-i \omega ^{\prime } t}$, i.e. set A(x, t) = a_o and ϕ(x, t) = 0 in Eq. 9 to get

$$ \eta (x,t) = - \frac{{\gamma {{{a}_{0}^{2}}}}}{{4{k_{o}}\sigma_{o} }} + a_{o} \cos \theta +\frac{{\delta {{{a}_{o}^{2}}}}}{{4{k_{o}}\sigma_{o} }}\cos 2\theta + \ldots $$

(68)

And we have seen that the modulated Stokes wave is given by Eq. 64, whose dynamics is given by NLS (2). Furthermore, we have learned that by first removing the Stokes wave nonlinearity from the surface wave elevation (by the first of Eq. 65), we can determine the NLFT to obtain the nonlinear spectrum for the NLS equation, directly from the Floquet solution of the eigenvalue problem.

We have also discussed that the solution to the NLS equation is written as the ratio of two theta functions as seen in Eq. 23. The latter expression together with (24) can be put in the form of a multidimensional, quasiperiodic Fourier series (Osborne 2017):

$$ \psi(x,t) = \sum\limits_{{\mathbf{n}} \in {\mathbf{Z}^{N}}} {{\psi_{\mathbf{n}}}{e^{i{\mathbf{n}} \cdot {\mathbf{K}} x - i{\mathbf{n}} \cdot \boldsymbol{\Omega}(\mathbf{K}) t + i{\mathbf{n}} \cdot \pmb{\upphi}}}} $$

(69)

Here, the coefficients ψ_n are functions of the parameters τ, K, Ω and ϕ. Thus, the so-called Riemann spectrum is contained in the coefficients ψ_n. Notice that the above equation is a function of the modulational wavenumber K and frequency Ω(K), just as we would expect.

To understand the physics of this expression, let us write the complex surface wave elevation as

$$ {\Xi} (x,t) =\eta(x,t) + i \tilde{\eta}(x,t)= \psi (x,t)Z $$

(70)

where $Z =e^{i{k_{o}}x - i{\omega _{o}}t}$. Then, the quasiperiodic Fourier series has the form:

$$ {\Xi}(x,t) = \sum\limits_{{\mathbf{n}} \in {\mathbf{Z}^{N}}} {{{\Xi}_{\mathbf{n}}}{e^{i{\mathbf{n}} \cdot {\mathbf{k}} x - i{\mathbf{n}} \cdot \pmb{\upomega}(\mathbf{k}) t + i{\mathbf{n}} \cdot \pmb{\upphi}}}} $$

(71)

for which

$$\begin{array}{@{}rcl@{}} {\mathbf{n}}\cdot{\mathbf{k}} &=& {k_{o}} + {\mathbf{n}}\cdot{\mathbf{K}}\\ {\mathbf{n}}\cdot\pmb{\upomega} &=& {\omega_{o}} + {\mathbf{n}}\cdot \boldsymbol{\Omega}({\mathbf{K}}) + \omega^{\prime} \end{array} $$

(72)

These are important relations because they say that the spectrum of the modulational envelope is the same as the Fourier spectrum of the surface elevation, apart from a shift in the spectral domain. This is the shifting theorem of Fourier analysis. The surface elevation spectrum is in terms of of the conventional wavenumber and frequency (k, ω) and is centered about (k_o, ω_o) (the peak of the spectrum) while the modulation spectrum is in terms of the modulational wavenumber and frequency (K,Ω) and the modulational spectrum has its peak centered about zero ((K,Ω) = 0). Further discussion will be given with regard to Fig. 14 below.

Let us return to the solution of Eq. 69 and show that it is a multidimensional, quasiperiodic Fourier series of interacting NLS Stokes waves, the goal of this section. First note that we are excluding the modulated Stokes wave field (64) from this analysis. Instead, in this section we are discussing the actual Stokes wave solutions of the NLS equation. Suppose that we extract terms in Eq. 69 for which the summation vectors n have only a single nonzero component. Terms of this type will have the form

$$ {S_{n}}(x,t) = \sum\limits_{m = - \infty }^{\infty} {{u_{m}^{n}}{e^{im[{k_{n}}x - i[{\omega_{n}}({k_{n}}) + {{\omega^{\prime}}_{n}}]t + i{\phi_{n}}]}}} $$

(73)

These are just the Stokes waves in the NLFT spectrum. Indeed (64) can, to leading order, be easily written:

$$ {\Xi} (x,t) = \sum\limits_{n = 1}^{N} {{S_{n}}(x,t) + {\Xi}_{int} (x,t)} $$

(74)

where Ξ_int(x, t) are pairwise nonlinear interactions among the Stokes waves. Thus, we have Fourier analysis of the NLS equation as a summation of Stokes waves, plus their nonlinear mutual interactions. This is the appropriate perspective about nonlinear Fourier analysis with Stokes waves. The main new feature in the formulation is the surprising appearance of phase-locked Stokes waves that form breathers and superbreathers, as already mentioned above. Details on this phase locking can be found in Osborne (2010).

Let us return to the work of Benjamin and Feir (1967) and Whitham, together with a whole body of literature over the past 50 years to give an overview of the physics of the modulational instability for water waves. What does the full theory say? It says that if one takes a Stokes wave Eq. 68 and nonlinearly modulates it, one will obtain a modulated Stokes wave Eq. 64. If one simultaneously asks the question: What are the dynamics of the modulation? One finds that it is governed by the NLS equation (Eq. 2). The combination of Eqs. 2 and 64 is a dynamical system which tells us the space/time behavior of the surface wave elevation and the modulation of the wave train. If we analyze this system for instabilities using linear instability analysis, we find, for small times, exponential growth in the modulation of a Stokes wave.

If on the other hand we use NLFA to analyze the instability properties for large time, we find that the early exponential growth slows and turns around to give recurrence, i.e., breathing of localized wave packets: We call these phenomena breather trains. Exponential growth at small times gives way to recurrence dynamics for long times and the formation of coherent wave packets. The way to think about the modulation of ocean waves is that it is a very general representation of a near Rayleigh random process governed by the NLS equation. The underlying surface elevation Eq. 64 will be near Gaussian (with a tail due to the Stokes and NLS nonlinearities). If the BF parameter is greater than 1, then the Stokes wave expansion Eq. 64 is unstable and any modulation will grow according to the dynamics of the NLS equation. Therefore, the implication is that any Stokes wave expansion of water waves for which I_BF > 1 is unstable! Therefore, any such Stokes wave in a wave flume will be unstable. This is the remarkable conclusion of Benjamin and Feir who essentially created our modern day understanding about the instabilities of Stokes waves. Today, we understand the problem much more, because we realize that for I_BF > 1, to leading order the disintegration is nothing more than the formation and appearance of nonlinear modes such as breather trains, whose properties are spectral invariants according to NLS evolution. Additional issues occur because of higher order physics, including dissipation and two-dimensional effects, which we will address in future papers (many of these issues are discussed in detail in chapter 29 of Osborne (2010)). The remarkable property of this physics is that even with the presence of instabilities, the NLS equation is perfectly integrable. This raises the ante on the use of the NLFT to clarify the actual nonlinear dynamics in experimental measurements, both in the laboratory and in the ocean. The surprising new features are of course the breathers, their pairwise interactions with other breathers, and recurrence.

3.12 Perspective on how to interpret the NLFA spectrum

Here, we want to show how the NLFT method graphically presents sine waves, NLS Stokes waves and breathers for a particular measured wave train. In practical applications of the NLFA method, all three kinds of spectral components can appear in the same spectrum. Figure 13 shows how this can happen. Generally, the sine waves lie in the tails of the spectrum, Stokes waves occur at intermediate amplitudes and finally the breathers are clustered around the peak. This ranking of the spectral components is quite natural for wave dynamics of the NLS equation and in many data analysis problems, we might expect to see a NLFA spectrum of this type. Of course in a particular situation, we could find very small waves with small BF parameter that would show only sine and Stokes waves, but no breathers. It is unlikely in our opinion that only sine waves would ever appear in an NLFT spectrum.

Fig. 13

Schematic of nonlinear Fourier spectrum for ocean surface waves in the presence of the modulational instability, for a variety of Stokes wave components in the spectrum. The sine waves are the smallest components far to the right and left of the peak (the spines are vertical lines connecting to the frequency axis). The Stokes waves are of intermediate amplitude closer to the peak (see curved spines connecting to the frequency axis). The breather trains occur in a band about the spectral peak, where two points of simple spectrum are directly connected by a spine that does not cross the real axis. A NLFT ocean wave spectrum would not necessarily have the components ordered in exactly this way, but this general perspective is reflected in the analysis of data as seen below

In Fig. 14, we give a summary of many of the features of NLFA which can be important in the analysis of data. Some of these ideas come from linear instability analysis, while others come from the nonlinear instability analysis of NLFA as already discussed above. Figure 14 shows a spectrum with a band of instability (green components) about the peak of the spectrum, the region where the breathers occur. Also shown are three important curves:

• (1) The instability curve of the modulational dispersion relation, the real part of Eq. 53, in shown in blue in Fig. 14 (see also Fig. 6). These curves define not only the width of the unstable region in the spectrum, but also how unstable the particular NLFA modes are. For a particular frequency, the higher the blue curve, the higher is the rate of instability and the faster the unstable modes grow.

• (2) The rise time curves, essentially the inverse of the modulational dispersion relation (1/ |Ω|), are shown in red. This information tells us how long it takes for a particular breather to rise up and how far it propagates in the process. On the average, the unstable modes nearest the peak of the spectrum take much longer to rise up than those further away (while at the same time being in the green unstable band), so the highest breathers nearest the peak may take hours, not minutes, to rise up from a quiescent initial state.

• (3) The amplitude enhancement curves, Equation 55, is in brown. This curve tells us what the maximum height of the breather packets is, for example, 2, 3, or 4 times the carrier amplitude. Note that this curve spans the entire unstable (green) region of the spectrum and that breathers near the peak of the spectrum are the largest. Intuitively, the NLFA components near the peak should be most nonlinear, and the brown curve theoretically demonstrates this. This is the dynamics of the NLS equation.

Fig. 14

Schematic of the Fourier spectrum for ocean surface waves in the presence of the modulational instability, combining ideas from both linear and nonlinear instability analyses discussed herein. The focus of this graph, together with Fig. 13, is to aid the reader in interpreting the nonlinear Fourier transform of the Currituck Sound data given below in Fig. 28. The spectrum is characterized by a central band of components (green) where the modulational instability occurs: This happens naturally because the most nonlinear part of the spectrum lies near the peak and then the nonlinearity subsequently decreases as one moves away from the peak. Thus, breathers tend to occur near the peak, sine waves occur in the tails and the intermediate regions have Stokes waves (see also Fig. 13). The instability diagram (Fig. 6) is shown here as the double lobed curve (blue) centered about the peak of the spectrum: this defines the width of the green band of spectral components where the breathers reside. The rise time or cycle time curves are shown in red: Note that the largest breathers occur near the peak and that they have the largest rise times, so that they come up more slowly than the smaller breathers. The maximum amplitudes of the breather packets are shown in brown: We see that there is an enhancement of the wave amplitudes (see Fig. 7) about the peak of the spectrum, caused by the spatially/temporally dynamically oscillating breather amplitudes there, a result already well known in the field of wind waves where the parameter γ gives a peak enhancement in the JONSWAP spectrum. We see here that it is the modulational instability that causes the enhancement of the spectral peak, normally accounted for in an ad hoc manner by the parameter γ

The I_BF parameter used in this paper is an estimate of the number of breathers in a wave train. This estimate corresponds to the so called zero field approximation for small amplitude modulations as discussed in Tracy and Chen (1988), which is then here treated in the limit of a Gaussian process. How is this estimate for I_BF computed? We recognize that the breathers occur in a band around the peak of the spectrum whose half-width is that of the modulational instability diagram shown in Fig. 6. Breathers occur under the curve of Fig. 6, which corresponds to the double lobe (in blue) of Fig. 14. The center of this double lobe occurs at zero modulational wavenumber (in Fig. 6), here converted to the modulational frequency appropriate for the analysis of time series. This can be seen explicitly in the actual nonlinear Fourier spectrum shown in Fig. 14. The modulational instability diagram of Fig. 6 is graphed both to the right (its actual image) and to the left (the mirror image) of the peak frequency as two blue arcs: We can actually see the double modulational lobe connecting the peak frequency f_o (on the frequency axis) to a red dot to the right, and its image to the red dot on the left. This is the central band of spectrum for which the waves are most nonlinear and hence unstable. Here, the spectral components are indicated by green vertical lines. These are the Stokes waves in the spectrum. We know that Stokes waves pair off to make a breather, so the rule to find the number of breathers in the unstable band is to count the Stokes waves in the green band and divide by 2 to get the number of breathers. This estimate of the number of breathers allows one to a priori guess the number of breathers in a time series from the simple parameters H_s and T_p. However, we note that the actual number of breathers comes from the spectral eigenvalue problem as used to determine the NLFT spectral components. This spectral number of breathers is discussed in detail with regard to the Currituck Sound spectrum shown in Fig. 28 below.

As just discussed, the instability curve gives the band of spectrum over which instabilities happen (blue curve, Fig. 14), i.e., those that initiate phase locking and therefore breather formation by the pair-wise binding of NLS Stokes waves. The rise time curves (red curve, Fig. 14) tell us how long it will take the breathers to “rise up” to their maximum heights. One can see in Fig. 14, the red curve, that the rise time increases for the larger, more energetic breathers. The larger the breathers are, and the closer they are to the peak of the spectrum, the slower they rise up. Thus, a low lying breather might take only 20 min to rise up to its maximum height, while a large breather might take much longer, even an hour or more. The brown curve tells us how high the breathers maximum height will be. We see how this curve acts effectively as an enhancement of the peak of the spectrum: The modulational instability effectively enhances the spectral peak in a “nonequilibrium sea” due to the presence of the modulational instability and the resultant breather dynamics. Oceanographers already know about this effect and take it into account in an ad hoc manner with the well-known parameter called γ in the JONSWAP spectrum. In the present dynamical scenario, the breather part of the spectrum is the theoretical, analytical, and experimental manifestation of the nonequilibrium nature of the sea state that occurs when the BF parameter is large. A future paper will discuss the relationship of γ to I_BF.

3.13 Application to spectral solutions of nonlinear wave equations

Let us briefly give an overview for the solutions of water wave equations in terms of quasiperiodic Fourier series such as Eq. 71, which we write again here:

$${\Xi}(x,t) = \sum\limits_{{\mathbf{n}} \in {\mathbf{Z}^{N}}} {{{\Xi}_{\mathbf{n}}}{e^{i{\mathbf{n}} \cdot {\mathbf{k}} x - i{\mathbf{n}} \cdot \pmb{\upomega}(\mathbf{k}) t + i{\mathbf{n}} \cdot \pmb{\upphi}}}} $$

We are thinking of applications of this series not only to a wide range of nonlinear integrable wave equations such as the KdV, NLS, and KP equations, but also to the Euler equations, the prototypical nonintegrable system. The advantage of a quasiperiodic Fourier series is that it has all infinity harmonics in a particular wave equation and the spectrum consists of a Riemann matrix for which the diagonal elements are Stokes waves and the off-diagonal elements are the pair-wise interactions between Stokes waves. The basic notion is that all nonlinear wave equations with well-defined dispersion relations (which is the case for water waves) must have single modes or degrees of freedom that are Stokes waves (see further discussion in Section 3.11 above). This is a lesson in the study of nonlinear wave equations, first discovered by Stokes for the Euler equations in the mid 1800s. When one treats the case for two degrees of freedom, we find two interacting Stokes waves. For the integrable equations, there is a symmetric 2x2 Riemann matrix whose diagonal elements correspond to Stokes waves and whose off-diagonal elements carry the pair-wise interactions. One also has to include the influence of nonlinearity on the frequency and phase. The influence of nonlinearity on the frequency is just the quadratic correction to the linear dispersion relation, the main result of Stokes, but here generalized to two or more interacting Stokes waves. When the modulational instability occurs, two Stokes waves phase lock and the frequency becomes imaginary, allowing exponential growth in the associated breather train. The influence of the BF instability, which causes strong phase interactions or coupling between two Stokes wave components, is a feature of nonlinear interactions at higher than linear order. Below the modulational threshold, I_BF < 1 (Eq. 36), for a particular NLFT component there are two independent Stokes waves that nonlinearly interact: This means that the sum of two Stokes waves must include a nonlinear interaction term in a kind of nonlinear superposition principle formally given by the theta functions and Eq. 23. But, as the I_BF parameter increases, the two phases are dynamically drawn together and at I_BF = 1 they become locked, so that the two Stokes waves form a coherent waveform or breather. This threshold for the formation of breathers is referred to as the Tracy threshold, after its discoverer (Tracy and Chen 1988). Sea states which substantially exceed the Tracy threshold are referred to as rogue seas.

In traditional numerical spectral models, one uses the FFT to integrate the motion forward in time. For a numerical spectral model, one typically assumes spatially periodic boundary conditions. This assumption results in a standard Fourier series for the wave motion with time-dependent Fourier coefficients, the latter of which are associated with a set of nonlinear ordinary differential equations (odes). One numerically integrates the nonlinear odes (normally with a Runge-Kutta algorithm) and then uses the time varying coefficients in the Fourier series (numerically the FFT) to get the wave motion.

Another type of spectral model follows from Eq. 71 again by assuming spatially periodic boundary conditions, for which we obtain (see chapter 32, Osborne (2010)):

$$ {\Xi} (x,t) = \sum\limits_{n = - \infty }^{\infty} {{{\Xi}_{n}}(t){e^{i{k_{n}}x}}} $$

(75)

$$ {{\Xi}_{n}}(t) = \sum\limits_{\{ {\textbf{n}} \in \mathbf{Z}^{N}: n = L {\textbf{n}}\cdot{\textbf{k}}/2\pi \} } {{{\Xi}_{\textbf{n}}}{e^{- i {\textbf{n}}\cdot \pmb{\upomega}(\mathbf{k}) t + {\textbf{n}}\cdot\pmb{\upphi} }}} $$

(76)

This result says that the wave motion is governed by a spatially periodic Fourier series (75) with time varying Fourier coefficients (76). As just mentioned, these coefficients are governed by a set of nonlinear odes in a standard spectral model. However, in the present model (75, 76), the time-dependent coefficients Ξ_n(t) are themselves quasiperiodic Fourier series that explicitly have the Riemann spectrum, with sine wave, Stokes waves and breather components! Thus, in the new model (75, 76), there is no longer any mystery about the physics hidden in a set of nonlinear odes, because the nonlinear physics is explicitly written in terms of the coherent waveforms of water waves (76).

In the model just given, there is one great advantage: The quasiperiodic Fourier series contains the coherent waveforms such as the Stokes wave and the breathers (76), whereas traditional models do not explicitly retain this information in the nonlinear odes. Therefore, only in the new class of models like that just given above do we actually retain the coherent waveforms as encoded information. One should read (Osborne 2010) (chapter 32) for an overview of this newer method as applied to a shallow water model.

In summary, only in multiply periodic Fourier series can we maintain the spectral information related to the individual Stokes waves, i.e., that information on the diagonal of the Riemann matrix. The off-diagonal elements give the interactions between the pairs of Stokes waves. One therefore concludes that to have the fundamental information about Stokes waves and breathers in the numerical integration of a nonlinear wave equation, one must use the NLFT (75, 76), not traditional spectral methods, to carry out the numerics. In this way, one has at all stages of the computation the Stokes waves and breathers. If such a model would be driven by the wind, then the nonlinear components themselves would have their spectra (Riemann matrix, frequencies, and phases) vary as a function of time. From an initial sea state with small amplitude sine wave components, one would find that as the wind blows the sine waves, especially near the peak of the spectrum, would grow into Stokes waves and with further wind/wave growth the Stokes waves would continue to grow and would eventually begin to phase lock near the peak of the spectrum, creating breathers. A rogue sea would result after sufficient energy has been injected into the sea surface that the NLFT spectrum would be BF unstable over a large band about the peak of the spectrum. In this case, most of the NLFT components in the nonlinear spectrum would be breather trains. We refer to a wind/wave model of this type as a phase resolving model. Traditional wind/wave models use a kinetic equation that does not retain phase information.

3.14 Application to wind/wave models

Typical wind/wave models use the Hasselmann kinetic equation with driving terms (nonlinearity, wind forcing, breaking dissipation, etc.) to compute the four-wave interactions among sine waves. However, in a 3G wave model, one finds that the nonlinear driving term S_nl goes to zero for one-dimensional wave motion: Zakharov and coworkers have written extensively on this result, i.e., that S_nl = 0 in the case of no spreading. This means that there is no Benjamin-Feir instability, even in 1D for 3G models because the nonlinearities are not included! This spells the death of any predictability for the Benjamin-Feir instability in modern 3G models. One cannot even study the one-dimensional problem with a 3G model and find the BF instability. This should not be too surprising because of the nature of the kinetic equation, i.e., that one is dealing only with interacting sine waves.

In order to get the coherent waveforms (Stokes waves, breathers, or super breathers) into a 3G model, one needs to have the capability to couple together sine waves (as a series) to create Stokes waves and then to pairwise couple Stokes waves to obtain breathers. These coherent waveforms are distinct features of higher order nonlinearity. The best way to do this, from a spectral point of view, is with the Riemann theta functions (see Eq. 24). The NLFA spectrum is then the Riemann matrix whose diagonal elements are sine waves or Stokes waves: To form a breather train two Stokes waves must bind together to form a coherent waveform with a 2×2 Riemann matrix. Higher bindings (super breathers) would be 3×3 or 4×4, etc. Thus, one could think of a 3G+ model (or possibility 4G) that would include the BF instability, by using a multiply periodic Fourier series of the type Eq. 71, as derived from Eqs. 23, 24, and 25. A model of this type could be developed, but has not had high priority in the field of wind waves up to now. In such a wind/wave model, one would deal with Stokes wave basis functions instead of sine waves as in the standard kinetic equation.

An alternative approach would be to reformulate the full Boltzmann integration in such a way that the quasiperiodic properties would be retained in the formulation. This approach would provide the full Boltzmann interactions with the coherent waveforms integrated into the formulation and would heavily depend theoretically and numerically on the Riemann theta functions to fully formulate the modulational instability. Formulations of this type would have to rely on the numerical acceleration of the theta functions using methods in Osborne (2010).

3.15 Possible directions of research for wave breaking

We consider the issue of wave breaking from a physical, but qualitative, point of view. We have conducted the preliminary analysis of a breather train solution of the NLS equation while it is initially small in amplitude during its early evolution (middle panel of Fig. 11) and have passed this solution to a computational fluid dynamical (CFD) model (this of course requires the construction of the particle velocity field as input). Then, we observed the breather evolution according to the CFD model. The breather begins to grow according to the small-amplitude physics of the NLS equation and eventually becomes even larger that the NLS equation would predict, due to higher order nonlinearities in the CFD dynamics. Finally, the packet rises to breaking amplitude and, being a deep-water wave, it undergoes behavior consistent with spilling breaker dynamics. Finally, due to the breaking dissipation, the packet drops below the breaking level and it continues its FPU cycle (qualitatively according to the NLS equation), but is slightly reduced in maximum amplitude. After the breaking stage, the packet is still a breather, but in the case studied, with its amplitude, a few percent smaller in the NLFT spectral domain. It appears that after at most a few breathing/breaking cycles, the wave will no longer rise above the breaking level, but will continue its breathing dynamics without further breaking. Thus, the breather concept seems to be robust to wave breaking in the sense just discussed, implying that the breather packet remains phase locked during its evolution. The breaking energy is removed from the maximum breather amplitude and the breather packet NLFT parameters change only slightly. We thus suspect that a nonlinear random wave spectrum would have its maximum breather amplitudes reduced by breaking events. The amazing robustness of the breathers is a conclusion of this preliminary study. Of course, if the breather falls below the Tracy threshold, the breather will fission into two separate Stokes waves. A future paper will provide details of this work.

4 The Currituck Sound data set

We now discuss the Currituck Sound data set that we are analyzing in this paper (Section 2 discusses the instrumentation). An important aspect of this data set is that the instruments were bottom founded and therefore not subject to the wave dynamics themselves, as are for example buoys. The Currituck Sound experiment also does not suffer from an important source of noise for wave staffs on offshore platforms that are subject to interference from structural members. The high resolution in frequency and direction are also important attributes of the instrument and data. While the wave heights are not large in terms of oceanic scales, the periods are small and hence we find large values for the steepness and the BF parameter. We recognize that, in spite of the smaller scale of waves in Currituck Sound, with respect to the North Sea, say, the physics is nevertheless the same as that of waves at larger scales. The importance of this high-resolution data set is its significance for the purposes of understanding the nonlinear physics. Here, we are studying this physics from the point of view of the modulated Stokes wave expansion (64) and the nonlinear Schrödinger Eq. 2: This is the simplest nonlinear modulational model of ocean waves. The fact that this model can be interpreted as a kind of nonlinear Fourier analysis, here exploited fully as the NLFT, is an important aspect of this work.

Figure 15 shows the significant wave height H_s and peak period T_p graphed as a function of time for the duration of the storm on 4 February 2002. The peak of the storm is seen to last for roughly 15 h, from about 15:00 until well past midnight and through the morning hours of the next day. The values graphed in Fig. 15 were obtained from half-hour time series and were averaged over the 9 probes of the experimental apparatus.

Fig. 15

Significant wave height (red) and peak period (black) as a function of time (from midnight) during the Currituck Sound storm of 4 February 2002

Figure 16 shows a graph of the significant wave height H_s and BF parameter I_BF for the storm period in Fig. 15. We see that the BF parameter varies between about 80 and 130, rough indications of the number of breather trains in each of the half-hour time series. This simple computation of I_BF indicates that the data are quite nonlinear, and that there is a large density of breather trains in the data, suggesting a priori an interpretation in terms of breather turbulence, even before the NLFT analysis discussed below. One can see from the figure that away from the peak of the storm I_BF is substantially lower and this suggests that the breather trains will go away in sufficiently low sea states with longer periods.

Fig. 16

The significant wave height and Benjamin-Feir parameter as a function of time (from midnight) during the Currituck Sound storm of 4 February 2002

The steepness values were also found to be rather high, based on H_s and T_p (${S} = \left ({{\pi ^{5/2}}/g} \right ){H_{s}}/{T_{p}^{2}}$), up to 0.17, with some of the individual waves near wave breaking. While the significant wave height varies from about 0.2 m up to over 0.5 m, the peak period ranges from about 1.6 s up to nearly 1.8 s. These relative parameter values ensure that the BF parameter remains large for the duration of the measurements.

5 Nonlinear Fourier analysis of the Currituck Sound data set

The nonlinear Fourier analysis of the Currituck Sound data set is shown in Figs. 17, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, and 28. Because of limited space here, we have elected to analyze only a single time series, but in great detail. We apply the knowledge that we have discussed earlier about the physics of nonlinear waves. We have taken a sample time series from the storm on 4 February 2018, that which was recorded beginning at 21:00. This time series occurs near the peak of the storm and was chosen because it has the largest measured wave height of 114 cm during the storm.

Fig. 17

Time series of 8192 points from Currituck Sound at 21:00 on 4 February 2002. The length of the time series is 1677.72 s = 27.962 min and the discretization interval is 0.2048 s. The standard deviation is σ = 13.7 cm, the significant wave height is H_s = 4σ = 54.7 cm, the peak period is T_p = 2.51 s (spectral average over 9 probes) and the zero crossing period is T_z = 2.38 s, giving 705 zero crossing waves. The blue horizontal lines correspond to the number of standard deviations above and below the zero mean. The largest measured wave amplitude is 86 cm (over six standard deviations tall) and the largest wave height (the same wave) is 114 cm, which corresponds to 2.08H_s

Fig. 18

Histogram of positive wave amplitudes (normalized by the standard deviation) compared to a Gaussian probability density function for the Currituck Sound time series at 21:00 on 4 February 2002. Statistics were obtained from all nine probes (12,288 points in each time series) in the instrument array, with a total of 110,592 amplitudes included in the histogram, of which only the positive values are shown

Fig. 19

Blow up of time series of Fig. 17 which centers about the point interval (3584–4096) to show the largest measured wave with crest height 86 cm and trough of −28 cm and height of 114 cm. The length of this section of the total time series is 104.86 s

Fig. 20

Time series of Fig. 17 after the removal of the low frequency part of the spectrum, whose physics is not described by the NLS equation, but instead by the low frequency soliton dynamics of the Korteweg-deVries equation (Costa et al. 2014). Here, the region of the left-hand power law f^− 1 in the spectrum of Fig. 4 has been removed by a high-pass filter. The standard deviation of the filtered time series is 13.45 cm and significant wave height is 53.8 cm. The largest wave height is 111 cm, corresponding to 2.06H_s

Fig. 21

Time series of Fig. 20 has been expanded about the point interval (3584–4096) to show the largest measured wave at the center, here after the soliton low frequency part of the spectrum has been filtered out of the measured time series of Fig. 17. The length of this section of the total time series is 104.86 s. The largest wave has its crest and trough values shown

Fig. 22

The measured time series of Fig. 17 has been first high-pass filtered (to remove the low frequency oscillations not described by the NLS equation) to obtain the time series of Fig. 20. Then, the inverse nonlinear Stokes operator of Eqs. 65 and 67 has been used to obtain the present time series. Also shown (red) is the modulational envelope $A(0,t) = |\eta (0,t) + i \tilde \eta (0,t)|$ found by the Hilbert transform of the above time series for which the carrier amplitude is a_o = 16.0 cm (see Fig. 24 below for an expanded, detailed view). The significant wave height of this time series is 52.0 cm. The height of the largest wave (labeled 1) is 2.04H_s

Fig. 23

Shown is the phase time series ϕ(0, t) of the complex envelope $\psi (0,t)=A(0,t) \exp [i \phi (0,t)]$ of the Currituck Sound time series shown in Fig. 22

Fig. 24

Time series of Fig. 22 has been expanded about the point interval (3584–4096) to show the largest measured wave at the center. The length of this section of the total time series is 104.86 s

Fig. 25

Time series of Fig. 23 has been expanded about the point interval (3584–4096) to show the modulational phases. The length of this section of the total time series is 104.86 s. This figure should be compared to the packets of Fig. 24. It is instructive to note that the phases have regions of relative constancy beneath some of the large packets, but undergo phase jumps between many packets

Fig. 26

The measured time series of Fig. 17 is first high-pass filtered (to remove the low frequency oscillations not described by the NLS equation) to obtain the time series of Fig. 20 and then the nonlinear Stokes filter (the first of of Eqs. 65 and 67) is used to obtain the time series of Fig. 22. Shown in this figure is the complex envelope function ψ(0, t) = ψ_R(0, t) + iψ_I(0, t) found by the Hilbert transform of Fig. 22 and Eq. 63. ψ_R(0, t) is shown in red and ψ_I(0, t) is shown in blue

Fig. 27

The time series of Fig. 26 has been expanded about the point interval (3584–4096) to show the complex modulation function in detail. The length of this section of the total time series is 104.86 s

Fig. 28

The nonlinear Fourier spectrum for the complex modulation function shown in Fig. 26. This is the actual NLFT spectrum of the Currituck Sound time series. Note that there are two vertical axes. The one on the left is the actual eigenvalue obtained in the computation of the NLFT spectrum and has units of meters. The right-hand vertical axis is dimensionless and is effectively the maximum amplitude of a breather normalized by the carrier amplitude. This means that the actual carrier amplitude is 0.16 m (left vertical axis, see horizontal red line in Fig. 22) and the normalized amplitude is 3 (the normalized amplitude of the Peregrine breather (Fig. 9), see right-hand vertical axis). The actual positions of the three theoretical breathers discussed herein (Akmediev, Peregrine and Ma-Kuznetsov) are shown in blue. Spectral data points above 2.2H_s (there are three of them) are considered to be rogue waves by the definition of (Dean 1990)

Figure 17 shows the time series analyzed with the various methods in this paper. To get a measure of the nonlinear behavior in this time series, we have placed horizontal blue lines that are spaced by a single standard deviation σ, both above and below the zero mean. For crests, we have marked up to over 6σ on the graph and for the troughs, we have labeled down to nearly − 3σ. The largest crest rises to 86 cm, which is 6.3σ. The up-crossing trough just to the left of this peak extends downward to −0.28 m. The actual height of this wave is 114 cm. An expanded view of the wave is shown in Fig.19.

In the time series of Fig. 17, there are a total of 36 wave crests above 3σ, 3 crests above 4σ, and 1 crest above 5σ and 6σ, all suggesting non Gaussian behavior. The fact that there are 6 pairs of crests above 3σ and 2 triples above 4σ, suggests that the large waves are correlated and related to nonlinear packet formation dynamics.

A histogram of the probability density for the positive wave amplitudes is given in Fig. 18, where the Gaussian density function is shown as a solid line. Waves from the 9 probes of the entire array were included in the histogram. We see that there is a substantial tail to the data, considerably above the Gaussian density for wave amplitude/σ greater than about 2.5. An exploded view of the time series about the largest wave is shown in Fig. 19. This wave, due to its very high crest, provides a startling contrast to the other lower waves in the time series. The height of this wave is 2.09 H_s.

Figure 20 shows the measured time series after the low frequency part of the signal has been removed by a high-pass filter. This is consistent with Costa et al. (2014) who argued that the low frequency power law f^− 1 in Fig. 4 can be interpreted as soliton turbulence. While this component of the wave train has been evidently driven energetically by the high frequency waves near the peak of the spectrum, we note that these low frequency waves are small and the energetics of the spectrum are governed by the region around the peak of the spectrum where the dynamics are governed to leading order by the NLS equation. Figure 4 shows the relevant physical parameters of the spectrum, including the peak frequency, the region of relevance at low frequency for the KdV equation and the frequency band about the peak of the spectrum appropriate for the dynamics of the NLS equation. After removing the low frequency content, we note from Fig. 20 that the highest crests have been reduced in amplitude by a few percent and the troughs have been deepened slightly. For example, the largest wave crest is reduced from 85 to 73 cm and the associated trough has been reduced from −27 to −38 cm as indicated in the figure. Thus, the height of the largest wave has been reduced from 114 to 111 cm by the high pass filtering operation. These details are more easily seen in the exploded view of the largest wave shown in Fig. 21. After having removed the low frequency content of the measured data, we are one more step closer to the nonlinear Fourier analysis.

The next step is to remove the Stokes wave nonlinearity from the wave train of Fig. 20. To remove the Stokes component, we use the inverse Stokes operator of Eqs. 65 and 67. The goal is to remove the Stokes wave nonlinearity (which is up/down antisymmetric) from the time series of Fig. 20, so that the resultant time series is up/down symmetric and therefore appropriate for analysis with the NLS eigenvalue problem Eq. 32. Indeed, the resultant time series, given in Fig. 22, has the required up/down symmetry. As pointed out earlier, we must meet the requirement that the physics of the NLS equation has only up/down symmetric wave trains, a requirement for the subsequent NLFT analysis. The up/down symmetry of Fig. 22 contrasts to the original measured time series in Fig. 17 which is up/down antisymmetric, clearly showing the Stokes wave nonlinearity. This sequence of events simply emphasizes the fact that the global Stokes wave nonlinearity and the dynamics of the NLS equation are experimentally separable from each other at the approximation given here. Alternatively, one might say that the wave dynamics, to this order, are governed by a complex NLS equation solution which is then “dressed” after the fact with the Stokes wave nonlinearity via the Stokes operator (the second of Eqs. 65, 66). As will be seen below, the Stokes wave modes of the NLS equation will be evident in the NLFT spectrum discussed in Fig. 28. This is an interesting lesson in nonlinear wave dynamics.

We now take the Hilbert transform of the wave train of Fig. 22 and then apply Eq. 63 to remove the carrier oscillation to obtain the complex envelope (see discussion in Section 3.10). The modulus A(0, t) of the time series, related to the complex modulation ψ(x, t) = A(x, t)exp[iϕ(x, t)], is shown in red in Fig. 22. Figure 23 shows the time series of the complex modulational phase time series ϕ(0, t) obtained from the data in Fig. 22. We have found that there are two types of activity that are apparent in this graph of the phases:

• (1) Clumps of dense points that tend to fall beneath packets in Fig. 22.

• (2) Phase jumps that occur from one packet to the other. The clumps of points suggest the coherent nature of the packets (many of them are actually breathers) and the phase jumps indicate that the phase tends to leap from one value to another as one passes from one wave group to another across the time series of Fig. 22. An expanded view of Fig. 22 is shown in Fig. 24. Here we see the largest wave in the center together with the modulus of the complex envelope which is shown in red.

Figure 25 shows an exploded view of Fig. 23, i.e., of the complex modulation phases centered about the largest wave. The phases of Fig. 25 should be compared to the wave amplitudes of Fig. 24, which has the same time scale. Again we note, and perhaps it is easier to see on the expanded time scale, that the phases under many of the packets tend to remain relatively constant, while there tend to be phase jumps between many of the packets. It may be that such behavior is indicative of nonlinear packet dynamics and suggests that many of the packets are not dispersive in nature, but instead behave coherently.

In Fig. 26, we show the complex envelope ψ(0, t) = ψ_R(0, t) + iψ_I(0, t) obtained from Fig. 22 with Eq. 63. Both the real part ψ_R(0, t) and the imaginary part ψ_I(0, t) are shown. An exploded view of the Fig. 26 is shown in Fig. 27.

We are now ready to obtain the NLFT spectrum of the complex function ψ(0, t) shown in Fig. 26: ψ(0, t) is the input complex function to the eigenvalue problem, Eq. 32, which we use to obtain the NLFA spectrum by the methods of Section 3.6. To this end, finally, the resultant NLFT spectrum of the Currituck Sound time series of 21:00 on 4 February 2002 is graphed in Fig. 28. The horizontal axis is the usual frequency axis in Hertz, while the left-hand vertical axis consists of the NLFT mode amplitudes in meters. The right-hand vertical axis shows the maximum breather amplitudes normalized by the carrier amplitude. For a particular breather mode in the graph, one can therefore instantly read off its maximum amplitude on the right-hand vertical scale.

We first discuss the least energetic modes in the spectrum of Fig. 28. The small nonlinear modes near the frequency axis can be identified by a red dot (point of simple spectrum) with a spine (thin black line) dropping to the frequency axis. These latter are small NLS sine and Stokes waves. When two red dots (again, points of simple spectrum) are connected by a spine (thin black curve, not crossing the real axis), we have the spectral signature of a small breather. A close inspection of the graph indicates that there are quite a number of these small amplitude breathers in the lower part of the graph near the frequency axis. A small box on the lower left shows simple pictograms for these simple modes.

The most important and energetic nonlinear modes in Fig. 28 are the NLFT modes λ_I above about 0.08 m: These are the red dots corresponding to breather modes that exceed about twice the carrier amplitude, as can be seen on the vertical axis to the right of the graph. For these energetic modes, the two points of simple spectrum are very near each other, so that the spine cannot be seen by eye because it is too short. Modes of this type are called “nearly homoclinic” because they are very close to each other, i.e., they are nearly “double points.” Of course, in real applications of the NLFT, the two points are never double points, but instead they are slightly separated, but this is not seen at graphical resolution. Note that the carrier amplitude a_o = 0.16 m is shown on the graph. Any breather of amplitude a_o has a maximum amplitude of 3a_o, as we have seen in particular for the Peregrine breather. The maximum amplitudes are easily found on the vertical axis on the right, which has these amplitudes on a scale of 1.0–4.0. Note also the positions of the three classical breathers for Akhmediev, Peregrine, and Kuznetsov-Ma that were discussed at length in Section 3.8. Shown in the upper right of Fig. 28 is an example of a breather train: There are arrows that point to examples of breathers in the spectrum. The number of breathers above 2.0a_o (twice the carrier amplitude of a_o= 16.0 cm) is 45, i.e., these are the subset of all the breathers in the spectrum whose maximum amplitudes range from twice to four times the carrier amplitude.

Note the horizontal lines in Fig. 28 for H_max = 2.0H_s and H_max = 2.2H_s, two common values often used to define “rogue waves,” see (Dean 1990). Note also that in Fig. 28, there are three modes above 2.2H_s (3.49a_o) so that we have three rogue waves (by the Dean definition) in the Currituck Sound time series. There are six modes above 1.86H_s (2.97a_o) in the data set. The latter discovery of six modes above 1.86H_s is a significant result, for indeed a linear Gaussian stochastic process has only one of these large waves in a time series of 1000 waves. In the present case for Currituck sound, we have six waves larger than the design height in a time series of 700 waves. Since the factor 1.86H_s is used as the defined size of the design wave for both the oil and shipping industries, the present findings have significant implications on the choice of the design wave for offshore structures and ships, here found for Currituck Sound to have a risk level an order of magnitude higher (about 6(1000/700)= 9) than the chosen industry standard. The fact that the measured data are also from a typical winter storm, not the one-in-one-hundred year storm, suggests also that there would be considerable additional risk should one use the actual one-in-one-hundred year storm.

We now look closely at the eight largest breathers, which rise above 2.7a_o in Fig. 28. These eight waves correspond to the breather packets already marked in Fig. 22, seen there to all lie above three standard deviations. The results are given in Table 2, where a number (left column) is associated with each breather, starting with the largest breather in the NLFT spectrum. These numbers are used to label the breathers in Fig. 22, from which one can directly see the packet amplitudes and heights at the instrument location. From Table 2, we see that the first two breathers have maximum heights that are quite large, 2.5H_s and 2.45H_s. These two packets, as they rise up, will likely be forced into breaking, essentially driven by the BF instability. From the right-hand column, we see that these two packets are due to rise up over periods of 40–60 min and 5–8 km. These are clearly appropriate space and time scales suited to investigation inside Currituck sound, which is about 20-km wide (see Fig. 1). Two of the breathers have close proximity to the carrier wave frequency and therefore take a long time to rise up. These are the two breathers numbered 3 and 8 in Table 2. The long distances and times mean that these waves will never be seen in the basin formed by Currituck Sound, for they are due to rise up only after they impact the far shore. Of the eight breathers in the table, six of them are due to rise to their maximum heights within the confines of Currituck Sound.

The time series analyzed here is 1677.7 s long and the waves at the peak frequency have wavelength of about 8.86 m. The time series have about 687 peak frequency wavelengths, are 6.09 km long based on the phase speed and are 3.59 km long based on the linear group speed of 2.14 m/s. These simple numbers characterize the measurement domain for which Table 2 shows that four of the eight breathers will propagate beyond the length of the time series. This interesting idea provides an estimate of the risk level for the largest breathers outside of the measurement domain, a result not obtainable with linear Fourier analysis.

6 Summary

Traditionally, the linear Fourier transform is used to analyze ocean surface wave data, here a time series η(0, t). A measured wave train is then viewed as a linear superposition of sine waves with random Fourier phases. Such a field is Gaussian in the wave amplitudes and, if sufficiently narrow banded, Rayleigh in its modulational envelope.

The goal of this paper is instead to analyze the surface wave amplitude η(0, t) for nonlinear effects such that coherent waveforms are important in the analysis. We do this by first computing the auxiliary wave field $\tilde \eta (0,t)$, which is the Hilbert transform of η(0, t), yielding the complex surface elevation${\Xi }(0,t)=\eta (0,t)+i \tilde \eta (0,t)$. This function is viewed as analytic in the complex plane because the Hilbert transform guarantees the Cauchy conditions are satisfied. We are then able to compute the complex modulational envelope$\psi (0,t) = {\Xi } (0,t){e^{i{\omega _{o}}t}}$, where ω_o is the carrier or peak spectral frequency of the wave train.

Given the above two complex fields ${\Xi }(0,t)=\eta (0,t)+i \tilde \eta (0,t)$ and ψ(0, t), we apply a method (Osborne 2010) that we call nonlinear Fourier analysis (NLFA) which is based on two sources of nonlinearity in the surface wave field:

• (1) The Stokes wave nonlinearity of the complex surface elevation Ξ(x, t) that is modulated by the complex fieldψ(x, t) (Eq. 64).

• (2) The nonlinear Schrödinger equation which governs the nonlinear dynamics of ψ(x, t) (Eq. 2). We have found that the first type of nonlinearity, that of the globally modulated Stokes wave, can be removed by a particular Stokes operator that we determine (the first of Eqs. 65 and 67).

After removal of the global Stokes wave nonlinearity in a time series, we obtain the up/down symmetric wave train which is governed to leading order by the nonlinear Schrödinger (NLS) equation. The NLS equation can be written as a boundary value problem which we call the tNLS equation (Eq. 17). The associated eigenvalue problem for tNLS (Eq. 32) is referred to as the nonlinear Fourier transform (NLFT), whose spectral structure then provides us with tools to nonlinearly analyze time series. The spectrum of the tNLS equation has three types of nonlinear Fourier components: (1) sine waves, (2) NLS Stokes waves and (3) breather packets (two phase locked NLS Stokes waves).

The NLFT spectrum reduces, in the limit of small amplitude waves, to the linear Fourier transform traditionally used to analyze time series (the FFT). As the wave field grows above this linear state, we find that, in addition to sine waves, Stokes waves began to appear in the spectrum. Further growth in the wave field results in the spontaneous formation of breather states. Thus, the NLFT spans the full range of nonlinearity from sine waves, to NLS Stokes waves to breathers in a natural and continuous way. Sufficiently increasing the global modulational parameter I_BF results in a sea state saturated by breather trains and is often referred to as a rogue sea, further characterized by breather turbulence.

We have applied the above NLFT method to the analysis of Currituck Sound time series measured during a storm on 4 February 2002. Surprisingly, we have found the time series to be energetically dominated by breather trains in the nonlinear spectrum. There are 195 breathers in the time series analysed herein and these nonlinear components contain about 95% of the energy in the spectrum. The breather trains are found to have NLFT phases that are uniformly distributed between 0 and 2π. This fact suggests a stochastic paradigm for these highly nonlinear wave trains: A wave field which is dominated by breather packets that are randomly distributed in their NLFT phases. This nonlinear random phase approximation contains breathers as “coherent waveforms,” the natural nonlinear modes in the formulation, together with the nonlinear pairwise interactions among the breathers.

The energetic dominance of the breather packets and their random phases leads us to the description of ocean waves in Currituck Sound as being characterized by breather turbulence. Breather turbulence at the order of the nonlinear Schrödinger equation is referred to as integrable turbulence because the tNLS equation is exactly integrable by the periodic inverse scattering transform as described herein. This new nonlinear random phase approximation is governed by Eq. 23 where the phases for the breather components are themselves taken to be uniformly distributed random numbers. Future work will determine properties of breather turbulence based on the approximation for the wave motion used herein: The wave field η(x, t) is taken to be a Stokes wave with a complex modulation function ψ(x, t) (Eq. 64), such that ψ(x, t) is a breather-dominated solution of the NLS equation (23) with random NLFT phases.

What are the implications of this new perspective on the nonlinear behavior of ocean surface waves? It means that many of the traditional arguments, based on observing individual waves in a time series, about whether a single wave is a sine wave, Stokes wave or something else, are all mute. Now, we can use modern tools, here mainly the NLFT, to determine what is really happening in a particular time series. No longer will we look at a time series and declare that a particular wave, on the basis of pure opinion, is a breather, Stokes wave, soliton or other kind of nonlinear coherent wave form. Now, we can determine the actual configuration of a nonlinear random sea state without guessing. Such a sea state might be a small amplitude wave train described by the Gaussian random phase approximation with its superposition of sine waves. Or a slightly more energetic sea state might be more complex, such that sine waves and Stokes waves occur together. More energetic near Gaussian sea states might simultaneously have sine waves, Stokes waves, and breathers for their NLFT components. Or we might have cases where primarily breathers dominant the spectrum, such as in Currituck Sound, giving what we might also call a rogue sea condition, because a sea state dominated by breather turbulence is also a precursor of extreme waves (Osborne 2010).

It nevertheless seems clear that we are arriving at a new age of perception about the behavior of energetic nonlinear ocean waves. In our opinion, we are only at the beginning of this new research and of the resultant consequences on our understanding of ocean wave dynamics. Thus, the approach of taking the Fourier transform of a time series and assuming random phases, thus destroying any possible coherency, seems much less desirable. The paradigm of the nonlinear random phase approximation introduced here will provide us with tools for a better understanding of the coherent nature of ocean surface waves. Furthermore, the search for superbreathers in ocean surface waves should have a high priority. Finally, nonlinear Fourier methods for the study of fully two-dimensional wave data must also be pursued.