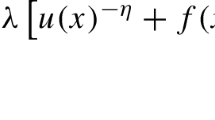Some local properties of subsolution and supersolutions for a doubly nonlinear nonlocal p-Laplace equation

Abstract

We establish a local boundedness estimate for weak subsolutions to a doubly nonlinear parabolic fractional p-Laplace equation. Our argument relies on energy estimates and a parabolic nonlocal version of De Giorgi’s method. Furthermore, by means of a new algebraic inequality, we show that positive weak supersolutions satisfy a reverse Hölder inequality. Finally, we also prove a logarithmic decay estimate for positive supersolutions.

1 Introduction

This work studies the local behavior of subsolutions and supersolutions to the doubly nonlinear parabolic nonlocal problem

$$\begin{aligned} \partial _t(u^{p-1})+\mathcal {L}u=0\text { in }\Omega \times (0,T), \quad p>2, \end{aligned}$$

(1.1)

where $\Omega \subset \mathbb {R}^n$ is a bounded smooth domain, $T>0$ and the operator $\mathcal {L}$ is defined by

$$\begin{aligned} \mathcal {L}u(x,t)=\text {P.V.}\int _{\mathbb {R}^n}|u(x,t)-u(y,t)|^{p-2}(u(x,t)-u(y,t))K(x,y,t)\,dy, \end{aligned}$$

and where P.V. stands for the principal value. We assume that K is a symmetric kernel with respect to x and y satisfying

$$\begin{aligned} \frac{\Lambda ^{-1}}{|x-y|^{n+sp}}\le K(x,y,t)\le \frac{\Lambda }{|x-y|^{n+sp}}, \end{aligned}$$

(1.2)

uniformly in $t\in (0,T)$ for some $\Lambda \ge 1$ and $s\in (0,1)$. If $K(x,y,t)=|x-y|^{-(n+sp)}$, then $\mathcal {L}$ becomes the fractional p-Laplace operator $(-\Delta _p)^{s}$, which further reduces to the fractional Laplacian $(-\Delta )^s$ for $p=2$.

The partial differential equation in (1.1) constitutes a nonlocal counterpart of the doubly nonlinear equation,

$$\begin{aligned} \partial _t(u^{p-1})-\text {div}(|\nabla u|^{p-2}\nabla u)=0. \end{aligned}$$

(1.3)

We refer the reader to [1,2,3,4,5,6,7] and the references therein. To the best of our knowledge, there is no literature available concerning the corresponding nonlocal equation. This paper is a first step toward a regularity theory where we prove a local boundedness estimate for weak subsolutions to (1.1) when $p>2$. To this end, we establish an energy estimate (Lemma 3.1) and apply De Giorgi’s method to obtain our main result (Theorem 2.15). We also prove a reverse Hölder inequality for strictly positive weak supersolutions (Theorem 2.17) by means of a new algebraic inequality (Lemma 2.9) and a logarithmic decay estimate (Lemma 5.3). In particular, Lemma 2.9 generalizes an inequality due to Felsinger and Kassmann for $p=2$, see Lemma 3.3 in [8]. Finally, we note that in the local case as for (1.3), such a reverse Hölder property as well as the logarithmic estimate constitute some of the key ingredients in the proof of weak Harnack inequality, see for instance [4]. To the best of our knowledge, weak Harnack inequality seems to be an open question in the nonlocal case for the doubly nonlinear equation (1.1) and therefore we believe that our results will be important in investigating such question along with further qualitative and quantitative properties of weak solutions to (1.1).

Fractional Laplace equations have been a topic of considerable attention recently. We refer to the survey [9] by Di Nezza, Palatucci and Valdinoci for an elementary introduction to the theory of the fractional Sobolev spaces and fractional Laplace equations. For globally nonnegative solutions of the elliptic fractional Laplace equation $(-\Delta )^s u=0$, Landkof [10] obtained scale-invariant Harnack inequality, which fails for sign-changing solutions as shown by Kassman [11]. Indeed, an additional tail term appears in the Harnack estimate. Di Castro, Kuusi and Palatucci studied local boundedness and H$\ddot{\text {o}}$lder continuity results for the equation $(-\Delta _p)^s u=0$ with $p>1$ in [12]. They also obtained Harnack inequality with a tail dealing with sign-changing solutions in [13]. The nonhomogeneous case $(-\Delta _p)^s u=f$ has been settled for local and global boundedness along with a discussion of eigenvalue problem by Brasco and Parini [14]. Moreover in this case, Brasco, Lindgren and Schikorra established higher and optimal regularity results in [15]. See also [16, 17] and the references therein.

In the parabolic setting, for the fractional heat equation, $\partial _t u+(-\Delta )^s u=0,$ weak Harnack inequality has been established by Felsinger and Kassman in [8], see also [18, 19] for related results. Caffarelli, Chan and Vasseur established boundedness and H$\ddot{\text {o}}$lder continuity results in [20] for different type of kernels. For regularity results up to the boundary, see [21]. Bonforte, Sire and Vázquez established optimal existence and uniqueness results in [22], along with a scale-invariant Harnack inequality for globally positive solutions. For sign-changing solutions, Strömqvist proved Harnack inequality with a tail in [23], see [24] for a different approach.

In the nonlinear framework, we mention the work of Vázquez [25] where global boundedness results for the equation

$$\begin{aligned} \partial _t u+(-\Delta _p)^{s} u=0 \end{aligned}$$

have been obtained. See also [26]. For such an equation, local boundedness result with a tail term has been investigated by Strömqvist in [27]. More recently, H$\ddot{\text {o}}$lder continuity results have been established for the same equation by Brasco, Lindgren and Strömqvist in [28]. In the doubly nonlinear case, Hynd and Lindgren [29] addressed the question of pointwise behavior of viscosity solutions for the following doubly nonlinear equation

$$\begin{aligned} |\partial _t u|^{p-2}\partial _t u+(-\Delta _p)^s u=0. \end{aligned}$$

See also [30, 31] for related results in the local case.

This paper is organized as follows: In Sect. 2, we introduce some basic notations, gather some preliminary results that are relevant to our work and then state our main results. In Sect. 3–5, we prove our main results. Finally, in Sect. 6, appendix, we give a proof of the algebraic inequality in Lemma 2.9 which is applied in the proof of Theorem 2.17.

2 Preliminaries and main results

We first present some facts about fractional Sobolev spaces. For more details we refer the reader to [9].

Definition 2.1

Let $1<p<\infty$ and $0<s<1$ and assume that $\Omega \subset \mathbb {R}^n$ is an open and connected subset of $\mathbb R^n$. The fractional Sobolev space $W^{s,p}(\Omega )$ is defined by

$$\begin{aligned} W^{s,p}(\Omega )=\Big \{u\in L^p(\Omega ):\frac{|u(x)-u(y)|}{|x-y|^{\frac{n}{p}+s}}\in L^p(\Omega \times \Omega )\Big \} \end{aligned}$$

and endowed with the norm

$$\begin{aligned} \Vert u\Vert _{W^{s,p}(\Omega )}=\Big (\int _{\Omega }|u(x)|^p\,dx+\int _{\Omega }\int _{\Omega }\frac{|u(x)-u(y)|^p}{|x-y|^{n+sp}}\,dx\,dy\Big )^\frac{1}{p}. \end{aligned}$$

The fractional Sobolev space with zero boundary values is defined by

$$\begin{aligned} W_{0}^{s,p}(\Omega )={\big \{u\in W^{s,p}(\mathbb {R}^n):u=0\text { on }\mathbb {R}^n\setminus \Omega \big \}}. \end{aligned}$$

Both $W^{s,p}(\Omega )$ and $W_{0}^{s,p}(\Omega )$ are reflexive Banach spaces, see [9]. The parabolic Sobolev space $L^p(0,T;W^{s,p}(\Omega ))$ is the set of measurable functions u on $\Omega \times (0,T)$, $T>0$, such that

$$\begin{aligned} ||u||_{L^p(0,T;W^{s,p}(\Omega ))}=\Big (\int _{0}^{T} ||u(\cdot ,t)||^p_{W^{s,p}(\Omega )}\,dt\Big )^\frac{1}{p}<\infty . \end{aligned}$$

The spaces $W^{s,p}_{\mathrm {loc}}(\Omega )$ and $L^p_{\mathrm {loc}}(0,T;W^{s,p}_{\mathrm {loc}}(\Omega ))$ are defined analogously. Next we discuss Sobolev embedding theorems, see [9]. We write by C to denote a positive constant which may vary from line to line or even in the same line depending on the situation. If C depends on $r_1,r_2,\dots ,r_k$, we write $C=C(r_1,r_2,\dots ,r_k)$.

Theorem 2.2

Let $1<p<\infty$ and $0<s<1$ with $sp<n$ and $\kappa ^{*}=\frac{n}{n-sp}$. For every $u\in W^{s,p}(\mathbb {R}^n)$, we have

$$\begin{aligned} \Vert u\Vert ^p_{L^{\kappa ^{*} p}(\mathbb {R}^n)}\le C\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}\frac{|u(x)-u(y)|^p}{|x-y|^{n+sp}}\,dx\,dy, \end{aligned}$$

for some positive constant $C=C(n,p,s)$. If $\Omega$ is a bounded extension domain for $W^{s,p}$ and $u\in W^{s,p}(\Omega )$, then for any $\kappa \in [1, \kappa ^*]$,

$$\begin{aligned} \Vert u\Vert _{L^{\kappa p}(\Omega )}\le C||u||_{W^{s,p}(\Omega )}, \end{aligned}$$

for some positive constant $C(n,p,s,\Omega )$. If $sp=n,$ then the second inequality hold for any $\kappa \in [1,\infty )$ and for $sp>n$, the second inequality holds for any $\kappa \in [1,\infty ]$ respectively.

The following Sobolev type inequality follows by arguing similarly as in the proof of [27, Lemma 2.1]. We give a brief sketch of the proof below. For $x_0\in \mathbb {R}^n$ and $r>0$, $B_r(x_0)=\{x\in \mathbb R^n:|x-x_0|<r\}$ denotes the ball in $\mathbb {R}^n$ of radius r and center $x_0$. The barred integral sign denotes the corresponding integral average.

Lemma 2.3

Let $1<p<\infty$ and $0<s<1$. Assume that $u\in W^{s,p}(B_r)$, where $B_r=B_r(x_0)$, and let $\kappa ^{*}=\frac{n}{n-sp}$, if $sp<n$, and $\kappa ^{*}=2$, if $sp\ge n$. There exists a constant $C=C(n,p,s)$ such that for every $\kappa \in [1,\kappa ^{*}]$, we have

$$\begin{aligned} \Big (\fint _{B_r}|u(x)|^{\kappa p}\,dx\Big )^\frac{1}{\kappa } \le Cr^{sp-n}\int _{B_r}\int _{B_r}\frac{|u(x)-u(y)|^p}{|x-y|^{n+sp}}\,dx\,dy+C\fint _{B_r}|u(x)|^p\,dx. \end{aligned}$$

Proof

Let $0<s<1$ and $\kappa ^*$ be as given by the hypothesis. Suppose $u\in W^{s,p}(B_1(0))$, then by choosing $\Omega =B_1(0)$ in Theorem 2.2, for every $\kappa \in [1,\kappa ^*]$, we have

$$\begin{aligned} \Big (\int _{B_1(0)}|u(x)|^{\kappa p}\,dx\Big )^\frac{1}{\kappa }\le C\Big (\int _{B_1(0)}\int _{B_1(0)}\frac{|u(x)-u(y)|^p}{|x-y|^{n+sp}}\,dx dy+\int _{B_1(0)}|u(x)|^p\,dx\Big ), \end{aligned}$$

(2.1)

for some positive constant $C=C(n,p,s)$. Using change of variable in (2.1) the result follows. $\square$

Next, we state and prove the parabolic Sobolev inequality, whose proof is similar to the proof of [27, Lemma 2.2].

Lemma 2.4

Let p, s and $\kappa ^{*}$ be as in Lemma 2.3. Assume that $u\in L^p(t_1,t_2;W^{s,p}(B_r))$. There exists a constant $C=C(n,p,s)$ such that for every $\kappa \in [1,\kappa ^{*}]$, we have

$$\begin{aligned}&\int _{t_1}^{t_2}\fint _{B_r}|u(x,t)|^{\kappa p}\,dx\,dt \le C\Bigr (r^{sp-n}\int _{{t_1}}^{{t_2}}\int _{B_r}\int _{B_r}\frac{|u(x, t)-u(y,t)|^p}{|x-y|^{n+sp}}\,dx\,dy\,dt\\&\quad +\int _{t_1}^{t_2}\fint _{B_r}|u(x,t)|^p\,dx\,dt\Bigl )\\&\quad \cdot \Bigl (\sup _{t_1<t<t_2}\fint _{B_r}|u(x,t)|^\frac{p\kappa ^{*}(\kappa -1)}{\kappa ^{*}-1}\,dx\Bigr )^\frac{\kappa ^{*}-1}{\kappa ^{*}}. \end{aligned}$$

Proof

Let $0<s<1$ and $\kappa ^{*}$ be as given by the hypothesis. Using Hölder’s inequality with exponents $\kappa ^{*}$ and $\frac{\kappa ^{*}}{\kappa ^{*}-1}$, for every $\kappa \in [1,\kappa ^*]$, we obtain

$$\begin{aligned} \begin{aligned}&\int _{t_1}^{t_2}\int _{B_r}|u(x,t)|^{\kappa p}\,dx dt\\&\quad =\int _{t_1}^{t_2}\int _{B_r}|u(x,t)|^p |u(x,t)|^{(\kappa -1)p}\,dx dt\\&\quad \le \int _{t_1}^{t_2}\Big (\int _{B_r}|u(x,t)|^{\kappa ^* p}\,dx\Big )^\frac{1}{\kappa ^*}\Big (\int _{B_r}|u(x,t)|^\frac{p\kappa ^*(\kappa -1)}{\kappa ^{*}-1}\,dx\Big )^\frac{\kappa ^{*}-1}{\kappa ^*}\,dt\\&\quad =r^{n-\frac{n}{\kappa ^*}}\int _{t_1}^{t_2}\Big (\int _{B_r}|u(x,t)|^{\kappa ^* p}\,dx\Big )^\frac{1}{\kappa ^*}\,dt\Big (\sup _{t_1<t<t_2}\fint _{B_r}|u(x,t)|^\frac{p\kappa ^*(\kappa -1)}{\kappa ^{*}-1}\,dx\Big )^\frac{\kappa ^{*}-1}{\kappa ^*}. \end{aligned} \end{aligned}$$

(2.2)

We now bound the following term in (2.2),

$$\begin{aligned} \int _{t_1}^{t_2}\Big (\int _{B_r}|u(x,t)|^{\kappa ^* p}\,dx\Big )^\frac{1}{\kappa ^*}\,dt, \end{aligned}$$

using Lemma 2.3 and consequently we obtain,

$$\begin{aligned} \begin{aligned} \int _{t_1}^{t_2}\fint _{B_r}|u(x,t)|^{\kappa p}\,dx dt&\le C\Big (r^{sp-n}\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}\frac{|u(x,t)-u(y,t)|^p}{|x-y|^{n+sp}}\,dx dy dt\\&\quad +\int _{t_1}^{t_2}\fint _{B_r}|u(x,t)|^p\,dx dt\Big )\\&\quad \cdot \Big (\sup _{t_1<t<t_2}\fint _{B_r}|u(x,t)|^\frac{p\kappa ^*(\kappa -1)}{\kappa ^{*}-1}\,dx\Big )^\frac{\kappa ^{*}-1}{\kappa ^*}, \end{aligned} \end{aligned}$$

for some positive constant $C=C(n,p,s)$. This completes the proof. $\square$

We now state the following weighted Poincaré inequality in fractional Sobolev spaces, see [32, Corollary 6].

Lemma 2.5

Let $1<p<\infty$, $0<s_0\le s<1$. Assume that $\phi (x)=\Phi (|x|)$ is a radially decreasing function on $B_1=B_1(0)$. Then there exists a constant $C=C(p,n,s_0,{\phi })$ such that for all $f\in L^p(B_1)$,

$$\begin{aligned} \int _{B_1}|f(x)-f^{\phi }_{B_1}|^p \phi (x)\,dx\le C(1-s)\int _{B_1}\int _{B_1}\frac{|f(x)-f(y)|^p}{|x-y|^{n+sp}}\min \{\phi (x),\phi (y)\}\,dx\,dy, \end{aligned}$$

where

$$\begin{aligned} f_{B_1}^{\phi }=\frac{\int _{B_1}f(x)\phi (x)\,dx}{\int _{B_1}\phi (x)\,dx}. \end{aligned}$$

Using change of variables in Lemma 2.5, we obtain the following weighted Poincaré inequality which will be useful in establishing a logarithmic estimate for weak supersolutions ( see Lemma 5.3).

Lemma 2.6

Let $1<p<\infty$, $0<s<1$ and $\psi (x)=\Psi (|x-x_0|)$ be a radially decreasing function on $B_r=B_r(x_0)$. Then there exists a constant $C=C(n,p,s)$ such that for every $f\in L^p(B_r)$,

$$\begin{aligned} \int _{B_r}|f(x)-f^{\psi }_{B_r}|^{p}\psi (x)\,dx\le Cr^{sp}\int _{B_r}\int _{B_r}\frac{|f(x)-f(y)|^p}{|x-y|^{n+sp}}\min \{\psi (x),\psi (y)\}\,dx\,dy, \end{aligned}$$

where

$$\begin{aligned} {f^{\psi }_{B_r}=\frac{\int _{B_r}f(x)\psi (x)\,dx}{\int _{B_r}\psi (x)\,dx}}. \end{aligned}$$

We also need the following real analysis lemmas. For the proof of Lemma 2.7, see [33, Lemma 4.1].

Lemma 2.7

Let $(Y_j)_{j=0}^{\infty }$ be a sequence of positive real numbers satisfying $Y_{j+1}\le c_0 b^{j} Y_j^{1+\beta }$, for some constants $c_0>1$, $b>1$ and $\beta >0$. If $Y_0\le c_{0}^{-\frac{1}{\beta }}b^{-\frac{1}{\beta ^2}}$, then $\lim _{j\rightarrow \infty }\,Y_j=0$.

The next inequality is as in [12, Lemma 3.1].

Lemma 2.8

Let $p\ge 1$ and $\epsilon \in (0,1]$. Then for every $a,b\in \mathbb {R}^n$, we have

$$\begin{aligned} |a|^p\le |b|^p+C(p)\epsilon |b|^p+\big (1+C(p)\epsilon \big )\epsilon ^{1-p}|a-b|^p, \end{aligned}$$

where $C(p)=(p-1)\Gamma (\max \{1,p-2\})$ and $\Gamma$ denotes the gamma function.

The following elementary inequality will play a crucial role in the proof of reverse H$\ddot{\text {o}}$lder inequality for supersolutions as in Theorem 2.17. A proof for Lemma 2.9 is given in appendix. This generalizes an inequality of Felsinger and Kassmann [8] to the p-case.

Lemma 2.9

Let $a,b>0$, $\tau _1,\tau _2\ge 0$. Then for any $p>1$, there exists a constant $C=C(p)>1$ large enough such that

$$\begin{aligned} \begin{aligned}&|b-a|^{p-2}(b-a)(\tau _1^{p}a^{-\epsilon }-\tau _2^{p}b^{-\epsilon }) \ge \frac{\zeta (\epsilon )}{C(p)}\Big |\tau _2 b^\frac{p-\epsilon -1}{p}-\tau _1 a^\frac{p-\epsilon -1}{p}\Big |^p\\&\quad -\Big (\zeta (\epsilon )+1+\frac{1}{\epsilon ^{p-1}}\Big )\big |\tau _2-\tau _1\big |^p\big (b^{p-\epsilon -1}+a^{p-\epsilon -1}\big ), \end{aligned} \end{aligned}$$

(2.3)

where $0<\epsilon <p-1$ and $\zeta (\epsilon )=\epsilon (\frac{p}{p-\epsilon -1})^p$. If $0<p-\epsilon -1<1$, we may choose $\zeta (\epsilon )=\frac{\epsilon p^p}{p-\epsilon -1}$ in (2.3).

For $v,k>0$, the auxiliary function defined by

$$\begin{aligned} \xi ((v-k)_{+})=\int _{k^{p-1}}^{v^{p-1}}\big (\eta ^\frac{1}{p-1}-k\big )_{+}\,d\eta =(p-1)\int _{k}^{v}(\eta -k)_{+}\eta ^{p-2}\,d\eta , \end{aligned}$$

(2.4)

would be very useful to deduce the energy estimate below. Indeed, from [2, Lemma 2.2], we have the following result.

Lemma 2.10

There exists a constant $\lambda =\lambda (p)>0$ such that for all $v,k>0$, we have

$$\begin{aligned} \frac{1}{\lambda }(v+k)^{p-2}(v-k)_{+}^2\le \xi ((v-k)_{+})\le \lambda (v+k)^{p-2}(v-k)_{+}^2. \end{aligned}$$

For more applications of such functions in the doubly nonlinear context, we refer to [2, 3, 6].

For $t_0\in (r^{sp},T-r^{sp})$, we consider the space-time cylinders

$$\begin{aligned} U^{-}(r)=U^{-}(x_0,t_0,r)=B_r(x_{0})\times (t_0-r^{sp},t_0) \end{aligned}$$

and

$$\begin{aligned} U^{+}(r)=U^{+}(x_0,t_0,r)=B_r(x_0)\times (t_0,t_0+r^{sp}). \end{aligned}$$

We denote the positive and negative parts of u by

$$\begin{aligned} u_{+}(x,t)=\max \{u(x,t),0\} \quad \text {and}\quad u_{-}(x,t)=\max \{-u(x,t),0\}, \end{aligned}$$

respectively. For any $a,b\in \mathbb {R}$, we have $|a_{+}-b_{+}|\le |a-b|$ which implies $u_{+}\in W^{s,p}(\Omega )$ when $u\in W^{s,p}(\Omega )$. Analogously, we have $u_{-}\in W^{s,p}(\Omega )$. Throughout the paper, we denote by

$$\begin{aligned} \mathcal {A}(u(x,y,t))=|u(x,t)-u(y,t)|^{p-2}(u(x,t)-u(y,t)) \quad \text {and}\quad d\mu =K(x,y,t)\,dx\,dy. \end{aligned}$$

It is well known that a tail term appears in nonlocal problems. If u is a measurable function in $\mathbb {R}^n\times (0,T)$ and $x_0\in \mathbb {R}^n$, $r>0$, $0<t_1<t_2<T$, the parabolic tail of u with respect to $x_0$, r, $t_1$ and $t_2$ is defined by

$$\begin{aligned} \mathrm {Tail}_{\infty }(u;x_0,r,t_1,t_2)=\Bigr (r^{sp}{\sup _{t_1<t<t_2}}\int _{\mathbb {R}^n\setminus B_r(x_0)}\frac{|u(x,t)|^{p-1}}{|x-x_0|^{n+sp}}\,dx\Bigl )^\frac{1}{p-1}. \end{aligned}$$

(2.5)

Next we define the notion of weak sub- and supersolution.

Definition 2.11

A function $u\in L^\infty (0,T;L^{\infty }(\mathbb {R}^n))$, with $u>0\text { in }\mathbb {R}^n\times (0,T)$, is a weak subsolution (or supersolution) of the equation (1.1) in $\Omega \times (0,T)$ if $u\in C_{\mathrm {loc}}(0,T;L^p_{\mathrm {loc}}(\Omega ))\cap L^p_{\mathrm {loc}}(0,T;W_{\mathrm {loc}}^{s,p}(\Omega ))$ and for every $\Omega '\times (t_1,t_2)\Subset \Omega \times (0,T)$, and nonnegative test function $\phi \in W^{1,p}_{\mathrm {loc}}(0,T;L^p(\Omega '))\cap L^p_{\mathrm {loc}}(0,T;W_{0}^{s,p}(\Omega '))$, one has

$$\begin{aligned} \begin{aligned}&\int _{\Omega '}u(x,t_2)^{p-1}\phi (x,t_2)\,dx -\int _{\Omega '}u(x,t_1)^{p-1}\phi (x,t_1)\,dx\\&\quad -\int _{t_1}^{t_2}\int _{\Omega '}u(x,t)^{p-1}\partial _t\phi (x,t)\,dx\,dt\\&\quad + \int _{t_1}^{t_2}\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}\mathcal {A}(u(x,y,t)){(\phi (x,t)-\phi (y,t))}\,d\mu \,dt\le 0\quad (\text {or } \ge 0) \end{aligned} \end{aligned},$$

(2.6)

respectively.

Remark 2.12

The assumption $u\in L^\infty (0,T;L^{\infty }(\mathbb {R}^n))$ ensures that the last term in the left-hand side of (2.6) and $\mathrm {Tail}_{\infty }(u;x_0,r,t_1,t_2)$ defined by (2.5) are finite for every $x_0\in \mathbb {R}^n$ and every $0<t_1<t_2<T$.

Remark 2.13

Moreover, we would like to emphasize that the global boundedness assumption $u\in L^\infty (0,T;L^{\infty }(\mathbb {R}^n))$ in Definition 2.11 can be replaced with the local boundedness assumption $u\in L^\infty _{\mathrm {loc}}(0,T;L^{\infty }_{\mathrm {loc}}(\mathbb {R}^n))$ together with the boundedness of $\mathrm {Tail}_{\infty }(u;x_0,r,t_1,t_2)$ defined by (2.5), for every $x_0\in \mathbb {R}^n$ and every $0<t_1<t_2<T$. Furthermore, the hypothesis $\phi _t\in L^p_{\mathrm {loc}}(0,T;L^p(\Omega '))$ in Definition 2.11 can be replaced with $\phi _t\in L^1_{\mathrm {loc}}(0,T;L^1(\Omega '))$.

Remark 2.14

To establish energy estimates for weak subsolutions or supersolutions of (1.1), we choose test functions $\phi$ that depend on the weak subsolution or supersolution itself and thus $\phi _t$ may not exist as a $L^{p}$ function as opposed to what Definition 2.11 requires. This aspect can, however, be rectified by using the following mollification in time,

$$\begin{aligned} f_h(x,t)=\frac{1}{h}\int _{0}^{t}e^{\frac{s-t}{h}}f(x,s)\,ds, \end{aligned}$$

(2.7)

combined with a limiting argument, i.e., by eventually letting $h \rightarrow 0$. See for instance the proof of Lemma 3.1. For more details on such a mollification, we refer to [2, 34].

2.1 Statement of the main results

Below, we state our main results. Our first main result is following local boundedness estimate for subsolutions.

Theorem 2.15

Let $p>2$, $x_0\in \mathbb {R}^n$, $r>0$ and $t_0\in (r^{sp},T)$. Assume that $u\in L^\infty (0,T;L^\infty (\mathbb {R}^n)) \cap C_{\mathrm {loc}}(0,T;L^p_{\mathrm {loc}}(\Omega ))\cap L^p_{\mathrm {loc}}(0,T;W_{\mathrm {loc}}^{s,p}(\Omega ))$ is a weak subsolution of (1.1) in $\Omega \times (0,T)$ such that $U^-(r)=U^-(x_0,t_0,r)=B_r(x_0)\times (t_0-r^{sp},t_0)\Subset \Omega \times (0,T)$ with $u>0\text { in }\mathbb {R}^n\times (t_0-r^{ps},t_0).$ Then there exists a positive constant $C=C(n,p,s,\Lambda )$ such that for any $\delta \in (0,1)$, we have

$$\begin{aligned} \sup _{(x,t)\in U^{-}(\frac{r}{2})}u(x,t) \le C \delta ^{-\frac{(p-1)\kappa }{p(\kappa -1)}}\Big (\fint _{U^{-}(r)}u(x,t)^p\,dx\,dt\Big )^\frac{1}{p}+\delta \,\mathrm {Tail}_{\infty }(u;x_0,\frac{r}{2},t_0-r^{sp},t_0), \end{aligned}$$

where $\kappa =\frac{n+sp}{n}$, if $sp<n$, and $\kappa =\frac{3}{2}$, if $sp\ge n$.

Remark 2.16

One should note that even when $\Omega =\mathbb {R}^n$, Theorem 2.15 will remain valid and the global boundedness assumption on $u\in L^\infty (0,T;L^\infty (\mathbb {R}^n))$ can be replaced by the local boundedness assumption $u\in L^\infty _{\mathrm {loc}}(0,T;L^{\infty }_{\mathrm {loc}}(\mathbb {R}^n))$ together with the boundedness of $\mathrm {Tail}_{\infty }(u;x_0,r,t_1,t_2)$ defined by (2.5), for every $x_0\in \mathbb {R}^n$ and every $0<t_1<t_2<T$.

Our second main result constitutes the following reverse Hölder inequality for positive supersolutions.

Theorem 2.17

Let $p>2$, $x_0\in \mathbb {R}^n$, $r>0$ and $t_0\in (0,T-r^{sp})$. Suppose that $u\in L^\infty (0,T;L^\infty (\mathbb {R}^n))\cap C_{\mathrm {loc}}(0,T;L^p_{\mathrm {loc}}(\Omega ))\cap L^p_{\mathrm {loc}}(0,T;W_{\mathrm {loc}}^{s,p}(\Omega ))$ is a weak supersolution of (1.1) in $\Omega \times (0,T)$ such that $U^+(r)=U^+(x_0,t_0,r)=B_r(x_0)\times (t_0,t_0+r^{sp})\Subset \Omega \times (0,T)$ with $u\ge \rho >0$ in $\mathbb {R}^n\times (t_0,t_0+r^{ps})$. Then for any $\theta \in [\frac{1}{2},1)$ there exists positive constants $\mu =\mu (\kappa ,p)$ and $C=C(n,p,q, s,\Lambda )\ge 1$ such that

$$\begin{aligned} \Big (\fint _{U^{+}(\theta r)}{u(x,t)^{q}\,dx\,dt}\Big )^\frac{1}{q} \le \Big (\frac{C}{(1-\theta )^{\mu }}\fint _{U^{+}(r)}u(x,t)^{\bar{q}}\,dx\,dt\Big )^\frac{1}{\bar{q}}, \end{aligned}$$

(2.8)

for all $0<\bar{q}<q<q_0$ where $q_0=\kappa (p-1)$ with $\kappa =\frac{n+sp}{n},$ if $sp<n$ and $\kappa =\frac{3}{2},$ if $sp\ge n$.

Remark 2.18

We would like to emphasize that the constant C in the reverse Hölder inequality (2.8) is independent of $\bar{q}$ as $\bar{q} \rightarrow 0$ and this is precisely where the algebraic lemma 2.9 plays a crucial role. It is well known that such a stable behavior of the constant C is needed in order to establish the Harnack inequality for local equations using the approach of Bombieri as in [35] (see also [4] for an adaptation of such an idea in the case of (1.3)). We therefore believe that such a reverse Hölder inequality will have similar future applications in the nonlocal case.

3 Energy estimate

To prove Theorem 2.15, we need the following Caccioppoli type estimate for subsolutions.

Lemma 3.1

Let $p>2$, $x_0\in \mathbb {R}^n$, $0<\tau _1<\tau _2$ and $l>0$ with $B_r=B_r(x_0)\Subset \Omega$ and $0<\tau _1-l<\tau _2<T$. Assume that $u\in L^\infty (0,T;L^\infty (\mathbb {R}^n))\cap C_{\mathrm {loc}}(0,T;L^p_{\mathrm {loc}}(\Omega ))\cap L^p_{\mathrm {loc}}(0,T;W_{\mathrm {loc}}^{s,p}(\Omega ))$ is a weak subsolution of (1.1) in $\Omega \times (0,T)$ with $u>0\text { in }\mathbb {R}^n\times (\tau _1-l,\tau _2)$. Let $k>0$ and denote $w(x,t)=(u-k)_{+}(x,t)$. Then there exists a positive constant $C=C(n,p,s,\Lambda )$ such that

$$\begin{aligned}&\int _{\tau _1-l}^{\tau _2}\int _{B_r}\int _{B_r}|w(x,t)\psi (x)-w(y,t)\psi (y)|^p \eta (t)^{p}\,d\mu \,dt\\&\quad +C\sup _{\tau _1<t<\tau _2}\int _{B_r}w(x,t)^p\psi (x)^p\,dx\\&\quad \le \int _{\tau _1-l}^{\tau _2}\int _{B_r}\int _{B_r}|w(x,t)\psi (x)-w(y,t)\psi (y)|^p \eta (t)^{p}\,d\mu \,dt\\&\quad +C\sup _{\tau _1<t<\tau _2}\int _{B_r}\xi (w)(x,t)\psi (x)^p\,dx\\&\quad \le C\Bigg (\int _{\tau _1-l}^{\tau _2}\int _{B_r}\int _{B_r}{\max \{w(x,t),w(y,t)\}^p|\psi (x)-\psi (y)|^p}\eta (t)^p\,d\mu \,dt\\&\qquad +\Big (\sup _{x\in \mathrm {supp}\,\psi ,\,\tau _1-l<t<\tau _2}\int _{{\mathbb {R}^n\setminus B_r}}{\frac{w(y,t)^{p-1}}{|x-y|^{n+sp}}}\,dy\Big ) \int _{\tau _1-l}^{\tau _2}\int _{B_r}w(x,t)\psi (x)^p\eta (t)^p\,dx\,dt\\&\qquad +\int _{\tau _1-l}^{\tau _2}\int _{B_r}\xi (w)\psi (x)^p\partial _t\eta (t)^p\,dx\,dt\Bigg ), \end{aligned}$$

for all nonnegative $\psi \in C_{0}^{\infty }(B_r)$ and nonnegative $\eta \in C^{\infty }(\mathbb {R})$ such that $\eta (t)=0$ for $t\le \tau _1-l$ and $\eta (t)=1$ for $t\ge \tau _1$ where $\xi$ is as in (2.4) defined as follows,

$$\begin{aligned} \xi (w)=\int _{k^{p-1}}^{u^{p-1}}\big (\eta ^\frac{1}{p-1}-k\big )_{+}\,d\eta =(p-1)\int _{k}^{u}(\eta -k)_{+}\eta ^{p-2}\,d\eta . \end{aligned}$$

Proof

Since $p>2$, we observe that the first inequality, i.e.,

$$\begin{aligned}&\int _{\tau _1-l}^{\tau _2}\int _{B_r}\int _{B_r}|w(x,t)\psi (x)-w(y,t)\psi (y)|^p \eta (t)^{p}\,d\mu \,dt +C\sup _{\tau _1<t<\tau _2}\int _{B_r}w(x,t)^p\psi (x)^p\,dx\\&\quad \le \int _{\tau _1-l}^{\tau _2}\int _{B_r}\int _{B_r}|w(x,t)\psi (x)-w(y,t)\psi (y)|^p \eta (t)^{p}\,d\mu \,dt\\&\quad +C\sup _{\tau _1<t<\tau _2}\int _{B_r}\xi (w)(x,t)\psi (x)^p\,dx \end{aligned}$$

follows directly from Lemma 2.10. Therefore, it is enough to prove the second inequality.

Let $t_1=\tau _1-l$ and $t_2=\tau _2$ and for fixed $t_1<l_1<l_2<t_2$ and $\epsilon >0$ small enough, following [2] we define the function $\zeta _{\epsilon }\in W^{1,\infty }\big ((t_1,t_2),[0,1]\big )$ by

$$\begin{aligned} \zeta _{\epsilon }(t) := {\left\{ \begin{array}{ll} 0 &{} \text { for } t_1\le t\le l_1-\epsilon ,\\ 1+\frac{t-l_1}{\epsilon } &{} \text {for }l_1-\epsilon<t\le l_1, \\ 1, &{} \text {for } l_1<t\le l_2, \\ 1-\frac{t-l_{2}}{\epsilon }, &{} \text {for }l_2<t\le l_2+\epsilon , \\ 0, &{} \text {for } l_2 +\epsilon <t\le t_2, \end{array}\right. } \end{aligned}$$

and we choose

$$\begin{aligned} \phi (x,t)=w(x,t)\psi (x)^p\zeta _{\epsilon }(t)\eta (t)^p \end{aligned}$$

as a test function in (2.6). Recalling the definition of $(\cdot )_h$ from (2.7), we denote by

$$\begin{aligned} v_{h}^{p-1}=(u^{p-1})_h \quad \text {and}\quad \mathcal {V}(u(x,y,t))=\mathcal {A}(u(x,y,t))K(x,y,t). \end{aligned}$$

Then following [2, 34], we observe that the subsolution u of (1.1) satisfies the following mollified inequality

$$\begin{aligned} \lim _{\epsilon \rightarrow 0}\lim _{h\rightarrow 0}(I_{h,\epsilon }+J_{h,\epsilon })\le 0, \end{aligned}$$

(3.1)

where

$$\begin{aligned} I_{h,\epsilon }=\int _{t_1}^{t_2}\int _{B_r}\partial _t{v_{h}^{p-1}}\phi (x,t)\,dx\,dt =\int _{t_1}^{t_2}\int _{B_r}\partial _t{v_{h}^{p-1}}w(x,t)\psi (x)^p\zeta _{\epsilon }(t)\eta (t)^p\,dx\, dt, \end{aligned}$$

and

$$\begin{aligned} J_{h,\epsilon }&=\int _{t_1}^{t_2}\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}\big (\mathcal {V}(u(x,y,t))\big )_{h}(\phi (x,t)-\phi (y,t))\,dx\,dy\,dt\\&=\int _{t_1}^{t_2}\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}\big (\mathcal {V}(u(x,y,t))\big )_{h}\big (w(x,t)\psi (x)^p-w(y,t)\psi (y)^p\big )\zeta _{\epsilon }(t)\eta (t)^p\,dx\,dy\,dt. \end{aligned}$$

Estimate of $I_{h,\epsilon }$: Proceeding similarly as in the proof of [2, Proposition 3.1], we have

$$\begin{aligned} \begin{aligned} \lim _{\epsilon \rightarrow 0}\lim _{h\rightarrow 0}I_{h,\epsilon }\ge \int _{B_r}\xi (w)(x,l_2)\psi (x)^p\eta (l_2)^p\,dx-\int _{B_r}\xi (w)(x,l_1)\psi (x)^p\eta (l_1)^p\,dx\\ -\int _{l_1}^{l_2}\int _{B_r}\xi (w)(x,t)\psi (x)^p\partial _t\eta (t)^p\,dx\, dt. \end{aligned} \end{aligned}$$

(3.2)

Estimate of $J_{h,\epsilon }$: First, we claim that $\lim _{h\rightarrow 0}J_{h,\epsilon }=J_{\epsilon },$ where

$$\begin{aligned} J_{\epsilon }=\int _{t_1}^{t_2}\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}\mathcal {V}(u(x,y,t))\big (w(x,t)\psi (x)^p-w(y,t)\psi (y)^p\big )\zeta _{\epsilon }(t)\eta (t)^p\,dx\,dy\,dt. \end{aligned}$$

Indeed, we can write

$$\begin{aligned} J_{h,\epsilon }-J_{\epsilon }=L_{h,\epsilon }+N_{h,\epsilon }, \end{aligned}$$

(3.3)

where

$$\begin{aligned} L_{h,\epsilon }=\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}\big (\big (\mathcal {V}(u(x,y,t))\big )_h-\mathcal {V}(u(x,y,t))\big )\big (w(x,t)\psi (x)^p-w(y,t)\psi (y)^p\big )\zeta _{\epsilon }(t)\eta (t)^p\,dx\,dy\,dt, \end{aligned}$$

and

$$\begin{aligned} N_{h,\epsilon }=2 \int _{t_1}^{t_2}\int _{B_r}\int _{\mathbb {R}^n\setminus B_r}\big (\big (\mathcal {V}(u(x,y,t))\big )_h-\mathcal {V}(u(x,y,t))\big )w(x,t)\psi (x)^p\zeta _{\epsilon }(t)\eta (t)^p\,dx\,dy\,dt. \end{aligned}$$

Estimate of $L_{h,\epsilon }$: We can rewrite $L_{h,\epsilon }$ as

$$\begin{aligned}&L_{h,\epsilon }=\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}\big (\big (\mathcal {V}(u(x,y,t))\big )_h-\mathcal {V}(u(x,y,t))\big )\\&\quad \frac{\big (w(x,t)\psi (x)^p-w(y,t)\psi (y)^p\big )\zeta _{\epsilon }(t)\eta (t)^p}{|x-y|^{-\frac{(n+sp)}{p}}|x-y|^\frac{n+sp}{p}}\,dx\,dy\,dt, \end{aligned}$$

and using Hölder’s inequality with exponents $p'=\frac{p}{p-1}$ and p, we obtain

$$\begin{aligned} \begin{aligned} L_{h,\epsilon }\le \Big (\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}\Big |\big (\big (\mathcal {V}(u(x,y,t))\big )_h-\mathcal {V}(u(x,y,t))\big )|x-y|^\frac{n+sp}{p}\Big |^{p'}\,dx\,dy\,dt\Big )^\frac{1}{p'}\\ \cdot \Big (\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}\frac{\big |\big (w(x,t)\psi (x)^p-w(y,t)\psi (y)^p\big )\zeta _{\epsilon }(t)\eta (t)^p\big |^p}{|x-y|^{n+sp}}\,dx\,dy\,dt\Big )^\frac{1}{p}. \end{aligned} \end{aligned}$$

(3.4)

Now using the property (1.2), we observe that

$$\begin{aligned} |x-y|^\frac{n+sp}{p}|\mathcal {V}(u(x,y,t)|\le \Lambda \frac{|u(x,t)-u(y,t)|^{p-1}}{|x-y|^\frac{n+sp}{p'}}\in L^{p'}((t_1,t_2)\times B_r\times B_r), \end{aligned}$$

From [34, Lemma 2.9], we have

$$\begin{aligned} \big (\big (\mathcal {V}(u(x,y,t))\big )_h-\mathcal {V}(u(x,y,t))\big )|x-y|^\frac{n+sp}{p}\rightarrow 0 \text { in } L^{p'}((t_1,t_2)\times B_r\times B_r), \end{aligned}$$

and therefore from (3.4), it follows that $\lim _{h\rightarrow 0}L_{h,\epsilon }=0$.

Estimate of $N_{h,\epsilon }$: We note that given the pointwise convergence of mollified functions together with the fact that $u\in L^{\infty }((t_1,t_2);L^{\infty }(\mathbb {R}^n))$, we can therefore apply the Lebesgue dominated convergence theorem to conclude that $\lim _{h\rightarrow 0}N_{h,\epsilon }=0$.

Estimate of $J_{\epsilon }$: We can rewrite $J_{\epsilon }=J^{1}_{\epsilon }+J^{2}_{\epsilon }$, where

$$\begin{aligned} J^{1}_{\epsilon }=\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}\mathcal {A}(u(x,y,t))(w(x,t)\psi (x)^p-w(y,t)\psi (y)^p)\zeta _{\epsilon }(t)\eta (t)^p\,d\mu \,dt, \end{aligned}$$

and

$$\begin{aligned} J^{2}_{\epsilon }=2\int _{t_1}^{t_2}\int _{\mathbb {R}^n\setminus B_r}\int _{B_r}\mathcal {A}(u(x,y,t))w(x,t)\psi (x)^p\zeta _{\epsilon }(t)\eta (t)^p\,d\mu \,dt. \end{aligned}$$

Estimate of $J^{1}_{\epsilon }$: To estimate the integral $J^{1}_{\epsilon }$, we mainly adapt an idea from the proof of [12, Theorem 1.4]. By symmetry we may assume $u(x,t)\ge u(y,t)$. In this case, for every fixed t, we observe that

$$\begin{aligned}&|u(x,t)-u(y,t)|^{p-2}(u(x,t)-u(y,t))\big (w(x,t)\psi (x)^p-w(y,t)\psi (y)^p\big )\eta (t)^p\\&=(u(x,t)-u(y,t))^{p-1}\big (w(x,t)\psi (x)^p-w(y,t)\psi (y)^p\big )\eta (t)^p\\&={\left\{ \begin{array}{ll} (w(x,t)-w(y,t))^{p-1}\big (w(x,t)\psi (x)^p-w(y,t)\psi (y)^p\big )\eta (t)^p,\text { if }u(x,t),u(y,t)>k,\\ (u(x,t)-u(y,t))^{p-1}w(x,t)\psi (x)^p\eta (t)^p,\text { if }u(x,t)>k,\,u(y,t)\le k,\\ 0,\text { otherwise. } \end{array}\right. } \end{aligned}$$

Thus

$$\begin{aligned}&|u(x,t)-u(y,t)|^{p-2}(u(x,t)-u(y,t))\big (w(x,t)\psi (x)^p-w(y,t)\psi (y)^p\big )\eta (t)^p\\&\qquad \ge |w(x,t)-w(y,t)|^{p-1}(w(x,t)\psi (x)^p-w(y,t)\psi (y)^p)\eta (t)^p. \end{aligned}$$

This implies,

$$\begin{aligned} J^{1}_{\epsilon }\ge \int _{t_1}^{t_2}\int _{B_r}\int _{B_r}(w(x,t)-w(y,t))^{p-1}(w(x,t)\psi (x)^p-w(y,t)\psi (y)^p)\zeta _{\epsilon }(t)\eta (t)^p\,d\mu \, dt. \end{aligned}$$

Let us now consider the case when $w(x,t)>w(y,t)$ and $\psi (x)\le \psi (y)$. By Lemma 2.8 we obtain

$$\begin{aligned} \psi (x)^p\ge (1-C(p)\epsilon )\psi (y)^p-(1+C(p)\epsilon )\epsilon ^{1-p}|\psi (x)-\psi (y)|^p \end{aligned}$$

(3.5)

for any $\epsilon \in (0,1]$ where $C(p)=(p-1)\Gamma (\max \{1,p-2\})$. Now by letting

$$\begin{aligned} \epsilon =\frac{1}{\max \{1,2C(p)\}}\frac{w(x,t)-w(y,t)}{w(x,t)}\in (0,1], \end{aligned}$$

we deduce from above that the following inequality holds for some positive constant $C=C(p)$,

$$\begin{aligned}&(w(x,t)-w(y,t))^{p-1}w(x,t)\psi (x)^p \ge (w(x,t)-w(y,t))^{p-1}w(x,t)\max \{\psi (x),\psi (y)\}^p\\&\qquad -\frac{1}{2}(w(x,t)-w(y,t))^p\max \{\psi (x),\psi (y)\}^p\\&\quad -C\max \{w(x,t),w(y,t)\}^p|\psi (x)-\psi (y)|^p. \end{aligned}$$

Note that over here, we used that under the assumption $\psi (x)\le \psi (y)$, we have $\max \{\psi (x),\psi (y)\}=\psi (y)$. In the other cases $w(x,t)\ge w(y,t)$, $\psi (x)\ge \psi (y)$ or $w(x,t)=w(y,t)$, the above estimate is clear. Therefore, when $w(x,t)\ge w(y,t)$, we have

$$\begin{aligned} \begin{aligned}&(w(x,t)-w(y,t))^{p-1}(w(x,t)\psi (x)^p-w(y,t)\psi (y)^p)\\&\quad \ge (w(x,t)-w(y,t))^{p-1}(w(x,t)\max \{\psi (x),\psi (y)\}^p-w(y,t)\psi (y)^p)\\&\qquad -\frac{1}{2}(w(x,t)-w(y,t))^p\max \{\psi (x),\psi (y)\}^p\\&\quad -C\max \{w(x,t),w(y,t)\}^p|\psi (x)-\psi (y)|^p\\&\quad \ge \frac{1}{2}(w(x,t)-w(y,t))^p\max \{\psi (x),\psi (y)\}^p\\&\quad -C\max \{w(x,t),w(y,t)\}^p|\psi (x)-\psi (y)|^p. \end{aligned} \end{aligned}$$

(3.6)

If $w(x,t)<w(y,t)$, we may interchange the roles of x and y above to obtain (3.6). We then observe that

$$\begin{aligned} \begin{aligned} |w(x,t)\psi (x)-w(y,t)\psi (y)|^p\le 2^{p-1}|w(x,t)-w(y,t)|^{p}\max \{\psi (x),\psi (y)\}^p\\ +2^{p-1}\max \{w(x,t),w(y,t)\}^p|\psi (x)-\psi (y)|^p. \end{aligned} \end{aligned}$$

(3.7)

Now (3.6) and (3.7) gives

$$\begin{aligned} \begin{aligned} J_{\epsilon }^{1}&\ge c\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}|w(x,t)\psi (x)-w(y,t)\psi (y)|^p\zeta _{\epsilon }(t)\eta (t)^p\,d\mu \, dt\\&\quad -C\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}\max \{w(x,t),w(y,t)\}^p|\psi (x)-\psi (y)|^p\zeta _{\epsilon }(t)\eta (t)^p\,d\mu \, dt, \end{aligned} \end{aligned}$$

(3.8)

for some positive constants $c=c(p), C=C(p)$.

Estimate of $J_{\epsilon }^{2}$: To estimate $J_{\epsilon }^{2}$, we observe that

$$\begin{aligned} |u(x,t)-u(y,t)|^{p-2}(u(x,t)-u(y,t))w(x,t)&\ge -(u(y,t)-u(x,t))^{p-1}w(x,t)\\&\ge -(u(y,t)-k)^{p-1}_{+}w(x,t)\\&\ge -w(y,t)^{p-1}w(x,t). \end{aligned}$$

As a consequence, we obtain,

$$\begin{aligned} \begin{aligned} J_{\epsilon }^{2}&\ge -\int _{t_1}^{t_2}\int _{\mathbb {R}^n\setminus B_r}\int _{B_r}K(x,y,t)w(y,t)^{p-1}w(x,t)\psi (x)^p\zeta _{\epsilon }(t)\eta (t)^p\,dx\,dy\,dt\\&\ge -\Lambda \Big (\sup _{{t_1<t<t_2},\,x\in \mathrm {supp}\,\psi }\int _{\mathbb {R}^n\setminus B_r}\frac{w(y,t)^{p-1}}{|x-y|^{n+sp}}\,dy\Big ) \int _{t_1}^{t_2}\int _{B_r}w(x,t)\psi (x)^p\zeta _{\epsilon }(t)\eta (t)^p\,dx\,dt. \end{aligned} \end{aligned}$$

(3.9)

Therefore from (3.8) and (3.9), we obtain for some positive constants $c=c(p)$ and $C=C(p)$,

$$\begin{aligned} \begin{aligned}&\lim _{\epsilon \rightarrow 0}\lim _{h\rightarrow 0}J_{h,\epsilon } =\lim _{\epsilon \rightarrow 0}J_{\epsilon } =\lim _{\epsilon \rightarrow 0}(J_{\epsilon }^{1}+J_{\epsilon }^{2})\\&\ge c\int _{l_1}^{l_2}\int _{B_r}\int _{B_r}|w(x,t)\psi (x)-w(y,t)\psi (y)|^p\eta (t)^p\,d\mu \, dt\\&\qquad -C\int _{l_1}^{l_2}\int _{B_r}\int _{B_r}\max \{w(x,t),w(y,t)\}^p|\psi (x)-\psi (y)|^p\eta (t)^p\,d\mu \,dt\\&\qquad -\Lambda \Big (\sup _{{t_1<t<t_2},\,x\in \mathrm {supp}\,\psi }\int _{\mathbb {R}^n\setminus B_r}\frac{w(y,t)^{p-1}}{|x-y|^{n+sp}}\,dy\Big ) \int _{l_1}^{l_2}\int _{B_r}w(x,t)\psi (x)^p\eta (t)^p\,dx\,dt. \end{aligned} \end{aligned}$$

(3.10)

Now employing the estimates (3.2) and (3.10) into (3.1) and then first letting $l_1\rightarrow t_1$ and then by $l_2\rightarrow t_2$, we get

$$\begin{aligned} \begin{aligned}&\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}|w(x,t)\psi (x)-w(y,t)\psi (y)|^p \eta (t)^{p}\,d\mu \,dt\\&\le C\Bigg (\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}{\max \{w(x,t),w(y,t)\}^p|\psi (x)-\psi (y)|^p}\eta (t)^p\,d\mu \,dt\\&\qquad +\Big (\sup _{x\in \mathrm {supp}\,\psi ,\,t_1<t<t_2}\int _{{\mathbb {R}^n\setminus B_r}}{\frac{w(y,t)^{p-1}}{|x-y|^{n+sp}}}\,dy\Big ) \int _{t_1}^{t_2}\int _{B_r}w(x,t)\psi (x)^p\eta (t)^p\,dx\,dt\\&\qquad +\int _{t_1}^{t_2}\int _{B_r}\xi (w)\psi (x)^p\partial _t\eta (t)^p\,dx\,dt\Bigg ). \end{aligned} \end{aligned}$$

(3.11)

Again using (3.2) and (3.10) and then first letting $l_1\rightarrow t_1$ and then by choosing $l_2 \in (\tau _1, \tau _2)$ such that

$$\begin{aligned} \int _{B_r}\xi (w)(x,l_2)\psi (x)^p\,dx \ge \frac{1}{2} \sup _{\tau _1< t< \tau _2} \int _{B_r}\xi (w)(x,t)\psi (x)^p\,dx, \end{aligned}$$

we observe that

$$\begin{aligned} \begin{aligned}&\sup _{\tau _1< t< \tau _2} \int _{B_r}\xi (w)(x,t)\psi (x)^p\,dx\\&\le C\Bigg (\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}{\max \{w(x,t),w(y,t)\}^p|\psi (x)-\psi (y)|^p}\eta (t)^p\,d\mu \,dt\\&\qquad +\Big (\sup _{x\in \mathrm {supp}\,\psi ,\,t_1<t<t_2}\int _{{\mathbb {R}^n\setminus B_r}}{\frac{w(y,t)^{p-1}}{|x-y|^{n+sp}}}\,dy\Big ) \int _{t_1}^{t_2}\int _{B_r}w(x,t)\psi (x)^p\eta (t)^p\,dx\,dt\\&\qquad +\int _{t_1}^{t_2}\int _{B_r}\xi (w)\psi (x)^p\partial _t\eta (t)^p\,dx\,dt\Bigg ). \end{aligned} \end{aligned}$$

(3.12)

Now from (3.11) and (3.12), we get the required estimate. $\square$

4 Proof of Theorem 2.15

Let $0<s<1$ and $\kappa =\frac{n+sp}{n}$, if $sp<n$ and $\kappa =\frac{3}{2}$ in the case when $sp\ge n$. For $j=0,1,2,\ldots$, we denote by

$$\begin{aligned} r_j =\frac{1+2^{-j}}{2}r, \quad s_j =\frac{r_j+r_{j+1}}{2}, \end{aligned}$$

and

$$\begin{aligned} B_j=B_{r_j}(x_0), \quad \bar{B}_j=B_{s_j}(x_0), \quad \Gamma _j=(t_0-r_j^{sp},t_0), \quad \bar{\Gamma }_j=(t_0-{s}_j^{sp},t_0). \end{aligned}$$

Moreover, for $\bar{k}>0$ to be chosen later, we let

$$\begin{aligned} k_j=(1-2^{-j})\bar{k},\quad \bar{k}_j=\frac{k_{j+1}+k_j}{2},\quad w_j=(u-k_j)_{+} \quad \text {and}\quad \bar{w}_j=(u-\bar{k}_j)_{+}. \end{aligned}$$

We observe that since $\bar{k}_j>k_j,\,w_j\ge \bar{w_j}$, one has that the following inequality holds,

$$\begin{aligned} w_j^p\ge (\bar{k}_j-k_j)^{p-1}\bar{w}_j = (2^{-j-2}\bar{k})^{p-1}\bar{w_j}. \end{aligned}$$

(4.1)

Indeed, (4.1) can be seen as follows. Suppose $u<\bar{k}_j$, then $\bar{w}_j=0$ and thus (4.1) holds. Instead if $u\ge \bar{k}_j$, then one has that $\bar{k}_j-k_j\le u-k_j\le w_j$ and also by using $\bar{k}_j-k_j=2^{-j-2}\bar{k}$ and $\bar{w}_j\le w_j$, we obtain

$$\begin{aligned} (2^{-j-2}\bar{k})^{p-1}\bar{w_j}=(\bar{k}_j-k_j)^{p-1}\bar{w}_j\le w_j^{p-1}\bar{w}_j\le w_j^{p}, \end{aligned}$$

which proves (4.1). Additionally, we choose $\psi _j\in C_{0}^\infty (B_j),\,\eta _j\in C^{\infty }(\Gamma _j)$ such that $0\le \psi _j\le 1$ in $B_{j}$, $\psi _j\equiv 1$ on $B_{j+1}$, $|\nabla \psi _j|<\frac{2^{j+3}}{r}$ in $B_j$ and $0\le \eta _j\le 1$ in $\Gamma _{j}$, and $\eta _j(t)=1$ if $t\ge t_0-r_{j+1}^{sp}$ with $\eta _{j}(t)=0$ if $t\le t_0-s_{j}^{sp}$ and $|\partial _t\eta _j|\le \frac{2^{jps}}{r^{ps}}\text { in }\Gamma _j$. Let $\kappa =\frac{n+sp}{n}$ and $\kappa ^*=\frac{n}{n-sp}$ if $sp<n$, and $\kappa =\frac{3}{2}$, $\kappa ^*=2$ if $sp\ge n$. Then noting that $\frac{p\kappa ^*(\kappa -1)}{\kappa ^*-1}=p$, by Lemma 2.4 we have for some positive constant $C=C(n,p,s)$ that the following inequality holds,

$$\begin{aligned} \begin{aligned}&\int _{\Gamma _{j+1}}\fint _{B_{j+1}}\bar{w_j}^{p\kappa }\,dx\,dt\\&\le Cr_{j+1}^{sp-n}\int _{\Gamma _{j+1}}\int _{B_{j+1}}\int _{B_{j+1}}\frac{|\bar{w}_j(x,t)-\bar{w}_j(y,t)|^p}{|x-y|^{n+sp}}\,dx\,dy\,dt\cdot \Big (\sup _{\Gamma _{j+1}}\fint _{B_{j+1}}\bar{w}_{j}^p\,dx\Big )^{\kappa -1}\\&\qquad +C\int _{\Gamma _{j+1}}\fint _{B_{j+1}}\bar{w}_j^p\,dx\,dt\cdot \Big (\sup _{\Gamma _{j+1}}\fint _{B_{j+1}}\bar{w}_{j}^p\,dx\Big )^{\kappa -1}\\&=Cr_{j+1}^{sp-n}I_1\cdot \Big (\frac{I_2}{|B_{j+1}|}\Big )^{\kappa -1}+C\int _{\Gamma _{j+1}}\fint _{B_{j+1}}|\bar{w}_j|^p\,dx\,dt\cdot \Big (\frac{I_2}{|B_{j+1}|}\Big )^{\kappa -1}, \end{aligned} \end{aligned}$$

(4.2)

where

$$\begin{aligned} I_1=\int _{\Gamma _{j+1}}\int _{B_{j+1}}\int _{B_{j+1}}\frac{|\bar{w}_j(x,t)-\bar{w}_j(y,t)|^p}{|x-y|^{n+sp}}\,dx\,dy\,dt \quad \text {and}\quad I_2=\sup _{\Gamma _{j+1}}\int _{B_{j+1}}|\bar{w}_j|^p\,dx. \end{aligned}$$

Let $U_j=B_j\times \Gamma _j$ and $\bar{U}_j=\bar{B}_{j}\times \bar{\Gamma }_j$. Since $r_{j+1}<r_j,\,s_j<r_j$, we have $\bar{B_j}\subset B_j$, $\bar{\Gamma }_j\subset \Gamma _{j}$, $B_{j+1}\subset B_j$ and $\Gamma _{j+1}\subset \Gamma _j$. To estimate $I_1$ and $I_2$ we apply Lemma 3.1 with $r={r_j}$, $\tau _2=t_0$, $\tau _1=t_0-r_{j+1}^{sp}$, $l=s_j^{sp}-r_{j+1}^{sp}$ and $\phi _j(x,t)=\psi _j(x)\eta _{j}(t)$ with $\eta _j(t)=0\text { if }t\le \tau _1-l$ and $\eta _j(t)=1$ if $t\ge \tau _1$. Observing that $B_{j+1}\subset \bar{B_j}$ and $\Gamma _{j+1}\subset \bar{\Gamma }_{j}$, using Lemma 3.1, for some positive constant $C=C(n,p,s,\Lambda )$ we get

$$\begin{aligned} \begin{aligned} I_1+C\,I_2&\le \int _{\bar{\Gamma }_j}\int _{B_j}\int _{B_j}|\bar{w}_j(x,t)\psi _j(x)-\bar{w}_j(y,t)\psi _j(y)|^p\eta _j(t)^p\,d\mu \,dt\\&\qquad +C\sup _{\Gamma _{j+1}}\int _{B_j}\bar{w}_j(x,t)^{p}\psi _{j}(x)^p\,dx\\&\le C(J_1+J_2+J_3), \end{aligned} \end{aligned}$$

(4.3)

where

$$\begin{aligned}&J_1=\int _{\Gamma _j}\int _{B_j}\int _{B_j}\max \{\bar{w}_j(x,t)^p,\bar{w}_j(y,t)^p\}|\psi _j(x)-\psi _{j}(y)|^p\eta _j(t)^p\,d\mu \,dt, \\&J_2=\sup _{t\in \Gamma _j,\,x\in \text {supp}\,\psi _j}\int _{\mathbb {R}^n\setminus B_j} \frac{\bar{w}_j(y,t)^{p-1}}{|x-y|^{n+sp}}\,dy\int _{B_j}\bar{w}_j(x,t)\psi _j(x)^p\eta _j(t)^p\,dx, \end{aligned}$$

and

$$\begin{aligned} J_3=\int _{\Gamma _j}\int _{B_j}\xi (\bar{w}_j)(x,t)\psi _j(x)^p\partial _t\eta _j(t)^p\,dx dt. \end{aligned}$$

Now we estimate each $J_i$, $i=1,2,3$ separately.

Estimate of $J_1$: Using $r_j<r$ and $\bar{w}_j\le w_j$, we have

$$\begin{aligned} \begin{aligned} J_1&=\int _{\Gamma _j}\int _{B_j}\int _{B_j}\max \{\bar{w}_j(x,t)^p,\bar{w}_j(y,t)^p\}|\psi _j(x)-\psi _{j}(y)|^p\eta _j(t)^p\,d\mu \,dt\\&\le C(n,p,s,\Lambda )\Big (\sup _{x\in B_j}\int _{B_j}\frac{|\psi _j(x)-\psi _j(y)|^p}{|x-y|^{n+sp}}\,dy\Big )\int _{\Gamma _j}\int _{B_j}\bar{w}_j(x,t)^p\,dx\,dt\\&\le C(n,p,s,\Lambda )\frac{2^{j(n+sp+p)}}{r_j^{sp}}\int _{\Gamma _j}\int _{B_j}w_{j}(x,t)^p\,dx\,dt. \end{aligned} \end{aligned}$$

(4.4)

Estimate of $J_2$: Without loss of generality, we may assume $x_0=0$. Using the fact that $\bar{w}_j\le w_0$, under the assumptions on $\psi _j$, we have for $x\in \text {supp}\,\psi _j$, and $y\in \mathbb {R}^n\setminus B_j$,

$$\begin{aligned} \frac{1}{|x-y|}=\frac{1}{|y|}\frac{|x-(x-y)|}{|x-y|}\le \frac{1}{|y|}\big (1+2^{j+3}\big )\le \frac{2^{j+4}}{|y|}. \end{aligned}$$

This implies

$$\begin{aligned} \begin{aligned} J_2&=\sup _{t\in \Gamma _j,\,x\in \text {supp}\,\psi _j}\int _{\mathbb {R}^n\setminus B_j}\frac{\bar{w}_j(y,t)^{p-1}}{|x-y|^{n+sp}}\,dy \int _{\Gamma _j}\int _{B_j}\bar{w}_j(x,t)\psi _j(x)^p\eta _j(t)^p\,dx\,dt\\&\le C\frac{2^{j(n+sp+p)}}{r^{sp}\bar{k}^{p-1}}\mathrm {Tail}_{\infty }^{p-1}(w_0;x_0,\frac{r}{2},t_0-r^{sp},t_0)\int _{\Gamma _j}\int _{B_j}w_j(x,t)^{p}\,dx\,dt\\&\le C\frac{2^{j(n+sp+p)}}{\delta ^{p-1}r_{j}^{sp}}\int _{\Gamma _j}\int _{B_j}w_j(x,t)^{p}\,dx\,dt, \end{aligned} \end{aligned}$$

(4.5)

where we also used the fact $\bar{w}_j\le \Big (\frac{2^{j+2}}{\bar{k}}\Big )^{p-1}w_j^{p}$ from (4.1) and also that $\bar{k}$ would be chosen finally such that $\bar{k}\ge \delta \,\mathrm {Tail}_{\infty }(w_0;x_0,\frac{r}{2},t_0-r^{sp},t_0)$.

Estimate of $J_3$: To estimate $J_3$, we first note that by Lemma 2.10 and the fact that $p>2$ we have

$$\begin{aligned} \begin{aligned} J_3&=\int _{\Gamma _j}\int _{B_j}\xi (\bar{w}_j)(x,t)\psi _{j}(x)^p\partial _t\eta _{j}(t)^p\,dx\,dt\\&\le C(p)\int _{\Gamma _j}\int _{B_j}(\bar{w}_j(x,t)+\bar{k}_j)^{p-2}\bar{w}_j(x,t)^{2}\psi _j(x)^p|\partial _t\eta _j(t)^{p}|\,dx\,dt\\&=J_4+J_5, \end{aligned} \end{aligned}$$

(4.6)

where

$$\begin{aligned} J_4=\int _{(\Gamma _j\times B_j)\cap \{0<u-\bar{k}_j<\bar{k}_j\}}(\bar{w}_j(x,t)+\bar{k}_j)^{p-2}\bar{w}_j(x,t)^{2}\psi _j(x)^p|\partial _t\eta _j(t)^{p}|\,dx\,dt, \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} J_5&=\int _{(\Gamma _j\times B_j)\cap {\{\bar{w}_j\ge \bar{k}_j}\}}(\bar{w}_j(x,t)+\bar{k}_j)^{p-2}\bar{w}_j(x,t)^{2}\psi _j(x)^p|\partial _t\eta _j(t)^{p}|\,dx\,dt\\&\le 2^{p-2}\int _{(\Gamma _j\times B_j)\cap {\{\bar{w}_j\ge \bar{k}_j}\}}\bar{w}_j(x,t)^p\psi _j(x)^p|\partial _t\eta _j(t)^p|\,dx\,dt\\&\le C(p,s)\frac{2^{j(n+sp+p)}}{r_j^{sp}}\int _{\Gamma _j}\int _{B_j}w_j(x,t)^p\,dx\,dt, \end{aligned} \end{aligned}$$

(4.7)

where to deduce the estimate (4.7) we have again used the fact that $p>2$.

Estimate of $J_4$: Now we estimate $J_4$ by adapting some ideas from [3]. Indeed, we denote by $A_j=(\Gamma _j\times B_j)\cap \{0<u-\bar{k}_j<\bar{k}_j\}$ and using binomial expansion we observe that,

$$\begin{aligned} \begin{aligned} J_4&=\int _{A_j}(\bar{w}_j(x,t)+\bar{k}_j)^{p-2}\bar{w}_j(x,t)^{2}\psi _j(x)^p|\partial _t\eta _j(t)^{p}|\,dx\,dt\\&=\sum _{d=0}^{\infty }\int _{A_j}\left( {\begin{array}{c}p-2\\ d\end{array}}\right) \bar{k}_j^{p}\left( \frac{\bar{w}_j(x,t)}{\bar{k}_j}\right) ^{d+2}|\partial _t\eta _j(t)^{p}|\,dx\,dt\\&=J_4^{1}+J_4^{2}, \end{aligned} \end{aligned}$$

(4.8)

where

$$\begin{aligned} J_4^{1}=\sum _{d=0}^{[p-2]}\int _{A_j}\left( {\begin{array}{c}p-2\\ d\end{array}}\right) \bar{k}_j^{p}\left( \frac{\bar{w}_j(x,t)}{\bar{k}_j}\right) ^{d+2}|\partial _t\eta _j(t)^{p}|\,dx\,dt, \end{aligned}$$

and

$$\begin{aligned} J_4^{2}=\sum _{d=[p-2]+1}^{\infty }\int _{A_j}\left( {\begin{array}{c}p-2\\ d\end{array}}\right) \bar{k}_j^{p}\left( \frac{\bar{w}_j(x,t)}{\bar{k}_j}\right) ^{d+2}|\partial _t\eta _j(t)^{p}|\,dx\,dt. \end{aligned}$$

Estimate of $J_4^{1}$: Let us estimate $J_4^{1}$ as follows. Using H$\ddot{\text {o}}$lder’s inequality, we obtain

$$\begin{aligned} J_4^{1}\le \sum _{d=0}^{[p-2]}\left| \left( {\begin{array}{c}p-2\\ d\end{array}}\right) \right| (\bar{k}_j)^{p-2-d}\Big (\int _{A_j}\bar{w}_j^{p}(\partial _t\eta ^p_{j})^\frac{p}{d+2}\,dx\,dt\Big )^\frac{d+2}{p}|A_j|^{1-\frac{d+2}{p}}. \end{aligned}$$

Now, since $u>\bar{k}_j$ in $A_j$, we observe that

$$\begin{aligned} \int _{A_j}w_j^p\,dx\,dt\ge \Big (\bar{k}_j-k_j\Big )^p|A_j|=\Big (\frac{\bar{k}}{2^{j+2}}\Big )^p|A_j|. \end{aligned}$$

Therefore, we obtain

$$\begin{aligned} |A_j|\le \Big (\frac{2^{j+2}}{\bar{k}}\Big )^p\int _{A_j}w_j^p\,dx\,dt. \end{aligned}$$

(4.9)

Now using (4.9) together with the fact $\bar{w}_j\le w_j$, $\bar{k}_j<\bar{k}$, $r_j<r$ and also by using the bounds on $|\partial _t \eta _j|$, we get

$$\begin{aligned} \begin{aligned} J_4^{1}&\le C(p)\sum _{d=0}^{[p-2]}\left| \left( {\begin{array}{c}p-2\\ d\end{array}}\right) \right| 2^{jp}\Big (\int _{A_j}w_j^{p}|\partial _t \eta _j|^\frac{p}{d+2}\,dx\,dt\Big )^\frac{d+2}{p} \Big (\int _{A_j}w_j^{p}\,dx\,dt\Big )^{1-\frac{d+2}{p}}\\&\le C(p)\frac{2^{jp(s+1)}}{r_j^{sp}}\int _{A_j}w_j^{p}\,dx dt. \end{aligned} \end{aligned}$$

(4.10)

Estimate of $J_4^{2}$: Now since $\bar{w}_j<\bar{k}_j$, therefore for all $d\ge [p-2]+1$, we have that $\bar{w}_j^{d-[p-2]-1}\le \bar{k}_j^{d-[p-2]-1}$. Thus $\bar{k}_j^{p-2-d}\bar{w}_j^{d+2}\le \bar{k}_{j}^{p-3-[p-2]}\bar{w}_j^{[p-2]+3}$ and consequently we obtain

$$\begin{aligned} J_4^{2}\le \sum _{d=[p-2]+1}^{\infty }\left| \left( {\begin{array}{c}p-2\\ d\end{array}}\right) \right| \int _{A_j}\bar{k}_j^{p-3-[p-2]}\bar{w}_j^{[p-2]+3}|\partial _t\eta _j^p|\,dx\,dt. \end{aligned}$$

Finally by using $\bar{k}_j^{p-3-[p-2]}<\bar{w}_j^{p-3-[p-2]}$, we have

$$\begin{aligned} \begin{aligned} J_4^{2}&\le \sum _{d=[p-2]+1}^{\infty }\left| \left( {\begin{array}{c}p-2\\ d\end{array}}\right) \right| \int _{A_j}\bar{w}_j^{p}|\partial _t\eta _j^p|\,dx\,dt\\&\le C(p)\frac{2^{jsp}}{r_j^{ps}}\int _{A_j}\bar{w}_j^p\,dx\,dt\\&\le C(p)\frac{2^{jsp}}{r_j^{sp}}\int _{\Gamma _j}\int _{B_j}{w}_j^p\,dx\,dt, \end{aligned} \end{aligned}$$

(4.11)

where we have also used the fact that the series $\sum _{d=0}^{\infty }|\left( {\begin{array}{c}p-2\\ d\end{array}}\right) |$ is convergent. Therefore, using (4.10) and (4.11) into (4.8), we obtain

$$\begin{aligned} J_4\le C(p)\frac{2^{jp(s+1)}}{r_j^{ps}}\int _{\Gamma _j}\int _{B_j}{w}_j^p\,dx\,dt. \end{aligned}$$

(4.12)

Now using the estimates (4.7) and (4.12) in (4.6) we conclude

$$\begin{aligned} J_3\le C(p,s)\frac{2^{j(n+sp+p)}}{r_j^{ps}}\int _{\Gamma _j}\int _{B_j}{w}_j^p\,dx\,dt. \end{aligned}$$

(4.13)

Then using $\bar{w}_j^{p\kappa }\ge (2^{-j-2}\bar{k})^{p(\kappa -1)}w_{j+1}^p$ in (4.2), we get

$$\begin{aligned} \begin{aligned} I&=(2^{-j-2}\bar{k})^{p(\kappa -1)}\fint _{\Gamma _{j+1}}\fint _{B_{j+1}}w_{j+1}^p\,dx\,dt\\&\le \frac{Cr_{j+1}^{ps-n}}{|\Gamma _{j+1}|}I_1\cdot \Big (\frac{I_2}{|B_{j+1}|}\Big )^{\kappa -1}+C\fint _{\Gamma _{j+1}}\fint _{B_{j+1}}w_{j}^p\,dx\,dt\cdot \Big (\frac{I_2}{|B_{j+1}|}\Big )^{\kappa -1}. \end{aligned} \end{aligned}$$

(4.14)

Plugging the estimates (4.4), (4.5) and (4.13) into (4.3), we have

$$\begin{aligned} I_1,I_2\le C(n,p,s,\Lambda )\frac{2^{j(n+sp+p)}}{\delta ^{p-1} r_j^{sp}}\int _{\Gamma _{j}}\int _{B_j}w_j^{p}\,dx\,dt. \end{aligned}$$

(4.15)

Then using (4.15) in (4.14), we get

$$\begin{aligned} I\le C(n,p,s,\Lambda )\Big (\frac{2^{j(n+sp+p)}}{\delta ^{p-1}}\fint _{\Gamma _{j}}\fint _{B_{j}}w_j^{p}\,dx\,dt\Big )^{\kappa } \end{aligned}$$

We now let

$$\begin{aligned} A_j=\Big (\fint _{U_j}w_j^p\,dx\,dt\Big )^\frac{1}{p}. \end{aligned}$$

Then we have

$$\begin{aligned} (2^{-j-2}\bar{k})^{p(\kappa -1)}A_{j+1}^p\le C(n,p,s,\Lambda )\Big (\frac{2^{j(n+sp+p)}}{\delta ^{p-1}}A_j^{p}\Big )^{\kappa }.\end{aligned}$$

Then for some positive constant $C=C(n,p,s,\Lambda )$ we have

$$\begin{aligned} \frac{A_{j+1}}{\bar{k}}&\le \frac{C}{\bar{k}^\kappa }2^{j(\kappa -1)}\Big (\frac{2^{j(n+sp+p)}}{\delta ^{p-1}}A_{j}^p\Big )^\frac{\kappa }{p}=C\frac{2^{j\big (\kappa -1+(n+sp+p)(\frac{\kappa }{p})\big )}}{\delta ^{(p-1)\frac{\kappa }{p}}}\Big (\frac{A_j}{\bar{k}}\Big )^{\kappa }. \end{aligned}$$

Noting that $w_0=u$, we now let

$$\begin{aligned} \bar{k}=\delta \mathrm {Tail}_{\infty }(u;x_0,\frac{r}{2},t_0-r^{ps},t_0)+C^\frac{1}{\kappa -1}b^\frac{1}{(\kappa -1)^2}\delta ^{-\frac{(p-1)\kappa }{p(\kappa -1)}}\Big (\fint _{U^{-}(r)}u^p\,dx\,dt\Big )^\frac{1}{p}, \end{aligned}$$

such that for

$$\begin{aligned} \beta =\kappa -1, \quad c_0=\frac{C}{\delta ^{(p-1)\frac{\kappa }{p}}}>1, \quad b=2^{\kappa -1+(n+sp+p)(\frac{\kappa }{p})}>1 \quad \text {and}\quad Y_j=\frac{A_j}{\bar{k}}, \end{aligned}$$

the hypothesis of Lemma 2.7 is satisfied and consequently we have that

$$\begin{aligned}\sup _{U^{-}(\frac{r}{2})}\,u\le \bar{k},\end{aligned}$$

which proves Theorem 2.15.

5 Some qualitative and quantitative properties of supersolutions

In this section, we prove some qualitative and quantitative properties of supersolutions which are strictly bounded away from zero. Throughout this section, by a global supersolution u in $\mathbb {R}^n \times (0, T)$, we refer to a bounded positive function u which satisfies the hypothesis of Definition 2.11 in $\Omega \times (0, T)$ where $\Omega$ is any bounded domain in $\mathbb {R}^n$.

The following lemma is the nonlocal analogue of Lemma 3.1 in [4] which states that the inverse of a supersolution is a subsolution.

Lemma 5.1

Let $p>2$ and $u\in L^\infty (0,T;L^\infty (\mathbb {R}^n))\cap C_{\mathrm {loc}}(0,T;L^p_{\mathrm {loc}}(\Omega ))\cap L^p_{\mathrm {loc}}(0,T;W_{\mathrm {loc}}^{s,p}(\Omega ))$ be a supersolution of (1.1) in $\Omega \times (0,T)$ such that $u\ge \rho >0$ in $\mathbb {R}^n\times (0,T)$, then $u^{-1}$ is a subsolution of (1.1).

Proof

Let $v=u^{-1}$, $\Omega '\Subset \Omega$ and $\psi \in W^{1,p}_{\mathrm {loc}}(0,T;L^p(\Omega '))\cap L^p_{\mathrm {loc}}(0,T;W_{0}^{s,p}(\Omega '))$ be nonnegative. Since u is a weak supersolution of (1.1), by formally choosing $\phi (x,t)=u(x,t)^{2(1-p)}\psi (x,t)$ as a test function in (2.6) which can be justified by mollifying in time as in the proof of Lemma 3.1, we obtain for every $(t_1,t_2)\Subset (0,T)$,

$$\begin{aligned} 0\le I_1+I_2, \end{aligned}$$

(5.1)

where

$$\begin{aligned} I_1&=\int _{\Omega '}u(x,t_2)^{p-1}\phi (x,t_2)\,dx-\int _{\Omega '}u(x,t_1)^{p-1}\phi (x,t_1)\,dx\\&\quad -\int _{t_1}^{t_2}\int _{\Omega '}u(x,t)^{p-1}\partial _t\phi (x,t)\,dx\,dt,\\&=\int _{\Omega '}u(x,t_2)^{1-p}\psi (x,t_2)\,dx-\int _{\Omega '}u(x,t_1)^{1-p}\psi (x,t_1)\,dx-I_3, \end{aligned}$$

with

$$\begin{aligned} I_3&=\int _{t_1}^{t_2}\int _{\Omega '}u(x,t)^{p-1}\big (u(x,t)^{2(1-p)}\partial _t\psi (x,t)\\&\quad -2(p-1)\psi (x,t)u(x,t)^{1-2p}\partial _t u(x,t)\big )\,dx\,dt\\&=\int _{t_1}^{t_2}\int _{\Omega '}u(x,t)^{1-p}\partial _t\psi (x,t)\,dx\, dt -2(p-1)\int _{t_1}^{t_2}\int _{\Omega '}\psi (x,t)u(x,t)^{-p}\partial _t u(x,t)\,dx\, dt\\&=\int _{t_1}^{t_2}\int _{\Omega '}u(x,t)^{1-p}\partial _t\psi (x,t)\,dx\, dt -2\int _{t_1}^{t_2}\int _{\Omega '}u(x,t)^{1-p}\partial _t\psi (x,t)\,dx\, dt+2I_4, \end{aligned}$$

and

$$\begin{aligned} I_4&=\int _{\Omega '}u(x,t_2)^{1-p}\psi (x,t_2)\,dx-\int _{\Omega '}u(x,t_1)^{1-p}\psi (x,t_1)\,dx. \end{aligned}$$

We thus obtain from above,

$$\begin{aligned} I_1&=-\Big (\int _{\Omega '}v(x,t_2)^{p-1}\psi (x,t_2)\,dx-\int _{\Omega '}v(x,t_1)^{p-1}\psi (x,t_1)\,dx\\&\quad -\int _{t_1}^{t_2}\int _{\Omega '}v^{p-1}\partial _t\psi \,dx\,dt\Big ). \end{aligned}$$

Here

$$\begin{aligned} I_2&=\int _{t_1}^{t_2}\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}\mathcal {A}(u(x,y,t)){(\phi (x,t)-\phi (y,t))}\,d\mu \, dt\\&=\int _{t_1}^{t_2}\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}|u(x,t)-u(y,t)|^{p-2}(u(x,t)-u(y,t))\\&\qquad \cdot (u(x,t)^{2(1-p)}\psi (x,t)-u(y,t)^{2(1-p)}\psi (y,t))\,d\mu \, dt\\&=-\int _{t_1}^{t_2}\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}\mathcal {A}(v(x,y,t)){\Big (\Big (\frac{v(x,t)}{v(y,t)}\Big )^{p-1}\psi (x,t)-\Big (\frac{v(y,t)}{v(x,t)}\Big )^{p-1}\psi (y,t)\Big )}\,d\mu \,dt. \end{aligned}$$

Now we estimate $I_2$. Let us first consider the case when $v(x,t)\ge v(y,t)$. In this case, we have

$$\begin{aligned}&\mathcal {A}(v(x,y,t)){\Big (\Big (\frac{v(x,t)}{v(y,t)}\Big )^{p-1}\psi (x,t)-\Big (\frac{v(y,t)}{v(x,t)}\Big )^{p-1}\psi (y,t)\Big )}\\&\quad \ge \mathcal {A}(v(x,y,t))\big (\psi (x,t)-\psi (y,t)\big ). \end{aligned}$$

Likewise when $v(x,t)<v(y,t)$, we have

$$\begin{aligned}&\mathcal {A}(v(x,y,t)){\Big (\Big (\frac{v(x,t)}{v(y,t)}\Big )^{p-1}\psi (x,t)-\Big (\frac{v(y,t)}{v(x,t)}\Big )^{p-1}\psi (y,t)\Big )}\\&=|v(y,t)-v(x,t)|^{p-2}(v(y,t)-v(x,t))\Big (\Big (\frac{v(y,t)}{v(x,t)}\Big )^{p-1}\psi (y,t)-\Big (\frac{v(x,t)}{v(y,t)}\Big )^{p-1}\psi (x,t)\Big )\\&\ge \mathcal {A}(v(y,x,t))(\psi (y,t)-\psi (x,t)). \end{aligned}$$

Therefore in either case, we obtain

$$\begin{aligned} I_2&\le -\int _{t_1}^{t_2}\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}\mathcal {A}(v(x,y,t))(\psi (x,t)-\psi (y,t))\,d\mu \, dt. \end{aligned}$$

By inserting the above estimates for $I_1$ and $I_2$ into (5.1), we get

$$\begin{aligned}&\int _{\Omega '}v(x,t_2)^{p-1}\psi (x,t_2)\,dx-\int _{\Omega '}v(x,t_1)^{p-1}\psi (x,t_1)\,dx\\&\quad -\int _{t_1}^{t_2}\int _{\Omega '}v(x,t)^{p-1}\partial _t\psi (x,t)\,dx\,dt\\&\quad +\int _{t_1}^{t_2}\int _{\mathbb {R}^n}\int _{\mathbb {R}^n}\mathcal {A}(v(x,y,t))(\psi (x,t)-\psi (y,t))\,d\mu \, dt\le 0. \end{aligned}$$

Hence $v=u^{-1}$ is a subsolution of (1.1). $\square$

Now we prove an energy estimate for strictly positive supersolutions of (1.1) which is the key ingredient needed to deduce reverse Hölder inequality for strictly positive supersolutions.

Lemma 5.2

Let $p>2$, $x_0\in \mathbb {R}^n$, $r>0$ and $\alpha \in (0,{p-1})$ with $B_r=B_r(x_0)\Subset \Omega$ and $(\tau _1,\tau _2+l)\Subset (0,T)$. Suppose that $u\in L^\infty (0,T;L^\infty (\mathbb {R}^n))\cap C_{\mathrm {loc}}(0,T;L^p_{\mathrm {loc}}(\Omega ))\cap L^p_{\mathrm {loc}}(0,T;W_{\mathrm {loc}}^{s,p}(\Omega ))$ is a weak supersolution of (1.1) in $\Omega \times (0,T)$ with $u\ge \rho >0$ in $\mathbb {R}^n\times (\tau _1,\tau _2+l)$. Then there exists positive constants $C=C(n,p,s,\Lambda )$ and $c=c(p)$ large enough such that

$$\begin{aligned} \begin{aligned}&\frac{p-1}{\alpha }\sup _{\tau _1<t<\tau _2}\int _{B_r}\psi (x)^p u(x,t)^\alpha \,dx\\&+\frac{\zeta (\epsilon )}{c(p)}\int _{\tau _1}^{\tau _2+l}\int _{B_r}\int _{B_r}\big |\psi (x)u(x,t)^\frac{\alpha }{p}-\psi (y)u(y,t)^\frac{\alpha }{p}\big |^p \eta (t)\,d\mu \,dt\\&\le \Big (\zeta (\epsilon )+1+\frac{1}{\epsilon ^{p-1}}\Big )\int _{\tau _1}^{\tau _2+l}\int _{B_r}\int _{B_r}|\psi (x)-\psi (y)|^p(u(x,t)^\alpha +u(y,t)^\alpha )\eta (t)\,d\mu \,dt\\&\qquad +C(\Lambda )\sup _{x\in \text { supp }\psi }\int _{\mathbb {R}^n\setminus B_r}\frac{dy}{|x-y|^{n+sp}}\int _{\tau _1}^{\tau _2+l}\int _{B_r}u(x,t)^\alpha \psi (x)^p\eta (t)\,dx\,dt\\&\qquad +\frac{p-1}{\alpha }\int _{\tau _1}^{\tau _2+l}\int _{B_r}u(x,t)^\alpha \psi (x)^p|\partial _t\eta (t)|\,dx\,dt, \end{aligned} \end{aligned}$$

where $\epsilon =p-\alpha -1$ and $\zeta (\epsilon )=\frac{\epsilon p^p}{\alpha ^p}$, if $\alpha \ge 1$ and $\zeta (\epsilon )=\frac{\epsilon p^p}{\alpha }$ if $\alpha \in (0,1)$. Moreover, $\psi \in C_{0}^{\infty }(B_r)$ is taken to be nonnegative and $\eta \in C^\infty (\mathbb {R})$ is also nonnegative such that $\eta (t)= 1$ if $\tau _1\le t\le \tau _2$ and $\eta (t)= 0$ if $t\ge \tau _2+l$.

Proof

Let $t_1\in (\tau _1,\tau _2)$ and $t_2=\tau _2+l$. We consider $\eta \in C^\infty (t_1,t_2)$ such that $\eta (t_2)=0$ and $\eta (t)= 1$ for all $t\le t_1$. Let $\epsilon \in (0,p-1)$ and $\alpha =p-\epsilon -1$. Then since u is a strictly positive weak supersolution of (1.1), choosing $\phi (x,t)=u(x,t)^{-\epsilon }\psi (x)^p\eta (t)$ as a test function in (2.6) (which is again justified by mollifying in time), we obtain

$$\begin{aligned} \begin{aligned} 0\le I_1+I_2+2 I_3, \end{aligned} \end{aligned}$$

(5.2)

where

$$\begin{aligned}&I_1=\int _{t_1}^{t_2}\int _{B_r}\frac{\partial }{\partial t}(u^{p-1})\phi (x,t)\,dx\,dt, \\&I_2=\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}\mathcal {A}(u(x,y,t))(u(x,t)^{-\epsilon }\psi (x)^p-u(y,t)^{-\epsilon }\psi (y)^p)\eta (t)\,d\mu \,dt, \end{aligned}$$

and

$$\begin{aligned} I_3=\int _{t_1}^{t_2}\int _{\mathbb {R}^n\setminus B_r}\int _{B_r}\mathcal {A}(u(x,y,t))u(x,t)^{-\epsilon }\psi (x,t)^p\eta (t)\,d\mu \,dt. \end{aligned}$$

We observe that for any $x\in B_r$ and $y\in \mathbb {R}^n\setminus B_r$, we have that the integrand in $I_3$ is nonnegative precisely in the set where $u(x, t) \ge u(y, t)$. In view of this, we observe that $I_3$ can be estimated from above in the following way,

$$\begin{aligned} \begin{aligned} I_3&=\int _{t_1}^{t_2}\int _{\mathbb {R}^n\setminus B_r}\int _{B_r}|u(x,t)-u(y,t)|^{p-2}(u(x,t)-u(y,t))u(x,t)^{-\epsilon }\psi (x)^p\eta (t)\,d\mu \,dt\\&\le \int _{t_1}^{t_2}\int _{\mathbb {R}^n\setminus B_r}\int _{B_r} u(x,t)^{p-\epsilon -1}\psi (x)^p\eta (t)\,d\mu \,dt\\&\le C(\Lambda )\sup _{x\in \text {supp}\,\psi }\int _{\mathbb {R}^n\setminus B_r}\frac{dy}{|x-y|^{n+sp}}\int _{t_1}^{t_2}\int _{B_r}u(x,t)^{p-\epsilon -1}\psi (x)^p\eta (t)\,dx\,dt. \end{aligned} \end{aligned}$$

(5.3)

Then we note that $I_2$ can be estimated using Lemma 2.9 as follows,

$$\begin{aligned} \begin{aligned} I_2&\le -\frac{\zeta (\epsilon )}{C(p)}\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}\big |\psi (x)u(x,t)^\frac{\alpha }{p}-\psi (y)u(y,t)^\frac{\alpha }{p}\big |^p\eta (t)\,d\mu \, dt\\&\qquad +\Big (\zeta (\epsilon )+1+\frac{1}{\epsilon ^{p-1}}\Big )\int _{t_1}^{t_2}\int _{B_r}\int _{B_r}|\psi (x)-\psi (y)|^p(u(x,t)^\alpha +u(y,t)^\alpha )\eta (t)\,d\mu \, dt. \end{aligned} \end{aligned}$$

(5.4)

For $I_1$ we have

$$\begin{aligned} \begin{aligned} I_1&=-\frac{p-1}{p-\epsilon -1}\int _{B_r}u^{p-\epsilon -1}(x,t_1)\psi (x)^p\,dx\\&\qquad -\frac{p-1}{p-\epsilon -1}\int _{t_1}^{t_2}\int _{B_r}u(x,t)^{p-\epsilon -1}\psi (x)^p\partial _{t}\eta (t)\,dx\,dt. \end{aligned} \end{aligned}$$

(5.5)

Now using (5.3), (5.4), (5.5) into (5.2) and letting $t_1\rightarrow \tau _1$, we obtain

$$\begin{aligned} \begin{aligned}&\frac{\zeta (\epsilon )}{C(p)}\int _{\tau _1}^{\tau _2+l}\int _{B_r}\int _{B_r}\big |\psi (x)u(x,t)^\frac{\alpha }{p}-\psi (y)u(y,t)^\frac{\alpha }{p}\big |^p \eta (t)\,d\mu \,dt\\&\le \Big (\zeta (\epsilon )+1+\frac{1}{\epsilon ^{p-1}}\Big )\int _{\tau _1}^{\tau _2+l}\int _{B_r}\int _{B_r}|\psi (x)-\psi (y)|^p(u(x,t)^\alpha +u(y,t)^\alpha )\eta (t)\,d\mu \,dt\\&\qquad +C(\Lambda )\sup _{x\in \text { supp }\psi }\int _{\mathbb {R}^n\setminus B_r}\frac{dy}{|x-y|^{n+sp}}\int _{\tau _1}^{\tau _2+l}\int _{B_r}u(x,t)^\alpha \psi (x)^p\eta (t)\,dx\,dt\\&\qquad +\frac{p-1}{\alpha }\int _{\tau _1}^{\tau _2+l}\int _{B_r}u(x,t)^\alpha \psi (x)^p|\partial _t\eta (t)|\,dx\,dt. \end{aligned} \end{aligned}$$

(5.6)

We then choose $t_1$ such that

$$\begin{aligned} \int _{B_r}u(x,t_1)^{p-\epsilon -1}\psi (x)^p\,dx\ge \frac{1}{2}\sup _{\tau _1<t<\tau _2}\int _{B_r}u(x,t)^{p-\epsilon -1}\psi (x)^p\,dx. \end{aligned}$$

(5.7)

Again using (5.3), (5.4), (5.5) and (5.7), we get

$$\begin{aligned} \begin{aligned}&\frac{p-1}{\alpha }\sup _{\tau _1<t<\tau _2}\int _{B_r}\psi (x)^p u(x,t)^\alpha \,dx\\&\le \Big (\zeta (\epsilon )+1+\frac{1}{\epsilon ^{p-1}}\Big )\int _{\tau _1}^{\tau _2+l}\int _{B_r}\int _{B_r}|\psi (x)-\psi (y)|^p(u(x,t)^\alpha +u(y,t)^\alpha )\eta (t)\,d\mu \,dt\\&\qquad +C(\Lambda )\sup _{x\in \text { supp }\psi }\int _{\mathbb {R}^n\setminus B_r}\frac{dy}{|x-y|^{n+sp}}\int _{\tau _1}^{\tau _2+l}\int _{B_r}u(x,t)^\alpha \psi (x)^p\eta (t)\,dx\,dt\\&\qquad +\frac{p-1}{\alpha }\int _{\tau _1}^{\tau _2+l}\int _{B_r}u(x,t)^\alpha \psi (x)^p|\partial _t\eta (t)|\,dx\,dt. \end{aligned} \end{aligned}$$

(5.8)

Therefore from (5.6) and (5.8) we get the required estimate. $\square$

Following the energy estimate, we now proceed with the proof of the reverse H$\ddot{\text {o}}$lder inequality for strictly positive supersolutions as in Theorem 2.17.

Proof of Theorem 2.17 Let $0<s<1$ and $\kappa =\frac{n+sp}{n}$ if $sp<n$ and $\kappa =\frac{3}{2}$ if $sp\ge n$. Let us denote by

$$\begin{aligned} r_0=r, \quad r_j=\Big (1-(1-\theta )\frac{1-2^{-j}}{(1-2^{-m})}\Big )r, \quad \delta _j=2^{-j}r,\quad j=1,2,\dots ,m \end{aligned}$$

and $U_j=B_j\times \Gamma _j=B_{r_j}(x_0)\times (t_0,t_0+r_{j}^{sp})$. We shall fix m later. Now we choose nonnegative test functions $\psi _j\in C_{0}^\infty (B_j)$ such that $0\le \psi _j\le 1$ in $B_j$, $\psi _j\equiv 1$ in $B_{j+1}$, $|\nabla \psi _j|\le \frac{2^{j+3}}{(1-\theta )r}$ and $\text {dist}\,(\text {supp}\,\psi _j,\mathbb {R}^n\setminus B_j)\ge \frac{\delta _j(1-\theta )}{2}$. Moreover, we choose $\eta _j\in C^\infty (\Gamma _j)$ such that $0\le \eta _j\le 1$ in $\Gamma _j$, $\eta _j\equiv 1$ in $\Gamma _{j+1}$, and $|\partial _t\eta _j|\le \frac{2^{sp(j+3)}}{(1-\theta )r^{sp}}$, $\eta _j(t)=0$ if $t\ge t_0+r_j^{sp}$. Let $\alpha =p-\epsilon -1$ where $\epsilon \in (0,p-1)$. Then $\alpha \in (0,p-1)$. Denote by $v=u^\frac{\alpha }{p}$. Let $r=r_j$, $\tau _1=t_0$, $\tau _2=t_0+r_{j+1}^{sp}$, $l=r_j^{sp}-r_{j+1}^{sp}$. Let $\kappa =\frac{n+sp}{n}$ and $\kappa ^*=\frac{n}{n-sp}$ if $sp<n$, and $\kappa =\frac{3}{2}$, $\kappa ^*=2$ if $sp\ge n$. Then noting that $\frac{p\kappa ^*(\kappa -1)}{\kappa ^*-1}=p$, by the Sobolev embedding theorem (Lemma 2.4), we obtain for some positive constant $C=C(n,p,s)$ that the following inequality holds,

$$\begin{aligned} \begin{aligned} \int _{\Gamma _{j+1}}\fint _{B_{j+1}}v^{p\kappa }\,dx\,dt&\le C\Big (r_{j+1}^{sp-n} I_1+\int _{\Gamma _{j+1}}\fint _{B_{j+1}}v^p\,dx dt\Big )\cdot \Big (\frac{I_2}{|B_{j+1}|}\Big )^{\kappa -1}, \end{aligned} \end{aligned}$$

(5.9)

where

$$\begin{aligned} I_1=\int _{\Gamma _{j+1}}\int _{B_{j+1}}\int _{B_{j+1}}\frac{|v(x,t)-v(y,t)|^p}{|x-y|^{n+sp}}\,dx\,dy\,dt, \end{aligned}$$

and

$$\begin{aligned} I_2=\sup _{\Gamma _{j+1}}\int _{B_{j+1}}v^p\,dx. \end{aligned}$$

Using the fact that $\psi _j \equiv 1$ on $B_{j+1}$ and also that $\eta _j \equiv 1$ on $\Gamma _{j+1}$, we obtain using Lemma 5.2 that the following holds,

$$\begin{aligned} I_1, I_2\le C(J_1+J_2+J_3), \end{aligned}$$

(5.10)

for some positive constant C which is independent of $\alpha$ as long as $\alpha$ is away from $p-1$, where

$$\begin{aligned} \begin{aligned} J_1&=\int _{\Gamma _j}\int _{B_j}\int _{B_j}(v(x,t)^p+v(y,t)^p)\frac{|\psi _j(x)-\psi _j(y)|^p}{|x-y|^{n+sp}}\eta _j(t)\,dx\,dy\,dt\\&\le C\frac{2^{j(n+sp+p)}}{(1-\theta )^p r_j^{sp}}\int _{\Gamma _j}\int _{B_j}v(x,t)^p\,dx\,dt, \end{aligned} \end{aligned}$$

(5.11)

since $r_j<r$,

$$\begin{aligned} \begin{aligned} J_2&=\sup _{x\in \text {supp}\,\psi _{j}}\int _{\mathbb {R}^n\setminus B_j}\frac{dy}{|x-y|^{n+sp}}\int _{\Gamma _j}\int _{B_j}v(x,t)^p\psi _j(x)^p\eta _j(t)\,dx\,dt\\&\le C\frac{2^{j(n+sp+p)}}{r_j^{sp}}\int _{\Gamma _j}\int _{B_j}v(x,t)^p\,dx\,dt, \end{aligned} \end{aligned}$$

(5.12)

and

$$\begin{aligned} J_3=\int _{\Gamma _j} \int _{B_j}\psi _j(x)^p v(x,t)^p|\partial _{t}\eta _j(t)|\,dx\,dt \le C\frac{2^{ps(j+3)}}{(1-\theta )r_j^{sp}}\int _{\Gamma _j}\int _{B_j}v(x,t)^{p}\,dx\,dt, \end{aligned}$$

(5.13)

again since $r_j < r$.

Therefore, using (5.11), (5.12) and (5.13) into (5.10) we obtain

$$\begin{aligned} \begin{aligned} I_1, I_2&\le C\frac{2^{j(n+sp+p)}}{(1-\theta )^pr_j^{sp}}\int _{\Gamma _j}\int _{B_j}v(x,t)^p\,dx\,dt, \end{aligned} \end{aligned}$$

(5.14)

for some positive constant C independent of $\alpha$ as long as $\alpha$ is away from $p-1$, but may depend on $n,p,s,\Lambda$.

Using the estimate (5.14) and the fact that $r_{j+1}<r_j<2 r_{j+1}$ for every j, we obtain from (5.9), since $v=u^\frac{\alpha }{p}$ that

$$\begin{aligned} \fint _{U_{j+1}}u^{\kappa \alpha }\, dx\, dt\le C\Big (\frac{2^{j(n+sp+p)}}{(1-\theta )^{p}}\fint _{U_{j}}u^{\alpha }\,dx\, dt\Big )^\kappa , \end{aligned}$$

(5.15)

for some positive constant C independent of $\alpha$ (given that our choice of $\alpha$ will be away from $p-1$ ) but may depend on $n,p,s,\Lambda$. Now we use Moser iteration technique into (5.15). Let us fix $q,\bar{q}$ such that $0<\bar{q}<q<q_0=\kappa (p-1)$ and m such that $\bar{q}\kappa ^{m-1}\le q\le \bar{q}\kappa ^{m}$. Let $t_0=\frac{q}{\kappa ^m}$, then $t_0\le \bar{q}$. Denote by $t_j=\kappa ^{j}t_0$ for $j=0,1,\cdots ,m$. Then observing that $r_m=\theta r$ and $r_0=r$, we get $U_m=U^{+}(\theta r)$ and $U_0=U^{+}(r)$. Hence by (5.15), we obtain

$$\begin{aligned} \Big (\fint _{U^{+}{(\theta r)}}u^q\,dx\, dt\Big )^\frac{1}{q}&=\Big (\fint _{U_{m}}u^q\,dx\, dt\Big )^\frac{1}{q}\\&\le \Big (\frac{C 2^{\frac{(n+sp+p)m}{p}}}{(1-\theta )}\Big )^\frac{p}{t_{m-1}}\Big (\fint _{U_{m-1}}u^{t_{m-1}}\,dx\, dt\Big )^\frac{1}{t_{m-1}}\\&\le \Big (\frac{C_{\text {prod}}(m)}{(1-\theta )^{m^{*}}}\fint _{U^{+}(r)}u^{t_0}\,dx\, dt\Big )^\frac{1}{t_0}, \end{aligned}$$

where

$$\begin{aligned} C_{\text {prod}}(m)= C^{m^{*}}\prod _{j=0}^{m-1}\Big (2^{{\frac{n+sp+p}{p}}(j+1)}\Big )^{p\kappa ^{-j}}, \end{aligned}$$

and

$$\begin{aligned} m^{*}=p\sum _{j=0}^{m-1}\kappa ^{-j}=\frac{p\kappa }{\kappa -1}(1-\kappa ^{-m}). \end{aligned}$$

It can be easily seen that $C_{\text {prod}}(m)$ is a positive constant uniformly bounded on m, where C is independent of $\bar{q}$ but depends on q due to the singularity of the constants involved in the energy inequality in Lemma 5.2 at $\epsilon =0$. Finally using H$\ddot{\text {o}}$lder’s inequality, we obtain

$$\begin{aligned} \begin{aligned} \Big (\fint _{U^{+}(\theta r)}u^{q}\,dx\, dt\Big )^\frac{1}{q}\le \Big (\frac{C}{(1-\theta )^{m^{*}}}\Big )^\frac{1}{t_0}\Big (\fint _{U^{+}(r)}u^{\bar{q}}\,dx\, dt\Big )^\frac{1}{\bar{q}}. \end{aligned} \end{aligned}$$

Now, since $\bar{q}\kappa ^{m-1}\le t_0\kappa ^{m}$, we have $t_0\ge \frac{\bar{q}}{\kappa }$. As a consequence the required estimate follows with $\mu =\frac{p\kappa ^2}{\kappa -1}$.

In closing, we prove the following logarithmic estimate for strictly positive supersolutions which constitutes the nonlocal analogue of Lemma 6.1 in [4] and also constitutes one of the key ingredients in the proof of weak Harnack in the local case.

Lemma 5.3

Let $p>2$, $x_0\in \mathbb {R}^n$, $r>0$ and $t_0\in (r^{ps},T-r^{ps})$ with $B_{\frac{3r}{2}}=B_{\frac{3r}{2}}(x_0)\Subset \Omega$ and $(t_0-r^{sp},t_0+r^{sp})\Subset (0,T)$. Suppose that $u\in L^\infty (0,T;L^\infty (\mathbb {R}^n))\cap C_{\mathrm {loc}}(0,T;L^p_{\mathrm {loc}}(\Omega ))\cap L^p_{\mathrm {loc}}(0,T;W_{\mathrm {loc}}^{s,p}(\Omega ))$ is a weak supersolution of (1.1) in $\Omega \times (0,T)$ with $u\ge \rho >0$ in $\mathbb {R}^n\times (t_0-r^{sp},t_0+r^{sp})$. Then for every $\lambda >0$, there exists a positive constant $C=C(n,p,s,\Lambda )$ such that

$$\begin{aligned} \big |\{(x,t)\in U^{+}(x_0,t_0,r):\log u(x,t)<-\lambda -b\}\big |\le \frac{Cr^{n+sp}}{\lambda ^{p-1}} \end{aligned}$$

(5.16)

and

$$\begin{aligned} \big |\{(x,t)\in U^{-}(x_0,t_0,r):\log u(x,t)>\lambda -b\}\big |\le \frac{Cr^{n+sp}}{\lambda ^{p-1}} \end{aligned}$$

(5.17)

where

$$\begin{aligned} b=b(u(\cdot ,t_0))= - \frac{\int _{B_{\frac{3r}{2}}(x_0)} \log u(x,t_0)\psi (x)^p\,dx}{\int _{B_{\frac{3r}{2}}(x_0)}\psi (x)^{p}\,dx}. \end{aligned}$$

Proof

Following Lemma 6.1 in [4], we only prove (5.16) because the proof of (5.17) is analogous. Without loss of generality, we may assume $x_0=0$. Let $\psi \in C_0^{\infty }(B_{\frac{3r}{2}})$ be a nonnegative radially decreasing function such that $0\le \psi \le 1$ in $B_\frac{3r}{2}$, $\psi \equiv 1$ in $B_r$, $|\nabla \psi |\le \frac{C}{r}$ in $B_\frac{3r}{2}$. Since u is a strictly positive supersolution of (1.1), choosing $\phi (x,t)=\psi (x)^p u(x,t)^{1-p}$ as a test function in (2.6), we get

$$\begin{aligned} I_1+I_2+2I_3\ge 0, \end{aligned}$$

(5.18)

where for any $t_0-r^{sp}\le t_1<t_2\le t_0+r^{sp}$, we have

$$\begin{aligned}&I_1=\int _{t_1}^{t_2}\int _{B_{\frac{3r}{2}}}\frac{\partial }{\partial t}(u(x,t)^{p-1})\phi (x,t)\,dx\, dt =(p-1)\int _{B_{\frac{3r}{2}}}\log \,u(x,t)\psi (x)^p\,dx\Big |_{t=t_1}^{t_2}, \nonumber \\&I_2=\int _{t_1}^{t_2}\int _{B_{\frac{3r}{2}}}\int _{B_{\frac{3r}{2}}}\mathcal {A}(u(x,y,t))(\phi (x,t)-\phi (y,t))\,d\mu \, dt, \end{aligned}$$

(5.19)

and

$$\begin{aligned} I_3=\int _{t_1}^{t_2}\int _{\mathbb {R}^n\setminus B_{\frac{3r}{2}}}\int _{B_{\frac{3r}{2}}}\mathcal {A}(u(x,y,t))\phi (x,t)\,d\mu \, dt. \end{aligned}$$

Following the arguments in the proof of [12, Lemma 1.3], we obtain for some positive constant $C=C(p)$,

$$\begin{aligned} \begin{aligned} I_2&=\int _{t_1}^{t_2}\int _{B_{\frac{3r}{2}}}\int _{B_{\frac{3r}{2}}}\mathcal {A}(u(x,y,t))(\phi (x,t)-\phi (y,t))\,d\mu \, dt\\&\le -\frac{1}{C}\int _{t_1}^{t_2}\int _{B_{\frac{3r}{2}}}\int _{B_{\frac{3r}{2}}}K(x,y,t)|\log \,u(x,t)-\log \,u(y,t)|^p \psi (y)^p\,dx\, dy\, dt\\&\qquad +C\int _{t_1}^{t_2}\int _{B_{\frac{3r}{2}}}\int _{B_{\frac{3r}{2}}}K(x,y,t)|\psi (x)-\psi (y)|^p\,dx\, dy\, dt\\&\le -\frac{1}{C}\int _{t_1}^{t_2}\int _{B_{\frac{3r}{2}}}\int _{B_{\frac{3r}{2}}}K(x,y,t)|\log \,u(x,t)-\log \,u(y,t)|^p \psi (y)^p\,dx\, dy\, dt\\&\qquad +C(t_2-t_1)r^{n-sp}, \end{aligned} \end{aligned}$$

(5.20)

where the last inequality is obtained using the properties of $\psi$. Again following the proof of [12, Lemma 1.3], we get that

$$\begin{aligned} I_3=\int _{t_1}^{t_2}\int _{\mathbb {R}^n\setminus B_{\frac{3r}{2}}}\int _{B_{\frac{3r}{2}}}\mathcal {A}(u(x,y,t))\phi (x,t)\,d\mu \, dt \le C(t_2-t_1)r^{n-sp}. \end{aligned}$$

(5.21)

Therefore using the estimates (5.19), (5.20) and (5.21) into (5.18), we obtain

$$\begin{aligned} \begin{aligned} \frac{1}{C}\int _{t_1}^{t_2}\int _{B_{\frac{3r}{2}}}\int _{B_{\frac{3r}{2}}}K(x,y,t)|\log \,u(x,t)-\log \,u(y,t)|^p \psi (y)^p\,dx\, dy\, dt\\ -(p-1)\int _{B_{\frac{3r}{2}}}\log \,u(x,t)\psi (x)^p\,dx\Big |_{t=t_1}^{t_2}\le C(t_2-t_1)r^{n-sp}. \end{aligned} \end{aligned}$$

(5.22)

Let $v(x,t)=-\log \,u(x,t)$ and

$$\begin{aligned} V(t)=\frac{\int _{B_{\frac{3r}{2}}}v(x,t)\psi (x)^p\,dx}{\int _{B_{\frac{3r}{2}}}\psi (x)^{p}\,dx}. \end{aligned}$$

Since $0\le \psi \le 1$ in $B_{\frac{3r}{2}}$ and $\psi \equiv 1$ in $B_r$, therefore we have that $\int _{B_{\frac{3r}{2}}}\psi (x)^p\,dx\approx r^n$. Hence dividing by $\int _{B_{\frac{3r}{2}}}\psi (x)^p\,dx$ on both sides of (5.22), we obtain using the weighted Poincaré inequality in Lemma 2.6 that the following holds,

$$\begin{aligned} V(t_2)-V(t_1)+\frac{r^{-sp}}{c(p-1)}\int _{t_1}^{t_2}\fint _{B_r}|v(x,t)-V(t)|^p\,dx\, dt\le \frac{cr^{-sp}}{p-1}(t_2-t_1). \end{aligned}$$

Let $A_1=C(p-1)$, $A_2=\frac{C}{p-1}$,

$$\begin{aligned} \bar{w}(x,t)=v(x,t)-A_2 r^{-sp}(t-t_1) \quad \text {and}\quad \bar{W}(t)=V(t)-A_2 r^{-sp}(t-t_1). \end{aligned}$$

Therefore $v(x,t)-V(t)=\bar{w}(x,t)-\bar{W}(t)$. Hence, we get

$$\begin{aligned} \bar{W}(t_2)-\bar{W}(t_1)+\frac{1}{A_1 r^{n+sp}}\int _{t_1}^{t_2}\int _{B_r}|\bar{w}(x,t)-{\bar{W}(t)}|^p\, dx\, dt\le 0. \end{aligned}$$

(5.23)

Therefore, $\bar{W}(t)$ is a monotone decreasing function in $t_0-r^{sp}\le t_1<t_2\le t_0+r^{sp}$. Hence, $\bar{W}(t)$ is differentiable almost everywhere with respect to t. Dividing by $t_2-t_1$ on both sides of (5.23), we obtain after letting $t_2\rightarrow t_1$,

$$\begin{aligned} \bar{W}'(t)+\frac{1}{A_1 r^{n+sp}}\int _{B_r}\big |\bar{w}(x,t)-\bar{W}(t)\big |^p\,dx\le 0. \end{aligned}$$

(5.24)

Let $t_1=t_0$, then $\bar{W}(t_0)=V(t_0)$ and we denote by $b(u(\cdot ,t_0))= \bar{W}(t_0)$. Let

$$\begin{aligned} \Omega _{t}^{+}(\lambda )=\big \{x\in B_r:\bar{w}(x,t)>b+\lambda \big \}. \end{aligned}$$

Then for any $x\in \Omega _{t}^{+}(\lambda )$ and $t\ge t_0$, since $\bar{W}(t)\le \bar{W}(t_0)=b$, we have

$$\begin{aligned} \bar{w}(t,x)-\bar{W}(t)\ge b+\lambda -\bar{W}(t)\ge b+\lambda -\bar{W}(t_0)=\lambda >0. \end{aligned}$$

Hence from (5.24), we have

$$\begin{aligned} \bar{W}'(t)+\frac{|\Omega _{t}^{+}(\lambda )|}{A_1 r^{n+sp}}\big (b+\lambda -\bar{W}(t)\big )^p\le 0. \end{aligned}$$

Therefore, we have

$$\begin{aligned} |\Omega _{t}^{+}(\lambda )|\le -\frac{A_1 r^{n+sp}}{p-1}\partial _{t}\big (b+\lambda -\bar{W}(t)\big )^{1-p}. \end{aligned}$$

Integrating over $t_0$ to $t_0+r^{sp}$, we obtain

$$\begin{aligned}&\big |\{(x,t)\in B_r\times (t_0,t_0+r^{sp}):\bar{w}(x,t)>b+\lambda \}\big |\\&\quad \le -\frac{A_1 r^{n+sp}}{p-1}\int _{t_0}^{t_0+r^{sp}}\partial _{t}\big (b+\lambda -\bar{W}(t)\big )^{1-p}\,dt, \end{aligned}$$

which gives

$$\begin{aligned} \big |\{(x,t)\in B_r\times (t_0,t_0+r^{sp}):\log \,u(x,t)+A_2 r^{-sp}(t-t_0)<-\lambda -b\}\big |\le \frac{A_1}{p-1}\frac{r^{n+sp}}{\lambda ^{p-1}}. \end{aligned}$$

(5.25)

Finally, we note that

$$\begin{aligned} \big |\{(x,t)\in B_r\times (t_0,t_0+r^{sp}):\log \,u(x,t)<-\lambda -b\}\big |\le A+B, \end{aligned}$$

(5.26)

where

$$\begin{aligned} A=\big |\{(x,t)\in B_r\times (t_0,t_0+r^{sp}):\log \,u(x,t)+A_2 r^{-sp}(t-t_0)<-\tfrac{\lambda }{2}-b\}\big | \le \frac{Cr^{n+sp}}{\lambda ^{p-1}}, \end{aligned}$$

which follows from (5.25) and

$$\begin{aligned} B=\big |\{(x,t)\in B_r\times (t_0,t_0+r^{sp}):A_2 r^{-sp}(t-t_0)>\tfrac{\lambda }{2}\}\big | \le \Big (1-\frac{\lambda }{2A_2}\Big )r^{n+sp}. \end{aligned}$$

If $\frac{\lambda }{2 A_2}<1$, then

$$\begin{aligned}B\le \Big (1-\frac{\lambda }{2A_2}\Big )r^{n+sp}<r^{n+sp}<\Big (\frac{2 A_2}{\lambda }\Big )^{p-1}r^{n+sp}.\end{aligned}$$

If $\frac{\lambda }{2 A_2}\ge 1$, then $B = 0$. Hence in either case we have

$$\begin{aligned} B\le \frac{Cr^{n+sp}}{\lambda ^{p-1}}. \end{aligned}$$

Inserting the above estimates of A and B into (5.26), we obtain

$$\begin{aligned} \big |\{(x,t)\in B_r\times (t_0,t_0+r^{sp}):\log \,u(x,t)<-\lambda -b\}\big |\le \frac{Cr^{n+sp}}{\lambda ^{p-1}}, \end{aligned}$$

for some positive constant $C=C(n,p,s,\Lambda )$, which proves (5.16). The proof of (5.17) is analogous. $\square$

Appendix

In this section, we prove Lemma 2.9. To this end, we establish the following auxiliary lemmas. Throughout this section, we assume $p>1$.

Lemma 6.1

Let $f,g\in C^1([a,b])$. Then

$$\begin{aligned} \frac{f(b)-f(a)}{b-a}+\Big |\frac{g(b)-g(a)}{b-a}\Big |^p\le \max _{t\in [a,b]}\big [f'(t)+|g'(t)|^p\big ]. \end{aligned}$$

Proof

Suppose the result does not hold, then by contradiction, we get

$$\begin{aligned} \frac{f(b)-f(a)}{b-a}+\Big |\frac{g(b)-g(a)}{b-a}\Big |^p>f'(t)+|g'(t)|^p, \end{aligned}$$

for all $t\in [a,b]$. Integrating over a to b, we obtain

$$\begin{aligned} \Big |\frac{g(b)-g(a)}{b-a}\Big |^p>\frac{1}{b-a}\int _{a}^{b}|g'(t)|^p\,dt, \end{aligned}$$

which contradicts Jensen’s inequality. $\square$

Lemma 6.2

Let $a,b>0$, $0<\epsilon <p-1$. Then we have

$$\begin{aligned} |b-a|^{p-2}(b-a)(a^{-\epsilon }-b^{-\epsilon })\ge \zeta (\epsilon )\Big |b^\frac{p-\epsilon -1}{p}-a^\frac{p-\epsilon -1}{p}\Big |^p, \end{aligned}$$

where $\zeta (\epsilon )=\frac{p^p\epsilon }{(p-\epsilon -1)^p}$. Moreover, if $0<p-\epsilon -1<1$, then we may choose $\zeta (\epsilon )=\frac{p^p\epsilon }{p-\epsilon -1}$.

Proof

Let $0<\epsilon <p-1$ and $\zeta (\epsilon )=\frac{p^p\epsilon }{(p-\epsilon -1)^p}$. Let $f(t)=\frac{t^{-\epsilon }}{\zeta (\epsilon )}$ and $g(t)=t^\frac{p-\epsilon -1}{p}$. By Lemma 6.1, we have

$$\begin{aligned} \frac{1}{\zeta (\epsilon )}\frac{b^{-\epsilon }-a^{-\epsilon }}{b-a}+\Big |\frac{b^\frac{p-\epsilon -1}{p}-a^\frac{p-\epsilon -1}{p}}{b-a}\Big |^p\le 0. \end{aligned}$$

If $b\ge a$, multiplying by $(b-a)^p$, we obtain

$$\begin{aligned} (b-a)^{p-1}(a^{-\epsilon }-b^{-\epsilon })\ge \zeta (\epsilon )\big |b^\frac{p-\epsilon -1}{p}-a^\frac{p-\epsilon -1}{p}\big |^p. \end{aligned}$$

(6.1)

If $b<a$, interchanging a and b, the Lemma follows. If $0<p-\epsilon -1<1$, then we have $0<(p-\epsilon -1)^p<p-\epsilon -1$, therefore $\zeta (\epsilon )\ge \frac{p^p\epsilon }{p-\epsilon -1}$ and (6.1) implies

$$\begin{aligned} (b-a)^{p-1}(a^{-\epsilon }-b^{-\epsilon })\ge \frac{p^p\epsilon }{p-\epsilon -1}\Big |b^\frac{p-\epsilon -1}{p}-a^\frac{p-\epsilon -1}{p}\Big |^p. \end{aligned}$$

Hence the claim follows with $\zeta (\epsilon )=\frac{p^p\epsilon }{p-\epsilon -1}$ when $0<p-\epsilon -1<1$. $\square$

1.1 Proof of Lemma 2.9

We denote the left-hand and right-hand sides of (2.3) by L.H.S and R.H.S, respectively. Let $\zeta _1(\epsilon )=\frac{\zeta (\epsilon )}{c(p)}$ and $\zeta _2(\epsilon )=\zeta (\epsilon )+1+\frac{1}{\epsilon ^{p-1}}$. Then $\zeta _1(\epsilon )-\zeta _2(\epsilon )<-1$ since $C(p)>1$ (to be finally chosen appropriately).

Case 1. If $\tau _1=\tau _2=0$, then (2.3) holds trivially.

Case 2. If $\tau _1>0$ and $\tau _2=0$. In this case, we note that if $b>a$, then

$$\begin{aligned} \text {L.H.S}=|b-a|^{p-2}(b-a)(\tau _1^{p}a^{-\epsilon }-\tau _2^{p}b^{-\epsilon })=(b-a)^{p-1}\tau _1^{p}a^{-\epsilon } \end{aligned}$$

and

$$\begin{aligned} \text {R.H.S}&=\zeta _1(\epsilon )\tau _1^{p}a^{p-\epsilon -1}-\zeta _2(\epsilon )\tau _1^{p}(b^{p-\epsilon -1}+a^{p-\epsilon -1})\\&=(\zeta _1(\epsilon )-\zeta _2(\epsilon ))\tau _1^{p}a^{p-\epsilon -1}-\zeta _2(\epsilon )\tau _1^{p}b^{p-\epsilon -1}. \end{aligned}$$

Now L.H.S is positive and since $\zeta _1(\epsilon )-\zeta _2(\epsilon )<0$ and $\zeta _2(\epsilon )>0$, the R.H.S is negative. Therefore, we have L.H.S $\ge$ R.H.S. On the other hand if $b\le a$, then

$$\begin{aligned} \text {L.H.S}&=-(a-b)^{p-1}\tau _1^{p}a^{-\epsilon }\ge -\tau _1^{p}a^{p-\epsilon -1}, \end{aligned}$$

and since $\zeta _1(\epsilon )-\zeta _2(\epsilon )<-1$ and $\zeta _2(\epsilon )>0$, we have

$$\begin{aligned} \text {R.H.S}=(\zeta _1(\epsilon )-\zeta _2(\epsilon ))\tau _1^{p}a^{p-\epsilon -1}-\zeta _2(\epsilon )\tau _1^{p}b^{p-\epsilon -1} <-\tau _1^{p}a^{p-\epsilon -1} \le \text {L.H.S}. \end{aligned}$$

Case 3. If $\tau _1=0$ and $\tau _2>0$. Then we have

$$\begin{aligned} \text {L.H.S}=-|b-a|^{p-2}(b-a)\tau _2^{p}b^{-\epsilon }, \end{aligned}$$

and

$$\begin{aligned} \text {R.H.S}&=(\zeta _1(\epsilon )-\zeta _2(\epsilon ))\tau _2^{p}b^{p-\epsilon -1}-\zeta _2(\epsilon )\tau _2^{p}a^{p-\epsilon -1}. \end{aligned}$$

If $b>a$, then

$$\begin{aligned} \text {L.H.S}=-(b-a)^{p-1}\tau _2^{p}b^{-\epsilon }\ge -\tau _2^{p}b^{p-\epsilon -1}, \end{aligned}$$

and since $\zeta _1(\epsilon )-\zeta _2(\epsilon )<-1$ and $\zeta _2(\epsilon )>0$, we have

$$\begin{aligned} \text {R.H.S}=(\zeta _1(\epsilon )-\zeta _2(\epsilon ))\tau _2^{p}b^{p-\epsilon -1}-\zeta _2(\epsilon )\tau _2^{p}a^{p-\epsilon -1}\\ <-\tau _2^{p}b^{p-\epsilon -1} \le \text {L.H.S}. \end{aligned}$$

If $b\le a$, then the L.H.S is nonnegative and the R.H.S is negative. Therefore, we have $\text {L.H.S}\ge \text {R.H.S}$.

Case 4. Let both $\tau _1,\tau _2>0$. By symmetry, we may assume that $b\ge a$. Let $t=\frac{b}{a}\ge 1$, $s=\frac{\tau _2}{\tau _1}>0$ and $\lambda =s^{p}t^{-\epsilon }$. It can be easily seen that the inequality (2.3) is equivalent to the following inequality

$$\begin{aligned} \zeta _1(\epsilon )|s t^\frac{p-\epsilon -1}{p}-1|^p\le (t-1)^{p-1}(1-\lambda )+\zeta _2(\epsilon )|s-1|^p(t^{p-\epsilon -1}+1). \end{aligned}$$

(6.2)

We first estimate the following term.

$$\begin{aligned} |st^\frac{p-\epsilon -1}{p}-1|^p&=|st^\frac{p-\epsilon -1}{p}-t^\frac{p-\epsilon -1}{p}+t^\frac{p-\epsilon -1}{p}-1|^p\\&=|(s-1)t^\frac{p-\epsilon -1}{p}+(t^\frac{p-\epsilon -1}{p}-1)|^p\\&\le 2^{p-1}|s-1|^p t^{p-\epsilon -1}+2^{p-1}|t^\frac{p-\epsilon -1}{p}-1|^p\\&=A+B, \end{aligned}$$

where

$$\begin{aligned} A=2^{p-1}|s-1|^p t^{p-\epsilon -1}\text { and }B=2^{p-1}|t^\frac{p-\epsilon -1}{p}-1|^p. \end{aligned}$$

By Lemma 6.2, we have

$$\begin{aligned} B\le \frac{2^{p-1}(t-1)^{p-1}(1-t^{-\epsilon })}{\zeta (\epsilon )}. \end{aligned}$$

As a consequence, we obtain

$$\begin{aligned} |st^\frac{p-\epsilon -1}{p}-1|^p\le 2^{p-1}|s-1|^p t^{p-\epsilon -1}+\frac{2^{p-1}(t-1)^{p-1}(1-t^{-\epsilon })}{\zeta (\epsilon )}. \end{aligned}$$

We observe that

$$\begin{aligned} 1-t^{-\epsilon }&=1-\lambda +\lambda -t^{-\epsilon } =1-\lambda +(s^p-1)t^{-\epsilon }\\&=1-\lambda +|s-1|^p t^{-\epsilon }+(s^p-1-|s-1|^p)t^{-\epsilon }. \end{aligned}$$

Therefore, we get

$$\begin{aligned} \begin{aligned}&|s t^\frac{p-\epsilon -1}{p}-1|^p \le 2^{p-1}\big (1+\frac{1}{\zeta (\epsilon )}\big )|s-1|^p t^{p-\epsilon -1}\\&\qquad +\frac{2^{p-1}}{\zeta (\epsilon )}(t-1)^{p-1}(1-\lambda )+\frac{2^{p-1}}{\zeta (\epsilon )}(t-1)^{p-1}(s^p-1-|s-1|^p)t^{-\epsilon }. \end{aligned} \end{aligned}$$

(6.3)

Next we estimate the term $T=\frac{2^{p-1}}{\zeta (\epsilon )}(t-1)^{p-1}(s^p-1-|s-1|^p)t^{-\epsilon }$ for different values of t and s.

Case (a). If $t>1$ and $s\ge 2$. Then using the fact that $s\ge 2$, it can be easily seen that there exists constant C(p) large enough such that $s^p-1-(s-1)^p\le C(p)(s-1)^p$. Therefore, we get

$$\begin{aligned} T\le \frac{C(p)}{\zeta (\epsilon )}|s-1|^p t^{p-\epsilon -1}. \end{aligned}$$

(6.4)

By inserting (6.4) into (6.3), we get

$$\begin{aligned} \begin{aligned} |s t^\frac{p-\epsilon -1}{p}-1|^p\le C(p)\big (1+\frac{1}{\zeta (\epsilon )}\big )|s-1|^p t^{p-\epsilon -1}+\frac{C(p)}{\zeta (\epsilon )}(t-1)^{p-1}(1-\lambda ). \end{aligned} \end{aligned}$$

(6.5)

Case (b). If $t=1$ or $0<s\le 1$. Then $T\le 0$. Hence, we get the estimate in (6.5).

Case (c). If $t>1$, $s\in (1,2)$. Let $r\ge p$ be the nearest integer to p. Again it follows that there exists a positive constant C(p) large enough such that $s^p-1-|s-1|^p\le C(p)|s-1|$. We have further subcases.

Case (i). If

$$\begin{aligned}t-1<\frac{r 2^{r-1}}{\epsilon }t(s-1).\end{aligned}$$

Note that we can choose C(p) large enough such that $r 2^{r-1}\le C(p)$. Hence, we have

$$\begin{aligned} T\le \frac{C(p)}{\epsilon ^{p-1}\zeta (\epsilon )}t^{p-\epsilon -1}|s-1|^p. \end{aligned}$$

(6.6)

By inserting (6.6) into (6.3), we get

$$\begin{aligned} |s t^\frac{p-\epsilon -1}{p}-1|^p \le C(p)\Big (1+\frac{1}{\zeta (\epsilon )}\Big (1+\frac{1}{\epsilon ^{p-1}}\Big )\Big )|s-1|^p t^{p-\epsilon -1}+\frac{C(p)}{\zeta (\epsilon )}(t-1)^{p-1}(1-\lambda ). \end{aligned}$$

(6.7)

Case (ii). If

$$\begin{aligned}t-1\ge \frac{r 2^{r-1}}{\epsilon }t(s-1).\end{aligned}$$

Since r is an integer, we observe that

$$\begin{aligned} s^r+s-2=(s-1)(s^{r-1}+s^{r-2}+\cdots +s+2). \end{aligned}$$

By the mean value theorem there exists $\eta \in (1,t)$ such that $t^\epsilon -1=\epsilon \eta ^{\epsilon -1}(t-1)$ and so $\epsilon =\frac{t^\epsilon -1}{\eta ^{\epsilon -1}(t-1)}$. Now, we have

$$\begin{aligned} \frac{s^r+s-2}{t-1}&=\frac{s-1}{t-1}(s^{r-1}+s^{r-2}\cdots +s+2)\\&\le \frac{\epsilon }{r 2^{r-1}t}(s^{r-1}+s^{r-2}+\cdots +s+2)\\&\le \frac{\epsilon }{t} \le \frac{t^\epsilon -1}{t\eta ^{\epsilon -1}(t-1)}, \end{aligned}$$

which gives $t\eta ^{\epsilon -1}(s^r+s-2)\le t^\epsilon -1$.

Now, the fact $\epsilon >0$ and $1<\eta <t$ gives $t\eta ^{\epsilon -1}>\eta ^\epsilon >1$. Therefore since $r\ge p$ and $s>1$, we get $s^p+s-2<s^r+s-2<t\eta ^{\epsilon -1}(s^r+s-2)\le t^\epsilon -1$. Hence, we have $s-1\le t^\epsilon -s^p=t^\epsilon (1-\lambda )$. Thus

$$\begin{aligned} T\le \frac{C(p)}{\zeta (\epsilon )}(t-1)^{p-1}(1-\lambda ). \end{aligned}$$

(6.8)

Using (6.8) into (6.3) we get

$$\begin{aligned} |s t^\frac{p-\epsilon -1}{p}-1|^p\le C(p)\big (1+\frac{1}{\zeta (\epsilon )}\big )|s-1|^p t^{p-\epsilon -1}+\frac{C(p)}{\zeta (\epsilon )}(t-1)^{p-1}(1-\lambda ). \end{aligned}$$

(6.9)

Finally from the estimates (6.5), (6.7) and (6.9), we obtain

$$\begin{aligned} \begin{aligned} |st^\frac{p-\epsilon -1}{p}-1|^p\le C(p)\Big (1+\frac{1}{\zeta (\epsilon )}(1+\frac{1}{\epsilon ^{p-1}})\Big )|s-1|^p (t^{p-\epsilon -1}+1)\\+\frac{C(p)}{\zeta (\epsilon )}(t-1)^{p-1}(1-\lambda ). \end{aligned} \end{aligned}$$

(6.10)

Multiplying $\frac{\zeta (\epsilon )}{C(p)}$ on both sides of (6.10), we obtain

$$\begin{aligned} \frac{\zeta (\epsilon )}{C(p)}|st^\frac{p-\epsilon -1}{p}-1|^p\le \Big (\zeta (\epsilon )+1+\frac{1}{\epsilon ^{p-1}}\Big )|s-1|^p(t^{p-\epsilon -1}+1)+(t-1)^{p-1}(1-\lambda ), \end{aligned}$$

which corresponds to the inequality (6.2). The lemma thus follows.