1 The introduction

We compare the indirect utility of individuals without and with access to annuities and measure the relative loss of wealth for an individual with access to annuities who loses that access. We characterize the loss explicitly and study its sensitivity toward the interest rate, the market price of financial risk, the market price of insurance risk, and the level of uncertainty in the survival model. We characterize the loss for individuals with time-additive utility and individuals with separated time and risk preferences. Finally, we include in the comparison a particular suboptimal consumption plan without access to annuities, which might seem to be an appealing product design. All value functions are characterized explicitly such that all comparisons can be calculated directly as a solution to a nonlinear equation, and all numerical illustrations are presented accordingly.

A standard question in pensions is whether and when to annuitize pension savings. If annuities are flexible and market returns drive payments, the question is whether the individual should put his wealth at stake and pick up so-called mortality credits. This depends on what the individual wants to leave behind when he dies. If he does not annuitize, his wealth goes to his inheritors. If he annuitizes, he leaves nothing. What is optimal depends on the individual’s so-called utility from a bequest.

When discussing annuitization, it is relevant to quantify the benefit of annuitization to the annuitant. For example, if he has no demand for annuitization because his utility from bequest urges him not to annuitize, the value of the annuity market is zero. But what about the other extreme, where an annuitant wishes to annuitize fully? What is the maximal value of the annuity market to the annuitant? And how does this value depend on various parameters of the market and the mortality? These are the questions we wish to answer in this paper.

We answer these questions in a continuous-time life-cycle model where the annuitant can choose optimal consumption and investment in the decumulation phase. First, we calculate the individual’s lifetime utility in the decumulation phase in markets without and with access to annuitization. We then compare these lifetime utility measures by translating them into wealth proportions using certainty equivalents.

We focus on the decumulation phase exclusively. It is not until the decumulation phase that the annuity market becomes valuable to the individual, simply because mortality rates in the accumulation phase are so low that they can probably be partly neglected. Then we can appropriately avoid the mathematical complication it would take to study the accumulation phase. The point is that we need to be able to calculate lifetime consumption in a market without access to annuitization to compare the situations with and without annuitization. However, with uncertain lifetime and labor income in the saving phase, this problem has no explicit solution. This is disturbing both if the saving rate is residual to optimal consumption and if it is a fixed ratio of the labor income. In both cases, we need a unique financial value of a fixed payment stream, which does not exist in a market without access to annuitization. Therefore, we focus on the decumulation phase and avoid resorting to numerics for non-explicit solutions.

For optimizing consumption and investment, we work with the power utility function. We consider two different cases. One case is the so-called time-additive utility, where the risk aversion parameter covers both aversions toward risk and variation in consumption over time. Aversion toward time variation is the reciprocal of the so-called elasticity of intertemporal substitution. In another case, we separate risk and time preferences. There is no consensus about how this should be done under an uncertain lifetime. We briefly review the different proposals in the literature and continue to work with one of them.

The optimal consumption and investment without access to life insurance are purely flexible bank savings products. Therefore, one can speak of the optimal consumption and investment plan as an optimal banking product design. There are, of course, many different suboptimal product designs of both bank and annuity products, but we pay attention to a particular suboptimal bank product. That behaves as an annuity-certain based on the conditional residual expected lifetime. However, since the conditional residual expected lifetime does not decrease linearly with age, it works as an annuity-certain with a moving time horizon. We compare the individuals consuming optimally with and without access to annuitization, respectively, to the individual offered the ingenious suboptimal product.

The bibliographical starting point of our work is Richard (1975), who merged the consumption–insurance results by Yaari (1965) with the consumption–investment results by Merton (1971). This consumption–investment–insurance problem has been generalized in various directions since its revival in both the financial literature (see Pliska and Ye (2007)), and in the insurance literature, see Kraft and Steffensen (2008), contributing to closing some gaps between the financial and the insurance literature. These directions of generalizations include the market (see Duarte et al. (2014) and Shen and Wei (2014)); the preferences (see Tang et al. (2018), Zhang et al. (2021) and Steffensen and Søe (2023)); the inclusion of health risk (see Kraft and Steffensen (2008), Koijen et al. (2015), Hambel et al. (2016) and Steffensen and Søe (2023)); and constraints (see Nielsen and Steffensen (2008), Hambel et al. (2016) and Di Liddo and Bari (2022)).

Duffie and Epstein (1992) formalized the continuous-time version of the separation of time and risk preferences introduced as a recursive utility by Epstein and Zin (1989, 1991). Local separation of time and risk preferences under lifetime uncertainty is studied in Aase (2016) and Jensen (2019). In contrast, the approach taken in Jensen and Steffensen (2015) is based on the global separation and the equilibrium control and also analyzed by Fahrenwaldt et al. (2020). These are significant background results as we wish to analyze the impact of separation.

Mitchell et al. (1999) also quantified the welfare loss of not annuitizing. That work initiated a vast amount of economic literature with positivistic explanations of the lack of annuitization, including Einav et al. (2010), Hosseini (2015) and Brown et al. (2017). In contrast to Mitchell et al. (1999), we work in continuous time, study the sensitivity to market and mortality parameters, analyze the performance of a particular suboptimal bank product, and pay special attention to non-time additive utility.

Other studies related to our scope are Milevsky and Young (2007) and Milevsky (2018). Common for Mitchell et al. (1999), Milevsky and Young (2007) and Milevsky (2018) is that the annuity market does not give full flexibility of the consumption–investment profile as we have in our setup. Annuities are there either fixed annuities or variable annuities with some degree of investment freedom but not the full freedom to choose both the investment portfolio and payout profile optimally. This means that annuitization in their works is always a trade-off between losing flexibility and gaining access to mortality credits. Annuitization in our work, in contrast, means full flexibility. Annuitization is, therefore, in their works, in general, less attractive than in our work, where there is no tradeoff; annuitizing has no downside, only the upside of getting access to mortality credits.

The paper is structured as follows. In Sect. 2, we present the four optimization problems that later are the fundament of our comparison. In Sect. 3, we offer the solutions to their problems. Section 4 presents the suboptimal banking products we include in the comparison, which is then performed in Sect. 5. Section 6 concludes.

2 The problems

In this section, we present the various optimization problems, the solutions of which we will later give and compare. The problems have two variations in the insurance market’s and objective function’s dimensions. Thus, we face four different problems.

For all four different problems, the underlying financial market is the same. Thus, only the insurance market depends on the market available to the investor. In all fours problems, the underlying financial market is a classical Black–Scholes financial market with price processes,

$$\begin{aligned} {\textrm{d}} S^0(t)&= S^0(t) r {\textrm{d}}t,\\ {\textrm{d}} S(t)&= S(t) \left( \alpha {\textrm{d}}t + \sigma {\textrm{d}} W(t)\right) . \end{aligned}$$

Here, W is a Brownian motion, and \(r, \alpha , \sigma > 0\) are constants. We assume that \(\alpha \ge r\) such that the market price of risk defined by \(\theta := (\alpha -r)/\sigma \) is non-negative.

The individual invests a proportion \(\pi (t)\) of his wealth in the stock at time t, and the process \(\pi \) is called the stock proportion. The individual consumes at rate c(t) at time t, and the process c is called the consumption rate.

We assume that the individual has an uncertain lifetime and denote by \(\mu {(t)}\) the individual’s mortality rate. Furthermore, we assume that the mortality rate is deterministic and increases with age. Thus, we do not model the so-called longevity risk where the mortality rate is stochastic. However, not modeling longevity risk does not mean we cannot model longevity, i.e., that mortality for a given age decreases with calendar time. If it is deterministic, we can quickly implement such an effect by letting the age-dependent mortality rate vary with birth year.

We distinguish between two different situations in the insurance market. In one case, there exists no insurance market. Thus the market is fully described by the financial market above. On the other hand, with lifetime uncertainty present in the individual’s objective, the market is incomplete, and we can formulate contingent claims that are not hedgeable in the market. An example is so-called pure endowment insurance that pays out one unit upon survival until time n. Letting I indicate survival such that \(I(t)=1\) if the individual is alive at time t, the non-hedgeable claim payable at time n is I(n). This claim is not hedgeable in the Black–Scholes market, where one cannot trade the survival risk of the individual. However, our goal is not to price contingent claims. Instead, our goal is to make optimal decisions, and the investment–consumption problem below is well-posed in this incomplete market.

We consider an individual after retirement when labor income has fallen away. The retirement phase is crucial for accessing the explicit solution for the investment–consumption problem below. Otherwise, the non-hedgeability of the labor income, which is only earned before retirement as long as the individual is alive, prevents an explicit solution. Of course, it is possible to work with a problem with non-hedgeable income and no access to insurance, but then one has to resort to a numerical solution of the HJB equation. The alternative idea is to assume that the mortality rate is zero until retirement. In that case, the otherwise incomplete market is, in a sense, ‘sufficiently complete’ to make the labor income hedgeable; we still have access to solutions in closed form. However, since we are interested in understanding the value of access to insurance, which comes from lifetime uncertainty, modeling over ages with zero mortality does not add value to our study. Therefore, we entirely disregard labor income by moving our problem’s starting point to retirement age.

In the problem described above, the individual consumes his wealth invested in the financial market. The dynamics of the wealth of that individual, as long as he is alive, becomes

$$\begin{aligned} {\textrm{d}} X(t)= & {} X(t) (r+ \pi (t) (\alpha -r)){\textrm{d}}t + X(t)\pi (t) \sigma {\textrm{d}} W(t)-c(t){\textrm{d}}t, \end{aligned}$$
(1)

where \(X(0)=x_0>0\) is the given initial wealth.

The individual’s objective is to maximize the expected utility from consumption until death. Thus, we have a value function in the following form

$$\begin{aligned} V(t,x)= & {} \sup _{c,\pi } E_{t,x} \left[ \int _{t}^\infty u(t,s,c(s))I(s){\textrm{d}}s \right] , \end{aligned}$$
(2)

where we remind the reader that the process I indicates survival. The subscript (t, x) denotes that the expectation is taken conditional on \(X(t)=x\) and \(I(t)=1\), i.e., conditional on the individual being alive at time t.

Note that there is no so-called utility from the bequest. Then the retiree does not achieve any utility from leaving money behind. In (2), this appears as the individual gets utility during survival only. The no-bequest case is a corner case that has several benefits. First, it prevents us from discussing what that utility from bequest different from zero should be. Second, it severely simplifies some elegant solutions to the consumption problem, as they appear in the coming sections. Finally, we can say that this is a clear case where we can measure the value of the annuity market in a situation where the individual has no economic dependants that he also has to take into account in his objective.

We are going to work with a constant relative risk aversion \(\gamma \) in combination with exponential discounting of the utility with the discount rate \(\rho \) such that

$$\begin{aligned} u(t,s,c)= & {} e^{-\rho (s-t)}\frac{1}{1-\gamma }c^{1-\gamma }. \end{aligned}$$
(3)

We speak of the individual with wealth dynamics given by (1), the value function (2), and the utility function (3) as the uninsured individual with time-additive preferences.

The next individual has the same objective as the first, namely the one presented through the value function (2). Thus, neither he has any utility from the bequest. He distinguishes himself from the first individual by having access to the insurance market. Instead of introducing the insurance sum as a decision process and optimizing it, we implement the optimal solution directly. The optimal solution for an individual with no utility from the bequest and access to life insurance is to sell an insurance contract that pays out current wealth at any point in time. This position is called annuitization. Access to an insurance market and an annuity market are two sides of the same story and are just a matter of the sign of the insurance sum paid out. If the individual is willing to give up his wealth upon death, he receives a premium based on the pricing mortality rate used by the life annuity provider. We denote that mortality by \(\mu ^*\) and the premium rate he receives at time t is \(\mu ^*(t) X(t)\) where X(t) is current wealth. The dynamics of the wealth of that individual, as long as he is alive, then becomes

$$\begin{aligned} {\textrm{d}} X(t)= & {} X(t) (r+ \mu ^*(t) + \pi (t) (\alpha -r)){\textrm{d}}t + X(t) \pi (t) \sigma {\textrm{d}} W(t)-c(t){\textrm{d}}t, \end{aligned}$$
(4)

where \(X(0)=x_0>0\) is the given initial wealth. The premium rate from annuitization appears in the return term of the dynamics because the premium is assumed to be proportional to wealth itself, corresponding to the linear pricing of the insurance contract.

We speak of the individual with wealth dynamics given by (4) in combination with the value function (2) as the insured individual with time-additive preferences. The appearance of \(\mu ^*\) in the dynamics (4) makes it seem as if the insured behaves as the uninsured with an addition of the mortality rate to the interest rate. But we have to be careful here. Since the interest rate also appears in the term stemming from stock investment, without the mortality rate, the correct statement is instead: The insured individual behaves as the non-insured individual with an addition of the mortality rate to both the interest rate and the stock return. Then, these additions offset correctly in the term \(\alpha -r\).

The uninsured and the insured individual above share the objective formalized through the value function (2). It is, however, well known that this objective misses an essential point about time and risk preferences. It assumes the parameter \(\gamma \), spoken of as risk aversion, as a parameter that characterizes preferences toward both risks, i.e., variation of consumption over outcomes of stochastic variables, and time, i.e., variation of consumption over time. We see this quickly by considering the particular case of no mortality risk (\(\mu =0\)) and no financial risk (\(\alpha =r\) and \(\sigma =0\)). Given the objective of the paper, this is an odd particular case. Still, it unveils the role of \(\gamma \) as a parameter that (in general but in this case of no risk only) characterizes preferences concerning time variation. That odd version of the problem has an internal solution that depends on \(\gamma \). The parameter \(\gamma \) reflects aversion toward the variation of consumption over time. If \(\gamma \) is large, the investor is not as willing to postpone consumption to pick up (deterministic) capital gains from interest payments as if \(\gamma \) is smaller. That is true, even if that would allow him to consume more. Note that this pattern of thinking works well without risk. We speak of the parameter as covering both risk aversion and variation aversion.

Epstein and Zin (1989, 1991) formalized the disentanglement of risk and variation aversion in the objective formalized by (2) in discrete time and Duffie and Epstein (1992) translated the concepts to continuous time. In the case of no lifetime uncertainty, they derive a so-called aggregator f(c, v) such that the value function has the implicit representation,

$$\begin{aligned} V(t,x)= & {} \sup _{c,\pi } E_{t,x} \left[ \int _{t}^\infty {f(c(s),V(s,X(s)))}{\textrm{d}}s \right] . \end{aligned}$$
(5)

The aggregator function f depends on the underlying structure of preferences toward risk and variation, respectively. They work with a parameter \(\phi \) for the elasticity of intertemporal substitution, which is the reciprocal of variation aversion. If both the relative risk aversion and the relative variation aversion are constant, they derive the aggregator

$$\begin{aligned} {f(c,v)}= & {} \frac{1-\gamma }{1-\phi } \delta {v} \left( \left( \frac{\frac{1}{1-\gamma }c^{1-\gamma }}{{v}}\right) ^{\frac{1-\phi }{1-\gamma }}-1\right) . \end{aligned}$$
(6)

Now comes the question of how to generalize the disentanglement of risk and time preferences by Duffie and Epstein (1992) to the case of an uncertain lifetime. They showed how to construct the aggregator for diffusive markets only. Others have worked on generalizing to other markets and more general risk and variation preferences. Yet, there is no consensus about how to implement lifetime uncertainty. The literature contains (at least) three proposals that we now explain.

The simplest generalization to an uncertain lifetime is the one obtained by simply replacing the value function (5) by

$$\begin{aligned} V(t,x)= & {} \sup _{c,\pi } E_{t,x} \left[ \int _{t}^\infty {f(c(s),V(s,X(s)))}I(s){\textrm{d}}s \right] . \end{aligned}$$
(7)

Again, the expectation is conditional on both current wealth and upon survival until time t, like how we read it in (2). Aase (2016) proposed this and studied the impact of insurance markets. However, the value function appearing as an argument in the aggregator in (7) is certainly different from the value function in (5). So, is there an argument that the same aggregator f with an updated argument V properly considers possible aversion toward lifetime uncertainty?

Jensen and Steffensen (2015) proposed a different generalization. They drop the idea of working with (local) aggregators as the fundamental ingredient in the (local) disentanglement. Instead, they form a global objective with a global risk and time variation disentanglement. Their version without mortality risk reads

$$\begin{aligned} V(t,x)= & {} \int _{t}^\infty v\left( u^{-1}\left( E_{t,x}\left[ u(t,s,c(s))\right] \right) \right) {\textrm{d}}s, \end{aligned}$$
(8)

where u is the utility function containing risk aversion and v is a time preference function containing variation aversion. It is probably an insinuation to call what we construct below a generalization of recursive utility to an uncertain lifetime. However, the consumption–investment strategy formed from the value function (8) does coincide with the consumption–investment strategy formed from (5). At least, this is the case for the Black–Scholes market. Both Fahrenwaldt et al. (2020) and Jensen and Steffensen (2015) obtain this result. So, in that sense, we present a generalization of the consumption–investment strategy obtained in recursive utility.

In two steps, we construct the value function in (8). The argument of the function v, \(u^{-1}(E_{t,x}\left[ u(t,s,c(s))\right] )\), is the so-called certainty equivalent. The first step is to form these certainty equivalents. They turn the utility of uncertain future consumption rates into certain consumption rates from which the individual obtains the same utility. Thus, in a sense, these certainty equivalence operations ‘delete’ uncertainty from the objective. The function v expresses preferences concerning time variation of certain (or rather certainty equivalent) consumption rates. There is a crucial difference between the recursive utility approach to the disentanglement of time and risk preferences and ours. The certainty equivalent is here based on the utility of actual consumption. In contrast, the certainty equivalent in recursive utility is based on indirect utility.

From a mathematical point of view, this construction radically changes the optimization problem. Suppose v and u are the same functions, such that the operation \(v(u^{-1}(\cdot ))\) vanishes. In that case, the expectation goes outside the integral, and we are back with a standard objective (corresponds to (2) without the survival indicator). But v and u being different functions, the integral forms a sum of nonlinear functions of conditional expectations. Time consistency and standard dynamic programming break down. But other methods are ready to take over. Jensen and Steffensen (2015) attack the problem with equilibrium theory, corresponding to how the so-called sophisticated individual thinks when facing a time-inconsistent problem. The technical details are beyond the level of ambition in that direction for this exposition. But this explains why we add in the equilibrium sense whenever we speak of an optimal solution below.

The following is the generalization of (8) to include lifetime uncertainty suggested by Jensen and Steffensen (2015). We compose the optimal value function in the equilibrium sense as

$$\begin{aligned} V(t,x)= & {} \int _{t}^\infty v\left( u^{-1}\left( E_{t,x}\left[ u(t,s,c(s))I(s)\right] \right) \right) {\textrm{d}}s, \end{aligned}$$
(9)

and we see how the utility function operates on both financial risk and lifetime uncertainty.

We mention that Jensen and Steffensen (2015) also works with utility from a bequest. Their approach to this and its consequences for consumption and insurance is a crucial idea of their work. They introduce an elasticity between consuming as dead (the bequest) or alive (like our consumption above). When working with time-additive utility, one usually works with additive utility across the states, dead and alive. But suppose we, in addition to disentangling time and risk preferences, also introduce an elasticity between consuming as dead or alive. Following Jensen and Steffensen (2015), this has exciting consequences and interpretations. However, when there is no utility from the bequest, the elasticity between consuming as dead or alive vanishes from the problem and, therefore, without utility from the bequest, only the parameters of the functions u and v appear in the solution.

Jensen (2019) proposes the third generalization of recursive utility to lifetime uncertainty and separation of preferences. Jensen (2019) extends the original derivation of the aggregator by Duffie and Epstein (1992). We shall not present the formalism behind it. But as mentioned above, a certainty equivalent based on indirect utility appears in classical recursive utility. Similarly to when Jensen and Steffensen (2015) introduced elasticity between consumption as dead or alive, it is natural in recursive utility to introduce elasticity between bequest (consumption as dead) and indirect utility conditional on surviving the next small time interval. However, since indirect utility upon survival contains both future consumption and future bequest, that elasticity does not explicitly concern bequest and consumption. Therefore, it should also be clear, as is also discussed in Jensen (2019), that Jensen and Steffensen (2015) and Jensen (2019) are fundamentally different approaches. In contrast to Jensen and Steffensen (2015), the elasticity between a bequest and indirect utility given survival appears in the solution by Jensen (2019), even in the case of no utility from the bequest we consider here.

When we work with separated preferences in the next section, our individual has an objective corresponding to (9). Suppose this individual does not have access to life insurance (unlike the situation in Jensen and Steffensen 2015) and therefore cannot annuitize and must realize the wealth dynamics (1). In that case, we speak of the uninsured individual with separated preferences. Finally, suppose the individual with an objective corresponding to (9) has access to life insurance (like the situation in Jensen and Steffensen 2015) and therefore fully annuitizes and realizes the wealth dynamics (4). In that case, we speak of the insured individual with separated preferences.

We have now presented four different individuals, namely the uninsured individual with time-additive preferences, the insured individual with time-additive preference, the uninsured individual with separated preferences, and the insured individual with separated preferences. In the next section, we present and discuss their optimal investment and consumption processes.

3 The solutions

In this section, we present the solutions to the problems presented in the previous section. These problems can be seen as special cases of Jensen and Steffensen (2015), here presented in our setting to enable an easier and more comprehendible comparison.

We start by considering the investment decision. The solutions for all four individuals are the same well-known Merton proportion given by

$$\begin{aligned} \pi =\frac{1}{\gamma }\frac{\alpha -r}{\sigma ^2} =\frac{1}{\gamma }\frac{\theta }{\sigma }. \end{aligned}$$
(10)

The expected return from the investment equals \(r+\pi (\alpha -r) = r+\frac{1}{\gamma }\theta ^2\). However, a return rate with half of the excess return obtained from stock investments added to the risk-free return shows up in the solution again and again, and we denote this by R such that \(R=r+\frac{1}{2}\pi (\alpha -r) = r+\frac{1}{2\gamma }\theta ^2\).

We now turn to the consumption rate. All individuals withdraw a fraction of their wealth for consumption. The fraction for all individuals is the reciprocal of an annuity, i.e., for all individuals, we can write \(c(t)=X(t)/a(t)\), where a(t) is a specific annuity that depends on which individual we consider. The uninsured individual with time-additive preferences withdraws optimally in accordance with the annuity

$$\begin{aligned} a^{\textrm{ua}}(t)= \int _t^\infty e^{-\int _t^s \delta ^{\textrm{a}} + \mu ^{\textrm{ua}}}{\textrm{d}}s, \end{aligned}$$
(11)

where

$$\begin{aligned} \delta ^{\textrm{a}}= & {} \frac{1}{\gamma }\rho +\left( 1-\frac{1}{\gamma }\right) R,\end{aligned}$$
(12)
$$\begin{aligned} \mu ^{\textrm{ua}}= & {} \frac{1}{\gamma }\mu \end{aligned}$$
(13)

The letters in the top script u and a abbreviate uninsured and time-additive. Decorating \(\delta \) with just an a reflects that this is the same for uninsured and insured individuals. Only the \(\mu \) in the annuity depends on whether the individual is insured. In the annuity, we use the slightly informal notation \(e^{-\int _t^s \delta ^{\textrm{a}} + \mu ^{\textrm{ua}}}\) representing \( e^{-\int _t^s ({\delta ^{\textrm{a}} + \mu ^{\textrm{ua}}(\tau )}){\textrm{d}}\tau }\), for notational ease, where the transition intensity is time-dependent, but \(\delta \) is not, we continue to use the abbreviated notation. We recognize the annuity formula as the actuarial formula for a life annuity with the design interest rate \(\delta ^{\textrm{a}}\) and the design mortality rate \(\mu ^{\textrm{ua}}\). We call these elements design elements as they form different annuity product designs. In that formula, the interest rate is a weighted average of the impatience rate \(\rho \) and the return rate R. The weights are \(\frac{1}{\gamma }\) and \(1-\frac{1}{\gamma }\), respectively. We also note how mortality impacts \(\rho \). Namely, we cover the case with an uncertain lifetime by the case without uncertainty lifetime by simply adding \(\mu \) to \(\rho \).

We also present the optimal consumption rate dynamics for each individual. For all four individuals, the optimal consumption rate follows a geometric Brownian motion. The uninsured individual with time-additive preferences consumes according to the dynamics

$$\begin{aligned} \frac{{\textrm{d}}c^{\textrm{ua}}(t,X(t))}{c^{\textrm{ua}}(t,X(t))}= & {} \frac{r-\rho -\mu +\frac{1}{2\gamma }(1+\gamma )\theta ^2}{\gamma }{\textrm{d}}t+\frac{\theta }{\gamma }{\textrm{d}}W(t). \end{aligned}$$
(14)

We now consider the uninsured individual with separated preferences. He also consumes a proportion of his wealth corresponding to the annuity,

$$\begin{aligned} a^{\textrm{us}}(t)&= \int _t^\infty e^{-\int _t^s \delta ^{\textrm{s}}+\mu ^{\textrm{us}}}{\textrm{d}}s, \end{aligned}$$
(15)

where

$$\begin{aligned} \delta ^{\textrm{s}}= & {} \frac{1}{\phi }\rho +\left( 1-\frac{1}{\phi }\right) R,\end{aligned}$$
(16)
$$\begin{aligned} \mu ^{\textrm{us}}= & {} \frac{1}{\phi }\frac{1-\phi }{1-\gamma }\mu . \end{aligned}$$
(17)

Again, we have the actuarial formula for the life annuity formed by a design interest rate and a design mortality rate. However, the weights on \(\rho \) and R in forming the design interest rate are now replaced by \(\frac{1}{\phi }\) and \(1-\frac{1}{\phi }\). The design mortality rate is replaced by \(\frac{1}{\phi }\frac{1-\phi }{1-\gamma }\mu \). As it should be, we find that the design rates of the uninsured individual with time-additive preferences equal those of the uninsured individual with separated preferences in the special case \(\phi =\gamma \).

The dynamics of consumption for the uninsured individual with separated preferences are

$$\begin{aligned} \frac{{\textrm{d}}c^{\textrm{us}}(t,X(t))}{c^{\textrm{us}}(t,X(t))}= & {} \frac{r-\rho -\frac{1-\phi }{1-\gamma }\mu +\frac{1}{2\gamma } (1+\phi )\theta ^2}{\phi }{\textrm{d}}t+\frac{\theta }{\gamma }{\textrm{d}}W(t). \end{aligned}$$
(18)

Again, we note how the dynamics of the uninsured individual with separated preferences collapse into those of the uninsured individual with time-additive preferences in the particular case \(\phi =\gamma \).

We now turn to the individuals with access to the life annuity market. We first consider the insured individual with time-additive preferences. He consumes a fraction of his wealth based on the annuity

$$\begin{aligned} a^{\textrm{ia}}(t)&= \int _t^\infty e^{-\int _t^s \delta ^{\textrm{a}}+\mu ^{\textrm{ia}}}{\textrm{d}}s, \end{aligned}$$
(19)

where

$$\begin{aligned} \mu ^{\textrm{ia}}= & {} \frac{1}{\gamma }\mu +\left( 1-\frac{1}{\gamma }\right) \mu ^*. \end{aligned}$$
(20)

Thus, we base the annuity of the insured individual with time-additive preferences on a design interest rate that is the same as that of the uninsured with the same preferences. However, we replace the design mortality rate of the uninsured individual \(\mu /\gamma \) by a weighted average of the actual mortality intensity and the pricing mortality intensity with weights given by \(\frac{1}{\gamma }\) and \(1-\frac{1}{\gamma }\). Note that the design mortality rate of the uninsured individual is obtained as the design mortality rate of the insured individual in the particular case \(\mu ^*=0\).

The dynamics of the consumption rate for the insured individual with time-additive preferences are

$$\begin{aligned} \frac{{\textrm{d}}c^{\textrm{ia}}(t,X(t))}{c^{\textrm{ia}}(t,X(t))}= & {} \frac{r-\rho +\mu ^*-\mu +\frac{1}{2\gamma }(1+\gamma )\theta ^2}{\gamma }{\textrm{d}}t+\frac{\theta }{\gamma }{\textrm{d}}W(t). \end{aligned}$$
(21)

Note that the dynamics of consumption for the uninsured individual follow from the special case \(\mu ^*=0\).

Finally, we consider the insured individual with separated preferences. He consumed a fraction of his wealth based on the annuity

$$\begin{aligned} a^{\textrm{is}}(t)&= \int _t^\infty e^{-\int _t^s \delta ^{\textrm{s}}+\mu ^{\textrm{is}}}{\textrm{d}}s, \end{aligned}$$
(22)

with

$$\begin{aligned} \mu ^{\textrm{is}}= & {} \frac{1}{\phi }\frac{1-\phi }{1-\gamma }\mu +\left( 1-\frac{1}{\phi }\right) \mu ^*. \end{aligned}$$
(23)

Thus, as was the case for time-additive utility, we can reuse the design interest rate \(\delta ^{\textrm{s}}\) for this uninsured individual. And, as was the case for time-additive utility, we have to update the design mortality rate. Now, for the case of separated preferences, the introduction of the life annuity market allows us to replace the design mortality rate \(\frac{1}{\phi }\frac{1-\phi }{1-\gamma }\mu \) by \(\frac{1}{\phi }\frac{1-\phi }{1-\gamma }\mu +(1-\frac{1}{\phi })\mu ^*\). Note how we obtain the design mortality rate of the insured individual with time-additive preferences as a particular case of the insured individual with separated preferences in the case of \(\phi =\gamma \). Also, note how we obtain the design mortality rate of the uninsured individual with separated preferences as a particular case of the insured individual with separated preferences in the specific case of \(\mu ^*=0\).

The dynamics of the consumption rate of the insured individual with separated preferences are

$$\begin{aligned} \frac{{\textrm{d}}c^{\textrm{is}}(t,X(t))}{c^{\textrm{is}}(t,X(t))}= & {} \frac{r-\rho +\mu ^*-\frac{1-\phi }{1-\gamma }\mu +\frac{1}{2\gamma } (1+\phi )\theta ^2}{\phi }{\textrm{d}}t+\frac{\theta }{\gamma }{\textrm{d}}W(t). \end{aligned}$$
(24)

Note that we obtain the consumption dynamics for the individual with time-additive preferences by the particular case \(\phi =\gamma \). Note that the dynamics of consumption for the uninsured individual is the specific case \(\mu ^*=0\).

All the above results follow Jensen and Steffensen (2015) with properly specifying special cases. As discussed in Sect. 2, Jensen (2019) provides a different disentanglement of time and risk preferences under lifetime uncertainty than Jensen and Steffensen (2015). In the case of no consumption upon death, the additional parameter considered to deal with an uncertain lifetime does not appear in the optimal controls in Jensen and Steffensen (2015), in contrast to what Jensen (2019) obtains. It is difficult to unravel the optimal control of Jensen (2019)’s approach in the case of no utility from a bequest since the utility from a bequest there cannot immediately be set to zero. However, it seems that we can base the optimal control on the annuity

$$\begin{aligned} a^{\textrm{is}}(t)&= \int _t^\infty e^{-\int _t^s \delta ^{\textrm{s}}+\mu ^{\textrm{is}}}{\textrm{d}}s, \end{aligned}$$
(25)

with

$$\begin{aligned} \mu ^{\textrm{is}}= & {} \frac{1}{\phi }\frac{1-\phi }{1-\kappa }\mu +\left( 1-\frac{1}{\phi }\right) \mu ^*, \end{aligned}$$
(26)

where \(\kappa \) is what Jensen (2019) speaks of as the reciprocal elasticity of substitution between a bequest and future utility. Jensen (2019) also provides a different interpretation of \(\kappa \). We can think of the distinction between \(\gamma \) and \(\kappa \) as working with different risk aversion concerning market risk and mortality risk, respectively, where \(\gamma \) is the former, and \(\kappa \) is the latter. Based on the annuity above, the dynamics of consumption are then in Jensen (2019) given by

$$\begin{aligned} \frac{{\textrm{d}}c^{\textrm{is}}(t,X(t))}{c^{\textrm{is}}(t,X(t))}= & {} \frac{r-\rho +\mu ^*-\frac{1-\phi }{1-\kappa }\mu +\frac{1}{2\gamma }(1+\phi )\theta ^2}{\phi }{\textrm{d}}t+\frac{\theta }{\gamma }{\textrm{d}}W(t). \end{aligned}$$
(27)

In our numerical studies, we stick to the approach by Jensen and Steffensen (2015), i.e., corresponding to (22), (23), and (24). However, as it can be seen through (25), (26), and (27), this can be thought of as a particular case of Jensen (2019) where \(\kappa =\gamma \), i.e.,+ according to the interpretation by Jensen (2019), as the particular case where the preferences for financial and insurance risk are identical.

In all the annuity formulas above, we recognize the actuarial life annuity formula with specific design interest and mortality rates that depend on the individual and whether he has access to an annuity market. With access to an annuity market, the design mortality rate is a weighted average of the actual mortality rate and the pricing mortality rate, depending on whether the individual has time-additive or separated preferences.

One may think that such a construction can be generalized to multi-state models. Indeed, it can. But from Kraft and Steffensen (2008) and Steffensen and Søe (2023), one can learn that the design mortality rates cannot be directly generalized based on the construction of a weighted average. They both work with time-additive utility and access to insurance, so we should compare with (19), (20), and (21). From there, one learns that the more general representation follows from adjusting the calculation interest rate by the difference between the arithmetic and the geometric weighted mean of mortalities and then using the geometric weighted mean as the mortality rate in the actuarial formula. That is, we should redefine \(\delta ^{\textrm{a}}\) and \(\mu ^{\textrm{ia}}\) by

$$\begin{aligned} \delta ^{\textrm{ag}}=&\delta ^{\textrm{a}}+\mu ^{\textrm{ia}}-\mu ^{\textrm{iag}},\end{aligned}$$
(28)
$$\begin{aligned} \mu ^{\textrm{iag}}=&\mu ^{\frac{1}{\gamma }}(\mu ^*)^{1-\frac{1}{\gamma }}. \end{aligned}$$
(29)

These design interest and mortality rates can be directly generalized to multi-state models. Obviously, in our studies, they form the same control processes since \(\delta ^{\textrm{a}}+\mu ^{\textrm{ia}}=\delta ^{\textrm{ag}}+\mu ^{\textrm{iag}}\).

4 The sub-optimal product design

The uninsured individuals above decide optimally in the market they face. Of course, there are many sub-optimal ways to determine, e.g., the consumption plan. We now pay special attention to one of them, which has some merits in its construction. Although the construction is sub-optimal, we derive the dynamics of the consumption plan such that we can compare its structure to the optimal one. The idea behind the design is to have a problem with deterministic finite time horizon n in mind. We use the letter n for the finite time point to reserve the otherwise frequently used T as the stochastic lifetime of the individual. For the problem with finite-time horizon n, the solution is to consume a fraction of your wealth according to the annuity

$$\begin{aligned} a(t)&= \int _t^n e^{-\int _t^s {\tilde{r}}}{\textrm{d}}s. \end{aligned}$$
(30)

As interest rate in the annuity, we introduce a rate of return \({\tilde{r}}\), which we can adjust to accommodate the individual’s preferences. If, e.g., the individual has time-additive preferences, and n is the actual time horizon, then \(\tilde{r}=\delta ^{\textrm{a}}\) is optimal.

Now, we acknowledge that the lifetime is uncertain, but what is our best estimate of that lifetime? The answer is the conditional expectation \(E_t[T]\) where the subscript t denotes survival until time t. We have that

$$\begin{aligned} E_t[T]&=t+\int _{t}^{\infty } e^{-\int _t^s {\mu }}{\textrm{d}}s, \end{aligned}$$
(31)

Now we replace n in our annuity construction by \(E_t[T]\) as this is our best estimate of our time horizon. Thus, we suggest the consumption rate X(t)/a(t) with

$$\begin{aligned} a(t)&= \int _t^{E_t[T]} e^{-\int _t^s {\tilde{r}} }{\textrm{d}}s. \end{aligned}$$
(32)

However, this is not an optimal consumption under any problem with a stochastic lifetime. It just seems to be a good idea. Note carefully that the expected lifetime is continuously updated with the conditioning on survival. This means that there is no risk of outliving your wealth, and there is nothing particular about dying before or after the expected lifetime, conditional on survival to some earlier age.

To derive the dynamics of c, we have to decide which dynamics of X to use. Since the product is proposed here as an alternative to the optimal consumption for the uninsured individual, we go with the dynamics in (1). We can then derive the dynamics of the consumption rate to be

$$\begin{aligned} \frac{{\textrm{d}} c(t,X(t))}{ c(t,X(t))}= & {} \left( r-\tilde{r}-{\tilde{\mu }}+\frac{\theta ^2}{\gamma }\right) {\textrm{d}}t+\frac{\theta }{\gamma }{\textrm{d}}W(t), \end{aligned}$$
(33)

where

$$\begin{aligned} {\tilde{\mu }}=\frac{e^{-\int _t^{E_t[T]} {{\tilde{r}}}}(E_t[T]-t)}{ a(t)} \mu , \end{aligned}$$
(34)

since

$$\begin{aligned} \frac{{\textrm{d}} a(t)}{{\textrm{d}}t}=\mu (E_t[T]-t)e^{-\int _t^{E_t[T]}{\tilde{r}} }-1+{\tilde{r}} a(t). \end{aligned}$$

We formulate the dynamics of the consumption rate by constructing an odd mortality rate \({\tilde{\mu }}\) to make it comparable with the optimal consumption patterns we have seen in the previous section.

We want to compare the performance of the proposed consumption strategy with those with and without insurance access. We must calculate the sub-optimal value function based on the suboptimal consumption strategy. We compare the suboptimal strategy to the optimal one under time-additive preferences. Thus, the objective is as defined in (2), such that

$$\begin{aligned} V(t,x)&=E_{t,x}\left[ \int _t^\infty u(t,s, c(s))I(s){\textrm{d}}s\right] \\&=E_{t,x}\left[ \int _t^\infty \frac{1}{1-\gamma } c(s)^{1-\gamma }e^{-\rho (s-t)}I(s){\textrm{d}}s\right] \\&=\int _t^\infty \frac{1}{1-\gamma }E_{t,x}\left[ c(s)^{1-\gamma }\right] e^{-\rho (s-t)}e^{-\int _t^s \mu }{\textrm{d}}s. \end{aligned}$$

To calculate the expectation, we write down the solution to (33) as

$$\begin{aligned} c(s,X(s))= c(t,X(t))e^{\int _t^s((r-{\tilde{r}}-{{\tilde{\mu }}} +\frac{\theta ^2}{\gamma } -\frac{1}{2}\frac{\theta ^2}{\gamma ^2})du+\frac{\theta }{\gamma }{\textrm{d}}W(t))}. \end{aligned}$$

We achieve

$$\begin{aligned}&E_{t,x}\left[ c(s,X(s))^{1-\gamma }\right] \\&\quad =E_{t,x}\left[ c(t,X(t))^{1-\gamma }e^{(1-\gamma )\int _t^s((r-\tilde{r}-{{\tilde{\mu }}} + \frac{\theta ^2}{\gamma } -\frac{1}{2}\frac{\theta ^2}{\gamma ^2})du+\frac{\theta }{\gamma }{\textrm{d}}W(u))}\right] \\&\quad = c(t,x)^{1-\gamma }E_{t,x}\left[ e^{(1-\gamma )\int _t^s((r-{\tilde{r}}-\tilde{\mu }+ \frac{\theta ^2}{\gamma } -\frac{1}{2}\frac{\theta ^2}{\gamma ^2})du+\frac{\theta }{\gamma }{\textrm{d}}W(u))}\right] \\&\quad = c(t,x)^{1-\gamma }e^{\int _t^s(1-\gamma )(r-{\tilde{r}}-{{\tilde{\mu }}} +\frac{1}{2}\frac{\theta ^2}{\gamma }){\textrm{d}}u}. \end{aligned}$$

By rewriting the power coefficient,

$$\begin{aligned} (1-\gamma )\left( r-{\tilde{r}}-{{\tilde{\mu }}} + \frac{\theta ^2}{2\gamma }\right) = -\gamma \delta ^{\textrm{a}}+\rho -(1-\gamma ) {{\tilde{\mu }}}- (1-\gamma ){\tilde{r}}, \end{aligned}$$

we conclude that

$$\begin{aligned}&\int _t^\infty \frac{1}{1-\gamma }E_{t,x}[ c(s,X(s))^{1-\gamma }]e^{-\rho (s-t)}e^{-\int _t^s \mu }{\textrm{d}}s \\&\quad = \frac{1}{1-\gamma } c(t,x)^{1-\gamma }\int _t^\infty e^{-\int _t^s \mu +\gamma \delta ^{\textrm{a}} + (1-\gamma )({\tilde{r}}+{{\tilde{\mu }}} ) }{\textrm{d}}s \\&\quad =\frac{1}{1-\gamma }x^{1-\gamma } a(t)^\gamma \frac{\int _t^\infty e^{-\int _t^s \mu +\gamma \delta ^{\textrm{a}} + (1-\gamma )({\tilde{r}}+{{\tilde{\mu }}} ) }{\textrm{d}}s}{ a(t)}. \end{aligned}$$

Note we have used the consumption rate \(c(t,x)=x/a(t)\). We define a function f(t) to simplify notation,

$$\begin{aligned} f(t)=\frac{\int _t^\infty e^{-\int _t^s \mu +\gamma \delta ^{\textrm{a}} + (1-\gamma )({\tilde{r}}+{{\tilde{\mu }}} ) }{\textrm{d}}s}{ a(t)}, \end{aligned}$$

such that we can write the sub-optimal value function as

$$\begin{aligned} V(t,x)=\frac{1}{1-\gamma }x^{1-\gamma } a(t)^\gamma f(t). \end{aligned}$$

This expression deviates from the structure of the other presented value functions because of the extra function f.

5 The comparison

In this section, we compare formally the explicit value functions such that the relative loss can be calculated directly and well as compared numerically, the individuals. In particular, we measure the welfare lost from losing access to an annuity market. We calculate the welfare loss for individuals with time-additive and separated preferences.

5.1 Comparison of the optimal solutions

We can compare the uninsured and insured individuals with either time-additive or separated preferences by comparing their optimal value functions, called indirect utility. One should be careful with comparing optimal value functions. Only if the same preferences underlie, the optimal value functions are they comparable. This is the case for the uninsured and insured individuals with time-additive and separated preferences, respectively. Only the markets are different, namely, through access to life annuities. However, for the same reason, we cannot, e.g., compare the value functions from the time-additive and separated preferences since the preferences are not the same.

We have presented the uninsured individual as an individual who behaves optimally in a market without insurance. However, we can also think of that individual as an individual who behaves sub-optimally in a market with insurance. His sub-optimal decision is not to buy any insurance. In that sense, we calculate the welfare loss from deciding sub-optimally rather than optimally in the market with insurance. Also, in such cases, one can compare the value functions corresponding to optimal and sub-optimal decisions. For most sub-optimal decisions, this is an utterly complicated numerical task. Whereas some problem formulations allow for closed-form expressions for the optimal value function, value functions for most sub-optimal decisions cannot be calculated directly. In our case, we can because the sub-optimal decision is optimal in the restricted market, and we have access to an explicit value function there.

The value functions are given by

$$\begin{aligned} V^{\textrm{ua}}(t,x)=&\big (a^{\textrm{ua}}(t)\big )^{\gamma }\frac{1}{1-\gamma }x^{1-\gamma },\\ V^{\textrm{us}}(t,x)=&\big (a^{\textrm{us}}(t)\big )^{\frac{1-\gamma }{1-\phi }\phi }\frac{1}{1-\gamma }x^{1-\gamma },\\ V^{\textrm{ia}}(t,x)=&\big (a^{\textrm{ia}}(t)\big )^{\gamma }\frac{1}{1-\gamma }x^{1-\gamma },\\ V^{\textrm{is}}(t,x)=&\big (a^{\textrm{is}}(t)\big )^{\frac{1-\gamma }{1-\phi }\phi }\frac{1}{1-\gamma }x^{1-\gamma }, \end{aligned}$$

respectively, for the four individuals we study. Thus, by specifying all the annuities in the previous section, we have all the ingredients we need to compare and calculate welfare gains from access to the insurance market.

For the individual with time-additive preferences, we form the equation

$$\begin{aligned} V^{\textrm{ia}}(0,x(1-\epsilon ))=&V^{\textrm{ua}}(0,x), \end{aligned}$$

which we then want to solve concerning \(\epsilon \). This is the relative loss of wealth that the insured individual would suffer from losing access to the insurance market. By plugging in the value functions above, it is easy to obtain

$$\begin{aligned} \epsilon =1-&\left( \frac{a^{\textrm{ua}}(0)}{a^{\textrm{ia}}(0)}\right) ^{\frac{\gamma }{1-\gamma }}. \end{aligned}$$

We speak of \(\epsilon \) as the relative value of the annuity market. We calculate it here as the value of that market to someone who has access to it. We could have calculated the relative value in terms of the gain experienced by an individual without access if that individual would get this access. It is just a convention whether to use one or the other as long as we use the same one in all calculations.

Correspondingly, for the individual with separate preferences, we form the equation

$$\begin{aligned} V^{\textrm{is}}(0,x(1-\epsilon ))=&V^{\textrm{us}}(0,x), \end{aligned}$$

again solving for \(\epsilon \). The relative value in terms of the loss experienced by someone with separated preferences and access in case they lose this access is

$$\begin{aligned} \epsilon =1-&\left( \frac{a^{\textrm{us}}(0)}{a^{\textrm{is}}(0)}\right) ^{\frac{\phi }{1-\phi }}. \end{aligned}$$
Table 1 The parameters used in the numerical examples
Full size table

In the forthcoming illustrations, we use parameters from Table 1, with true mortality intensity defined by the Gompertz law with \(\mu (t)=A\cdot B^{(z+t)}.\) These parameters and transition intensities are chosen as a baseline case, where we study the effect of their values in the numerical examples by varying them. By studying the variations of the parameters, we can isolate and evaluate their effect and impact on the relative loss. The illustrations below show the time-additive case with \(\gamma =2\). The separated case is calculated with \(\gamma =2\) and \(\phi =6\). These values are chosen based on previously performed studies, such as Burgaard and Steffensen (2020) where the average risk aversion for males is 1.9 and for females 2.3. In Burgaard and Steffensen (2020), they also discuss the values of \(\phi \) and that it should be greater than the risk aversion. Further, we remind the reader that the time-additive preferences correspond to the case of the separated preferences where \(\gamma =\phi \). Thus, in the illustration, the individual with separated preferences has a stronger aversion toward time variability than risk.

Fig. 1
figure 1

The relative loss \(\epsilon \), as a function of the interest rate for a fixed market price of risk. For time-additive preferences (\(\gamma =\phi =2\)) and for separated preferences (\(\gamma =2\), \(\phi =6\))

Full size image

In the baseline case, the relative loss is 22,2% for time-additive preferences and 15,8% for separated preferences. Thus, separated preferences lead here to a reduction of the relative loss. The reason is that the individual with separated preferences demands, for our choice of parameters, growth in the consumption rate, which is relatively smaller. Therefore, he consumes faster than the individual with time-additive preferences, and his capital is generally lower. But then his mortality credits are relatively lower, and his loss from giving up the annuity option is smaller.

We start by varying the interest rate, r, in Fig. 1. The market price of risk, defined by \(\theta _0=\frac{\alpha - r_0}{\sigma }\), where \(r_0\), is defined in Table 1. The relative loss decreases with the interest rate since a higher interest rate means that (risk-free) capital gains finance a higher proportion of total income. When capital gains finance a higher proportion of total income, the additional return from mortality credits plays a smaller role, and the relative loss from losing the annuity becomes smaller. The line for separated preferences is lower than the line for time-additive preferences with the same argument as the one for the baseline case above.

Now we vary the market price of risk and keep the interest rate constant as \(r_0\) in Fig. 2. We see how the relative loss decreases with the increasing market price of risk. Again the explanation is that a higher market price of risk leads to a higher part of the consumption being financed by (risky) capital gains.

Fig. 2
figure 2

The relative loss \(\epsilon \), as a function of the market price of risk for a fixed interest rate, for time-additive preference (\(\gamma =\phi =2\)) and separated preferences (\(\gamma =2\), \(\phi =6\))

Full size image

In Fig. 3, we study the impact of insurance pricing. So far, we have assumed that \(\mu ^* = \mu \). Now we define \(\mu ^*=(1-\xi )\mu \) with \(\xi \in [0,1]\). When \(\xi =0\), there is no risk loading in the price, and we are back with \(\mu ^* = \mu \). When \(\xi \ge 0\), the insurance company has a risk loading in the pricing. We can see that the larger the risk loading, the less attractive the mortality credits and, thus, the less is lost if we lose the annuity market. When \(\xi =1 \), there are no mortality credits. In that case, there is no benefit from access to the annuity market.

Fig. 3
figure 3

The relative loss \(\epsilon \), for time-additive preferences (\(\gamma =\phi =2\)) and separated preferences (\(\gamma =2\), \(\phi =6\)) as a function of the reduction from \(\mu \) to \(\mu ^*\)

Full size image

It is also interesting to study the loss as a function of the lifetime’s uncertainty. Intuitively, if the lifetime were certain, there should be no difference between insured and uninsured individuals as both would have to buy the same annuity-certain. In the Gompertz model we have used so far, it is difficult to control the uncertainty level by changing the parameters. We, therefore, consider a so-called hyperbolic mortality model defined by \(\mu _K(t,n)=\frac{1}{K(n-t)}\), where n is the maximum age possible (we let \(n=120\)) and where K is a measure of certainty. When K increases, the mortality for all ages earlier than n decreases. However, the maximum age is still n. Thus, we see how the uncertainty decreases in K, and for K increasing, we approach a model where the lifetime ends deterministically at age n.

Figure 4 shows how the relative loss decreases when K increases. The intuition is that the larger the K, the less lifetime uncertainty, and, naturally, the less is lost from losing access to the insurance market.

Fig. 4
figure 4

The relative loss \(\epsilon \), for time-additive preferences (\(\gamma =\phi =2\)) and separated preferences (\(\gamma =2\), \(\phi =6\)) as a function of the constant K defining the certainty of survival until time \(n=120\)

Full size image

Finally, we study the sensitivity of the relative loss toward the assumptions about risk aversion and EIS. We perform two different sensitivity analyses. For time-additive preferences, we vary \(\gamma \). For separated preferences, we fix \(\gamma =2\) and vary \(\phi \).

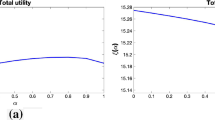
Figure 5 the sensitivity toward these assumptions. Note that the x-axis means something different for the two curves. We see that the loss is relatively robust with respect to risk aversion in the case of time-additive preferences. A slight upward trend can be explained by the fact that the bank actually uses smaller risk aversions to slope the consumption profile as well as they can. If the risk aversion is high, this feature vanishes as \(\mu ^{\textrm{ia}}\) tends to zero for the banking case, \(\mu ^{*}=0\). For separated preferences, we see that the loss is relatively robust but slightly decreasing in \(\phi \) when this is larger than \(\gamma \). However, it increases drastically for \(\phi \) smaller than \(\gamma \). As \(\phi \) tends to 1, \(\mu ^{\textrm{is}}\) tends to zero for both the bank and insurance products. Then the loss is the pure impact of mortality credits since the bank does not deviate from the insurance company’s assumption about \(\mu ^{\textrm{is}}\) to compensate for the loss of mortality credits. It should also be noted, as mentioned earlier, the value of \(\phi \) is known to be bigger than \(\gamma \).

Fig. 5
figure 5

The relative loss \(\epsilon \), for time-additive preferences and separated preferences as a function of either \(\gamma \) or fixing \(\gamma =2\) and as a function of \(\phi \)

Full size image

5.2 Comparison to the sub-optimal product design

We now wish to compare the relative loss of being equipped with the suboptimal product design. We want to calculate both the loss from optimality with access to life insurance to the suboptimal product and the loss from optimality without access to life insurance to the suboptimal product.

The value function for the suboptimal consumption is formulated as

$$\begin{aligned} V(t,x)=( a(t))^{\gamma } f(t) \frac{1}{1-\gamma }x^{1-\gamma }, \end{aligned}$$
(35)

such that we can form the two loss quantification problems as

$$\begin{aligned} V^{\textrm{ia}}(0,x(1-\epsilon ))&= V(0,x),\\ V^{\textrm{ua}}(0,x(1-\epsilon ))&= V(0,x), \end{aligned}$$

respectively. Corresponding to when comparing the optimal controls, we get relative losses in the form,

$$\begin{aligned} \epsilon&= 1- \left( \frac{a(0)}{a^{\textrm{ia}}(0)} \right) ^{\frac{\gamma }{1-\gamma }}f(0)^{\frac{1}{1-\gamma }}, \\ \epsilon&= 1- \left( \frac{a(0)}{a^{\textrm{ua}}(0)} \right) ^{\frac{\gamma }{1-\gamma }}f(0)^{\frac{1}{1-\gamma }}, \end{aligned}$$

respectively.

When comparing the suboptimal product design, we must decide which interest rate \(\tilde{r}\) to use. There are two natural alternatives. One is to determine with which interest rate the product performs the best. With the baseline parameters, we have calculated that by static optimization to be \(\tilde{r}=-0.00835\). An alternative is, of course, to use \(\delta ^{\textrm{a}}\). For the baseline case, this is \(\delta ^{\textrm{a}}=0.02281\).

In Table 2, we present the results for the two interest rate choices in the two lines. The loss from insured to uninsured is unrelated to the suboptimal product and is in the baseline case 22%. This corresponds to, e.g., the point in Fig. 3 for time-additive preferences and \(\xi =0\). If the insured is offered the suboptimal design with the best possible interest rate instead of optimality with insurance, he loses \(29\%\). If the uninsured individual is provided a suboptimal design with the best possible interest rate instead of the best possible design without insurance, he loses \(9\%\). These two losses, \(22\%\) and \(9\%\), do not add up to the \(29\%\) since they are relative losses stemming from nonlinear functions.

Table 2 Table for values of relative loss in the three cases with \(\gamma =2\), age at 65 and in the case of using \({\tilde{r}}\) and \(\delta ^{\textrm{a}}\)
Full size table

It is clear from the suboptimal control that this performs optimally if the mortality is deterministic. To compare the three consumption plans as a function of the level of lifetime uncertainty, we consider the hyperbolic mortality rate underlying Fig. 4 again. In Fig. 6, all three relative losses converge toward zero as K becomes larger and mortality becomes less uncertain. The interest rate level \(\tilde{r}\) is chosen equal to \(\delta ^{\textrm{a}}\) for greater comparability to the optimal and suboptimal consumption. Like in Table 2, we do not have additivity in the sense that the relative loss from insured to suboptimal is not the sum of the relative loss from insured to uninsured and the relative loss from uninsured to suboptimal. The relative loss from uninsured to suboptimal decreases steeply toward zero. Similarly, the loss of the life annuity is not so different depending on whether the alternative is the optimal consumption plan without insurance or the suboptimal plan. For \(K<2.5\), the loss is more than 20% in both cases.

Fig. 6
figure 6

The relative loss for the individual in the three situations, as a function of the constant K defining the certainty of surviving until time \(T=120\) for \(\gamma =2\) and \(\tilde{r}=\delta ^{\textrm{a}}\)

Full size image

5.3 Comparison of consumption profiles

It is interesting to study the consumption profiles from each of the three cases, insured, uninsured, and sub-optimal. This adds time to the dimension, and we limit ourselves to the baseline assumptions of the time-additive individual. For the insured individual, the uninsured individual, and the sub-optimal product design, we get from (14), (21), and (33), where the sub-optimal consumption is not decorated with topscripts,

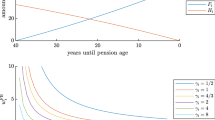
$$\begin{aligned} E_{t,x}\left[ c^{\textrm{ua}}(s,X(s))\right]&=c^{\textrm{ua}}(t,x)e^{\int _t^s\frac{1}{\gamma }(r-\rho -\mu +\frac{(1+\gamma )\theta ^2}{\gamma }{\textrm{d}}u)}\\&=\frac{a^{\textrm{ua}}(t)}{x}e^{\int _t^s\frac{1}{\gamma } (r-\rho -\mu +\frac{(1+\gamma )\theta ^2}{\gamma }{\textrm{d}}u)},\\ E_{t,x}\left[ c^{\textrm{ia}}(s,X(s))\right]&=c^{\textrm{ia}}(t,x)e^ {\int _t^s\frac{1}{\gamma }(r-\rho +\mu ^*-\mu +\frac{(1+\gamma )\theta ^2}{\gamma }){\textrm{d}}u} \\&=\frac{a^{\textrm{ia}}(t)}{x}e^{\int _t^s\frac{1}{\gamma } (r-\rho +\mu ^*-\mu +\frac{(1+\gamma )\theta ^2}{\gamma }){\textrm{d}}u},\\ E_{t,x}\left[ c(s,X(s))\right]&=c(t,x)e^{\int _t^s (r-{\tilde{r}}-{{\tilde{\mu }}} +\frac{\theta ^2}{\gamma }){\textrm{d}}u} \\&=\frac{a(t)}{x}e^{\int _t^s(r-{\tilde{r}} -{{\tilde{\mu }}} +\frac{\theta ^2}{\gamma }){\textrm{d}}u.} \end{aligned}$$

The expected consumption profiles are illustrated in Fig. 7, assuming the parameters presented in Table 1, \(\gamma =2\), and the interest rate in the sub-optimal case chosen as \(\delta ^{\textrm{a}}\). The wealth at time 0 is taken to be 1. The insured individual demands an exponentially increasing consumption rate. The uninsured individual starts out at a lower level because \(\gamma >1\) and demands a hump-shaped as a consequence of the drift of \(c^{\textrm{ua}}\) crossing zero from above when mortality increases. The sub-optimal design starts out at a higher level than the uninsured individual. However, after approximately 10 ears, the consumption rate of the uninsured individual becomes larger than that in the sub-optimal design. The value of the insured benefit rate equals the initial wealth of 1. The values of the two other benefit rates are smaller and mutually different since in both cases, some wealth is left behind upon death.

Fig. 7
figure 7

The expected consumption rates as a function of time, with the preference \(\gamma =2\) and wealth equal to 1 at retirement

Full size image

6 The conclusion

We have specified the optimal payout profiles of retirement products with and without mortality credits. The preference parameters, as well as the insurance and financial market parameters, determine the optimal drift and volatility of the consumption/benefit profiles in the two cases. In the product design, these are determined by the proportion invested in risky assets and the interest and mortality basis used in the annuity when spreading out current wealth during the ’rest of the life.’

We have compared the cases with and without mortality credits numerically. We found, for realistic parameters, a considerable loss of wealth if an individual without utility from bequest does not annuitize, and we studied and discussed its dependence on preference and market parameters.

The results generally contribute to the optimal design of annuity contracts, both life annuities offered by pension funds and annuity contracts offered by banks. The results can help both financial regulators in reconsidering their framework for annuity designs and financial institutions in redesigning their product range and arguing for (or against) life annuitization. All of this contributes to the generation of welfare for retirees.

Future works along the lines include, in unprioritized order, (a) evaluation of the sub-optimal product design under separated preferences; (b) more fundamental understanding and comparison of the different approaches to separated preference under mortality risk; (c) further numerical studies to illustrate the various consumption profiles arising from different market conditions; (d) formalizing and discussing the impact of longevity risk in the sense of a stochastic process for \(\mu \), both with and without the individual’s access to longevity derivatives; (e) the impact of asymmetric information about health that could undermine the extreme payout flexibility assumed; (f) more profound discussions about institutional and policy impact of the study.