Behavioral premium principles

Abstract

We define a premium principle under the continuous cumulative prospect theory which extends the equivalent utility principle. In prospect theory, risk attitude and loss aversion are shaped via a value function, whereas a transformation of objective probabilities, which is commonly referred as probability weighting, models probabilistic risk perception. In cumulative prospect theory, probabilities of individual outcomes are replaced by decision weights, which are differences in transformed, through the weighting function, counter-cumulative probabilities of gains and cumulative probabilities of losses, with outcomes ordered from worst to best. Empirical evidence suggests a typical inverse-S shaped function: decision makers tend to overweight small probabilities, and underweight medium and high probabilities; moreover, the probability weighting function is initially concave and then convex. We study some properties of the behavioral premium principle. We also assume an alternative framing of the outcomes; then, we discuss several applications to the pricing of insurance contracts, considering different value functions and probability weighting functions proposed in the literature, and an alternative mental accounting. Finally, we focus on the shape of the probability weighting function.

1 Introduction

According to prospect theory, individuals do not always take their decisions consistently with the maximization of expected utility. Decision makers are risk averse when they evaluate gains and risk seeking with respect to losses. They are also loss averse, as they are more sensitive to losses than gains of comparable magnitude. Investment opportunities are evaluated based on potential gains and losses relative to a reference point, rather than in terms of final wealth. Moreover, decision makers apply decision weights that are biased with respect to objective probabilities; in particular, they tend to underweight medium and high probabilities and overweight low probabilities of extreme outcomes (Quiggin 1993), they are more sensitive to changes in the probability of extreme outcomes than mid outcomes. Kahneman and Tversky (1979) and many other studies based on survey data reported such behaviors.

Risk attitude and loss aversion are shaped via a value function and objective probabilities through a probability weighting (or distortion) function, which models probabilistic risk perception. In cumulative prospect theory, decision weights are differences in transformed, through the weighting function, counter-cumulative probabilities of gains and cumulative probabilities of losses, with outcomes ordered from worst to best, and not the probabilities of individual outcomes.

In this contribution, we define a premium principle under the continuous cumulative prospect theory (Tversky and Kahneman 1992; Davies and Satchell 2007) based on the equivalent utility, or zero utility, principle introduced by Gerber (1979), extending previous work of Kaluszka and Krzeszowiec (2012).

A few contributions study premium principles under rank-dependent utility theory (e.g., Heilpern 2003, and Goovaerts et al. 2010); van der Hoek and Sherris (2001) consider different probability weighting functions for gains and losses, with linear utility; Kaluszka and Krzeszowiec (2012) extend the equivalent premium principle under cumulative prospect theory for linear and exponential utility functions; Kaluszka and Krzeszowiec (2013) study iterativity conditions of the premium principle defined in Kaluszka and Krzeszowiec (2012). Also Sung et al. (2011) apply cumulative prospect theory in order to study the optimality of insurance from the viewpoint of the insured maximizing her/his prospect value subject to a proportional premium principle adopted by the insurer.

The premium principles we discuss have some common features with respect to the approach based on distortion risk measures. Distorted probabilities were introduced by Wang (1996) in the definition of a premium principle based on a proportional hazard transform of the decumulative distribution function of the insurance risk. Wang (2000) applies distortion operators in order to price financial and insurance risks; the approach is more related to the dual theory of Yaari (1987). Along the same line of research, one may include the contributions of van der Hoek and Sherris (2001), Hamada and Sherris (2003), Balbás et al. (2009), Tsanakas (2009), Belles-Sampera et al. (2013) and Belles-Sampera et al. (2016).

We also discuss some examples under the rank-dependent utility and the dual theory as particular cases. Differently from previous contributions, here we focus on the representation of the cumulative prospect theory value for continuous distributions (Davies and Satchell 2007). We study some properties of the premium principle, providing alternative proofs under continuous cumulative prospect theory.

Moreover, we introduce the assumption that alternative framing (see Thaler 1985) of the results may be evaluated by the insurer into different mental accounts. Decision makers may aggregate or segregate outcomes, leading to different premium principles. In the segregated model, we obtain explicit solutions for the premium. Under specific assumptions on the value function and the probability weighting function, the premium has an integral representation and can be computed by numerical approximation.

Then, we discuss several applications to the pricing of insurance contracts, considering alternative value functions and probability weighting functions proposed in the literature, and different mental accounting.

Finally, we focus on the transformation of objective probabilities and provide some remarks on the shape of the probability weighting function. Empirical evidence suggests a typical inverse-S shaped function: decision makers tend to overweight small probabilities, and underweight medium and high probabilities; moreover, the probability weighting function is initially concave and then convex. We will see that curvature and elevation of the weighting function have an interesting interpretation in terms of probabilistic optimism and pessimism.

The paper is organized as follows. Section 2 summarizes the main features of cumulative prospect theory. Section 3 introduces the behavioral premium principles and some of their properties. Section 4 analyzes applications to the evaluation of insurance contracts. Section 5 presents a review on probability weighting functions suggested in the literature. Section 6 discusses an example assuming particular functional forms for the value function, the probability weighting function and the continuous distribution of the claim. Section 7 concludes.

2 Cumulative prospect theory

Prospect theory has been proposed by Kahneman and Tversky (1979) as an alternative to expected utility theory to explain actual behaviors. Formally, prospect theory relies on two key transformations: the value functionv, which replaces the utility function for the evaluation of outcomes, and a probability weighting, or probability distortion, function for objective probabilities w, which models probabilistic risk behavior. Risk attitudes are derived from the shapes of these functions as well as their interaction.

Prospect theory,¹ in its formulation initially proposed by Kahneman and Tversky (1979), is based on the subjective evaluation of prospects. A preference relation is introduced over the set of all prospects; originally prospect theory deals only with a limited set of prospects. With n possible future outcomes $\{ x_1,x_2,\ldots ,x_n\}$, a prospect is a vector of pairs $(\Delta \,x_i,\,p_i)$, for $i=1,2,\ldots ,n$. A probability $p_i$ is assigned to each outcome. Assume $\Delta \,x_i\le \Delta \,x_j$, for $i<j$, with $\Delta \,x_i\le 0$ for $i\le k$ and $\Delta \,x_i>0$ for $i>k$. Infinitely many outcomes may also be considered (Schmeidler 1989).

Outcome $\Delta x_i$ is defined relative to a certain reference point$x^*$; $x_i$ being the absolute outcome, we have $\Delta x_i = x_i - x^*$. Zero is usually taken as a reference point (the status quo), even though prospect theory does not explain clearly how to locate such reference points (see Shiller 1999; Werner and Zank 2018). It is also relevant to separate gains from losses, as negative and positive outcomes may be evaluated differently by decision makers: results are evaluated through a strictly increasing value function v, which is typically convex and steeper in the range of losses (loss aversion) and concave in the range of gains. An important feature of prospect theory, with respect to expected utility, is the discontinuity in the slope of v in correspondence of the reference point. The curvature of the value function represents sensitivity to values away from the reference point, rather than marginal returns (see Davies and Satchell 2007).

Specific parametric forms have been suggested in the literature for the value function. Let x be an outcome, a function which is used in Tversky and Kahneman (1992) and in many empirical studies is

$$\begin{aligned} v(x) = \left\{ \begin{array}{ll} v^+(x) = x^a &{} \quad x \ge 0 \\ v^-(x) = -\lambda (-x)^b &{} \quad x < 0, \end{array} \right. \end{aligned}$$

(1)

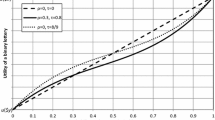
with positive parameters that control risk attitude (curvature), $0<a\le 1$ and $0<b\le 1$, and loss aversion, $\lambda \ge 1$. $v^-$ and $v^+$ denote the value function for losses and gains, respectively. Function (1) is continuous, strictly increasing, has zero as reference point; it is concave for positive outcomes and convex for negative ones, it is steeper for losses. Parameters values equal to one imply risk and loss neutrality. Figure 1 shows the value function defined in Eq. (1) with parameters $\lambda =2.25$ and $a = b = 0.88$ as estimated by Tversky and Kahneman (1992).

Fig. 1

Value function $v^+(x) = x^a$ ($x \ge 0$), $v^-(x) = -\lambda (-x)^b$ ($x < 0$) with parameters $\lambda = 2.25$ and $a = b = 0.88$

Subjective values $v(\Delta x_i)$ are not multiplied by objective probabilities $p_i$, but using decision weights$\pi _i = w(p_i)$, computed via a probability weighting (or probability distortion) function. The shape of the value function and the weighting function becomes significant in capturing the full complexity of actual choice patterns.

A weighting function w is a strictly increasing function which maps the probability interval [0, 1] into [0, 1], with $w(0)=0$ and $w(1)=1$. In this work, we will assume continuity of w on [0, 1], even thought in the literature discontinuous weighting functions are also considered. Evidence suggests a typical inverse-S shape: small probabilities of extreme events are overweighted, $w(p)>p$, whereas medium and high probabilities are underweighted, $w(p)<p$. The curvature of the weighting function is related to the risk attitude toward probabilities; the function is initially concave (probabilistic risk seeking or optimism) for probabilities in the interval $(0,p^*)$, and then convex (probabilistic risk aversion or pessimism) in the interval $(p^*,1)$, for a certain value of $p^*$. A linear weighting function describes probabilistic risk neutrality or objective sensitivity toward probabilities, which characterizes expected utility. Empirical findings indicate that the intersection (elevation) between the weighting function and the 45 degrees line, $w(p)=p$, is for p around 1 / 3.

Let us now denote with $\Delta x_i$, for $-m \le i < 0$, negative outcomes and for $0 < i \le n$ positive outcomes, with $\Delta x_i \le \Delta x_j$ for $i<j$. The subjective value of a prospect is displayed as follows:

$$\begin{aligned} V = \sum _{i=-m}^n \pi _i \cdot v(\Delta x_i), \end{aligned}$$

(2)

with decision weights $\pi _i$ and values $v(\Delta x_i)$ based on relative outcomes. In the case of expected utility, the weights are $\pi _i = p_i$ and a utility function is considered. In the following, in order to simplify the notation, it will be convenient to write $x_i$ instead of $\Delta x_i$ for the net outcomes, but still considering outcomes interpreted as deviations from a reference point.

Cumulative prospect theory developed by Tversky and Kahneman (1992) overcomes some drawbacks (such as violations of first-order stochastic dominance) of the original prospect theory. In cumulative prospect theory, the prospect value depends also on the rank of the outcomes, and decision weights $\pi _i$ are defined as differences in transformed (through the function w) cumulative probabilities of losses and counter-cumulative probabilities of gains. Formally:

$$\begin{aligned} \pi _i = \left\{ \begin{array}{ll} w^-(p_{-m}) &{} \quad i = -m \\ w^-\left( \sum _{j=-m}^i p_j \right) - w^-\left( \sum _{j=-m}^{i-1} p_j \right) &{} \quad i=-m+1,\ldots ,-1 \\ w^+\left( \sum _{j=i}^n p_j \right) - w^+\left( \sum _{j=i+1}^{n} p_j \right) &{} \quad i=0,\ldots ,n-1 \\ w^+(p_n) &{} \quad i = n,\\ \end{array} \right. \end{aligned}$$

(3)

where $w^-$ denotes the weighting function for losses and $w^+$ for gains, respectively. As above, we consider outcomes ranked from worst to best.

As Quiggin (1993) pointed out:²“The general notion of a weighting function depending on the entire vector of probabilities rather than on the probabilities of individual events was first proposed by Allais (1953). Allais did not, at that time, suggest a functional form or a set of axioms, and the idea remained undeveloped for another 25 years”. Later Quiggin (1982) introduced the rank-dependent expected utility theory; Yaari (1987) developed the dual theory; Allais (1988) discussed his cardinal utility; Tversky and Kahneman (1992) proposed the cumulative version of prospect theory (Kahneman and Tversky 1979). All such theories have been developed almost independently and share the idea that individual probabilities are distorted through a weighting function and the degree of risk aversion or risk seeking appears to depend not only on the values, but also on the probability and ranking of the outcomes.

Different parametric forms for the weighting function with the above-mentioned features have been proposed in the literature, and their parameters have been estimated in many empirical studies. Some forms are derived axiomatically or are based on psychological factors. Single parameter and two (or more) parameter weighting functions have been suggested; some functions have linear, polynomial or other forms, and there is also some interest for discontinuous (such as neo-additive) weighting functions. Two commonly applied weighting functions are those proposed by Tversky and Kahneman (1992) $w(p)= \tfrac{p^\gamma }{\left( p^\gamma +(1-p)^\gamma \right) ^{1/\gamma }}$, with $w(0)=0$ and $w(1)=1$, and $\gamma > 0$ (with some constraint in order to have an increasing function); and Prelec (1998) $w(p) = e^{- \delta (-\ln p)^\gamma }$, with $w(0)=0$ and $w(1)=1$, $0< \delta < 1$, $\gamma > 0$. When $\gamma < 1$, one obtains the inverse-S shape. Figure 2 shows some examples of the weighting function used in Tversky and Kahneman (1992).

A short discussion on the shape of the probability weighting function is postponed to Sect. 5.

Fig. 2

Weighting function $w(p)= \tfrac{p^\gamma }{\left( p^\gamma +(1-p)^\gamma \right) ^{1/\gamma }}$ for different values of the parameter $\gamma < 1$. As $\gamma$ approaches the value 1, w tends to the identity function

2.1 Cumulative prospect theory for continuous distributions

Prospects may involve a continuum of values, in particular when considering applications in finance and insurance; hence, prospect theory cannot be applied directly in its original or cumulative versions. In this work, we consider the cumulative prospect value for a continuous random variable as defined by Davies and Satchell (2007).³ Let $w^+$ and $w^-$ be strictly increasing functions with $w^+(0)=w^-(0)=0$ and $w^+(1)=w^-(1)=1$, and v a strictly increasing function (denoting $v^+(x)$ for $x>0$ and $v^-(x)$ for $x<0$, with $v(0)=0$). A preference relation can be expressed by the continuous cumulative prospect value

$$\begin{aligned} V (v(X)) = \int _{-\infty }^0 v^-(x)\, \psi ^- [F(x)] \, f(x)\, \mathrm{{d}}x + \int _0^{+\infty } v^+(x)\, \psi ^+ [1-F(x)] \, f(x)\, \mathrm{{d}}x,\nonumber \\ \end{aligned}$$

(4)

where $\psi = \frac{\mathrm{{d}}w(p)}{\mathrm{{d}}p}$ is the derivative of the weighting function w with respect to the probability variable, F is the cumulative distribution function and f is the probability density function of the random outcomes X. If we use the notation ${\mathbb {E}}_w(v(X))$ (when $w^+=w^-=w$) and ${\mathbb {E}}_{w^+w^-}(v(X))$, in much analogy with the notation in Heilpern (2003) and Kaluszka and Krzeszowiec (2012), we can also define the continuous cumulative prospect value as $V (v(X)) = {\mathbb {E}}_{w^+w^-}(v(X))$.

A special case of (4) is when the value function is linear and, in particular, $v(x)=x$:

$$\begin{aligned} V (X) = {\mathbb {E}}_{w^+w^-}(X) = \int _{-\infty }^0 x\, \psi ^- [F(x)] \, f(x)\, \mathrm{{d}}x + \int _0^{+\infty } x\, \psi ^+ [1-F(x)] \, f(x)\, \mathrm{{d}}x;\nonumber \\ \end{aligned}$$

(5)

and when $w^+=w^-=w$, we have

$$\begin{aligned} V (X) = {\mathbb {E}}_{w}(X) = \int _{-\infty }^{+\infty } x\, \psi [1-F(x)] \, f(x)\, \mathrm{{d}}x. \end{aligned}$$

(6)

For an arbitrary random variable, the cumulative prospect value can also be defined using the generalized Choquet integral:

$$\begin{aligned} {\mathbb {E}}_{w^+w^-}(v(X))= & {} \int _0^{+\infty } w^+ \left( {\mathbb {P}}(v^+(X)>y)\right) \,\mathrm{{d}}y \\&- \int _{-\infty }^0 \left[ 1 - w^-\left( {\mathbb {P}}(v^-(X)>y)\right) \right] \,\mathrm{{d}}y; \end{aligned}$$

with special cases

$$\begin{aligned} {\mathbb {E}}_{w^+w^-}(X) = \int _0^{+\infty } w^+ \left( {\mathbb {P}}(X>x)\right) \,\mathrm{{d}}x - \int _{-\infty }^0 \left[ 1 - w^-\left( {\mathbb {P}}(X>x)\right) \right] \,\mathrm{{d}}x \end{aligned}$$

and

$$\begin{aligned} {\mathbb {E}}_{w}(X) = \int _{-\infty }^{+\infty } w\left( {\mathbb {P}}(X>x)\right) \,\mathrm{{d}}x. \end{aligned}$$

3 A behavioral premium principle under continuous cumulative prospect theory

Let u denote the utility function, and W be the initial wealth; the utility indifference priceP is the premium from the insurer’s viewpoint which satisfies (if it exists) the condition:

$$\begin{aligned} u(W) = {\mathbb {E}}[u(W + P - X)], \end{aligned}$$

(7)

where X is the claim amount; the severity of the loss caused by a risk event can be modeled by a non-negative random variable. The premium P makes indifferent the insurance company about accepting the risky position and not selling the insurance policy. The well-known equivalent utility principle has been introduced by Gerber (1979) for concave utility functions; we refer to the zero utility principle when the initial wealth is $W=0$ or the utility function is defined with respect to the a reference point which is set equal to the status quo ${\hat{u}}(x)=u(W+x)$ (see Heilpern 2003).

Differently from expected utility theory, in prospect theory individuals are risk averse when considering gains and risk seeking with respect to losses; moreover, they are more sensitive to losses than to gains of comparable magnitude (loss aversion). The final result $W + P - X$ in (7) could be positive or negative. The relative result $W + P - X$ will be considered through a value function v, which is continuous and strictly increasing, with $v(0)=0$. Objective probabilities are replaced by decision weights, as defined in the previous section.

The equivalent utility principle (7) under cumulative prospect theory becomes

$$\begin{aligned} v^+(W) = V[v(W + P - X)] = {\mathbb {E}}_{w^+w^-}[v(W + P - X)]. \end{aligned}$$

(8)

Heilpern (2003) introduces a zero utility principle under rank-dependent utility theory, Kaluszka and Krzeszowiec (2012) extend the definition of the premium principle in a cumulative prospect framework, discussing some special cases with linear and exponential utility functions and the properties of the related premium.

In the present work, we adopt the continuous cumulative prospect theory representation as defined in (4). Let the loss severity X be modeled by a non-negative continuous random variable, with distribution function $F_X$ and probability density function $f_X$,⁴ then condition (8) becomes

$$\begin{aligned} \begin{aligned} v^+(W)&= \int _0^{W+P} v^+(W + P - x)\, \psi ^+ [F_X(x)] \, f_X(x)\, \mathrm{{d}}x\, \\&\quad +\,\int _{W+P}^{+\infty } v^-(W + P - x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x. \end{aligned} \end{aligned}$$

(9)

As already pointed out, in prospect theory results are evaluated considering potential gains and losses relative to a reference point, rather than in terms of final wealth; the value function may be non differentiable at the reference point. When zero is assumed as reference point (the status quo), or taking $W=0$ in (9), then the premium P for insuring X is defined by the condition

$$\begin{aligned} V[v(P - X)] = {\mathbb {E}}_{w^+w^-}[v(P - X)] = 0, \end{aligned}$$

and is implicitly determined by the following equation

$$\begin{aligned} 0&= \int _0^{P} v^+(P - x)\, \psi ^+ [F_X(x)] \, f_X(x)\, \mathrm{{d}}x\, \nonumber \\&\quad +\,\int _{P}^{+\infty } v^-(P - x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x. \end{aligned}$$

(10)

Condition (10) defines the zero prospect value premium principle based on cumulative prospect theory for continuous random variables.

3.1 Properties of the behavioral premium principle

We discuss some properties of the principles defined above. It is easy to show that, when the utility or value functions are identity functions, $u(x)=x$ or $v(x)=x$, and probabilities are not distorted, $w(p)=p$, then the behavioral premium is equal to the equivalence premium,

$$\begin{aligned} P = {\mathbb {E}}(X). \end{aligned}$$

When probabilities are not distorted and we consider a utility function u, we have

$$\begin{aligned} V(u(W+P-X)) = {\mathbb {E}}[u(W+P-X)], \end{aligned}$$

and the equivalent utility premium principle follows.

Let $u(x)=x$ and $w=w^+=w^-$, which corresponds to the dual utility model (see Yaari 1987); then $V(Y)={\mathbb {E}}_w(Y)$ as defined in (6), for any continuous random variable,

$$\begin{aligned} V (Y) = {\mathbb {E}}_{w}(Y) = \int _{-\infty }^{+\infty } y\, \psi [1-F_Y(y)] \, f_Y(y)\, \mathrm{{d}}y. \end{aligned}$$

Define $Y = W + P - X$, then

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_{w}(W + P - X)&= \int _{0}^{+\infty } (W + P - x)\, \psi [F_X(x)] \, f_X(x)\, \mathrm{{d}}x\\&= (W+P)[w(1)-w(0)] - \int _{0}^{+\infty } x\, \psi [F_X(x)] \, f_X(x)\, \mathrm{{d}}x \\&= (W+P) - {\mathbb {E}}_{\overline{w}}(X), \end{aligned} \end{aligned}$$

where $\overline{w}$ is the dual probability weighting function $\overline{w}(p) = 1 - w(1-p)$, with $\overline{w}^\prime (p) = w^\prime (1-p)$. Note that ${\mathbb {E}}_w(-X) = -{\mathbb {E}}_{\overline{w}}(X)$. If we impose condition

$$\begin{aligned} u(W) = {\mathbb {E}}_w[u(W + P - X)] \end{aligned}$$

(we can also consider $W=0$), the solution is the following premium principle

$$\begin{aligned} P = {\mathbb {E}}_{\overline{w}}(X). \end{aligned}$$

(11)

It is worth noting that when w is concave (convex), $\overline{w}$ is convex (concave).⁵ More generally, if w has an inverse-S shape (S-shape), $\overline{w}$ has an S-shape (inverse-S shape). The shape of the probability weighting function, and its interpretation in terms of probabilistic optimism and pessimism, will be explained later in Sect. 5. In Sect. 4, we will discuss the case with linear utility and different probability distortions for positive and negative outcomes $w^+ \ne w^-$, and two cases with exponential utility functions with both $w^+ = w^-$ and $w^+ \ne w^-$.

The premium principle under continuous cumulative prospect theory satisfies the following properties.

No unjustified safety (or risk) loading:$P(a)=a$, for all constants a.

This is a consequence of the definition of the premium principle, strict monotonicity of v, and property ${\mathbb {E}}_{w^+w^-}(c)=c$, so that

$$\begin{aligned} v(W) = {\mathbb {E}}_{w^+w^-}(v(W+P(a)-a)) = v(W+P(a)-a), \end{aligned}$$

thus $P=a$. $\square$

Non-excessive loading: when v is a continuous and increasing function, with $v(0)=0$, and $w^+$ and $w^-$ are probability weighting functions, $P(X) \le \sup (X)$.

Given ${\mathbb {E}}_{w^+w^-}c=c$, for all c, and ${\mathbb {E}}_{w^+w^-}(X)\le {\mathbb {E}}_{w^+w^-}(Y)$, if $X\le Y$, then

$$\begin{aligned} v(W)= & {} {\mathbb {E}}_{w^+w^-}(v(W+P-X))\\\ge & {} {\mathbb {E}}_{w^+w^-}(v(W+P-\sup X))\\= & {} v(W+P-\sup X), \end{aligned}$$

hence $P \le \sup (X)$. $\square$

Translation invariance:$P(X+b) = P(X) + b$, for all b.

Indeed, we have

$$\begin{aligned} v(W)= & {} {\mathbb {E}}_{w^+w^-}[v(W + P(X+b)-(X+b))] \\= & {} {\mathbb {E}}_{w^+w^-}[v(W + P(X)+b - (X+b))], \end{aligned}$$

or using the representation (4) we can prove that

$$\begin{aligned} \begin{aligned} v(W)&= \int _0^{W+P(X+b)-b} v^+(W+P(X+b)-(X+b))\psi ^+(F_X(x))\,f_X(x)\,\mathrm{{d}}x\, \\&\quad +\, \int _{W+P(X+b)-b}^{+\infty } v^-(W+P(X+b)-(X+b))\psi ^-(1-F_X(x))\,f_X(x)\,\mathrm{{d}}x \\&= \int _0^{W+P(X)} v^+(W+P(X)+b-(X+b))\psi ^+(F_X(x))\,f_X(x)\,\mathrm{{d}}x\, \\&\quad +\, \int _{W+P(X)}^{+\infty } v^-(W+P(X)+b-(X+b))\psi ^-(1-F_X(x))\,f_X(x)\,\mathrm{{d}}x, \end{aligned} \end{aligned}$$

so that $P(X+b) = P(X) + b$. $\square$

Positive scale invariance:$P(aX) = aP(X)$, for $a>0$.

This property holds under rank-dependent utility if and only if the value function is linear (for the proof, see Heilpern 2003). Under cumulative prospect theory, Kaluszka and Krzeszowiec (2012) prove that scale invariance holds when: (i) $W=0$, if and only if $v^-=c_1(-x)^d$ and $v^+=c_2(x)^d$, for $d>0$, $c_1< 0 < c_2$; (ii) $W>0$, for a random variable X such that ${\mathbb {P}}(X=0)=1-q$ and ${\mathbb {P}}(X=s)=q$ ($s>0$, $q\in [0,1]$), if and only if $v(x)=cx$, $c>0$ and $\overline{w}^+=w^-$. $\square$

Additivity for independent risks, additivity for comonotonic risks, sub-additivity, stop-loss order preserving are studied and proved under rank-dependent utility and cumulative prospect theory (see Gerber 1985; Heilpern 2003; Goovaerts et al. 2004, 2010; Kaluszka and Krzeszowiec 2012) for a class of functions including linear and exponential utility, with some restrictions on the value function and on the shape of the probability weighting function. The assumptions we make about v and w are more general; in particular, for the shape of the probability weighting function, an inverse-S is more realistic.

3.2 Behavioral premium principle and framing

In this contribution, we also assume that decision makers are not indifferent among frames of cash flows: the framing of alternatives exerts a crucial effect on actual choices. People may keep different mental accounts for different types of outcomes, and when combining these accounts to obtain overall result, typically they do not simply sum up all monetary amounts, but intentionally use hedonic framing (Thaler 1985) such that the combination of the outcomes appears more favorable and increases their utility. The term framing is also used to refer to the way in which alternatives (e.g., outcomes from financial investments, products sold in-bundle, insurance or derivatives embedded in some other contracts) are presented and explained to the decision maker, and may influence mental accounting.

Outcomes are aggregated $v(x+y)$ or segregated $v(x)+v(y)$ depending on what leads to the highest possible prospect value: multiple gains are preferred to be segregated, $v^+(x)+v^+(y)$ (with $x>0$, $y>0$); losses are preferred to be integrated with other losses, $v^-(x+y)$ (with $x<0$, $y<0$), or large gains, in order to ease the pain of the loss. Mixed outcomes would be integrated in order to cancel out losses when there is a net gain or a small loss; for large losses and a small gain, they usually are segregated in order to preserve the silver lining.⁶ This is due to the shape of the value function in prospect theory, characterized by risk seeking or risk aversion, diminishing sensitivity and loss aversion.

Regarding the valuation of insurance contracts, different aggregations or segregations of the results are possible. One can consider a single position (narrow framing) or a portfolio of insurance policies. In the premium principle defined by (10) narrow framing is applied, where X is the random amount that will be paid by the insurer to settle each claim; moreover, the random result on a single policy is considered in a mental account separated from the wealth own by the insurance company and zero is the reference point.

It is also possible to segregate results across time: e.g., one can evaluate separately the cashed premium and the final loss. Moreover, when time is relevant,⁷ one can assume that the premium received at time $t=0$ is invested at the risk-free interest rate r, obtaining $Pe^{rT}$ at some maturity T of the contract.

If we segregate the cashed premium from the possible loss and evaluate the results in two separate mental accounts, condition (10) becomes

$$\begin{aligned} 0 = v^+(P) + \int _0^{+\infty } v^-(-x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x, \end{aligned}$$

(12)

and the premium can be determined as

$$\begin{aligned} P = \varphi ^{-1}\left( - {\mathbb {E}}_{w^-}(v^-(-X))\right) , \end{aligned}$$

(13)

where $\varphi =v^+$, and ${\mathbb {E}}_{w^-}(v^-(-X))=\int _0^{+\infty } v^-(-x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x$.

Equation (12) defines an alternative premium principle based on continuous cumulative prospect theory when the premium is segregated from the random loss. Hence, premium principle in (10) is the one determined in the aggregated model.

It is worth noting that, when the value function is linear, in particular $a = b = 1$ and $\lambda = 1$ for function (1), and there is no probability distortion, $w^+(p)=w^-(p)=p$, the resulting premium is $P = {\mathbb {E}}(X)$. Properties discussed in the previous subsection for the premium principle obtained in the aggregated model may be in general no longer valid.

4 Applications of the behavioral premium principle

Alternative functional forms both for the utility or value function and the probability weighting function, embedded in rank-dependent utility and cumulative prospect theory, yield different models with potentially different implications for choice behavior. In this section, we discuss several examples and some properties of the related premium principle.

In the first example, we consider the premium principle defined by (8) with a linear value function. This case generalizes a property previously discussed and it has also been analyzed by Kaluszka and Krzeszowiec (2012).

Example 1

Let $v(x)=c\,x$, with $c > 0$. Consider also $W\ge 0$. Condition (8) is satisfied when⁸

$$\begin{aligned} \begin{aligned} W&= \int _0^{W+P} (W + P - x)\, \psi ^+ [F_X(x)] \, f_X(x)\, \mathrm{{d}}x \, \\&\quad +\, \int _{W+P}^{+\infty } (W + P - x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x. \end{aligned} \end{aligned}$$

It is possible to show that⁹

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_{w^+w^-}(W+P-X)&= - \int _0^{+\infty } x \psi ^-(1-F_X(x))\,f_X(x)\,\mathrm{{d}}x\, +\, (W+P) \, \\&\quad +\, \int _0^{W+P} (W+P-x)[\psi ^+(F_X(x))-\psi ^-(1-F_X(x))]\,\mathrm{{d}}x \\&= - {\mathbb {E}}_{w^-}(X) + (W+P) \, \\&\quad +\, \int _0^{W+P} [w^-(1-F_X(x))-\overline{w}^+(1-F_X(x))]\,\mathrm{{d}}x, \end{aligned} \end{aligned}$$

where ${\mathbb {E}}_{w^-}(X) = \int _0^{+\infty } x \psi ^-(1-F_X(x))\,f_X(x)\,\mathrm{{d}}x$.

Hence, condition (8) can also be expressed as follows

$$\begin{aligned} W + {\mathbb {E}}_{w^-}(X) = (W+P) + \int _0^{W+P} [w^-(1-F_X(x))-\overline{w}^+(1-F_X(x))]\,\mathrm{{d}}x. \end{aligned}$$

Let us denote $t=W+P$, then the right-hand side is a function G(t) with $G^\prime = 1 + (w^-(1-F_X(t)) - 1 + w^+(F_X(t))) > 0$.

The resulting premium is solution of

$$\begin{aligned} P = G^{-1}(W+{\mathbb {E}}_{w^-}(X)) - W, \end{aligned}$$

and for $W=0$ we have

$$\begin{aligned} P = G^{-1}({\mathbb {E}}_{w^-}(X)), \end{aligned}$$

(14)

which requires numerical computation. $\square$

In the next two examples, we consider the behavioral premium principle with exponential utility functions under rank-dependent utility theory (see also Heilpern 2003, and Tsanakas 2009) and cumulative prospect theory (see also Kaluszka and Krzeszowiec 2012); we provide also an alternative discussion of the results based on the continuous representation (4).

Example 2

Exponential premium principle under rank-dependent utility theory

Assume a utility function¹⁰$u(x)=(1-e^{-bx})/a$, with $a>0$ and $b>0$. With $W\ge 0$, we have $u(W)=(1-e^{-bW})/a$. When $w^+=w^-=w$, the right-hand side of condition (8) is equal to

$$\begin{aligned} \begin{aligned} V(u(W+P-X))&= \int _0^{+\infty } u(W+P-x)\,\psi (F_X(x))\,f_X(x)\,\mathrm{{d}}x\\&= \int _0^{+\infty } \frac{1}{a} \left( 1-e^{-b(W+P-x)}\right) \,\psi (F_X(x))\,f_X(x)\,\mathrm{{d}}x \\&= \frac{1}{a} \left( 1 -e^{-b(W+P)}\,\int _0^{+\infty } e^{bx}\,\psi (F_X(x))\,f_X(x)\,\mathrm{{d}}x \right) \\&= \frac{1}{a} \left( 1 -e^{-b(W+P)}\, {\mathbb {E}}_{\overline{w}} \left( e^{bX}\right) \right) . \end{aligned} \end{aligned}$$

Given the definition and properties of the Choquet integral, one obtains the same result:

$$\begin{aligned} {\mathbb {E}}_w(u(W+P-X)) = {\mathbb {E}}_w \left( \frac{1-e^{-b(W+P-X)}}{a} \right) = \frac{1}{a}\left( 1-e^{-b(W+P)} {\mathbb {E}}_{\overline{w}} \left( e^{bX}\right) \right) , \end{aligned}$$

where ${\mathbb {E}}_{\overline{w}} \left( e^{bX}\right) = \int _0^{+\infty } e^{bx}\,\psi (F_X(x))\,f_X(x)\,\mathrm{{d}}x$.

By imposing the condition $u(W)={\mathbb {E}}_w(u(W+P-X))$ and after some algebraic manipulation,¹¹ we obtain the following exponential premium principle under rank-dependent utility theory:

$$\begin{aligned} P = \frac{1}{b} \, \ln {\mathbb {E}}_{\overline{w}} \left( e^{bX}\right) . \end{aligned}$$

(15)

Using analogous arguments, one can derive an exponential premium principle adopting the utility function¹²$u(x)=(e^{bx}-1)/a$, with $a>0$ and $b>0$. With $W\ge 0$, we have $u(W)=(e^{bW}-1)/a$. When $w^+=w^-=w$, the right-hand side of condition (8) is equal to

$$\begin{aligned} \begin{aligned} V(u(W+P-X))&= \int _0^{+\infty } u(W+P-x)\,\psi (F_X(x))\,f_X(x)\,\mathrm{{d}}x \\&= \int _0^{+\infty } \frac{1}{a} \left( e^{b(W+P-x)}-1 \right) \,\psi (F_X(x))\,f_X(x)\,\mathrm{{d}}x \\&= \frac{1}{a} \left( -1 + e^{b(W+P)}\,\int _0^{+\infty } e^{-bx}\,\psi (F_X(x))\,f_X(x)\,\mathrm{{d}}x \right) \\&= \frac{1}{a} \left( -1 + e^{b(W+P)}\, {\mathbb {E}}_{\overline{w}} \left( e^{-bX}\right) \right) . \end{aligned} \end{aligned}$$

Equivalently, we have

$$\begin{aligned} {\mathbb {E}}_w \left( \frac{1}{a}\left( e^{b(W+P-X)} -1 \right) \right) = \frac{1}{a} e^{b(W+P)} {\mathbb {E}}_{\overline{w}} \left( e^{-bX}\right) - \frac{1}{a}, \end{aligned}$$

where ${\mathbb {E}}_{\overline{w}} \left( e^{-bX}\right) = \int _0^{+\infty } e^{-bx}\,\psi (F_X(x))\,f_X(x)\,\mathrm{{d}}x$. Condition (8) yields

$$\begin{aligned} P = - \frac{1}{b} \, \ln \left( {\mathbb {E}}_{\overline{w}} \left( e^{-bX}\right) \right) , \end{aligned}$$

(16)

an alternative exponential premium principle under rank-dependent utility theory. $\square$

Example 3

Exponential premium principle under continuous cumulative prospect theory

Assume a utility function $u(x)=(1-e^{-bx})/a$, with $a>0$ and $b>0$. With $W\ge 0$, we have $u(W)=(1-e^{-bW})/a$. When $w^+\ne w^-$, the right-hand side of condition (8) is equal to

$$\begin{aligned} \begin{aligned}&V(u(W+P-X)) =\\&\quad = \frac{1}{a} \int _0^{W+P} (1-e^{-b(W+P-x)})\,\psi ^+(F_X(x))\,f_X(x)\,\mathrm{{d}}x \\&\quad \quad +\, \frac{1}{a} \int _{W+P}^{+\infty } \left( 1-e^{-b(W+P-x)}\right) \,\psi ^-(1 - F_X(x))\,f_X(x)\,\mathrm{{d}}x \\&\quad = \frac{1}{a}{\mathbb {E}}_{w^-}\left( 1-e^{-b(W+P-X)}\right) \\&\quad \quad +\, \frac{1}{a} \int _0^{W+P} (1-e^{-b(W+P-x)})\,[\psi ^+(F_X(x))-\psi ^-(1 - F_X(x))]\,f_X(x)\,\mathrm{{d}}x \\&\quad = \frac{1}{a} - \frac{1}{a} e^{-b(W+P)}{\mathbb {E}}_{w^-} \left( e^{bX}\right) \\&\quad \quad +\, \frac{1}{a} \int _0^{W+P} (1-e^{-b(W+P-x)})\,[\psi ^+(F_X(x))-\psi ^-(1 - F_X(x))]\,f_X(x)\,\mathrm{{d}}x. \end{aligned} \end{aligned}$$

Using the same result as in the first example, it is possible to show that

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_{w^+w^-}\left( 1-e^{-b(W+P-X)}\right)&= 1 - {\mathbb {E}}_{w^-}\left( e^{-b(W+P-X)}\right) \, \\&\quad +\, \int _0^1 [w^-(1-F_Y(y))-\overline{w}^+(1-F_Y(y))]\,\mathrm{{d}}y, \end{aligned} \end{aligned}$$

where $Y=e^{-b(W+P-X)}$, and

$$\begin{aligned} {\mathbb {E}}_{w^-}\left( e^{-b(W+P-X)}\right) = \int _0^{+\infty } e^{-b(W+P-x)} \psi ^-(1-F_X(x))\,f_X(x)\,\mathrm{{d}}x. \end{aligned}$$

After substitution into (8)

$$\begin{aligned} 1 - e^{-bW} = 1 - e^{-b(W+P)}{\mathbb {E}}_{w^-}\left( e^{bX}\right) + \int _0^{1} [w^-(1-F_Y(y))-\overline{w}^+(1-F_Y(y))]\,\mathrm{{d}}y\, \end{aligned}$$

and a transformation of random variable,

$$\begin{aligned} \begin{aligned}&e^{-b(W+P)}{\mathbb {E}}_{w^-}\left( e^{bX}\right) = e^{-bW} \\&\quad +\, e^{-b(W+P)} \int _0^{\exp (b(W+P))} [w^-({\mathbb {P}}(e^{bX}>s))-\overline{w}^+({\mathbb {P}}(e^{bX}>s))]\,\mathrm{{d}}s, \end{aligned} \end{aligned}$$

we obtain

$$\begin{aligned} {\mathbb {E}}_{w^-}\left( e^{bX}\right) = e^{bP} + \int _0^{\exp (b(W+P))} [w^-({\mathbb {P}}(e^{bX}>s))-\overline{w}^+({\mathbb {P}}(e^{bX}>s))]\,\mathrm{{d}}s. \end{aligned}$$

When $W=0$, we have

$$\begin{aligned} \begin{aligned} {\mathbb {E}}_{w^-}\left( e^{bX}\right)&= e^{bP} + \int _0^{\exp (bP)} [w^-({\mathbb {P}}(e^{bX}>s))-\overline{w}^+({\mathbb {P}}(e^{bX}>s))]\,\mathrm{{d}}s \\&= e^{bP} + \int _0^{\exp (bP)} e^{bx}[\psi ^+(F_X(x))-\psi ^-(1-F_X(x))]\,\mathrm{{d}}x. \end{aligned} \end{aligned}$$

Let us denote $t=e^{bP}$, then the right-hand side is a function G(t) with $G^\prime > 0$, and the premium is solution of

$$\begin{aligned} P = \frac{1}{b} \ln \left( G^{-1}\left( {\mathbb {E}}_{w^-}(e^{bX})\right) \right) , \end{aligned}$$

which generalizes the exponential premium principle (15) obtained in the case $w^+=w^-$.

As an alternative, if we consider the utility function $u(x)=(e^{bx}-1)/a$, we can derive a premium which is solution of

$$\begin{aligned} P = -\frac{1}{b} \ln \left( G^{-1}\left( {\mathbb {E}}_{w^+}(e^{-bX})\right) \right) , \end{aligned}$$

where G(t) is a function of $t=e^{-bP}$ for which $G^{-1}$ exists. $\square$

The value function under cumulative prospect theory should display a combination of risk aversion for gains and risk seeking for losses, and loss aversion. A function with these features is (see also Davies and Satchell 2007)

$$\begin{aligned} v(x) = \left\{ \begin{array}{ll} v^+(x) = \dfrac{1 - e^{-ax}}{a} &{} \qquad x \ge 0 \\ \\ \lambda v^-(x) = \lambda \dfrac{e^{bx}-1}{b} &{} \qquad x < 0, \end{array} \right. \end{aligned}$$

(17)

where $\lambda \ge 1$ is the loss aversion parameter; parameters a and b govern curvature. When $a>0$ and $b>0$, the function v is convex for negative results, concave for positive outcomes, steeper for losses depending on the value of the parameter $\lambda$ ($\lambda > 1$ implies loss aversion). This function could be used in the case discussed in the previous example. In Sect. 6, we will obtain an explicit solution for the premium combining the value function defined in Eq. (17), a probability weighting function proposed by Prelec (1998) and a Weibull distribution under cumulative prospect theory in the segregated model.

A usual choice for the value function, widely applied in the literature, is defined by (1) presented above,

$$\begin{aligned} v(x) = \left\{ \begin{array}{ll} v^+(x) = x^a &{} \quad x \ge 0 \\ v^-(x) = -\lambda (-x)^b &{} \quad x < 0. \end{array} \right. \end{aligned}$$

In the following examples, we adopt such a value function.

Example 4

Let v be defined by (1); then Eq. (10) becomes

$$\begin{aligned} 0 = \int _0^{P} (P - x)^a\, \psi ^+ [F_X(x)] \, f_X(x)\, \mathrm{{d}}x - \lambda \int _{P}^{+\infty } (x - P)^b\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x, \end{aligned}$$

which requires numerical solution for P.

In the segregated model, equating at zero and solving for P, gives the explicit formula

$$\begin{aligned} P = \left( \lambda \int _0^{+\infty } x^b\, \psi ^- [1-F_X(x)]f_X(x)\, \mathrm{{d}}x \right) ^{1/a}, \end{aligned}$$

which requires numerical approximation of the integral. The premium is increasing with loss aversion $\lambda$, which appears not so obvious in the aggregated case; given that $0<a\le 1$ and $0 < b\le 1$. $\square$

Remember the property $P\,{\le }\,\sup X$ (non-excessive loading) presented above. Kaluszka and Okolewski (2008) analyze a premium principle when the utility function is linear and the function $w^+$ and $w^-$ are neo-additive weighting functions, $w^-=a+bp$ and $w^+=c+dp$ ($b,\,d>0$, $a+b<1$, $c+d<1$), and $\sup X = W$. In the next example, we assume that the random variable X is bounded.

Example 5

If the set of possible outcomes for the claim X is $[0,\overline{x}]$, for some limit value $\overline{x}>0$, then the premium in the aggregated model is defined by

$$\begin{aligned} 0 = \int _0^{P} v^+(P - x)\, \psi ^+ [F_X(x)] \, f_X(x)\, \mathrm{{d}}x + \int _{P}^{\overline{x}} v^-(P - x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x, \end{aligned}$$

and considering the value function (1) yields

$$\begin{aligned} 0 = \int _0^{P} (P - x)^a\, \psi ^+ [F_X(x)] \, f_X(x)\, \mathrm{{d}}x - \int _{P}^{\overline{x}} \lambda (x - P)^b\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x. \end{aligned}$$

In the segregated model (12), the premium is the solution of

$$\begin{aligned} 0 = v^+(P) + \int _0^{\overline{x}} v^-(-x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x; \end{aligned}$$

substituting (1), we have

$$\begin{aligned} P = \left( \lambda \int _{0}^{\overline{x}} x^b\, \psi ^- [1-F_X(x)] f_X(x)\, \mathrm{{d}}x \right) ^{1/a}. \end{aligned}$$

Also in this case, the higher the loss aversion of the insurer, the higher the premium. $\square$

Premium principles (10) and (12) can be adjusted in order to take into consideration some policy conditions such as deductibles. The next two examples discuss the cases of fixed-percentage and fixed-amount deductibles.

Example 6

Fixed-percentage deductible

If we consider a fixed-percentage deductible, the part of the risk $\theta X$ is retained by the insured, while $(1-\theta )X$ is transferred to the insurer, for $0\le \theta \le 1$. In the aggregated model (10), the premium can be determined from the following equation

$$\begin{aligned} \begin{aligned} 0&= \int _0^{P/(1-\theta )} v^+\left( P - (1-\theta )x\right) \, \psi ^+ [F_X(x)] \, f_X(x)\, \mathrm{{d}}x \\&\quad +\, \int _{P/(1-\theta )}^{+\infty } v^-\left( P - (1-\theta )x\right) \, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x, \end{aligned} \end{aligned}$$

solving numerically for P. Taking v as in (1) as a special case, we have

$$\begin{aligned} \begin{aligned} 0&= \int _0^{P/(1-\theta )} \left( P - (1-\theta )x\right) ^a\, \psi ^+ [F_X(x)] \, f_X(x)\, \mathrm{{d}}x \\&\quad -\, \lambda \int _{P/(1-\theta )}^{+\infty } \left( (1-\theta )x - P\right) ^b\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x. \end{aligned} \end{aligned}$$

In the segregated model (12), the premium is defined by

$$\begin{aligned} 0 = v^+(P) + \int _0^{+\infty } v^-(-(1-\theta )x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x; \end{aligned}$$

in particular, we have the following result

$$\begin{aligned} P = \left( \lambda \,(1-\theta )^b \int _{0}^{+\infty } x^b\, \psi ^- [1-F_X(x)] f_X(x)\, \mathrm{{d}}x \right) ^{1/a}. \end{aligned}$$

It is interesting to observe that, in the last explicit formula, not only is the premium increasing with loss aversion, modeled by the parameter $\lambda$, but also it is higher the lower the retention $\theta$ is, which is also an intuitive result. In the aggregated model, the resulting premium depends on the combined effect of risk-aversion and risk seeking behaviors, together with loss aversion, of the value function. $\square$

Example 7

Deductible of fixed amount

If a deductible of fixed amount $d\ge 0$ is considered, any loss less than or equal to d is entirely retained by the insured, $\min (X,d)$, while losses higher than d are transferred to the insurer for the amount exceeding the deductible, $\max (X-d,0)$. In such a case, it can be shown that in the aggregated model (10) the premium can be determined from the following equation¹³

$$\begin{aligned} \begin{aligned} 0&= v^+(P) w^+\left( F_X(d)\right) + \int _d^{d+P} v^+ \left( P-(x-d) \right) \, \psi ^+ \left( F_X(x)\right) f_X(x)\, \mathrm{{d}}x \\&\quad +\, \int _{d+P}^{+\infty } v^-\left( P-(x-d) \right) \, \psi ^- \left( 1-F_X(x)\right) f_X(x)\, \mathrm{{d}}x, \end{aligned} \end{aligned}$$

solving numerically for P.

In the segregated model (12), the premium is defined by

$$\begin{aligned} 0 = v^+(P) + \int _{d}^{+\infty } v^-(d-x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x; \end{aligned}$$

and, in particular, we have the following result

$$\begin{aligned} P = \left( \lambda \int _{d}^{+\infty } (x-d)^b\, \psi ^- [1-F_X(x)] f_X(x)\, \mathrm{{d}}x \right) ^{1/a}. \end{aligned}$$

Also in this case, the premium is decreasing with respect to the fixed deductible d and increasing with loss aversion of the insurer. $\square$

All the results presented above depend on the choice of the weighting function. So far, we have assumed that $w^+$ and $w^-$ were increasing functions $w:[0,1]\rightarrow [0,1]$, with $w(0)=0$ and $w(1)=1$. Weighting functions are a key element in modeling decisions under risk and uncertainty when one tries to capture behavioral patterns which departure from expected utility theory. In the literature related to prospect theory, in its original and cumulative versions, and rank-dependent utility theory, several functional forms of probability weighting functions have been proposed and tested in many theoretical and empirical studies. Different functional forms yield different models; in particular, when the weighting function has an inverse-S shape, very low probability of extreme events are overweighted, with possible implications for the resulting premium.

5 Some remarks on the shape of the probability weighting function

In this section, we discuss some features of the probability weighting function (see Nardon and Pianca 2018), which models probabilistic risk behavior. We recall from previous sections that w is uniquely determined, it maps the probability interval [0, 1] into [0, 1], and is strictly increasing, with $w(0)=0$ and $w(1)=1$. Here, we consider continuous weighting functions.¹⁴

The curvature of the weighting function is related to the risk attitude toward probabilities. Empirical evidence suggests a particular shape of probability weighting functions: small probabilities are overweighted $w(p)>p$, whereas individuals tend to underestimate large probabilities $w(p)<p$. The function is initially concave (probabilistic risk seeking or optimism) for probabilities in the interval $(0,p^*)$, and convex (probabilistic risk aversion or pessimism) in the interval $(p^*,1)$, for a certain value of $p^*$. This turns out in a typical inverse-S shape. A linear weighting function describes probabilistic risk neutrality or objective sensitivity toward probabilities, which characterizes expected utility. Empirical findings¹⁵ indicate that the intersection (elevation) between the weighting function and the $45^\text {o}$ line, $w(p)=p$, is for p in the interval (0.3, 0.4).

The sensitivity toward probability is increased if (see Abdellaoui et al. 2010) $w(p)/p>1$, for $p\in (0,\delta )$, and $(1-w(p))/(1-p)>1$, for $p\in (1-\epsilon , 1)$, whereas a weighting function exhibits decreased sensitivity if $w(p)/p<1$, for $p\in (0,\delta )$, and $(1-w(p))/(1-p)<1$, for $p\in (1-\epsilon , 1)$, for some arbitrary small $\delta >0$ and $\epsilon >0$. Some weighting functions (e.g., the functions suggested by Goldstein and Einhorn 1987; Tversky and Kahneman 1992; Prelec 1998) display extreme sensitivity, in the sense that w(p) / p and $(1-w(p))/(1-p)$ are unbounded as p tends to 0 and 1, respectively.

An inverse-S shape of w combines the increased sensitivity with concavity for small probabilities and convexity for medium and large probabilities. In particular, such a form captures the fact that individuals are extremely sensitive to changes in (cumulative) probabilities which approach to 0 and 1. Abdellaoui et al. (2010) discuss how optimism and pessimism are possible sources of increased sensitivity.

Different parametric forms for the weighting function with the above-mentioned features have been proposed in the literature, and their parameters have been estimated in many empirical studies. Single parameter probability weighting functions are those proposed by Karmarkar (1978, 1979), Röell (1987), Currim and Sarin (1989), Tversky and Kahneman (1992), Luce et al. (1993), Hey and Orme (1994), Prelec (1998), Safra and Segal (1998), and Luce (2000). Two (or more) parameter probability weighting functions have been proposed by Bell (1985), Goldstein and Einhorn (1987), Allais (1988), Currim and Sarin (1989), Lattimore et al. (1992), Wu and Gonzalez (1996), Prelec (1998), Luce (2001), Loomes et al. (2002), Walther (2003), Rieger and Wang (2006), Diecidue et al. (2009), Abdellaoui et al. (2010), and Pfiffelmann (2011).

Karmarkar (1978) considers the following function

$$\begin{aligned} w(p) = \frac{p^{\gamma }}{p^{\gamma } + (1-p)^{\gamma }}, \end{aligned}$$

(18)

with $\gamma > 0$. Function (18) is a special case (when $\delta = 1$) of the two parameter family proposed by Wu and Gonzalez (1996),

$$\begin{aligned} w(p) = \frac{p^{\gamma }}{\left( p^{\gamma } + (1-p)^{\gamma } \right) ^\delta }, \end{aligned}$$

(19)

with $\delta$ and $\gamma$ positive.

Allais (1988) suggests the expression

$$\begin{aligned} w(p) = \frac{m'p}{a-p} \frac{[1+(m'-1)a](a-p) - a(a-1)(m\,m'-1)(1-p)}{[1+(m'-1)a][1+(m'-1)p] - (a-1)(m\,m'-1)(1-p)},\nonumber \\ \end{aligned}$$

(20)

with $w(0)=0$, $w(1)=1$, $m'=\frac{\partial w}{\partial p} \Big |_{p=0}$, $m=\frac{\partial w}{\partial p} \Big |_{p=1}$. The function depends on three parameters: m, $m'$, and a. Based on observed data (subjective answer to questionnaires) and the properties of function (20), the parameters are such that $m > 1$, $0< m' < m$, $m\,m'>1$, $1<a<m/(m-1)$. Parameters m and $m'$ govern curvature of the weighting function. In particular, Allais (1988) points out that m can be interpreted as an indicator of the preference for security and $m'$ as an indicator of preference for risk for small probabilities. As $\partial w/\partial a <0$, the parameter a can be viewed as an indicator of the preference for security given the values of m and $m'$; hence, it controls elevation.

Tversky and Kahneman (1992) use the Quiggin (1982) functional of the form

$$\begin{aligned} w(p) = \frac{p^{\gamma }}{\left( p^{\gamma } + (1-p)^{\gamma } \right) ^{1/{\gamma }}}, \end{aligned}$$

(21)

where $\gamma$ is a positive constant. The parameter $\gamma$ captures the degree of sensitivity toward changes in probabilities from impossibility (zero probability) to certainty (Tversky and Kahneman 1992). When $\gamma < 1$, one obtains the typical inverse-S shape form; the lower the parameter, the higher is the curvature of the function. Note that $w(0)=0$ and $w(1)=1$ for the above defined functions.

Prelec (1998) suggests a two parameter compound-invariant function¹⁶ of the form

$$\begin{aligned} w(p) = e^{- \delta (-\ln p)^\gamma }, \qquad \qquad p\in (0,1), \end{aligned}$$

(22)

with $w(0)=0$ and $w(1)=1$. The parameter $\delta$ (with $0< \delta < 1$) governs elevation of the weighting function relative to the $45^\text {o}$ line, while $\gamma$ (with $\gamma > 0$) governs curvature and the degree of sensitivity to extreme results relative to medium probability outcomes. When $\gamma < 1$, one obtains the inverse-S shape function. In this model, the parameter $\delta$ influences the tendency of over- or underweighting the probabilities, but it has no direct meaning.

As an alternative, one can also consider the more parsimonious single parameter Prelec’s weighting function

$$\begin{aligned} w(p) = e^{-(-\ln p)^\gamma }, \qquad \qquad p\in (0,1), \end{aligned}$$

(23)

which only allows for curvature to be varied. Note that, in this case, the unique solution of equation $w(p)=p$ for $p\in (0,1)$ is $p=1/e\simeq 0.367879$ and does not depend on the parameter $\gamma$.

In an empirical study, Wu and Gonzalez (1999) consider both the Prelec (1998) weighting function and the linear in log odds function proposed by Goldstein and Einhorn (1987),

$$\begin{aligned} w (p) = \frac{\delta \, p^{\gamma }}{\delta \, p^{\gamma } + (1-p)^{\gamma }}. \end{aligned}$$

(24)

Function (24) has also been used by Lattimore et al. (1992) in a variant functional form, Tversky and Fox (1995), Birnbaum and McIntosh (1996), and Kilka and Weber (2001). The weighting function proposed by Karmarkar (1978, 1979) is a special case of (24) with $\delta =1$.

An interesting parametric function is the switch-power weighting function proposed by Diecidue et al. (2009), which consists in a power function for probabilities below a certain value ${\hat{p}}\in (0,1)$ and a dual power function for probabilities above ${\hat{p}}$; formally w is defined as follows:

$$\begin{aligned} w(p) = \left\{ \begin{array}{ll} cp^a &{} \qquad \hbox {if }\ 0 \le p \le {\hat{p}}, \\ 1-d(1-p)^b &{} \qquad \hbox {if }\ {\hat{p}} < p \le 1, \end{array} \right. \end{aligned}$$

(25)

with five parameters a, b, c, d, and ${\hat{p}}$. All the parameters are strictly positive, assuming continuity and monotonicity of w. When ${\hat{p}}$ approaches 1 or 0, w reduces to a power or a dual power probability weighting function, respectively. Diecidue et al. (2009) provide preference foundation for such a family of parametric weighting functions and inverse-S shape under rank-dependent utility based on testable preference conditions.

Fig. 3

Instances of the two parameter constant relative sensitivity probability weighting function, with different elevation (left) for $\gamma =0.3$ and $\delta =0.1,0.3,0.5,0.7$ (for higher values of $\delta$ the function is more elevated), and curvature (right) for $\delta =0.3$ and $\gamma =0.1,0.3,0.5,0.7$ (for lower values of $\gamma$ the function exhibits higher curvature)

Parameters in (25) reduce to three (a, b, and ${\hat{p}}$) by assuming continuity of w(p) at ${\hat{p}}$ and differentiability. For $a,b \le 1$, the function w is concave on $(0,{\hat{p}})$ and convex on $({\hat{p}},1)$ (it has an inverse-S shape), while for $a,b\ge 1$ the weighting function is convex for $p < {\hat{p}}$ and concave for $p>{\hat{p}}$ (it has an S-shape). Both parameters a and b govern the curvature of w when $a\ne b$. In particular, parameter a describes probabilistic risk attitude for small probabilities; whereas parameter b describes probabilistic risk attitude for medium and large probabilities. In the case with $a\ne b$, parameter ${\hat{p}}$, which signals the point where probabilistic risk attitudes change from risk aversion to risk seeking (for an inverse-S shape function), may not lie on the $45^\text {o}$ line, hence it has not the meaning of dividing the region of over- and underweighting of the probability.

When $a = b$, one obtains a two parameter probability weighting function, which intersects the $45^o$ line at ${\hat{p}}$. The parameter ${\hat{p}}$ separates the regions of over- and underweighting of probabilities. If we denote $\delta = {\hat{p}}$ and $a = \gamma$, the result is the constant relative sensitivity weighting function considered by Abdellaoui et al. (2010):

$$\begin{aligned} w(p) = \left\{ \begin{array}{ll} \delta ^{1-\gamma } p^\gamma &{} \qquad \hbox {if } 0 \le p \le \delta , \\ 1 - (1-\delta )^{1-\gamma }(1-p)^\gamma &{} \qquad \hbox {if } \delta < p \le 1, \end{array} \right. \end{aligned}$$

(26)

with $\gamma >0$ and $\delta \in [0,1]$. For $\gamma < 1$ and $0< \delta < 1$, it has an inverse-S shape. The derivative of w at $\delta$ equals $\gamma$; this parameter controls for the curvature of the weighting function. The parameter $\delta$ indicates whether the interval for overweighting probabilities is larger than the interval for underweighting, and therefore controls for the elevation. Hence, such a family of weighting functions allows for a separate and direct modeling of these two features. Figure 3 shows the plots of the constant relative sensitivity weighting function for different values of the parameters.

Remember that a convex weighting function characterizes probabilistic risk aversion and a concave weighting function characterizes probabilistic risk proneness, whereas a linear weighting function characterizes probabilistic risk neutrality. Then, the role of $\delta$ is to demarcate the interval of probability risk seeking from the interval of probability risk aversion.¹⁷ In such a case, overweighting corresponds to risk seeking (or optimism) and underweighting corresponds to risk proneness (or pessimism). Elevation represents the relative strength of optimism versus pessimism, hence it is a measure of relative optimism, and $\delta$ may be interpreted as an index of relative optimism.

Figure 4 shows the dependence of the decision weights $\pi$ on rank r, when results are ordered from best to worst, for the weighting function defined in Eq. (26). The decision weights $w(p+r)-w(r)$ can be approximated by $p\,w'(r)$ for objective individual probability p (such a probability is represented by the dashed line which depicts neutral psychology). The curvature parameter is $\gamma = 0.6$, and we consider different values for the elevation parameter. For $\delta =0.2$, the dotted curve illustrates relative pessimism (probabilities of extreme good outcomes and small probabilities of bad outcomes are overweighted), for $\delta =0.5$ the solid line illustrates that good and bad outcomes are overweighted, while intermediate results are underweighted, and for $\delta =0.8$ the dashed-dotted curve illustrates relative optimism (small probabilities of good outcomes are overweighted, probabilities of extreme bad outcomes are overweighted). As $\gamma$ approaches the value 1 (for lower curvature), the weights tend to the objective probabilities.

Fig. 4

Dependence of the decision weights on rank r (from best to worst) for w(p) defined as in Eq. (26), with weights $w(p+r)-w(r)\approx p\,w'(r)$ for objective probability $p=0.01$ (the dashed line depicts neutral psychology). The parameters of probability weighting w are: $\gamma =0.6$, letting elevation vary, $\delta =0.2$ (the dotted line curve illustrates relative pessimism), $\delta =0.5$ (the solid line illustrates that good and bad outcomes are overweighted while intermediate results are underweighted) and $\delta =0.8$ (the dashed-dotted curve illustrates relative optimism)

Gonzalez and Wu (1999) and Abdellaoui et al. (2010) find that the weighting function is more elevated for losses than for gains. In Abdellaoui et al. (2010), the relative index of optimism for gains $\delta ^+$ is lower than the relative index of pessimism for losses $\delta ^-$.

Curvature is a measure of the degree of sensitivity to changes from impossibility to possibility (Tversky and Kahneman 1992), it represents the diminishing effect of optimism and pessimism when moving away from extreme probabilities 0 and 1. Hence, parameter $\gamma$, controlling for curvature, measures the relative sensitivity of the weighting function. This suggests an interpretation for such a parameter as a measure of relative risk aversion. The index of relative sensitivity (see Abellaoui et al. 2010) of w as defined in (26) is $- p \frac{\partial ^2 w(p)}{\partial p^2}\big /\frac{\partial w(p)}{\partial p}$ for $p \in (0,\delta ]$ and $- (1-p) \frac{\partial ^2(1- w(p))}{\partial (1-p)^2}\big / \frac{\partial (1- w(p))}{\partial (1-p)}$ for $p \in (\delta ,1)$, it is constant and equals $1-\gamma$.

The constant relative sensitivity weighting function has been used by Nardon and Pianca (2018) in a behavioral model for the evaluation of European options. The choice of the probability weighting function should be driven by the following motivations: its empirical properties, intuitive and empirically testable preference conditions, nonlinear behavior of the probability weighting function. Moreover, a parametric probability weighting function should be parsimonious (remaining consistent with the properties suggested by empirical evidence), in particular when we consider different parameters for the weighting of probability of gains and losses. Two parameters allow for separate control of curvature and elevation, and the constant relative sensitivity weighting function, which governs distinctly these two features, is of particular interest also for the premium principle in order to model probabilistic pessimism and optimism of the insurer.

6 Behavioral premium principle with Weibull distribution and Prelec’s probability weighting function

Let us recall the premium principle in the segregated model defined by condition (12),

$$\begin{aligned} 0 = v^+(P) + \int _0^{+\infty } v^-(-x)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x; \end{aligned}$$

with $v^+$ a strictly increasing function, the premium P is solution to the previous equation.

Assume a piecewise exponential value function as defined in (17),

$$\begin{aligned} v(x) = \left\{ \begin{array}{ll} v^+(x) = \frac{1 - e^{-ax}}{a} &{} \qquad x \ge 0 \\ \lambda v^-(x) = \lambda \frac{e^{bx}-1}{b} &{} \qquad x < 0, \end{array} \right. \end{aligned}$$

where $\lambda >1$, $a>0$, and $b>0$. Function v is continuous and strictly increasing, convex for losses and concave for gains, steeper for losses.

Then, we obtain the following explicit solution for the premium

$$\begin{aligned} P = -\frac{1}{a} \ln \left( 1 - \lambda \frac{a}{b} \int _0^{+\infty } (e^{-bx} - 1)\, \psi ^- [1-F_X(x)] \, f_X(x)\, \mathrm{{d}}x \right) , \end{aligned}$$

(27)

where X is a non-negative continuous random variable, with cumulative distribution $F_X$ and probability density function $f_X$.

Consider the one parameter probability weighting function proposed by Prelec (1998):

$$\begin{aligned} w(p)=e^{-(-\ln p)^\gamma }, \end{aligned}$$

with

$$\begin{aligned} \psi (p) = w^\prime (p) = \frac{1}{p} \gamma (-\ln p)^{\gamma - 1} e^{-(-\ln p)^\gamma }. \end{aligned}$$

In what follows, for simplicity, we write w, $\psi$ and $\gamma$ instead of $w^-$, $\psi ^-$ and $\gamma ^-$, as only the weighting function for probability of losses is involved in the computations.

Assume that the random variable X has a Weibull distribution with parameters $\alpha > 0$ and $\beta > 0$, with density

$$\begin{aligned} f_X (x) = \alpha \beta ^{-\alpha } x^{\alpha - 1}e^{-x^\alpha \beta ^{-\alpha }} = \frac{\alpha }{\beta } \left( \frac{x}{\beta }\right) ^{\alpha - 1} e^{- \left( \frac{x}{\beta }\right) ^{\alpha }} \end{aligned}$$

and cumulative distribution function

$$\begin{aligned} F_X (x) = 1 - e^{-\left( \frac{x}{\beta }\right) ^{\alpha }}. \end{aligned}$$

So that

$$\begin{aligned} w(1-F_X(x)) = e^{- \left( \frac{x}{\beta }\right) ^{\alpha \gamma }}, \end{aligned}$$

and

$$\begin{aligned} \psi (1-F_X(x)) = \gamma \left( \frac{x}{\beta }\right) ^{\alpha (\gamma -1)} e^{\left( \frac{x}{\beta }\right) ^{\alpha } - \left( \frac{x}{\beta }\right) ^{\alpha \gamma }}. \end{aligned}$$

Substitution into (27), combining the Weibull distribution with the Prelec’s probability weighting function and an exponential value function, after a change of variable $z = (x/\beta )^{\alpha \gamma }$, and some simplifications, give the resulting premium

$$\begin{aligned} P = -\frac{1}{a} \ln \left( 1 - \lambda \frac{a}{b} \int _0^{+\infty } e^{-z} \left( e^{-b\beta \, z^{1/(\alpha \gamma )}} - 1 \right) \, \mathrm{{d}}z \right) , \end{aligned}$$

(28)

which requires numerical computation. An analogous result for the premium P can be obtained also adopting the more flexible two parameter Prelec’s weighting function $w(p)=e^{-\delta (-\ln p)^\gamma }$. Observe that the premium principle (28) is of similar form of premia discussed in Examples 2 and 3.

7 Conclusions

Prospect theory has begun to attract increasing interest in the insurance theory literature and, in its cumulative version, it seems a promising alternative to other models (such as the ranked dependent expected utility theory, the dual theory and risk measures based on distorted probabilities) for its potential to explain observed behaviors. In this framework, we define a premium principle under cumulative prospect theory based on the equivalent utility principle of Gerber (1979), extending behavioral premium principles presented in the literature. In particular, we adopted the representation of the cumulative prospect theory for continuous distributions, which allows us to review and provide alternative proofs of previous results and properties of the related premium principles.

We then assumed that framing of the alternatives matters: we apply the notion of hedonic framing introduced by Thaler (1985) in order to define two different models where the results are aggregated or segregated into separate mental accounts. In the segregated model, we obtain explicit solutions for the premium. We also introduce and discuss several applications, under specific assumptions on the value function and the probability weighting function.

As future research, it will be interesting to study the decision problem also from the viewpoint of the insured willing to buy protection, analyzing applications to other form of insurance, with extensions to reinsurance and the choice of optimal retention both in the proportional and non proportional case.