Introduction

Model parameters in health economic evaluations are generally based on results from published studies, which typically report summary statistics (e.g., the mean and standard error) at an aggregate level. In the field of health economics, probabilistic analysis refers to specifying sampling distributions of sample mean as the model input parameters in order to capture uncertainty around the parameters [1]. Deterministic analysis assigns point estimates to the model input parameters (i.e., often represented by the sample mean). When model parameter values are based on studies with large sample size, the sampling distribution around the mean tends to appear approximately normal, distributing tightly around the mean; in this case, the model outputs or results of the probabilistic and deterministic analyses are likely to be similar. However, when the study sample size that is used for estimation the model parameter values is not large, probabilistic and deterministic analyses may yield different results. As an example, re-intervention rate on the truncal vein was one of the key clinical parameters in a cost–utility analysis comparing seven treatments for patients with varicose veins [2]. The network meta-analysis informing this study showed that the odds ratio (OR) of re-intervention for mechanochemical ablation (MOCA) versus high-ligation surgery was 0.46 (95% confidence interval [CI] is 0.01–29.92). That is, the point estimate was favoring MOCA with a very wide 95%CI [2]. The OR is assumed to follow log-normal distribution, and the expected OR in a probabilistic analysis of these data is 3.7 (see Formula (1) below). Thus, drastically different findings of the analysis may be arrived at when the model input in deterministic analysis favored MOCA while the inputs in probabilistic analyses favored high-ligation surgery. The results from probabilistic analyses are inconsistent with what is noted broadly in the literature or reported by many clinicians because the risk of neovascularization and reintervention after surgery is generally higher after surgery than endovenous therapy (e.g., MOCA) [3].

The MOCA case is probably an example of inappropriate application of probabilistic analyses given the circumstances. The parameters of OR, risk ratio (RR) and hazard ratio (HR) are generally defined in log-normal distributions in a probabilistic analysis. The log-normal distribution follows right-skewed data that typically have extremely low measurements which affects the median less than the mean. Thus, in this situation, the median of log-normal data is a more meaningful central tendency measure than the mean.

Economic evaluation guidelines from some institutions (e.g., National Institute for Health and Care Excellence, and Canadian Agency for Drugs and Technologies in Health) state that probabilistic analysis provides less biased estimates than a deterministic analysis due to the non-linear relationship of model inputs and model outputs and, therefore, recommend probabilistic analysis to estimate the expected costs and clinical outcomes (e.g., using the estimates of mean cost and health outcomes from Monte Carlo simulations) [4,5,6]. The guidelines make recommendations in favour of probabilistic analysis based on publications that [7, 8] cite the presence of non-linear relationships as the main rationale. Despite the advantages of probabilistic analysis over deterministic analysis, the evidence cited by the guidelines did not use sophisticated approaches to compare the bias of model parameters or model results from probabilistic analysis versus deterministic analysis. However, other factors besides the non-linear relationship of model functions can also impact the magnitude of bias for model results. Deterministic analysis uses point estimates which are often best fitted with the observed data (i.e., maximum likelihood estimation) [9] and represents the "best guess" for the model input. When the information that the data contain about the parameter is less certain (i.e., derived from small sample size), the parameter estimates may not be precise and thus have a large standard error. In such circumstances, simulated model inputs used in the probabilistic analysis may generate data which are quite different from the maximum likelihood estimators. For parameters which do not follow normal distributions (e.g., log-normal distributed data), the expected values of model inputs in probabilistic analyses may be different than those in deterministic analysis. One such example in varicose vein treatment is mentioned above. Ultimately, probabilistic analysis in which the model inputs may have smaller likelihood to fit the observed data will not necessarily yield more reliable model outputs than deterministic analysis.

Simulations from probabilistic analyses may yield more extreme values that can bias the results. For example, the expected value of an exponentially distributed random variable \(X\) (e.g., years of survival) with a constant rate parameter \(\lambda\) (e.g., mortality rate per person-year) is equal to \(E\left( X \right) = \frac{1}{\lambda }\). When the variance is large (e.g., data derived from a study with a small sample size), probabilistic analyses can yield some simulations with small values for \(\lambda\) and can substantially impact the \(E\left( X \right)\). A deterministic analysis using the point estimate of \(\lambda\) may avoid this problem. Thus, a probabilistic model may result in larger bias in model outputs than the deterministic model.

We aim to understand potential bias in probabilistic and deterministic analysis through simulations. Given that probabilistic analysis and deterministic analysis are generally associated with similar results when parameter uncertainty is small, we mainly discuss the bias related to the two types of analyses when the variance of parameter is relatively large (e.g., the sample size of 100 for each hypothetical trial and the risk of events are moderate, 0.1 or greater). We further explored the impact of bias in probabilistic and deterministic analysis according to sample size (i.e., 300 and 1,000 patients in each hypothetical trial). Section 2 evaluates biases associated with using RR as the effect measure in probabilistic versus deterministic analysis. Section 3 evaluates biases of mean cost estimates using smearing estimator in both types of analyses. In Sect. 4, we compare bias in expected life-years in a two-state Markov model in probabilistic versus deterministic analysis and further compare the bias in incremental net monetary benefit (INMB) in cost-effectiveness analysis. Finally, we discuss our findings and provide reflections for areas of inappropriate application of probabilistic analysis in Sect. 5.

We used SAS 9.4 (SAS Institute, Cary, North Carolina) to generate datasets for the deterministic and probabilistic analysis [10]. The SAS code of our simulation studies is enclosed in the supplementary materials.

Risk ratio in probabilistic analysis versus deterministic analysis: a simulation study

Expected value of log normal data

Measures of comparative clinical effectiveness are often expressed on a relative scale, such as a RR, OR, or HR. To calculate confidence intervals, one uses the standard error of the log-transformed measure. Therefore, the parameters of RR, OR, and HR are generally defined in log-normal distributions in a probabilistic analysis. The expected arithmetic mean of a log-normally distributed variable \(X\) is given by Formula (1).

$$E\left[ X \right] = {\text{exp}}\left( {\mu + \frac{{\sigma^{2} }}{2}} \right),$$
(1)

where \(\mu\) is the mean of variable \(X\) after natural log transformation, and \(\sigma\) is the standard deviation of variable \(X\) after natural log transformation. In the Mathematical Supplement, we provide the further details of probability distributions used in the article.

The point estimate of the relative measure (i.e., variable \(X\) representing any of the measures above) is equal to \({\text{exp}}\left( \mu \right)\). According to Formula (1), the expected values \(E\left[ X \right]\) of RR, OR, and HR are always larger than the corresponding point estimates \({\text{exp}}\left( \mu \right)\) by the factor of \({\text{exp}}\left( {\sigma^{2} /2} \right)\). When the variance \(\sigma^{2}\) is large, it may lead to discordance between the expected values of RR, OR, or HR from the probabilistic analysis and the point estimate (mean) from observed data.

Evaluation of bias in probabilistic versus deterministic analyses: study design

Consider two Bernoulli populations (binary outcomes 0s and 1s) that we denote as Population A (control) and Population B (invention) with risks of the events (proportions) \(TP_{A}\) and \(TP_{B}\), respectively. These population distributions are considered to be the true distributions of parameters in this simulation study. Samples from these populations are denoted as Group A (control group) and Group B (intervention group), respectively. We are interested in the estimation of the ratio of the proportions; that is, in \(TRR = \frac{{TP_{B} }}{{TP_{A} }}\) (i.e., the true risk ratio).

Estimation of RR is biased, and the bias tends to be small when the sample size is large; see, for example Ngamkham et al. [11] We conducted a simulation study to evaluate the magnitude of the bias of RR in probabilistic versus deterministic analyses. The design of our simulation study followed a tutorial article by Morris et al. 2019 [12]. The estimand of interest is the risk ratio estimated from the deterministic and probabilistic analyses. The notation, data generation and performance measures of the simulation study are organized in the following way:

The following are the steps for data generation of the simulation study on risk Ratio in deterministic and probabilistic analyses: (a) The total number of patients in each hypothetical trial \(N_{pt} = 100\) in Scenario 1.

(b) The number of repetitions used for hypothetical trials (the simulation sample size) \(N_{sim} = 100,000\).

(c) The amount \(B\) of random numbers that follow the specified distribution in Step 4 in probabilistic analysis as \(B = 2,000\).

Step 1: Assign the true value of the risks of event (proportions) \(TP_{A}\) for Population A and \(TP_{B}\) for Population B and then calculate the corresponding true risk ratio \(TRR = \frac{{TP_{B} }}{{TP_{A} }}\). Assume that \(N_{pt}\) is even and let the number of patients in Groups A and B equal \(NA = NB = N_{pt} /2\).

Begin the simulation for the \(i\) th hypothetical trial, \(i = 1,2, \ldots ,N_{sim}\) .

Step 2: Generate the numbers of patients with events for Group A as \(EA_{i} \sim {\text{}}binomial\left[ {NA,TP_{A} } \right])\) and for Group B as \(EB_{i} \sim {\text{}}binomial\left[ {NB,TP_{B} } \right])\).

Step 3: Deterministic analysis: Calculate the risk for Group A \(\widehat{{PA_{i} }} = \frac{{EA_{i} }}{NA}\) and Group B \(\widehat{{PB_{i} }} = \frac{{EB_{i} }}{NB}\), and the risk ratio \(\widehat{{DRR_{i} }}\) of the event for Group B versus Group A \(\widehat{{RR_{i} }} = \frac{{\widehat{{PB_{i} }}}}{{\widehat{{PA_{i} }}}}\).

Step 4: Probabilistic analysis: it is assumed that the risk ratio follows log normal distribution

$${\text{}}lognormal\left( {{\text{ln}}\left( {\widehat{{DRR_{i} }}} \right),\left( {\frac{1}{{EA_{i} }} + \frac{1}{{EB_{i} }}} \right) - \left( {\frac{1}{NA} + \frac{1}{NB}} \right)} \right).$$

Simulate \(B\) random numbers that follow this distribution. Then \(\widehat{{PRR_{i} }}\) is the average of these \(B\) values. Namely, let \(\left\{ {W_{,} j = 1,2, \ldots B} \right\}\) be random numbers from \({\text{}}lognormal\left( {{\text{ln}}\left( {\widehat{{DRR_{i} }}} \right),\left( {\frac{1}{{EA_{i} }} + \frac{1}{{EB_{i} }}} \right) - \left( {\frac{1}{NA} + \frac{1}{NB}} \right)} \right)\) distribution. Then,

$$\widehat{{PRR_{i} }} = \frac{1}{B}\sum\nolimits_{j = 1}^{B} {W_{j} } .$$

End the simulation for a hypothetical trial \(i\) .

Step 5: Repeat Steps 2 to 4 for \(N_{sim}\) times.

Step 6: Calculate \(\widetilde{DRR}\) as the average value of \(\widehat{{DRR_{i} }}\) and \(\widetilde{PRR}\) as the average value of \(\widehat{{PRR_{i} }},i = 1,2, \ldots ,N_{sim}\). Namely,

$$\widetilde{DRR} = \frac{1}{{N_{sim} }}\sum\limits_{i = 1}^{{N_{sim} }} {\widehat{{DRR_{i} }}} \,{\text{and}}\,\,\widetilde{PRR} = \frac{1}{{N_{sim} }}\sum\limits_{i = 1}^{{N_{sim} }} {\widehat{{PRR_{i} }}} .\,$$

Performance assessment: The main performance measures are Bias and the Mean Square Error (MSE). We compared these two accuracy and precision characteristics for the RR using both deterministic and probabilistic analysis. [13]

$$\begin{gathered} {\text{}}Bias_{D} = \widetilde{{DRR{ }}} - TRR \hfill \\ {\text{}}Bias_{P} = \widetilde{PRR} - TRR \hfill \\ \end{gathered}$$
(2)
$$\begin{gathered} MSE_{D} = \frac{1}{{N_{sim} }}\sum\limits_{i = 1}^{{N_{sim} }} {\left( {\widehat{{DRR_{i} }} - TRR} \right)^{2} } \hfill \\ MSE_{P} = \frac{1}{{N_{sim} }}\sum\limits_{i = 1}^{{N_{sim} }} {\left( {\widehat{{PRR_{i} }} - TRR} \right)^{2} } , \hfill \\ \end{gathered}$$
(3)

where \({\text{}}Bias_{D}\) is the bias of the deterministic analysis, \({\text{}}Bias_{P}\) is the bias of the probabilistic analysis, \(MSE_{D}\) is the MSE for the deterministic analysis, and \(MSE_{P}\) is the MSE for the probabilistic analysis. We also reported the Monte Carlo Standard Error (MCSE) of biases and MSEs. [12].

The notations of the simulation study are shown in Table 1. We considered the following six scenarios:

Table 1 Description of notation for risk ratio estimation in deterministic and probabilistic analyses
Full size table

Scenario 1: \(N_{pt} = 100;\, TP_{A} = 0.16;\, \text{and }\, TP_{B} { } = 0.10\).

Scenario 2: \(N_{pt} = 300;\,TP_{A} = 0.16;\,\text{and }\, TP_{B} { } = 0.10\).

Scenario 3: \(N_{pt} = 1000;\,TP_{A} = 0.16;\,\text{and }\, TP_{B} { } = 0.10\).

Scenario 4: \(N_{pt} = 100;\,TP_{A} = 0.10;\,\text{and }\,TP_{B} { } = 0.20\).

Scenario 5: \(N_{pt} = 300;\,TP_{A} = 0.10;\,\text{and }\,TP_{B} = 0.20\).

Scenario 6: \(N_{pt} = 1000;\,TP_{A} = 0.10;\,\text{and }\,TP_{B} = 0.20\).

Results of simulation study

Both probabilistic and deterministic analyses produced biased estimates for TRR. The magnitude of bias and MSE in both analyses markedly decreased with a larger number of patients in each hypothetical trial. The biases and the MSEs in both analyses were small in Scenario 3 and 6 (\(N_{pt} = 1000\); see Table 2). The biases and MSEs in the probabilistic analyses were greater in all scenarios. The median bias in RRs in probabilistic and deterministic analyses were less than \({\text{}}Bias_{D}\) and \({\text{}}Bias_{P}\), respectively. The median bias of RRs deterministic analysis was also smaller than the probabilistic analysis. The proportion of absolute bias in the probabilistic analysis greater than that in the deterministic analysis in Scenario 1 (\(N_{pt} = 100\)), Scenario 2 (\(N_{pt} = 300\)) and Scenario 3 (\(N_{pt} = 1000\)) was 0.554, 0.526 and 0.519, respectively.

Table 2 Comparison of deterministic and probabilistic analyses for risk ratio: results of simulation study 1 (with scenarios of N = 100, N = 300, and N = 1000)
Full size table

We also drew density plots of bias of RRs for probabilistic and deterministic analyses in Scenarios 1, 2 and 3 (Fig. 1). With an increased the sample size (e.g., \(N_{pt} = 1000\) in Scenario 3), the distributions of bias were subject to normal distributions in both probabilistic and deterministic analyses.

Fig. 1
figure 1

Bias of Risk Ratios of Deterministic and Probabilistic Analysis With Histograms and Density Plots. N sample size (i.e., total number of patients in each hypothetical trial); STD, standard deviation. True risk ratio = 0.625. We randomly selected 1000 simulations in each scenario for this plot.

Full size image

Mean costs estimated from a regression model: a simulation study

A function of cost and predictors

In this section, we compare the predicted estimate of mean costs in a given condition (e.g., treatment, patients’ characteristics etc.) using probabilistic analysis and deterministic analysis. We firstly define the function of cost and predictors. We generate data of the predictors and costs for 100, 300, and 1000 hypothetical patients for Scenario 1, 2 and 3, respectively. Then we conduct regression analysis and develop a model to predict the mean costs using the smearing estimator. Subsequently, we estimate the mean costs using probabilistic and deterministic analyses separately. Finally, we compare the performance of two types of analyses. Figure 2 outlines the process of data simulation and evaluating the performance of probabilistic analysis and deterministic analyses.

Fig. 2
figure 2

The Process of Simulating Data and Assessing the Bias of Probabilistic Analysis versus Deterministic Analysis for Cost Estimates Using the Smearing Estimator

Full size image

We followed the methods introduced by Wicklin [14] to generate data for the regression analysis. We modeled natural log transformed costs as a linear function of two independent variables \(X_{1}\) and \(X_{2}\) with errors:

$${\text{log}}\left( C \right) = \beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{2} + \varepsilon ,$$
(4)

where \(C\) is the total cost of treatment, \(X_{1}\) is the first predictor, \(X_{2}\) is the second predictor, and \(\varepsilon\) is the random error term (e.g., residual). Next, \(\beta_{0}\) is the constant, and \(\beta_{1}\) and \(\beta_{2}\) are the coefficients which represent the relative change of cost for each unit change in \(X_{1}\) and \(X_{2}\), respectively. In our simulations, we chose the values of coefficients for the model and the distributions of predictors based on a published cost study of treatments for prostate cancer (\(\beta_{0} = 7.15138,\beta_{1} = 0.153807,\beta_{2} = 0.352548\)) [15]. Then, we derived the cost (Canadian dollar, $) from formula (3) for each patient:

$$C = { }e^{{7.15138 + 0.153807X_{1} + 0.352548X_{2} + \varepsilon }} ,$$
(5)

where \(X_{1}\) is the binary variable for the treatment (0 for control group and 1 for intervention group) which follows Bernoulli distribution \({\text{}}bernoilli\left( \frac{1}{2} \right)\), and \(X_{2}\) is the variable for the severity of disease (0 for non-severe and 1 for severe) which also follows Bernoulli distribution \({\text{}}bernoulli\left( {0.3} \right)\) (probability of severe = 0.3).

We often encounter outliers within cost data. Therefore, we assigned a contaminated normal distribution for \(\varepsilon\). A contaminated normal distribution is a specific case of a two-component mixture distribution in which both components are normally distributed with a common mean [14]. We assumed that \(\varepsilon\) follows one normal distribution with mean 0 and standard deviation 0.5 in 90% simulations, and the other normal distribution with mean 0 and standard deviation 1 in 10% simulations. Mathematically, we consider that \(\varepsilon\) has normal distribution with random variance parameters \(N\left( {0,{\Sigma }^{2} } \right)\), where \(P\left( {{\Sigma } = 0.5} \right) = 0.9\) and \(P\left( {{\Sigma } = 1} \right) = 0.1\).

Note that if a random variable \(Y\) has normal distribution \(N\left( {\mu ,\sigma^{2} } \right)\), then

$$E\left( {e^{Y} } \right) = {\text{exp}}\left( {\mu + \frac{{\sigma^{2} }}{2}} \right).$$
(6)

Estimand of interest

The estimands are the mean costs for four groups (group 1, \(X_{1}\) = 0 and \(X_{2}\) = 0; group 2, \(X_{1}\) = 1 and \(X_{2}\) = 0; group 3, \(X_{1}\) = 0 and \(X_{2}\) = 1; and group 4: \(X_{1}\) = 1 and \(X_{2}\) = 1) from the probabilistic and deterministic analyses (see Sect. 3.1). For example, according to Formula (5), the expectation of cost for severe case in the intervention group (i.e., the true estimand in group 4) is:

$$E(C|X_{1} = 1,X_{2} = 1) = E\left( {e^{7.15138 + 0.153807 + 0.352548 + \varepsilon } } \right) = e^{7.657735} E\left( {e^{\varepsilon } } \right)$$
$$= e^{7.657735} \left\{ {P\left( {{\Sigma } = 0.5} \right)E\left( {e^{{\varepsilon |{\Sigma } = 0.5}} } \right) + P\left( {{\Sigma } = 1} \right)E\left( {e^{{\varepsilon |{\Sigma } = 1}} } \right)} \right\}$$
$$= e^{7.657735} \left( {0.9e^{{0.5^{2} /2}} + 0.1e^{{1^{2} /2}} } \right){\text{ by Formula }}\left( 6 \right){ }$$
$$= 2507.97.$$

Similarly, we can calculate the true estimands in the other 3 groups (see Table 3).

We also simulated 100 million hypothetical patients using Formula (5) and calculated the average cost in four groups of the hypothetical patients. The mean costs from simulations in each group are very close to the theoretical value calculated above.

Data generation and data analysis

We simulated 100,000 hypothetical trials (i.e., 100,000 repetitions) in all three scenarios. In Scenario 1, for each hypothetical trial, we simulated 100 patients with independent random \(X_{1} ,X_{2}\), and \(\varepsilon\), and then derived \(C\) and \({\text{log}}\left( C \right)\) using Formula (5). Each hypothetical trial had 300 patients in Scenario 2 and 1000 patients in Scenario 3. Except for the number of patients per hypothetical trial, the other parameters in Scenario 2 and 3 were same as in Scenario 1. We conducted linear regression analysis with independent variables \(X_{1}\) and \(X_{2}\) and dependent variable of \({\text{log}}\left( C \right)\) in each trial. We applied the smearing estimator to the median costs from the model to calculate the mean cost [16]. We used the following formulas to estimate the mean cost of each simulated trial. [15]

$$C = e^{{\beta_{0} + \beta_{1} X_{1} + \beta_{2} X_{2} }} \times S,$$
(7)

where \(C\) is the mean cost, \(\beta_{0} ,\beta_{1}\), and \(\beta_{2}\) are the coefficients obtained from the regression analyses, and \(S\) is the smearing estimator: [16]

$$S = \frac{1}{n}\sum\nolimits_{i = 1}^{n} {e^{{\widehat{{\varepsilon_{l} }}}} } ,$$
(8)

where \(n\) is the sample size of the trial (e.g., 100 in Scenario 1) and \(\widehat{{\varepsilon_{i} }} = {\text{log}}\left( {C_{i} } \right) - x_{i} \hat{\beta }\). \(\hat{\beta }\) is the vector of the estimates of the coefficients from linear regression model, \(x = (x_{1} , \ldots , x_{p} )\) is the vector of independent variables. Then, \(x\hat{\beta }\) is the predicted value of log (C). The differences between observed log transformed costs and the predicted log transformed costs is the least squares residual.

For the deterministic analysis, we used \(\beta_{0} ,\beta_{1}\), and \(\beta_{2}\) from the linear regression and \(S\) as the fixed values to calculate the mean cost for patients with different characters (i.e., different \(X_{1}\) and \(X_{2}\) values) for four groups. For the probabilistic analysis, \(\beta_{0} ,\beta_{1}\), and \(\beta_{2}\) and \(S\) were assigned a normal distribution based on the mean and standard error of each parameter in the linear regression, and the average value of 2,000 iterations was used as the estimate of mean cost in the probabilistic analysis.

We repeated the above steps of generating data and analysing data for a single hypothetical trial 100,000 times in each scenario.

Results of a simulation study

We summarized the data from 100,000 repetitions in three scenarios and evaluated the performance in Table 3. Three scenarios showed that the mean cost estimates obtained from the deterministic analysis had smaller bias and MSE than the probabilistic analysis in four groups. Overall, the magnitude of bias increases with the larger true estimands, when the number of patients per trial remains the same. Among all analyses, the maximum bias was $50.60 (relative bias = 2%) for the probabilistic analysis of \(X_{1}\) = 1 and \(X_{2}\) = 1, and \(N_{pt}\) = 100. When the sample size per hypothetical trial was 1000, the biases in both probabilistic and deterministic analyses were small. The distributions of biases for \(X_{1}\) = 1 and \(X_{2}\) = 1 with different numbers of patients per trial can be found in Figure S1 in Supplementary materials. In addition, when defining a larger \(\varepsilon\), the bias in probabilistic analysis increased considerably while the impact on the deterministic analysis was smaller (data not shown).

Table 3 Comparison of mean costs ($) using the smearing estimator by deterministic and probabilistic analyses: results of simulation study 2 (with scenarios of N = 100, N = 300, and N = 1000)
Full size table

Life-years in a two-state Markov model: a simulation study

Total life-years in a two-state Markov model

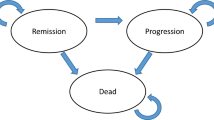
We evaluate the bias in the estimate of life-years in probabilistic and deterministic analyses using Markov model in this section. We briefly describe the process of simulation and evaluate both types of analyses in Fig. 3.

Fig. 3
figure 3

The Process of Simulating Data and Assessing the Bias of Probabilistic Analysis versus Deterministic Analysis in a Two-state Markov Model

Full size image

More precisely, we consider a simple Markov model with two health states: alive and dead. In our Markov model, let \(0 < p < 1\) represent a constant yearly transition probability from alive to dead. Let the reward (i.e., model output) be survival time, or the accumulated time in the alive health state from the beginning of a Markov cycle. We assume that all people start in the alive state. The total reward (life-years) over a lifetime time horizon is an infinite geometric series:

$$LY = 1 + \left( {1 - p} \right) + (1 - p)^{2} + \ldots + (1 - p)^{n} + \ldots$$
$$= \sum\nolimits_{k = 0}^{\infty } {\left( {1 - p} \right)}^{k} = \frac{1}{{p^{} }},$$
(9)

where \(LY\) is the total life-years over the time horizon.

Conceptually, this two-state Markov model is approximately equivalent to an exponential survival model with a constant hazard function, but the survival time of an individual is discrete with a fixed interval (the Markov cycle). The life-years can be modelled by a random variable \(Y\) with First Success (geometric) distribution \({\text{}}FS\left( p \right)\). It is well known that \(E\left( Y \right) = \frac{1}{p}\).

A simulation study: methods and results

The true estimands from a true transition probability

We consider a fixed \(p\) for the true transition probability in our simulation study. The true \(p\) can be interpreted as the population mean. The estimand of interest was LYs. We defined a fixed \(p\) of 0.10. By (formula 9), the true \(LY = 10\).

We can also approximate the true estimands at a given true \(p\). We define that the \(P\) follows a beta distribution, P ~ \(beta \left( {\alpha , \beta } \right)\). When \(\alpha\) and \(\beta\) are large, the shape of the probability density function becomes very narrow. In Supplementary materials, we provide the derivation for the mean values of the Beta-First Success distribution. The mean values of the Beta-First Success distribution is as follows:

$$E\left( Y \right) = \frac{\alpha + \beta - 1}{{\alpha - 1}}$$
(10)

Let both \(\alpha\) and \(\beta\) be large, and let \(n = \alpha + \beta .\) For a beta distribution of expected \(E\left( P \right) = 0.10\), \(\alpha = 0.1n \,\text{ and }\, \beta = 0.9n.\) Then, when n tends to infinity and \(P\) is close to a fixed value, \(E\left( Y \right) = \frac{n - 1}{{0.1n - 1}} \cong 10\).

A simulation study: data generation

Here, we briefly introduce the process of generating data in each scenario (Fig. 3). In the simulation study, X denotes the number of mortality events of interest from the cohort of patients (n: cohort size) at 1 year for a given true transition probability. X is a random variable, so the values may vary in different simulations. Except the different n (\(N_{pt}\) = 100 for Scenario 1, \(N_{pt}\) = 300 for Scenario 2, and \(N_{pt}\) = 1000 for Scenario 3), all other parameters in three scenarios were same.

We estimated the transition probabilities for the deterministic analysis; that is, \(p = \frac{X}{n}\). We then calculated LY using formula (9) above for this simulation. We also defined the distributions of transition probabilities for the probabilistic analysis (i.e., \(P \sim Beta \left( {X, n - X} \right)\)). The \(LYs\) of the probabilistic analysis were calculated from the average value of \(B = 2,000\) simulations.

We repeated the above steps 100,000 times (\(N_{sim} = 100,000\)) in three scenarios and then compared the performance of deterministic and probabilistic analyses.

A simulation study: results

We present the results of our simulations in Table 4. We note that the bias and MSE of deterministic analysis were smaller than that in the probabilistic analysis, in three scenarios. When the cohort size was small (\(N_{pt}\) = 100 in Scenario 1), the bias of LYs in the probabilistic analysis was much greater than the deterministic analysis (3.19 versus 1.16). However, when the cohort size was large (\(N_{pt}\) = 1000 in Scenario 3), the biases were much smaller in both approaches (probabilistic: 0.19; and deterministic: 0.09). When the cohort size was moderate (\(N_{pt}\) = 300 in Scenario 2), the bias and MSE of LYs were close to Scenario 3 of \(N_{pt}\) = 1000, rather than the Scenario 1 of \(N_{pt}\) = 100.

Table 4 Comparison of life-years of two-state Markov model by deterministic and probabilistic analyses: results of simulation study 3 (with scenarios of N = 100, N = 300, and N = 1000)
Full size table

Other cost-effectiveness outcomes in the Markov model

In economic evaluation, both the costs and quality-adjusted life-years (QALYs) are linked to life-years. Thus, it is expected that the biases of costs and QALYs in probabilistic analysis would also be greater than in the deterministic analysis if we extend the example in 4.2 to QALYs and costs. Our simulation considered a single group. When comparing the cost-effectiveness of two groups (i.e., the incremental cost [IC], incremental effectiveness [IE], incremental cost-effectiveness ratio [ICER], or INMB), it becomes more complex. There are more parameters involved in the estimation process, and there are different approaches to model the efficacy of the intervention. Elbasha and Chhatwal [17] evaluate curvature of health economic outcomes as functions of several types of model parameters and direction of bias in a three-state Markov model and showed that different parameters can result in different directions of bias. Thus, it would be case by case which analysis (probabilistic analysis or deterministic analysis) is associated with less bias.

To understand the bias of probabilistic analysis and deterministic analysis in economic evaluations, we conducted a simulation study to evaluate the magnitude of bias of IC, IE and INMB. The INMB was calculated using the following formula: INMB = WTP × IE – IC, where WTP is willingness-to-pay threshold, IE is the difference in QALYs between the new intervention and the control and IC is the difference in cost between the new intervention and the control. We assumed that new treatment B is more effective and more costly than the traditional treatment A. After treatment A or B, patients would enter the two-state Markov model (i.e., alive or dead, same as that in Sect. 4.2). For patients who are alive with either treatment, they have the same health utility. We considered one-time treatment costs for treatment A and B, and the yearly costs for any patients who are alive. In Supplementary materials, we provided the SAS code for this simulation study which includes the annotation with detailed introductions of model and parameters. We ran simulations in several scenarios by changing the true values of costs, utilities and transition probabilities. Our simulations showed that the biases of IC, IE and INMB were smaller in deterministic analysis than probabilistic analysis (data not shown), and the differences in bias can be large when the number of patients of each hypothetical trial was small (e.g., n = 100). With the increase of sample size of the hypothetical trial, the bias of IC, IE and INMB substantially decreased in both probabilistic and deterministic analyses. When the number of patients of each hypothetical trial was large (e.g., n = 1000), the magnitude of bias was small in both probabilistic analysis and deterministic analysis.

Discussion

We used three examples to illustrate that, compared with deterministic analyses, probabilistic analyses may be associated with greater biases in model inputs (Sects. 2 and 3), and model outputs (Sect. 4). However, this does not mean that deterministic analysis generally produces less biased results than probabilistic analysis. Many aspects, including the methodological approaches for defining the true estimand and generating random variables, and the function of the model, affected the results of simulation studies which aim to evaluate the performance of deterministic and probabilistic analyses in terms of bias and precision. The magnitude of bias decreased with a larger sample size of the hypothetical trial. Model-based economic evaluation includes many variables and numerous non-linear functions. The different variables and non-linear functions may impact the bias of cost-effectiveness results in different directions. Owing to this, it is reasonable to expect that the bias will be partially cancelled out. Therefore, except for the main model parameters based on small sample evidence, we may not need to worry too much about the magnitude of bias when selecting deterministic analyses or probabilistic analyses for cost-effectiveness analysis.

Probabilistic analysis has numerous advantages over deterministic analysis. It yields cost-effectiveness estimates with uncertainty which is an important issue to be considered in decision-making. The expected value of perfect information from probabilistic analysis provides the upper bound of the net health or net monetary benefits for future research. Although health data are often correlated, we did not explore correlated model parameters in the present simulation studies. The correlations between model inputs directly impact the variance of model outputs and may impact the expected values of model results [18]. Probabilistic analysis can better incorporate the correlations between model parameters (e.g., use the coefficients and covariance–correlation matrix from a regression model1) and may lead the smaller bias of cost-effectiveness estimates than deterministic analysis. However, if the correlations between model parameters are unknown and omitted from the probabilistic analysis, this would not be an ideal application of this technique and is difficult to comment how it will impact the bias of results, compared with deterministic analysis.

There is no definitive answer on which approach (probabilistic or deterministic analysis) is associated with a less biased estimate in non-linear models. Probabilistic analysis is generally recommended as the base case analysis due to several obvious advantages. However, we may caution the application of probabilistic analysis under some conditions when deterministic analysis may be more appropriate for these cases, for instance:

  • When the key model parameters have wide, asymmetric confidence intervals, such as ORs of clinical effects from network meta-analysis. In this case, the point estimates represent the most likely values of the parameter in the population and may result in less biased model outputs

  • When the variance of a model parameter is large, such as parameter estimates based on data from a small sample size. Here, simulations from probabilistic analyses may yield extreme values that tend to bias the results of some non-linear models and may not be meaningful. Deterministic analysis can avoid extreme values that probabilistic analysis may encounter and hence, may provide a less biased estimate

It has been acknowledged that probabilistic analysis as a tool is advantageous in several ways, namely its ability to incorporate parameter uncertainty. However, the limitations of probabilistic analysis have not been well discussed in literature. It is necessary to understand the limitations of probabilistic approach when selecting a tool for this type of analysis. Economic modelers should select the most suitable approach for their analyses.