Expectation–maximization algorithm for system-based lifetime data with unknown system structure

Abstract

In science and engineering, we are often interested in learning about the lifetime characteristics of the system as well as those of the components that made up the system. However, in many cases, the system lifetimes can be observed but not the component lifetimes, and so we may not also have any knowledge on the structure of the system. Statistical procedures for estimating the parameters of the component lifetime distribution and for identifying the system structure based on system-level lifetime data are developed here using expectation–maximization (EM) algorithm. Different implementations of the EM algorithm based on system-level or component-level likelihood functions are proposed. A special case that the system is known to be a coherent system with unknown structure is considered. The methodologies are then illustrated by considering the component lifetimes to follow a two-parameter Weibull distribution. A numerical example and a Monte Carlo simulation study are used to evaluate the performance and related merits of the proposed implementations of the EM algorithm. Lognormally distributed component lifetimes and a real data example are used to illustrate how the methodologies can be applied to other lifetime models in addition to the Weibull model. Finally, some recommendations along with concluding remarks are provided.

1 Introduction

In science and engineering, systems are made up of different components and these systems can be complex in form and structure. Reliability engineers and researchers are often interested in the lifetime distribution of the system as well as the lifetime distribution of the components that form the system. In many cases, the lifetimes of a n-component system can be observed, but not the lifetimes of the components themselves. This problem may arise when it is not possible to put the individual components on a life test after the n-component system is already built. A system with specified performance characteristics but unknown or unspecified constituents and means of operation is also known as a black-box system. For example, an integrated circuit (IC) is made up of different electrical components, such as transistors, resistors, capacitors and diodes, that are connected to each other in different ways. Manufacturers of IC are not only interested in the lifetime of the IC, but also the lifetime distributions of the electrical components that form the IC. Once the IC is built, it may not be possible to test these electronic components inside the IC individually. Therefore, in this situation, the development of statistical inference for the component reliability characteristics based on system lifetime data becomes necessary.

In recent years, parametric and nonparametric inferential methods for the lifetime distribution of components based on system lifetimes have been developed by many authors. Coherent systems (i.e., each component contributes to the functioning/failure of the system and the reliability of the system is monotone) are commonly considered in these studies. For nonparametric inference, Bhattacharya and Samaniego (2010) considered the nonparametric estimation of component lifetime distributions from system failure-time data, while Balakrishnan et al. (2011a) developed exact nonparametric confidence intervals for population quantiles as well as tolerance intervals. Al-Nefaiee and Coolen (2013) discussed nonparametric inference for system lifetimes with exchangeable components. For parametric inference, Eryilmaz et al. (2011) considered the analysis of consecutive k-out-of-n systems with exchangeable components. Ng et al. (2012) discussed the estimation of parameters in the component lifetime distribution under a proportional hazard rate model. Balakrishnan et al. (2011b) developed the best linear unbiased estimation method for the location and scale parameters of the lifetime distribution of components based on complete and censored system lifetime data. Zhang et al. (2015) discussed different estimation methods for the parameters when the component lifetime distribution is in the location-scale family of distributions or log-location-scale family of distributions. In these existing works, the structure of the systems under investigation was assumed to be known. However, in some practical situations, the system of interest is a black box, in which case there is a lack of knowledge on the system’s internal structure. System identification is the subject that tries to estimate a black box based on observed experimental system lifetime data. There is a rich literature on system identification based only on data (data driven) without having previous knowledge of the system (see, for example, Eykhoff 1974; Ljung 1999; Tangirala 2015). In this paper, we are interested in developing statistical inferential procedures for estimating the parameters of the component lifetime distribution as well as for identifying the system structure based on the system-level lifetime data.

Based on the special features of the system lifetime data, we treat the system-level data as incomplete data and apply the expectation–maximization (EM) algorithm (Dempster et al. 1977; McLachlan and Krishnan 2008) to obtain the maximum likelihood estimates (MLEs). EM algorithm is an iterative method for finding the MLEs of the parameters in statistical models that involve some unobserved latent variables. It is based on the idea of replacing a difficult likelihood maximization with a sequence of easier maximization steps which will ultimately converge to the value obtainable by direct maximization of the likelihood. It is particularly useful for solving missing data problems. EM algorithm has been widely used in lifetime data analysis, for example, in the analysis of progressively censored data (Ng et al. 2002), for hybrid censored data (Dube et al. 2011), and for left- truncated and right-censored data (Balakrishnan and Mitra 2012). Based on the representations of the system structure, system signature (Samaniego 2007) and minimal signature (Navarro et al. 2007), we propose here different ways of implementing the EM algorithm and evaluate relative merits of these implementations.

The rest of this paper is organized as follows. Section 2 provides the details of the form of system lifetime data and the notion of system signature. In Sect. 3, we discuss the statistical inference based on maximum likelihood method and present the framework of the EM algorithm when considering the system lifetime distribution as a mixture distribution. Different implementations of the EM algorithm based on system-level and component-level likelihood functions are presented in Sects. 3.1–3.3. Then, in Sect. 4, we discuss the applications of the EM algorithm when the system is known to be a coherent system with an unknown system structure. In Sect. 5, we illustrate the methodologies by considering the lifetimes of the components in the system to follow a two-parameter Weibull distribution. An illustrative example is presented in Sect. 5.2, and a Monte Carlo simulation study is carried out in Sect. 5.3 to evaluate the performance of the proposed implementations of the EM algorithm when the component lifetimes follow the Weibull distribution. In Sect. 6, we consider the case when the component lifetimes follow a lognormal distribution to further illustrate how the methodologies can be applied to different lifetime models in addition to the Weibull model. A real data example of water-reservoir control system is used to verify the performance of the proposed estimation procedures. Finally, some concluding remarks are made in Sect. 7.

2 System lifetime data and system signature

Let the random variable T be the lifetime of a coherent system with independent and identically distributed (i.i.d.) component lifetimes $X_1, X_2,\ldots , X_n$ from a common absolutely continuous cumulative distribution function (c.d.f.) $F_X(\cdot )$, probability density function (p.d.f.) $f_X(\cdot )$ and survival function (s.f.) ${{\bar{F}}}_X (\cdot )=1 - F_X(\cdot )$. We denote the order statistics corresponding to the n component lifetimes by $X_{1:n}< X_{2:n}< \cdots < X_{n:n}$. We shall further denote the c.d.f., p.d.f. and s.f. of the i-th order statistic by ${F}_{i:n}(\cdot )$, ${f}_{i:n}(\cdot )$ and ${{\bar{F}}}_{i:n}(\cdot )$, and the c.d.f., p.d.f. and s.f. of the lifetime of the system T by $F_{T}(\cdot )$, $f_{T}(\cdot )$ and ${{\bar{F}}}_{T}(\cdot )$, respectively. Now, let us assume m independent such n-component coherent systems are placed on a life-testing experiment and their lifetimes are observed, with the corresponding ordered system lifetimes being $T_{1:m}< T_{2:m}< \cdots < T_{m:m}$.

System signature (Samaniego 2007) is an index that characterizes a system without using complex structure function. The system signature of a coherent n-component system is a n-dimensional probability vector, ${{\varvec{s}}} = (s_{1}, s_{2}, \ldots , s_{n})$, defined by

$$\begin{aligned} s_{i}= & {} \Pr ( {\text{ system } \text{ fails } \text{ upon } \text{ the } \text{ failure } \text{ of } \text{ the }} i-{\text{ th } \text{ component }}) \\= & {} \Pr (T = X_{i:n}), \end{aligned}$$

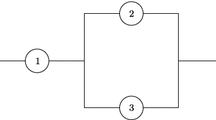
where $0 \le s_i \le 1$, $i = 1, 2, \ldots , n$, and $\sum \nolimits _{i=1}^{n} s_{i} = 1$. System signature is a distribution-free representation (Kochar et al. 1999) of the system structure meaning that ${\varvec{s}}$ does not depend on the distribution of the component lifetimes. For example, let us consider a 3-component series-parallel system, as shown in Fig. 1. The signature for this system is (1/3, 2/3, 0). Once we establish a system signature ${\varvec{s}}$, the distribution function of the system lifetime T can be expressed readily in terms of ${\varvec{s}}$ and $F_X$ alone. For a n-component system with i.i.d. components, the p.d.f. and s.f. of the system lifetime T can be expressed as

$$\begin{aligned} f_{T}(t|{\varvec{\theta }}, {\varvec{s}}) = \sum \limits _{i=1}^{n} s_{i} f_{i:n}(t| {\varvec{\theta }}) = \sum \limits _{i=1}^{n} s_{i} \left( {\begin{array}{c}n\\ i\end{array}}\right) i f_{X}(t | {\varvec{\theta }}) [F_{X}(t|{\varvec{\theta }})]^{i-1} [{{\bar{F}}}_{X}(t|{\varvec{\theta }})]^{n-i} \end{aligned}$$

(1)

and

$$\begin{aligned} {{\bar{F}}}_{T}(t| {\varvec{\theta }}, {\varvec{s}}) = \sum \limits _{i=1}^{n} s_{i} {{\bar{F}}}_{i:n}(t| {\varvec{\theta }}) = \sum \limits _{i=1}^{n} s_{i} \sum \limits _{j=0}^{i-1} \left( {\begin{array}{c}n\\ j\end{array}}\right) [F_{X}(t|{\varvec{\theta }})]^{j} [{{\bar{F}}}_{X}(t|{\varvec{\theta }})]^{n-j}, \end{aligned}$$

(2)

respectively, where ${\varvec{\theta }}$ is the vector of model parameters. For more discussions on the system signatures and their applications, one may refer to Samaniego (2007) and the references therein.

Fig. 1

A 3-component parallel-series system

Suppose m independent n-component systems with the same but unknown structure are placed on a life-testing experiment and the censoring time for the k-th system is $\tau _k$. That is, the experiment is terminated at $T_k^{*}=\min \{T_k, ~ \tau _k\}$ for the k-th system. Let $d_k$ be the censoring indicator, i.e., $d_{k} = 1$ if $T_k < \tau _k$ and $d_{k} = 0$ otherwise. Then, the observation can be expressed as $T_k^{*} = d_k T_k+(1-d_k) \tau _k$, $k = 1, 2, \ldots , m$, and we denote the observed values as $t_k^{*} = d_k t_k+(1-d_k) \tau _k$, $k = 1, 2, \ldots , m$. In this paper, we consider the system structure to be unknown but unchanged over time, i.e., ${\varvec{s}}$ is considered as a vector of parameters. Our aim is to estimate the system signature ${\varvec{s}}$ and the model parameter ${\varvec{\theta }}$ simultaneously based on the censored system-based lifetime data $({\varvec{t}}^{*}, {\varvec{d}})=((t_1^{*}, d_1), \ldots , (t_m^{*}, d_m))$.

3 Maximum likelihood estimation and EM algorithm

Suppose $\mathbf U$ is the observed data which are generated from the distribution $f(u|{\varvec{\theta }})$, and $\mathbf V$ is the missing data. Then, the complete data are $(\mathbf U , \mathbf V )$ with a joint distribution $f(\mathbf u , \mathbf v |{\varvec{\theta }})=f(\mathbf v |\mathbf u , {\varvec{\theta }})f(\mathbf u |{\varvec{\theta }})$, where ${\varvec{\theta }}$ is the vector of model parameters. The problem of interest is to estimate the parameter vector ${\varvec{\theta }}$. The log-likelihood based on the observed data $\mathbf u$ is

$$\begin{aligned} \ell ({\varvec{\theta }}) = \ln f(\mathbf u |{\varvec{\theta }}). \end{aligned}$$

(3)

The MLE of ${\varvec{\theta }}$ can be obtained by direct maximization of the log-likelihood function in Eq. (3). However, in some cases, the direct maximization of the log-likelihood function based on the observed data may not be straightforward. An alternative method to obtain the MLE of ${\varvec{\theta }}$ is by applying the EM algorithm. Consider the log-likelihood function based on the complete data $(\mathbf U , \mathbf V )$ given by $\ln f(\mathbf u , \mathbf v |{\varvec{\theta }})$. The log-likelihood function of $(\mathbf U , \mathbf V )$ is in fact a random variable because $\mathbf V$ is unobserved. The EM algorithm first takes the conditional expectation of the complete data log-likelihood with respect to the unobserved data $\mathbf V$, given the observed data $\mathbf U$ and the parameter estimate in the h-th iteration ${\varvec{\theta }}^{(h)}$. Let us define

$$\begin{aligned} Q({\varvec{\theta }}, {\varvec{\theta }}^{(h)})= & {} E_{\mathbf {V}} \left( \ln f(\mathbf u ,\mathbf V |{\varvec{\theta }})|\mathbf u , {\varvec{\theta }}^{(h)} \right) =\int _{\mathbf {v}} \ln f(\mathbf u ,\mathbf v |{\varvec{\theta }}) f(\mathbf v |\mathbf u ,{\varvec{\theta }}^{(h)}) \mathrm {d} \mathbf {v}, \end{aligned}$$

where $f(\mathbf v |\mathbf u ,{\varvec{\theta }}^{(h)})$ is the conditional marginal distribution of the unobserved data $\mathbf V$, given the observed data $\mathbf U$ and the current parameter estimate ${\varvec{\theta }}^{(h)}$. The evaluation of the expectation $Q({\varvec{\theta }}, {\varvec{\theta }}^{(h)})$ is the E-step of the EM algorithm. The first argument ${\varvec{\theta }}$ in $Q({\varvec{\theta }}, {\varvec{\theta }}^{(h)})$ corresponds to the variable that maximizes the function $Q({\varvec{\theta }}, {\varvec{\theta }}^{(h)})$, and the second argument ${\varvec{\theta }}^{(h)}$ is treated as a constant in each iteration.

Then, the M-step of the EM algorithm maximizes the expected log-likelihood function obtained from the E-step, i.e.,

$$\begin{aligned} {\varvec{\theta }}^{(h+1)}=\arg \max _{{\varvec{\theta }}} Q({\varvec{\theta }}, {\varvec{\theta }}^{(h)}). \end{aligned}$$

The MLE of the parameter vector ${\varvec{\theta }}$ is obtained by iterating the E-step and the M-step successively until convergence. Each iteration in the EM algorithm is guaranteed to increase the log-likelihood. Detailed discussions on the convergence of the EM algorithm can be found in Dempster et al. (1977) and Wu (1983). An estimate of the asymptotic variance–covariance matrix of the MLE of parameter vector ${\varvec{\theta }}$, denoted by ${\varvec{{{\hat{\theta }}}}}$, can be obtained by inverting the observed (local) Fisher information matrix (see, for example, Zhang et al. 2015)

$$\begin{aligned} \mathbf{I }_\mathbf{U }({\varvec{{{\hat{\theta }}}}}) = \left. \left( - \frac{\partial ^{2} \ell ({\varvec{\theta }})}{ \partial {\varvec{\theta }}\partial {\varvec{\theta }}^{T} } \right) \right| _{{\varvec{\theta }}= {\varvec{{{\hat{\theta }}}}}}. \end{aligned}$$

While the EM algorithm is used to find the MLE of ${\varvec{\theta }}$, an alternative way to obtain the observed Fisher information matrix is through the use of the missing information principle (Louis 1982; Tanner 1993):

$$\begin{aligned} {\text{ Observed } \text{ information }}= & {} {\text{ Complete } \text{ information }} - {\text{ Missing } \text{ information }}; \end{aligned}$$

that is,

$$\begin{aligned} \mathbf{I }_\mathbf{U }({\varvec{{{\hat{\theta }}}}})= & {} \mathbf{I }_{(\mathbf U , \mathbf V )}({\varvec{{{\hat{\theta }}}}}) - \mathbf{I }_\mathbf{V |\mathbf U }({\varvec{{{\hat{\theta }}}}}), \end{aligned}$$

where $\mathbf{I }_{(\mathbf U , \mathbf V )}({\varvec{{{\hat{\theta }}}}}) = E_\mathbf{V } \left. \left( - \frac{\partial ^{2} \ln f(\mathbf u , \mathbf V | {\varvec{\theta }})}{ \partial {\varvec{\theta }}\partial {\varvec{\theta }}^{T} } \right) \right| _{{\varvec{\theta }}= {\varvec{{{\hat{\theta }}}}}}$ is the complete information and $\mathbf{I }_\mathbf{V |\mathbf U }({\varvec{{{\hat{\theta }}}}}) = E_\mathbf{V } \left. \left( - \frac{\partial ^{2} \ln f(\mathbf V | \mathbf u , {\varvec{\theta }})}{ \partial {\varvec{\theta }}\partial {\varvec{\theta }}^{T} } \right) \right| _{{\varvec{\theta }}= {\varvec{{{\hat{\theta }}}}}}$ is the missing information. In the following subsections, we describe different approaches of implementing the EM algorithm based on the censored system-level lifetime data.

3.1 EM algorithm based on system-level likelihood function

Based on the censored system lifetime data $({\varvec{t}}^{*}, {\varvec{d}})=((t_1^{*}, d_1), \ldots , (t_m^{*}, d_m))$, the log-likelihood function is

$$\begin{aligned} \ell ({\varvec{\theta }}, {\varvec{s}})= & {} \sum _{k=1}^m d_k \ln \left( \sum _{i=1}^n s_i f_{i:n}(t_k |{\varvec{\theta }}) \right) + \sum _{k=1}^m (1- d_k) \ln \left( \sum _{i=1}^n s_i \bar{F}_{i:n}(\tau _k |{\varvec{\theta }}) \right) .\qquad \end{aligned}$$

(4)

The MLEs of ${\varvec{\theta }}$ and ${\varvec{s}}$ can be obtained by maximizing the log-likelihood function in (4) with respect to ${\varvec{\theta }}$ and ${\varvec{s}}$. However, direct maximization of (4) with respect to ${\varvec{\theta }}$ and ${\varvec{s}}$ simultaneously is not an easy task, especially when the number of components n is large. For this reason, we consider an alternative iterative procedure in which we fix one parameter vector at a time and maximize the log-likelihood function with respect to the other parameter vector.

First, we consider the parameter vector ${\varvec{\theta }}$ to be fixed (i.e., assume that $\varvec{\theta }$ is known) and then maximize the log-likelihood function with respect to ${\varvec{s}}$. Here, maximizing Eq. (4) with respect to ${\varvec{s}}$ with the constraint $\sum \limits _{i=1}^{n} s_{i} = 1$ can be done by maximizing

$$\begin{aligned}&\sum _{k=1}^m d_k \ln \left( \sum _{i=1}^n s_i f_{i:n}(t_k|{\varvec{\theta }}) \right) + \sum _{k=1}^m (1-d_k) \ln \left( \sum _{i=1}^n s_i \bar{F}_{i:n}(\tau _k|{\varvec{\theta }})\right) \nonumber \\&\quad -\,\upsilon \left( \sum _{i=1}^n s_i -1\right) , \end{aligned}$$

(5)

where $\upsilon$ is the Lagrange multiplier. Taking the derivative of Eq. (5) with respect to $s_i$, and setting the derivative to 0, we obtain

$$\begin{aligned} \sum _{k=1}^m d_k \dfrac{ f_{i:n}(t_k|{\varvec{\theta }})}{\sum _{l=1}^n s_l f_{l:n}(t_k|{\varvec{\theta }})} + \sum _{k=1}^m (1-d_k) \dfrac{ \bar{F}_{i:n}(\tau _k|{\varvec{\theta }})}{\sum _{l=1}^n s_l \bar{F}_{l:n}(\tau _k|{\varvec{\theta }})} -\upsilon =0, \end{aligned}$$

(6)

for $i=1, \ldots , n$. Multiplying both sides of Eq. (6) by $s_i$, and summing over all $s_i$, for $i=1, \ldots , n$, we can obtain $\upsilon =m$ and

$$\begin{aligned} s_i= & {} \frac{1}{m} \left[ \sum _{k=1}^m d_k \dfrac{ s_i f_{i:n}(t_k|{\varvec{\theta }})}{\sum _{l=1}^n s_l \ f_{l:n}(t_k|{\varvec{\theta }})} + \sum _{k=1}^m (1-d_k) \dfrac{ s_i \bar{F}_{i:n}(\tau _k|{\varvec{\theta }})}{\sum _{l=1}^n s_l \bar{F}_{l:n}(\tau _k|{\varvec{\theta }})} \right] , \end{aligned}$$

(7)

for $i=1, \ldots , n.$

Second, we consider the system signature ${\varvec{s}}$ to be fixed (i.e., assume that ${\varvec{s}}$ is known) and then maximize the log-likelihood function with respect to ${\varvec{\theta }}$. Taking the first derivative of $\ell ({\varvec{\theta }}, {\varvec{s}})$ in Eq. (4) with respect to the parameter ${\varvec{\theta }}$, we obtain

$$\begin{aligned} \frac{\partial \ell ({\varvec{\theta }}, {\varvec{s}})}{\partial {\varvec{\theta }}}= & {} \sum _{k=1}^m d_k \left( \sum _{i=1}^n \dfrac{s_i f_{i:n}(t_k|{\varvec{\theta }})}{\sum _{l=1}^n s_l f_{l:n}(t_k|{\varvec{\theta }})} \dfrac{\partial \ln f_{i:n} (t_k|{\varvec{\theta }})}{ \partial {\varvec{\theta }}} \right) \nonumber \\&+\,\sum _{k=1}^m (1-d_k) \left( \sum _{i=1}^n \dfrac{s_i \bar{F}_{i:n}(\tau _k|{\varvec{\theta }})}{\sum _{l=1}^n s_l \bar{F}_{l:n}(\tau _k|{\varvec{\theta }})} \dfrac{\partial \ln \bar{F}_{i:n} (\tau _k|{\varvec{\theta }})}{ \partial {\varvec{\theta }}} \right) . \end{aligned}$$

(8)

Defining

$$\begin{aligned} \delta _{ki}( {\varvec{\theta }}, {\varvec{s}})= \dfrac{s_i f_{i:n}(t_k|{\varvec{\theta }})}{\sum _{l=1}^n s_l f_{l:n}(t_k|{\varvec{\theta }})}\quad { \text{ and } }\quad \tilde{\delta }_{ki}({\varvec{\theta }}, {\varvec{s}})=\dfrac{s_i \bar{F}_{i:n}(\tau _k|{\varvec{\theta }})}{\sum _{l=1}^n s_l \bar{F}_{l:n}(\tau _k|{\varvec{\theta }})}, \end{aligned}$$

for $k=1, \dots , m, ~i=1, \ldots , n$, Eq. (8) can be rewritten as

$$\begin{aligned} \frac{\partial \ell ({\varvec{\theta }}, {\varvec{s}})}{\partial {\varvec{\theta }}}= & {} \sum _{k=1}^m d_k \left( \sum _{i=1}^n \delta _{ki}({\varvec{\theta }}, {\varvec{s}}) \dfrac{\partial \ln f_{i:n} (t_k|{\varvec{\theta }})}{ \partial {\varvec{\theta }}} \right) \\ \nonumber&+\,\sum _{k=1}^m (1-d_k) \left( \sum _{i=1}^n \tilde{\delta }_{ki}({\varvec{\theta }}, {\varvec{s}}) \dfrac{\partial \ln \bar{F}_{i:n} (\tau _k|{\varvec{\theta }})}{ \partial {\varvec{\theta }}} \right) . \end{aligned}$$

Here, the observed data $\mathbf{U }$ is the system lifetimes or censoring times ${\varvec{t}}^{*} =(t_1^{*}, t_{2}^{*}, \ldots , t_m^{*})$ and the censoring indicators ${\varvec{d}}= (d_1, d_{2}, \ldots , d_m)$, and the missing (unobserved) data $\mathbf{V }$ is the number of failed components at the time of the system failure for each of the m systems. Let the number of failed components at the time of the system failure for system k be $I_k$ and $\mathbf{I } = (I_1, I_2, \ldots , I_m)$. Here, $\mathbf{I }$ can be considered as the latent variable and the complete sample for the system-level EM algorithm is $(\mathbf U , \mathbf V ) = ({\varvec{t}}^{*}, {\varvec{d}}, \mathbf{I })$.

With an initial estimate of the parameter vector ${\varvec{\theta }}$ and an initial estimate of the system signature ${\varvec{s}}$, say ${\varvec{\theta }}^{(0)}$ and ${\varvec{s}}^{(0)}$, respectively, and the estimates at the h-th iteration $({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)})$, the $(h+1)$-th iteration of the EM algorithm based on the system-level likelihood function can be described as follows:

E-step :

Evaluate the conditional probability of latent variable ${\varvec{I}}$ as

$$\begin{aligned} \Pr (I_k=i|T_k=t_k,{\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)})= & {} {\delta }_{ki}({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} ) \nonumber \\= & {} \dfrac{s_i^{(h)} f_{i:n}(t_k|{\varvec{\theta }}^{(h)})}{\sum _{l=1}^n s_l^{(h)} f_{l:n}(t_k|{\varvec{\theta }}^{(h)})}~ \text{ for } d_k=1, \end{aligned}$$

(9)

$$\begin{aligned} \Pr (I_k=i|T_k>\tau _k,{\varvec{\theta }}^{(h)},{\varvec{s}}^{(h)} )= & {} \tilde{\delta }_{ki}({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} ) \nonumber \\= & {} \dfrac{ s_i^{(h)} \bar{F}_{i:n}( \tau _k|{\varvec{\theta }}^{(h)})}{\sum _{l=1}^n s_l^{(h)} \bar{F}_{l:n}( \tau _k|{\varvec{\theta }}^{(h)})} ~ \text{ for } d_k=0, \end{aligned}$$

(10)

$k=1, 2, \ldots , m$, $i=1, 2, \ldots , n$. Then, we obtain the expectation of the complete data on system-level log-likelihood as

$$\begin{aligned} Q({\varvec{\theta }}, ({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}))= & {} \sum _{k=1}^m \sum _{i=1}^n d_k {\delta }_{ki}({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} ) \ln f_{i:n}(T_k=t_k|{\varvec{\theta }}) \nonumber \\&+ \,\sum _{k=1}^m \sum _{i=1}^n (1-d_k) \tilde{\delta }_{ki}({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} ) \ln \bar{F}_{i:n}(\tau _k|{\varvec{\theta }}). \end{aligned}$$

(11)

M-step :

Step 1. Maximize $Q({\varvec{\theta }}, ({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}) )$ in Eq. (11) with respect to ${\varvec{\theta }}$ to obtain ${\varvec{\theta }}^{(h+1)}$;

Step 2. The updated estimate of ${\varvec{s}}$ can be obtained as

$$\begin{aligned} s_i^{(h+1)}= & {} \frac{1}{m} \sum _{k=1}^m \left[ d_k{\delta }_{ki}({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} ) + (1-d_k) \tilde{\delta }_{ki}({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} ) \right] , \end{aligned}$$

(12)

for $i=1, \ldots , n$.

The above E-step and M-step are repeated until convergence occurs to the desired level of accuracy. The MLEs of the model parameter ${\varvec{\theta }}$ and the system signature ${\varvec{s}}$ based on the EM algorithm are the convergent values of the sequence ${\varvec{\theta }}^{(h)}$ and ${\varvec{s}}^{(h)}$, respectively. In the following comparative study, we denote this implementation of the EM algorithm based on system-level likelihood function by EM-sys.

3.2 EM algorithm based on component-level likelihood function

Due to the complexity of the distribution of order statistics, maximizing the function in Eq. (11) usually does not yield an explicit solution. The EM algorithm will lose its advantage if the M-step in each iteration is not straightforward. Therefore, we consider here a different way of applying the EM algorithm by considering the component-level likelihood function.

When all the n component lifetimes in a system are observed, finding the MLE is simply reduced to maximizing the likelihood function based on a complete sample from the component lifetime distribution $f_{X}$, which is a much simpler problem because computational algorithms to compute MLEs of parameters of commonly used lifetime distributions are well-known.

Consider a single n-component system, say system k, with system lifetime $T_{k} = t_{k}$ and the system fails due to the failure of the $I_{k}$-th ordered component failure. Let ${\varvec{x}}_k = (x_{k1}, x_{k2}, \ldots , x_{kn})$ be the vector of the n component lifetimes in system k. If all the n component lifetimes in system k are observed, the log-likelihood function can be expressed as

$$\begin{aligned} \ell _{k}({\varvec{\theta }}) = \sum \limits _{j=1}^{n} \ln f_X(x_{kj}|{\varvec{\theta }}). \end{aligned}$$

(13)

If the lifetime of system k is observed as $T_{k} = t_{k}$, then the system lifetime must correspond to one of the n component lifetimes, i.e., $t_{k} = x_{k(I_{k}:n)}$. In this case, the number of component failures at the time of the system failure ($I_{k}$) and the lifetimes of the other $n-1$ component lifetimes ($x_{k({1:n})}$, $x_{k({2:n})}$, $\ldots$, $x_{k({I_k-1:n})}$, $x_{k({I_k+1:n})}$, $\ldots$, $x_{k({n:n})}$) can be considered as missing data and the EM algorithm can then be applied in this framework. On the other hand, if the lifetime of system k is right censored at $\tau _{k}$, then all the n component lifetimes, ${\varvec{x}}_k = (x_{k({1:n})}, x_{k({2:n})}, \ldots , x_{k({n:n})})$, can be considered as missing data and the EM algorithm can then be applied. We will describe now the ways of handling these two situations in the following subsections.

3.2.1 Observed system failures

Suppose the lifetime of system k is observed as $T_{k} = t_{k}$. For notational simplicity, we use $x_{k1}<$$x_{k2} < \ldots$$< x_{k(I_k-1)}$$< t_k = x_{kI_k}$$< x_{k(I_k+1)}<$$\ldots < x_{k,n}$ to denote the ordered component lifetimes in system k. Let us further denote the observed system lifetime by $U_k$, i.e., $U_k = T_k$, the missing data by ${{\varvec{V}}}_{k} = (V_{k1}, {{\varvec{V}}}_{k2})$, where $V_{k1} = I_{k}$ is the number of component failures at the time of the system failure and ${{\varvec{V}}}_{k2} =$ ($X_{k1}$, $X_{k2}$, $\ldots$, $X_{k(I_k-1)}$, $X_{k(I_k+1)}$, $\ldots$, $X_{kn}$) is the vector of unobserved component lifetimes. From Eq. (13), the log-likelihood function of the complete data $(U_k, V_{k1}, {{\varvec{V}}}_{k2})$ for system k is

$$\begin{aligned}&\ell _{k}({\varvec{\theta }}| U_{k}, V_{k1}, {{\varvec{V}}}_{k2}) \nonumber \\&\quad = \,\ell _{k}({\varvec{\theta }}| T_{k} = x_{kI_{k}}, I_{k}, (x_{k1}, \ldots , x_{k(I_{k} - 1)}, x_{k(I_{k} + 1)}, \ldots , x_{km})) \nonumber \\&\quad = \,\sum _{j=1}^{I_k-1} \ln f_X(x_{kj}|{\varvec{\theta }})+ \ln f_X(t_k|{\varvec{\theta }})+\sum _{j=I_k+1}^n \ln f_X(x_{kj}|{\varvec{\theta }}). \end{aligned}$$

(14)

As mentioned in Sect. 2, the EM algorithm first takes the conditional expectation of the log-likelihood function based on complete data with respect to the missing data $(V_{k1}, {{\varvec{V}}}_{k2})$. Suppose the estimates of ${\varvec{\theta }}$ and ${\varvec{s}}$ after the h-th iteration are ${\varvec{\theta }}^{(h)}$ and ${\varvec{s}}^{(h)}$, respectively. We then need to evaluate the function

$$\begin{aligned}&Q_k({\varvec{\theta }}, ({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)})) \nonumber \\&\quad = \,E_{(V_{k1}, {{\varvec{V}}}_{k2})| U_k} \left( \ell _{k}({\varvec{\theta }}| U_{k}, V_{k1}, {{\varvec{V}}}_{k2})|u_k, {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} \right) \nonumber \\&\quad = \,E_{{{\varvec{V}}}_{k2}|U_k} \left[ E_{V_{k1}|({{\varvec{V}}}_{k2}, U_k)} \left( \ell _{k}({\varvec{\theta }}| U_{k}, V_{k1}, {{\varvec{V}}}_{k2}) |u_k, {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}\right) \right] . \end{aligned}$$

(15)

We first consider the inner layer of the expectation

$$\begin{aligned}&E_{V_{k1}|({{\varvec{V}}}_{k2}, U_k)} \left( \ell _{k}({\varvec{\theta }}| U_{k}, V_{k1}, {{\varvec{V}}}_{k2}) |u_k, {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} \right) \nonumber \\&\quad = \,\sum _{i=1}^n \Pr (I_k = i|T_k=t_k, {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}) \ell _{k}({\varvec{\theta }}| U_{k}, V_{k1} = I_{k} = i, {{\varvec{V}}}_{k2}). \end{aligned}$$

(16)

Next, we consider the outer layer of the expectation in Eq. (15). The conditional distribution of the first $(I_k - 1)$ ordered component lifetimes, given $t_{k}$, is i.i.d. random variables from a right-truncated distribution

$$\begin{aligned} g_{RX}(x_{kj}| {\varvec{\theta }}, t_k)=\frac{f_X(x_{kj} | {\varvec{\theta }})}{F_X(t_k | {\varvec{\theta }})}, ~x_{kj} < t_k, \end{aligned}$$

for $j=1, \ldots , I_k-1$; see Arnold et al. (1992). The outer layer of the expectation of the log-likelihood in Eq. (15) with respect to the components failed before the system failure (i.e., $X < t$) can be written as

$$\begin{aligned} E_{X|X < t}[\ln f_{X}(x | {\varvec{\theta }})] = \int _{-\infty }^{t} \ln f_{X}(x | {\varvec{\theta }}) g_{RX}(x | {\varvec{\theta }}, t) \text {d}x. \end{aligned}$$

Similarly, given the lifetime of the system k, $t_{k}$, the last $(n-I_{k})$ ordered component lifetimes are i.i.d. random variables from a left-truncated distribution

$$\begin{aligned} g_{LX}(x_{kj}|{\varvec{\theta }}, t_k)=\frac{f_X(x_{kj} | {\varvec{\theta }})}{\bar{F}_X(t_k | {\varvec{\theta }})}, ~x_{kj} > t_k, \end{aligned}$$

for $j=I_k+1, \ldots , n$; see Arnold et al. (1992). The outer layer of the expectation of the log-likelihood in Eq. (15) with respect to the components survived at the time of system failure (i.e., $X > t$) can be written as

$$\begin{aligned} E_{X|X > t}[\ln f_{X}(x | {\varvec{\theta }})] = \int _{t}^{\infty } \ln f_{X}(x | {\varvec{\theta }}) g_{LX}(x | {\varvec{\theta }}, t) \text {d}x. \end{aligned}$$

Then, Eq. (15) can be expressed as

$$\begin{aligned}&Q_k({\varvec{\theta }}, ({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)})) \nonumber \\&\quad = \,\sum _{i=1}^n \Pr \left( I_k=i|T_k=t_k, {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}\right) \nonumber \\&\qquad \left[ (i-1) \int _{-\infty }^{t_k} \ln f_X(x|{\varvec{\theta }}) g_{RX}(x| {\varvec{\theta }}^{(h)}, t_k) \text {d}x + f_X(t_k|{\varvec{\theta }}) \right. \nonumber \\&\qquad \quad \left. +\, (n-i) \int _{t_k}^{\infty } \ln f_X(x|{\varvec{\theta }}) g_{LX}(x| {\varvec{\theta }}^{(h)}, t_k) \text {d}x \right] . \end{aligned}$$

(17)

3.2.2 Censored system lifetimes

Suppose the component lifetimes in system k are ${\varvec{x}}_k = (x_{k1}, \ldots , x_{kn})$, and the system lifetime $T_k$ is right censored at time $\tau _k$. Let $\varLambda _k$ be the random variable that denotes the number of failed components in system k before time $\tau _k$. $\varLambda _k$ is a discrete random variable with support on $\{0, 1, \ldots , n-1\}$. In this case, the observed data are $U_k = \tau _k$ and the missing data are ${\varvec{V}}_{k} = (V_{k1}, {\varvec{V}}_{k2})$, where $V_{k1} = \varLambda _k$ and ${\varvec{V}}_{k2} = (X_{k1}, \ldots , X_{k \varLambda _k}, X_{k (\varLambda _k+1)}, \ldots , X_{kn})$. From Eq. (13), the log-likelihood function of the complete data $(U_k, V_{k1}, {{\varvec{V}}}_{k2})$ can be written as

$$\begin{aligned} \ell _{k}({\varvec{\theta }}| U_{k}, V_{k1}, {{\varvec{V}}}_{k2}) = \sum _{j=1}^{\varLambda _k} \ln f_X(x_{k(j:n)}|{\varvec{\theta }})+ \sum _{j=\varLambda _k+1}^n \ln f_X(x_{k(j:n)}|{\varvec{\theta }}). \end{aligned}$$

(18)

As in the case when the system failure is observed, the conditional distribution of the first $\varLambda _k$ ordered component lifetimes, given the censoring time $\tau _{k}$, are i.i.d. random variables from a right-truncated distribution

$$\begin{aligned} g_{RX}(x_{kj}| {\varvec{\theta }}, \tau _k)=\frac{f_X(x_{kj} | {\varvec{\theta }})}{F_X(\tau _k | {\varvec{\theta }})}, ~x_{kj} < \tau _k, \end{aligned}$$

for $j=1, \ldots , \varLambda _k$. Given the censoring time of system k, $\tau _{k}$, the last $(n-\varLambda _{k})$ ordered component lifetimes are i.i.d. random variables from a left-truncated distribution

$$\begin{aligned} g_{LX}(x_{kj}|{\varvec{\theta }}, \tau _k)=\frac{f_X(x_{kj} | {\varvec{\theta }})}{\bar{F}_X(\tau _k | {\varvec{\theta }})}, ~x_{kj} > \tau _k, \end{aligned}$$

for $j=\varLambda _k+1, \ldots , n$. Suppose the estimates of ${\varvec{\theta }}$ and ${\varvec{s}}$ after the h-th iteration are ${\varvec{\theta }}^{(h)}$ and ${\varvec{s}}^{(h)}$, respectively. We then need to evaluate the function

$$\begin{aligned}&Q_k({\varvec{\theta }}, ({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)})) \nonumber \\&\quad = \, \sum _{\lambda =0}^{n-1} \Pr (\varLambda _k=\lambda |T_k>\tau _k, {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}) \left[ \lambda \int _{-\infty }^{\tau _k} \ln f_X(x|{\varvec{\theta }}) g_{RX}(x| {\varvec{\theta }}^{(h)}, \tau _k) \text {d}x \right. \nonumber \\&\qquad \quad \left. +\, (n-\lambda ) \int _{\tau _k}^{\infty } \ln f_X(x|{\varvec{\theta }}) g_{LX}(x| {\varvec{\theta }}^{(h)}, \tau _k) \text {d}x \right] , \end{aligned}$$

(19)

where

$$\begin{aligned}&\Pr (\varLambda _{k}=\lambda | T_k>\tau _k, {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}) = \frac{\Pr (\varLambda _{k}=\lambda , T_k>\tau _k| {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)})}{\Pr (T_k > \tau _k| {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)})}\nonumber \\&\quad = \,\dfrac{(1-\sum _{l=1}^\lambda s_l^{(h)}) \left( {\begin{array}{c}n\\ \lambda \end{array}}\right) [F_X(\tau _k| {\varvec{\theta }}^{(h)})]^{\lambda }[\bar{F}_X (\tau _k|{\varvec{\theta }}^{(h)})]^{n-\lambda }}{\bar{F}_T(\tau _k| {\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)})} {\mathop {=}\limits ^{def}} \delta _{k \lambda }^c({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}),\nonumber \\ \end{aligned}$$

(20)

$(1-\sum _{l=1}^\lambda s_l^{(h)})$ is the probability that the system did not fail due to the i-th ordered component failure, $i = 1,2, \ldots , \lambda$, and $\left( {\begin{array}{c}n\\ \lambda \end{array}}\right) [F_X(\tau _k| {\varvec{\theta }}^{(h)})]^{\lambda }[\bar{F}_X (\tau _k|{\varvec{\theta }}^{(h)})]^{n-\lambda }$ is the probability that $\lambda$-out-of-n components are failed at time $\tau _{k}$.

3.2.3 Implementation of the EM algorithm

Based on the results presented in Sects. 3.2.1 and 3.2.2, when the system signature ${\varvec{s}}$ is unknown and given the estimates of ${\varvec{\theta }}$ and ${\varvec{s}}$ after the h-th iteration are ${\varvec{\theta }}^{(h)}$ and ${\varvec{s}}^{(h)}$, respectively, the $(h+1)$-th iteration of the EM algorithm on component-level can be described as follows:

E-step :

Compute the conditional probabilities $\delta _{ki}({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} )$ in Eq. (9) for $d_{k} = 1$, $i = 1, \ldots , n$, and $\delta _{k \lambda }^c({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)})$ in Eq. (20) for $d_{k} = 0$, $\lambda = 0, \ldots , n-1$, $k = 1, \ldots , m$. We then have

$$\begin{aligned} Q({\varvec{\theta }}, ({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}))= & {} \sum _{k=1}^m d_k \sum _{i=1}^n \delta _{ki}({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} ) \nonumber \\&\times \, \left[ (i-1) \int _{-\infty }^{t_k} \ln f_X(x|{\varvec{\theta }}) g_{RX}(x| {\varvec{\theta }}^{(h)}, t_k) \text {d}x + f_X(t_k|{\varvec{\theta }}) \right. \nonumber \\&\left. +\, (n-i) \int _{t_k}^{\infty } \ln f_X(x|{\varvec{\theta }}) g_{LX}(x| {\varvec{\theta }}^{(h)}, t_k) \text {d}x \right] \nonumber \\&+ \,\sum _{k=1}^m (1-d_k) \sum _{\lambda =0}^{n-1} \delta _{k \lambda }^c({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}) \nonumber \\&\times \,\left[ \lambda \int _{-\infty }^{\tau _k} \ln f_X(x|{\varvec{\theta }}) g_{RX}(x| {\varvec{\theta }}^{(h)}, \tau _k) \text {d}x \right. \nonumber \\&\left. + \,(n-\lambda ) \int _{\tau _k}^{\infty } \ln f_X(x|{\varvec{\theta }}) g_{LX}(x| {\varvec{\theta }}^{(h)}, \tau _k) \text {d}x \right] . \end{aligned}$$

(21)

M-step :

Step 1. Maximize $Q({\varvec{\theta }}, ({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)} ))$ in Eq. (21) with respect to ${\varvec{\theta }}$ to obtain ${\varvec{\theta }}^{(h+1)}$;

Step 2. The updated estimate of ${\varvec{s}}$ can be obtained by Eq. (12) for $i=1, \ldots , n$.

The MLEs of the model parameter ${\varvec{\theta }}$ and the system signature ${\varvec{s}}$ can be obtained by repeating the E-step and M-step until convergence occurs to the desired level of accuracy. In the following comparative study, we denote this implementation of the EM algorithm based on component-level likelihood function by EM-comp.

3.3 Alternate implementation based on component-level likelihood function

Suppose a Type II censored system lifetime data, ${\varvec{t}}=(t_{1:m}< t_{2:m}< \ldots <t_{r:m})$, $r\le m$, are observed. According to the results in order statistics (Arnold et al. 1992, pp. 23), the censored system lifetimes $T_{r+1:m}, \ldots , T_{m:m}$ have the same distribution as order statistics $Z_{1:m-r}, \ldots , Z_{m-r:m-r}$, where $Z_1, \ldots , Z_{m-r}$ are generated from

$$\begin{aligned} g_{L}(z| t_{r:m}) = \frac{f_T(z)}{1-F_T(t_{r:m})},~~~z > t_{r:m}. \end{aligned}$$

Then, the distribution of order statistic $T_{r+j:m}$ is simply

$$\begin{aligned} g_{(r+j):m}(z|t_{r:m})= & {} \frac{(m-r)!}{(j-1)!(m-r-j)!} \\&\times \,g_L(z|t_{r:m}) G_L(z|t_{r:m})^{j-1} (1-G_L(z|t_{r:m}))^{m-r-j}, z\ge t_{r:m}, \end{aligned}$$

$j=1, 2, \ldots , (m-r)$, where $G_L(z|t_{r:m})=\int _{t_{r:m}}^z g_L(x|t_{r:m}) \text {d}x$. The expectation of $T_{r+j:m}$ can then be expressed as

$$\begin{aligned} E(T_{(r+j):m})=\int _{t_{r:m}}^{\infty } x g_{(r+j):m}(x|t_{r:m})\text {d}x, ~j=1, \ldots , m-r. \end{aligned}$$

Once we have the expectation of the censored system lifetimes, those expectations could be used to replace the censored system lifetimes, i.e., assuming the observed system lifetimes to be $T_{1:m}, \ldots , T_{r:m}, E(T_{r+1:m}), \ldots , E(T_{m:m})$ as an approximation. The theoretical basis of this approximation is approximating $E[\ln f_{T}(T) | T > t_{r:m}]$ by $\ln f_{T}[E(T| T > t_{r:m})]$ based on the first-order Taylor expansion of $\ln f_{T}(T)$ at $E(T| T > t_{r:m})$. Then, the EM algorithm discussed in Sects. 3.1 and 3.2 can be applied with $d_1=1, \ldots , d_m=1$ on the system lifetimes. We denote this implementation of the EM algorithm by EM-exp.

4 Coherent systems with unknown structure

In the preceding sections, when the system signature is unknown, we have developed different implementations of the EM algorithm for the estimation of the model parameter ${\varvec{\theta }}$ and the system signature ${\varvec{s}}$, but we did not put any restriction on the estimate of the system signature except $\sum _{i=1}^{n} {{\hat{s}}_{i}} = 1$. However, in practice, if we have the information that the observed system lifetimes are coming from a coherent system with n components, there are a limited number of possible system signatures that need to be considered. For example, if the system is a 3-component coherent system, then there are only 5 possible arrangements, as shown in Table 1.

Table 1 All possible 3-component coherent system

If the system is a 4-component coherent system, then there are 20 possible arrangements (Navarro et al. 2007, p. 184). Therefore, we should take into account the restriction on the limited possible system signatures in the parameter estimation procedures. This can be achieved by applying the proposed EM algorithms with known system signature for each of the possible system signature and then choose the system signature that results in the largest likelihood value. Specifically, if there are L possible system signatures, ${\varvec{s}}_{l}, l = 1, 2, \ldots , L$, we can apply the proposed implementations of EM algorithms by fixing the system signature as ${\varvec{s}}_{l}$ to obtain the MLE of ${\varvec{\theta }}$ as ${\varvec{{{\hat{\theta }}}}}_{l}$, $l = 1, 2, \ldots , L$, and then computing the value of the log-likelihood in Eq. (4) as $\ell ({{\varvec{{{\hat{\theta }}}}}}_{l}, {\varvec{s}}_{l})$. Then, suppose

$$\begin{aligned} \ell ({{\varvec{{{\hat{\theta }}}}}}_{l^{*}}, {\varvec{s}}_{l^{*}}) = \max _{l = 1, 2, \ldots , L} \{ \ell ({{\varvec{{{\hat{\theta }}}}}}_{l}, {\varvec{s}}_{l}) \}, \end{aligned}$$

the final estimates of the parameter vector and the system signature will be ${{\varvec{{{\hat{\theta }}}}}}_{l^{*}}$ and ${\varvec{s}}_{l^{*}}$, respectively.

5 Weibull distributed component lifetime data

To illustrate the methodologies developed in the preceding sections, we consider the lifetimes of the components in an n-component system to follow a two-parameter Weibull distribution. Then, Monte Carlo simulations and a numerical example are used here to evaluate the performance of different implementations of the EM algorithm in obtaining the MLEs of the parameters in the subsequent sections.

5.1 Implementations of the EM algorithm

Suppose that the component lifetimes follow a two-parameter Weibull distribution (see, for example, Weibull 1951; Murthy et al. 2004; Rinne 2010) with c.d.f. and p.d.f.

$$\begin{aligned} F_X(x| \alpha , \beta )= & {} 1 - \exp \left[ -\left( \frac{x}{\beta }\right) ^\alpha \right] , x> 0 \\ {\text{ and } } f_X(x| \alpha , \beta )= & {} \frac{\alpha }{x} \left( \frac{x}{\beta } \right) ^\alpha e^{- \left( \frac{x}{\beta } \right) ^\alpha }, x > 0, \end{aligned}$$

respectively, where $\alpha > 0$ is the shape parameter and $\beta > 0$ is the scale parameter. The log-transformation of the component lifetimes follows the smallest extreme value (SEV) distribution. Let $W = \ln X$ be the log-lifetime of the component. Then, the c.d.f. and p.d.f. of the log-transformed component lifetimes are

$$\begin{aligned} F_W(w| \mu , \sigma )= & {} 1 - \exp \left\{ -\exp \left[ \frac{w-\mu }{\sigma }\right] \right\} , -\infty< w< \infty \\ {\text{ and } } f_W(w| \mu , \sigma )= & {} \frac{1}{\sigma } e^{\frac{w-\mu }{\sigma }} \exp \left[ -e^{\frac{w-\mu }{\sigma }} \right] , -\infty< w < \infty , \end{aligned}$$

respectively, with location parameter $-\infty< \mu = \ln \beta < \infty$ and scale parameter $\sigma = 1/\alpha > 0$.

The p.d.f. and c.d.f. of the i-th order statistic $W_{i:n}$ are, respectively,

$$\begin{aligned} f_{i:n}(w|\mu , \sigma )= & {} \left( {\begin{array}{c}n\\ i\end{array}}\right) i \left( F_W(w|\mu , \sigma ) \right) ^{i-1} f_W(w|\mu , \sigma ) \left( 1-F_W(w|\mu , \sigma )\right) ^{n-i}\quad \nonumber \\= & {} \frac{1}{\sigma } \left( {\begin{array}{c}n\\ i\end{array}}\right) i \exp \left( \frac{w-\mu }{\sigma }\right) \left\{ \exp \left[ -\exp \left( \frac{w-\mu }{\sigma }\right) \right] \right\} ^{n-i+1} \nonumber \\&\times \,\left\{ 1 - \exp \left[ -\exp \left( \frac{w-\mu }{\sigma }\right) \right] \right\} ^{i-1}, -\infty< w < \infty \end{aligned}$$

(22)

$$\begin{aligned} {\text{ and } } F_{i:n}(w|\mu , \sigma )= & {} \sum _{l=i}^n \left( {\begin{array}{c}n\\ l\end{array}}\right) [F_W(w|\mu , \sigma )]^{l} [1-F_W(w|\mu , \sigma )]^{n-l}\nonumber \\= & {} \sum _{l=i}^n \left( {\begin{array}{c}n\\ l\end{array}}\right) \left\{ 1 - \exp \left[ -\exp \left( \frac{w-\mu }{\sigma }\right) \right] \right\} ^{l} \nonumber \\&\times \,\left\{ \exp \left[ -\exp \left( \frac{w-\mu }{\sigma }\right) \right] \right\} ^{n-l}, -\infty< w < \infty , \end{aligned}$$

(23)

where $-\infty<\mu < \infty$ and $\sigma > 0$. Here after, we consider the log-transformed system and component lifetimes instead of the original lifetimes as it is more convenient. For notational simplicity, we still use X to denote the log-transformed component lifetime and T to denote the log-transformed system lifetime, unless stated otherwise.

In the following subsections, we illustrate different implementations of the EM algorithm described earlier in Sect. 3 when the component lifetime distribution is Weibull. The algorithms and the required computational formulae for the conditional expectations are presented.

5.1.1 EM-sys algorithm

The EM-sys algorithm is realized by directly applying Eqs. (22) and (23) to the algorithm described earlier in Sect. 3.1. Suppose the estimates of the parameter vector and the system signature in the h-th iteration are, respectively, ${\varvec{\theta }}^{(h)}=(\mu ^{(h)}$, $\sigma ^{(h)})$ and ${\varvec{s}}^{(h)}$. Then, the $(h+1)$-th iteration of the EM-sys algorithm can be described as follows:

E-step :

Evaluate the conditional probability of ${\varvec{I}}$ in Eq. (9) by plugging in the p.d.f. in Eq. (22) and the c.d.f. in Eq. (23);

M-step :

Step 1. Maximize $Q({\varvec{\theta }}, ({\varvec{\theta }}^{(h)}, {\varvec{s}}^{(h)}))$ in Eq. (11) with respect to $\mu$ and $\sigma$ to obtain $\mu ^{(h+1)}$ and $\sigma ^{(h+1)}$;

Step 2. Obtain the updated ${\varvec{s}}^{(h)}$ by Eq. (12).

5.1.2 EM-comp algorithm

Suppose a sample ${\varvec{w}}=(w_1, w_2, \ldots , w_n)$ follows SEV distribution with location parameter $\mu$ and scale parameter $\sigma$. Then, the MLEs of $\mu$ and $\sigma$ can be obtained by solving the following equation (Lawless 2011):

$$\begin{aligned}&\hat{\sigma }=\frac{\sum _{i=1}^n w_i \exp (w_i/ \hat{\sigma })}{\sum _{i=1}^n \exp (w_i/ \hat{\sigma })}- \frac{1}{n} \sum _{i=1}^n w_i, \end{aligned}$$

(24)

and then substituting the solution ${\hat{\sigma }}$ into

$$\begin{aligned}&\hat{\mu }=\,\hat{\sigma } \ln \left[ \frac{1}{n} \sum _{i=1}^n \exp \left( \frac{w_i}{\hat{\sigma }} \right) \right] . \end{aligned}$$

(25)

The M-step of the EM algorithm based on component-level likelihood function can be simplified to solve Eq. (24).

In order to compute the conditional expectations in the E-step, we consider a random variable $Z_k$ that follows a left-truncated SEV distribution with truncation at time $t_k$ (see, for example, Ng et al. 2002). The p.d.f. of $Z_k$ is then given by

$$\begin{aligned} \begin{aligned} f_{Z_k}(z_k|Z_k> t_k, \mu , \sigma )&=\frac{f_X(z_k|\mu , \sigma )}{1-F_X(t_k|\mu , \sigma )}\\&=\frac{\exp [ \exp (\xi _k) ]}{\sigma } \exp \left[ \frac{z_k-\mu }{\sigma }-\exp \left( \frac{z_k-\mu }{\sigma } \right) \right] ,~z_k>t_k,\\&\quad -\, \infty<\mu <\infty , \sigma >0, \end{aligned} \end{aligned}$$

where $\xi _k=\frac{t_k-\mu }{\sigma }$.

Let $Z^*_k=\frac{Z_k-\mu }{\sigma }$ and $\eta _k=\exp \left[ \exp (\xi _k) \right]$. Then, the p.d.f. of $Z^*_k$ could be expressed as

$$\begin{aligned} f_{Z_k^*}(z^*_k|Z^*_k> \xi _k, \mu , \sigma )=\eta _k \exp \left[ z^*_k-\exp (z^*_k)\right] , z_k^*> \xi _k, - \infty<\mu <\infty , \sigma >0. \end{aligned}$$

The moment generating function of $Z^*_k$, conditional on $Z^*_k>\xi _k$, is given by

$$\begin{aligned} M_{Z^*_k}(s)= & {} \eta _k \varGamma (s+1, e^{\xi _k}) = \varGamma (s+1) \left[ \eta _k- \sum _{p=0}^{+\infty } \frac{e^{(s+p+1) \xi _k}}{\varGamma (s+p+2)} \right] , \end{aligned}$$

where $\varGamma (\alpha )=\int _0^{\infty } u^{\alpha -1} e^{-u} \mathrm {d} u$ is the gamma function and $\varGamma (\alpha ,x)=\int _x ^{\infty } u^{\alpha -1} e^{-u} \mathrm {d} u$ is the incomplete gamma function. Then, we have the following expectations:

(26)

where

$$\begin{aligned} E_{R,1,k}= & {} E\left( Z^*_k | \xi _k, \mu , \sigma \right) \nonumber \\= & {} \psi (1) \eta _k + \sum _{p=0}^{+\infty } \frac{e^{(p+1) \xi _k} \psi (p+2)}{\varGamma (p+2)} - [ \xi _k +\psi (1) ] \sum _{p=0}^{+\infty } \frac{e^{(p+1) \xi _k} }{\varGamma (p+2)}, \\ E_{R,2,k}= & {} E\left( e^{Z^*_k} | \xi _k, \mu , \sigma \right) \nonumber \\= & {} e^{\xi _k}+1\\ {\text{ and } } E_{R,3,k}= & {} E\left( Z^*_k e^{Z^*_k} | \xi _k, \mu , \sigma \right) \nonumber \\= & {} \psi (2) \eta _k + \sum _{p=0}^{+\infty } \frac{e^{(p+2) \xi _k} \psi (p+3)}{\varGamma (p+3)} - [ \xi _k +\psi (2) ] \sum _{p=0}^{+\infty } \frac{e^{(p+2) \xi _k} }{\varGamma (p+3)}, \end{aligned}$$

$\psi ( \cdot )=\frac{\mathrm {d}}{\mathrm {d}x} \ln \varGamma (x)$ is the digamma function.

Similarly, let $Y_k$ be a random variable with a right-truncated SEV distribution at time $t_k$. The p.d.f. of $Y_k$ is then

$$\begin{aligned} f_{Y_k}(y_k|Y_k< t_k, \mu , \sigma )= & {} \frac{f_X(y_k|\mu , \sigma )}{F_X(t_k|\mu , \sigma )}\\= & {} \frac{1}{\sigma [1-\exp ( \exp (\xi _k) )]} \exp \left[ \frac{y_k-\mu }{\sigma }-\exp (\frac{y_k-\mu }{\sigma })\right] ,\\&\quad y_k<t_k, - \infty<\mu <\infty , \sigma >0. \end{aligned}$$

If $Y^*_k=\frac{Y_k-\mu }{\sigma }$, the p.d.f. of $Y^*_k$ can be expressed as

$$\begin{aligned} f_{Y^*_k}(y^*_k|Y^*_k< \xi _k, \mu , \sigma )= \frac{1}{ [1-\exp ( \exp (\xi _k) )]} \exp \left[ y^*_k-\exp (y^*_k)\right] ,\\ y_k^*>\xi _k, - \infty<\mu <\infty , \sigma >0. \end{aligned}$$

The moment generating function of $Y^*_k$, conditional on $Y^*_k <\xi _k$, is given by

$$\begin{aligned} \begin{aligned} M_{Y^*_k}(s)&=(\eta _k-1)^{-1} [ \eta _k \varGamma (s+1) -M_{Z^*_k}(s)]. \end{aligned} \end{aligned}$$

The conditional expectations of interest are then given by

(27)

where

$$\begin{aligned} E_{L,1,k}= & {} E(Y^*_k| \xi _k, \mu , \sigma )\\= & {} (\eta _k-1)^{-1} \left[ \eta _k \psi (1) - E(Z^*_k|\xi _k, \mu , \sigma )\right] , \\ E_{L,2,k}= & {} E(e^{Y^*_k}| \xi _k, \mu , \sigma )\\= & {} (\eta _k-1)^{-1} \left[ \eta _k - E(e^{Z^*_k}|\xi _k, \mu , \sigma )\right] \\ {\text{ and } } E_{L,3,k}= & {} E(Y^*_k e^{Y^*_k}| \xi _k, \mu , \sigma )\\= & {} (\eta _k-1)^{-1} \left[ \eta _k \psi (2) - E(Z^*_k e^{Z^*_k}|\xi _k, \mu , \sigma )\right] . \end{aligned}$$

As mentioned in Sect. 3.2, suppose system k failed at time $t_k$. Then, the components still working at time $t_k$ have the same distribution as the random variable $Z_k$, and the components failed before time $t_k$ have the same distribution as the random variable $Y_k$. If system k is censored at time $\tau _k$, with $\xi ^*_k=\frac{\tau _k-\mu }{\sigma }$, the above formulations are still applicable.

Following the notation and setting described earlier in Sect. 3.1, the $(h+1)$-th iteration of the EM-comp is as follows:

E-step :

Evaluate the conditional probabilities $\delta _{ki}(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})$ in Eq. (9) for $i=1, \ldots , n$, and $\delta _{k \lambda }^c(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})$ in Eq. (20), for $\lambda =0, \ldots , n-1$, $k=1, \ldots , m$;

M-step :

Step 1. Update the estimates of the parameters by Eqs. (24) and (25) as

$$\begin{aligned} \sigma ^{(h+1)}= & {} \dfrac{\sum _{k=1}^m \left( \rho _{ 3}(k|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})) \right) }{\sum _{k=1}^m \left( \rho _{ 2}(k|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})\right) } \nonumber - \dfrac{\sum _{k=1}^m \left( \rho _{ 1}(k|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) ) \right) }{ mn } \nonumber \\ {\text{ and } } \mu ^{(h+1)}= & {} \sigma ^{(h+1)} \ln \left[ \dfrac{\sum _{k=1}^m \left( \rho _{ 2}(k|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \right) }{mn} \right] , \end{aligned}$$

where

$$\begin{aligned} \rho _{ l}(k|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} d_k \sum _{i=1}^n E_{o,l}(k, i|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \\&+\, (1-d_k)\sum _{\lambda =0}^{n-1} E_{c,l}(k, \lambda |\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}), \end{aligned}$$

for $l=1, 2, 3$, and

$$\begin{aligned} E_{o,1}(k, i|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} \delta _{ki}(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \left[ (i-1) E(Y_k |\xi _k, \mu ^{(h)}, \sigma ^{(h)}) \right. \\&\left. + \,t_k +(n-i) E(Z_k|\xi _k, \mu ^{(h)}, \sigma ^{(h)} ) \right] ,\\ E_{c,1}(k, \lambda |\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} \delta _{k \lambda }^c(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \left[ \lambda E(Y_k|\xi ^*_k, \mu ^{(h)}, \sigma ^{(h)} ) \right. \\&\left. +\,(n-\lambda ) E(Z_k |\xi _k^*, \mu ^{(h)}, \sigma ^{(h)} ) \right] , \\ E_{o,2}(k, i|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} \delta _{ki}(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \left[ (i-1) E(e^{Y_k/ \sigma ^{(h)}} |\xi _k, \mu ^{(h)}, \sigma ^{(h)}) \right. \\&\left. +\, e^{t_k /\sigma ^{(h)}} +(n-i) E(e^{Z_k / \sigma ^{(h)}} |\xi _k, \mu ^{(h)}, \sigma ^{(h)}) \right] , \\ E_{c,2}(k, \lambda |\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} \delta _{k \lambda }^c(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \left[ \lambda E(e^{Y_k/ \sigma ^{(h)}}|\xi _k^*, \mu ^{(h)}, \sigma ^{(h)} ) \right. \\&\left. +\,(n-\lambda ) E( e^{Z_k / \sigma ^{(h)}} |\xi _k^*, \mu ^{(h)}, \sigma ^{(h)}) \right] , \\ E_{o,3}(k, i|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} \delta _{ki}(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \left[ (i-1) E(Y_ke^{Y_k/ \sigma ^{(h)}}|\xi _k, \mu ^{(h)}, \sigma ^{(h)} ) \right. \\&\left. + \,t_k e^{t_k /\sigma ^{(h)}} +(n-i) E(Z_k e^{Z_k / \sigma ^{(h)}} |\xi _k, \mu ^{(h)}, \sigma ^{(h)}) \right] \\ {\text{ and } } E_{c,3}(k, \lambda |\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} \delta _{k \lambda }^c(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \left[ \lambda E(Y_ke^{Y_k/ \sigma ^{(h)}}|\xi ^*_k, \mu ^{(h)}, \sigma ^{(h)} ) \right. \\&\left. +\,(n-\lambda ) E(Z_k e^{Z_k / \sigma ^{(h)}} |\xi _k^*, \mu ^{(h)}, \sigma ^{(h)}) \right] ; \end{aligned}$$

Step 2. Update ${\varvec{s}}^{(h+1)}$ by Eq. (12).

5.1.3 EM-exp algorithm

The algorithm of EM-exp based on Weibull distributed component lifetimes can be described as follows:

E-step :

Step 1. Evaluate the expectations if the system lifetimes $t_k$ are censored, for $k= r+1, \ldots , m$, obtaining the pseudo-complete system lifetimes $t_1$, $t_{2}$, $\ldots$, $t_r$, $E(T_{r+1}), \ldots , E(T_m)$;

Step 2. Evaluate the conditional probabilities $\delta _{ki}(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})$ in Eq. (9) for $i=1, \ldots ,n$, $k=1, \ldots , m$;

M-step :

The same as the M-step in Sect. 5.1.2 with $d_k =1$ for $k=1, \ldots , m$.

5.2 Illustrative example

A numerical example is given here to illustrate the three different implementations of the EM algorithm: EM-sys, EM-comp and EM-exp, proposed in Sects. 3.1, 3.2 and 3.3 by assuming the component lifetime distribution to be Weibull. A sample of $m = 30$ system lifetimes was simulated from a 4-component system with system signature $\mathbf s = (1/4, 1/4, 1/2, 0)$, and the component lifetimes follow a Weibull distribution with scale parameter $\beta = 1$ and shape parameter $\alpha = 1$. In other words, the logarithm of the component lifetimes is assumed to follow a SEV distribution with location parameter $\mu =0$ and scale parameter $\sigma =1$. The ordered log-transformed system lifetimes are presented in Table 2. We consider the estimation of parameters and the system signature when the system structure is unknown with different censoring proportions in the following subsections.

Table 2 Logarithm of $m = 30$ simulated system lifetimes of a 4-component system with system signature $\mathbf s = (1/4, 1/4, 1/2, 0)$ when the component lifetimes are from Weibull(1, 1)

We are interested in estimating both the system signature ${\varvec{s}}$ and the model parameters $\mu$ and $\sigma$. We apply the three different implementations of the EM algorithm proposed in Sects. 3.1, 3.2 and 3.3, and the numerical maximization to obtain the MLEs based on the dataset presented in Table 2 with censoring proportions $q = 0, 10$ and 30%. We consider four different combinations of initial values for these algorithms:

• (i) ${\varvec{\theta }}^{(0)} = ({{\hat{\mu }}}^{(0)}, {{\hat{\sigma }}}^{(0)}) = (0, 1), {\varvec{s}}^{(0)} = (0.25, 0.25, 0.50, 0.00)$;

• (ii) ${\varvec{\theta }}^{(0)} = ({{\hat{\mu }}}^{(0)}, {{\hat{\sigma }}}^{(0)}) = (2, 3), {\varvec{s}}^{(0)} = (0.25, 0.25, 0.50, 0.00)$;

• (iii) ${\varvec{\theta }}^{(0)} = ({{\hat{\mu }}}^{(0)}, {{\hat{\sigma }}}^{(0)}) = (0, 1), {\varvec{s}}^{(0)} = (0.40, 0.30, 0.20, 0.10)$;

• (iv) ${\varvec{\theta }}^{(0)} = ({{\hat{\mu }}}^{(0)}, {{\hat{\sigma }}}^{(0)}) = (2, 3), {\varvec{s}}^{(0)}= (0.40, 0.30, 0.20, 0.10)$.

The algorithm is considered to have converged when

$$\begin{aligned} \max (|{{\hat{\mu }}}^{(h+1)} - {{\hat{\mu }}}^{(h)}|, |{{\hat{\sigma }}}^{(h+1)} - {{\hat{\sigma }}}^{(h)}|, |\hat{s}_i^{(h+1)}-\hat{s}_i^{(h)} |, i=1, 2, 3, 4) < 10^{-6}. \end{aligned}$$

The parameter estimates (say, $\hat{{\varvec{\theta }}}=(\hat{\mu }, \hat{\sigma })$) and the estimate of system signature $\hat{{\varvec{s}}}$ of the three different implementations of the EM algorithm and the parameter estimates obtained from direct maximization of the log-likelihood function are presented in Table 3. In addition, to assess which method results in estimates with the largest likelihood, the values of the log-likelihood in Eq. (4) are evaluated at the parameter estimates and are denoted by $\ell (\hat{{\varvec{\theta }}}, \hat{{\varvec{s}}})$. The largest value of $\ell (\hat{{\varvec{\theta }}}, \hat{{\varvec{s}}})$ for each setting is marked with an asterisk $^*$. We can observe from Table 3 that different initial values $({\varvec{\theta }}^{(0)}, {\varvec{s}}^{(0)})$ result in different estimates of the parameters and the system signature. The initial value of the system signature, ${\varvec{s}}^{(0)}$, plays an important role in the resulting estimates, especially in the estimation of the system signature. It is noteworthy that the elements set to be zero in the initial values of the system signature ${\varvec{s}}^{(0)}$ will never become nonzero in the algorithm, and hence, the final estimate of those elements is always equal to zero. From Table 3, the estimate of ${\varvec{\theta }}$ is very close to the true value when the censoring proportion is small, regardless of the initial values. We will further investigate the effect of the initial values on the final estimates by using a Monte Carlo simulation study in the following section.

Table 3 MLEs obtained by three different implementations of the EM algorithm with unknown system signature

For Type II censored sample, the first r-out-of-m system failures are observed, and thus, we define the censoring proportion by $q = (m-r)/m$. For Type II censored sample with $r = 27$ (i.e., $q = 10\%$) in Table 2 with initial values $({{\hat{\mu }}}^{(0)}, {{\hat{\sigma }}}^{(0)}) = (2, 3)$ and ${\varvec{s}}^{(0)} = (0.25, 0.25, 0.50, 0.00)$, the implementations EM-sys, EM-comp and EM-exp take 78 iterations (in 17.54 s), 176 iterations (in 1.06 s) and 205 iterations (in 1.22 s), respectively, to converge to the final estimates. In this example, we can see that the implementations of EM algorithm based on component-level likelihood function, EM-comp and EM-exp, take less time to converge to the final estimates. This is because the M-step of EM-sys requires a two-dimensional numerical optimization, while the M-step in EM-comp and EM-exp only requires solving one nonlinear equation.

Since these three proposed implementations of the EM algorithm converge to different values, to evaluate the correctness of the estimates obtained by these implementations, we compute the values of the log-likelihood function in Eq. (4), $\ell ({{\hat{{\varvec{\theta }}}}}, {{\hat{{\varvec{s}}}}})$ and compare these values. These values of the log-likelihood function are also presented in Table 3 with “$*$” to indicate the largest log-likelihood among the three implementations. We do observe that these values of log-likelihood based on different implementations are quite close to each other.

5.3 Monte Carlo simulation study

In this subsection, we evaluate the performance of the proposed implementations of the EM algorithm using Monte Carlo simulation. Once again, the component lifetime distribution is assumed to be Weibull, and hence, the logarithm of the component lifetimes follows SEV distribution. Without loss of generality, we set $\mu = 0$ and $\sigma = 1$ in the following simulation studies.

5.3.1 Coherent systems with unknown system signature

In Sect. 4, we described the procedure to estimate the parameter vector and the system signature when we have the information that the systems are coherent systems. A Monte Carlo simulation study is conducted here to evaluate the performance of the proposed implementations of the EM algorithm in correctly identifying the system signature.

We consider the 3-component coherent systems with sample sizes $m = 10$ and 100. The five possible coherent systems and their corresponding system signatures are presented in Table 1. We generate samples of m system lifetimes with system signature ${\varvec{s}}_{l}$, $l = 1, 2, 3, 4, 5$, presented in Table 1. Then, we apply the procedure described in Sect. 4 to obtain the estimate of ${\varvec{\theta }}$. Since all three implementations of the EM algorithm converge to the same value when the system signature is assumed to be known, we present the results based only on EM-comp in this simulation study. The simulation results were based on 10,000 Monte Carlo runs.

The obtained results are summarized in Tables 4 and 5, where the sample sizes are $m = 10$ and 100, respectively. The values in Tables 4 and 5 represent the percentages that the data sampled from the row category have the largest likelihood value assuming it is sampled from the column category. For example, the cell in row 1 (Series) column 2 (Series-parallel) in Table 4 is 0.292, which means of the 10,000 iterations that the data are generated from a series system, the value of the likelihood of a series-parallel system is the largest 2920 times compared to the other four likelihoods (series, 2-out-of-3, parallel-series and parallel systems).

From Tables 4 and 5, we observe that the EM algorithm could not correctly detect which system the data are generated from when the sample size is small (say $m=10$). When $m=100$, the percentage of correctly detecting the system structure increases. It may also be seen that when the sample size is small, the most unlikely choices are parallel-series and 2-out-of-3 systems.

To investigate this problem further, a sample of size 30 was generated from a series-parallel system with signature (1/3, 2/3, 0), and with log-transformed components following a SEV distribution with location $\mu =0$ and scale $\sigma =1$. The EM algorithm is then used to estimate the parameters $\mu$ and $\sigma$ for each of the five possible system signatures separately. Figure 2 presents the p.d.f. of the log-system lifetime for each of the possible system, when log-component lifetimes follow SEV distribution with $\mu =0$ and $\sigma =1$. Figure 3 presents the estimated system lifetime distribution by assuming different underlying system structures and the parameter estimates are also presented. From Fig. 3, it can be seen that the estimated distribution of the log-transformed system lifetime under different assumptions is very similar, even when the parameter estimates vary.

Table 4 The proportion of correct detection of system signature when the sample size is 10

Table 5 The proportion of correct detection of system signature when the sample size is 100

Fig. 2

Distributions of log-system lifetimes, when log-component lifetimes follow SEV distribution with $\mu =0$ and $\sigma =1$, based on different system signatures

Fig. 3

Estimated $f_T(t)$ with parameters estimated from different system signatures

5.3.2 Unknown system signature

Simulation studies are used in this subsection to evaluate the performance of the proposed methodologies. The log-component lifetimes in the system with system signature ${\varvec{s}}= (.25, .25, .5, 0)$ are generated from SEV distribution with $\mu =0$ and $\sigma =1$ with sample size $m = 20, 30$, and proportion of censoring $q = 0, 10, 30, 50\%$. Different initial values are considered. The stopping criterion used is

$$\begin{aligned} \max (|{{\hat{\mu }}}^{(h+1)} - {{\hat{\mu }}}^{(h)}|, |{{\hat{\sigma }}}^{(h+1)} - {{\hat{\sigma }}}^{(h)}|, |\hat{{\varvec{s}}}^{(h+1)}-\hat{{\varvec{s}}}^{(h)}|, i=1, 2, 3, 4) < 10^{-4}. \end{aligned}$$

The simulation results are based on 10,000 Monte Carlo runs, and these results are presented in Tables 6 and 7. We have also considered different system signatures in the simulation study, and since the results demonstrate similar behavior, for the sake of brevity, we only present here the results for ${\varvec{s}}= (.25, .25, .5, 0)$. The average of parameter estimates and the mean square errors (MSEs) of the estimates were obtained. Moreover, the values of the likelihood function in Eq. (4) were evaluated with the estimates of the component lifetime distribution parameters and system signature, i.e., $\ell (\hat{{\varvec{\theta }}}, \hat{{\varvec{s}}})$. The proportions of cases in which the implementation results in estimates with the largest likelihood function among the three proposed implementations, denoted as “Prop”, are also presented in Tables 6 and 7. The obtained results are presented in Tables 6 and 7 in which the starting values of $(\mu , \sigma )$ and ${\varvec{s}}$ are {(0, 1), (.25, .25, .5, 0)} and {(0, 1), (.1, .4, .3, .2)}, respectively. The results for starting values {(1, 2), (.25, .25, .5, 0)}, {(1, 2), (.1, .4, .3, .2)} are not presented here for the sake of conciseness.

It is observed that those estimates obtained from the three implementations of the EM algorithm depend on the choice of the initial values, especially the initial value of the system signature, when the system lifetimes are Type II censored. When the censoring proportions are small (say, $q < 30 \%$), the effect of the initial values to the final estimates is relatively small, and the three proposed implementations EM-sys, EM-comp and EM-exp all give quite similar estimates which are indeed close to the true value.

For the cases when the true value of the unknown system signature is used as the starting value of the EM algorithm (see Table 6), EM-sys has the largest proportion of times that the likelihood function is the largest in most of the cases, especially for small censoring proportion $q \le 10\%$. For the estimation of the parameters of the component lifetime distribution, EM-exp gives the smallest MSEs in most of the cases.

For the cases when the starting value of the unknown system signature is different from the true value (see Table 7), EM-exp has the largest proportion of times that the likelihood function is the largest when the censoring proportion is moderate to large ($q \ge 30\%$). EM-exp also gives the smallest MSEs for the estimation of the parameters of the component lifetime distribution in most of the cases. If the estimation of the parameters of the component lifetime distribution is the major focus, we would therefore recommend the use of EM-exp method.

Table 6 Estimates of the parameters and the proportions of $\ell (\hat{{\varvec{\theta }}}, \hat{{\varvec{s}}})$ being the largest based on EM-sys, EM-comp, EM-exp when the starting values for $(\mu , \sigma )$ and ${\varvec{s}}$ are (0, 1) and (.25, .25, .5, 0), respectively

Table 7 Estimates of the parameters and the proportions of $\ell (\hat{{\varvec{\theta }}}, \hat{{\varvec{s}}})$ being the largest based on EM-sys, EM-comp, EM-exp when the starting values for $(\mu , \sigma )$ and ${\varvec{s}}$ are (0, 1) and (.1, .4, .3, .2), respectively

6 Lognormal distributed component lifetime data

In order to illustrate how the proposed methodologies can be applied to different lifetime models in addition to the Weibull model, we consider the case when the component lifetimes follow lognormal distribution in this section. The component lifetime X is assumed to follow a lognormal distribution with c.d.f. and p.d.f.

$$\begin{aligned} F_{X}(x| \mu , \sigma ) = \varPhi \left[ \frac{\ln x - \mu }{\sigma } \right] \quad {\text{ and } }\quad f_{X}(x| \mu , \sigma ) = \frac{1}{\sigma x} \phi \left( \frac{\ln x - \mu }{\sigma } \right) ,\quad x > 0, \end{aligned}$$

respectively, where $\phi (z)= e^{-(z^2/2)}/\sqrt{2\pi }$ is the p.d.f. and $\varPhi (z) = \int _{-\infty }^z \phi (u) \mathrm {d} u$ is the c.d.f. of the standard normal distribution, $\exp (\mu )$ is a scale parameter and $\sigma > 0$ is a shape parameter. The log-transformation of the component lifetimes, $W = \ln X$, follows the normal distribution with location parameter $\mu \in (-\infty , \infty )$ and scale parameter $\sigma > 0$.

Based on a complete sample of the log-lifetimes $(w_{1}, w_{2}, \ldots , w_{n})$ from a normal distribution, the MLEs of $\mu$ and $\sigma$ can be simply obtained as

$$\begin{aligned} {{\hat{\mu }}}= & {} \frac{1}{n} \sum _{i=1}^n w_i { \text{ and } } \hat{\sigma } = \left[ \frac{1}{n} \sum _{i=1}^n (w_i -\hat{\mu })^2 \right] ^{1/2}, \end{aligned}$$

(28)

respectively.

Following the formulations presented in Sect. 5, to implement the EM-comp algorithm, the expectations of a truncated normally distributed random variable are needed. Let $Z_k$ be the left-truncated normal random variable at time $t_k$, and $Y_k$ be the right-truncated normal random variable. The required expectations could be obtained as

$$\begin{aligned} E(Z_k|\xi _k, \mu , \sigma )= & {} \mu + \sigma \lambda (\xi _k), \nonumber \\ E(Z_k^2| \xi _k, \mu , \sigma )= & {} \sigma ^2 [ 1+ \xi _k \lambda (\xi _k)] +2\mu \sigma \lambda (\xi _k) +\mu ^2, \nonumber \\ E(Y_k|\xi _k, \mu , \sigma )= & {} \mu - \sigma \lambda (-\xi _k) \nonumber \\ {\text{ and } } E(Y_k^2| \xi _k, \mu , \sigma )= & {} \sigma ^2 [ 1- \xi _k \lambda (-\xi _k)] -2\mu \sigma \lambda (-\xi _k) +\mu ^2, \end{aligned}$$

where $\xi _k = \frac{t_k - \mu }{\sigma }$ and $\lambda (s) = \frac{\phi (s)}{1-\varPhi (s)}$ is the hazard function of the standard normal distribution.

The Step 1 in M-step at the $(h+1)$-th iteration of the EM-comp can be described as follows:

M-step :

Step 1. Update the estimates of the parameters by Eq. (28) as

$$\begin{aligned} \mu ^{(h+1)}= & {} \frac{1}{mn} \sum _{k=1}^m \left[ \rho ^{*}_{ 1}(k|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) ) \right] \\ {\text{ and } }\sigma ^{(h+1)}= & {} \left[ \frac{1}{mn} \sum _{k=1}^m \rho ^{*}_{ 2}(k|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) -(\mu ^{(h+1)})^2 \right] ^{1/2}, \end{aligned}$$

where

$$\begin{aligned} \rho ^{*}_{ l}(k|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} d_k \sum _{i=1}^n E^{*}_{o,l}(k, i|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \\&+ \,(1-d_k)\sum _{\lambda =0}^{n-1} E^{*}_{c,l}(k, \lambda |\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}),\\ E^{*}_{o,l}(k, i|\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} \delta _{ki}(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \left[ (i-1) E(Y_k^l |\xi _k, \mu ^{(h)}, \sigma ^{(h)}) \right. \\&\left. +\, t_k +(n-i) E(Z_k^l|\xi _k, \mu ^{(h)}, \sigma ^{(h)} ) \right] \\ {\text{ and } } E^{*}_{c,l}(k, \lambda |\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)})= & {} \delta _{k \lambda }^c(\mu ^{(h)}, \sigma ^{(h)}, {\varvec{s}}^{(h)}) \left[ \lambda E(Y_k^l|\xi ^*_k, \mu ^{(h)}, \sigma ^{(h)} ) \right. \\&\left. +\,(n-\lambda ) E(Z_k^l |\xi _k^*, \mu ^{(h)}, \sigma ^{(h)} ) \right] , \end{aligned}$$

for $l= 1, 2$

Here, we present a real data example to illustrate when the component lifetimes follow a lognormal distribution. The failure times of a simple software control logic for a water-reservoir control system presented in Pham and Pham (1991) and Teng and Pham (2002) are used here to illustrate the EM algorithm. Water is supplied via a source pipe controlled by a source valve and removed via a drain pipe controlled by a drain valve. There are two level sensors in the control system that maintain the water level between the high and low limits in the water reservoir. The water-reservoir control system achieves fault tolerance by using a two-version programming software control logic in which the system fails only when both of its components (software versions) fail. The control system can be treated as a two-component parallel system with system signature ${\varvec{s}}= (0, 1)$. The original dataset presented in Table IV of Teng and Pham (2002) contains the failure times of the two individual components. In order to verify the performance of the proposed estimation procedures discussed here, we assume that the system failure times are observed, but not the individual component lifetimes and the component lifetimes follow a lognormal distribution. The dataset is presented in Table 8.

Since the complete component lifetimes are available, we can obtain the estimates of the parameters based on the component lifetimes as $\hat{\mu } = 3.4608$ and $\hat{\sigma } = 0.9582$. The standard errors of ${{\hat{\mu }}}$ and ${\hat{\sigma }}$ obtained from the method using the missing information principle described in Sect. 3 are 0.1336 and 0.0981, respectively. In this example, we can observe that the parameter estimates based on system-level data (Table 9) are close to the parameter estimates based on component-level data, while the system-level data contain less information compared to the component-level data. As expected, the standard errors of the estimates based on system-level data are larger than those based on component-level data.

Table 8 Failure times of water-reservoir control systems and the 2 components (software versions) in the system (Teng and Pham 2002)

Table 9 MLEs obtained by direct maximization and the proposed EM algorithms with known system signature based on the data in Table 8

7 Concluding remarks

In this paper, we develop the EM algorithm for estimating the parameters of the component lifetime distribution and the system structure simultaneously based on censored system-level lifetime data. We propose three different implementations of the EM algorithm based on the system-level likelihood function and the component-level likelihood function. These implementations are illustrated when the component lifetimes follow a two-parameter Weibull distribution. The performances of these three implementations of the EM algorithm are evaluated by Monte Carlo simulations. As shown in the simulation results and the illustrative example given in Sects. 5.2 and 5.3, the final estimates depend on the initial value of the system signature. Among the three different implementations, EM-comp is the one that is most computationally efficient. Overall, we recommend the use of EM-exp method for estimating the parameters when we have no information on the system structure or when the censoring proportion is large. If one is more concerned about the computational efficiency, the EM-comp method is the best choice.

Since the estimate of the system structure is dependent on the initial estimate, if more information could be collected, for example, if one can use autopsy on some of the failed systems in order to observe the number of failed components, then a better estimate of the system signature can be obtained and used as an initial estimate. However, when little or no information is available on the system structure, we would suggest using different system signatures as the initial value for the EM algorithm and then comparing the resulting estimates. It will be of practical interest to see how a reliable starting value can be obtained for the implementation of the EM algorithm.