Fourier methods for analyzing piecewise constant volatilities

Abstract

We develop procedures for testing whether a sequence of independent random variables has constant variance. If this is fulfilled, the modulus of a Fourier-type transformation of the volatility process is identically equal to one. Our approach takes advantage of this property considering a canonical estimator for the modulus under the assumption of piecewise identically distributed zero mean observations. Using blockwise variance estimation, we introduce several test statistics resulting from different weight functions. All of them are given by simple explicit formulae. We prove the consistency of the corresponding tests and compare them to alternative procedures on extensive Monte Carlo experiments. According to the results, our proposals offer fairly high power, particularly in the case of multiple structural breaks. They also allow for an adequate estimation of the change point positions. We apply our procedure to gold mining data and also briefly discuss how it can be modified to test for the stationarity of other distributional parameters.

1 Introduction

Let us consider a real-valued sequence of independent random variables $X_t$ corresponding to the times $t = 1,\ldots , n$ for some $n \in {\mathbb {N}}$. In addition, let $\sigma ^2(t)$ denote the variance of $X_t$ for each $t = 1,\ldots , n$. We are interested in testing whether the random variables under study have a constant volatility as opposed to the alternative of one or several changes of the variance. This is expressed by the hypotheses

$$\begin{aligned} {{\mathbb {H}}}_0: \forall t, t'=1,\ldots , n: \sigma ^2(t) = \sigma ^2(t') \text { vs. } {{\mathbb {H}}}_1: \exists t, t'=1,\ldots , n: \sigma ^2(t)\ne \sigma ^2(t'). \end{aligned}$$

Testing for changes in the volatility is a topic studied for the most part in the last forty years. First papers on this problem often rely on distributional assumptions in order to derive appropriate decision rules. For example, for the Gaussian case Hsu (1977) constructs a test using cumulative sums of $\chi ^2$-type random variables, while Jandhyala et al. (2002) and others propose likelihood based procedures. To weaken the distributional assumptions later articles such as Wied et al. (2012) consider asymptotic CUSUM-type tests, while Ross (2013) and others introduce nonparametric alternatives. It should be noted that most of these methods split the sample into two parts and are therefore constructed to detect at most one change at a time. This can be quite problematic in cases where several change points lead to comparable variances for any split of the data in two parts.

The method proposed in the following tries to circumvent this problem by using a test statistic calculated from several nonoverlapping blocks of data. It performs quite well on data with several structural breaks, but is also competitive in case of only one change point. In addition, it does not make any assumptions on the distribution of the data and keeps the significance level for any sample size.

We adopt a framework within which marginal distributional features are locally stationary, but globally nonconstant. A blockwise constant volatility has drawn attention in Mercurio and Spokoiny (2004) , Davies et al. (2012) and Fried (2012), among others, but there are also more general frameworks such as that of blockwise local stationarity suggested in Guégan (2015). The assumption of a blockwise constant variance can be formulated using some specified time points $0=t_0<t_1<\cdots <t_{N}=n$. They are understood as possible change point positions. If external knowledge allowing us to choose them appropriately is not available, one can select $t_0, \ldots , t_{N}$ equidistantly. The possible change point positions correspond to important events which may trigger an upward or downward change in the volatility. The values of the volatility process $\sigma ^2(\cdot )$ are thus allowed to differ for some of the time blocks $B_j=\left\{ t_{j-1}+1, t_{j-1}+2, \ldots , t_{j}\right\}$, $j=1,\ldots ,N$. Within each time block the volatility is assumed to be approximately constant.

In accordance with this model, we work under the assumption of independent zero mean random variables with identical distribution up to scale. In other words, we assume that the relation $P(X_t\le x)= F\left( x/\sqrt{\sigma ^2(t)}\right)$ holds for some unknown but fixed distribution function F for $t=1,\ldots , n$ and $x \in {\mathbb {R}}$. The centered Gaussian distribution is thus contained as a special case, but heavy tails are also included. The zero mean assumption is justifiable when dealing with returns or similar data obtained from differences of consecutive observations. In other cases, it can be relaxed to blockwise constant means with known block structure, so that zero mean data results from preprocessing. For a detailed discussion of the other assumptions in the context of volatility, see for example Spokoiny (2009) and the references given therein.

The paper is structured as follows: in Sect. 2 a new statistic for testing changes in the volatility process is motivated. The corresponding test is introduced in Sect. 3, along with alternative procedures available in the literature. In Sect. 4, all methods presented before are compared in several simulation scenarios. Hereafter, the best methods are applied to quality control data concerning face sampling in South African gold mines. Section 5 summarizes the main results and provides an outlook on possible future work. A proof for the consistency of our test procedure is given in the Appendix.

2 Test statistics

In this section, we introduce a class of test statistics for testing the constancy of the volatility process. We then derive explicit representations for some members of this class.

2.1 Motivation

A reasonable first step in order to test ${{\mathbb {H}}}_0$ is the estimation of the local volatilities. Since all random variables are assumed to have zero mean, a natural estimator for the variance within the j-th block $B_j$, $j = 1,\ldots , N,$ is given by

$$\begin{aligned} {\widehat{\sigma }}^2_j=\frac{1}{\tau _j} \sum _{t\in B_j} X_t^2. \end{aligned}$$

(1)

Thereby, $\tau _j = |B_j|$ denotes the number of random variables corresponding to the j-th block $B_j$, $j=1,\ldots ,N$. These block lengths must be sufficiently large to ensure a reasonable accuracy of the variance estimations.

Instead of considering the estimated volatilities themselves, we rather work with their logarithms. This allows us to construct scale independent test procedures, as we demonstrate in the following. Under the null hypothesis of constant variance, the logarithmized volatility process $\log \left( \sigma ^2(\cdot )\right)$ constantly equals $\log \left( \sigma ^2\right)$ for some unknown $\sigma ^2>0$. In this case, the function $\varphi : {\mathbb {R}}\times \left\{ 1,\ldots , n\right\} \rightarrow {\mathbb {C}}$ defined by $\varphi (u,t)= e^{i u \log \left( \sigma ^2(t)\right) }$, where $i=\sqrt{-1}$, does not depend on t. Hence, for any $t = 1, \ldots , n$ it can be estimated by

$$\begin{aligned} {{\varphi }}_n(u)= \sum _{j=1}^N \frac{\tau _j}{n} e^{i u \log \left( {\widehat{\sigma }}_j^2\right) } \end{aligned}$$

(2)

in a straightforward way. Here, each $\tau _j/n=\tau _j/(\sum _{i=1}^N \tau _i)$ weights the corresponding summand according to the number of observations in the j-th block for $j=1,\ldots ,N$. If all blocks contain the same number of observations, all weights are equal to $\frac{1}{N}$. The applied transformation $f:{\mathbb {R}} \rightarrow {\mathbb {C}}, f(x) =e^{iux}$ is closely related to the Fourier transform and characteristic functions. In our situation, it has the following nice and intuitive behavior: under ${\mathbb {H}}_0$, the blockwise estimations are closer to each other than under the alternative. Therefore, they are mapped to points on the unit circle close to each other. Consequently, the weighted mean ${\varphi }_n(u)$ lies relatively close to the unit circle for every $u \in {\mathbb {R}}$ and thus has a modulus near one. Under the alternative, the logarithmized blockwise estimations differ more than under ${\mathbb {H}}_0$. They are thus mapped to comparatively distant points on the unit circle for most $u \in {\mathbb {R}}$. Hence, for most $u \in {\mathbb {R}}$, the weighted mean ${\varphi }_n(u)$ is closer to the origin than under the null hypothesis. Because of that, ${\varphi }_n(u)$ has a small modulus under the alternative. This behavior is related to the well-known property that the modulus of a characteristic function takes on its maximum value one, identically in u, if and only if the underlying random variable is degenerate; see Loéve (1977, §14.1). In view of this fact, we propose to use statistics of the form

$$\begin{aligned} V_n=\int \left( 1-|{{\varphi }}_n(u)|^2\right) w(u) \hbox {d}u \end{aligned}$$

to test for global constant volatility, whereby here and henceforth integration is meant over the entire real line. $V_n$ is nonnegative because of $|{{\varphi }}_n(u)|^2\le 1$. The weight function $w:{\mathbb {R}} \rightarrow {\mathbb {R}}_0^+$ is chosen such that a finite $V_n$ is ensured. More details on the weight function along with explicit representations of $V_n$ for several choices of w are given in the next subsection.

To the best of our knowledge, the idea of utilizing the property of a Fourier transform taking on its maximum modulus constantly over u is new in the literature. Nevertheless, similar transformations and characteristic functions have been used before for change point detection, and to a good effect; see for instance Hušková and Meintanis (2006a, b), Hlávka et al. (2012), and Hlávka et al. (2015). Specifically in these papers, it is shown that approaches based on Fourier-type transformations are convenient from the computational point of view, lead to theoretically sound asymptotics, and are competitive compared to more classical procedures. We want to stress the fact that the aforementioned Fourier-type tests are constructed by comparing the two subsamples before and after each candidate change point using two-sample techniques (Meintanis 2005). This approach is based on the implicit assumption of only one or at least one dominant change point in the data. If the latter assumption does not hold, the corresponding methods may lose a considerable amount of power. As opposed to this, our test is designed to handle multiple structural changes by splitting the data set into several subsamples.

2.2 Explicit representation and weight functions

In this section, we derive a representation of $V_n$ allowing to calculate it in a convenient way. To handle the integral figuring in $V_n$, we work with integrable weight functions w and set $W=\int w(u) \hbox {d}u <\infty$. Then, $V_n$ can be rewritten to

$$\begin{aligned} V_n=W-\int |{{\varphi }}_n(u)|^2 w(u) \hbox {d}u. \end{aligned}$$

Since the constant W does not depend on the data, it can be dropped for testing. Using the definition of ${\varphi }$ in (2), the integral above reduces to

$$\begin{aligned} T_\mathrm{Four} = \int |{{\varphi }}_n(u)|^2 w(u) \hbox {d}u= \frac{1}{n^2} \sum _{j, k=1}^N \tau _j \tau _k I_w\left( \log \left( \widehat{\sigma }_j^2\right) -\log \left( {\widehat{\sigma }}_k^2\right) \right) , \end{aligned}$$

(3)

where

$$\begin{aligned} I_w(x)=\int \cos (ux)w(u)\hbox {d}u. \end{aligned}$$

Since small values of V support the null hypothesis, ${{\mathbb {H}}}_0$ is rejected for small values of $T_\mathrm{Four}$. This test statistic depends on the data only via the terms $\log \left( {\widehat{\sigma }}_j^2\right) -\log \Big ({\widehat{\sigma }}_k^2\Big ) = \log \left( {\widehat{\sigma }^2_j}/{\widehat{\sigma }^2_k}\right) , 1\le j\ne k\le N$. Therefore, thanks to taking the logarithm, any scale factor is canceled out and thus $T_\mathrm{Four}$ is scale invariant. For that reason, we propose to use the logarithmized estimated volatilities instead of the estimated volatilities themselves.

The function $I_w$ can be expressed explicitly for several standard choices of w. These are the uniform, the Laplace and the Gaussian weighting with corresponding weight functions

$$\begin{aligned} w_{U}(u)=\mathbf{{1}}_{(-a,a)}(u) , w_{L}(u)=e^{-a|u|} \quad \text { and } \quad w_{G}(u)=e^{-au^2}, \end{aligned}$$

respectively. All of them depend on a parameter $a>0$. Straightforward computations lead to

$$\begin{aligned} I_{w_{U}}(x) = \frac{2\sin (ax)}{x}, \quad I_{w_{L}}(x) = \frac{2a}{a^2 + x^2}, \quad \mathrm{{and}} \quad I_{w_{G}}(x) = \sqrt{\frac{\pi }{a}} \exp \left( \frac{-x^2}{4a} \right) \end{aligned}$$

for the uniform, Laplace and Gaussian weighting, respectively (Hušková and Meintanis 2006a). Thereby, $I_{w_{U}}(0)$ is defined by its limit $\lim \nolimits _{x\rightarrow 0} \frac{2\sin (ax)}{x} = 2a$.

There also exist alternative choices for w. One example is the data adaptive weighting scheme proposed by Meintanis et al. (2014) for goodness-of-fit testing. Another weight function is studied in Matteson and James (2014) in the context of multivariate nonparametric detection of general distributional changes. Both weight functions were considered in our simulations. The corresponding results are not included in this paper, since, in accordance with our simulations in Sect. 4.1, the choice of the weight function does not seem to have a large impact on the performance of our tests. In particular, the data adaptive weighting leads to slightly worse and the weighting proposed by Matteson and James to essentially the same rejection rates as the three standard weight functions introduced above. These results match earlier work suggesting that the performance of similar Fourier-type procedures does not depend much on the particular functional form of w; see for instance Hušková and Meintanis (2006a) and Hlávka et al. (2012).

In general, the parameter a figuring in the weight function might also influence the method’s results. For the weight functions presented before, a large value of a lets w decay more sharply while the opposite is true for smaller values of a. In the former case (resp. latter case), more emphasis is placed on $\widehat{\varphi }(u)$ for u near the origin (resp. away from the origin). Note that the behavior of a characteristic function near the origin reflects the tail behavior of the underlying distribution. Therefore, caution must be exercised in choosing a. If a is chosen too large, then we might overemphasize the tail of the underlying law, whereas in the opposite case of a being too small, these tails will be obscured; see for instance Epps (1993). Other than that, the whole issue of making an educated guess for a is typically highly technical. It has been theoretically investigated only under very stringent parametric assumptions both about the hypothesis being tested as well as about the direction of possible deviation from this hypothesis; see Epps (1999) and Tenreiro (2009). Fortunately, the simulations in Sect. 4.1 illustrate that our test seems not to be influenced much by the choice of a, so that this problem is alleviated.

3 Testing for constant volatility

In this section, we first show how the hypothesis of global constant volatility can be tested using the statistics defined in Sect. 2. Hereafter, we present a natural estimator of the structural break position in case of rejection is defined. The procedure allows for the location of several presumable structural break positions. The section closes by briefly introducing four alternative methods for the testing problem taken from or inspired by the literature.

3.1 Testing procedure

The distribution of our test statistic strongly depends on the distribution of the random variables $X_1, \ldots , X_n$. Getting critical values without imposing distributional assumptions is thus not possible, at least for small sample sizes. In such situations, resampling strategies are often of great help. Since under the null hypothesis the $X_1, \ldots , X_n$ are independent and identically distributed, we propose to test the stationarity of the variance using the permutation principle introduced by Fisher (1935). Research in various fields shows that this approach can lead to quite powerful tests; see Good (2005) for a monograph treatment with applications to various fields and Hušková and Meintanis (2006b) in the context of characteristic functions. In our setting, the method is applied as follows: given the complete original sample, first generate p new samples by randomly permuting the observations p times. Then, determine the test statistic $T_\mathrm{Four}$ for each of the $p+1$ samples assuming that the data was observed in the respective order. Thereby, the block lengths $\tau _1, \ldots , \tau _N$ as well as N, w and a are the same for each computation. Under the null hypothesis, the $p+1$ test statistics are observations of identically distributed random variables. Thus, the permutation test rejects ${{\mathbb {H}}}_0$ at the predefined significance level $\alpha$, if the test statistic determined on the original sample falls below the empirical $\alpha$-quantile of all $p+1$ test statistics. A formal proof of the consistency of this testing procedure is given in the Appendix.

3.2 Estimation of structural break positions

If our test rejects ${{\mathbb {H}}}_0$ in favor of at least one variance change, we typically want to find out where the structural breaks occur. Therefore, our goal is to locate the presumable change point positions. A rough approximation for the position of the dominant change in variance is given by $t_{j^*}$, where $j^*= {\text {argmax}}\left| \log \left( \widehat{\sigma }_j^2\right) - \log \left( \widehat{\sigma }_{j+1}^2\right) \right|$ and the maximization is performed over $j = 1,\ldots , N-1$. The resolution of this estimator is obviously limited by the block lengths $\tau _j, j=1,\ldots ,N$. This is particularly problematic, if the block boundaries $t_1,\ldots , t_N$ are not determined by a priori knowledge. In order to alleviate this problem the presumable position of the dominant change in variance can be fine tuned as follows: since we expect a structural break near the rough estimate $t_{j^*}$, we consider the union of the two blocks around $t_{j^*}$, $B=\left\{ t_{j^*-1},t_{j^*-1}+1, \ldots , t_{j^*}-1, t_{j^*}, t_{j^*}+1, \ldots , t_{j^*+1}\right\}$. For the moment, we focus solely on the observations with indices in B and exclude the ones from the remaining blocks from this part of the analysis. Our goal is to find the index $t^* \in B$ such that the empirical variance before $t^*$, $\widehat{\sigma }_1^2(t^*)$, differs the most from the empirical variance after $t^*$, $\widehat{\sigma }_2^2(t^*)$. Thereby, both $\widehat{\sigma }_1^2(t^*)$ and $\widehat{\sigma }_2^2(t^*)$ are computed analogously to (1) using observations from B only. The position of the presumable structural break is thus estimated by

$$\begin{aligned} t^*=\underset{t\in B }{{\text {argmax}}} \left| \log \left( \widehat{\sigma }_1^2(t)\right) - \log \left( \widehat{\sigma }_2^2(t)\right) \right| . \end{aligned}$$

To ensure meaningful estimations $\hat{\sigma }_1^2(t)$ and $\hat{\sigma }_2^2(t)$ we do not maximize over all $t \in B$ but leave out values of t near the boundaries of B.

Several structural break positions are located in a recursive manner in the spirit of Vostrikova (1981): after identifying the presumable position of the dominant change in variance as described above, the sample is split into two parts at that point. The test procedure is then conducted on each of the two subsets, as long as they are large enough to ensure reasonable estimations. In case of new rejections, the corresponding presumable change point positions are determined and the splitting continues. As soon as the test does not reject ${\mathbb {H}}_0$ on all current subsamples, the original sample appears to be split into homogeneous subsamples and the procedure stops. This approach indeed yields a level $\alpha$ test, since under ${\mathbb {H}}_0$ the permutation test conducted on the complete sample rejects in only $\alpha$ percent of the cases.

3.3 Alternative methods

The literature offers several approaches checking the stationarity of the variance for a series of random variables. One of them is the CUSUM procedure. It is a standard tool in the detection of structural breaks and hence a lot of work is available in this context. We choose the method proposed by Wied et al. (2012) as a representative for this class of tests. It is based on the CUSUM statistic

$$\begin{aligned} T_\mathrm{CUS} = \underset{1\le t\le n}{\max }\left| \widehat{D} \frac{t}{\sqrt{n}}\left( \widehat{\sigma }^2_{1:t} - \widehat{\sigma }^2_{1:n}\right) \right| , \end{aligned}$$

where $\widehat{\sigma }^2_{1:l}$ denotes the empirical variance computed from the first l observations, $l=1, \ldots , n$. The normalizing scalar $\widehat{D}$ is necessary to attain the asymptotic distribution. The CUSUM approach compares the discrepancies between the estimated variance on the whole sample to all estimated variances on proper subsamples. It then determines the maximal deviation signaling a possible structural break. The test is designed to detect at most one change in volatility. Critical values are derived from asymptotics.

Peña (2005) also compares variances estimated on subsamples to a measure of volatility estimated on the complete sample. He proposes a test statistic built in a blockwise manner, namely

$$\begin{aligned} T_\mathrm{Log}= n\log \left( \sum _{t=1}^n X_t^2\right) - \sum _{j=1}^N \tau _j\log \left( \widehat{\sigma }_j^2\right) . \end{aligned}$$

As for our test statistic, the distribution of $T_\mathrm{Log}$ under ${\mathbb {H}}_0$ heavily depends on the data. We therefore again apply the permutation principle to obtain a distribution-free test.

Another approach checking the hypothesis of global constant volatility is given by Ross (2013). It is motivated by the classical distribution-free procedure proposed by Mood (1954). Instead of using $X_1, \ldots , X_n$, their ranks in the complete sample, denoted by $r_1, \ldots , r_n$, are determined. Hereafter, the sample is divided into two subsamples for each possible split position $t=1, \ldots , n$. For each of these splittings, the standardized statistic of the Mood test is calculated. Its expected value $\mu _t=t(n^2-1)/12$ and the standard deviation $\sigma _t=\sqrt{t(n-t)(n+1)(n^2-4)/180}$ hold under the null hypothesis. Taking the maximum over the possible split positions $t=1, \ldots , n$ results in

$$\begin{aligned} T_\mathrm{Mood} = \underset{t=1,\ldots , n}{\max } \frac{\left| \sum _{h=1}^t \left( r_h - \frac{n+1}{2}\right) ^2-\mu _t\right| }{\sigma _t}. \end{aligned}$$

Since only the ranks of the observations contribute to the test statistic, the procedure is distribution-free. Appropriate critical values depend solely on the sample size n and can be derived by simulations. For several critical values and more details, we refer to Ross (2013).

In addition, we consider the monitoring procedure based on characteristic functions proposed by Steland and Rafajłowicz (2014). The authors develop a test statistic comparable to ours. It has the advantage that changes in the location process do not affect the monitoring of the volatility and vice versa. According to the authors,

$$\begin{aligned} S_j = \int \left[ \left( \widehat{U}_j(u)\right) ^2 + \left( \widehat{V}_j(u)\right) ^2\right] w(u)\hbox {d}u \end{aligned}$$

is an estimator in the context of characteristic functions which reflects the volatility in the j-th data block, $j=1,\ldots , N$. Thereby, w is a weight function and may be chosen as suggested in Sect. 2.2. The statistics $\widehat{U}_j$ and $\widehat{V}_j$ denote the standard estimators of the real and imaginary part of the characteristic function for the random variables in the j-th block, $j=1,\ldots , N$:

$$\begin{aligned} \widehat{U}_j(u) = \frac{1}{\tau _j}\sum _{t \in B_j} \cos \left( u \cdot X_t\right) \quad \text { and }\quad \widehat{V}_j(u) = \frac{1}{\tau _j}\sum _{t \in B_j} \sin \left( u \cdot X_t\right) . \end{aligned}$$

We transfer the monitoring procedure of Steland and Rafajłowicz (2014) to the retrospective case in the following way: since ${\mathbb {H}}_0$ should be rejected if the volatilities in two blocks are substantially different, we propose to use

$$\begin{aligned} T_\mathrm{cf} = \underset{1\le j<k\le N}{\max } \left| S_j - S_{k}\right| \end{aligned}$$

to test the null hypothesis via the permutation principle.

Note that for any $j=1, \ldots , N$ one can express $S_j$ as

$$\begin{aligned} S_j = \frac{1}{\tau _j^2} \sum _{t, t' \in B_j} I_w\left( X_t-X_t'\right) , \end{aligned}$$

so that by (3) our statistic $T_\mathrm{Four}$ can be interpreted as a weighted version of $S_j$ computed on the pseudo-observations $\log \left( \widehat{\sigma }_1^2\right) , \ldots , \log \left( \widehat{\sigma }_N^2\right)$.

All four methods presented in this section reject the hypothesis of a global constant volatility for large values of the corresponding test statistic.

4 Evaluation of the methods

In this section, we compare the performance of our permutation tests based on $T_\mathrm{Four}$ to its competitors listed in Sect. 3.3. For this purpose, we compute the empirical power of each procedure for different data cases. We thereby address the choice of parameters and weighting functions. Hereafter, the best methods are applied to gold mining data.

4.1 Choice of settings

As a first step of the analysis, we assess the influence of the weight function w, its parameter a and the number of the blocks N on the tests based on the Fourier-type statistics $T_\mathrm{Four}$ and $T_\mathrm{cf}$, respectively. Since both methods are constructed using the permutation principle, they attain a predefined significance level $\alpha$ under the null hypothesis of global constant volatility. We thus consider their empirical power under various alternatives as an adequate measure of performance.

The tests are evaluated on datasets consisting of 200 observations each. The first half of every sample is generated from the standard Gaussian distribution. The second 100 observations are sampled from the Gaussian distribution with increased standard deviation 1.5 and mean 0. In this manner, we proceed generating 1000 datasets and apply both tests to them. Following the discussion in Sect. 2.2, appropriate values for the weight parameter $a>0$ are chosen from the literature on empirical characteristic functions, which are comparable to our quantity $\widehat{\varphi }_N$; see for instance Jiménez-Gamero et al. (2009), Potgieter and Genton (2013) and Pardo-Fernández et al. (2015). In accordance with this prior experience, we consider the values $a=0.5,\; 1,\; 1.5$ for the uniform ($w_U$), Laplacian ($w_L$) and Gaussian ($w_G$) weight functions. The number of equidistant blocks is set to $N=5$ and $N=10$ and 2000 permutations are conducted for both test procedures. The resulting rejection rates are shown in Table 1.

Table 1 Rejection rates given in rounded percent for data with one increase in the variance in the middle of the sample for the permutation tests based on $T_\mathrm{Four}$ and $T_\mathrm{cf}$, respectively

According to Table 1, the choice of the weight function w and its parameter a do not have a large influence on the performance of our test based on $T_\mathrm{Four}$. The second method seems to be more strongly affected by these settings. Unsurprisingly, both procedures heavily depend on the splitting of the data into blocks. For the considered data scenario, the tests lead to lower rejection rates for $N=10$ than for $N=5$ although for $N=5$ the true structural break lies in the middle of one block. We also observe that our newly proposed test considerably outperforms the procedure using $T_\mathrm{cf}$ in all cases. In the following, we restrict ourselves to the Gaussian weighting and $a=1.5$ for both tests due to the results in the previous analysis. Repeating the simulation for $N=2,\ldots , 10$ yields the rejection rates in Table 2.

Table 2 Rejection rates given in rounded percent for data with one increase in the variance in the middle of the sample for the permutation tests based on $T_\mathrm{Four}$ and $T_\mathrm{cf}$ for different numbers of initial equidistant blocks $N=2,\ldots ,10$

As expected, the choice of $N=2$ blocks leads to the highest rejection rates, since this data splitting perfectly fits the true volatility clusters. For the same reason, even values of N attain better results than the corresponding odd neighbors $N-1$ and $N+1$. In general, the rejection rates decrease with N, since many small blocks lead to worse estimates of the volatility in the individual blocks. Also, for large N some blocks estimate the same volatility. The difference of the corresponding logarithmized blockwise estimates figuring in $T_\mathrm{Four}$ is thus not equal to 0 solely due to sampling error. Therefore, more terms than necessary contribute to the mean $T_\mathrm{Four}$, so that the impact of the terms reflecting actual changes of the volatility are downweighted. Lastly, we observe that, up to a certain degree, the correct position of the blocks is more relevant than their actual number. For example, even though $N=2$ is optimal in this case, $N=6$ is preferable to $N=3$ and $N=5$ for the test using $T_\mathrm{Four}$.

To study the latter point in more detail, we repeat the simulation presented above with the structural change now taking place after 20% of the observations rather than in the middle of the sample. Table 3 provides the corresponding rejection rates.

Table 3 Rejection rates given in rounded percent for data with one increase in the variance after 20% of the observations for the permutation tests based on $T_\mathrm{Four}$ and $T_\mathrm{cf}$ for different numbers of initial equidistant blocks $N=2,\ldots ,10$

According to the results, choosing a few oversized blocks can be more problematic than using many small blocks. In the scenario investigated, $N=5$ blocks free of structural breaks attain the best results, although actually just two volatility regions exist. For $N=2$, the correct number of blocks, the data is split at the wrong position leading to worse performance of both methods. As before, one can observe a general decrease in power after the optimal choice $N=5$ and relatively good results for its multiple $N=10$. These findings consistently apply for both tests. Thereby, $T_\mathrm{Four}$ leads to increasingly higher rejection rates compared to $T_\mathrm{cf}$ as N, the number of blocks increases. We will revisit the problem of block-choice in the discussion.

4.2 Method comparison

We now apply all tests introduced in Sect. 3 in six different data scenarios. To present the settings in a clear and compact way, let the notation $\left| n=n_1, \sigma =s_1\right| n=n_2, \sigma =s_2|$ describe $n_1$ observations with standard deviation $s_1$ followed by $n_2$ observations with standard deviation $s_2$. Generalizing this representation to the case of several data blocks allows us to represented the scenarios under study in the following way:

• (1) $\left| n=200, \sigma =1\right|$

• (2) $\left| n=100, \sigma =1\right| \left. n=100, \sigma =1.5\right|$

• (3) $\left| n=100, \sigma =1\right| n=100, \sigma =1.5\left| n=100, \sigma =1\right|$

• (4) $\left| n=100, \sigma =1\right| n=100, \sigma =1.4\left| n=100, \sigma =1\right| n=100, \sigma =1.4\left| n= 100, \sigma =1\right|$

• (5) $\left| n=100, \sigma =1\right| n=50\phantom {0}, \sigma =1.6\left| n=100, \sigma =1\right| n=150, \sigma =1.2\left| n=100, \sigma =1\right|$

• (6) Four random structural breaks in 500 observations

The first five of them correspond to the null hypothesis and the case of one, two, four and four nonequidistant changes in volatility, respectively. In scenario (6), we randomize both the positions of the structural breaks as well as the variances within the blocks for every sample. The four change point positions are sampled uniformly from the values 40, 41, ..., 460 such that the resulting blocks contain at least 40 observations. The corresponding variances are randomly chosen from the values 0.6, 0.8, 1.0, 1.2, 1.4. Thereby, we make sure that subsequent blocks do not share the same variance. For each of these six scenarios, three distributions are considered. These are the standard Gaussian distribution (G), the t-distribution with 5 degrees of freedom (t5) and the exponential distribution with parameter $\lambda =1$ (exp) shifted to have zero mean. In order to obtain the desired standard deviations, scaling is applied. The six data scenarios and the three distributions yield 18 data cases in total. For each of them, 10,000 replications are generated. All five tests introduced in Sect. 3 are applied to this data at a significance level of 5%. The permutation tests are executed with 2000 permutations. The procedures involving blocks are conducted using $N=10$ equidistant data blocks on the original data and all subsamples. To reduce the computational burden, the tests based on $T_\mathrm{Four}$ and $T_\mathrm{cf}$ are carried out only for $a=1.5$ and $w=w_G$ due to the analysis in the previous subsection. The resulting rejection rates are listed in Table 4.

Table 4 Rejection rates given in percent for all tests introduced in Sect. 3 for the six different volatility scenarios on page 11 and for Gaussian (G), t-distributed (t5) and exponential data (exp)

Under the null hypothesis, all methods roughly keep the significance level of 5%. For non-Gaussian data, however, the asymptotic of the CUSUM test does not provide a good approximation so that its rejection rates are somehat low under ${\mathbb {H}}_0$. As expected, the CUSUM procedure leads to the best results for Gaussian data with one volatility change, but loses a considerable amount of power in presence of multiple structural breaks due to masking effects. We observe a similar loss of efficiency for the Mood-type test. Much like the CUSUM approach, the distribution-free procedure is based on a two-sample test. It therefore also implicitly anticipates one structural break at a time. Nevertheless, the procedure proposed by Ross (2013) clearly outperforms its competitors in the case of exponential data in all but the fifth data scenario. In the latter setting, its rejection rate is still fine, but the procedure does not dominate its competitors any longer. The tests based on $T_\mathrm{Four}$ and $T_\mathrm{Log}$ overall lead to competitive results. In particular, their performance often improves when multiple structural breaks occur, in contrast to the CUSUM and the Mood-type test. As a consequence, they clearly outperform the CUSUM test for all distributions under study and the test proposed by Ross for the symmetric distributions in case of more than one volatility change. Among the two, $T_\mathrm{Log}$ leads to slightly higher rejection rates. The test using $T_\mathrm{cf}$ performs similarly to $T_\mathrm{Four}$ and $T_\mathrm{Log}$, but is inferior to both in all but two considered scenarios. This is in accordance with the results discussed in Sect. 4.1. In general, the rejection rates of all tests are lower for t-distributed data than for the corresponding Gaussian case. This indicates that heavier tails make the detection of the breaks more difficult.

A good test for structural breaks should have high rejection rates under various alternatives. However, it also must adequately determine the causes of the heterogeneity causing the rejection. Otherwise, it connects the correct rejection with an irrelevant event leading to false conclusions. We therefore take a closer look at the estimated number and location of the structural breaks of the methods. Thereby, we focus on the results for the blockwise procedures based on $T_\mathrm{Four}$ and $T_\mathrm{Log}$, which showed the best overall performance in our opinion. Both tests are conducted in the recursive manner as explained in Sect. 3.2. Their mean numbers of estimated change points are listed in Table 5 for the six data scenarios investigated above for t-distributed samples:

Table 5 Mean number of detected structural breaks for the permutation tests using the blockwise statistics $T_\mathrm{Four}$ and $T_\mathrm{Log}$ on data generated by the t-distribution with five degrees of freedom for the six data cases introduced on page 11. In brackets, the mean number of detected structural breaks among the samples with rejection is given

To interpret the results correctly keep in mind that each data case was chosen such that the rejection rates of all tests are below 100$\%$ so that the tests are comparable. Therefore, unsurprisingly, both tests do not detect all structural breaks, since the volatility changes are simply not that clear by construction of the setting. Quite intuitively it seems harder to detect all structural changes the more of them occur. The test based on $T_\mathrm{Log}$ rejects more often and thus estimates more structural breaks on average. The differences are quite small though. We also provide the mean numbers of estimated structural breaks only considering the samples where the tests reject. As indicated by the values in brackets, both methods determine a reasonable number of presumable structural breaks if they reject at all. Their results are again quite similar.

The estimated change point positions for the case of two and four equidistant structural breaks for t-distributed data are presented in Fig. 1 for both methods. Note that both tests estimate presumable change points in the same way in case of rejection, see Sect. 3.2. The different results are thus mainly a consequence of additional rejections of the method based on $T_\mathrm{Log}$ on subsamples. Figure 1 reveals that the test based on $T_\mathrm{Four}$ estimates the true change point positions much more precisely than the one using $T_\mathrm{Log}$. Consequently, the estimated change points due to additional rejections of the latter method do not coincide with the true structural breaks for the most part. This suggests that tackling the detection of structural breaks via Fourier-type transformations is advantageous in comparison with a simpler blockwise approach. The price paid by a somewhat smaller rejection rate is outweighed by a more exact estimation of the change point position.

Fig. 1

Change point positions estimated by the permutation procedure for two (top) and four (bottom) present structural changes for the test based on $T_\mathrm{Four}$ (left) and $T_\mathrm{Log}$ (right)

Next, we investigate how the structural break position influences the methods’ performance. Therefore, we repeat the simulation for Gaussian data and one volatility change increasing from $\sigma =1$ to $\sigma =1.5$. This time we let the structural break occur after 10, 20, ..., 80$\%$, or 90$\%$ of the 200 observations. We apply all tests presented, but leave out the permutation test based on $T_\mathrm{cf}$ due to its poor results in the previous simulations. The corresponding rejection rates based on 1000 replications are presented in Table 6.

Table 6 Rejection rates given in rounded percent for different volatility tests in case of one volatility change occurring after different proportions of the data

The best results for all methods are attained when the structural break is in the middle of a sample. The rejection rates decrease the more the volatility clusters differ in size. The best procedure for a break in the middle of the sample, the CUSUM test, is most severely affected by this fact. Its rejection rates drop the most when the data is almost exclusively generated from one model. In general, better results are achieved for all tests if the majority of the data has a standard deviation of 1 rather than 1.5. The overall variance of the data in this case is smaller leading to a more precise decision process.

The simulation presented next allows to assess the importance of our zero mean assumption. As before, we induce one or two structural breaks on 1000 Gaussian samples of size 200, respectively, and apply our test based on $T_\mathrm{Four}$ to the data. Hereafter, the data sets are centered by their arithmetic means and again passed to the permutation test. In case of one volatility change, we get rejection rates of 70.3$\%$ for the uncentered data and 70.2$\%$ for the centered equivalents. For two strucural breaks, the results are 76.0 and 75.2$\%$. We thus conclude that demeaning has a negligible effect on the performance of our test even for comparatively small numbers of observations. Instead of zero mean data, it is thus possible to assume an unknown constant mean.

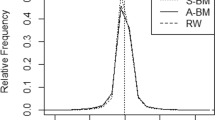
Finally, we compare the tests on artificial data with linearly increasing variance. For this purpose, we simulate 500 datasets containing 200 observations each. The first 100 observations for each of them are generated from the standard Gaussian distribution. The remaining ones are drawn from Gaussian distributions with mean zero and a variance increasing by 0.025, that is, $\sigma ^2(101)=1.025, \sigma ^2(102)=1.05, \ldots , \sigma ^2(200)=3.5$. The corresponding rejection rates for the test under study are 83% for $T_\mathrm{Four}$, 94% for $T_\mathrm{CUS}$, 89 % for $T_\mathrm{Mood}$ and 88% for $T_\mathrm{Log}$. We repeat the simulation now increasing the variance by 0.1 each time. This time all tests reject the null hypotheses of constant variance in all cases. Kernel density estimates of the estimated change point positions for each test are given in Fig. 2. Hereby, we use the Gaussian kernel and the default bandwidth selection for the kernel routine in R.

Fig. 2

Kernel density estimates of the estimated positions of potential structural changes for different tests in case of a linear increase in the variance by 0.025 (upper row) and 0.1 (lower row) after 100 observations

The test based on $T_\mathrm{Four}$ does not detect the structural break position well in case of a comparatively small linear increase in the variance. In contrast, the other tests correctly estimate potential change points almost exclusively after the 100th observation. In case of increased variance growth, our procedure performs much better than before relatively to its competitors. It is more sensitive to the first change of the variance and does not get distracted by the linear increase after the 100th observation.

4.3 Application

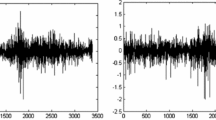
For further illustration of the methods, we consider a data set related to gold mining in South Africa introduced in Rowland and Sichel (1960). The extraction and processing of gold are quite expensive. Therefore, ore samples are collected in mines and checked for their gold content by chemical examinations to discover promising cultivating regions. However, taking representative samples is quite complicated due to the highly irregular gold concentration. This leads to unreliable results in particular for new samplers. Thus, experienced supervisors resample part of the work. The data considered in the following and presented in Fig. 3 are taken from Jandhyala et al. (2002). It consists of 157 logarithmised ratios of gold contents in samples collected by a junior sampler to samples mined by a supervisor at the same locations. The data are arranged in chronological order. Values with a large modulus therefore indicate a high disagreement between the two corresponding samples. Such a result is interpreted as nonrepresentative sampling by the junior sampler. We follow the arguments of Jandhyala et al. (2002) stating that unreliable sampling does not induce a bias in the data, but rather leads to more unstable results. In accordance with these authors, we thus assume zero mean observations. To evaluate the work of the junior sampler, we check the constancy of the variance of the data applying the tests performing best on artificial data.

Fig. 3

Logarithmised ratios of gold contents in samples collected by a junior sampler to samples mined by a supervisor at the same 157 locations (Jandhyala et al. 2002)

Using $N=5$ almost equidistant blocks, the Gaussian weighting and $a=1$ the test based on $T_\mathrm{Four}$ detects a variance change at observation 81. This seems plausible in view of the data and is in accordance with the results in Jandhyala et al. (2002). Note that last-named authors propose a method relying on Gaussianity, while our procedure is valid regardless of this assumption. The test based on $T_\mathrm{Log}$ detects only one change point at observation 42. It thereby neglects both the region of comparatively high variance around observation 55 as well as the high peak at observation 77. Therefore, the procedure based on $T_\mathrm{Four}$ appears to be more favorable in this application.

5 Conclusion and outlook

In this work, we consider the problem of testing whether a sequence of random variables has constant volatility over time. In accordance with Spokoiny (2009), Davies et al. (2012) and other authors we assume that the volatility is approximately piecewise constant. We thus propose a new test based on blockwise volatility estimates and a Fourier-type transformation. According to our extensive simulations, it performs competitively in comparison with alternative procedures from the literature in case of data from symmetric distributions. In particular, our test is recommendable if several structural changes may occur. In case of rejection, it determines the structural break positions adequately. An application to gold mining data also leads to meaningful results.

Our concept can easily be adapted for testing the constancy of other distributional properties such as skewness, kurtosis or tail behavior. This can be achieved in a straightforward way: one simply substitutes the estimator of the local variance presented in (1) by another measure reflecting the quantity of choice. Robust estimators of scale can also be incorporated in this way, if outliers are an issue. Simulation results for the case of kurtosis not reported here show that the corresponding method performs similar to the volatility case.

In forthcoming work, we would like to further explore the asymptotic behavior of our test statistic. First results in this regard indicate that under certain additional assumptions, the asymptotic distribution of $T_\mathrm{Four}$ for a particular weight function is Gaussian under the null hypothesis. These investigations however are the subject of ongoing work. Also, we are interested in extending our methods to dependent observations considering a more general framework; see for instance Brooks et al. (2005); Feunou and Tédongap (2012); Harvey and Siddique (1999). In this connection, appropriate resampling techniques might be of great help. Finally, our procedure might benefit from a more refined choice of data blocks. We have considered two initial approaches for this purpose. The first one pre-estimates potential structural breaks by applying a fast heuristic to the data. For any possible split position, the heuristic estimates the variance both shortly before as well as shortly after the split position. It then returns the positions with the largest discrepancies between the two corresponding estimated local variances. To avoid representing the same structural break several times, we thereby exclude positions close to ones with even greater local variance changes. The second approach determines the best of several given data partitions by maximizing a properly standardized version of our test statistic. The choice of $N=10$ fixed equidistant blocks performed almost equal or better than both alternative strategies for the simulation settings presented in this manuscript and in particular for the case of four randomized structural breaks. Thus, for the moment, we recommend to use somewhat more than twice as many equidistant blocks as the expected number of structural breaks. In this way, the majority of the blocks are free of structural breaks so that the test’s power should be decent. Nevertheless, there is certainly room for further improvement.

Appendix

In this subsection, we prove the consistency of our permutation test based on $V_n$ against a change in volatility alternative, as specified in ${\mathbb {H}}_1$.

Let us first recall our definitions

$$\begin{aligned} {{\varphi }}_n(u)= \sum _{j=1}^N \frac{\tau _j}{n} e^{i u \log \left( {\widehat{\sigma }}_j^2\right) } \quad \text { and } \quad V_n=\int \left( 1-|{{\varphi }}_n(u)|^2\right) w(u) \hbox {d}u, \end{aligned}$$

whereby $\widehat{\sigma }_j^2 = \frac{1}{\tau _j} \sum _{k\in B_j} X_k^2$ for $j=1,\ldots ,N$. The $X_1,\ldots , X_n$ are assumed to be independent zero mean random variables. The corresponding variances remain constant within each block $B_j$, i.e., $\mathrm{{Var}}(X_t)=\sigma ^2_j, \forall t \in B_j, j=1,\ldots ,N$. We consider weight functions w which are integrable and positive, except possibly over a set of measure zero.

We prove consistency of our test in scenarios with an arbitrary but fixed (in n) number of change points, where the number of observations inbetween the change points grows linearly with the same rate (infill asymptotics). Assume that N equidistant blocks are chosen, with $N=N_n$ growing slower than linearly in n, such that the block length grows in n, too. Then the fraction of the blocks corresponding to the same true variance asymptotically equals the fraction $\kappa _j, j=1,\ldots , \nu$ of observations with this variance. Thereby, $\nu$ denotes the number of different true variances. We then have

$$\begin{aligned} \varphi _n(u) \rightarrow \varphi (u)=\sum _{j=1}^\nu {\kappa _j e^{iu \log \sigma ^2_j}}. \end{aligned}$$

$\varphi$ is the characteristic function of a random variable, say Y, which satisfies

$$\begin{aligned} {\mathbb {P}}\left( Y=\log \sigma ^2_j\right) =\kappa _j \quad \text { for } \quad j=1,\ldots ,\nu . \end{aligned}$$

By taking into account that $1-|\varphi _n(u)|^2\le 1$ and that w is integrable, the Lebesgue theorem of dominated convergence entails

$$\begin{aligned} V_n= \int _{-\infty }^\infty \left( 1-|\varphi _n(u)|^2\right) w(u)\hbox {d}u \rightarrow \int _{-\infty }^\infty \left( 1-|\varphi (u)|^2\right) w(u)\hbox {d}u=V, \end{aligned}$$

almost surely. Clearly $|\varphi (u)|^2\le 1$ holds. Along with $w>0$ this implies that V is positive unless $|\varphi (u)|^2=1$, identically in u. However, the latter would mean that $\varphi$ is the characteristic function of a degenerate random variable, i.e., ${\mathbb {P}}(Y=c)=1$ for some $c \in {\mathbb {R}}$; see Loéve (1977, §14.1). Since this does not hold under ${\mathbb {H}}_1$, our test statistic $V_n$ converges toward $V>0$ for any alternative.

Let us now consider a random sample $\tilde{X}_1,\ldots , \tilde{X}_n$ generated from the original sample via permutation. Define $\tilde{V}_n$ in analogy $V_n$, but computed on the permuted rather than the original sample. For any $n\in {\mathbb {N}}$, the $\tilde{X}_1,\ldots , \tilde{X}_n$ are strictly stationary. Thus we get $\tilde{V}_n \rightarrow 0$ using similar arguments as above. Hence, the permutation test rejecting ${{\mathbb {H}}}_0$ for large values of $V_n$ is strongly consistent against a general change-point alternative such as ${{\mathbb {H}}}_1$. An analogous result holds for the permutation test based on $T_\mathrm{Four}$, since $T_\mathrm{Four}$ and $V_n$ are identical up to constants.